Arterial Coordination Control Optimization Based on AM–BAND–PBAND Model

Abstract

The green wave coordinated control model has evolved from the basic bandwidth maximization model to the multiweight approach to an asymmetrical multiband model and a general signal progression model with phase optimization to improve the operational efficiency of urban arterial roads and reduce driving delays and the amount of exhaust gas generated by vehicles queuing at intersections. However, most of the existing green wave models of arterial roads are based on a single phase pattern and little consider the optimization of the combination of multiple phase patterns. Initial queue clearing time is also considered at the green wave progression line in the time–space diagram, which leads to a waste of green light time. This study proposes a coordination control optimization method based on an asymmetrical multiband model with phase optimization to address the abovementioned problem. This model optimizes four aspects in the time–distance diagram: phase pattern selection, phase sequence, offset, and queue clearing time. Numerical experiments were conducted using the VISSIM micro traffic simulation tool for intersections along Kunlunshan South Road in Qingdao, and the effect of green wave coordination was evaluated using hierarchical analysis and compared with the signal-timing schemes generated by the four models: the multiweight approach, the improved multiweight approach, an asymmetrical multiband model, and a general signal progression model with phase optimization. The results show that an asymmetrical multiband model with phase optimization obtains a total bandwidth of 314 s in both directions. In the outbound direction, average number of stops, average travel speed, average travel time, and average delay time improve by 16%, 7.9%, 17.9%, and 15.6%, respectively. In the inbound direction, they improve by 43.7%, 16.1%, 40.7%, and 36%, respectively. Polluting gas emissions and fuel consumption improve by 17.9%. The applicability of the optimization method under different traffic flow conditions is analyzed, and results indicate a clear control effect when the traffic volume is moderate and the turning vehicles on the feeder roads are few. This work can provide a reference for the optimization of subsequent arterial signal coordination and also has indirect significance for environmental protection to a certain extent.

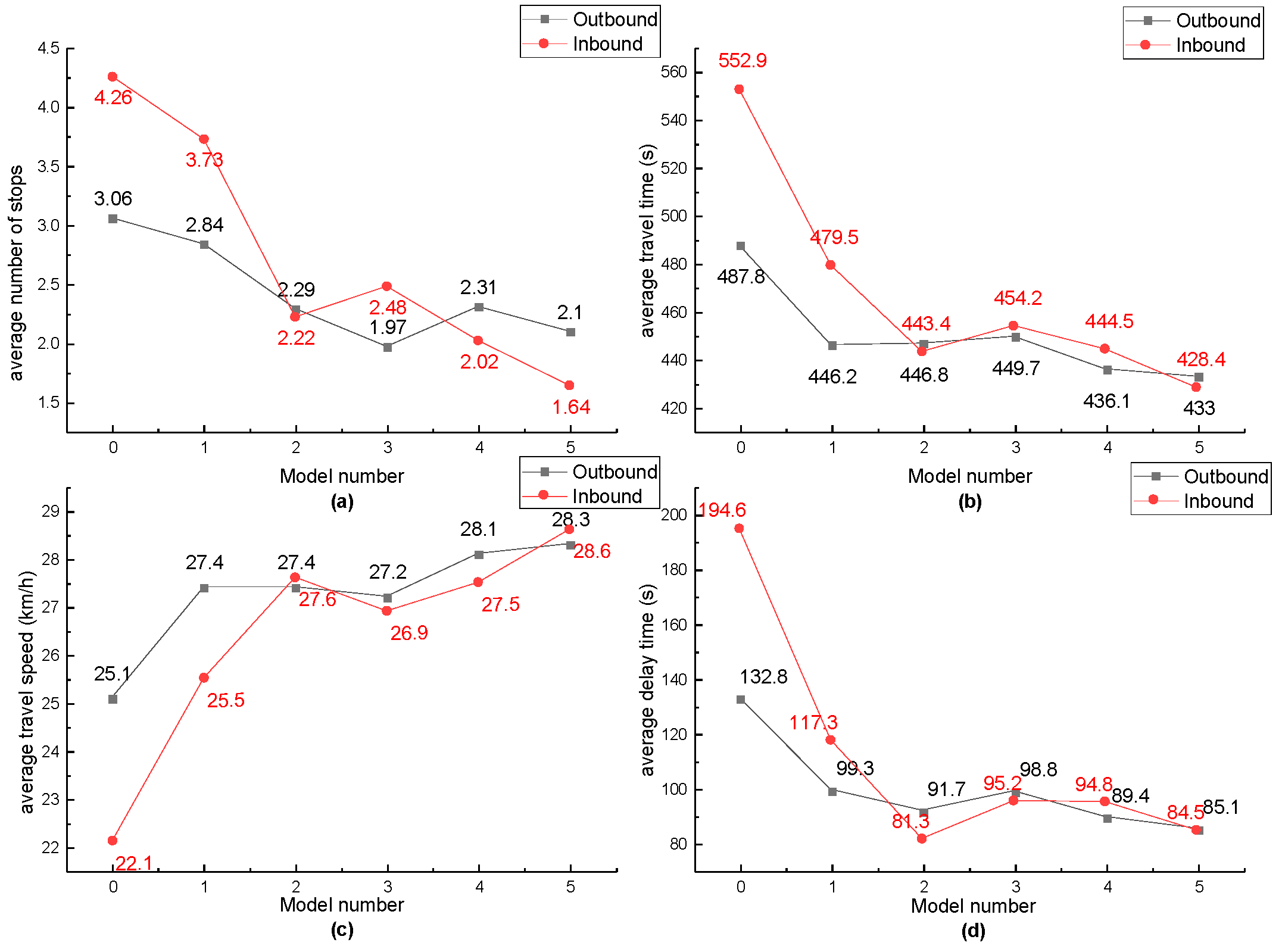
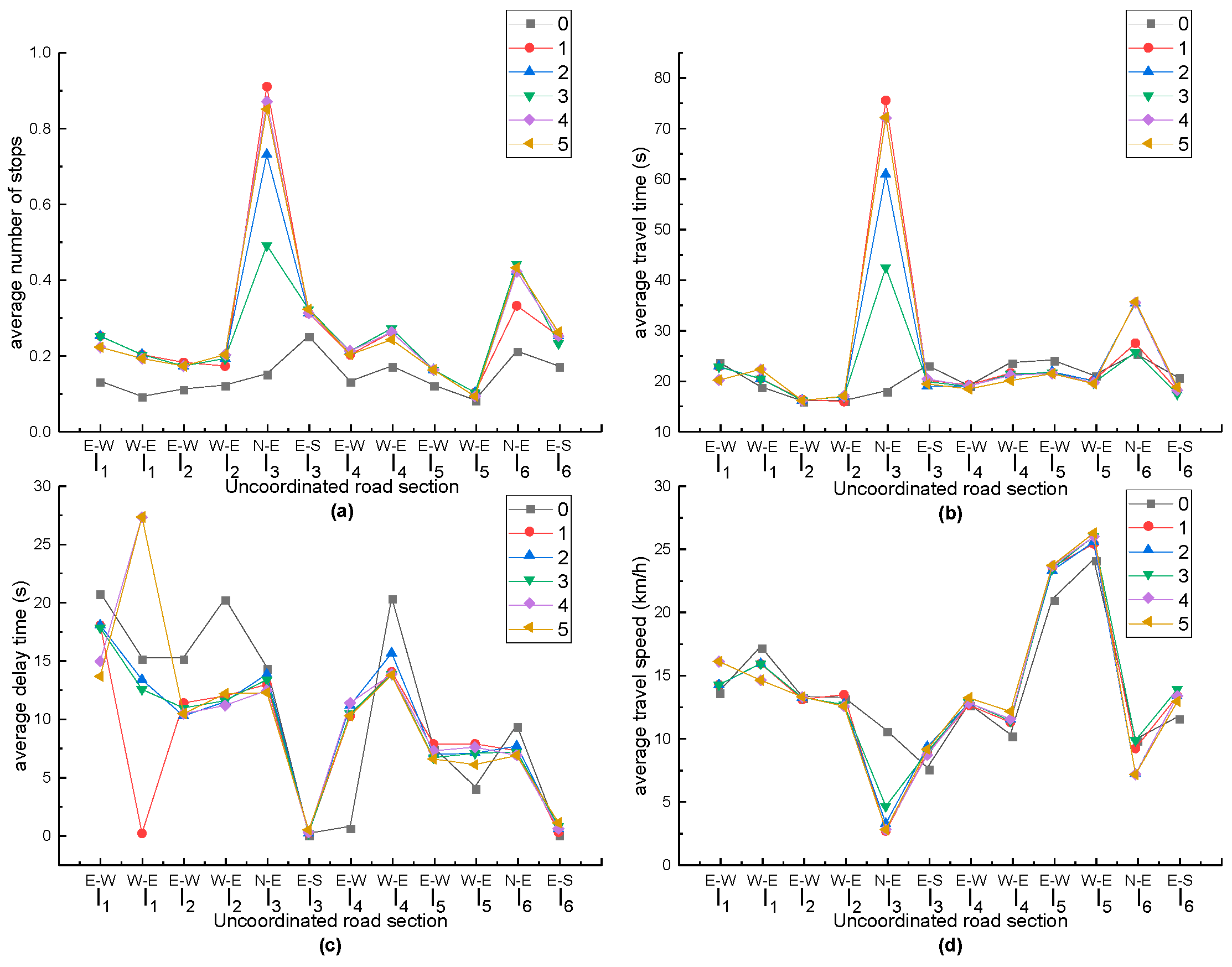
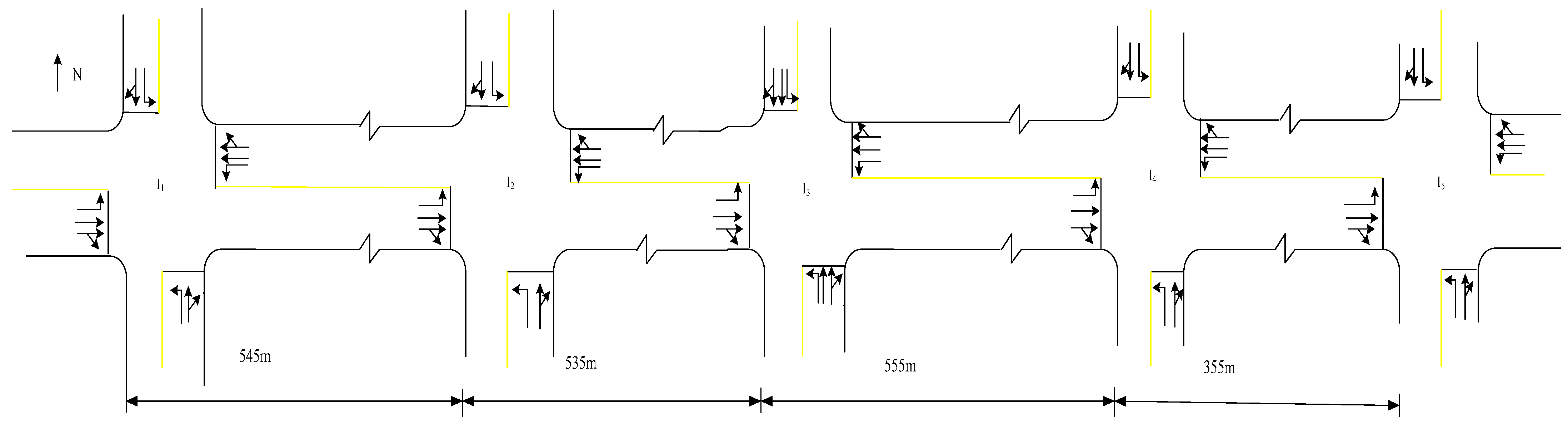
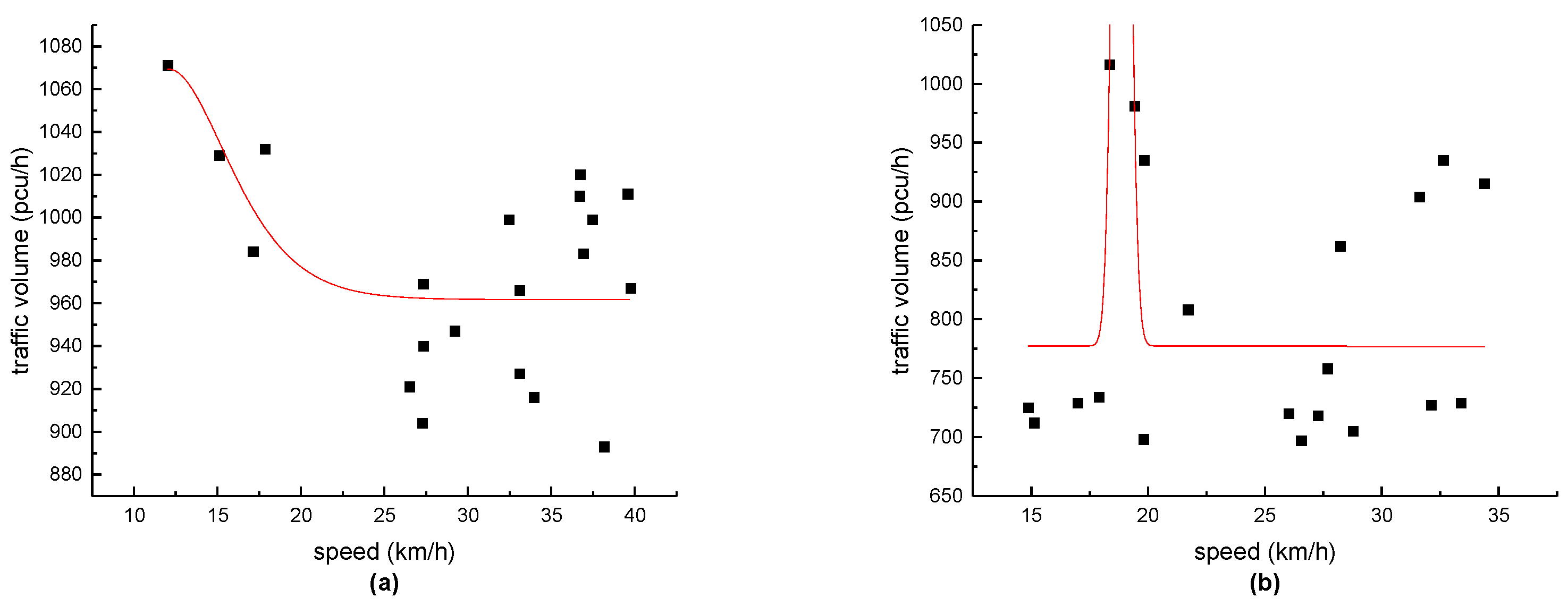1. Introduction

Continuous economic development and the gradual increase in motor vehicle ownership have resulted in various urban traffic problems. Coordinated control of urban arterial roads has long been favored by traffic managers for relieving road traffic congestion because it is one of the most effective, most economical, and fastest ways to reduce traffic time costs [1] and pollutant gas emissions. Coordinated control of urban arterial roads can ensure that vehicles pass multiple intersections without stopping when they reach the coordinated control area. It can also reduce vehicle delays, the number of stops, and pollution emissions from vehicles stopping at intersections, which is important for improving travel efficiency and environmental protection.

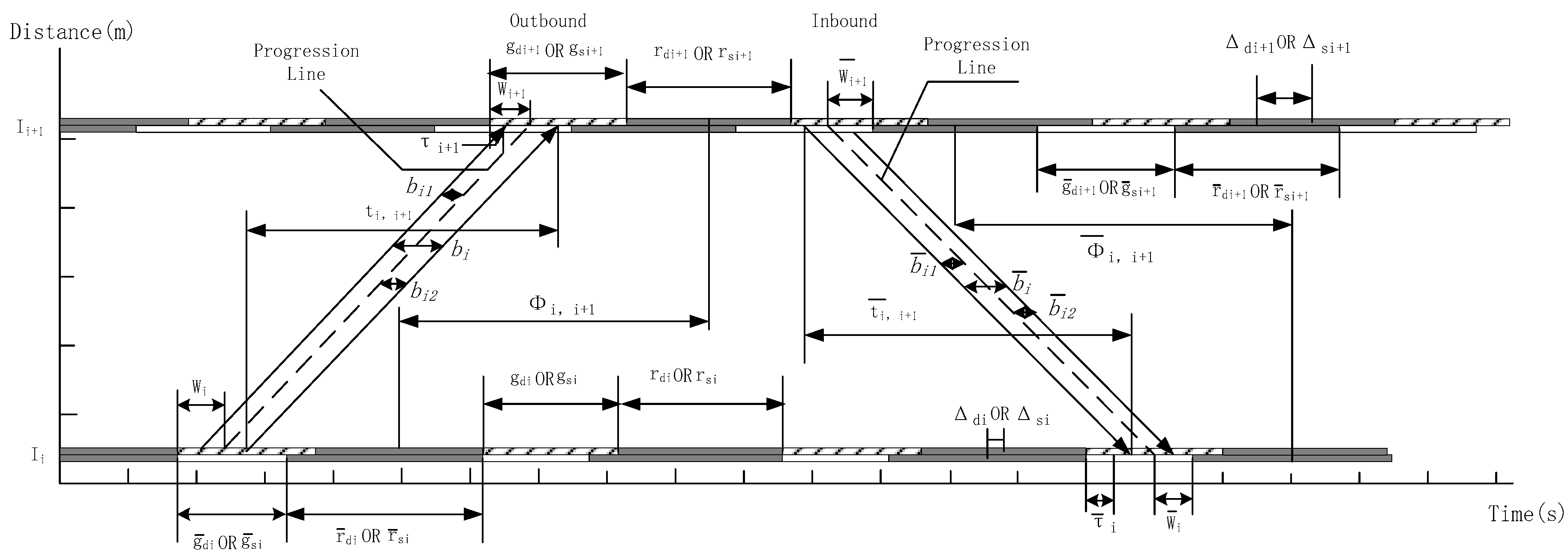
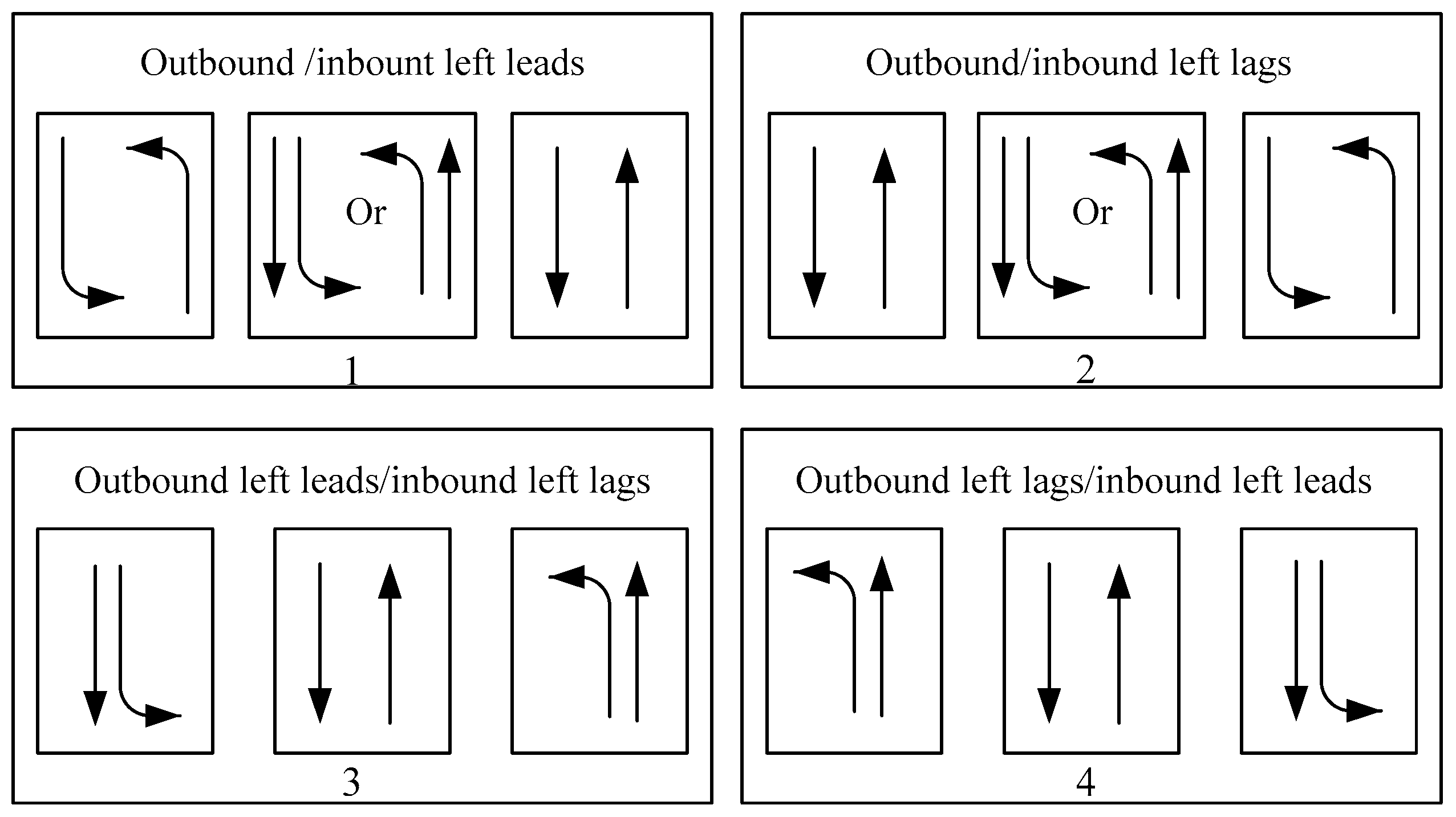
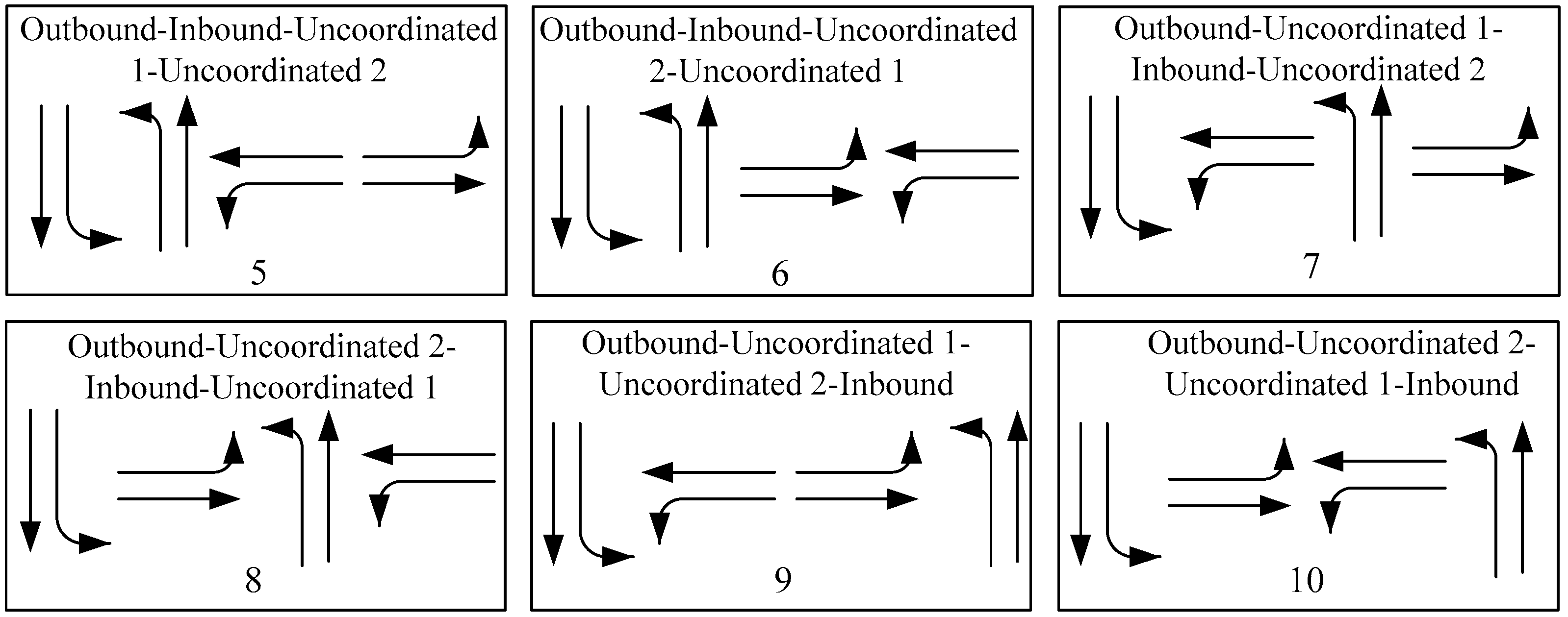
According to the different optimization objectives, coordinated control methods for urban roads are usually divided into two categories [2]: one is to maximize the green wave bandwidth; the other is to minimize the traffic performance index. The green wave width refers to the width of the green light time when a car traveling at the specified speed can continuously pass through the intersection. In this study, a coordination control method based on an asymmetrical multiband model with phase optimization (AM–BAND–PBAND model) is proposed with the maximum green wave bandwidth as the optimization objective. The model is optimized for the current stage of research based mainly on a single phase pattern, the location of the initial queuing clearing time in the time–space diagram, and the possibility of model insolvency due to the green wave centrosymmetry constraint. Specifically, the focus is on the phase sequence optimization, phase pattern selection, and queue clearing time in the time–space diagram between adjacent intersections in the arterial coordinated control system. A comprehensive analysis is also performed from the perspective of cycle and offset. The model improves the possibility of obtaining larger green wave bandwidths by generating asymmetric bandwidths along the green wave progression lines and by extending the optimization space for phase sequence and pattern selection between adjacent intersections. The case study shows that the model can obtain a larger green wave bandwidth, and the optimization effect is remarkable in average number of stops, average travel speed, average travel time, and average delay time. It has certain advantages in reducing emission of polluting gases and fuel consumption, and can provide a reference for optimization of subsequent arterial signal coordination control.

The rest of the paper is organized as follows. Section 2 is a literature review. Section 3 introduces the research methodology, including hypothetical conditions, AM–BAND–PBAND model, optimization principles, and solution methods. Section 4 is a case study and simulation comparison of the intersection along Kunlunshan South Road in Qingdao City by applying the optimization model. Section 5 is a sensitivity analysis. Section 6 extends numerical experiments. Section 7 offers managerial insights. Section 8 is the conclusion and recommendations.

2. Literature Review

The optimization objective is to maximize the green wave bandwidth. Morgan et al. [3] proposed the MAXBAND model to obtain a balanced and uniform green wave bandwidth at each intersection in the coordinated direction of the arterial. Yao et al. [4] introduced the concept of the green wave bandwidth coordination rate based on the MAXBAND model and developed an improved model for coordinated control of multiplexed signals. In response to the shortcomings of the MAXBAND model, Gartner et al. [5] extended the model to account for the presence of nonuniform bandwidths in different directions on different road sections, considered variable left-turn phases, and proposed the MULTIBAND model. To address the shortcomings of the MULTIBAND model, Zhang et al. [6] removed the bandwidth symmetry constraint and developed an asymmetric unequal-width bidirectional green wave coordinated control model, namely, AM–BAND model. Peng et al. [7] proposed a coordinated control model for arterials with asymmetric traffic demands in both oversaturated and unsaturated directions to alleviate the congestion caused by the tidal traffic. Ma et al. [8] proposed a partition-based PM–BAND model to solve the signal coordination problem between general vehicles and transit vehicles in the arterial direction. Zhang et al. [9] proposed an extended green wave optimization model by considering branch roads and pedestrian crossing time. Wang [10] eliminated the centrosymmetric constraint and green wave progression lines on the basis of the MULTIBAND model. They also included the consideration position of the queuing clearing time to the lower limit of the green waveband, which achieved good results. However, existing maximum green wave bandwidth models generally consider the location of the queue clearing time at the center of the green wave, which leads to the significant waste of green light time. The optimization objective is the minimization of traffic performance index. Hillier [11] analyzed the vehicle queue dissipation process between adjacent intersections based on the traffic flow information collected from the inlet lane, established the function relationship between total delay time and coordination control systematic offset, and proposed a coordinated control model based on the minimum total delay time. Qu et al. [12] optimized the key parameters of arterial control based on traffic wave theory. Zheng et al. [13] proposed two arterial traffic coordination control methods, namely, DDPG–BAND and ES–BAND. Yao et al. [14] proposed a coordinated control model based on trajectory data. Yang et al. [15] proposed a signal coordination control method based on an improved genetic algorithm. Khanchehzarrin et al. [16] proposed a mixed-integer nonlinear programming model for a time-dependent vehicle routing problem with time windows. The model could be applied to transportation services by determining the optimal path and minimizing the total cost. For the solution of a mixed-integer nonlinear programming models, Askari et al. [17] used two metaheuristic algorithms to demonstrate the effectiveness of the approaches by generating various instances in a variety of dimensions. Rafael et al. [18] developed two metaheuristic algorithms that showed excellent performance in terms of average marginal improvement and runtime. Gharaei et al. [19] used the null-space method (NSM) to solve nonlinear programming (NLP) problems. Li et al. [20] developed a two-phase approach to solve bandwidth optimization models.

The maximum green waveband method and the minimum performance index method achieve coordinated control, but they essentially focus on the optimization of offset and give less consideration to the phase sequence and phase pattern between adjacent intersections. Wang et al. [21] combined vehicle speed and signal timing to develop a joint queuing and coordination control model. Gu et al. [22] proposed a reinforcement learning-based optimization model for multiple intersection signal control while fixing the conventional phase phasing. Joo et al. [23] proposed an intelligent traffic signal phase assignment system based on deep Q-networks to determine the optimal phase sequence of green light signals. Arsava et al. [24] proposed the OD–NETBAND model, and Yan et al. [25] proposed the NMBSC method to optimize the phase sequence and offset simultaneously. Yang [26] and Chen [27] considered the simultaneous optimization of phase sequence and offset to provide green bands for local paths of trunk lines. Lu et al. [28,29,30] proposed a two-way green wave coordination control algorithm for the different phase design methods of the coordination direction at each intersection of the arterial in terms of separate release and mixed release. Liang et al. [31] proposed an overlapping phase method for bus signal priority control to solve the problem of uneven traffic volume at urban trunk road intersections. Wang et al. [32] proposed a phase optimization design method based on multiple swarm genetic algorithms to reduce vehicle delays at intersections. Jing et al. [33] simultaneously proposed a bidirectional green wave bandwidth maximization model from the perspective of overlapping phase, split phase, phase sequence, and offset optimization, namely, PBAND model. The existing arterial coordination control methods for phase sequence and phase pattern are mainly based on a single phase pattern and reduce the possibility of phase pattern selection and optimization between adjacent intersections in the arterial coordination system. Thus, the coordination control effect is not optimal.

As people become more aware of environmental protection, some scholars have started to consider the effect of pollutant gas emissions while optimizing signal-timing schemes. Li et al. [34] analyzed the relationship among emissions, fuel consumption, vehicle delays, and signal cycle lengths at isolated intersections to optimize green light timing and signal cycle lengths. Liao et al. [35], Park et al. [36], and Stevanovic et al. [37] used traffic simulation software to optimize a signal-timing scheme that greatly reduced fuel consumption and pollutant emissions. Madireddy et al. [38] combined the microscopic traffic simulation model PARAMICS with the emission model VERSIT+ and achieved a decrease in pollutant emissions by reducing the travel speed in the study area. Kwak et al. [39] used genetic algorithms to optimize traffic signal schemes and combined the microscopic traffic simulation model TRANSIMS with the VT-Micro model, which had a positive effect on the reduction of vehicle fuel consumption and pollutant emissions. Ding et al. [40] used VISSIM simulation software to calculate emission factors and developed a bi-objective offset optimization model for reducing vehicle delays and exhaust emissions on urban arterial roads. These studies consider environmental factors and quantify pollutant gas emissions using the proposed models.

On the basis of the abovementioned research, this study regards the maximum green waveband width as the optimization objective. An optimization method based on AM–BAND–PBAND model is proposed. Phase sequence optimization, phase pattern selection, and the position of queue clearing time in the time–space diagram between adjacent intersections in the arterial coordinated control system are considered as well. The number of stops, delay time, travel time, travel speed, fuel consumption, and pollution emissions are also taken as evaluation indexes.

3. Methodology

3.1. Hypothetical Conditions

Considering the random uncertainty of traffic conditions, the following assumptions are set when establishing the optimization model:

• The traffic demand of each intersection on urban arterial roads is in a relatively stable unsaturated state.
• The distance between adjacent intersections on arterial roads is generally less than 1200 m to ensure a high degree of correlation between intersections.
• The left-turn traffic volume in the coordinated direction of each intersection is less than the straight traffic volume. In addition, the right-turn traffic flow is not controlled by signal scheme, and the volume is small.
• Motor vehicles strictly obey traffic rules. This does not take into account the impacts of bus stops, pedestrians and nonmotorized vehicles.
• The signal-timing scheme is fixed. The phase interval time is not set.

3.2. AM–BAND–PBAND Model

AM–BAND model [6] optimizes the available green light time obtained by generating an asymmetric bandwidth along the green wave progression line while ignoring the different phase patterns between adjacent intersections. The location of the initial queue clearing time is considered at the green wave progression line, which is inconsistent with the realistic situation because the initial queuing vehicles are stranded due to insufficient green time in the previous cycle. Moreover, the queuing vehicles in the previous cycle will be the first to utilize the green light time when the green light of the next cycle starts. PBAND model [33] takes overlapping and split phases as the research objects simultaneously, which increases the possibility of obtaining a larger green wave bandwidth. However, the model removes the green waveband progression line and increases the queue clearing time constraints on the green waveband and the time interval between the edge of the green waveband and the midpoint of the red light. This condition may not guarantee the continuity of the green waveband at the intersection and make the model unsolvable. Considering the advantages and disadvantages of each of the two models above, this study proposes an optimized method of arterial coordination control based on AM–BAND–PBAND model by redefining the arterial coordination control variables between adjacent intersections and studying the quantitative mathematical relationships between green wave coordination parameters and vehicle trajectory parameters with time–space diagram. The space–time diagrams between two adjacent intersections are given in Figure 1 for convenience of model description. The key notations involved in AM–BAND–PBAND are defined in

Table 1. Descriptions of the key notations.

Notation	Unit	Description
${\mathrm{b}}_{\mathrm{i}} ({\overline{\mathrm{b}}}_{\mathrm{i}}$)	s	The outbound (inbound) green wave bandwidth between intersection Ii and intersection Ii+1
${\mathrm{g}}_{\mathrm{di}} ({\overline{\mathrm{g}}}_{\mathrm{di}}$)	s	The outbound (inbound) straight green time at intersection Ii under the overlapping phase pattern
${\mathrm{g}}_{\mathrm{dLi}} ({\overline{\mathrm{g}}}_{\mathrm{dLi}}$)	s	The outbound (inbound) left-turn green time in the overlapping phase pattern at intersection Ii
${\mathrm{g}}_{\mathrm{si}} ({\overline{\mathrm{g}}}_{\mathrm{si}}$)	s	The outbound (inbound) green time in the split phase pattern at intersection Ii
${\mathrm{g}}_{\mathrm{s}\mathrm{i}1} ({\mathrm{g}}_{\mathrm{s}\mathrm{i}2}$)	s	The green time of uncoordinated phase 1 (uncoordinated phase 2) at intersection Ii in split phase pattern
mi,i+1	-	An integer variable, representing an integer multiple of the signal period
n		Number of intersections on the arterial road
${\mathrm{r}}_{\mathrm{di}} ({\overline{\mathrm{r}}}_{\mathrm{di}}$)	s	The outbound (inbound) straight red time at intersection Ii under the overlapping phase pattern
${\mathrm{r}}_{\mathrm{si}} ({\overline{\mathrm{r}}}_{\mathrm{si}}$)	s	The outbound (inbound) red time in the split phase pattern at intersection Ii
${\mathrm{r}}_{\mathrm{s}\mathrm{i}1} ({\mathrm{r}}_{\mathrm{s}\mathrm{i}2}$)	s	The red time of uncoordinated phase 1 (uncoordinated phase 2) at intersection Ii in split phase pattern
${\mathrm{t}}_{\mathrm{i},\mathrm{i}+1} ({\overline{\mathrm{t}}}_{\mathrm{i},\mathrm{i}+1}$)	s	The outbound (inbound) travel time from the intersection Ii (Ii+1) to the intersection Ii+1 (Ii)
${\mathrm{w}}_{\mathrm{i}} ({\overline{\mathrm{w}}}_{\mathrm{i}}$)	s	$\mathrm{The} \mathrm{time} \mathrm{interval} \mathrm{between} \mathrm{the} \mathrm{progression} \mathrm{line} \mathrm{of} \mathrm{outbound} \left(\mathrm{inbound}\right) \mathrm{green} \mathrm{waveband} \mathrm{b}{\mathrm{i}}_{ }\left({\overline{\mathrm{b}}}_{\mathrm{i}}\right)$ and the right (left) edge of the adjacent red time at intersection Ii
${\mathrm{w}}_{\mathrm{i}+1} ({\overline{\mathrm{w}}}_{\mathrm{i}+1}$)	s	$\mathrm{The} \mathrm{time} \mathrm{interval} \mathrm{between} \mathrm{the} \mathrm{progression} \mathrm{line} \mathrm{of} \mathrm{outbound} \left(\mathrm{inbound}\right) \mathrm{green} \mathrm{waveband} {\mathrm{b}}_{\mathrm{i}} \left({\overline{\mathrm{b}}}_{\mathrm{i}}\right)$ and the right (left) edge of the adjacent red time at intersection Ii+1
xi, xi′	-	0–1 variable. xi represents overlapping phase pattern, xi′ represents split phase pattern
${\mathsf{\tau }}_{\mathrm{i}} ({\overline{\mathsf{\tau }}}_{\mathrm{i}}$)	s	The initial queue clearing time at intersection Ii when the vehicle is in outbound (inbound) direction
${\mathsf{\Phi }}_{\mathrm{i},\mathrm{i}+1} ({\overline{\mathsf{\Phi }}}_{\mathrm{i},\mathrm{i}+1}$)	s	The time interval between the midpoint of the outbound (inbound) red time at intersection Ii and the midpoint of the outbound (inbound) red time at intersection Ii+1
Δdi (Δsi)	s	The time interval between the midpoint of the outbound red time and the midpoint of the closest inbound red time in the overlapping phase pattern (split phase pattern). If the midpoint of the outbound red time is to the right of the midpoint of the inbound red time, take a positive value
δi1, δi2, δi3, δi4, δi5	-	0–1 variable. δi1, δi2 are binary variables in the overlapping phase pattern; δi3, δi4, δi5 are binary variables in the split phase pattern

.

3.2.1. Objective Function

We maximize the weighted sum of the bandwidth between adjacent intersections on both directions of the arterial road with the objective of maximum green waveband width. Similar to AM–BAND model, the green wave progression line is introduced to ensure the continuity of the green wave band at the intersection, while the symmetric bandwidth constraint is removed to optimize the available green light time obtained. The outbound green waveband is divided into two components along the progress line, that is, b_i = b_i1 + b_i2, where b_i1 and b_i2 are not required to be equal. b_i1 indicates the left component of the outbound green waveband along the progress line, and b_i2 indicates the right component of the outbound green waveband along the progress line. The inbound green waveband along the progress line is also divided into two components, that is, ${\overline{\mathrm{b}}}_i$ = ${\overline{b}}_{i1}$ + ${\overline{b}}_{i2}$, where the two components ${\overline{b}}_{i1}$ and ${\overline{b}}_{i2}$ do not need to be equal. ${\overline{b}}_{i1}$ represents the left component of the inbound green waveband along the progress line, and ${\overline{b}}_{i2}$ represents the right component of the inbound green waveband along the progress line. The objective function is expressed as follows:

$$\max {\displaystyle \sum _{i=1}^{n-1}[{\alpha }_i(b_{i1}+b_{i2})+\overline{{\alpha }_i}(\overline{b_{i1}}+\overline{b_{i2}})}]$$

(1)

where α_i (${\overline{\alpha }}_i$) is the weighting coefficient of the outbound (inbound) bandwidth, which is the ratio between the outbound (inbound) total volume and outbound (inbound) total saturation flow.

3.2.2. Constraints

Similar to the PBAND model, the overlapping phase and split phase are studied. With the assumption that all intersections on the arterial roads use a common cycle time, the internode offsets Φ_i,i+1 and ${\overline{\mathsf{\Phi }}}_{\mathrm{i},\mathrm{i}+1}$ can be expressed by:

$${\mathsf{\Phi }}_{i,i+1}=0.5\left(x_i{r}_{di}+x_i^{\prime }{r}_{\mathrm{si}}^{}\right)+w_i+t_{i,i+1}-w_{i+1}-0.5\left(x_{i+1}{r}_{\mathrm{di}+1}+x_{i+1}^{\prime }{r}_{\mathrm{si}+1}^{}\right)$$

(2)

$${\overline{\mathsf{\Phi }}}_{i,i+1}=0.5\left(x_i{\overline{r}}_{di}+x_i^{\prime }{\overline{r}}_{\mathrm{si}}^{}\right)+{\overline{w}}_i+{\overline{t}}_{i,i+1}-{\overline{w}}_{i+1}-0.5\left(x_{i+1}{\overline{r}}_{\mathrm{di}+1}+x_{i+1}^{\prime }{\overline{r}}_{\mathrm{si}+1}^{}\right)$$

(3)

Similar to the conventional bandwidth, the internode and intranode offsets along the loop can be formulated by:

$${\mathsf{\Phi }}_{i,i+1}+\left(x_i{\mathsf{\Delta }}_{di}+x_i^{\prime }{\mathsf{\Delta }}_{si}^{}\right)+{\overline{\mathsf{\Phi }}}_{i,i+1}-\left(x_{i+1}{\mathsf{\Delta }}_{di+1}+x_{i+1}^{\prime }{\mathsf{\Delta }}_{si+1}^{}\right)=m_{i,i+1}$$

(4)

Substituting Equations (2)–(4) to eliminate internode offsets, the equation periodicity constraint is as follows:

$$\begin{array}{l}\begin{array}{l}0.5\left[\left(x_i{r}_{di}+x_i{}^{\prime }{r}_{\mathrm{si}}^{}\right)+\left(x_i{\overline{r}}_{di}+x_i{}^{\prime }{\overline{r}}_{\mathrm{si}}^{}\right)\right]-\\ 0.5\left[\left(x_{i+1}{r}_{\mathrm{di}+1}+x_{i+1}^{\prime }{r}_{\mathrm{si}+1}^{}\right)+\left(x_{i+1}{\overline{r}}_{\mathrm{di}+1}+x_{i+1}^{\prime }{\overline{r}}_{\mathrm{si}+1}^{}\right)\right]+\\ \left(w_i+{\overline{w}}_i\right)-\left(w_{i+1}+{\overline{w}}_{i+1}\right)+\left(t_{i,i+1}+{\overline{t}}_{i,i+1}\right)+\left(x_i{\mathsf{\Delta }}_{di}+x_i^{\prime }{\mathsf{\Delta }}_{si}^{}\right)-\end{array}\hfill \\ \left(x_{i+1}{\mathsf{\Delta }}_{di+1}+x_{i+1}^{\prime }{\mathsf{\Delta }}_{si+1}^{}\right)=m_{i,i+1}\hfill \end{array}$$

(5)

The general formula for the possible release of the overlapping phase pattern is:

$${\mathsf{\Delta }}_{di}={\delta }_{i1}{g}_{\mathrm{dL}i}-0.5g_{\mathrm{dLi}}-{\delta }_{i2}{\overline{g}}_{\mathrm{dL}i}+0.5{\overline{g}}_{\mathrm{dL}i}$$

(6)

The general formula for the possible release of split phase pattern is:

$${\Delta }_{si}^{}=\{\begin{array}{l}\begin{array}{l}0.5\left[\left(2{\delta }_{i3}-1\right)g_{\mathrm{s}i}^{}-\left(2{\delta }_{i4}-1\right){\overline{g}}_{\mathrm{s}i}^{}\right]+\left(2{\delta }_{i3}{\delta }_{i5}-{\delta }_{i5}\right)g_{si2},\\ 0.5\left(g_{\mathrm{s}i}^{}+{\overline{g}}_{\mathrm{s}i}^{}\right)+g_{si2}\le 0.5\end{array}\hfill \\ \begin{array}{l}0.5\left[\left(2{\delta }_{i3}-1\right)g_{\mathrm{s}i}^{}-\left(2{\delta }_{i4}-1\right){\overline{g}}_{\mathrm{s}i}^{}\right]+\left(2{\delta }_{i3}{\delta }_{i5}-{\delta }_{i5}\right)g_{si1},\\ 0.5\left(g_{\mathrm{s}i}^{}+{\overline{g}}_{\mathrm{s}i}^{}\right)+g_{si1}\le 0.5\end{array}\hfill \end{array}$$

(7)

Constraint (8) excludes the remaining four unqualified combinations of split phase pattern and presents the actual valid four split phase methods:

$$\{\begin{array}{l}1\le {\delta }_{i3}+{\delta }_{i4}+{\delta }_{i5}\le 2\\ {\delta }_{i4}-{\delta }_{i5}+{\delta }_{i3}\ge 0\\ {\delta }_{i3}+{\delta }_{i4}\le 1\end{array}$$

(8)

Constraint (9) limits the selection of one of split phase pattern or overlapping phase pattern, which is due to that only one pattern is possible at each intersection at the same time:

$$x_i+x_i^{\prime }=1$$

(9)

By dividing outbound (inbound) green waveband into their respective components and advancing the initial queue clearing time to the start of each cycle of green time, the interference constraint is changed accordingly. To keep the left and right edges of the green band within the green time and prevent the green band from crossing at the red time, the interference constraint is as follows:

$$\{\begin{array}{l}{w}_{i+1}-{\tau }_{i+1}\ge 0\\ b_{i1}\le w_i\le 1-(x_i{r}_{di}+x_i^{\prime }{r}_{si}^{})-b_{i2}\\ {\overline{b}}_{i2}\le {\overline{w}}_i\le 1-(x_i{\overline{r}}_{di}+x_i^{\prime }{\overline{r}}_{si}^{})-{\overline{\tau }}_i-{\overline{b}}_{i1}\\ b_{i1}\le w_{i+1}\le 1-(x_{i+1}{r}_{di+1}+x_{i+1}^{\prime }{r}_{si+1}^{})-b_{i2}\\ {\overline{b}}_{i2}\le {\overline{w}}_{i+1}\le 1-(x_{i+1}{\overline{r}}_{di+1}+x_{i+1}^{\prime }{\overline{r}}_{si+1}^{})-{\overline{b}}_{i1}\end{array}$$

(10)

To ensure that the left and right components of the outbound (inbound) green bands along the progression line are not zero, the following constraint is imposed on AM–BAND–PBAND model:

$$\{\begin{array}{l}\frac{1}{N1}\cdot b_{i2}\le b_{i1}\le N1\cdot b_{i2}\\ \frac{1}{N2}\cdot {\overline{b}}_{i2}\le {\overline{b}}_{i1}\le N2\cdot {\overline{b}}_{i1}\end{array}$$

(11)

where N1 and N2 can be any positive real number. The upper and lower limits of the ratio between the two components of the outbound or inbound green band can be determined by adjusting the values of N1 and N2.

Constraint (12) restricts the value to positive numbers; constraint (13) restricts the value to integers; constraints (14) and (15) indicate that both are binary variables and take the value of 0 or 1.

$$b_i,b_{i1},b_{i2},{\overline{b}}_i,{\overline{b}}_{i1},{\overline{b}}_{i2},t_{i,i+1},{\overline{t}}_{i,i+1}\ge 0$$

(12)

$$m_{i,i+1}\mathrm{int}\mathrm{eger}$$

(13)

$$x_i,x_i^{\prime } 0/1$$

(14)

$${\delta }_{i1},{\delta }_{i2},{\delta }_{i3},{\delta }_{i4},{\delta }_{i5} 0/1$$

(15)

3.3. Optimization Principles for AM-BAND-PBAND Model

AM–BAND–PBAND model takes overlapping phase pattern and split phase pattern as the research objects, and it selects the best phase pattern of each intersection by introducing binary variables. The binary variables are x_i and x_i′. When x_i =1, x_i′ = 0, the best phase pattern obtained is overlapping phase pattern at intersection I_i; when x_i =0, x_i′ = 1, the best phase pattern obtained is split phase pattern at intersection I_i.

Different phase sequences correspond to different values of Δ_di or Δ_si. Four-phase and six-phase sequences are possible under overlapping and split phase patterns, respectively, as shown in Figure 2 and Figure 3.

A general formula for Δ_di or Δ_si can be expressed by introducing different binary variables. The binary variables are δ_i1, δ_i2, δ_i3, δ_i4, and δ_i5. They can achieve the optimal selection of phase sequences. The phase sequence optimization principles of the two phase patterns are shown in

Table 2. Relationship between δ_i1-δ_i5 and phase sequences.

Phase Sequence	Δdi(Δsi)	δi1	δi2	δi3	δi4	δi5	Note
1	${\mathsf{\Delta }}_{\mathrm{di}}=-0.5 ({\mathrm{g}}_{\mathrm{dLi}}-{\overline{\mathrm{g}}}_{\mathrm{dLi}}$)	0	0
2	${\mathsf{\Delta }}_{\mathrm{di}}=0.5 ({\mathrm{g}}_{\mathrm{dLi}}-{\overline{\mathrm{g}}}_{\mathrm{dLi}}$)	1	1
3	${\mathsf{\Delta }}_{\mathrm{di}}=-0.5 ({\mathrm{g}}_{\mathrm{dLi}}+{\overline{\mathrm{g}}}_{\mathrm{dLi}}$)	0	1
4	${\mathsf{\Delta }}_{\mathrm{di}}=0.5 ({\mathrm{g}}_{\mathrm{dLi}}+{ \mathrm{g} ¯}_{\mathrm{dLi}})$	1	0
5	${\mathsf{\Delta }}_{\mathrm{si}}=-0.5 ({\mathrm{g}}_{\mathrm{si}}+{\overline{\mathrm{g}}}_{\mathrm{si}}$)			0	1	0	$0.5 ({\mathrm{g}}_{\mathrm{si}}+{\overline{\mathrm{g}}}_{\mathrm{si}}$) + gsi2 ≤ 0.5 OR $0.5 ({\mathrm{g}}_{\mathrm{si}}+{\overline{\mathrm{g}}}_{\mathrm{si}}$) + gsi1 ≤ 0.5
6
7	${\mathsf{\Delta }}_{\mathrm{si}}=0.5 ({\mathrm{g}}_{\mathrm{si}}+{\overline{\mathrm{g}}}_{\mathrm{si}}$) + gsi2			1	0	1	$0.5 ({\mathrm{g}}_{\mathrm{si}}+{\overline{\mathrm{g}}}_{\mathrm{si}}$) + gsi2 ≤ 0.5
	${\mathsf{\Delta }}_{\mathrm{si}}=-0.5 ({\mathrm{g}}_{\mathrm{si}}+{\overline{\mathrm{g}}}_{\mathrm{si}}$) − gsi1			0	1	1	$0.5 ({\mathrm{g}}_{\mathrm{si}}+{\overline{\mathrm{g}}}_{\mathrm{si}}$) + gsi1 ≤ 0.5
8	${\mathsf{\Delta }}_{\mathrm{si}}=-0.5 ({\mathrm{g}}_{\mathrm{si}}+{\overline{\mathrm{g}}}_{\mathrm{si}}$) − gsi2			0	1	1	$0.5 ({\mathrm{g}}_{\mathrm{si}}+{\overline{\mathrm{g}}}_{\mathrm{si}}$) + gsi2 ≤ 0.5
	${\mathsf{\Delta }}_{\mathrm{si}}=0.5 ({\mathrm{g}}_{\mathrm{si}}+{\overline{\mathrm{g}}}_{\mathrm{si}}$)+ gsi1			1	0	1	$0.5 ({\mathrm{g}}_{\mathrm{si}}+{\overline{\mathrm{g}}}_{\mathrm{si}}$) + gsi1 ≤ 0.5
9	${\mathsf{\Delta }}_{\mathrm{si}}=0.5 ({\mathrm{g}}_{\mathrm{si}}+{\overline{\mathrm{g}}}_{\mathrm{si}}$)			1	0	0	$0.5 ({\mathrm{g}}_{\mathrm{si}}+{\overline{\mathrm{g}}}_{\mathrm{si}}$) + gsi2 ≤ 0.5 OR $0.5 ({\mathrm{g}}_{\mathrm{si}}+{\overline{\mathrm{g}}}_{\mathrm{si}}$) + gsi1 ≤ 0.5
10

.

3.4. Solution Method

Three signal phase patterns are available: symmetrical, overlapping, and split. Different phase patterns will have different effects on intersection operation efficiency. The specific algorithm flow is as follows:

Step 1: According to the channelization, road conditions, and geographical distribution of each intersection, the Webster method [41] is used to calculate the optimal signal cycle of each intersection. The maximum cycle is selected as the common cycle of the arterial road. At the same time, the green time allocation ratio in the different phase patterns is determined according to the traffic volume in each direction of each entrance road at the intersection.

Step 2: The green time allocation ratio obtained by the overlapping phase pattern of each intersection, the green time allocation ratio obtained by the split phase pattern of each intersection, the common signal cycle, and the designed green wave speed are used as input data. According to the model by LINGO software programming solution, the optimal phase pattern and phase sequence of each intersection are obtained. It is worth pointing out that we discuss the most suitable phase pattern and phase sequence for the coordinated control direction (north-south). The non-coordinated direction (east-west) adopts symmetrical phase pattern.

Step 3: The results of the solution are combined with the relationships between each parameter in the model and offset in the time–space diagram to find offset indirectly. The time–space diagram of the model is plotted by the results of each parameter of the solution.

4. Case Study

4.1. Data Collection

This study demonstrates the applicability of AM–BAND–PBAND model by taking the intersections along Kunlunshan South Road in Qingdao City as an example.

4.1.1. Channelization Scheme and Current Signal-Timing Scheme

Six signal intersections on Kunlunshan South Road in Qingdao (Huaihe West Road-Huanghe Middle Road-Yihe Road-Weihe Road-Qianwangang Road-Songhua River Road) were selected for the study. According to field survey and topographic map calculation, the distances of two adjacent intersections from north to south are 859 m, 460 m, 462 m, 952 m, and 666 m respectively. The intersections on the arterial road from north to south are denoted as I₁, I₂, I₃, I₄, I₅ and I₆ for the convenience of description (e.g., I₁ for the intersection of Kunlunshan South Road-Huaihe West Road, I₂ for the intersection of Kunlunshan South Road-Huanghe Middle Road, and so on). Vehicles travel from intersection I₁ (intersection I₆) to intersection I₆ (intersection I₁) in the outbound (inbound) direction of the arterial road. The geographical distribution of each intersection is shown in Figure 4. The current signal control scheme is based on a single-point fixed cycle, and the phase setting and timing scheme are shown in Figure 5.

4.1.2. Time Correlation Analysis of Traffic Flow

Given that traffic flow has uncertainty and periodicity characteristics, the total traffic volume data of each intersection for 3 days before and after the working day from 14:40 to 16:40 were selected for the study time correlation of traffic flow according to the actual survey. Traffic volume was collected by manual counting method and video recording method, counting every 5 min. A 5 min time interval sequence of traffic flow for three consecutive days is shown in Figure 6.

By comparing and analyzing the traffic volume data of the 3 days before and after, we can visually see that there is a difference in the time-varying trend of traffic flow between the 3 days before and after. To more accurately and effectively measure the traffic volume of the road section and design a practical coordinated control scheme, the traffic volume of the above before and after 3 days is divided into intersections, entrances, turn direction, and vehicle types (the vehicle types are divided into three categories: small cars, medium cars, and large cars) and converted into standard small car equivalents (conversion factor—small cars: medium cars: large cars = 1:1.5:2.5) as each intersection along the route the traffic volume of each turn in each entrance. The actual and statistical traffic volumes of each cross section often differ because manual counting has a certain inaccuracy. Thus, the data obtained from the statistics are fine-tuned to obtain the traffic flow of each intersection, as shown in

Table 3. Summary of turning vehicles at intersections-case study.

Intersection	South			North			East			West
	Left	Straight	Right	Left	Straight	Right	Left	Straight	Right	Left	Straight	Right
I1	134	526	60	174	576	46	239	276	133	91	299	125
Sum	720			796			648			515
I2	209	441	75	214	637	89	284	421	38	241	396	45
Sum	725			940			743			682
I3		700	18	69	897		113		25
Sum	718			966			138
I4	265	558	81	186	762	62	124	338	34	126	201	41
Sum	904			1010			496			368
I5	283	622	30	121	770	36	192	639	50	232	543	67
Sum	935			927			881			842
I6		881	125	273	756		262		54
Sum	1006			1029			316

. The unit of traffic volume in Table 3 is pcu/h (pcu = passenger car unit, and it represents the equivalent traffic volume with a passenger car as the standard model; h represents an hour). The table shows that the volume of straight traffic is much larger than the volume of left-turn traffic in the coordinated control direction, and considering this road section with arterial coordination control has some practical value.

4.1.3. Vehicle Speed Distribution

The test vehicle following speed measurement method was selected to measure the vehicle speed. At the same time of measuring the traffic volume, the road section was measured back and forth six times for a total of 3 days. The average value of the average vehicle speed between the intersection sections in the 3 days was taken as the average vehicle speed between the intersection sections, as shown in

Table 4. Average speed of each section of intersection.

Outbound		Inbound
Road Section	Average Travel Speed (km/h)	Road Section	Average Travel Speed (km/h)
I1-I2	27	I2-I1	26
I2-I3	33	I3-I2	15
I3-I4	37	I4-I3	27
I4-I5	33	I5-I4	32
I5-I6	15	I6-I5	20
Average travel speed	29.1	Average travel speed	23.9

.

The data in Table 4 show that a great difference exists in the average travel speed between different road sections of the outbound and inbound directions (e.g., I₃-I₄ and I₅-I₆). The finding may be due to the fact that single-point timing control is used between all intersections, which results in poor coordination and large stopping delays for each vehicle passing through an intersection. This condition ultimately increases the gap in the average travel speed. At the same time, the average travel speed gap between the same road section in the outbound and inbound direction is large (e.g., I₂-I₃ and I₃-I₂), which may be due to the differences in traffic volume between the intersections in the outbound and inbound directions. Furthermore, the signal-timing scheme is based mainly on symmetrical phase pattern, which results in insufficient green time in one direction. Ultimately, the possibility of stopping delay when vehicles pass through the intersection increases. Therefore, the gap between the average travel speed of outbound and inbound direction on the same road section is increased. In response to the current shortage, different phase patterns of two-way green wave coordinated control method can be considered.

4.1.4. Relationship between Speed and Traffic Volume

A correlation often exists between speed and traffic volume. In this study, the six intersections along the route are viewed as a whole, and the traffic volume and the average travel speed measured for 3 days before and after each road section are used as the base data for fitting to explore the mechanism within the whole system. The fit is better when more data are considered during fitting. However, the limited data obtained in this study can only show the approximate relationship between speed and traffic volume. Figure 7 shows the fitting curves between speed and traffic volume when vehicles are in outbound and inbound directions.

As shown in Figure 7a, the traffic volume corresponding to the apex of the curve is the capacity of the whole system in outbound direction. The value is 1069 pcu/h. It corresponds to a speed of 12 km/h at this point. The left side of the apex indicates the unsteady flow state. Theoretically, as the number of vehicles inside the system continues to increase, it starts to queue until traffic is paralyzed and the speed of vehicles inside the system drops to zero. The right side indicates the stable flow state. In this state, the arrival of vehicles is within the tolerance range of the system. Drivers and passengers obtain a better driving experience, and the internal operation of the traffic flow is good. Theoretically, the traffic volume is 0 at the beginning of the right part of the vertex, and the corresponding speed is the free flow speed at this moment. The speed gradually decreases as the traffic volume increases until the traffic volume reaches the capacity of the system.

As shown in Figure 7b, the traffic volume corresponding to the apex of the curve is the capacity of the whole system in inbound direction. The value is 1681 pcu/h. It corresponds to a speed of 19 km/h at this point. The left part of the apex indicates that the arrival flow exceeds the capacity of the system in inbound direction and vehicles are queued. Theoretically, as the number of vehicles continues to increase, the system internally causes severe congestion, and the speed gradually decreases until it reaches zero. The arrival of vehicles in the right part of the apex is within the tolerance range of the system, and the internal operation of the traffic flow is good. Theoretically, the traffic volume in the right part of the apex is 0 at the beginning, and the speed gradually decreases as the traffic volume increases until the traffic volume reaches the capacity of the system.

4.2. Test Design and Results Analysis

AM–BAND–PBAND model is evaluated and compared with the MULTIBAND [5], improved MULTIBAND [10], AM–BAND [6], and PBAND [33] models. The traffic volume at each intersection is derived from Table 3. The single-lane traffic capacity of left turn lane is 1450 pcu/h, and the traffic capacity of other single lanes is 1500 pcu/h. According to Webster method [41], the public signal cycle of each intersection is determined to be 88 s. The green time allocation ratio for each intersection’s overlapping phase pattern is shown in

Table 5. Green time allocation ratio of each intersection under overlapping phase pattern.

Intersection	East		West		South		North
	Left	Straight	Left	Straight	Left	Straight	Left	Straight
I1	0.32788	0.19826	0.32788	0.19826	0.08943	0.35607	0.11779	0.38442
I2	0.28277	0.20260	0.28277	0.20260	0.12714	0.34650	0.16814	0.38750
I3	0.20675	-	-	-	-	0.72207	0.06479	0.79325
I4	0.18366	0.24633	0.18366	0.24633	0.14708	0.42751	0.14250	0.42293
I5	0.14885	0.34258	0.14885	0.34258	0.13668	0.42575	0.08282	0.37189
I6	0.31995	-	-	-	-	0.51917	0.16088	0.68005

. The green time allocation ratio for each intersection’s split-phase pattern is shown in

Table 6. Green time allocation ratio of each intersection under split phase pattern.

Intersection	East		West		South		North
	Left	Straight	Left	Straight	Left	Straight	Left	Straight
I1	0.22727	0.22727	0.13636	0.13636	0.30682	0.30682	0.32955	0.32955
I2	0.20455	0.20455	0.19318	0.19318	0.27273	0.27273	0.32955	0.32955
I3	0.10227	-	-	-	-	0.38636	0.51136	0.51136
I4	0.26136	0.26136	0.19318	0.19318	0.26136	0.26136	0.28409	0.28409
I5	0.18182	0.18182	0.29545	0.29545	0.26136	0.26136	0.26136	0.26136
I6	0.17045	-	-	-	-	0.40909	0.42045	0.42045

. Outbound and inbound speeds are set to 40 km/h.

4.2.1. Time–Space Diagrams

The results of green wave coordination control at the intersection of South Kunlunshan Road (West Huaihe Road-Songhua River Road) are shown in

Table 7. Progression bandwidths of each model (unit: s).

Number	Model	b1	${\overline{\mathbf{b}}}_1$	b2	${\overline{\mathbf{b}}}_2$	b3	${\overline{\mathbf{b}}}_3$	b4	${\overline{\mathbf{b}}}_4$	b5	${\overline{\mathbf{b}}}_5$	∑
1	MULTIBAND	25	13	16	6	37	38	32	31	33	4	235
2	Improved MULTIBAND	31	0	34	23	35	34	31	33	30	26	277
3	AM–BAND	31	8	34	27	37	38	28	29	33	17	282
4	PBAND	26	23	32	30	32	38	29	33	31	25	299
5	AM–BAND–PBAND	26	23	34	30	37	38	33	37	30	26	314

(model number 1 indicates MULTIBAND, model number 2 indicates improved MULTIBAND, model number 3 indicates AM–BAND, model number 4 indicates PBAND, model number 5 indicates AM–BAND–PBAND). Table 7 shows that the green wave bandwidths obtained based on AM–BAND–PBAND model is the largest and the best optimized, followed by those of the PBAND model and AM–BAND model.

The time–space diagrams of AM–BAND model, PBAND model, and AM–BAND–PBAND model are plotted, as shown in Figure 8, Figure 9 and Figure 10, respectively, to compare the gap between the green wave bandwidth of each road segment more intuitively. In time–space diagrams, offset _i,i+1 indicates the time interval between the starting point of the green time at intersection I_i in outbound direction and the starting point of the green time at intersection I_i+1 in outbound direction.

As shown in Figure 8, the sum of the outbound green wave bandwidth is much larger than the sum of the inbound green wave bandwidth, where the difference in the outbound and inbound direction bandwidths between intersection I₁ and intersection I₂ is the largest, followed by those in intersection I₅ and intersection I₆. This condition results in more wasted green time in the inbound direction and a poor optimization effect on the two directions. As shown in Figure 9, the sums of the outbound and inbound green wave bandwidths insignificantly differ. However, the green wave bandwidth in outbound direction between intersection I₂ and intersection I₅ is not optimal. Comparing Figure 8 and Figure 10 reveals that the optimization effect between intersection I₁ and intersection I₂ using split phase pattern is more significant than overlapping phase pattern. As a result, the difference between outbound and inbound green wave bandwidths is small, and the difference between outbound and inbound green wave bandwidth of intersection I₅ and intersection I₆ is also relatively reduced. Thus, the combination of different phase patterns can obtain a larger green wave bandwidth than a single phase pattern. The green wave bandwidth between intersection I₂ and intersection I₅ in Figure 9 is larger and better optimized than that in Figure 10.

4.2.2. VISSIM Simulation Results

Evaluation indexes such as number of stops, delay time, travel time, and travel speed are difficult to obtain by manual counting and calculation, and inaccuracies inevitably exist in obtaining them based on actual surveys of road sections. Therefore, this study compares and analyzes the evaluation indexes before and after optimization using simulation software VISSIM based on the solution results of each model and current signal control scheme. This way determines the degree of merit of the arterial coordinated control system optimization method. Different random seeds are selected to simulate each model for 10 times to avoid randomness of the simulation, and the average value is finally taken as the final simulation result. The results of the arterial coordination direction are shown in Figure 11 (model number 0 indicates current signal control scheme).

Compared with the current signal control scheme, each model was optimized in each index to different degrees. The coordination effect is evaluated in the same way as in the literature [42], and the weights of average number of stops, average travel speed, average travel time, and average delay were calculated using hierarchical analysis, which are 0.07, 0.19, 0.34, and 0.4, respectively. Then, they are evaluated using a comprehensive evaluation index model. The improvement of each model after green wave coordination compared with current signal control scheme is shown in

Table 8. Green wave coordination evaluation of each model.

Number	Model	Improvement Rate of Average Number of Stops		Improvement Rate of Average Travel Speed		Improvement Rate of Average Travel Time		Improvement Rate of Average Delay Time		Comprehensive Index
		Outbound	Inbound	Outbound	Inbound	Outbound	Inbound	Outbound	Inbound	Outbound	Inbound
1	MULTIBAND	3.7%	8.8%	5.8%	8.5%	13.6%	24.0%	10.9%	25.3%	9.9%	20.0%
2	Improved MULTIBAND	12.8%	34.0%	5.8%	13.7%	13.4%	35.8%	13.4%	37.0%	11.6%	30.7%
3	AM-BAND	18.2%	29.7%	5.3%	12.0%	12.4%	32.3%	11.1%	32.5%	10.6%	27.1%
4	PBAND	12.5%	37.3%	7.4%	13.5%	16.9%	35.4%	14.2%	32.6%	13.0%	29.3%
5	AM-BAND-PBAND	16%	43.7%	7.9%	16.1%	17.9%	40.7%	15.6%	36.0%	14.3%	32.8%

.

The results for sub-indicators in Table 8 show that AM–BAND–PBAND model has the best improvement effect on the average travel speed, average travel time, and average delay time in outbound and inbound directions. In terms of the improvement effect of average number of stops, the improvement effect in outbound direction is better those of, and the improvement effect in inbound direction is the best. With regard to the comprehensive indexes, the outbound and inbound green wave coordination effects are better those of than with other models.

The results in Table 7 and Table 8 indicate that the green wave bandwidth obtained by each model is incompletely consistent with the optimization effect of comprehensive indicators in outbound and inbound directions, such as AM–BAND and PBAND. Theoretically, the evaluation index should be better when the obtained green wave bandwidth is larger. The reason for the abnormality may be that the green wave band is incompletely consistent with the vehicle’s travel trajectory, or that not all the vehicle’s trajectory is within the green wave band. This condition results in some vehicles not being able to drive within the green wave band, which affects the original vehicle’s travel within the green wave band. Ultimately, the evaluation effect is poor. Moreover, many vehicles on the branch road may be turning to the coordinated direction, which causes vehicles to queue in the coordinated direction. This condition destroys the green wave belt. The randomness of the simulation software may also be another affecting factor.

The results of the uncoordinated direction are shown in Figure 12 (I₁ E-W means that vehicles drive from the east entrance to the west entrance at intersection I₁, and so on). Compared with current signal control scheme, each model has different degrees of superiority and inferiority in the indicators of average travel speed and average delay time and is at a disadvantage in average number of stops and average travel time. Each model has a greater disadvantage than the current signal control scheme in terms of various evaluation indicators in the north-to-east direction of intersection I₃. The disadvantages of the uncoordinated direction may be due to the coordinated control method for bandwidth maximization, which focuses on the optimization of the evaluation indicators of the coordinated direction and pays less attention to the uncoordinated direction. Even if the objective function of bandwidth maximization reaches the optimal, this optimization method cannot guarantee to minimize travel delay time or the number of stops of the arterial line or the whole network. If traffic volume in the uncoordinated direction is high, then it will need to be reviewed again.

As pollutants continue to be emitted and environmental problems become increasingly serious, considering the effect of pollutant emissions while optimizing signal-timing schemes is particularly important. The simulation software VISSIM was used to set “node” at 60 m from the signal light at each entrance of each intersection, and the average value was taken as the fuel consumption and emission (sum of all intersections) for each model after 10 simulations with different random seeds, as shown in

Table 9. Fuel consumption and emissions for each model-case study.

Number	Model	CO (g)	NOX (g)	VOX (g)	Fuel Consumption (US Liquid Gallon)
0	Current	16,914.7	3291.0	3920.2	242.0
1	MULTIBAND	13,893.6	2703.2	3220.0	198.8
2	Improved MULTIBAND	13,727.4	2670.9	3181.5	196.4
3	AM-BAND	14,164.5	2755.9	3282.8	202.6
4	PBAND	14,084.5	2740.3	3264.2	201.5
5	AM-BAND-PBAND	13,886.5	2701.8	3218.3	198.7

.

As shown in Table 9, each model has been optimized to varying degrees in terms of pollutant gas emissions and fuel consumption compared with current signal control scheme. The improved MULTIBAND model has the best optimization results, followed by AM–BAND–PBAND model. The reason may be that less consideration is given to the uncoordinated direction in improving the coordination efficiency of the arterial line. This way sacrifices the green time of some branches roads, which results in an increase in the parking time and delay of vehicles on the branches roads. Ultimately, the emission of pollutants and fuel consumption are increased.

5. Sensitivity Analysis

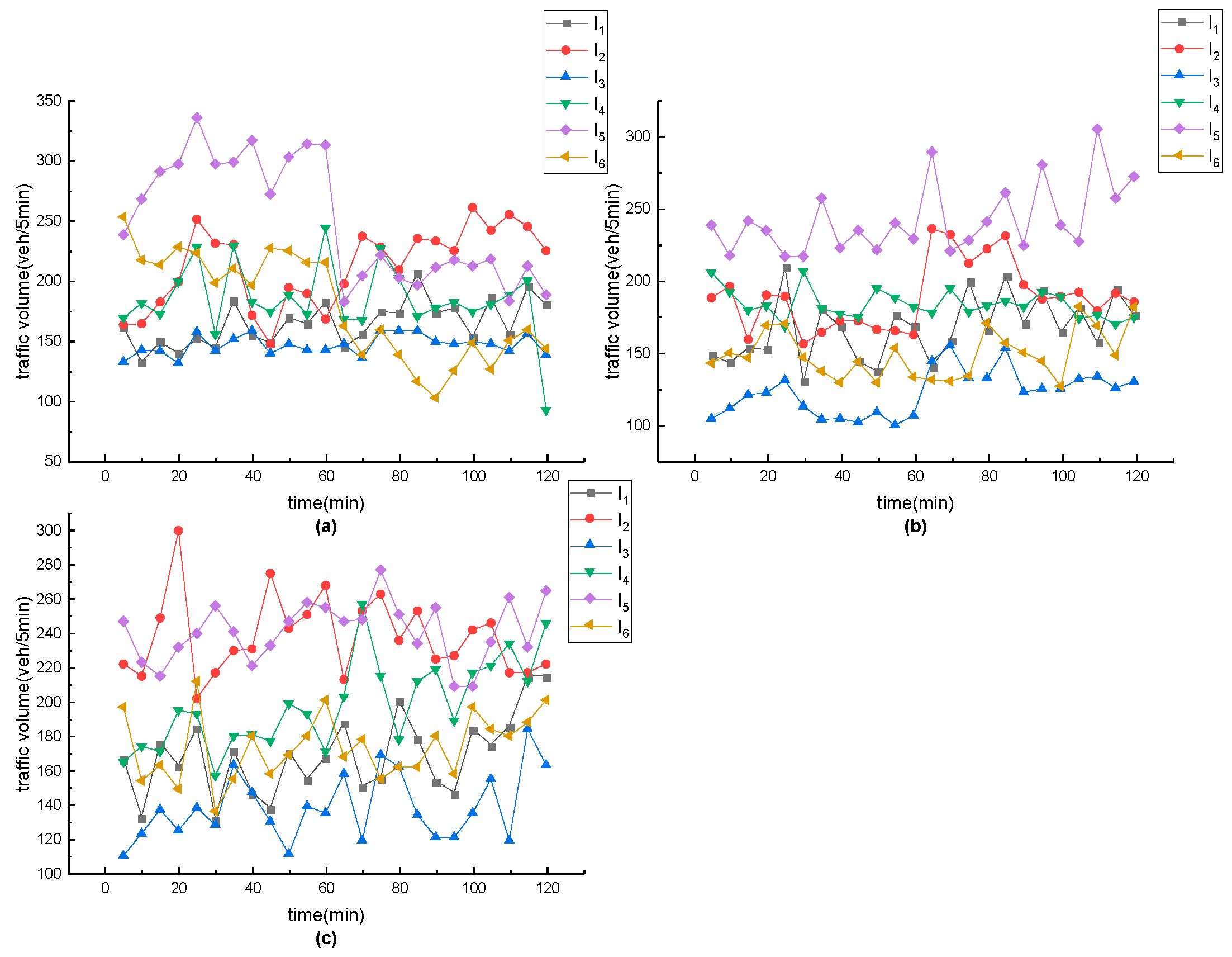
AM–BAND–PBAND model achieves better results in terms of green wave bandwidth, evaluation index improvement, pollutant emission, and fuel consumption. Thus, a sensitivity analysis of its applicability conditions is conducted to provide a reference for the optimization of the subsequent signal coordination control. We refer to the literature [43] in analyzing the sensitivity of AM–BAND–PBAND model under different traffic flow conditions. The data in Table 3 are used as the basis, with traffic flow coefficients set to 0.4, 0.5, 0.6, 0.8, 1.0, 1.1, 1.2, 1.4, and 1.6 to obtain 10 different scenarios. 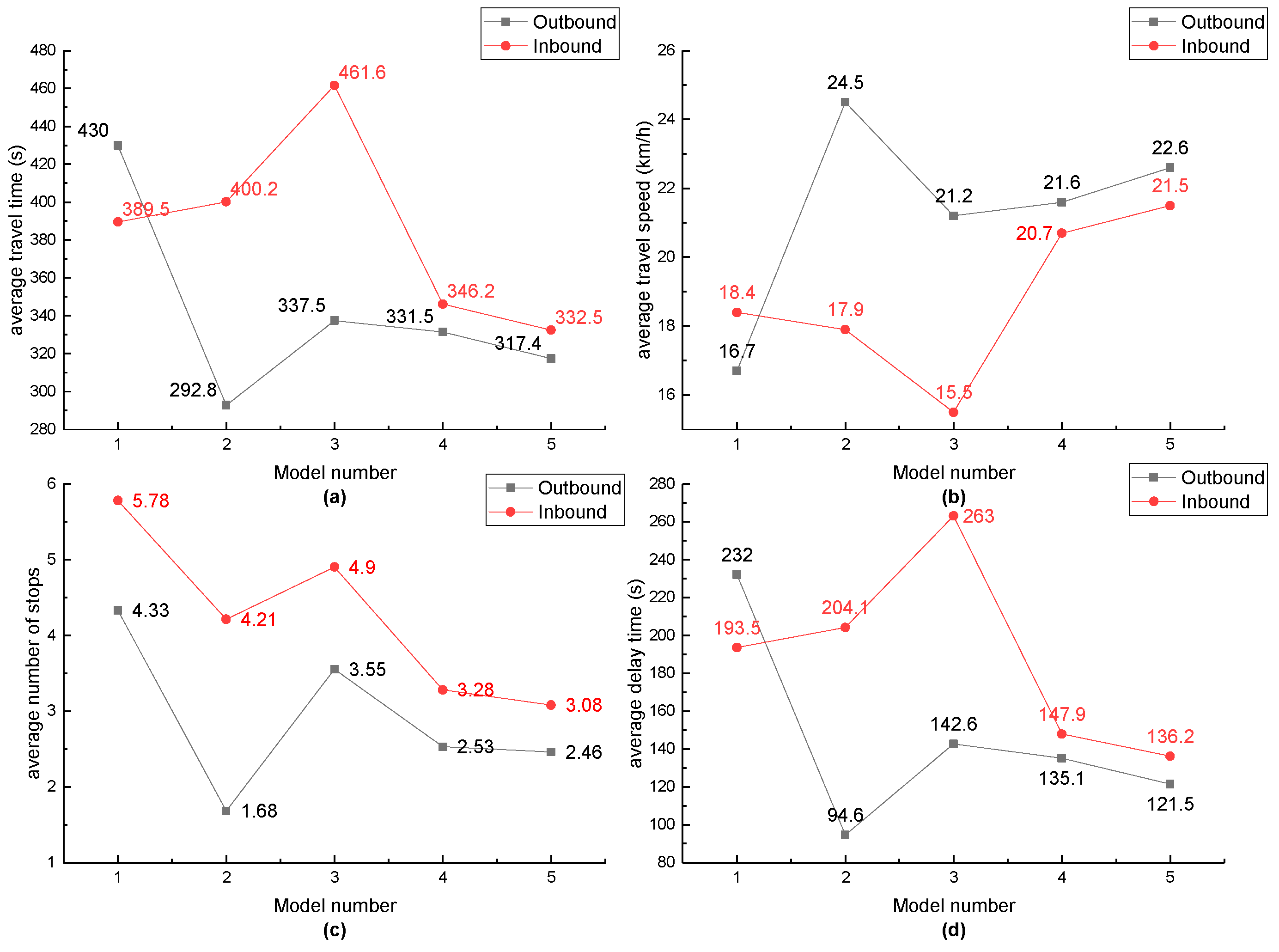Section 4 implies that the AM–BAND and PBAND models have better optimized effects than the MULTIBAND and improved MULTIBAND models. Thus, the AM–BAND and PBAND models are chosen as the comparison models. At the same time, the average number of stops, average travel time, and average delay time have the same trend, and the average travel speed is inversely related to the first three indicators. Therefore, any of the four performance indicators can be used to measure the effectiveness of the different methods of control. In this study, the average delay time along the arterial road is used as the evaluation index, and the results are shown in

Table 10. Average delay under different scenarios (unit: s).

Traffic Flow Coefficient	AM–BAND		PBAND		AM–BAND–PBAND
	Outbound	Inbound	Outbound	Inbound	Outbound	Inbound
0.4	68.4	95.2	62.0	71.9	60.7	74.9
0.5	75.8	99.9	68.4	73.8	66.8	80.1
0.6	79.9	101.7	72.5	79.3	70.1	77.5
0.8	88.6	99.3	79.0	84.3	77.8	83.4
1	98.8	95.2	89.4	94.8	85.1	84.5
1.1	90.5	104.8	91.4	92.0	87.5	88.7
1.2	102.9	100.4	94.5	92.5	92.3	95.9
1.4	107.8	106.9	101.9	97.9	101.6	99.3
1.6	112.7	108.4	108.7	100.9	109.1	104.7

.

Table 10 shows that the traffic flow coefficients are between 0.6 and 1.1, and that AM–BAND–PBAND model can achieve better results in outbound and inbound directions than AM–BAND and PBAND. This finding verifies the control effect of the method proposed in this study. However, AM–BAND–PBAND model cannot achieve the best coordination effect in outbound and inbound directions when the traffic flow coefficients are between 0.4 and 0.5 or greater than or equal to 1.2. Especially, the method is not optimal in terms of coordination control effect when the traffic coefficient is 1.6. The results of fuel consumption and pollutant emissions for different scenarios are shown in

Table 11. Fuel consumption and emissions under different scenarios.

Traffic Flow Coefficient	AM–BAND				PBAND				AM–BAND–PBAND
	CO (g)	NOX (g)	VOX (g)	Fuel Consumption (US Liquid Gallon)	CO (g)	NOX (g)	VOX (g)	Fuel Consumption (US Liquid Gallon)	CO (g)	NOX (g)	VOX (g)	Fuel Consumption (US Liquid Gallon)
0.4	5396.5	1050.0	1250.7	77.2	5325.0	1036.0	1234.1	76.2	5268.2	1025.0	1220.9	75.4
0.5	6802.5	1323.5	1576.6	97.3	6693.7	1302.3	1551.3	95.8	6603.4	1284.8	1530.4	94.5
0.6	8174.4	1590.4	1894.5	116.9	8032.3	1562.8	1861.6	114.9	7923.6	1541.7	1836.4	113.4
0.8	11,009.1	2142.0	2551.5	157.5	10,790.0	2099.3	2500.7	154.4	10,625.1	2067.3	2462.5	152.0
1	14,164.5	2755.9	3282.8	202.6	14,084.5	2740.3	3264.2	201.5	13,886.5	2701.8	3218.3	198.7
1.1	16,566.9	3223.3	3839.5	237.0	16,450.4	3200.6	3812.5	235.3	16,234.0	3158.5	3762.4	232.2
1.2	18,964.4	3689.8	4395.2	271.3	19,581.7	3809.9	4538.3	280.1	19,346.7	3764.2	4483.8	276.8
1.4	23,768.0	4624.4	5508.5	340.0	24,719.2	4809.5	5728.9	353.6	24,461.6	4759.3	5669.2	350.0
1.6	30,405.6	5915.8	7046.8	435.0	30,892.0	6010.5	7159.5	441.9	30,621.2	5957.8	7096.8	438.1

.

Table 11 shows that AM–BAND–PBAND model has the least fuel consumption and pollutant emissions when the traffic flow coefficient is between 0.4 and 1.1. However, the effect is not optimal when the traffic flow coefficient is greater than 1.1. The reason may be that the traffic volume in the arterial coordination direction increases with a rise in traffic flow coefficient, and the vehicles flowing into the arterial coordination direction in the branch direction also increases. Vehicles start to queue in the arterial coordination direction, and local blockage occurs in severe cases. Thus, the coordination control method is unsatisfactory. At the same time, the pollution emission generated by vehicle queuing and delay also increase. In summary, the proposed method has better control effect when the traffic volume is moderate and there are fewer turning vehicles on the branch road.

To ensure that each “left” or “right” part of the green wave progression line is not zero, the upper and lower limits of the respective component ratios of the outbound and inbound green wave bandwidths can be determined by adjusting the values of N1 and N2 in AM–BAND–PBAND model. On the basis of the traffic volume data in Table 3, the effects of different N1 and N2 are discussed. Different N1 and N2 can generate the corresponding traffic signal control scheme, which VISSIM then evaluates. The average delay time in the coordinated direction is taken as the evaluation index (the sum of the average delays in outbound and inbound directions). The results are shown in

Table 12. Average delay times in AM–BAND–PBAND model under different N1 and N2 (unit = s).

	N1	1	1.5	2	2.5	3	3.5	4	5	∑
N2
1		178.7	178.7	175.1	173.9	174.2	179.1	175.1	173.9	1408.6
1.5		175.8	178.7	177.6	173.9	173.9	173.2	175.8	176.7	1405.6
2		173.9	173.9	174.1	174.8	168.6	173.2	182.2	173.2	1393.8
2.5		182.5	175.1	173.9	176.7	173.9	173.2	173.9	175.1	1404.1
3		178.7	174.1	173.9	169.7	174.6	183.9	173.9	173.2	1402.1
4		179.3	173.9	173.2	176.7	182.3	173.2	174.8	174.6	1407.9
5		180.4	173.9	175.3	179.6	178.7	180.9	174.1	183.2	1426.1
6		173.9	173.9	179.1	174.1	173.2	174.8	174.2	173.9	1397.1
∑		1423.3	1402.2	1402.1	1399.5	1399.3	1411.3	1404.1	1403.7

.

As shown in Table 12, the performance of the model varies with the values of N1 and N2. The average delay is larger when N1 = 1 or N2 = 5. When N1 changes between 2.5 and 3 or N2 changes between 2 and 3, the performance of the model is relatively good. This result indicates that the difference between the two respective components of the outbound and inbound bandwidth should be within a reasonable range, within which the advantage of the model is obvious. In general, when N1 changes between 1.5 and 5 or N2 changes between 1 and 4, the change in model performance is not very significant, which indicates that the model performance is stable.

6. Numerical Experiments Extension

In this paper, the applicability and performance of the proposed model under different traffic conditions are verified by the extended numerical experiment with road conditions as shown in Figure 13 and traffic volume as shown in

Table 13. Summary of turning vehicles at intersections-numerical experiments extension.

Intersection	South			North			East			West
	Left	Straight	Right	Left	Straight	Right	Left	Straight	Right	Left	Straight	Right
I1	248	244	46	236	256	38	317	554	28	180	662	58
Sum	538			530			898			900
I2	277	272	45	265	293	86	228	536	140	244	634	67
Sum	594			643			904			945
I3	272	709	84	276	704	96	210	536	124	256	566	121
Sum	1065			1076			870			943
I4	232	276	141	226	282	40	320	598	140	342	446	114
Sum	649			548			1058			902
I5	272	272	102	270	286	78	334	706	93	244	488	106
Sum	646			634			1133			838

.

AM-BAND-PBAND model is evaluated and compared with the MULTIBAND [5], improved MULTIBAND [10], AM-BAND [6], and PBAND [33] models. The traffic capacity of single lane is 1800 pcu/h. According to Webster method [41], the public signal cycle of each intersection is determined to be 120 s. Outbound and inbound speeds are set to 45 km/h. Green wave coordination control results are shown in

Table 14. Progression bandwidth of each model (unit: s).

Number	Model	b1	${\overline{\mathbf{b}}}_1$	b2	${\overline{\mathbf{b}}}_2$	b3	${\overline{\mathbf{b}}}_3$	b4	${\overline{\mathbf{b}}}_4$	∑
1	MULTIBAND	29	29	12	13	27	28	15	18	171
2	Improved MULTIBAND	33	31	13	12	27	28	27	6	177
3	AM–BAND	26	19	31	28	29	28	27	29	217
4	PBAND	32	31	30	28	29	26	26	31	233
5	AM–BAND–PBAND	34	31	30	28	28	27	27	31	236

. Simulation results in coordination direction are shown in Figure 14. Simulation results in uncoordination direction are shown in Figure 15. Fuel and pollution gas emission results are shown in

Table 15. Fuel consumption and emissions for each model-numerical experiments extension.

Number	Model	CO (g)	NOX (g)	VOX (g)	Fuel Consumption (US Liquid Gallon)
1	MULTIBAND	20,650.1	4017.8	4785.9	295.4
2	Improved MULTIBAND	21,792.5	4240.0	5050.6	311.8
3	AM–BAND	21,859.9	4253.1	5066.2	312.7
4	PBAND	21,255.4	4135.5	4926.1	304.1
5	AM–BAND–PBAND	20,043.8	3899.8	4645.3	286.8

.

From the above results, it can be seen that AM–BAND–PBAND model can obtain a larger green wave bandwidth than other models. It has a significant optimization effects in the average number of stops, average delay time, average travel time and average travel speed, and it has a better optimization effect in fuel consumption and emissions, which can provide support for subsequent traffic management.

7. Managerial Insights

With the rapid development of the economy and the accelerating pace of urbanization, building or expanding urban roads can no longer meet the growing traffic demands in the new era. The unbreakable old urban area planning and the high cost of reconstruction and construction also limit traffic managers to a certain extent. When the development of a city reaches a certain stage and the roads can no longer be expanded, the importance of signal coordination control becomes apparent. It allows vehicles entering urban arterial roads to drive through each intersection in a timely, smooth, and safe manner. It can avoid traffic congestion, improve traffic efficiency, improve the level of urban traffic services, and effectively improve the urban environment. It can further reduce vehicle exhaust emissions, strengthen atmospheric environmental protection and governance, and improve urban environmental quality. Traffic managers consider the coordinated control of traffic signals and appropriate construction or expansion of urban roads, which is of great significance to urban operation and improvement of the environment. For drivers, it reduces the number of stops at intersections and the time cost caused by parking and waiting. It can enhance the driving experience and reduce drivers’ emotional fluctuation caused by queuing or parking many times, which has practical significance for driving safety and reducing traffic accident rates [44,45].

8. Conclusions and Recommendations

Considering the respective advantages and disadvantages of AM–BAND and PBAND models, this study proposes a coordinated control method for urban arterial roads based on AM–BAND–PBAND model. The method optimizes the available green time obtained by advancing the initial queue clearing time and generating an asymmetric bandwidth along the green wave progression line, considering adjacent intersections in a different phase pattern, increasing the possibility of obtaining a larger green wave bandwidth, and making the arterial coordination control effective. Six intersections along Kunlunshan South Road in Qingdao were selected for numerical experiments, and the signal-timing schemes formed by four models, MULTIBAND, improved MULTIBAND, AM–BAND, and PBAND, were implemented. Simulation software VISSIM verifies the feasibility and applicability of AM–BAND–PBAND model. AM–BAND–PBAND model can produce a larger green wave bandwidth than other models. From the perspective of coordinated control, the optimization effects for average parking time, average delay time, average travel time, and average travel speed are remarkable. From the perspective of fuel consumption and emissions, the optimization effect is better than the current situation. At the same time, the sensitivity analysis of AM–BAND–PBAND model under different traffic flow scenarios shows that the optimization effects for this method is obvious when the traffic volume is medium and there are few turning vehicles on the branches, which can provide a reference for the subsequent optimization of arterial-signal coordination control. To verify applicability and performance of the proposed model in different traffic conditions, numerical experiments were conducted. The results show that the proposed model has a better optimization effect on the green wave bandwidth and various evaluation indicators. Traffic managers can consider the coordinated control of traffic signals and the appropriate expansion of urban roads to improve the operational efficiency of urban traffic. In the future, we will consider using different speeds to optimize different sections in the coordinated direction. At the same time, we will consider turning vehicles in uncoordinated direction, zone coordination, and traffic safety-related factors.