Analysis of the Working Response Mechanism of Wrapped Face Reinforced Soil Retaining Wall under Strong Vibration
Abstract
:1. Introduction
| Reference | Test Type a | Height Model | Length to Height Ratio | Input Motion b | Reinforcement | Amax c |
|---|---|---|---|---|---|---|
| Krishna [8,9] | ST | 0.60 m | 1.25 | Sine. | geotextile | 0.2 g |
| Sakaguchi [10] | ST | 1.50 m | 2.30 | Sine. | geogrid | 0.72 g |
| Sakaguchi [10] | CST | 0.15 m | 2.30 | Sine. | geotextile | 12 g |
| Ramakrishnan [11] | ST | 0.81 m | 2.50 | Sine. | geotextile | 0.6 g |
| Huang [12] | ST | 0.60 m | 1.40 | Sine. | geotextile | 1.72 g |
| Roessing [13,14] | CST | 0.38 m | 1.60 | EQ | geotextile/metallic strips | 1.0 g |
| Yang [15] | CST | 0.16 m | 1.20 | Sine. | geotextile | 1.0 g |
| Zhu [16] | ST | 1.60 m | 1.56 | EQ | geogrid | 0.616 g |
| Duan [17] | ST | 2.00 m | 1.40 | EQ | geogrid | 0.616 g |
| Sabermahani [22] | ST | 1.00 m | - | Sine. | geotextile/geogrid | 0.3 g |
2. Shaking Table Model Test
2.1. Similitude Laws
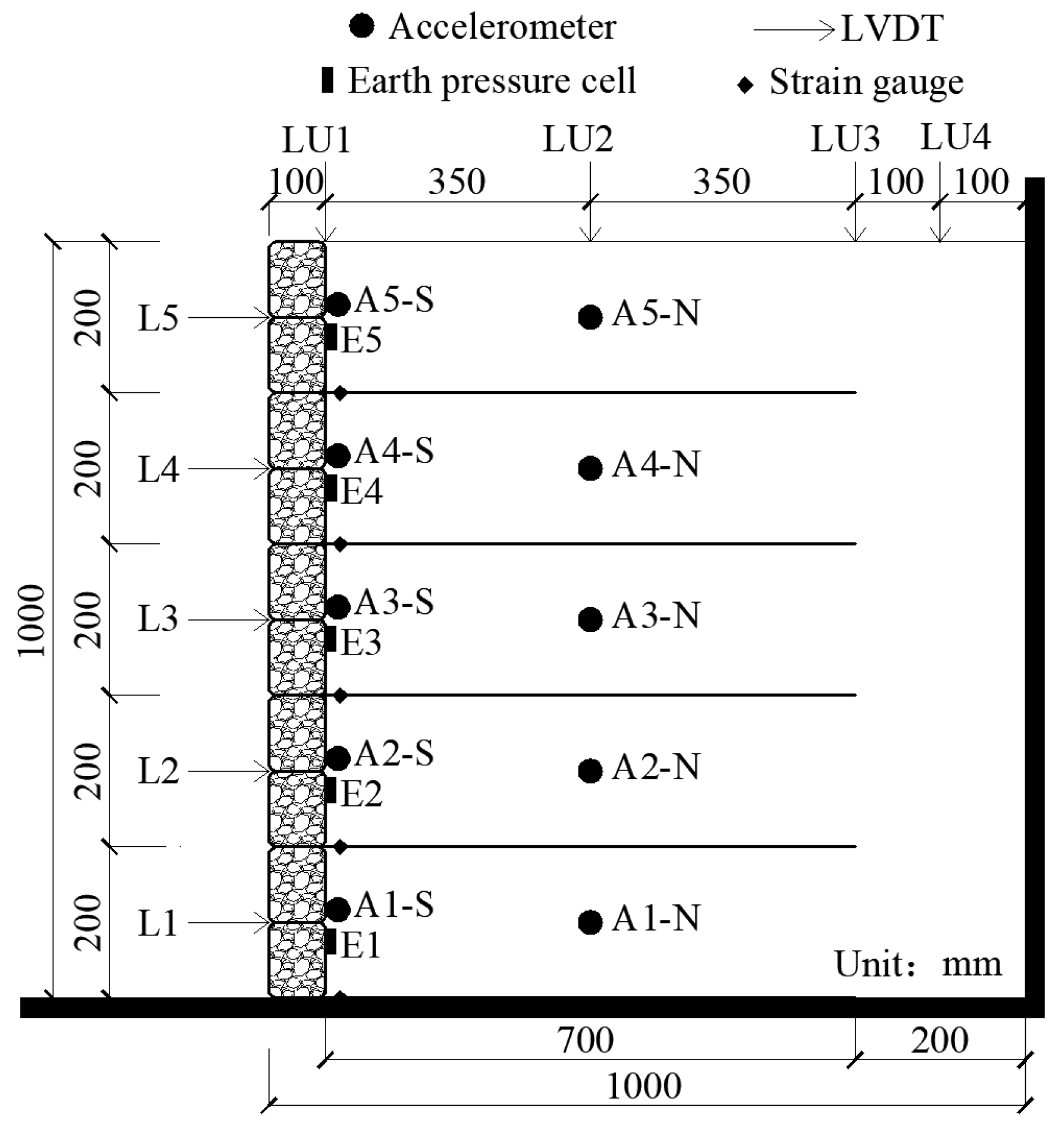
2.2. Model Design
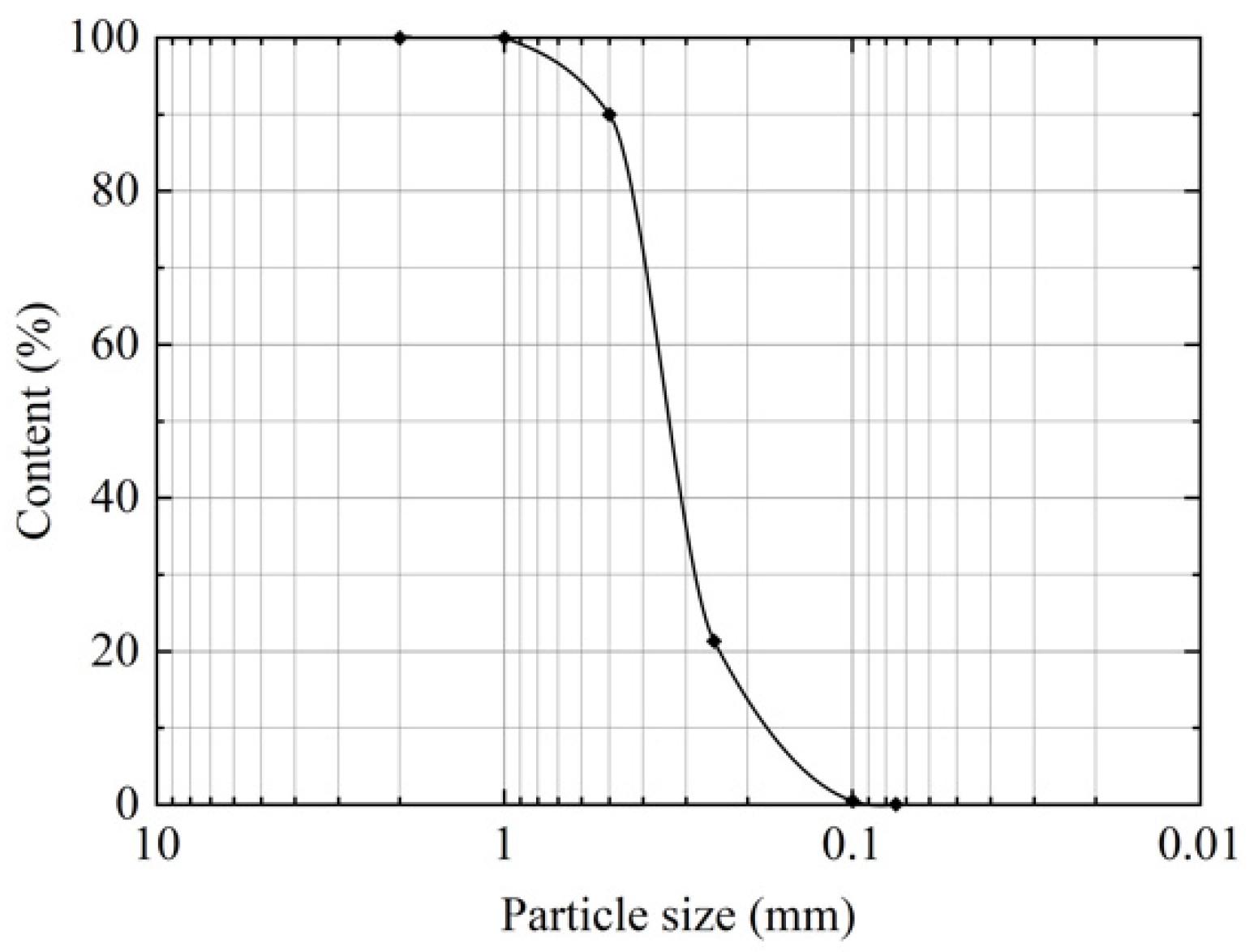
2.3. Backfill Material
2.4. Reinforcement
2.5. Panel
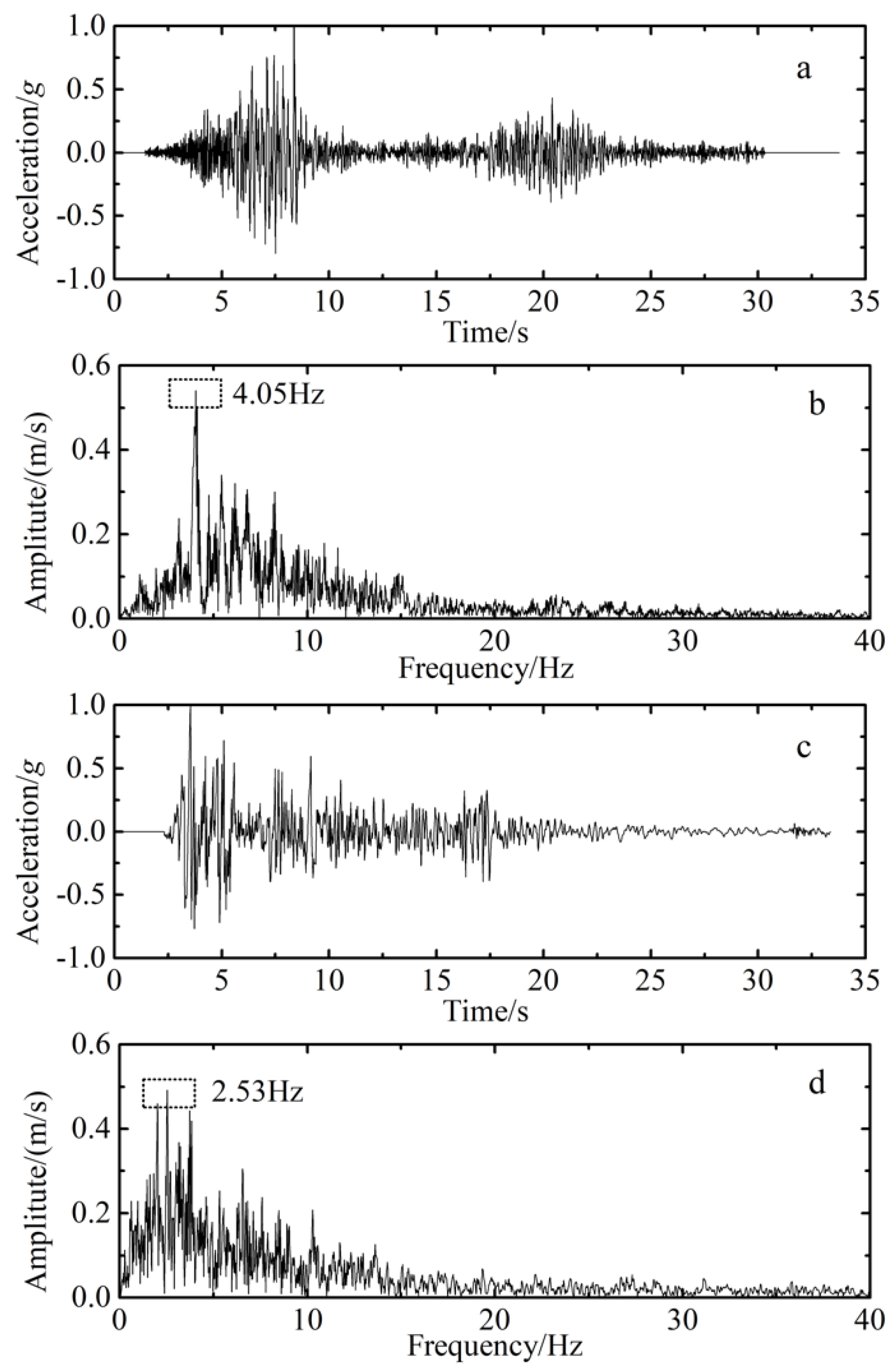
2.6. Input Motions
3. Results
3.1. Model Damage Phenomena
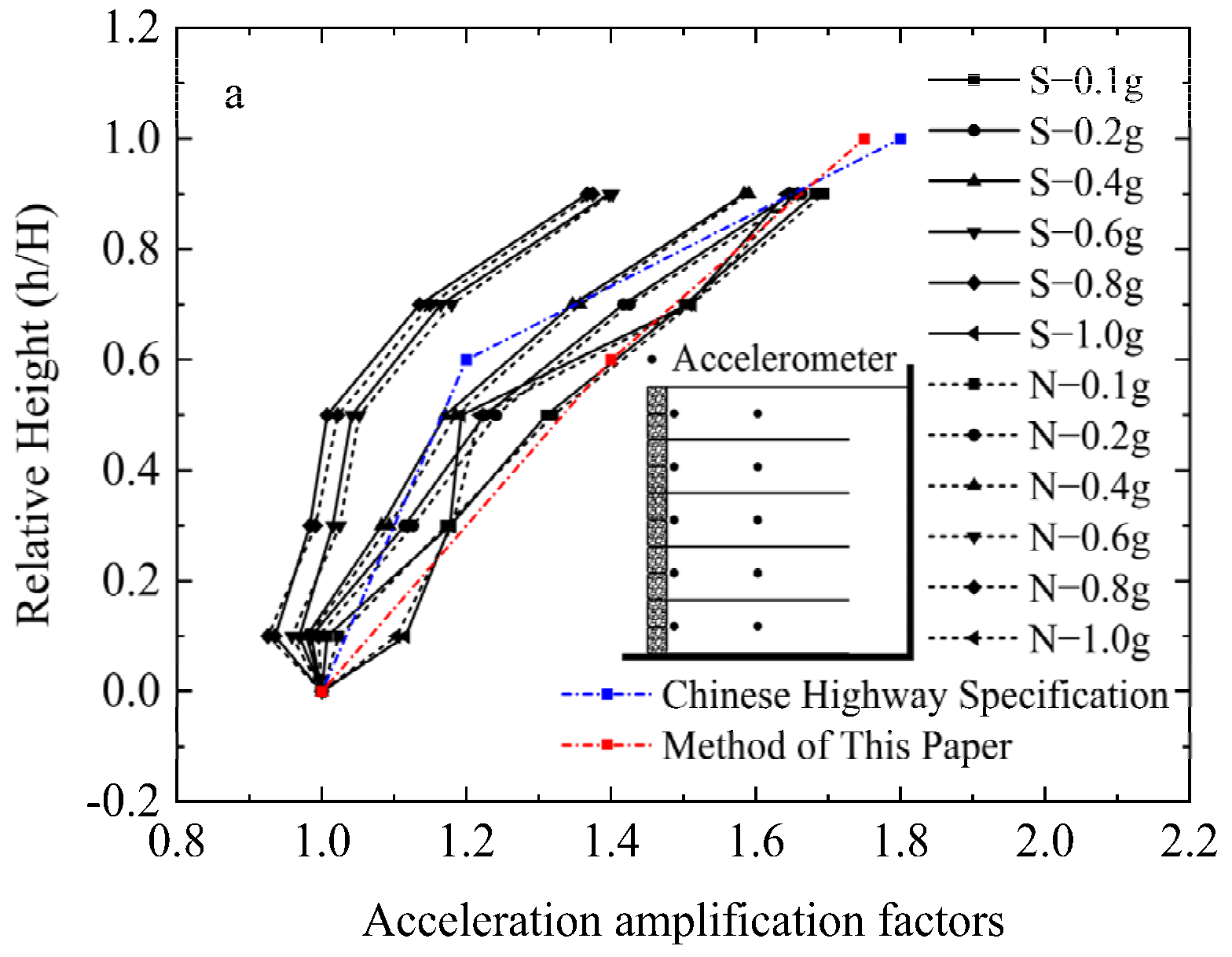
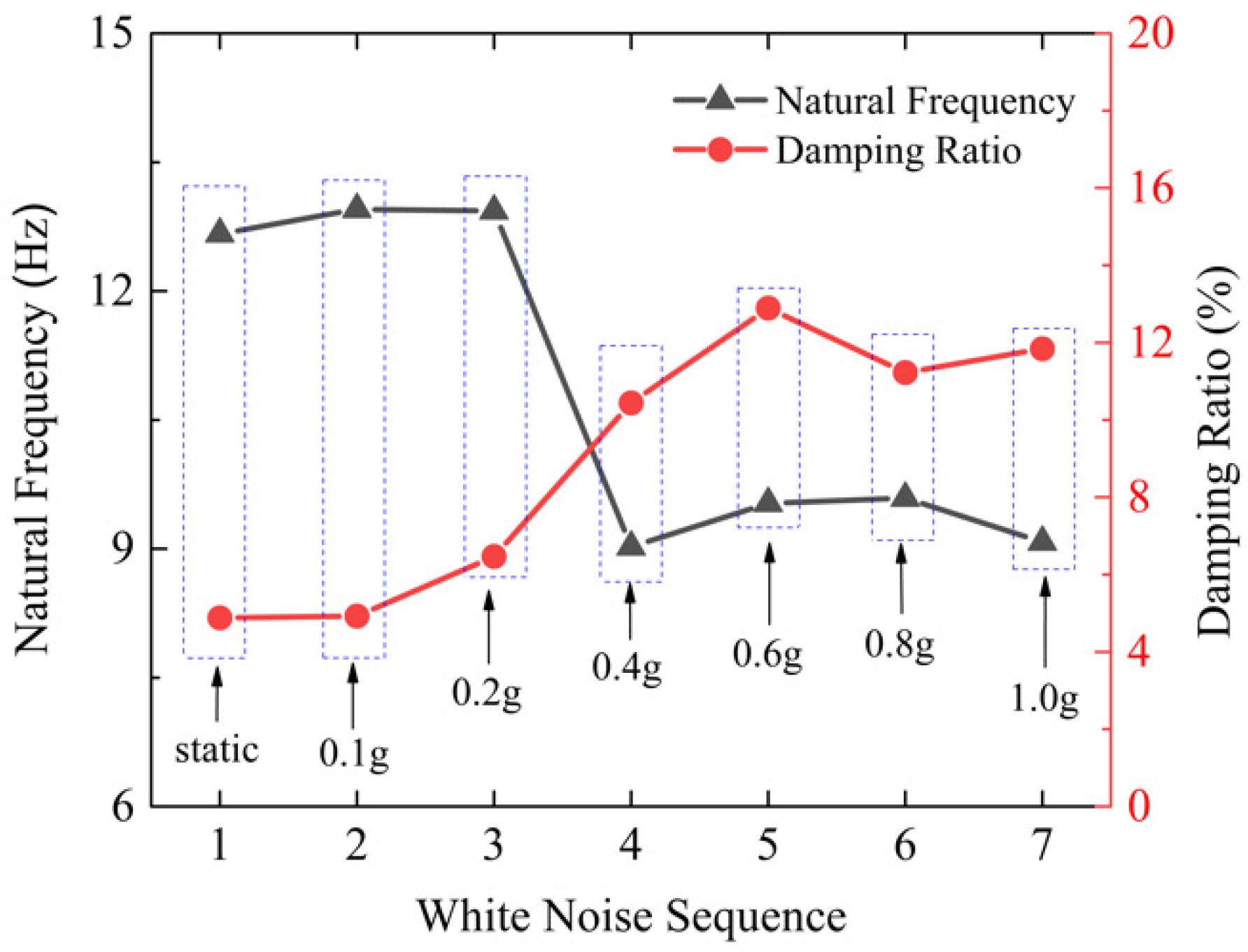
3.2. Acceleration Response
3.3. Deformation
3.4. Earth Pressure
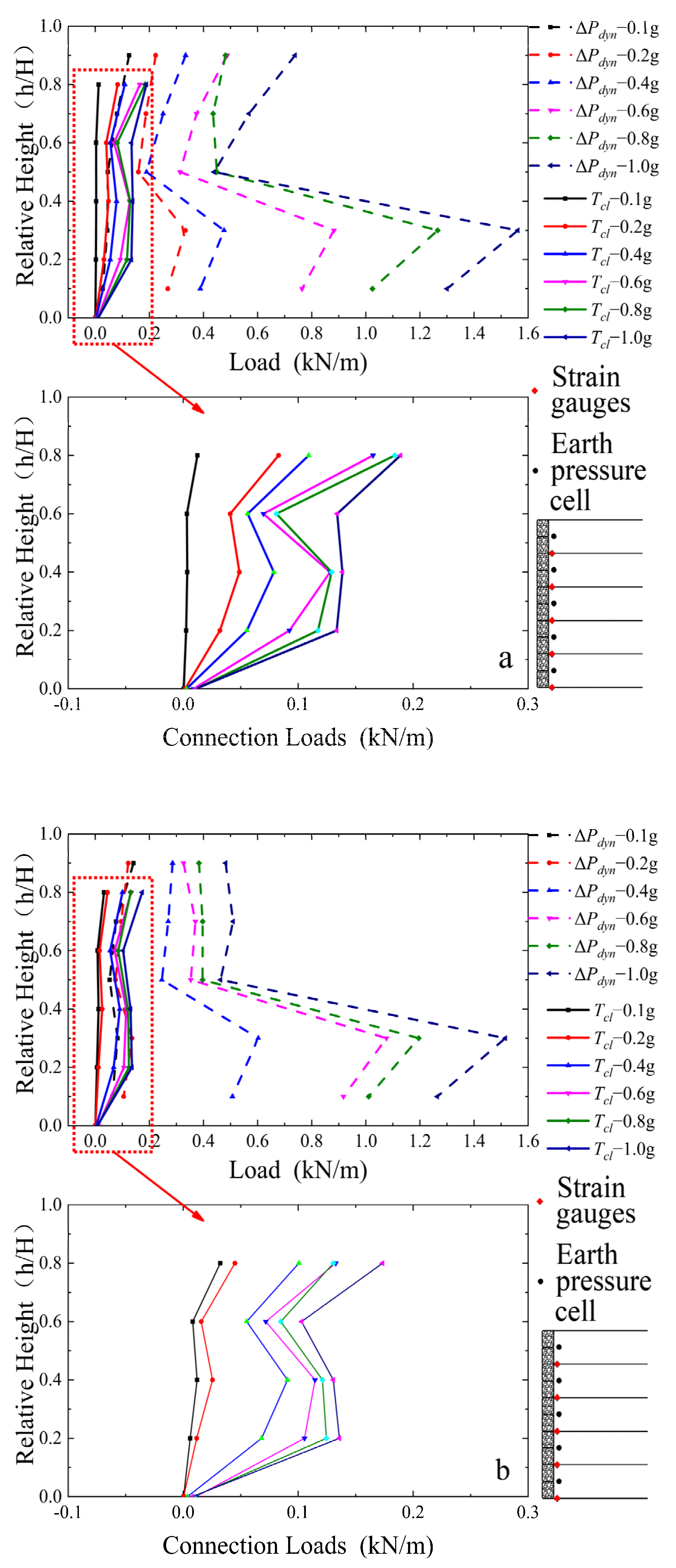
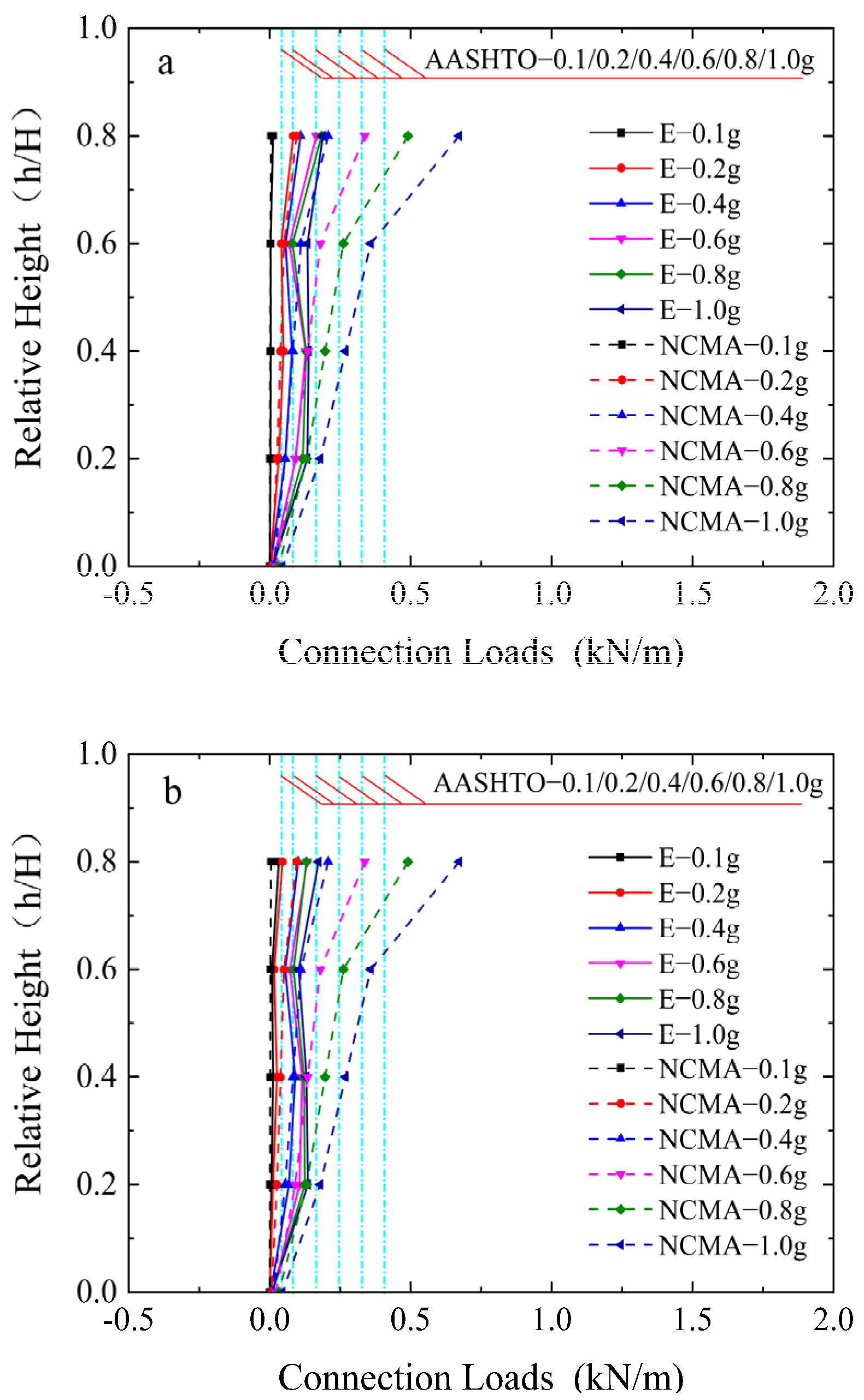
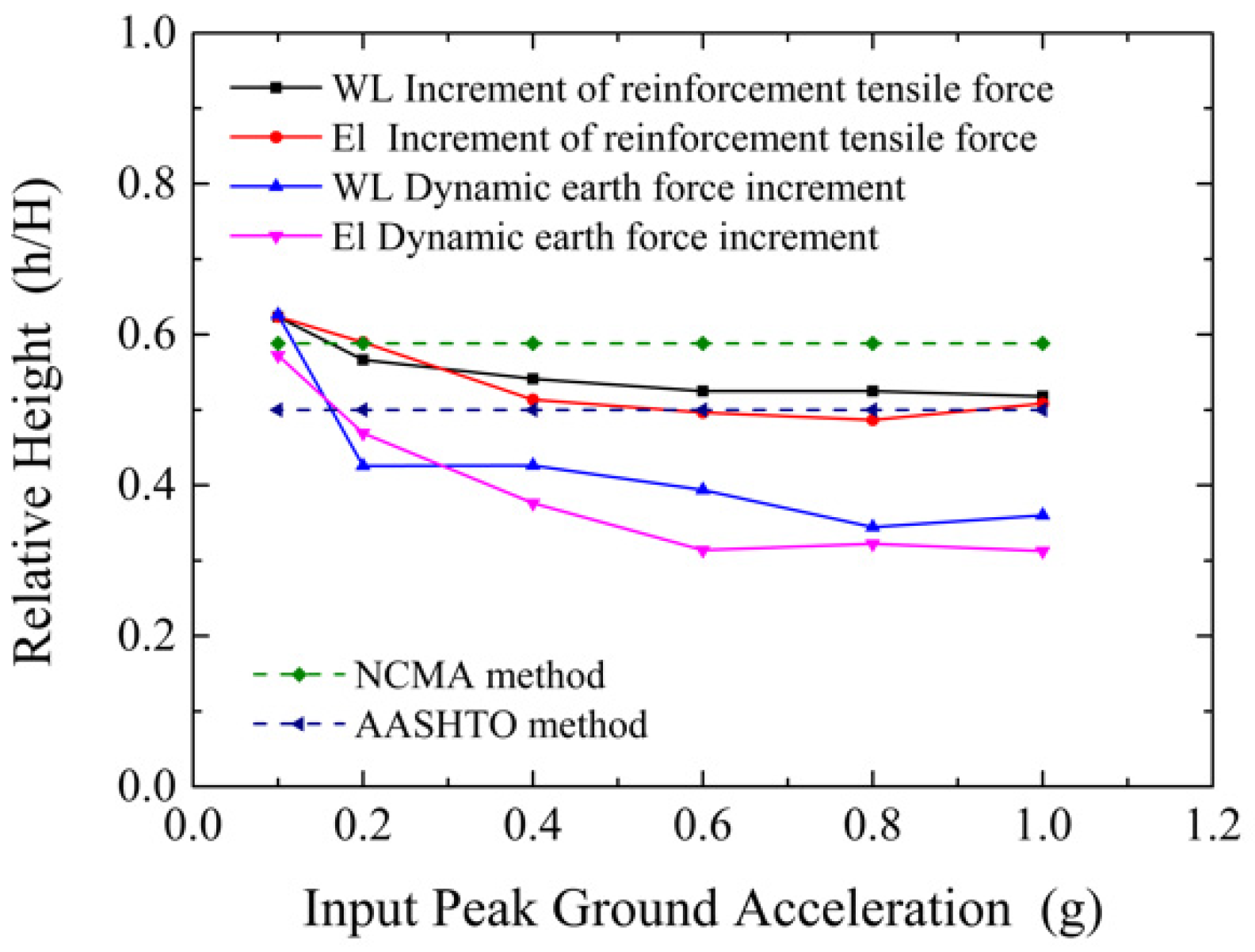
3.5. Connection Loads
4. Discussion
5. Conclusions
- (1)
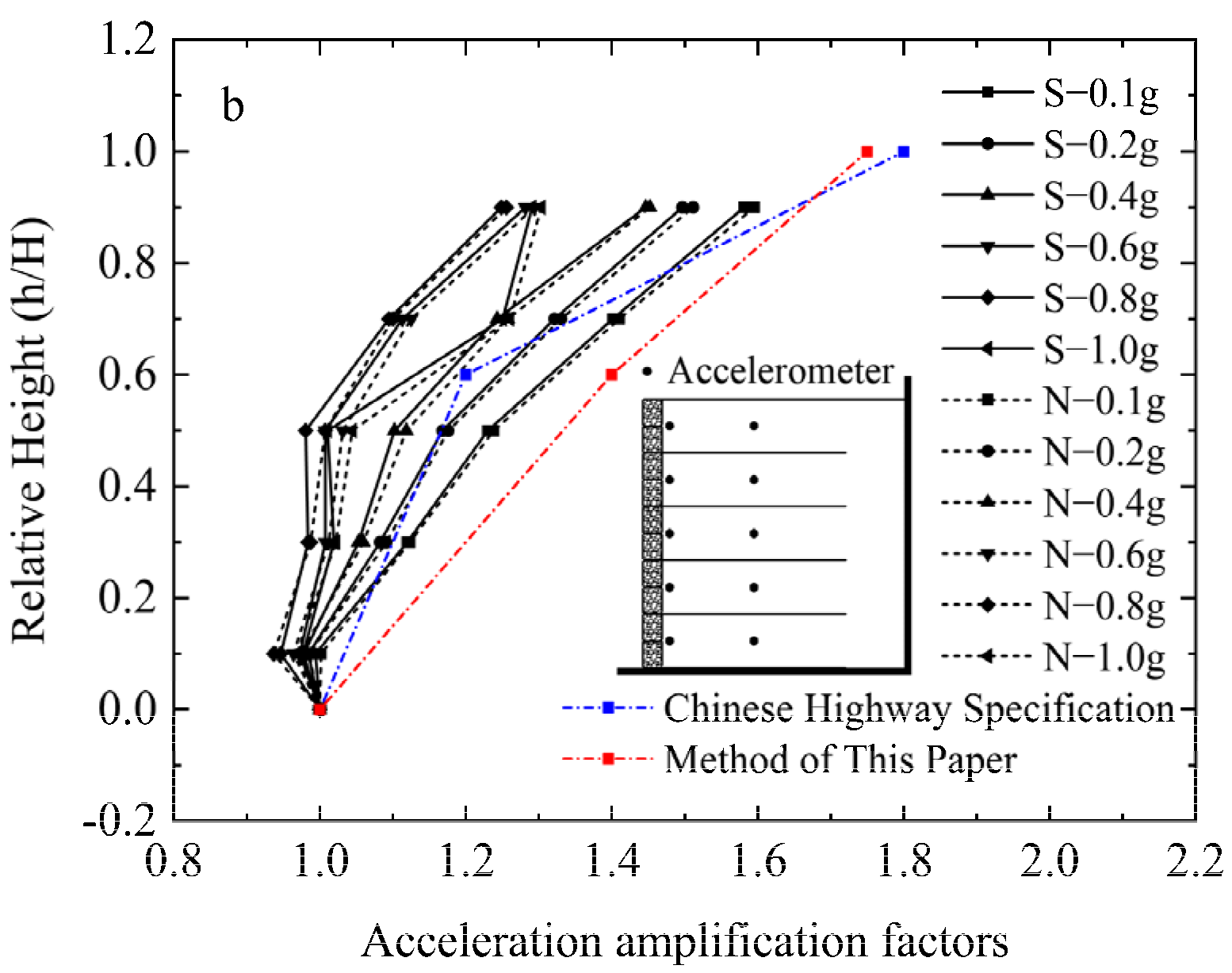
- Affected by the nonlinear characteristics of soil, the acceleration amplification coefficient decreases with the increase of peak acceleration, and the maximum acceleration appears at the top of the retaining wall, which is consistent with the whiplash effect of high-rise structures. When HPGA reaches 1.0 g, the acceleration amplification coefficient increases, the range of acceleration amplification coefficient at the top of the wall is 1.36–1.69. Based on the Chinese Highway Specification and test results, this paper suggests that the acceleration amplification factor distribution formula is suitable for the reinforced soil-retaining wall with wrapped-face.
- (2)
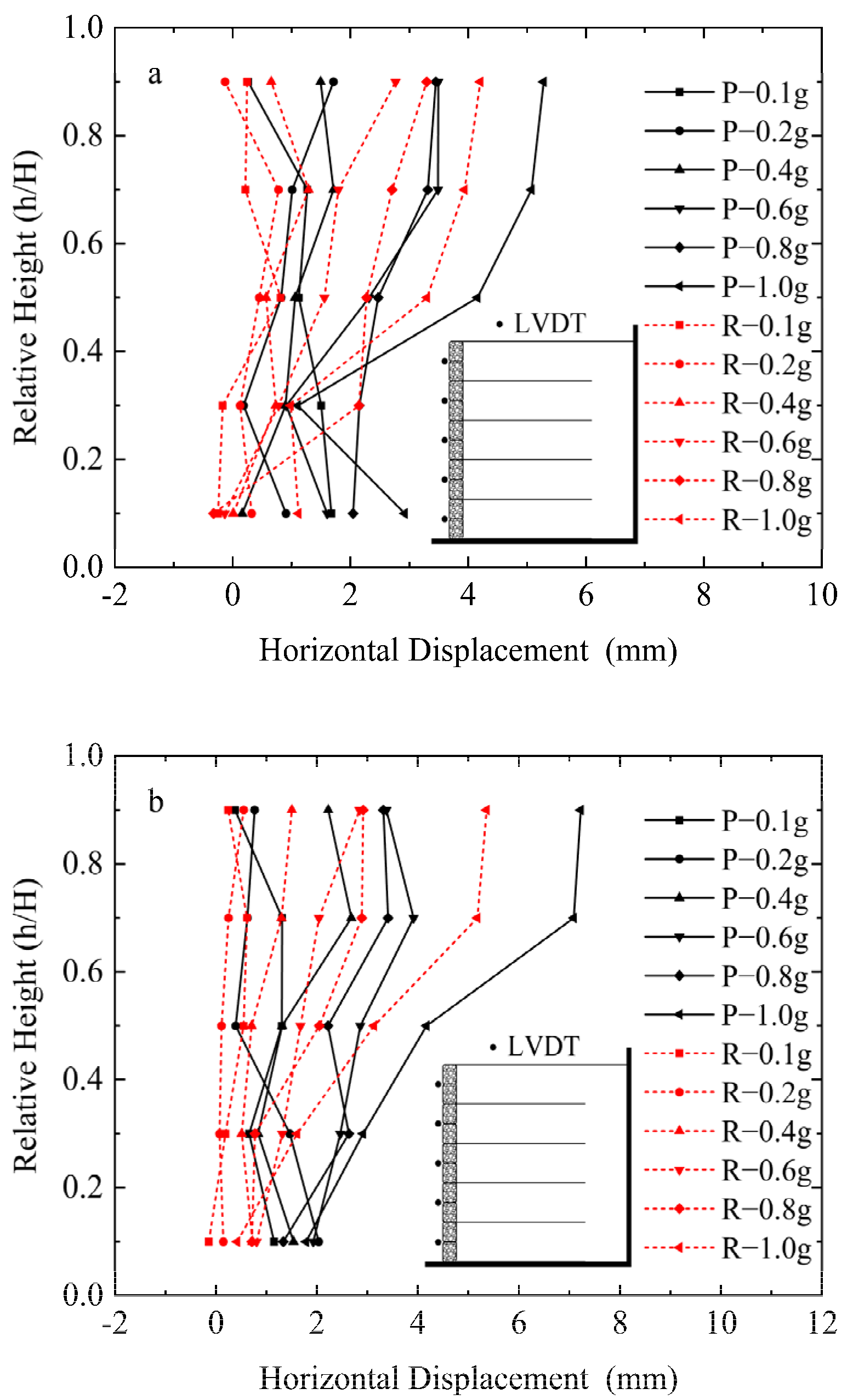
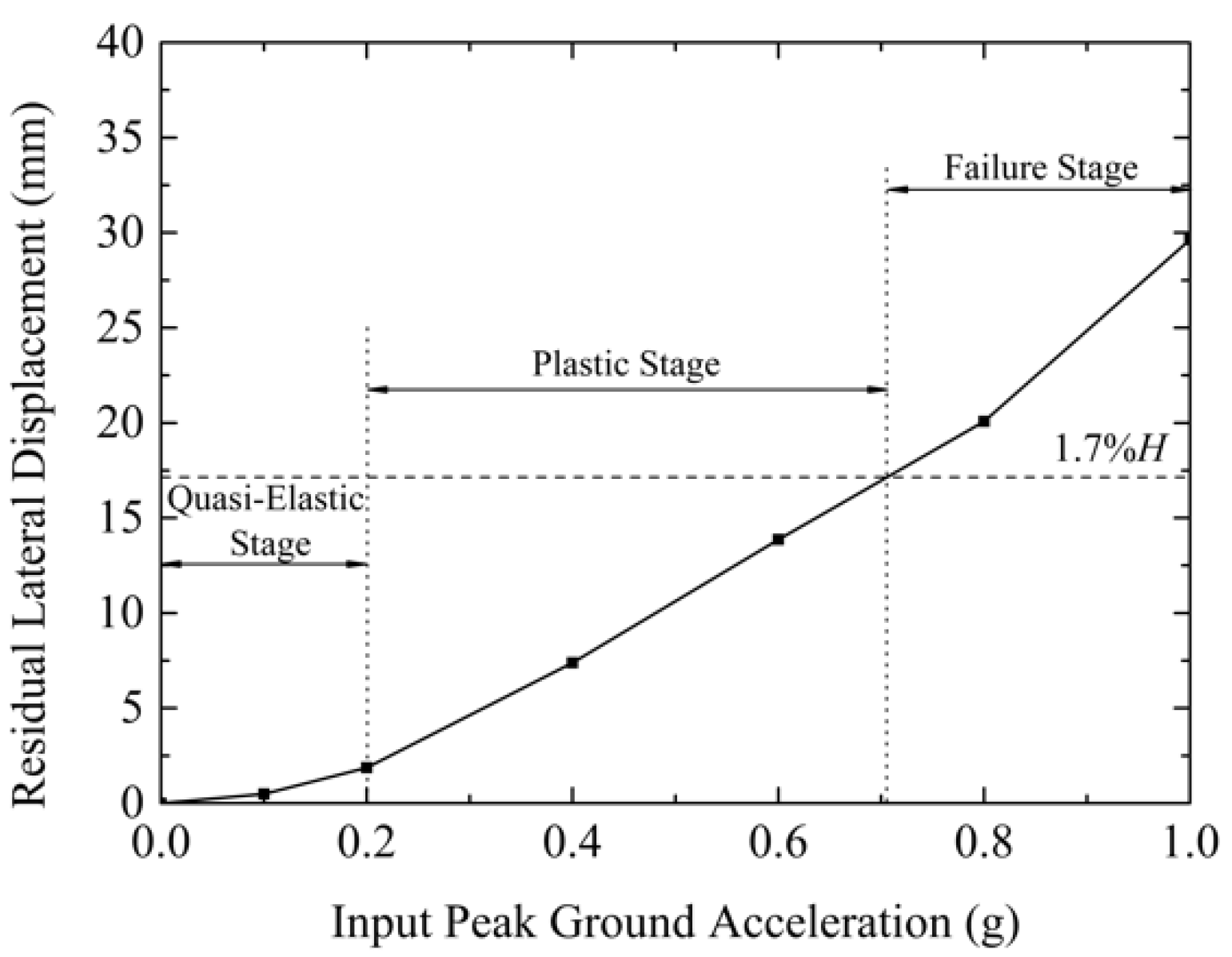
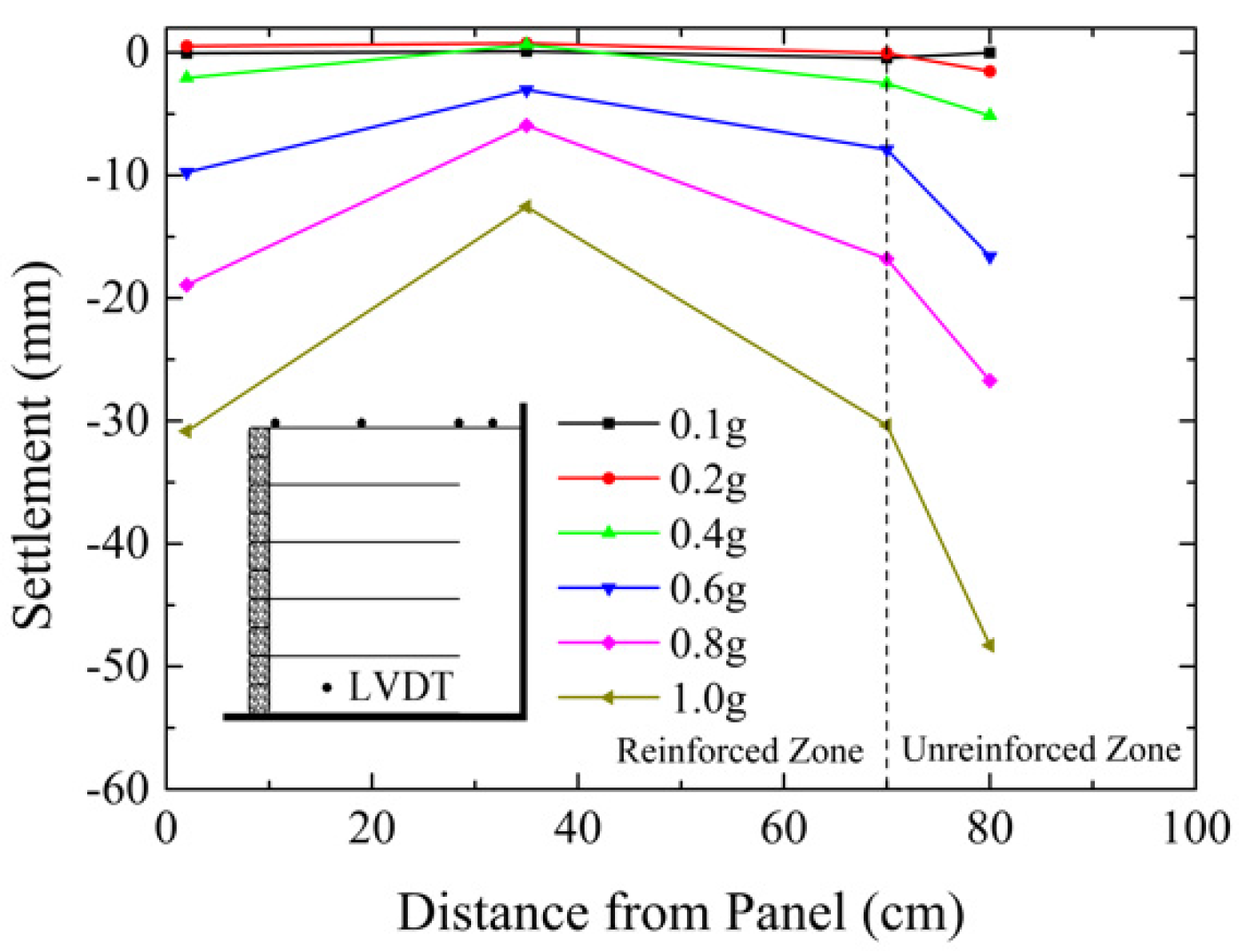
- The lateral residual displacement increases with the increase of peak acceleration, and the residual displacement at the top of the retaining wall is the largest. When HPGA is 1.0 g, the maximum cumulative residual displacement is 2.96% H, exceeding the failure index of WSDOT, and the maximum uneven settlement of sand is 3.57% H, exceeding the limit value of AASHTO. According to the WSDOT lateral displacement control index, the deformation range of the reinforced soil-retaining wall with wrapped-face is divided into three stages: quasi-elastic stage, plastic stage, and failure stage.
- (3)
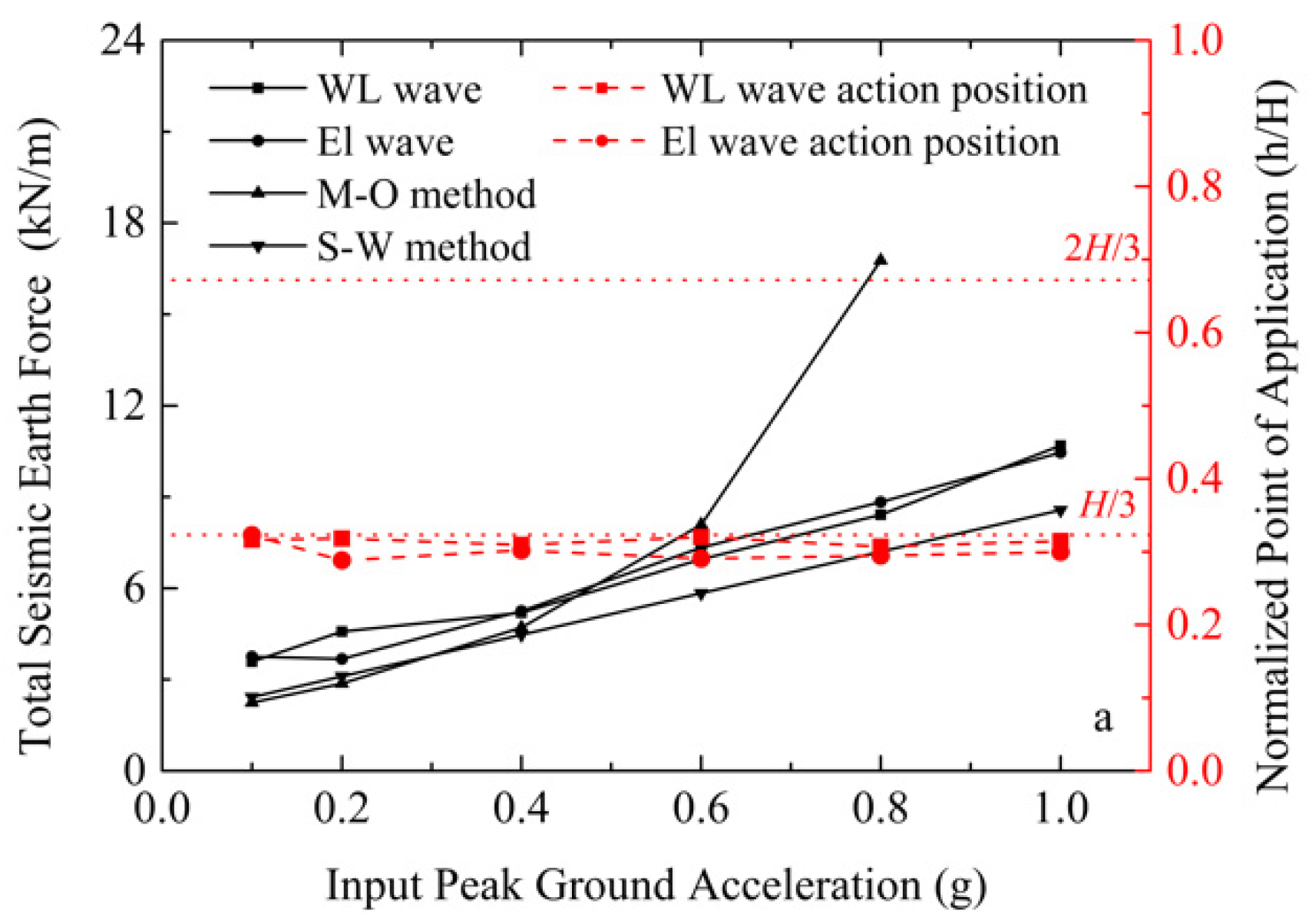
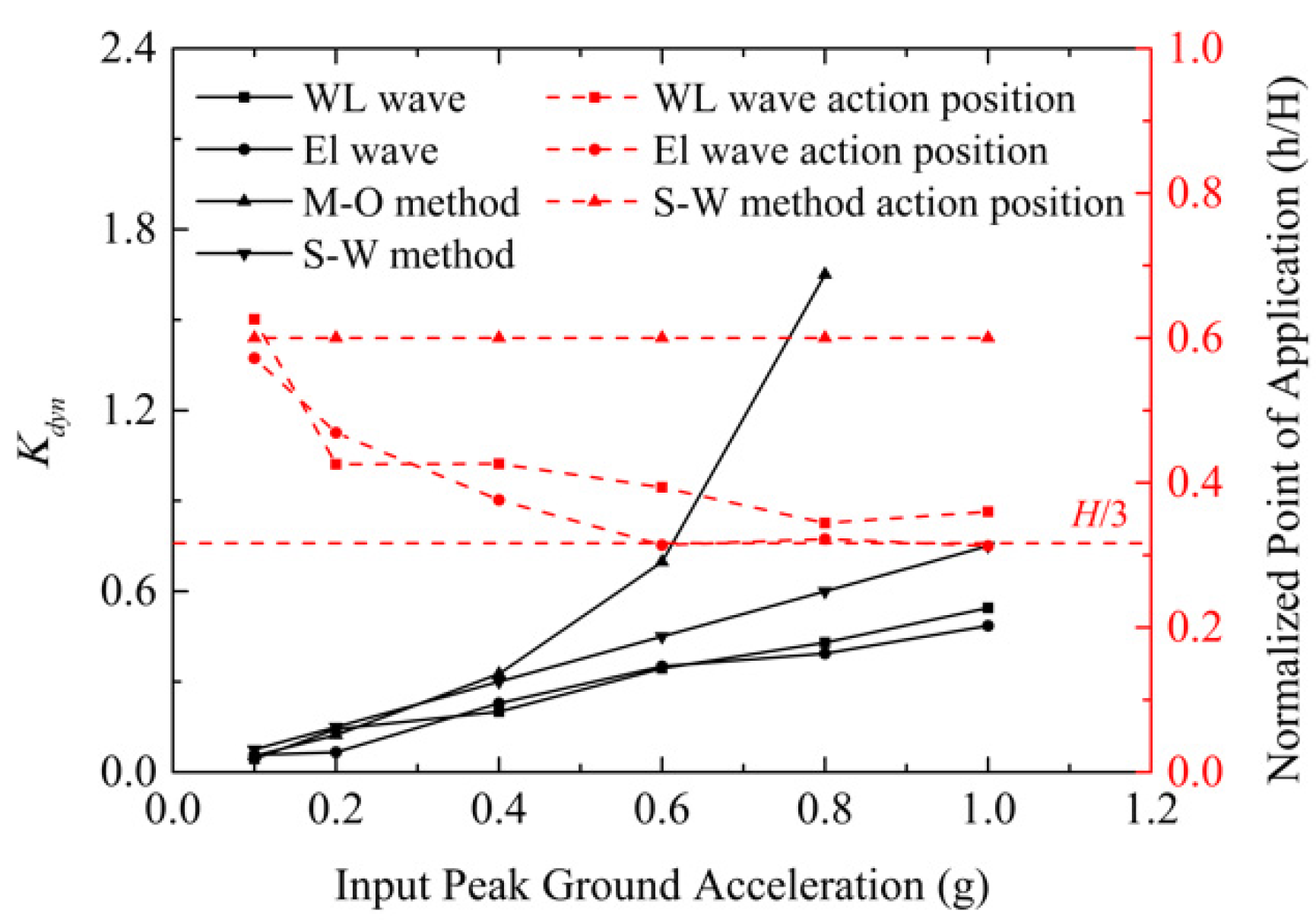
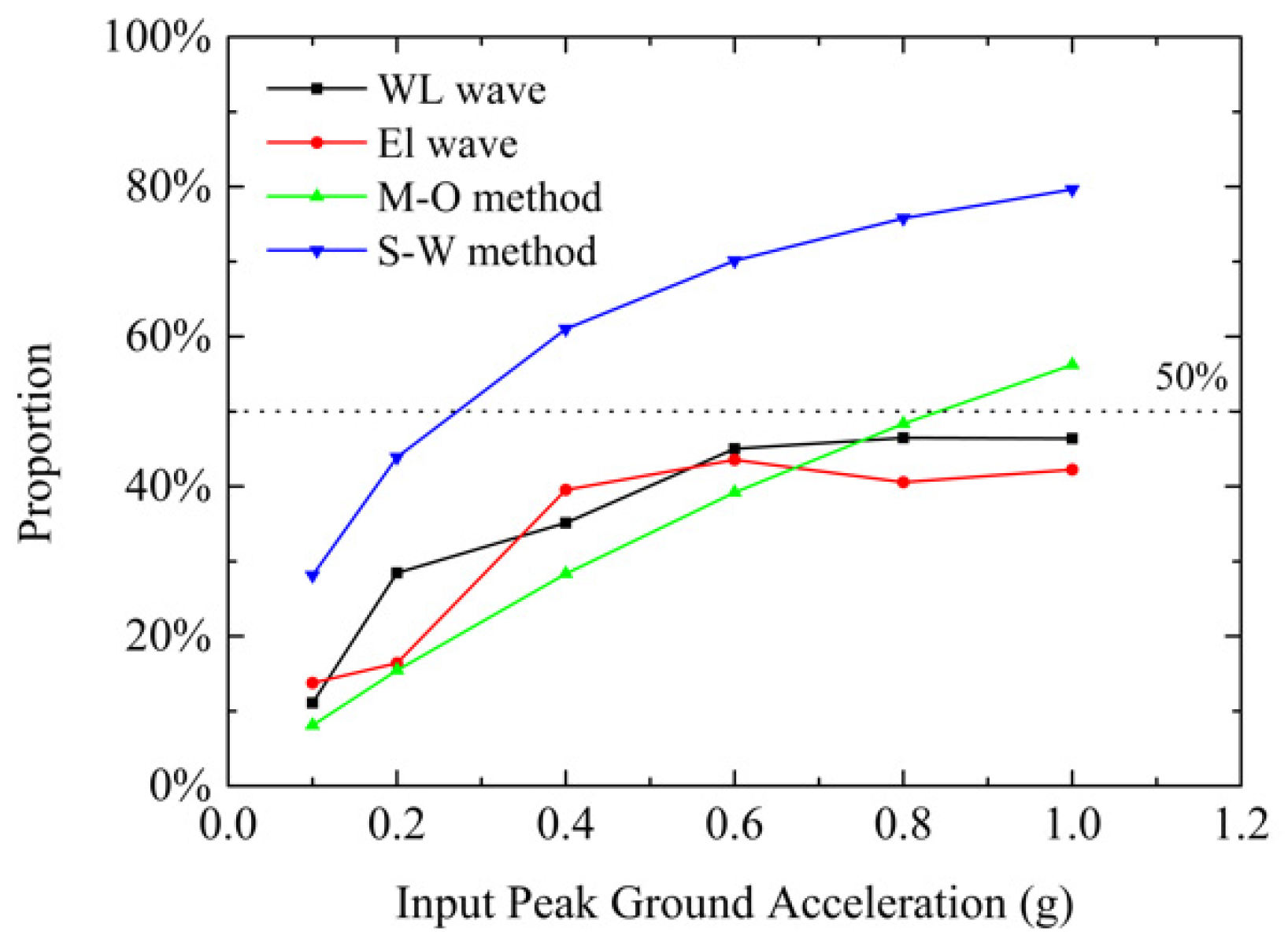
- When HPGA is 1.0 g, the measured total dynamic earth force is 10.68 kN/m, which is greater than 8.57 kN/m predicted by the S-W method, but the measured Kdyn is slightly smaller than the theoretical value of the S-W method. This is because the traditional S-W and M-O methods do not consider the reinforcement effect of geogrid on sand, resulting in a gap between the predicted value and the actual value. The calculation of earth pressure of reinforced soil-retaining walls still needs to be studied.
- (4)
- AASHTO and NCMA guidelines check the stress distribution of geosynthetics based on the limit equilibrium theory, allowable stress, and safety factor. This method is designed for the limit working state of retaining walls, it is considered that the load and resistance are in the limit state, and it is assumed that all reinforcements can reach the same stress state, which will lead to conservative results. The measured maximum value is 0.189 kN/m, less than the predicted values of the two guidelines.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Shi, M.; Wang, Z.; Yang, G.; Li, D. Calculation and evaluation of carbon emission from different types of retaining structures. Railw. Investig. Surv. 2020, 46, 41–48. [Google Scholar]
- Liu, Z. Test Study and Numerical Analysis on the Static and Dynamic Characteristics of Eco-Reinforced Earth Retaining Wall. Ph.D. Thesis, Central South University, Changsha, China, 2012. [Google Scholar]
- Yang, G. Study on Horizontal Deformation of Geogrid Reinforced Soil Retaining Wall. Ph.D. Thesis, Beijing Jiaotong University, Beijing, China, 2005. [Google Scholar]
- Wang, A. Application of Three Dimensional Drainage Flexible and Ecological Reinforced Construction in High-speed Railway Station Roadbed. In Advanced Materials Research; Trans Tech Publications Ltd.: Freienbach, Switzerland, 2012. [Google Scholar]
- Kazimierowicz-Frankowska, K. A case study of a geosynthetic reinforced wall with wrap-around facing. Geotext. Geomembr. 2005, 23, 107–115. [Google Scholar] [CrossRef]
- Wang, Z. Application of Reverse Geogrid Reinforced Soil Retaining Wall in High Retaining Wall Substation in Mountain Area. China Hyd. Elect. 2008, 6, 48–52. [Google Scholar]
- Koseki, J. Use of geosynthetics to improve seismic performance of earth structures. Geotext. Geomembr. 2012, 34, 51–68. [Google Scholar] [CrossRef]
- Krishna, A.M.; Latha, G.M. Modeling the dynamic response of wrap-faced reinforced soil retaining walls. Int. J. Geomech. 2012, 12, 439–450. [Google Scholar] [CrossRef]
- Murali Krishna, A.; Madhavi Latha, G. Seismic response of wrap-faced reinforced soil-retaining wall models using shaking table tests. Geosynth. Int. 2007, 14, 355–364. [Google Scholar] [CrossRef]
- Sakaguchi, M. A Study of the Seismic Behavior of Geosynthetic Reinforced Walls in Japan. Geosynth. Int. 1996, 3, 13–30. [Google Scholar] [CrossRef]
- Ramakrishnan, S.; Budhu, M.; Britto, A. Laboratory Seismic Tests of Geotextile Wrap-Faced and Geotextile- Reinforced Segmental Retaining Walls. Geosynth. Int. 1998, 5, 55–71. [Google Scholar] [CrossRef]
- Huang, C.C. Seismic responses of vertical-faced wrap-around reinforced soil walls. Geosynth. Int. 2019, 26, 146–163. [Google Scholar] [CrossRef]
- Nova-Roessig, L. Centrifuge Studies of the Seismic Response of Reinforced Soil Slopes. Ph.D. Thesis, University of California, Los Angeles, CA, USA, 1999. [Google Scholar]
- Nova-Roessig, L.; Sitar, N. Centrifuge Model Studies of the Seismic Response of Reinforced Soil Slopes. J. Geotech. Geoenviron. 2006, 132, 380–400. [Google Scholar] [CrossRef]
- Yang, K.H.; Hung, W.Y.; Kencana, E.Y. Acceleration-Amplified Responses of Geosynthetic-Reinforced Soil Structures with a Wide Range of Input Ground Accelerations. In Proceedings of the Geo-Congress, San Diego, CA, USA, 3–7 March 2013. [Google Scholar]
- Zhu, H.W.; Yao, L.K.; Liu, Z.S. Analysis of deformation characteristics of flexible retaining wall under earthquake. Chin. J. Rock. Mech. Eng. 2012, 31, 2829–2838. [Google Scholar]
- Duan, Z.C. Experimental Study on Seismic Characteristics of Encapsulated Reinforced Soil Retaining Wall. Master’s Thesis, Southwest Jiaotong University, Chengdu, China, 2011. [Google Scholar]
- Wang, L.M.; Xia, K.; Liu, K.; Wang, Q.; Jia, P.; Chai, S.F. A Review of Research Trends and Progress in Geotechnical Earthquake Engineering: The 16h European Conference on Earthquake Engineering. China Earthq. Eng. J. 2018, 40, 1133–1152. [Google Scholar]
- Li, S.H. Dynamic Response of Reinforced Soil Retaining Walls and Seismic Design Methods. Ph.D. Thesis, Institute of Engineering Mechanics, China Earthquake Administration, Harbin, China, 2021. [Google Scholar]
- Xue, J.; Aloisio, A.; Lin, Y.; Fragiacomo, M.; Briseghella, B. Optimum design of piles with pre-hole filled with high-damping material: Experimental tests and analytical modeling. Soil Dyn. Earthq. Eng. 2021, 151, 106995. [Google Scholar] [CrossRef]
- Fiorentino, G.; Cengiz, C.; De Luca, F.; Mylonakis, G.; Karamitros, D.; Dietz, M.; Nuti, C. Integral abutment bridges: Investigation of seismic soil-structure interaction effects by shaking table testing. Earthq. Eng. Struct. Dyn. 2021, 50, 1517–1538. [Google Scholar] [CrossRef]
- Sabermahani, M.; Ghalandarzadeh, A.; Fakher, A. Experimental study on seismic deformation modes of reinforced-soil walls. Geotext. Geomembr. 2009, 27, 121–136. [Google Scholar] [CrossRef]
- Eftekhari, Z.; Panah, A.K. 1-g shaking table investigation on seismic performance of polymeric-strip reinforced-soil retaining walls built on rock slopes with limited reinforced zone. Soil Dyn. Earthq. Eng. 2021, 147, 106758. [Google Scholar] [CrossRef]
- ASTM D6637; Standard Test Method for Determining Tensile Properties of Geogrids by the Single or Multi-rib Tensile Method. American Society of Testing Materials: West Conshohocken, PA, USA, 2015.
- Viswanadham, B.; Konig, D. Studies on scaling and instrumentation of a geogrid. Geotext. Geomembr. 2004, 22, 307–328. [Google Scholar] [CrossRef]
- El-Emam, M.M.; Bathurst, R.J. Facing contribution to seismic response of reduced-scale reinforced soil walls. Geosynth. Int. 2005, 12, 215–238. [Google Scholar] [CrossRef]
- Cai, X.G.; Li, S.H.; Xu, H.L.; Jing, L.P.; Huang, X.; Zhu, C. Shaking Table Study on the Seismic Performance of Geogrid Reinforced Soil Retaining Wall. Adv. Civ. Eng. 2021, 2021, 6668713.28. [Google Scholar] [CrossRef]
- Koseki, J.; Munaf, Y.; Tatsuoka, F.; Tateyama, M.; Kojima, K.; Sato, T. Shaking and Tilt Table Tests of Geosynthetic-Reinforced Soil and Conventional-Type Retaining Walls. Geosynth. Int. 1998, 5, 73–96. [Google Scholar] [CrossRef]
- Li, S.H.; Cai, X.G.; Jing, L.P.; Xu, H.L.; Huang, X.; Zhu, C. Lateral displacement control of modular-block reinforced soil retaining walls under horizontal seismic loading. Soil Dyn. Earthq. Eng. 2020, 141, 106485. [Google Scholar] [CrossRef]
- El-Emam, M.M.; Bathurst, R.J. Influence of reinforcement parameters on the seismic response of reduced-scale reinforced soil retaining walls. Geotext. Geomembr. 2007, 25, 33–49. [Google Scholar] [CrossRef]
- Yünkül, K.; Gürbüz, A. Shaking table study on seismic behavior of MSE wall with inclined backfill soils reinforced by polymeric geostrips. Geotext. Geomembr. 2022, 50, 116–136. [Google Scholar] [CrossRef]
- Xu, P.; Hatami, K.; Jiang, G. Shaking table study on the influence of ground motion frequency on the performance of MSE walls. Soil Dyn. Earthq. Eng. 2021, 142, 106585. [Google Scholar] [CrossRef]
- Athanasopoulos-Zekkos, A.; Vlachakis, V.S.; Athanasopoulos, G.A. Phasing issues in the seismic response of yielding, gravity-type earth retaining walls—Overview and results from a FEM study. Soil Dyn. Earthq. Eng. 2013, 55, 59–70. [Google Scholar] [CrossRef]
- Jo, S.B.; Ha, J.G.; Yoo, M.; Choo, Y.W.; Kim, D.S. Seismic behavior of an inverted T-shape flexible retaining wall via dynamic centrifuge tests. Bull. Earthq. Eng. 2014, 12, 961–980. [Google Scholar] [CrossRef]
- Bathurst, R.J.; Cai, Z. Pseudo-Static Seismic Analysis of Geosynthetic-Reinforced Segmental Retaining Walls. Geosynth. Int. 1995, 2, 787–830. [Google Scholar] [CrossRef]
- Wilson, P.; Elgamal, A. Shake table lateral earth pressure testing with dense c-phi backfill. Soil Dyn. Earthq. Eng. 2015, 71, 13–26. [Google Scholar] [CrossRef]
- Niu, X.D.; Yang, G.Q.; Wang, H.; Ding, S.; Feng, F. Field tests on structural properties of reinforced retaining walls with different panels. Rock Soil Mech. 2021, 42, 245–254. [Google Scholar]
- Jamnani, A.R.; Yazdandoust, M.; Sabermahani, M. Effect of a two-tiered configuration on the seismic behavior of reinforced soil walls. Geosynth. Int. 2022, in press. [CrossRef]
- Ren, F.F.; Zhang, F.; Xu, C.; Wang, G. Seismic evaluation of reinforced-soil segmental retaining walls. Geotext. Geomembr. 2016, 44, 604–614. [Google Scholar] [CrossRef]
- El-Emam, M.M.; Bathurst, R.J. Experimental Design, Instrumentation and Interpretation of Reinforced Soil Wall Response Using a Shaking Table. Int. J. Phys. Model. Geotech. 2004, 4, 13–32. [Google Scholar]
- Kilic, I.E.; Cengiz, C.; Edincliler, A.; Guler, E. Seismic behavior of geosynthetic-reinforced retaining walls backfilled with cohesive soil. Geotext. Geomembr. 2021, 49, 1256–1269. [Google Scholar] [CrossRef]
- Sizkow, S.F.; Shamy, U.E. Discrete-Element Method Simulations of the Seismic Response of Flexible Retaining Walls. J. Geotech. Geoenviron. 2021, 147, 04020157. [Google Scholar] [CrossRef]
- Liu, S.H.; Jia, F.; Chen, X.L.; Li, L.J. Experimental study on seismic response of soilbags-built retaining wall. Geotext. Geomembr. 2020, 48, 603–613. [Google Scholar] [CrossRef]
- NCMA TR 127B; Design Manual for Segmental Retaining Walls. National Concrete Masonry Association: Herndon, VA, USA, 2012.
- AASHTO LRFDUS-8; Bridge Design Specifications. American Association of State Highway and Transportation Officials: Washington, DC, USA, 2017.



| Parameter | Unit | Scale Factor (Prototype/Model) | Scale Factor Used in This Study (Prototype/Model) |
|---|---|---|---|
| Length | m | N * | 3 |
| Elastic modulus | kPa | 1 | 1 |
| Density | Kg/m3 | 1 | 1 |
| Stress | kPa | 1 | 1 |
| Time | s | N0.5 | 1.73 |
| Velocity | m/s | N0.5 | 1.73 |
| Acceleration | g | 1 | 1 |
| Gravity | g | 1 | 1 |
| Frequency | Hz | N−0.5 | 0.58 |
| Case Number | Input Wave | PGA/g | Case Code |
|---|---|---|---|
| 1, 2 | WL, El | 0.1 | WL 0.1 g, El 0.1 g |
| 3, 4 | WL, El | 0.2 | WL 0.2 g, El 0.2 g |
| 5, 6 | WL, El | 0.4 | WL 0.4 g, El 0.4 g |
| 7, 8 | WL, El | 0.6 | WL 0.6 g, El 0.6 g |
| 9, 10 | WL, El | 0.8 | WL 0.8 g, El 0.8 g |
| 11, 12 | WL, El | 1.0 | WL 1.0 g, El 1.0 g |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xu, H.; Cai, X.; Wang, H.; Li, S.; Huang, X.; Zhang, S. Analysis of the Working Response Mechanism of Wrapped Face Reinforced Soil Retaining Wall under Strong Vibration. Sustainability 2022, 14, 9741. https://doi.org/10.3390/su14159741
Xu H, Cai X, Wang H, Li S, Huang X, Zhang S. Analysis of the Working Response Mechanism of Wrapped Face Reinforced Soil Retaining Wall under Strong Vibration. Sustainability. 2022; 14(15):9741. https://doi.org/10.3390/su14159741
Chicago/Turabian StyleXu, Honglu, Xiaoguang Cai, Haiyun Wang, Sihan Li, Xin Huang, and Shaoqiu Zhang. 2022. "Analysis of the Working Response Mechanism of Wrapped Face Reinforced Soil Retaining Wall under Strong Vibration" Sustainability 14, no. 15: 9741. https://doi.org/10.3390/su14159741
APA StyleXu, H., Cai, X., Wang, H., Li, S., Huang, X., & Zhang, S. (2022). Analysis of the Working Response Mechanism of Wrapped Face Reinforced Soil Retaining Wall under Strong Vibration. Sustainability, 14(15), 9741. https://doi.org/10.3390/su14159741






