Optimization of Ramp Locations along Freeways: A Dynamic Programming Approach
Abstract
1. Introduction
2. Problem Statement and Model Development
2.1. Total Travel Cost
2.1.1. Access Cost
2.1.2. Freeway Travel Cost
2.2. Construction Cost
2.3. Safety Issue
2.4. Model Development
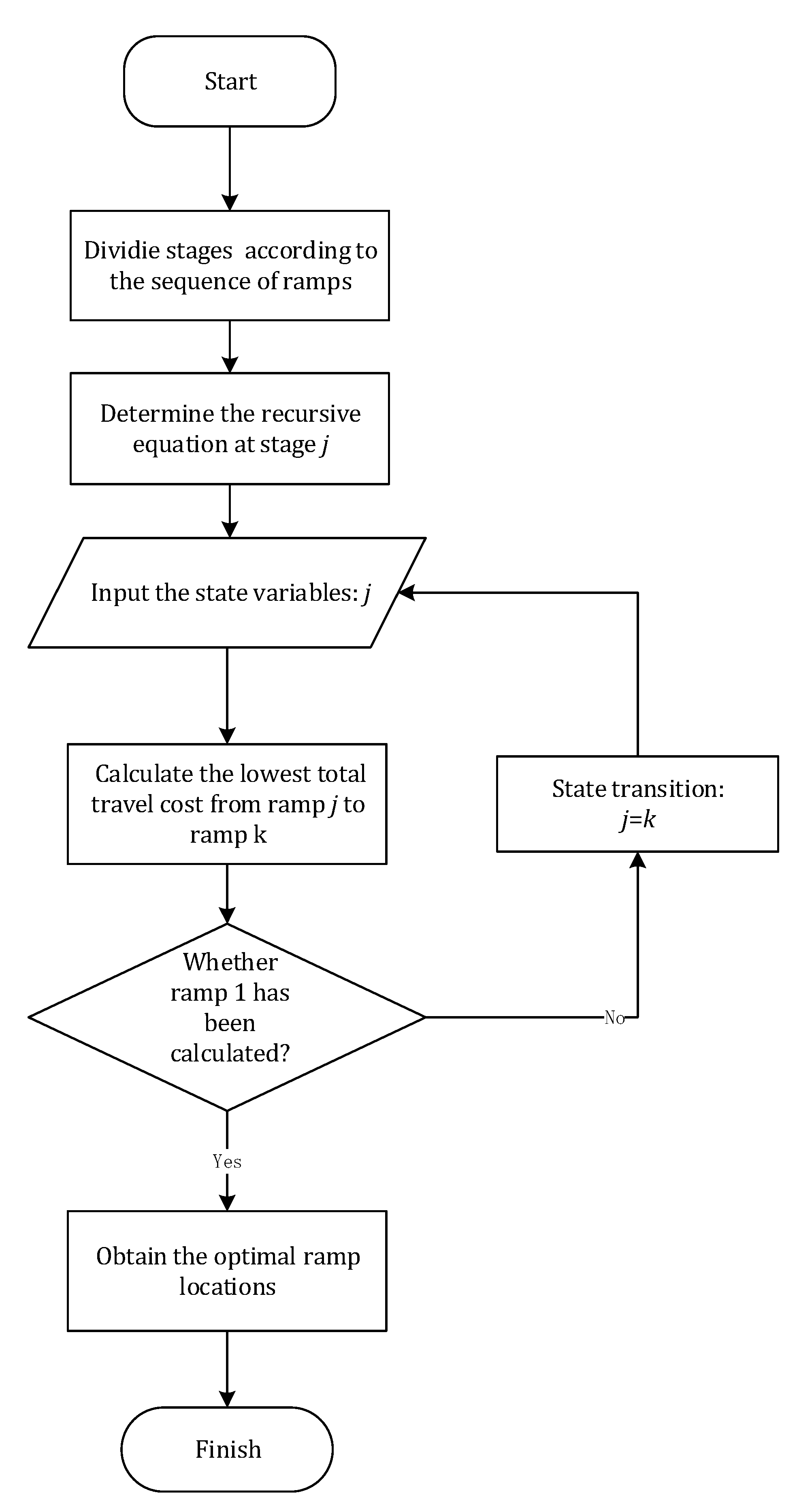
3. Dynamic Programming Approach
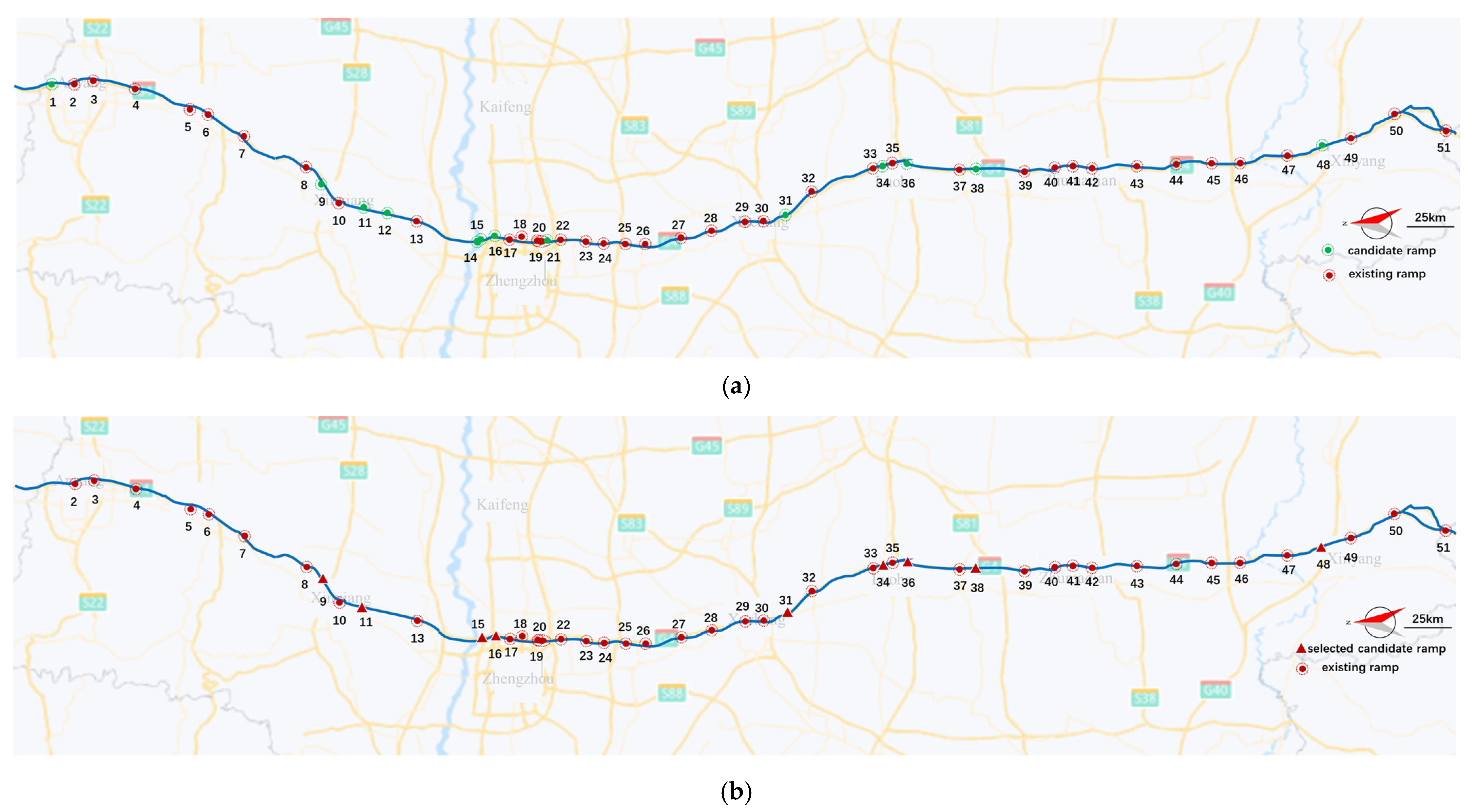
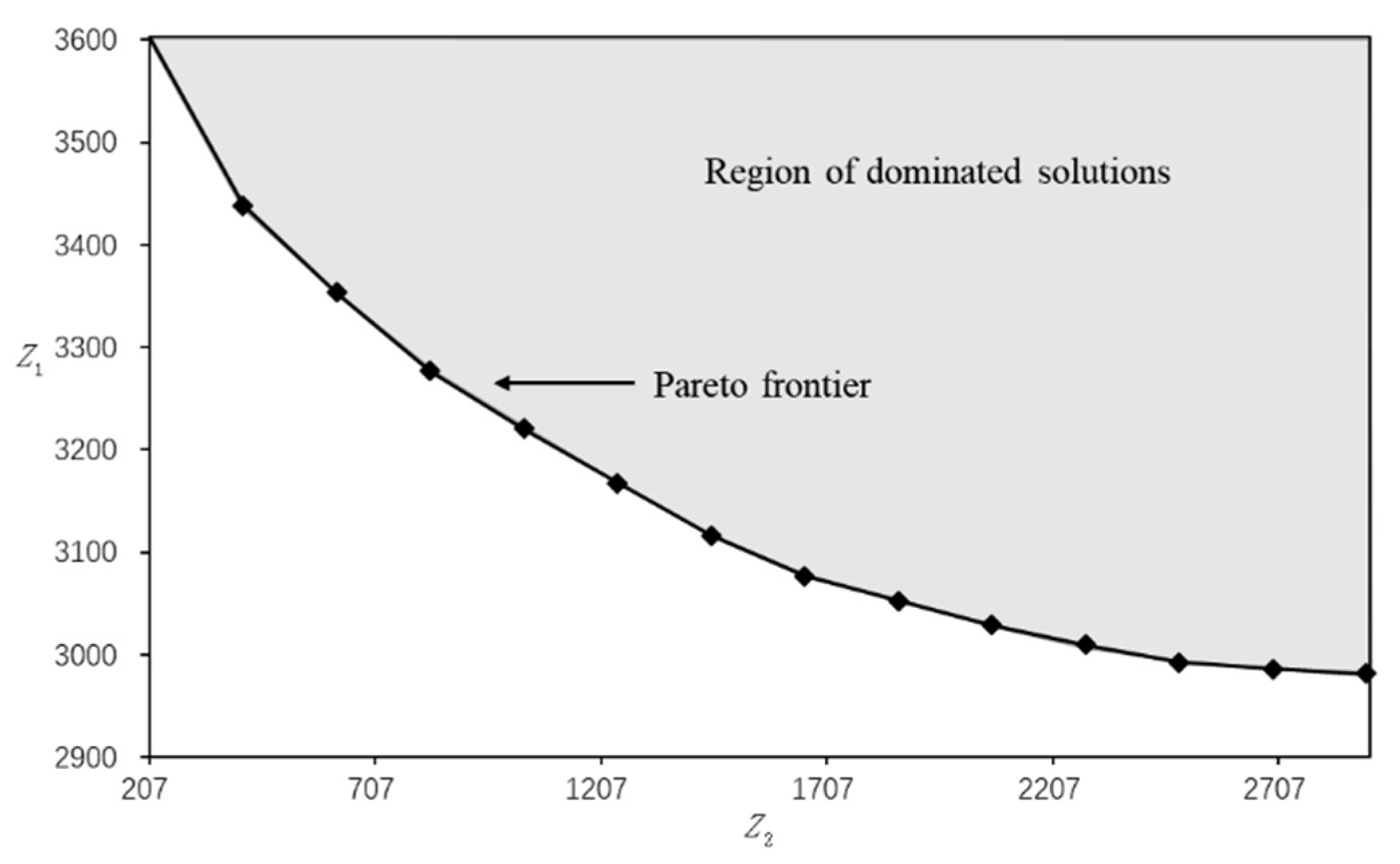
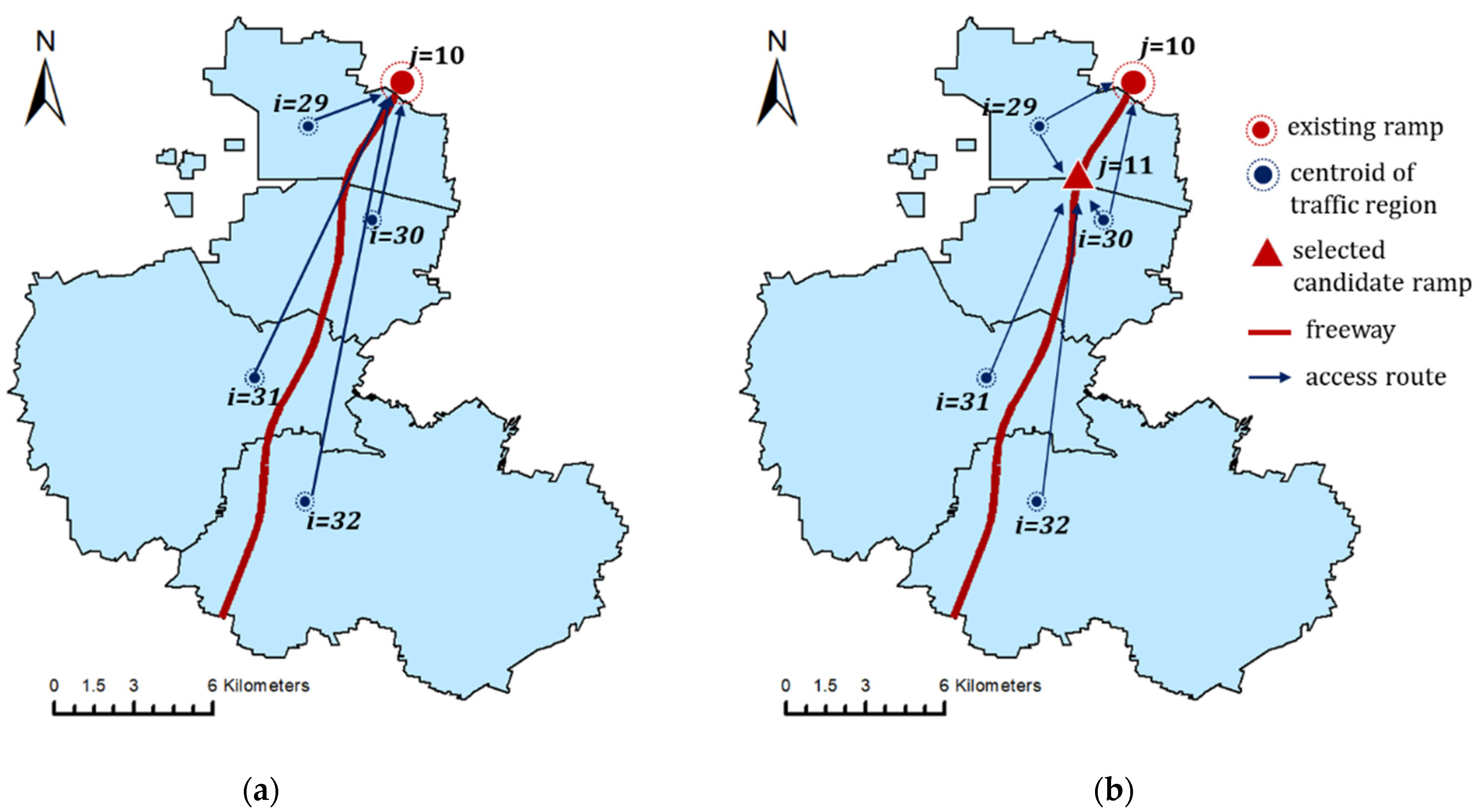
4. Case Study
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Blair, J.M.; Ijawka, K.D. Evaluating success in urban freeway planning. J. Plan. Educ. Res. 2001, 21, 40–51. [Google Scholar] [CrossRef]
- Weber, J. Continuity and change in american urban freeway networks. J. Transp. Geogr. 2017, 58, 31–39. [Google Scholar] [CrossRef]
- Abdel-Aty, M.; Huang, Y. Exploratory spatial analysis of expressway ramps and its effect on route choice. J. Transp. Eng. 2004, 130, 104–112. [Google Scholar] [CrossRef]
- Hunter, M.; Machemehl, R.; Tsyganov, A. Operational evaluation of freeway ramp design. Transp. Res. Rec. 2001, 1751, 90–100. [Google Scholar] [CrossRef]
- Lederer Paul, R.; Cohn Louis, F.; Guensler, R.; Harris Roswell, A. Effect of on-ramp geometric and operational factors on vehicle activity. J. Transp. Eng. 2005, 131, 18–26. [Google Scholar] [CrossRef]
- Park, B.-J.; Fitzpatrick, K.; Lord, D. Evaluating the effects of freeway design elements on safety. Transp. Res. Rec. 2010, 2195, 58–69. [Google Scholar] [CrossRef]
- Bhouri, N.; Haj-Salem, H.; Kauppila, J. Isolated versus coordinated ramp metering: Field evaluation results of travel time reliability and traffic impact. Transp. Res. Part C Emerg. Technol. 2013, 28, 155–167. [Google Scholar] [CrossRef]
- Pasquale, C.; Sacone, S.; Siri, S.; De Schutter, B. A multi-class model-based control scheme for reducing congestion and emissions in freeway networks by combining ramp metering and route guidance. Transp. Res. Part C Emerg. Technol. 2017, 80, 384–408. [Google Scholar] [CrossRef]
- Fitzpatrick, K.; Porter, R.J.; Pesti, G.; Chu, C.-L.; Park, E.S.; Le, T. Guidelines for Spacing between Freeway Ramps. Transp. Res. Rec. J. Transp. Res. Board 2011, 2262, 3–12. [Google Scholar] [CrossRef]
- Van Beinum, A.; Hovenga, M.; Knoop, V.; Farah, H.; Wegman, F.; Hoogendoorn, S. Macroscopic traffic flow changes around ramps. Transp. A: Transp. Sci. 2017, 14, 598–614. [Google Scholar] [CrossRef]
- National Research Council (U.S.). HCM 2010: Highway Capacity Manual, 5th ed.; Transportation Research Board: Washington, DC, USA, 2010. [Google Scholar]
- American Association of State Highway and Transportation Officials (AASHTO). A Policy on Geometric Design of Highways and Streets; AASHTO: Washington, DC, USA, 2001. [Google Scholar]
- Forschungsgesellschaft für Straßen- und Verkehrswesen (FGSV). Richtlinie für die Anlage von Autobahnen (RAA); FGSV: Köln, Germany, 2008. [Google Scholar]
- Pei, Y.; Jin, Y.; Wang, Y. A calculation method for minimum spacing between entrances and exits on expressways considering number of lanes on mainline and ramp speed. J. Transp. Inf. Saf. 2019, 37, 59–66. [Google Scholar]
- Golob, T.F.; Recker, W.W.; Alvarez, V.M. Freeway safety as a function of traffic flow. Accid. Anal. Prev. 2004, 36, 933–946. [Google Scholar] [CrossRef]
- Shea, M.S.; Le, T.Q.; Porter, R.J. Combined crash frequency–crash severity evaluation of geometric design decisions. Transp. Res. Rec. 2015, 2521, 54–63. [Google Scholar] [CrossRef]
- Le, T.Q.; Porter, R.J. Safety evaluation of geometric design criteria for spacing of entrance–exit ramp sequence and use of auxiliary lanes. Transp. Res. Rec. 2012, 2309, 12–20. [Google Scholar] [CrossRef]
- Liu, P.; Chen, H.; Lu Jian, J.; Cao, B. How lane arrangements on freeway mainlines and ramps affect safety of freeways with closely spaced entrance and exit ramps. J. Transp. Eng. 2010, 136, 614–622. [Google Scholar] [CrossRef]
- Guo, Y. Effects of ramp spacing on freeway mainline crashes. Appl. Mech. Mater. 2011, 97-98, 95–99. [Google Scholar] [CrossRef]
- Chen, S.-K.; Mao, B.-H.; Liu, S.; Sun, Q.-X.; Wei, W.; Zhan, L.-X. Computer-aided analysis and evaluation on ramp spacing along urban expressways. Transp. Res. Part C Emerg. Technol. 2013, 36, 381–393. [Google Scholar] [CrossRef]
- Yan, Y.; Guo, T.; Wang, D. Dynamic accessibility analysis of urban road-to-freeway interchanges based on navigation map paths. Sustainability 2021, 13, 372. [Google Scholar] [CrossRef]
- Akinradewo, O.; Aigbavboa, C.; Oke, A.; Coffie, H. Modelling a cost profile for road projects. Can. J. Civ. Eng. 2021, 48, 366–376. [Google Scholar] [CrossRef]
- Creedy Garry, D.; Skitmore, M.; Wong Johnny, K.W. Evaluation of risk factors leading to cost overrun in delivery of highway construction projects. J. Constr. Eng. Manag. 2010, 136, 528–537. [Google Scholar] [CrossRef]
- Liu, S.; Niu, C.; Liu, S. Study on the interchange hinge location problems based on fuzzy analytic hierarchy process method. Traffic Transp. 2009, z1, 25–28. [Google Scholar]
- Liu, F.; Li, Y.; Li, P.; Mo, Z. Comprehensive evaluation of the connection between entrance and exit of expressway and urban road network. Highway 2018, 63, 187–193. [Google Scholar]
- Wang, H.; Zhou, W. Research on freeway jieke structure and attributes. J. Highw. Transp. Res. Dev. 2011, 28, 101–105. [Google Scholar]
- Deng, K. A bi-level optimization model for freeway entrance/exit site selection. J. Hunan City Univ. Nat. Sci. 2011, 20, 20–22. [Google Scholar]
- Yang, S.; Liu, X.; Wu, Y.-J.; Woolschlager, J.; Coffin, S.L. Can freeway traffic volume information facilitate urban accessibility assessment?: Case study of the city of st. Louis. J. Transp. Geogr. 2015, 44, 65–75. [Google Scholar] [CrossRef]
- Chen, Z.; Jin, F.; Yang, Y.; Wang, W. Distance-decay pattern and spatial differentiation of expressway flow: An empirical study using data of expressway toll station in fujian province. Prog. Geogr. 2018, 37, 1086–1095. [Google Scholar]
- Cui, H.; Ren, Z.; Zhu, M.; Wang, Z.; He, M. Analysis and application of highway travel distance characteristics. Sci. Technol. Eng. 2020, 20, 3323–3329. [Google Scholar]
- Jolovic, D.; Stevanovic, A.; Sajjadi, S.; Martin, P.T. Assessment of level-of-service for freeway segments using hcm and microsimulation methods. Transp. Res. Procedia 2016, 15, 403–416. [Google Scholar] [CrossRef][Green Version]
- Jin-Tae, K.; Joonhyon, K.; Myungsoon, C. Lane-changing gap acceptance model for freeway merging in simulation. Can. J. Civ. Eng. 2008, 35, 301–311. [Google Scholar]
- Yi, H.; Mulinazzi, T.E. Urban freeway on-ramps invasive influences on main-line operations. Transp. Res. Rec. 2007, 2023, 112–119. [Google Scholar] [CrossRef]
- Love, P.E.D.; Ahiaga-Dagbui, D.D.; Irani, Z. Cost overruns in transportation infrastructure projects: Sowing the seeds for a probabilistic theory of causation. Transp. Res. Part A Policy Pract. 2016, 92, 184–194. [Google Scholar] [CrossRef]
- Cassidy, M.; May, A. Proposed analytical technique for estimating capacity and level of service of major freeway weaving. Transp. Res. Rec. 1991, 1320, 99–109. [Google Scholar]
- Sulejic, D.; Jiang, R.; Sabar, N.R.; Chung, E. Optimization of lane-changing distribution for a motorway weaving segment. Transp. Res. Procedia 2017, 21, 227–239. [Google Scholar] [CrossRef]
- Diao, T. Safety on Traffic Flow Characteristics of Weaving Segments of Interchange Base On Traffic Safety. Master’s Thesis, Southeast University, Nanjing, China, 2017. [Google Scholar]
- Bellman, R. Dynamic programming. Science 1966, 153, 34–37. [Google Scholar] [CrossRef]
- Carraway, R.L.; Morin, T.L. Theory and applications of generalized dynamic programming: An overview. Comput. Math. Appl. 1988, 16, 779–788. [Google Scholar] [CrossRef][Green Version]
- Bellman, R. The theory of dynamic programming. Bull. Am. Math. Soc. 1954, 60, 503–515. [Google Scholar] [CrossRef]
- Halffmann, P.; Schäfer, L.E.; Dächert, K.; Klamroth, K.; Ruzika, S. Exact algorithms for multiobjective linear optimization problems with integer variables: A state of the art survey. J. Multi-Criteria Decis. Anal. 2022, n/a, 1–23. [Google Scholar] [CrossRef]
- Tian, X.; Niu, H. A dynamic programming approach to synchronize train timetables. Adv. Mech. Eng. 2017, 9, 1–11. [Google Scholar] [CrossRef]
- Sitarz, S. Dynamic programming with ordered structures: Theory, examples and applications. Fuzzy Sets Syst. 2010, 161, 2623–2641. [Google Scholar] [CrossRef]
- Wang, S.; Qu, X. Rural bus route design problem: Model development and case studies. KSCE J. Civ. Eng. 2014, 19, 1–5. [Google Scholar] [CrossRef]
- Chen, J.; Wang, S.; Liu, Z.; Wang, W. Design of suburban bus route for airport access. Transp. A Transp. Sci. 2017, 13, 568–589. [Google Scholar] [CrossRef]
- Karimi, M.; Sadjadi, S.J. Optimization of a multi-item inventory model for deteriorating items with capacity constraint using dynamic programming. J. Ind. Manag. Optim. 2022, 18, 1145–1160. [Google Scholar] [CrossRef]
- Ritzinger, U.; Puchinger, J.; Hartl, R.F. Dynamic programming based metaheuristics for the dial-a-ride problem. Ann. Oper. Res. 2016, 236, 341–358. [Google Scholar] [CrossRef]
- Villarreal, B.; Karwan, M.H. Multicriteria dynamic programming with an application to the integer case. J. Optim. Theory Appl. 1982, 38, 43–69. [Google Scholar] [CrossRef]
- Furth, P.G.; Rahbee, A.B. Optimal bus stop spacing through dynamic programming and geographic modeling. Transp. Res. Rec. 2000, 1731, 15–22. [Google Scholar] [CrossRef]

| Variable | Notation |
|---|---|
| Indices | |
| i | Index of traffic regions |
| j | Index of existing ramps and candidate ramps |
| g | Index of traffic regions along the freeway section between ramp j and ramp k |
| Parameters | |
| Cost of access time | |
| Cost of freeway travel time | |
| Construction cost | |
| Distance between traffic region g and ramp j | |
| Distance decay probability between traffic region g and ramp j | |
| Travel demand of travel region g | |
| Traffic demand between traffic region g and ramp j | |
| Unit value of access cost | |
| Average access speed | |
| Traffic volume between ramp j and ramp k | |
| Travel time between ramp j and ramp k | |
| Average free-flow travel speed on the freeway | |
| c | Freeway capacity |
| Travel delay existing in the location between ramp j and ramp k | |
| Critical gap acceptance for vehicles entering or exiting the ramps | |
| Average waiting interval between ramp j and ramp k | |
| Average non-gap duration between ramp j and ramp k | |
| Average vehicle arrival rate of ramp j | |
| Unit value of freeway travel cost | |
| Construction cost of ramp j | |
| Service life of freeway | |
| Number of lane-changing behaviors between ramp j and ramp k | |
| Maximum number of lane changes | |
| Spacing between ramp j and ramp k (j = 1, 2, …, N − 1) | |
| Lower limit of the spacing | |
| Sets | |
| Set of available ramp locations of traffic region g | |
| S | Set of existing ramps |
| Set of existing ramps and selected candidate ramps | |
| Variables | |
| Binary variable that equals 1 if ramp j (∉) is selected to be newly constructed ramps and 0 if otherwise | |
| j | Index of existing ramps and candidate ramps |
| k | Downstream ramp of ramp j |
| Ramp Number (j) | Service Area | ||
|---|---|---|---|
| Traffic Region Number (i) | |||
| 1 | 1 | 8 | 103 |
| 2 | 2 | 84 | |
| 3 | 5.5 | 107 | |
| 4 | 5.4 | 232 | |
| Symbol | Description | Value |
|---|---|---|
| Unit value of access cost | 10 | |
| Average access speed | 50 km/h | |
| c | Freeway capacity | 3600 pcu/h |
| Critical gap acceptance for vehicles entering or exiting the ramps | 4 s | |
| Value of freeway travel cost | 5 | |
| Construction cost of ramp j | $590,000 | |
| Service life of the freeway | 15 years |
| Existing Locations | Optimized Locations | |
|---|---|---|
| Total number of ramps | 38 | 46 |
| Average access time (h per vehicle) | 0.169 | 0.157 (7% reduction) |
| Average freeway travel time (h per vehicle) | 1.667 | 1.207 (27.6% reduction) |
| Total travel cost (USD) | 3603 | 3052 (15.3% reduction) |
| Construction cost (USD) | 2472 | 22,252 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, D.; Mo, F.; Chen, Y.; Zhang, J.; You, X. Optimization of Ramp Locations along Freeways: A Dynamic Programming Approach. Sustainability 2022, 14, 9718. https://doi.org/10.3390/su14159718
Chen D, Mo F, Chen Y, Zhang J, You X. Optimization of Ramp Locations along Freeways: A Dynamic Programming Approach. Sustainability. 2022; 14(15):9718. https://doi.org/10.3390/su14159718
Chicago/Turabian StyleChen, Dawei, Fangxu Mo, Ye Chen, Jun Zhang, and Xinyu You. 2022. "Optimization of Ramp Locations along Freeways: A Dynamic Programming Approach" Sustainability 14, no. 15: 9718. https://doi.org/10.3390/su14159718
APA StyleChen, D., Mo, F., Chen, Y., Zhang, J., & You, X. (2022). Optimization of Ramp Locations along Freeways: A Dynamic Programming Approach. Sustainability, 14(15), 9718. https://doi.org/10.3390/su14159718





