Abstract
A virtual energy storage system (VESS) logically shares a physical energy storage system among multiple units. In resource sharing, the distribution of benefits is a critical problem. As a resolution, this study proposes a fair VESS operation method for smart energy communities that involve groups of energy consumption units. First, the cost and resource fairness indices are defined as the benefit and VESS usage proportional to the investment cost, respectively. The fair VESS operation problem is formulated considering the fairness indices that could be solved optimally by applying gradient methods without additional computational burden. The simulation results using the dataset in Korea demonstrate that the proposed operation allows the fair distribution of the benefit and resource usage among units with a marginal benefit reduction of approximately 5% in relation to the VESS operation to maximize the benefit. Moreover, it is shown that the resource fairness that controls the VESS usage limits the total benefit, and the cost fairness distributes the benefit among units according to the cost contribution. Furthermore, the proposed VESS operation can manage the VESS lifetime and improve the system performance of the utility grid.
1. Introduction
1.1. Motivation
Electrification is a rapidly growing technique that addresses climate change by replacing final energy consumption with electricity [1]. It facilitates the usage of clean energy. However, increased electrification can lead to broad and significant impacts across energy systems [2]. Demand side management strategies, such as energy efficiency improvement and adaptive load control, are more economical for reducing the energy system burden than supply side management strategies, such as effective bulk generation control and unit commitment [3].
Smart energy communities (SECs) are intelligent local demand organizations formed through energy integration techniques [4]. They have dedicated energy service providers (SPs) or energy management systems (EMSs) and function to achieve their individual and collective economic, environmental, and social goals [5]. The peak-demand shaving and load-shifting of SECs provide benefits such as minimizing the electricity bills of community units and increasing grid utilization and efficiency of the utility grid [6]. The energy storage system (ESS) is an essential component for the demand management of SECs; however, its expensive cost is a limitation [7].
Recently, energy storage sharing (i.e., the virtual energy storage system (VESS)) has been introduced as a sharing economy business model [8]. It involves the logical sharing of a physical ESS in multiple units, similar to cloud data storage services, that provide benefits by allowing units to store massive amounts of data on demand in a cost-effective way [9]. The VESS provides the SEC with a cost-effective option to employ an ESS [10].
The operation of hybrid energy storage systems combining variable resources, such as ESS, PV, and wind power generations, have been researched based on fuzzy logic and fractional-order proportional-integral-derivative [11], direct reactive power control [12], and high order sliding mode control [13]. However, this study focused on the fact that VESS operation involves the sharing of one physical ESS, which is different from the use of individual ESSs that units individually install and operate. Therefore, the allocation of shared resources becomes an important issue. Particularly, fairness is a necessary condition for the continuous service participation of units [14,15]. However, conventional research on VESS operation focuses on maximizing the total benefit to units without considering fairness. By contrast, this study deals with fairness and how it should be considered in VESS operation for SECs.
1.2. Prior Works
The objective of VESS research is to effectively operate VESS resources for multiple units. Methodology based on optimization is a classical approach for VESS operation [16,17,18,19]. Zhu et al. presented a VESS model including electrical and thermal energy storages and proposed a charging/discharging VESS operation method to reduce operational costs and improve system stability [16]. The problem is formulated as a binary mixed-integer linear programming model, which is solved using the MATLAB software and CPLEX toolbox. Zhao et al. formulated a two-stage optimization problem that determines VESS investment and pricing in the first and VESS operation in the second stage [17]. They showed that upon using the VESS, the investment and usage costs of units are reduced in relation to those by the individual implementation of the ESS by each unit. Cheng et al. proposed an optimal VESS operation method to improve the operating economy of a building-integrated photovoltaic microgrid [18]. The results indicate that the operating cost is reduced by applying the VESS. Ding et al. designed a multi-stage distributional system for the VESS to address temporal uncertainties in the day-ahead economic dispatch [19], which is solved using stochastic dual programming, indicating that the VESS operation reduces the operation cost. Oh and Son proposed a VESS operation for SECs considering the usage-limited constraint rather than the capacity allocation constraint [20]. The results showed that the utilization of the VESS is related to the degree of freedom of the operation.
Game theoretical approaches have also been used for the VESS operation [21,22,23,24,25]. Tushar et al. designed a modified auction-based system for energy storage sharing, resulting in the net benefit maximization of units and the cost saving maximization of SP [21]. The auction is determined by a non-cooperative Stackelberg game formula for units and SP. Zaidi et al. introduced a VESS model based on a combinatorial auction for a small neighborhood in a community [22]. The auction is operated by applying the genetic algorithm with particle swarm optimization to maximize the social welfare of the community. Chakraborty et al. modeled an electricity consumption cost problem using a cooperative game and showed that the VESS effectively saves the cost in a cooperative manner [23]. Jo and Park proposed an energy capacity trading and operation game to minimize the energy operation cost for ESS sharing; they showed that the operation of a shared ESS can decrease the total energy operation cost and the average peak-to-peak ratio of energy [24]. Building on the work in [24], Xiao et al. proposed a VESS framework considering the storage and power capacity constraints [25]. They determined a generalized Nash equilibrium for the VESS operation using an alternating direction multiplier and the heavy ball method.
Machine-learning-based methods, particularly reinforcement leaning methods for decision making, have also been implemented for the VESS operation [26,27]. A previously reported reinforcement-learning-based VESS operation method involved the application of an expected state-action-reward-state-action approach and showed that the VESS operation is efficient to manage the renewable energy forecasting uncertainty [26]. He et al. proposed a VESS operation method in a peer-to-peer (P2P) energy market, and Q-learning is utilized to obtain the optimal pricing policy [27]. They showed that the VESS operation enhances the economic benefits by increasing the P2P energy transaction.
From previous studies, the benefits of the VESS operation are summarized as follows: (1) According to economies of scale, the VESS reduces the cost barrier of ESS usage. It enhances the economic benefit of units that use the VESS service. (2) According to the multi-user diversity of units, the operation room of the VESS is larger than those of individual ESSs. The VESS operation improves system utilization. However, these studies are considered only in terms of total cost/benefit or social welfare. In particular, these do not touch on the fairness issues, as summarized in Table 1.

Table 1.
Summary of VESS research.
A few studies have discussed fairness in SECs [28,29,30]. Oh and Son considered fairness as equally distributing economic benefits among energy transaction pairs in a P2P energy transaction system for an SEC [28]. Yang et al. defined fairness as the minimization of the minimal dissatisfaction of all community units [29]. However, these studies discuss the effects of fairness only numerically. Dai et al. proposed a biobjective optimization approach considering effectiveness and fairness [30]. However, they assumed a case wherein energy storage is shared between two units only. The present study overcomes the limitations of existing studies by defining fairness and elucidating how it should be considered for VESS operation.
1.3. Contributions
This study focuses on a fair VESS operation method for an SEC considering fairness. The main contributions of this study are summarized as follows:
- Definition of the fairness index for a VESS operation: Fairness refers to the problem of dividing a set of resources among several units. No single principle is universally accepted; however, the fundamental theory suggests that resources should be allocated in proportion to some pre-existing claims [31]. In this study, the fairness of costs and resources was considered. Basically, fairness is defined according to the contribution of units. Cost fairness is defined as the reward of a unit given in proportion to the invested cost of the unit, and resource fairness is defined as the VESS usage of a unit in proportion to its allocated VESS capacity. Using these definitions, a fairness index that can be used for VESS operation is presented in Section 2.3.
- Fair VESS operation for the SEC: Two VESS operation problems for an SEC are formulated by considering fairness in Section 2.4. The first problem (P1) involves maximizing social welfare under VESS operation and resource fairness constraints. In P1, the resource fairness constraint prevents the VESS operation from being biased toward a specific unit; thus, welfare is softly distributed among the units. The second problem (P2) involves maximizing the minimum bound of the cost fairness index with the VESS operation constraints and resource and cost fairness constraints. In this case, welfare among units is distributed hardly, owing to the cost fairness constraint. Moreover, by maximizing the minimum bound, social welfare is increased while ensuring cost fairness among units. These two fair VESS operation problems satisfy convexity; thus, a solution can be obtained using the iterative method.
- Experimental results and discussions about a real data set: The performance of the proposed VESS operation is verified using a real data set measured in Korea. To confirm the impact in terms of SECs, the total benefit, cost, and resource fairness indices were measured by varying the VESS capacity; this is described in Section 3.2. In order to demonstrate the effect on the VESS and utility grid, the VESS operation cycle and the peak demand reduction were measured and are described in Section 3.3 and Section 3.4, respectively. The experimental results show that upon the application of the proposed VESS operation, units in the SEC can achieve fairly distributed benefits, and the benefit reduction is marginal at about 5% in relation to the VESS operation to maximize the benefit. Hence, the ways in which the proposed VESS operation achieves this benefit distribution upon varying the implemented VESS capacity and the effect of fairness constraints are investigated. Moreover, future research prospects of the VESS for SECs are discussed in Section 4, including ownership of VESS and its profit distribution, cost-effective VESS size and implementation, and energy transaction cost and large-scale expansion.
2. Methods
The VESS of the SEC consisted of the following three components: SEC, VESS, and the utility grid, as shown in Figure 1. The SEC is a customer group of commercial or residential units. A smart energy service provider (SESP) is a demand aggregator for the community units. The SESP manages the energy transactions between the units and energy producers of the VESS and the utility grid. The VESS can be implemented by either an SESP or a third-party service provider. In this study, it was assumed that the VESS is implemented by the former, the SESP. Therefore, the SESP managed the VESS operation for community units, and determined individual ESS operation actions for each unit according to the objective and constraints. The actions were combined into a single action at each operation time and applied to the VESS operation. The SESP decided multiple logical actions for the community units and operated a physical ESS using the combined single action. The utility grid was connected to the SESP for the energy balance of the community units and VESS.
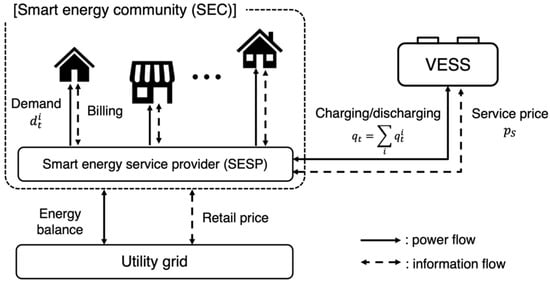
Figure 1.
Constitution of a virtual energy storage system (VESS) for the smart energy community (SEC).
2.1. SEC
The units that participated in the SEC reduced the electricity bill through effective demand management using the ESS operation.
Let be the demand of unit at time . The electricity bill of unit is measured as
where is the billing period such as one month, is the demand price for the billing period, and is the energy price at time .
When unit participates in the SEC and utilizes the VESS capacity of , the electricity bill is modified as
where is the charging and discharging quantity of unit . The quantity is determined using the VESS operation action for unit , , and round-trip efficiency , as follows:
where the positive value, i.e., , becomes the charging operation of the VESS, and vice versa. The VESS operation for unit is restricted by capacity .
The reward of unit with capacity is the electricity bill saving, i.e., the difference between (1) and (2),
and the cost of unit using capacity is
where is the service price of the VESS.
The reward and cost of (4) and (5) are used to design the objective function for the VESS operation.
2.2. VESS
Although the VESS was logically serviced to multiple units, it was physically operated as one ESS. Therefore, the VESS operation is decided by the aggregated action of each unit,
where is the unit set of the SEC.
The VESS operation action was limited by the implemented VESS capacity of the power subsystem (PS) and energy subsystem (ES). The PS constructed as the power conversion system constraints the instantaneous charging and discharging action at each operation time,
where is the maximum PS capacity.
Moreover, the VESS operation action was operated in the stored energy range. The stored energy, referred to as the state-of-charge (SoC), is the accumulated action with the initial state, ,
where is the operation time interval such as 1 h. The SoC is limited by the ES capacity,
where and are the minimum and maximum operable ES capacity ranges, respectively. This was determined within the implemented VESS capacity range in consideration of the depth of discharge (DoD). On assuming 100% DoD, and were set to and , i.e., the implemented VESS capacity, respectively.
The PS and ES constraints of (7) and (9) were used to determine the VESS operation range to achieve its objective.
2.3. Fairness
The following two types of fairness were considered: cost and resource. The cost fairness is defined as a reward of unit given in proportion to the invested cost of unit. This is analogous to return on investment (RoI), which is used as an indicator of the efficiency of an investment [32]. Using (4) and (5), the cost fairness index of unit is calculated as
Similarly, the resource fairness is defined as the VESS usage of unit proportional to its allocated VESS capacity. The resource fairness of unit is measured as
and it is rewritten as
It is similar to the ESS cycle constraint that manages the ESS lifetime [33]. This is because it controls the usage of VESS.
Using (12), the resource fairness index of unit is presented as
The fairness indices of (10) and (13) are used as indicators to verify the performance of a fair VESS operation.
2.4. Fair VESS Operation for SEC
The community energy systems were designed with the objective of maximizing the social welfare of the community, i.e., the total reward of units [15]. In the VESS operation for the SEC, the social welfare maximization problem is formulated as
where is the VESS operation action set of the units, and the constraints are the PS and ES capacity constraints of VESS expressed in (7) and (9). P0 is a mixed integer linear programming problem that satisfies the convexity [34]. Therefore, the problem can be optimally and iteratively solved using the gradient method [35].
Note that problem P0 is of a basic form considered in existing research on VESS operation for SECs with VESS constraints [15,20]. The fair VESS operation problem is formulated by modifying the existing problem by adding a fairness constraint and adjusting the objective function. Therefore, the solution obtained through P0 is used as an index to compare the performance of the proposed fair VESS operation for SECs.
Using the solution of P0, the SEC can achieve the maximum social welfare; however, its distribution among units is not guaranteed. The first fair VESS operation to control welfare distribution is to consider the resource fairness constraint in the existing problem. In this case, for the purpose of social welfare maximization, the distribution of the welfare can be indirectly controlled by considering the resource fairness as follows:
In problem P1, the third constraint of the resource fairness index limits the VESS usage of each unit. It prevents the VESS operation from being biased toward a specific unit. Through this constraint, the welfare is softly distributed among the units. This problem is also a mixed integer linear programming problem, which can be solved similarly to P0.
In contrast, cost fairness is directly related to welfare. Therefore, in order to consider cost fairness, the objective function is modified in the second fair VESS operation problem. Using cost fairness, the welfare among units can be directly ensured as follows:
In problem P2, each unit is guaranteed the minimum reward on the invested cost by the fourth constraint of the cost fairness index. In addition, by maximizing the minimum bound, the social welfare is increased while ensuring the cost fairness among units. This problem is one of the max–min fairness problems of sharing a resource with multiple units [36]. This problem satisfies the convexity; thus, the solution is obtained using the iterative method [37].
In this subsection, two fair VESS operations for an SEC were suggested by modifying the existing VESS operation to maximize social welfare without considering fairness. However, the proposed VESS operations considering fairness satisfy the convexity requirement; thus, they can be optimally solved using the iterative method. This means that the VESS can be effectively operated considering fairness without additional computational burden.
3. Results
3.1. Experimental Environment
To perform the simulations, the SEC was considered to have 116 units. The demand was recorded at 1 h resolution as a part of the Korea Micro Grid Energy Project (K-MEG) [38]. Figure 2 shows the average daily demand distribution of the units in the SEC. The implemented VESS capacity, , is assumed to be 232 kWh, which is the capacity of Powerpack, i.e., Tesla’s utility and business energy storage [39]. The performance of the VESS operation upon varying the VESS capacity is discussed through the simulation results. The VESS parameters are set as , , , and considering the use of a lithium-ion battery [39,40]. The time-of-use tariff (ToU) for the medium general demand-metered service of the Pacific Gas and Electric Company (PG&E) is used to calculate the electricity bill, as shown in Table 2 [41]. For the ToU tariff under consideration, the energy price for mid-peak time and on-peak time is equal.
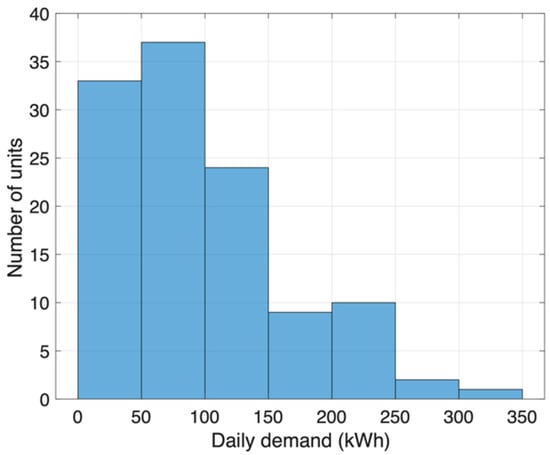
Figure 2.
Average daily demand distribution of units in the SEC.

Table 2.
Time-of-use tariff of Pacific Gas and Electric Company.
3.2. SEC
Although fairness is the main consideration of this study, the basic purpose of the VESS operation from the perspective of the SEC is to increase the benefit of the units. The benefit, i.e., the net reward, is calculated as the reward after deducting the cost:
Figure 3 shows the total benefit of units in the SEC from the VESS operations upon varying the implemented VESS capacity. The blue with circle, red with square, and black with diamond curves show the results obtained using the solutions of P0, P1, and P2, respectively. In addition, the solid and dashed curves indicated in red and black represent the results when the resource fairness constraints are set as and , respectively.
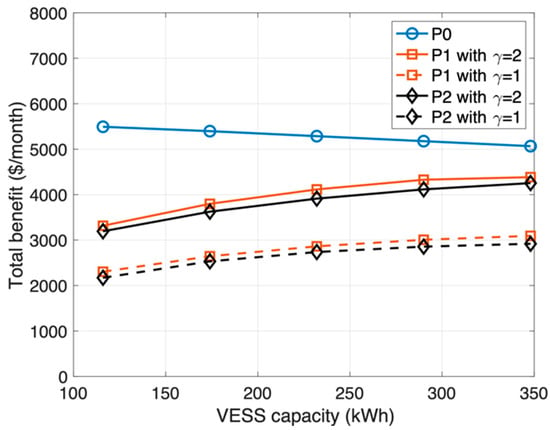
Figure 3.
Total benefit of units in the SEC upon varying the implemented VESS capacity.
In Figure 3, the VESS capacity is directly proportional to the total benefit, except that for P0. The VESS capacity limits the VESS operational room. On increasing the VESS capacity, the VESS can be operated more effectively while enhancing the benefit. For P0, the reward of units improves with increasing the VESS capacity; however, the benefit decreases as the cost increases steeply. However, in all cases, the total benefit is maximized with respect to P0, as indicated by the blue curve. This is because the VESS operation with respect to P0 aims to maximize the total reward without considering the fairness constraints. P1 also aims to maximize the total reward, but it is limited by the resource fairness constraint. Therefore, the VESS operation with respect to P1 achieves the second maximum benefit as indicated by the red curves, and the benefit increases when the resource fairness constraint is set to large and VESS capacity. The VESS operation with respect to P2 considers the resource and cost fairness. Because of the hard constraints, the results of P2 achieve the lowest total benefit. However, the gap of the total benefit between P1 and P2 is less than 5.2%, as shown in Figure 4.
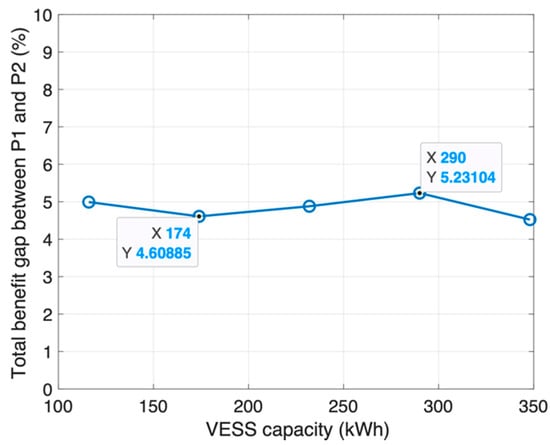
Figure 4.
Total benefit gap between P1 and P2.
Table 3 and Table 4 list the cost and resource fairness indices of the solutions from the VESS operation methods, respectively. From Table 3, the cost fairness index is observed to decrease on increasing the VESS capacity in all cases. The cost fairness index is the ratio of the reward to the cost. These results show that as the VESS capacity increases, the increase rate of the cost grows faster than that of the reward. The mean of the cost fairness index has the highest value for P0, followed by P1 and P2, which is identical to the order observed for the total reward, as shown in Figure 3. The standard deviation of the cost fairness index shows the highest value in the order of its mean. In particular, for P0, the standard deviation of the cost fairness index is approximately three times the mean of the cost fairness index. This indicates that the units by the VESS operation applying P0 achieve a higher reward than the cost on average; however, the distribution of the reward among the units is very unfair in that the reward is concentrated on specific units. In the case of P1, which maximizes the total reward considering the resource fairness, the mean of the cost fairness index is reduced in relation to that of P0. However, the cost fairness is enhanced and its standard deviation is half its mean. However, using P2, all units can achieve the same cost fairness index with marginal reward degradation in relation to that upon the use of P1.

Table 3.
Results of the cost fairness index.

Table 4.
Results of the resource fairness index.
As shown in Table 4, the resource and cost fairness indices show similar trends. For P0, the average VESS usage of the units is very high, and it is biased to specific units as represented in the standard deviation of the resource fairness index. However, for P1 and P2, the VESS usage is guaranteed to be the same for all units. This is because P1 and P2 consider the resource fairness constraint. Additionally, the VESS usage of each unit presented as the resource fairness index expresses the logical VESS usage. The physical VESS operation usage is reflected in the aggregate logical usage discussed in the next subsection.
To ascertain the impact on the welfare of each unit when applying the fair VESS operation for SECs, Figure 5 shows the probability distribution of the welfare change. Figure 5a,b present the welfare change distribution for each unit, namely the welfare difference between the case of applying P0 and that of applying P1 and P2, respectively. In Figure 5a, the sharpness increases with increasing VESS capacity. This is because the welfare gap between the P0 and P1 cases reduces with increasing VESS capacity, as shown in Figure 3. The sharpness also increases in Figure 5b, similar to the case of Figure 5a, but it is not critical. This is because welfare is hardly constrained; thus, there is little welfare change.
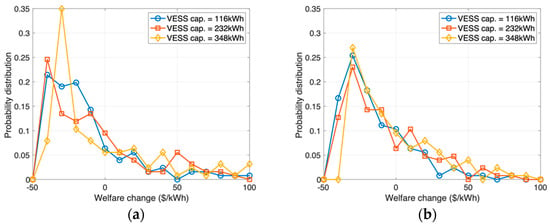
Figure 5.
Probability distribution of the welfare change in each unit. (a) Welfare changes between the P0 and P1 cases with γ = 2. (b) Welfare changes between the P0 and P2 cases with γ = 2.
To determine the dominant factor affecting welfare change, Table 5 shows Pearson’s linear correlation coefficient (PLCC) [42] between welfare change and various parameters. Notably, the welfare changes are highly related to the peak demand rather than the mean demand. This shows that welfare saving the electricity bill is achieved to reduce the peak demand through the VESS operation. Further, the welfare changes between the cases of P0 and P1 are correlated to the allocated capacity when the VESS capacity is small (116 kWh), but the correlation decreases rapidly with increasing VESS capacity. This means that the resource constraint in P1 is limited in terms of the welfare of units when the VESS capacity is small, but it relaxes with increasing VESS capacity. However, the welfare changes between the P0 and P2 cases are highly correlated to the allocated capacity in all cases. This is because the allocated capacity is the main factor determining the cost contribution, and in the case of P2, the VESS is operated to satisfy cost fairness. This result shows that the welfare of units is fairly established by P2 according to the cost contribution.

Table 5.
PLCC between welfare change and various parameters.
3.3. VESS
For the ESS service, ESS lifetime, i.e., the replacement time of the ESS, is an important factor. It is related to the extent of the ESS charging/discharging operation [43]. The VESS operation is determined by the aggregate operation of individual units, as expressed in (6). Therefore, the VESS operation cycle is measured as
Figure 6 shows the VESS operation cycle upon varying the implemented VESS capacity. The results indicate trends similar to those of the resource fairness index in Table 4. The VESS using P0 is operated to maximize the total benefit without fairness constraints; thus, it is operated more frequently than other cases. For P1 and P2, the VESS operation cycle has similar values. Setting the hard resource fairness constraint as , the VESS operation cycle is lower than that with , which implies that the resource fairness constraint limits the VESS operation. However, in the entire range of P1 and P2, the VESS operation cycle is less than 1, which enhances the ESS lifetime [40].
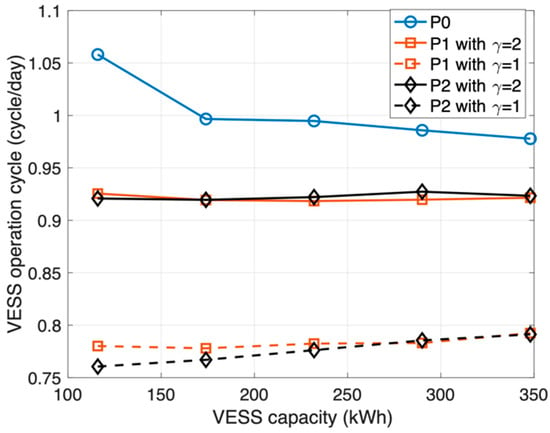
Figure 6.
VESS operation cycle upon varying the implemented VESS capacity.
3.4. Utility Grid
For units in the SEC, the benefit of the VESS operation is the reduction in electricity bills using peak-demand shaving and demand shifting. The former is a major concern of utility grids for increasing the grid system efficiency [44]. It implies that the VESS operation for the SEC benefits the utility grid. Figure 7 shows the peak-demand reduction upon varying the implemented VESS capacity. On increasing the VESS capacity, the peak demand reduces. From Figure 3, the VESS operates more effectively on increasing the VESS capacity. For P0 and P1, the first- and second-most peak demands are reduced because the peak demand is an important factor in determining the electricity bill, which is minimized using P0 and P1. For P2, the peak demand reduces with a marginal gap, i.e., less than 1%, to that of P1. Hence, the fair VESS operation enhances the benefit of the utility grid and the units in the SEC.
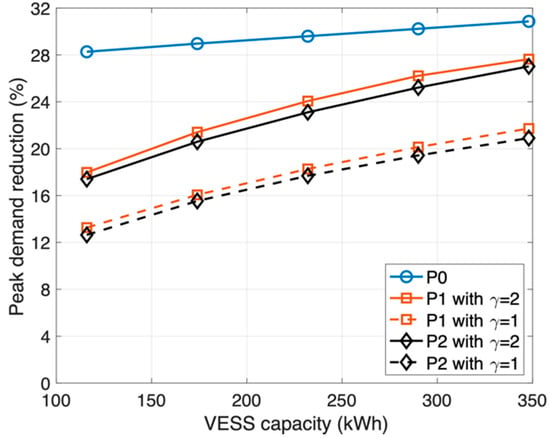
Figure 7.
Peak-demand reduction upon varying the implemented VESS capacity.
4. Discussion
From Section 3, it is evident that the proposed fair VESS operation using P2 fairly distributes rewards and resources to the units in the SEC with marginal benefit reduction in relation to the benefit-maximized VESS operation using P0 and P1. Based on these results, the following key points can be stated for the VESS operation in SECs:
- The benefit or the net reward is directly proportional to the VESS capacity, and the cost using the VESS increases more rapidly, except for P0, as shown in Figure 3. The VESS is operated to achieve the maximum benefit using P0.
- The cost fairness index that represents the cost efficiency decreases with increasing VESS capacity, as shown in Table 3. This validates the previous point. The result indicates that the ESS cost is still high enough to act as a burden on ESS utilization.
- The comparison results of P1 and P2 as shown in Figure 4 and Table 3 indicate that the proposed fair VESS operation considering the cost and resource fairness can achieve approximately 95% of the total benefit performance of the VESS operation for the maximum benefit with the resource fairness constraint. It implies that the resource fairness limits the total benefit, and the cost fairness distributes the benefits to each unit. Figure 5 and Table 4 also show that the resource fairness distributes the welfare to units softly, but the cost fairness distributes the welfare hardly according to the cost contribution.
- As shown in Figure 6, the resource fairness constraint limits the VESS usage, which decides the VESS lifetime that is crucial for determining the ESS cost. The result states that the resource fairness constraint can be used as a management index for the VESS lifetime, which affects the VESS cost.
- Finally, using the VESS operation, the peak demand is effectively reduced, as shown in Figure 7. Peak-demand reduction can improve the system efficiency and defer the facility investment cost of the utility grid. It implies that the units in the SEC and the utility grid benefit enhancement can be used to measure the social welfare improvement.
This study presents a fair VESS operation for SECs, and the following future research directions can be suggested:
- In this study, the SESP is considered to own and directly operate the VESS. It can be extended to the case of the third-party service provider owning the VESS, and the SESP rents the VESS capacity, where the benefit distribution between the third-party service provider and the units in the SEC can be researched as a new problem.
- This study defines cost fairness as the ratio of the reward to cost, and resource fairness as the ratio of the VESS usage to cost. In actuality, fairness is defined in various ways, and this study can be extended to various fairness formulations. For instance, proportional and balanced fairness can be studied [36].
- This study focuses on the VESS operation when the SEC and VESS are set up. Implementation issues such as cost-effective VESS sizing and selection of the appropriate size of community units can be studied further.
- This study did not include the energy transaction costs, such as distribution and transmission fees. This is because the SEC comprises units located in adjacent areas. It can be extended to large-scale grid connection systems considering the energy transaction costs.
5. Conclusions
This study proposed a fair VESS operation method for SEC considering cost and resource fairness. The VESS was considered for the SEC model comprising the VESS, SEC, and utility grid as the main components. The fair VESS operation problem considering the fairness and VESS operation constraints was formulated as a mixed-integer linear problem that can be solved optimally by applying gradient methods and dual decomposition. The simulation results using the real dataset in Korea demonstrated that the units served by the proposed VESS operation achieved a fair benefit distribution. Moreover, the total benefit achieved by the proposed VESS operation was marginal at ∼5% in relation to that of the VESS operation to maximize the total benefit. Additionally, it was shown that the proposed VESS operation improves the benefit of the VESS and the utility grid. The VESS usage is limited according to the resource fairness constraint; thus, the VESS lifetime can be managed for reducing the VESS replacement cost. The peak-demand reduction provides the possibility of improving the system performance of the utility grid.
In this study, basic environments for the VESS, SEC, and utility grid were considered, which can be extended to more complex environments. For the SEC model, only passive units were considered as energy consumers, which can be extended to the environment of active units, such as prosumers with distributed renewable generators. For the VESS model, the problems related to the ownership and cost-effective size of the VESS capacity can be considered. Finally, the utility grid model can be extended to more realistic environments by including power system requirements.
Funding
This research was funded by the National Research Foundation of Korea grant, funded by the Korean Government, Ministry of Science and ICT, under Grant 2020R1A2B5B01095044.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Conflicts of Interest
The author declares no conflict of interest.
References
- Luderer, G.; Madeddu, S.; Merfort, L.; Ueckerdt, F.; Pehl, M.; Pietzcker, R.; Rottoli, M.; Schreyer, F.; Bauer, N.; Baumstark, L.; et al. Impact of declining renewable energy costs on electrification in low-emission scenarios. Nat. Energy 2022, 7, 32–42. [Google Scholar] [CrossRef]
- Zhou, E.; Mai, T. Electrification Futures Study: Operational Analysis of US Power Systems with Increased Electrification and Demand-Side Flexibility; Technical Report NREL/TP-6A20-79094; National Renewable Energy Laboratory (NREL): Golden, CO, USA, 2021.
- Jabir, H.J.; Teh, J.; Ishak, D.; Abunima, H. Impacts of demand-side management on electrical power systems: A review. Energies 2018, 11, 1050. [Google Scholar] [CrossRef] [Green Version]
- Ceglia, F.; Esposito, P.; Marrasso, E.; Sasso, M. From smart energy community to smart energy municipalities: Literature review, agendas and pathways. J. Clean. Prod. 2020, 254, 120118. [Google Scholar] [CrossRef]
- Gjorgievski, V.Z.; Cundeva, S.; Georghiou, G.E. Social arrangements, technical designs and impacts of energy communities: A review. Renew. Energy 2021, 169, 1138–1156. [Google Scholar] [CrossRef]
- Jabir, H.J.; Teh, J.; Ishak, D.; Abunima, H. Impact of demand-side management on the reliability of generation systems. Energies 2018, 11, 2155. [Google Scholar] [CrossRef] [Green Version]
- Tronchin, L.; Manfren, M.; Nastasi, B. Energy efficiency, demand side management and energy storage technologies–A critical analysis of possible paths of integration in the built environment. Renew. Sustain. Energy Rev. 2018, 95, 341–353. [Google Scholar] [CrossRef]
- Kalathil, D.; Wu, C.; Poolla, K.; Varaiya, P. The sharing economy for the electricity storage. IEEE Trans. Smart Grid 2019, 10, 556–567. [Google Scholar] [CrossRef]
- Zhou, L.; Varadharajan, V.; Hitchens, M. Trust enhanced cryptographic role-based access control for secure cloud data storage. IEEE Trans. Inf. Forensics Secur. 2015, 10, 2381–2395. [Google Scholar] [CrossRef]
- Koirala, B.P.; van Oost, E.; van der Windt, H. Community energy storage: A responsible innovation towards a sustainable energy system? Appl. Energy 2018, 231, 570–585. [Google Scholar] [CrossRef]
- Al Alahmadi, A.A.; Belkhier, Y.; Ullah, N.; Abeida, H.; Soliman, M.S.; Khraisat, Y.S.H.; Alharbi, Y.M. Hybrid wind/PV/battery energy management-based intelligent non-integer control for smart DC-microgrid of smart university. IEEE Access 2021, 9, 98948–98961. [Google Scholar] [CrossRef]
- Sahri, Y.; Belkhier, Y.; Tamalouzt, S.; Ullah, N.; Shaw, R.N.; Chowdhury, M.S.; Techato, K. Energy management system for hybrid PV/wind/battery/fuel cell in microgrid-based hydrogen and economical hybrid battery/super capacitor energy storage. Energies 2021, 14, 5722. [Google Scholar] [CrossRef]
- Soliman, M.S.; Belkhier, Y.; Ullah, N.; Achour, A.; Alharbi, Y.M.; Al Alahmadi, A.A.; Habti, A.; Khraisat, Y.S.H. Supervisory energy management of a hybrid battery/PV/tidal/wind sources integrated in DC-microgrid energy storage system. Energy Rep. 2021, 7, 7728–7740. [Google Scholar] [CrossRef]
- Seiders, K.; Berry, L.L. Service fairness: What it is and why it matters. Acad. Manag. Perspect. 1998, 12, 8–20. [Google Scholar] [CrossRef]
- Tomin, N.; Shakirov, V.; Kozlov, A.; Sidorov, D.; Kurbatsky, V.; Rehtanz, C.; Lora, E.E. Design and optimal energy management of community microgrids with flexible renewable energy sources. Renew. Energy 2022, 183, 903–921. [Google Scholar] [CrossRef]
- Zhu, X.; Yang, J.; Liu, Y.; Liu, C.; Miao, B.; Chen, L. Optimal scheduling method for a regional integrated energy system considering joint virtual energy storage. IEEE Access 2019, 7, 138260–138272. [Google Scholar] [CrossRef]
- Zhao, D.; Wang, H.; Huang, J.; Lin, X. Virtual energy storage sharing and capacity allocation. IEEE Trans. Smart Grid 2020, 11, 1112–1123. [Google Scholar] [CrossRef]
- Cheng, Z.; Li, X.; Li, Z.; Si, J.; Xu, S.; Nie, R. Optimal scheduling strategy of building integrated photovoltaic microgrid considering virtual energy storage. Appl. Sci. 2020, 10, 6176. [Google Scholar] [CrossRef]
- Ding, T.; Zhang, X.; Lu, R.; Qu, M.; Shahidehpour, M.; He, Y.; Chen, T. Multi-stage distributionally robust stochastic dual dynamic programming to multi-period economic dispatch with virtual energy storage. IEEE Trans. Sustain. Energy 2022, 13, 146–158. [Google Scholar] [CrossRef]
- Oh, E.; Son, S.Y. Dynamic virtual energy storage system operation strategy for smart energy communities. Appl. Sci. 2022, 12, 2750. [Google Scholar] [CrossRef]
- Tushar, W.; Chai, B.; Yuen, C.; Huang, S.; Smith, D.B.; Poor, H.V.; Yang, Z. Energy storage sharing in smart grid: A modified auction-based approach. IEEE Trans. Smart Grid 2016, 7, 1462–1475. [Google Scholar] [CrossRef] [Green Version]
- Zaidi, B.H.; Bhatti, D.M.S.; Ullah, I. Combinatorial auctions for energy storage sharing amongst the households. J. Energy Storage 2018, 19, 291–301. [Google Scholar] [CrossRef]
- Chakraborty, P.; Baeyens, E.; Poolla, K.; Khargonekar, P.P.; Varaiya, P. Sharing storage in a smart grid: A coalitional game approach. IEEE Trans. Smart Grid 2019, 10, 4379–4390. [Google Scholar] [CrossRef] [Green Version]
- Jo, J.; Park, J. Demand-side management with shared energy storage system in smart grid. IEEE Trans. Smart Grid 2020, 11, 4466–4476. [Google Scholar] [CrossRef]
- Xiao, J.W.; Yang, Y.B.; Cui, S.; Liu, X.K. A new energy storage sharing framework with regard to both storage capacity and power capacity. Appl. Energy 2022, 307, 118171. [Google Scholar] [CrossRef]
- Oh, E. Reinforcement-learning-based virtual energy storage system operation strategy for wind power forecast uncertainty management. Appl. Sci. 2020, 10, 6420. [Google Scholar] [CrossRef]
- He, L.; Liu, Y.; Zhang, J. Peer-to-peer energy sharing with battery storage: Energy pawn in the smart grid. Appl. Energy 2021, 297, 117129. [Google Scholar] [CrossRef]
- Oh, E.; Son, S.Y. Peer-to-peer energy transaction mechanisms considering fairness in smart energy communities. IEEE Access 2020, 8, 216055–216068. [Google Scholar] [CrossRef]
- Yang, Y.; Hu, G.; Spanos, C.J. Optimal sharing and fair cost allocation of community energy storage. IEEE Trans. Smart Grid 2021, 12, 4185–4194. [Google Scholar] [CrossRef]
- Dai, R.; Charkhgard, H.; Rigterink, F. A robust biobjective optimization approach for operating a shared energy storage under price uncertainty. Int. Trans. Oper. Res. 2022, 29, 1627–1658. [Google Scholar] [CrossRef]
- Bertsimas, D.; Farias, V.F.; Trichakis, N. The price of fairness. Oper. Res. 2011, 59, 17–31. [Google Scholar] [CrossRef] [Green Version]
- Friedlob, G.T.; Plewa, F.J., Jr. Understanding Return on Investment; John Wiley & Sons: Hoboken, NJ, USA, 1996. [Google Scholar]
- Zhang, L.; Yu, Y.; Li, B.; Qian, X.; Zhang, S.; Wang, X.; Zhang, X.; Chen, M. Improved cycle aging cost model for battery energy storage systems considering more accurate battery life degradation. IEEE Access 2021, 10, 297–307. [Google Scholar] [CrossRef]
- Boyd, S.; Boyd, S.P.; Vandenberghe, L. Convex Optimization; Cambridge University Press: Cambridge, UK, 2004. [Google Scholar]
- Giselsson, P.; Doan, M.D.; Keviczky, T.; De Schutter, B.; Rantzer, A. Accelerated gradient methods and dual decomposition in distributed model predictive control. Automatica 2013, 49, 829–833. [Google Scholar] [CrossRef] [Green Version]
- Bonald, T.; Massoulie, L.; Proutiere, A.; Virtamo, J. A queueing analysis of max-min fairness, proportional fairness and balanced fairness. Queueing Syst. 2006, 53, 65–84. [Google Scholar] [CrossRef]
- Radunovic, B.; Le Boudec, J.Y. A unified framework for max-min and min-max fairness with applications. IEEE/ACM Trans. Netw. 2007, 15, 1073–1083. [Google Scholar] [CrossRef] [Green Version]
- Yang, W.; Kang, H.; Kwon, Y.; Yoon, Y. Energy Moving the World: Micro Energy Grid; K-MEG R&D Center: Seoul, Korea, 2004; ISBN 978-89-94792-95-815320. [Google Scholar]
- Powerpack: Utility and Business Energy Storage—Overall Sysem Specs. Tesla. 2020. Available online: https://www.tesla.com/powerpack (accessed on 15 June 2022).
- Lazard’s Levelized Cost of Storage Analysis. Lazard. 2021. Available online: https://www.lazard.com/media/451882/lazards-levelized-cost-of-storage-version-70-vf.pdf (accessed on 15 June 2022).
- A-10 Medium General Demand-Metered Service. Pacific Gas and Electric Company (PG&E). 2021. Available online: https://www.pge.com/tariffs/assets/pdf/tariffbook/ELEC_SCHEDS_A-10.pdf (accessed on 28 July 2022).
- Lee Rodgers, J.; Nicewander, W.A. Thirteen ways to look at the correlation coefficient. Am. Stat. 1988, 42, 59–66. [Google Scholar] [CrossRef]
- Torkashvand, M.; Khodadadi, A.; Sanjareh, M.B.; Nazary, M.H. A life cycle-cost analysis of Li-ion and lead-acid BESSs and their actively hybridized ESSs with supercapacitors for islanded microgrid applications. IEEE Access 2020, 8, 153215–153225. [Google Scholar] [CrossRef]
- Danish, S.M.S.; Ahmadi, M.; Danish, M.S.S.; Mandal, P.; Yona, A.; Senjyu, T. A coherent strategy for peak load shaving using energy storage systems. J. Energy Storage 2020, 32, 101823. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).