Abstract
This paper presents a study on the optimal district integration of a distributed generation (DG) system for an energy community (EC) and the implementation of sharing electricity (SE) between users. In recent years, the scientific community has frequently discussed potential pathways to achieve a 100% renewable energy source (RES) scenario, mainly through increasing electrification in all sectors. However, cooling-, heat-, and power-related technologies are expected to play a crucial role in the transition to a 100% RES scenario. For this reason, a research gap has been identified when it comes to an optimal SE solution and its effects on the optimal district heating and cooling network (DHCN) allowing both electrical and thermal integration among users. The considered system includes several components for each EC user, with a central unit and a DHCN connecting them all. Moreover, the users inside the EC can exchange electricity with each other through the existing electric grid. Furthermore, the EC considers cooling storage as well as heat storage systems. This paper applies the Mixed Integer Linear Programming (MILP) methodology for the single-objective optimization of an EC, in Northeast Italy, considering the total annual cost for owning, operating, and maintaining the entire system as the economic objective function. After the optimization, the total annual CO2 emissions were calculated to evaluate the environmental effects of the different solutions. The energy system is optimized in different scenarios, considering the usage of renewable resources and different prices for the purchase of electricity and natural gas, as well as different prices for selling electricity. Results showed that, without changing utility prices, the implementation of SE allowed for a reduction of 85% in the total electricity bought from the grid by the EC. Moreover, the total annual EC costs and CO2 emissions were reduced by 80 k€ and 280 t, respectively.
1. Introduction
A country’s economic development is directly connected to its level of primary energy consumption. As stated by Vogel et al. [1] in a research study that gathered data from 106 countries, economic growth and extractivism activities (which includes fossil fuels) are associated with high levels of energy requirements. Indeed, during the past 50 years, global energy consumption has increased by over 200% [2]. Consequently, greenhouse gas (GHG) emissions have also risen, resulting in serious environmental impacts, especially global warming [3]. With this in mind, the scientific community has raised efforts in order to produce new solutions and technologies that address both economic and environmental interests.
1.1. Literature Review
Amongst the solutions presented in the literature, energy communities stand as a method of saving primary energy and a potential solution to contribute to the transition process to a 100% renewable energy source (RES) scenario, although unavoidable challenges are apparent due to the irregular pattern of such sources [4]. The intended meaning for an energy community (EC), in this paper, is described by Bauwens et al. [5], i.e., the community as a place where users are able to share energy amongst each other (which is the case, for instance, of a District Heating Network—(DHN) and a district heating and cooling network (DHCN)) with the aim to pursue not only economic objectives, but also environmental ones. Moreover, to reach such objectives, many studies have employed the Mixed Integer Linear Programming (MILP) methodology. This is the case, for instance, of Casisi et al. [6] which applied the MILP method to a community comprising nine tertiary sector buildings.
Over the past 50 years, the scientific community’s interest in using the MILP methodology to optimize energy systems has increased exponentially. To have an idea of this, according to Google Scholar, the number of studies in the 1990s related to the optimization of energy systems through the MILP methodology was almost 45% higher compared to the 1980s. In 2010, the number was 10-times higher compared to the previous decade and, nowadays, the number is about 22 times compared to that of 2010. The energy systems analysed in those studies included several types, such as combined cooling heat and power (CHP) systems comprised by boiler and steam turbine [7], the integration of absorption chillers to a CHP plant [8], the incorporation of a condensation turbine and heat pump to a turbine/boiler CHP plant [9], and an optimization of by-product gas distribution in the iron and steel industry [10].
The versatility of MILP optimizations allows one to apply them not only to energy communities, but also to different types of energy systems such as seaports [11,12], wine cellars, ships [13], and so on. The research developed by Pivetta et al. [14], for instance, used MILP optimization to optimize the energy system of a wine cellar in the Northeast Italy so that it produce with the most efficient system configuration from the point of view of profit maximization and share of RE utilization. In another study performed by Pivetta et al. [15], they developed an MILP model to optimize the design and operation of a small-size ferry. The optimization was focused on minimizing the fuel cells’ and batteries’ degradation, as well as minimizing the capital expenses and the operation cost.
As mentioned before, the range of applicability of MILP models also includes the optimization of energy communities. In most cases, the multi-objective functions target the economic optimization of purchasing, maintaining, and operating the whole system as well as the total annual emissions. For example, the authors in reference [6] performed their optimization for the total annual cost and emissions of a DHCN serving a nine-building energy community. They compared this solution with what they called the “conventional solution”, i.e., all thermal, cooling, and electricity demands met, respectively, by a boiler, an electric compression chiller, and electricity bought from the grid. As for the cost optimization, the comparison resulted in a 32% reduction in the DHCN solution with respect to the conventional one, whereas the emissions optimization led to a 41% reduction for the same comparison.
The role of DHNs in achieving better economic results for energy systems as well as reducing environmental emissions has been widely considered and studied by the scientific community [16,17,18]. More specifically, DHNs have also been considered when the transition to a 100% RE scenario is considered. For instance, the work developed by Lund et al. [19], analysed a set of scenarios in which the Danish energy system is converted to a 100% RE scenario by 2060. In such scenario, amongst 10 heating technology types, the DHN one was demonstrated to have the second lowest annual cost (the first was the individual electric heating), and it resulted in the lowest annual fuel consumption option. Still, according to the authors, the best solution for the transition would be achieved through continuing the growth of the DHNs combined with individual heat pumps for areas not covered by DHNs themselves.
In the same direction, another largely discussed concept (in the past decade) is the “4th generation district heating”. According to Lund et al. [20], the so-called first (1880s to 1930s), second (1930s to 1970s), and third (from the 1980s) generations of district heating were mostly fed by fossil fuels and based, respectively, on steam, pressurized hot water (over 100 °C), and pressurized hot water (below 100 °C) as the energy carrier. Nonetheless, in accordance with the same authors, the fourth generation of district heating is the one capable of meeting sustainability requirements, i.e., low heat losses, low-temperature supply, the capacity to recover low-temperature heat sources, the integration of renewable heat sources, the ability to be integrated into smart energy systems (such as electricity and gas grids), and that is economically viable and feasible. This last requirement is particularly important since, according to Volkova et al. [21], one of the most important barriers preventing the massive transition to this new generation of DH is the economic aspect, which can be overcome through financial incentives. Moreover, the fourth generation of district heating has the potential to reduce costs, primary energy consumption [22], and CO2 emissions [23].
Sharing electricity (SE) between users is an additional topic that has demonstrated the potential for the improvement of DHCNs. This SE approach essentially intends to reduce the amount of electricity bought from the grid by sharing the electricity produced by each member of a given energy community. Such a procedure might aim, for instance, to share the electricity produced by local photovoltaic (PV) plants in order to feed heat pumps and circulation pumps, as in the case of the research conducted by Vivian et al. [24], which are their main source of operation costs. In the work developed by Kim et al. [25], they proposed an “energy prosumer concept” in order to raise the self-consumption of a community in terms of thermal and electrical energies. The shared electricity was generated by distributed PV plants and fed a simultaneous heating and cooling heat pump (SHCHP), which in turn supplied heat and cooling to the DHCN. Still, according to the authors, before the implementation of this concept, the power sold to the grid was around 60% of the PV power production, whereas the implementation resulted in 12.5% of electricity sold to the grid, which shows the increase of self-consumption. Kayo et al. [26] investigated the energy sharing approach (which also included the SE) applied to four types of buildings that could generate and consume electricity and heat from each other. Since each building had its own CHP system, one of their main conclusions was that the larger the CHP system, the greater the possibility of sharing electricity with other buildings and the greater the primary energy savings. Another interesting conclusion is that the operation strategy of the CHP system plays a key role when it comes to energy sharing improvements.
As observed, the literature has dealt with the SE methodology from different points of view, including also the presence of a DHN. Further advancements have also analysed how the community is established, the presence of non-prosumers [27], and the financial attractiveness in terms of incentives when it comes to SE between users with residential electricity storage [28]. In the same line, Wu et al. [29] claimed that SE does not always lead to a reduction in storage investments, since it will depend on applied taxes. Somma et al. [30] have also analysed local energy systems with sharing electricity and their interactions with the electricity market through an MILP optimization; however, no heating or cooling distribution systems were considered. There are other authors who also consider the cost of optimization when it comes to the interaction of local users with the main grid, as with the authors in the references [31,32,33]; however, they have not considered heating and/or cooling district systems as well.
1.2. Novelty and Goals
From the literature review depicted above, one can observe that it has approached the topic of optimal sharing electricity (SE) between local users in a wide variety of ways. Furthermore, in recent years, the scientific community has frequently discussed potential pathways to achieve a 100% RES scenario by the middle of this century, mainly through an increasing in electrification of all sectors. However, as discussed in a previous study [34], cooling-, heat-, and power-related technologies are expected to play a crucial role in the transition to a 100% RES scenario. On top of that, an overview of EC-related literature demonstrated the difficulty of finding studies dealing, at the same time, with the optimization of the following aspects:
- District heating and cooling network;
- Thermal and cooling storage;
- Electricity sharing among EC members;
- Renewable sources considered;
- Considerable number of heating-, cooling-, and power-related technologies.
As can be observed in Table 1, the reviewed literature has applied different optimization methodologies and objective functions to analyse ECs. Nevertheless, the implementation of SE among EC members and its effects on the optimal cost-related solution of the district heating and cooling network (DHCN) and adopted technologies have not been evaluated yet.

Table 1.
Comparison of the EC-related literature regarding key modelling aspects.
For this reason, it comes to light that the literature has still a research gap regarding:
- Optimal SE solution for an EC and its effects on the optimal DHCN solution;
- Amount of electricity exchanged between EC and the national electric grid according to utility price variations and, consequently, to the adopted technologies in the solution;
- Evaluation of the EC performance in relation to the possibility of moving towards a self-sufficient scenario in terms of electricity production/consumption.
The study is developed by performing a single-objective MILP optimization to define the optimal synthesis, design, and operation of a distributed generation (DG) system in an EC, in the northeast of Italy, in a similar way as presented in a previous work of this research group [6]. Such an EC comprises nine tertiary sector buildings connected through a DHCN. The single-objective optimization of the DG energy system considers the total annual cost for owning, operating, and maintaining the whole system as the economic objective function, while the total annual CO2 emissions have been calculated after optimization to evaluate the environmental effect of the different solutions. Within such a context, the SE between EC users is implemented in order to assess the economic and environmental impacts of this option. The optimal results obtained for a test case are compared with and without SE. Then, an investigation is performed to analyse the behaviour of the optimal solution by varying the prices of the energy vectors through six sensitive scenarios. This approach made it possible to highlight the extent to which the EC option effectively allows one to obtain fewer emissions and reduced exchanges with the external electricity grid, even without the need to introduce objectives other than simple economic convenience.
Section 2 is dedicated to the description of the model, presenting the equations of the components, energy balances, objective functions, and the sharing electricity methodology. Section 3 describes the energy community case study, whereas Section 4 presents the results and discussions about the simulations and comparisons mentioned in the previous paragraph.
2. Model Description
As mentioned in the last section, the definition of the optimal synthesis, design, and operation of the DHCN was performed through the Mixed Integer Linear Programming (MILP) optimization method. In summary, the synthesis refers to the selection of the equipment that is going to be included in the final optimal structure; the design process concerns the sizing of each selected equipment, and the operation definition has the objective of setting the on/off status of each piece of selected equipment.
The MILP method can be divided into three main parts: decision variables, constraints, and objective functions. Decision variables can be of two types: binary or continuous. Binary variables express the selection and on/off status of equipment, whereas continuous variables express the sizing of each selected equipment and auxiliary components, as well as energy quantities and streams. Constraints are mathematical expressions with the aim of determining the model and what its limitations are in terms of equipment size, performance, and energy balance. The objective functions represent the main target of the analysis, which is, for this work, the minimization of the total costs regarding the DHCN and the nine users.
As depicted in Figure 1, the superstructure is divided in three main elements. The first one is related to the maximum set of equipment (Polygeneration Unit k) that can be dedicated to a given user building (denoted as “User k”). The second part is associated to the central unit, which is a user-independent structure and can comprise a set of equipment to benefit the energy community with heating and electricity. The third element is “User i”, which represents the other users within the energy community. These three elements are connected through a DHCN, for thermal related energy exchange, and a distribution substation (DS), as an electricity concentrator. The pipeline connections between users, the central unit, and the DHCN are one of the optimized characteristics performed by the model. The users and central unit are not connected directly to the electricity grid. Instead, they are all connected to the DS, the purpose of which is to manage the electricity flow for the three elements. In other words, based on an electricity balance, the DS sends electricity to a given user (if its polygeneration unit did not fulfil its demand), receives electricity from a given user (if its polygeneration unit has fulfilled its demand and now it has an electricity surplus), buys electricity from the grid (if the electricity surplus from the users is not enough to cover the electricity deficit of the other users), and sells electricity to the grid (if there is a surplus and all electricity users demands are covered).
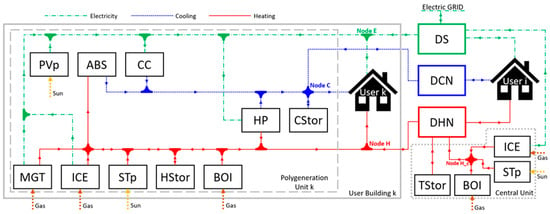
Figure 1.
Schematic diagram of the energy community.
Heating, electricity, and cooling have specific origins, destinations, and paths within the polygeneration unit superstructure. Starting from heating connections, the heat is produced from two types of primary energy: natural gas and solar energy. Natural gas drives micro gas turbines (MGT), internal combustion engines (ICE), and boilers (BOI), whereas solar thermal panels (STp) are obviously driven by solar energy. As can be observed in Figure 1, absorption chillers (ABS) can only be powered by the heat coming from MGT and ICE. The heat thermal storage (TStor) is allowed to store the heat coming only from MGT, ICE, and STp, and, on the other hand, it can supply heat only to User k or to DHN. If the heat supplied by MGT, ICE, STp, TStor, and the heat pump (HP) is not enough to cope with the User k thermal demand, the BOI comes to the scene to cover this deficit. The electricity is produced by MGT, ICE, and photovoltaic panels (PVp). This electricity can feed the compression chiller (CC), HP, and User k demand. At the same time, this User Building k is allowed to send or receive electricity to/from the DS. The cooling energy can be produced by ABS, CC, and/or HP and is sent to the cooling storage (CStor), to User k, and/or to the DCN. As observed in Figure 1, CStor is allowed to send cooling only to User k or DCN.
Regarding the central unit, it has a smaller superstructure and has connections only with the DS and DHN. It also comprises a TStor (that is allowed to send/receive heating only to/from the DHN), a BOI, STp, and ICE (that send heating directly to the DHN). The ICE of the central unit can also send its produced electricity to the DS in order to increase the electricity supply for the users and prevent them from buying electricity from the grid.
2.1. Components
As mentioned in the introduction, the energy community, taken into account in this study, is made up of nine users located in a medium town in Northeast Italy. Every user is allowed to install several devices in order to satisfy their own energy demands, as described in the previous section. The sizes of MGT, ICE, ABS, and HP are fixed and have been chosen a priori as described in Section 3. BOI and CC have been left free in size and it is upon the model to optimize their installation and sizes as well. STp and PVp are of variable size and have a limitation of a maximum of 200 m2 per user. All the central unit devices are of variable size, except for the ICE. Every user can adopt in parallel up to j components of the same size.
A set of binary variables is expressed at each time interval for the whole year, at every user location, and for each device. Equations (1)–(34) represent the base formula setting regarding component, DHCN, and thermal storage modelling, which is similar to our previous work [6]. The variable “X” expresses the existence of a given component, while the variable “O” expresses its on/off operation. The component j is allowed to be installed only if the component j − 1 has been already taken into account (Equation (1)), and it cannot be turned on if it is not installed (Equation (2)).
Xchp(j,u) ≤ Xchp(j − 1,u)
Ochp(m,d,h,j,u) ≤ Xchp(j,u)
The partial load performance of cogeneration devices is represented by the set of linear relations presented in Equations (3) and (4).
Hchp(m,d,h,j,u) = Khchp(m,d,h,1)·Echp(m,d,h,j,u) + Khchp(m,d,h,2)·Ochp(m,d,h,j,u)
Fchp(m,d,h,j,u) = Kfchp(m,d,h,1)·Echp(m,d,h,j,u) + Kfchp(m,d,h,2)·Ochp(m,d,h,j,u)
The coefficients Khchp and Kfchp have been obtained with a linear regression of the devices characteristic load curves, and the electric energy produced is limited above and below the device’s performance limits.
The subscript “chp” represents the ICE and MGT devices for a given user. For that reason, in Equations (1)–(4), such subscript can be changed to “ice” or “mgt” to obtain the equations related to both devices. The ICE at the central unit is described by different equations because both load and size are decision variables, and it is then mandatory to introduce further constraints to maintain the problem a linear one.
The ICE size and the relation between the operation and the device existence are expressed by Equation (5).
Sice,lim,c(1)·Xice,c ≤ Sice,c ≤ Sice,lim,c(2)·Xice,c
Oice,c(m,d,h) ≤ Xice,c
The relations among the fuel consumed by the central ICE (Fice,c), the main (Eice,c), and the secondary (Hice,c) products are as follows:
where the variable ξice,c is introduced to set a linear equation with two independent variables. Therefore, in order to avoid inconsistencies in the results when the engine is turned off, it is necessary to constrain ξice,c through the following equations:
Fice,c(m,d,h) = Kfice,c(m,d,h,1)·Eice,c(m,d,h) + Kfice,c(m,d,h,2)·Oice,c(m,d,h) + Kfice,c(m,d,h,3)·ξice,c(m,d,h)
Hice,c(m,d,h) = Khice,c(m,d,h,1)·Eice,c(m,d,h) + Khice,c(m,d,h,2)·Oice,c(m,d,h) + Khice,c(m,d,h,3)·ξice,c(m,d,h)
Sice,c + Sice,lim,c(2)·(Oice,c(m,d,h) − 1) ≤ ξice,c(m,d,h) ≤ Sice,c
Sice,lim,c(1)·Oice,c(m,d,h) ≤ ξice,c(m,d,h) ≤ Sice,lim,c(2)·Oice,c(m,d,h)
Eice,c(m,d,h) ≤ Sice,c
The central BOI is modelled in an analogous way to the central ICE, with the introduction of the auxiliary variable ψboi,c (with a minimum load limit of Hboi,lim,c = 0.1). The fuel consumption, described by Equation (12), is affected by the BOI’s efficiency. Analogously, the CC, at the user level, is modelled through its COP. Both BOI and CC have no load limits.
Fboi,c(m,d,h) = Hboi,c(m,d,h)/ηboi,c(m,d,h)
Hboi,lim,c·ψboi,c(m,d,h) ≤ Hboi,c(m,d,h) ≤ ψboi,c(m,d,h)
Sboi,c + Sboi,lim,c(2)·(Oboi,c(m,d,h) − 1) ≤ ψboi,c(m,d,h) ≤ Sboi,c
Sboi,lim,c(1)·Xboi,c ≤ Sboi,c ≤ Sboi,lim,c(2)·Xboi,c
The ABS devices are allowed to exist only at the user locations where there is the presence of ICE and MGT. Another important constraint is the cooling produced by the ABS, since it must not be greater than the heat supplied by both ICE and MGT (Equation (17)).
Xabs(j,u) ≤ Xice(j,u) + Xmgt(j,u)
Cabs(m,d,h,j,u) ≤ Hice(m,d,h,j,u) + Hmgt(m,d,h,j,u)
The heat pump modelling is a bit more complicated since, besides its existence (Equation (18)), its operation should be managed properly, as the heating and cooling production cannot happen at the same time (Equations (19)–(21)). The linear equations regarding the heating (Equation (22)) and cooling (Equation (23)) production as a function of the electricity input are also presented. Equations (24)–(26) represent the operation limits, as well as the limitation about the electricity input for both operation modes.
Xhp(j,u) ≤ Xhp(j − 1,u)
Ohp,h(m,d,h,j,u) ≤ Xhp(j,u)
Ohp,c(m,d,h,j,u) ≤ Xhp(j,u)
Ohp,h(m,d,h,j,u) + Ohp,c(m,d,h,j,u) ≤ 1
Hhp(m,d,h,j,u) = Khp(m,d,h,u,1)·Ehp,h(m,d,h,j,u) + Khp(m,d,h,u,2)·Ohp,h(m,d,h,j,u)
Chp(m,d,h,j,u) = Khp(m,d,h,u,3)·Ehp,c(m,d,h,j,u) + Khp(m,d,h,u,4)·Ohp,c(m,d,h,j,u)
Shp,lim(m,d,h,u,1)·Ohp,h(m,d,h,j,u) ≤ Ehp,h(m,d,h,j,u) ≤ Shp,lim(m,d,h,u,2)·Ohp,h(m,d,h,j,u)
Shp,lim(m,d,h,u,1)·Ohp,c(m,d,h,j,u) ≤ Ehp,c(m,d,h,j,u) ≤ Shp,lim(m,d,h,u,2)·Ohp,c(m,d,h,j,u)
Ehp(m,d,h,j,u) = Ehp,h(m,d,h,j,u) + Ehp,c(m,d,h,j,u)
PVp and STp plants are proportional to the user and central unit available surface sizes. They are estimated a priori through the hourly insolation, inclination, and orientation angle of installed panels.
2.2. District Heating and Cooling Network
In order to have an effective working DHCN, the user location has to be geographically near the DHCN pipelines (within the distance of about 1.5 km) in order to avoid large amounts of thermal losses through the pipelines themselves. The definition of the DHCN layout and the maximum capacity of pipelines (considering the whole system operation) are two of the aims of the DG energy system optimization, since the network strongly affects the optimal solution.
Equation (27) describes the heat flowing into each DHCN pipeline:
in which the velocity vp is supposed to be constant (ranging from 1.5 to 2.5 m/s), so that the heat flowing through the pipeline () is a function of the pipeline cross section area (Ap) and the temperature difference Δt between the inlet/outlet of the pipeline itself. This temperature difference is assumed to be fixed (ranging into the 15–25 °C interval), as is the network temperature, while the pipeline length and maximum flow ratio introduced by the model are constant. The network layout and size are decision variables for which the pipeline flow rate limits, and the superstructure are the constraints. The thermal losses are expressed by Equation (28) and depend on the pipeline length lp(u,v) and a coefficient of proportionality (δt).
pt(u,v) = δt·lp(u,v)
Another important constraint is the one represented by Equation (29). It does not allow the model to connect two users (e.g., user u and user v) with two pipelines sending thermal energy.
Xtp(u,v) + Xtp(u,v) ≤ 1
The maximum heat flow rate is constrained by the pipelines size, while the energy flow into each pipeline is bounded between a lower and an upper limit:
Hnet,lim(1)·Xtp(u,v) ≤ SH,net(u,v) ≤ Hnet,lim(2)·Xtp(u,v)
Hnet(m,d,h,u,v) ≤ SH,net(u,v)
By suitably changing the subscripts of the preceding expressions, it is possible to obtain the District Cooling Network model.
2.3. Thermal Storages
The natural intermittence characteristic of the sunlight associated with its scarcity during the winter make the thermal storage (TStor) systems good solutions to overcome such a problem. Moreover, when associated with cogeneration devices, as is the case of the present work, TStor systems can support the users to reduce the usage of the BOIs when the cogeneration devices are shut down. Thus, the consumption of fossil fuels is reduced and, consequently, the environmental impact also decreases.
We hypothesise that the residual energy of a not-fully discharged storage is accumulated at the same temperature that a DHN requires. For this reason, it is needed to introduce the assumption of the perfect stratification of the water (the working fluid) into the TStor. The following equation gives the thermal energy stored into a TStor:
where the temperature difference Δt is constant as in Equation (27) and shows that Qts is a decision variable proportional to the volume of the stored working fluid. Unlike the other components, it is not possible to use the concept of typical day to group a set of comparable days; however, it is necessary to model the TStor without any time decomposition for the whole year to consider the charging and discharging phases.
Qts = Vts·ρp·cp·Δt
Equation (33) shows how the TStor energy balance considers the energy stored at the time t equal to the one contained at the time t − 1 by a thermal loss coefficient with the addition of the energy coming from the network at the time t:
Hts(m,d,h,u) = Qts(m,s,d,r,h,u) − Klos,ts(u)·Qts(m,s,d,r,h − 1,u)
Hts(m,d,h,u) = Qts(m,s,d,r,h,u) − Klos,ts(u)·Qts(m,s,d,r − 1,24,u)
Equation (34) states that two days of the same kind must be connected to allow for the whole year representation, as well as the fact that any other end of a time period has to be connected to the beginning of the following one. Further, going through working and non-working days, or different weeks and months, needs some additional constraints. Moreover, the heat stored is limited by the TStor size itself. Equations (32)–(34) can be used to model both heat and cooling storage devices.
2.4. Energy Balances
The energy balances considered for this work have the objective to tell the model what the constraints are when it comes to heating, cooling, and electricity balance. Taking Figure 1 as orientation, the energy balances are applied at the User Building k, central unit, and DS levels. For User Building k, all three types of energy balance are needed, and they are applied at Node H (heating), Node C (cooling), and Node E (electricity), as observed in Figure 1. In the case of the central unit, the only balance required is the heating one, since the electricity produced by the central ICE is sent directly to the DS. The DS works as an electricity manager and, for this reason, the only balance applied here is the electricity one. The DS is also responsible for the promotion of sharing electricity among users, and this is explained in more detail in the next section. Equations (35), (36) and (38)–(40) are also part of this work basis and may be found in our previous work [6] as well. Equation (37) represents the modification that had to be implemented in the user electricity balance, i.e., there is no terms representing the electricity bought or sold from/to the electric grid. These terms are now two of the components in the DS electricity balance (Equation (41)).
Following the same order, the User Building k balance regarding the heating, cooling, and electrical types of energy are obtained through Equations (35)–(37).
Hmgt(m,d,h,u) + Hice(m,d,h,u) + Hstp(m,d,h,u) + Hboi(m,d,h,u) + Hhp(m,d,h,u)
+ Hnet(m,d,h,v,u)(1 − pt(v,u)) = Hts(m,d,h,u) + Habs(m,d,h,u) + Hdem(m,d,h,u) + Hnet(m,d,h,u,v)
+ Hnet(m,d,h,v,u)(1 − pt(v,u)) = Hts(m,d,h,u) + Habs(m,d,h,u) + Hdem(m,d,h,u) + Hnet(m,d,h,u,v)
The term pt in Equation (35) refers to the thermal losses, throughout the pipelines, per unit of length (km−1).
Cabs(m,d,h,u) + Ccc(m,d,h,u) + Chp(m,d,h,u) = Cdem(m,d,h,u) + Cts(m,d,h,u)
Eut(m,d,h,u) = Eice(m,d,h,u) + Emgt(m,d,h,u) + Epvp(m,d,h,u) − Ecc(m,d,h,u)
− Ehp(m,d,h,u) − Edem(m,d,h,u)
− Ehp(m,d,h,u) − Edem(m,d,h,u)
Some other constraints are needed to specify to the model, the boundaries, and where a given energy flow should come from. With that in mind, Equation (38) states that the heat energy feeding the heat thermal storage should be originated from the MGT, ICE, and/or STp. Analogously, Equation (39) expresses that the cooling energy for the cooling thermal storage should come from the ABS, CC, and/or HP.
when it comes to the central unit, the thermal balance is done at Node H_c (Figure 1), and it is translated into the Equation (40).
Hmgt(m,d,h,u) + Hice(m,d,h,u) + Hst(m,d,h,u) − Hts(m,d,h,u) ≥ 0
Cabs(m,d,h,u) + Ccc(m,d,h,u) + Chp(m,d,h,u) − Cts(m,d,h,u) ≥ 0
Hice,c(m,d,h) + Hboi,c(m,d,h) + Hstp,c(m,d,h) = Hnet,c(m,d,h) + Hts,c(m,d,h)
The variables related to heat thermal storage (Hts), cooling thermal storage (Cts), central heat thermal storage (Hts,c), and the total net electricity sent/received by a given user () are the only variables also allowed to hold negative values. For the thermal storage variables, a negative value means that thermal energy is leaving the device, whereas positive values mean the input of thermal energy. Regarding the total net electricity of a given user, positive values mean that the user is sending electricity to the DS, while negative values mean that the user is receiving electricity from the DS.
2.5. Electricity Sharing
As shown in the introduction section, sharing electricity (SE) amongst the users of a given energy community (EC) has the potential to benefit EC members. The main objective of such a methodology is to reduce the amount of electricity exchange (bought and sold) between EC and the electric grid and, consequently, to reduce the overall costs and environmental impacts associated with that EC.
The electricity sharing methodology proposed in this work is presented in Figure 2. Electricity produced by MGT, ICE, and PVp devices, if present in a given user, is intended to feed that same user and, in the case of electricity surplus, to be sent to the DS. Once in the DS, this electricity can be either sent to another EC member with an electricity deficit or sold to the grid. The electricity balance for each user is obtained through Equation (37), i.e., if the summation of the electricity produced by MGT, ICE, and PVp devices minus the electricity consumed by CC and HP is greater than the user electricity demand, then that user has an electricity surplus which can be sent to the DS (Eut is positive). On the other hand, if the user electricity demand is greater than the electricity produced by that same user’s devices, it has an electricity deficit and it should be compensated by receiving electricity from the DS (Eut is negative).
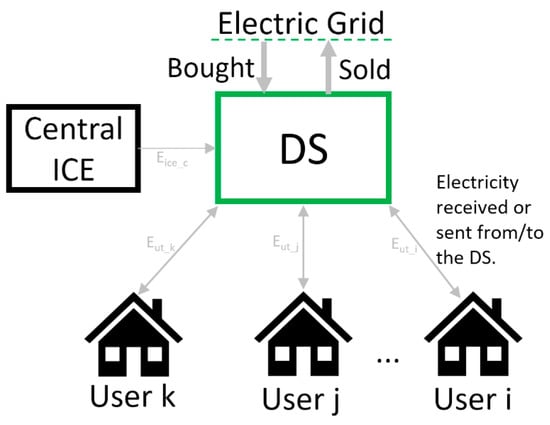
Figure 2.
Electricity sharing diagram.
Another important electricity balance within this methodology is the DS balance (Equation (41)). The first term (∑Eut(m,d,h,u)) refers to the net electricity exchanged between all users and the DS throughout a whole year. This term is allowed to be positive or negative. When it is positive, it means that all users have their electricity demand fulfilled and that such electricity surplus can be sold to the grid. When it is negative, it means that not all users have their electricity demand satisfied, and that electricity should be bought from the grid (by the DS) in order to cope with such a deficit. The second term (∑Eice,c(m,d,h)) is regarded as the total electricity produced and sent by the ICE in the central unit to the DS, which is allowed to be only equal or greater than zero. The third term (∑Ebgt(m,d,h)) is the total electricity bought from the grid by the DS, while the fourth term (∑Esel(m,d,h)) is the total electricity sold to the grid by the DS.
∑Eut(m,d,h,u) + ∑Eice,c(m,d,h) + ∑Ebgt(m,d,h) − ∑Esel(m,d,h) = 0
2.6. Objective Function
The considered objective function is the minimization of the total costs related to the EC, i.e., the costs related to the operation, maintenance, and capital investment of all users plus the central unit. Moreover, since all electricity exchanged with the main electric grid is managed by the DS (no user has direct connection with the main electric grid), the cost relative to the total electricity bought and the income relative to the total electricity sold should be two additional terms considered in the total EC costs (Equation (42)). The calculation of the costs related to the first three terms of Equation (42) are detailed through Equations (43)–(49), which are adapted from our previous work [6].
cann,tot = cinv + cman + cope + celec,bgt − relec,sold
The total annual investment costs can be separated into three investment parts.
The first part regards the users, obtained through Equation (43). The first term of this equation shows the contributions of MGTs, ICEs, HPs, and ABSs to the investment costs of the users. Each component contribution term comprises the amortization factor (f), a binary variable (X) to express the existence of such component, and the purchase cost of the component (c). Each user u is allowed to install j components of the same type up to a maximum of six. The other terms in Equation (43) present the contributions of BOIs, CCs, PVp, STp, TStor, and CS (which are dependent of the installed capacity needed for a given optimal solution). These terms include the amortization factor, the size of the component (S [kW]), and the specific cost of the component (c [€/kW]).
The second part concerns the investments in the central unit (Equation (44)). As observed, this equation includes the variable and fixed costs related to the ICE, BOI, and DHN of the central unit, as well as the investment costs associated to STp and TStor.
The third part is concerned with the investment costs of the DHCN pipeline network (Equation (45)). This equation comprises the fixed costs (related to the existence or absence of a given pipeline connection) and the variable costs (related to the actual size of each pipeline connection and whether it is for heating or cooling).
cinv,u(u) = ∑j [fmgt Xmgt(j,u)·cmgt(j,u) + fice·Xice(j,u)·cice(j,u) + fhp·Xhp(j,u)·chp(j,u) + fabs·Xabs(j,u)·cabs(j,u)] + fboi·Sboi(u)·cboi+ fcc·Scc(u)·ccc + fpvp·Spvp(u)·cpvp + fstp·Sstp(u)·cstp + fts·Sts(u)·cts + fts·Scs(u)·cts
cinv,c = fice (Sice,c·cice,v + Xice,c·cice,f) + fboi·(Sboi,c·cboi,v + Xboi,c·cboi,f) + fstp·Sstp,c·cstp,c + fts Sts,c·cts,c + fnet·(cnet,f,c·Xnet,c + cnet,v,c·SH,net,c)
cnet = fnet·∑u,v[cnet,f,c(1)·(Xtp(u,v) + Xcp(u,v)) + cnet,f,c(1)·Xnet(u,v) + cnet,v·(SH,net,c(u,v) + SC,net(u,v))]
The total annual maintenance cost is obtained by the summation of Equations (46) and (47). Equation (46) represents the total annual maintenance cost related to a given user and comprises the maintenance cost associated to each considered component. This latter cost is considered proportional to the total amount of product from the component. Equation (47) contains the terms related to the maintenance costs of ICE and BOI, both from the central unit. These costs are also proportional to the total amount of product from each component.
cman,u(u) = cman,mgt(u) + cman,ice(u) + cman,abs(u) + cman,hp(u) + cman,boi(u) + cman,cc(u) + cman,pvp(u) + cman,stp(u)
cman,c = cman,ice,c + cman,boi,c
Since the user’s electricity connection, in this case, has no direct link with the main electricity grid, all the operation costs/incomes related to buying/selling electricity to the grid is now concentrated exclusively in the DS (Equation (42)). With that in mind, the total annual operation cost is derived only from fuel-related costs and can also be split into the operation costs of the users (Equation (48)) and the operation costs of the central unit (Equation (49)).
cope,u(u) = ∑m,d,h [cfue,chp(m)·(Fice(m,d,h,u) + Fmgt(m,d,h,u)) + cfue,boi(m)·Fboi(m,d,h,u)]
cope,c = ∑m,d,h [cfue,ice,c·Fice,c(m,d,h) + cfue,boi(m)·Fboi,c(m,d,h)]
The total annual CO2 emission due to electricity and fuel consumption is obtained through Equation (50).
emtot = emel·∑m,d,h [Ebgt(m,d,h) − Esel(m,d,h)] + emf,chp ·∑m,d,h,u [Fice(m,d,h,u) + Fmgt(m,d,h,u)] + emf,boi ·∑m,d,h,u [(Fboi(m,d,h,u) + Fboi,c(m,d,h)] + emf,cen ·∑m,d,h Fice,c(m,d,h)
The CO2 emissions related to each type of fuel considered in this work (electricity and natural gas) are obtained in the specialized literature [47].
3. Case Study
Performing a MILP optimization through a mathematical model could be very time consuming, based on the detail level and the model complexity. One of the most influential characteristics is the time resolution (hours, weeks, months), which is strongly related to the energy demands to be considered. Since environmental conditions are relevant for residential and tertiary sector energy systems, they require demand data based on an hourly period, whereas the industrial sector could only require a weekly or monthly time resolution.
In order to reduce the model complexity, which needs an hourly period, some typical days have been introduced to represent the whole year [48]. Therefore, in this case study, the year has been divided into 24 typical days of 24 h each, namely 12 working days and 12 non-working days, resulting in each month being composed of one working and one non-working day. This time subdivision works for all the variables used, excluding the variables related to the thermal storages, both heating and cooling, that take into account the whole year instead (please refer to Section 2.3).
The nine users taken into account are: town hall, main theatre, library, primary school, retirement home, town hall archive, main hospital, secondary school, and swimming pool (private owning).
The location of the nine users is shown in Figure 3, as well as the DHCN path (in red colour) that could be built. This path has been sketched taking into account road layouts, boiler rooms’ locations, and underground utilities’ positions (waterworks, gas network, etc.). The maximum distance between users and the central unit (C) is the one related to the town hall (user 1), which is roughly 2.5 km far from it.
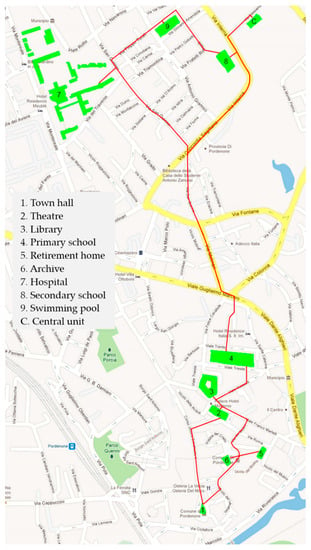
Figure 3.
Possible connections for the DHCN pipelines.
The thermal energy needed by buildings is used for space heating (demanded at a temperature of 65–70 °C) and for sanitary hot water and is supplied by the BOIs. On the other hand, CCs provide the cooling energy demanded just for space cooling during the summer period. The DHN and DCN operation temperature values have been set up for the simulations at 82 °C and 12 °C, respectively.
Through electricity sharing, users constitute an EC in which the aim is to fulfil the whole electric energy demand. Users that are producing an energy surplus send it to a distribution substation (cabled with the grid), which distributes the electricity to other EC users using the grid structure. This energy sharing avoids electricity purchasing from the grid until the demands are satisfied. If more energy is needed, users can purchase it from the grid; alternatively, if there is an unconsumed surplus, they can sell it to the grid, both through the distribution substation.
Inside the EC, the user receiving electricity does not pay for the energy received from a producing user. Such a sharing structure could allow users to save money because not all of them need to install cogeneration devices and PVp; furthermore, it allows them to choose the size of the devices more appropriately according to the users’ demands. The type and size of the devices must fit these demands, otherwise their installation will not be appropriate.
Table 2 shows the yearly demands of electric, thermal, and cooling energies of the nine users considered. The electricity demands do not take into account the CCs’ requirement regarding the cooling energy production. Hospital electricity demand represents 75% of the total amount, followed by the theatre, with 7%, while others are around 2–4% each. Regarding thermal and cooling demands, the hospital is the most energy-intensive user, which is followed by the secondary school with 11% (thermal demand) and by the retirement home with 7% (cooling demand). The summer break in the school activities leads to no cooling demands for both the institutes, just as the swimming pool, which does not need cooling all year long.

Table 2.
Energy demands for each user (all values in kWh).
The energy demands for all users have profiles typical of European continental climate. In fact, as observed in Figure 4, since the summer daylight is longer than in winter, there are more electricity requirements during the winter season. A similar trend is noticeable for the heating demands. The cooling demands are considerable from May to September instead, with June, July, and August being the most cooling-intensive months. The other months of the year comprise a lower cooling demand (around 700 kWh per day) due to the hospital needs. The building energy patterns are different from one another because of the thermal insulation, the occupancy factor, night lighting, etc.
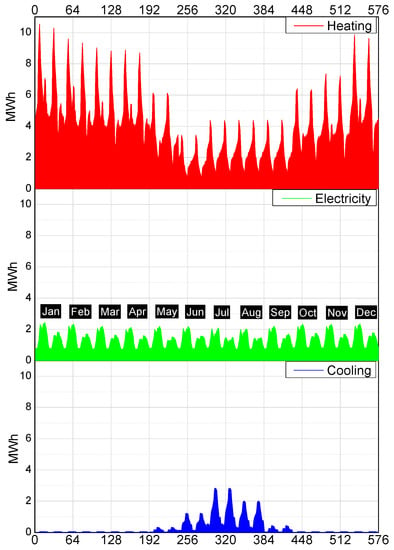
Figure 4.
Heating, electricity, and cooling demands for the nine buildings together. Two representative days per month.
As stated in Section 2.1, the installed devices should have fixed and variable sizes, depending on the model. The optimization process gives the number of fixed size machines and the final dimension of the variable size ones (CCs, BOIs, TStors). Up to six devices of the same kind can be installed at each user location, choosing from a look-up table (reported in Table 3) containing the size values which are based on the user peak demands.

Table 3.
Sizes of components for each user in accordance with their peak demands [kW] (Adapted from [6]).
The devices investment costs are comprehensive of transportation, installation, commissioning, etc., while maintenance costs have been considered proportional to the energy produced by the devices.
Operating costs have been taken into account as proportional to the fuels and electricity costs, while the investment costs’ amortization factors are based on the components lifespans and on the interest rate. The latter have been set up to 6% as a summation of the real interest rate (4%) and of a risk rate (2%). DHCN lifespan duration has been chosen to be 30 years long, 20 years for PVp and STp, 15 years for MGTs, ICEs, ABSs, and HPs, and, finally, 10 years for CCs and BOIs.
Currently, it is not possible to consider the energy market prices because they do not reflect the common conditions that should be found in a normal dynamic before the pandemic. Natural gas average market values of 0.06 €/kWh and 0.045 €/kWh have been adopted for BOIs and cogeneration devices, respectively, while a value of 0.17 €/kWh has been assumed for the purchase of electricity. Since the prices for selling electricity to the main grid depend on the contract conditions, a significantly lower price of 0.10 €/kWh has been selected with respect to the one relating to the purchase of electricity.
CO2 emissions are proportional to the electricity and natural gas consumption. A value of 0.356 kg CO2/kWh has been adopted for the electricity purchased from the grid as an average between the values relative to the period 2011–2017 [47], while a value of 0.200 kg CO2/kWh has been selected for the natural gas used to feed BOIs and cogeneration devices [49].
4. Results and Discussions
The optimization conducted in this study has an hourly resolution and considers two typical days per month to represent an entire year of operation for the EC. The two typical days are intended to correspond to one working and one non-working day for each month. In each studied case, the optimization determined the optimal configuration and operation strategy for the EC. The aim of the objective function was to optimize the total annual cost for owning, operating, and maintaining the whole EC system.
In a previous study (Casisi et al. [6]), the model was developed and optimized. However, in order to perform comparisons, new simulations were performed using their model, though now with updated energy demand inputs (electricity, heat, cooling). Then, with the modifications made to this model (as described in Section 2), it was possible to simulate a scenario where all users within the EC share electricity among them. For that reason, this section focuses on the comparison of three optimal solutions for the following EC scenarios:
- Conventional solution (CS);
- Energy Community Solution (ECS);
- Sharing Electricity Solution (SES).
ECS refers to the most complete scenario analysed by Casisi et al. [6]. SES is based on ECS but with the implementation of the sharing electricity methodology described in Section 2.5. CS is also based on ECS; however, when it comes to equipment, the model is allowed to deal only with BOIs, CCs, and TStors at the user level (there is no district pipelines network). All simulations were performed through X-press software [50], using Mosel programming language [51], and accepting a 2% gap. The PC used to run all simulations is provided with an Intel Xeon CPU 3.3 GHz, 32 GB of RAM memory, and Windows 10 Pro for Workstations. Although using a relatively good computer, the computation time may be as short as a few hours or as long as one week, as it depends on several aspects; moreover, a previous research published in 2019 [52] presented a possible alternative to cope with such a situation.
4.1. Superstructure for Each EC Scenario Plus DHCN Diagrams
Before examining the figures of the results, it is relevant to keep in mind the pictured scenarios and the main differences among them. All scenarios are designed to fully cover the electricity, heat, and cooling demands of each user within the EC. As mentioned in the last section, the scenarios are CS, ECS, and SES.
The CS scenario has the aim of representing reality for most cases nowadays. Here, all the electricity, heat, and cooling demands are covered by electricity bought from the electric grid, a local BOI, and a local CC, respectively. In order to support the BOI and CC, heat and cooling storages were also considered (Figure 5). As observed, in this case, there is no connection among the users, i.e., there are no DHCN pipelines connecting them. This scenario was included to serve as a base case for the other two scenarios, i.e., to help in the assessment of the actual improvements provided by the proposed enhanced scenarios.
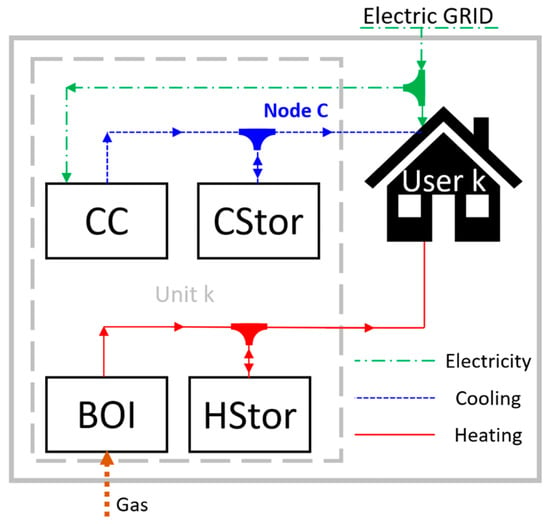
Figure 5.
Superstructure for the conventional solution.
The ECS scenario refers to the most complete one proposed by Casisi et al. [6]. In this scenario (Figure 6), each user can own a set of polygeneration components to cover their demands and share energy with the other users within the EC (through the DHCN). The ECS scenario is also provided with a central unit which is also connected to the DHN (a detailed explanation of this superstructure is presented in Section 2). However, a crucial limitation of this scenario is the lack of sharing electricity among the users.
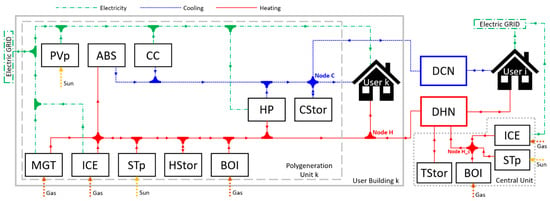
Figure 6.
Superstructure for the complete distributed solution without sharing electricity.
For this reason, and based on the ECS scenario, the SES one (Figure 1) was developed so that users have no direct connection with the electric grid. Instead, the electricity connection of all nine users with the electric grid is managed by the distribution substation (DS). The DS has the task of covering the electricity demand of each user by either buying it from the electric grid or by transferring the electricity surplus from other user(s) within the EC (the methodology is better described in Section 2.3).
As specified in Section 3, the EC comprises nine users distributed throughout the city centre of Pordenone, Italy (Figure 3). The simulated ECS and SES scenarios also provided an optimal configuration for the pipelines of the DHCN (Figure 7), i.e., based on the minimization of the economic objective function, the optimizer decided which users can be interconnected and the amount of energy transferred through these pipelines.
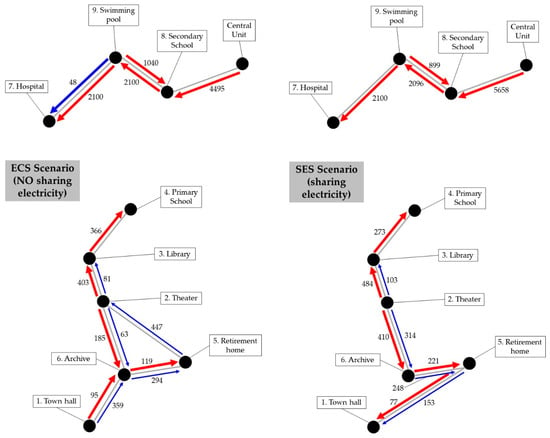
Figure 7.
Schematic diagram for the DHCN pipelines: ECS scenario: complete distributed solution without sharing electricity. All values in kW.
The DHCN configuration presented in Figure 7 shows the interconnections among users for the optimal solution derived from the ECS scenario (left) and SES scenario (right). As observed, in both cases, the users were divided into two parts: (1) users from 1 to 6; (2) users from 7 to 8 plus a central unit. The reason for this is most likely the physical distance between the users comprising these two parts. To have an idea, the shortest distance between users from the two parts (user 4 to user 8) is about 1000 m, while the average distance among users within each part is about 400 m. Installing pipelines between them would certainly increase the total cost objective function as well as the heat losses from thermal energy transferred through pipelines. Comparing both scenarios, it is possible to recognize that the scenario with the implementation of sharing electricity has one interconnection less (grey lines). It represents a reduction of 7.2% in the total annual cost with the DHCN (which corresponds to about 77.6 k€). Moreover, although both optimal solutions resulted in the same number of heating pipeline connections (red arrows in Figure 7), the solution derived from the implementation of sharing electricity resulted in only four cooling pipeline connections (blue arrows in Figure 7), while the other solution resulted in six cooling pipeline connections.
4.2. The Three Scenarios: Results and Comparison
This section is intended to present the results of the three scenarios, since a comparison among them could be more meaningful to the reader. Table 4, Table 5, Table 6 and Table 7 present the results regarding the total installed capacities of each component for both user k and the central unit, the number of DHCN pipelines, the required/produced energy quantities, the main related costs, as well as the main related CO2 emissions.

Table 4.
Total installed capacities for all nine users. Optimal components’ configuration for the three studied scenarios.

Table 5.
Optimal configuration for the central unit and DHCN pipelines.

Table 6.
Optimal energy magnitudes for the three analysed scenarios. Values refer to the total energy for a whole year.

Table 7.
Optimal economic and environmental results of the three studied scenarios.
Table 4 shows the total installed capacities for the nine EC users and the three analysed scenarios, while Table 5 presents the optimal configuration for the central unit and DHCN pipelines. Based on the superstructure presented in Figure 1, Figure 5 and Figure 6, the optimizer defined the best configuration in terms of the minimization of the total annual cost. As depicted in Figure 5 and presented in Table 4 and Table 5, the CS scenario is allowed to work only at the user level (no central unit or DHCN pipelines) and is limited to four types of components to cover heating and cooling demands plus the electricity bought from the grid. By comparing these results with the other two scenarios, it is possible to observe the substantially higher capacities needed for BOI and CC. Although fewer components are needed in the CS scenario, its total annual cost is almost doubled when compared to the other two scenarios. As can be easily inferred, this is due to the higher amounts of gas and electricity required, although the optimal solution has also included heat storage.
An analysis of the total installed capacity results from the ECS and SES scenarios can be achieved by keeping the focus on Table 4. By comparing their respective columns, it is possible to observe that the total installed capacity of each component was reduced with the implementation of the sharing electricity methodology, except for the ABSs and HPs.
Although the total installed capacity of the ABSs is increased (by 20%), the number of installed units is actually reduced (by 17%). The results from the ECS scenario show that the total installed capacity of 875 kW for ABSs is, in reality, divided among five users. Users 1–3 (see Figure 7) received one ABS unit each, while users 5 and 7 received four and five ABS units, respectively. When it comes to the SES scenario, the results show that the 1050 kW of the total installed capacity of ABS is spread between only two users. Users 2 and 7 received five ABS units each. As depicted in Figure 7, the ABS units installed for user 2 are intended to feed part of its cooling demand and send the remaining cooling energy to nearby users through the DCN, whereas the ABS units installed for user 7 are intended to only feed part of its cooling demand. In summary, on one hand, the optimal solution installed 12 ABS units for the ECS scenario (spread among five users), while, on the other hand, it installed 10 ABS units for the SES scenario (divided into two users).
When it comes to HPs, the optimal solution increased the total installed capacity by 16% and also increased the total number of installed HP units by 25% when comparing the ECS and SES scenarios. In order to understand this result, it is essential to keep in mind the following: one of the main achievements (for the EC) derived from the implementation of the sharing electricity methodology presented in Section 2.5 was the increased amount of consumed electricity originated from self-production within the EC. To have a clearer picture of such a fact, the reader may look at Table 6. This table is divided into four sections dedicated to the electricity, heat, cooling, and fuel energy magnitudes. From the electricity section, it is possible to observe that, comparing the optimal results from the ECS and SES scenarios, the total electricity bought and sold by the EC decreased by 85% and 32%, respectively, when users are allowed to share electricity among each other. In other words, the EC is relying substantially less on the external electric grid to cover its electricity demands, and about 1/3 of the electricity sold in the scenario without sharing electricity is used within the EC based on sharing electricity.
Table 5 shows the optimal configuration when it comes to the central unit and DHCN pipelines. The amount of heat transmitted through the central pipeline and the size of the solar thermal field installed in the central unit are, respectively, 26% and 16% higher for the scenario with sharing electricity. In fact, the optimal solution for the SES scenario reduced the installed capacities of cogeneration systems and boilers. User 7 (hospital), for example, did not receive MGT in the solution with sharing electricity. As user 7 makes part of the group of users connected with the central unit (Figure 7), and it is possible to infer that the reduction in cogeneration systems and BOIs had compensation, with more heat coming from the central unit. Regarding the number of DHCN pipelines, the reader is invited to refer to Section 4.1.
Table 6 presents the optimal total energy magnitudes for the three scenarios. Rows-wise, the table is divided into four main sections concerning electricity, heat, cooling, and fuel figures. As mentioned in Section 4.1, the CS scenario comprises only BOIs, CCs, TStors and CStors, which means that the whole demand must be taken from the utility supplier. For this reason, the amount of electricity and gas that must be purchased is substantially higher when compared to the other scenarios. Consequently, the amount of CO2 emissions in this scenario is 44% and 49% higher when compared to the ECS and SES scenarios, respectively (see Table 7).
Before analysing the ECS and SES scenarios, it is important to properly understand the meaning of the rows “Total IN” and “Total OUT” (Table 6). For the case of electricity, the first one means the total amount produced locally (by the EC) plus the amount purchased from the electric grid. The second one means the amount of electricity required by the CCs and HPs plus the total electricity sold to the grid. As observed in Table 6, the total electricity IN, for the scenario with sharing electricity (SES), is 8.5% lower compared to the one without sharing electricity (ECS), while the total electricity OUT is 24% lower. If the focus is kept only on the electricity bought/sold from/to the grid (SES scenario), it is possible to see that they were 85%/32% lower, respectively, if compared to the ECS scenario. This result shows the effect on the energy dispatch in the electric grid, i.e., less electricity is allocated to the grid by the EC and less electricity must be found in the grid in order to cover the EC demand.
With the aim to make the effect on the electricity exchange more evident to the reader, Figure 8 and Figure 9 were included to demonstrate the behaviour of the electricity bought and sold throughout a year. Figure 8 represents the electricity exchange between the EC and the electric grid for the scenario without sharing electricity (ECS), while Figure 9 represents the scenario with sharing electricity (SES). Since the hourly behaviour of an entire year is represented by 12 months made of two typical days each (working and non-working days), the total number of hours presented in both graphs is 576.
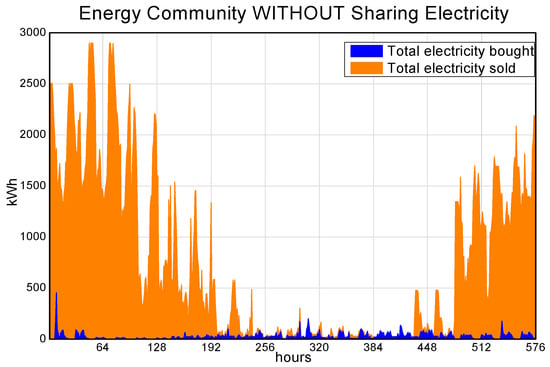
Figure 8.
Total electricity bought and sold by all EC users together (ECS scenario—without sharing electricity).
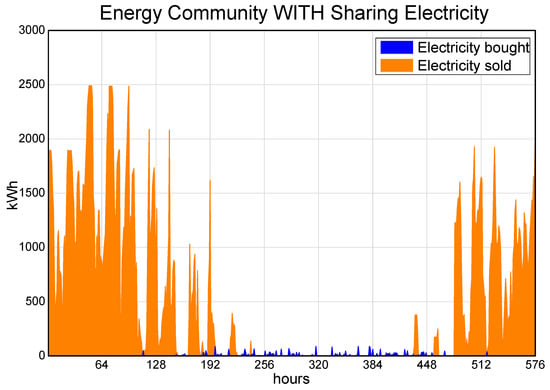
Figure 9.
Total electricity bought and sold by the DS (SES scenario—with sharing electricity).
Another crucial aspect to bear in mind is that the curves in Figure 8 represent the total electricity bought and sold by all users together. In other words:
- Total electricity bought curve (blue one) → summation of the electricity bought hourly by each building;
- Total electricity sold curve (orange one) → summation of the electricity sold hourly also by each building.
Figure 9 also represents the total electricity bought and sold by the EC. However, there is a vital difference here. Since Figure 9 represents the EC with sharing electricity, the users have no direct connection with the main electric grid. Instead, as described in Section 2.3, the users are all connected to a distribution substation (DS) which manages the connection with the electric grid, i.e., the processes of buying and/or selling all the electricity demanded and/or produced by the EC. In other words, Figure 9 represents:
- Electricity bought curve (blue one) → total electricity bought by the DS;
- Electricity sold curve (orange one) → total electricity sold by the DS.
By comparing Figure 8 and Figure 9, the effect of the presented sharing electricity methodology is evident. The total electricity sold in Figure 8 (without sharing electricity) is more prominent if compared with the equivalent curve in Figure 9 (with sharing electricity). Moreover, as observed also in Figure 8, the curves of total electricity bought and sold overlap throughout almost the entire year. This happens because, as the users in the ECS scenario are individually connected to the electric grid, at a given moment, a certain user might have an electricity surplus (and sell electricity to the grid) while another user does not cover its electricity demand with self-production (and buy electricity from the grid). On the contrary, this cannot happen to the EC based on the SES scenario. As explained in Section 2.5, the DS cannot buy and sell electricity at the same time. If there is an electricity surplus in the DS, the priority must be given to fulfil the electricity demand of the users within the EC. Only when every single user is fulfilled and there is still an electricity surplus is the DS allowed to sell it. This is the reason why Figure 9 does not present an overlap of the curves. Therefore, it is possible to infer that the EC based on sharing electricity (SES scenario) provides a higher amount of self-produced electricity available to its users. Thus, the optimizer can install more electricity-based components (CCs and HPs) to the detriment of the cogeneration ones. Such a fact can be observed in Table 6, where the EC based on the SES scenario supplied 43% and 45% more electricity to CCs and HPs, respectively.
The heat section in Table 6 shows the figures for produced, consumed, and demanded heat. The first thing that should be kept in mind is the fact that each heat-producing component has its efficiency, and, for that reason, they should produce more heat concerning the heat demand (as clearly observed in the column regarding the CS scenario). The second thing is the higher amount of heat produced by BOIs (+36%), HPs (+86%), and STp (+15%) when comparing ECS and SES scenarios. A higher amount of heat derived from HPs is consistent with the fact that more self-produced electricity is used within the EC. Although the optimizer devoted fewer STp to the EC users, the central unit received 16% more STp in the SES scenario. This increase in STp in the central unit together with a higher amount of heat produced by BOIs can assist in the compensation of fewer installed cogeneration components. Consequently, with higher amounts of produced heat and transported heat through the DHN (Figure 7), the heat wasted resulted in a 21.5% higher rate in the SES scenario.
The cooling section in Table 6 gives the values for produced, wasted, and demanded cooling energy. The cooling produced by CCs and ABSs is 43% and 8% higher for the SES scenario. The higher amount of cooling produced by CCs demonstrates the higher consumption of self-produced electricity within the EC, while the higher amount of cooling produced by the ABSs is a consequence of the higher amount of heat required by them. However, the cooling produced by the HPs was 21% lower for the SES scenario, which shows that the emphasis given to HPs had heat production as the focus. The cooling waste was considerably reduced (−66%) in the SES scenario, which is explained by the reduction in DCN pipelines from six to four.
Table 7 displays the optimal economic and environmental results obtained from simulations performed under the three considered scenarios. From the CS scenario outcomes, the only values that are lower than the respective ones from the other two scenarios are total maintenance cost, total recovered capital, total annual investment cost, and emissions from NG combustion. The first three figures are explained by the substantially lower number of components considered in the CS superstructure (Figure 5). The fourth figure (emissions from NG combustion) is explained by the same reason; however, in this scenario, a higher amount of electricity must be bought from the electric grid. Such a fact contributes to the total annual emissions that are, at least, 44% (or 3430 t/y) higher than the total ones from the other two scenarios.
By comparing the ECS and SES scenarios, Table 7 reveals the effect of the sharing electricity methodology, introduced in this paper, on the costs and emissions of the studied EC. Starting from the objective function (total annual cost), the optimization results showed a reduction of 80 k€/y (−3.4%). Such a decrease was achieved by reductions in the installed components (with consequent decline of the maintenance and investment costs), number of DCN pipelines, and NG consumed by cogeneration systems. Another important contributor to such a reduction was the decreased total annual cost with electricity bought from the grid. The EC based on sharing electricity spent 85% less money buying less electricity from the grid, which allowed saving around 33 k€/y. The revenue from selling electricity to the grid was 32% lower; however, it is compensated by the higher self-consumption electricity within the EC. Despite such a total cost diminution, the total operation cost increased by 20% due to the higher amount of NG consumed by BOIs.
The situation regarding the total emissions was also improved. Dealing with the same comparison of scenarios, the total emissions derived from the electricity bought from the grid was reduced in 70 t CO2/y (−85%), while the total emissions from NG combustion was reduced in 858 t CO2/y (−9%). This last figure highlights the lower emissions at local level, i.e., the EC tends to burn less NG with the implementation of sharing electricity. Such a fact is made more evident with the sensitive analysis performed for the SES scenario (next section). Since the saved emissions due to electricity sold to the grid was also reduced (−32%), the effect on the total annual emissions was not so large. The implementation of the SES scenario allowed for a reduction of 280.1 t CO2/y (−4%) in the total annual emissions.
4.3. Sensitive Analysis of the Sharing Electricity Solution
This section aims to investigate the performance behaviour of the EC, based on sharing electricity (SES scenario), when the prices of the utilities are altered. The optimization model receives, as inputs, the utility prices for gas, electricity bought, and electricity sold. As explained in Section 3, the price for gas is divided into two categories: gas for CHP components (ICEs and MGTs) and gas for BOIs. As shown in Figure 10, six scenarios were created to simulate variations in the utility prices and to compare these variations with the original sharing electricity scenario (SES).
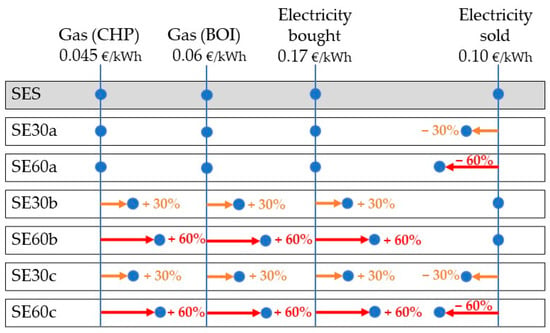
Figure 10.
Illustration of the original scenario (SES) plus the six additional ones where the sensitive analysis was based.
The original scenario (SES) was configured with the following utility prices (Figure 10): 0.045 €/kWh for gas-feeding CHP components, 0.06 €/kWh for gas-feeding boilers, 0.17 €/kWh for electricity bought, and 0.10 €/kWh for electricity sold. The sensitive scenarios were divided essentially into two categories: SE30 for price variations of 30% and SE60 for price variations of 60%. Then, these two categories were distributed into three subcategories: “a” (variations only in the price of electricity sold), “b” (variations only in the price of gas and electricity bought), and “c” (variations “a” and “b” together). For an easier understanding, Table 8 presents the values of the utility prices for each scenario.

Table 8.
Utility prices for the original scenario (SES) plus the six additional ones. All values expressed in €/kWh.
Figure 11, Figure 12 and Figure 13 report the optimal configuration, in terms of installed capacity, for each component in each scenario (for both users and central unit). Figure 11 shows the behaviour of installed capacities for engines, absorption chillers, heat pumps, and PV panels (all of them at user level). As observed, the installed capacity of engines (ICE) is around the same for both reference scenarios (ECS and SES). However, the sensitive analysis showed that all scenarios with altered utility prices resulted in a reduction of around 15% of the installed capacity of engines. In order to understand it, the reader should keep in mind the increase in the prices for gas and electricity bought and the decrease in the price of electricity sold for the six scenarios presented in Table 8. With such price alterations, the optimizer does not identify the same advantage as before to self-produce more electricity to obtain the revenue by selling electricity to the grid. Instead, the optimizer suggests a configuration where the EC produces and sells less electricity. As an alternative, the optimizer proposes to use the non-sold electricity to feed more HPs. Indeed, the total installed capacity of HPs increases by 75% on average for the six sensitive scenarios. Moreover, the amount of electricity destined to feed HPs increased by almost three times (see Table 9).
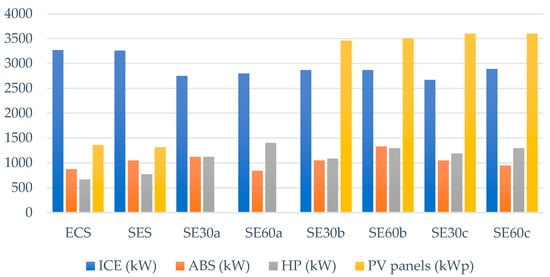
Figure 11.
Total installed capacities for engines, ABSs, HPs, and PVp in the 9 users together. Sensitive analysis for the two reference scenarios (ECS and SES) plus the results for six additional scenarios.
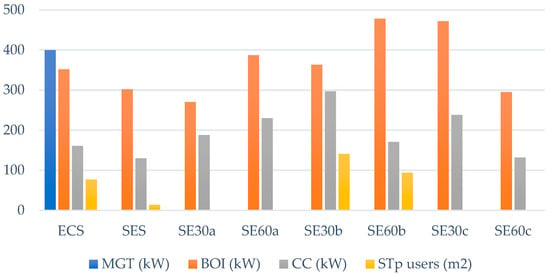
Figure 12.
Total installed capacities for MGTs, BOIs, CCs, and STp in the 9 users together. Sensitive analysis for the two reference scenarios (ECS and SES) plus the results for six additional scenarios.
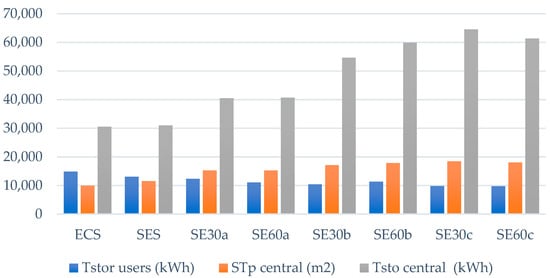
Figure 13.
Total installed capacities for heat storage in the 9 users together, ST panels in the central unit, and heat storage in the central unit. Sensitive analysis for the two reference scenarios (ECS and SES) plus the results for six additional scenarios.

Table 9.
Total annual energy magnitudes for electricity, heat, cooling, and fuel of the ECS (without sharing electricity) and SES (with sharing electricity) scenarios, as well as the six scenarios for the sensitive analysis. All values in MWh.
The decrease in gas consumption by BOIs and the increase in heat storage in the central unit are two key consequences for such an increase in the HPs’ installed capacity. Such a fact shows the tendency that the EC has to store electricity when there is no convenience to sell it to the grid. Since no electricity storage was considered for this EC, the optimal solution suggests the storage of heat by powering more HPs. Nevertheless, even in this way, the presence of a higher heat storage capacity prevents the optimizer to install even more HPs, since the EC can take part of the demanded heat from the heat storage.
The reference scenarios (ECS and SES) installed around 1340 kWp of PVp each. However, the scenarios SE30a and SE60a did not consider the installation of PVp in their optimal solution, as observed in Figure 11 also. These are the scenarios with alterations only in the price of electricity sold. Therefore, there is no advantage in putting PVp when such a low price for selling electricity is considered, since it is possible to obtain more electricity from the engines. Moreover, installing any additional component means higher costs in purchase, operation, and maintenance. On the contrary, the scenarios SE30b, SE60b, SE30c, and SE60c suggest a lot more PVp compared to the reference scenarios. The reason for this is the increase in the price required to buy gas and electricity. Now, the disadvantage is to install more CHP components and/or buy electricity from the grid. Even with the mentioned costs related to any additional component, producing a percentage of the electricity demand from PVp is now more advantageous since the objective function (total EC annual cost) can be kept at the lower possible value, given the imposed gap.
The installed capacity of ABSs did not present a substantial variation (Figure 11). Comparing the reference scenarios (ECS and SES) with the six sensitive scenarios, the ABS-installed capacity increased by approximately 9% on average, while its produced cooling increased by around 5% (Table 9). Bearing in mind the same comparison, the installed capacity of CCs increased, on average, by 23% (Figure 12), and its produced cooling increased by 44% (Table 9). This is consistent with the same explanation for HPs, i.e., the optimizer suggests selling less electricity in order to feed not only more HPs, but also more CCs. Regarding MGTs, as the ECS scenario is not provided with sharing electricity, the optimization found a better solution where two 200 kW MGTs each are placed in building 7 (hospital). However, none of the other scenarios comprise MGTs. One of the reasons for this fact is the higher purchasing price of MGTs, which are between 12% and 43% more expensive if compared with ICEs. Moreover, it is more economically advantageous when using the electricity received from other users rather than installing more CHP components (whether they are ICEs or MGTs).
The installed capacity of BOIs is defined so that it can cover the heat gap (between heat produced by other components and the heat demand) when it is economically viable. In order to have an idea, BOIs cover the total heat demand in the CS scenario. For this one, the installed capacity of BOIs was 9460 kW (Table 4) while the average between all the other scenarios is around 360 kW (Table 9). Comparing the reference scenarios (ECS and SES) and the six sensitive ones (Figure 12), the installed capacity of BOIs varies up to an increment of about 55%. However, by analysing the amount of heat produced by BOIs (Table 9), it is possible to see that, for the same comparison, the heat produced decreases in the range of 37–70%, except for scenario SE30c, where the optimal size of the ICEs is the minimum. A possible reason is the substantial increase in heat storage in the central unit (Figure 13). Although the heat storage at the user’s level decreases in a range between 5% and 24%, the heat storage at the central unit increases by up to 100%. This higher storage capacity can compensate for the necessity of burning more gas to obtain the desired amount of heat. This effect is even more evident for the sub-DHN made up by the buildings 7–9, for which total heat demand amounts to 87% of the total heat demand of the entire EC. These buildings are directly connected to the central unit through one of the two sub-DHN (Figure 7), and this is the main reason why the optimization result suggests such an increase in the heat storage of the central unit, as well as an increase in the STp installed in the central unit, as explained next.
Solar thermal panels (STp) should be evaluated at both user (Figure 12) and central level (Figure 13). Moreover, two crucial aspects should be kept in mind: the model is configured to install more PVp than STp at user level; and there is a restriction regarding the total available rooftop area at user location. This can be observed in Figure 11 and Figure 12, i.e., a lot more PVp are installed to the detriment of STp, except for scenarios SE30a and SE60a. Therefore, the alteration only in the price of electricity sold results in more heat and electricity being obtained from ICEs (Table 9), i.e., the optimizer concludes that it is more economically advantageous to give more fuel to the ICEs rather than installing PVp and STp. Nevertheless, the total heat produced by STp (Table 9) increased by 58%, on average, for the six sensitive scenarios in comparison with the two reference ones. Figure 13 adds additional pieces of information to explain this fact. As noted, the installed capacity of STp in the central unit also increased by around 58%, which provides a great amount of heat to be distributed to users through the DHN.
Figure 14 shows the behaviour of the total cost of electricity bought and total revenue obtained from electricity sold to the grid by the entire EC. What stands out in the figure is the influence that the implementation of sharing electricity among users (by comparing ECS and SES scenarios) imposes on the overall performance of the EC. The SES scenario allowed the EC to spend 85% less money per year by buying less electricity from the grid, although the revenue from electricity sold to the grid decreased by 32%. However, this lower income is an indication that the EC is using a higher percentage of the self-produced electricity to feed its members.
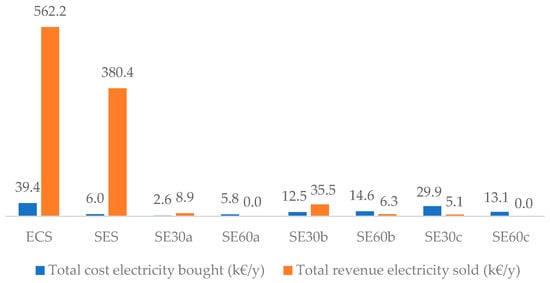
Figure 14.
Total annual cost of electricity bought and sold by the EC. Sensitive analysis for the two reference scenarios (ECS and SES) plus the results for six additional scenarios.
Figure 14 also presents the behaviour of the six sensitive scenarios for the EC. It is apparent from this figure that the variation on the utility prices plays an important role in the amount of electricity exchanged between EC and electric grid. As explained in the assessment of Figure 11, the variation of utility prices tends to guide the optimization to a solution where a greater amount of self-produced electricity is used within the EC.
Still, in Figure 14, the EC buys and sells very few amounts of electricity in the SE30a and SE60a scenarios. As shown in Table 9, the “Total electricity IN” for these two scenarios is around 15% lower when compared to the SES scenario. This is directly related to the lower electricity produced from ICEs. With the lower price for selling electricity, the optimizer finds that there is no longer advantage on selling electricity produced by ICEs. Instead, the EC can burn a lower amount of gas to generate electricity and heat, buy few amounts of electric energy when it is needed, and still use a considerable amount of self-produced electricity to drive electric-based equipment.
The scenarios SE30b, SE60b, SE30c, and SE60c presented the same tendency as the first two scenarios, i.e., lower electricity produced from ICEs. Another important aspect from the results of these four scenarios is the presence of a considerable amount of electricity produced from PVp. As can be noted in Table 9, in these four cases, the optimizer found it more interesting to lower the amount of electricity generated from ICEs to compensate it with PVp. Then, the following question may arise: considering that these four scenarios have higher prices for gas and electricity, why does the EC buy more electricity (comparing to the SES scenario) in these four scenarios? The answer is relatively simple: at some hours of the year, the optimizer finds that it is more economically advantageous to buy the missing amount of electricity needed to cover the demand from the grid rather than installing more ICE and/or PVp units. Then, the different behaviours of the total electricity sold, among the six sensitive scenarios, will depend on whether the solution prescribes a higher or lower electricity consumption by HPs and/or CCs.
Figure 15 provides an overview of the total costs related to the operation, maintenance, and purchase of the energy systems of the entire EC, as well as the total cost of the DHCN and the total annual recovered capital. Starting by comparing the scenarios ECS and SES, it is possible to observe that the costs were slightly affected by the implementation of the sharing electricity. The maintenance costs remained the same, while the investment with components and the network (DHCN) costs decreased, respectively, by 6% and 7%. This is explained by the lower installed capacity (SES scenario) for some of the components. However, the operation costs increased by around 20%. The reason for this is twofold: (1) increase in the installed capacity of some of the components; (2) increase of 35% in the fuel requested by BOIs.
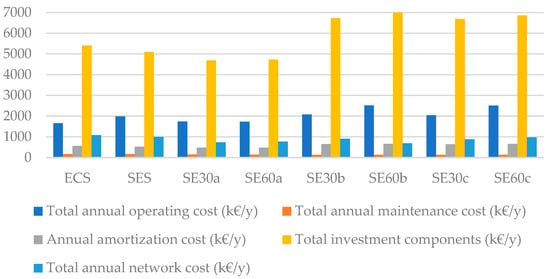
Figure 15.
Total annual cost of operation, maintenance, and investment for the EC energy system. Sensitive analysis for the two reference scenarios (ECS and SES) plus the results for six additional scenarios.
The reader is now invited to keep the focus on the six sensitive scenarios (Figure 15). The first and easier analysis is about the lower values for scenarios SE30a and SE60a. The purchase utility prices were not varied; however, only the price of electricity sold. Therefore, it is straightforward to observe that, in these cases, the total annual costs reported in Figure 15 are slightly lower compared to the reference SES scenario. In contrast, the remaining four sensitive scenarios (subcategories “b” and “c”) presented the higher annual cost results, which are directly related to the higher prices of gas and electricity. This is especially true for the total annual operating costs, which were 32% higher (on average) than the “a” scenario and are directly associated to the price of the gas. Bearing the same comparison in mind, the total investment costs with components were, on average, 42% higher in the subcategories “b” and “c”. This is due to the considerable increase in the installed capacity of components such as ABSs, HPs, PVp, STp, and TStors.
One of the results presented in Figure 16 is the total annual cost of the entire EC. As noted, the three subcategories (“a”, “b”, and “c”) present approximately the same behaviour of the costs reported in Figure 15. By comparing with the scenario without sharing electricity (ECS), the scenarios SES, SE30a, and SE60a provide savings of 80, 31.6, and 23.2 k€/y, respectively, while the scenarios SE30b, SE60b, SE30c, and SE60c resulted in total annual cost increase of 456.8, 930.5, 457.4, and 929.6 k€/y. Analogously, as also reported in Figure 16, the scenarios SES, SE30a, and SE60a resulted in approximately the same level of total annual CO2 emissions. However, in the scenarios SE30b, SE60b, SE30c, and SE60c, the EC emitted, on average, 9% less CO2 per year (or 690 t CO2/y), which is in agreement with the lower gas consumption in these scenarios (Table 9 and Figure 17).
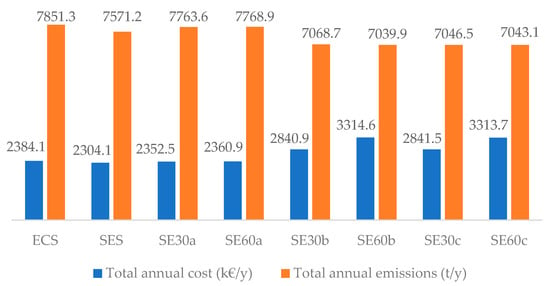
Figure 16.
Total annual CO2 emissions and costs of the EC. Sensitive analysis for the two reference scenarios (ECS and SES) plus the results for six additional scenarios.
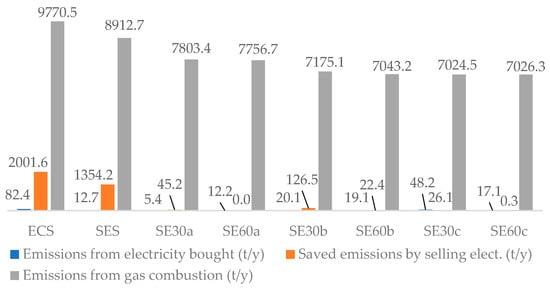
Figure 17.
Total annual CO2 emissions from electricity bought and gas combustion, as well as saved emissions due to electricity sold. Sensitive analysis for the two reference scenarios (ECS and SES) plus the results for six additional scenarios.
Figure 17 shows the emissions picture in more detail. It is possible to note that, although the scenarios SE30a and SE60a resulted in the same level of total annual emissions as scenario SES (Figure 16), the emissions due to gas combustion in this scenario was about 14% higher if compared to the same emissions for scenarios SE30a and SE60a (Figure 17). However, scenario SES (and scenario ECS) was provided with a compensation due to saved emissions by selling electricity. It is also easy to recognize that the emissions from gas combustion (Figure 17) follow the same pattern as the total annual emissions (Figure 16).
The effect on the electricity exchange between DS and electric grid is presented for each sensitive scenario (Figure 18). Following the same pattern of Figure 8 and Figure 9, the behaviour of the electricity bought and sold, throughout a year, is represented by 12 months made of two typical days each (working and non-working days), so that the total number of hours presented in the graphs is 576.
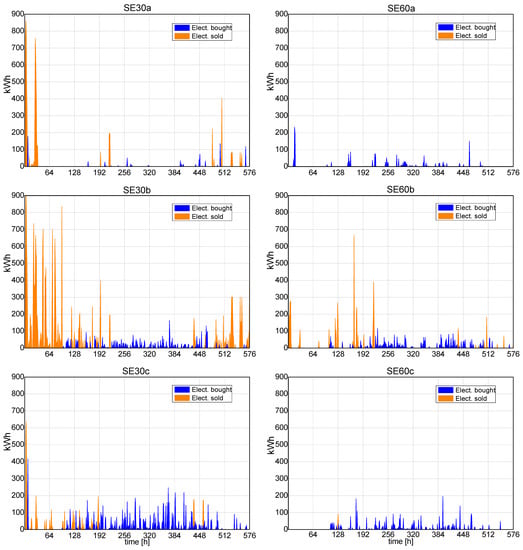
Figure 18.
Total electricity bought and sold by the DS. Behaviour according to sensitive scenarios SE30a, SE30b, SE30c, SE60a, SE60b, and SE60c.
In order to understand the reasons for such variations (Figure 18), the reader is encouraged to first analyse and compare subcategories “a” and “c”. Both of them are set up with reductions in the electricity sold price (Table 8); however, only subcategory “c” is set up with increases in the prices of gas and electricity bought. Thus, it is possible to note that subcategory “a” bought less electricity than “c”, even though “c” has higher utility prices. One reason for this is that, as the prices are higher, not only for electricity, but also for gas, the optimization is conducted to a solution where less gas is supplied to ICEs. In fact, the solutions for “c” received, on average, 10% less gas for ICEs than the solutions for “a” (Table 9). A consequence for this is less self-produced electricity within the EC, which leaves no choice if one cannot buy more electricity.
Subcategory “b” has no changes in the price of electricity sold; it has them only in the prices of gas and electricity bought (Table 8). In this scenario, the optimizer still finds advantages in selling more electricity and, in fact, scenario SE30b sells more electricity than all the other scenarios. When it comes to the electricity bought, subcategory “b” found a middle term between “a” and “c”, i.e., solutions in “b” suggest more gas to ICEs with respect to “c” but, at the same time, less gas to ICEs with respect to “a”. That is why scenario “b” bought more electricity than scenario “a” and less than scenario “c”.
5. Conclusions
The aim of the present research study was to apply a sharing electricity (SE) option to an energy community (EC) previously studied by our research group and to evaluate the effects on the performance of the EC from a technical, economical, and environmental viewpoint. In the mentioned previous study, the EC shares thermal energy among its users; however, each user is connected individually to the electric grid. In the present study, users have no direct connection with the electric grid; instead, they are connected to a distribution substation (DS) which manages the exchanges of electricity between users and the connection with the electric grid.
The optimization was performed through a Mixed Integer Linear Programming (MILP) model running in the X-press software and written in the Mosel language. The EC comprises nine tertiary sector buildings connected through a DHCN, in a small city in the northeast of Italy. The model optimization allowed the definition of the optimal solution for three types of scenarios: conventional solution (CS), Energy Community Solution (ECS)—without sharing electricity—and Sharing Electricity Solution (SES). The optimal configuration for all scenarios was determined in a way that minimizes the total annual cost of the entire EC.
The CS scenario has been added to represent the reality of most current cases and to serve as a reference when analysing the other two scenarios. The scenarios ECS and SES provided a substantial reduction in the total annual costs and total annual CO2 emissions when compared to the CS scenario. ECS allowed reductions of 45.4% and 30.4% in the total annual cost and total annual emissions, respectively, while SES provided reductions of 47.3% and 32.9% in the same parameters.
The effect of the sharing electricity implementation is evaluated by comparing scenarios ECS and SES. The results revealed improvements both in the total annual costs (−3.4%) and total annual emissions (−3.6%) when the SE is applied to the EC, which represent reductions of 80 k€/y and 280.1 t CO2/y, respectively. Moreover, the SE implementation allowed the following:
- Reduction by 84.6% of the total electricity bought from the grid;
- Reduction of 32.4% of the total electricity sold to the grid, which indicates a higher consumption of self-produced electricity within the EC, corroborated by higher installed capacity and electricity consumption of HPs;
- Reduction of emissions at local level, i.e., emissions due to combustion of gas were reduced by 9%;
- Reductions on the annual amortization cost (−6.7%), total investment costs with components (−5.8%), and total annual costs with the DHCN (−7.2%);
- Reduction in installed capacity of components such as MGTs (−100%), BOIs (−14.2%), CCs (−22%), and DCN (−33.3%).
Regarding the reductions on the total electricity bought and sold, it is possible to conclude that the SE implementation is effective in reducing the electricity exchange with the electric grid, i.e., it is moving the EC towards a more “isolated” scenario where it would become gradually independent from the main grid. Such a scenario could also contribute to a better dispatch on the main grid, i.e., less electricity would be allocated in the main electric grid by the EC and also less electricity would have to be demanded from the main grid to feed the EC.
The sensitive analysis of the EC based on SE was performed by varying the utility prices, i.e., the prices for buying gas and electricity, as well as the price for selling the self-produced electricity. The following highlights show the main crucial results from the analysis of the six sensitive scenarios presented in Section 4.3.
- Both the increases in the gas and electricity prices and the decrease in the price of electricity sold lead the optimization process to a solution where less cogeneration systems are installed. Hence, the EC has a lower gas consumption and lower CO2 emissions;
- The substantial increase in the HPs’ installed capacity (and electricity consumption) along with heat storage (especially in the central unit) and the decrease in gas consumption by BOIs demonstrate the tendency of the EC to store electricity when there is no convenience to sell it. Since no electricity storage was considered for the studied EC, the results show that it stores the electricity in the form of heat by powering more HPs. Then, the heat is used when it is needed. Therefore, if electricity storage was considered, it could increase the positive effect for the EC, because it would allow a more flexible usage of the stored energy;
- No PVp are considered if only the price of the electricity sold is reduced (without increasing the prices of the gas and electricity bought). The solutions for the first two sensitive scenarios (SE30a and SE60a) demonstrate that it is better to supply more gas to ICEs to obtain slightly more electricity than installing PVp plants;
- Variations in the utility prices play a crucial role in the amount of electricity exchanged between the DS and the main electric grid, further reducing the electricity exchange with the electric grid and moving the EC towards an even more “isolated” condition;
- Lower total emission levels are achieved by the EC when higher cost levels of utilities have to be considered. By comparing subcategories “b” and “c” with “a”, it is possible to observe that the total annual emissions were reduced by 9.3% with a consequent increase of 30.6% in the total annual costs (both on average).
Therefore, even from the perspective of an increase in the electrification of all energy sectors, the integration of thermal products from cogeneration systems is expected to play a crucial role in the management of the entire energy system and in a reduction in emissions [34]. The solutions obtained from the MILP model show that introducing the SE option in the EC may allow for a reduction in the total annual cost and in CO2 emissions. Such an option strongly contributes to a better dispatch on the main grid. The expectation is that the adoption of renewable fuels and the introduction of electricity storage could further improve the positive effect of the EC with respect to CO2 emissions and the management of the national electricity grid.
Author Contributions
Conceptualization, M.C. and M.R.; methodology, R.D.S., M.C., E.N. and M.R.; investigation, R.D.S., E.N. and M.C.; resources, M.C. and M.R.; data curation, R.D.S., E.N. and M.C.; writing—original draft preparation, R.D.S., E.N.; writing—review and editing, R.D.S., M.C., E.N. and M.R.; visualization, R.D.S., E.N. and M.C.; supervision, M.R. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
Nomenclature
| δt | Thermal losses percentage |
| Δt | Difference between outlet and inlet temperatures (K) |
| ηboi,c | Central BOI efficiency |
| ψboi,c | Additional variable for the centralized BOI |
| ρp | Medium density (kg/m3) |
| ξice,c | Additional variable for the centralized Internal Combustion Engine (ICE) |
| Ap | Diameter of the pipeline (m2) |
| c | Central unit |
| Cabs | Cold produced by the Absorption Chiller (ABS) (kWh) |
| cabs | ABS investment cost (€) |
| cboi | BOI investment cost (€) |
| cboi,f | BOI fixed investment cost (€) |
| cboi,v | BOI variable investment cost (€/kW) |
| Ccc | Cold produced by the Compression Chiller (CC) (kWh) |
| Cdem | User cooling demand (kWh) |
| celec,bgt | Cost of electricity bought from the main grid (€) |
| cfue,boi | BOI fuel cost (€/kWh) |
| cfue,chp | Combined Cooling Heat and Power (CHP) fuel cost (€/kWh) |
| cfue,ice,c | Central ICE fuel cost (€/kWh) |
| chp | HP investment cost (€) |
| Chp | Cold produced by the HP (kWh) |
| cice | ICE investment cost (€) |
| cice,f | ICE fixed investment cost (€) |
| cice,v | ICE variable investment cost (€/kW) |
| cinv | Investment annual cost (€/y) |
| cinv,c | Central unit annual investment cost (€/y) |
| cinv,u | Site annual investment cost (€/y) |
| cman | Maintenance annual cost (€/y) |
| cman,abs | ABS maintenance annual cost (€/y) |
| cman,boi | BOI maintenance annual cost (€/y) |
| cman,boi,c | Central BOI maintenance annual cost (€/y) |
| cman,c | Central unit maintenance annual cost (€/y) |
| cman,cc | CC maintenance annual cost (€/y) |
| cman,hp | HP maintenance annual cost (€/y) |
| cman,ice | ICE maintenance annual cost (€/y) |
| cman,ice,c | Central ICE maintenance annual cost (€/y) |
| cman,mgt | MGT maintenance annual cost (€/y) |
| cman,pvp | PV panels maintenance annual cost (€/y) |
| cman,stp | ST panels maintenance annual cost (€/y) |
| cman,u | Site maintenance annual cost (€/y) |
| cmgt | Micro Gas Turbine (MGT) investment cost (€) |
| cnet | DHCN annual investment cost (€/y) |
| cnet,f,c | Fixed cost of the DHCN pipeline (€/m) |
| cnet,v | Variable cost of the DHCN pipeline (€/kW m) |
| cnet,v,c | Variable cost of the central DHN pipeline (€/kW m) |
| cope | Operating annual cost (€/y) |
| cope,c | Central unit annual operation cost (€/y) |
| cope,u | Unit annual operation cost (€/y) |
| cp | Specific heat (KJ/kg K) |
| cpvp | PV panels investment cost (€/m) |
| cstp | Solar thermal panels (ST panels) investment cost (€/m2) |
| cstp,c | Central ST panels investment cost (€/m2) |
| cann,tot | Total annual cost (€/y) |
| Cts | Cooling energy storage input (kWh) |
| cts | Thermal Storage (TS) investment cost (€/kWh) |
| cts,c | Central TS investment cost (€/kWh) |
| d | Generic day |
| Ebgt | Electricity bought from the network (kWh) |
| Ecc | Electricity required by the CC (kWh) |
| Echp | Electricity produced by the CHP (kWh) |
| Ehp,c | Electricity required by the HP when producing cold (kWh) |
| Edem | User electricity demand (kWh) |
| Ehp,h | Electricity required by the HP when producing heat (kWh) |
| Ehp | Electricity required by the HP (kWh) |
| Eice | Electricity produced by the ICE (kWh) |
| Eice,c | Electricity produced by the centralized ICE (kWh) |
| Emgt | Electricity produced by the MGT (kWh) |
| Epv | Electricity produced by the Photovoltaic panels (kWh) |
| Eut | Electricity exchanged between user and distribution substation (kWh) |
| Esel | Electricity sold the network (kWh) |
| emel | Electricity carbon intensity (kgCO2/kWh) |
| emf,boi | BOI fuel carbon intensity (kgCO2/kWh) |
| emf,cen | Central CHP fuel carbon intensity (kgCO2/kWh) |
| emf,chp | CHP fuel carbon intensity (kgCO2/kWh) |
| Emgt | Electricity produced by the MGT (kWh) |
| emtot | Total annual CO2 emissions (kg) |
| Epvp | Electricity produced by the PV panels (kWh) |
| Esel | Electricity sold to the network (kWh) |
| fabs | ABS amortization factor (y−1) |
| Fboi | Fuel required by the BOI (kWh) |
| fboi | BOI amortization factor (y−1) |
| Fboi,c | Fuel required by the central BOI (kWh) |
| fcc | CC amortization factor (y−1) |
| Fchp | Fuel required by the CHP (kWh) |
| fhp | HP amortization factor (y−1) |
| Fice | Fuel required by the ICE (kWh) |
| fice | ICE amortization factor (y−1) |
| Fice,c | Fuel required by the centralized ICE (kWh) |
| Fmgt | Fuel required by the MGT (kWh) |
| fmgt | MGT amortization factor (y−1) |
| fnet | DHCN amortization factor (y−1) |
| fpvp | PV panels amortization factor (y−1) |
| fstp | ST panels amortization factor (y−1) |
| fts | TS amortization factor (y−1) |
| h | Generic hour |
| Habs | Heat required by the ABS (kWh) |
| Hboi | Heat produced by the BOI (kWh) |
| Hboi,c | Heat produced by the central BOI (kWh) |
| Hboi,lim,c | Centralized BOI operation limits (kW) |
| Hchp | Heat produced by the CHP (kWh) |
| Hdem | User thermal demand (kWh) |
| Hhp | Heat produced by the HP (kWh) |
| Hice | Heat produced by the ICE (kWh) |
| Hice,c | Heat produced by the centralized ICE (kWh) |
| Hmgt | Heat produced by the MGT (kWh) |
| Hnet | Thermal energy transferred through the pipeline (kWh) |
| Hnet,c | Thermal energy transferred through the pipeline of the central DHN (kWh) |
| Hnet,lim | Size limits of the pipelines (kWh) |
| Hstp | Solar panel thermal production (kWh) |
| Hstp,c | Centralized solar field thermal production (kWh) |
| Hts | Thermal energy storage input (kWh) |
| Hts,c | Thermal energy storage input (kWh) |
| j | Generic component |
| k | Generic site/user |
| Kfchp | CHP Performance curve linearization coefficient |
| Kfice,c | Centralized ICE Performance curve linearization coefficient |
| Khchp | CHP Performance curve linearization coefficient |
| Khice,c | Central ICE performance curve linearization coefficient |
| Khp | HP Performance curve linearization coefficient |
| Klos,ts | Percentage thermal loss coefficient |
| lp | Length of the pipeline (m) |
| m | Generic month |
| Oboi,c | Central BOI operation (binary) |
| Ochp | Combined heat and power operation (binary) |
| Ohp,c | HP cold operation (binary) |
| Ohp,h | HP heat operation (binary) |
| Oice,c | Centralized ICE operation (binary) |
| pt | Pipeline thermal loss per unit length (km−1) |
| Heat flux transferred by a DHCN pipeline (kW) | |
| Qts | Thermal energy stored in a thermal storage (kWh) |
| r | type of the day index: working or non-working day |
| relec,sold | Revenue of electricity sold to the grid (€) |
| s | Generic week |
| Sboi | BOI size (kW) |
| Sboi,c | Central BOI size (kW) |
| Sboi,lim,c | Central BOI size limits (kW) |
| Scc | CC size (kW) |
| SC,net | Size of the cooling pipeline (kW) |
| Scs | Cooling storage size (kWh) |
| SH,net | Size of the thermal pipeline (kW) |
| SH,net,c | Size of the central DHN pipeline (kW) |
| Shp,lim | HP operation limits (kW) |
| Sice,c | Centralized ICE size |
| Sice,lim,c | Centralized ICE size limits (kW) |
| Spvp | Size of the PV panels equipment (m2) |
| Sstp | Size of the solar equipment |
| Sstp,c | Size of the central solar field |
| Sts | Thermal storage size (kWh) |
| Sts,c | Central thermal storage size (kWh) |
| u, v | Generic unit |
| vp | Velocity of the medium inside the pipeline (m/s) |
| Vts | Thermal storage volume (m3) |
| Xabs | ABS existence (binary) |
| Xboi,c | Central BOI existence (binary) |
| Xcp | Existence of the cooling pipeline (binary) |
| Xchp | Existence of the combined heat and power device (binary) |
| Xhp | HP existence (binary) |
| Xice | ICE existence (binary) |
| Xice,c | Centralized ICE existence (binary) |
| Xmgt | MGT existence (binary) |
| Xnet | Existence of a network pipeline (binary) |
| Xnet,c | Existence of the central DHN (binary) |
| ABS | Absorption Chiller |
| BOI | Boiler |
| CC | Compression Chiller |
| COP | Coefficient of Performance |
| CPU | Central Processing Unit |
| CS | Conventional Solution |
| CStor | Cooling Storage |
| DCN | District Cooling Network |
| DG | Distributed Generation |
| DHCN | District Heating and Cooling Network |
| DHN | District Heating Network |
| DS | Distribution Substation |
| EC | Energy Community |
| ECS | Energy Community Solution |
| ES | Electricity storage |
| GA | Genetic algorithm |
| GHG | Green House Gases |
| HP | Heat Pump |
| ICE | Internal Combustion Engine |
| MGT | Micro Gas Turbine |
| MILP | Mixed Integer Linear Programming |
| NG | Natural Gas |
| NLP | Nonlinear programming |
| NSGA-II | Non-dominated sorting genetic algorithm-II |
| PC | Personal Computer |
| PVp | Photovoltaic panels |
| RAM | Random Access Memory |
| RE | Renewable Energy |
| RES | Renewable Energy Sources |
| SE | Sharing Electricity |
| SES | Sharing Electricity Solution |
| SHCHP | Simultaneous Heating and Cooling Heat Pump |
| SLP | Successive linear programming |
| STp | Solar Thermal panels |
| TStor | Thermal Storage |
| WT | Wind turbine |
References
- Vogel, J.; Steinberger, J.K.; O’Neill, D.W.; Lamb, W.F.; Krishnakumar, J. Socio-economic conditions for satisfying human needs at low energy use: An international analysis of social provisioning. Glob. Environ. Chang. 2021, 69, 102287. [Google Scholar] [CrossRef]
- IEA—International Energy Agency. Key World Energy Statistics 2017. Available online: http://www.iea.org/statistics/ (accessed on 2 February 2022).
- Waters, C.N.; Zalasiewicz, J.; Summerhayes, C.; Barnosky, A.D.; Poirier, C.; Gałuszka, A.; Cearreta, A.; Edgeworth, M.; Ellis, E.C.; Ellis, M.; et al. The Anthropocene is functionally and stratigraphically distinct from the Holocene. Science 2016, 351, aad2622. [Google Scholar] [CrossRef]
- Oree, V.; Hassen, S.Z.S.; Fleming, P.J. Generation expansion planning optimisation with renewable energy integration: A review. Renew. Sustain. Energy Rev. 2017, 69, 790–803. [Google Scholar] [CrossRef]
- Bauwens, T.; Schraven, D.; Drewing, E.; Radtke, J.; Holstenkamp, L.; Gotchev, B.; Yildiz, Ö. Conceptualizing community in energy systems: A systematic review of 183 definitions. Renew. Sustain. Energy Rev. 2022, 55, 111999. [Google Scholar] [CrossRef]
- Casisi, M.; Buoro, D.; Pinamonti, P.; Reini, M. A Comparison of Different District Integration for a Distributed Generation System for Heating and Cooling in an Urban Area. Appl. Sci. 2019, 9, 3521. [Google Scholar] [CrossRef]
- Bojić, M.; Stojanović, B. MILP optimization of a CHP energy system. Energy Convers. Manag. 1998, 39, 637–642. [Google Scholar] [CrossRef]
- Bruno, J.C.; Miquel, J.; Castells, F. Optimization of energy plants including water/lithium bromide absorption chillers. Int. J. Energy Res. 2000, 24, 695–717. [Google Scholar] [CrossRef]
- Bojić, M.; Dragičević, S. MILP optimization of energy supply by using a boiler, a condensing turbine and a heat pump. Energy Convers. Manag. 2002, 43, 591–608. [Google Scholar] [CrossRef]
- Kong, H.; Qi, E.; Li, H.; Li, G.; Zhang, X. An MILP model for optimization of byproduct gases in the integrated iron and steel plant. Appl. Energy 2010, 87, 2156–2163. [Google Scholar] [CrossRef]
- Iris, Ç.; Lam, J.S.L. A review of energy efficiency in ports: Operational strategies, technologies and energy management systems. Renew. Sustain. Energy Rev. 2019, 112, 170–182. [Google Scholar] [CrossRef]
- Iris, Ç.; Lam, J.S.L. Optimal energy management and operations planning in seaports with smart grid while harnessing renewable energy under uncertainty. Omega 2021, 103, 102445. [Google Scholar] [CrossRef]
- Gnes, P.; Pinamonti, P.; Reini, M. Bi-Level Optimization of the Energy Recovery System from Internal Combustion Engines of a Cruise Ship. Energies 2020, 10, 6917. [Google Scholar] [CrossRef]
- Pivetta, D.; Rech, S.; Lazzaretto, A. Choice of the Optimal Design and Operation of Multi-Energy Conversion Systems in a Prosecco Wine Cellar. Energies 2020, 13, 6252. [Google Scholar] [CrossRef]
- Pivetta, D.; Dall’Armi, C.; Taccani, R. Multi-objective optimization of hybrid PEMFC/Liion battery propulsion systems for small and medium size ferries. Int. J. Hydrog. Energy 2021, 46, 35949–35960. [Google Scholar] [CrossRef]
- Dorfner, J.; Hamacher, T. Large-Scale District Heating Network Optimization. IEEE Trans. Smart Grid 2014, 5, 1884–1891. [Google Scholar] [CrossRef]
- Vesterlund, M.; Toffolo, A.; Dahl, J. Optimization of multi-source complex district heating network, a case study. Energy 2017, 126, 53–63. [Google Scholar] [CrossRef]
- Sartor, K.; Quoilin, S.; Dewallef, P. Simulation and optimization of a CHP biomass plant and district heating network. Appl. Energy 2014, 130, 474–483. [Google Scholar] [CrossRef]
- Lund, H.; Möller, B.; Mathiesen, B.V.; Dyrelund, A. The role of district heating in future renewable energy systems. Energy 2010, 35, 1381–1390. [Google Scholar] [CrossRef]
- Lund, H.; Werner, S.; Wiltshire, R.; Svendsen, S.; Thorsen, J.E.; Hvelplund, F.; Mathiesen, B.V. 4th Generation District Heating (4GDH): Integrating smart thermal grids into future sustainable energy systems. Energy 2014, 68, 1–11. [Google Scholar] [CrossRef]
- Volkova, A.; Mašatin, V.; Siirde, A. Methodology for evaluating the transition process dynamics towards 4th generation district heating networks. Energy 2018, 150, 253–261. [Google Scholar] [CrossRef]
- Sorknæs, P.; Østergaard, P.A.; Thellufsen, J.Z.; Lund, H.; Nielsen, S.; Djørup, S.; Sperling, K. The benefits of 4th generation district heating in a 100% renewable energy system. Energy 2020, 213, 119030. [Google Scholar] [CrossRef]
- Ziemele, J.; Gravelsins, A.; Blumberga, A.; Vigants, G.; Blumberga, D. System dynamics model analysis of pathway to 4th generation district heating in Latvia. Energy 2016, 110, 85–94. [Google Scholar] [CrossRef]
- Vivian, J.; Chinello, M.; Zarrella, A.; De Carli, M. Investigation on Individual and Collective PV Self-Consumption for a Fifth Generation District Heating Network. Energies 2022, 15, 1022. [Google Scholar] [CrossRef]
- Kim, M.-H.; Lee, D.-W.; Kim, D.-W.; An, Y.-S.; Yun, J.-H. Energy Performance Investigation of Bi-Directional Convergence Energy Prosumers for an Energy Sharing Community. Energies 2021, 14, 5544. [Google Scholar] [CrossRef]
- Kayo, G.; Hasan, A.; Siren, K. Energy sharing and matching in different combinations of buildings, CHP capacities and operation strategy. Energy Build. 2014, 82, 685–695. [Google Scholar] [CrossRef]
- Duvignau, R.; Heinisch, V.; Göransson, L.; Gulisano, V.; Papatriantafilou, M. Benefits of small-size communities for continuous cost-optimization in peer-to-peer energy sharing. Appl. Energy 2021, 301, 117402. [Google Scholar] [CrossRef]
- Müller, S.C.; Welpe, I.M. Sharing electricity storage at the community level: An empirical analysis of potential business models and barriers. Energy Policy 2018, 118, 492–503. [Google Scholar] [CrossRef]
- Wu, C.; Kalathil, D.; Poolla, K.; Varaiya, P. Sharing electricity storage. In Proceedings of the 2016 IEEE 55th Conference on Decision and Control (CDC), Las Vegas, NV, USA, 12–14 December 2016; pp. 813–820. [Google Scholar] [CrossRef]
- Di Somma, M.; Graditi, G.; Siano, P. Optimal Bidding Strategy for a DER Aggregator in the Day-Ahead Market in the Presence of Demand Flexibility. IEEE Trans. Ind. Electron. 2019, 66, 1509–1519. [Google Scholar] [CrossRef]
- Zhong, X.; Zhong, W.; Liu, Y.; Yang, C.; Xie, S. Coalition Game Approach for Electricity Sharing in Multi-Energy Multi-Microgrid Network. In Proceedings of the 2021 IEEE International Smart Cities Conference (ISC2), Manchester, UK, 7–10 December 2021; pp. 1–6. [Google Scholar] [CrossRef]
- Ramos, J.S.; Moreno, M.P.; Rodríguez, L.R.; Delgado, M.G.; Domínguez, S.A. Potential for exploiting the synergies between buildings through DSM approaches. Case study: La Graciosa Island. Energy Convers. Manag. 2019, 194, 199–216. [Google Scholar] [CrossRef]
- Perger, T.; Wachter, L.; Fleischhacker, A.; Auer, H. PV sharing in local communities: Peer-to-peer trading under consideration of the prosumers’ willingness-to-pay. Sustain. Cities Soc. 2021, 66, 102634. [Google Scholar] [CrossRef]
- De Souza, R.; Casisi, M.; Micheli, D.; Reini, M. A Review of Small–Medium Combined Heat and Power (CHP) Technologies and Their Role within the 100% Renewable Energy Systems Scenario. Energies 2021, 14, 5338. [Google Scholar] [CrossRef]
- Buoro, D.; Casisi, M.; De Nardi, A.; Pinamonti, P.; Reini, M. Multicriteria optimization of a distributed energy supply system for an industrial area. Energy 2013, 58, 128–137. [Google Scholar] [CrossRef]
- Haikarainen, C.; Pettersson, F.; Saxén, H. A model for structural and operational optimization of distributed energy systems. Appl. Therm. Eng. 2014, 70, 211–218. [Google Scholar] [CrossRef]
- Zeng, J.; Han, J.; Zhang, G. Diameter optimization of district heating and cooling piping network based on hourly load. Appl. Therm. Eng. 2016, 107, 750–757. [Google Scholar] [CrossRef]
- Vesterlund, M.; Toffolo, A. Design Optimization of a District Heating Network Expansion, a Case Study for the Town of Kiruna. Appl. Sci. 2017, 7, 488. [Google Scholar] [CrossRef]
- Delangle, A.; Lambert, R.S.C.; Shah, N.; Acha, S.; Markides, C.N. Modelling and optimising the marginal expansion of an existing district heating network. Energy 2017, 140, 209–223. [Google Scholar] [CrossRef]
- Lamaison, N.; Collette, S.; Vallée, M.; Bavière, R. Storage influence in a combined biomass and power-to-heat district heating production plant. Energy 2019, 186, 115714. [Google Scholar] [CrossRef]
- Vand, B.; Ruusu, R.; Hasan, A.; Delgado, B.M. Optimal management of energy sharing in a community of buildings using a model predictive control. Energy Convers. Manag. 2021, 239, 114178. [Google Scholar] [CrossRef]
- Iqbal, S.; Nasir, M.; Zia, M.F.; Riaz, K.; Sajjad, H.; Khan, H.A. A novel approach for system loss minimization in a peer-to-peer energy sharing community DC microgrid. Int. J. Electr. Power Energy Syst. 2021, 129, 106775. [Google Scholar] [CrossRef]
- Rashidizadeh-Kermani, H.; Vahedipour-Dahraie, M.; Shafie-khah, M.; Siano, P. Optimal bidding of profit-seeking virtual associations of smart prosumers considering peer to peer energy sharing strategy. Int. J. Electr. Power Energy Syst. 2021, 132, 107175. [Google Scholar] [CrossRef]
- Dal Cin, E.; Carraro, G.; Volpato, G.; Lazzaretto, A.; Danieli, P. A multi-criteria approach to optimize the design-operation of Energy Communities considering economic-environmental objectives and demand side management. Energy Convers. Manag. 2022, 263, 115677. [Google Scholar] [CrossRef]
- Liu, Z.; Fan, G.; Sun, D.; Wu, D.; Guo, J.; Zhang, S.; Yang, X.; Lin, X.; Ai, L. A novel distributed energy system combining hybrid energy storage and a multi-objective optimization method for nearly zero-energy communities and buildings. Energy 2022, 239, 122577. [Google Scholar] [CrossRef]
- Herenčić, L.; Kirac, M.; Keko, H.; Kuzle, I.; Rajšl, I. Automated energy sharing in MV and LV distribution grids within an energy community: A case for Croatian city of Križevci with a hybrid renewable system. Renew. Energy 2022, 191, 176–194. [Google Scholar] [CrossRef]
- IEA—International Energy Agency. CO2 Emissions from Fuel Combustion. 2019. Available online: https://www.oecd-ilibrary.org/energy/co2-emissions-from-fuel-combustion-2019_2a701673-en (accessed on 5 April 2022).
- Ortiga, J.; Bruno, J.C.; Coronas, A. Selection of typical days for the characterisation of energy demand in cogeneration and trigeneration optimisation models for buildings. Energy Convers. Manag. 2011, 52, 1934–1942. [Google Scholar] [CrossRef]
- Our World in Data. Carbon Dioxide Emissions. 2017. Available online: https://ourworldindata.org/grapher/carbon-dioxide-emissions-factor?tab=table (accessed on 23 June 2022).
- X-Press Software. Available online: https://www.fico.com/en/products/fico-xpress-optimization (accessed on 23 June 2022).
- Mosel Language. Available online: https://www.fico.com/fico-xpress-optimization/docs/latest/mosel/mosel_lang/dhtml/moselreflang.html (accessed on 23 June 2022).
- Casisi, M.; Costanzo, S.; Pinamonti, P.; Reini, M. Two-Level Evolutionary Multi-Objective Optimization of a District Heating System with Distributed Cogeneration. Energies 2019, 12, 114. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).