A Load-Independent Output Current Method for Wireless Power Transfer Systems with Optimal Parameter Tuning
Abstract
1. Introduction
- Contribution of this study
- -
- This study elaborates a mathematical method for achieving a Load-Independent Output Current.
- -
- This study proposes a parameter-design method by adjusting the proportion of active power to reactive power ratios as an index to optimize the topology size as well as reduction of voltage/current stresses on their elements. Due to preventing the increase in power losses and reducing the damage to the devices, the analysis of compensating topologies from the perspective of voltage and current stresses is important.
- -
- According to the above-mentioned findings, this is the first paper that improves a systematic investigation to identify and explore an immittance conditions-qualified family of PRN, which is associated with a more appropriate topological description in WPT applications. Moreover, their conditions are specified with their topological superiority description.
- Outlines
2. Theoretical Analysis of the IPRN
2.1. Analysis of an RN
2.2. Analysis of an IPRN
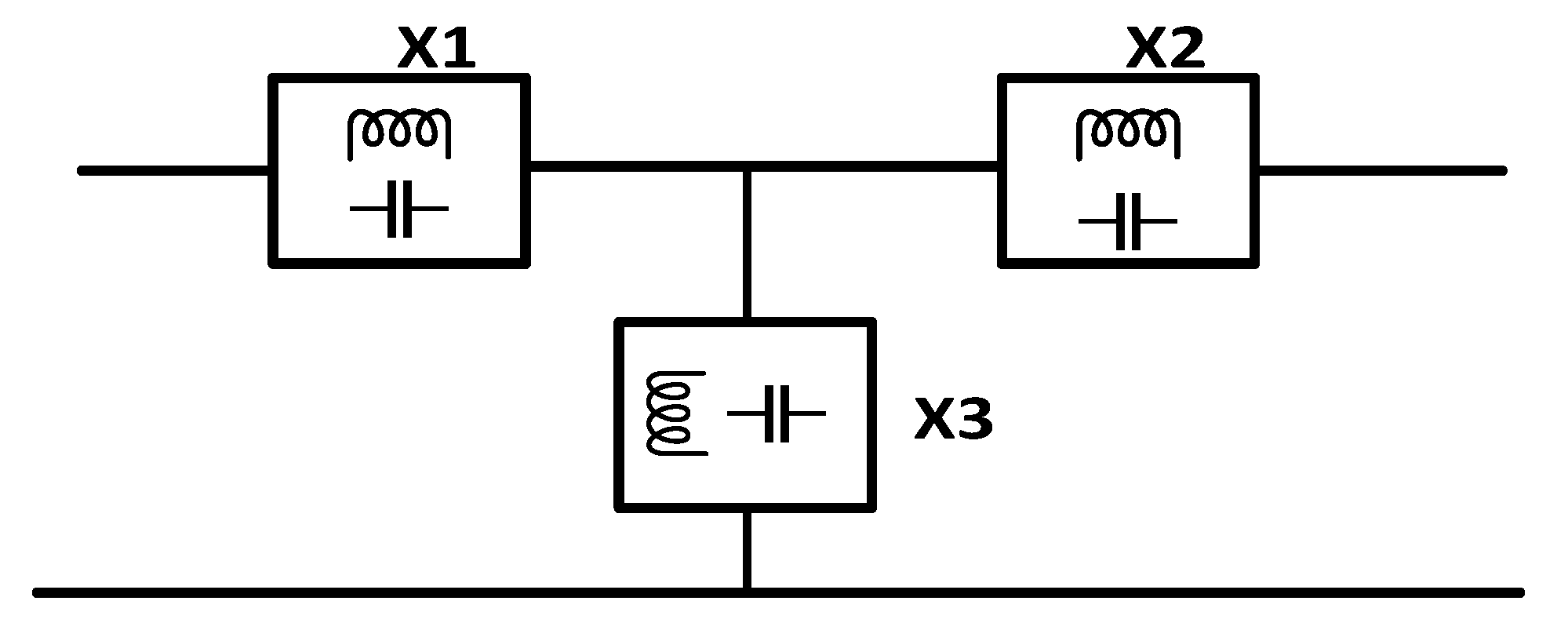
3. Design Conditions of IPRN Topologies in WPT System
3.1. Analysis of the Proposed IPRN
3.2. Achieving Mathematical Equations
3.3. Parameter-Tuning Process
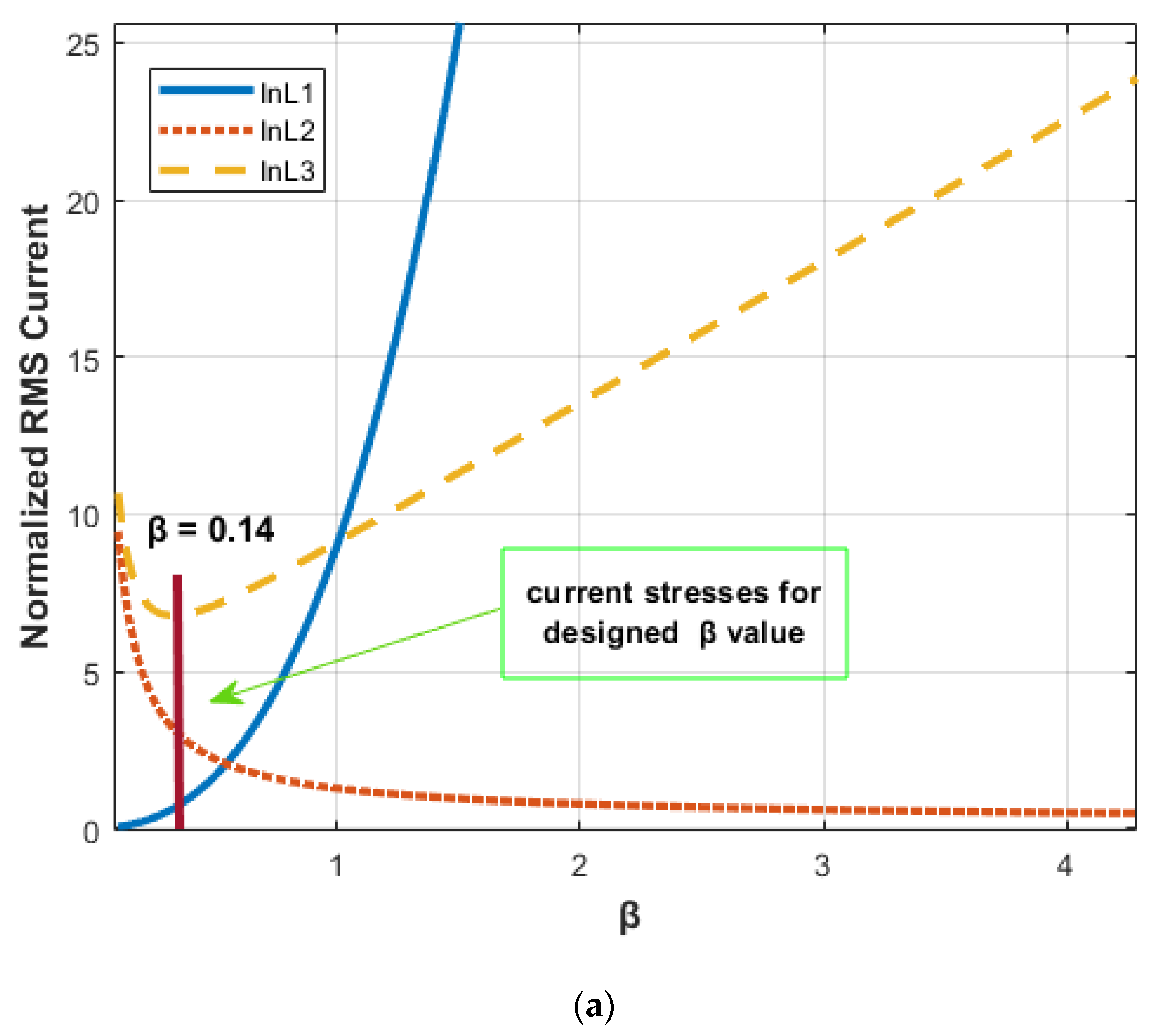
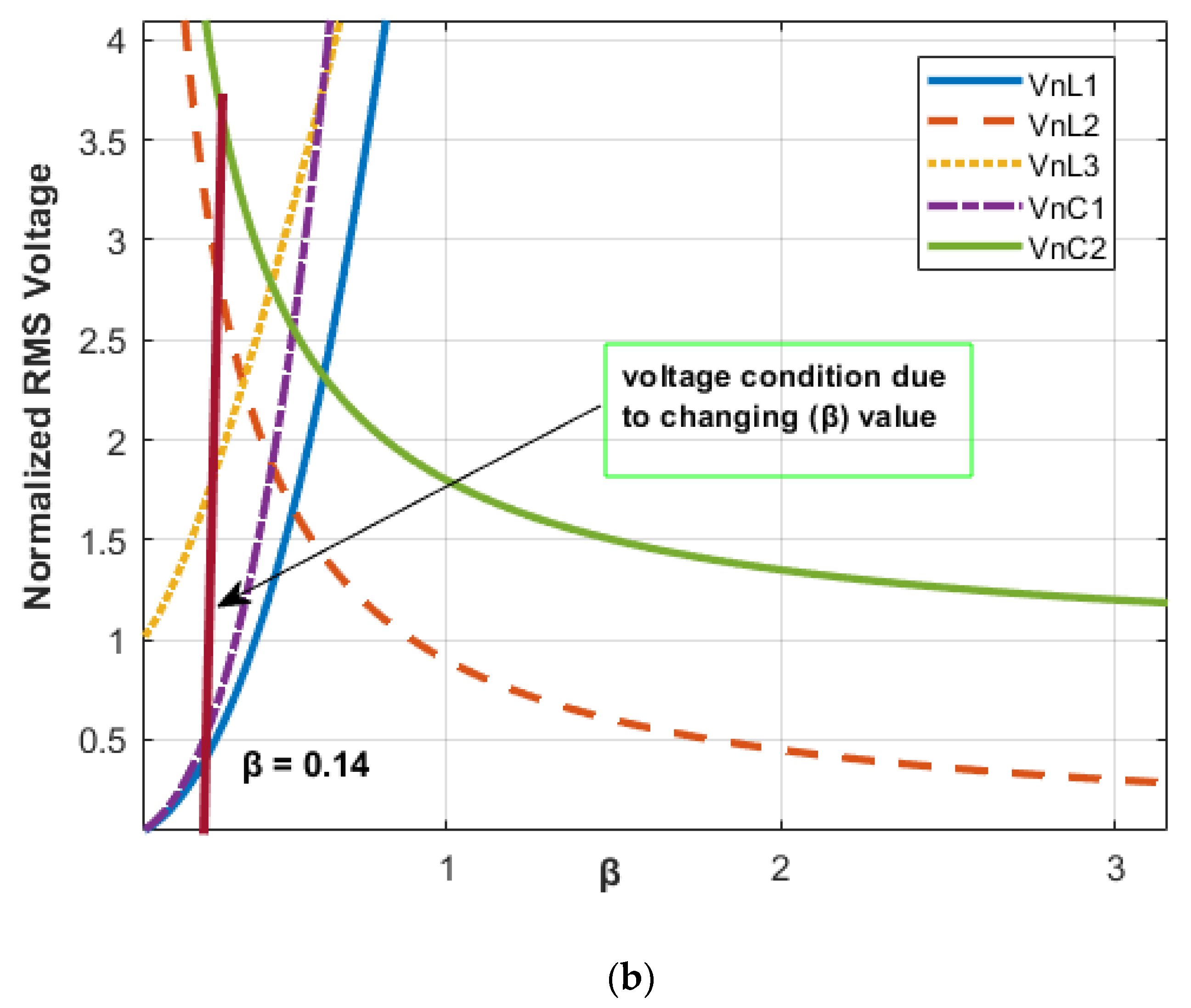
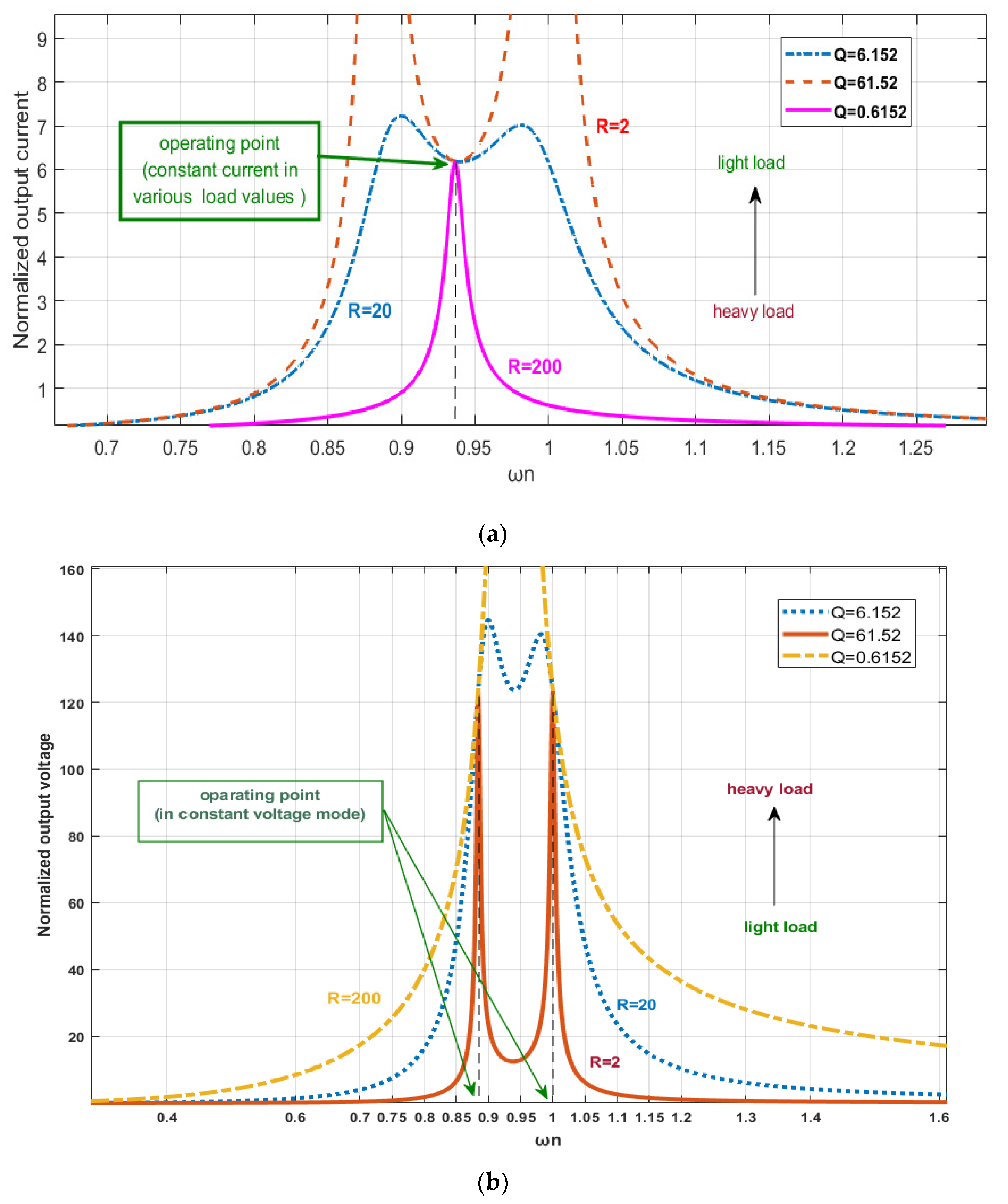
- The minimum voltage and current stresses can be realized with well-designed parameters. Table 2 shows that selecting the proper can considerably decrease the voltage/current stresses on the components. The stresses of voltage/current parameters are directly related to (). Due to the relationship between L1 and L2 with Lp and Ls (based on Section 3.1), therefore, the possible value range of should be selected according to the rated Lp and Ls and subsequently, is related to the volumes and dimensions of primary and secondary coils. According to practical limitations, the values obtained at the 30 mm air gap for the proposed ferrite core in the laboratory, the value of 0.14 is appropriate for (). It is noteworthy that regulated voltage/current stresses on T1 components under different () values, which are within immittance mode under the steady-state output circumstances, were presented and compared in Figure 7. These diagrams are extracted from Table 3. A significant observation from Figure 7 is that the current and voltage stresses decrease with the reduction.
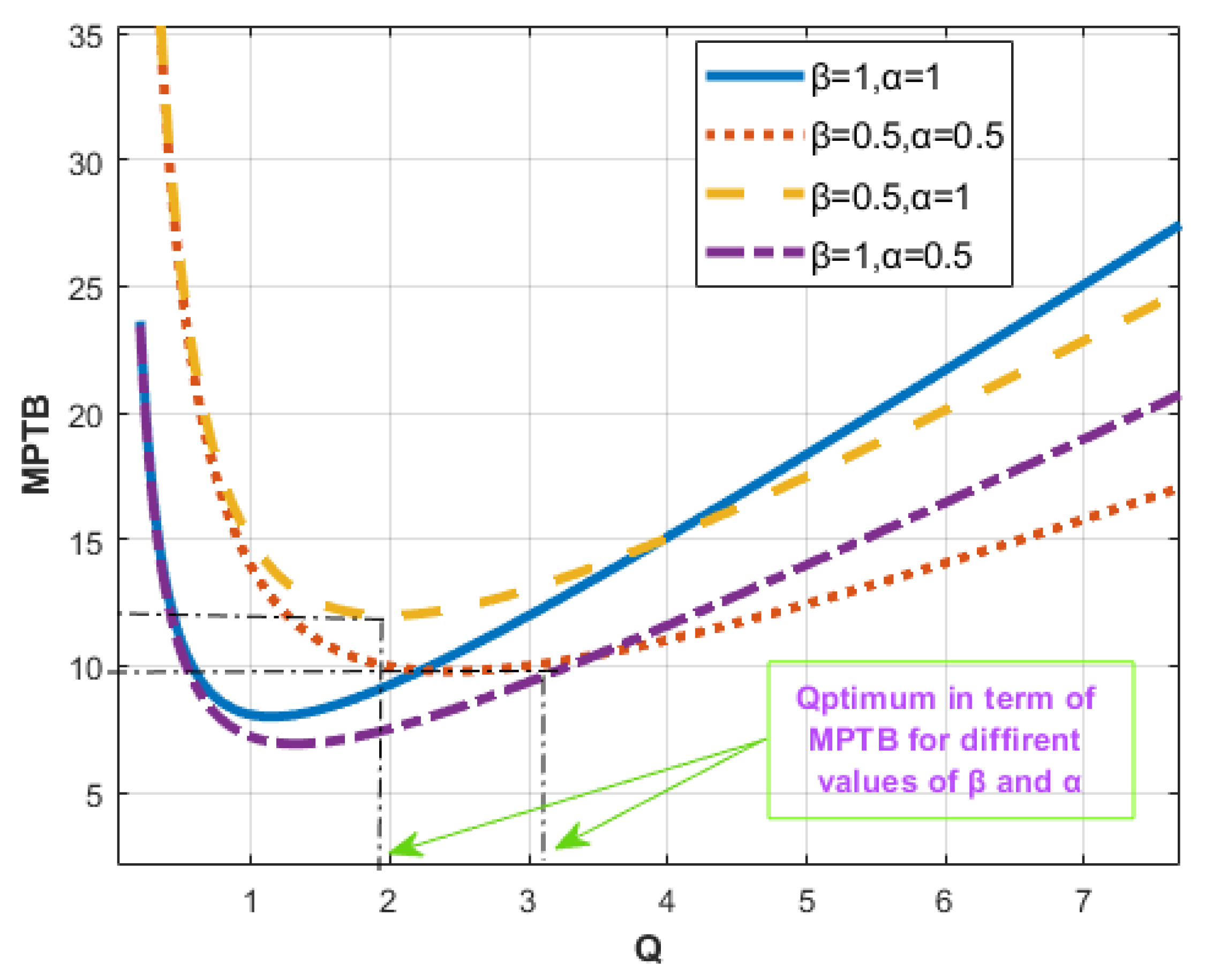
- K0 selection must be carried out to decrease the stresses resulting from voltage/current. Therefore, the regulated voltage/current values of components with respect to K0 and Qoptimum are summarized in Table 3. According to (17), the Qoptimum is the function of and . Using Figure 8, proper values for and can be achieved. Figure 8 indicates the relationship between MPTB and Q of various quantities of and . It can be inferred that higher and lower values of and must be considered, respectively, while performing the designing procedure. Also, to achieve a reduction in the physical size of the circuit, it is necessary to select the lower Qoptimum value. Since is proportional to K0, the regulation procedure must be conducted with the purpose of achieving the appropriate coupling coefficient.
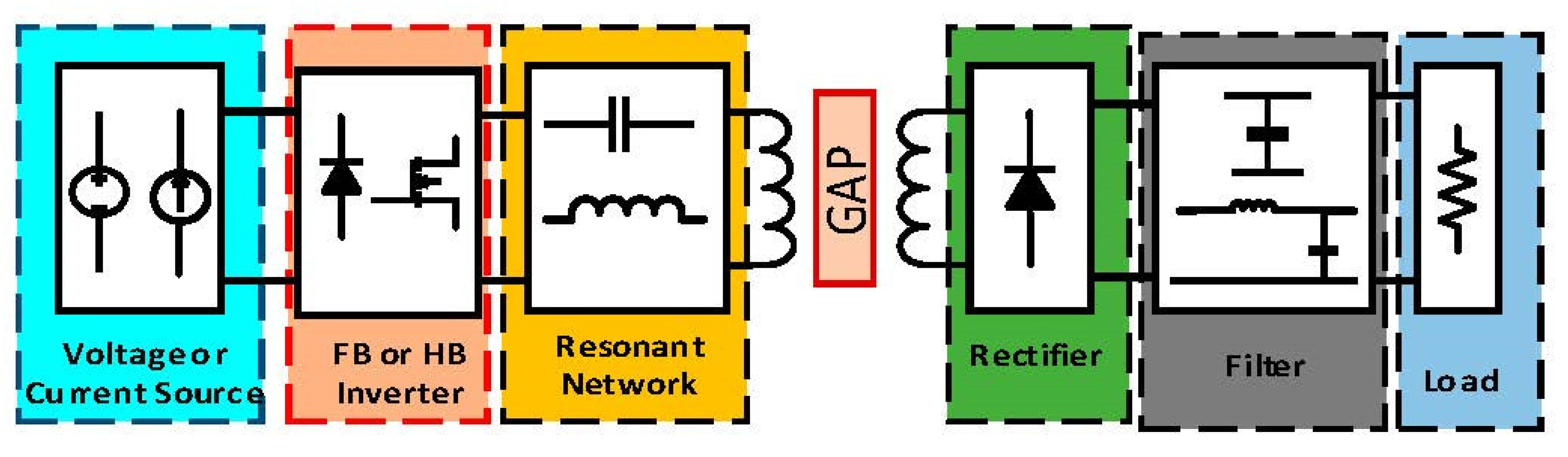
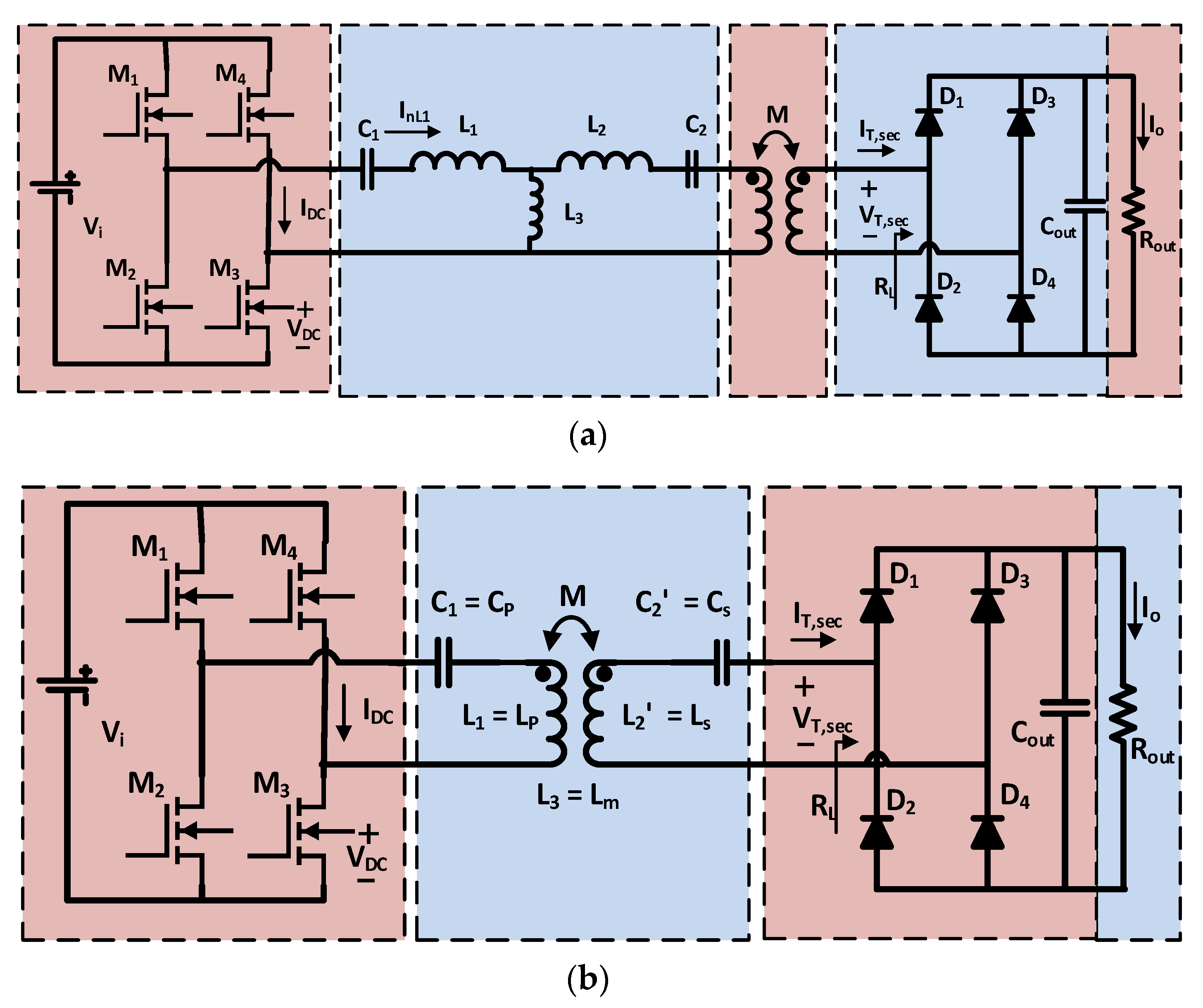
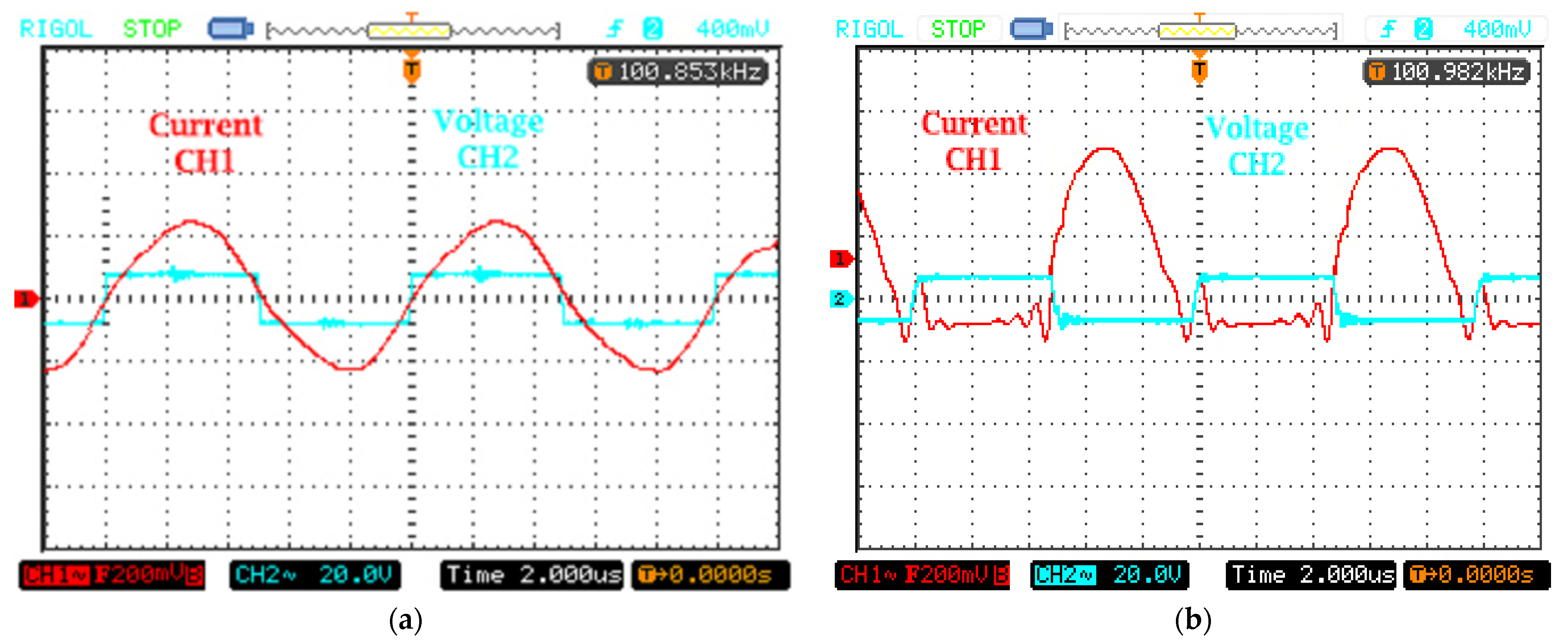
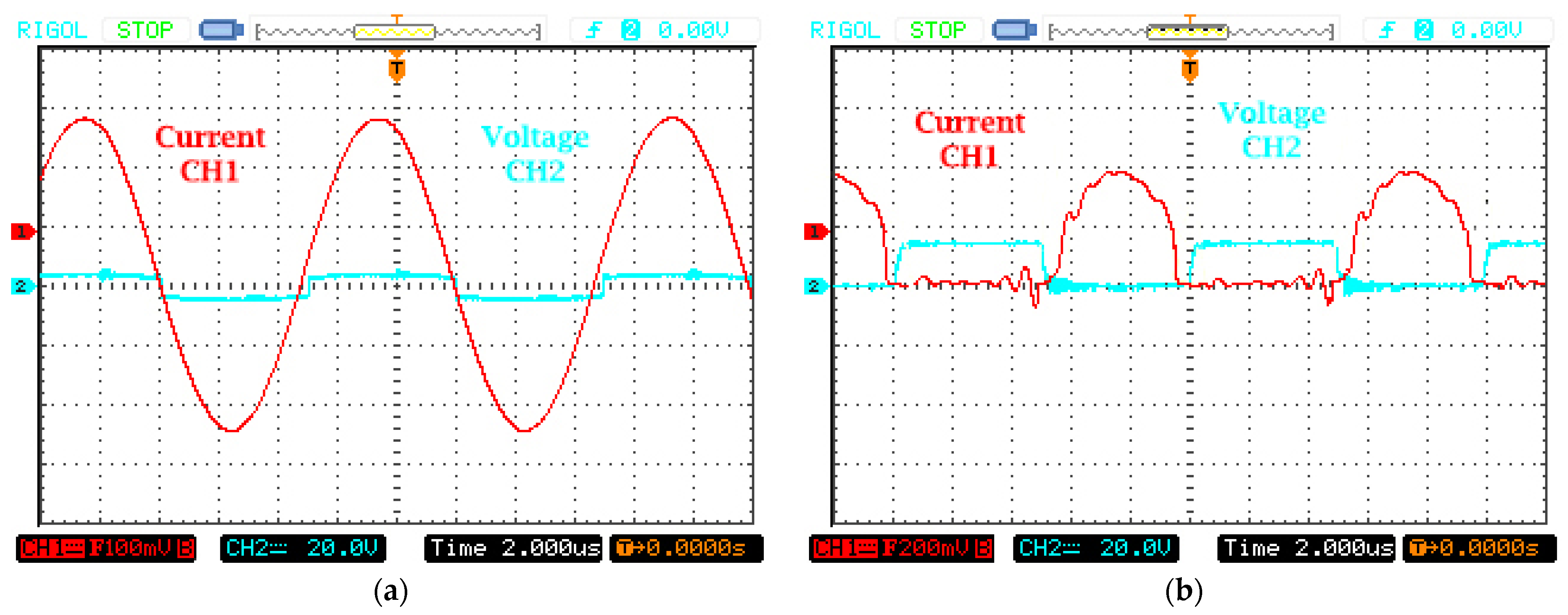
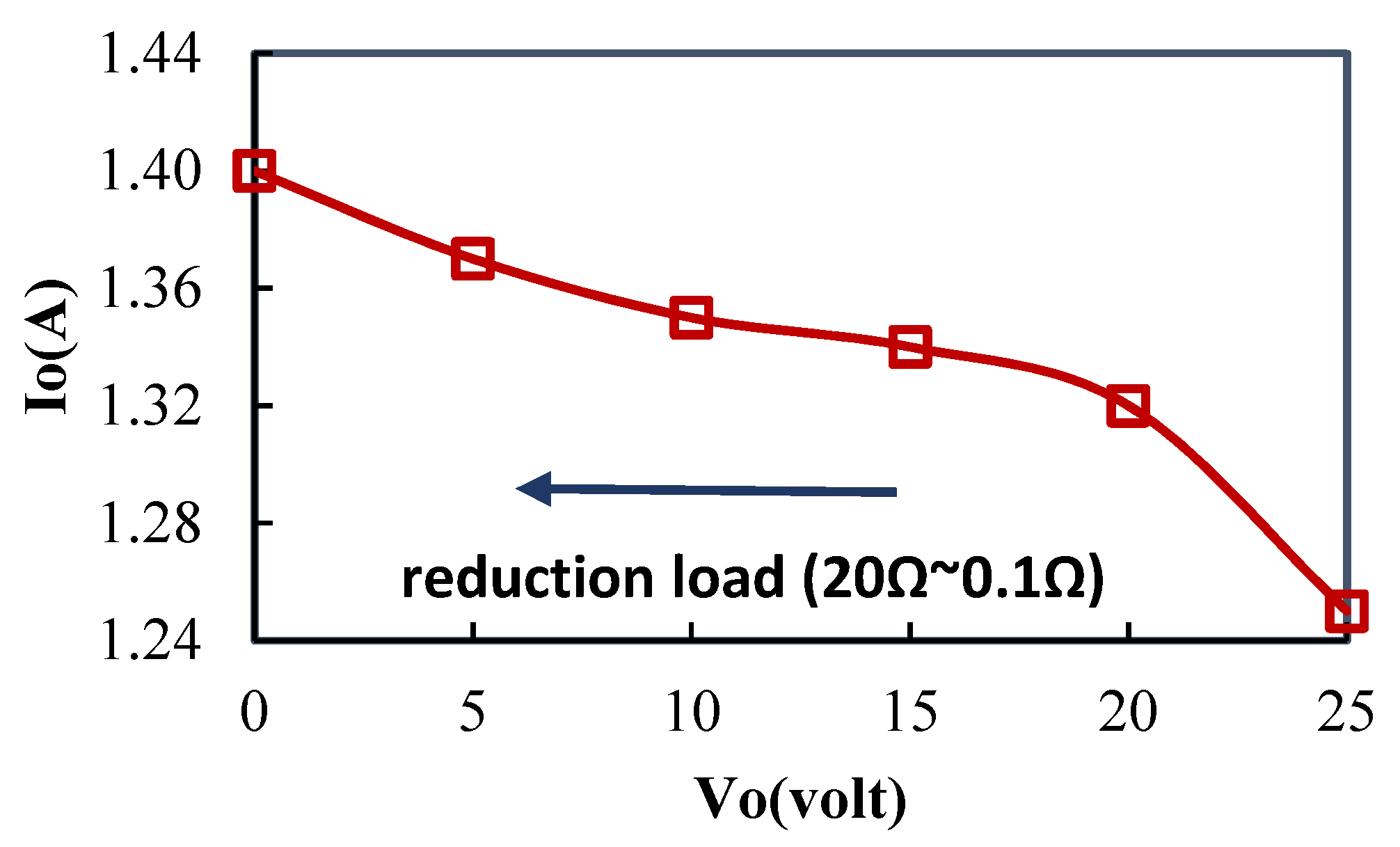
4. Experimental Verification
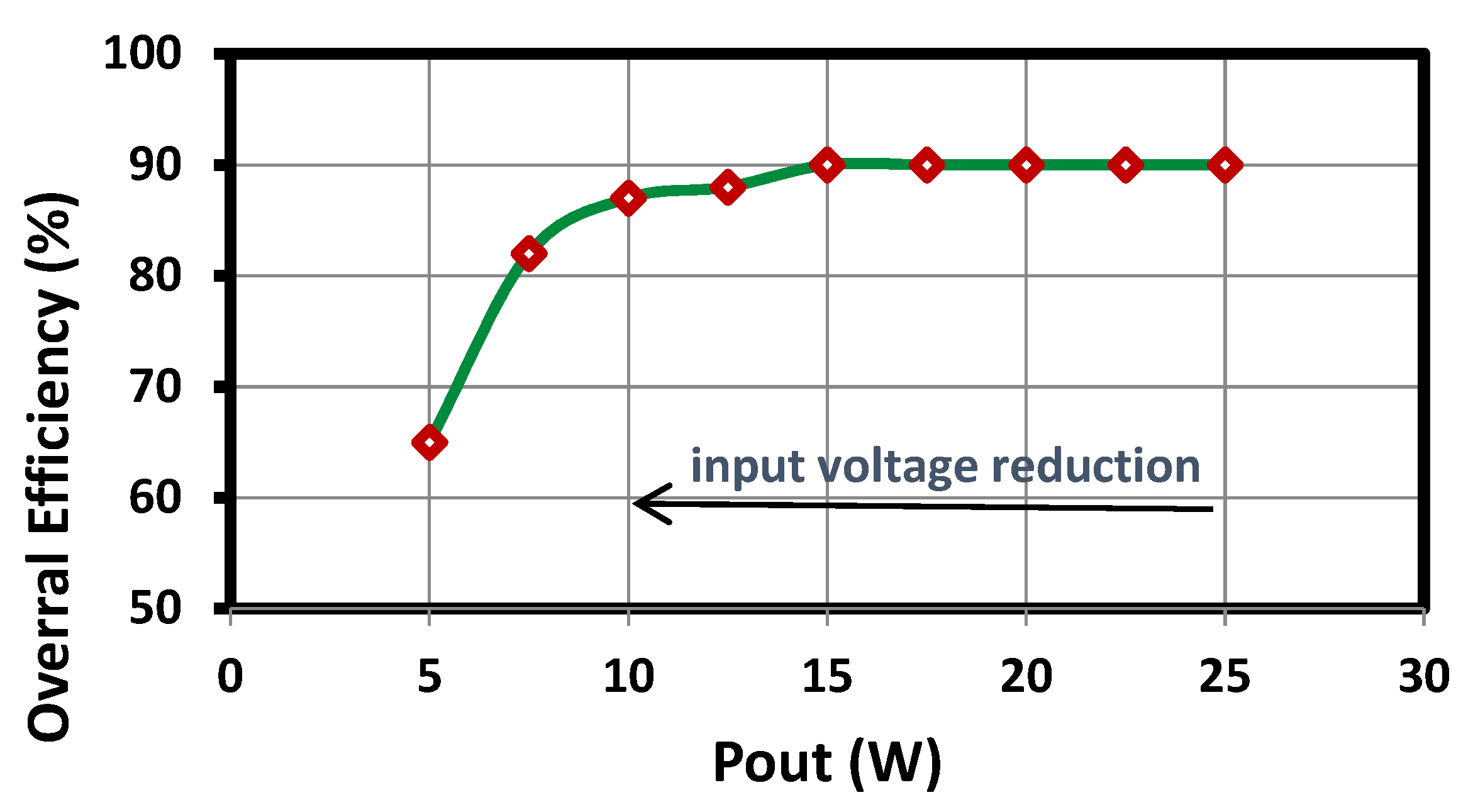
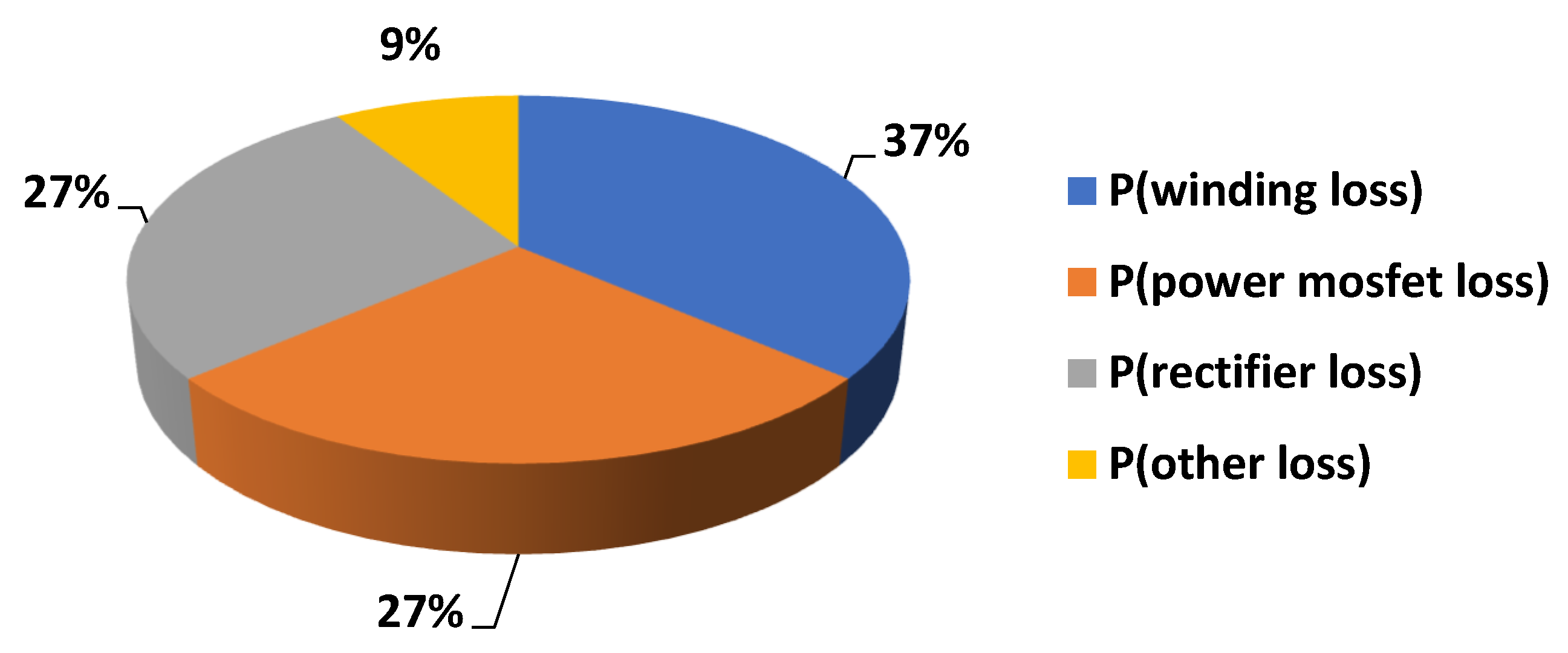
4.1. Practical Result
4.2. Discussion and Comparison
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Liu, H.; Huang, X.; Tan, L.; Guo, J.; Wang, W.; Yan, C.; Xu, C. Dynamic Wireless Charging for Inspection Robots Based on Decentralized Energy Pickup Structure. IEEE Trans. Ind. Inform. 2018, 14, 1786–1797. [Google Scholar] [CrossRef]
- Zhang, Y.; Tian, G.; Lu, J.; Zhang, M.; Zhang, S. Efficient Dynamic Object Search in Home Environment by Mobile Robot: A Priori Knowledge-Based Approach. IEEE Trans. Veh. Technol. 2019, 68, 9466–9477. [Google Scholar] [CrossRef]
- Huang, S.; Lee, T.; Li, W.; Chen, R. Modular On-Road AGV Wireless Charging Systems Via Interoperable Power Adjustment. IEEE Trans. Ind. Electron. 2019, 66, 5918–5928. [Google Scholar] [CrossRef]
- Siroos, A.; Sedighizadeh, M.; Afjei, E.; Fini, A.S. Comparison of different controllers for wireless charging system in AUVs. In Proceedings of the 2022 13th Power Electronics, Drive Systems, and Technologies Conference (PEDSTC), Tehran, Iran, 1–3 February 2022; pp. 155–160. [Google Scholar]
- Tang, Y.; Chen, Y.; Madawala, U.K.; Thrimawithana, D.J.; Ma, H. A New Controller for Bidirectional Wireless Power Transfer Systems. IEEE Trans. Power Electron. 2018, 33, 9076–9087. [Google Scholar] [CrossRef]
- Esmaeil, J.; Salehizadeh, M.R.; Rahimikian, A. Optimal control of the power ramp rate with flicker mitigation for directly grid connected wind turbines. Simulation 2020, 96, 141–150. [Google Scholar]
- Chen, X.; Huang, D.; Li, Q.; Lee, F.C. Multichannel LED driver with CLL resonant converter. IEEE J. Emerg. Sel. Top. Power Electron. 2015, 3, 589–598. [Google Scholar] [CrossRef]
- Haga, H.; Kurokaw, F. Modulation method of a full-bridge three-level LLC resonant converter for battery charger of electrical vehicles. IEEE Trans. Power Electron. 2017, 32, 2498–2505. [Google Scholar] [CrossRef]
- Hou, J.; Chen, Q.; Zhang, Z.; Wong, S.; Tse, C.K. Analysis of Output Current Characteristics for Higher-Order Primary Compensation in Inductive Power Transfer Systems. IEEE Trans. Power Electron. 2018, 33, 6807–6821. [Google Scholar] [CrossRef]
- Li, Y.L.; Sun, Y.; Dai, X. μ-Synthesis for Frequency Uncertainty of the ICPT System. IEEE Trans. Ind. Electron. 2013, 60, 291–300. [Google Scholar] [CrossRef]
- Huang, Z.; Lam, C.; Mak, P.; Martins, R.P.d.S.; Wong, S.; Tse, C.K. A Single-Stage Inductive-Power-Transfer Converter for Constant-Power and Maximum-Efficiency Battery Charging. IEEE Trans. Power Electron. 2020, 35, 8973–8984. [Google Scholar] [CrossRef]
- Lourdusami, S.S.; Viaramani, R. Analysis, design and experimentation of series-parallel LCC resonant converter for constant current source. IEICE Electron. Exp. 2014, 11, 20140711. [Google Scholar] [CrossRef][Green Version]
- Duan, F.; Xu, M.; Yang, X.; Yao, Y. Canonical model and design methodology for LLC DC/DC converter with constant current operation capability under shorted load. IEEE Trans. Power Electron. 2016, 31, 6870–6883. [Google Scholar] [CrossRef]
- Li, Y.; Xu, Q.; Lin, T.; Hu, J.; He, Z.; Mai, R. Analysis and Design of Load-Independent Output Current or Output Voltage of a Three-Coil Wireless Power Transfer System. IEEE Trans. Transp. Electrif. 2018, 4, 364–375. [Google Scholar] [CrossRef]
- Salehizadeh, M.R.; Koohbijari, M.A.; Nouri, H.; Taşcıkaraoğlu, A.; Erdinç, O.; Catalao, J.P. Bi-objective optimization model for optimal placement of thyristor-controlled series compensator devices. Energies 2019, 12, 2601. [Google Scholar] [CrossRef]
- Naghash, R.; Alavi, S.M.M.; Afjei, S.E. Robust Control of Wireless Power Transfer Despite Load and Data Communications Uncertainties. IEEE J. Emerg. Sel. Top. Power Electron. 2021, 9, 4897–4905. [Google Scholar] [CrossRef]
- Jamakani, B.E.; Afjei, E.; Mosallanejad, A. A Novel Triple Quadrature Pad for Inductive Power Transfer Systems for Electric Vehicle Charging. In Proceedings of the 2019 10th International Power Electronics, Drive Systems and Technologies Conference (PEDSTC), Shiraz, Iran, 12–14 February 2019; pp. 618–623. [Google Scholar]
- Zhang, W.; Mi, C.C. Compensation topologies of high-power wireless power transfer systems. IEEE Trans. Vehicular Tech. 2016, 65, 4768–4778. [Google Scholar] [CrossRef]
- Mahdizadeh, A.H.; Afjei, E. LLC Resonant Converter Utilizing Parallel-Series Transformers Connection. In Proceedings of the 2019 International Power System Conference (PSC), Tehran, Iran, 9–11 December 2019; pp. 472–477. [Google Scholar]
- Ramezani, A.; Farhangi, S.; Iman-Eini, H.; Farhangi, B.; Rahimi, R.; Moradi, G.R. Optimized LCC-Series Compensated Resonant Network for Stationary Wireless EV Chargers. IEEE Trans. Ind. Electron. 2019, 66, 2756–2765. [Google Scholar] [CrossRef]
- Nagatsuka, Y.; Ehara, N.; Kaneko, Y.; Abe, S.; Yasuda, T. Compact contactless power transfer system for electric vehicles. In Proceedings of the The 2010 International Power Electronics Conference-ECCE ASIA-, Sapporo, Japan, 21–24 June 2010; pp. 807–813. [Google Scholar]
- Wang, C.-S.; Covic, G.A.; Stielau, O.H. Power transfer capability and bifurcation phenomena of loosely coupled inductive power transfer systems. IEEE Trans. Ind. Electron. 2004, 51, 148–157. [Google Scholar] [CrossRef]
- Zhang, W.; Wong, S.C.; Tse, C.K.; Chen, Q. Analysis and Comparison of Secondary Series- and Parallel-Compensated Inductive Power Transfer Systems Operating for Optimal Efficiency and Load-Independent Voltage-Transfer Ratio. IEEE Trans. Power Electron. 2014, 29, 2979–2990. [Google Scholar] [CrossRef]
- Qu, X.; Han, H.; Wong, S.C.; Tse, C.K.; Chen, W. Hybrid IPT Topol-ogies with Constant Current or Constant Voltage Output for Battery Charging Applications. IEEE Trans. Power Electron. 2015, 30, 6329–6337. [Google Scholar] [CrossRef]
- Borage, M.; Nagesh, K.V.; Bhatia, M.S.; Tiwari, S. Resonant immittance converter topologies. IEEE Trans. Ind. Electron. 2011, 58, 771–778. [Google Scholar] [CrossRef]
- Irie, H.; Yamana, H. Immittance converters suitable for power electronics. Electr. Eng. Jpn. 1998, 124, 53–62. [Google Scholar] [CrossRef]
- Sakamoto, Y.; Wada, K.; Shimizu, T. A 13.565 MHz current output type inverter utilizing an immittance conversion element. In Proceedings of the 2008 13th International Power Electronics and Motion, Poznan, Poland, 1–3 September 2008; pp. 288–294. [Google Scholar]
- Zhang, E. Inverter design shines in photovoltaic systems. Power Electron. Technol. 2008, 34, 20–25. [Google Scholar]
- Kimura, N.; Morizane, T.; Taniguchi, K.; Irie, H. Dynamic performance of current sourced forced commutation HVDC converter with immitance conversion link. In Proceedings of the IEEE/PES Transmission and Distribution Conference and Exhibition, Yokohama, Japan, 6–10 October 2002; Volume 3, pp. 1937–1942. [Google Scholar]
- Irie, H.; Minami, N.; Minami, H.; Kitayoshi, H. Non-contact energy transfer system using immittance converter. Elect. Eng. Jpn. 2001, 136, 58–64. [Google Scholar] [CrossRef]
- Borage, M.; Tiwari, S.; Kotaiah, S. Analysis and design of LCL-T resonant converter as a constant-current power supply. IEEE Trans. Ind. Electron. 2005, 52, 1547–1554. [Google Scholar] [CrossRef]
- Borage, M.; Tiwari, S.; Kotaiah, S. LCL-T resonant converter with clamp diodes: A novel constant-current power supply with inherent constant-voltage limit. IEEE Trans. Ind. Electron. 2007, 54, 741–746. [Google Scholar] [CrossRef]
- Borage, M.; Tiwari, S.; Kotaiah, S. A constant-current, constant voltage half-bridge resonant power supply for capacitor charging. Proc. Inst. Elect. Eng. Elect. Power. Appl. 2006, 153, 343–347. [Google Scholar] [CrossRef]
- Borage, M.; Nagesh, K.V.; Bhatia, M.S.; Tiwari, S. Characteristics and design of an asymmetrical duty-cycle controlled LCL-T resonant converter. IEEE Trans. Power Electron. 2009, 24, 2268–2275. [Google Scholar] [CrossRef]
- Borage, M.; Nagesh, K.V.; Bhatia, M.S.; Tiwari, S. Design of LCL T resonant converter including the effect of transformer winding capacitance. IEEE Trans. Ind. Electron. 2009, 56, 1420–1427. [Google Scholar] [CrossRef]
- Tamate, M.; Ohguchi, H.; Hayashi, M.; Takagi, H.; Ito, M. A novel approach of power converter topology based on immittance conversion theory. In Proceedings of the ISIE’2000. Proceedings of the 2000 IEEE International Symposium on Industrial Electronics (Cat. No.00TH8543), Cholula, Puebla, Mexico, 4–8 December 2000; pp. 482–487. [Google Scholar]
- Braun, W.D.; Perreault, D.J. A High-Frequency Inverter for Variable-Load Operation. IEEE J. Emerg. Sel. Top. Power Electron. 2019, 7, 706–721. [Google Scholar] [CrossRef]
- Sinha, S.; Kumar, A.; Afridi, K.K. Optimized Design of High-Efficiency Immittance Matching Networks for Capacitive Wireless Power Transfer Systems. In Proceedings of the 2021 IEEE PELS Workshop on Emerging Technologies: Wireless Power Transfer (WoW), San Diego, CA, USA, 1–4 June 2021; pp. 1–6. [Google Scholar]
- Batarseh, I. Resonant converter topologies with three and four energy storage elements. IEEE Trans. Power Electron. 1994, 9, 64–73. [Google Scholar] [CrossRef]
- Kim, M.; Kim, J.; Lee, B. Adjustable frequency–duty-cycle hybrid control strategy for full-bridge series resonant converters in electric vehicle chargers. IEEE Trans. Ind. Electron. 2014, 61, 5354–5361. [Google Scholar]
- Irie, H.; Yamana, H. Immittance converter suitable for power electronics. Trans. Inst. Elect. Eng. Jpn. 1997, 117, 962–969. [Google Scholar] [CrossRef]
- Yang, L.; Li, X.; Liu, S.; Xu, Z.; Cai, C. Analysis and Design of an LCCC/S-Compensated WPT System with Constant Output Characteristics for Battery Charging Applications. IEEE J. Emerg. Sel. Top. Power Electron. 2021, 9, 1169–1180. [Google Scholar] [CrossRef]
- Zhang, W.; Wong, S.C.; Tse, C.K.; Chen, Q. Load-independent duality of current and voltage outputs of a series- or parallel-compensated inductive power transfer converter with optimized efficiency. IEEE J. Emerg. Sel. Topics in Power Electron. 2015, 3, 137–146. [Google Scholar]
- Khoshsaadat, A.; Moghani, J.S. Fifth-Order T-Type Passive Resonant Tanks Tailored for Constant Current Resonant Converters. IEEE Trans. Circuits Syst. I Regul. Pap. 2017, 65, 842–853. [Google Scholar] [CrossRef]

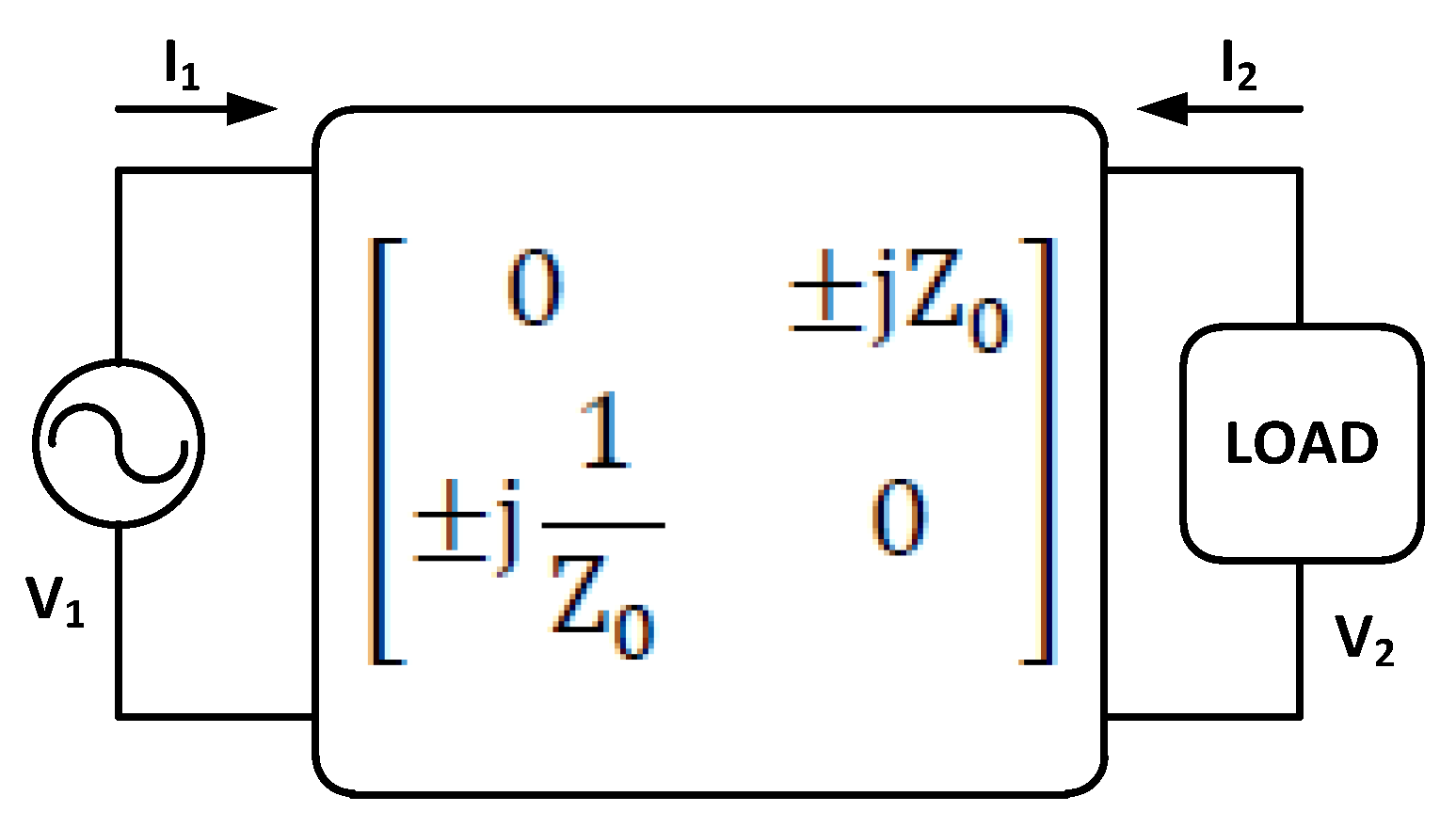
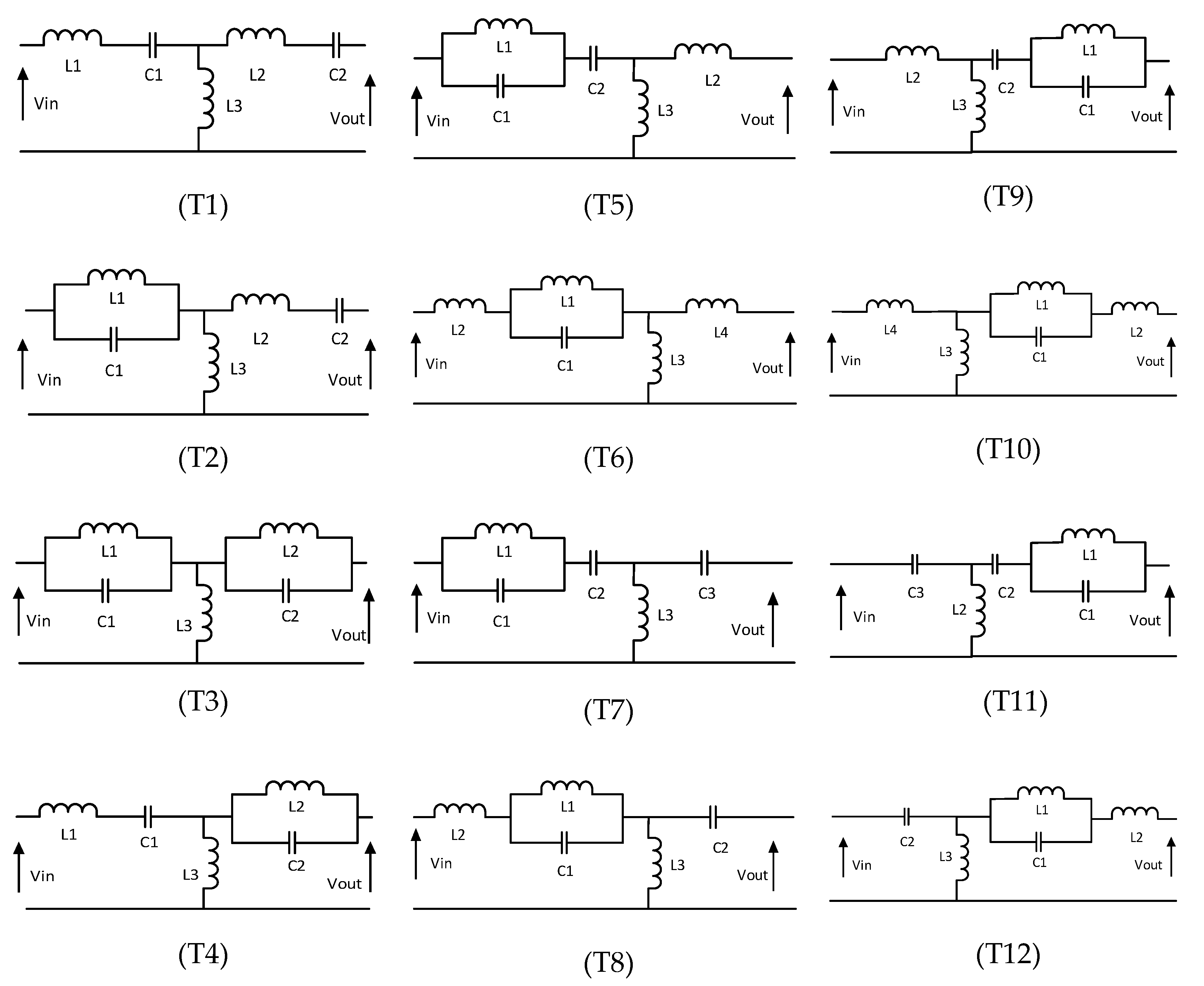


| Name | SOF | SRE |
|---|---|---|
| T1 | ||
| T2 | ||
| T3 | ||
| T4 | ||
| T7 | ||
| T8 | ||
| T11 | ||
| T12 |
| Normalized I & V of Elements | Conventional Mode | Immittance Mode |
|---|---|---|
| Parameters | Values According to Different Coupling Coefficients in IPRN Conditions |
|---|---|
| Elements | Designed Value by the IPRN Method |
|---|---|
| L1(uH) | 103.69 |
| L2(uH) | 183.42 |
| L3(uF) | 14.5 |
| C1(nF) | 21.43, (MKP type) |
| C2(nF) | 12.11, (MKP type) |
| n | 1.33 |
| M1~M4 | IRFP150 |
| D1~D4 | MBR20100 |
| R0ut(Ω) | 20 |
| K | 0.14 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yarmohammadi, L.; Hosseini, S.M.H.; Olamaei, J.; Mozafari, B. A Load-Independent Output Current Method for Wireless Power Transfer Systems with Optimal Parameter Tuning. Sustainability 2022, 14, 9391. https://doi.org/10.3390/su14159391
Yarmohammadi L, Hosseini SMH, Olamaei J, Mozafari B. A Load-Independent Output Current Method for Wireless Power Transfer Systems with Optimal Parameter Tuning. Sustainability. 2022; 14(15):9391. https://doi.org/10.3390/su14159391
Chicago/Turabian StyleYarmohammadi, Leila, S. Mohammad Hassan Hosseini, Javad Olamaei, and Babak Mozafari. 2022. "A Load-Independent Output Current Method for Wireless Power Transfer Systems with Optimal Parameter Tuning" Sustainability 14, no. 15: 9391. https://doi.org/10.3390/su14159391
APA StyleYarmohammadi, L., Hosseini, S. M. H., Olamaei, J., & Mozafari, B. (2022). A Load-Independent Output Current Method for Wireless Power Transfer Systems with Optimal Parameter Tuning. Sustainability, 14(15), 9391. https://doi.org/10.3390/su14159391






