Prediction of China’s Economic Structural Changes under Carbon Emission Constraints: Based on the Linear Programming Input–Output (LP-IO) Model
Abstract
:1. Introduction
2. Literature Review
3. Methodology
3.1. Input–Output Model and I-O Table
3.1.1. Basic Framework
3.1.2. Basic Calculation Rules
3.1.3. Influence and Sensitivity Coefficients
3.1.4. RAS Updating Technique
3.2. Carbon Emission Intensity Factor
3.3. LP-IO Model
4. Data and Empirical Analysis
4.1. Carbon Emission Data and I-O Table
4.2. Economic Growth Target Data
4.3. Coefficient Matrix of 2030
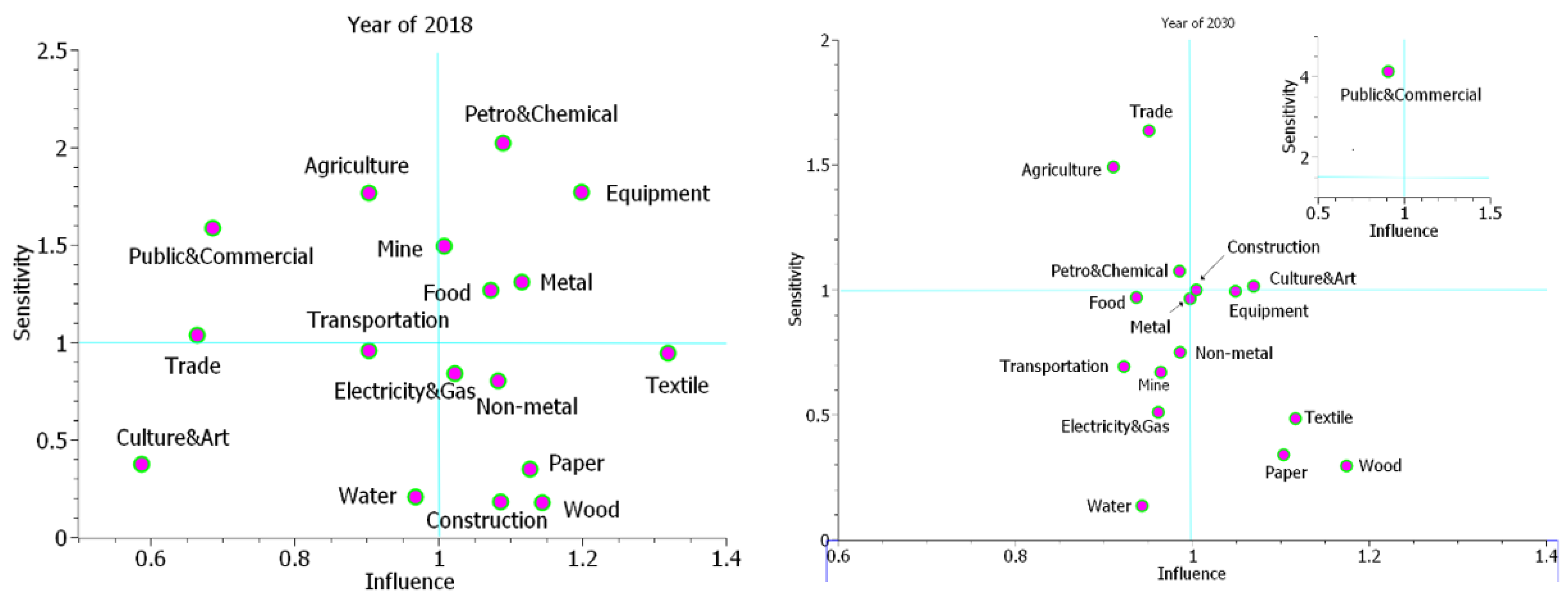
4.4. Influence and Sensitivity Coefficients
5. Discussion and Recommendations
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A
| NO. | Sectors in OECD Database | Sectors in CEAD Database | Adjusted Sectors | Abbreviation |
|---|---|---|---|---|
| 1 | 01 Agriculture, hunting, forestry 02 Fishing and aquaculture | 01 Farming, Forestry, Animal Husbandry, Fishery, and Water Conservancy | Agriculture, Fishery, and Forestry | Agriculture |
| 2 | 03 Mining and quarrying, energy-producing products 04 Mining and quarrying, non-energy-producing products 05 Mining support service activities | 02 Coal Mining and Dressing 03 Petroleum and Natural Gas Extraction 04 Ferrous Metals Mining and Dressing 05 Nonferrous Metals Mining and Dressing 06 Nonmetal Minerals Mining and Dressing 07 Other Minerals Mining and Dressing | Mining and Quarrying | Mine |
| 3 | 06 Food products, beverages and tobacco | 09 Food 10 Processing Food Production 11 Beverage Production 12 Tobacco Processing | Food product, Beverage, and Tobacco | Food |
| 4 | 07 Textiles, textile products, leather, and footwear | 13 Textile Industry 14 Garments and Other Fiber Products 15 Leather, Furs, Down, and Related Products | Textile, Leather Industries | Textile |
| 5 | 08 Wood and products of wood and cork | 08 Logging and Transport of Wood and Bamboo 16 Timber Processing, Bamboo, Cane, Palm Fiber, and Straw Products 17 Furniture Manufacturing | Manufacture of Wood and Wood products | Wood |
| 6 | 09 Paper products and printing | 18 Papermaking and Paper Products 19 Printing and Record Medium Reproduction | Manufacture of Paper and Paper Products, Printing, and Publishing | Paper |
| 7 | 10 Coke and refined petroleum products 11 Chemical and chemical products 12 Pharmaceuticals, medicinal chemical and botanical products | 21 Petroleum Processing and Coking 22 Raw Chemical Materials and Chemical Products 23 Medical and Pharmaceutical Products 24 Chemical Fiber | Manufacture of Industrial Chemicals and petrochemicals | Petroleum and Chemical |
| 8 | 13 Rubber and plastics products 14 Other non-metallic mineral products | 25 Rubber Products 26 Plastic Products 27 Nonmetal Mineral Products | Manufacture of Non-metallic Mineral Products | Non-metal |
| 9 | 15 Basic metals 16 Fabricated metal products | 28 Smelting and Pressing of Ferrous Metals 29 Smelting and Pressing of Nonferrous Metals 30 Metal Products | Basic Metal Industries | Metal |
| 10 | 17 Computer, electronic, and optical equipment 18 Electrical equipment 19 Machinery and equipment 20 Motor vehicles, trailers, and semi-trailers 21 Other transport equipment 22 Manufacturing; repair and installation of machinery and equipment 34 Telecommunications 35 IT and other information | 31 Ordinary Machinery 32 Equipment for Special Purposes 33 Transportation Equipment 34 Electric Equipment and Machinery 35 Electronic and Telecommunications Equipment 36 Instruments, Meters, Cultural and Office Machinery 37 Other Manufacturing Industry | Equipment | Equipment |
| 11 | 23 Electricity, gas, steam, and air conditioning supply | 39 Production and Supply of Electric Power, Steam and Hot Water 40 Production and Supply of Gas | Electricity | Electricity and Gas |
| 12 | 24 Water supply; sewerage, waste management, and remediation activities | 38 Scrap and waste 39 Production and Supply of Tap Water | Water supply and waste | Water |
| 13 | 25 Construction 37 Real estate activities | 42 Construction | Construction | Construction |
| 14 | 26 Wholesale and retail trade; repair of motor vehicles | 44 Wholesale, Retail Trade, and Catering Services | wholesale and retail trade | Trade |
| 15 | 27 Land transport and transport via pipelines 28 Water transport 29 Air transport 30 Warehousing and support activities for transportation 31 Postal and courier activities | 43 Transportation, Storage, Post, and Telecommunication Services | Transportation | Transportation |
| 16 | 32 Accommodation and food service activities 33 Publishing, audiovisual and broadcasting activities 36 Financial and insurance activities 39 Administrative and support services 40 Public administration and defence; compulsory social security 42 Human health and social work activities 44 Other service activities | 45 Others | Commercial, public services, and others | Public and Commercial |
| 17 | 41 Education 43 Arts, entertainment, and recreation 38 Professional, scientific, and technical activities | 20 Culture, Education, and Sports | Culture, Education, and Sports | Culture and Art |
References
- United Nations Environment Programme. Emissions Gap Report 2020. Nairobi. 2020. Available online: https://www.unep.org/emissions-gap-report-2020 (accessed on 26 March 2022).
- The State Council of China. China Releases White Paper on Climate Change Response, 28 October 2021. Available online: http://english.www.gov.cn/news/videos/202110/28/content_WS617a1072c6d0df57f98e4115.html (accessed on 10 April 2022).
- The World Bank. World Development Indicators. Available online: https://pip.worldbank.org/country-profiles/CHN (accessed on 26 March 2022).
- The State Council. Report on the Work of the Government. 2022. Available online: http://www.china.org.cn/chinese/2022-03/14/content_78106770.htm (accessed on 14 March 2022). (In Chinese and English).
- Morgan, J.P. Five Questions about China’s Economy in 2022. Available online: https://www.jpmorgan.com/insights/research/china-economy-2022 (accessed on 17 March 2022).
- European Commission; Joint Research Centre; Olivier, J.G.J.; Guizzardi, D.; Schaaf, E.; Solazzo, E.; Crippa, M.; Vignati, E.; Banja, M.; Muntean, M.; et al. GHG Emissions of All World: 2021 Report, Publications Office of the European Union, 2021. Available online: https://data.europa.eu/doi/10.2760/173513 (accessed on 16 June 2022).
- Leontief, W.W. Quantitative Input and Output Relations in the Economic Systems of the United States. Rev. Econ. Stat. 1936, 18, 105–125. [Google Scholar] [CrossRef] [Green Version]
- Leontief, W. An Alternative to Aggregation in Input-Output Analysis and National Accounts. Rev. Econ. Stat. 1967, 49, 412–419. [Google Scholar] [CrossRef]
- Klinsrisuk, R.; Pechdin, W. Evidence from Thailand on Easing COVID-19’s International Travel Restrictions: An Impact on Economic Production, Household Income, and Sustainable Tourism Development. Sustainability 2022, 14, 3423. [Google Scholar] [CrossRef]
- Choi, J.; Kim, W.; Choi, S. The Economic Effect of the Steel Industry on Sustainable Growth in China—A Focus on Input–Output Analysis. Sustainability 2022, 14, 4110. [Google Scholar] [CrossRef]
- Allan, G.J.; Hanley, N.D.; Mcgregor, P.G.; Kim Swales, J.; Turner, K.R. Augmenting the Input–Output Framework for ‘Common Pool’ Resources: Operationalizing the Full Leontief Environmental Model. Econ. Syst. Res. 2007, 19, 1–22. [Google Scholar] [CrossRef]
- Andrew, R.; Peters, G.P.; Lennox, J. Approximation and regional aggregation in multi-regional input-output analysis for national carbon footprint accounting. Econ. Syst. Res. 2009, 21, 311–335. [Google Scholar] [CrossRef]
- Li, J.; Crawford-Brown, D.; Syddall, M.; Guan, D. Modeling Imbalanced Economic Recovery Following a Natural Disaster Using Input-Output Analysis. Risk Anal. 2013, 33, 908–1921. [Google Scholar] [CrossRef]
- Elorri, I.; Rugani, B.; Rege, S.; Benetto, E.; Drouet, L.; Zachary, D.S. Combination of equilibrium models and hybrid life cycle-input–output analysis to predict the environmental impacts of energy policy scenarios. Appl. Energy 2015, 145, 234–245. [Google Scholar] [CrossRef] [Green Version]
- Liu, X.; Moreno, B.; SaloméGarcía, A. A grey neural network and input-output combined forecasting model. Primary energy consumption forecasts in Spanish economic sectors. Energy 2016, 115, 1042–1054. [Google Scholar] [CrossRef]
- Vogstad, K.O. Input-Output Analysis and Linear Programming. In Handbook of Input-Output Economics in Industrial Ecology; Eco-Efficiency in Industry and Science; Suh, S., Ed.; Springer: Dordrecht, The Netherlands, 2009; Volume 23. [Google Scholar] [CrossRef]
- Wang, T.-F.; Miller, R.E. The economic impact of a transportation bottleneck: An integrated input-output and linear programming approach. Int. J. Syst. Sci. 1994, 26, 1617–1632. [Google Scholar] [CrossRef]
- Ten Ra, T.; Steel, M.F. Revised stochastic analysis of an input–output model. Reg. Sci. Urban Econ. 1994, 24, 161–175. [Google Scholar] [CrossRef] [Green Version]
- San Cristóbal, J.R. An environmental input-output linear programming model to reach the targets for greenhouse gas emissions set by the Kyoto protocol. Econ. Syst. Res. 2010, 22, 223–236. [Google Scholar] [CrossRef]
- Chen, L. Identifying lowest-emission choices and environmental pareto frontiers for wastewater treatment wastewater treatment input–output model based linear programming. J. Ind. Ecol. 2011, 15, 367–380. [Google Scholar] [CrossRef]
- Yu, K.D.; Aviso, K.B.; Promentilla, M.A.B.; Santos, R.J.; Tan, R.R. A weighted fuzzy linear programming model in economic input–output analysis: An application to risk management of energy system disruptions. Environ. Syst. Decis. 2016, 36, 183–195. [Google Scholar] [CrossRef]
- Nguyen, H.T.; Aviso, K.B.; Le, D.Q.; Kojima, N.; Tokai, A. A linear programming input–output model for mapping low-carbon scenarios for Vietnam in 2030. Sustain. Prod. Consum. 2018, 16, 134–140. [Google Scholar] [CrossRef]
- Kang, J.; Ng, T.S.; Su, B. Optimizing electricity mix for CO2 emissions reduction: A robust input-output linear programming model. Eur. J. Oper. Res. 2020, 287, 280–292. [Google Scholar] [CrossRef]
- Su, Y.; Liu, X.; Ji, J.; Ma, X. Role of economic structural change in the peaking of China’s CO2 emissions: An input–output optimization model. Sci. Total Environ. 2021, 761, 143306. [Google Scholar] [CrossRef]
- Yu, S.; Zheng, S.; Li, X.; Li, L. China can peak its energy-related carbon emissions before 2025: Evidence from industry restructuring. Energy Econ. 2018, 73, 91–107. [Google Scholar] [CrossRef]
- Ronald, E.M.; Peter, D.B. Input–Output Analysis Foundations and Extensions, 2nd ed.; Cambridge University Press: Cambridge, UK, 2009; p. 555. [Google Scholar]
- Stone, R. Input-Output and National Accounts; Organization for European Economic Cooperation: Paris, France, 1961. [Google Scholar]
- Bacharach, M. Biproportional Matrices and Input-Output Change; Cambridge University Press: Cambridge, UK, 1970; p. 4. [Google Scholar]
- Chansombat, S.; Pongcharoen, P.; Hicks, C. A mixed-integer linear programming model for integrated production and preventive maintenance scheduling in the capital goods industry. Int. J. Prod. Res. 2019, 57, 61–82. [Google Scholar] [CrossRef]
- Emeç, Ş.; Akkaya, G. Developing a new optimization energy model using fuzzy linear programming. J. Intell. Fuzzy Syst. 2021, 40, 9529–9542. [Google Scholar] [CrossRef]
- Shan, Y.; Guan, D.; Zheng, H.; Ou, J.; Li, Y.; Meng, J.; Mi, Z.; Liu, Z.; Zhang, Q. China CO2 Emission Accounts 1997–2015. 2018. Available online: https://www.nature.com/articles/sdata2017201 (accessed on 16 January 2018).
- Shan, Y.; Huang, Q.; Guan, D.; Hubacek, K. China CO2 Emission Accounts 2016–2017. Scientific Data. 2020. Available online: https://www.nature.com/articles/s41597-020-0393-y (accessed on 13 February 2022).
- Guan, Y.; Shan, Y.; Huang, Q.; Chen, H.; Wang, D.; Hubacek, K. Assessment to China’s recent emission pattern shifts. Earth’s Future 2021, 9, e2021EF002241. [Google Scholar] [CrossRef]
- OECD. Input-Output Table. 2021. Available online: https://stats.oecd.org/Index.aspx?DataSetCode=IOTS_2021 (accessed on 30 April 2022).
- Xu, L.; Chen, N.; Chen, Z. Will China make a difference in its carbon intensity reduction targets by 2020 and 2030? Appl. Energy 2017, 203, 874–882. [Google Scholar] [CrossRef]
- Cui, L.; Li, R.; Song, M.; Zhu, L. Can China achieve its 2030 energy development targets by fulfilling carbon intensity reduction commitments? Energy Econ. 2019, 83, 61–73. [Google Scholar] [CrossRef]
- Li, P.; Ouyang, Y. Quantifying the role of technical progress towards China’s 2030 carbon intensity target. J. Environ. Plan. Manag. 2021, 64, 379–398. [Google Scholar] [CrossRef]
- International Energy Agency (IEA). An Energy Sector Roadmap to Carbon Neutrality in China. Available online: https://www.iea.org/reports/an-energy-sector-roadmap-to-carbon-neutrality-in-china/executive-summary (accessed on 20 January 2022).
- Sun, Z.; Liu, Y.; Yu, Y. China’s carbon emission peak pre-2030: Exploring multi-scenario optimal low-carbon behaviors for China’s regions. J. Clean. Prod. 2019, 231, 963–979. [Google Scholar] [CrossRef]
- Statistical Communiqué of the People’s Republic of China on National Economic and Social Development in 2021. China National Bureau of Statistics. Available online: https://www.stats.gov.cn/tjsj/zxfb/202202/t20220227_1827960.html (accessed on 28 February 2022).
- Hamaguchi, Y. Polluting firms’ location choices and pollution havens in an R&D-based growth model for an international emissions trading market. J. Int. Trade Econ. Dev. 2021, 30, 625–642. [Google Scholar] [CrossRef]
- Hamaguchi, Y. Positive effect of pollution permits in a variety expansion model with social status preference. Manch. Sch. 2019, 87, 591–606. [Google Scholar] [CrossRef]
- Nakada, M. Does Environmental Policy Necessarily Discourage Growth? J. Econ. 2004, 81, 249–275. [Google Scholar] [CrossRef]
- Grimaud, A.; Tournemaine, F. Why can an environmental policy tax promote growth through the channel of education? Ecol. Econ. 2007, 62, 27–36. [Google Scholar] [CrossRef] [Green Version]
- Nakada, M. Environmental Tax Reform and Growth: Income Tax Cuts or Profits Tax Reduction. Environ. Resour. Econ. 2010, 47, 549–565. [Google Scholar] [CrossRef]
- International Energy Agency (IEA). Global Energy Review: CO2 Emissions in 2021. Available online: https://www.iea.org/reports/global-energy-review-co2-emissions-in-2021-2 (accessed on 31 March 2022).
| Intermediate Demand | Final Demand | Total Output | |||||
|---|---|---|---|---|---|---|---|
| 1 | 2 | … | n | ||||
| Intermediate Input | 1 | … | |||||
| 2 | … | ||||||
| … | … | … | … | … | |||
| n | … | ||||||
| Initial Input (GDP) | |||||||
| Total Input | |||||||
| No. | Sector | Influence Coefficient | Sensitivity Coefficient | ||||
|---|---|---|---|---|---|---|---|
| Year of 2018 | Year of 2030 (Prediction) | Changing Trend | Year 2018 | Year 2030 (Prediction) | Changing Trend | ||
| 1 | Agriculture, Fishery, and Forestry | 0.904813799 | 0.911193495 | ↓ | 1.762027066 | 1.488778679 | ↓ |
| 2 | Mining and Quarrying | 1.009079544 | 0.965229629 | ↓ | 1.489040976 | 0.665824097 | ↓ |
| 3 | Food product, Beverage, and Tobacco | 1.07347282 | 0.937524512 | ↓ | 1.260593194 | 0.96751964 | ↓ |
| 4 | Textile, Leather Industries | 1.320953003 | 1.117117863 | ↓ | 0.940646051 | 0.481975322 | ↓ |
| 5 | Manufacture of Wood and Wood products | 1.144890402 | 1.17549248 | ↑ | 0.173149877 | 0.291590586 | ↑ |
| 6 | Manufacture of Paper and Paper Products, Printing and Publishing | 1.128036709 | 1.103835222 | ↓ | 0.344761535 | 0.337072054 | ↓ |
| 7 | Manufacture of Industrial Chemicals and petrochemicals | 1.090738039 | 0.986463947 | ↓ | 2.018706162 | 1.071174135 | ↓ |
| 8 | Manufacture of Non-metallic Mineral Products | 1.084037308 | 0.986846186 | ↓ | 0.795797208 | 0.747015255 | ↓ |
| 9 | Basic Metal Industries | 1.117413045 | 0.998128947 | ↓ | 1.304609116 | 0.960560485 | ↓ |
| 10 | Equipment | 1.199747846 | 1.049484139 | ↓ | 1.76799118 | 0.992071028 | ↓ |
| 11 | Electricity | 1.024260271 | 0.962016243 | ↓ | 0.832964451 | 0.507226756 | ↓ |
| 12 | Water supply and waste | 0.969568481 | 0.943859788 | ↓ | 0.201398544 | 0.13147807 | ↓ |
| 13 | Construction | 1.08760903 | 1.005504157 | ↓ | 0.17441818 | 0.997242957 | ↑ |
| 14 | Wholesale and retail trade | 0.665885129 | 0.951670374 | ↑ | 1.0317304 | 1.632107876 | ↑ |
| 15 | Transportation | 0.904065837 | 0.923489878 | ↑ | 0.95291135 | 0.689591594 | ↓ |
| 16 | Commercial, public services, and others | 0.687125641 | 0.911856852 | ↑ | 1.579653219 | 4.118776369 | ↑ |
| 17 | Culture, Education, Sports, Art | 0.588303097 | 1.070286291 | ↑ | 0.369601491 | 1.009995095 | ↑ |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xu, X.; Liao, M. Prediction of China’s Economic Structural Changes under Carbon Emission Constraints: Based on the Linear Programming Input–Output (LP-IO) Model. Sustainability 2022, 14, 9336. https://doi.org/10.3390/su14159336
Xu X, Liao M. Prediction of China’s Economic Structural Changes under Carbon Emission Constraints: Based on the Linear Programming Input–Output (LP-IO) Model. Sustainability. 2022; 14(15):9336. https://doi.org/10.3390/su14159336
Chicago/Turabian StyleXu, Xiaoxiang, and Mingqiu Liao. 2022. "Prediction of China’s Economic Structural Changes under Carbon Emission Constraints: Based on the Linear Programming Input–Output (LP-IO) Model" Sustainability 14, no. 15: 9336. https://doi.org/10.3390/su14159336
APA StyleXu, X., & Liao, M. (2022). Prediction of China’s Economic Structural Changes under Carbon Emission Constraints: Based on the Linear Programming Input–Output (LP-IO) Model. Sustainability, 14(15), 9336. https://doi.org/10.3390/su14159336





