Abstract
The study of the impact of the high-speed railway (HSR) on enterprise financing costs (EFCs) contributes to understanding the economic impact of transportation facilities, by analyzing the coordinated development of the regional economy and studying the influencing factors in enterprise operation. By using data of Chinese listed companies from 2008 to 2019, this paper analyzes the impact of HSR on EFCs and examines the role of central cities (CCs) in the whole process through methods of the DID model, panel threshold model, PSM-DID, parallel trend test and so on. The research results are as follows: first, HSR led to a significant decrease in the level of corporate debt financing. The regression coefficient of HSR is −0.002, which is significant at a 5% level. Second, there exists a heterogeneous effect of HSR on CCs. Mid-region enterprises suffered more than small enterprises, low-growth enterprises and enterprises with a low return on assets. Third, HSR affects EFCs, which leads to the diffusion effect of CCs, resulting in an increase in EFCs in CCs and a decrease in non-CCs. It was found that there is a single threshold of the panel threshold regression based on per capita GDP, and the regression coefficient of HSR below the threshold is −0.001, which is significant at the 5% level. Additionally, the regression coefficient of HSR above the threshold is 0.002, which is significant at the 1% level. The interaction term and group regression both also confirm the above conclusion. Fourth, the impact of HSR on EFCs is limited by geographic distance. When the geographic distance between a non-CC and a single CC is greater than 500 km, and the total distance between a non-CC and four CCs is greater than 3500 km, the effect of HSR is remarkable. The above conclusions prove the significant impact of HSR on EFCs and reveal the role of CCs and geographic distance in this process. These provide new ideas and evidence for corporate financing management as well as planning for urban development and the HSR network.
1. Introduction
The endless stream of literature on high-speed rail (HSR) suggests that, due to its space-time compression effect, HSR can not only change transportation and lifestyles but affect enterprise financing costs (EFCs) [1]. As an important mode of transportation, HSR has a faster running speed than the ordinary railway and operates better than airplanes in terms of convenience and punctuality. Consequently, HSR can accelerate the interregional flowing of capital and personnel, make the communication between banks and enterprises more effective and reduce the degree of information asymmetry in the process of financing. Several studies have revealed the impact of HSR on EFCs. For instance, HSR can affect a corporation’s options for financing methods, increase debt financing and reduce equity financing; it can also adjust the distribution of banks’ credit resources, increase the loan limit to enterprises in other places and enhance the communication between banks and enterprises [2,3,4,5]. However, available research is deficient in revealing the process of HSR with EFCs. Many important issues are not mentioned, such as the mechanism, heterogeneity, interfering factors, etc. In view of the increasing economic impact of HSR and the importance of EFCs on corporate and regional development, it will be vital to analyze the above topics.
The role of CCs should be meticulously considered when it comes to the impact of HSR on EFCs. HSR affects EFCs by promoting regional resource flow, such as people and capital. Therefore, it is necessary to understand the role of CCs in the flow of resources. According to a new economic geography theory, CCs are agglomeration economies with unique economic expertise, abundant labor resources, relatively large markets and other types of resources in the region, and they also operate as the economic growth poles of the region. CCs can influence other cities in two different ways. On the one hand, CCs may have a radiation effect of spreading resources to the surrounding area, which will promote the development of other cities. On the other hand, CCs may have a siphon effect of absorbing resources from the surrounding area, which will cause the economic development of other cities to be restricted. For the same reason, the impact of HSR on EFCs will change due to CCs’ different effects. If it is radiation effect, enterprises in non-CCs will receive resources from CCs, and EFCs will decrease; in the case of siphon effect, EFCs of non-CCs will increase. In this case, analyzing the effects of CCs will help us to better understand the impact of HSR, and provide targeted strategies for different cities. Regrettably, theoretical research is still insufficient in this field.
The impact of HSR on EFCs also needs to take geographic distance into consideration. In the process of interregional resource flowing, there will be mobility efficiency issues due to urban distance. Urban economics have confirmed that city interrelationships obey the law of distance decay, that is, the farther from the central city, the weaker the radiation ability of the central city will be. In the process of HSR affecting EFCs, geographic distance between CCs and other cities will be crucial, resulting in geographical distance restrictions on the impact [6]. Prior studies have focused on this topic and proved that there is an optimal geographical distance radius for the effect of HSR on urban innovation. However, similar results have not yet been achieved, from the perspective of EFCs. Hence, studying the role of geographic distance may be necessary to analyze the impact of HSR, and also provide a decision-making basis for HSR network planning and site setting.
Given the above background, this paper, based on the data of 281 cities and 1443 listed companies in China from 2008 to 2019, examines the relationship among HSR, CCs and EFCs. The information our study contributes to the field may be compared with previous studies as follows. First, we confirm the impact of HSR on EFCs. We adopt the DID Mode to test the impact of HSR and use replacement variables, PSM-DID, parallel trend testing and counterfactual testing for robustness. The results all prove that HSR can reduce EFCs. Second, we explore the effect of CCs on the impact of HSR. We employ threshold regression and other methods to test whether radiation effect or siphon effect will occur in CCs and compare different changes in EFCs in CCs and other cities. We found that in high-income areas, HSR had a small effect on EFCs, and even led to an increase in EFCs; in low-income areas, HSR led to a decrease in EFCs, and the effect was significant. This result proves that the central city has a diffusion effect during the opening of HSR. Third, we analyze the role of geographic distance in the impact of HSR. We analyze whether the geographic distance between cities (distance from one city to single CC, total distance from one city to four CCs) impacts the effect of HSR through interaction item setting and group regression. The results confirm the effect of geographic distance. Compared to the existing research, this paper will provide insightful ideas and new evidence to better comprehend the economic impact of HSR, corporate financing decisions and urban development planning.
The rest of the paper is organized as follows. The second part is the literature review and theoretical assumptions; the third part is the econometric model, data and indicators description; the fourth part is the empirical results and explanations; the last part is the conclusion.
2. Literature Review and Theoretical Assumptions
2.1. HSR and EFCs
HSR has important impacts on economic development owing to its time-space compression effect, such as driving regional economic growth, promoting regional economic integration and improving urbanization levels. HSR also affects the development of micro-enterprises, by reducing enterprise costs, promoting technological innovation, weakening the stickiness of human capital, improving investment efficiency and so on.
HSR has an impact on corporate financing while strengthening regional linkages. The circulation and coordination of financing parties and the transmission of financing information will be affected by geographical distance, which will be impacted by the space-time compression effect of HSR. For instance, it increases the level of competition among banks and reduces the cost of debt financing for companies, enabling enterprises to obtain more favorable credit conditions with a larger credit scale, longer term and lower cost; this, in turn, allows banks to lend more to businesses outside the region [2,3,5]. Other studies also confirmed the impact of HSR indirectly. For example, HSR leads to an increase in the company’s perceived risk of operating and default, which leads to an increase in bank loan costs; it also leads to a faster adjustment of the company’s capital structure and a change in the ratio of debt financing to equity financing [7,8].
HSR may affect EFCs in the following ways. First, HSR promotes the flow of information. HSR can improve the convenience of communication, the efficiency of information circulation, the quality of company information release, and reduce the cost of information search and supervision for capital suppliers [8]. Numerous studies confirmed that HSR can promote face-to-face communication between investors and enterprises; improve the transparency of company information; prevent the accumulation of negative information [9]; reduce information asymmetry and supervision costs; improve accounting conservatism [10,11]. Second, HSR promotes the role of regulatory agencies. Studies have proved that HSR improves independent directors’ travel convenience and work enthusiasm; enhances their supervision effect [12]; increases the probability of companies hiring auditors from different places; improves audit quality [13,14]; increases the company’s attention and improves the quality of financial reports. Third, HSR will improve the operation effect of enterprises. HSR reduces the communication cost of enterprise management, increases the scale of branches, and enhances the professionalism of production, thereby improving the company’s operating efficiency, enhancing its value, increasing investors’ willingness to invest, and reducing financing costs [12,15,16].
Based on the above analysis, this paper proposes Hypothesis 1:
Hypothesis 1.
HSR promotes the flow of resources, and thereby reduces EFCs.
2.2. HSR and CCs
HSR enhances the connection between regions but generates different effects. According to urban economics and new economic geography, the developmental impact of CCs on other cities produces different effects. On the one hand, CCs have a radiation effect on surrounding cities, other cities gain the resource radiation. That is, HSR promotes the flowing of resource elements from CCs to other cities, thereby promoting the economic development of other cities. On the other hand, CCs have a siphon effect on the surrounding cities. HSR promotes the flow of resources such as production factors to CCs and has a negative impact on the development of other cities.
There is still no consistent conclusion on whether HSR will lead to radiation effect or siphon effect. Some studies confirmed the siphoning effect of HSR, as firstly, it accelerates the flow of production factors from peripheral cities to CCs, promotes economic growth in CCs, and inhibits economic growth in small and medium-sized cities [17,18,19,20]; secondly, it is beneficial for the development of cities in central Europe, but the impact on other cities is just the opposite, especially cities in peripheral countries such as Spain and Portugal [21]; thirdly, it promotes the development of the service industry in the Tokyo metropolitan area of Japan, but the peripheral regional service industry tends to shrink. Other studies believe that there is a diffusion effect. For example, HSR can accelerate the flow of factors and knowledge spillovers, thus promoting economic growth and employment growth in cities along the route, strengthening regional trade linkages and narrowing the economic development gap between regions [22,23,24]; highways also promote population migration from urban centers to suburban areas, leading to urban “suburbanization”.
There is still plenty of room for discussing whether there will be a diffusion effect or a siphon effect in terms of HSR’s impact on EFCs. Several studies have found relevant evidence that HSR increased EFCs by 2.2% in non-node cities, and it is more obvious for enterprises in eastern China [5,25]; that it reduced EFCs in regions with a low level of financial marketization [2]. Other studies demonstrated the different impacts of HSR. For example, it promotes the flow of capital from small and medium cities to large cities, resulting in a siphon effect [1]; makes VC investment spread from central cities to other cities, resulting in a radiation effect [26]; makes the capital of enterprises in other regions spill over to the region [8] and has more a obvious effect on promoting innovation investment of enterprises in areas with a low degree of marketization [27].
Based on the above analysis, this paper proposes Hypothesis 2:
Hypothesis 2.
HSR leads to the diffusion of resources from CCs to other cities, which will reduce the EFCs in other cities.
2.3. HSR and Geographic Distance
Geographical distance is an important factor affecting corporate financing [27]. Some studies consider the quality of “soft information” available to banks as a decreasing function of the distance between the bank and the borrower, that is, the closer the geographic distance, the higher the quality of “soft information” available to the bank and the greater the likelihood that the borrower will receive a loan [28,29,30,31]. Studies concerning the information advantage of local bank customers compared to those coming from a distance have revealed that these differences can lead to changes in loan amount and loan cost [32,33,34]. Other studies have explored the relationship between corporate banks, loan banks and other competing banks, arguing that the transportation cost caused by geographic distance leads to regional price discrimination [35].
There are a few studies on the impact of distance from CCs, especially about EFCs. It is worth highlighting that the geographic distance in this paper is different from the previous studies. Previous studies analyzed the geographic distance between financing entities, especially the distance between companies and lending institutions, while this study analyzes the geographic distance between CCs and other cities. Some pertinent research covers the following aspects. Ye, et al. (2020) found that the optimal radius for HSR to affect urban innovation is about 200 km away from CCs, and urban innovation within 100 km around CCs exhibits a “siphon effect” [6]. Wang, et al. (2021) analyzed the impact of HSR on enterprise innovation and found that the distance of transportation will affect its effect. There is a non-linear relationship between the influence of CCs on non-central cities in terms of transportation distance, with significant effects within 3 h of transportation distance and the greatest effect within the 1-h circle [36]. Chen, et al. (2021) analyzed the impact of Shanghai–Kunming HSR in China, and found that if the distance between cities and towns is 0–18 min away from the HSR station, economic development will be promoted; within the time distance of 18–64 min, the economic development will show a siphon effect; within the distance of 64–151 min, the economic development will generate a promoting effect; if the distance exceeds 151 min, the effect will be not significant [37].
Based on the above analysis, this paper proposes Hypothesis 3:
Hypothesis 3.
Geographical distance between CCs and other cities will influence the effect of HSR.
2.4. Research Gap
Previous studies have analyzed the relationship between HSR and corporate financing, and their relative results have laid foundations for this paper. Additionally, there are differences between this paper and previous studies, which are mainly reflected in the following aspects.
First, this paper specifically analyzes the impact of HSR on corporate financing costs. In the past, scholars mainly studied the social impacts of HSR by analyzing its impact on regional economic coordination, human resources flow, and technology spreading. Seldom did they analyze the impact of HSR on microeconomic management especially EFCs, and that is the main focus of this paper. Because EFCs are of great significance to the operation of enterprises, the research of this paper has strong theoretical value.
Second, this paper uses CCs to explore the role of HSR. Previous studies have analyzed the effect of HSR on regional economic development, overlooking the specific processes and mechanisms. However, this paper takes CCs into consideration, especially geographic distance, making it better suited to understand how HSR affects corporate financing costs.
Third, this paper makes use of analyzing methods and tools such as geographic distance. This paper measures the geographic distance between cities and introduces geographic distance as an important variable in the analysis process. These practices can not only make the research more accurate but also provide new ideas and methods for HSR research.
3. Methods and Materials
3.1. Methodology
3.1.1. Research Framework
This paper analyzes the impact of HSR on EFCs, with the research content involving benchmark regression, robustness test, heterogeneity analysis and extensional analysis, and uses the methods of DID model, panel threshold model, PSM-DID, parallel trend test, and placebo test. The research thought is shown in Figure 1.
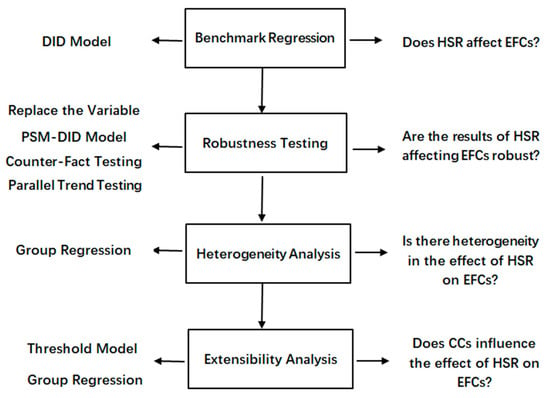
Figure 1.
Research framework.
First, benchmark regression analysis. This paper uses the DID model as the benchmark analysis model, inspecting whether HSR has an impact on EFCs.
Second, robustness test. In order to ensure the accuracy of the benchmark analysis model, this paper uses the following methods to conduct the robustness test. Among them, the method of replacing indicators ensures the validity of the data indicators by replacing the indicators of the explained variables. The parallel trend test is used to check whether the DID model conforms to the parallel trend characteristics during the usage process; PSM-DID is used to check whether the DID model confronts selection bias during the usage process. Counterfactual testing, relying on counterfactual settings, is used to test the analysis results of the DID model as a whole.
Third, heterogeneous analysis. In this paper, the total samples are grouped according to specific indicators to construct heterogeneous sample groups, and the benchmark model is used to perform grouping regression so as to compare the heterogeneous effects of HSR.
Fourth, extensional analysis. This paper analyzes, in the process of HSR affecting EFCs, what impacts will CCs (whether it is a CC, or the geographic distance between non- CCs and CCs) exert? In the research process, this paper turns to panel threshold regression to analyze whether HSR affects EFCs and stirs a nonlinear transformation and the grouping regression is used to compare the differences between different samples (CCs and non-CCs samples, groups with different geographical distances).
3.1.2. DID Model
This paper adopts the well-established difference-in-difference model (DID) in the field of policy evaluation as a benchmark model [38]. Due to the differences in time of HSR development in different cities, we select a multi-period DID model. The specific model is as follows.
where represents the city and year; represents the cost of debt financing; is a dummy variable for grouping, if HSR is opened in the region where the company is located, the value is 1, otherwise it is 0; is a time dummy variable, the year after the regional HSR is opened takes the value of 1, otherwise it is 0; are the control variables; is the regional fixed effect; is the time fixed effect; is the random error. We focus on the coefficient . When is greater than 0, it indicates that HSR will lead to an increase in EFCs; when is less than 0, it indicates that HSR will lead to a decrease in EFCs.
3.1.3. Panel Threshold Model
When analyzing the effect of CCs, we adopt the panel threshold model for analysis. The panel threshold model can find the threshold characteristics generated by the structural mutation in the economic system, and automatically identify the sample data to determine the threshold value. At the same time, it has the good characteristics of the general panel data model [39,40]. This paper studies whether there is a nonlinear effect in the effect of HSR on EFCs. That is, whether there are different city scale thresholds, resulting in differences in the sample regression results above and below the threshold. The specific model is as follows:
where is the threshold variable, is the threshold value, and is the indicative function; other variables are the same as Formula (1). By comparing the size of the threshold variable and the threshold value , the sample observations are divided into two sample regions, and the difference between the different regions is the difference between the regression coefficients and . When , , otherwise . Arbitrary is assigned to as the initial value, and each regression coefficient is estimated by the least square method OLS, and the corresponding residual square sum is obtained at the same time. If is selected from small to large in the range of value in turn, multiple different can be obtained, so that the minimum value of the residual square sum is the threshold value , that is,.
3.2. Data Sources
This paper uses data from cities and listed companies in China from 2008 to 2019 for research. The data of listed companies comes from the CSMAR and Wind database; the cities’ data comes from the Wind database; HSR data are compiled according to the data published by the Chinese traffic management agency. Since China’s first HSR, the Beijing-Tianjin Intercity Railway, was officially completed in 2008, we select 2008–2019 as the research interval.
We process data as follows: remove listed companies in finance, insurance, and real estate; remove ST, *ST listed companies; remove companies that were listed during the investigation period and with incomplete data; 1% and 99% winsorize for company-level continuous metrics. Finally, 1443 listed companies and cities in 281 prefecture-level cities are matched with annual observation data.
3.3. Indicator Selection
3.3.1. HSR
HSR has had an important impact on China’s economic development. Since the official completion of China’s first HSR in 2008, China has built a relatively complete national expressway network within 20 years. In 2012, China’s expressway mileage ranked first in the world. By the end of 2019, the operating mileage of HSR reached 35,000 km, accounting for 70% of the total operating mileage of HSR in the world. As shown in Figure 2, in 2008, there were 76 cities with HSR in China, and in 2019, the number of cities reached 250.
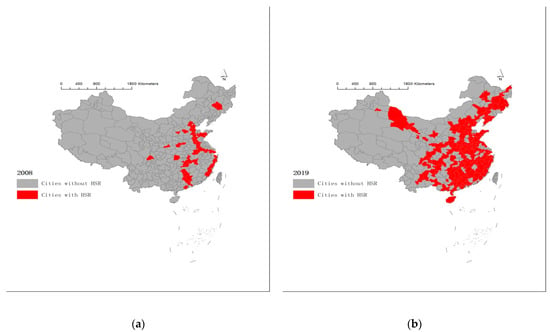
Figure 2.
Cities with HSR in China. (a) Cities with HSR in 2008; (b) Cities with HSR in 2019.
This study draws on the practice of theoretical circles to set up dummy variables for HSR. If HSR is opened in the area where the company is located, it will be assigned a value of 1 in the year of opening and subsequent years, otherwise, it will be assigned a value of 0 [2,41,42,43].
3.3.2. EFCs
EFCs are not the only important factor affecting the operation and development of enterprises, but an important content of economic development and capital market. Considering that debt financing is an important way of corporate financing, this paper mainly analyzes the cost of debt financing in the process of analyzing EFCs. According to research conventions, this paper uses the following method to measure EFCs [2,7,28]. In the process of robustness testing, this paper will also use other financing cost indicators for analysis.
EFCs = (Detailed interest expense of financial expenses + detailed handling fee of financial expenses + detail of financial expenses and others)/Total liabilities
3.3.3. CCs
This study uses two methods to define CCs. On one hand, Beijing, Shanghai, Guangzhou and Shenzhen are listed as central cities, and other areas are non-central cities. The above classification mainly considers the prominence of the four cities in China’s economic and social development. On the other hand, CCs are measured by the size of the city, especially the level of economic development, that is, the per capita GDP of the city is used as the measurement standard, and the city with a high per capita GDP is determined to be a CC, otherwise, it is a non-central city.
3.3.4. Control Variables
The cost of corporate debt financing is affected by other factors, including company characteristics and regional characteristics. On one hand, company characteristics include company size, company debt ratio, and company age, etc. On the other hand, regional characteristics include regional GDP, regional population, regional financial development level and so on. The specific indicators are described in Table 1.

Table 1.
Description of indicators.
4. Results
4.1. Descriptive Statistics
Table 2 presents descriptive statistics results. Among them, the mean value of EFCs is 0.024, the maximum value is 0.102, the minimum value is −0.02, and the standard deviation is 0.017, which are similar to previous studies. The mean value of HSR is 0.773, indicating that 77.3% of the areas where listed companies are located have HSR in 2019 in China. Other indicators are detailed in the table.

Table 2.
Descriptive Statistics.
4.2. Baseline Results
This paper uses model (1) to test the impact of HSR on EFCs. The results are shown in Table 3. Among them, column (1) does not add any control variables, only controls the fixed effects of time and region, and the HSR coefficient is negative and significant at the 1% level, indicating that HSR can reduce EFCs. Column (2) controls company characteristic variables such as enterprise scale, debt ratio, tangible asset ratio, etc. The HSR regression coefficient is still negative and significant. Column (3) further adds a regional control variable, HSR is significant at the 5% level, and the regression coefficient is negative, which still shows that HSR significantly reduces EFCs.

Table 3.
Estimates of the impact of HSR on EFCs.
The benchmark regression results support research Hypothesis 1, which proves that HSR can reduce EFCs by strengthening the flow of people and capital, reducing the degree of information asymmetry, and enhancing the convenience of communication. This result is consistent with previous research results, such as Wu, et al. (2021), Chu, et al.2019), and Wang, et al. (2020) [2,3,5]. Of course, this conclusion still needs more robustness checks.
When it comes to the control variables, the financial liability ratio is significantly negative at the level of 1%, suggesting that the higher the level of the financial liability ratio, the lower the degree of EFCs. The company’s establishment time is significantly negative at the level of 5%, which means that the longer the company’s existence period, the lower its financing cost. Other control variables such as company size, company market value, regional per capita GDP, regional household registration population, regional financial deposits and loans and return on assets are not significant.
4.3. Robustness Checks
4.3.1. Measurements of Replacing Explained Variables
Considering the influence of index selection on regression results, it is necessary to replace the measurement index for the robustness test. In this paper, we replace the metrics for EFCs. According to the theoretical practice, we use the following two methods to replace the EFC and use the benchmark model for regression to analyze whether the previous conclusions are affected by the measurement indicators [2,7,28].
EFCs1 = Financial expenses/total liabilities
EFCs2 = Interest expense details of financial expenses/average value of long-term and short-term liabilities
Table 4 shows the regression results, and columns (1) and (2) are the regression results of the above indicators, respectively. The results show that when the explained variables are replaced, the effect of HSR is still salient, and the regression coefficients are negative and significant at the 10% and 5% levels, respectively. This is consistent with the benchmark regression results. The above results prove that the previous analysis results are robust and are not affected by the way the indicators are measured.

Table 4.
Estimates of changing variables for EFCs.
4.3.2. Parallel Trend Test
In order to ensure the rationality of DID model, the parallel trend test needs to be satisfied between the experimental group and the control group, that is, the experimental group and the control group should have parallel trends before the event. Referring to the practice of Beck (2010), Wang, et al. (2020) [44,45], we examine whether there is a parallel trend in the changes between the experimental group and the control group before and after the opening of the high-speed rail. As shown in Figure 3, before the opening of HSR, the difference in financing cost between the experimental group and the control group was not large; but after the opening of HSR, the financing cost of listed companies in the experimental group increased significantly and showed an obvious growth trend, indicating that the quasi-natural experiment constructed in this paper satisfies the parallel trend test.
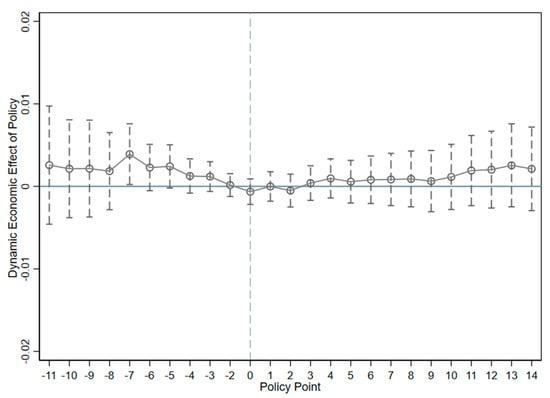
Figure 3.
Parallel trend test results.
4.3.3. PSM-DID
The DID model may be subject to “selectivity bias”, i.e., it does not ensure that the experimental and control groups have the same individual characteristics prior to policy implementation. The above bias is more likely to appear when the data sample size is large [46]. The samples in this paper include 17,316 samples from 281 prefecture-level cities in China, and their regional differences and individual differences are relatively large. Therefore, it is necessary to use the propensity score matching method (PSM) to use the control variables as the identification features of the sample points. Groups of cities were matched (Heckman et al., 1998; Rosenbaum et al., 1983) [47,48].
This paper first uses the nearest neighbor 1:1 and no replacement method to match the samples year by year. In the matching process, the covariates are company size, company debt ratio, tangible asset ratio, operating cash flow and property rights. This paper uses model (1) to analyze the impact of the opening of HSR on the company’s debt financing cost. The regression results of the model are shown in Table 5. The HSR coefficient is still significantly negative, and the hypothesis in this paper is still valid.

Table 5.
Estimates of PSM-DID.
4.3.4. Counterfactual Testing
The premise of using the DID method is that the experimental group and the control group should be comparable, that is, if there is no impact of HSR, the financing cost of the experimental group and the control group will not change significantly over time. To verify the above premise, this paper draws on the research of Hung et al. (2013) [49], where the opening of HSR is carried out 1 and 2 years ahead of the time of policy implementation and regressed using a benchmark model. The test results are shown in Table 6. Columns (1) and (2) are the regression results of pushing forward the opening time of high-speed rail by 1 year and 2 years, respectively. From the results, the HSR coefficients are not significant. The above counterfactual test results show that HSR significantly decreases EFCs.

Table 6.
Estimates of counterfactual testing.
4.4. Heterogeneity Results
4.4.1. Regions
To deepen the understanding of the nexus between HSR and EFCs, this section further investigates the heterogeneity of region and company. Specifically, we analyze the heterogeneity results of the impact of HSR on EFCs in terms of regions, return on assets, Tobin’s Q, and enterprise assets.
This part divides the total sample into samples from the eastern, central, western and northeastern regions, and analyzes the differences in the impact of HSR. The results are shown in Table 7, and columns (1)–(4) are the results of the western region, the northeastern region, the central region and the eastern region.

Table 7.
Estimates of heterogeneity by regions.
The results show that HSR has a significant impact in the central region, with an impact coefficient of −0.004, which is significant at the 10% level; the impact effect in other regions is not significant. The results may be due to economic differences in different regions. Geographically, the central region is close to the economically developed eastern region. High-speed rail can strengthen the flow of resources and economic exchanges between the two regions. Affected by the diffusion effect, enterprises in the central region can obtain external resources and funds, thus significantly reducing EFCs. Concurrently, the eastern region has the opposite effect. Because of the spread of its own resources, the eastern region cannot produce the promotion effect of its own development in the process of strengthening its connection with other regions, so the EFCs of enterprises in this region have not been reduced. The western region and the northeastern region are far away from the eastern region due to their geographical location. As a result, HSR failed to bring external resources and EFCs failed to decrease. The research on the diffusion effect of CCs in this paper confirms the above analysis.
4.4.2. Enterprise Scale
This part considers the impact of enterprise scale on the opening of high-speed rail. According to the scale of enterprise assets, the total sample is divided into a large-scale sample (above the median) and a small-scale sample (below the median). Then, the two sets of samples are used for regression estimation, and the results are shown in columns (1) and (2) of Table 8.

Table 8.
Estimates of heterogeneity by enterprise scale, growth and assets.
The results show that there are significant differences between the different samples. HSR has a significant impact on EFCs of small-scale enterprises, and the impact coefficient is −0.002, which is significant at the 5% level. The regression coefficients of large-scale samples are also negative, but not significant. HSR does not have an impact on the EFCs of such companies. The above results show that, compared to large-scale enterprises, small-scale enterprises will be able to make better use of external resources for financing. Judging from the reasons, small-scale enterprises are less difficult to obtain financing due to their small financing scale and low financing threshold.
4.4.3. Growth of Enterprises
This section analyzes the heterogeneity caused by the growth of enterprises. Using Tobin’s Q of the firm as a variable, all companies are divided into low growth (below the median) and high growth (above the median). Then, the two sets of samples are used for regression estimation, and the results are shown in columns (3) and (4) of Table 8.
The results show that HSR has a significant impact on EFCs of low-growth companies, with an impact coefficient of −0.002, which is significant at the 5% level. Conversely, the impact of HSR on enterprises with high growth is not significant. The above results show that, compared with high-growth companies, low-growth companies are more likely to reduce their EFCs by obtaining resources when they obtain effective external financing channels.
4.4.4. Return on Assets
This section analyzes the heterogeneity caused by firm assets. Using the return on assets of the firm as a variable, all companies are divided into low return on assets (below the median) and high return on assets (above the median). Then, the two sets of samples are used for regression estimation, and the results are shown in columns (5) and (6) of Table 8.
The results show that HSR has a significant impact on EFCs for enterprises with low return on assets, and the coefficient is −0.002, which is significant at the level of 5%. Conversely, the impact of HSR on enterprises with a high return is not significant. Generally speaking, enterprises with a higher return on assets have easy access to funds and lower financing costs, so HSR has little impact on their financing costs. In contrast, enterprises with lower returns on assets are more affected by HSR, as they present the possibility of obtaining funding from other regions.
4.5. Analysis of Expansion Based on CCs
4.5.1. Diffusion Effect of CCs
This part examines whether the radiation effect or siphon effect occurs in CCs during the opening of HSR, and what impact it has on FCEs. During the analysis, the definition of CCs needs to be explained. Since Beijing, Shanghai, Guangzhou and Shenzhen all have HSR in 2008, it is difficult to analyze the impact of HSR in the above-mentioned central cities through DID. In this case, we use the per capita GDP of the city as the measurement variable between CCs and other cities, that is, the high per capita GDP cities are CCs, otherwise they are considered non-central cities. According to the above definition, we adopt threshold regression, interaction item setting, and grouping for analysis.
First, the threshold regression results. In this paper, the urban per capita GDP is used as the threshold for regression to test whether there is a threshold, and at the same time, the regression results above and below the threshold are analyzed. The results are shown in Table 9. There is a single threshold value based on regional per capita GDP in the process of HSR affecting FCEs. The specific value is 11.321; when it is lower than the threshold value, the HSR regression coefficient is −0.001, which is significant at the 5% level. In the case of higher than the threshold value, the regression coefficient of HSR is 0.002, which is significant at the 1% level. For the samples above the threshold of regional per capita GDP, that is, high-income cities or CCs, HSR leads to an increase in FCEs. For samples below the threshold or non-CCs, HSR leads to a decrease in FCEs. The above results show that the radiation effect of CCs occurs during the opening of HSR, which causes non-CCs to obtain resources from CCs, thereby reducing FCEs in the region. CCs have the opposite result. The above conclusions confirm Hypothesis 2.

Table 9.
Estimates of threshold regression based on per capita GDP.
Second, the interaction term regression. Based on the benchmark regression model, we add the interaction term between regional per capita GDP and HSR. The regression results are shown in column (1) of Table 10. The results show that the regression coefficient of the interaction term is 0.002, which is significant at the 5% level, indicating that the per capita GDP has a negative adjustment effect on the effect of HSR on reducing FCEs. The higher the regional per capita GDP level, the lower the effect of HSR on the reduction of FCEs. The above results can be understood as the radiation effect in CCs. This conclusion may also be regarded as the confirmation of the hypothesis (2).

Table 10.
Estimates of interaction terms and group regression.
Third, group regression. This part sorts the quartiles according to the regional per capita GDP and uses the benchmark regression model to regress the 75th, 50th, and 25th quantile samples respectively. The results are shown in columns (2)–(4) of Table 10. The results showed that regression results of the 75th percentile and 50th percentile samples were not significant; the 25th percentile sample regression coefficient is −0.004, and significant at the 10% level. Compared with other grouped samples, the 25% sample with the lowest per capita GDP level has a significant effect on reducing FCEs. That is, in cities with lower income levels, or non-CCs, the impact of the decline in FCEs is more obvious. This result can be regarded as proof of the previous conclusion.
4.5.2. Geographical Distance of CCs
In order to analyze the influence of geographic distance on HSR, this paper uses the interaction term of geographic distance, the shortest distance of a single central city, and the total distance of four central cities to analyze. First, the interaction term is added to the benchmark mode, that is, the intersection of the shortest geographical distance between other cities and a single central city and HSR, and the interaction effect is used to analyze the impact of geographic distance. Secondly, use the benchmark model to perform grouping regression. The grouping standard is the minimum geographic distance between other cities and four central cities (Beijing, Shanghai, Guangzhou, Shenzhen), and then use 100 km as the dividing line to divide the total sample into 10 subsections, and then regression analysis on each group of samples. Finally, the total geographic distance between other cities and the four central cities was calculated, and then the total sample was divided into subsamples, and each group of samples was regressed separately.
The results of the interaction term regression are shown in column (1) of Table 11. The regression coefficient of the interactive term is positive and significant at the 5% level. The shortest distance from CCs has a negative impact on the effect of HSR, that is, for two cities that also have HSR, the farther the geographical distance from CCs, the higher the possibility of lowering FCEs in the region. This result confirms that geographic distance will be an important factor affecting the effect of HSR.

Table 11.
Estimates of the effect of minimum geographic distance on HSR.
The regression results of the geographic distance grouping of a single central city are shown in columns (2)–(11). The regression coefficients of HSR in columns (2)–(5) are not significant, that is, when the minimum distance from CCs is less than 500 km, HSR has no significant effect. The regression coefficients of HSR in columns (6)–(11) are negative and significant, that is, when the minimum distance from CCs is higher than 500 km, HSR has a significant effect, which can reduce FCEs in the region.
The regression results based on the total geographic distance are shown in columns (1)–(5) of Table 12. The coefficients of HSR in columns (1) and (2) are not significant, that is, when the total distance from CCs is less than 3800 km, HSR has no significant effect. The coefficients of HSR in columns (3)–(6) are significant and negative, which means HSR can reduce FCEs in the region. This is consistent with the results in Table 4.

Table 12.
Estimates of the effect of geographic distances on HSR.
The above results show that HSR affects FCEs with an effective radius based on geographic distance, which confirms Hypothesis 3. From the interpretation of the results, the possible result is that the substitution effect of HSR is relative to other means of transportation. For example, when the geographic distance between cities is less than 500 km (total distance is less than 3800 km), it is difficult for HSR to effectively replace other transportation. Other tools such as ordinary railways, self-driving cars and passenger cars may have comparative time advantages in this range. HSR stations are often far from the city center in China. In this case, if the passenger needs to make a journey within 500 km, self-driving may be a better choice than HSR. The above phenomenon will affect the effect of HSR. In addition, the possible reason is the siphoning effect, that is, when the geographical distance is low (500 km), the siphoning effect occurs in CCs, and the effect of HSR is not significant. This is similar to the reason why Ye, (2020) explained that HSR affects urban innovation [6].
5. Discussion
How to effectively play the role of HSR in promoting the economy is a very important issue. Regrettably, the theoretical community has not done enough in this regard. At present, research on the impact of HSR mainly focuses on transportation efficiency, regional coordination, factors flow, etc., and there is a lack of research on the micro-level of enterprises. Although some papers have explored the impacts of HSR on enterprise development, there are still few findings. In this paper, the impact of HSR on EFCs is analyzed, and the role of CCs is studied in this process. This paper provides a new perspective and new evidence for analyzing the economics of HSR and corporate financing theory, which can be regarded as an application and expansion for new geographic economics. Our empirical findings also provide a decision-making basis for public agencies, financial institutions and transportation management agencies, so as to let them better understand the impact of HSR on enterprises and different cities, as well as the impact of geographic distance on the role of HSR. The above research provides implications for corporate financing, local economic development, and HSR network planning.
First, financing behaviors are affected by HSR. This requires enterprises, banks and investment institutions to pay attention to the impact of HSR, and make adjustments in terms of financing information, behaviors, channels, and areas according to changes in transportation facilities. Enterprises should make full use of the HSR, contact more banks and investment institutions, obtain more funds from outside the region and improve their own financing structures. Banks should acquire accurate investment and risk information by conducting field investigations, field visits and on-site communication. Investment institutions should pay attention to the impact of HSR on the operation of enterprises in this region and analyze possible investment opportunities.
Second, HSR leads to the diffusion effect of CCs. The central government should promote regional economic growth by planning HSR lines, building urban agglomerations with CCs as its core and exerting the diffusion effect of CCs by using HSR to drive economic growth in surrounding areas. CCs’ governments should position the regional development of HSR lines and adjust the industrial structure to avoid adverse effects caused by resource spillage. Non-CCs’ governments should adjust industrial structure, optimize the business environment and introduce preferential policies under the condition of opening up HSR, so as to better undertake the proliferation of human and capital resources.
Third, the impact of HSR is limited by geographic distance. Attention should be paid to geographic distance factors, especially when planning regional transport development, building HSR networks and setting up HSR stations. For example, when considering the setting of HSR stations people should think about the geographical distance between cities, the carrying capacity of trains, cars and other means of transportation between cities, so as to effectively substitute other tools. At the same time, it is necessary to consider the geographical distance between HSR stations and city centers and reduce the time and space cost of transferring between HSR and urban traffic, so as to better support the role of HSR and accelerate the diffusion of factors.
6. Conclusions
This paper analyzes the impact of HSR on business operations and explores the role of CCs in this process. This paper uses the data of Chinese listed companies from 2008 to 2019, and uses DID model, panel threshold model, PSM-DID, parallel trend test, and placebo test to study the following questions: Does HSR lead to changes in EFCs? Does HSR have different impacts on different types of enterprises? How does HSR affect EFCs in CCs and non-CCs? We considered whether the geographic distance between CCs and non-CCs affects the impact of HSR. Through the above research, this paper draws the following conclusions.
First, HSR will reduce EFCs. Due to the compression of time and space, HSR facilitates the flow of resources, information and people between regions, thereby reducing EFC. The study found that the regression coefficient of HSR is −0.002, which is significant at a 5% level, indicating that HSR leads to a significant decrease in EFCs. The above conclusions were drawn through the DID model, and the robustness was tested successively through methods of measurement index replacement, parallel trend testing, PSM-DID and counterfactual testing.
Second, there is heterogeneity in the effects of HSR on EFCs. Central-region enterprises, small enterprises, low-growth enterprises and enterprises with low return on assets are affected more by HSR than others. The study found that the regression coefficient of HSR in the sample from the central region was −0.004, which was significant at a 10% level, while regression results for samples from the eastern, western, and northeastern regions were not significant. The regression coefficient for the sample of small enterprises is −0.002, which is significant at a 5% level. And the sample of large enterprises is not significant. The regression coefficient of the sample of low-growth enterprises is −0.002, which is significant at a 5% level, and the sample of high-growth enterprises is not significant. The regression coefficient of the sample of low-asset regression enterprises is −0.002, which is significant at a 5% level, and the sample of high-asset regression enterprises is not significant.
Third, when HSR affects EFCs, there is a diffusion effect in CCs. The urban per capita GDP is taken as the measurement variable between CC and other cities, and analysis is conducted by using panel thresholds, interaction items, group regression and other methods. The study found that there is a single threshold effect based on per capita GDP. The regression coefficient of HSR below the threshold is −0.001, which is significant at a 5% level, and the regression coefficient of high-speed rail above the threshold is 0.002, which is significant at a 1% level. The regression coefficient of per capita GDP and HSR of the interaction term is 0.002, which is significant at a 5% level, indicating that per capita GDP wedges a negative adjustment effect on HSR reducing financing costs. Group regression based on per capita GDP shows that compared with other groups samples, the 25% sample with the lowest level of per capita GDP showed a significant reduction in decreasing financing costs. The above results show that the radiation effect of CCs occurs during the opening of HSR, which causes non-CCs to obtain resources from CCs, thereby reducing the EFCs in this region, while CCs in face of the opposite result.
Fourth, when HSR affects EFCs, it is limited by geographical distance. When the shortest distance between a city and a single CC exceeds 500 km, the regression coefficient of HSR is negative, and both are significant at a 5% level. When the total distance between a city and four CCs exceeds 3800 km, the regression coefficient of HSR is negative, and all of them are significant at a 10% level.
7. Limitation of the Study
This study also has some limitations. Firstly, this paper does not analyze how HSR leads to EFCs, that is, the mode and means of the impact of HSR. Secondly, when analyzing the diffusion effect of CCs, there are other methods such as spatial DID that can make research more accurate. In the future research process, we will continue to explore the above issues.
Author Contributions
Conceptualization, S.L. and X.Y.; methodology, S.L. and X.Y.; validation, Q.L.; formal analysis, S.L. and Q.L.; writing, S.L. and X.Y. All authors have read and agreed to the published version of the manuscript.
Funding
This research was supported by the Educational Commission of Guangdong Province Projects (Grant NO. 2019WQNCX038, Q18278, 2020KZDZX1113).
Data Availability Statement
The data used in this paper can be found at www.wind.com.cn. The data presented in this study are available on request from the corresponding author.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Ma, G.; Cheng, X.; Yang, E. How Does Transportation Infrastructure Affect Capital Flows—A Study from High-speed Rail and Cross-region Investment of Listed Companies. Econ. Ind. Democr. 2020, 6, 5–23. [Google Scholar]
- Wu, Y.; Zhang, Y.; Li, G. High-Speed Railway Opening, Bank Competition and Corporate Debt Financing Cost. Financ. Forum 2021, 26, 27–36. [Google Scholar]
- Chu, J.; Fang, J. Improvement of Transport Infrastructure and Bank Loan Decision:Based on a Quasi-natural Experiment of High-speed Railway in China. Acc. Econ. Res. 2019, 33, 38–60. [Google Scholar]
- Chen, J.; Fang, J. Transportation Infrastructure Improvement and Dynamic Adjustment of Firm Capital Structure: Empirical Evidence Based on High-speed Railway Coverage. Foreign Econ. Manag. 2022, 44, 138–152. [Google Scholar]
- Wang, G. Research on the impact of the opening of high-speed rail on corporate financing—Analysis based on space effect and time effect. Price Theory Pract. 2020, 11, 153–156. [Google Scholar]
- Ye, D.; Pan, S.; Wu, W.; Zhou, H. Distance, Accessibility and Innovation: A Study on the Optimal Working Radius of High-speed Railway Opening for Urban Innovation. Financ. Trade Econ. 2020, 41, 146–161. [Google Scholar]
- Chen, S.; Liu, X. High-Speed Railway and the Cost of Bank Loans—Based on the Perspective of Customer Concentration Risk. Q. Chin. Econ. 2020, 20, 173–192. [Google Scholar]
- Sahu, S.; Verma, A. Quantifying wider economic impacts of high-speed connectivity and accessibility: The case of the Karnataka high-speed rail. Transp. Res. Part A Policy Pract. 2022, 158, 141–155. [Google Scholar] [CrossRef]
- Zhao, J.; Huang, J.; Liu, F. China High-Speed Railways and Stock Price Crash Risk. Manag. World 2018, 34, 157–168. [Google Scholar]
- Wu, K.; Kong, D.; Yang, W. The Opening of High-speed Railway and Accounting Conservatism:A Quasi-natural Experiment. J. Zhongnan Univ. Econ. Law 2019, 4, 13–24. [Google Scholar]
- Yang, Q.; Ji, Z.; Wang, Y. Can High-speed Railway Improve the Accuracy of Analysts’ Earnings Forecasts? Evidence from Listed Companies. J. Financ. Res. 2019, 3, 168–188. [Google Scholar]
- Zhang, H.; Ping, F. Independent Directors’ Geographic Distance, High Speed Rail and Financial Restatemen. Acc. Econ. Res. 2019, 33, 21–37. [Google Scholar]
- Du, X.; Peng, M. Do High-Speed Trains Motivate the Flow of Corporate Highly Educated Talents? BMJ 2017, 39, 89–107. [Google Scholar] [CrossRef]
- Cai, C.; Hunag, H.; Zhao, L. High-speed Railway and Audit Delay. AR 2019, 6, 72–78. [Google Scholar]
- Charnoz, P.; Lelarge, C.; Trevien, C. Communication costs and the internal organisation of multi-plant businesses: Evidence from the impact of the French high-speed rail. Econ. J. 2018, 128, 949–994. [Google Scholar] [CrossRef]
- Bernard, A.B.; Moxnes, A.; Saito, Y.U. Production networks, geography, and firm performance. J. Polit. Econ. 2019, 127, 639–688. [Google Scholar] [CrossRef] [Green Version]
- Zhang, K.; Tao, D. The economic Distribution effect of transportation infrastructure: Evidence from the opening of high-speed rail. Econ. Perspect. 2016, 6, 62–73. [Google Scholar]
- Qin, Y. ‘No county left behind?’ The distributional impact of high-speed rail upgrades in China. J. Econ. Geogr. 2017, 17, 489–520. [Google Scholar] [CrossRef] [Green Version]
- Bian, Y.; Wu, L.; Bai, J. Does High-speed Rail Improve Regional Innovation in China? J. Financ. Res. 2019, 6, 132–149. [Google Scholar]
- Wei, Z.; Sun, J. Can High-speed Railway Opening Promote FDI Attraction in Chinese Central and Western Regions? South Chin. J. Econ. 2020, 1, 33–45. [Google Scholar]
- Coto-Millán, P.; Inglada, V.; Rey, B. Effects of network economies in high-speed rail: The Spanish case. Ann. Reg. Sci. 2007, 41, 911–925. [Google Scholar] [CrossRef]
- Li, Z.; Xu, H. High-speed railroads and economic geography: Evidence from Japan. J. Reg. Sci. 2018, 58, 705–727. [Google Scholar] [CrossRef]
- Lin, X. High-Speed Railway and the New Pattern of Economic and Social Development; SSAP: Beijing, China, 2015. [Google Scholar]
- Liu, Y.; Yan, L. High-speed Rails and City Economic Growth in China. Financ. Res. 2017, 11, 18–33. [Google Scholar]
- Wang, Y.; Liang, S.; Kong, D.; Wang, Q. High-speed rail, small city, and cost of debt: Firm-level evidence. Pacific-Basin Financ. J. 2019, 57, 101194. [Google Scholar] [CrossRef]
- Long, Y.; Zhao, H.L.; Zhang, X.; Li, Y. High-speed Railway and Venture Capital Investment. Econ. Res. J. 2017, 52, 195–208. [Google Scholar]
- Liu, H.; Li, J.; Xia, D. The Relationship between High-Speed Railway Construction and Enterprise Technology Innovation under the Background of Dual Circulation—From the perspective of information asymmetry and financing constraints. JXTU J. 2021, 45, 62–68. [Google Scholar]
- Petersen, M.A.; Rajan, R.G. The benefits of lending relationships: Evidence from small business data. J. Financ. 1994, 49, 3–37. [Google Scholar] [CrossRef]
- Berger, A.N.; Miller, N.H.; Petersen, M.A.; Rajan, R.G.; Stein, J.C. Does function follow organizational form? Evidence from the lending practices of large and small banks. J. Financ. Econ. 2005, 76, 237–269. [Google Scholar] [CrossRef] [Green Version]
- Hauswald, R.; Marquez, R. Competition and Strategic Information Acquisition in Credit Markets. Rev. Financ. Stud. 2006, 19, 967–1000. [Google Scholar] [CrossRef]
- Agarwal, S.; Hauswald, R. Distance and Private Information in Lending. Rev. Financ. Stud. 2010, 23, 2757–2788. [Google Scholar] [CrossRef]
- Stiglitz, J.E.; Weiss, A. Credit rationing in markets with imperfect information. Am. Econ. Rev. 1981, 71, 393–410. [Google Scholar]
- Bharath, S.T.; Dahiya, S.; Saunders, A.; Srinivasan, A. Lending relationships and loan contract terms. Rev. Financ. Stud. 2011, 24, 1141–1203. [Google Scholar] [CrossRef]
- Hollander, S.; Verriest, A. Bridging the gap: The design of bank loan contracts and distance. J. Financ. Econ. 2016, 119, 399–419. [Google Scholar] [CrossRef]
- Degryse, H.; Ongena, S. Distance, lending relationships, and competition. J. Financ. 2005, 60, 231–266. [Google Scholar] [CrossRef]
- Wang, Y.; Ni, P.; Zhao, J.; Wang, Y. Travel Distance, Commuting Frequency and Corporate Innovation from the Perspective of High-Speed Rail and Spatial Relationship with Central Cities. Financ. Trade Econ. 2021, 42, 150–165. [Google Scholar]
- Chen, M.; Zhang, W.; Zheng, R. Does High Speed Railway Promote the Economic Activities of Cities and Towns along the Line—Evidence from Dual Source Night Lighting. J. China Univ. Geosci. 2021, 21, 119–133. [Google Scholar]
- Deng, R.; Zhang, A.; Chen, M. Impact and Spatial Spillover Effect of Low-carbon Pilot Policy on Ecological Efficiency—Empirical Analysis Based on SDID. World Surv. Res. 2022, 1, 38–47. [Google Scholar]
- Liu, H.; Yan, T. An Analysis on the “Threshold Effect” in the Relationship between OFDI and Enterprise R&D Investment—Based on the Perspective of Government Intervention. East China Econ. Manag. 2014, 28, 59–62. [Google Scholar]
- Peng, Z. Analysis on the Management Strategies of Chinese Enterprises’ Foreign Direct Investment. Enterp. Econ. 2013, 32, 40–43. [Google Scholar]
- Guo, X.; Sun, W.; Yao, S.; Zheng, S. Does high-speed railway reduce air pollution along highways?—Evidence from China. Transp. Res. D Transp. Environ. 2020, 89, 102607. [Google Scholar] [CrossRef]
- Kong, D.; Liu, L.; Liu, S. Market information traveling on high-speed rails: The case of analyst forecasts. Pacific-Basin Financ. J. 2020, 61, 101320. [Google Scholar] [CrossRef]
- Jin, M.; Lin, K.C.; Shi, W.; Lee, P.T.; Li, K.X. Impacts of high-speed railways on economic growth and disparity in China. Transp. Res. Part A Policy Pract. 2020, 138, 158–171. [Google Scholar] [CrossRef]
- Beck, T.; Levine, R.; Levkov, A. Big bad banks? The winners and losers from bank deregulation in the United States. J. Financ. 2010, 65, 1637–1667. [Google Scholar] [CrossRef] [Green Version]
- Wang, J.; Li, Q.; Liu, J. High-Speed Rail and the Expansion of Enterprises Business Space: An Empirical Study Based on the Geographical Information of Listed Companies in 2004–2018. Econ. Geogr. 2020, 40, 114–122. [Google Scholar]
- Shi, D.; Li, S.L. Emissions Trading System and Energy Use Efficiency—Measurements and Empirical Evidence for Cities at and Above The Prefecture Level. China Ind. Econ. 2020, 9, 5–23. [Google Scholar]
- Heckman, J.J.; Ichimura, H.; Todd, P. Matching as an econometric evaluation estimator. Rev. Econ. Stud. 1998, 65, 261–294. [Google Scholar] [CrossRef]
- Rosenbaum, P.R.; Rubin, D.B. The central role of the propensity score in observational studies for causal effects. Biometrika 1983, 70, 41–55. [Google Scholar] [CrossRef]
- Hung, M.; Shi, J.; Wang, Y. The Effect of Mandatory CSR Disclosure on Information Asymmetry: Evidence from a Quasi-Natural Experiment in China. Available online: https://papers.ssrn.com/sol3/papers.cfm?abstract_id=2206877 (accessed on 19 June 2022).
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).