The Use of Macro-Level Safety Performance Functions for Province-Wide Road Safety Management
Abstract
:1. Introduction
Related Work
2. Methods
2.1. Data Description
2.1.1. Spatial Aggregation in the Context of a Province-Wide Sustainable Urban Mobility Plan
2.1.2. Safety Performance Indicators and Predictor Variables
- fatal + injury (FI) crash frequency (crashes/year);
- fatal (F) crash frequency (crashes/year);
- pedestrian crash frequency (crashes/year);
- bicyclist crash frequency (crashes/year).
- population,
- population density,
- area width,
- mean elevation of the area above sea level (see, e.g., [25]).
2.2. Statistical Methods
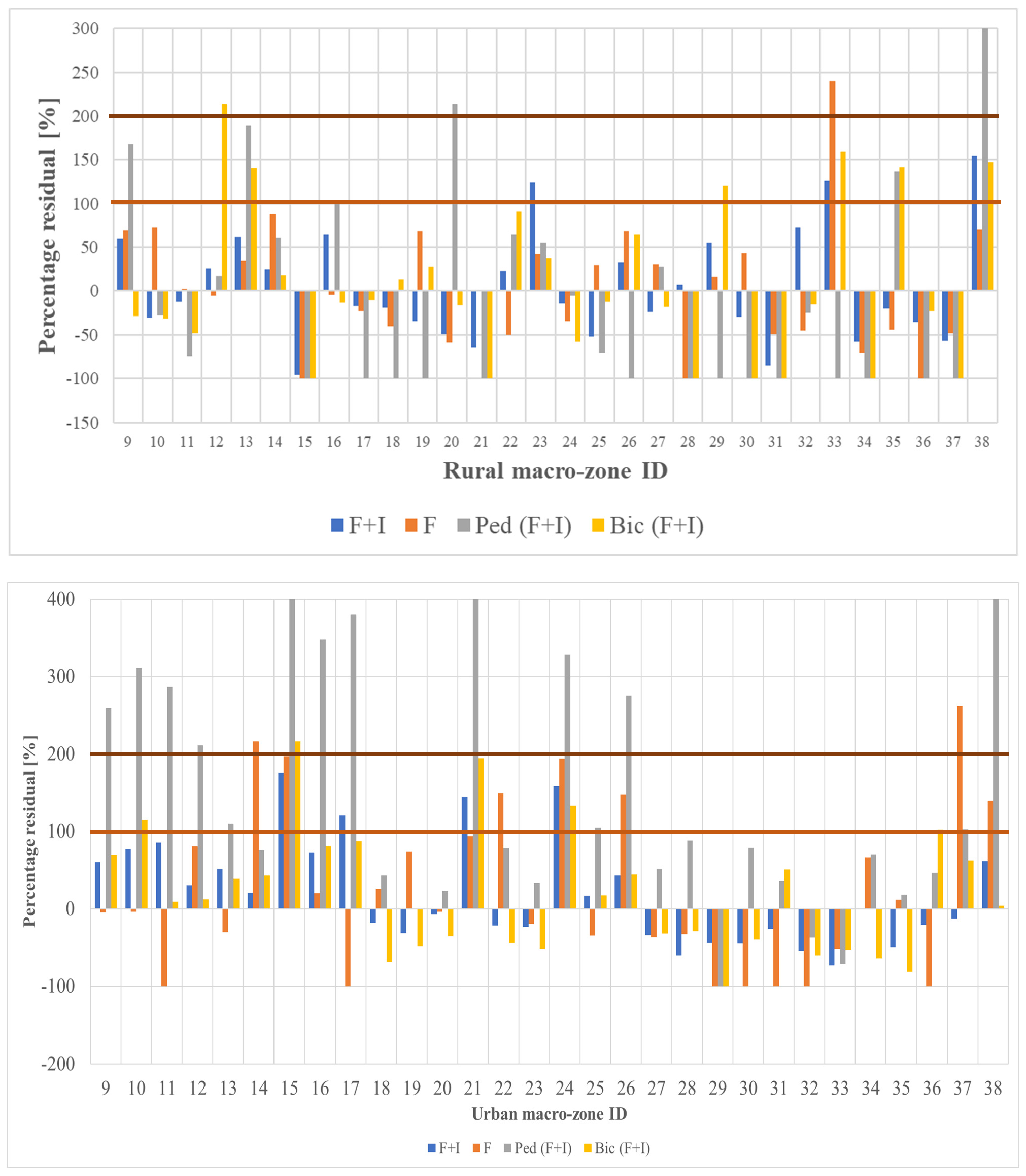
3. Results
3.1. Models for the Rural Environment
3.2. Models for the Urban Environment
4. Discussion
4.1. Influential Factors on Crash Frequency
4.2. Practical Implications
- Nobs is the annual average observed crash frequency;
- Npred is the annual average predicted crash frequency.
5. Conclusions
- the increase in population and area width can be related to an increase in each of the considered urban traffic crash types, while the same variables were not selected for rural models, in which the increase in population density is instead related to an increase in bicycle and pedestrian fatal + injury crashes.
- The mean elevation of the macro-zones is consistently related to a decrease in traffic crashes in both the urban and rural environment, possibly hiding other factors not considered in this study.
- The increase in the network length is generally related to an increase in rural crashes and a decrease in urban crashes (with some exceptions in which it is irrelevant), which was explained according to previous research and by considering the simultaneous effect of the other predictors. The freeway network length seems irrelevant for predicting crashes at this aggregation level.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- AASHTO (American Association of State Highway and Transportation Officials). Highway Safety Manual, 1st ed.; AASHTO: Washington, DC, USA, 2010. [Google Scholar]
- Lee, J.; Abdel-Aty, M.M.; De Blasiis, R.; Wang, X.; Mattei, I. Mattei International transferability of macro-level safety performance functions: A case study of the United States and Italy. Transp. Saf. Environ. 2019, 1, 68–78. [Google Scholar] [CrossRef] [Green Version]
- Lee, J.; Abdel-Aty, Q.M. Cai Intersection crash prediction modeling with macro-level data from various geographic units. Accid. Anal. Prev. 2017, 102, 213–226. [Google Scholar] [CrossRef] [PubMed]
- Montella, A.; Marzano, V.; Mauriello, F.; Vitillo, R.; Fasanelli, R.; Pernetti, M.; Galante, F. Development of macro-level safety performance functions in the city of Naples. Sustainability 2019, 11, 1871. [Google Scholar] [CrossRef] [Green Version]
- Demasi, F.; Loprencipe, G.; Moretti, L. Road safety analysis of urban roads: Case study of an Italian municipality. Safety 2018, 4, 58. [Google Scholar] [CrossRef] [Green Version]
- Saha, D.; Alluri, P.; Gan, A.; Wu, W. Spatial analysis of macro-level bicycle crashes using the class of conditional autoregressive models. Accid. Anal. Prev. 2018, 118, 166–177. [Google Scholar] [CrossRef] [PubMed]
- Cai, Q.; Abdel-Aty, M.; Lee, J. Macro-level vulnerable road users crash analysis: A Bayesian joint modeling approach of frequency and proportion. Accid. Anal. Prev. 2017, 107, 11–19. [Google Scholar] [CrossRef] [PubMed]
- Cai, Q.; Abdel-Aty, M.; Lee, J.; Eluru, N. Comparative analysis of zonal systems for macro-level crash modeling. J. Saf. Res. 2017, 61, 157–166. [Google Scholar] [CrossRef]
- Lee, J.; Abdel-Aty, X.M. Jiang Development of zone system for macro-level traffic safety analysis. J. Transp. Geogr. 2014, 38, 13–21. [Google Scholar] [CrossRef]
- Lee, J.; Abdel-Aty, X.M. Jiang Multivariate crash modeling for motor vehicle and non-motorized modes at the macroscopic level. Accid. Anal. Prev. 2015, 78, 146–154. [Google Scholar] [CrossRef]
- Pirdavani, A.; Daniels, S.; van Vlierden, K.; Brijs, K.; Kochan, B. Socioeconomic and sociodemographic inequalities and their association with road traffic injuries. J. Transp. Health 2017, 4, 152–161. [Google Scholar] [CrossRef]
- Wang, X.; Yang, J.; Lee, C.; Ji, Z.; You, S. Macro-level safety analysis of pedestrian crashes in Shanghai, China. Accid. Anal. Prev. 2016, 96, 12–21. [Google Scholar] [CrossRef] [Green Version]
- Quddus, M.A. Modelling area-wide count outcomes with spatial correlation and heterogeneity: An analysis of London crash data. Accid. Anal. Prev. 2008, 40, 1486–1497. [Google Scholar] [CrossRef] [Green Version]
- Siddiqui, C.; Abdel-Aty, M.; Choi, K. Macroscopic spatial analysis of pedestrian and bicycle crashes. Accid. Anal. Prev. 2012, 45, 382–391. [Google Scholar] [CrossRef]
- Farid, A.; Abdel-Aty, M.; Lee, J.; Eluru, N.; Wang, J.H. Exploring the transferability of safety performance functions. Accid. Anal. Prev. 2016, 94, 143–152. [Google Scholar] [CrossRef]
- Intini, P.; Berloco, N.; Binetti, R.; Fonzone, A.; Ranieri, V.; Colonna, P. Transferred versus local Safety Performance Functions: A geographical analysis considering two European case studies. Saf. Sci. 2019, 120, 906–921. [Google Scholar] [CrossRef]
- Hasanat-E-Rabbi, S.; Hamim, O.F.; Debnath, M.; Hoque, M.S.; McIlroy, R.C.; Plant, K.L.; Stanton, N.A. Exploring the Relationships between Demographics, Road Safety Attitudes, and Self-Reported Pedestrian Behaviours in Bangladesh. Sustainability 2021, 13, 10640. [Google Scholar] [CrossRef]
- Intini, P.; Berloco, N.; Colonna, P.; De Gennaro, D.; Ranieri, V.; Ryeng, E. Self-reported route familiarity and road safety negative outcomes: First results from a transnational survey-based study. Transp. Res. Procedia 2020, 45, 46–53. [Google Scholar] [CrossRef]
- Lee, J.; Nam, M.B. Abdel-Aty Effects of pavement surface conditions on traffic crash severity. J. Transp. Eng. 2015, 141, 04015020. [Google Scholar] [CrossRef]
- Lee, J.; Abdel-Aty, M.; Shah, I. Evaluation of surrogate measures for pedestrian trips at intersections and crash modeling. Accid. Anal. Prev. 2019, 130, 91–98. [Google Scholar] [CrossRef]
- Wefering, F.; Rupprecht, S.; Bührmann, S.; Böhler-Baedeker, S. Guidelines. In Developing and Implementing a Sustainable Urban Mobility Plan; European Platform on Sustainable Urban Mobility Plans; European Commission: Brussels, Belgium, 2014. [Google Scholar]
- Kiba-Janiak, M.; Witowski, J. Sustainable urban mobility plans: How do they work? Sustainability 2019, 11, 4605. [Google Scholar] [CrossRef] [Green Version]
- ISTAT. Istituto Nazionale di Statistica. Available online: https://www.istat.it/it/archivio/104317 (accessed on 12 April 2022).
- Jones, A.P.; Haynes, R.; Kennedy, V.; Harvey, I.M.; Jewell, T.; Lea, D. Geographical variations in mortality and morbidity from road traffic accidents in England and Wales. Health Place 2008, 14, 519–535. [Google Scholar] [CrossRef] [PubMed]
- Azimian, A.; Pyrialakou, V.D.; Lavrenz, S.; Wen, S. Exploring the effects of area-level factors on traffic crash frequency by severity using multivariate space-time models. Anal. Methods Accid. Res. 2021, 31, 100163. [Google Scholar] [CrossRef]
- Intini, P.; Berloco, N.; Colonna, P.; Ottersland Granås, S.; Olaussen Ryeng, E. Influence of road geometric design consistency on familiar and unfamiliar drivers’ performances: Crash-based analysis. Transp. Res. Rec. 2019, 2673, 489–500. [Google Scholar] [CrossRef]
- Intini, P.; Berloco, N.; Ranieri, V.; Colonna, P. Geometric and operational features of horizontal curves with specific regard to skidding proneness. Infrastructures 2019, 5, 3. [Google Scholar] [CrossRef] [Green Version]
- Osama, A.; Sayed, T. Evaluating the impact of bike network indicators on cyclist safety using macro-level collision prediction models. Accid. Anal. Prev. 2016, 97, 28–37. [Google Scholar] [CrossRef] [PubMed]
- Lord, D.; Mannering, F. The statistical analysis of crash-frequency data: A review and assessment of methodological alternatives. Transp. Res. Part A Policy Pract. 2010, 44, 291–305. [Google Scholar] [CrossRef] [Green Version]
- Venables, W.N.; Ripley, B.D. Exploratory multivariate analysis. In Modern Applied Statistics with S; Springer: New York, NY, USA, 2002. [Google Scholar]
- Wei, F.; Lovegrove, G. An empirical tool to evaluate the safety of cyclists: Community based, macro-level collision prediction models using negative binomial regression. Accid. Anal. Prev. 2013, 61, 129–137. [Google Scholar] [CrossRef] [PubMed]
- Clark, D.E. Effect of population density on mortality after motor vehicle collisions. Accid. Anal. Prev. 2003, 35, 965–971. [Google Scholar] [CrossRef]
- Gedeborg, R.; Thiblin, I.; Byberg, L.; Melhus, H.; Lindbäck, J.; Michaelsson, K. Population density and mortality among individuals in motor vehicle crashes. Inj. Prev. 2010, 16, 302–308. [Google Scholar] [CrossRef]
- Choi, J.; Kim, S.; Heo, T.Y.; Lee, J. Safety effects of highway terrain types in vehicle crash model of major rural roads. KSCE J. Civ. Eng. 2011, 15, 405–412. [Google Scholar] [CrossRef]
- Haynes, R.; Jones, A.; Kennedy, V.; Harvey, I.; Jewell, T. District variations in road curvature in England and Wales and their association with road-traffic crashes. Environ. Plan. A 2007, 39, 1222–1237. [Google Scholar] [CrossRef]
- Ukkusuri, S.; Miranda-Moreno, L.F.; Ramadurai, G.; Isa-Tavarez, J. The role of built environment on pedestrian crash frequency. Saf. Sci. 2012, 50, 1141–1151. [Google Scholar] [CrossRef]
- Elvik, R. Why some road safety problems are more difficult to solve than others. Accid. Anal. Prev. 2010, 42, 1089–1096. [Google Scholar] [CrossRef]
- Marshall, W.E.; Garrick, N.W. Street network types and road safety: A study of 24 California cities. Urban Des. Int. 2010, 15, 133–147. [Google Scholar] [CrossRef]
- Guerra, E.; Dong, X.; Kondo, M. Do denser neighborhoods have safer streets? population density and traffic safety in the Philadelphia Region. J. Plan. Educ. Res. 2019, 0739456X19845043. [Google Scholar] [CrossRef]
- Thomas, L.; Lan, B.; Sanders, R.L.; Frackelton, A.; Gardner, S.; Hintze, M. Changing the future?: Development and application of pedestrian safety performance functions to prioritize locations in Seattle, Washington. Transp. Res. Rec. 2017, 2659, 212–223. [Google Scholar] [CrossRef]
- Colonna, P.; Intini, P.; Berloco, N.; Fedele, V.; Masi, G.; Ranieri, V. An integrated design framework for safety interventions on existing urban roads—Development and case study application. Safety 2019, 5, 13. [Google Scholar] [CrossRef] [Green Version]
- Ranieri, V.; Berloco, N.; Intini, P.; Ottomanelli, M. Methods for road infrastructure planning in areas close to hospitals at the regional level. Paper presented at the AIIT TIS 2022 International Conference, Rome, Italy, 15–16 September 2022. [Google Scholar]
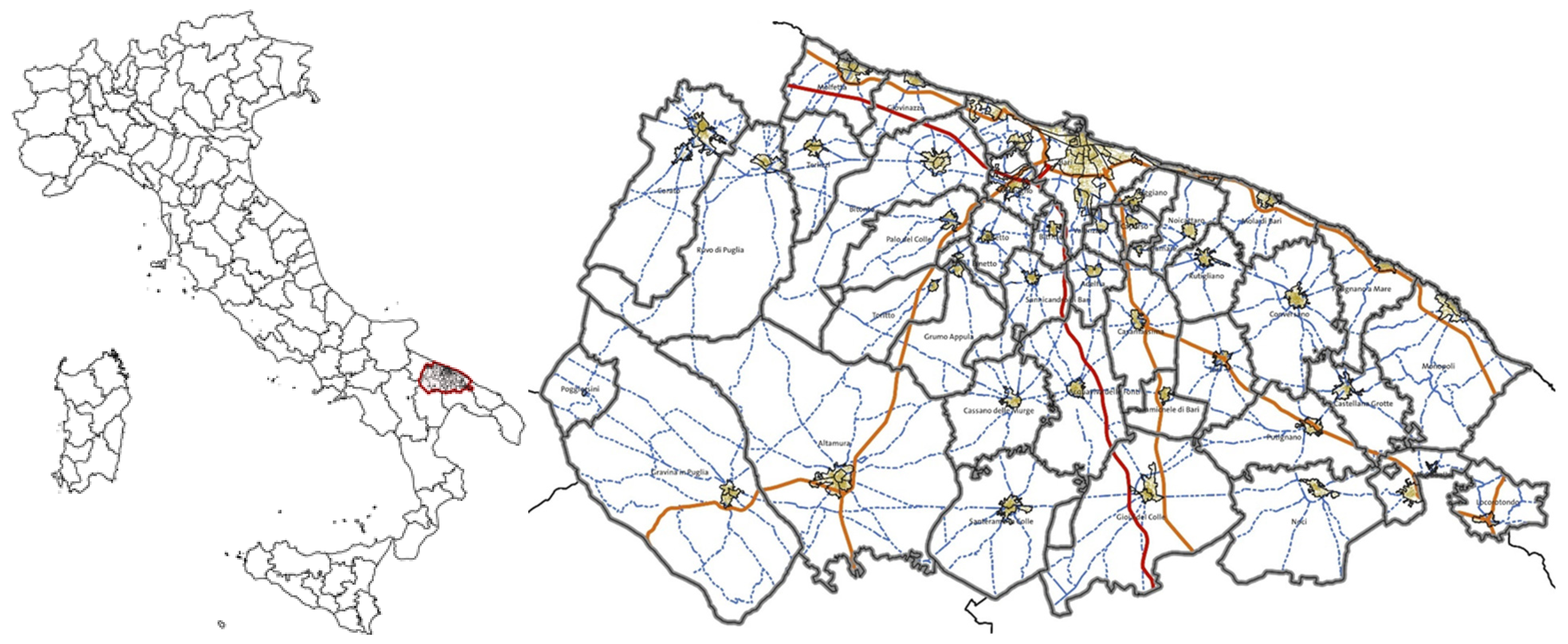

| Safety Performance Indicator | Total (Rural + Urban) (Crashes/Year) | Rural (Crashes/Year) | Urban (Crashes/Year) |
|---|---|---|---|
| Total crash frequency | 3418.6 | 1112.4 | 2306.2 |
| Fatal crash frequency | 51.0 | 34.4 | 16.6 |
| Pedestrian crash frequency | 399.2 | 14.6 | 384.6 |
| Bicyclist crash frequency | 171.0 | 26.2 | 144.8 |
| Variable Type | Independent Variable | Source | Rural Environment | Urban Environment | ||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Mean | St. dev. | Max. | Min. | Mean | St. dev. | Max. | Min. | |||
| Geographic | Population (inhabitants) | ISTAT | 7945.1 | 6760.3 | 19,340.0 | 196.0 | 14,446.6 | 3804.4 | 22,661.0 | 1418.0 |
| Total area (m2) | GIS | 85.4·106 | 88.3·106 | 419.7·106 | 5.4·106 | 1.9·106 | 1.3·106 | 7.9·106 | 0.2·106 | |
| Density (inhabitants/m2) | ISTAT/ GIS | 0.3 | 0.4 | 2.1 | 0.0 | 10.1 | 5.5 | 35.4 | 2.2 | |
| Mean elevation (m) | ISTAT | 199.3 | 144.2 | 489.0 | 5.0 | 162.3 | 161.0 | 489.0 | 5.0 | |
| Road network | Secondary network length (m) | OSM/ GIS | 38.8·103 | 34.7·103 | 163.2·103 | 1.3·103 | 1.0·103 | 1.5·103 | 9.1·103 | 0.0 |
| Primary network length (m) | OSM/ GIS | 5.2·103 | 6.6·103 | 29.7·103 | 0.0 | 0.3·103 | 0.8·103 | 4.3·103 | 0.0 | |
| Freeway network length (m) | OSM/ GIS | 1.6·103 | 3.7·103 | 15.6·103 | 0.0 | |||||
| Urban network length (m) | OSM/ GIS | 30.2·103 | 13.8·103 | 74.2·103 | 4.3·103 | |||||
| Independent Variables | Coefficient Estimates (Standard Errors in Parenthesis) | |||
|---|---|---|---|---|
| Total (F + I) Crashes | Fatal Crashes | Pedestrian (F + I) Crashes | Bicyclist (F + I) Crashes | |
| (Intercept) | 2.980 (9.145·10−2) | −5.309·10−1 (1.579·10−1) | −1.456 (3.424·10−1) | −6.764·10−1 (1.957·10−1) |
| Population density | - | - | 8.741·10−1 (3.219·10−1) | 4.760·10−1 (2.141·10−1) |
| Mean elevation | −2.492·10−3 (3.949·10−4) | −1.681·10−3 (7.111·10−4) | −3.985·10−3 (1.238·10−3) | −3.339·10−3 (7.973·10−4) |
| Length of the secondary road network | 8.963·10−6 (1.872·10−6) | 1.376·10−5 (2.428·10−6) | - | 1.492·10−5 (2.835·10−6) |
| Length of the primary road network | 4.832·10−5 (8.926·10−6) | - | 9.222·10−5 (2.402·10−5) | - |
| Goodness of fit measures | ||||
| Nagelkerke R2 | 0.494 | 0.151 | 0.212 | 0.162 |
| Mean square error (MSE) | 231.61 | 0.25 | 0.28 | 0.18 |
| Independent Variables | Coefficient Estimates (Standard Errors in Parenthesis) | |||
|---|---|---|---|---|
| Total (F + I) Crashes | Fatal Crashes | Pedestrian (F + I) Crashes | Bicyclist (F + I) Crashes | |
| (Intercept) | 1.823 (1.350·10−1) | −2.596 (5.450·10−1) | 3.657·10−1 (2.008·10−1) | −7.611·10−1 (2.563·10−1) |
| Area | 3.421·10−7 (3.839·10−8) | 4.403·10−7 (1.23·10−7) | 2.264·10−7 (5.484·10−8) | 1.858·10−7 (6.127·10−8) |
| Population | 1.267·10−4 (1.029·10−5) | 8.142·10−5 (4.039·10−5) | 1.360·10−4 (1.527·10−5) | 1.268·10−4 (1.925·10−5) |
| Mean elevation | −2.273·10−3 (2.093·10−4) | - | −1.441·10−3 (3.043·10−4) | −2.521·10−3 (4.002·10−4) |
| Length of the urban road network | −2.123·10−5 (3.925·10−6) | −3.625·10−5 (1.500·10−5) | −3.194·10−5 (5.718·10−6) | −1.599·10−5 (6.680·10−6) |
| Length of the secondary road network | −1.459·10−4 (2.221·10−5) | - | −1.544·10−4 (3.440·10−5) | −1.571·10−4 (4.323·10−5) |
| Goodness of fit measures | ||||
| Nagelkerke R2 | 0.714 | 0.059 | 0.361 | 0.345 |
| Mean square error (MSE) | 564.13 | 0.05 | 22.69 | 2.28 |
| Variable Type | Predictors | Rural | Urban | ||||||
|---|---|---|---|---|---|---|---|---|---|
| F + I | F | Ped. (F + I) | Bic. (F + I) | F + I | F | Ped. (F + I) | Bic. (F + I) | ||
| Geographic | Population | + | + | + | + | ||||
| Total area | + | + | + | + | |||||
| Population density | + | + | |||||||
| Mean elevation | − | − | − | − | − | − | − | ||
| Road network | Urban road network length | − | − | − | − | ||||
| Secondary road network length | + | + | + | − | − | − | |||
| Primary road network length | + | + | |||||||
| Freeway road network length | |||||||||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Intini, P.; Berloco, N.; Coropulis, S.; Gentile, R.; Ranieri, V. The Use of Macro-Level Safety Performance Functions for Province-Wide Road Safety Management. Sustainability 2022, 14, 9245. https://doi.org/10.3390/su14159245
Intini P, Berloco N, Coropulis S, Gentile R, Ranieri V. The Use of Macro-Level Safety Performance Functions for Province-Wide Road Safety Management. Sustainability. 2022; 14(15):9245. https://doi.org/10.3390/su14159245
Chicago/Turabian StyleIntini, Paolo, Nicola Berloco, Stefano Coropulis, Roberta Gentile, and Vittorio Ranieri. 2022. "The Use of Macro-Level Safety Performance Functions for Province-Wide Road Safety Management" Sustainability 14, no. 15: 9245. https://doi.org/10.3390/su14159245
APA StyleIntini, P., Berloco, N., Coropulis, S., Gentile, R., & Ranieri, V. (2022). The Use of Macro-Level Safety Performance Functions for Province-Wide Road Safety Management. Sustainability, 14(15), 9245. https://doi.org/10.3390/su14159245





