Multi-Objective Optimization of the Organization’s Performance for Sustainable Development

Abstract

Sustainable development can be defined in terms of three main components: ecologically sustainable, economically sustainable, and socially sustainable. Conflicting objectives are involved in sustainable development issues, of which the economic, environmental, and social objectives are the most important. Multi-criteria decision-making provides a systematic methodology that combines these conflicting objectives and can provide a rational compromise solution to complex decision-making issues. Using multi-objective optimization, this paper integrated three major objectives of organizational performance, maximizing sales, minimizing expenses, and maximizing productivity, all of which are combined for the sustainable development of the organization. All these conflicting problems were included in an objective function that allowed for solving the three objectives simultaneously and, thus, achieving economic, environmental, and social performance, in order to sustainably develop the organization. The input data included the objectives planned by the company regarding the turnover to be achieved, the production and delivery costs, and the productivity achieved by employees. Customer orders, production capacity, delivery costs, and resource consumption were also taken into account for optimization. With the help of multi-objective linear programming, the optimal number of parts produced and delivered by the company was determined so as to reach its economic, environmental, and social performance.

1. Introduction

Performance and sustainability are two areas of great interest and echo for all socio- economic entities. The interdependence between sustainability and performance is an indestructible one, a sine qua non condition to approach the concept of sustainability in an overall manner. In its current sense, sustainable development comprises three broad categories: economic performance, environmental protection, and social responsibility, all three of which are based on an educational process in the spirit of sustainable development (Figure 1). In using these branches, the ability of a system to thrive, by maintaining economic viability and by limiting resource consumption to meet the needs of present and future generations, is created.

Sustainability is a paradigm in which the future is thought of as a balance between the environment, society, and economy, in order to develop and improve quality of life. In other words, an enterprise with financial performance is not compulsorily sustainable, meaning that the financial performance does not guarantee or prove clear indications on the achievement of social or environmental objectives, in case they have been taken into account [1]. A sustainable management is defined as the application of sustainable practices in commerce, agriculture, environment, production, and other fields by management, in a manner that is beneficial to present and future generations.

To be sustainable, an enterprise must manage its resources to have good results not only in the short term, during a financial year, but also especially in the long term. Moreover, the performance of an organization not only indicates the maximizing of results, but also the contribution to the improvement of the couple’s cost-value [2]. Given the need to simultaneously meet several performance requirements, translated into performance objectives, companies are moving towards optimization through multi-criteria decision methods [3].

Multiple-criteria decision-making (MCDM) is a subdomain of operations research concerned with designing mathematical and computational tools to support the subjective assessment of performance criterion by decision. MCDM is an assemblage of methodologies to compare, select, or rank alternatives, where various and conflicting criteria involve both tangible and intangible factors [4].

MCDM can be divided in between multi-objective decision-making (MODM) and multi-attribute decision-making (MADM) methods. The goal in MADM problems is to design the best alternative, considering the assessment of the whole set of attributes that are difficult to quantify or to compare [5]. In MODM, alternatives are not predetermined, but instead a set of objective functions is optimized, subject to a set of constraints, with a number of alternatives effectively infinite. The most satisfactory and efficient solution is the goal. In this solution, it is not possible to improve the performance of any objective without degrading the performance of others [6].

There are several classification criteria for MCDM, for example, Castro [4] uses the following classification for MADM:

• Evaluating (DEMATEL, ISM, SEM);
• Weighting (analytic hierarchy process);
• Normalization (TOPSIS, SAW, ELECTRE);
• MODM–multi-attribute utility analysis.

The same author classifies the MODM as follows:

• Multi-attribute utility analysis;
• Goal programming;
• Genetic algorithm and neural network.

Multi-criteria decision-making methods are a valuable tool in the sustainable development decision-making process. Multi-objective decision-making methods, also known as multi-objective programming, are much more suitable for an infinite number of continuous variants defined by a set of constraints [7]. According to Velasquez [8], the most common methods used in performance-type problems and optimization problems in the field of engineering and planning are analytic hierarchy process (AHP), ELECTRE, TOPSIS, and linear programming.

AHP is a theory of measurement through pairwise comparisons that relies on the judgments of experts to derive priority scales [8]. It is one of the more popular methods of MCDM and has many advantages, as well as some disadvantages. One of its advantages is its ease of use. Its use of pairwise comparisons can allow decision-makers to weight coefficients and compare alternatives with relative ease. It is scalable and can easily adjust in size to accommodate decision-making problems due to its hierarchical structure. One of its biggest criticisms is that the general form of AHP is susceptible to rank reversal. Due to the nature of comparisons for rankings, the addition of alternatives at the end of the process could cause the final rankings to flip or reverse. AHP has seen much use in performance-type problems, resource management, corporate policy and strategy, public policy, political strategy, and planning.

TOPSIS is an approach to identify an alternative that is closest to the ideal solution and farthest to the negative ideal solution in a multi-dimensional computing space [8]. It has numerous advantages. It has a simple process, and it is easy to use and programmable. The number of steps remains the same regardless of the number of attributes. A disadvantage is that it is difficult to weight attributes and keep consistency of judgment, especially with additional attributes. TOPSIS has been used in supply chain management and logistics, design, engineering and manufacturing systems, business, and marketing.

ELECTRE, along with its many iterations, is an outranking method based on concordance analysis. Its major advantage is that it takes into account uncertainty and vagueness. One disadvantage is that its process and outcomes can be hard to explain in layman’s terms. Further, due to the way preferences are incorporated, the lowest performances under certain criteria are not displayed. The outranking method causes neither the strengths and weaknesses of the alternatives to be directly identified nor the results and impacts to be verified [8]. ELECTRE has been used in energy, economics, environmental, water management, and transportation problems. Like other methods, it also takes uncertainty and vagueness into account, which many of the mentioned applications appear to need.

This paper proposes a method to optimize the performance of the organization by using multiple-criteria decision-making. In order to make up for shortcomings in any single particular method, two methods of MCDM were used. Thus, in addition to utilizing the analytic hierarchy process (AHP) to define coefficients for optimization functions, a Multi-Objective Linear Programming was used to express the main objectives of the company. For sustainable development in the automotive field and beyond, the optimization requires considering environmental issues in economic decisions. As a component of the economy significantly influencing the environment, resource consumption and transport require paying particular attention to environmental issues.

Therefore, this paper is devoted to the study of the applicability potential of selected multi-objective decision-making methods in the field of automotive engineering. In the beginning, a review of the literature on the latest applications of the selected methods in various decision-making processes was performed. Then, computational examples were developed through a case study on optimizing the main performance objectives of a multinational company: maximizing sales, minimizing costs (focusing on reduction of material consumption and transport costs that have a major impact on environment), and maximizing productivity. Finally, based on multiobjective linear programming, the number of products to be made and delivered to customers was determined, in order to simultaneously satisfy the three conflicting performance objectives.

2. Literature Review

Generally, optimization represents the action of obtaining the best result in certain imposed conditions. By definition, the procedure can be applied to an extremely wide variety of problems, such as aerospace design (minimum mass issues), civil engineering (sizing of resistance structures, sizing of beams in metal structures, sizing of useful spaces in constructions), design of mechanical parts, design of units or production lines, or design of energy equipment and energy networks.

During the design stages, optimization has become a necessary, mandatory component when the performance requirements of the realized product are imposed. The problem area is not limited to engineering, being known in a number of economic applications, from evaluating and optimizing the performance of an investment to banking applications or insurance. In recent years, when profit optimization has become a common language term, optimization applications, whether explicit or implicit (for example, programs that control automatic cutting/cutting machines in the wood industry or the garment industry), are increasingly present.

From a historical point of view, the classical foundations of optimization techniques, based on derivative operators, were laid out by the works of Newton, Filipacci, and Euler, but especially by the research of Cauchy and Lagrange. The latter succeeded in sec. 19 to theoretically cover the classical domain of optimization problems, not only for linear and nonlinear functions but also for the case of applications that suffer restrictions [9].

By the middle of the 20th century, advances in the theoretical and practical field of optimization techniques were insignificant. The advent of the numerical computer fundamentally changed the direction of mathematical research and accelerated, in the 1950s and 1960s, the research of the English school of mathematics that focused on the field of numerical algorithms. The second impetus came from the direction that can be called “artificial intelligence” [10].

The general elements of formulating an optimization problem involve prior knowledge of design rules in a specific field and the ability to describe the design in mathematical terms. This means variable design, parameter design, and objective function design.

In the case of classical optimization problems, the objective function is unique. This optimizes only one aspect, considered essential, of the problem (for example, in the case of designing electric cars, only the efficiency is chosen as an objective function). However, practice requires a product or a human action to simultaneously fulfill several quality indices and objective functions [11]. In the example of electric car design, the cost element can be added as a significant direction of the global optimal design. This type of design is called a multi-objective design. Obviously, the objectively chosen functions are imposed by the requirements of the design theme, which we can find along with efficiency or price, mass, maximum temperature, vibration level, harmonic content, and maximum speeds. According to general perception, we expect these objective functions to be concurrent and contradictory. However, there are also situations in which they are cooperating targets. From the point of view of the current interest, the problems of multi-objective optimization are the most important, and the interest for multi-objective techniques and algorithms existing in the first place. Many real-world optimization problems possess several, often-conflicting objectives that have to be optimized simultaneously.

Multi-objective optimization, also known as multi-criteria or vector optimization, is the discipline that is concerned with analyzing the mathematical structure of these problems and designing appropriate solution methods. This multidisciplinary field of research connects mathematics, computer science, economics, and operations research. As a consequence of its multi-disciplinarity and universality, multi-objective optimization is utilized in applications across various domains. Many authors [4,5,6,7,8,9,10] refer the interested reader to one of several surveys of applications of multi-objective optimization to get an overview.

Table 1. Summary of MCDM methods used for optimization problems in automotive engineering.

Method	Advantages	Disadvantages/Limits	Main Areas of Application
Analytic Hierarchy Process (AHP)	Easy to use; scalable; hierarchy structure can easily adjust to fit many sized problems; possibility of integration with other methods; not data intensive.	Problems due to interdependence between criteria and alternatives; can lead to inconsistencies between judgment and ranking criteria.	Performance-type problems, resource management, political strategy, and planning.
Technique for Order Preferences by Similarity to Ideal Solutions (TOPSIS)	Has a simple process; easy to use and program; the number of steps remains the same regardless of the number of attributes.	Difficult to weight and keep consistency of judgment.	Supply chain management and logistics, engineering, manufacturing systems, business, marketing, and environment.
Linear Programming (LP)	Capable of handling large-scale problems; can produce infinite alternatives.	Needs to be used in combination with other MCDM methods to weight coefficients.	Production planning, scheduling, distribution systems, energy planning, scheduling, and wildlife management.
PROMETHEE	Easy to use; possibility of taking into account both quantitative and qualitative criteria; does not require assumption that criteria are proportionate; possibility of integration with other methods.	Does not provide a clear method by which to assign weights; need to weigh decision factors using other methods.	Environmental, hydrology, water management, business and finance, chemistry, logistics, transportation, and manufacturing.

presents the main methods of MCDM used in automotive engineering.

Authors such as [12] developed an optimal decision model for diversified industrial management using linear programming methods. The decision target was not only to maximize the enterprise’s profit but also to consider the social and environmental benefits.

Ref. [13] used a multi-criteria modeling approach using the linear programming problem framework for the simultaneous optimization of the gross domestic product, electricity consumption, and greenhouse gas emissions.

Others authors [14] used fuzzy linear programming to analyze the problem of route optimization when delivering urban road-network products.

Also, a mixed integer non-linear programming model for the green lock-scheduling problem at the Three Gorges Dam was proposed by other authors [15]. The model aims at minimizing the carbon emissions and the waiting time in the lockage process, by scheduling the vessels in a fairer and more efficient manner.

Table 2. Results of using the MCDM/MCDA methods in various fields.

Author	MCDM/MCDA Methods Used	Main Subject of the Research
Behzadian, M. et al. [5]	TOPSIS	A state-of-the-art literature survey to taxonomize the research on TOPSIS applications and methodologies.
Broniewicz, E.; Ogrodnik, K. A. [6]	DEMATEL, REMBRANDT, and VIKOR	The utilization of the application potential of MCDM/MCDA methods in decision-making problems in the field of transport, in light of sustainable development.
Halffmann, P. et al. [11]	Multi-objective mixed-integer and integer linear	State-of-the-art multiobjective mixed-integer programming.
Li, C.-M. et al. [12]	Linear programming	Optimal decision model for diversified industrial management (optimal scales of coal, electric power, chemical, and equipment manufacturing).
Gupta, S. et al. [13]	Fuzzy goal programming	A fuzzy goal programming model to study the sustainable development goals of GDP growth, electricity consumption, and GHG emission across different economic sectors of India by the year 2030.
Zhao, X. et al. [15]	Mixed-integer non-linear programming	Model for the green lock-scheduling problem at the Three Gorges Dam (minimizing the carbon emissions and the waiting time in the lockage process).
Zhou, W. et al. [16]	Mixed-integer linear programming	Multi-periodic train timetabling and routing, by optimizing the routes of trains at stations and their entering time and leaving time on each chosen arrival–departure track at each visited station.
Sarwar, S. et al. [17]	Mixed-integer linear programming	Providing an efficient load-shedding technique for an islanded distribution system.
Al-Quradaghi, S. et al. [18]	Mixed-integer programming	Optimizing the exchange of material flows in the network (maximize reusable/recyclable material output, while minimizing network costs)
Fechete, F.; Nedelcu, A.	AHP and multi-objective linear programming	Optimization model that integrates three major objectives of organizational performance: maximizing sales, minimizing expenses, and maximizing productivity, all combined for the sustainable development of the organization.

presents a summary of the results of using the MCDM/MCDA methods used in various fields.

It is observed that multi-objective optimization is used in various fields, but especially for economic development, taking into account the environmental component.

This paper aims to use multi-objective linear programming to optimize three performance objectives: sales made by the company, production and transportation costs, and employee productivity. Given that sustainable development focuses on the congruence between economic, environmental, and social objectives, the ultimate goal’s function is to increase economic performance by maximizing sales, increase environmental performance by minimizing resources used, and increase social performance by maximizing productivity and motivating employees.

Thus, by the optimization proposed in this paper, the monthly production planning will be obtained, namely, the number of parts that must be made and delivered monthly, so that the three performance objectives are satisfied simultaneously.

3. Materials and Methods

3.1. Methods

The mathematical model of the multiobjective linear programming problem, also called the multiobjective decision problem, is given by a lot of constraints (inequalities, equalities) for n variables X₁, X₂, …, X_n, which generally represents the quantities to be manufactured from n products in a production system (workshop, section, enterprise) in which m resources (raw materials, energy, machinery, human resources) are limited to bi, i = 1, 2, …, m, and the specific consumption is a_ij, a vector function f(X) with components that must be maximized or minimized.

The mathematical model of the multiobjective linear-programming problem is given by relations (1) [19]. Decisions in multicriteria decision-making processes with an infinite number of possible solutions (variants) are called multiobjective decisions.

$$\begin{array}{c}{\displaystyle \sum _{j=1}^n}{a}_{ij}·X_j\le b_{i, }i=1,2, \dots , m;\\ X_j\ge 0, j=1,2, \dots , n;\\ f_k\left(X_1, X_2, \dots , X_n\right)={\displaystyle \sum _{j=1}^n}{c}_{kj}·X_j, k=1,2,\dots , p;\\ optimum f_k \left(X_1,X_2, \dots , X_n\right), k=1,2, \dots , p.\end{array}$$

(1)

where: a_ij—is the consumption of the resource R_i available in the quantity b_i, b_i ≥ 0, of product unit P_j, a_ij ≥ 0, i = 1, 2, …, m, j = 1, 2, …, n,

and optimum ∈ {max, min}, so some of the components of f(X) are maximized and some are minimized. The constraints can include the relations ≤, ≥, or =, which can all be brought to the use of the relation ≤.

There are several ways to solve the problem of multi-objective linear programming. In general, an optimal solution for the linear-programming problem with a single objective function from the p functions of the model (1) [19] is not optimal, and for the other objective functions of the vector function f(X), it can be very unfavorable.

$$f\left(X\right)=\left(\begin{array}{c}\begin{array}{c}{f}_1\left(X\right)\\ \begin{array}{c}{f}_2\left(X\right)\\ \dots \end{array}\end{array}\\ f_p\left(X\right)\end{array}\right)$$

The model in relation (1) can also be written as a matrix:

$$\begin{array}{c}A·X\le b\\ X\ge 0\\ f\left(X\right)=C·X\\ optimum f \left(X\right)\end{array}$$

(2)

where:

$$\begin{array}{c}A=(a_{ij}), i=1,2, \dots , m;, j=1,2, \dots , n;\\ C=(c_{kj}), k=1,2, \dots , p;, j=1,2, \dots , n;\end{array}$$

(3)

$$X=\left(\begin{array}{c}\begin{array}{c}{X}_1\\ \begin{array}{c}{X}_2\\ \dots \end{array}\end{array}\\ X_n\end{array}\right)b=\left(\begin{array}{c}\begin{array}{c}{b}_1\\ \begin{array}{c}{b}_2\\ \dots \end{array}\end{array}\\ b_m\end{array}\right) f\left(X\right)=\left(\begin{array}{c}\begin{array}{c}{f}_1\left(X\right)\\ \begin{array}{c}{f}_2\left(X\right)\\ \dots \end{array}\end{array}\\ f_p\left(X\right)\end{array}\right)$$

$$optimum \in \left\{max, min\right\}$$

$$f_k\left(X\right)={\displaystyle \sum }_{j=1}^n{c}_{kj}·X_j, k=1,2,\dots , p;$$

The solution of the multi-objective linear programming problem can be done through algorithms: STEP, POP, maximizing the global utility, the weighting method, game theory, the lexicographic method, etc.

The components of the vector function f(X) can have as concrete economic meanings:

• profit, which will be maximized;
• turnover, which will be maximized;
• production costs, which will be minimized;
• the time of non-use of the equipment, which will be minimized;
• labor productivity, which will be maximized;
• working capital, which must be minimized.

Obviously, each f_k(X), a component of f(X), can have other concrete meanings. In general, an optimal solution to the linear-programming problem with a single objective function f_k(X), of those p of f(X), is not optimal for the other (p − 1) objective functions, since as components of the vector function f(X), they can be conflicting and very unfavorable.

For the multiobjective models given by relations (1) and (2), there is, in general, no optimal solution that optimizes all the objective functions simultaneously. The notion of optimal solution is replaced in this case by the notion of “best” from the point of view of the set of objective component functions of f(X). The notion of “best solution” is ambiguous, but there are various equivalent notions, such as: Pareto-optimal solution, undominated solution, and efficient solution, which is in fact a possible solution that achieves the best compromise in solving the models given by relations (1) and (2).

Non-dominant solutions can be found by various methods, of which the weighting method will be used.

The weighting method (parametric) consists of constructing a linear model with a single objective function given by the relations (3), from the multi-objective models (1), respectively (2), with the help of some weights $w_k$:

$$A·X\le b$$

$$X\ge 0$$

$$F\left(X\right)={\displaystyle \sum }_{k=1}^p{w}_k·f_k\left(X\right)={\displaystyle \sum }_{k=1}^p{w}_k·{\displaystyle \sum }_{k=1}^p{c}_{kj}·X_j \left(5.6\right)$$

$$\max F\left(X\right)$$

(4)

$$w_k\ge 0, k=1,2, \dots , p;$$

The parametric variation of the weights obtains the set of non-dominated solutions of the multiobjective linear model given by the relations (1), respectively (2). The weights w_k were determined using the vector of importance coefficients.

In several methods for solving the problem of multiattribute decisions, the vector of the coefficients of importance $p=w_1, w_2,\dots , w_n$ with ${{\displaystyle \sum }}_{i=1}^n{w}_i=1$ is used, which expresses the importance given to decide each criterion.

The evaluation of these coefficients, taking into account the relative importance of the criteria can be done by several methods, in this paper using the method of its own vector [16].

The matrix has been established:

$$B=\left(\begin{array}{ccc}{p}_1/p_1& p_1/p_2& p_1/p_n\\ p_2/p_1& p_2/p_2& p_2/p_n\\ \dots & \dots & \dots \\ p_n/p_1& p_n/p_2& p_n/p_n\end{array}\right)$$

(5)

which expresses the relative importance of the criteria. The b_ij elements of the matrix B have the properties:

b_ij = 1/b_ij,
b_ij = b_ik/b_jk, i, j, k = 1,2,…, n.

(6)

Calculating

BP^T = mP^T

(7)

where P^T is the column vector:

$$P^T=\left(\begin{array}{c}\begin{array}{c}{p}_1\\ \begin{array}{c}{p}_2\\ \dots \end{array}\end{array}\\ p_n\end{array}\right)$$

It results in (B − nE) P^T = 0, where E is the unit matrix. The P^T vector is an eigenvector of matrix B. The P^T values are obtained as follows:

1. It starts from the matrix B estimated by the decision-maker and finds its eigenvalues, solving the characteristic equation

$$det\left(B-\lambda E\right)=0.$$

(8)

2. The following equation is solved

BP^T = λ_maxP^T,

(9)

where $\lambda$_max is its highest value.

3.2. Materials

This paper aims to improve the performance of the organization for sustainable development. Improving performance can be achieved by solving an optimization problem by applying MCDM methods. We considered a total of 15 scientific articles in which MCDM/MCDA methods were applied to decision-making problems in the field of planning in automotive worldwide. After studying the literature, it was identified that AHP, TOPSIS, ELECTRE, and linear programming are still the most popular methods of multi-criteria decision-making in the performance-type problems in the automotive field.

To eliminate the shortcomings of one of the methods, it was decided to combine two MCDM methods: AHP to determine the weight of objective function coefficients and multi-objective linear programming to optimize functions. It was identified that for sustainable development, the organization must combine economic, social, and environmental performance. Thus, the three objective functions that will enter the optimization process are: the function of maximizing sales, the function of minimizing resource consumption and delivery costs, and the function of maximizing productivity. The three functions were integrated, by applying the weights determined by the AHP method, in a final function, the resolution of which allowed the simultaneous satisfaction of the three conflicting objectives. In order to eliminate the subjectivity of the evaluation of the criteria, the weights of the three functions were also determined with the help of MCDA weight calculator software [20], using the standard deviation and the critical method. The values obtained were extremely close, which confirms the accuracy of the method (AHP) used.

Objective functions and related restrictions were resolved using QM (Quantitative Management) software. The implementation of the determined methods was achieved by applying the mathematical model obtained in a multinational company in automotive engineering. Economic and technical data achieved by the company during 12 months were taken into account, indicators such as: customer orders, production capacity of the organization, production costs, delivery costs, productivity achieved by employees, or sales made by the company. The results obtained by solving the multi-objective function allowed the simultaneous optimization of the economic, social, and environmental performances of the organization.

4. Results

In order to optimize, the following economic, environmental, and social performances were taken into account as objective functions:

• Turnover, in order to maximize sales volume;
• Delivery costs, in order to minimize the consumption of materials, energy, and fuel;
• Productivity, in order to maximize the added value achieved by employees.

Optimization will be achieved by integrating the three objective functions in a linear programming model, where each objective function has a weight established by its own vector method. The importance scale in the table below (

Table 3. The scale of importance.

Intensity of Importance $({\mathit{w}}_{\mathit{i}}$$/{\mathit{w}}_{\mathit{j}})$	Definition	Explanation
1	Equal importance	The two criteria contribute equally to the goal.
3	Weak importance	Experience shows the slight importance of one criterion over another.
5	Strong importance	Experience demonstrates the stronger importance of one criterion over another.
7	Demonstrated importance	Practice has proven the importance of one criterion over another.
9	Absolute importance	Obviously one criterion is more important than another.
2, 4, 6, 8	Importance of intermediate values	Used when a compromise is needed.

) was used to determine the relative importance $w_i$/$w_j.$

Using the importance scale to determine the relative importance $w_i$/$w_j$ the matrix was established:

$$B=\left(\begin{array}{ccc}1& 1/5& 1/3\\ 5& 1& 5\\ 3& 1/5& 1\end{array}\right)$$

(10)

Characteristic equation:

$$det\left(B-\lambda E\right)=\left(\begin{array}{ccc}1-\lambda & 1/5& 1/3\\ 5& 1-\lambda & 5\\ 3& 1/5& 1-\lambda \end{array}\right)$$

(11)

It will obtain $\lambda$_max = 3.135 and the matrix equation BP^T = λ_maxP^T results:

$$\left(\begin{array}{ccc}-2.135& 1/5& 1/3\\ 5& -2.135& 5\\ 3& 1/5& -2.135\end{array}\right).\left(\begin{array}{c}{w}_1\\ w_2\\ w_3\end{array}\right)=0$$

(12)

From (13), it is obtained as p = (0.132; 0.612; 0.256). Therefore, the function of maximizing sales will have a weight of 0.132, the function of minimizing costs will have a weight of 0.612, and the function of maximizing productivity will have a weight of 0.256.

In order to eliminate the subjectivity of the evaluation of the criteria, the weights of the three functions were also determined with the help of MCDA weight-calculator software [20], using the standard deviation (0.103; 0.552; 0.345) and the critical method (0.096; 0.714; 0.189). The values obtained were extremely close, which confirms the accuracy of the method (AHP) used.

The case study was conducted in the automotive sector of an industrial organization, which manufactures parts with revolution shapes, thus grouped, taking into account similarities in size, shape, technology, and material.

• Maximizing turnover

For the function of maximizing turnover, knowing the quantity of parts to be delivered in the next 12 months, according to the contracts with customers, the production capacity for each month (

Table 4. Data used to maximize turnover.

Month	Sales Volume Achieved [T-Ron]	Customer Orders [pcs]	Production Capacity [pcs]
January	1438	2,548,556	2,700,000
February	1309	2,550,855	2,500,000
March	1157	2,735,389	2,700,000
April	1811	2,503,787	2,800,000
May	1089	2,750,643	2,800,000
June	1078	2,624,632	2,700,000
July	1088	2,682,187	2,800,000
August	1025	2,563,748	3,000,000
September	1003	2,451,276	2,800,000
October	1200	2,992,994	3,000,000
November	1117	2,761,731	2,800,000
December	927	2,258,991	2,100,000

) determined using linear programming, and the optimum level of production, so that the turnover is maximized.

Notations:

${\mathrm{x}}_1,{\mathrm{x}}_2,{\mathrm{x}}_3,\dots ,{\mathrm{x}}_{12}=$ quantity of parts to be delivered in the next 12 months.

The objective function restrictions have been determined, following the customers’ orders and the capacity of production:

$$\{\begin{array}{c}{\mathrm{x}}_{\mathrm{i}}>0,i=\stackrel{\_}{1,12}\\ {\mathrm{x}}_1\le 2700000\\ {\mathrm{x}}_2+({\mathrm{x}}_1-2700000)\le 2500000\\ {\mathrm{x}}_3+({\mathrm{x}}_1+{\mathrm{x}}_2-5200000)\le 2700000\\ {\mathrm{x}}_4+({\mathrm{x}}_1+{\mathrm{x}}_2+{\mathrm{x}}_3-7900000)\le 2800000\\ {\mathrm{x}}_5+({\mathrm{x}}_1+\dots +{\mathrm{x}}_4-10700000)\le 2800000\\ {\mathrm{x}}_6+({\mathrm{x}}_1+\dots +{\mathrm{x}}_5-13500000)\le 2700000\\ {\mathrm{x}}_7+({\mathrm{x}}_1+\dots +{\mathrm{x}}_6-16200000)\le 2800000\\ {\mathrm{x}}_8+({\mathrm{x}}_1+\dots +{\mathrm{x}}_7-19000000)\le 3000000\\ {\mathrm{x}}_9+({\mathrm{x}}_1+\dots +{\mathrm{x}}_8-22000000)\le 2800000\\ {\mathrm{x}}_{10}+({\mathrm{x}}_1+\dots +{\mathrm{x}}_9-24800000)\le 3000000\\ {\mathrm{x}}_{11}+({\mathrm{x}}_1+\dots +{\mathrm{x}}_{10}-27800000)\le 2800000\\ {\mathrm{x}}_{12}+({\mathrm{x}}_1+\dots +{\mathrm{x}}_{11}-30600000)\le 2100000\\ {\mathrm{x}}_1\ge 2548556\\ {\mathrm{x}}_2\ge 2550855\\ {\mathrm{x}}_3\ge 2735389\\ {\mathrm{x}}_4\ge 2503787\\ {\mathrm{x}}_5\ge 2750643\\ {\mathrm{x}}_6\ge 2624632\\ {\mathrm{x}}_7\ge 2563748\\ {\mathrm{x}}_8\ge 2563748\\ {\mathrm{x}}_9\ge 2451276\\ {\mathrm{x}}_{10}\ge 2992994\\ {\mathrm{x}}_{11}\ge 2761731\\ {\mathrm{x}}_{12}\ge 2258991\end{array}$$

(13)

Considering the sales volume and production capacity, the objective function becomes:

max f(x) = 1450x₁ + 1320x₂ + 1167x₃ + 1820x₄ + 1097x₅ + 1085x₆ + 1094x₇ + 1030x₈ + 1007x₉ + 1203x₁₀ + 1119x₁₁ + 928x₁₂ − 32700000

(14)

The objective function and related restrictions have been resolved using QM software.

Table 5. The solutions obtained by solving the objective function of maximizing turnover.

	Orders Delivered per Month (Pieces/Month)
X1	2,548,556
X2	2,550,855
X3	2,735,389
X4	2,865,200
X5	2,750,643
X6	2,624,632
X7	2,682,187
X8	2,563,748
X9	2,451,276
X10	3,906,792
X11	2,761,731
X12	2,258,991

shows the monthly quantities that must be delivered by the company in order for the company’s turnover to be maximum.

2.

Minimizing delivery costs, minimizing used resources

For the function of minimizing costs and resource consumption, knowing the quantity of parts to be delivered in the next 12 months, according to the contracts with customers, the production planned for each month, and the price per piece, will all be determined using linear programming for the optimum level of production, so that delivery costs are minimal.

The required data are presented in the table below (

Table 6. Data required for the minimizing cost function.

Month	Customer Orders [pcs]	Production Capacity [pcs]	Total Cost/min (RON/min)
January	2,548,556	2,700,000	25
February	2,550,855	2,500,000	25
March	2,735,389	2,700,000	25
April	2,503,787	2,800,000	25
May	2,750,643	2,800,000	25
June	2,624,632	2,700,000	25
July	2,682,187	2,800,000	25
August	2,563,748	3,000,000	25
September	2,451,276	2,800,000	25
October	2,992,994	3,000,000	25
November	2,761,731	2,800,000	25
December	2,258,991	2,100,000	25

).

$$\{\begin{array}{c}{\mathrm{x}}_{\mathrm{i}}>0,i=\stackrel{\_}{1,12}\\ {\mathrm{x}}_1\ge 2548556\\ {\mathrm{x}}_2+({\mathrm{x}}_1-2548556)\ge 2550855\\ {\mathrm{x}}_3+({\mathrm{x}}_1+{\mathrm{x}}_2-5099411)\ge 2735389\\ {\mathrm{x}}_4+({\mathrm{x}}_1+{\mathrm{x}}_2+{\mathrm{x}}_3-7834800)\ge 2503787\\ {\mathrm{x}}_5+({\mathrm{x}}_1+\dots +{\mathrm{x}}_4-10338587)\ge 2750643\\ {\mathrm{x}}_6+({\mathrm{x}}_1+\dots +{\mathrm{x}}_5-13089230)\ge 2624632\\ {\mathrm{x}}_7+({\mathrm{x}}_1+\dots +{\mathrm{x}}_6-15713862)\ge 2682187\\ {\mathrm{x}}_8+({\mathrm{x}}_1+\dots +{\mathrm{x}}_7-18396049)\ge 2563748\\ {\mathrm{x}}_9+({\mathrm{x}}_1+\dots +{\mathrm{x}}_8-20959797)\ge 2451276\\ {\mathrm{x}}_{10}+({\mathrm{x}}_1+\dots +{\mathrm{x}}_9-23411073)\ge 2992994\\ {\mathrm{x}}_{11}+({\mathrm{x}}_1+\dots +{\mathrm{x}}_{10}-26404067)\ge 2761731\\ {\mathrm{x}}_{12}+({\mathrm{x}}_1+\dots +{\mathrm{x}}_{11}-29165798)\ge 2258991\\ {\mathrm{x}}_1\le 2700000\\ {\mathrm{x}}_2\le 2500000\\ {\mathrm{x}}_3\le 2700000\\ {\mathrm{x}}_4\le 2800000\\ {\mathrm{x}}_5\le 2800000\\ {\mathrm{x}}_6\le 2700000\\ {\mathrm{x}}_7\le 2800000\\ {\mathrm{x}}_8\le 3000000\\ {\mathrm{x}}_9\le 2800000\\ {\mathrm{x}}_{10}\le 3000000\\ {\mathrm{x}}_{11}\le 2800000\\ {\mathrm{x}}_{12}\le 2100000\end{array}$$

(15)

Notations:

${\mathrm{x}}_1,{ \mathrm{x}}_{2,}{ \mathrm{x}}_3,\dots ,{ \mathrm{x}}_{12}$ = quantity of parts to be delivered in the next 12 months;

restrictions are shown in Equation (15).

It is known that the cost of obtaining the piece is 25 RON/min, and the delivery cost of the remaining parts based on a special transport is 5 RON/piece.

Considering the production and transport costs, the objective function becomes:

min f(x) = 80x₁ + 75x₂ + 70x₃ + 65x₄ + 60x₅ + 55x₆ + 50x₇ + 45x₈ + 40x₉ + 35x₁₀ + 30x₁₁ + 25x₁₂ − 172961230,

(16)

By solving the objective function in the QM program, the results presented in

Table 7. The solutions obtained by solving the objective function of minimizing costs.

	Orders Delivered per Month (Pieces/Month)
X1	2,634,800
X2	2,500,000
X3	2,700,000
X4	2,503,790
X5	2,750,640
X6	2,624,630
X7	2,682,190
X8	2,563,750
X9	2,564,990
X10	3,000,000
X11	2,800,000
X12	2,100,000

are obtained.

Table 7 shows the monthly quantities that must be delivered by the company in order for the company’s delivery costs to be minimized.

3.

Maximizing productivity

For the function of maximizing productivity, knowing the quantity of parts to be delivered for the next 12 months, according to the contracts with customers, the production planned for each month, and the productivity will all be determined using linear programming for the optimum level of production, so that the productivity of employees are maximal. The required data are presented in the table below (

Table 8. Data required for maximizing the productivity function.

Month	Productivity [Pieces/Worker]	Customer Orders [pcs]	Production Capacity [Pieces]
January	9664	2,548,556	2,700,000
February	10,913	2,550,855	2,500,000
March	12,121	2,735,389	2,700,000
April	11,072	2,503,787	2,800,000
May	11,617	2,750,643	2,800,000
June	11,492	2,624,632	2,700,000
July	11,706	2,682,187	2,800,000
August	11,122	2,563,748	3,000,000
September	10,939	2,451,276	2,800,000
October	13,438	2,992,994	3,000,000
November	12,178	2,761,731	2,800,000
December	10,341	2,258,991	2,100,000

).

The objective function restrictions have been determined, following the customers’ orders and production capacity:

$$\{\begin{array}{c}{\mathrm{x}}_{\mathrm{i}}>0,i=\stackrel{\_}{1,12}\\ {\mathrm{x}}_1\le 2700000\\ {\mathrm{x}}_2+({\mathrm{x}}_1-2700000)\le 2500000\\ {\mathrm{x}}_3+({\mathrm{x}}_1+{\mathrm{x}}_2-5200000)\le 2700000\\ {\mathrm{x}}_4+({\mathrm{x}}_1+{\mathrm{x}}_2+{\mathrm{x}}_3-7900000)\le 2800000\\ {\mathrm{x}}_5+({\mathrm{x}}_1+\dots +{\mathrm{x}}_4-10700000)\le 2800000\\ {\mathrm{x}}_6+({\mathrm{x}}_1+\dots +{\mathrm{x}}_5-13500000)\le 2700000\\ {\mathrm{x}}_7+({\mathrm{x}}_1+\dots +{\mathrm{x}}_6-16200000)\le 2800000\\ {\mathrm{x}}_8+({\mathrm{x}}_1+\dots +{\mathrm{x}}_7-19000000)\le 3000000\\ {\mathrm{x}}_9+({\mathrm{x}}_1+\dots +{\mathrm{x}}_8-22000000)\le 2800000\\ {\mathrm{x}}_{10}+({\mathrm{x}}_1+\dots +{\mathrm{x}}_9-24800000)\le 3000000\\ {\mathrm{x}}_{11}+({\mathrm{x}}_1+\dots +{\mathrm{x}}_{10}-27800000)\le 2800000\\ {\mathrm{x}}_{12}+({\mathrm{x}}_1+\dots +{\mathrm{x}}_{11}-30600000)\le 2100000\\ {\mathrm{x}}_1\ge 2548556\\ {\mathrm{x}}_2\ge 2550855\\ {\mathrm{x}}_3\ge 2735389\\ {\mathrm{x}}_4\ge 2503787\\ {\mathrm{x}}_5\ge 2750643\\ {\mathrm{x}}_6\ge 2624632\\ {\mathrm{x}}_7\ge 2563748\\ {\mathrm{x}}_8\ge 2563748\\ {\mathrm{x}}_9\ge 2451276\\ {\mathrm{x}}_{10}\ge 2992994\\ {\mathrm{x}}_{11}\ge 2761731\\ {\mathrm{x}}_{12}\ge 2258991\end{array}$$

(17)

Considering the productivity and production capacity, the objective function becomes:

max f(x) = 9676x₁ + 10924x₂ + 12131x₃ + 11081x₄ + 11625x₅ + 11499x₆ + 11082x₇ + 11127x₈ + 10943x₉ + 13441x₁₀ + 12180x₁₁ + 10342x₁₂ − 32700000

(18)

Table 9. The solutions obtained by solving the objective function of maximizing productivity.

	Orders Delivered per Month (Pieces/Month)
X1	2,548,556
X2	2,550,855
X3	2,735,389
X4	2,503,787
X5	2,750,643
X6	2,624,632
X7	2,682,187
X8	2,563,748
X9	2,451,276
X10	4,268,205
X11	2,761,731
X12	2,258,991

shows the monthly quantities that must be delivered by the company in order for the company’s productivity to be maximal.

Having the three objective functions, it was possible to build the final objective function, applying the weights related to each: 0.132 for the function of maximizing the sales, 0.612 for the function of minimizing the costs, and 0.256 for the function of maximizing the productivity (all values were brought to the same unit, as the sales were expressed in thousands of RON):

max(X) = 0.132(1450000 x₁ + 1320000 x₂ + 1167000 x₃ + 1820000 x₄ + 1097000 x₅ + 1085000 x₆ + 1094000 x₇ + 1030000 x₈ + 1007000 x₉ + 1203000 x₁₀ + 1119000 x₁₁ + 92800 x₁₂ − 32700000) − 0.612 (80 x₁ + 75 x₂ + 70 x₃ + 65 x₄ + 60 x₅ + 55 x₆ + 50 x₇ + 45 x₈ + 40 x₉ + 35 x₁₀ + 30 x₁₁ + 25 x₁₂ − 172961230) + 0.256 (9676 x₁ + 10924 x₂ + 12131 x₃ + 1081 x₄ + 11625 x₅ + 11499 x₆ + 11082 x₇ + 11127 x₈ + 10943 x₉ + 13441 x₁₀ + 12180 x₁₁ + 10342 x₁₂ − 32700000),

(19)

The final objective function will be:

max(X) = 193828.1x₁ + 176990.6x₂ + 157106.7x₃ + 243037.9x₄ + 147743.3x₅ + 146130.1x₆ + 147214.4x₇ + 138780.9x₈ + 135700.9x₉ + 138455.58x₁₀ + 150807.7x₁₁ + 125128.3x₁₂ + 107561230,

(20)

Combining the constraints of the three functions that make up the final objective function, the following constraints emerged (21):

$$\{\begin{array}{c}{\mathrm{x}}_{\mathrm{i}}>0,\mathrm{i}=\stackrel{\_}{1,12}\\ {\mathrm{x}}_1\le 2700000\\ {\mathrm{x}}_2+({\mathrm{x}}_1-2700000)\le 2500000\\ {\mathrm{x}}_3+({\mathrm{x}}_1+{\mathrm{x}}_2-5200000)\le 2700000\\ {\mathrm{x}}_4+({\mathrm{x}}_1+{\mathrm{x}}_2+{\mathrm{x}}_3-7900000)\le 2800000\\ {\mathrm{x}}_5+({\mathrm{x}}_1+\dots +{\mathrm{x}}_4-10700000)\le 2800000\\ {\mathrm{x}}_6+({\mathrm{x}}_1+\dots +{\mathrm{x}}_5-13500000)\le 2700000\\ {\mathrm{x}}_7+({\mathrm{x}}_1+\dots +{\mathrm{x}}_6-16200000)\le 2800000\\ {\mathrm{x}}_8+({\mathrm{x}}_1+\dots +{\mathrm{x}}_7-19000000)\le 3000000\\ {\mathrm{x}}_9+({\mathrm{x}}_1+\dots +{\mathrm{x}}_8-22000000)\le 2800000\\ {\mathrm{x}}_{10}+({\mathrm{x}}_1+\dots +{\mathrm{x}}_9-24800000)\le 3000000\\ {\mathrm{x}}_{11}+({\mathrm{x}}_1+\dots +{\mathrm{x}}_{10}-27800000)\le 2800000\\ {\mathrm{x}}_{12}+({\mathrm{x}}_1+\dots +{\mathrm{x}}_{11}-30600000)\le 2100000\\ {\mathrm{x}}_1\ge 2548556\\ {\mathrm{x}}_2+({\mathrm{x}}_1-2548556)\ge 2550855\\ {\mathrm{x}}_3+({\mathrm{x}}_1+{\mathrm{x}}_2-5099411)\ge 2735389\\ {\mathrm{x}}_4+({\mathrm{x}}_1+{\mathrm{x}}_2+{\mathrm{x}}_3-7834800)\ge 2503787\\ {\mathrm{x}}_5+({\mathrm{x}}_1+\dots +{\mathrm{x}}_4-10338587)\ge 2750643\\ {\mathrm{x}}_6+({\mathrm{x}}_1+\dots +{\mathrm{x}}_5-13089230)\ge 2624632\\ {\mathrm{x}}_7+({\mathrm{x}}_1+\dots +{\mathrm{x}}_6-15713862)\ge 2682187\\ {\mathrm{x}}_8+({\mathrm{x}}_1+\dots +{\mathrm{x}}_7-18396049)\ge 2563748\\ {\mathrm{x}}_9+({\mathrm{x}}_1+\dots +{\mathrm{x}}_8-20959797)\ge 2451276\\ {\mathrm{x}}_{10}+({\mathrm{x}}_1+\dots +{\mathrm{x}}_9-23411073)\ge 2992994\\ {\mathrm{x}}_{11}+({\mathrm{x}}_1+\dots +{\mathrm{x}}_{10}-26404067)\ge 2761731\\ {\mathrm{x}}_{12}+({\mathrm{x}}_1+\dots +{\mathrm{x}}_{11}-29165798)\ge 2258991\end{array}$$

(21)

Solving the objective function using QM software, the number of pieces planned to deliver monthly are presented in

Table 10. The solutions obtained by solving the final objective function of optimization.

Variable	Orders Delivered per Month (Pieces/Month)
X1	2,700,000
X2	2,500,000
X3	2,634,800
X4	2,865,200
X5	2,389,230
X6	3,110,770
X7	2,800,000
X8	3,000,000
X9	1,411,070
X10	2,993,000
X11	4,195,930
X12	2,100,000

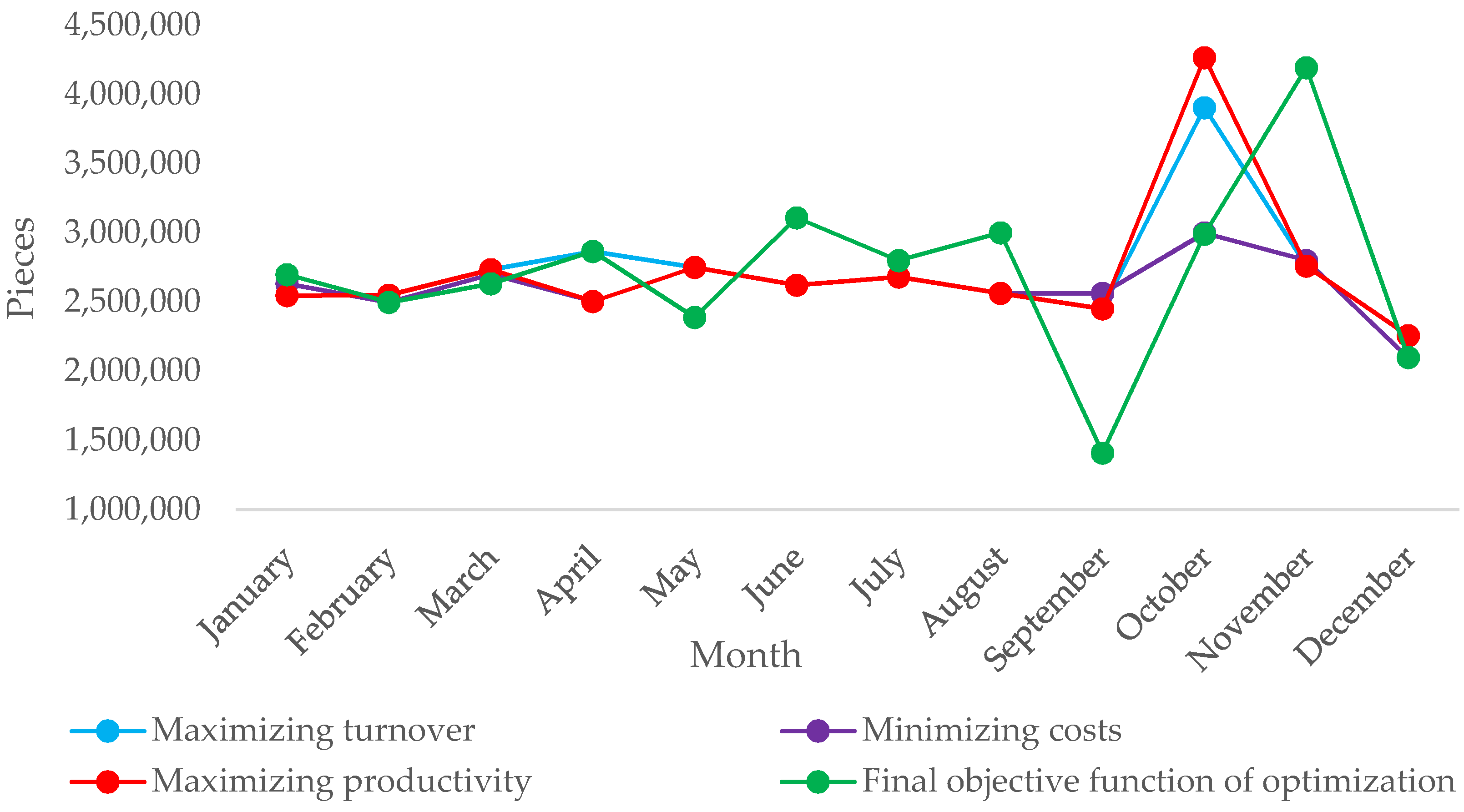
. Table 10 shows the solutions obtained by solving the final objective function of optimization. In order to satisfy all three objective functions simultaneously, a company must produce enough pieces in order to be able to deliver the following quantities each month: 2,700,000, 2,500,000, 2,634,800, 2,865,200, 2,389,230, 3,110,770, 2,800,000, 3,000,000, 1,411,070, 2,993,000, 4,195,930, and 2,100,000 pieces.

Applying these optimized values for each objective function, the maximum and minimum values were obtained, namely: the maximum value for sales will be RON 40,335,178,470,000 (before optimization it was RON 38,359,405,393,000, the) minimum value for costs and resource consumption will be RON 1,703,195,850 (before optimization it was RON 1,750,425,875) and the maximum value for maximizing productivity RON 375,152,423,220 (before optimization it was RON 359,399,430,070).

By solving the final objective function, the values to be achieved by a company each month were obtained, so as to satisfy all three objectives: maximizing turnover, minimizing delivery and consumption costs, and maximizing productivity achieved by employees. By realizing these values, the company can achieve its goals of economic, environmental, and social performance.

5. Discussion

Sustainable development in any organization provides the interdependence between economic, environmental, and social performance. In order to satisfy them all at the same time, the company needs to implement tools that allow multi-criteria decisions. The present paper aims to help the company to achieve the three performances simultaneously by applying multi-attribute optimization.

The optimization problems have been the attention of researchers because by applying the solutions offered by them, organizations can adapt more easily to the rapid changes that intervene in the market, which can improve their activity.

According to numerous studies [5,6,7,8,9], the analytic hierarchy process and linear programming are the most common methods used for optimization problems in automotive engineering. Thus, this paper aligns with recent studies and uses these two MCDM methods to improve the organization’s performance for a sustainable development. However, this paper is the only one in the automotive engineering field that combines AHP with multi-objective linear programming to optimize the organization’s performance.

In areas such as transportation, methods such as AHP, TOPSIS, and PROMETHEE [6] have been used for optimization or a mixed-integer linear-programming model [14]. Combined methods of MCDM, such as AHP and TOPSIS, were used by the authors of [21] for product ranking using customers’ reviews.

Linear programming has been used by many authors in various domains to optimize certain aspects, such as train traffic, such as the problem of multi-periodic train timetabling and routing at stations on a high-speed rail network, with the goal of minimizing the total travel time of trains [16].

In the field of electronics, a linear-programming optimization that produces an optimal load-shedding strategy based on the priority of the loads and a load ranking from the voltage-stability index of the loads was developed by Sarwar et al. [17].

In the economic and quality field, binary linear-programming optimization by minimization of the cost, while optimizing environmental pollution and the quality of products, was proposed by [22,23]. Moreover, in the electrical field, integer linear programming was used to maintain energy storage and prolong the battery life cycle, while minimizing load shedding [24]. Ref. [18] provided a mathematical programming model for sustainable end-of-life vehicle processing and recycling. The model selects the components that maximize reusable material output while minimizing network costs.

From the analysis of recent works, it is observed that the emphasis is on the product [17,18,19,20,21,22,23,24,25] and not on the organization. Thus, to eliminate all the shortcomings mentioned above, a multi-criterial optimization was conceived, focusing on economic, environmental, and social development. Therefore, this paper focuses on the three vital aspects of an organization, trying to combine them in order to meet the requirements of all stakeholders. At the same time, the work does not focus on the product but on the organization as a whole, being a useful tool in control and planning at the management level.

In addition, in a recent review, Refs. [26,27] show that the economic and environmental aspects of sustainability are the main context of sustainable supply chain and logistics where the social aspect is still limited. On the contrary, Ref. [28] focused on the social aspect, using the multi-objective function for optimizing productivity and worker well-being, but no other aspects were taken into account.

According to the papers mentioned above, numerous studies have shown that one of the main weaknesses of the performance-optimization models used by many companies is that they have adopted a single-dimensional focus. Thus, the optimization created in this paper starts from a multidimensional vision of performance, being consistent with the current studies [11,12,13,14,20].

The present research seeks to eliminate the above shortcomings by proposing a multi-criteria optimization and does not focus on a single aspect of an organization’s activity. Compared to these studies, this paper allowed the integration of the three essential elements at the organizational level, such as economic, environmental, and social performance, thus providing managers with a useful tool for business optimization. The case study was successfully implemented in an industrial organization in the automotive area, helping to improve the performance of the organization.

Figure 2 is a graphical representation that allows for comparison between the optimization results obtained both through linear programming for each objective function and by multi-objective linear programming for a multinational company. The final objective function shows the optimal quantities that must be delivered each month to achieve the overall performance of the organization. In order to satisfy all three objective functions simultaneously, maximizing sales, minimizing costs, and maximizing productivity, the company should deliver the following quantities each month: 2,700,000, 2,500,000, 2,634,800, 2,865,200, 2,389,230, 3,110,770, 2,800,000, 3,000,000, 1,411,070, 2,993,000, 4,195,930, and 2,100,000 pieces. By applying these optimized values for each objective function, the maximum and minimum values were obtained, namely: the maximum value for sales will be RON 40,335,178,470,000 (before optimization it was RON 38,359,405,393,000), the minimum value for costs and resource consumption will be RON 1,703,195,850 (before optimization it was RON 1,750,425,875), and the maximum value for productivity will be RON 375,152,423,220 (before optimization it was RON 359,399,430,070). A substantial improvement is observed both in the maximization and minimization functions, which shows the fact that the optimal final function allows an increase in both the unitary performances (sales, costs, and productivity) and the global performance of the organization.

Cost optimization is often targeted by researchers [22,29], profit optimization is the focus of specialists [12], and multi-objective optimization of the two indicators is also targeted [6,11,18,24]; however, a multi-objective vision that involves the optimization of sales, as well as costs and productivity, is the novelty brought by the current work. Analyzing the results obtained, it can be stated that the final multi-objective function allowed for the global optimization of the sustainable development of the organization. Increasing the performance of the organization simultaneously with sustainable development is in fact the target desired by specialists, such as [6,13,17,18,23,26,29].

In addition, the model offered can be an extremely useful tool in production planning and delivery according to customer requirements. By assessing the impacts of different objectives, this paper provided the readers with a reference for selecting the most applicable objective function combination, including different importance weights for each objective function. The paper also provides a framework for applying the optimization model, providing the sequence of all stages, which is extremely easy to implement in the organization.

6. Conclusions

An approach based on portfolio theory for production planning in the automotive industry, taking into account environmental and economic constraints, has been achieved through this research. An approach based on a multi-objective programming model for production planning and deliveries is presented.

The model takes into account economic performance, social performance, and environmental performance. The input data include the objectives planned by the company regarding the turnover to be achieved, the production and delivery costs, and the productivity achieved by employees. Customer requirements for orders, production capacity, delivery costs, and resource consumption are also taken into account for optimization.

Starting from the multi-objective model, several mono-objective optimization problems are formulated: the problem of maximizing turnover, the problem of minimizing costs and resources used, and the problem of maximizing productivity. All these problems were integrated into an objective function that allowed for solving the three objectives simultaneously and, thus, achieving economic, environmental, and social performance, in order to sustainably develop the organization.

However, several limitations of this study must be highlighted. First of all, the applicability of the model has been proven in the automotive industry for several segments of a multinational company, but, in other industries, the model may need adjustments in terms of the objective functions. Second, depending on the objectives pursued by the company, the objective functions may be subject to adjustments (the new objective functions may refer to maximizing profit or minimizing working capital).

Likewise, delivery scheduling may be disrupted by unexpected events, i.e., accidents that happen in the delivery process, equipment malfunctions, etc., so the development of a decision-support tool for reactive strategy is of interest, as the model does not consider this.

Even if the delay penalty is formulated in this paper, it has not been thoroughly tested in the experiments due to the lack of relevant information. Thus, future research may be conducted in order to test different economic means (e.g., different levels of a delay penalty), for ensuring the efficiency of delivery scheduling.

Although there are several sustainability and social factors mentioned, including the social and environmental benefits, the objective functions are still the sales maximization or the minimization of the costs in the optimization model. The next step will be quantifying the social and environmental impacts with objective functions.

Starting from these limitations, some proposals for future research on performance optimization are related to the object of activity of the company, with the analysis of other factors such as the firms’ size or the economic sector, to make additional contributions to the literature on sustainability. This may mean applying different weights, depending on the target desired, as well as determining other objective functions to achieve the desired performance. Furthermore, providing different weighting methods, with the possibility to compare them for users without specialized knowledge, may increase interest in such a system. The presented system is fully functional and delivers something not available in any other framework, by combining objective and subjective methods of MCDM. Additionally, more comparative methods could be presented, providing an even broader spectrum of data analysis.

The performed research shows that this system may serve as a helpful tool in solving multi-criteria decision-making problems using MCDM, ensuring that there is a need for such a framework. Combining other MCDM techniques with different metaheuristic algorithms and analyzing their effect on the algorithm’s performance can also be interesting for future research. The problem can also be extended in future studies by considering some other key performance indicators such as raw material stocks, scrap, and parts returned from the customer.

At the same time, the future research directions follow the development of the social pillar from the objective function, by integrating the motivation of employees as an indicator of the social performance. This variable is more difficult to define because it is a qualitative indicator that is harder to quantify.