An Assessment of the Impact of Temperature Rise Due to Climate Change on Asphalt Pavement in China
Abstract
:1. Introduction
2. Temperature-Related Parameters for Asphalt Pavement Performance Prediction
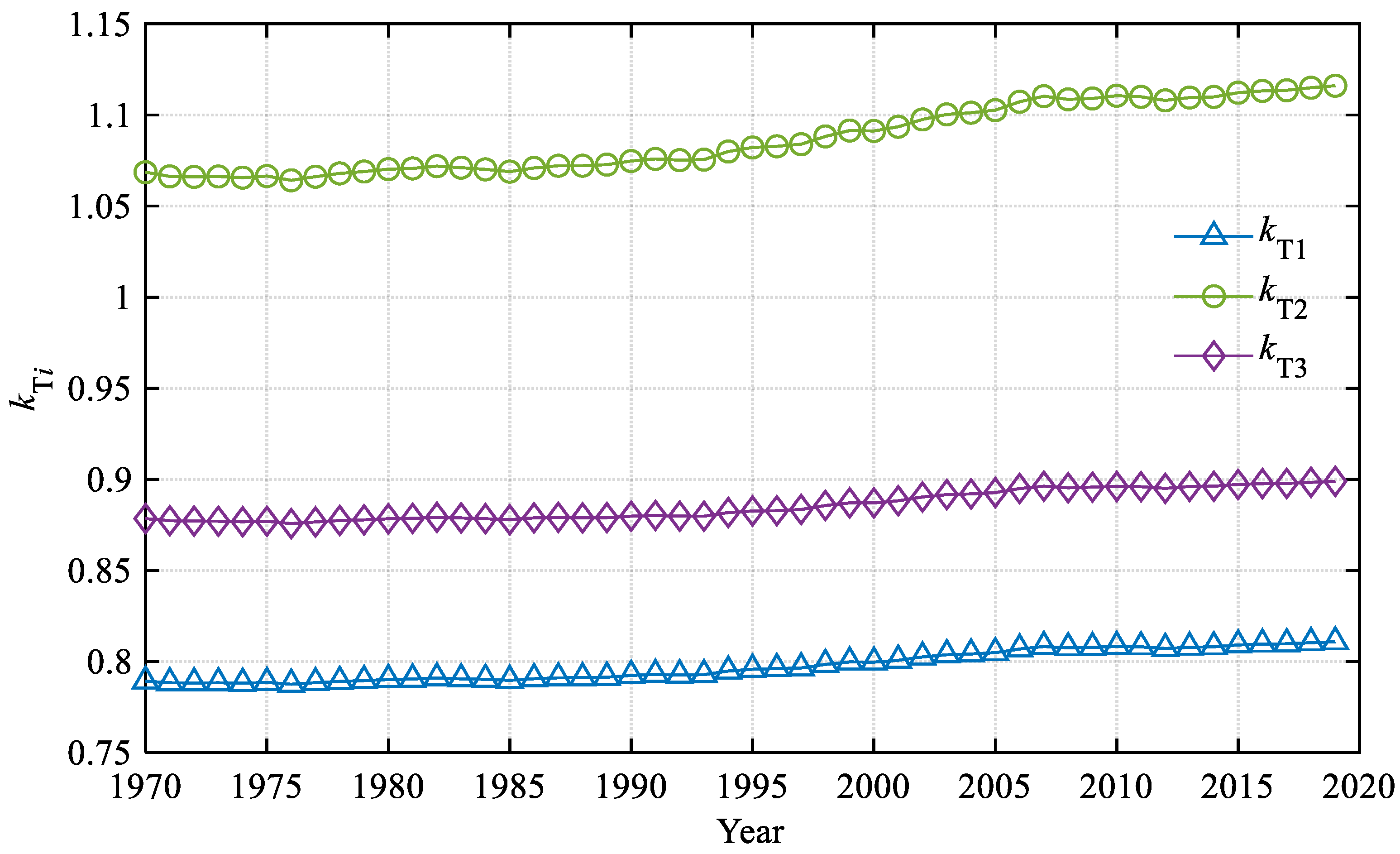
2.1. Temperature Calibration Coefficients
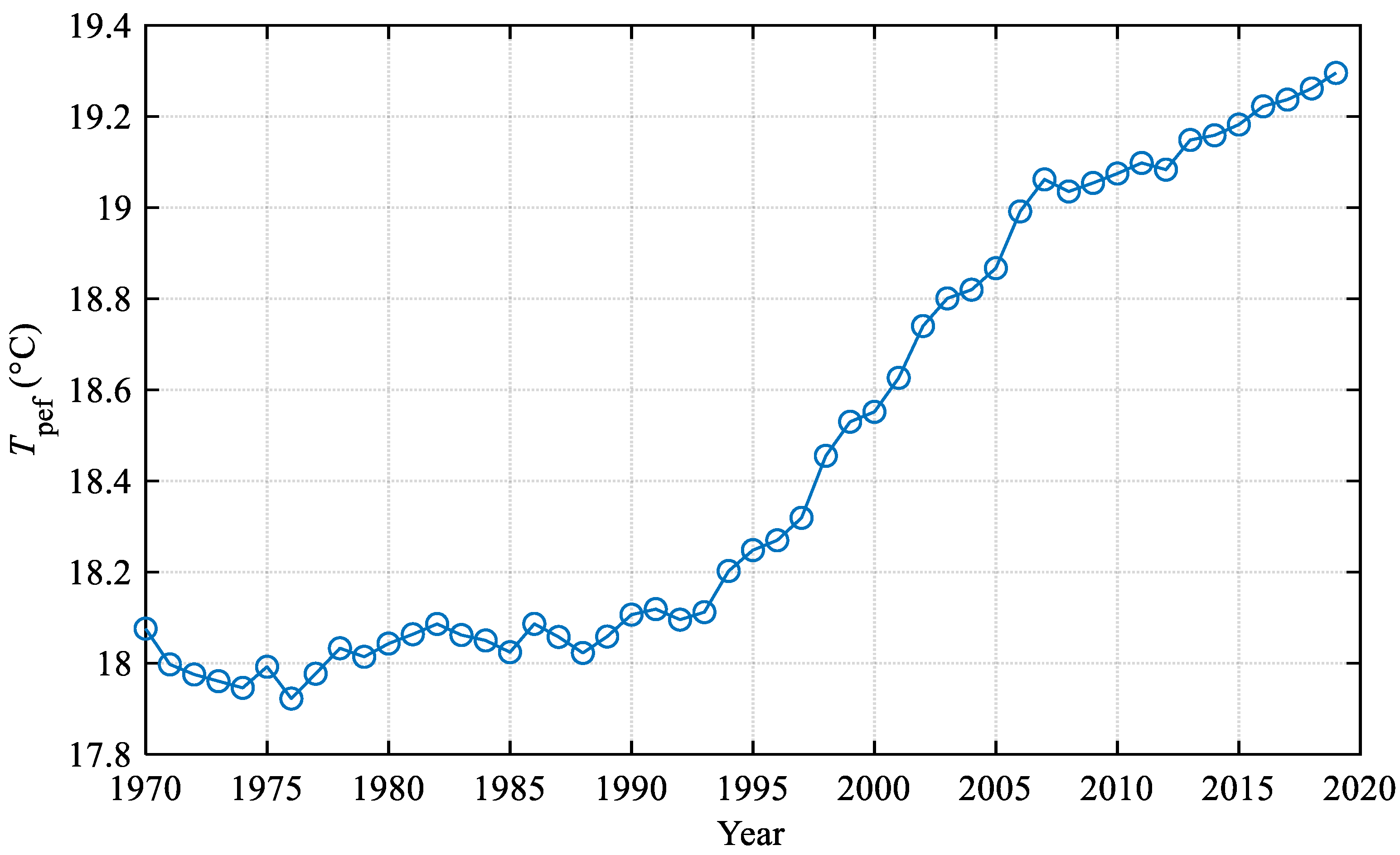
2.2. Equivalent Temperature
2.3. Design Low-Temperature
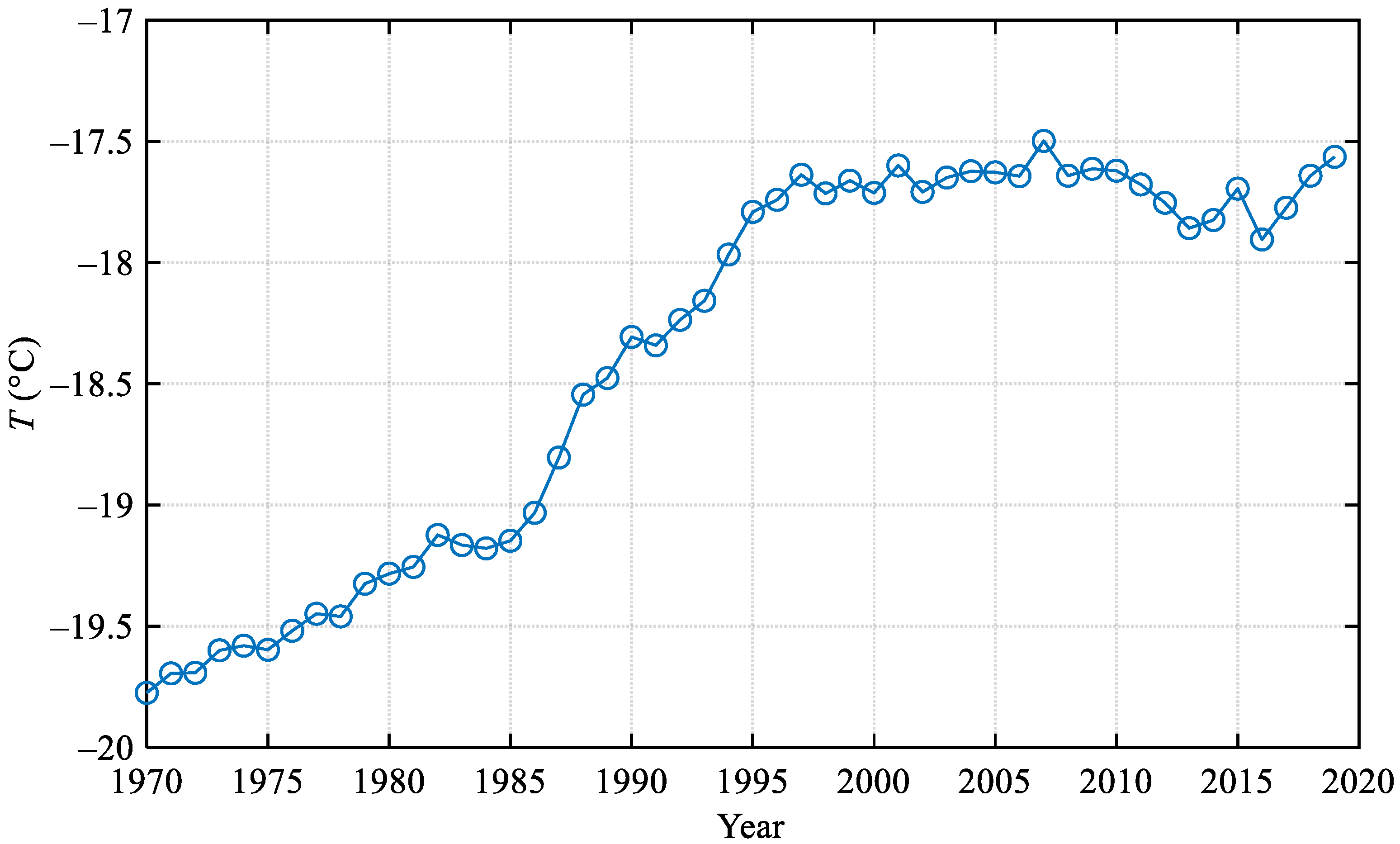
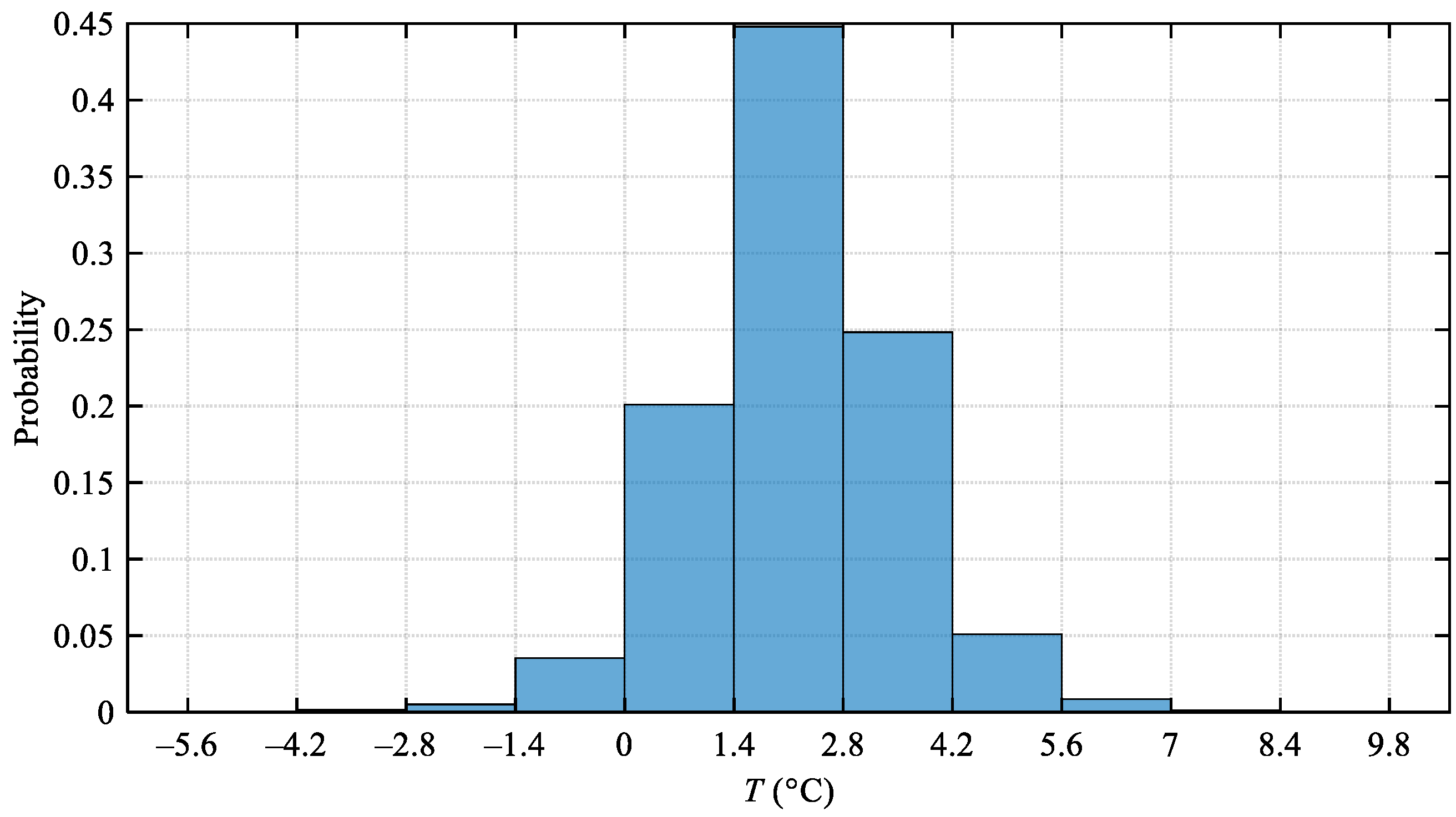
3. Impact of Temperature Rise on Asphalt Pavement in China from 1970 to 2019
3.1. Data Basis
3.2. Impact on the FLAL, FLIBSL, and AVCSSS
3.3. Impact on PDAL
3.4. Impact on LTCIASL
4. Potential Impact of Global Warming on Asphalt Pavement in China in the Future
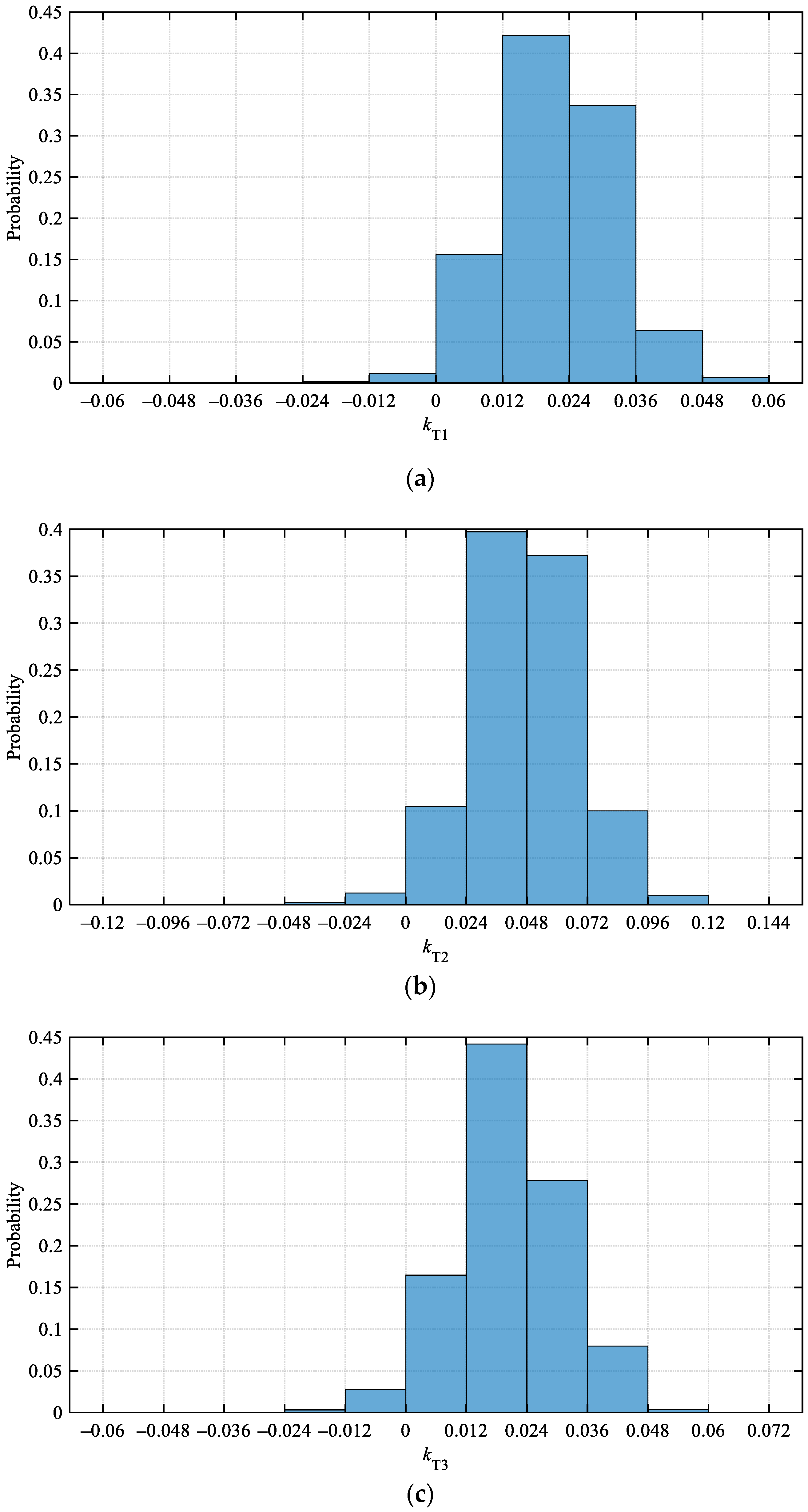
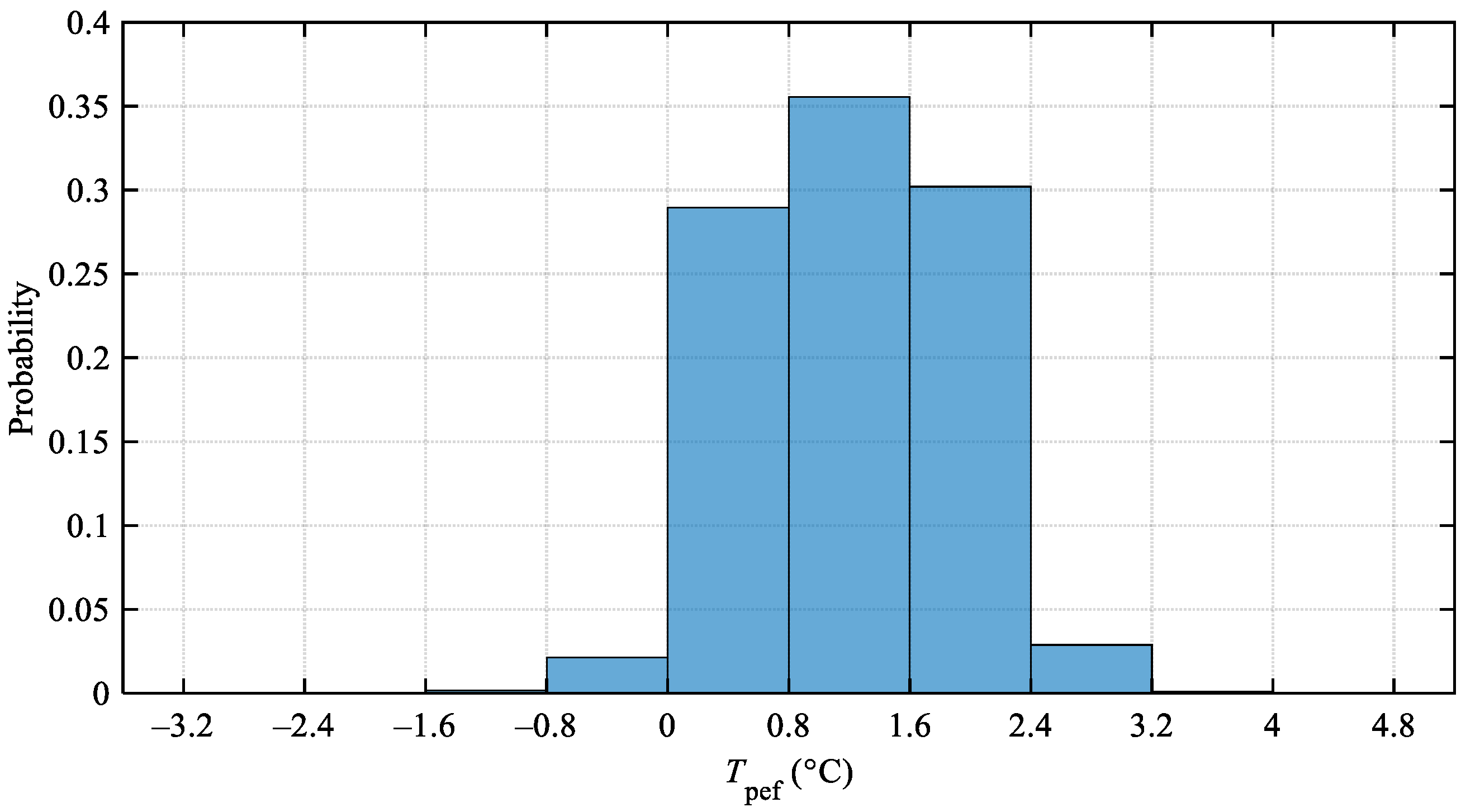
4.1. Relationship between GMST Anomaly and Temperature-Related Parameters for Asphalt Pavement Performance Prediction in China
4.2. Potential Impact of 1.5 °C and 2 °C Global Warming on Asphalt Pavement in China in the Future
5. Discussion
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- The National Academy of Sciences; The Royal Society. Climate Change: Evidence and Causes, Update 2020; The National Academy of Sciences: Washington, DC, USA; The Royal Society: London, UK, 2020. [Google Scholar]
- IPCC. Climate Change 2021: The Physical Science Basis; Intergovernmental Panel on Climate Change: Geneva, Switzerland, 2021. [Google Scholar]
- Taylor, K.E.; Stouffer, R.J.; Meehl, G.A. An Overview of CMIP5 and the Experiment Design. Bull. Am. Meteorol. Soc. 2012, 93, 485–498. [Google Scholar] [CrossRef] [Green Version]
- Giorgi, F.; Coppola, E.; Solmon, F.; Mariotti, L.; Sylla, M.B.; Bi, X.; Elguindi, N.; Diro, G.T.; Nair, V.; Giuliani, G.; et al. RegCM4: Model description and preliminary tests over multiple CORDEX domains. Clim. Res. 2012, 52, 7–29. [Google Scholar] [CrossRef] [Green Version]
- Mearns, L.O.; Sain, S.; Leung, L.R.; Bukovsky, M.S.; McGinnis, S.; Biner, S.; Caya, D.; Arritt, R.W.; Gutowski, W.; Takle, E.; et al. Climate change projections of the North American Regional Climate Change Assessment Program (NARCCAP). Clim. Chang. 2013, 120, 965–975. [Google Scholar] [CrossRef] [Green Version]
- Scinocca, J.F.; Kharin, V.V.; Jiao, Y.; Qian, M.W.; Lazare, M.; Solheim, L.; Flato, G.M.; Biner, S.; Desgagne, M.; Dugas, B. Coordinated global and regional climate modeling. J. Clim. 2016, 29, 17–35. [Google Scholar] [CrossRef]
- Morice, C.P.; Kennedy, J.J.; Rayner, N.A.; Jones, P.D. Quantifying uncertainties in global and regional temperature change using an ensemble of observational estimates: The HadCRUT4 data set. J. Geophys. Res. Atmos. 2012, 117, D08101. [Google Scholar] [CrossRef]
- Daniel, J.S.; Jacobs, J.M.; Douglas, E.; Mallick, R.B.; Hayhoe, K. Impact of climate change on pavement performance: Preliminary lessons learned through the infrastructure and climate network (ICNet). In Climatic Effects on Pavement and Geotechnical Infrastructure; Liu, J., Li, P., Zhang, X., Huang, B., Eds.; American Society of Civil Engineers (ASCE): Reston, VA, USA, 2014; pp. 1–9. [Google Scholar]
- Austroads. Impact of Climate Change on Road Infrastructure; Austroads Incorporated: Sydney, Australia, 2004. [Google Scholar]
- Austroads. Impact of Climate Change on Road Performance: Updating Climate Information for Australia; Austroads Incorporated: Sydney, Australia, 2010. [Google Scholar]
- Valle, O.; Qiao, Y.; Dave, E.; Mo, W. Life cycle assessment of pavements under a changing climate. In Pavement Life-Cycle Assessment; Al-Qadi, I.L., Ozer, H., Harvey, J., Eds.; CRC Press: London, UK, 2017; pp. 241–250. [Google Scholar]
- Knott, J.F.; Sias, J.E.; Dave, E.V.; Jacobs, J.M. Seasonal and Long-Term Changes to Pavement Life Caused by Rising Temperatures from Climate Change. Transp. Res. Rec. 2019, 2673, 267–278. [Google Scholar] [CrossRef]
- Stoner, A.M.K.; Daniel, J.S.; Jacobs, J.M.; Hayhoe, K.; Scott-Fleming, I. Quantifying the Impact of Climate Change on Flexible Pavement Performance and Lifetime in the United States. Transp. Res. Rec. 2019, 2673, 110–122. [Google Scholar] [CrossRef]
- Zareie, A.; Amin, M.S.R.; Amador-Jimenez, L.E. Thornthwaite Moisture Index Modeling to Estimate the Implication of Climate Change on Pavement Deterioration. J. Transp. Eng. 2016, 142, 04016007. [Google Scholar] [CrossRef]
- Tighe, S.L.; Smith, J.; Mills, B.; Andrey, J. Evaluating Climate Change Impact an Low-Volume Roads in Southern Canada. Transp. Res. Rec. 2008, 2053, 9–16. [Google Scholar] [CrossRef]
- Chen, X.; Wang, H.; Horton, R.; DeFlorio, J. Life-cycle assessment of climate change impact on time-dependent carbon-footprint of asphalt pavement. Transp. Res. Part D Transp. Environ. 2021, 91, 102697. [Google Scholar] [CrossRef]
- Lu, D.; Tighe, S.L.; Xie, W. Pavement Risk Assessment for Future Extreme Precipitation Events under Climate Change. Transp. Res. Rec. 2018, 2672, 122–131. [Google Scholar] [CrossRef]
- Mallick, R.B.; Jacobs, J.M.; Miller, B.J.; Daniel, J.S.; Kirshen, P. Understanding the impact of climate change on pavements with CMIP5, system dynamics and simulation. Int. J. Pavement Eng. 2018, 19, 697–705. [Google Scholar] [CrossRef]
- Nakicenovic, N.; Alcamo, J.; Davis, G.; de Vries, B.; Fenhann, J.; Gaffin, S.; Gregory, K.; Griibler, A.; Jung, T.Y.; Kram, T.; et al. Special Report on Emissions Scenarios; Intergovernmental Panel on Climate Change: Geneva, Switzerland, 2000. [Google Scholar]
- Moss, R.; Babiker, M.; Brinkman, S.; Calvo, E.; Carter, T.; Edmonds, J.; Elgizouli, I.; Emori, S.; Erda, L.; Hibbard, K.; et al. Towards New Scenarios for Analysis of Emissions, Climate Change, Impacts, and Response Strategies; Intergovernmental Panel on Climate Change: Geneva, Switzerland, 2008. [Google Scholar]
- Wistuba, M.P.; Walther, A. Consideration of climate change in the mechanistic pavement design. Road Mater. Pavement 2013, 14, 227–241. [Google Scholar] [CrossRef]
- Gudipudi, P.P.; Underwood, B.S.; Zalghout, A. Impact of climate change on pavement structural performance in the United States. Transp. Res. Part D Transp. Environ. 2017, 57, 172–184. [Google Scholar] [CrossRef]
- Qiao, Y.; Santos, J.; Stoner, A.M.K.; Flinstch, G. Climate change impacts on asphalt road pavement construction and maintenance: An economic life cycle assessment of adaptation measures in the State of Virginia, United States. J. Ind. Ecol. 2020, 24, 342–355. [Google Scholar] [CrossRef]
- Daniel, J.S.; Jacobs, J.M.; Miller, H.; Stoner, A.; Crowley, J.; Khalkhali, M.; Thomas, A. Climate change: Potential impacts on frost-thaw conditions and seasonal load restriction timing for low-volume roadways. Road Mater. Pavement 2018, 19, 1126–1146. [Google Scholar] [CrossRef]
- Viola, F.; Celauro, C. Effect of climate change on asphalt binder selection for road construction in Italy. Transp. Res. Part D Transp. Environ. 2015, 37, 40–47. [Google Scholar] [CrossRef]
- Li, Q.J.; Mills, L.; McNeil, S.; Attoh-Okine, N.O. Integrating potential climate change into the mechanistic-empirical based pavement design. Can. J. Civ. Eng. 2013, 40, 1173–1183. [Google Scholar] [CrossRef]
- Mills, B.N.; Tighe, S.L.; Andrey, J.; Smith, J.T.; Huen, K. Climate change implications for flexible pavement design and performance in Southern Canada. J. Transp. Eng. 2009, 135, 773–782. [Google Scholar] [CrossRef]
- Guest, G.; Zhang, J.; Maadani, O.; Shirkhani, H. Incorporating the impacts of climate change into infrastructure life cycle assessments: A case study of pavement service life performance. J. Ind. Ecol. 2020, 24, 356–368. [Google Scholar] [CrossRef]
- Qiao, Y.; Dawson, A.R.; Parry, T.; Flintsch, G.W. Evaluating the effects of climate change on road maintenance intervention strategies and Life-Cycle Costs. Transp. Res. Part D Transp. Environ. 2015, 41, 492–503. [Google Scholar] [CrossRef]
- Bilodeau, J.; Dore, G.; Drolet, F.P.; Chaumont, D. Correction of air freezing index for pavement frost protection design to consider future climate changes. Can. J. Civ. Eng. 2016, 43, 312–319. [Google Scholar] [CrossRef]
- Steyn, W.J.M.; Pretorius, T. The potential effects of climate change on selected flexible South African pavements. In Sustainability, Eco-Efficiency, and Conservation in Transportation Infrastructure Asset Management; Losa, M., Papagiannakis, T., Eds.; CRC Press: London, UK, 2014; pp. 469–477. [Google Scholar]
- Chai, G.; Van Staden, R.; Guan, H.; Kelly, G.; Chowdhury, S. The impacts of climate change on pavement maintenance in Queensland, Australia. In Materials and Infrastructures 2, 5B; Torrenti, J.M., La Torre, F., Eds.; ISTE Ltd.: London, UK, 2016; pp. 207–221. [Google Scholar]
- Jiang, X.; Gabrielson, J.; Titi, H.; Huang, B.; Bai, Y.; Polaczyk, P.; Hu, W.; Zhang, M.; Xiao, R. Field investigation and numerical analysis of an inverted pavement system in Tennessee, USA. Transp. Geotech. 2022, 35, 100759. [Google Scholar] [CrossRef]
- Qiao, Y.; Zhang, Y.; Zhu, Y.; Lemkus, T.; Stoner, A.M.K.; Zhang, J.; Cui, Y. Assessing impacts of climate change on flexible pavement service life based on Falling Weight Deflectometer measurements. Phys. Chem. Earth 2020, 120, 102908. [Google Scholar] [CrossRef]
- Qiao, Y.; Zhang, Y.; Elshaer, M.; Daniel, J.S. A method to assess climate change induced damage on flexible pavements with machine learning. In Bearing Capacity of Roads, Railways and Airfields; Loizos, A., Al-Qadi, I.L., Scarpas, A.T., Eds.; CRC Press: London, UK, 2017; pp. 2103–2108. [Google Scholar]
- Jeong, H.; Kim, H.; Kim, K.; Kim, H. Prediction of flexible pavement deterioration in relation to climate change using fuzzy logic. J. Infrastruct. Syst. 2017, 23, 04017008. [Google Scholar] [CrossRef]
- Mallick, R.B.; Radzicki, M.J.; Daniel, J.S.; Jacobs, J.M. Use of system dynamics to understand long-term impact of climate change on pavement performance and maintenance cost. Transp. Res. Rec. 2014, 2455, 1–9. [Google Scholar] [CrossRef] [Green Version]
- Chang, C.M.; Ortega, O. A methodology to quantify the impact of climate change on the state of good repair of pavements. In Bituminous Mixtures and Pavements VII; Nikolaides, A.F., Manthos, E., Eds.; CRC Press: London, UK, 2019; pp. 399–410. [Google Scholar]
- Wang, Y.; Huang, Y.; Rattanachot, W.; Lau, K.K.; Suwansawas, S. Improvement of pavement design and management for more frequent flooding caused by climate change. Adv. Struct. Eng. 2015, 18, 487–496. [Google Scholar] [CrossRef]
- Ministry of Transport, China. Specifications for Design of Highway Asphalt Pavement (JTG D50-2017); China Communications Press: Beijing, China, 2017. [Google Scholar]
- Climate Change Center of China Meteorological Administration. The Blue Paper of Climate Change in China 2020; Science Press: Beijing, China, 2020. [Google Scholar]
- World Meteorological Organization. WMO Statement on the State of the Global Climate in 2019; World Meteorological Organization: Geneva, Switzerland, 2020. [Google Scholar]
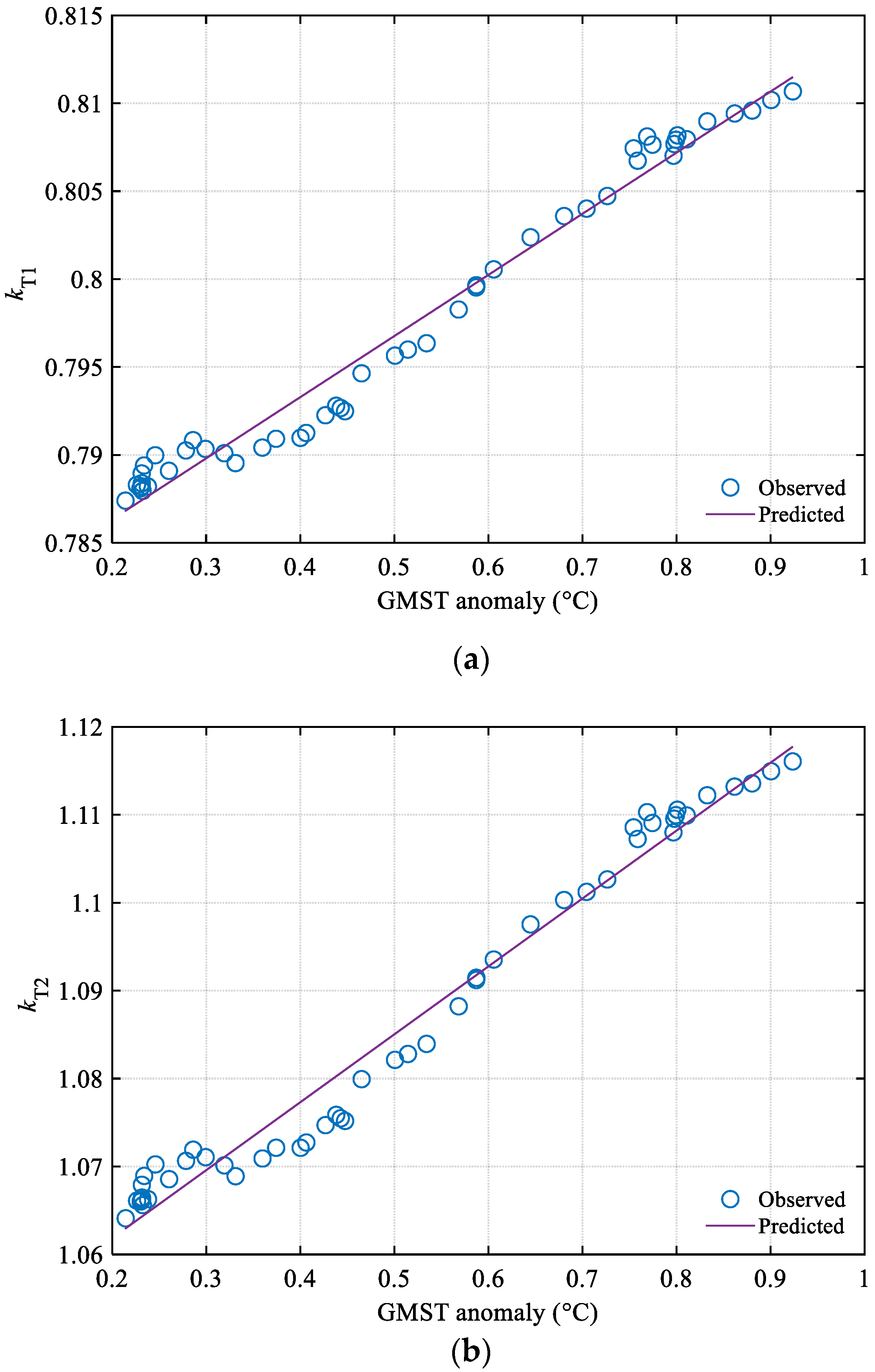
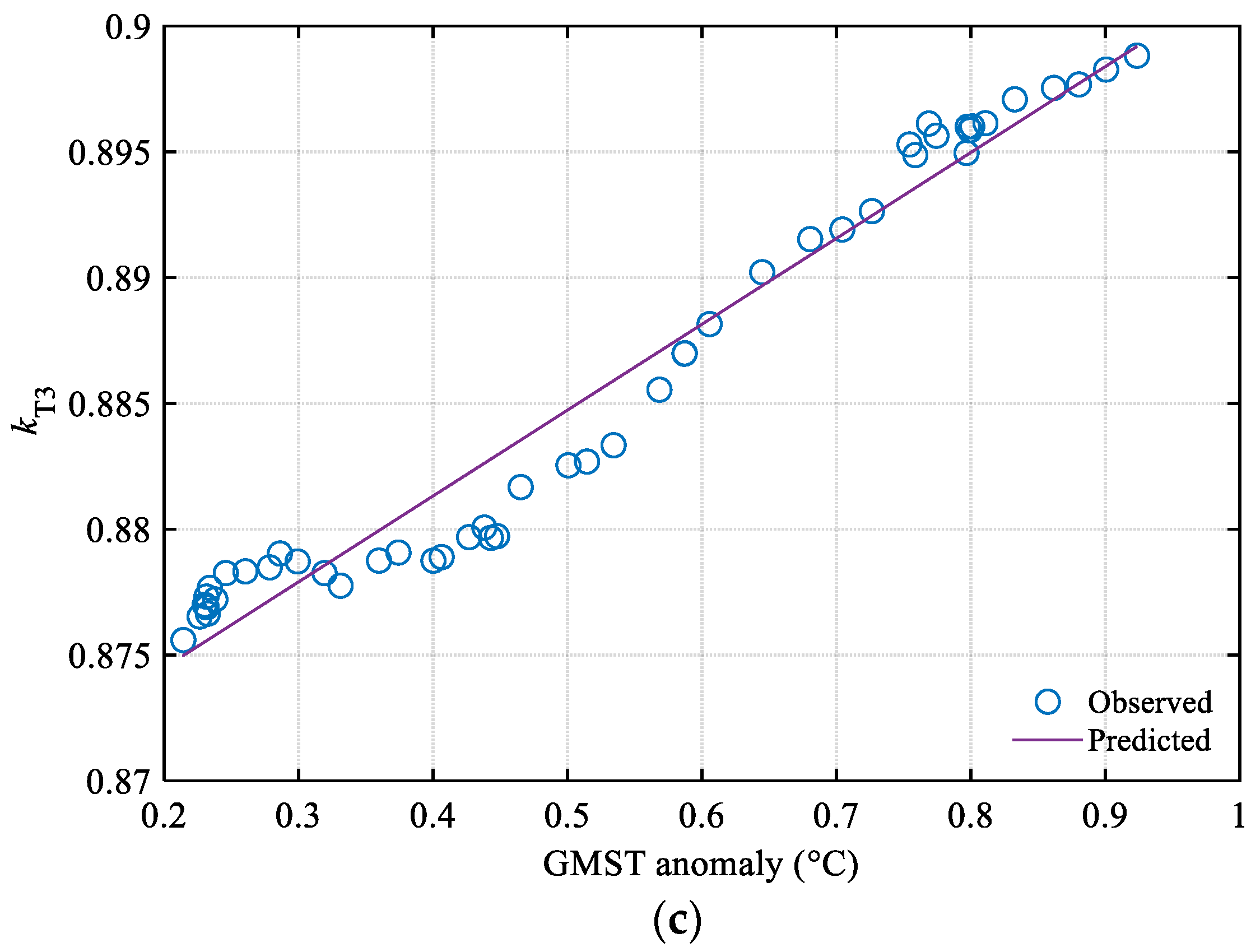
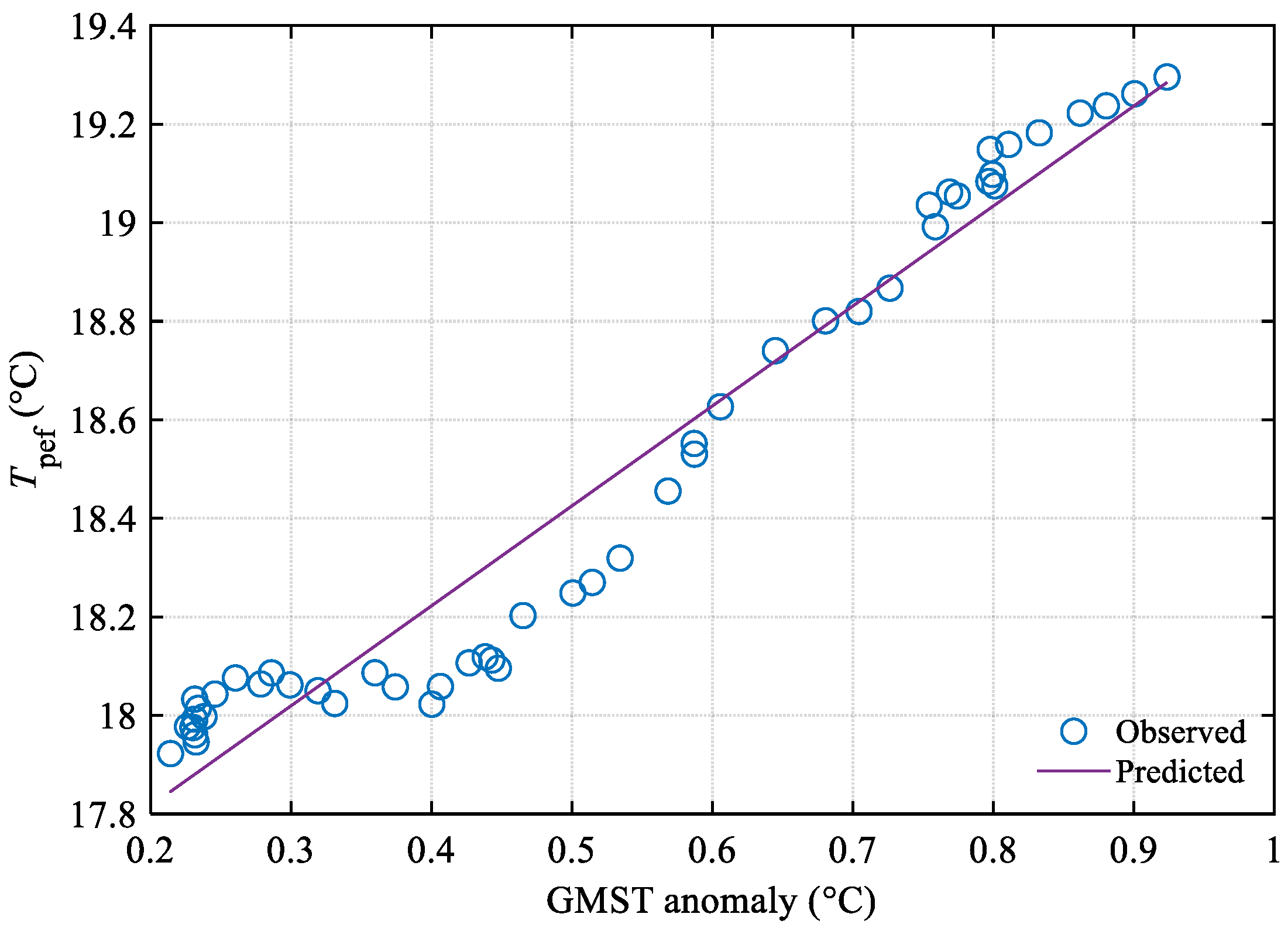
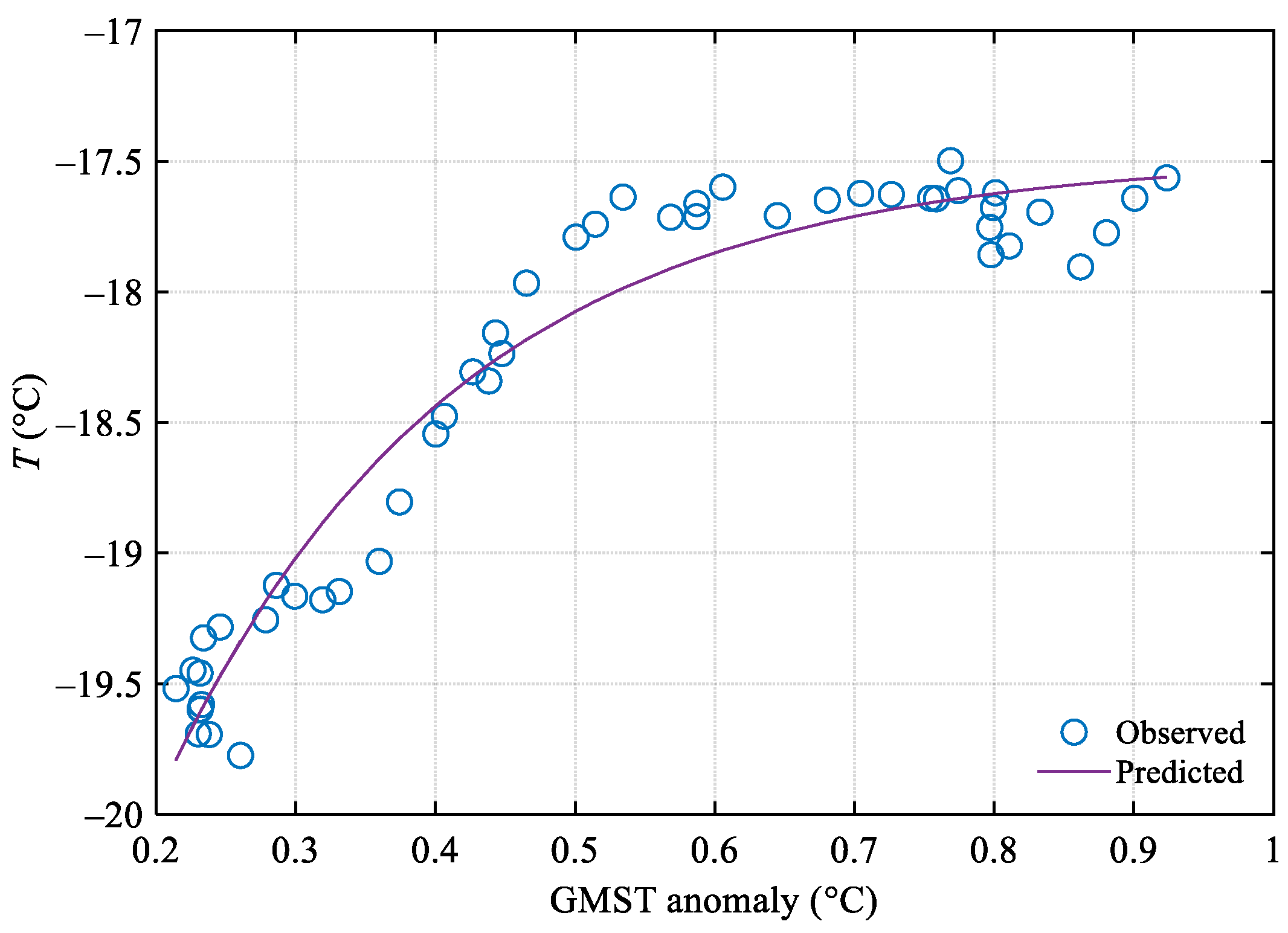
| Parameter | Regression Model | R Square | F Value | p < |
|---|---|---|---|---|
| kT1 | 0.9770 | 2078.5 | 0.0001 | |
| kT2 | 0.9747 | 1887.2 | 0.0001 | |
| kT3 | 0.9603 | 1187.6 | 0.0001 | |
| Tpef | 0.9464 | 865.9 | 0.0001 | |
| T | 0.9441 | 396.6 | 0.0001 |
| Design Indicator | 1.5 °C GMST Anomaly | 2 °C GMST Anomaly |
|---|---|---|
| Nf1 | −2.52% | −4.51% |
| Nf2 | −3.98% | −7.06% |
| [εz] | −0.46% | −0.85% |
| Ra | 18.63% | 36.71% |
| CI | −0.97% | −1.03% |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Miao, Y.; Sheng, J.; Ye, J. An Assessment of the Impact of Temperature Rise Due to Climate Change on Asphalt Pavement in China. Sustainability 2022, 14, 9044. https://doi.org/10.3390/su14159044
Miao Y, Sheng J, Ye J. An Assessment of the Impact of Temperature Rise Due to Climate Change on Asphalt Pavement in China. Sustainability. 2022; 14(15):9044. https://doi.org/10.3390/su14159044
Chicago/Turabian StyleMiao, Yinghao, Jiajia Sheng, and Jin Ye. 2022. "An Assessment of the Impact of Temperature Rise Due to Climate Change on Asphalt Pavement in China" Sustainability 14, no. 15: 9044. https://doi.org/10.3390/su14159044
APA StyleMiao, Y., Sheng, J., & Ye, J. (2022). An Assessment of the Impact of Temperature Rise Due to Climate Change on Asphalt Pavement in China. Sustainability, 14(15), 9044. https://doi.org/10.3390/su14159044






