Abstract
How to sustainably conduct intersection operations is a key issue of the current research. For an actuated control intersection, queued vehicles, control parameters, and phase schemes all affect the operation effect. This paper discusses queued vehicles at actuated intersections and their influence on signal timing. First, this paper establishes an improved traffic wave model and proposes a vehicle queuing model on this basis. Second, by analyzing the queuing and dispersion process of queued vehicles, a minimal green time calculation model is proposed. Then, this paper establishes a maximal green time calculation model aiming at minimizing average vehicle delay and maximizing traffic capacity under different phase schemes, and considers the influence of queued vehicles. Lastly, the models are verified separately; results show that the average error of the minimal green time model was 4.18%, and the average optimization rate of the maximal green time model was 9.27%. It is proved that the models achieved great accuracy and optimization effects, which could potentially improve intersection sustainability.
1. Introduction
A large amount of practical experience has proven that only increasing the supply level cannot essentially solve traffic congestion problems [1]. In contrast, using management and control strategies can achieve better results. As an important part of urban road systems, intersections are not only key to solving congestion, but also determine the entire system’s sustainability. Therefore, optimizing intersection signal control parameters is a hot issue in current research.
Intelligent methods such as deep learning [2,3], fuzzy control theory [4,5], and intelligent algorithms [6,7] have been proposed that highly rely on high-precision and real-time traffic data to ensure reliability. Some scholars believe that using these methods to solve congestions will become the main trend. However, the current intelligence and automation levels of most intersections cannot meet the requirements. In fact, more than 90% of the intersections in China are still not equipped with modern detectors such as video and radar detectors [8], so the methods above are not applicable at this stage.
Considering the above problem, this paper focuses on actuated signal control, an effective and widely used control strategy relying on traffic detectors to detect traffic flow and make corresponding control decisions [9]. In actuated control, the minimal green time ensures the dispersion of all queued vehicles, and the maximal green time limits the maximal time of the phase. These two basic parameters can avoid the secondary queuing of vehicles and the waste of green time, so it is greatly significant to optimize their value. Furthermore, in view of the current intelligent transportation development level in China, further exploration of actuated control optimization could be highly compatible with realistic needs.
The rest of the paper is organized as follows. Section 2 reviews the existing literature relevant to this paper. In Section 3, we establish an improved traffic wave model, and propose a vehicle queuing model on this basis. In Section 4, we construct a minimal green time calculation model by analyzing the queuing and dispersion process of queued vehicles, and construct a maximal green time calculation model considering the influence of queued vehicles. The solving algorithm for the model is given in Section 5. Verifications are conducted in Section 6, and our contributions are concluded in Section 7.
2. Literature Review
In the 1950s, Webster [10] first proposed an optimal cycle length model with minimal average vehicle delay, and suggested that the maximal cycle length is approximately 1.25–1.5 times the optimal cycle length, which provided a reference for setting the maximal green time. Pappis and Mamdani [11] first applied fuzzy logic in signal control, taking vehicle arrival and queuing information as inputs, and outputting the actuated green time. Murat and Gedizioglu [12] also established a fuzzy control model on the basis of that of Pappis [11] that considered the phase sequence influence. By obtaining the real-time vehicle delay and queue length, Cowan [13] improved actuated control, which could effectively evaluate the control effect. By studying vehicle arrival characteristics, traffic capacity, saturation flow, vehicle delay, queue length, and parking rate, Akcelik [14] proposed cycle length and green time calculation models that can be used for semiactuated and fully actuated control. Furth et al. [15] decomposed the cycle length into two parts: full utilization time and loss time, and a cycle length calculation model was constructed on this basis. Viti and Van Zuylen [16] proposed a green time calculation model based on probability theory that considered queue length. Moghimi et al. [17] analyzed different green time demand levels, and deduced the cycle length by using a time sequence forecast method. Shiri and Maleki [18] determined the maximal green time through fuzzy logic, and dynamically adjusted it by monitoring the traffic operating conditions. Jing [19] established a minimal green time optimization model considering the stochastic characteristics of traffic flow. Hao [20] proposed a framework for actuated control that took into account uncertainties in potential driver distraction issues that could reduce energy consumption and emissions. Bao [21] analyzed traffic flow according to collected data, including occupancy and vehicle queuing information, and then proposed an actuated control strategy that could reduce vehicle delay. Christian [22] designed a fully actuated control using logical controls that were able to perceive the pedestrian density on refuge islands, prioritizing pedestrians more. Wang [23] used RFID technology to record arrival flow and predict future traffic volume to obtain the cycle length of the actuated control. Wu [24] presented a new volume-occupancy-based actuated control system for a diamond interchange that used real-time traffic volume and occupancy to improve the traffic by adaptively adjusting the signal control plan.
Above all, we found the following: (a) The optimization models constructed in recent years mostly rely on the real-time data obtained by intelligent detectors, but these data are not easy to obtain in most intersections, and the accuracy and reliability of the data still need to be further studied. Therefore, these models lack certain applicability. (b) There is less research on the minimal green time, and these studies mainly focused on the arrival characteristics of vehicles, ignoring the impact of queued vehicles. (c) Studies on maximal green time mainly focused on traffic flow characteristics with no indepth discussion of phase schemes and queued vehicles.
To deal with the abovementioned issues, the following work is presented in this paper: (a) An improved traffic wave model is first established, and a vehicle queuing model is proposed on this basis. Then, a minimal green time calculation model considering queued vehicles is proposed that fully considers the impact of the queued vehicles on the control effect. (b) A maximal green time calculation model considering phase schemes and queued vehicles is established that deeply discusses the phase schemes and impact of queued vehicles. (c) The data needed in this paper can be accurately obtained at almost all intersections through coil detectors, which means that the constructed models in this paper have stronger practical value.
3. Vehicle Queuing Model Based on Improved Traffic Wave Model
3.1. Improved Traffic Wave Model
The starting wave transmission process is shown in Figure 1a. The traffic flow in front of the wave front was congested traffic flow with a speed of 0 and density of congestion density kj. The traffic flow behind the wave front was the traveling traffic flow with the speed of critical speed vm, density of critical density km, and headway of the saturated headway hm.
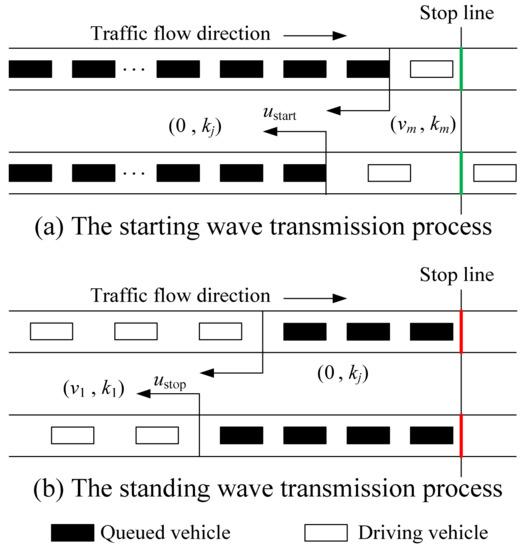
Figure 1.
Transmission process of the traffic wave.
The standing wave transmission process is shown in Figure 1b. The traffic flow in front of the wave front was the traveling traffic flow with speed v1, density k1, and headway h1. The traffic flow behind the wave front was the congested traffic flow with speed of 0 and the density of congested density kj.
There are three existing traffic wave calculation methods, namely, the Greenhill [25], the Greenberg traff [26] and the LWR [27,28] traffic wave models. The LWR traffic wave model is as follows:
where ustart represents the starting wave (m/s), and ustop represents the standing wave (m/s).
The relationship among traffic volume q, speed v, and density k is as follows:
The relationship between space headway s and headway h is as follows:
The relationship between space headway s and density k is as follows:
Combining Equations (1)–(5), the improved traffic wave model is shown in Equations (6) and (7).
As we can see in the LWR model’s Equations (1) and (2), traffic density k1 is needed for calculation, which is difficult to obtain directly. In the improved model, shown in Equations (6) and (7), headway h1 was adopted instead of k1, which could be accurately obtained in real time thanks to the widely used coil detectors in actuated control.
3.2. Vehicle Queuing and Dispersion Process
On the basis of unsaturated traffic flow, all vehicles queued in the previous cycle were assumed to be completely released. Figure 2 describes the vehicle-queuing and traffic wave transmission processes in the nth cycle.
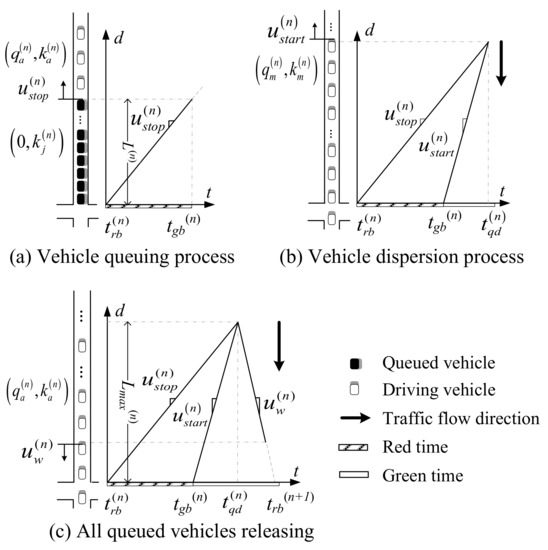
Figure 2.
Evolution of vehicle queuing process.
3.2.1. Vehicle Queuing Process
As shown in Figure 2a, when the red light turned on, the driving vehicles stopped in sequence behind the stop line. The standing wave formed at this time transmitted backward from the stop line, which is shown in Equation (8).
where va(n) is the average speed of the arriving vehicles (m/s), and ha(n) is the average headway (s).
3.2.2. Vehicle Dispersion Process
As shown in Figure 2b, when the green light turned on, the static vehicles started to leave the intersection. The starting wave formed at this time transmitted backwards from the stop line, which is as follows:
As shown in Figure 2c, when the starting wave and the standing wave met, all queued vehicles turned to the driving state and were released at critical speed vm.
3.3. Vehicle-Queuing Model
Assuming that the studied traffic flow started with red time in the nth cycle, and the vehicles queued in the previous cycle had been completely released, the distance between the leading vehicle and the stop line was ignored.
When trb(n) ≤ t ≤ tgb(n)
where trb(n) is the start time of the red light, tgb(n) is the start time of the green light, x0(n) is the position of the leading vehicle relative to the stop line (m), xl(n) is the position of the trailing vehicle relative to the stop line (m), and L(n) is the queue length (m).
When tgb(n) ≤ t ≤ tqd(n)
where tqd(n) is the moment when the starting wave and the standing wave meet, and is shown in Equation (12).
The longest queue length Lmax(n) formed at time tqd(n) is as follows:
After tqd(n), the vehicles passed through the intersection, as shown in Figure 2c. At this time, there were no queued vehicles.
4. Optimization Models of Basic Parameters
4.1. Minimal Green Time Optimization Model
In the actuated control, the minimal green time is defined as the time during which all queued vehicles can pass through the intersection [29]. As shown in Figure 3, the time for queued vehicles of length L to pass through includes two parts: (a) the time required for the starting wave to pass from the leading vehicle to the trailing vehicle, which was recorded as T1; and (b) the time required for vehicles gradually leave the intersection, which was recorded as T2.
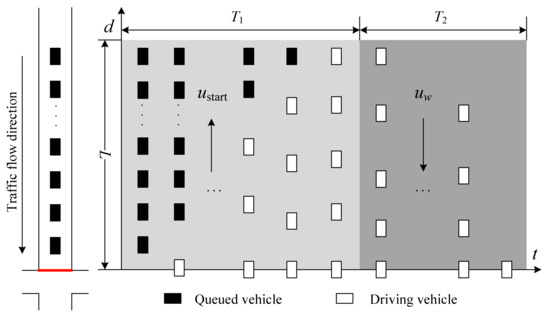
Figure 3.
Departure process of queuing vehicles.
Minimal green time Gp is as follows:
4.2. Maximal Green Time Optimization Model
This study establishes an optimization model for the maximal green time considering the queued vehicles, and gives the objective function and constraints under different phase schemes. The cycle length was calculated by the formula of Webster [10], and the objective function simultaneously pursued the smallest average vehicle delay and largest traffic capacity. In order to unify the dimensions and facilitate the solution, this study expresses the minimal average vehicle delay as the ratio of the optimized vehicle delay to the current vehicle delay, and the maximal capacity is expressed as the reciprocal of the ratio of the optimized capacity to the current capacity. The objective function is as follows:
where di is the average vehicle delay in flow direction i (s), qi is the traffic volume in flow direction i (pcu), D0 is the traffic capacity under current signal timing plan (pcu/h), si is the saturated flow in flow direction i (pcu/h), gei is the effective green time in flow direction i (s), c is the cycle length (s), 1 is the weight coefficient of the average vehicle delay, and 2 is the weight coefficient of the capacity. The traffic engineer can decide the weight coefficient according to the actual operating conditions of the intersection. In this study, 1 = 2/3 and 2 = 1/3 were chosen.
Average vehicle delay di was calculated with the Webster model [30], which is as follows:
where yi is the flow ratio in flow direction i, which equals to saturated flow dividing qi [10].
In the constraints, this study considers the length of queued vehicles, which is shown in Equation (17).
where H is the distance between the upstream and downstream intersections (m), and Lmax is the longest queue length calculated in Formula (13). Incorporating Equation (13) into Equation (17) is shown as Equation (18).
The basic constraints for signal timing are as follows:
where gi is the green time in flow direction i (s), A is the yellow time (s), li is the starting loss time in flowing direction i (s), gi(min) is the minimal green time in flow direction i (s), and gi(max) is the maximal green time in flow direction i (s).
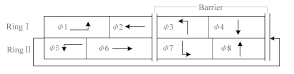
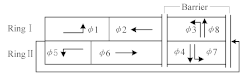
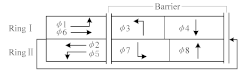
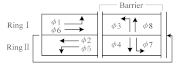
When considering the influence of phase schemes, this study adopted the NEMA phase structure [31]. Since its structure could be flexibly adjusted, such as Phases 1 and 5 shown in Table 1, it has better adaptability to different traffic situations.

Table 1.
Phase schemes.
The objective function and constraints under different phase schemes are shown in Table 2.

Table 2.
Objective function and constraints.
5. Solving Algorithm for the Optimization Model
The maximal green time calculation model is a nonlinear integer optimization model. For this model, there are many variables, and each variable must meet certain constraints. It is very difficult to apply traditional optimization methods to solve the problem, and heuristic algorithms are generally used. The more widely used methods are the genetic, simulated annealing, and particle swarm algorithms. Among them, the genetic algorithm has the advantages of good robustness and global search ability. Therefore, this study uses the genetic algorithm to solve the maximal green time calculation model [32].
5.1. Variable Coding
Since green time generally does not exceed two digits, the chromosome length of 16 consisting of 8 loci was chosen.
5.2. Fitness Function
When the optimization problem is a minimization problem, the fitness function takes the opposite value of the objective function. Therefore, this study takes −Z as the fitness function.
5.3. Genetic Manipulation
The manipulation procedures include selection, crossover, and mutation. The specific steps are as follows:
Step 1: Initialization. Set population number (100), chromosome length (16), number of iterations (800), crossover probability (0.8), mutation probability (0.001), and roulette selection operator.
Step 2: use real encoding to assign values to the parameters, and randomly generate 100 individuals that meet the constraints as the initial group.
Step 3: calculate the objective function and fitness value of each individual.
Step 4: perform selection operations on all individuals and select a new population.
Step 5: perform crossover operations on random paired individuals according to crossover probability.
Step 6: perform mutation operations on individuals according to mutation probability.
Step 7: if number of iterations g = 800, the individual with the best fitness is taken as the optimal solution output, and the algorithm can be terminated.
6. Verification
6.1. Verification of Minimal Green Time Calculation Model
In order to verify the calculation accuracy of the minimal green time calculation model, a VISSIM simulation experiment was designed as shown in Figure 4.

Figure 4.
Simulation settings.
Taking a signal lane as the research object, two data collection detectors were set at the stop line and distance L to collect parameters. The traffic volume input was set to be 800 pcu/h, the speed distribution was 40 and 50 km/h, and 25 s was set as the vehicle release time every 30 s. The control group was the minimal green time calculation model provided in the 2010 Highway Capacity Manual (HCM), which is as follows:
Taking the queue length L = 55 m as an example, the statistics of 30-period simulations are shown in Table 3.

Table 3.
Simulation results of 55m queue length.
In order to intuitively reflect the difference between the simulated and calculated values, the result was drawn as a scatter diagram, as shown in Figure 5.
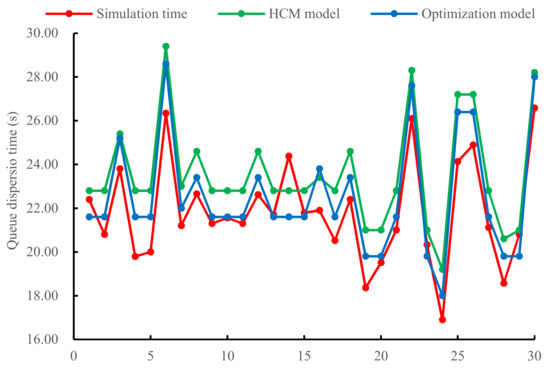
Figure 5.
Scatter plot of simulated and calculated values.
The figure shows that the minimal green time calculation model proposed in this paper was closer to the simulated value, while the traditional HCM calculation model had larger calculation errors.
A 30-period simulation was conducted for queue lengths L of 25, 35, 45, 55, and 65 m, and the simulation results are shown in Table 4.

Table 4.
Simulation results under different queue lengths.
Since we used the improved traffic wave model to calculate the queue length, the table shows that the minimal green time calculation model proposed in this paper (4.18% average relative error) was more accurate than the traditional HCM calculation model (10.44% average relative error) under different queue lengths, which verified the effectiveness and accuracy of the model.
6.2. Verification of Maximal Green Time Calculation Model
It was assumed that each flow direction of the intersection was released at the maximal green time, and this study did not consider the influence of the maximal green time on the overall control effect. Information of a certain intersection is shown in Table 5.

Table 5.
Intersection information.
We assumed that yellow time A = 3 s, all red period r = 1 s, and starting loss time l = 2 s. Two sets of experiments were designed as follows: (a) calculation results of traditional Webster method (traditional model); (b) calculation results of the maximal green time calculation model proposed in this paper (optimization model). The objective function and constraints were input into MATLAB, and the maximal green time of each flow direction was obtained as shown in Table 6.

Table 6.
Solution results.
Table 7 shows the optimization results of average vehicle delay and capacity under different phase schemes.

Table 7.
Optimization results of average delay and capacity.
We can see from the table that, under phase schemes F1, F2, and F3, the optimization ratios all exceeded 10%. Under phase scheme F4, since there were only two green time parameters that could be adjusted, it also had an optimization ratio of 2.10%. Thus, the maximal green time calculation model established in this paper could effectively reduce the average vehicle delay and improve traffic capacity (9.27% average optimization ratio), which verified the effectiveness of the model.
7. Conclusions
Compared with previous studies, this paper focused on the influence of queued vehicles, and two basic control parameters, namely, the minimal and maximal green times, were optimized to achieve a better control effect. Through this study, more reasonable control parameters could be obtained to avoid green loss, reduce vehicle delay, and improve traffic operation sustainability.
The main contributions of this paper are as follows: (a) According to the relationship between basic traffic flow parameters, an improved traffic wave model was established. Then, by analyzing the vehicle-queuing process, a vehicle-queuing model was proposed. (b) By analyzing the queuing and dispersion process of queued vehicles, a minimal green time calculation model was established. Through simulation, the average error between calculation and simulation values was 4.18%, verifying the model’s accuracy. (c) The maximal green time calculation model with the objective function of minimizing the average vehicle delay and maximizing traffic capacity under different phase schemes was established. The influence of queued vehicles was considered in the constraints, and the a genetic algorithm solution process was given. Through calculation, the average optimization rate was 9.27%, verifying its effeteness.
In summary, this paper proposed two basic parameter optimization models of actuated control, and verifications successfully proved their validity of improving green time utilization, reducing vehicle delay, and enlarging traffic capacity, which is essential for improving traffic sustainability.
Author Contributions
Conceptualization, J.L.; data curation, X.W. (Xinyue Wang); formal analysis, X.W. (Xinyue Wang); funding acquisition, X.W. (Xianyu Wu); methodology, X.W. (Xinyue Wang); project administration, X.W. (Xianyu Wu); resources, J.L.; supervision, X.W. (Xianyu Wu); writing—original draft, J.L.; writing—review and editing, X.W. (Xianyu Wu). All authors have read and agreed to the published version of the manuscript.
Funding
This research was supported by the Fundamental Research Funds for the Central Universities (no. 2022JBZY005).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data used to support the findings of this study are included within the article.
Conflicts of Interest
The authors declare that they have no conflict of interest.
References
- Downs, A. The law of peak-hour expressway congestion. Traffic 1962, 33, 347–362. [Google Scholar]
- Wang, Z.L. Multimodal Traffic Adaptive Signal Control Based on Deep Reinforcement Learning. Ph.D. Thesis, Southeast University, Nanjing, China, 2021. [Google Scholar]
- Han, Y. Research on Signal Optimization in Controlled Intersections Based on Deep Reinforcement Learning. Master’s Thesis, Beijing Jiaotong University, Beijing, China, 2021. [Google Scholar]
- Liu, J.J.; Zuo, X.Q. Research on fuzzy control and optimization for traffic lights at signal intersection. J. Syst. Simul. 2020, 32, 2401–2408. [Google Scholar]
- Xing, Y.; Hao, Y.Q.; Gao, Z.J.; Liu, W.D.; Li, Z.Z. Signal timing optimization of signal intersection based on fuzzy logic. China Sci. Pap. 2021, 16, 890–894. [Google Scholar]
- Cao, Y. Optimization of adaptive signal control using simulated annealing algorithm. J. Transp. Eng. Inf. 2018, 16, 49–55+60. [Google Scholar]
- Yan, L.P.; Zhang, M.K.; Guo, C.Y.; Zhu, L.L. Real time multi-intersection signal control based on quantum particle swarm optimization. Comput. Simul. 2021, 38, 180–184. [Google Scholar]
- AMAP. 2020 Traffic Analysis Report of China’s Major Cities. 2020. Available online: https://recordtrend.com/research-report/2020-traffic-analysis-report-of-major-cities-in-china-from-gaud-map/ (accessed on 16 November 2021).
- Zhou, T.M. Research on optimal design of intersection actuated signal control. J. Chin. People’s Public Secur. Univ. 2001, 2, 34–37. [Google Scholar]
- Webster, F.V. Traffic signal settings. In Road Research Technical Paper; HM Stationery Office: London, UK, 1958. [Google Scholar]
- Pappis, C.P.; Mamdani, E.H. A fuzzy logic controller for a traffic junction. IEEE Trans. Syst. Man Cybern. 1977, 7, 707–717. [Google Scholar] [CrossRef]
- Murat, Y.S.; Gedizioglu, E. A fuzzy logic multi-phase signal control model for isolate junctions. Transp. Res. Part C 2005, 13, 19–36. [Google Scholar] [CrossRef]
- Cowan, R. An improved model for signalized intersections with vehicle-actuated control. J. Appl. Probab. 1978, 15, 384–396. [Google Scholar] [CrossRef]
- Akcelik, R. Estimation of green times and cycle time for vehicle-actuated signals. Transp. Res. Rec. J. Transp. Res. Board 1994, 1457, 63–72. [Google Scholar]
- Furth, P.; Cesme, B.; Muller, T. Lost time and cycle length for actuated traffic signal. Transp. Res. Rec. J. Transp. Res. Board 2009, 2128, 152–160. [Google Scholar] [CrossRef] [Green Version]
- Viti, F.; van Zuylen, H.J. A Probabilistic model for traffic at actuated control signals. Transp. Res. Part C 2010, 8, 299–310. [Google Scholar] [CrossRef]
- Moghimi, B.; Safikhani, A.; Kamga, C.; Hao, W. Cycle-length prediction in actuated traffic-signal control using ARIMA model. J. Comput. Civ. Eng. 2018, 32, 04017083. [Google Scholar] [CrossRef]
- Shiri, M.; Maleki, H. Maximum green time settings for traffic-actuated signal control at isolated intersections using fuzzy logic. Int. J. Fuzzy Syst. 2017, 19, 247–256. [Google Scholar] [CrossRef]
- Jing, T. Research on Optimization of Single Intersection Actuated Control under Stochastic Conditions. Master’s Thesis, Lanzhou Jiaotong University, Lanzhou, China, 2014. [Google Scholar]
- Hao, P.; Wu, G.; Boriboonsomsin, K.; Barth, M.J. Developing a framework of eco-approach and departure application for actuated signal control. In Proceedings of the 2015 IEEE Intelligent Vehicles Symposium (IV), Seoul, Korea, 28 June–1 July 2015. [Google Scholar]
- Bao, L.J. Traffic Signal Actuation Strategy Based on RFID. Master’s Thesis, Shanghai Institute of Technology, Shanghai, China, 2016. [Google Scholar]
- Jauregui, C.; Torres, M.; Silvera, M.; Campos, F. Improving people’s accessibility through a fully actuated signal control at intersections with high density of pedestrians. In Proceedings of the 2020 Congreso Internacional de Innovación y Tendencias en Ingeniería (CONIITI), Bogota, Colombia, 30 September–2 October 2020. [Google Scholar]
- Wang, M.; Zhang, Y.; Ding, H. Research on real-time actuated signal control of intersection based on Internet of things technology. J. Gansu Sci. 2021, 33, 98–103. [Google Scholar]
- Wu, X.; Adhikari, B.; Chiu, S.; Yang, H.; Sajjadi, S.; Roy, U. Volume-occupancy-based actuated signal control system: Design and implementation to diamond interchanges in Houston. Int. J. Civ. Eng. 2022, 20, 337–348. [Google Scholar] [CrossRef]
- Gartner, N.H.; Messer, C.J.; Rathi, A.K. Revised Monograph on Traffic Flow Theory: A State-of-the-Art Report; The Federal Highway Administration (FHWA): Washington, DC, USA, 2005. [Google Scholar]
- Zhang, H.M. A theory of nonequilibrium traffic flow. Transp. Res. Part B 1998, 32, 485–498. [Google Scholar] [CrossRef]
- Lighthill, M.J.; Whitham, G.B. On kinematic waves I: Flow movement in long rivers. Proc. R. Soc. London. Ser. A Math. Phys. Sci. 1995, 229, 281–316. [Google Scholar]
- Lighthill, M.J.; Whitham, G.B. On kinematic waves II: A theory of traffic flow on long crowded roads. Proc. R. Soc. London. Ser. A Math. Phys. Sci. 1995, 22, 317–345. [Google Scholar]
- Xu, H.F.; Liu, S.; Zhang, D.; Zheng, Q.M. Configuring parameters of fully actuated control at isolated signalized intersections. J. Jilin Univ. Eng. Technol. Ed. 2019, 49, 45–52. [Google Scholar]
- Feng, S.L. Research on Signal Timing Optimization of Isolated Intersection Based on Multi-Phase Variable Phase Sequence. Master’s Thesis, Lanzhou Jiaotong University, Lanzhou, China, 2014. [Google Scholar]
- NEMA. NEMA Standards Publication TS-2; NEMA: Nairobi, Kenya, 2003. [Google Scholar]
- Cao, C.T.; Xu, J.M. Multi-object traffic signal control method for single intersection. Comput. Eng. Appl. 2010, 46, 20–22. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).