Research on Control of Levitation Force and Torque of a Maglev Device for Water-Turbine Generator Set
Abstract
:1. Introduction
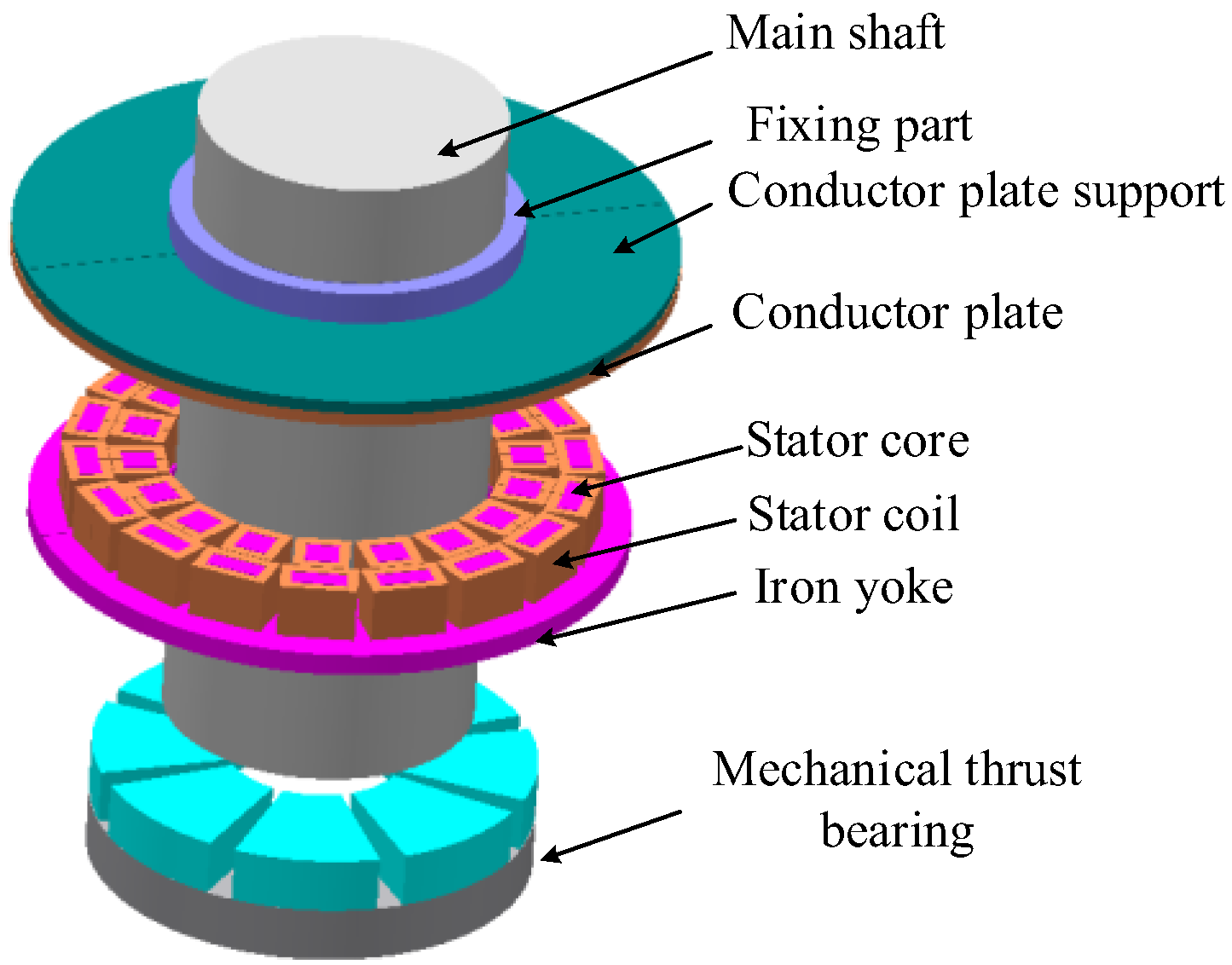
2. Structure and Principle of the Maglev Device
3. Torque Offsetting Design
4. Calculation and Relationship of the Levitation Force and Torque
4.1. Analytic Calculation of the Levitation Force and Torque
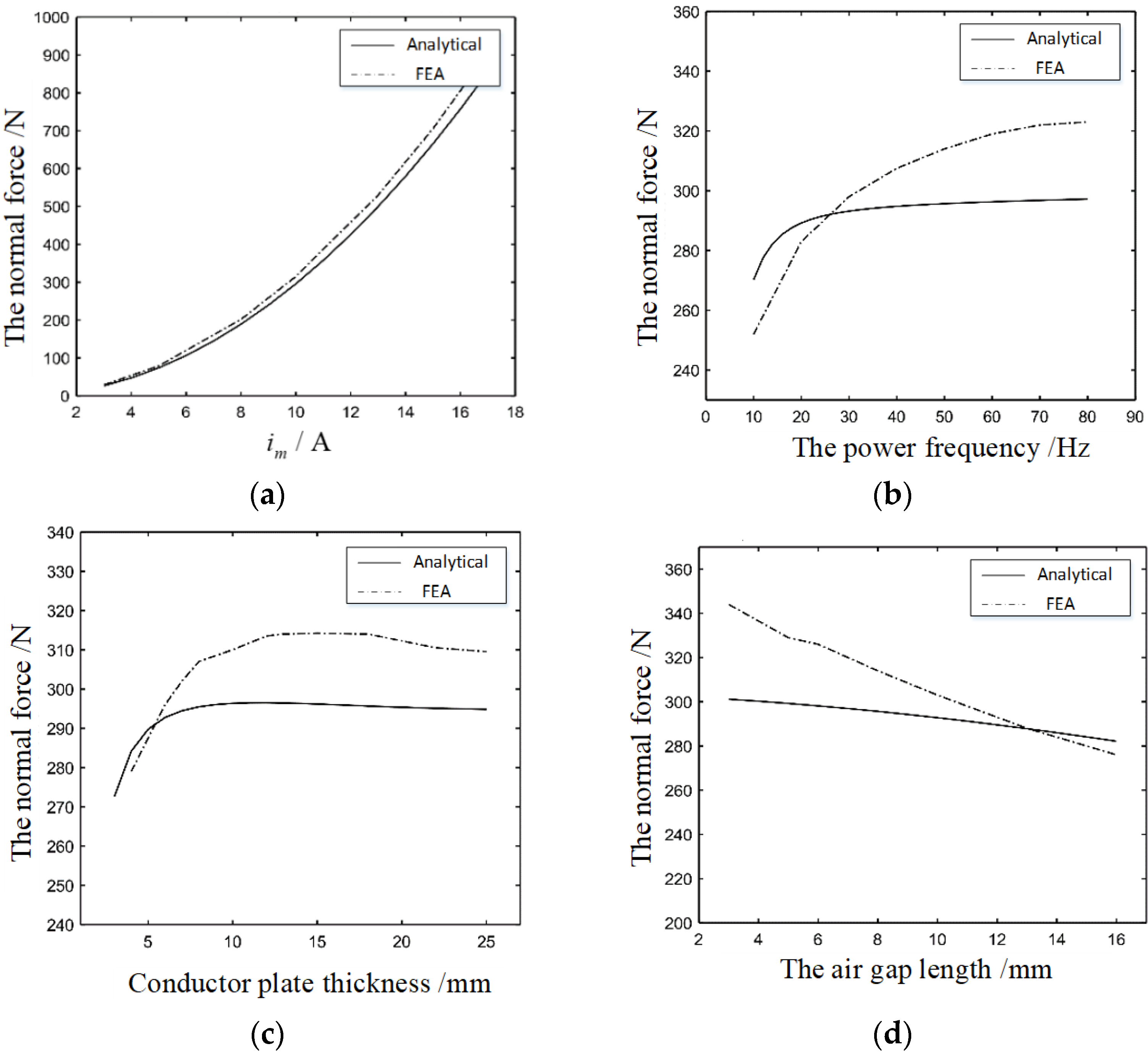
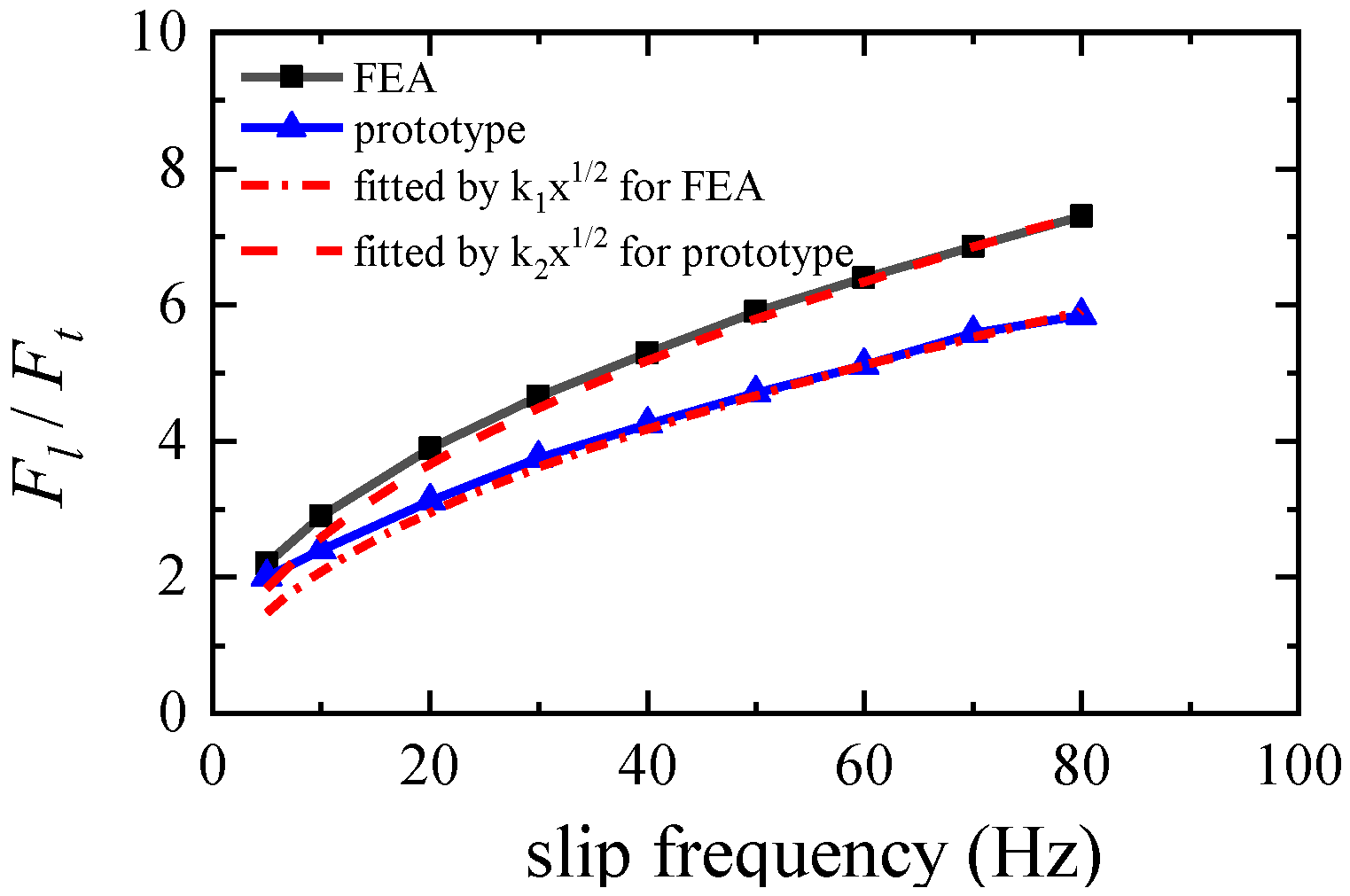
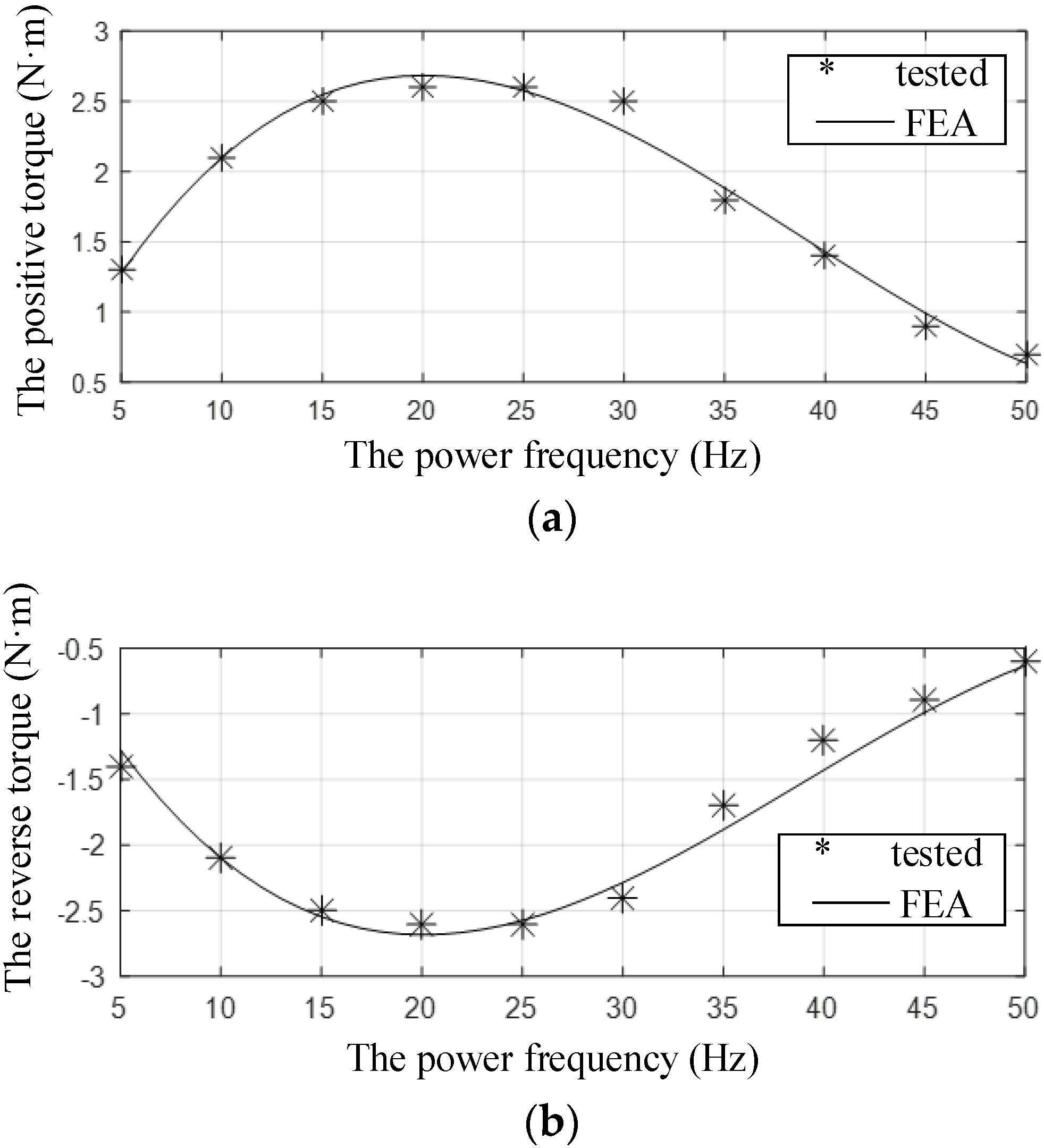
4.2. Relationship of the Levitation Force and Torque
5. Control of the Normal Force and the Torque
5.1. Dynamic Mathematical Model of the Torque
5.2. Dynamic Mathematical Model of the Normal Lift Force
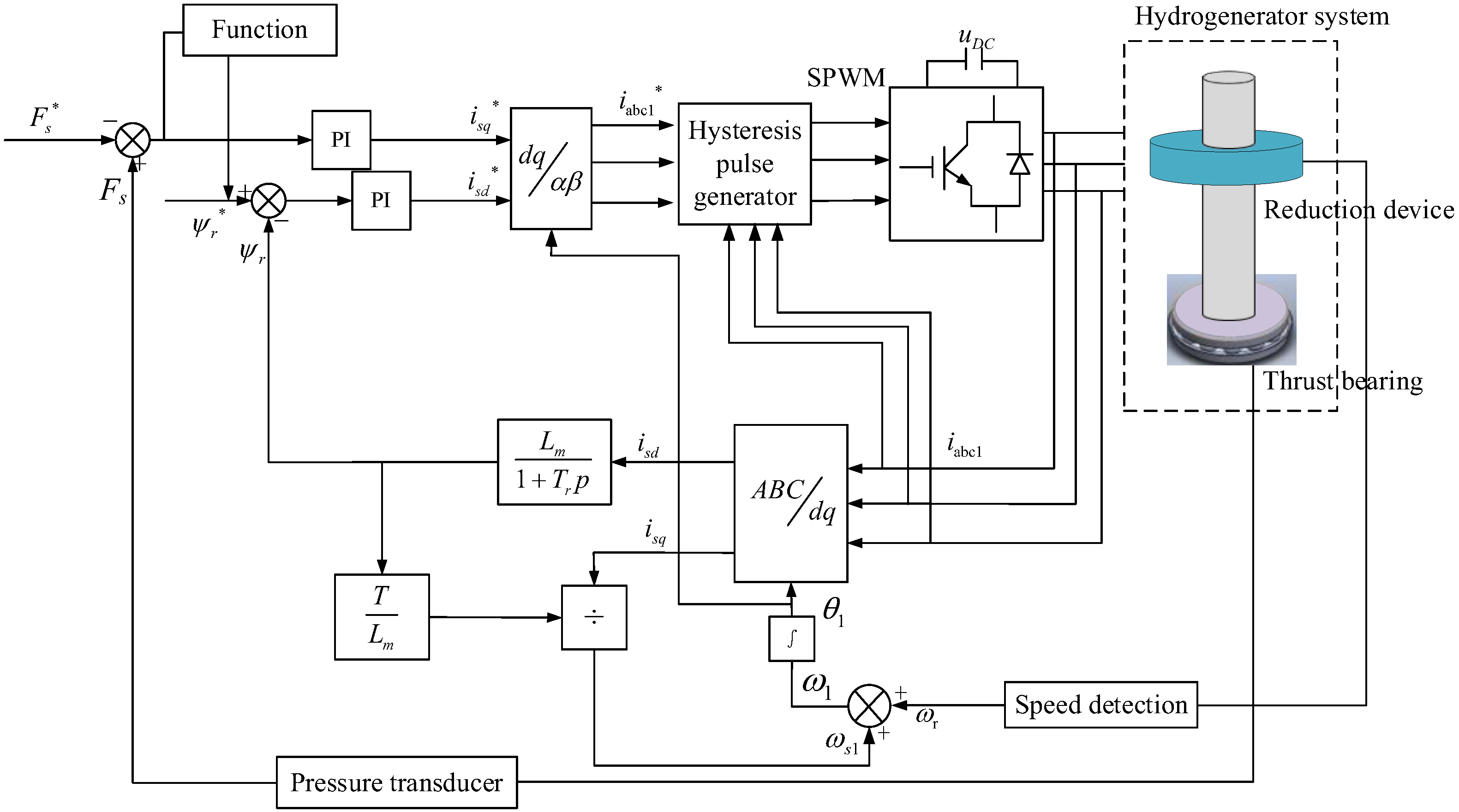
5.3. Control Strategy of the Normal Force and the Torque
6. Simulation and Experimental Verification of Control Strategy
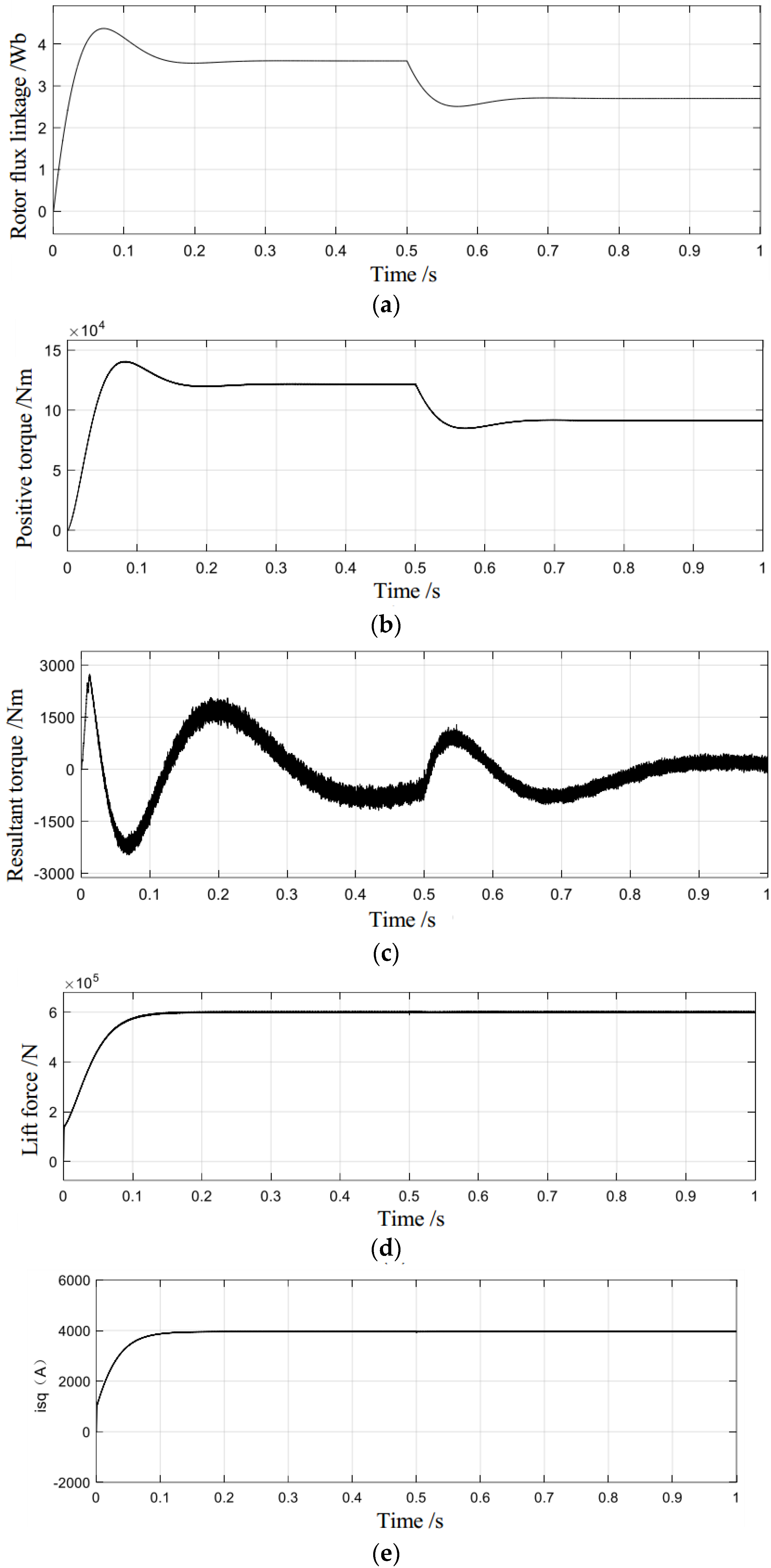
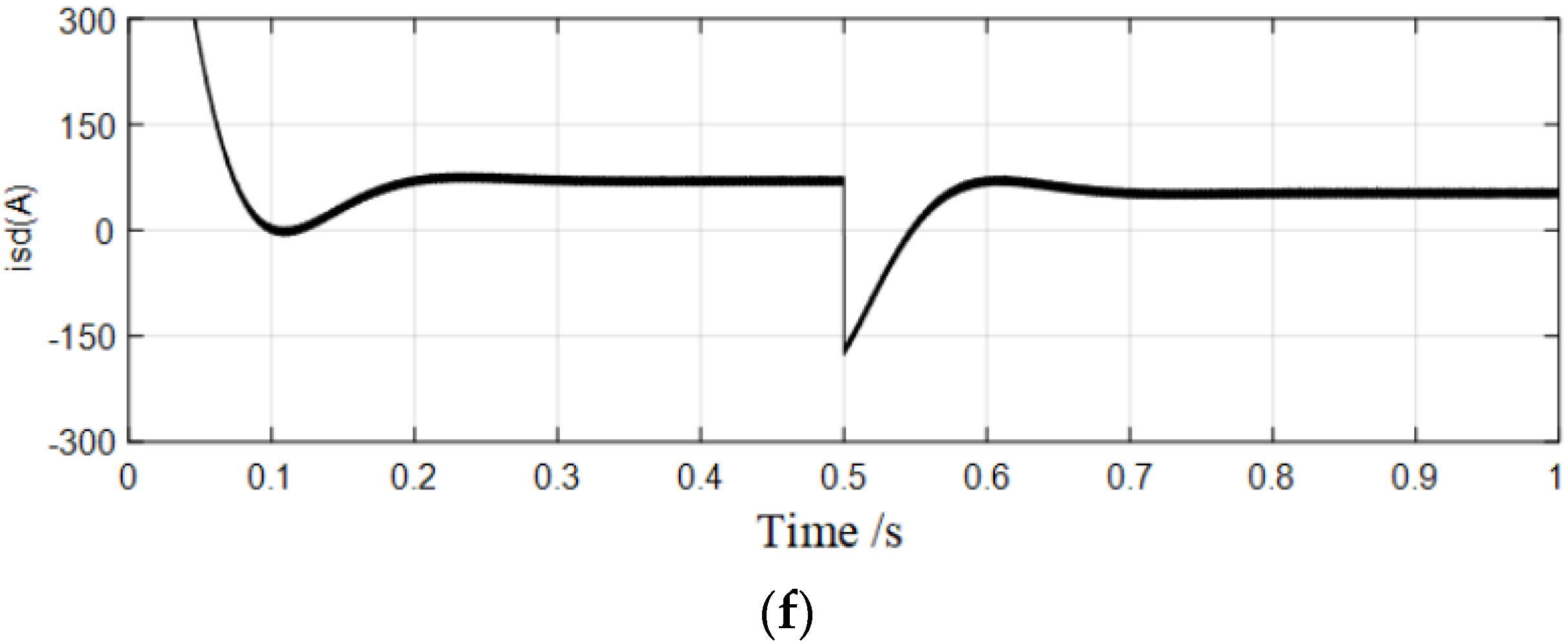
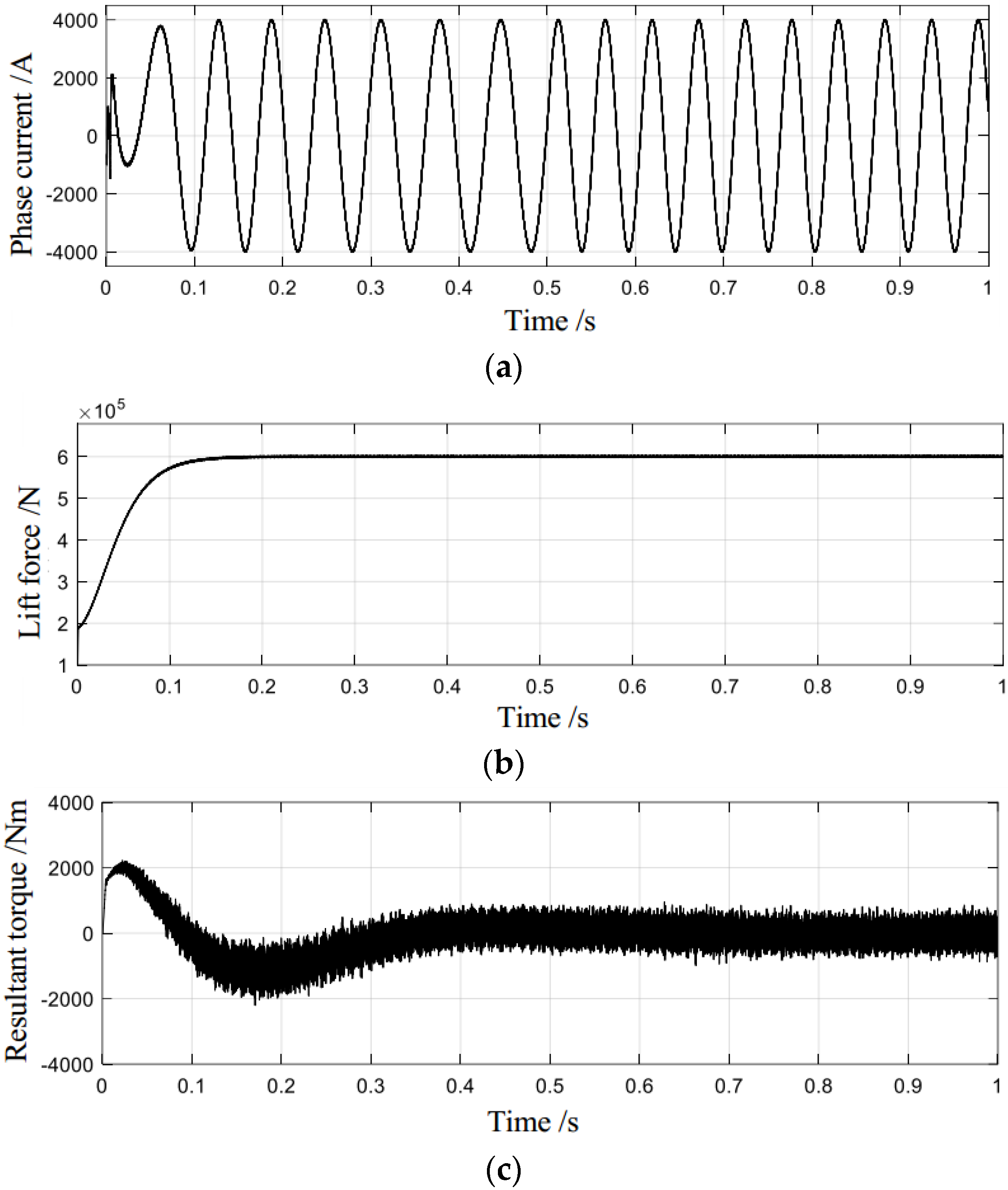
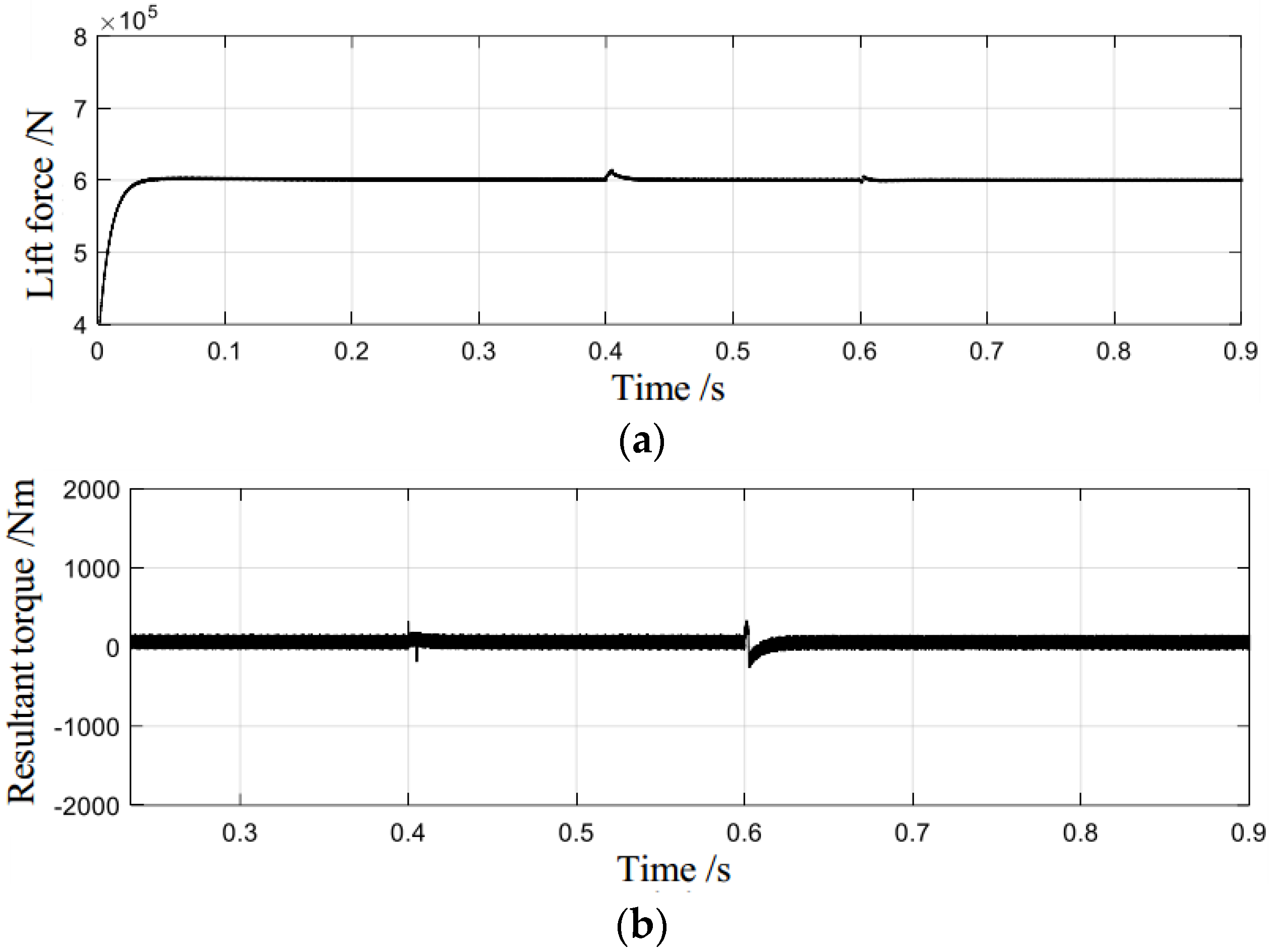
6.1. Simulation Verification of Control Strategy
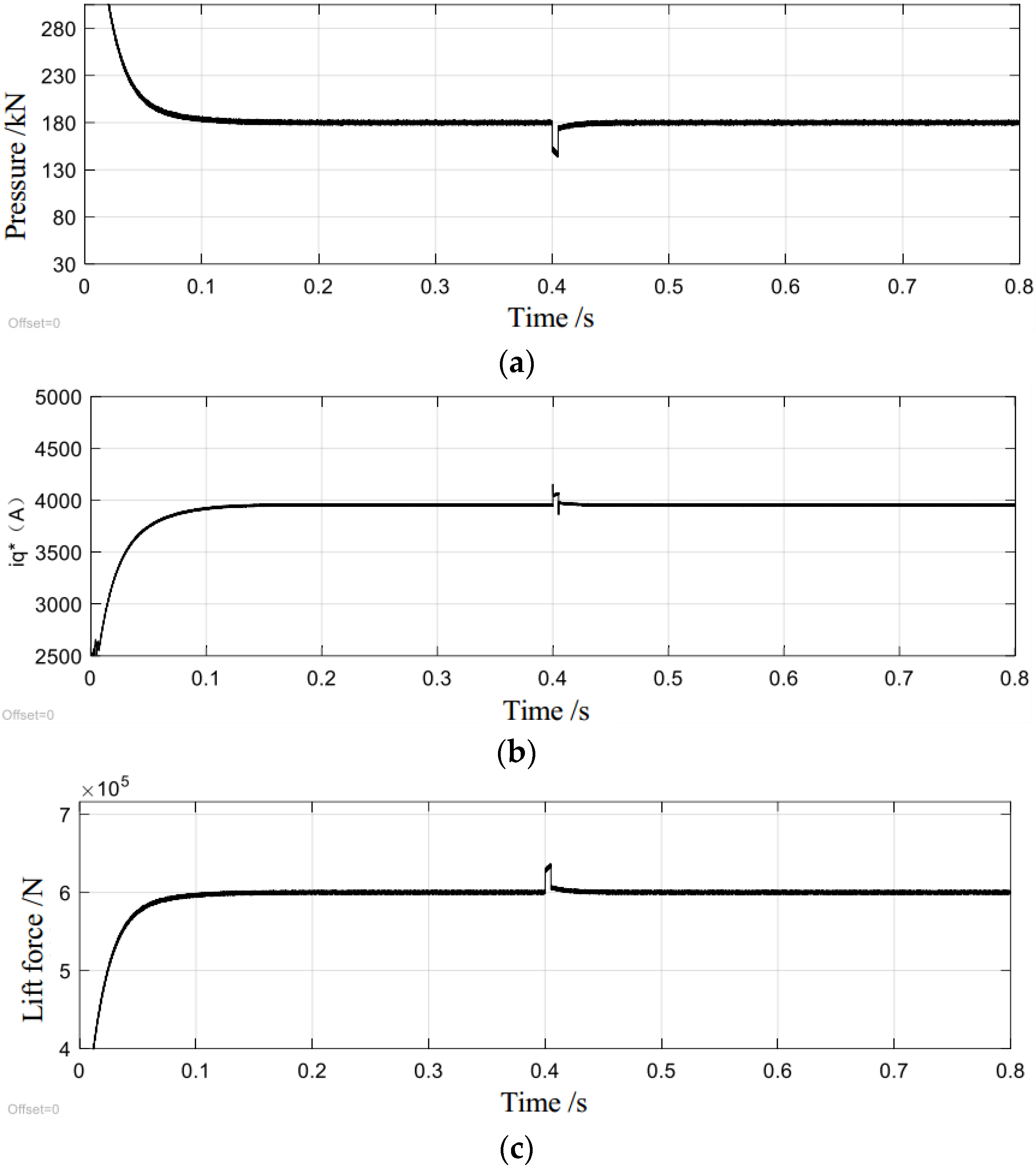
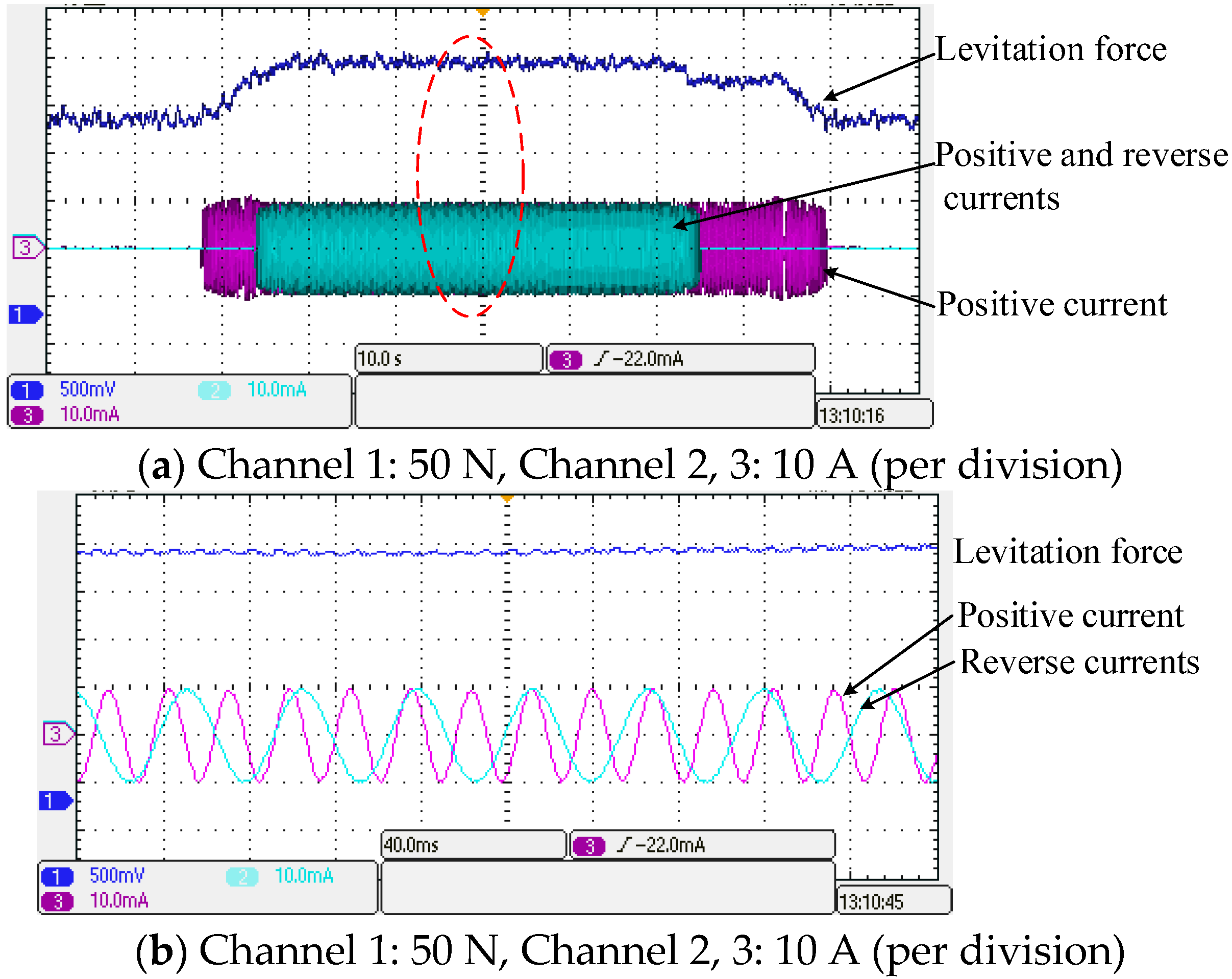
6.2. Experimental Verification of Control Strategy
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- National Energy Administration of China. Notification on the Completion of the Duty Weighting of Renewable Energy Electricity Consumption; National Energy Administration of China: Beijing, China, 2021.
- Chen, Y.Q.; Hu, W.M. New progress in research on 1000MW hydropower unit. Electr. Power Constr. 2011, 32, 62–66. [Google Scholar]
- Liu, Q.Y.; Fu, Y.C.; Wu, Z.D. Thrust bearing tile temperature of large hydraulic generator. Large Electr. Mach. Hydraul. Turbine 2010, 4, 14–15. [Google Scholar]
- Yu, K.S. Discussion on thrust bearing support structure and principle of hydrogenator. Mech. Electr. Tech. Hydropower Stn. 1996, 1, 1–7. [Google Scholar]
- Liu, J.; Ma, H.Z.; Zhang, Q.; Zhang, L.J.; Cai, B.P. Design and optimization of a magnetic levitation load reduction device for a hydropower unit. IEEE Access 2021, 9, 32019–32029. [Google Scholar] [CrossRef]
- Liu, J.; Wang, R.B.; Hu, J.L.; Zhang, Q.; Ma, H.Z.; Zhang, L.J.; Cai, B.P. Study on Improving the Levitation Force for a Maglev Load Reduction Machine. IEEE Trans. Appl. Supercond. 2021, 31, 4400805. [Google Scholar] [CrossRef]
- Morizane, T.; Tsujikawa, K.; Kimura, N. Control of Traction and Levitation of Linear Induction Motor Driven by Power Source with Frequency Component Synchronous with the Motor Speed. IEEE Trans. Magn. 2011, 47, 4302–4305. [Google Scholar] [CrossRef]
- Ghosh, M.K.; Gao, Y.; Dozono, H.; Muramatsu, K.; Guan, W.; Yuan, J.; Tian, C.; Chen, B. Proposal of Maxwell Stress Tensor for Local Force Calculation in Magnetic Body. IEEE Trans. Magn. 2018, 54, 7206204. [Google Scholar] [CrossRef]
- Long, X.L. Theory and Magnetic Design Method of Linear Induction Motor; Science: Beijing, China, 2006. [Google Scholar]
- Burnham, D.C. Asymptotic Lift to Drag Ratios for Magnetic Suspension Systems. J. Appl. Phys. 1971, 42, 3455–3457. [Google Scholar] [CrossRef]
- Gang, L. Research on Decoupling Optimal Control of Linear Induction Motor; Beijing Jiaotong University: Beijing, China, 2007; pp. 84–135. [Google Scholar]
- Reitz, J.R.; Davis, L.C. Force on a Rectangular Coil Moving above a Conducting Slab. J. Appl. Phys. 1972, 43, 1547–1553. [Google Scholar] [CrossRef]
- Wang, H.; Bao, J.; Xue, B.; Liu, J. Control of Suspending Force in Novel Permanent-Magnet-Biased Bearingless Switched Reluctance Motor. IEEE Trans. Ind. Electron. 2015, 62, 4298–4306. [Google Scholar] [CrossRef]
- Li, X.; Wang, X.; Gao, P.; Gu, Y. Model Predictive Current Control Algorithm Based on Joint Modulation Strategy for Low-Inductance PMSM. IEEE Trans. Power Electron. 2022, 37, 806–819. [Google Scholar] [CrossRef]
- Cruz, S.M.A.; Marques, G.D.; Gonçalves, P.F.C.; Iacchetti, M.F. Predictive Torque and Rotor Flux Control of a DFIG-DC System for Torque Ripple Compensation and Loss Minimization. IEEE Trans. Ind. Electron. 2018, 65, 9301–9310. [Google Scholar] [CrossRef] [Green Version]
- Hao, Z.; Yu, Q.; Cao, X.; Deng, X.; Shen, X. An Improved Direct Torque Control for a Single-Winding Bearingless Switched Reluctance Motor. IEEE Trans. Energy Convers. 2020, 35, 1381–1393. [Google Scholar] [CrossRef]
- Cho, Y.; Bak, Y.; Lee, K.-B. Torque-Ripple Reduction and Fast Torque Response Strategy for Predictive Torque Control of Induction Motors. IEEE Trans. Power Electron. 2018, 33, 2458–2470. [Google Scholar] [CrossRef]



Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, J.; Xu, C.; Zhu, J.; Huang, L.; Ma, H. Research on Control of Levitation Force and Torque of a Maglev Device for Water-Turbine Generator Set. Sustainability 2022, 14, 8742. https://doi.org/10.3390/su14148742
Liu J, Xu C, Zhu J, Huang L, Ma H. Research on Control of Levitation Force and Torque of a Maglev Device for Water-Turbine Generator Set. Sustainability. 2022; 14(14):8742. https://doi.org/10.3390/su14148742
Chicago/Turabian StyleLiu, Jing, Chongwang Xu, Jinnan Zhu, Lei Huang, and Hongzhong Ma. 2022. "Research on Control of Levitation Force and Torque of a Maglev Device for Water-Turbine Generator Set" Sustainability 14, no. 14: 8742. https://doi.org/10.3390/su14148742
APA StyleLiu, J., Xu, C., Zhu, J., Huang, L., & Ma, H. (2022). Research on Control of Levitation Force and Torque of a Maglev Device for Water-Turbine Generator Set. Sustainability, 14(14), 8742. https://doi.org/10.3390/su14148742






