Novel Axial Flux-Switching Permanent Magnet Machine for High-Speed Applications
Abstract
:1. Introduction
2. Design Evaluation of Proposed 6/4 FSPM Machines
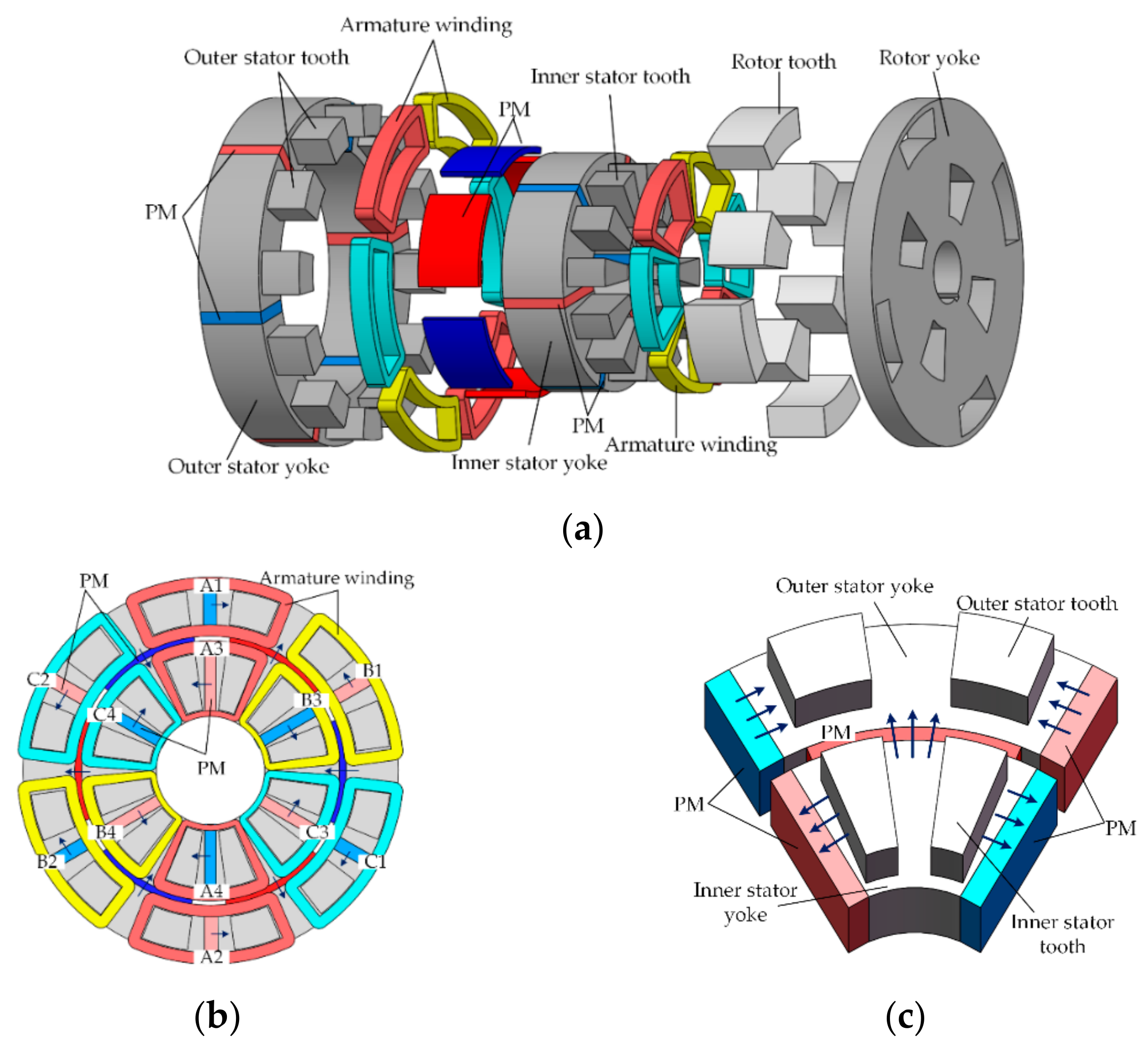
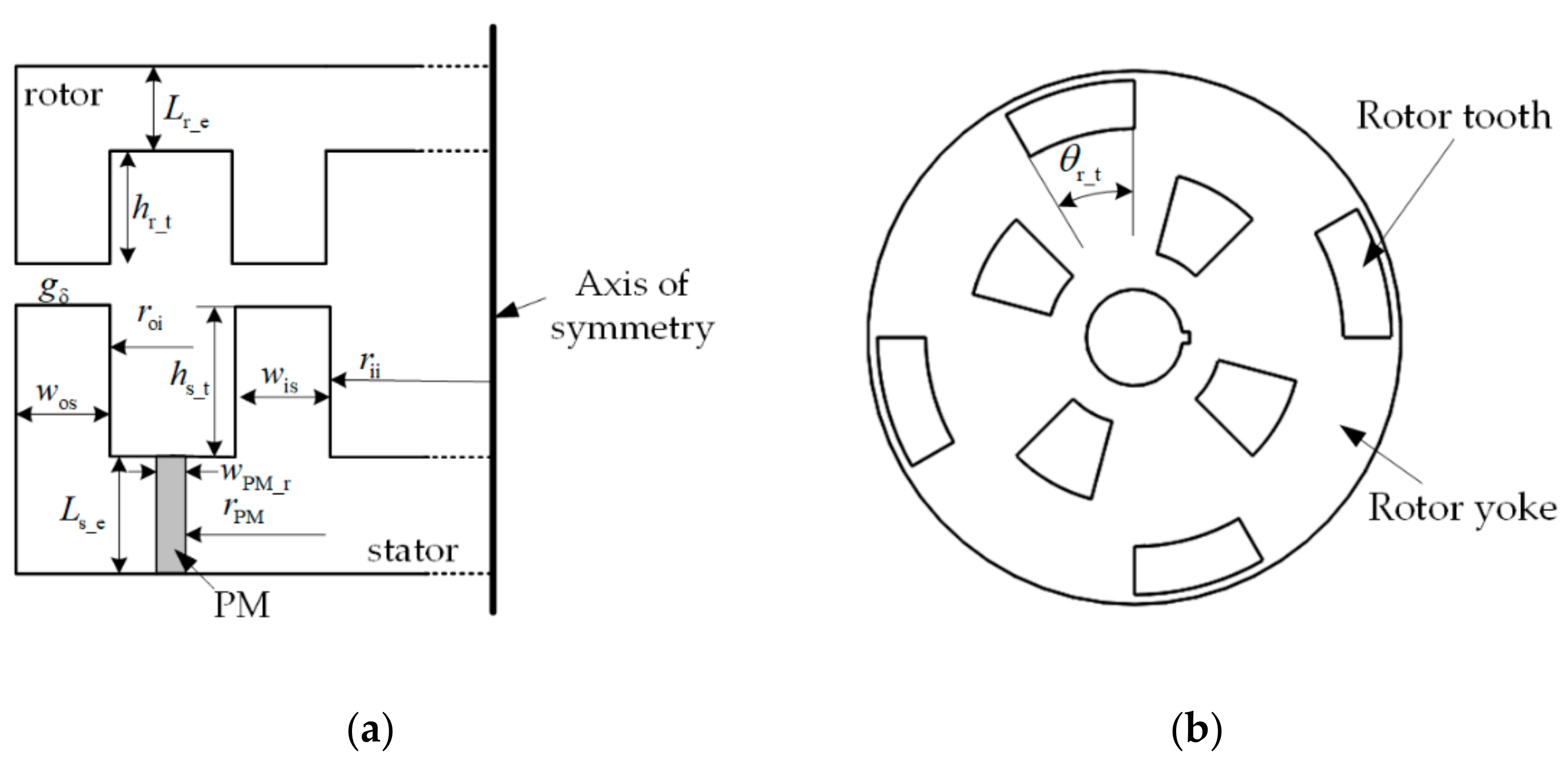
2.1. Fundamental Configuration
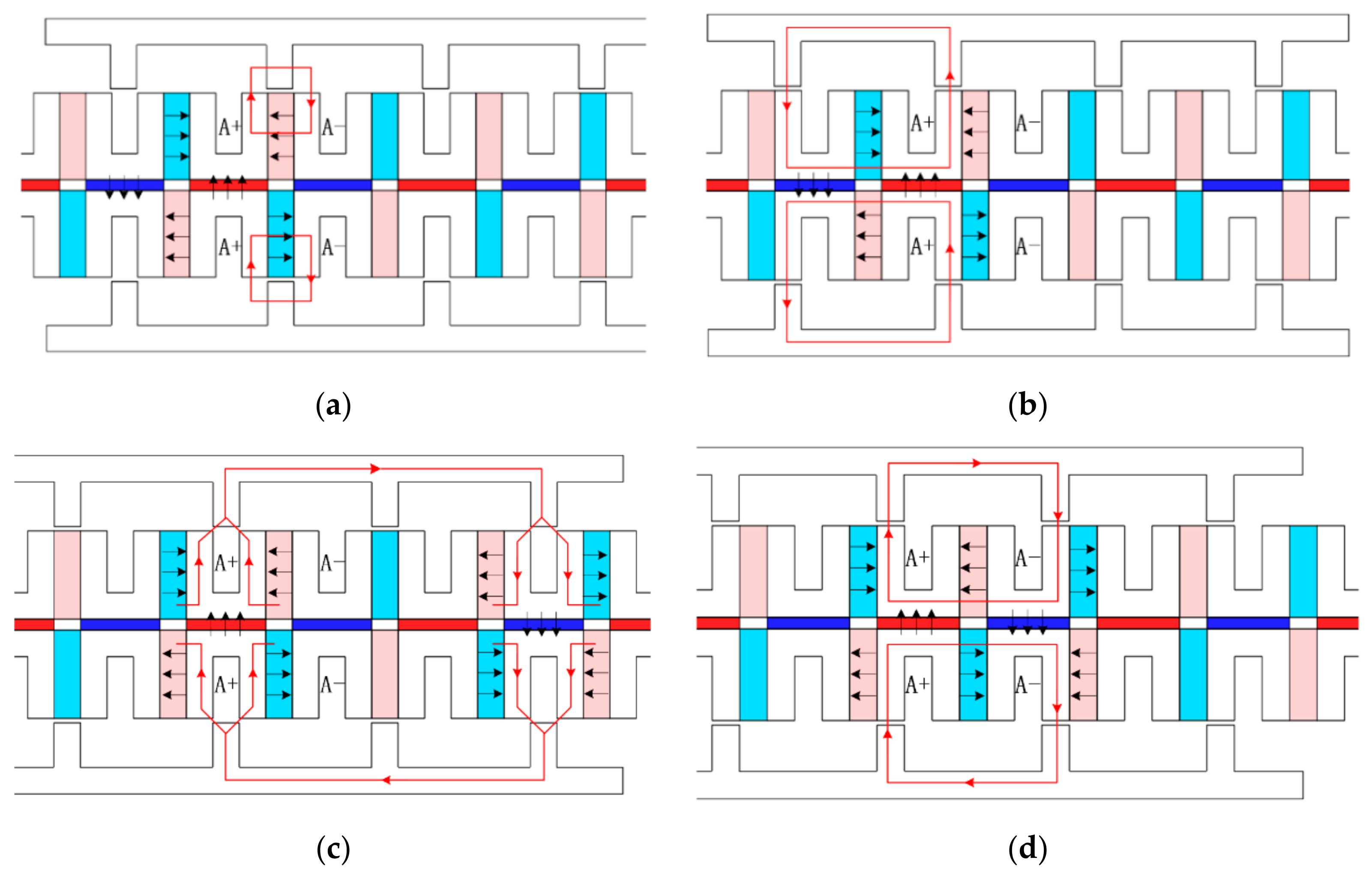
2.2. Operation Principle
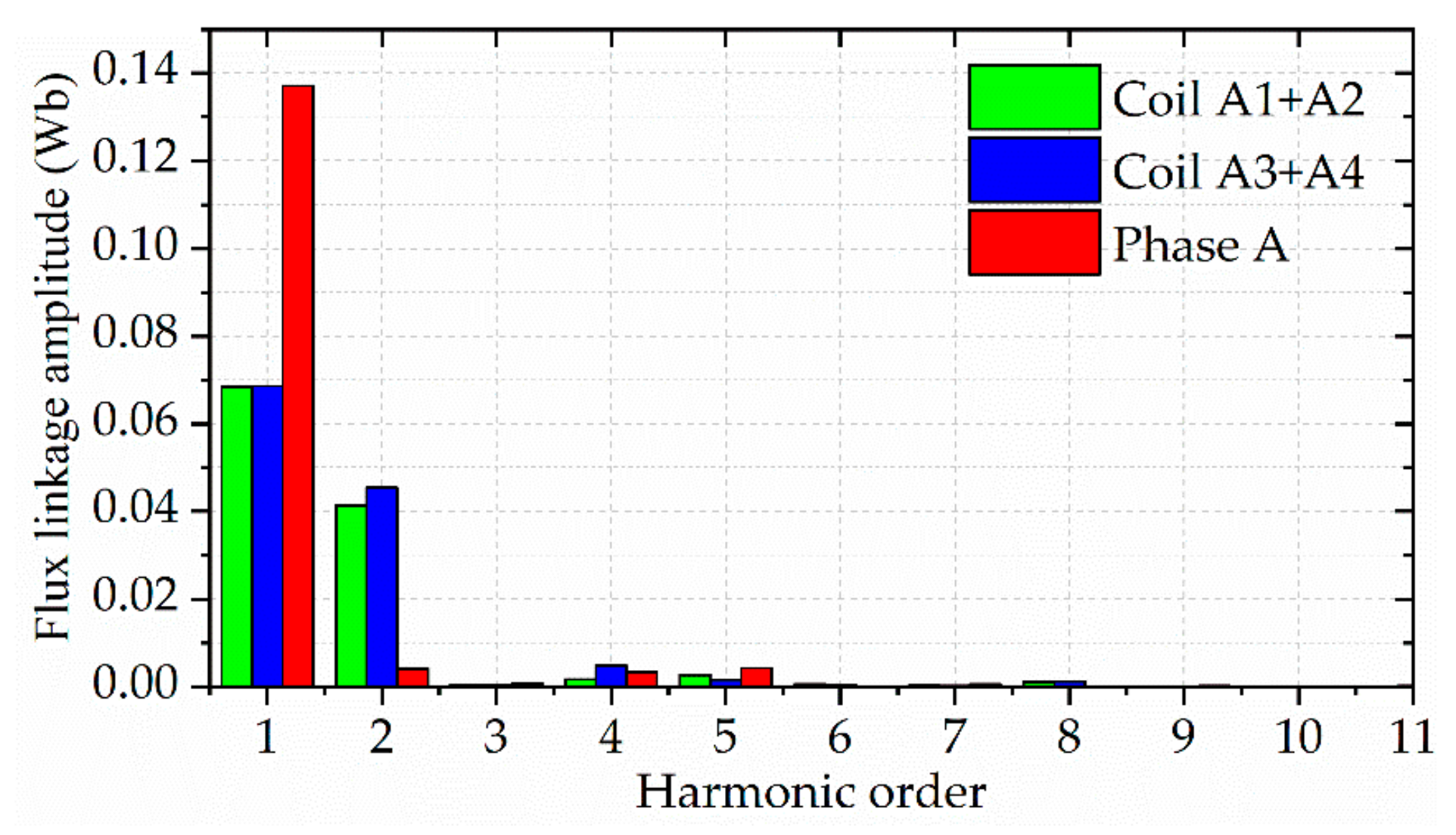
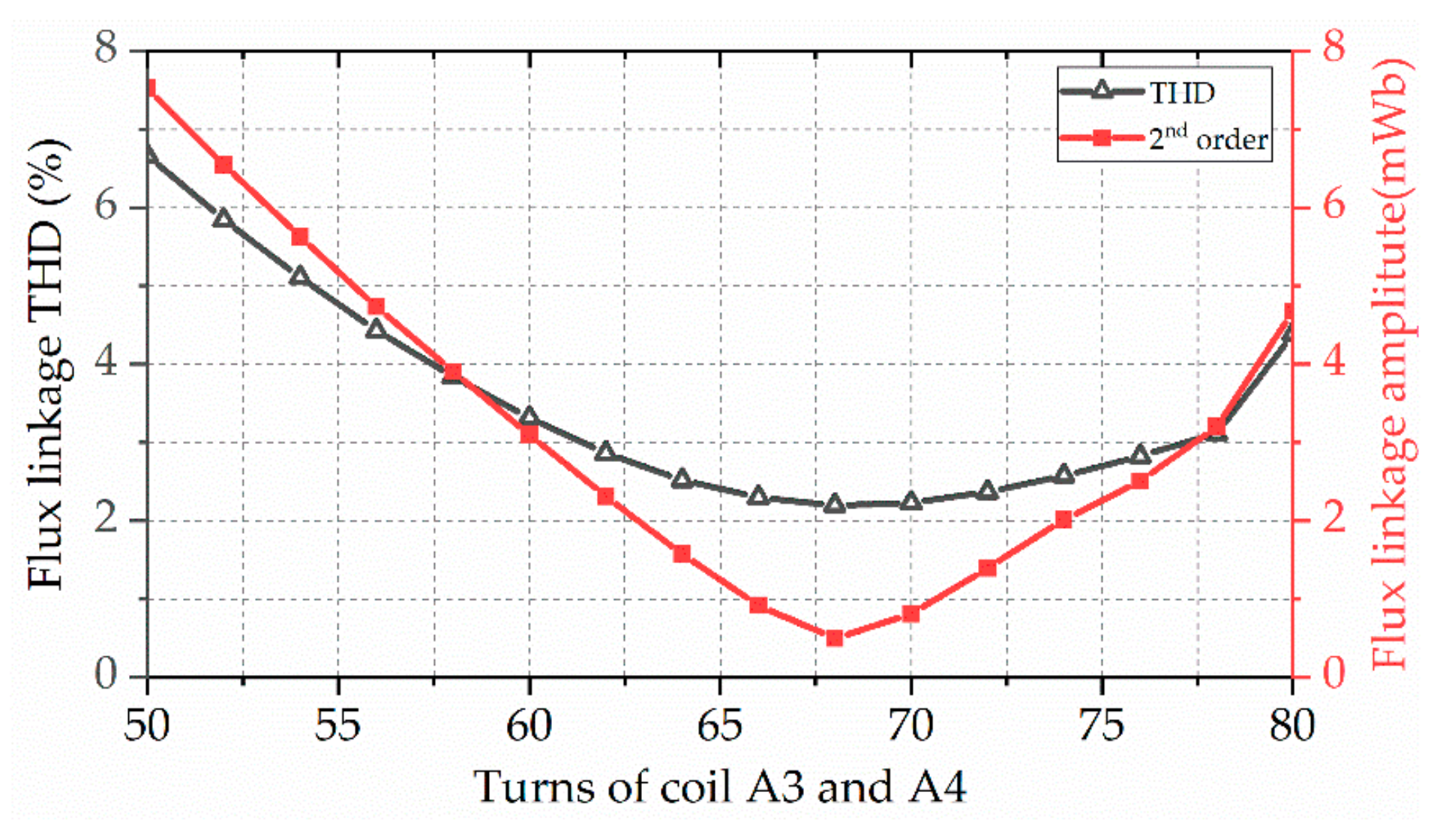
2.3. Even Harmonic Cancellation
3. Analytical Calculation of Proposed 6/4 FSPM Machine
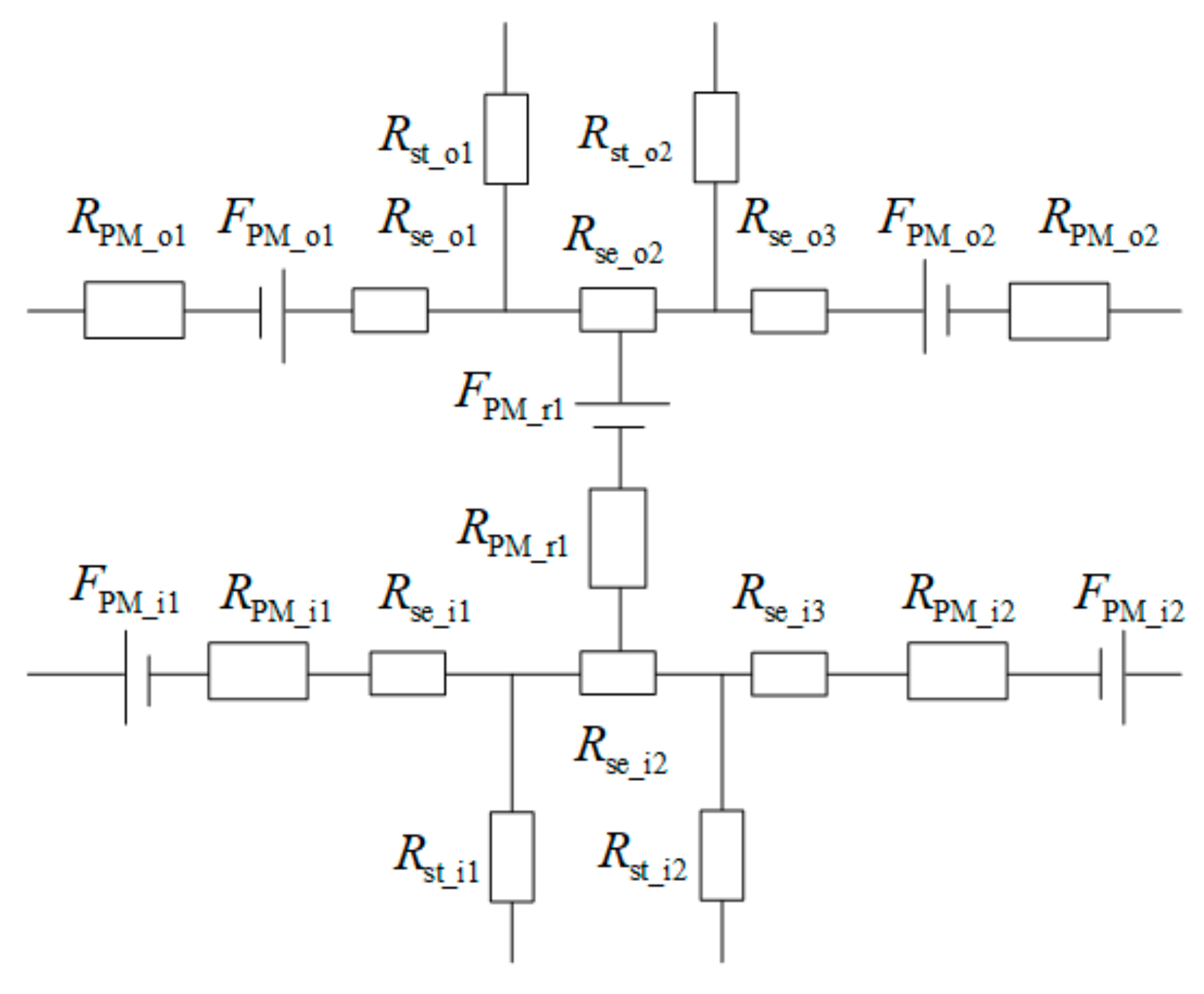
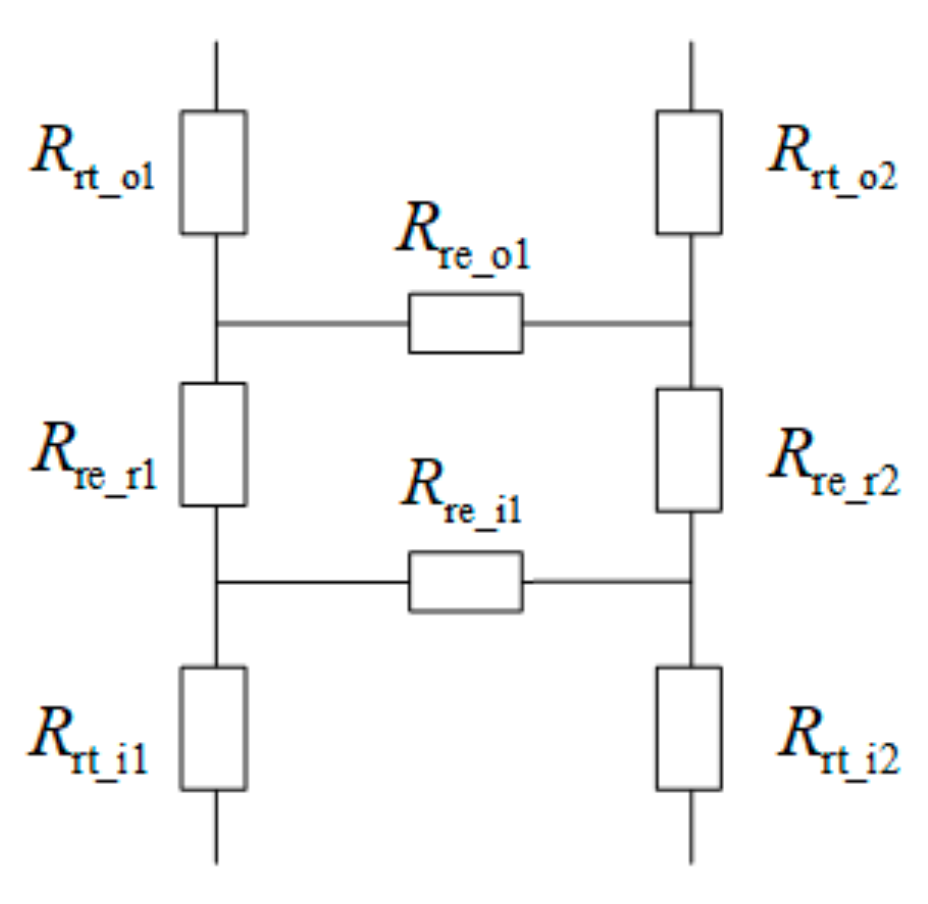
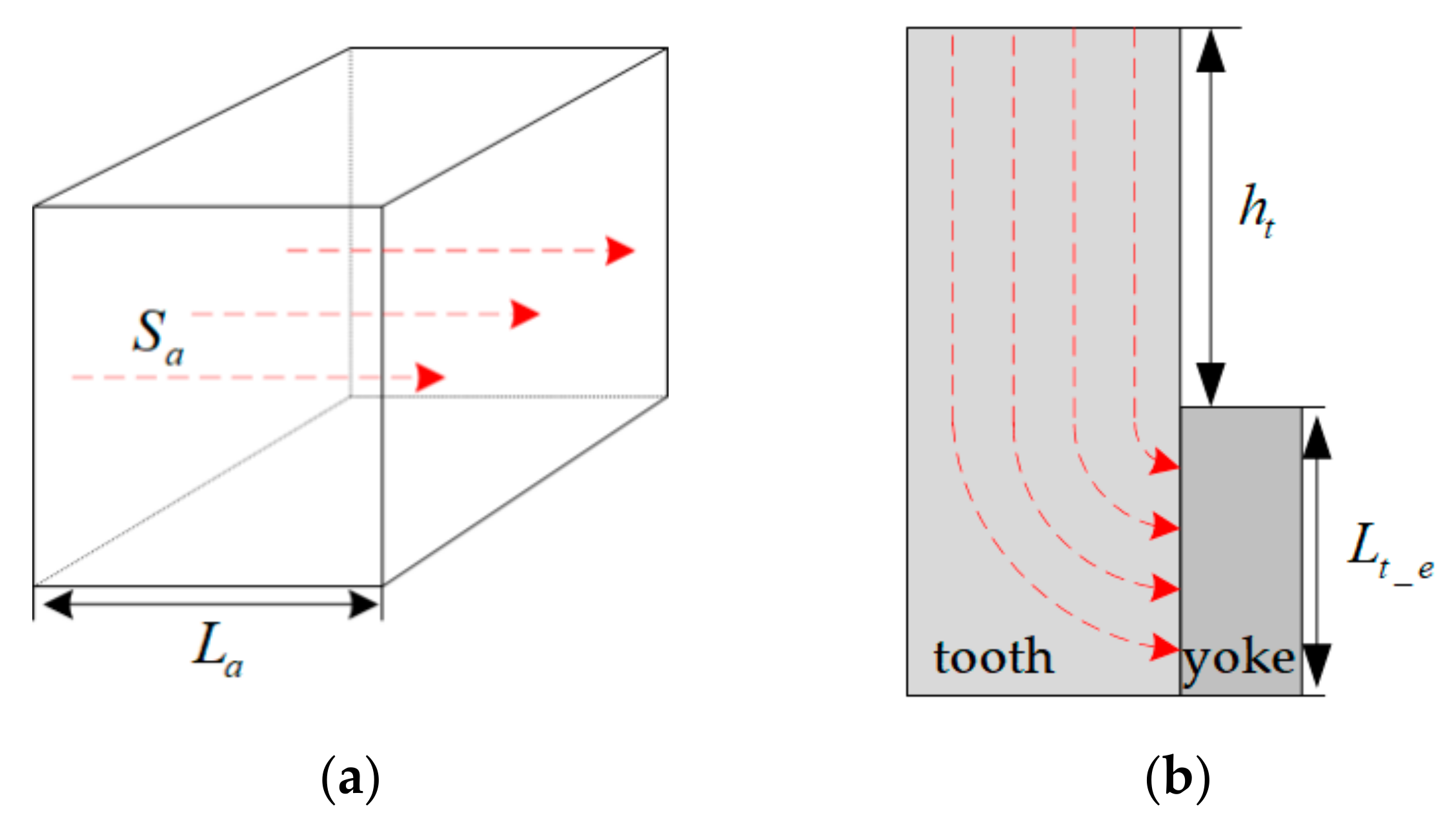
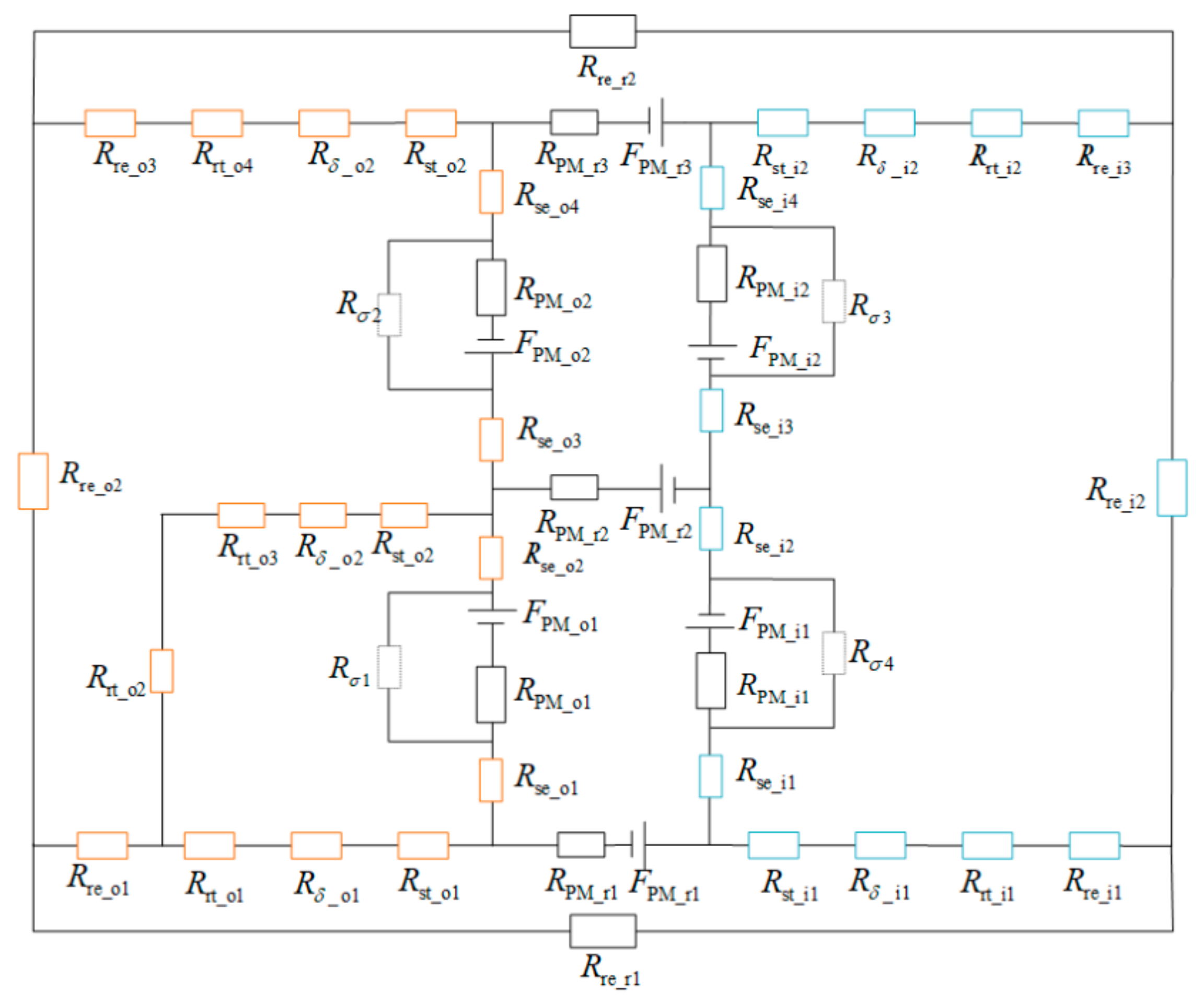
3.1. Magnetic Circuit Analysis
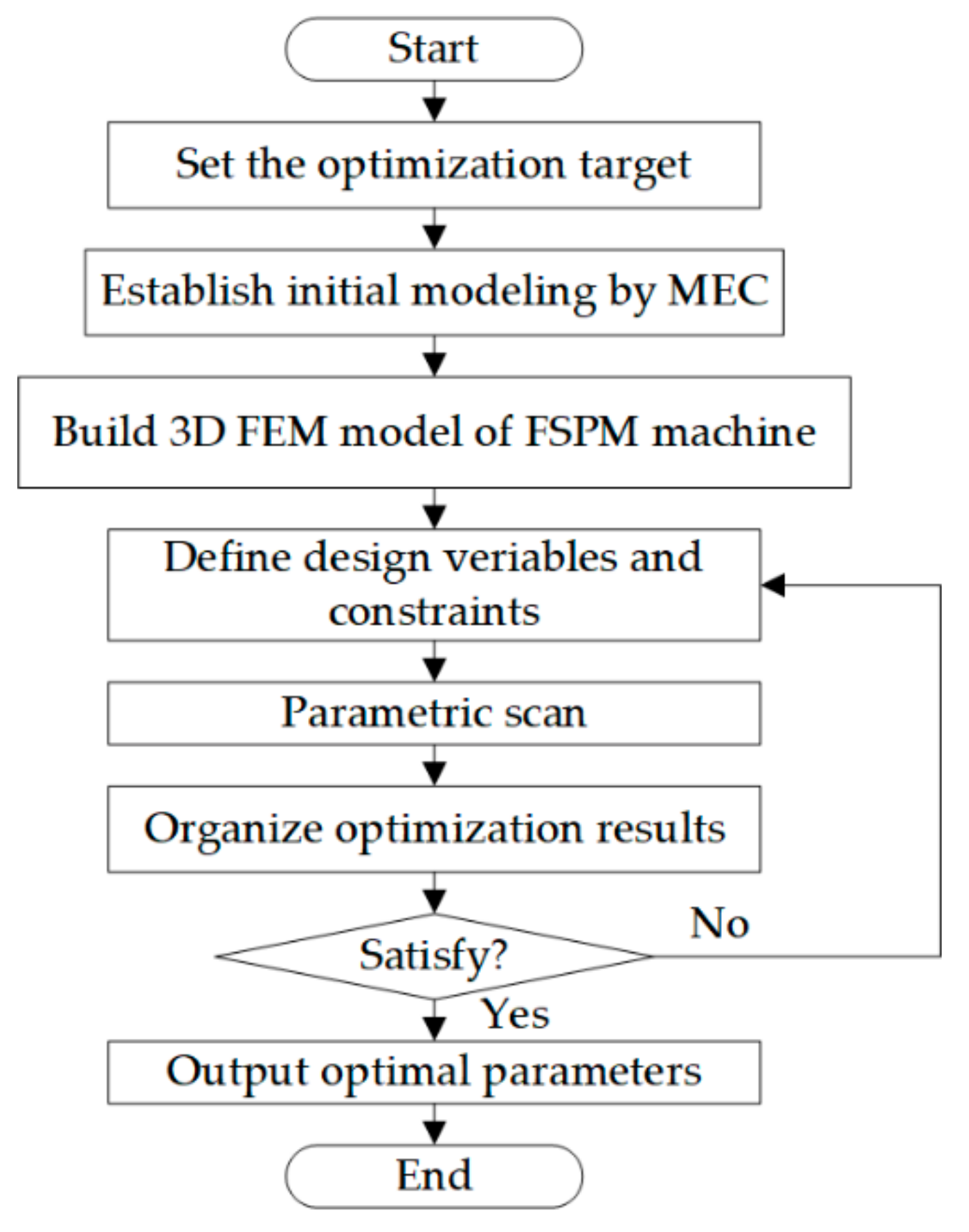
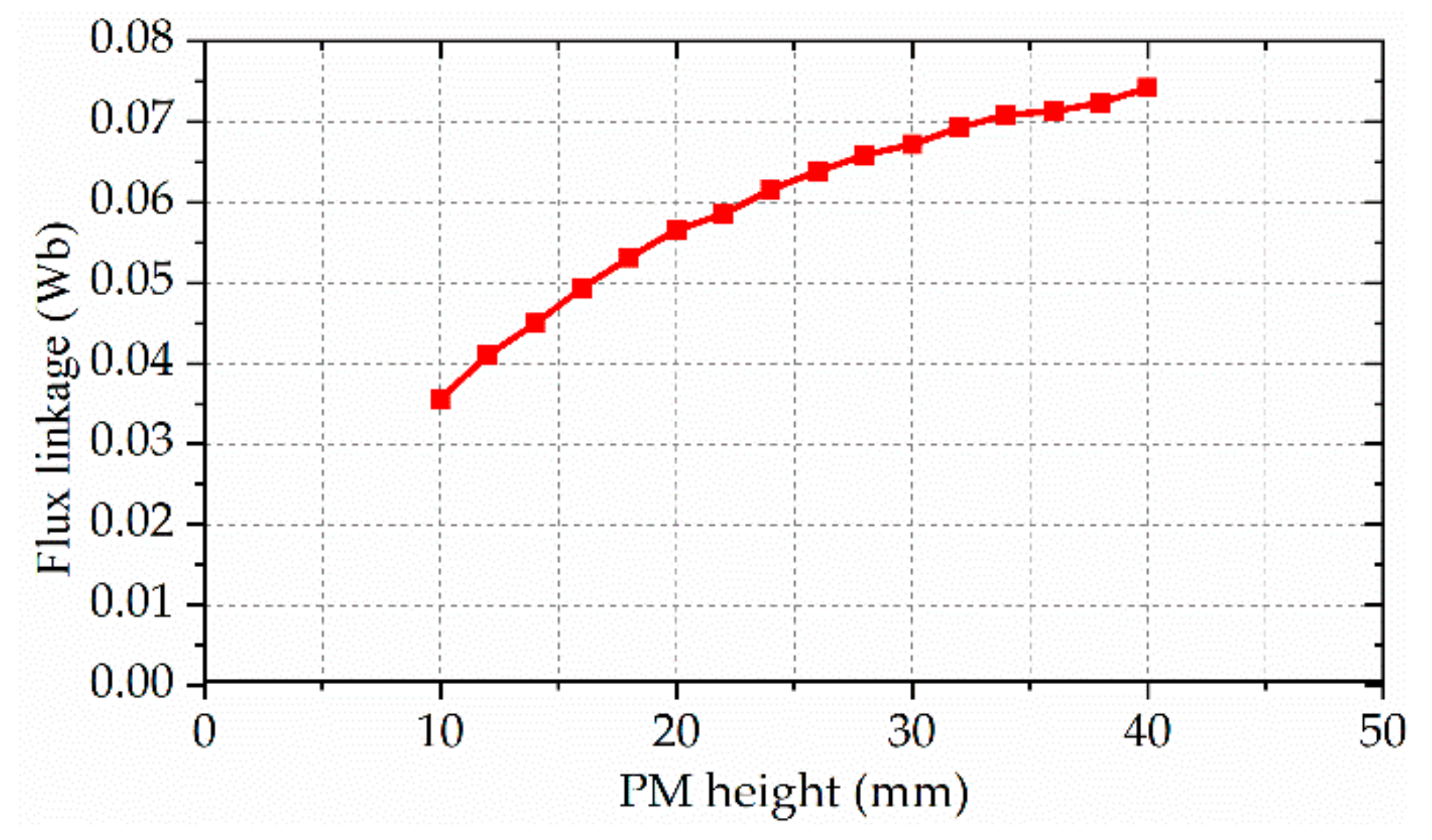
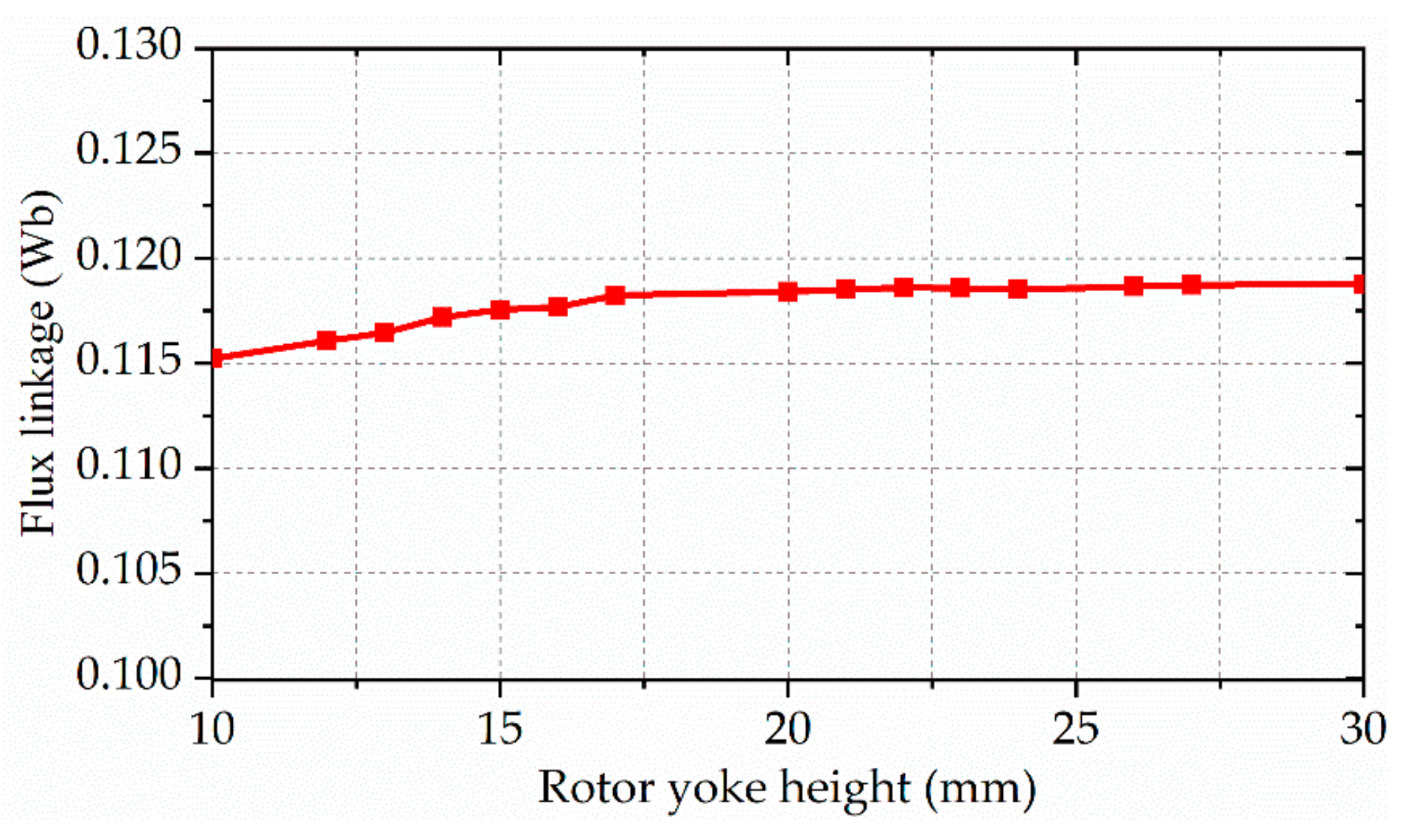
3.2. Parameter Optimization
4. Performance Evaluation
4.1. Open-Circuit Magnetic Field Distribution
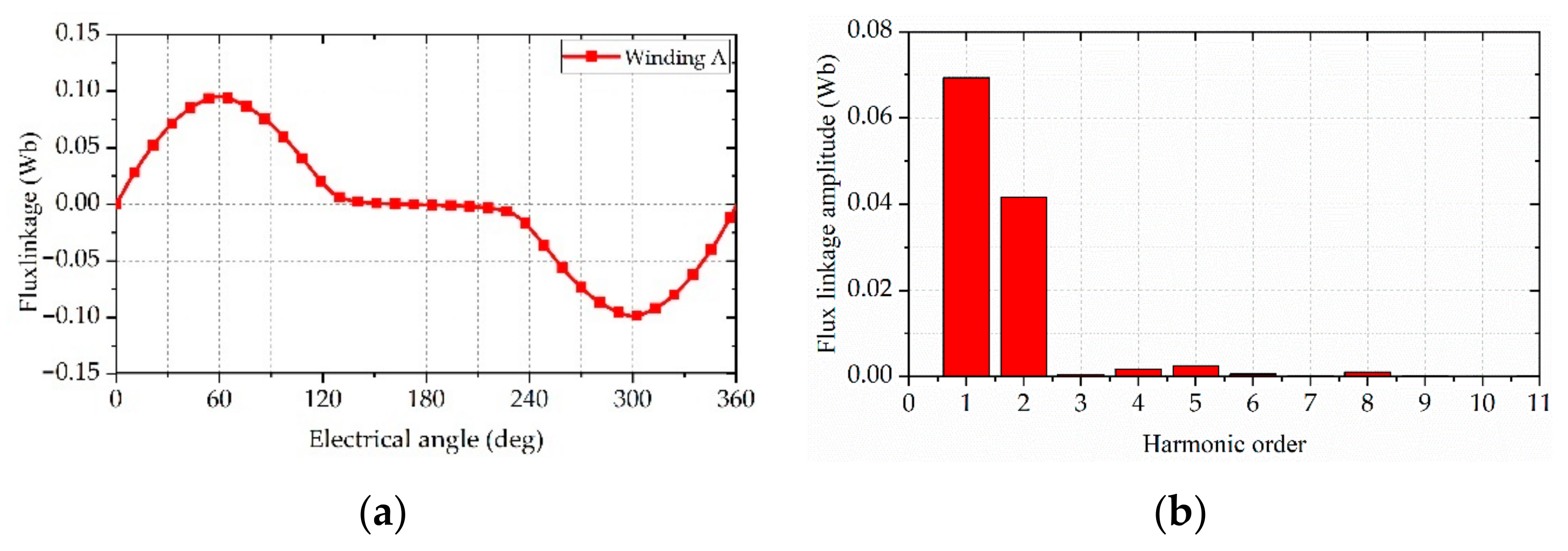
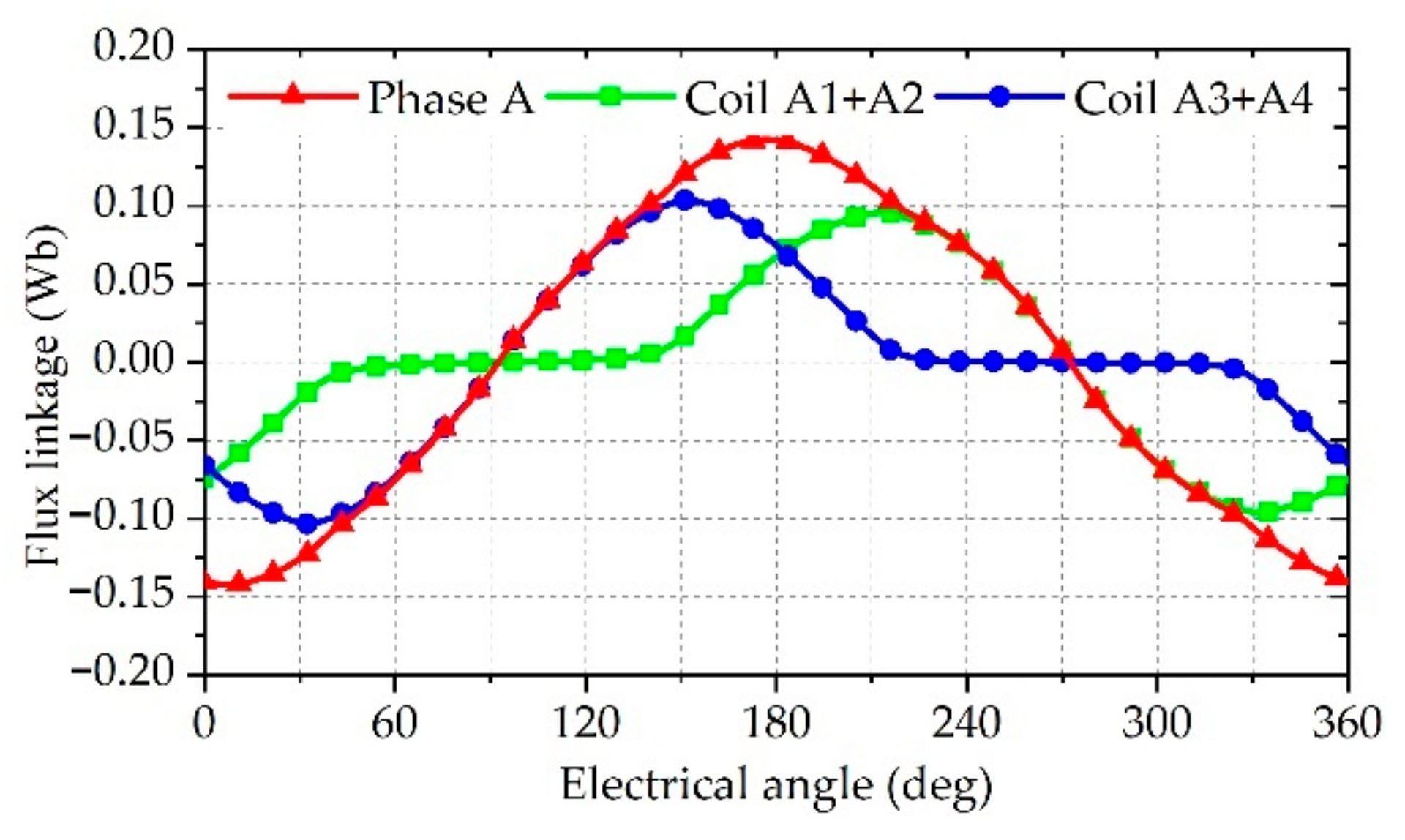
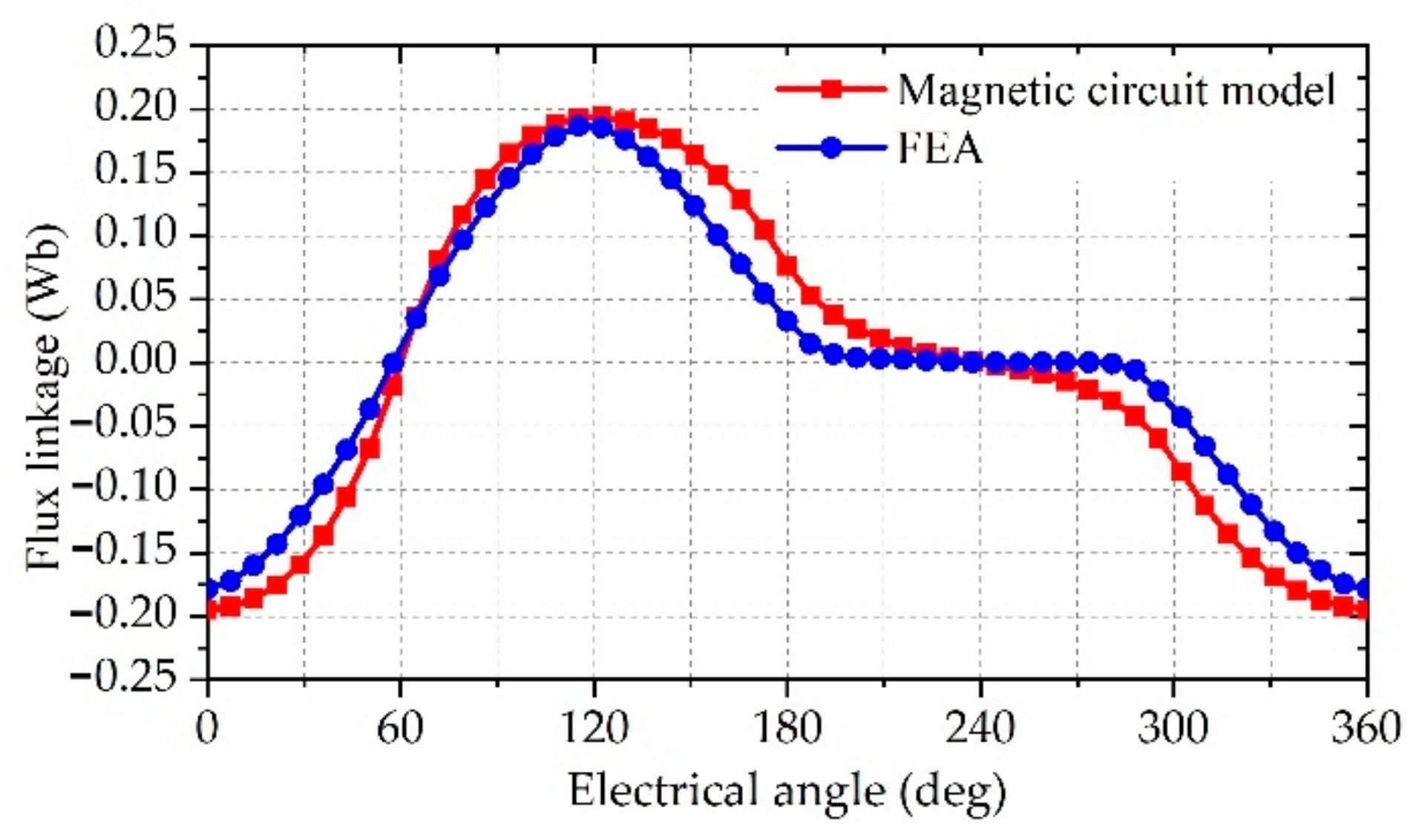
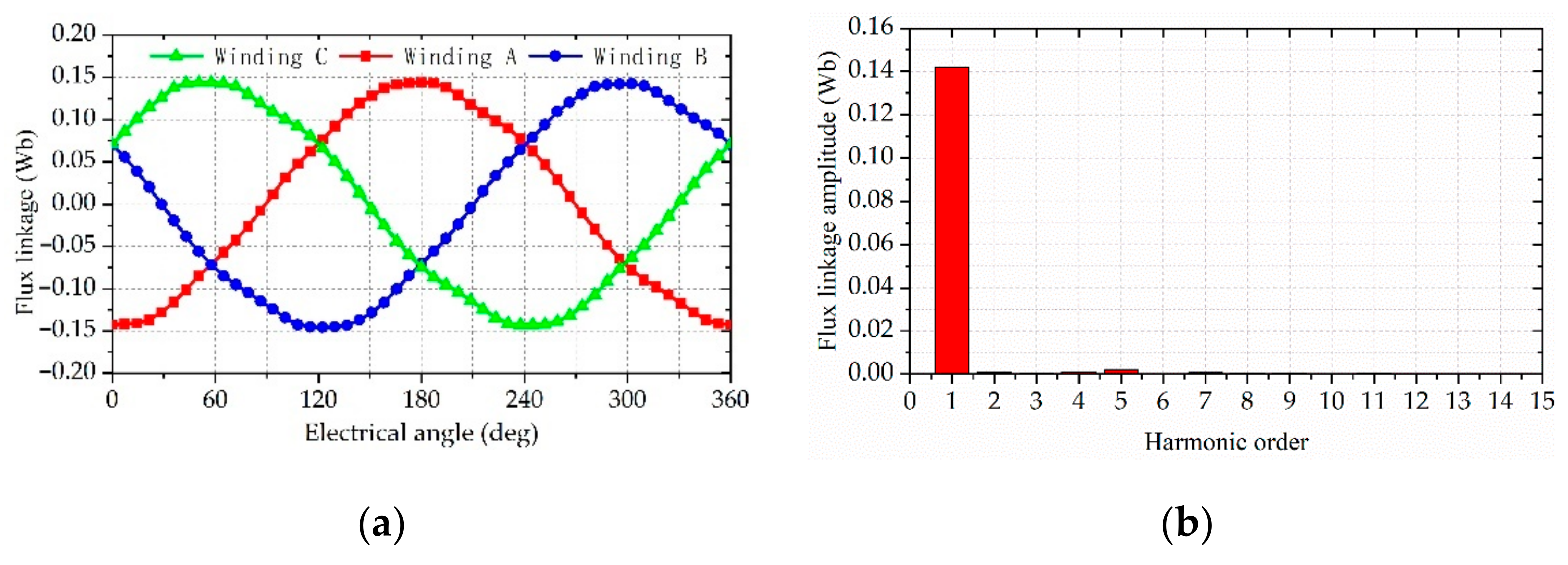
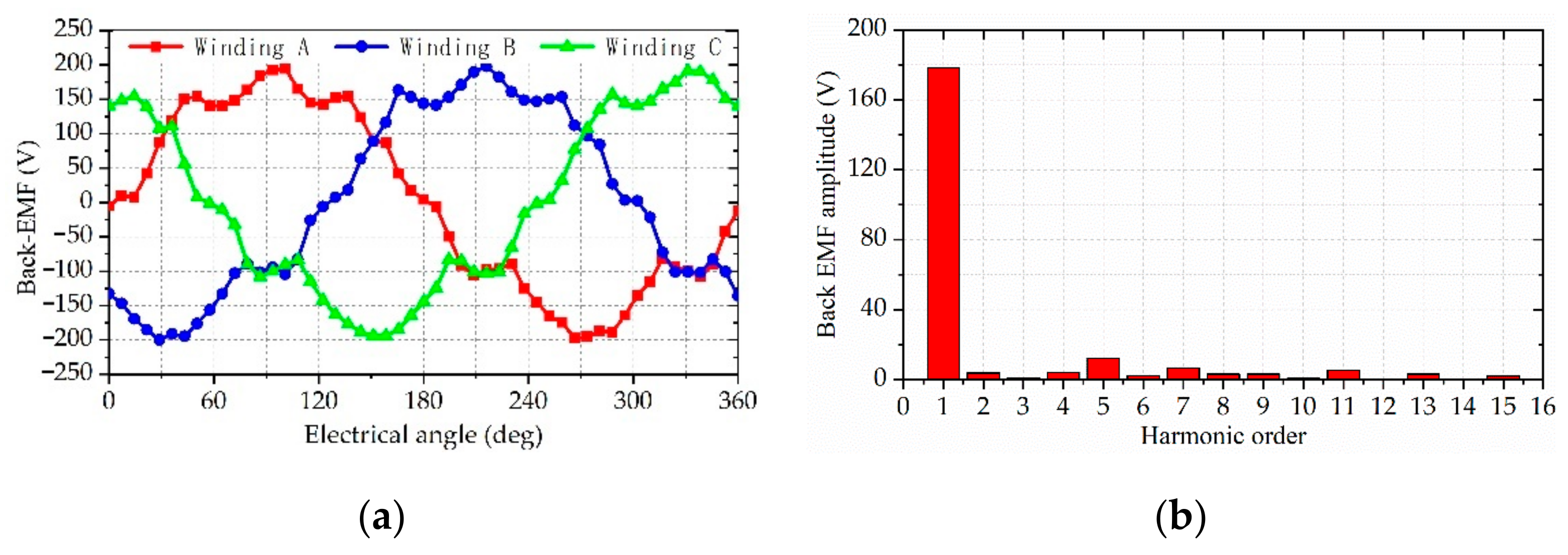
4.2. Open-Circuit Flux Linkage and Back-EMF
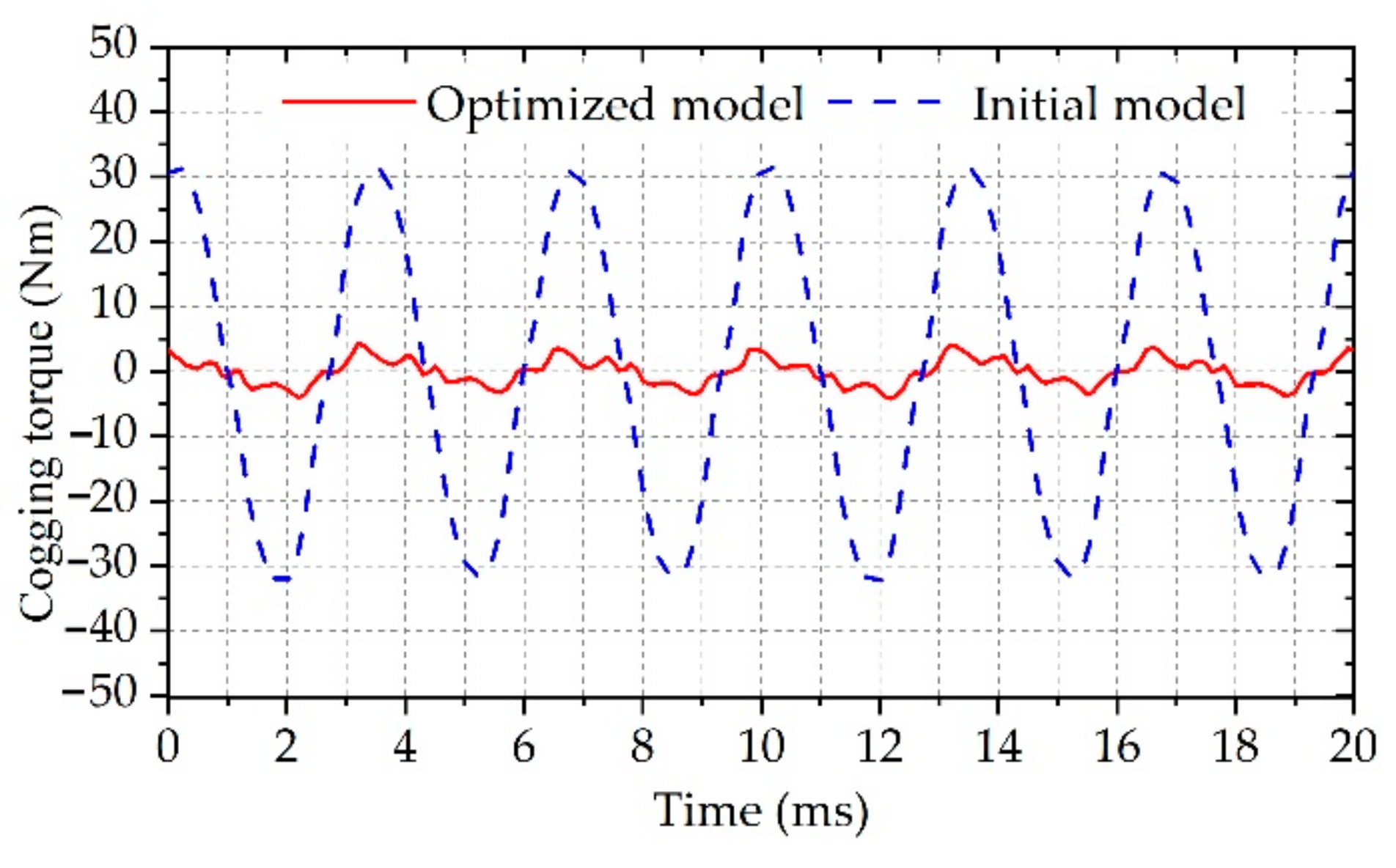
4.3. Cogging Torque
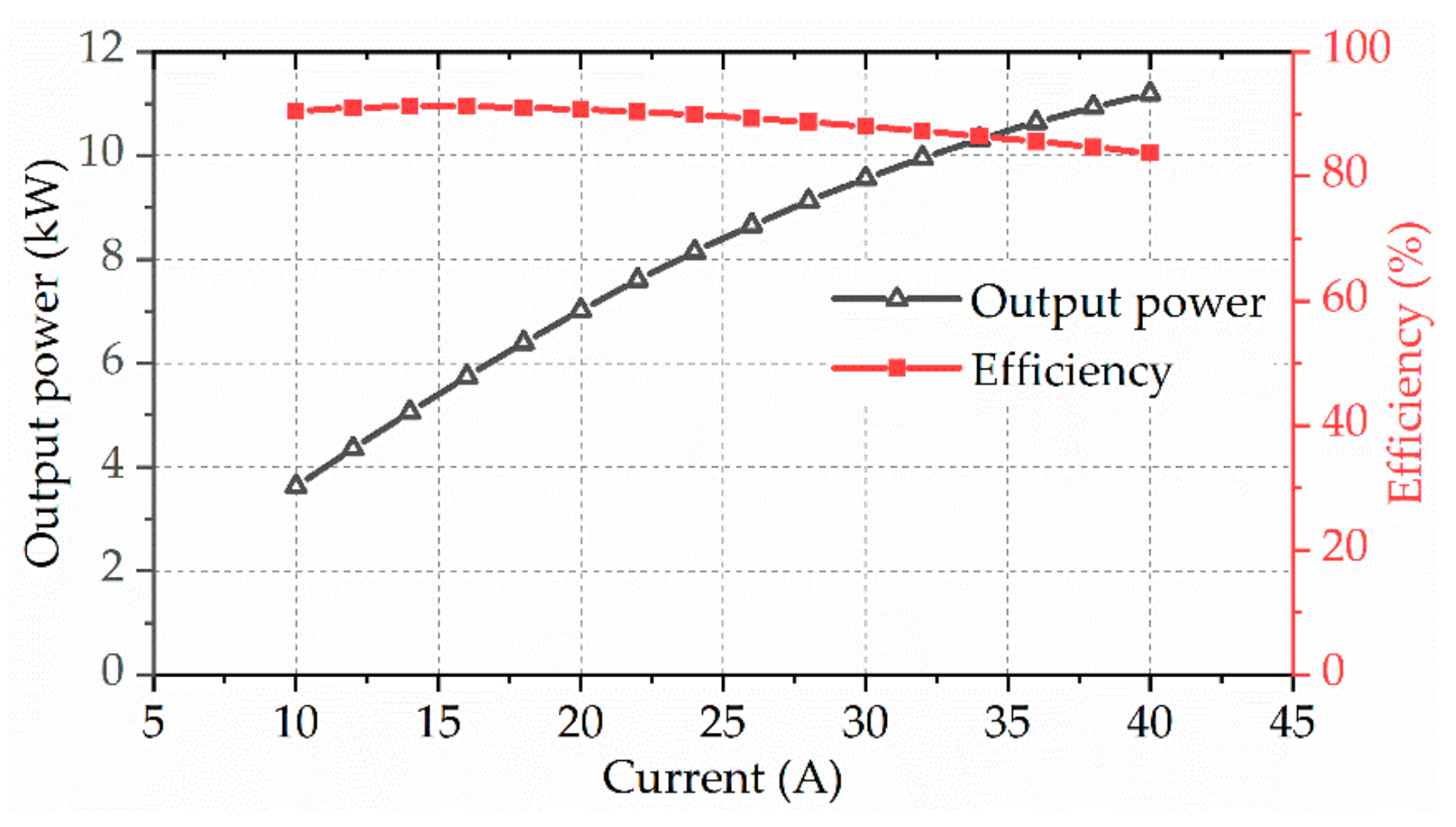
4.4. Output Power and Efficiency
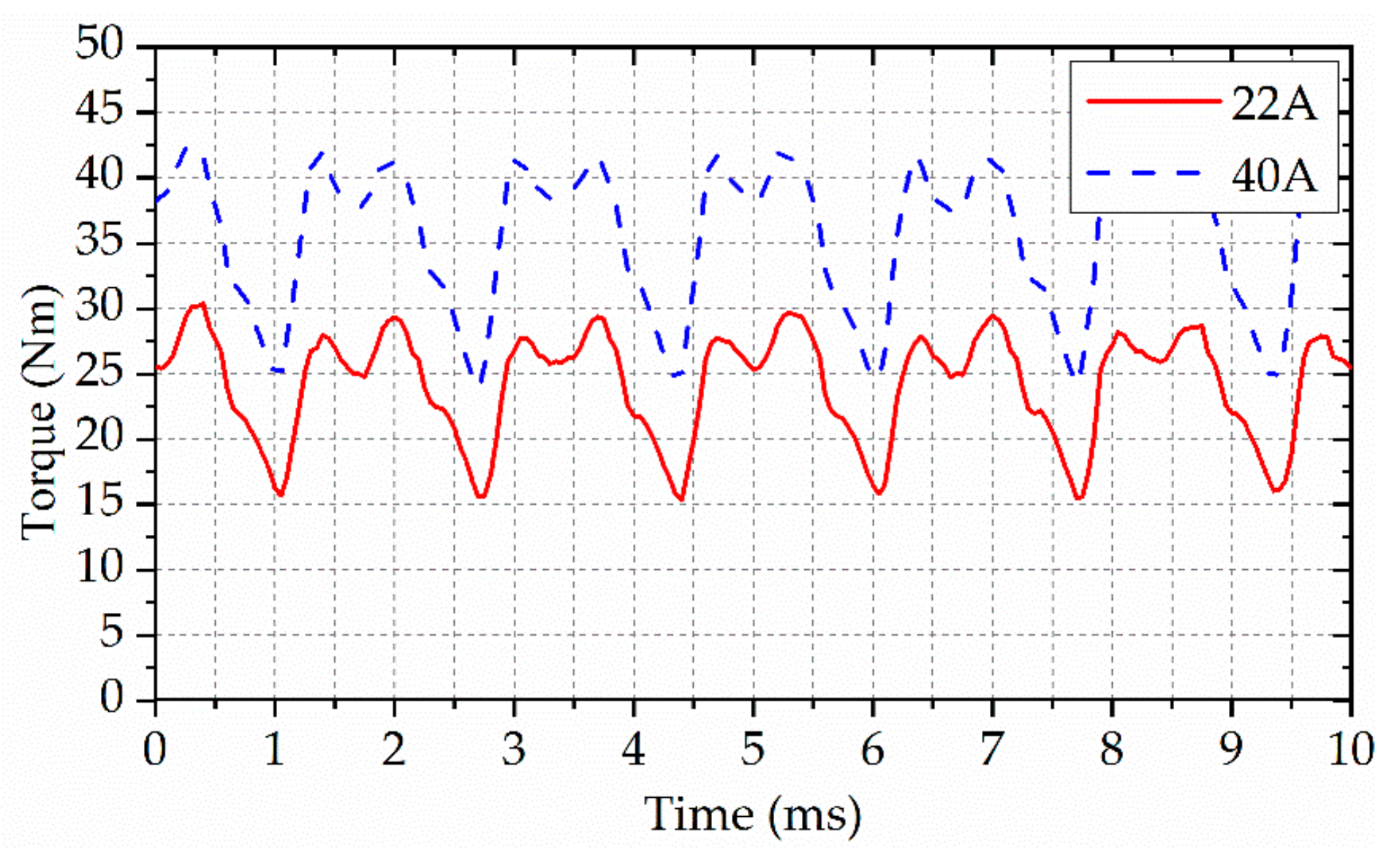
4.5. Output Torque
5. Discussion
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Li, S.; Li, Y.; Choi, W.; Sarlioglu, B. High-Speed Electric Machines: Challenges and Design Considerations. IEEE Trans. Transp. Electrif. 2016, 2, 2–13. [Google Scholar] [CrossRef]
- Bianchi, N.; Bolognani, S.; Luise, F. Potentials and Limits of High-Speed PM Motors. IEEE Trans. Ind. Appl. 2004, 40, 1570–1578. [Google Scholar] [CrossRef]
- Tenconi, A.; Vaschetto, S.; Vigliani, A. Electrical Machines for High-Speed Applications: Design Considerations and Tradeoffs. IEEE Trans. Ind. Electron. 2014, 61, 3022–3029. [Google Scholar] [CrossRef]
- Zhang, Z.; Wang, C.; Geng, W. Design and Optimization of Halbach-Array PM Rotor for High-Speed Axial-Flux Permanent Magnet Machine with Ironless Stator. IEEE Trans. Ind. Electron. 2020, 67, 7269–7279. [Google Scholar] [CrossRef]
- Ou, J.; Liu, Y.; Doppelbauer, M. Comparison Study of a Surface-Mounted PM Rotor and an Interior PM Rotor Made from Amorphous Metal of High-Speed Motors. IEEE Trans. Ind. Electron. 2021, 68, 9148–9159. [Google Scholar] [CrossRef]
- Thomas, A.; Zhu, Z.; Jewell, G.; Howe, D. Flux-Switching PM Brushless Machines with Alternative Stator and Rotor Pole Combinations. In Proceedings of the 11th International Conference on Electrical Machines and Systems (ICEMS), Wuhan, China, 17–20 October 2008; pp. 2986–2991. [Google Scholar]
- Zhu, Z.; Chen, J. Advanced Flux-switching Permanent Magnet Brushless Machines. IEEE Trans. Magn. 2010, 46, 1447–1453. [Google Scholar] [CrossRef]
- Li, X.; Shen, F.; Yu, S.; Xue, Z. Flux-Regulation Principle and Performance Analysis of a Novel Axial Partitioned Stator Hybrid-Excitation Flux-Switching Machine Using Parallel Magnetic Circuit. IEEE Trans. Ind. Electron. 2021, 68, 6560–6573. [Google Scholar] [CrossRef]
- Chen, J.; Zhu, Z. Winding Configurations and Optimal Stator and Rotor Pole Combination of Flux-Switching PM Brushless AC Machines. IEEE Trans. Energy Convers. 2010, 25, 293–302. [Google Scholar] [CrossRef]
- Zhao, J.; Quan, X.; Sun, X.; Lin, M.; Niu, S. Influence of Rotor-Pole Number on Electromagnetic Performance of Novel Double-Rotor Hybrid Excited Axial Switched-Flux Permanent-Magnet Machines for EV/HEV Applications. IEEE Trans. Magn. 2020, 56, 3. [Google Scholar] [CrossRef]
- Hua, W.; Cheng, M.; Zhu, Z. Analysis and Optimization of Back EMF Waveform of a Flux-Switching Permanent Magnet Motor. IEEE Trans. Energy Convers. 2008, 23, 727–733. [Google Scholar] [CrossRef]
- Li, Y.; Li, S.; Yang, Y.; Sarlioglu, B. Analysis of Flux Switching Permanent Magnet Machine Design for High-Speed Applications. In Proceedings of the 2014 IEEE Energy Conversion Congress and Exposition (ECCE), Pittsburgh, PA, USA, 14–18 September 2014; pp. 302–309. [Google Scholar]
- Li, Y.; Bobba, D.; Sarlioglu, B. A Novel Dual-Stator Flux Switching Permanent Magnet Machine with Six Stator Slots and Four Rotor Poles Configuration. In Proceedings of the 2015 IEEE International Electric Machines & Drives Conference (IEMDC), Coeur d’Alene, ID, USA, 10–13 May 2015; pp. 1566–1572. [Google Scholar]
- Liu, M.; Li, Y.; Sixel, W.; Sarlioglu, B. Design and Testing of Low Pole Dual-Stator Flux-Switching Permanent Magnet Machine for Electric Vehicle Applications. IEEE Trans. Veh. Technol. 2020, 69, 1464–1472. [Google Scholar] [CrossRef]
- Yu, W.; Liu, K.; Hua, W.; Hu, M.; Zhang, Z.; Hu, J. A New High-Speed Dual-Stator Flux Switching Permanent Magnet Machine with Distributed Winding. IEEE Trans. Magn. 2022, 58, 2. [Google Scholar] [CrossRef]
- Kim, J.; Li, Y.; Sarlioglu, B. Novel Dual-Rotor Single-Stator Axial Flux Switching Permanent Magnet Machine with Even Harmonic Elimination Topology. In Proceedings of the 2015 Int Aegean Conference on Electrical Machines and Power Electronics (ACEMP), Side, Turkey, 2–4 September 2015; pp. 506–512. [Google Scholar]
- Kim, J.; Li, Y.; Sarlioglu, B. Novel Six-Slot Four-Pole Axial Flux-Switching Permanent Magnet Machine for Electric Vehicle. IEEE Trans. Transp. Electrif. 2017, 3, 108–117. [Google Scholar] [CrossRef]
- Bobba, D.; Li, Y.; Sarlioglu, B. Harmonic Analysis of Low Stator-Slot and Rotor-Pole Combination FSPM Machine Topology for High Speed. IEEE Trans. Magn. 2015, 51, 11. [Google Scholar] [CrossRef]
- Capponi, G.; Donato, D.; Caricchi, F. Recent Advances in Axial-Flux Permanent-Magnet Machine Technology. IEEE Trans. Ind. Appl. 2012, 48, 2190–2205. [Google Scholar] [CrossRef]
- Zhao, J.; Ma, T.; Liu, X.; Zhao, G.; Dong, N. Performance Analysis of a Coreless Axial-Flux PMSM by an Improved Magnetic Equivalent Circuit Model. IEEE Trans. Energy Convers. 2021, 36, 2120–2130. [Google Scholar] [CrossRef]
- Lin, M.; Zhang, L.; Li, X. Analysis on Cogging Torque in Axial Field Flux-Switching Permanent Magnet Machine. Electr. Mach. Control 2009, 13, 787–791. [Google Scholar]
- Zhu, H.; Xu, Y. Permanent Magnet Parameter Design and Performance Analysis of Bearingless Flux Switching Permanent Magnet Motor. IEEE Trans. Ind. Electron. 2021, 68, 4153–4163. [Google Scholar] [CrossRef]
- Chen, C.; Ren, X.; Li, D.; Qu, R.; Liu, K.; Zou, T. Torque Performance Enhancement of Flux-Switching Permanent Magnet Machines with Dual Sets of Magnet Arrangements. IEEE Trans. Transp. Electrif. 2021, 7, 2623–2634. [Google Scholar] [CrossRef]

| Radial FSPM Machine | Axial FSPM Machine | Proposed Model | ||
|---|---|---|---|---|
| Slot/pole | 12/10 [12] | 6/4 [14] | 6/4 [17] | 6/4 |
| Axial length | Long | Long | Short | Shortest |
| Fundamental frequency | High | Low | Low | Low |
| Efficiency | low | High | High | High |
| Dissipate heat | Good | Bad | Better | Better |
| Parameter | Symbol | Lower | Upper | Units |
|---|---|---|---|---|
| Stator yoke height | 15 | 35 | mm | |
| Stator tooth height | 10 | 20 | mm | |
| Inner stator tooth internal diameter | 90 | 120 | mm | |
| Inner stator tooth width | 30 | 50 | mm | |
| Radial magnetized PMs inner diameter | 200 | 240 | mm | |
| Radial magnetized PMs thickness | 3 | 6 | mm | |
| Outer stator tooth internal diameter | 240 | 260 | mm | |
| Rotor yoke height | 10 | 30 | mm | |
| Rotor tooth angle | 15 | 45 | deg |
| Parameter | Value | Parameter | Value |
|---|---|---|---|
| Turns of outer winding | 50 | Angle between inner and outer rotor teeth/deg | 45 |
| Turns of inner winding | 68 | Rated speed (rpm) | 3000 |
| Stator yoke height (mm) | 28 | Outer stator tooth internal diameter (mm) | 252 |
| Stator tooth height (mm) | 20 | Outer stator tooth width (mm) | 25 |
| Inner stator tooth internal diameter (mm) | 114 | Tangential magnetized PMs width (mm) | 6 |
| Inner stator tooth width (mm) | 43.6 | Rotor yoke height (mm) | 17 |
| Radial magnetized PMs inner diameter (mm) | 220 | Rotor tooth height (mm) | 20 |
| Radial magnetized PMs thickness (mm) | 6 | Rotor tooth angle (mm) | 17 |
| Radial magnetized PMs angle (deg) | 55 | Air gap height (mm) | 1 |
| Radial FSPM Machine | Axial FSPM Machine | Proposed Model | ||
|---|---|---|---|---|
| Slot/pole | 12/10 [12] | 6/4 [14] | 6/4 [17] | 6/4 |
| Number of stators | 1 | 2 | 1 | 2 |
| Number of rotors | 1 | 1 | 2 | 1 |
| Axial length/outer diameter (mm) | 0.58 | 0.83 | 0.57 | 0.33 |
| Fundamental frequency (Hz) | 500 | 200 | 200 | 200 |
| Iron loss (W) | 524 | 412 | 425 | 423 |
| Efficiency (%) | 86 | 91 | 92 | 90 |
| Cogging torque (Nm) | 0.3 | 2.3 | 21.5 | 4.5 |
| THD of back-EMF (%) | 0.2 | 5.8 | 8.9 | 9.8 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, H.; Xu, Z.; Liu, C.; Jin, L.; Yu, H.; Xu, B.; Fang, S. Novel Axial Flux-Switching Permanent Magnet Machine for High-Speed Applications. Sustainability 2022, 14, 7774. https://doi.org/10.3390/su14137774
Zhang H, Xu Z, Liu C, Jin L, Yu H, Xu B, Fang S. Novel Axial Flux-Switching Permanent Magnet Machine for High-Speed Applications. Sustainability. 2022; 14(13):7774. https://doi.org/10.3390/su14137774
Chicago/Turabian StyleZhang, Hongbin, Zhike Xu, Chenglei Liu, Long Jin, Haitao Yu, Bingxin Xu, and Shuhua Fang. 2022. "Novel Axial Flux-Switching Permanent Magnet Machine for High-Speed Applications" Sustainability 14, no. 13: 7774. https://doi.org/10.3390/su14137774
APA StyleZhang, H., Xu, Z., Liu, C., Jin, L., Yu, H., Xu, B., & Fang, S. (2022). Novel Axial Flux-Switching Permanent Magnet Machine for High-Speed Applications. Sustainability, 14(13), 7774. https://doi.org/10.3390/su14137774







