Research on Linear Combination Models of BDS Multi-Frequency Observations and Their Characteristics
Abstract
:1. Introduction
2. Linear Combination of Carrier-Phase Observations
3. Integer Combinations of Carrier-Phase
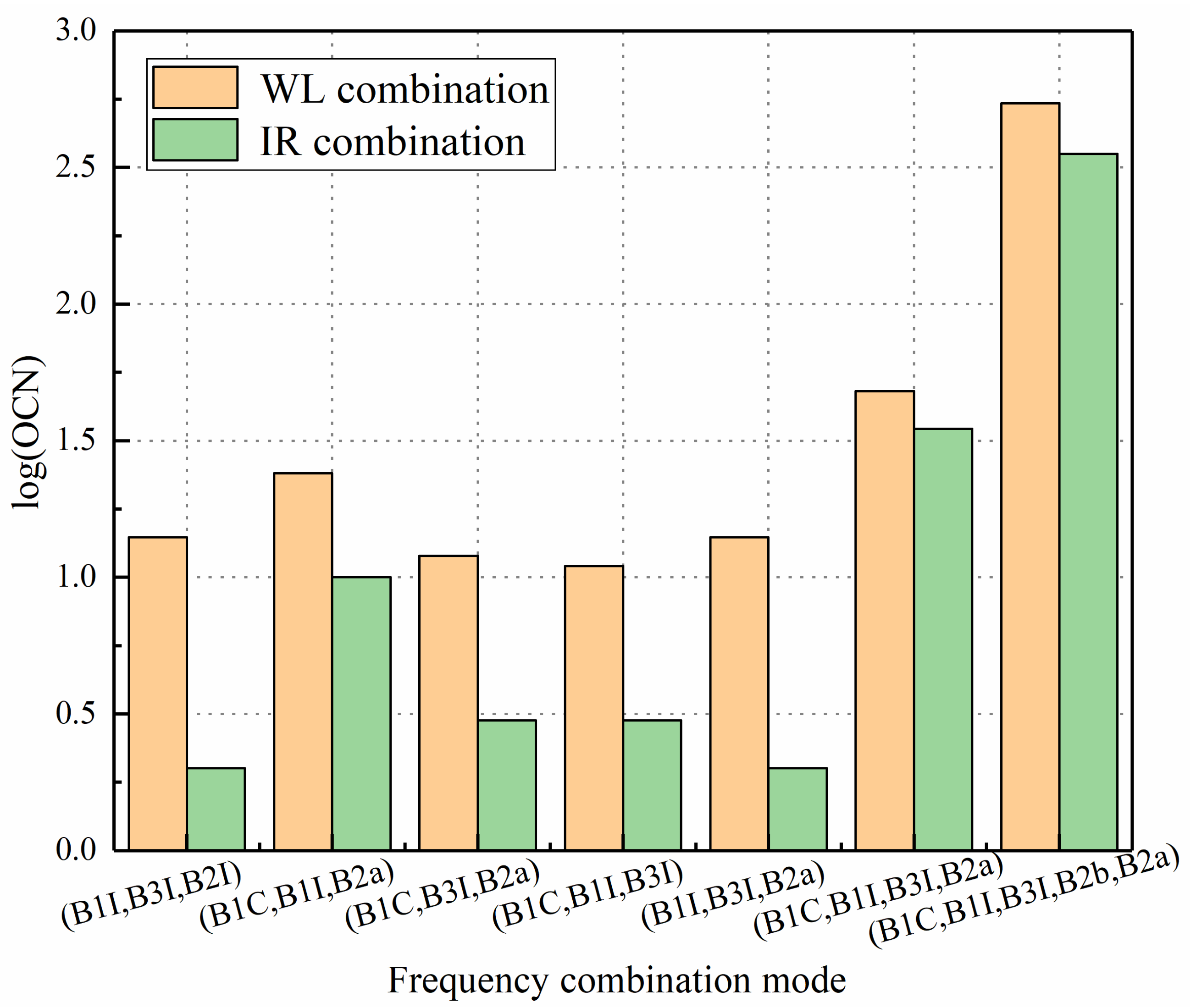
3.1. WL and IR Combinations
3.2. GF Combinations
3.3. IF Combinations
4. Optimal IF Real Combinations
4.1. Optimal GBIF Real Combination
4.2. Optimal GFIF Real Combination
5. Pseudorange Multipath Delay Combination
6. Summary and Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Hein, G. Status, perspectives and trends of satellite navigation. Satell. Navig. 2020, 1, 22. [Google Scholar] [CrossRef] [PubMed]
- Xie, J. Research on BDS’s big data technology development. Aerosp. China 2021, 1, 8–19. [Google Scholar]
- Yang, Y.; Yang, C.; Ren, X. PNT intelligent services. Acta Geod. Cartogr. Sin. 2021, 50, 1006–1012. [Google Scholar]
- Yang, Y.; Gao, W.; Guo, S.; Mao, Y.; Yang, Y. Introduction to BeiDou-3 navigation satellite system. Navigation 2019, 66, 7–18. [Google Scholar] [CrossRef] [Green Version]
- Yang, Y.; Xu, Y.; Li, J.; Yang, C. Progress and performance evaluation of BeiDou global navigation satellite system: Data analysis based on BDS-3 demonstration system. Sci. China Earth Sci. 2018, 61, 614–624. [Google Scholar] [CrossRef]
- Hu, C.; Wang, Z.; Rao, P.; Cheng, T. One-step correction strategy for BDS-2/BDS-3 satellite observation code bias and multipath delay. Acta Geod. Geophys. 2021, 56, 29–59. [Google Scholar] [CrossRef]
- Zhang, Z. Code and phase multipath mitigation by using the observation-domain parameterization and its application in five-frequency GNSS ambiguity resolution. GPS Solut. 2021, 25, 144. [Google Scholar] [CrossRef]
- Li, J.; Yang, Y.; He, H.; Guo, H. An analytical study on the carrier-phase linear combinations for triple-frequency GNSS. J. Geod. 2017, 91, 151–166. [Google Scholar] [CrossRef]
- Zhang, Z.; Li, B.; He, X. Geometry-free single-epoch resolution of BDS-3 multi-frequency carrier ambiguities. Acta Geod. Cartogr. Sin. 2020, 49, 1139–1148. [Google Scholar]
- Zhao, C.; Zhang, B.; Zhang, X. SUPREME: An open-source single-frequency uncombined precise point positioning software. GPS Solut. 2021, 25, 86. [Google Scholar] [CrossRef]
- Zou, J.; Wang, J. Mixed Application of Single and Dual Frequency Receivers in Single-Frequency Precise Point Position. J. Tongji Univ. (Nat. Sci.) 2021, 49, 731–736. [Google Scholar]
- Liu, C.; Tao, Y.; Xin, H.; Zhao, X.; Liu, C.; Hu, H.; Zhou, T. A Single-Difference Multipath Hemispherical Map for Multipath Mitigation in BDS-2/BDS-3 Short Baseline Positioning. Remote Sens. 2021, 13, 304. [Google Scholar] [CrossRef]
- Dong, Y.; Dai, P.; Wang, S.; Xing, J.; Xue, Y.; Liu, S.; Han, S.; Yang, Z.; Bai, X. A Study on the Detecting Cycle Slips and a Repair Algorithm for B1/B3. Electronics 2021, 10, 2925. [Google Scholar] [CrossRef]
- Wu, Z.; Wang, Q.; Hu, C.; Yu, Z.; Wu, W. Modeling and assessment of five -frequency BDS precise point positioning. Satell. Navig. 2022, 3, 8. [Google Scholar] [CrossRef]
- Guo, F.; Zhang, X.; Wang, J.; Ren, X. Modeling and assessment of triple-frequency BDS precise point positioning. J. Geod. 2016, 90, 1223–1235. [Google Scholar] [CrossRef]
- Blewitt, G. Carrier phase ambiguity resolution for the global positioning system applied to geodetic baselines up to 2000 km. J. Geophys. Res. Atmos. 1989, 94, 10187–10203. [Google Scholar] [CrossRef] [Green Version]
- Cocard, M.; Geiger, A. Systematic search for all possible widelanes. In Proceedings of the 6th International Geodetic Symposium on Satellite Positioning, Columbus, OH, USA, 17–20 March 1992; pp. 312–318. [Google Scholar]
- Han, S.; Rizos, C. The impact of two additional civilian GPS frequencies on ambiguity resolution strategies. In Proceedings of the ION 55th Annual Meeting, Alexandria, VA, USA, 25–27 January 1999; pp. 315–321. [Google Scholar]
- Teunissen, P.J.G.; Odijk, D. Rank-defect integer estimation and phase-only modernized GPS ambiguity resolution. J. Geod. 2003, 76, 523–535. [Google Scholar] [CrossRef] [Green Version]
- Richert, T.; El-Sheimy, N. Optimal linear combinations of triple-frequency carrier phase data from future global navigation satellite systems. GPS Solut. 2007, 11, 11–19. [Google Scholar] [CrossRef]
- Cocard, M.; Bourgon, S.; Kamali, O.; Collins, P. A systematic investigation of optimal carrier-phase combinations for modernized triple-Frequency GPS. J. Geod. 2008, 82, 555–564. [Google Scholar] [CrossRef]
- Henkel, P. Geometry-free linear combinations for Galileo. Acta Astronaut. 2009, 65, 1487–1499. [Google Scholar] [CrossRef]
- Chang, Q.; Yi, B.; Zhang, Q.; Xiao, Z. Study for Model of Inter-Frequency Combinations of Galileo and GPS. Chin. J. Space Sci. 2007, 1, 77–82. [Google Scholar]
- Wang, Z.; Liu, J. Model of Inter-Frequency Combinations of Galileo GNSS. Geomat. Inf. Sci. Wuhan Univ. 2003, 6, 723–727. [Google Scholar]
- Yang, X.; Dang, Y.; Cheng, Y. Approach to ambiguity resolution using Galileo/GPS combination observations. Sci. Surv. Mapp. 2009, 34, 40–42. [Google Scholar]
- Chen, J.; Yue, D.; Zhu, S.; Liu, Z.; Zhao, X.; Xu, W. A New Cycle Slip Detection and Repair Method for Galileo Four-Frequency Observations. IEEE Access 2020, 8, 56528–56543. [Google Scholar] [CrossRef]
- Xu, J.; Tao, T.; Gao, F. Research on three kinds of carrier frequency combination value of GLONASS. J. Geod. Geodyn. 2013, 33, 86–89. [Google Scholar]
- Guo, Z.; Gao, J.; Wang, J.; Cao, X. Research on Multi-Frequency Observation Linear Combination of GNSS. J. Geod. Geodyn. 2015, 35, 379–382. [Google Scholar]
- Sun, B.; Ou, J.; Sheng, C.; Liu, J. Optimal Multi-frequency Data Combination for Compass Cycle Slip Detection and Reparation. Geomat. Inf. Sci. Wuhan Univ. 2010, 35, 1157–1160. [Google Scholar]
- Huang, L.; Song, L.; Wang, Y.; Zhi, S. BeiDou Triple-frequency Geometry-Free Phase Combination for Cycle-slip Detection and Correction. Acta Geod. Cartogr. Sin. 2012, 41, 763–768. [Google Scholar]
- Li, J.; Yang, Y.; He, H.; Xu, J.; Guo, H. Optimal Carrier-phase Combinations for Triple-frequency GNSS Derived from an Analytical Method. Acta Geod. Cartogr. Sin. 2012, 41, 797–803. [Google Scholar]
- Zhang, X.; He, X. BDS triple-frequency carrier-phase linear combination models and their characteristics. Sci. China: Earth Sci. 2015, 58, 896–905. [Google Scholar] [CrossRef]
- Zhang, X.; Wu, M.; Liu, W.; Li, X.; Yu, S.; Lu, C.; Wickert, J. Initial assessment of the COMPASS/BeiDou-3: New-generation navigation signals. J. Geod. 2017, 91, 1225–1240. [Google Scholar] [CrossRef]
- Zhang, X.; Cai, W. BDS four frequency carrier phase combination models and their characteristics. Surv. Rev. 2018, 52, 97–106. [Google Scholar] [CrossRef]
- Li, J.; Yang, Y.; He, H.; Guo, H. Benefits of BDS-3 B1C/B1I/B2a triple-frequency signals on precise positioning and ambiguity resolution. GPS Solut. 2020, 24, 100. [Google Scholar] [CrossRef]
- Wang, H.; Pan, S.; Gao, W.; Ye, F.; Ma, C.; Tao, J.; Wang, Y. Real-time cycle slip detection and repair for BDS-3 triple-frequency and quad-frequency B1C/B1I/B3I/B2a signals. Acta Geodyn. Geomater. 2021, 18, 363–377. [Google Scholar] [CrossRef]
- Yuan, H.; Zhang, Z.; He, X.; Xu, T.; Xu, X.; Zeng, N. Real-time Cycle Slip Detection and Repair Method for BDS-3 Five-frequency Data. IEEE Access 2021, 9, 51189–51201. [Google Scholar] [CrossRef]
- Zhao, Q.; Wang, G.; Liu, Z.; Hu, Z.; Dai, Z.; Liu, J. Analysis of BeiDou Satellite Measurements with Code Multipath and Geometry-Free Ionosphere-Free Combinations. Sensors 2016, 16, 123. [Google Scholar] [CrossRef] [Green Version]
- Zhang, X.; Liu, G.; Guo, F. Model comparison and performance analysis of triple-frequency BDS precise point positioning. Geomat. Inf. Sci. Wuhan Univ. 2018, 43, 2124–2130. [Google Scholar]
- Zhou, F.; Xu, T. Modeling and assessment of GPS/BDS/Galileo triple-frequency precise point positioning. Acta Geod. Cartogr. Sin. 2021, 50, 61–70. [Google Scholar]
- Jin, S.; Su, K. PPP models and performances from single- to quad-frequency BDS observations. Satell. Navig. 2020, 1, 16. [Google Scholar] [CrossRef]
- Su, K.; Jin, S. Analysis and comparisons of the BDS/Galileo quad-frequency PPP models performances. Acta Geod. Cartogr. Sin. 2020, 49, 1189–1201. [Google Scholar]
- Zeng, T.; Sui, L.; Xu, Y.; Jia, X.; Xiao, G.; Tian, Y.; Zhang, Q. Real-time triple-frequency cycle slip detection and repair method under ionospheric disturbance validated with BDS data. GPS Solut. 2018, 22, 62. [Google Scholar] [CrossRef]
- Li, B.; Feng, Y.; Shen, Y. Three carrier ambiguity resolution: Distance-independent performance demonstrated using semi-generated triple frequency GPS signals. GPS Solut. 2010, 14, 177–184. [Google Scholar] [CrossRef]
- Chen, D.; Ye, S.; Xia, J.; Liu, Y.; Xia, P. A geometry-free and ionosphere-free multipath mitigation method for BDS three-frequency ambiguity resolution. J. Geod. 2016, 90, 703–714. [Google Scholar] [CrossRef]
- Kuang, K.; Wang, J.; Han, H. Real-Time BDS-3 Clock Estimation with a Multi-Frequency Uncombined Model including New B1C/B2a Signals. Remote Sens. 2022, 14, 966. [Google Scholar] [CrossRef]
- Zhang, F.; Chai, H.; Li, L.; Wang, M.; Feng, X.; Du, Z. Understanding the characteristic of GLONASS inter-frequency clock bias using both FDMA and CDMA signals. GPS Solut. 2022, 26, 63. [Google Scholar] [CrossRef]
- Guo, Z.; Yu, X.; Hu, C.; Yu, Z.; Jiang, C. Correction Model of BDS-3 Satellite Pseudorange Multipath Delays and Its Impact on Single-Frequency Precise Point Positioning. Math. Probl. Eng. 2021, 2021, 8189541. [Google Scholar] [CrossRef]
- Chen, C.; Chang, G.; Zheng, N.; Xu, T. GNSS Multipath Error Modeling and Mitigation by Using Sparsity-Promoting Regularization. IEEE Access 2019, 7, 24096–24108. [Google Scholar] [CrossRef]
- Zheng, K.; Zhang, X.; Li, P.; Li, X.; Ge, M.; Guo, F.; Sang, J.; Schuh, H. Multipath extraction and mitigation for high-rate multi-GNSS precise point positioning. J. Geod. 2019, 93, 2037–2051. [Google Scholar] [CrossRef]
- Tao, Y.; Liu, C.; Chen, T.; Zhao, X.; Liu, C.; Hu, H.; Zhou, T.; Xin, H. Real-Time Multipath Mitigation in Multi-GNSS Short Baseline Positioning via CNN-LSTM Method. Math. Probl. Eng. 2021, 2021, 6573230. [Google Scholar] [CrossRef]
- Jin, T.; Hu, B.; Sun, Y.; Huang, Z.; Wang, Q.; Wu, Q. Optimal Solution to Multi-Frequency BDS Code-Multipath Combination Measurement. J. Navig. 2019, 72, 1297–1314. [Google Scholar] [CrossRef]
- Zhang, R.; Gao, C.; Wang, Z.; Zhao, Q.; Shang, R.; Peng, Z.; Liu, Q. Ambiguity Resolution for Long Baseline in a Network with BDS-3 Quad-Frequency Ionosphere-Weighted Model. Remote Sens. 2022, 14, 1654. [Google Scholar] [CrossRef]
- Fan, X.; Tian, R.; Dong, X.; Shuai, W.; Fan, Y. Cycle Slip Detection and Repair for BeiDou-3 Triple-Frequency Signals. Int. J. Adv. Robot. Syst. 2020, 17, 1–14. [Google Scholar] [CrossRef]
- Zhu, S.; Yue, D.; He, L.; Chen, J.; Liu, Z. Modeling and Performance Assessment of BDS-2/BDS-3 Triple-Frequency Ionosphere-Free and Uncombined Precise Point Positioning. Measurement 2021, 180, 109564. [Google Scholar] [CrossRef]
- Zhang, S.; Fang, L.; Wang, G.; Li, W. The impact of second-order ionospheric delays on the ZWD estimation with GPS and BDS measurements. GPS Solut. 2020, 24, 41. [Google Scholar] [CrossRef]
- Li, J.; Yang, Y.; Xu, J.; He, H.; Guo, H. Ionosphere-free combinations for triple-frequency GNSS with application in rapid ambiguity resolution over medium-long baselines. In Proceedings of the China Sat Nav Conf (CSNC), Guangzhou, China, 17–20 May 2012; pp. 173–187. [Google Scholar]

| BDS-2 | BDS-3 | |||
|---|---|---|---|---|
| Frequency (MHz) | Wavelength (cm) | Frequency (MHz) | Wavelength (cm) | |
| f1 | B1I: 1561.098 | 19.20 | B1C: 1575.420 | 19.03 |
| f2 | B3I: 1268.520 | 23.63 | B1I: 1561.098 | 19.20 |
| f3 | B2I: 1207.140 | 24.83 | B3I: 1268.520 | 23.63 |
| f4 | / | / | B2b: 1207.140 | 24.83 |
| f5 | / | / | B2a: 1176.450 | 25.48 |
| BDS-2 | BDS-3 | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| B1I | B3I | B2I | B1C | B1I | B3I | B2b | B2a | ||
| B1I | 1:1 | 763:620 | 763:590 | B1C | 1:1 | 110:109 | 77:62 | 77:59 | 154:115 |
| B3I | 1:1 | 62:59 | B1I | 1:1 | 763:620 | 763:590 | 763:575 | ||
| B2I | 1:1 | B3I | 1:1 | 62:59 | 124:115 | ||||
| B2b | 1:1 | 118:115 | |||||||
| B2a | 1:1 | ||||||||
| Frequency Number | Combination Mode |
|---|---|
| TF | (B1I, B3I, B2I) |
| (B1C, B1I, B2a), (B1C, B3I, B2a), (B1C, B1I, B3I), (B1I, B3I, B2a) | |
| QF | (B1C, B1I, B3I, B2a) |
| FF | (B1C, B1I, B3I, B2b, B2a) |
| a1 | a2 | a3 | S_a | |||||||
|---|---|---|---|---|---|---|---|---|---|---|
| −1 | 6 | −5 | 0 | 20.932 | 84.286 | −8.963 | −0.428 | 164.821 | 7.874 | 1 |
| 1 | −5 | 4 | 0 | 6.371 | 25.652 | 0.652 | 0.102 | 41.287 | 6.481 | 1 |
| 0 | 1 | −1 | 0 | 4.884 | 19.667 | −1.591 | −0.326 | 6.907 | 1.414 | 1 |
| −1 | 7 | −6 | 0 | 3.960 | 15.946 | −2.986 | −0.754 | 36.725 | 9.274 | 1 |
| 1 | −4 | 3 | 0 | 2.765 | 11.132 | −0.618 | −0.223 | 14.097 | 5.099 | 1 |
| −3 | −2 | 6 | 1 | 13.321 | 53.636 | 159.400 | 11.966 | 93.244 | 7.000 | 1 |
| 4 | −3 | −2 | −1 | 12.211 | 49.167 | −144.867 | −11.864 | 65.756 | 5.385 | 1 |
| −4 | 4 | 1 | 1 | 8.140 | 32.778 | 93.925 | 11.538 | 46.763 | 5.745 | 1 |
| 3 | 3 | −7 | −1 | 7.712 | 31.053 | −94.797 | −12.292 | 63.125 | 8.185 | 1 |
| 5 | −8 | 2 | −1 | 4.186 | 16.857 | −49.240 | −11.762 | 40.373 | 9.644 | 1 |
| −3 | −1 | 5 | 1 | 3.574 | 14.390 | 41.601 | 11.641 | 21.143 | 5.916 | 1 |
| 4 | −2 | −3 | −1 | 3.489 | 14.048 | −42.527 | −12.190 | 18.787 | 5.385 | 1 |
| −4 | 5 | 0 | 1 | 3.053 | 12.292 | 34.227 | 11.212 | 19.546 | 6.403 | 1 |
| 3 | 4 | −8 | −1 | 2.990 | 12.041 | −37.732 | −12.618 | 28.211 | 9.434 | 1 |
| 4 | 2 | −5 | 1 | 0.109 | 0.440 | −0.003 | −0.025 | 0.732 | 6.708 | 1 |
| 5 | −3 | −1 | 1 | 0.107 | 0.432 | 0.008 | 0.077 | 0.635 | 5.916 | 1 |
| a1 | a2 | a3 | a4 | a5 | S_a | |||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| (B1C, B1I, B2a) | ||||||||||||
| 1 | −1 | / | / | 0 | 0 | 20.932 | 82.143 | −1.009 | −0.048 | 29.603 | 1.414 | 1 |
| 2 | 1 | / | / | −4 | −1 | 48.842 | 191.667 | −602.486 | −12.335 | 223.822 | 4.583 | 1 |
| −1 | −2 | / | / | 4 | 1 | 36.632 | 143.750 | 450.098 | 12.287 | 167.867 | 4.583 | 1 |
| 3 | 0 | / | / | −4 | −1 | 14.653 | 57.500 | −181.452 | −12.384 | 73.263 | 5.000 | 1 |
| 0 | −3 | / | / | 4 | 1 | 13.321 | 52.273 | 163.030 | 12.239 | 66.603 | 5.000 | 1 |
| 1 | −4 | / | / | 4 | 1 | 8.140 | 31.944 | 99.237 | 12.191 | 46.763 | 5.745 | 1 |
| 2 | −5 | / | / | 4 | 1 | 5.861 | 23.000 | 71.168 | 12.143 | 39.317 | 6.708 | 1 |
| 3 | −6 | / | / | 4 | 1 | 4.579 | 17.969 | 55.379 | 12.094 | 35.763 | 7.810 | 1 |
| 4 | −7 | / | / | 4 | 1 | 3.757 | 14.744 | 45.258 | 12.046 | 33.814 | 9.000 | 1 |
| 4 | −1 | / | / | −4 | −1 | 8.619 | 33.824 | −107.152 | −12.432 | 49.513 | 5.745 | 1 |
| 5 | −2 | / | / | −4 | −1 | 6.105 | 23.958 | −76.194 | −12.480 | 40.955 | 6.708 | 1 |
| 6 | −3 | / | / | −4 | −1 | 4.727 | 18.548 | −59.217 | −12.528 | 36.916 | 7.810 | 1 |
| 7 | −4 | / | / | −4 | −1 | 3.856 | 15.132 | −48.494 | −12.576 | 34.704 | 9.000 | 1 |
| −3 | −3 | / | / | 8 | 2 | 146.526 | 575.000 | 3607.851 | 24.623 | 1326.851 | 9.055 | 1 |
| 1 | 3 | / | / | −3 | 1 | 0.110 | 0.431 | 0.006 | 0.053 | 0.479 | 4.359 | 1 |
| 2 | 2 | / | / | −3 | 1 | 0.109 | 0.429 | 0.001 | 0.005 | 0.451 | 4.123 | 1 |
| 3 | 1 | / | / | −3 | 1 | 0.109 | 0.427 | −0.005 | −0.043 | 0.474 | 4.359 | 1 |
| 4 | 0 | / | / | −3 | 1 | 0.108 | 0.424 | −0.010 | −0.091 | 0.541 | 5.000 | 1 |
| (B1C, B3I, B2a) | ||||||||||||
| 1 | / | −4 | / | 3 | 0 | 9.768 | 38.333 | 2.549 | 0.261 | 49.809 | 5.099 | 1 |
| −1 | / | 5 | / | −4 | 0 | 4.884 | 19.167 | −3.769 | −0.772 | 31.653 | 6.481 | 1 |
| 0 | / | 1 | / | −1 | 0 | 3.256 | 12.778 | −1.663 | −0.511 | 4.605 | 1.414 | 1 |
| −2 | / | −4 | / | 7 | 1 | 29.305 | 115.000 | 370.550 | 12.645 | 243.427 | 8.307 | 1 |
| 3 | / | 0 | / | −4 | −1 | 14.653 | 57.500 | −181.452 | −12.384 | 73.263 | 5.000 | 1 |
| −4 | / | 5 | / | 0 | 1 | 7.326 | 28.750 | 85.073 | 11.612 | 46.911 | 6.403 | 1 |
| 4 | / | −4 | / | −1 | −1 | 5.861 | 23.000 | −71.052 | −12.123 | 33.669 | 5.745 | 1 |
| −3 | / | 1 | / | 3 | 1 | 4.186 | 16.429 | 49.705 | 11.873 | 18.248 | 4.359 | 1 |
| 2 | / | 5 | / | −8 | −1 | 3.663 | 14.375 | −48.190 | −13.155 | 35.326 | 9.644 | 1 |
| 5 | / | −8 | / | 2 | −1 | 3.663 | 14.375 | −43.452 | −11.862 | 35.326 | 9.644 | 1 |
| −2 | / | −3 | / | 6 | 1 | 2.931 | 11.500 | 35.558 | 12.134 | 20.514 | 7.000 | 1 |
| 3 | / | 1 | / | −5 | −1 | 2.664 | 10.455 | −34.352 | −12.894 | 15.761 | 5.916 | 1 |
| 2 | / | −7 | / | 5 | 0 | 1.954 | 7.667 | 0.022 | 0.011 | 17.254 | 8.832 | 1 |
| 4 | / | 0 | / | −3 | 1 | 0.108 | 0.424 | −0.010 | −0.091 | 0.541 | 5.000 | 1 |
| 6 | / | −7 | / | 2 | 1 | 0.102 | 0.402 | −0.008 | −0.080 | 0.967 | 9.434 | 1 |
| (B1C, B1I, B3I) | ||||||||||||
| 1 | −1 | 0 | / | / | 0 | 20.932 | 88.571 | −1.009 | −0.048 | 29.603 | 1.414 | 1 |
| 7 | −3 | −5 | / | / | −1 | 146.526 | 620.000 | −1722.644 | −11.757 | 1334.917 | 9.110 | 1 |
| −6 | 2 | 5 | / | / | 1 | 24.421 | 103.333 | 285.930 | 11.708 | 196.889 | 8.062 | 1 |
| −5 | 1 | 5 | / | / | 1 | 11.271 | 47.692 | 131.424 | 11.660 | 80.493 | 7.141 | 1 |
| −4 | 0 | 5 | / | / | 1 | 7.326 | 31.000 | 85.073 | 11.612 | 46.911 | 6.403 | 1 |
| −3 | −1 | 5 | / | / | 1 | 5.427 | 22.963 | 62.755 | 11.564 | 32.106 | 5.916 | 1 |
| −2 | −2 | 5 | / | / | 1 | 4.310 | 18.235 | 49.627 | 11.516 | 24.757 | 5.745 | 1 |
| −1 | −3 | 5 | / | / | 1 | 3.574 | 15.122 | 40.982 | 11.467 | 21.143 | 5.916 | 1 |
| 0 | −4 | 5 | / | / | 1 | 3.053 | 12.917 | 34.858 | 11.419 | 19.546 | 6.403 | 1 |
| 1 | −5 | 5 | / | / | 1 | 2.664 | 11.273 | 30.293 | 11.371 | 19.026 | 7.141 | 1 |
| 2 | −6 | 5 | / | / | 1 | 2.363 | 10.000 | 26.759 | 11.323 | 19.054 | 8.062 | 1 |
| 7 | −2 | −4 | / | / | 1 | 0.106 | 0.448 | 0.008 | 0.073 | 0.879 | 8.307 | 1 |
| 8 | −3 | −4 | / | / | 1 | 0.105 | 0.446 | 0.003 | 0.025 | 0.994 | 9.434 | 1 |
| (B1I, B3I, B2a) | ||||||||||||
| / | 1 | −4 | / | 3 | 0 | 18.316 | 71.875 | 5.559 | 0.304 | 93.392 | 5.099 | 1 |
| / | −1 | 5 | / | −4 | 0 | 3.960 | 15.541 | −3.188 | −0.805 | 25.665 | 6.481 | 1 |
| / | 0 | 1 | / | −1 | 0 | 3.256 | 12.778 | −1.633 | −0.502 | 4.605 | 1.414 | 1 |
| / | 1 | −3 | / | 2 | 0 | 2.765 | 10.849 | −0.547 | −0.198 | 10.344 | 3.742 | 1 |
| / | −4 | 4 | / | 1 | 1 | 48.842 | 191.667 | 572.132 | 11.714 | 280.576 | 5.745 | 1 |
| / | 5 | −8 | / | 2 | −1 | 29.305 | 115.000 | −334.384 | −11.410 | 282.609 | 9.644 | 1 |
| / | −3 | 0 | / | 4 | 1 | 13.321 | 52.273 | 160.079 | 12.017 | 66.603 | 5.000 | 1 |
| / | −2 | −4 | / | 7 | 1 | 7.712 | 30.263 | 95.018 | 12.321 | 64.060 | 8.307 | 1 |
| / | 2 | 5 | / | −8 | −1 | 5.636 | 22.115 | −72.263 | −12.823 | 54.348 | 9.644 | 1 |
| / | 3 | 1 | / | −5 | −1 | 4.310 | 16.912 | −53.952 | −12.519 | 25.496 | 5.916 | 1 |
| / | 4 | −3 | / | −2 | −1 | 3.489 | 13.690 | −42.616 | −12.215 | 18.787 | 5.385 | 1 |
| / | −4 | 5 | / | 0 | 1 | 3.053 | 11.979 | 34.227 | 11.212 | 19.546 | 6.403 | 1 |
| / | 5 | −7 | / | 1 | −1 | 2.931 | 11.500 | −34.908 | −11.912 | 25.379 | 8.660 | 1 |
| / | −3 | 1 | / | 3 | 1 | 2.617 | 10.268 | 30.132 | 11.516 | 11.405 | 4.359 | 1 |
| / | 4 | 0 | / | −3 | 1 | 0.110 | 0.433 | 0.011 | 0.100 | 0.552 | 5.000 | 1 |
| / | 5 | −3 | / | −1 | 1 | 0.106 | 0.417 | −0.010 | −0.098 | 0.628 | 5.916 | 1 |
| a1 | a2 | a3 | a4 | a5 | S_a | |||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| (B1C, B1I, B3I, B2a) | ||||||||||||
| 1 | −1 | 0 | / | 0 | 0 | 20.932 | 82.143 | −1.009 | −0.048 | 29.603 | 1.414 | 1 |
| 0 | 1 | −4 | / | 3 | 0 | 18.316 | 71.875 | 5.662 | 0.309 | 93.392 | 5.099 | 1 |
| −5 | 6 | −3 | / | 2 | 0 | 8.140 | 31.944 | 0.321 | 0.039 | 70.026 | 8.602 | 1 |
| −4 | 5 | −3 | / | 2 | 0 | 5.861 | 23.000 | −0.052 | −0.009 | 43.070 | 7.348 | 1 |
| −3 | 4 | −3 | / | 2 | 0 | 4.579 | 17.969 | −0.261 | −0.057 | 28.226 | 6.164 | 1 |
| 4 | −3 | −4 | / | 3 | 0 | 4.070 | 15.972 | 0.473 | 0.116 | 28.780 | 7.071 | 1 |
| −1 | 1 | 1 | / | −1 | 0 | 3.856 | 15.132 | −1.784 | −0.463 | 7.712 | 2.000 | 1 |
| −2 | 3 | −3 | / | 2 | 0 | 3.757 | 14.744 | −0.395 | −0.105 | 19.157 | 5.099 | 1 |
| 0 | 0 | 1 | / | −1 | 0 | 3.256 | 12.778 | −1.663 | −0.511 | 4.605 | 1.414 | 1 |
| −1 | 2 | −3 | / | 2 | 0 | 3.185 | 12.500 | −0.489 | −0.153 | 13.514 | 4.243 | 1 |
| 6 | −5 | −4 | / | 3 | 0 | 2.931 | 11.500 | 0.058 | 0.020 | 27.177 | 9.274 | 1 |
| 1 | −1 | 1 | / | −1 | 0 | 2.818 | 11.058 | −1.575 | −0.559 | 5.636 | 2.000 | 1 |
| 0 | 1 | −3 | / | 2 | 0 | 2.765 | 10.849 | −0.557 | −0.202 | 10.344 | 3.742 | 1 |
| 1 | 3 | 0 | / | −3 | 1 | 0.110 | 0.431 | 0.006 | 0.053 | 0.479 | 4.359 | 1 |
| 2 | 2 | 0 | / | −3 | 1 | 0.109 | 0.429 | 0.001 | 0.005 | 0.451 | 4.123 | 1 |
| 3 | 1 | 0 | / | −3 | 1 | 0.109 | 0.427 | −0.005 | −0.043 | 0.474 | 4.359 | 1 |
| −2 | 7 | −3 | / | −1 | 1 | 0.107 | 0.421 | 0.000 | −0.004 | 0.851 | 7.937 | 1 |
| (B1C, B1I, B3I, B2b, B2a) | ||||||||||||
| 1 | −1 | 0 | 0 | 0 | 0 | 20.932 | 82.143 | −1.009 | −0.048 | 29.603 | 1.414 | 1 |
| 1 | −1 | 2 | −6 | 4 | 0 | 20.932 | 82.143 | 0.078 | 0.004 | 159.416 | 7.616 | 1 |
| −4 | 5 | −3 | 0 | 2 | 0 | 5.861 | 23.000 | −0.052 | −0.009 | 43.070 | 7.348 | 1 |
| −1 | 2 | −4 | 2 | 1 | 0 | 4.727 | 18.548 | −0.002 | 0.000 | 24.101 | 5.099 | 1 |
| −3 | 4 | −1 | −6 | 6 | 0 | 4.579 | 17.969 | −0.023 | −0.005 | 45.329 | 9.899 | 1 |
| 2 | −1 | −5 | 4 | 0 | 0 | 3.960 | 15.541 | 0.031 | 0.008 | 26.859 | 6.782 | 1 |
| 2 | −1 | −6 | 7 | −2 | 0 | 3.960 | 15.541 | −0.072 | −0.018 | 38.395 | 9.695 | 1 |
| 0 | 1 | −2 | −4 | 5 | 0 | 3.856 | 15.132 | 0.012 | 0.003 | 26.152 | 6.782 | 1 |
| 3 | −2 | −3 | −2 | 4 | 0 | 3.330 | 13.068 | 0.038 | 0.012 | 21.582 | 6.481 | 1 |
| 3 | −2 | −4 | 1 | 2 | 0 | 3.330 | 13.068 | −0.048 | −0.014 | 19.418 | 5.831 | 1 |
| 0 | 0 | 1 | 0 | −1 | 0 | 3.256 | 12.778 | −1.663 | −0.511 | 4.605 | 1.414 | 1 |
| 6 | −5 | −4 | 0 | 3 | 0 | 2.931 | 11.500 | 0.058 | 0.020 | 27.177 | 9.274 | 1 |
| 6 | −5 | −5 | 3 | 1 | 0 | 2.931 | 11.500 | −0.018 | −0.006 | 28.713 | 9.798 | 1 |
| 4 | −3 | −2 | −5 | 6 | 0 | 2.873 | 11.275 | −0.031 | −0.011 | 27.256 | 9.487 | 1 |
| 2 | 1 | 2 | 4 | −8 | 1 | 0.112 | 0.441 | 2.0 × 10−4 | 1.8 × 10−3 | 1.061 | 9.434 | 1 |
| 2 | 2 | 1 | −3 | −1 | 1 | 0.109 | 0.429 | 3.4 × 10−3 | 3.1 × 10−2 | 0.476 | 4.359 | 1 |
| 0 | 4 | 3 | −8 | 2 | 1 | 0.109 | 0.428 | 5.0 × 10−5 | 4.6 × 10−4 | 1.053 | 9.644 | 1 |
| 3 | 1 | 0 | 0 | −3 | 1 | 0.109 | 0.427 | −4.7 × 10−3 | −4.3 × 10−2 | 0.474 | 4.359 | 1 |
| 1 | 4 | −4 | 2 | −2 | 1 | 0.107 | 0.419 | 4.8 × 10−4 | 4.5 × 10−3 | 0.684 | 6.403 | 1 |
| −1 | 6 | −1 | −6 | 3 | 1 | 0.107 | 0.419 | −3.8 × 10−6 | −3.6 × 10−5 | 0.972 | 9.110 | 1 |
| 1 | 7 | 1 | −2 | −5 | 2 | 0.055 | 0.215 | 9.6 × 10−5 | 1.8 × 10−3 | 0.490 | 8.944 | 1 |
| a1 | a2 | a3 | S_a | ||||
|---|---|---|---|---|---|---|---|
| −10 | 38 | −27 | 1 | 47.676 | 9.621 | 0.143 | 0.070 |
| 40 | −211 | 170 | −1 | 273.900 | 0.944 | 0.002 | 4.102 |
| −50 | 249 | −197 | 2 | 321.419 | 8.677 | 0.019 | 0.524 |
| 30 | −173 | 143 | 0 | 226.446 | 10.565 | 0.033 | 0.303 |
| −60 | 287 | −224 | 3 | 368.978 | 18.297 | 0.035 | 0.285 |
| 50 | −308 | 259 | 1 | 405.518 | 30.751 | 0.054 | 0.186 |
| 20 | −135 | 116 | 1 | 179.112 | 20.186 | 0.080 | 0.125 |
| 0 | −59 | 62 | 3 | 85.586 | 39.427 | 0.326 | 0.031 |
| a1 | a2 | a3 | a4 | a5 | S_a | ||||
|---|---|---|---|---|---|---|---|---|---|
| (B1C, B1I, B2a) | |||||||||
| −30 | 25 | / | / | 7 | 2 | 39.674 | 24.190 | 0.431 | 0.023 |
| 188 | −195 | / | / | 7 | 0 | 270.958 | 3.074 | 0.008 | 1.247 |
| −297 | 305 | / | / | −7 | 1 | 425.773 | 7.484 | 0.012 | 0.805 |
| 267 | −280 | / | / | 14 | 1 | 387.150 | 16.706 | 0.031 | 0.328 |
| −109 | 110 | / | / | 0 | 1 | 154.858 | 10.558 | 0.048 | 0.207 |
| 79 | −85 | / | / | 7 | 1 | 116.254 | 13.632 | 0.083 | 0.121 |
| −139 | 135 | / | / | 7 | 3 | 193.894 | 34.749 | 0.127 | 0.079 |
| 49 | −60 | / | / | 14 | 3 | 78.721 | 37.822 | 0.340 | 0.029 |
| (B1C, B3I, B2a) | |||||||||
| −10 | / | 5 | / | 8 | 3 | 13.748 | 36.379 | 1.871 | 0.005 |
| −94 | / | 369 | / | −272 | 3 | 467.954 | 0.161 | 0.000 | 41.000 |
| 97 | / | −382 | / | 282 | −3 | 484.620 | 1.132 | 0.002 | 6.054 |
| −91 | / | 356 | / | −262 | 3 | 451.288 | 1.455 | 0.002 | 4.387 |
| −88 | / | 343 | / | −252 | 3 | 434.623 | 2.748 | 0.004 | 2.236 |
| −85 | / | 330 | / | −242 | 3 | 417.958 | 4.042 | 0.007 | 1.462 |
| −79 | / | 304 | / | −222 | 3 | 384.631 | 6.629 | 0.012 | 0.821 |
| −76 | / | 291 | / | −212 | 3 | 367.969 | 7.922 | 0.015 | 0.657 |
| 3 | / | −13 | / | 10 | 0 | 16.673 | 1.293 | 0.055 | 0.182 |
| −49 | / | 174 | / | −122 | 3 | 218.085 | 19.564 | 0.063 | 0.158 |
| (B1C, B1I, B3I) | |||||||||
| −41 | 30 | 14 | / | / | 3 | 52.697 | 35.011 | 0.470 | 0.021 |
| 143 | −150 | 7 | / | / | 0 | 207.360 | 1.668 | 0.006 | 1.758 |
| −252 | 260 | −7 | / | / | 1 | 362.151 | 8.890 | 0.017 | 0.576 |
| 320 | −340 | 21 | / | / | 1 | 467.377 | 15.562 | 0.024 | 0.425 |
| 177 | −190 | 14 | / | / | 1 | 260.048 | 13.894 | 0.038 | 0.265 |
| 211 | −230 | 21 | / | / | 2 | 312.829 | 26.120 | 0.059 | 0.169 |
| 245 | −270 | 28 | / | / | 3 | 365.662 | 38.347 | 0.074 | 0.135 |
| (B1I, B3I, B2a) | |||||||||
| / | −10 | 29 | / | −18 | 1 | 35.567 | 9.391 | 0.187 | 0.054 |
| / | −65 | 246 | / | −179 | 2 | 311.098 | 1.112 | 0.003 | 3.957 |
| / | 55 | −217 | / | 161 | −1 | 275.744 | 8.280 | 0.021 | 0.471 |
| / | −75 | 275 | / | −197 | 3 | 346.495 | 10.503 | 0.021 | 0.467 |
| / | 45 | −188 | / | 143 | 0 | 240.454 | 17.671 | 0.052 | 0.192 |
| / | 80 | −347 | / | 268 | 1 | 445.683 | 44.733 | 0.071 | 0.141 |
| / | 35 | −159 | / | 125 | 1 | 205.258 | 27.062 | 0.093 | 0.107 |
| / | 25 | −130 | / | 107 | 2 | 170.218 | 36.453 | 0.151 | 0.066 |
| a1 | a2 | a3 | a4 | a5 | S_a | ||||
|---|---|---|---|---|---|---|---|---|---|
| (B1C, B1I, B3I, B2a) | |||||||||
| −2 | −5 | 4 | / | 5 | 2 | 8.367 | 24.265 | 2.051 | 0.005 |
| −8 | 5 | 1 | / | 3 | 1 | 9.950 | 12.114 | 0.861 | 0.012 |
| 14 | −15 | 2 | / | −1 | 0 | 20.640 | 0.037 | 0.001 | 7.795 |
| −39 | 45 | −19 | / | 13 | 0 | 63.844 | 1.181 | 0.013 | 0.764 |
| 45 | −45 | −7 | / | 7 | 0 | 64.405 | 1.406 | 0.015 | 0.648 |
| −25 | 30 | −17 | / | 12 | 0 | 44.249 | 1.219 | 0.019 | 0.514 |
| 31 | −30 | −9 | / | 8 | 0 | 44.788 | 1.368 | 0.022 | 0.463 |
| −11 | 15 | −15 | / | 11 | 0 | 26.306 | 1.256 | 0.034 | 0.296 |
| 17 | −15 | −11 | / | 9 | 0 | 26.758 | 1.331 | 0.035 | 0.284 |
| 20 | −15 | −24 | / | 19 | 0 | 39.522 | 2.624 | 0.047 | 0.213 |
| (B1C, B1I, B3I, B2b, B2a) | |||||||||
| 0 | 0 | 1 | −3 | 2 | 0 | 3.742 | 0.026 | 0.005 | 2.037 |
| 1 | 0 | −5 | 2 | 2 | 0 | 5.831 | 0.414 | 0.050 | 0.199 |
| −27 | 30 | −22 | 41 | −22 | 0 | 65.406 | 0.001 | 1 × 10−5 | 693.743 |
| −1 | 0 | 21 | −50 | 30 | 0 | 61.984 | 0.002 | 2 × 10−5 | 519.787 |
| 41 | −45 | 23 | −38 | 19 | 0 | 77.717 | 0.010 | 9 × 10−5 | 108.367 |
| 42 | −45 | 2 | 12 | −11 | 0 | 63.702 | 0.008 | 9 × 10−5 | 106.540 |
| −13 | 15 | −21 | 44 | −25 | 0 | 58.275 | 0.013 | 2 × 10−4 | 64.341 |
| 1 | 0 | −20 | 47 | −28 | 0 | 58.258 | 0.024 | 3 × 10−4 | 33.927 |
| 14 | −15 | 1 | 3 | −3 | 0 | 20.976 | 0.011 | 4 × 10−4 | 25.850 |
| 28 | −30 | 3 | 3 | −4 | 0 | 41.449 | 0.049 | 0.001 | 11.982 |
| −14 | 15 | 1 | −9 | 7 | 0 | 23.495 | 0.040 | 0.001 | 8.211 |
| 14 | −15 | 3 | −3 | 1 | 0 | 20.976 | 0.063 | 0.002 | 4.678 |
| 14 | −15 | 5 | −9 | 5 | 0 | 23.495 | 0.115 | 0.003 | 2.880 |
| 1 | 0 | −12 | 23 | −12 | 0 | 28.601 | 0.232 | 0.006 | 1.743 |
| 1 | 0 | −11 | 20 | −10 | 0 | 24.940 | 0.258 | 0.007 | 1.367 |
| 1 | 0 | −10 | 17 | −8 | 0 | 21.307 | 0.284 | 0.009 | 1.061 |
| a1 | a2 | a3 | S_a | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 62 | −59 | 0.000 | 10.590 | −9.590 | 40.365 | 85.586 | 3.455 | 14.286 | 3 | 1 |
| 763 | −620 | 0 | 2.944 | −1.944 | 0.000 | 0.741 | 983.142 | 0.728 | 3.527 | 143 | 1 |
| 763 | −558 | −59 | 2.891 | −1.718 | −0.173 | 0.728 | 947.108 | 0.689 | 3.367 | 146 | 1 |
| 763 | −186 | −413 | 2.609 | −0.517 | −1.092 | 0.657 | 887.318 | 0.583 | 2.875 | 164 | 1 |
| 763 | −124 | −472 | 2.567 | −0.339 | −1.228 | 0.646 | 905.720 | 0.585 | 2.865 | 167 | 1 |
| 763 | −248 | −354 | 2.652 | −0.700 | −0.951 | 0.667 | 876.920 | 0.585 | 2.903 | 161 | 1 |
| 763 | −310 | −295 | 2.696 | −0.890 | −0.806 | 0.679 | 874.811 | 0.594 | 2.952 | 158 | 1 |
| 763 | −62 | −531 | 2.526 | −0.167 | −1.360 | 0.636 | 931.651 | 0.592 | 2.874 | 170 | 1 |
| a1 | a2 | a3 | a4 | a5 | S_a | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| (B1C, B1I, B2a) | |||||||||||||||
| 110 | −109 | / | / | 0 | 55.25 | −54.25 | / | / | 0.00 | 95.58 | 154.86 | 14.80 | 77.43 | 1 | 1 |
| 154 | 0 | / | / | −115 | 2.26 | 0.00 | / | / | −1.26 | 2.79 | 192.20 | 0.54 | 2.59 | 39 | 1 |
| 44 | 109 | / | / | −115 | 0.67 | 1.63 | / | / | −1.30 | 2.88 | 164.44 | 0.47 | 2.19 | 38 | 1 |
| 242 | 218 | / | / | −345 | 1.21 | 1.08 | / | / | −1.29 | 0.95 | 474.46 | 0.45 | 2.07 | 115 | 1 |
| 286 | 327 | / | / | −460 | 1.07 | 1.22 | / | / | −1.29 | 0.71 | 632.71 | 0.45 | 2.07 | 153 | 1 |
| (B1C, B3I, B2a) | |||||||||||||||
| 154 | / | −496 | / | 345 | 12.57 | / | −32.59 | / | 21.03 | 15.53 | 623.50 | 9.68 | 40.77 | 3 | 1 |
| 77 | / | −186 | / | 115 | 5.87 | / | −11.42 | / | 6.55 | 14.51 | 231.84 | 3.37 | 14.42 | 6 | 1 |
| 77 | / | −62 | / | 0 | 2.84 | / | −1.84 | / | 0.00 | 7.03 | 98.86 | 0.69 | 3.39 | 15 | 1 |
| 385 | / | −62 | / | −230 | 2.36 | / | −0.31 | / | −1.05 | 1.17 | 452.74 | 0.53 | 2.60 | 93 | 1 |
| 616 | / | −124 | / | −345 | 2.38 | / | −0.39 | / | −1.00 | 0.74 | 716.84 | 0.53 | 2.61 | 147 | 1 |
| 693 | / | −62 | / | −460 | 2.31 | / | −0.17 | / | −1.15 | 0.64 | 834.08 | 0.53 | 2.59 | 171 | 1 |
| (B1C, B1I, B3I) | |||||||||||||||
| 187 | −109 | −62 | / | / | 6.43 | −3.72 | −1.72 | / | / | 6.55 | 225.15 | 1.47 | 7.62 | 16 | 1 |
| 297 | −218 | −62 | / | / | 9.56 | −6.95 | −1.61 | / | / | 6.13 | 373.60 | 2.29 | 11.93 | 17 | 1 |
| 121 | 109 | −186 | / | / | 1.53 | 1.36 | −1.89 | / | / | 2.40 | 247.22 | 0.59 | 2.79 | 44 | 1 |
| 440 | 327 | −620 | / | / | 1.66 | 1.22 | −1.89 | / | / | 0.72 | 827.60 | 0.59 | 2.80 | 147 | 1 |
| 407 | 436 | −682 | / | / | 1.40 | 1.49 | −1.89 | / | / | 0.66 | 906.02 | 0.59 | 2.79 | 161 | 1 |
| 44 | 109 | −124 | / | / | 0.84 | 2.07 | −1.91 | / | / | 3.65 | 170.86 | 0.62 | 2.94 | 29 | 1 |
| (B1I, B3I, B2a) | |||||||||||||||
| / | 0 | 124 | / | −115 | / | 0.00 | 7.15 | / | −6.15 | 13.62 | 169.12 | 2.30 | 9.43 | 9 | 1 |
| / | 763 | −620 | / | 0 | / | 2.94 | −1.94 | / | 0.00 | 0.74 | 983.14 | 0.73 | 3.53 | 143 | 1 |
| / | 763 | −124 | / | −460 | / | 2.42 | −0.32 | / | −1.10 | 0.61 | 899.52 | 0.55 | 2.67 | 179 | 1 |
| / | 763 | −248 | / | −345 | / | 2.53 | −0.67 | / | −0.86 | 0.64 | 873.33 | 0.56 | 2.76 | 170 | 1 |
| / | 763 | 0 | / | −575 | / | 2.31 | 0.00 | / | −1.31 | 0.58 | 955.40 | 0.56 | 2.66 | 188 | 1 |
| (B1C, B1I, B3I, B2a) | |||||||||||||||
| 187 | −109 | −186 | / | 115 | 12.38 | −7.15 | −9.92 | 0.00 | 5.69 | 12.60 | 307.69 | 3.88 | 18.31 | 7 | 1 |
| 110 | −109 | 124 | / | −115 | 6.89 | −6.77 | 6.26 | 0.00 | −5.38 | 11.92 | 229.31 | 2.73 | 12.71 | 10 | 1 |
| 121 | 109 | −62 | / | −115 | 1.30 | 1.16 | −0.54 | 0.00 | −0.92 | 2.04 | 208.78 | 0.43 | 2.04 | 53 | 1 |
| 165 | 218 | −62 | / | −230 | 1.04 | 1.36 | −0.31 | 0.00 | −1.08 | 1.19 | 362.62 | 0.43 | 2.04 | 91 | 1 |
| (B1C, B1I, B3I, B2b, B2a) | |||||||||||||||
| 0 | 0 | 62 | −177 | 115 | 0.00 | 0.00 | 284.74 | −773.56 | 489.81 | 1085.38 | 220.00 | 238.78 | 958.85 | 0 | 1 |
| 110 | −109 | −62 | 177 | −115 | 60.59 | −59.49 | −27.50 | 74.70 | −47.30 | 104.81 | 269.03 | 28.20 | 125.63 | 1 | 1 |
| 110 | −109 | 62 | −177 | 115 | 50.78 | −49.86 | 23.05 | −62.61 | 39.64 | 87.85 | 269.03 | 23.63 | 105.29 | 1 | 1 |
| 121 | 109 | 0 | −59 | −115 | 1.24 | 1.10 | 0.00 | −0.46 | −0.88 | 1.94 | 207.91 | 0.40 | 1.93 | 56 | 1 |
| 198 | 109 | −62 | −59 | −115 | 1.58 | 0.86 | −0.40 | −0.36 | −0.69 | 1.52 | 267.65 | 0.41 | 2.00 | 71 | 1 |
| 198 | 109 | 0 | −118 | −115 | 1.53 | 0.83 | 0.00 | −0.70 | −0.66 | 1.47 | 279.70 | 0.41 | 1.99 | 74 | 1 |
| 77 | 0 | 0 | −59 | 0 | 2.42 | 0.00 | 0.00 | −1.42 | 0.00 | 5.99 | 97.01 | 0.58 | 2.81 | 18 | 1 |
| Frequency Number | B1I | B3I | B2I | Ω |
|---|---|---|---|---|
| GBIF_1 mode | ||||
| DF | 2.944 | 1.944 | / | 3.527 |
| 2.487 | / | −1.487 | 2.898 | |
| / | 10.590 | −9.590 | 14.286 | |
| TF | 2.566 | −0.338 | −1.229 | 2.865 |
| GBIF_2 mode | ||||
| QF | 9.100 | −28.157 | 20.057 | 35.748 |
| Frequency Number | B1C | B1I | B3I | B2b | B2a | Ω |
|---|---|---|---|---|---|---|
| GBIF_1 mode | ||||||
| DF | / | 2.944 | −1.944 | / | / | 3.527 |
| 55.251 | −54.251 | / | / | / | 77.433 | |
| 2.844 | / | −1.844 | / | / | 3.389 | |
| 2.422 | / | / | −1.422 | 2.809 | ||
| 2.261 | / | / | / | −1.261 | 2.588 | |
| / | 2.314 | / | / | −1.314 | 2.662 | |
| / | 7.148 | / | −6.148 | 9.429 | ||
| TF | 1.503 | 1.388 | −1.891 | / | / | 2.786 |
| 1.172 | 1.115 | / | / | −1.287 | 2.067 | |
| 2.290 | / | −0.094 | / | −1.196 | 2.586 | |
| / | 2.343 | −0.089 | / | −1.254 | 2.659 | |
| QF | 1.224 | 1.171 | −0.336 | / | −1.058 | 2.025 |
| FF | 1.216 | 1.170 | −0.123 | −0.520 | −0.742 | 1.919 |
| GBIF_2 mode | ||||||
| TF | 201.948 | −206.108 | 5.161 | / | / | 288.600 |
| 158.661 | −160.121 | / | / | 2.460 | 225.428 | |
| 7.943 | / | −17.968 | / | 11.025 | 22.528 | |
| / | 8.438 | −18.915 | / | 11.477 | 23.679 | |
| QF | 5.532 | 2.561 | −18.256 | / | 11.162 | 22.249 |
| FF | 5.495 | 2.555 | −17.629 | −1.370 | 11.949 | 22.184 |
| Frequency Number | B1C | B1I | B3I | B2b | B2a | Ω |
|---|---|---|---|---|---|---|
| GFIF_1 mode | ||||||
| TF | 1.000 | −1.035 | 0.035 | / | / | 1.440 |
| 1.000 | −1.024 | / | / | 0.024 | 1.431 | |
| 1.000 | / | −3.162 | / | 2.162 | 3.959 | |
| / | 1.000 | −3.089 | / | 2.089 | 3.860 | |
| QF | 1.000 | −0.958 | −0.202 | / | 0.160 | 1.409 |
| FF | 1.000 | −0.958 | −0.210 | 0.020 | 0.148 | 1.409 |
| GFIF_2 mode | ||||||
| QF | 1.000 | −1.062 | 0.119 | / | −0.057 | 1.465 |
| FF | 1.000 | −1.061 | 0.102 | 0.037 | −0.078 | 1.464 |
| Frequency Number | P | L | Δ | ||||
|---|---|---|---|---|---|---|---|
| B1C | B1C | B1I | B3I | B2b | B2a | ||
| MP_1 mode | |||||||
| DF | 1 | −109.502 | 108.502 | / | / | / | 154.154 |
| 1 | −4.687 | / | 3.687 | / | / | 5.964 | |
| 1 | −3.844 | / | / | 2.844 | / | 4.782 | |
| 1 | −3.521 | / | / | / | 2.521 | 4.331 | |
| TF | 1 | −2.489 | −2.276 | 3.765 | / | / | 5.054 |
| 1 | −1.832 | −1.730 | / | / | 2.561 | 3.593 | |
| 1 | −3.644 | / | 0.389 | / | 2.255 | 4.303 | |
| QF | 1 | −1.951 | −1.858 | 0.774 | / | 2.035 | 3.464 |
| FF | 1 | −1.935 | −1.857 | 0.352 | 1.030 | 1.410 | 3.220 |
| MP_2 mode | |||||||
| TF | 1 | −113.491 | 112.631 | −0.140 | / | / | 159.894 |
| 1 | −112.314 | 111.381 | / | / | −0.067 | 158.178 | |
| 1 | −7.474 | / | 12.499 | / | −6.025 | 15.760 | |
| QF | 1 | −4.845 | −2.793 | 12.812 | / | −6.174 | 15.282 |
| FF | 1 | −4.802 | −2.785 | 12.080 | 1.600 | −7.092 | 15.153 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Guo, Z.; Yu, X.; Hu, C.; Jiang, C.; Zhu, M. Research on Linear Combination Models of BDS Multi-Frequency Observations and Their Characteristics. Sustainability 2022, 14, 8644. https://doi.org/10.3390/su14148644
Guo Z, Yu X, Hu C, Jiang C, Zhu M. Research on Linear Combination Models of BDS Multi-Frequency Observations and Their Characteristics. Sustainability. 2022; 14(14):8644. https://doi.org/10.3390/su14148644
Chicago/Turabian StyleGuo, Zhongchen, Xuexiang Yu, Chao Hu, Chuang Jiang, and Mingfei Zhu. 2022. "Research on Linear Combination Models of BDS Multi-Frequency Observations and Their Characteristics" Sustainability 14, no. 14: 8644. https://doi.org/10.3390/su14148644
APA StyleGuo, Z., Yu, X., Hu, C., Jiang, C., & Zhu, M. (2022). Research on Linear Combination Models of BDS Multi-Frequency Observations and Their Characteristics. Sustainability, 14(14), 8644. https://doi.org/10.3390/su14148644





