Effective Realization of Multi-Objective Elitist Teaching–Learning Based Optimization Technique for the Micro-Siting of Wind Turbines

Abstract

In this paper, the meta-heuristic multi-objective elitist teaching–learning based optimization technique is implemented for wind farm layout discrete optimization problem. The optimization of wind farm layout addresses the optimum siting among the wind turbines within the wind farm to accomplish economical, profitable, and technical features. The presented methodology is implemented with multi-objective optimization problem through different targets such as minimizing cost, power output maximization, and the saving of the number of turbines. These targets are investigated with some case studies of multi-objective optimization problems in three scenarios of wind (Scenario-I: fixed wind direction and constant speed, Scenario-II: variable wind direction and constant speed, and Scenario-III: variable wind direction and variable speed) for the optimal micro-siting of wind turbines in a given land area that maximizes the power production while minimizing the total cost. To check the effectiveness of the algorithm, firstly, the results obtained for the three different scenarios have been compared with past studies available in the literature. Secondly, the numbers of turbines have also been optimized by using teaching–learning based optimization. It has been observed that the proposed algorithm shows the optimal layouts along with the optimal number of turbines with minimum fitness evaluation. Finally, the concept of elitism has been introduced in the teaching–learning based optimization algorithm. It is proposed that if elitist-teaching–learning based optimization with elite size of 15% is used, computational expense can be significantly reduced. It can be concluded that that the results obtained by the proposed algorithm are more accurate and advantageous than others.

1. Introduction

With ever-increasing demand for energy, the energy sources such as oil, natural gas, coal have contributed to meeting the demands since the beginning of the last century. The growth in population and technologic and economic developments suggest that this growth will escalate in the near future [1,2]. Currently, the production of energy has a prominent impact on the environment, natural ecosystems, human communities, and many other areas [3]. Keeping in mind these impacts, many efforts are underway to minimize the consumption of oil, coal, and other non-renewable energy resources. On the other hand, renewable energy systems are becoming the major candidates to meet the energy demand [4,5]. The renewable energy systems are cost effective, reliable, and environment friendly as compared to the traditional fossil fuels. For the sustainable energy supply, the renewable energy sources are proven to be proficient and effective solutions. Among all the types of renewable energy systems, wind energy installation has been experiencing a tremendous demand in the past few decades [6,7]. It has certain benefits over the other resources for reducing the hydrocarbons for producing electricity.

More than 80% of humanity’s energy need is fulfilled with fossil fuels. However, the world’s reliance on fossil fuels is decreasing and shifting towards clean and green renewable energy. Wind turbines are the best option for clean energy. Placing turbines with expert estimates produces less energy than an optimized layout of turbines. Large difference in energy production can be created by wisely selecting the positions of turbines. This can be done using an optimization algorithm in a computer program.

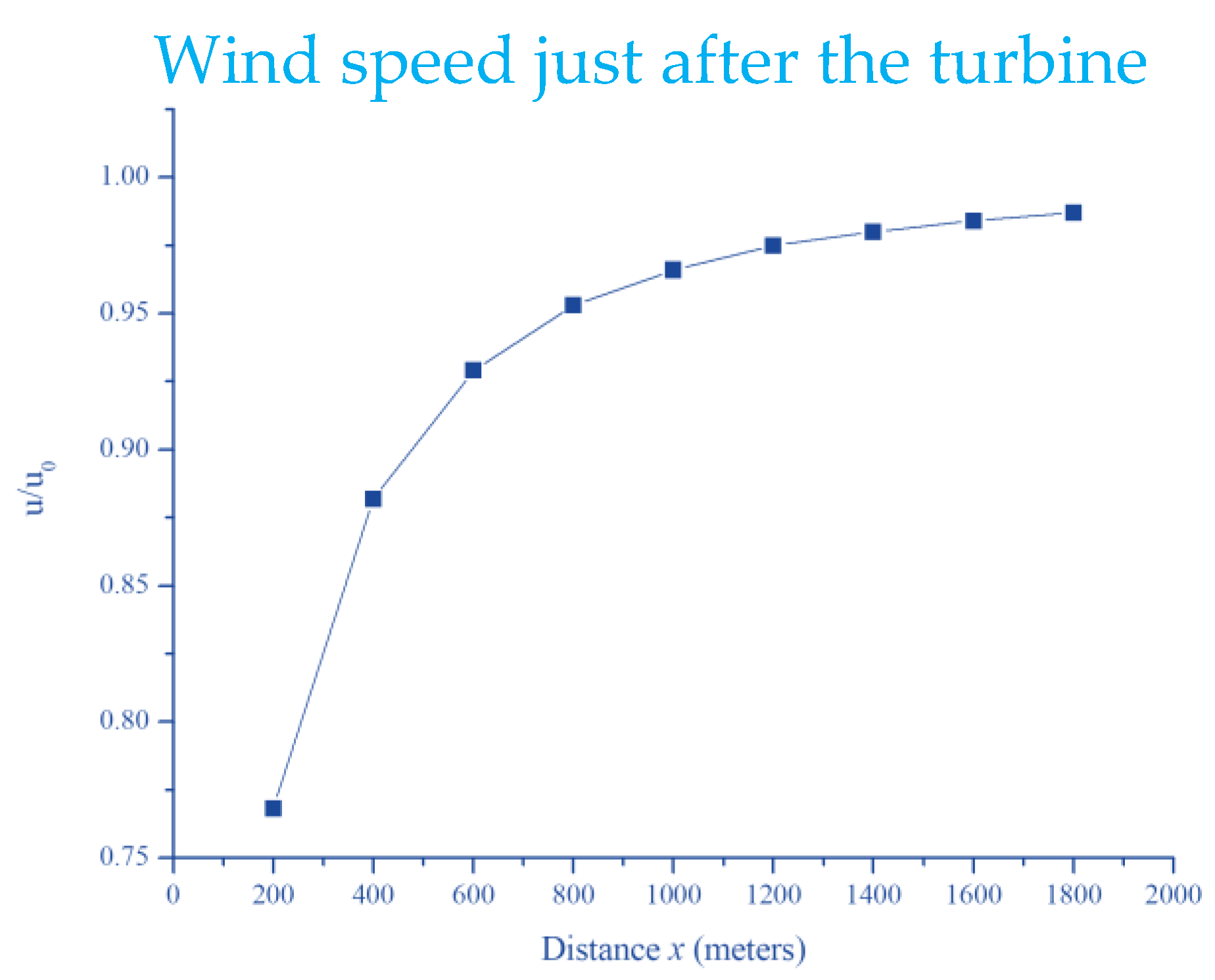
There are certain challenges faced by wind technology, such as the reduction in the wind speed caused by the significant interference of other neighboring turbines, resulting in reduced speed of the turbines and high wake effect, which possibly cause mechanical failure resulting in the increase in requirement of maintenance and decrease in the electricity production. Therefore, there is a need to find the optimal distance between the turbines to reduce the effect of wake generated by the wind turbines. Many studies in the past have proposed a rule that has gained support among the scientific community. The rule states that the turbines should not be placed at a distance less than 5 m rotor diameters to generate a minimum interference among the other turbines to produce the maximum power output [8,9,10]. With continuous development in computer technology, computational intelligence techniques are expanding their application area to the renewable energy resources. These techniques have been very effective in solving complex optimization problems and generating efficient solutions. During the last decade, these techniques have been widely used for the positioning optimization of wind turbines. To place a large number of wind turbines in the wind farm, it is necessary to find the optimal placement of these turbines to obtain the maximum expected power production at a minimized cost. Several studies have been performed to optimize the placement of wind turbines. Mosetti et al. employed the genetic algorithm to find the optimal wind turbine placement in a wind farm [1]. They used Jensen’s analytical wake model [11] for modelling the wake effect and their main objective was to minimize the value of cost per unit power. Mosetti et al. produced results for three different scenarios for fixed wind direction at constant speed, but with change in direction, variable wind speed, and variable direction with some preferred directions, respectively. Grady et al. [2] challenged the results of Mosetti et al. and claimed that the results produced by Mosetti et al. were sub-optimal. They suggested that the sufficient number of generations did not reach the optimum point. Rabia et al. [9] proposed a method for wind farm layout optimization by using definite point selection and genetic algorithm, which can improve the output power of a wind farm by changing the dimensions of a wind farm with an area size of $2 \mathrm{km} \times 2 \mathrm{km}$. They rotated the square shaped wind farm by 45 degrees towards the uniform direction of the wind and a definite point selection criterion was set in order to face upstream wind [9]. Several other evolutionary techniques such as viral based algorithm [12], greedy algorithm [8], particle swarm optimization algorithm [13], mixed integer linear programming technique [14], multi-population genetic algorithm [15], ant colony algorithm [16], random and local search algorithm [17,18,19], and many more have been used to find the optimal placement of the wind turbines to maximize the power output while minimizing the cost [20,21,22,23,24].

Wind energy presents one of the significant promising renewable energy sources and ranks as the best source of clean energy technology worldwide [25]. In order to reduce the cost/kW, the L-SHADE algorithm has been used to enhance the performance of the Differential Evolution (DE) process. SHADE is a DE parameter adaptation technique that is based on success history. LSHADE enhances SHADE’s performance by progressively and linearly reducing the population size. Historically, continuous variable optimization has been the principal use of DE [26,27]. Wind farm area shape optimization has been performed using newly developed multi-objective evolutionary algorithms [28,29]. The placement task of turbines can be seen as a combinatorial optimization problem that requires finding the optimum set of positioning among the available finite set (multi-positioning by discretizing the continuous wind farm) [30,31]. If it is necessary to allocate $q$turbines to n available placements, then there are $n!/ q!\left(n-q \right)!$ combinations. In this context, the computational complexity increases with increasing n. Thus, many exhaustive search methodologies and local search techniques such as Monte Carlo simulation and integer programming may fail. Therefore, the meta-heuristics methodologies pose higher searching capabilities in solving complex optimization tasks [32,33]. Many researchers have employed them to address the wind farm layout discrete optimization (WFL-DO) problems. Gao et al. [34,35] developed the Genetic Algorithm (GA) with many individuals within the population size to improve searching inside the search space and then obtain better output. Additionally, a hybrid GA by Rethore et al. [36], and Huang [37,38] was presented to address these problems. Pookpunt and Ongsakul [39] proposed a particle swarm optimizer (PSO) with binary formulation to achieve optimal wind turbines for the WFL-DO problem. Chen et al. [40] implemented the multi-objective GA for optimal wind turbines placement, but they utilized a micro-siting to replace the grid-based placement aspect. Mora et al. [41] presented an evaluative algorithm to the WFL-DO problem by maximizing the profits of the wind farm. Gonzalez et al. proposed an improved version of the evaluative algorithm, where the optimization process considered the wind farm cost with Mora’s model [42]. Decomposition based multi-objective evolutionary algorithm for windfarm layout optimization has been implemented by Biswas et al. [43]. Using an optimally designed parameters including rotor radius, hub height, and rated power, a strategy to reduce the cost of energy (COE) of wind turbines on high-altitude sites has been implemented by Song et al. [44]. Yang and Hu implemented modified GA based on Boolean code for wind farm layout optimization [45]. The water cycle algorithm [46], a novel equilibrium optimizer [47] for optimal placement of wind turbines, has also been implemented. A teaching–learning based optimization technique [48] has been implemented for core reload pattern optimization of a research reactor [49], solving complex constrained optimization problems [50], unconstrained optimization problems [51], and constrained mechanical design optimization problems [52]. Other novel approaches, such as the bat algorithm for numerical optimization [53] and particle swam optimization with new initialization technique, can also be applied for wind farm optimization [54,55]. Based on the previous studies, the teaching–learning based optimization technique has not been implemented to solve problems considered in this study. The effectiveness of the algorithm is checked by comparing the results with other studies and approaches.

The main objectives of this study are:

• To check the effectiveness of the multi-objective teaching–learning based optimization technique.
• To determine the optimal locations of the wind turbines in a given land area of $2 \mathrm{km}\times 2 \mathrm{km}$ to achieve the maximum energy production while minimizing the total cost.
• To find the optimal layouts along with the optimal number of turbines in a given land area of $2 \mathrm{km}\times 2 \mathrm{km}$ with minimum fitness evaluation.

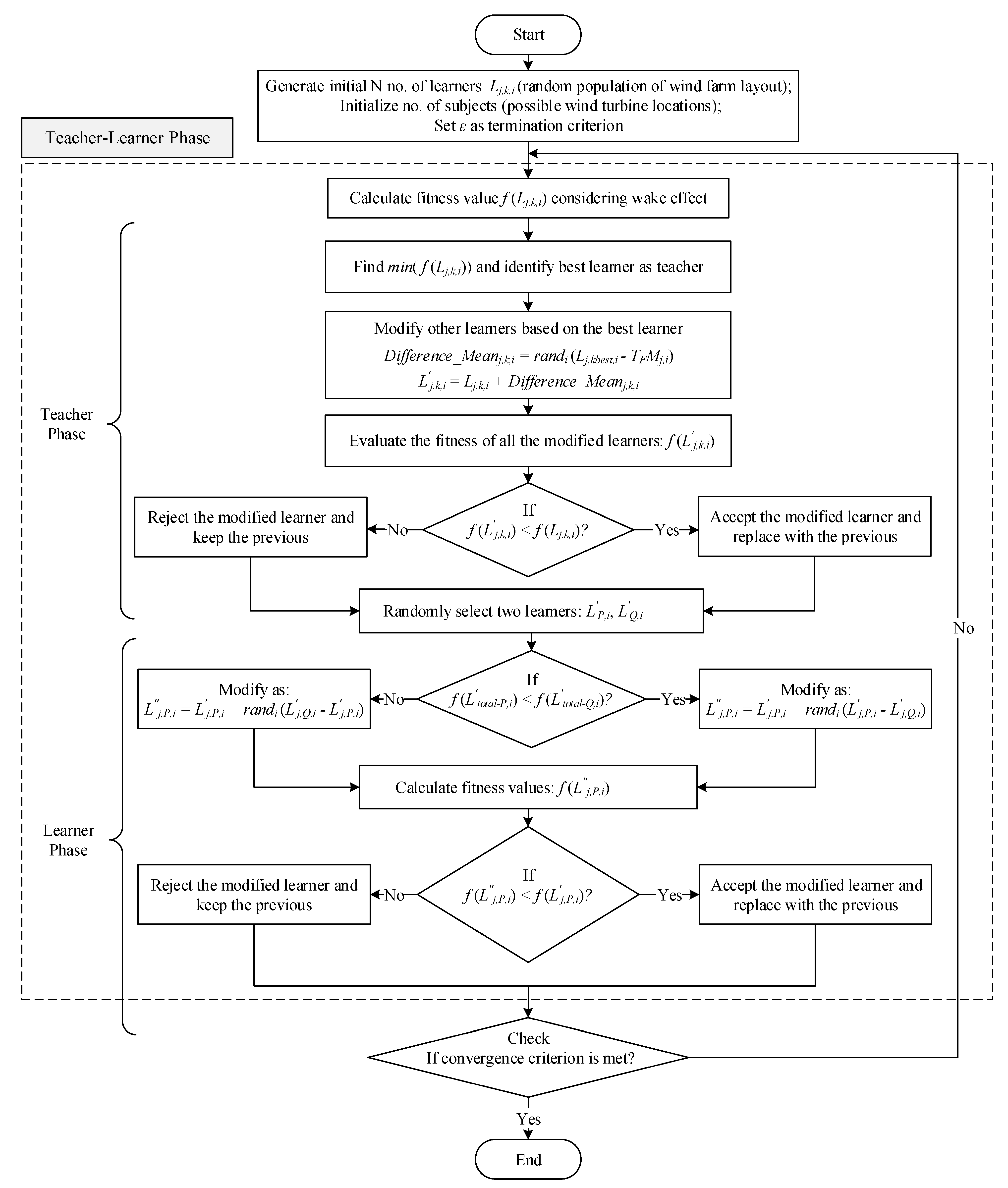
The selection of the algorithm was made due to its observed reliability, accuracy, robustness, less computational time, and consistency as compared to other optimization techniques. The most optimal placement of the turbines is performed for three different scenarios of wind (Scenario-I: fixed wind direction at constant speed, Scenario-II: variable wind direction at constant speed, and Scenario-III: variable wind direction at variable speed). The results obtained for these scenarios are compared with past studies available in the literature. In addition, the concept of elitism is implemented in TLBO. Results of TLBO and elitist-TLBO (ETLBO) are compared with those obtained by other studies for the same discrete optimization problems. The obtained results are observed to be more accurate and advantageous than the others and are discussed in detail in the subsequent sections.

2. Materials and Methods

2.1. The Analytical Model: Jensen’s Wake Modelling

The analytical Jensen’s wake model to find the optimal wind farm layout design is used in the present study as it was proposed initially by Mosetti et al. [1] and Grady et al. [2]. The assumptions made in the initial studies are still being used in recent studies. The schematic diagram of Jensen’s wake model is shown in the Figure 1.

The problem considered here is a square region of $2 \mathrm{km}\times 2 \mathrm{km}$, which is divided into 100 possible turbine positions, and each cell has a dimension of $5d\times 5d,$where d is the rotor diameter of the turbine. Each turbine is placed only at the center of each cell, so $x$ can be varied as $5d, 10d, 15d,\dots , 45d,$ where $d$ is the distance between 1st and 10th turbine (if there is a turbine).

The expression for calculating the velocity of air behind the turbine ($u$) after it has passed through the turbine is given by N. O. Jensen’s wake model [11] in Equation (1),

$$\frac{u}{u_0}=\left[1-\frac{2a}{1+\alpha \left(\frac{x}{r_1}\right)}\right]$$

(1)

where $u_0$ is undistributed/freestream wind speed, $a$ is the interference/ induction/ perturbation coefficient, $x$ is the wind stream distance, $\alpha$ is the entrainment constant, and $r_1$is the downstream rotor radius. For thrust coefficient $C_T=0.88=4a\left(1-a\right)$, the interference/induction/perturbation coefficient $a$is calculated as 0.3268, which is less than 0.5. The downstream rotor radius $r_1$ is calculated using the following expression:

$$r_1=r_r\sqrt{\frac{1-a}{1-2a}}$$

(2)

where $r_r$ is the rotor radius. The empirical expression for entrainment constant $\alpha$ is given by

$$\alpha h\frac{0.5}{ln\left(\frac{Z}{z_0}\right)}=\frac{0.5}{ln\left(\frac{60}{0.3}\right)}=0.09437$$

(3)

$$\alpha =tan\frac{\theta }{2}$$

(4)

$$\theta =2{tan}^{-1}0.09437=10.787$$

(5)

where $z_0$ is surface roughness and $Z$ is the hub/axis height of turbine.

This model predicts the velocity of air behind the turbine rotor at any distance $x$ from the turbine. It also predicts that the velocity of air is the smallest at just behind the rotor and it starts recovering as it moves away from the turbines. At large distance from turbines, velocity fully recovers and becomes equal to the free stream velocity. A change in velocity with distance is shown in Figure 2.

An important point to note here is that one column of turbines does not affect the other column of turbines. Therefore, one can determine the power from each column independently and adding the power from each column determines the power of whole layout. To determine the power of turbines placed in one column, the turbines will be set behind each other. Each turbine creates a wake effect for the turbine behind it. The velocity of air at any turbine will be given by the sum of wake effect from each upstream turbine.

The velocity of air at a turbine experiencing multiple wakes is calculated by assuming that the sum of kinetic energy (K.E.) deficit at the turbine being considered is equal to the K.E. deficit of mixed wake.

Equation (1) can be rewritten in the form

$$1-\frac{u}{u_0}=\frac{2a}{{\left(1+\alpha (\frac{x}{r_1})\right)}^2}$$

$${\left(1-\frac{u_{mixed wake}}{u_0}\right)}^2={\left(1-\frac{u_1}{u_0}\right)}^2+{\left(1-\frac{u_2}{u_0}\right)}^2+-x{\left(1-\frac{u_n}{u_0}\right)}^2$$

2.2. Fitness Evaluation

2.2.1. Estimation of Wind Farm Cost

Mosetti et al. presented an empirical relation to calculate cost/year dependent on number of turbines in Equation (7):

$$cost of Single turbine=\left(\frac{2}{3}+\frac{1}{3}{e}^{-0.00174N^2}\right)$$

(6a)

Mosetti et al. assumed that the above modeled cost/year of single turbine is $1$ with maximum reduction in cost of $1/3$ for each additional turbine.

$$\underset{N\to \infty }{lim}\left(\frac{2}{3}+\frac{1}{3}{e}^{-0.00174N^2}\right)=\frac{2}{3}$$

(6b)

$$cost of N turbines=N\left(\frac{2}{3}+\frac{1}{3}{e}^{-0.00174N^2}\right)$$

(7)

For a large number of turbines, the cost reduces from $1$ to $2/3$, i.e., $1/3$ cost reduction can be obtained for each additional turbine.

2.2.2. Estimation of Wind Farm Power

Power for wind turbine is given in Equations (8) and (9);

$$P=\frac{1}{2}\dot{m}{u}^2$$

(8)

$$P=\frac{1}{2}\left(\rho Au\right)u^2$$

$$P=\frac{1}{2}\rho A{u}^3$$

(9)

$\rho$ is considered to be constant here. $\rho$ is calculated according to general gas equation at fixed atmospheric conditions given by the Equation (10):

$$\rho =\frac{P}{RT}$$

(10)

Assuming efficiency of turbine to be 40%, the actual power (P) produced is calculated by using Equation (11a):

$$Efficiency=\frac{P}{P_{ideal}}=1.2 {\mathrm{kgm}}^{-3}$$

(11a)

$$P=0.3{\left(u_{wmwe}\right)}^3 \mathrm{KW}$$

(11b)

where, $u_{wmwe}$ is the velocity of the turbine with multiple wake effect. So, the Equation (11b) can be written as;

$$P\propto {\left(u_{wmwe}\right)}^3$$

(11c)

This shows that Power produced by the turbine is directly proportional to the cube of velocity.

2.2.3. Evaluation of Fitness Function

The main objective of the present study is the generation of optimal layout of the turbines at such positions so as to produce maximum power while minimizing the cost. Therefore, the objective of the layout optimization problem can be stated mathematically as

$$\begin{array}{c}objective function\\ =minimize\left(\frac{Total Cost}{Total Power}\right)\\ =minimize\left(\frac{N\left(\frac{2}{3}+\frac{1}{3}{e}^{-0.00174N^2}\right)}{0.3{\left(u_{wmwe}\right)}^3}\right)\end{array}$$

(12)

2.2.4. Calculation of Efficiency

Efficiency of the wind farm is the amount of energy extracted from the total energy of the wind farm without considering the effect of wake. It should not be confused with the efficiency of the wind turbine. It estimates the actual power produced from the wind farm compared to the power produced from the same number of turbines. The efficiency of the turbine is considered as the aerodynamic efficiency of the rotor or blade of the turbine. It is a measure of the energy extracted from the wind through blades. Mathematically, efficiency (η) of the wind farm installed with N number of turbines is estimated by the ratio of the total power with multiple wake effects, i.e., $P_{tot,wmwe}$ to the total power without wake effects, i.e., $P_{tot, wowe}$:

$$\eta =\frac{P_{tot,wmwe}}{P_{tot,wowe}}$$

(13a)

In case of Scenario-I with constant speed and constant direction, the formulations for the total power with multiple wake effects ($P_{wmwe}$) and without considering wake effects ($P_{wowe}$) are respectively given as:

$$P_{tot,wmwe}={\displaystyle \sum }_{i=1}^{N}0.3\times u_i{}^3; P_{tot,wowe}=N\left(0.3\times u^3\right)$$

(13b)

In case of Scenario-II with constant speed and variable direction, the formulations for the total power with multiple wake effects ($P_{wmwe}$) and without considering wake effects ($P_{wowe}$) are respectively given as:

$$P_{wmwe}={\displaystyle \sum }_{k=1}^{N_T}{\displaystyle \sum }_{ {\mathsf{\theta }}_i=1}^{36}0.3\times f_{\left( {\mathsf{\theta }}_i-1\right)\times 10,j}\times u_0{}^3\times {\left(\frac{v}{u}\right)}_k{}^3; {\mathsf{\theta }}_i==0, 10, 20,\dots , 350$$

(14)

$$P_{wowe}=N_T\times {\displaystyle \sum }_{ {\mathsf{\theta }}_i=1}^{36}0.3\times f_{\left( {\mathsf{\theta }}_i-1\right)\times 10,j}\times u_0{}^3; {\mathsf{\theta }}_i==0, 10, 20,\dots , 350$$

where

$$f_0=f_{10}=f_{20}=\dots =f_{350}=\frac{1}{36} \left(\mathrm{wind} \mathrm{ocurrence} \mathrm{probability} @ \mathrm{each} \mathrm{angle}\right)$$

(15)

$${\displaystyle \sum }_{ {\mathsf{\theta }}_i=1}^{36}{f}_{\left( {\mathsf{\theta }}_i-1\right)\times 10,j}=1$$

(16)

$$P_{wowe}=N_T\times 0.3\times u_0{}^3$$

(17)

While in case of Scenario-III with variable speed and variable direction, the formulations for the total power with multiple wake effects ($P_{wmwe}$) and without considering wake effects ($P_{wowe}$) are respectively given as:

$$P_{wmwe}={\displaystyle \sum }_{k=1}^{N_T}{\displaystyle \sum }_j{\displaystyle \sum }_{ {\mathsf{\theta }}_i=1}^{36}0.3\times f_{\left( {\mathsf{\theta }}_i-1\right)\times 10,j}\times u_j{}^3\times {\left(\frac{v}{u}\right)}_k{}^3$$

(18)

$$P_{wowe}=N_T\times {\displaystyle \sum }_j{\displaystyle \sum }_{ {\mathsf{\theta }}_i=1}^{36}0.3\times f_{\left( {\mathsf{\theta }}_i-1\right)\times 10,j}\times u_j{}^3$$

(19)

$\begin{array}{c}\mathrm{where}\\ {\mathsf{\theta }}_i=0,10,20\dots 350 \\ j=8, 12, 17 \left(\mathrm{wind} \mathrm{speed} \mathrm{values}\right)\\ k=1, 2, 3, \dots ,N_T \left(\mathrm{Number} \mathrm{of} \mathrm{Turbines}\right)\end{array}$

2.3. Elitist Teaching–Learning Based Optimization Algorithm

The problem of wind turbine placement optimization is solved many times by Genetic Algorithms (GAs) with specific improvement every time. Different algorithms have been applied to the same problem to see which optimization algorithm produces best results, i.e., converges quickly with a smaller number of iterations or produces even better results than other optimization algorithms. Teaching–learning based optimization algorithm (TLBO) is proposed by the Indian Researcher R. Venkata Rao [50,51,52]. This optimization algorithm mimics the teaching and learning process in the environment of the classroom to improve the average student performance. This teaching–learning based optimization algorithm (TLBO) has two phases of improvement, i.e., teacher phase and student/learner phase.

2.3.1. Teacher Phase

In this phase, the learners are being taught by a teacher who struggles hard to improve the average result of the class in a specific subject depending upon his knowledge and teaching capabilities. Let us assume that at any number of iterations “i”, there is “N” number of design variable, i.e., subjects.

In this particular study, the design variables are the number of turbines and total number of learners are “M” (i.e., population size$k=1, 2, 3,\dots , M$). Population size in this problem means the total number of arrangements of turbines which will imitate the class of learners. The average result of the class in a particular subject “j” (where,$j=1, 2, 3,\dots , N$) is $M_{j,i}$. The teacher is the most learned person in the class, who teaches the class so that the students can obtain better results. The best result is considered to be associated with the teacher in the class whose result is denoted by$L_{kbest,i}$.

The difference in the average result of a particular subject and the corresponding result of the teacher for that subject can be written in the following equation:

$$Difference\_Mea{n}_{j,k,i}=ran{d}_i\left(L_{j,kbest,i}-T_F{M}_{j,i}\right)$$

(20)

where, “$T_F$” is the teaching factor which will decide how much of the mean of the result is varied and ‘‘$ran{d}_i$” is the random number uniformly distributed between 0 and 1. $L_{j,kbest,i}$ is the best result in a particular subject “j”. In the teacher phase of the algorithm, the solution is evaluated according to the following equation:

$$L_{j,k,i}^{\prime }=L_{j,k,i}+Difference\_Mea{n}_{j,k,i}$$

(21)

$L_{j,k,i}^{\prime }$ will be accepted if it will give better fitness function value than the preceding case and be rejected otherwise. All the accepted values will be given as input to next phase i.e., the learner phase.

2.3.2. Learner Phase

In any class, learners/students not only learn from teacher but also by interacting with other fellow students in the form of group discussions and combined studies, etc. As discussed in last section, among the class with “M” number of students, two random students “P” and “Q” are selected, so that $L_{P,i}^{\prime } \ne L_{Q,i}^{\prime }$, where $L_{P,i}^{\prime }$ and $L_{Q,i}^{\prime }$ are the results of students P and Q at the end of the teacher phase considering all the subjects. The following two equations represent the learning process in this phase:

$$L_{j,P,i}^{″}=L_{j,P,i}^{\prime }+ran{d}_i(L_{j,P,i}^{\prime }-L_{j,Q,i}^{\prime })$$

(22)

$$L_{j,P,i}^{″}=L_{j,P,i}^{\prime }+ran{d}_i(L_{j,Q,i}^{\prime }-L_{j,P,i}^{\prime })$$

(23)

where $L_{j,P,i}^{″}$ is the updated result of student P after learner phase, it will be accepted if its corresponding fitness function value is better than the preceding case.

2.3.3. Evaluation of Fitness Function

For the solution of present research problems, a binary matrix of dimension $10\times 10$ with fixed number 1s represents the layout of the wind farm. The 1s in the layout show the presence of the turbine at the center of particular grid cell while 0s represent the absence of the wind turbine at the center of a particular grid cell. Figure 3 shows optimal wind farm layout presented by Mosetti et al. in binary format.

The teaching factor used in the TLBO algorithm plays a vital role in the slow or fast convergence of the algorithm. It is either 1 or 2. However, some researchers have shown that a random selection of teaching factor 1 or 2 throughout its iteration would produce better results. To ensure the successful convergence of the algorithm, the following two convergence criterions given in inequalties (24) and (25) are used.

Check if

$$\max \left(\left\{\left|f\left({L^{″}}_{j,P,i}\right)-f\left({L^{″}}_{j,P,i-1}\right)\right|;\hspace{0.17em}\hspace{0.17em}\forall \hspace{0.17em}j=1,2,3,...,N\right\}\right)<{\epsilon }_1$$

(24)

If condition given in inequality 24 is satisfied, then check

$$\left\{\left|f\left({L^{″}}_{j,P,i}\right)-f\left({L^{″}}_{j+1,P,i}\right)\right|;\hspace{0.17em}\hspace{0.17em}\forall \hspace{0.17em}j=1,2,3,...,N-1\right\}<{\epsilon }_2$$

(25)

It states that if the maximum difference between two successive iterations ($i^{\mathrm{th}}$ and ${\left(i-1\right)}^{\mathrm{th}}$ iterations) is less than ${\epsilon }_1$, which is set to be $1\times {10}^{-6},$ then at the $i^{\mathrm{th}}$ iteration it will further check whether the difference between two successive learners is less than ${\epsilon }_2$, which is set to be $1\times {10}^{-7}$. If both the criteria are met, then the algorithm will be stopped. The overall flow diagram of the algorithm is shown in Figure 4.

In basic TLBO algorithm, population size is the only controlling parameter. Elitism is yet another concept introduced by Rao and Patel in 2012 [50,51,52] in which a second controlling parameter of elite size was introduced. In elitist TLBO (ETLBO), at the end of each iteration worst solutions are replaced with the elite solutions which have been saved earlier. This replacement of worst solution with elite ones depends upon the controlling parameter of elite size. Thus, enriching the solution with best solutions helps in achieving the convergence criteria in a smaller number of iterations as compared to solution with no elitism. Figure 5 shows the flow of ETLBO algorithm for wind farm layout optimization. Same convergence criterion is applied as implemented in the TLBO algorithm.

2.4. Wind Scenarios

Scenario-I is the wind scenario with constant speed and constant direction. It is the simplest of all: wind blows from only one direction with constant wind speed of $12{ \mathrm{ms}}^{-1}$ or $3.3{ \mathrm{kmh}}^{-1}$. In this scenario, it is easy to find an optimal placement of a certain number of wind turbines in a given land area. Figure 6a shows the frequency distribution for Scenario-I. Scenario-II is the multi-directional wind with the identical velocity. Wind blows at constant speed but it may occur from any direction. The circle is divided into 36 segments. Each segment has equal probability of wind occurrence with speed of $12{ \mathrm{ms}}^{-1}$. The wind rose in Figure 6b shows the frequency distribution for Scenario-II. Scenario-III is the multi-directional wind with variable wind velocity. It is a relatively general case. Here, three wind speeds of $8{ \mathrm{ms}}^{-1},12{ \mathrm{ms}}^{-1} \mathrm{and} 17{ \mathrm{ms}}^{-1}$ are considered. These three speeds have different probabilities of occurrence from different sides. In real wind scenarios, wind speed does not have fixed value; rather, there are wind speed groups. The wind rose in Figure 6c shows the frequency distribution for Scenario-III.

3. Results and Discussion

3.1. Mosetti et al. vs. WFAO-ETLBO

Scenario-I considered by Mosetti et al. is used for the sensitivity analysis of the TLBO algorithm. Mosetti et al. used 26 turbines to find the optimal placement of the wind turbines. The same number of turbines is used to check the sensitivity of initial population size and the teaching factor in the following sections.

3.1.1. Sensitivity Analysis for Initial Population

To check the effect of the number of initial learners on the results, different initial population sizes of 20, 50, 100, and 150 were used.

Table 1. Population sensitivity with varying number of learners.

Number of Learners	Power (KW)	Fitness Value	Efficiency (%)
20	12,229	0.0016366	90.73
50	12,361	0.0016196	91.71
100	12,495	0.0016014	92.71
150	12,427	0.0016132	92.20

shows the sensitivity of initial population. Fifty independent runs were made and it was observed that 100 learners gave minimum fitness and highest efficiency. It was also observed that any increase in population size would increase computational cost without increasing the accuracy of results and would be unnecessary. Based on this sensitivity analysis, an initial population size of 100 is selected for further analysis in this research.

Figure 7 (left panel) shows the plot for differences in fitness values of the succeeding iterations. It can be noted that differences in fitness values at 1st iteration are much higher, while in the succeeding iterations, the differences start to decrease and become zero when the convergence criteria are met. This figure also shows that the whole class of learners is approaching the same result at 43rd iteration, which indicates the convergence of TLBO algorithm. Figure 7 (right panel) shows the convergence plot obtained using 100 numbers of learners. It is observed that after the 44th iteration the solution converges and shows the asymptotic behavior of the fitness.

3.1.2. Sensitivity of Teaching Factor

There is a teaching factor $\left(T_F\right)$ used in the TLBO algorithm which can have a constant value of either 1 or 2 or it can vary randomly (1 or 2) during TLBO search. In TLBO, a smaller value of teaching factor enables the algorithm to explore the search space in small steps, while in case of higher value, large steps are taken to explore the search space and the convergence time will be decreased. Figure 8 shows sensitivity analysis of these teaching factors performed in this study and it is observed that $T_F=1$ gives minimum fitness when the simulation is run with optimal 100 numbers of learners while other researchers proposed the random selection of 1 or 2. Based on these results, $T_F=1$ has been used for this study.

Table 2. Results obtained by TLBO with different values of teaching factor T_F.

Teaching Factor	Initial No. of Learners	Power (KW)	Fitness Value	Efficiency (%)	Converged No. of Iterations
1	100	12,374	0.0016152	91.89	30
2		12,267	0.0016309	91.05	50
Rand [1 2]		12,371	0.0016168	91.81	56

shows the detail of results obtained by TLBO with different values of teaching factor obtained by TLBO.

Table 1, using a coarse grid with five times the rotor diameter (i.e., 200 m) as the center-to-center distance between two adjacent wind turbines, compares the results obtained from TLBO algorithm using both coarse and fine grid meshing. TLBO produces good results with minimum fitness while producing maximum power and efficiency as compared to the results obtained by Mosetti et.al., Grady et al. and Mittal et al., with fewer iterations as well. It should be noted that Mosetti et al. used a population of 200 individuals and evolved up to 400 generations. Grady et.al. went even further and used the population of 600 individuals and evolved them over 3000 iterations. Mittal et al. did not report the number of individuals and converged the number of iterations used for their simulations. The results of all the three studies performed on the considered scenarios in this work are discussed in the subsequent sections.

In order to obtain the effectiveness of Multi-objective Elitist Teaching Learning Based Algorithm (MO-ETLBO) algorithm, only Scenario-1 as discussed in the Section 3.1.1 is considered. The same conditions of fixed wind direction at constant speed are considered to find the optimal number of turbines and turbine positioning that maximizes the expected power production. A 100 number of learners were taken as an initial population and different elite sizes were considered, i.e., 0, 5, 10, 15, and 20. The 0 elite size means no elitism, which is similar to TLBO discussed in last section.

Table 3. Results obtained from ETLBO using different elite sizes.

Elite Size (%)	Optimal Fitness Value	Efficiency (%)	Power (KW)	Optimal No. of Turbines	Converged No. of Iterations	Simulation Time (Sec)
0	0.0014256	92.99	19,284	40	44	6.3
5	0.0014285	92.11	20,056	42	23	3.3
10	0.0014329	93.38	18,395	38	16	2.9
15	0.0014262	92.95	19,275	40	14	1.8
20	0.0014539	92.04	18,131	38	13	1.6

illustrates the results obtained by ETLBO. It is evident from the table that elite size of 15 gives similar results to those obtained from TLBO but with significantly fewer iterations, i.e., 14. Figure 9 illustrates the convergence plot obtained using 100 numbers of learners simulated with different elite sizes. Figure 10 represents a selection of elite size corresponding to optimal number turbines and optimal fitness value.

3.2. Comparison Results of the MO-ETLBO

The comparisons of numerical results obtained for Scenario-I using TLBO algorithm with those obtained by different studies are discussed in the following sections.

3.2.1. Numerical Results for Scenario-I

This case deals with the uni-directional wind with an identical velocity of 12 m/s. The TLBO approach is applied to this case, and obtained results are compared with different reported methods in the literature. These methods include Mosetti [1], Grady [2], and Mittal [3]. In this regard, the comparative performances through some statistical measures in terms of the best, mean, median, worst values of the fitness and standard deviation (std. dev.) are presented and tabulated in

Table 4. Statistical performances of MO-ETLBO for Scenario-I.

Statistical Measures	TLBO
Minimum	1.3315 × 10−3
Mean	1.3152 × 10−3
Median	1.3136 × 10−3
Worst	1.3532 × 10−3
Std. Dev.	4.3342 × 10−3

. Furthermore, the TLBO algorithm is compared with different algorithms taken from the literature and recorded in

Table 5. Comparison among the performances of the literature studies and MO-ETLBO for Scenario-I.

Algorithm	Number of Turbines	Fitness Value × 10−3 ($/KW)	Total Power (KW/Year)	Efficiency (%)	Converged Number of Iterations	Saving by Present Study (%)	Average Power Produced by Unit Turbine (KW/Year)
Mosetti [1]	26	1.619	12,352	91.65	400	17.75	475.08
Grady [2]	30	1.5436	14,310	92.015	1203	13.74	477.00
Mittal [3]	44	1.3602	21,936	96.17	NA	2.11	498.55
MO-ETLBO	41	1.315	20,495	95.49	41	-	499.88

. In this case, optimal layouts are found via the minimization of the cost per unit power. It can be seen that the power produced by unit turbine is higher than the others.

Along with the obtained minimum value for the objective function, the total power (kW) and the farm’s efficiency are also computed. In terms of minimizing the fitness value (cost per unit power generated), the proposed EO-PS algorithm provides superior results over the other methods. Referring to Table 5, it can be observed that the MO-TLBO algorithm offers the best solution as it gives a minimum value for a total cost that is $1.3315 × 10⁻³/kW as well as the power of 20495 kW obtained by 41 turbines and efficiency of 95.49%. Additionally, the saving in the total cost over the compared algorithms is shown in Table 4. On the other hand, the optimal configurations for the wind farm layout reported by prominent studies, Mosetti [1], Grady [2], and Mittal [3], versus those achieved by the MO-TLBO algorithms are visualized in Figure 11a–d. Figure 11e shows convergence plot for proposed optimal number of turbines for Scenario-I. The plot shows the convergence of the optimal number of turbines for each learner iteration by iteration. For randomly selected iteration numbers, at iteration 1, it can be seen that all the learners have different fitness values; at iterations 10, 20, and 30 the fitness values of each learner are improved but do not satisfy the convergence criteria, while at iteration number 41, all the learners are approaching the same fitness value and successfully satisfying the convergence criteria.

3.2.2. Numerical Results of Scenario-II

This case deals with the multi-directional wind with an identical velocity of 12 m/s blowing during 36 rotational directions through a single probability of occurring in that direction. The MO-ETLBO approach is applied to this case, and obtained results are compared with different reported methods in the literature. These methods include Mosetti [1], Grady [2], Mittal [3], Feng [20], SSA [25], SBO [25], DE [25], GWO [25], WCA [25], BPSO-TVAC [22], L-SHADE [26], and Gao [15]. In this regard, the comparative performances through some statistical measures in terms of the best, mean, median, worst values of the fitness, and standard deviation (std. dev.) are presented and tabulated in

Table 6. Statistical performances of MO-ETLBO for Scenario-II.

Statistical Measures	TLBO
Minimum	1.5271 × 10−3
Mean	1.5352 × 10−3
Median	1.5336 × 10−3
Worst	1.5452 × 10−3
Std. Dev.	6.2507 × 10−3

. Furthermore, the MO-ETLBO algorithm is compared with different algorithms taken from the literature and recorded in

Table 7. Comparison among the performances of the literature studies and MO-ETLBO for Scenario-II.

Algorithm	Number of Turbines	Fitness Value × 10−3 ($/KW)	Total Power (KW/Year)	Efficiency (%)	Converged Number of Iterations	Saving by Present Study (%)	Average Power Produced by Unit Turbine (KW/Year)
Mosetti [1]	19	1.736	9244	NA	350	12.03	486.53
Grady [2]	39	1.567	17,220	85.174	3000	2.55	441.54
Mittal [3]	38	1.5273	17259	87.61	NA	0.01	454.18
Feng [20]	39	1.547	17,406	NA	NA	1.29	446.31
SSA [25]	39	1.567	17,175	85	NA	2.55	440.38
SBO [25]	40	1.593	17,254	82	NA	4.14	431.35
DE [25]	40	1.538	17,877	86	NA	0.71	446.93
GWO [25]	40	1.543	17,817	86	NA	1.03	445.43
WCA [25]	40	1.538	17,878.32	86.22	NA	0.71	446.96
BPSO-TVAC [22]	35	1.5648	15,796	87.06	NA	2.41	451.31
L-SHADE [26]	40	1.5341	17,920	86.42	NA	0.46	448.00
Gao [15]	39	1.619	15,333	77.83	NA	5.68	393.15
MO-ETLBO	36	1.5271	16,913.86	87.76	41	-	469.83

. In this case, optimal layouts are found via the minimization of the cost per unit power. It can also be seen that the power produced by unit turbine is higher than al l the others studies.

Along with the obtained minimum value for the objective function, the total power (kW) and the farm’s efficiency are also computed. In terms of minimizing the fitness value (cost per unit power generated), the MO-ETLBO algorithm provides superior results over the other methods. Referring to Table 6, it can be observed that the MO-ETLBO algorithm offers the best solution as it gives a minimum value for a total cost that is $1.5271 × 10⁻³/kW as well as the power of 16913.86 kW obtained by 36 turbines and efficiency of 87.76%. Additionally, the saving in the total cost over the compared algorithms is shown in Table 7, where the distribution achieved by the MO_ETLBO algorithm finds the better layout as regarding the total cost compared to the other methods by 20.89%, 3.99%, 0.02%, 1.99%, 3.99%, 6.59%, 1.09%, 1.59%, 1.09%, 3.77%, 0.7%, and 9.19%, for Mosetti [1], Grady [2], Mittal [3], Feng [20], SSA [25], SBO [25], DE [25], GWO [25], WCA [25], BPSO-TVAC [11], L-SHADE [26], and Gao, respectively. On the other hand, the optimal configurations for the wind farm layout reported by prominent literatures, Mosetti [1], Grady [2], and Mittal [3], versus those achieved by the MO-ETLBO are visualized in Figure 12a–d. Figure 12e shows convergence plot for proposed optimal number of turbines for Scenario-II. The plot shows the convergence of the optimal number of turbines for each learner, iteration by iteration. For randomly selected iteration numbers, at iteration 1, it can be seen that all the learners have significantly different fitness values, and at iterations 43, 86, and 129 the fitness values of each learner are improved but do not satisfy the convergence criteria. At iteration number 172, all the learners are approaching the same fitness value and successfully satisfying the convergence criteria.

3.2.3. Numerical Results of Scenario-III

This case presents a more realistic situation for the environmental wind. In this case, a multidirectional wind with varying velocities of 8 m/s, 12 m/s, and 17 m/s is considered. In this sense, 36 rotational directions are considered for the wind flow, where there is an unequal probability of occurrence for all wind velocities in each direction. The proposed algorithm’s computational results via some statistical performances are demonstrated in the form of best fitness (cost per unit power generated), mean of fitness, a median of fitness, worst value, and standard deviation, and summarized in

Table 8. Statistical performances of TLBO for Scenario-III.

Statistical Measures	MO-ETLBO
Minimum	8.2517 × 10−4
Mean	8.2782 × 10−4
Median	8.2716 × 10−4
Worst	8.2064 × 10−4
Std. Dev.	2.0059 × 10−6

. Further, the comparative performances of some methods taken from the literature are recorded in

Table 9. Comparison among the performances of the literature studies and MO-ETLBO for Scenario-III.

Algorithm	Number of Turbines	Fitness Value × 10−3 ($/KW)	Total Power (KW/Year)	Efficiency (%)	Converged Number of Iterations	Saving by Present Study (%)	Average Power Produced by Unit Turbine (KW/Year)
Mosetti [1]	15	0.99405	13,460	NA	400	16.99	897.33
Grady [2]	39	0.8403	31,850	86.619	1203	1.80	816.67
Mittal [3]	41	0.84379	21,936	86.729	NA	2.21	535.02
Feng [25]	39	0.839	32,096	NA	NA	1.65	822.97
SSA [25]	41	0.848	33,099	85	NA	2.69	807.29
SBO [25]	40	0.846	32,501.28	85	NA	2.46	812.53
DE [25]	40	0.836	32,901.41	86	NA	1.30	822.54
GWO [25]	38	0.837	31,498	86	NA	1.41	828.89
WCA [25]	40	0.833	33,005	87	NA	0.94	825.13
BPSO-TVAC [22]	46	0.8523	36,433	82.76	NA	3.18	792.02
L-SHADE [26]	39	0.8322	32,351	86.68	NA	0.84	829.51
MO-ETLBO	38	0.82517	31,086.86	87.59	66	-	839.13

. Based on obtained results, it can be observed that the layout obtained by the MO-ETLBO algorithm provides a better result concerning the objective function (cost per unit power generated) while comparing with the other state of the art algorithms, where it gives minimum value for a total cost that is $8.2517 × 10⁻⁴/kW as well as power of 31,086.86 kW obtained by 38 turbines and efficiency of 87.59%. Additionally, the saving in the total cost over the compared algorithms is shown in Table 5, where the distribution achieved by the proposed EOPS algorithm finds the layout which can save the total cost compared to the other methods by 16.89%, 1.51%, 1.86%, 1.38%, 2.28%, 2.08%, 1.08%, 1.18%, 2.71%, and 0.7% for Mosetti [1], Grady [2], Mittal [3], Feng [20], SSA [25], SBO [25], DE [25], GWO [25], WCA [25], BPSO-TVAC [11], and L-SHADE [26], respectively. For further validation, the fitness function’s behavior is illustrated by depicting the convergence behavior over the searching period as in Figure 13e. Additionally, the optimal wind turbine positioning obtained by Mosetti [1], Grady [2], and Mittal [3] versus that achieved by the MO-ETLBO algorithms is visualized in in Figure 13a–d. Figure 13e shows convergence plot for proposed optimal number of turbines for Scenario-III. The plot shows the convergence of the optimal number of turbines for each learner iteration by iteration. For randomly selected iteration numbers, at iteration 1, it can be seen that all the learners have different fitness values; at iterations 16, 33, and 49 the fitness values of each learner are improved but do not satisfy the convergence criteria. At iteration number 66, all the learners are approaching the same fitness value and successfully satisfying the convergence criteria. Finally, it can be concluded that the proposed MO-ETLBO algorithm has a high capability in solving the challenging combinatorial wind farm layout problems.

4. Conclusions

This paper presents MO-ETLBO to find the optimal placement of wind turbines in a specified land area of$2 \mathrm{km} \times 2 \mathrm{km}$ of the wind farm. The wind farm layout optimization is formulated as a multi-objective optimization problem. In this context, a multi-objective version of MO-ETLBO is accomplished to deal with the multi-objective optimization problem. The algorithm is investigated with three different scenarios of wind (Scenario-I: fixed wind direction at constant speed, Scenario-II: variable wind direction and constant speed, and Scenario-II: variable wind direction and variable speed) to find the optimal number of turbines and turbine positioning that maximizes the power production while minimizing the total cost. For Scenario-I, it can be seen that the average power produced by the unit turbine is 499.88 KW/year, which is higher than all the other three studies along with the lowest fitness evaluation of 1.315. For Scenario-II, it can be observed that the average power produced by the unit turbine is 469.83 KW/year, which is higher than all the other studies except Mosetti et al’s. However, the fitness evaluation is 1.5271, which is the lowest as compared to all other studies. For Scenario-III, it can be confirmed that the average power produced by the unit turbine is 839.13 KW/year, which is higher than all the other studies except Mosetti et al’s. However, the fitness evaluation is 0.82517, which is lowest as compared to all other studies. Based on the results obtained for the multi-objective problem with MO-ETLBO, its superiority can be confirmed over the other state-of-the-art algorithms with acceptable levels of economic, profitable, and technical merits. The economic concern is shown through the obtained saving reached by the algorithm. The profitable aspect is achieved by maximizing energy’s total power output and the technical benefit provided by visualizing the farm efficiency. MO-ETLBO results show the superiority over the other algorithms. It can improve the convergence and coverage capabilities while solving the wind farm layout optimization problem for multi-objective aspects. The salient features regarding the implemented methodology can be mentioned as follows:

• It has been efficiently implemented to solve the wind farm layout discrete optimization problem by considering the multiple objectives optimization.
• The MO-ETLBO provides superior and promising results for a single scenario of the WFL-DO problem.
• It can achieve a better convergence and well-distributed set of non-dominated solutions when dealing with multiple objectives of the wind farm layout discrete optimization problem. These characteristics are useful and can provide reasonable layouts for the decision-maker to extract the best compromise solution or operating solution from the available finite alternatives based on decision-making regulations or total cost obligations.
• It can be concluded that the present study can provide a twofold contribution. The first one is incorporating the pattern search technique, and the second one is caused by simultaneously considering many objectives of the wind farm layout optimization problem.

For future work, the optimization results of different nonlinear wake models can be investigated. Additionally, the realistic shapes of wind farms using more recent and sophisticated wake models along with the new formulations of objective function by taking into account the available number of turbines and the available budget must be examined. The effects of the uncertain nature regarding the speed and wind scenarios on the produced power may be worth future research.