A Novel Approach to Generate Hourly Photovoltaic Power Scenarios
Abstract
:1. Introduction
2. Photovoltaic Power Production
- (A)
- A direct model for photovoltaic power production. One possibility is to model photovoltaic power as a univariate time series [9] or to apply a stochastic state-space model [10]. Despite the advantage of considering only a one-dimensional data set, this approach comes with a few challenges. We have multiple seasonality with constantly varying periods and amplitude (sunrise and sunset change every day) and sudden disruptions, e.g., due to rain (which might also have a seasonal impact).
- (B)
- A separate model for all input parameters. The second option is to first design separate models for all relevant influence factors, especially for irradiation and temperature. Given the respective numbers, such as the solar panels’ tilt, we can then calculate the expected amount of photovoltaic power. Abdel-Nasser and Karrar [11] set up a model to forecast photovoltaic power based on neural networks and various input parameters. They ignore any knowledge about physical interactions and let the neural network decide. Miozzo et al. [12] apply a Markov process for simulation purposes. Barukčić et al. [13] propose an alternative stochastic approach. These ideas look promising because they are simple. Nonetheless, all models face the problem that temperature is relatively easy to model, but irradiation is not—mainly because of the dynamic seasonality described in Alternative (A).
- (C)
- Physical deterministic models. A physical deterministic model establishes a link between input factors such as temperature, cloudiness, albedo factor, and solar irradiation. Those factors are then modeled, including a stochastic component for each one, allowing simulations to be generated. Politaki and Alouf [14] proceed similarly by combining a deterministic model for solar power production under clear sky conditions with a Markov-based approach for cloudiness. A widely used fundamental model for modeling solar power is the clear sky model of Bird and Hulstrom [7], or the extension to cloudy conditions of Myers [6], which is accordingly called the Cloudy Sky Model (CSM). More complex solar irradiation models [15,16,17] for clear sky conditions are more accurate than Bird and Hulstrom’s [7] model. However, they require a much larger number of input data, making them inadequate for daily use. Often, detailed live data for atmospheric input factors are missing or potentially skewed, which is the advantage of simplified models such as the one of Bird and Hulstrom [7]. The approach in Hofmann and Seckmeyer [18] also includes the possibilities of clouded skies and tries to balance complexity (it considers aerosol depth, for example) and simplicity. Additionally, they give a good overview of alternative approaches and benchmark them. For another summary of different concepts, please refer to Zhang et al. [5] or Khatib et al. [19], which focus on forecasting models.
2.1. Solar Power Production Modeling
2.2. How to Incorporate Clouds into the Model
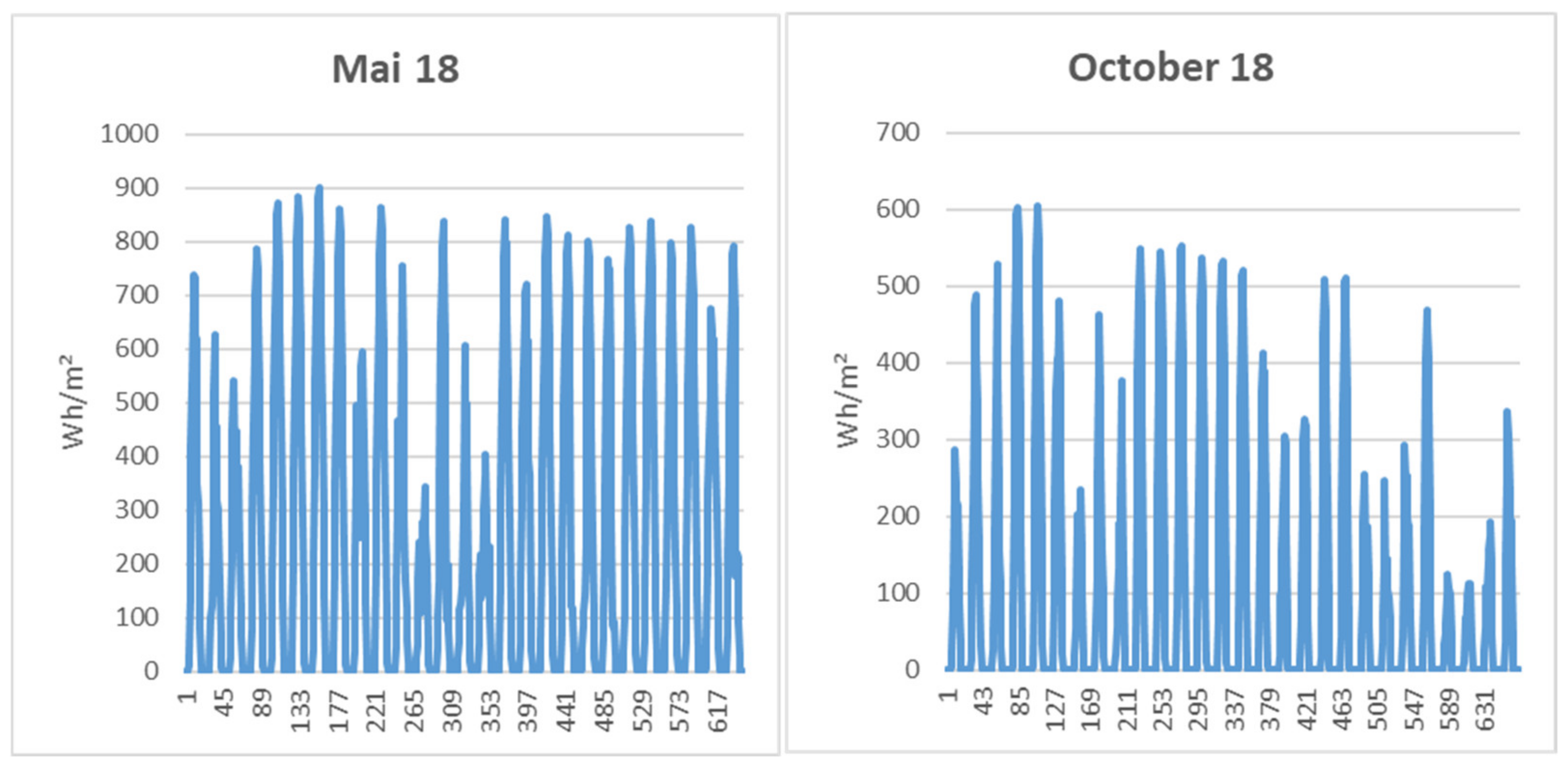
3. Modeling Temperature and Cloudiness
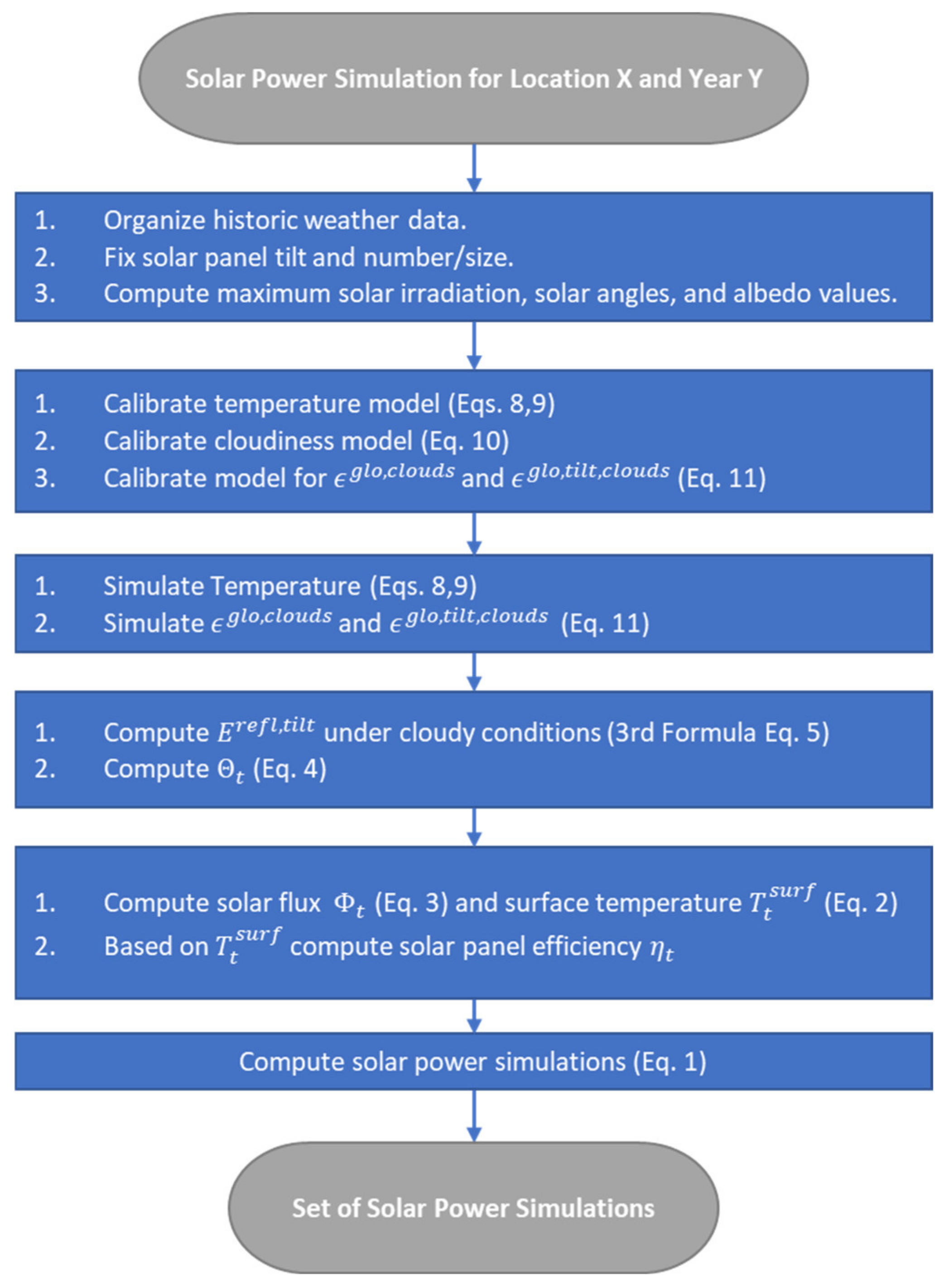
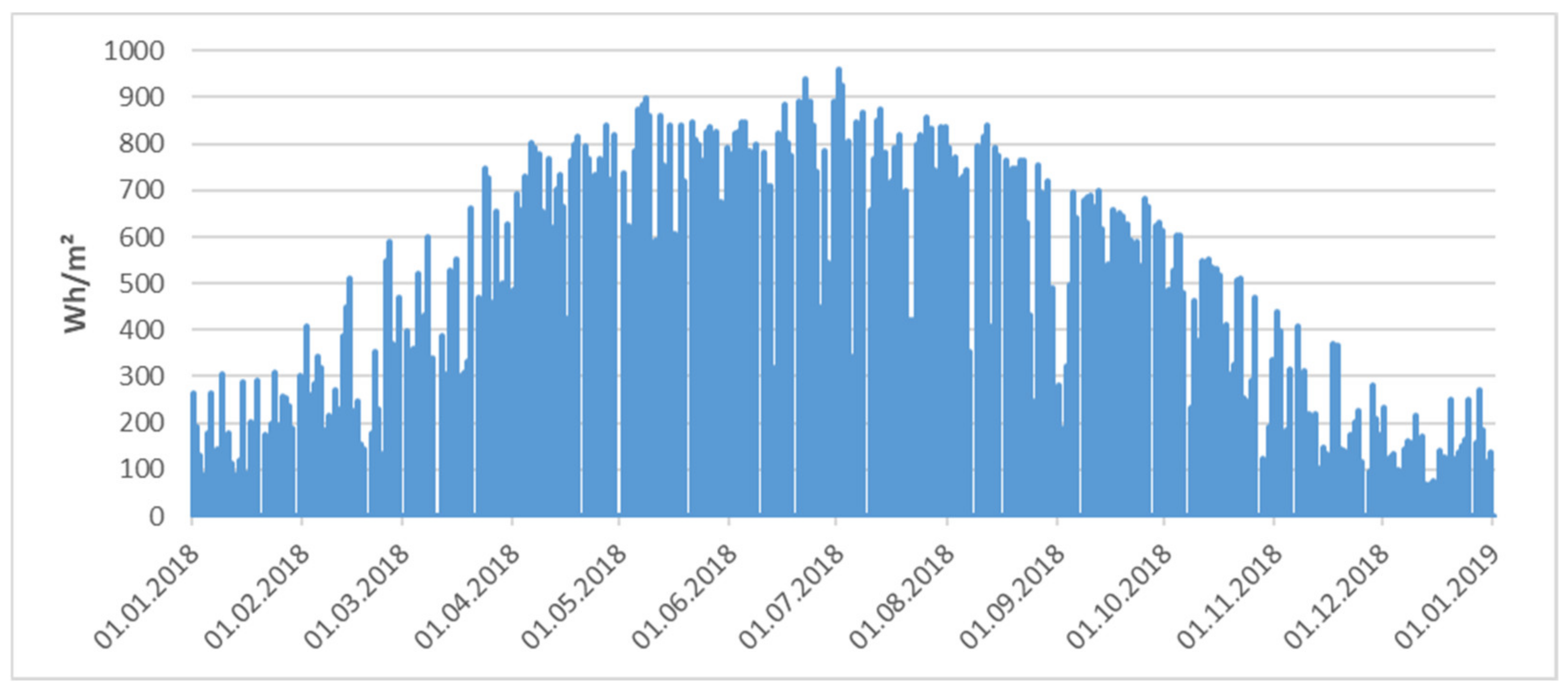
4. Application to Real-World Solar Irradiation Data
4.1. Data
4.2. Model Calibration and Results
5. Quality Control and Discussion
5.1. Quality Control
5.2. Discussion
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A

| From/To | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
|---|---|---|---|---|---|---|---|---|---|
| 0 | 68.93% | 7.95% | 4.70% | 3.41% | 2.78% | 2.58% | 2.45% | 4.26% | 2.94% |
| 1 | 31.02% | 12.98% | 9.95% | 7.90% | 8.29% | 7.51% | 4.98% | 9.27% | 8.10% |
| 2 | 18.11% | 11.19% | 12.31% | 10.99% | 8.95% | 10.27% | 7.53% | 11.50% | 9.16% |
| 3 | 12.40% | 7.66% | 9.66% | 9.66% | 12.31% | 11.58% | 9.39% | 16.13% | 11.21% |
| 4 | 8.62% | 6.81% | 7.80% | 10.92% | 12.56% | 13.63% | 12.64% | 15.68% | 11.33% |
| 5 | 6.38% | 4.77% | 7.18% | 9.09% | 11.22% | 12.46% | 12.10% | 20.09% | 16.72% |
| 6 | 4.36% | 3.37% | 6.20% | 7.66% | 9.64% | 10.03% | 13.14% | 26.67% | 18.94% |
| 7 | 1.99% | 1.82% | 1.60% | 2.73% | 3.08% | 4.14% | 6.34% | 32.27% | 46.03% |
| 8 | 0.58% | 0.46% | 0.47% | 0.65% | 0.80% | 1.06% | 1.38% | 14.44% | 80.16% |
| Hour | Intercept | Seasonality | ||||
|---|---|---|---|---|---|---|
| 6 | 0.8664 | −0.0447 | −0.1085 | 0.0041 | 0.0052 | 0.0565 |
| 7 | 0.9336 | −0.0466 | −0.1556 | 0.0061 | 0.0038 | 0.1519 |
| 8 | 1.1537 | −0.0460 | −0.0251 | 0.0002 | 0.0044 | 0.2764 |
| 9 | 1.1165 | −0.0449 | −0.0077 | −0.0003 | 0.0061 | 0.2492 |
| 10 | 0.8488 | −0.0423 | −0.0356 | 0.0014 | 0.0060 | 0.1797 |
| 11 | 0.7877 | −0.0377 | −0.0230 | 0.0009 | 0.0083 | 0.1552 |
| 12 | 0.7460 | −0.0325 | −0.0197 | 0.0008 | 0.0082 | 0.1694 |
| 13 | 0.7132 | −0.0306 | −0.0154 | 0.0006 | 0.0078 | 0.1571 |
| 14 | 0.6043 | −0.0285 | −0.0189 | 0.0008 | 0.0071 | 0.1300 |
| 15 | 0.5085 | −0.0232 | −0.0219 | 0.0009 | 0.0062 | 0.1297 |
| 16 | 0.2547 | −0.0184 | −0.0654 | 0.0031 | 0.0042 | 0.1147 |
| 17 | 0.0964 | −0.0134 | −0.0141 | 0.0010 | 0.0020 | 0.0379 |
| 18 | 0.0256 | −0.0084 | −0.0180 | 0.0013 | 0.0008 | 0.0592 |
| 19 | −0.0276 | −0.0044 | −0.0201 | 0.0015 | −0.0005 | 0.0320 |
| Hour | Intercept | Seasonality | ||||
|---|---|---|---|---|---|---|
| 6 | 0.3930 | 0.0063 | −0.2051 | 0.0089 | −0.0011 | −0.1730 |
| 7 | 0.8892 | −0.0336 | −0.0559 | 0.0017 | 0.0007 | 0.0954 |
| 8 | 0.9814 | −0.0427 | −0.0437 | 0.0013 | 0.0044 | 0.1819 |
| 9 | 1.0066 | −0.0452 | −0.0423 | 0.0014 | 0.0060 | 0.2181 |
| 10 | 0.7323 | −0.0451 | −0.0583 | 0.0027 | 0.0060 | 0.1548 |
| 11 | 0.7920 | −0.0403 | −0.0414 | 0.0018 | 0.0117 | 0.1808 |
| 12 | 0.9114 | −0.0354 | −0.0332 | 0.0012 | 0.0130 | 0.2369 |
| 13 | 0.9308 | −0.0398 | −0.0267 | 0.0009 | 0.0119 | 0.1983 |
| 14 | 0.8582 | −0.0449 | −0.0334 | 0.0013 | 0.0106 | 0.1491 |
| 15 | 0.6622 | −0.0401 | −0.0485 | 0.0021 | 0.0078 | 0.1243 |
| 16 | 0.2767 | −0.0271 | −0.1058 | 0.0050 | 0.0045 | 0.0870 |
| 17 | 0.1091 | −0.0173 | −0.1230 | 0.0058 | 0.0018 | 0.0498 |
| 18 | 0.01606 | −0.0060 | −0.0104 | 0.0009 | 0.0005 | 0.0273 |
| 19 | −0.0280 | 0.0007 | −0.0097 | 0.0009 | −0.0007 | 0.0174 |
References
- Mitić, P.; Kostić, A.; Petrović, E.; Cvetanović, S. The Relationship between CO2 Emissions, Industry, Services and Gross Fixed Capital Formation in the Balkan Countries. Eng. Econ. 2020, 31, 425–436. [Google Scholar] [CrossRef]
- Li, D.; Yang, D. Does Non-Fossil Energy Usage Lower CO2 Emissions? Empirical Evidence from China. Sustainability 2016, 8, 874. [Google Scholar] [CrossRef] [Green Version]
- Petrović-Ranđelović, M.; Mitić, P.; Zdravković, A.; Cvetanović, D.; Cvetanović, S. Economic growth and carbon emissions: Evidence from CIVETS countries. Appl. Econ. 2020, 52, 1806–1815. [Google Scholar] [CrossRef]
- Voyant, C.; Notton, G.; Kalogirou, S.; Nivet, M.L.; Paoli, C.; Motte, F.; Fouilloy, A. Machine learning methods for solar radiation forecasting: A review. Renew. Energy 2017, 105, 569–582. [Google Scholar] [CrossRef]
- Zhang, J.; Zhao, L.; Deng, S.; Xu, W.; Zhang, Y. A critical review of the models used to estimate solar radiation. Renew. Sust. Energy Rev. 2017, 70, 314–329. [Google Scholar] [CrossRef]
- Myers, D.R. Cloudy Sky Version of Bird’s Broadband Hourly Clear Sky Model. NREL Technical Report. In Proceedings of the SOLAR 2006 “Renewable Energy: Key to Climate Recovery”, Denver, CO, USA, 8–13 July 2006; Available online: https://www.nrel.gov/docs/fy06osti/40115.pdf (accessed on 7 February 2022).
- Bird, R.E.; Hulstrom, R.L. Simplified Clear Sky Model for Direct and Diffuse Insolation on Horizontal Surfaces (No. SERI/TR-642-761); Solar Energy Research Institute: Golden, CO, USA, 1981. Available online: https://www.nrel.gov/docs/legosti/old/761.pdf (accessed on 7 February 2022).
- Jasmin, B.; Taheri, P. An Origami-Based Portable Solar Pael System. In Proceedings of the 2018 IEEE 9th Annual Information Technology, Electronics and Mobile Communication Conference, Vancouver, BC, Canada, 1–3 November 2018. [Google Scholar]
- Benth, F.E.; Ibrahim, N. Stochastic Modelling of Photovoltaic Power Generation and Electricity Prices. J. Energy Mark. 2017, 10, 275–309. [Google Scholar] [CrossRef]
- Dong, J.; Olama, M.M.; Kuruganti, T.; Melin, A.M.; Djouadi, S.M.; Zhang, Y.; Xue, Y. Novel stochastic methods to predict short-term solar radiation and photovoltaic power. Renew. Energy 2020, 145, 333–346. [Google Scholar] [CrossRef]
- Abdel-Nasser, M.; Karar, M. Accurate photovoltaic power forecasting models using deep LSTM-RNN. Neural Comput. Appl. 2019, 31, 2727–2740. [Google Scholar] [CrossRef]
- Miozzo, M.; Zordan, D.; Dini, P.; Rossi, M. SolarStat: Modeling photovoltaic sources through stochastic Markov processes. In Proceedings of the 2014 IEEE International Energy Conference (ENERGYCON), Cavtat, Croatia, 13–16 May 2014. [Google Scholar] [CrossRef] [Green Version]
- Barukčić, M.; Hederić, Ž.; Hadžiselimović, M.; Seme, S. A simple stochastic method for modelling the uncertainty of photovotaic power production based on measured data. Energy 2018, 165, 246–256. [Google Scholar] [CrossRef]
- Politaki, D.; Alouf, S. Stochastic Models for Solar Power. In Computer Performance Engineering. EPEW 2017. Lecture Notes in Computer Science; Reinecke, P., Di Marco, A., Eds.; Springer: Cham, Switzerland, 2017; Volume 10497, pp. 282–297. [Google Scholar] [CrossRef] [Green Version]
- Gueymard, C.A. Parametrized transmittance model for direct beam and circumsolar spectral irradiance. Sol. Energy 2001, 71, 325–346. [Google Scholar] [CrossRef]
- Badescu, V.; Gueymard, C.A.; Cheval, S.; Oprea, C.; Baciu, M.; Dumitrescu, A.; Iacobescu, F.; Milos, I.; Rada, C. Accuracy analysis for fifty-four clear-sky solar radiation models using routine hourly global irradiance measurements in Romania. Renew. Energy 2013, 55, 85–103. [Google Scholar] [CrossRef]
- Ineichen, P. Validation of models that estimate the clear sky global and beam solar irradiance. Sol. Energy 2016, 132, 332–344. [Google Scholar] [CrossRef] [Green Version]
- Hofmann, M.; Seckmeyer, G. A New Model for Estimating the Diffuse Fraction of Solar Irradiance for Photovoltaic System Simulations. Energies 2017, 10, 248. [Google Scholar] [CrossRef] [Green Version]
- Khatib, T.; Mohamed, A.; Sopian, K. A review of solar energy modeling techniques. Renew. Sustain. Energy Rev. 2012, 16, 2864–2869. [Google Scholar] [CrossRef]
- Moharram, K.A.; Abd-Elhady, M.S.; Kandil, H.A.; El-Sherif, H. Enhancing the performance of photovoltaic panels by water cooling. Ain. Shams Eng. J. 2013, 4, 869–877. [Google Scholar] [CrossRef] [Green Version]
- Brecl, K.; Topič, M. Development of a Stochastic Hourly Solar Irradiation Model. Int. J. Photoenergy 2014, 2014, 376504. [Google Scholar] [CrossRef] [Green Version]
- SolarEdge. Available online: https://www.solaredge.com/sites/default/files/se-smart-modules-white-datasheet-aus.pdf (accessed on 7 February 2022).
- JinkoSolar. Available online: https://www.jinkosolar.com/uploads/CheetahPerc%20JKM325-345M-60H-(V)-A3-EN.pdf (accessed on 7 February 2022).
- Michalsky, J.J. The Astronomical Almanac’s algorithm for approximate solar position (1950–2050). Sol. Energy 1988, 40, 227–235. [Google Scholar] [CrossRef]
- Andreas, A.; Reda, I. Solar Position Algorithm for Solar Radiation Applications (Revised), Technical Report, NREL/TP-560-34302; National Renewable Energy Laboratory: Golden, CO, USA, 2008. Available online: https://www.nrel.gov/docs/fy08osti/34302.pdf (accessed on 7 February 2022).
- Duffie, J.A.; Beckman, W.A. Solar Engineering of Thermal Processes, 4th ed.; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2013; ISBN 978-047-087-366-3. [Google Scholar]
- Alboteanu, I.L.; Bulucea, C.A.; Degeratu, S. Estimating Solar Irradiation Absorbed by Photovoltaic Panels with Low Concentration Located in Craiova, Romania. Sustainability 2015, 7, 2644–2661. [Google Scholar] [CrossRef] [Green Version]
- Schönwiese, C.D. Klimatologie, 4th ed.; UTB GmbH: Stuttgart, Germany, 2013; ISBN 978-382-523-900-8. [Google Scholar]
- Richardson, C.W. Stochastic simulation of daily precipitation, temperature, and solar radiation. Water Resour. Res. 1981, 17, 182–190. [Google Scholar] [CrossRef]
- Campbell, G.S.; Norman, J.M.A. Introduction to Environmental Biophysics; Springer Science+Business Media: New York, NY, USA, 1998. [Google Scholar] [CrossRef]
- Parey, S. Generating a Set of Temperature Time Series Representative of Recent Past and Near Future Climate. Front. Environ. Sci. 2019, 7, 99. [Google Scholar] [CrossRef]
- Breinl, K.; Turkington, T.; Stowasser, M. Simulating daily precipitation and temperature: A weather generation framework for assessing hydrometeorological hazards. Meteorol. Appl. 2014, 22, 334–347. [Google Scholar] [CrossRef]
- Smith, K.; Strong, C.; Rassoul-Agha, F. A New Method for Generating Stochastic Simulations of Daily Air Temperature for Use in Weather Generators. J. Appl. Meteorol. Climatol. 2017, 56, 953–963. [Google Scholar] [CrossRef] [Green Version]
- McNeil, A.J.; Frey, R.; Embrechts, P. Quantitative Risk Management: Concepts, Techniques, and Tools—Revised Edition; Princeton University Press: Princeton, NJ, USA, 2015; ISBN 978-0-691-16627-8. [Google Scholar]
- Deutscher Wetterdienst. Available online: https://www.dwd.de (accessed on 7 February 2022).
- Global Modeling and Assimilation Office (GMAO). MERRA-2 tavg1 2d slv Nx: 2d,1-Hourly, Time-Averaged, Single-Level, Assimilation, Single-Level Diagnostics V5.12.4; Goddard Earth Sciences Data and Information Services Center (GES DISC): Greenbelt, MD, USA, 2015. [Google Scholar] [CrossRef]
- SoDa. Solar Radiation Data. Available online: https://www.soda-pro.com (accessed on 7 February 2022).
- Lockart, N.; Kavetski, D.; Franks, S.W. A New Stochastic Model for Simulating Daily Solar Radiation from Sunshine Hours. Int. J. Climatol. 2015, 35, 1090–1106. [Google Scholar] [CrossRef]
- Anand, M.P.; Rajapakse, A.; Bagen, B. Stoachstic Model for Generating Synthetic Hourly Global Horizontal Solar Radiation Data Sets Based on Auto Regression Characterization. Int. Energy J. 2020, 20, 181–200. [Google Scholar]
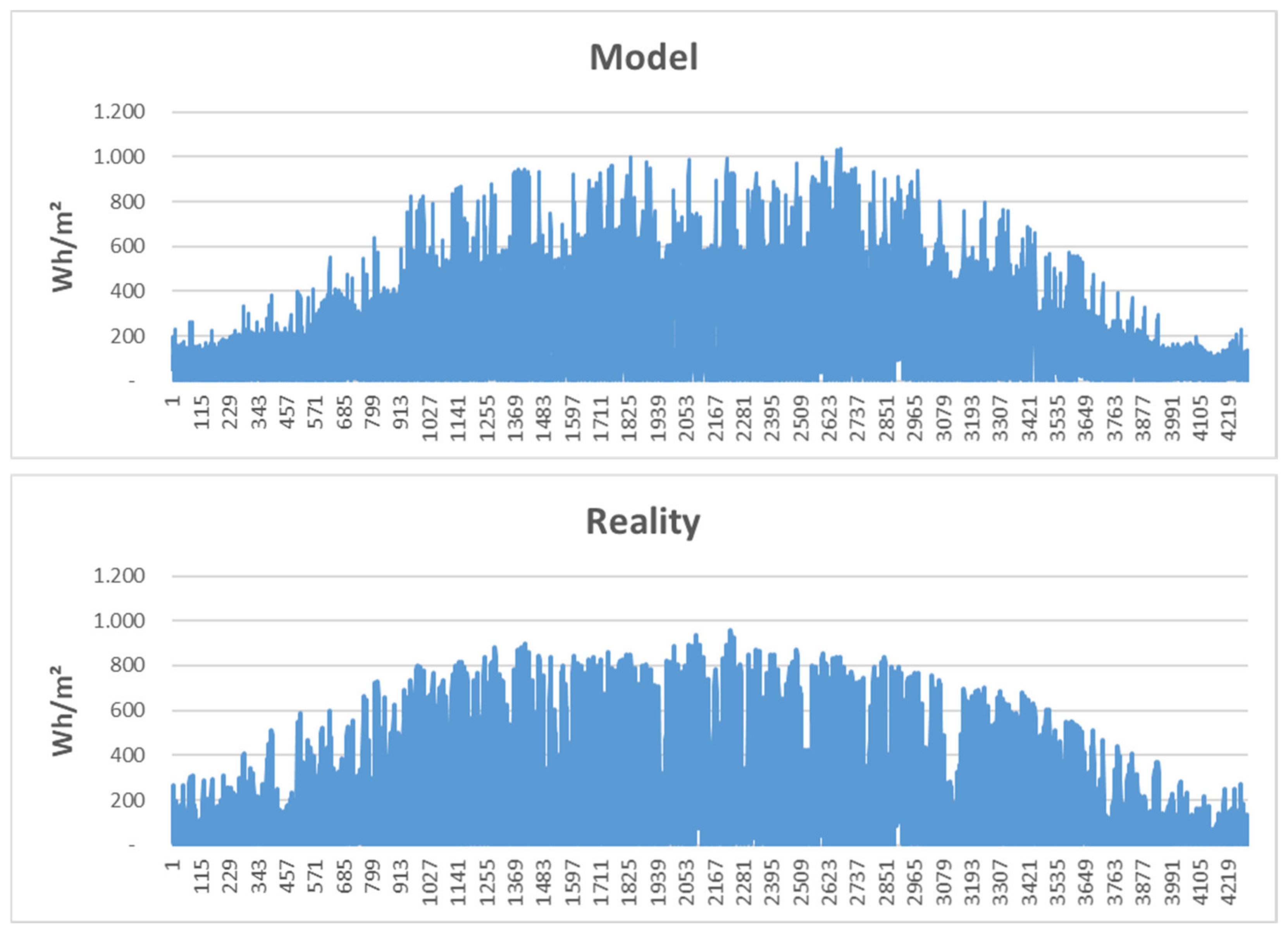

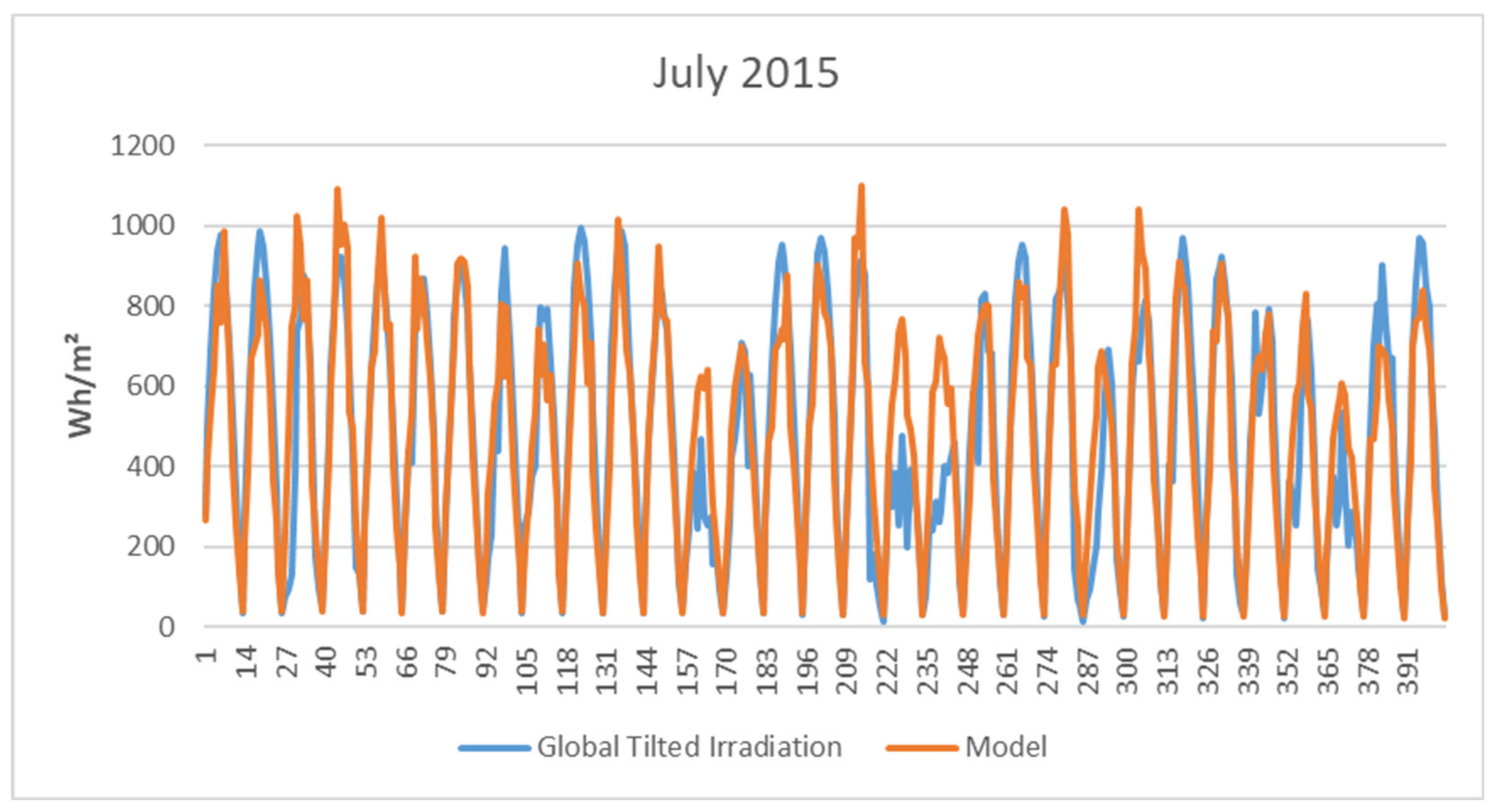
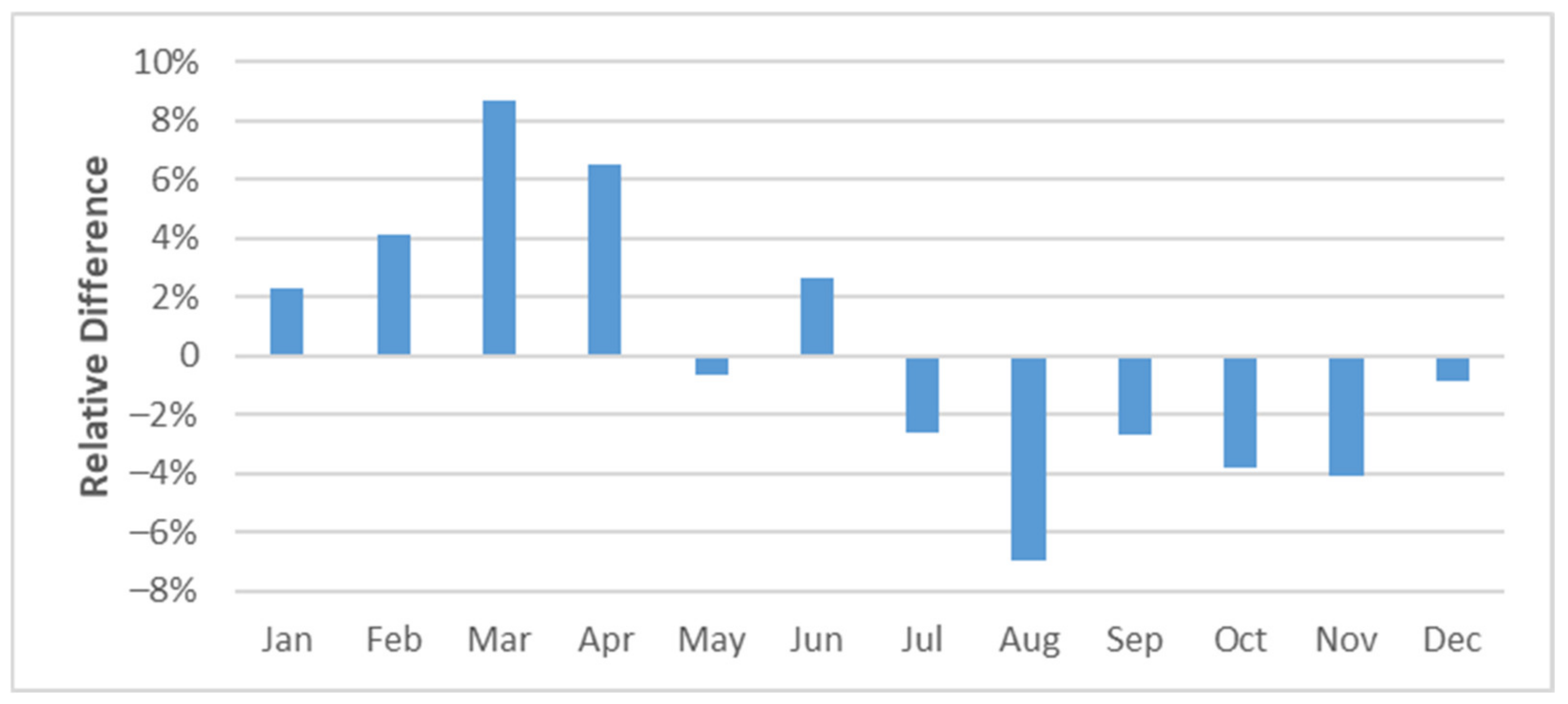

| Data Set | Source | From/To | Length |
|---|---|---|---|
| Temperature Ulm | www.dwd.de [35] | 1 January 2014–31 December 2018 | 37,924 |
| Cloud Cover Ulm | www.dwd.de [35] | 1 January 2014–31 December 2018 | 37,381 |
| Irradiation Ulm | www.soda-pro.com [37] | 1 January 2013–31 December 2018 | 52,584 |
| January | February | March | April | May | June | |
| RSE | 37.82% | 38.94% | 29.71% | 29.17% | 27.97% | 25.11% |
| MAPE | 29.01% | 30.78% | 25.96% | 22.27% | 19.85% | 17.74% |
| January | February | March | April | May | June | |
| RSE | 25.66% | 27.50% | 29.65% | 34.96% | 38.74% | 32.06% |
| MAPE | 17.18% | 17.86% | 21.55% | 29.48% | 32.05% | 33.55% |
| January | February | March | April | May | June | |
| RSE | 49.98% | 47.76% | 37.57% | 27.50% | 29.15% | 24.19% |
| MAPE | 37.44% | 39.14% | 31.12% | 24.62% | 23.07% | 18.95% |
| January | February | March | April | May | June | |
| RSE | 25.37% | 27.49% | 31.86% | 43.92% | 48.80% | 49.33% |
| MAPE | 17.74% | 20.01% | 25.14% | 37.65% | 43.23% | 39.13% |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Schlüter, S.; Menz, F.; Kojić, M.; Mitić, P.; Hanić, A. A Novel Approach to Generate Hourly Photovoltaic Power Scenarios. Sustainability 2022, 14, 4617. https://doi.org/10.3390/su14084617
Schlüter S, Menz F, Kojić M, Mitić P, Hanić A. A Novel Approach to Generate Hourly Photovoltaic Power Scenarios. Sustainability. 2022; 14(8):4617. https://doi.org/10.3390/su14084617
Chicago/Turabian StyleSchlüter, Stephan, Fabian Menz, Milena Kojić, Petar Mitić, and Aida Hanić. 2022. "A Novel Approach to Generate Hourly Photovoltaic Power Scenarios" Sustainability 14, no. 8: 4617. https://doi.org/10.3390/su14084617
APA StyleSchlüter, S., Menz, F., Kojić, M., Mitić, P., & Hanić, A. (2022). A Novel Approach to Generate Hourly Photovoltaic Power Scenarios. Sustainability, 14(8), 4617. https://doi.org/10.3390/su14084617







