Safety Assessment of Channel Seepage by Using Monitoring Data and Detection Information
Abstract
:1. Introduction
2. Project Overview and Analysis Methods
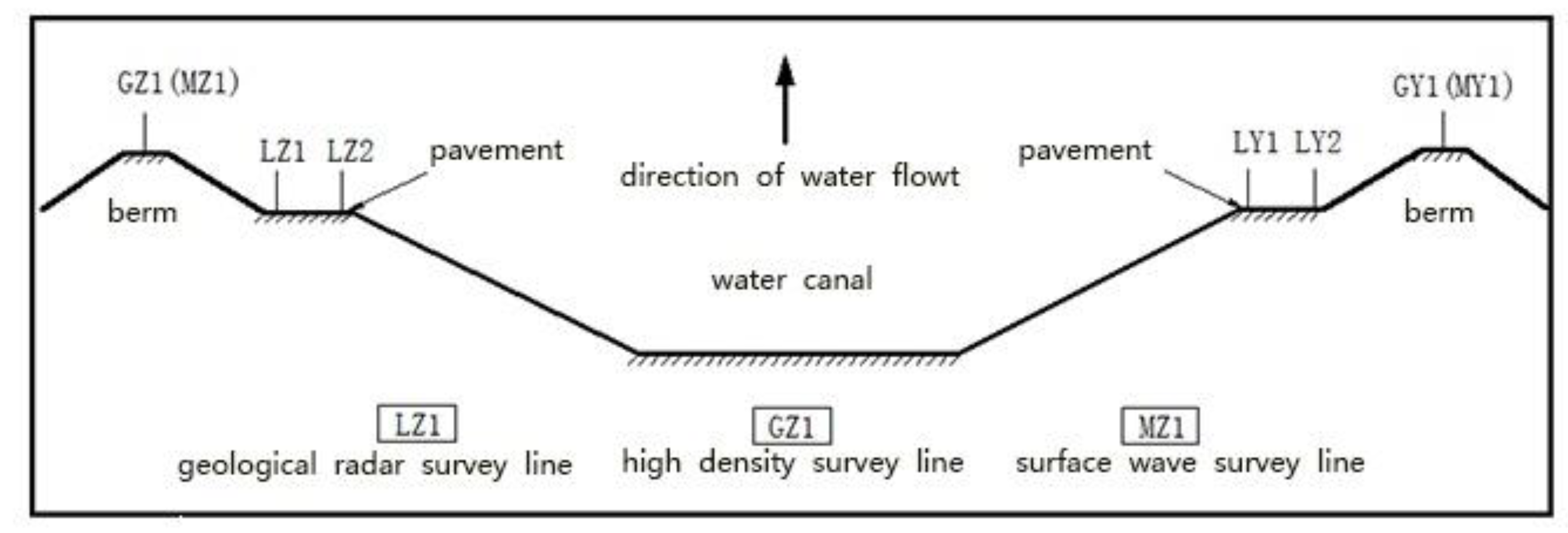
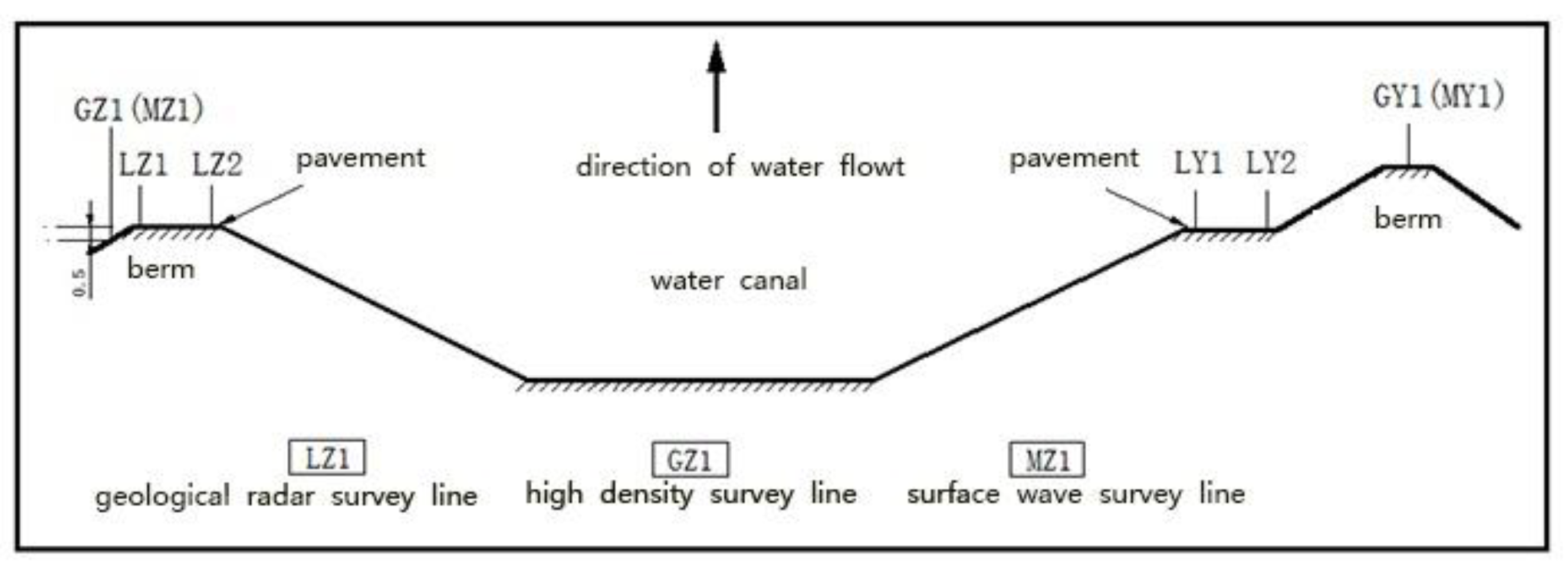
2.1. Project Overview
2.2. General Flow of the Set Pair Analysis Method Considering Data Uncertainty
2.2.1. Set-to-Set Determination
2.2.2. Determination of Indicator Weight
2.2.3. Calculation of Connection Degree
2.2.4. Computation of Potential Vector and Determination of Evaluation Grading in a Comprehensive Set
3. Key Indicators Safety Evaluation Criteria
3.1. Water Level and Temperature Safety Evaluation Standard
- (1)
- Water level safety evaluation standard in the canal
- (2)
- Temperature Evaluation Safety Standards
3.2. Osmotic Pressure Safety Evaluation Standard
- (1)
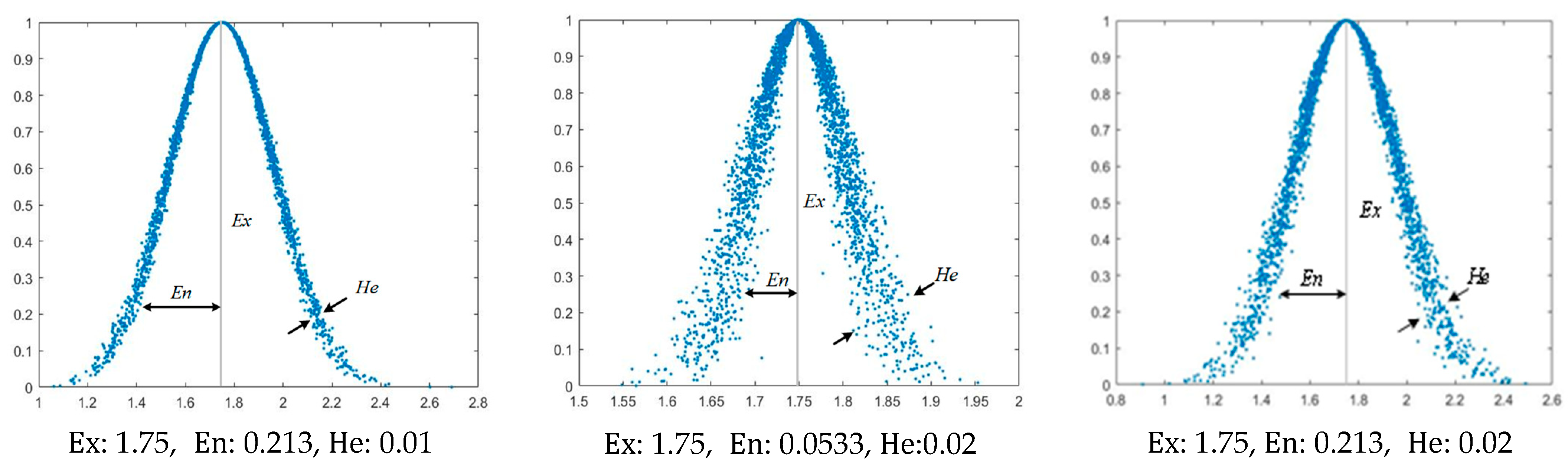
- Cloud model theory:
- Calculate the sample mean of the basic data according to , the absolute center distance of the first-order sample , and the sample variance
- (2)
- Determination of the osmotic pressure safety evaluation standard
4. Analysis of the Seepage Safety Evaluation of the Canal in a High-Fill Section
4.1. Establishment of Evaluation Index System and Evaluation Standard Set
4.2. Weight Distribution
4.3. Connection Calculation
- (1)
- Single index connection degree
| Water level data: | Osmometer P5-4: |
| Temperature change: | Osmometer P6-5: |
| Osmometer P4-6: | Osmometer P7-5: |
- (2)
- Comprehensive connection degree
4.4. Evaluation Results
4.5. Test Information Verification
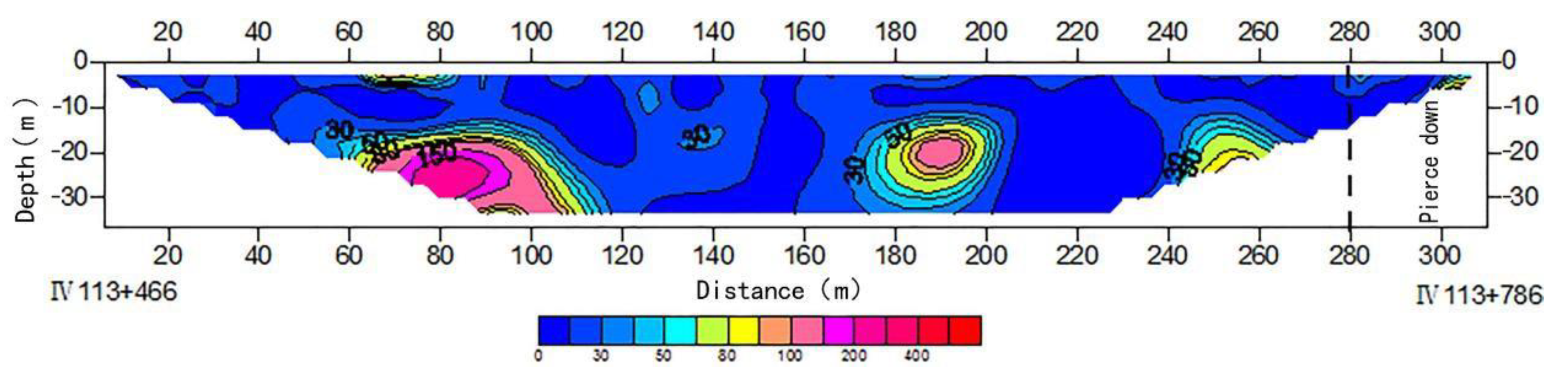
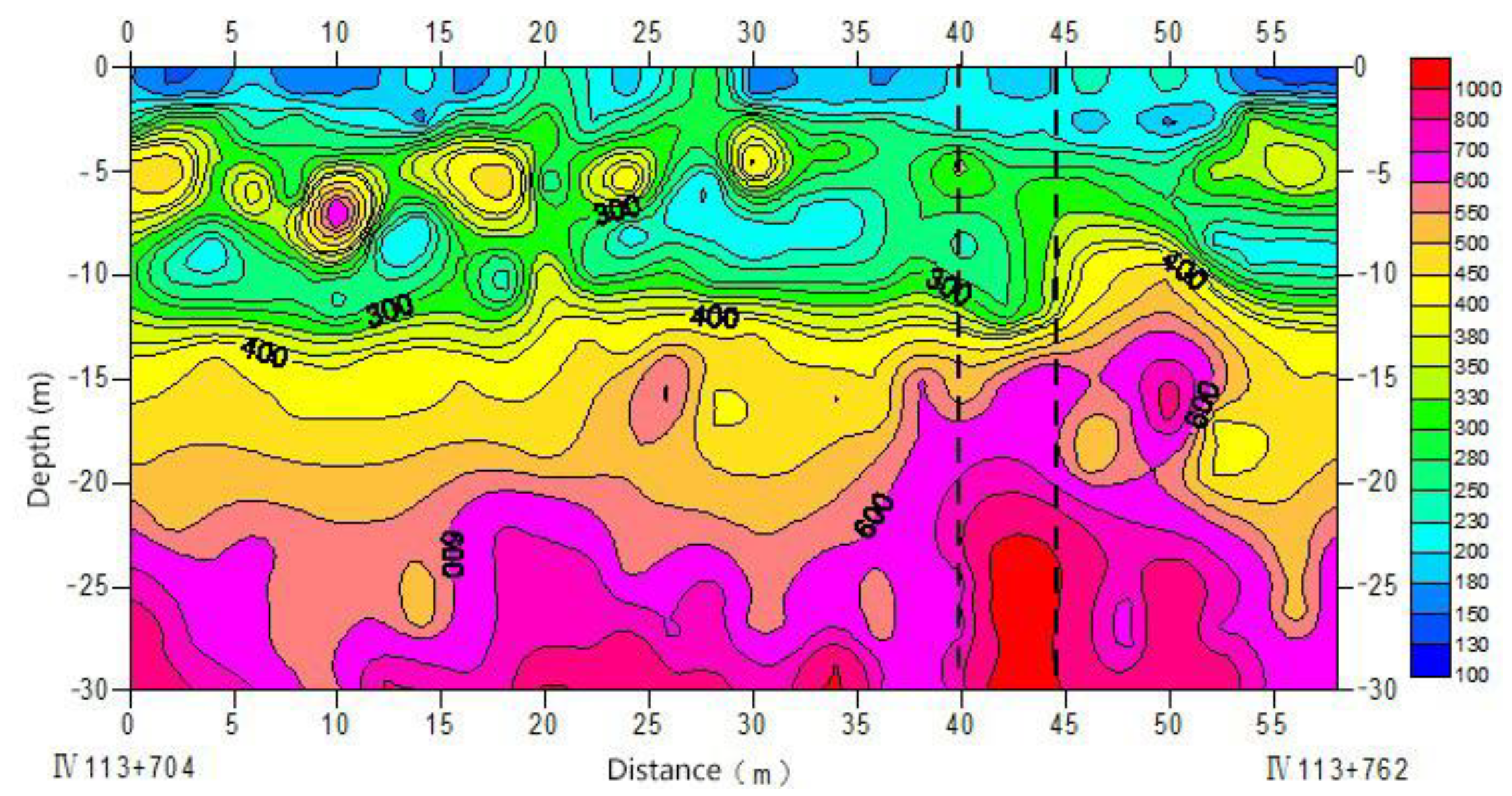
- (1)
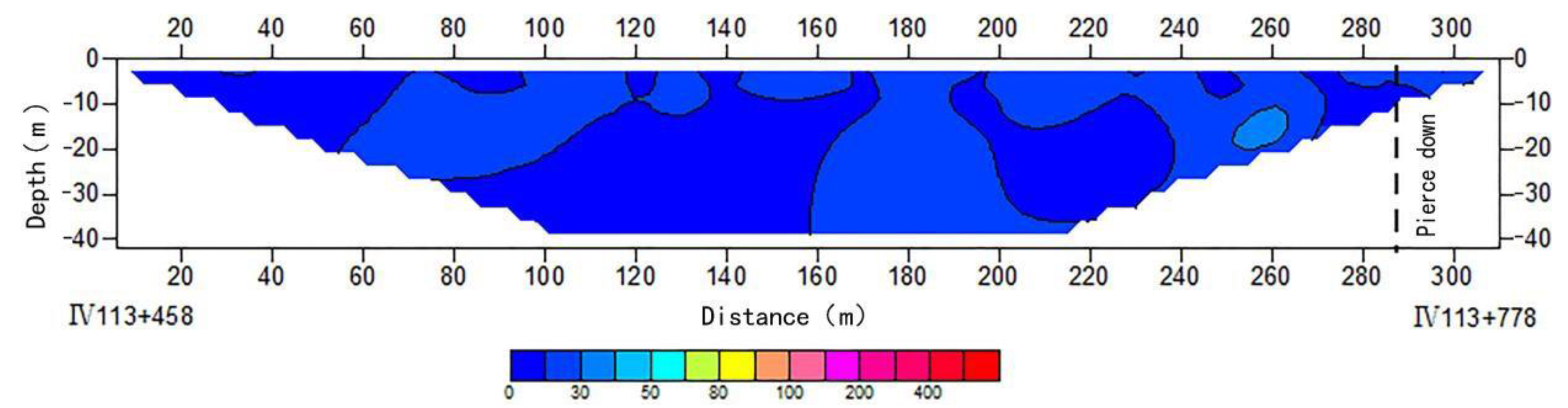
- Geological radar method
- (2)
- High-density electrical method
- (3)
- Surface wave method
4.6. Results of Fusion Analysis of Monitoring Data and Detection Information
5. Conclusions
- (1)
- Combining the monitoring index value method and the theoretical method of the cloud model, a single-point multi-factor aging model of the monitoring data can be established. Through statistical analysis of the monitoring data, the data mean Y, standard deviation value S, and cloud digital characteristics can be obtained. On the premise of clarifying the distribution interval of monitoring data, safety evaluation standards for factors such as water level, temperature, and osmotic pressure are obtained.
- (2)
- Integrating the single-point multi-factor aging model with the set pair analysis method can realize the determination of the evaluation level of monitoring data. Using the formula of the connection degree, the generalized set pair potential, and confidence intervals, etc., the safety level of the seepage monitoring data of the project is determined, and the safety evaluation result is “safety degree 50~75%”.
- (3)
- The detection of abnormal information could be realized. By collecting data a from a geological radar and using the high-density electrical and surface wave method to achieve an image output using tomography and other methods, the qualitative analysis of canal section safety is realized based on expert experience.
- (4)
- With the employment of the comprehensive analysis method, the relationship between environmental variables, monitoring data, and detection information is studied and considered, an adaptive evaluation method reflecting the working behavior of the channel is established, and corresponding diagnostic techniques are proposed.
Author Contributions
Funding
Informed Consent Statement
Conflicts of Interest
References
- Ge, W.; Li, Z.K.; Liang, R.Y.; Li, W.; Cai, Y.C. Methodology for Establishing Risk Criteria for Dams in Developing Countries, Case Study of China. Water Resour. Manag. 2017, 31, 4063–4074. [Google Scholar] [CrossRef]
- Matalas, N.C.; Nordin, C.F.; Ministry of Water Resources of the People’s Republic of China. First National Water Conservancy Survey Bulletin; China Water Resources and Hydropower Press: Beijing, China, 2013. [Google Scholar]
- Fan, Q.; Tian, Z.; Wang, W. Study on Risk Assessment and Early Warning of Flood-Affected Areas when a Dam Break Occurs in a Mountain River. Water 2018, 10, 1369. [Google Scholar] [CrossRef] [Green Version]
- Jie, J.; Sun, D. Statistics of Dam Damages in China and Analysis on Damage Causations. Water Resour. Hydropower Eng. 2009, 40, 124–128. [Google Scholar]
- Jiang, S.; Fan, Z. Earth-rockfill dam safety classification and risk rate assessment on flood control. J. Hydraul. Eng. 2008, 39, 35–40. [Google Scholar]
- Chen, S. The Damage Mechanism of Earth-Rock DAMS and the Simulation of Dam Damage Process; China Water &Power Press: Beijing, China, 2012. [Google Scholar]
- Mei, Y.; Zhong, Y. Fuzzy Extension Evaluation Model of Dam Osmotic Behavior Based on Entropy Weight. Water Resour. Power 2011, 29, 58–61. [Google Scholar]
- Wang, X.; Dai, L.; Lü, P.; Wang, C.; Cheng, Z. Study on Comprehensive Evaluation Model of Osmotic Safety Based on DSR-Extension Cloud. J. Tianjin Univ. 2019, 52, 52–61. [Google Scholar]
- Wang, X.; Yu, H.; Lv, P.; Wang, C.; Zhang, J.; Yu, J. Seepage Safety Assessment of Concrete Gravity Dam Based on Matter-Element Extension Model and FDA. Energies 2019, 12, 502. [Google Scholar] [CrossRef] [Green Version]
- Su, H.; Ou, B.; Fang, Z.; Gao, J.; Wen, Z. Dual criterion-based dynamic evaluation approach for dike safety. Struct. Health Monit. 2018, 18, 147592171881337. [Google Scholar] [CrossRef]
- Xiang, Y.; Fu, S.; Zhu, K.; Yuan, H.; Fang, Z. Seepage safety monitoring model for an earth rock dam under influence of high-impact typhoons based on particle swarm optimization algorithm. Water Sci. Eng. 2017, 10, 70–77. [Google Scholar] [CrossRef]
- Lan, Z.; Huang, M. Safety assessment for seawall based on constrained maximum entropy projection pursuit model. Nat. Hazards 2018, 91, 1165–1178. [Google Scholar] [CrossRef]
- Su, H.; Tian, S.; Kang, Y.; Xie, W.; Chen, J. Monitoring water seepage velocity in dikes using distributed optical fiber temperature sensors. Autom. Constr. 2017, 76, 71–84. [Google Scholar] [CrossRef]
- Keqin, Z. Set pair analysis and its prelimiary application SE. Explor. Nat. 1994, 13, 67–72. [Google Scholar]
- Cao, L.; Wang, H.Y.; Lu, F.X. Operational Capability Evaluation of Surface Warship Formation Based on Set Pair Analysis. In Proceedings of the 2016 8th International Conference on Intelligent Human-Machine Systems and Cybernetics (IHMSC), IEEE, Hangzhou, China, 27–28 August 2016. [Google Scholar]
- Yang, Y. Research on approximate inference method based on Set pair logic. CAAI Trans. Intell. Syst. 2015, 10, 921–926. [Google Scholar]
- Li, W. Application of AHP Analysis in Risk Management of Engineering Projects. J. Beijing Univ. Chem. Technol. 2009, 1, 46–48. [Google Scholar]
- Cui, D.H.; Zhang, X.Y. Application of Gray Analytic Hierarchy Process in Project Risk Evaluation. In Proceedings of the 2009 International Conference on Artificial Intelligence and Computational Intelligence, AICI ‘09, Shanghai, China, 7–8 November 2009. [Google Scholar]
- Liu, B.X.; Zhang, C.Y. The Situation Ordered Structure of IDO Connection Degree and ITS Application. In Proceedings of the IEEE 2006 International Conference on Machine Learning and Cybernetics, Dalian, China, 13–16 August 2006. [Google Scholar]
- Li, D.S.; Xu, K.L. IDO most superior pattern recognition model and its application in the safety assessment of the coal mine. Procedia Eng. 2011, 26, 2059–2064. [Google Scholar]
- Yang, Y.F.; Yang, A.M.; Zhang, H.C. Application of Set pair analysis in the Material Clustering. Appl. Mech. Mater. 2013, 443, 707–710. [Google Scholar] [CrossRef]
- Chen, S.; Wang, S.Y.; Sun, J.Z. Trusted software reliability measures based on cloud model. Appl. Res. Comput. 2014, 31, 2729–2731. [Google Scholar]
- Zhou, J.; Zhu, Y.Q.; Chai, X.D.; Tang, W.Q. Approach for analyzing consensus based on cloud model and evidence theory. Syst. Eng. Theory Pract. 2012, 32, 2756–2763. [Google Scholar]
- Zhang, Q.-W.; Zhang, Y.-Z.; Zhong, M. A cloud model base approach for multi-hierarchy fuzzy comprehensive evaluation of reservoir-induced seismic risk. J. Hydraul. Eng. 2014, 45, 87–95. [Google Scholar]
- Chen, H.; Bing, L.I. Gauss Cloud Model Based on Uniform Distribution. Comput. Sci. 2016, 43, 238-241, 246. [Google Scholar]
- Yu, L.; Li, D. Statistics on atomized feature of normal cloud model. J. Beijing Univ. Aeronaut. Astronaut. 2010, 36, 1320. [Google Scholar]
- Li, S.H.; Wang, S.Y.; Zhu, J.D.; Li, B.; Yang, J.; Wu, L.Z. Prediction of rock burst tendency based on weighted fusion and improved cloud model. Yantu Gong Cheng Xue Bao/Chin. J. Geotech. Eng. 2018, 40, 1075–1083. [Google Scholar]
- Gao, H.B.; Zhang, X.Y.; Zhang, T.L.; Liu, Y.C.; Li, D.Y. Research of Intelligent Vehicle Variable Granularity Evaluation Based on Cloud Model. Acta Electron. Sin. 2016, 44, 365–373. [Google Scholar]
- Fu, B.; Li, D.G.; Wang, M.K. Review and prospect on research of cloud model. Appl. Res. Comput. 2011, 2, 420–426. [Google Scholar]
- Wang, S.; Chi, H.; Feng, X.; Yin, J. Human Facial Expression Mining Based on Cloud Model. In Proceedings of the IEEE International Conference on Granular Computing, Nanchang, China, 17–19 August 2009. [Google Scholar]


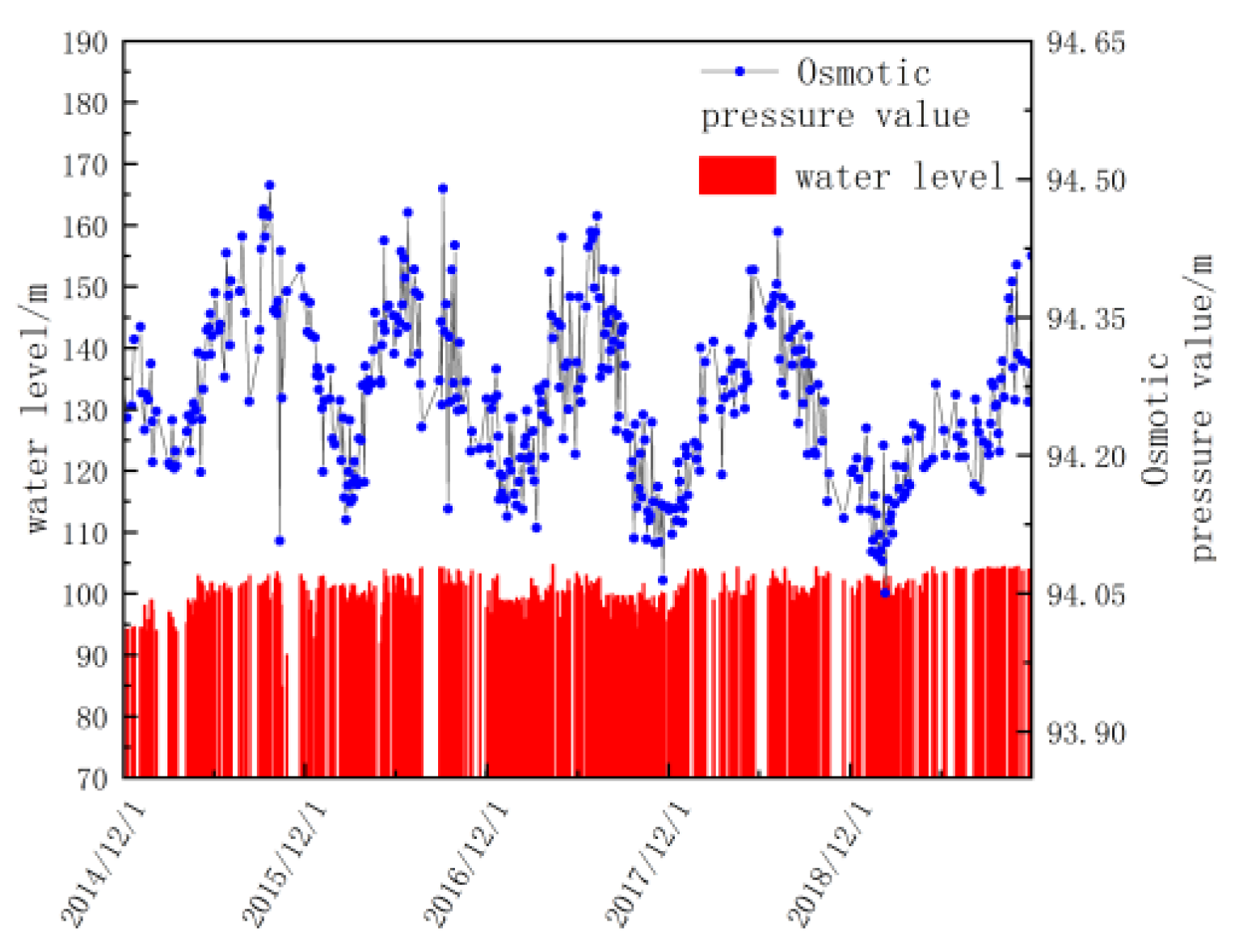
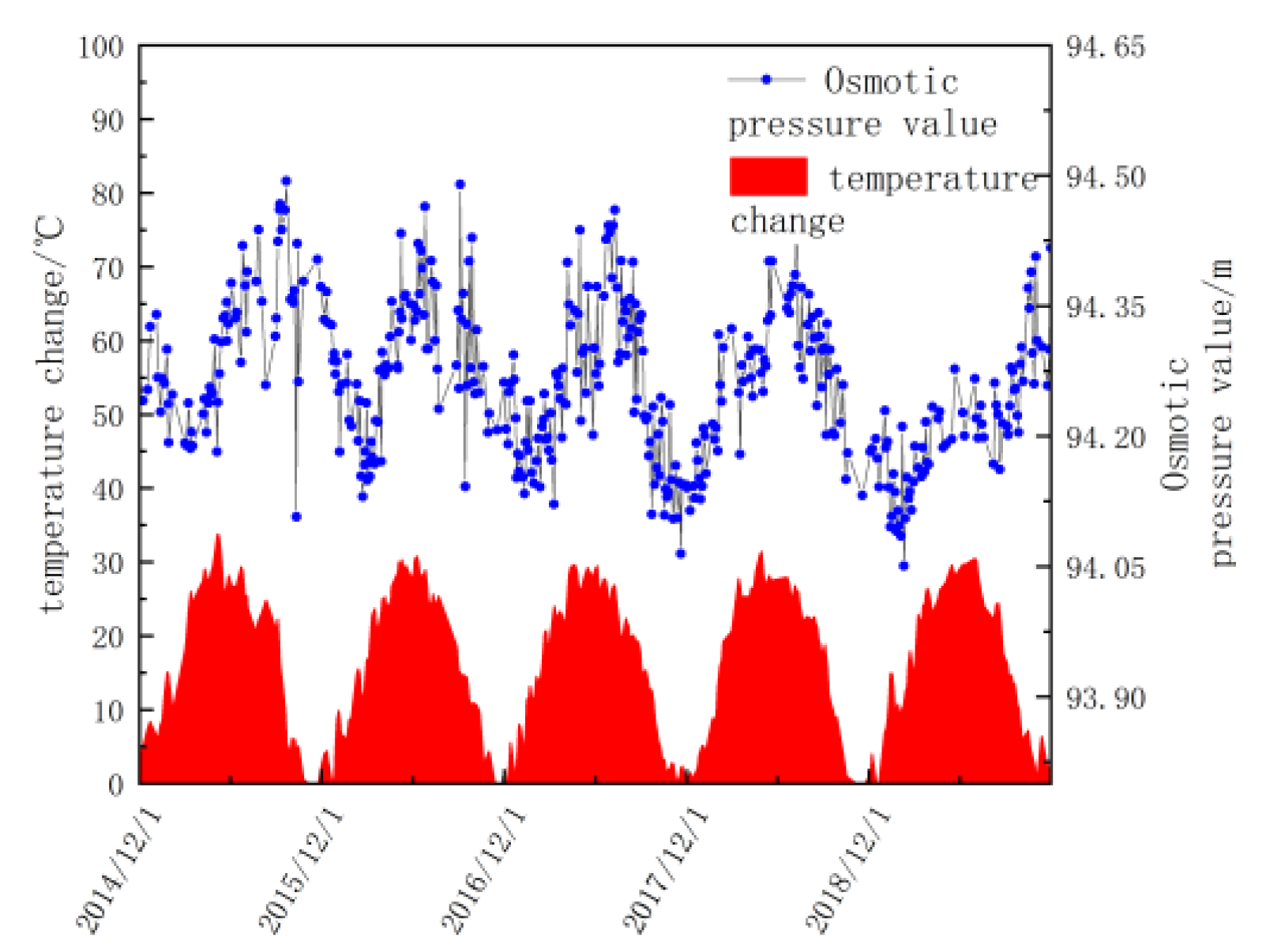

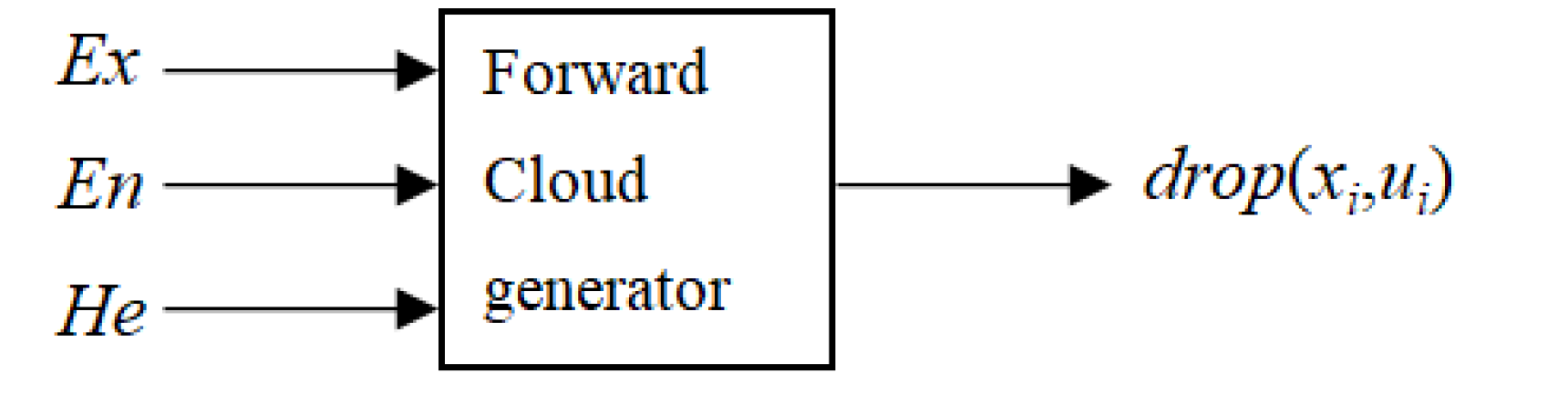
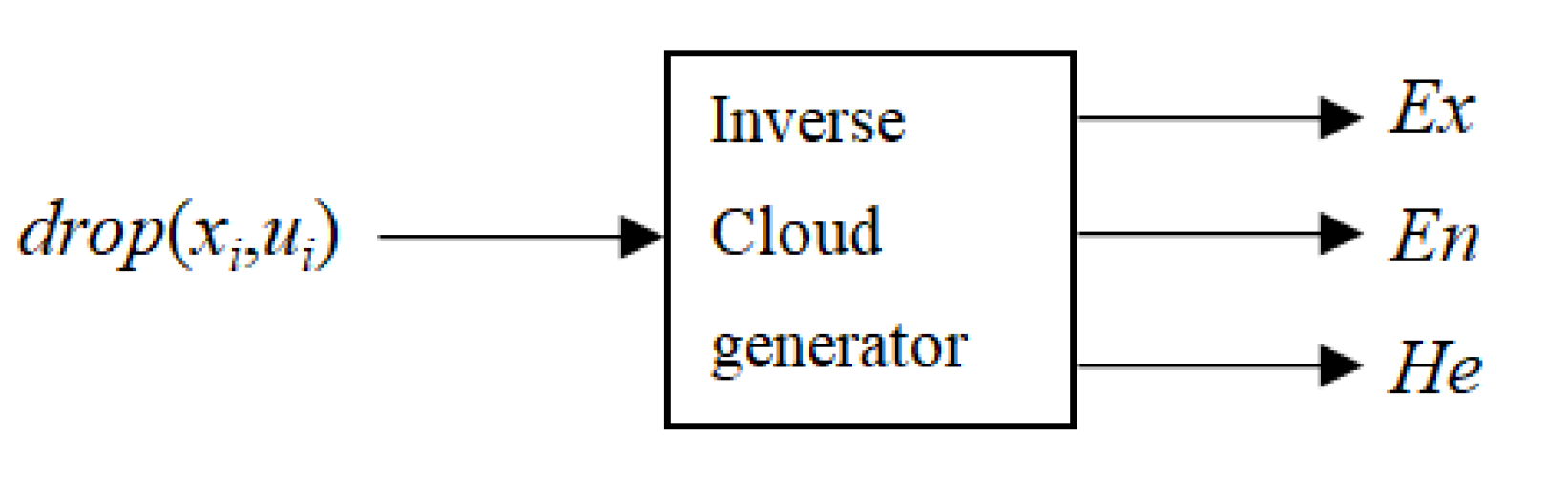









| Grading | Grading Standard |
|---|---|
| Safety 75~100% | |
| Safety 50~75% | |
| Safety 25~50% | |
| Safety 0~25% |
| Temperature Drop | Temperature Rise | ||
|---|---|---|---|
| Grading | Grading Standard | Grading | Grading Standard |
| Safety 75~100% | Safety 75~100% | ||
| Safety 50~75% | Safety 50~75% | ||
| Safety 25~50% | Safety 25~50% | ||
| Safety 0~25% | Safety 0~25% | ||
| Grading | Grading Standard | Grading | Grading Standard |
|---|---|---|---|
| Safety 75~100% | Safety 75~100% | ||
| Safety 50~75% | Safety 50~75% | ||
| Safety 25~50% | Safety 25~50% | ||
| Safety 0~25% | Safety 0~25% | ||
| Evaluation Index | Water Level Data | Temperature Change | Osmometer P4-6 | Osmometer P5-4 | Osmometer P6-5 | Osmometer P7-5 |
|---|---|---|---|---|---|---|
| Osmotic index value | 108.45 | 14.9 | 93.99 | 93.95 | 93.52 | 92.68 |
| Grading | Grading Standard |
|---|---|
| Safety 75~100% | [87.13, 109.18] |
| Safety 50~75% | (109.18, 111.43] |
| Safety 25~50% | (111.43, 112.17] |
| Safety 0~25% | (112.17, 115.15] |
| Temperature Drop | Temperature Rise | ||
|---|---|---|---|
| Grading | Grading Standard | Grading | Grading Standard |
| Safety 75~100% | [−1.49, 12.30] | Safety 75~100% | [2.30, 29.01] |
| Safety 50~75% | (−5.91, −1.49] | Safety 50~75% | (29.01, 36.91] |
| Safety 25~50% | (−10.40, −5.91] | Safety 25~50% | (36.91, 38.70] |
| Safety 0~25% | [−15.60, −10.40] | Safety 0~25% | (38.70, 41.50] |
| Osmometer Number | Mean (Ex) | Entropy (En) | Hyper-Entropy (He) | Max | Min |
|---|---|---|---|---|---|
| Osmometer P4-6 | 94.12 | 0.19 | 0.06 | 95.52 | 93.59 |
| Osmometer P5-4 | 93.47 | 0.18 | 0.03 | 94.09 | 92.90 |
| Osmometer P6-5 | 93.37 | 0.12 | 0.01 | 93.85 | 92.87 |
| Osmometer P7-5 | 92.63 | 0.16 | 0.05 | 93.32 | 92.14 |
| Osmometer P4-6 | Osmometer P5-4 | ||
|---|---|---|---|
| Grading | Grading standard | Grading | Grading standard |
| Safety 75~100% | [93.59, 94.31) | Safety 75~100% | [92.90, 93.65) |
| Safety 50~75% | [94.31, 94.50) | Safety 50~75% | [93.65, 93.83) |
| Safety 25~50% | [94.50, 94.70) | Safety 25~50% | [93.83, 94.01) |
| Safety 0~25% | [94.70, 95.52] | Safety 0~25% | [94.01, 94.09] |
| Osmometer P6-5 | Osmometer P7-5 | ||
| Grading | Grading standard | Grading | Grading standard |
| Safety 75~100% | [92.87, 93.49) | Safety 75~100% | [92.14, 92.79) |
| Safety 50~75% | [93.49, 93.61) | Safety 50~75% | [92.79, 92.95) |
| Safety 25~50% | [93.61,93.73) | Safety 25~50% | [92.95,93.11) |
| Safety 0~25% | [93.73,93.85] | Safety 0~25% | [93.11,93.32] |
| Evaluation Index | Water Level Data | Temperature Change | Osmometer P4-6 | Osmometer P5-4 | Osmometer P6-5 | Osmometer P7-5 |
|---|---|---|---|---|---|---|
| Weights | 0.0812 | 0.0673 | 0.2235 | 0.2171 | 0.2122 | 0.1987 |
| Grading Index | Safety 75~100% | Safety 50~75% | Safety 25~50% | Safety 0~25% |
|---|---|---|---|---|
| Osmotic | 2.7155 | 1.8904 | 1.3453 | 1.1228 |
| 0.3839 | 0.2672 | 0.1902 | 0.1587 | |
| Confidence interval | 0.6511 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhao, M.; Zhang, C.; Chen, S.; Jiang, H. Safety Assessment of Channel Seepage by Using Monitoring Data and Detection Information. Sustainability 2022, 14, 8378. https://doi.org/10.3390/su14148378
Zhao M, Zhang C, Chen S, Jiang H. Safety Assessment of Channel Seepage by Using Monitoring Data and Detection Information. Sustainability. 2022; 14(14):8378. https://doi.org/10.3390/su14148378
Chicago/Turabian StyleZhao, Mengdie, Chao Zhang, Shoukai Chen, and Haifeng Jiang. 2022. "Safety Assessment of Channel Seepage by Using Monitoring Data and Detection Information" Sustainability 14, no. 14: 8378. https://doi.org/10.3390/su14148378
APA StyleZhao, M., Zhang, C., Chen, S., & Jiang, H. (2022). Safety Assessment of Channel Seepage by Using Monitoring Data and Detection Information. Sustainability, 14(14), 8378. https://doi.org/10.3390/su14148378





