Fuel Cell Hybrid Locomotive with Modified Fuzzy Logic Based Energy Management System
Abstract
:1. Introduction
2. Methodology
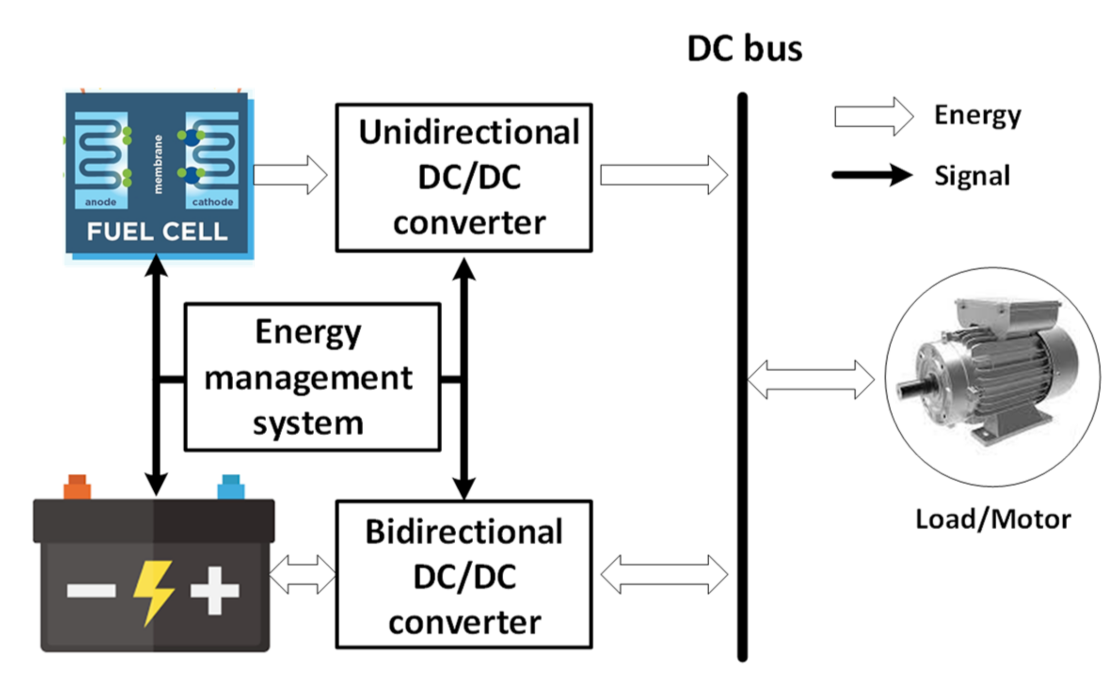
2.1. Modeling of Power System for Fuel Cell Hybrid Locomotive
2.1.1. Modeling of Fuel Cell
2.1.2. Modeling of Battery
2.1.3. Modeling of DC-DC Converters
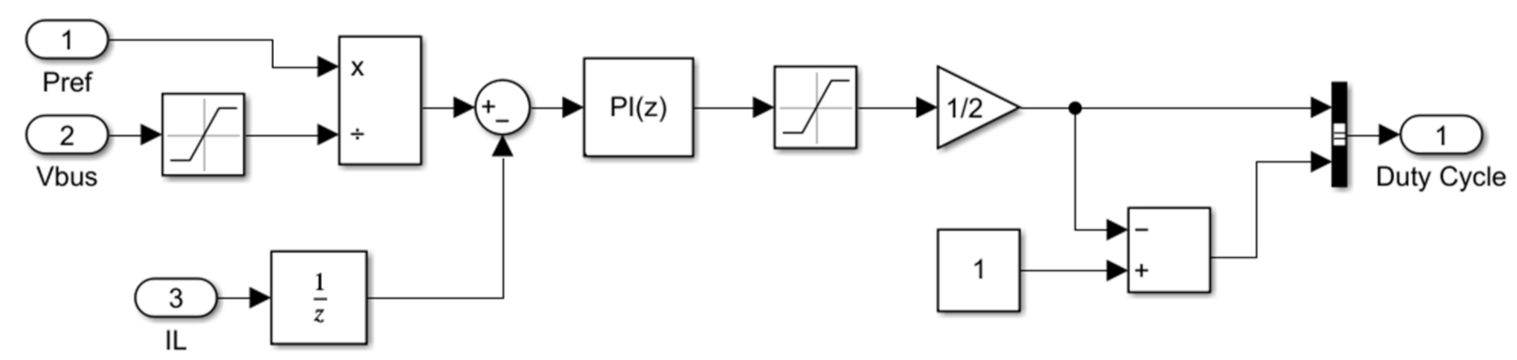
Unidirectional Converter
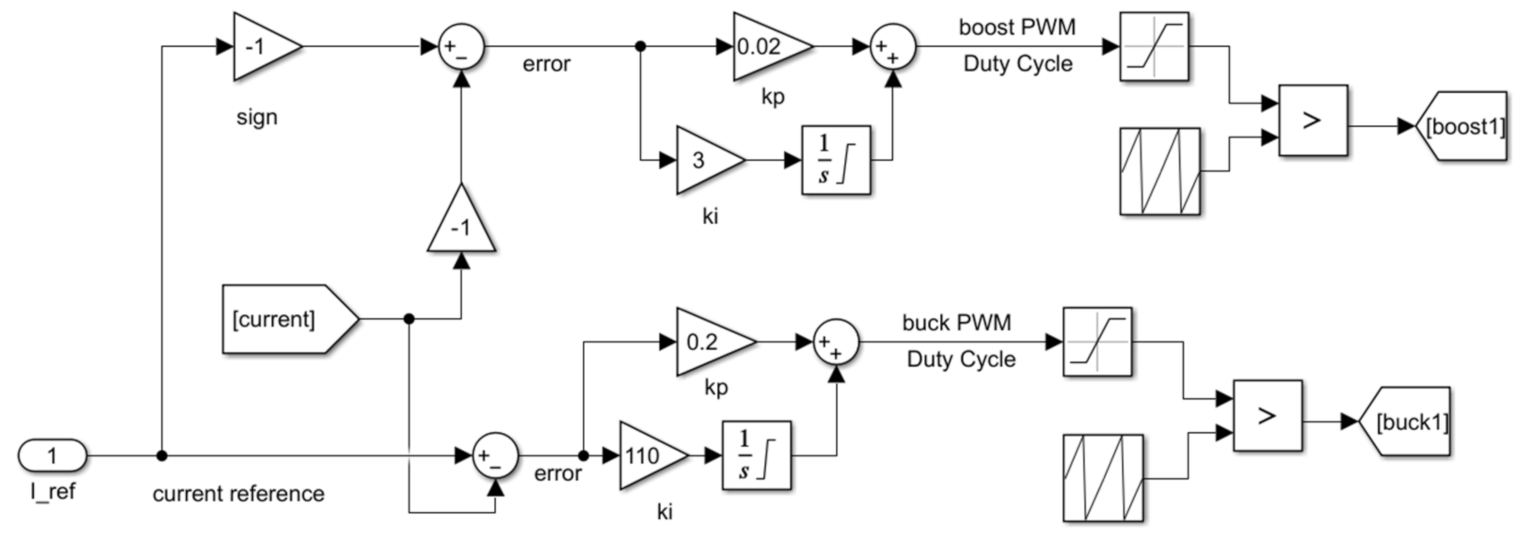
Bidirectional Converter
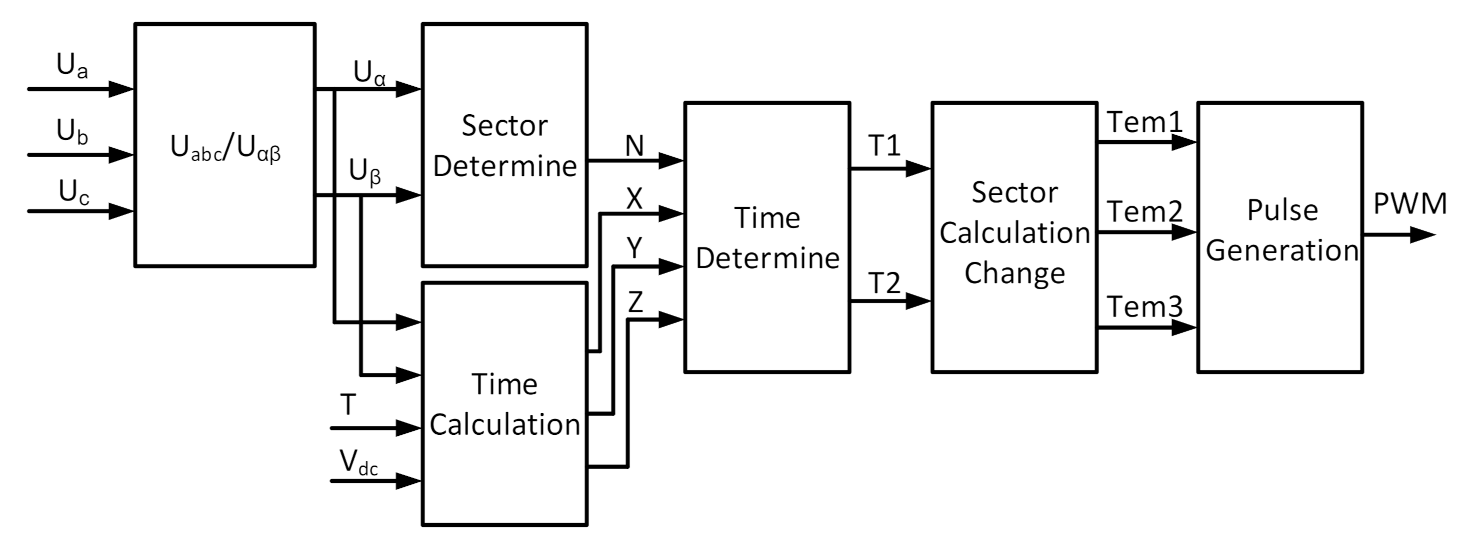
2.1.4. Modeling of DC-AC Converters
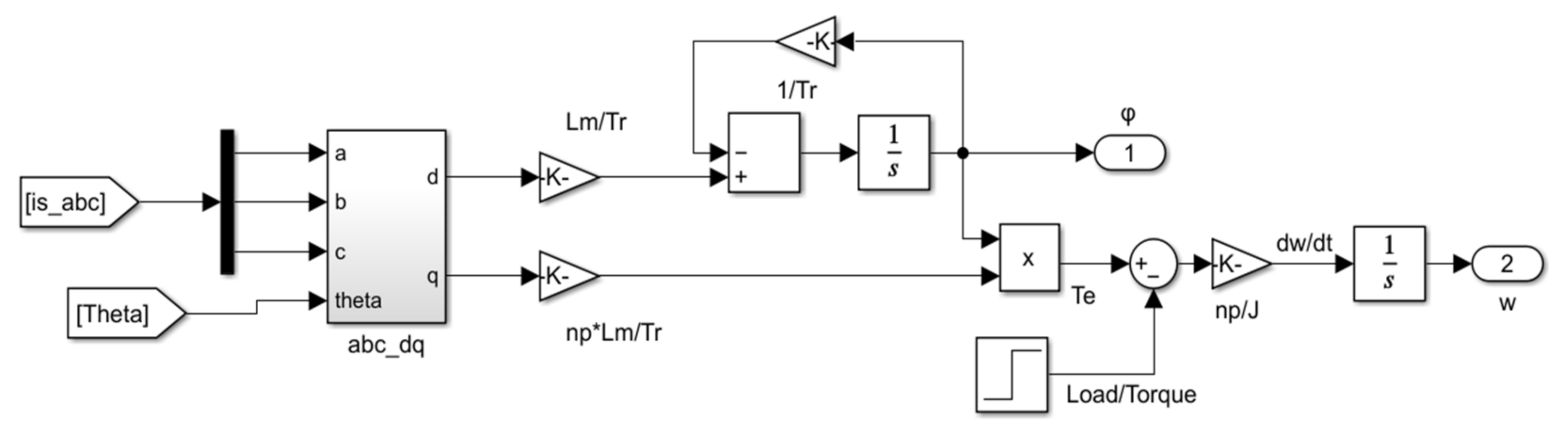
2.1.5. Modeling of Traction Motors
Space Vector Control Based on Rotor Field Orientation Control (FOC)
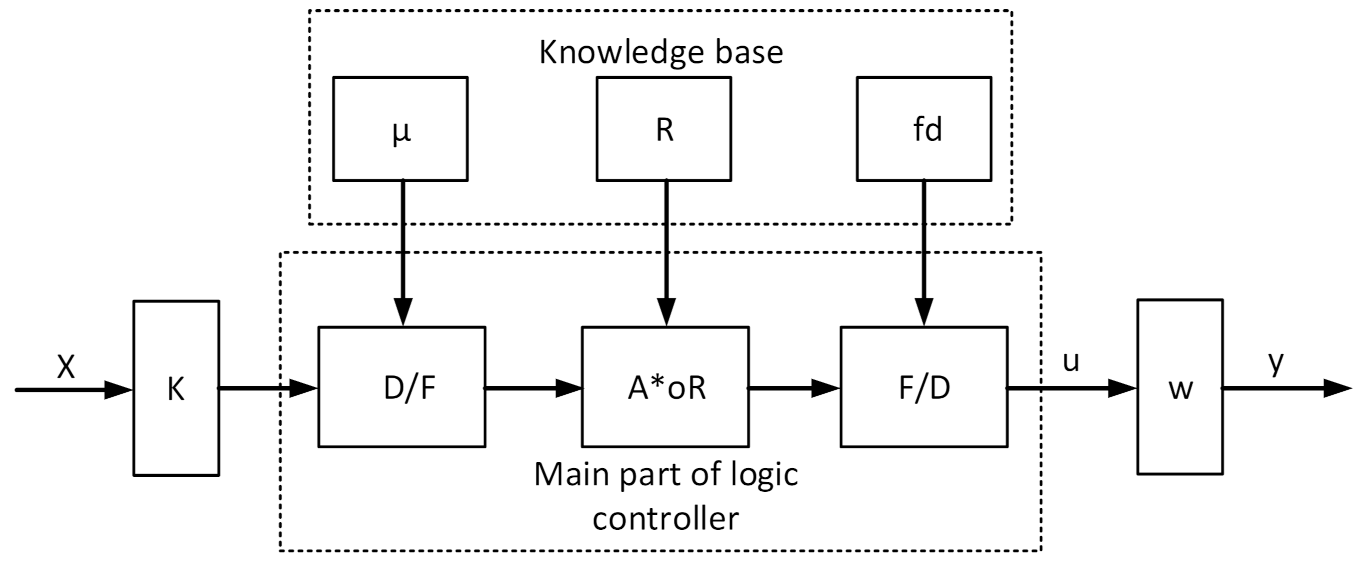
3. Fuzzy Logic-Based Modified Control Energy Management Strategy
3.1. Quantization Factor
3.2. Scale Factor
3.3. Approximate Reasoning and Clarification
3.4. Fuzzification
- Ensure the power demand of the hybrid locomotive;
- Reduce the dynamic load of the fuel cell and optimize its working performance;
- Maintain the state of charge of the battery near the expected value, and, at the same time, make full use of the energy stored and absorbed by the battery, reduce fuel costs, and improve the economy of the hybrid locomotive.
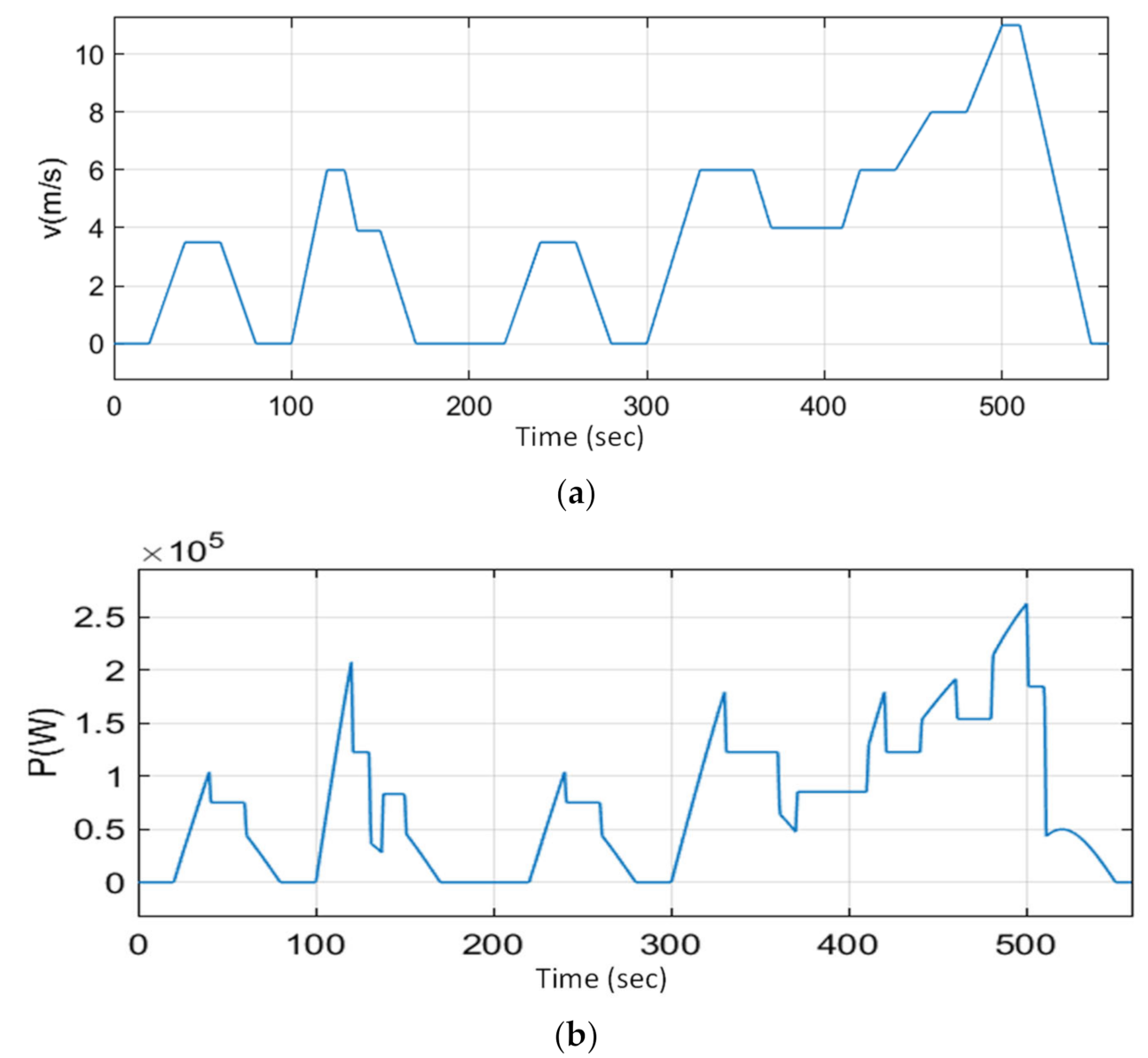
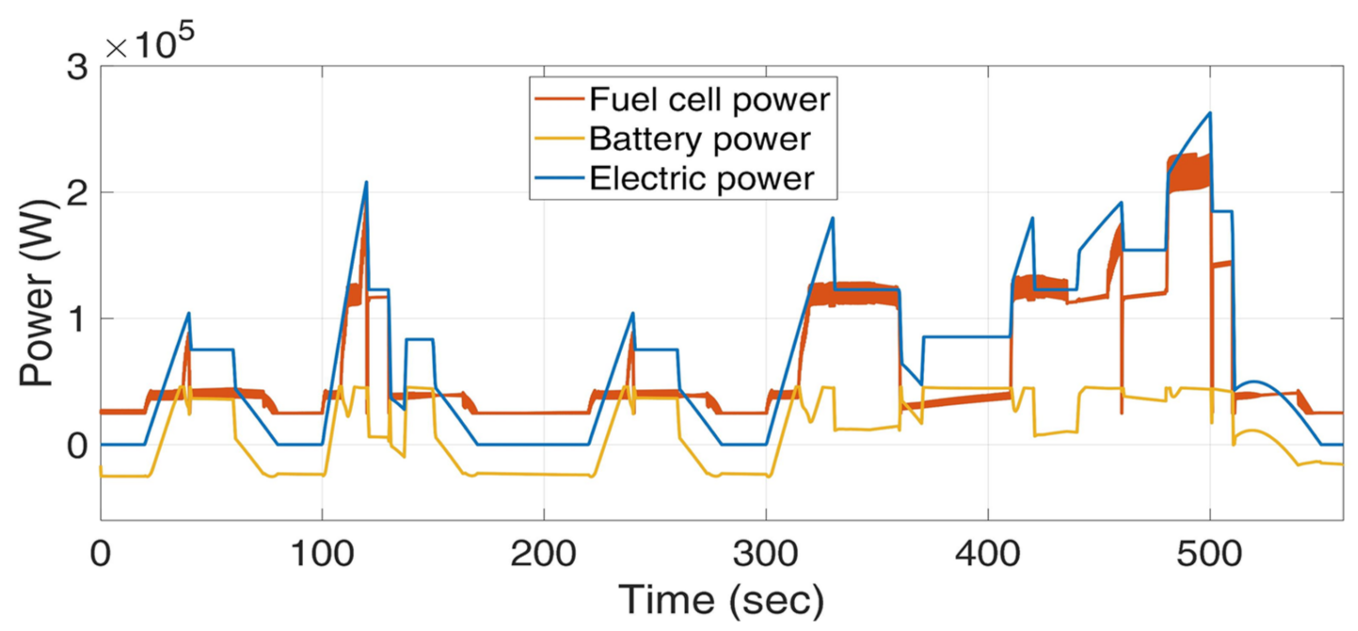
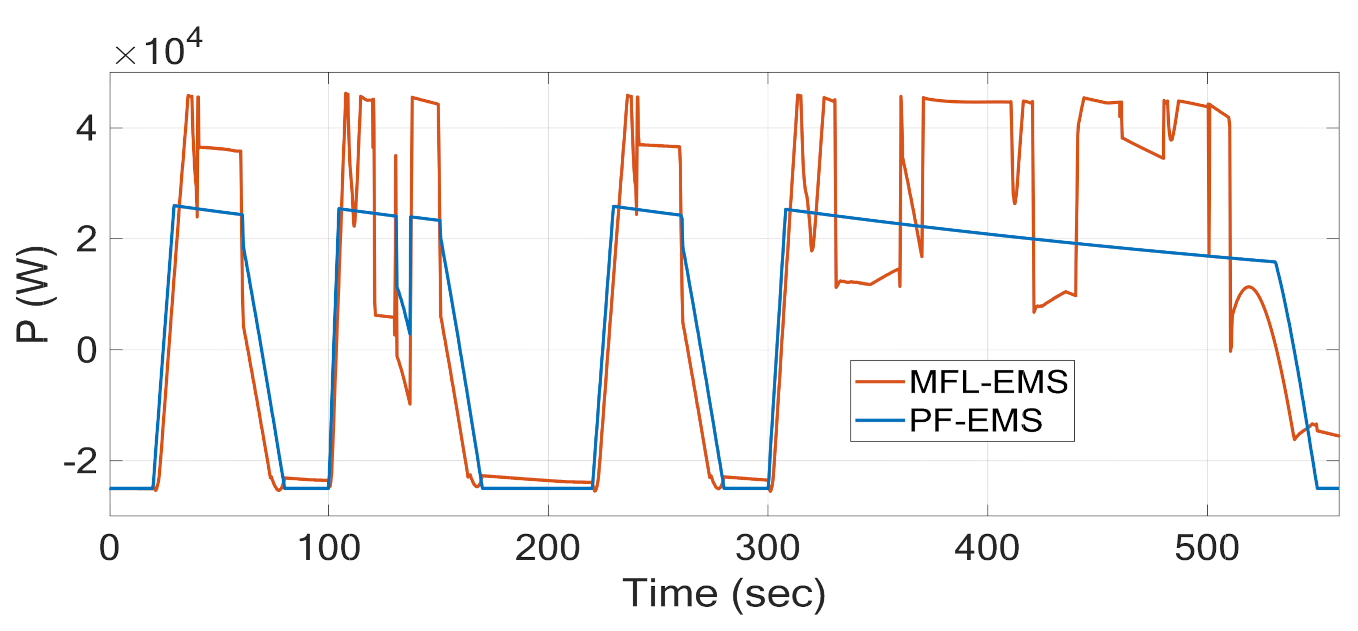
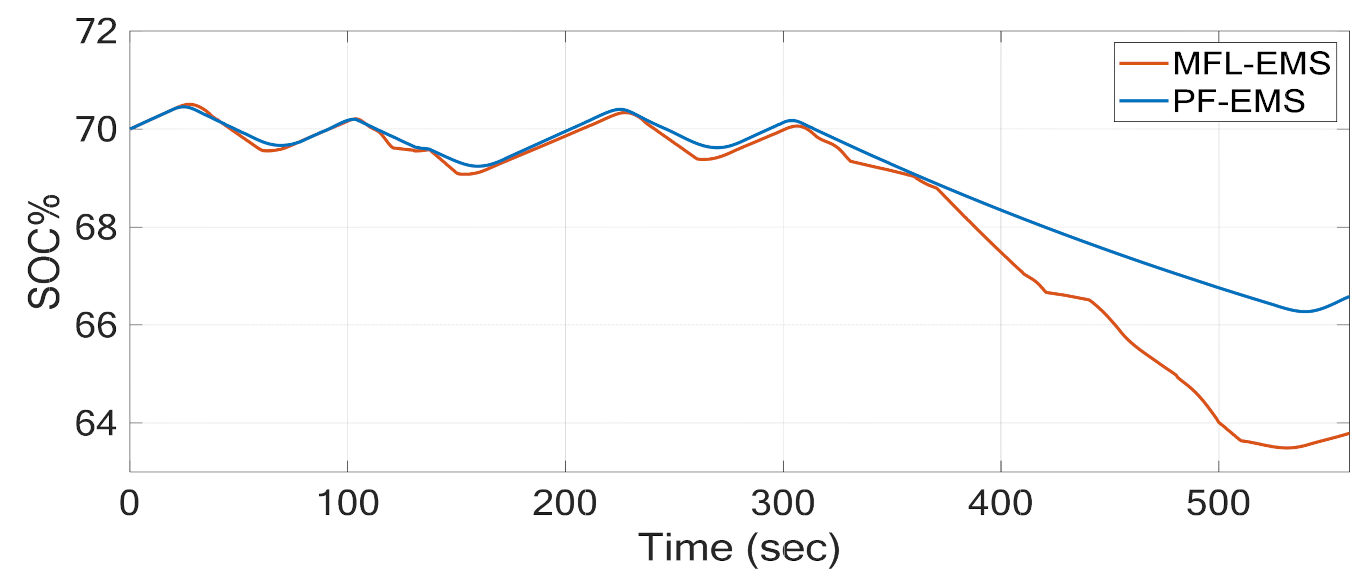
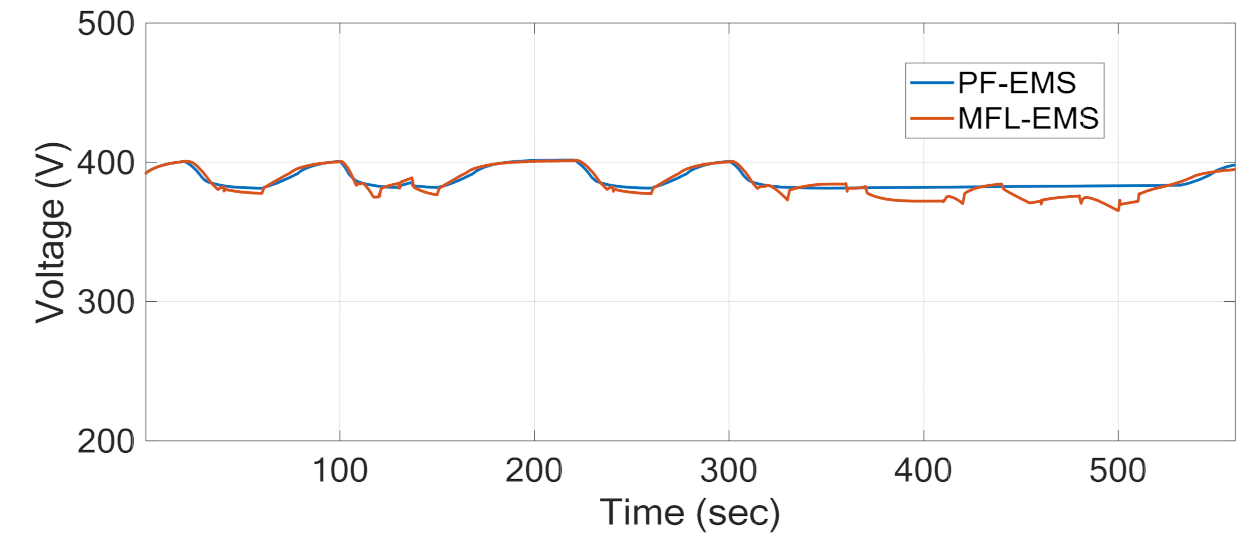
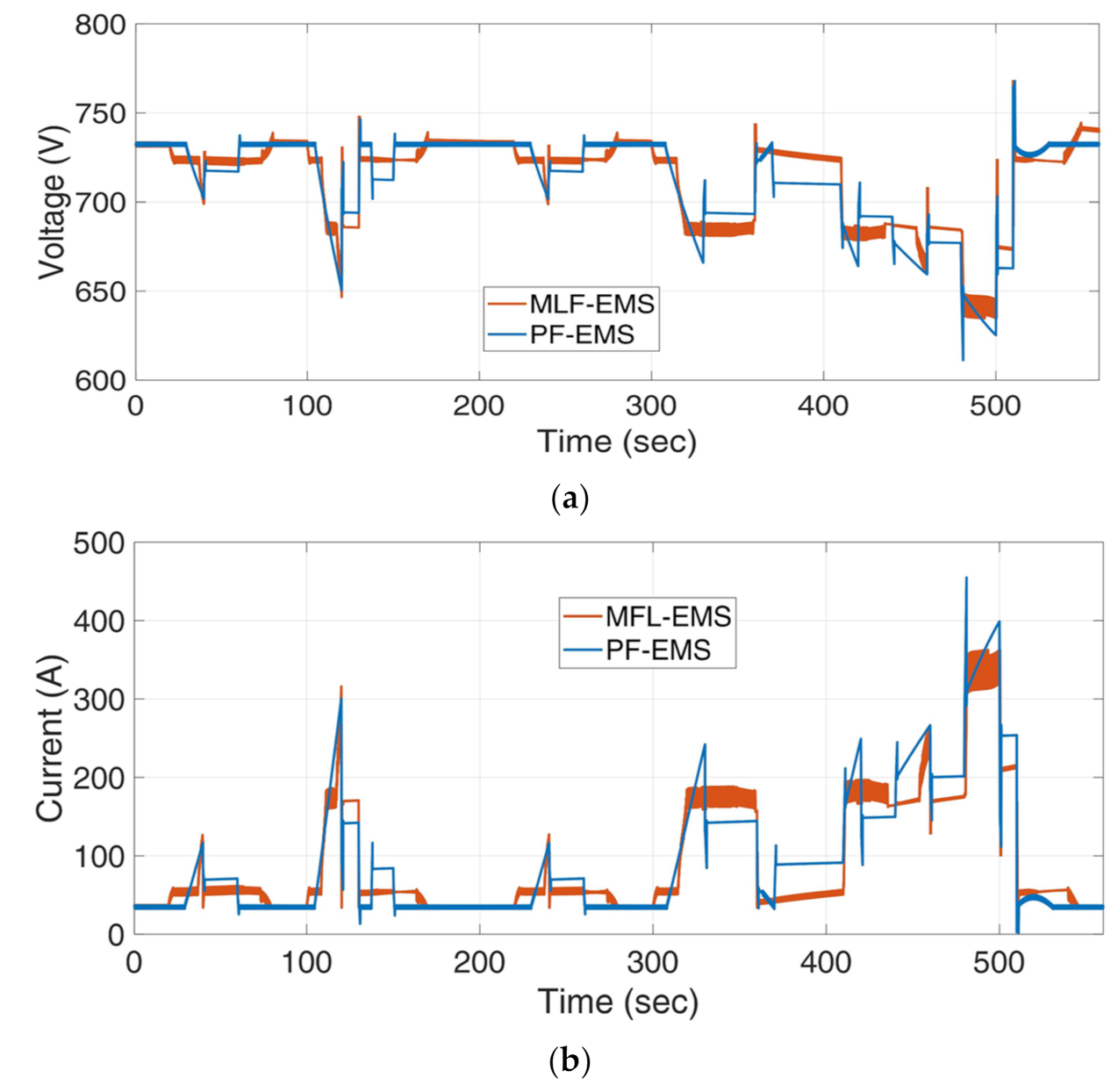
4. Results and Discussion
5. Conclusions and Future Work
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Nomenclature
| Acronyms | |
| BESS | battery energy storage system |
| BNSF | Burlington North America the Santa Fe |
| FCHL | fuel cell hybrid locomotive |
| MFL-EMS | fuzzy logic-based energy management system |
| PF-EMS | power flow energy management system |
| FCS | fuel cell stack |
| EMS | energy management strategy |
| FRC | fluffy rationale control |
| ECMS_DFC | EMS technique dependent on dynamic following coefficient |
| FCHPS | fuel cell hybrid power system |
| PEMFC | proton exchange membrane fuel cell |
| SOC | State of charge |
| SVPWM | space vector pulse width modulation |
| FOC | field orientation control |
| Indexes | |
| Vs [V] | stack voltage/output voltage |
| N | number of series-connected cells in the stack |
| ENernst [V] | reversible fuel cell voltage |
| Vact [V] | voltage drop at the lower currents |
| Vcon [V] | voltage drop at higher currents |
| Vohmic [V] | voltage drop at the intermediate currents |
| Td [K] | cell operating temperature in Kelvin |
| PH2 [Pa] | partial pressures of hydrogen |
| PO2 [Pa] | partial pressures of oxygen |
| F | Faraday constant |
| R | gas constant |
| A [mV/decade] | Tafel slope |
| io [A] | exchange current density |
| ifc [A] | fuel cell current |
| rohm [Ω] | equivalent internal resistance of the fuel cell |
| I [A] | output current of the battery |
| Q [Ah] | maximum capacity of the battery |
| Vdc [V] | DC bus voltage of converter |
| usa, usb, usc [V] | terminal voltage of stator windings |
| ura, urb, urc [V] | terminal voltage of rotor windings |
| isa, isb, isc [A] | terminal current of stator windings |
| ira, irb, irc [A] | terminal current of rotor windings |
| Ψsa, Ψsb, Ψsc [A] | terminal flux of stator windings |
| Ψra, Ψrb, Ψrc [Wb] | terminal flux of rotor windings |
| Wm [J] | magnetic energy |
| Te [N·m] | electromagnetic torque |
| np | number of pole pairs |
| TL [N·m] | load torque |
| J [kg·m2] | rotational inertia |
| D [N s/m] | damping coefficient |
| ωe [rad/s] | rotation speed |
| isq [A] | stator current in q axis |
| isd [A] | stator current in d axis |
| X | input signal vector of the fuzzy controller |
| M | physical theory domain of input signal |
| Aik | domain of the fuzzy subset |
| Ni | domain of the fuzzified fuzzy subset |
| ki | quantization factor |
| Pref [W] | reference power of the fuel cell |
| w | scale factor |
| A*o R | approximate reasoning module |
| F/D | clarification module |
| D/F | fuzzy module |
| μ | membership function information module |
| Pfcmin [W] | minimum output power of the fuel cell |
| Pfcmax [W] | maximum output power of the fuel cell |
| SOCh [%] | upper limit of the battery state of charge |
| SOCl [%] | lower limit of the battery state of charge |
References
- Craven, N.; Orsini, R.; Ciuffini, M.; Arena, D. UIC Low Carbon Rail Challenge. In Technical Report; United Nations Climate Summit: New York, NY, USA, 2014. [Google Scholar]
- Brenna, M.; Foiadelli, F.; Kaleybar, H.J. The Evolution of Railway Power Supply Systems Toward Smart Microgrids: The concept of the energy hub and integration of distributed energy resources. IEEE Electrif. Mag. 2020, 8, 12–23. [Google Scholar] [CrossRef]
- Miller, A.R.; Peters, J.; Smith, B.E.; Velev, O.A. Analysis of fuel cell hybrid locomotives. J. Power Sources 2006, 157, 855–861. [Google Scholar] [CrossRef]
- Sarma, U.; Ganguly, S. Modelling and Cost-Benefit Analysis of PEM Fuel-Cell-Battery Hybrid Energy System for Locomotive Application. In International Conference on Technologies for Smart City Energy Security and Power: Smart Solutions for Smart Cities, ICSESP 2018—Proceedings; IEEE: Piscataway, NJ, USA, 2018; pp. 1–5. [Google Scholar]
- Sun, L.; Chan, C.C.; Liang, R.; Wang, Q. State-of-Art of Energy System for New Energy Vehicles. In Proceedings of the 2008 IEEE Vehicle Power and Propulsion Conference, VPPC 2008, Harbin, China, 3–5 September 2008. [Google Scholar]
- Jafari Kaleybar, H.; Fazel, S.S. Three-Port Multifunctional Railway Power Conditioner Integrated with Energy Storage Systems for Regenerative Braking Energy and Power Quality Control. Int. J. Railw. Res. 2020, 7, 35–43. [Google Scholar]
- Ahmadi, M.; Jafari Kaleybar, H.; Brenna, M.; Castelli-Dezza, F.; Carmeli, M.S. Integration of Distributed Energy Resources and EV Fast-Charging Infrastructure in High-Speed Railway Systems. Electronics 2021, 10, 2555. [Google Scholar] [CrossRef]
- Khodaparastan, M.; Mohamed, A.A.; Brandauer, W. Recuperation of Regenerative Braking Energy in Electric Rail Transit Systems. IEEE Trans. Intell. Transp. Syst. 2019, 20, 2831–2847. [Google Scholar] [CrossRef] [Green Version]
- Miller, A.R.; Hess, K.S.; Barnes, D.L.; Erickson, T.L. System Design of a Large Fuel Cell Hybrid Locomotive. J. Power Sources 2007, 173, 935–942. [Google Scholar] [CrossRef]
- Ahmadi, S.; Bathaee, S.M.T. Multi-Objective Genetic Optimization of the Fuel Cell Hybrid Vehicle Supervisory System: Fuzzy Logic and Operating Mode Control Strategies. Int. J. Hydrogen Energy 2015, 40, 12512–12521. [Google Scholar] [CrossRef]
- Chen, Q.; Gao, L.; Dougal, R.A.; Quan, S. Multiple Model Predictive Control for a Hybrid Proton Exchange Membrane Fuel Cell System. J. Power Sources 2009, 191, 473–482. [Google Scholar] [CrossRef]
- Miller, A.R.; Hess, K.S.; Erickson, T.L.; Dippo, J.L. Demonstration of a Hydrogen Fuel-Cell Locomotive. In Proceedings of the Locomotive Maintenance Officers Association conference, Chicago, IL, USA; 2010; pp. 1–6. [Google Scholar]
- China Rolled Out Its First Self-Developed Hydrogen Fuel Cell Hybrid Locomotive. Available online: http://www.ecns.cn/news/sci-tech/2021-01-28/detail-ihafywhr7620669.shtml (accessed on 24 June 2022).
- Fadel, A.; Zhou, B. An Experimental and Analytical Comparison Study of Power Management Methodologies of Fuel Cell-Battery Hybrid Vehicles. J. Power Sources 2011, 196, 3271–3279. [Google Scholar] [CrossRef]
- Xie, C.; Ogden, J.M.; Quan, S.; Chen, Q. Optimal Power Management for Fuel Cell-Battery Full Hybrid Powertrain on a Test Station. Int. J. Electr. Power Energy Syst. 2013, 53, 307–320. [Google Scholar] [CrossRef]
- Xie, C.; Xu, X.; Bujlo, P.; Shen, D.; Zhao, H.; Quan, S. Fuel Cell and Lithium Iron Phosphate Battery Hybrid Powertrain with an Ultracapacitor Bank Using Direct Parallel Structure. J. Power Sources 2015, 279, 487–494. [Google Scholar] [CrossRef]
- Bassam, A.M.; Phillips, A.B.; Turnock, S.R.; Wilson, P.A. An Improved Energy Management Strategy for a Hybrid Fuel Cell/Battery Passenger Vessel. Int. J. Hydrogen Energy 2016, 41, 22453–22464. [Google Scholar] [CrossRef] [Green Version]
- Hong, Z.; Zhu, Y.; Shang, W.; Li, Q.; Chen, W. Research of Energy Management Strategy for Fuel Cell/Battery Hybrid Locomotive. In Proceedings of the 2017 IEEE Transportation Electrification Conference and Expo, Asia-Pacific, ITEC Asia-Pacific, Harbin, China, 7–10 August 2017. [Google Scholar]
- Peng, H.; Chen, Y.; Chen, Z.; Li, J.; Deng, K.; Thul, A.; Löwenstein, L.; Hameyer, K. Co-Optimization of Total Running Time, Timetables, Driving Strategies and Energy Management Strategies for Fuel Cell Hybrid Trains. eTransportation 2021, 9, 100130. [Google Scholar] [CrossRef]
- Sarma, U.; Ganguly, S. Determination of the Component Sizing for the PEM Fuel Cell-Battery Hybrid Energy System for Locomotive Application Using Particle Swarm Optimization. J. Energy Storage 2018, 19, 247–259. [Google Scholar] [CrossRef]
- Wang, Z.; Xie, Y.; Zang, P.F.; Wang, Y. Energy Management Strategy of Fuel Cell Bus Based on Pontryagin’s Minimum Principle. J. Jilin Univ. Eng. Technol. Ed. 2020, 50, 36–43. [Google Scholar]
- Song, K.; Wang, X.; Li, F.; Sorrentino, M.; Zheng, B. Pontryagin’s Minimum Principle-Based Real-Time Energy Management Strategy for Fuel Cell Hybrid Electric Vehicle Considering Both Fuel Economy and Power Source Durability. Energy 2020, 205, 118064. [Google Scholar] [CrossRef]
- Ajayan, S.; Immanuel Selvakumar, A. Metaheuristic Optimization Techniques to Design Solar-Fuel Cell-Battery Energy System for Locomotives. Int. J. Hydrogen Energy 2022, 47, 1845–1862. [Google Scholar] [CrossRef]
- Wang, W.; Qu, F.; Wang, Q.; Wu, C. Research on Energy Control Strategy of 4WD Hybrid Electric Vehicle Based on Fuzzy Control. In Proceedings of the 2018 2nd IEEE Advanced Information Management, Communicates, Electronic and Automation Control Conference, IMCEC 2018, Xi’an, China, 25–27 May 2018; pp. 1806–1811. [Google Scholar]
- Yuan, Z.; Li, H.; Yousefi, N. Optimal Hydrogen Consumption of Fuel Cell-Based Locomotive Using Speed Trajectory Optimization by Improved Pathfinder Algorithm. J. Clean. Prod. 2021, 278, 123430. [Google Scholar] [CrossRef]
- Shang, W.; Yu, S.; Zhang, G.; Li, Q.; Chen, W. Fuel Cell Hybrid Locomotive System Based on Equivalent Consumption Minimization Strategy. In Proceedings of the 2017 Chinese Automation Congress, CAC 2017, Jinan, China, 20–22 October 2017; pp. 2457–2461. [Google Scholar]
- Li, Q.; Chen, W.; Liu, Z.; Li, M.; Ma, L. Development of Energy Management System Based on a Power Sharing Strategy for a Fuel Cell-Battery-Supercapacitor Hybrid Tramway. J. Power Sources 2015, 279, 267–280. [Google Scholar] [CrossRef]
- Guaitolini, S.V.M.; Yahyaoui, I.; Fardin, J.F.; Encarnacao, L.F.; Tadeo, F. A Review of Fuel Cell and Energy Cogeneration Technologies. In Proceedings of the 2018 9th International Renewable Energy Congress, IREC 2018, Hammamet, Tunisia, 20–22 March 2018; pp. 1–6. [Google Scholar]
- Mo, Z.J.; Zhu, X.J.; Wei, L.Y.; Cao, G.Y. Parameter Optimization for a PEMFC Model with a Hybrid Genetic Algorithm. Int. J. Energy Res. 2006, 30, 585–597. [Google Scholar] [CrossRef]
- Isa, Z.M.; Nayan, N.M.; Arshad, M.H.; Kajaan, N.A.M. Optimizing PEMFC Model Parameters Using Ant Lion Optimizer and Dragonfly Algorithm: A Comparative Study. Int. J. Electr. Comput. Eng. 2019, 9, 5295–5303. [Google Scholar] [CrossRef]
- Barcellona, S.; Piegari, L. Lithium Ion Battery Models and Parameter Identification Techniques. Energies 2017, 10, 2007. [Google Scholar] [CrossRef] [Green Version]
- Oliveira, D.B.S.; Glória, L.L.; Kraemer, R.A.S.; Silva, A.C.; Dias, D.P.; Oliveira, A.C.; Martins, M.A.I.; Ludwig, M.A.; Gruner, V.F.; Schmitz, L.; et al. Mixed-Integer Linear Programming Model to Assess Lithium-Ion Battery Degradation Cost. Energies 2022, 15, 3060. [Google Scholar] [CrossRef]


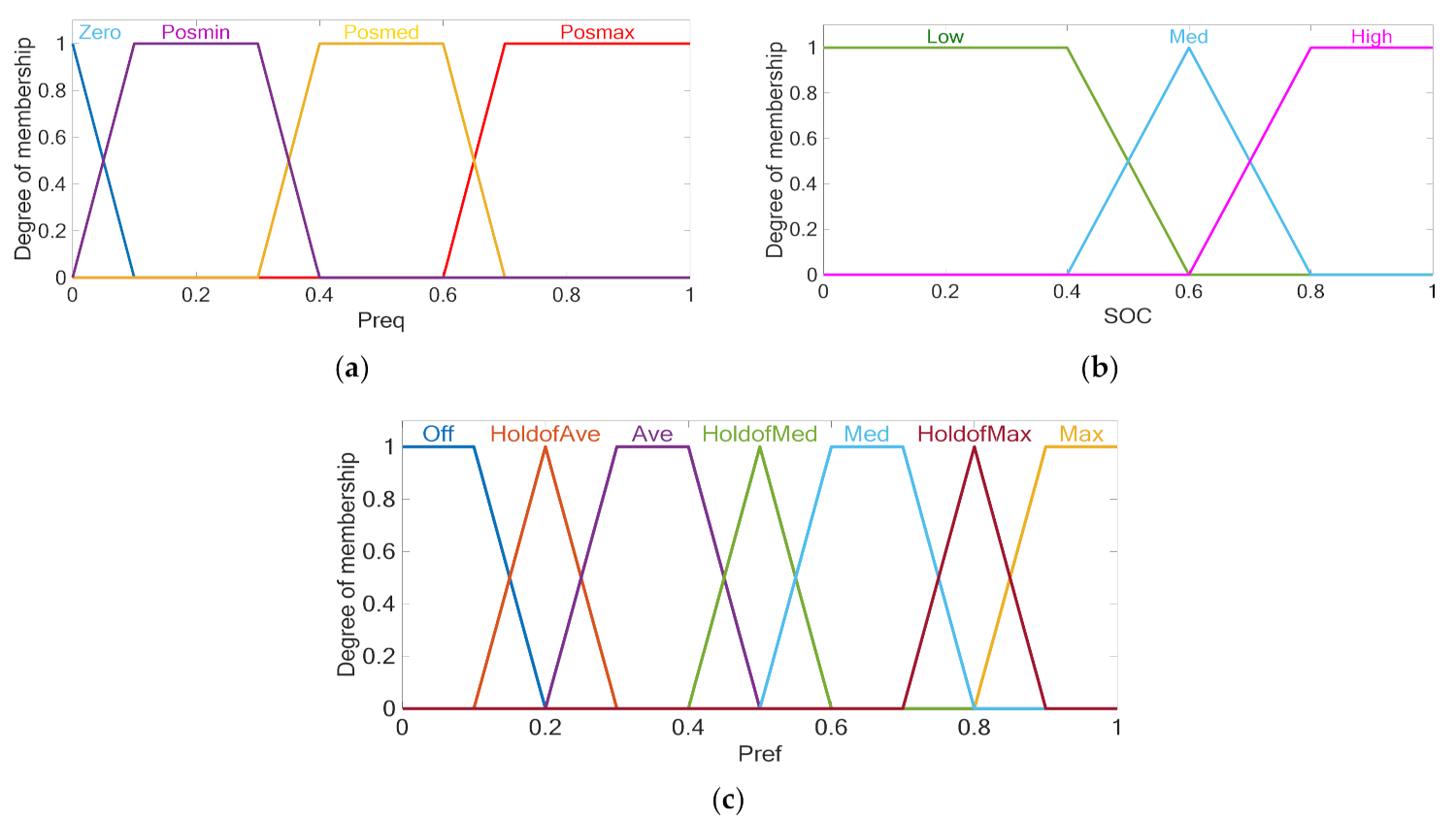


| SOC | Preq | |||
|---|---|---|---|---|
| Zero | Posmin | Posmed | Posmax | |
| Low | Hold of Ave | Ave | Med | Max |
| Med | Off | Hold of Ave | Hold of Med | Hold of Max |
| High | Off | Off | Ave | Med |
| Parameter | Value | |
|---|---|---|
| Fuel cell | Type | HD6 |
| Nominal power (kW) | 300 kW | |
| Rated working efficiency | 55% | |
| Fuel/oxidant | Hydrogen/Air | |
| Motor | Nominal/maximum power (kW) | 150/300 |
| Nominal/maximum speed (rpm) | 1500/3200 | |
| Maximum traction torque (n.m) | 430 | |
| Maximum braking torque (n.m) | 550 | |
| No-load current | 67 A | |
| Battery | Type | Lithium-ion |
| Rated Capacity (Ah) | 120 | |
| Maximum discharging rate (C) | 5 | |
| Internal impedance (mΩ) | 35 | |
| Rated voltage (V) | 380 | |
| Parameter | Value | Parameter | Value |
|---|---|---|---|
| Vehicle Mass | 45 t | Axle | B-B |
| Maximum Speed | 70 km/h | Maximum Gradient | 6.50% |
| Maximum Acceleration | 1 m/s2 | Maximum Grade Speed | 30 km/h |
| Inertia | 0.1 | Gravitational Acceleration | 9.8 N/kg |
| Critical Speed | 30 km/h | Transmission System Efficiency | 0.95 |
| Davis Coefficient A | 2.591 | Traction Inverter Efficiency | 0.95 |
| Davis Coefficient B | 0.00078 | Davis Coefficient C | 0.0911 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jafari Kaleybar, H.; Brenna, M.; Li, H.; Zaninelli, D. Fuel Cell Hybrid Locomotive with Modified Fuzzy Logic Based Energy Management System. Sustainability 2022, 14, 8336. https://doi.org/10.3390/su14148336
Jafari Kaleybar H, Brenna M, Li H, Zaninelli D. Fuel Cell Hybrid Locomotive with Modified Fuzzy Logic Based Energy Management System. Sustainability. 2022; 14(14):8336. https://doi.org/10.3390/su14148336
Chicago/Turabian StyleJafari Kaleybar, Hamed, Morris Brenna, Huan Li, and Dario Zaninelli. 2022. "Fuel Cell Hybrid Locomotive with Modified Fuzzy Logic Based Energy Management System" Sustainability 14, no. 14: 8336. https://doi.org/10.3390/su14148336
APA StyleJafari Kaleybar, H., Brenna, M., Li, H., & Zaninelli, D. (2022). Fuel Cell Hybrid Locomotive with Modified Fuzzy Logic Based Energy Management System. Sustainability, 14(14), 8336. https://doi.org/10.3390/su14148336







