Seismic Fragility Evaluation of Main Steam Piping of Isolated APR1400 NPP Considering the Actual Failure Mode
Abstract
:1. Introduction
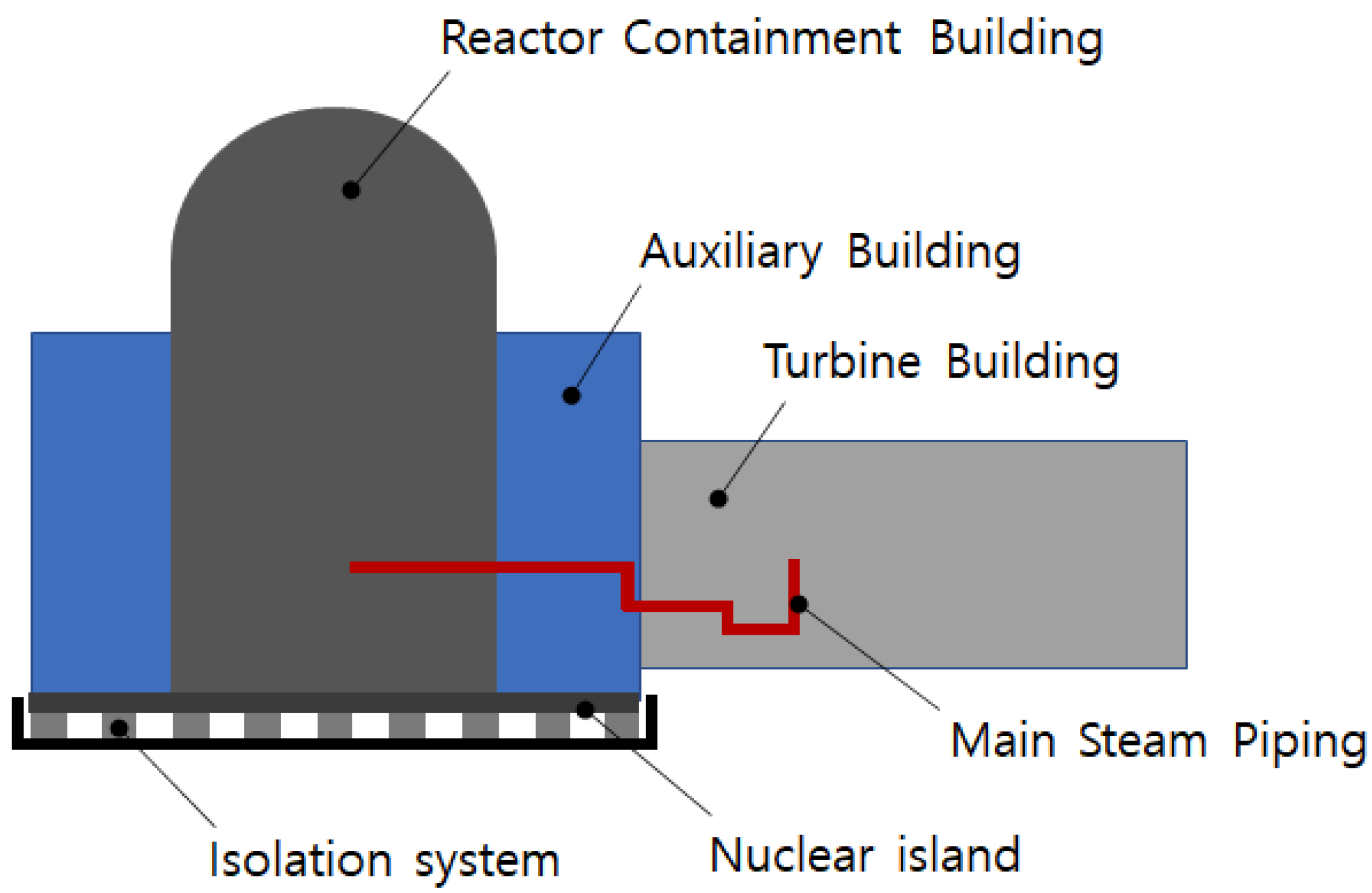
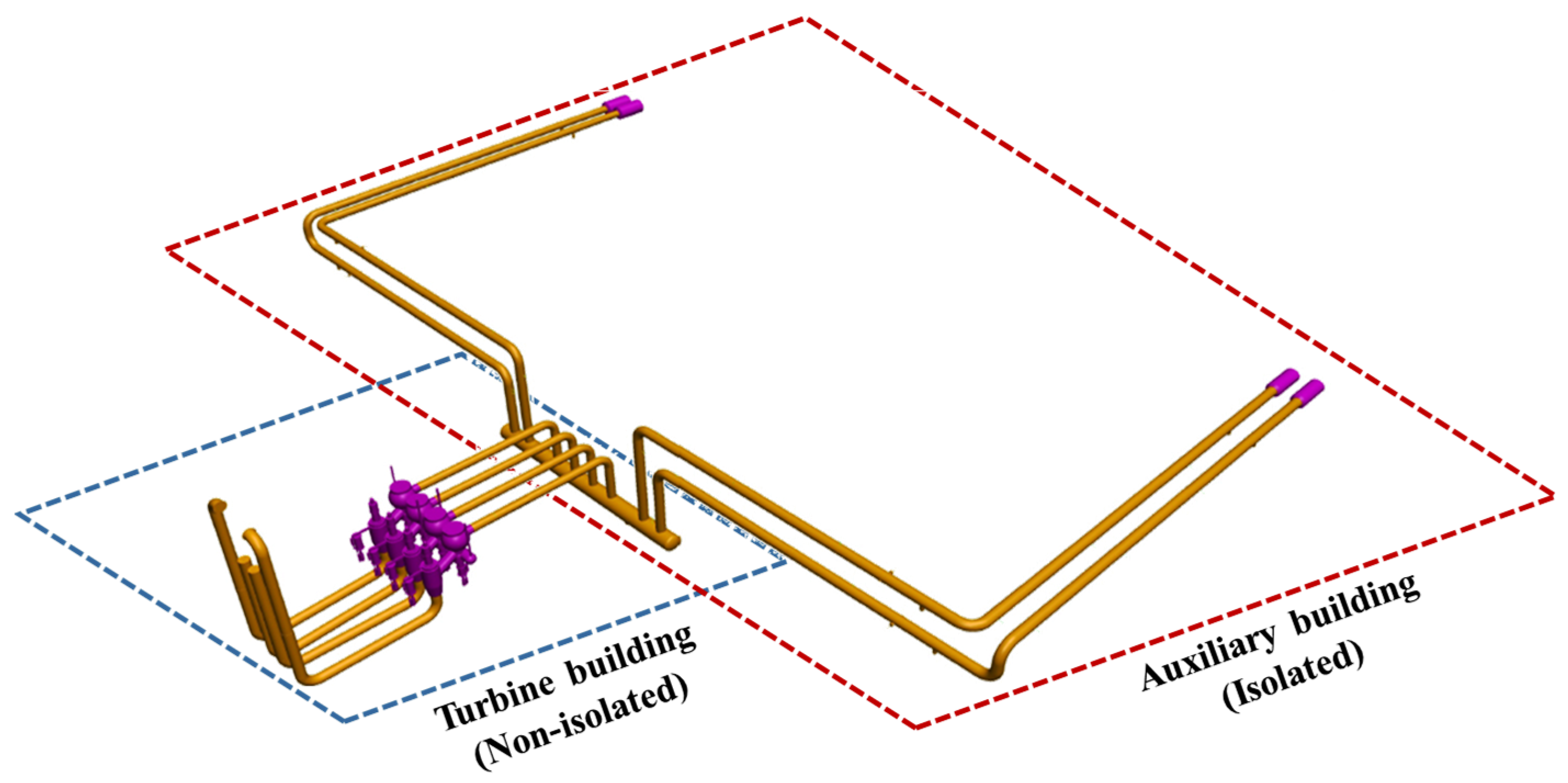
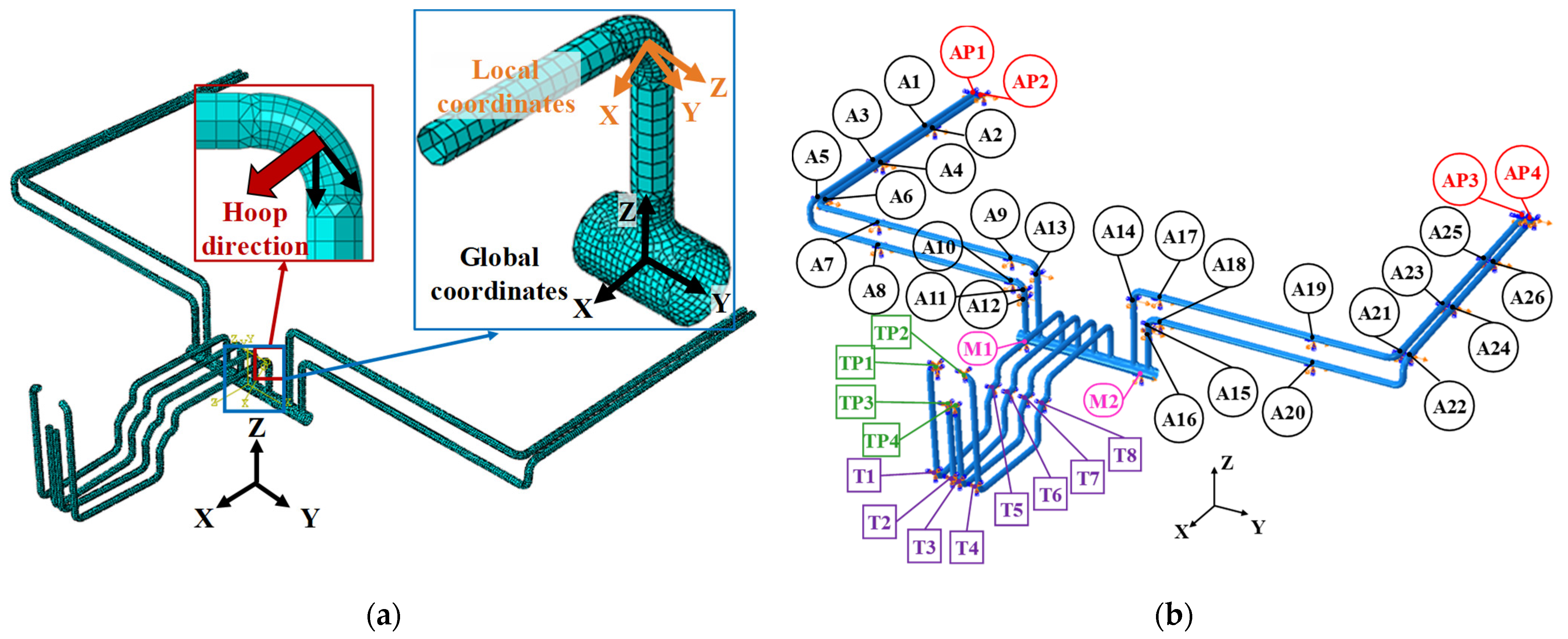
2. Main Steam Piping of Isolated APR1400 NPP
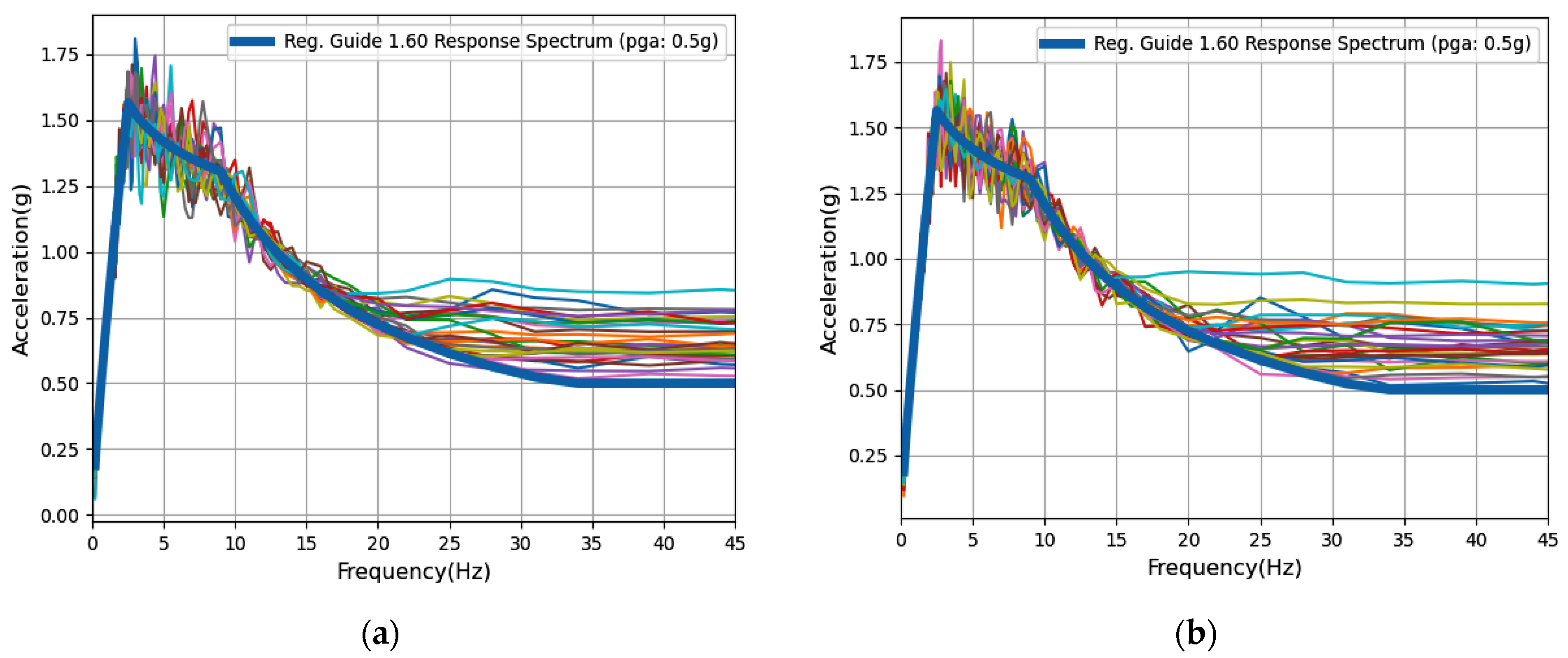
3. Results of Seismic Response Analysis
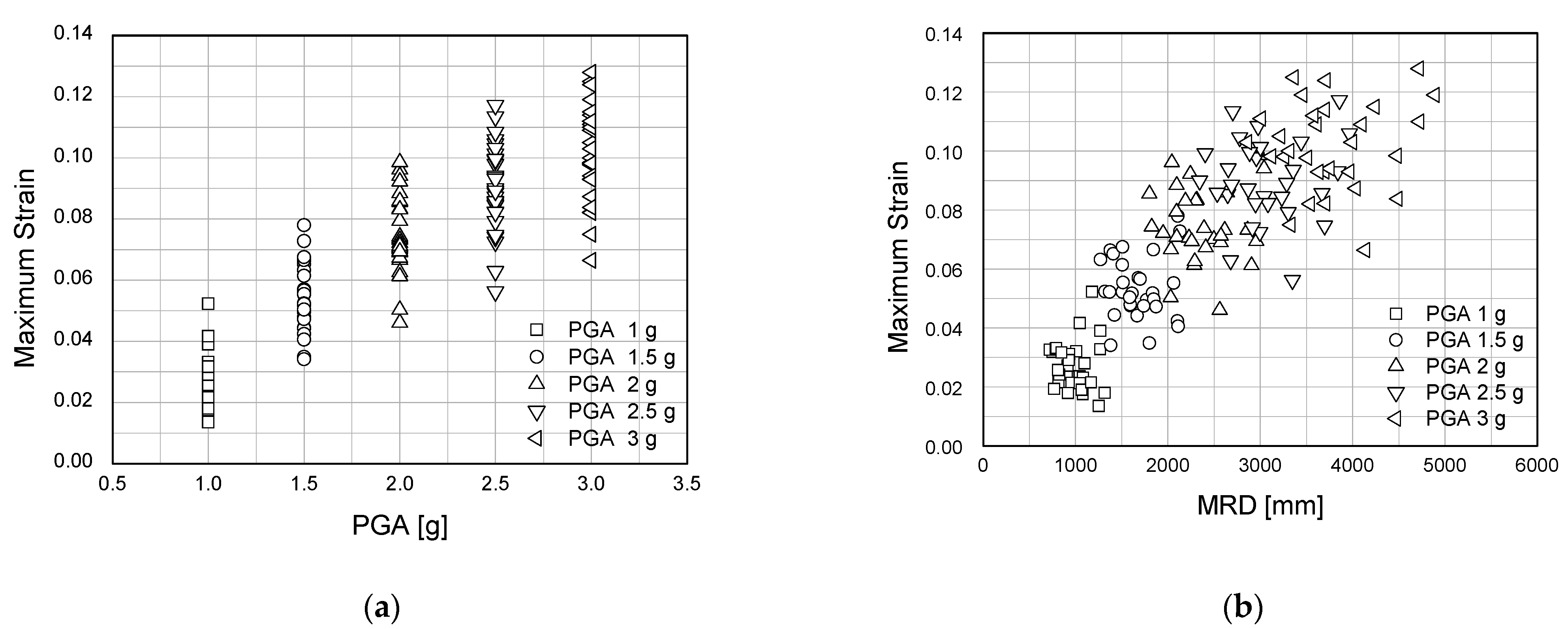
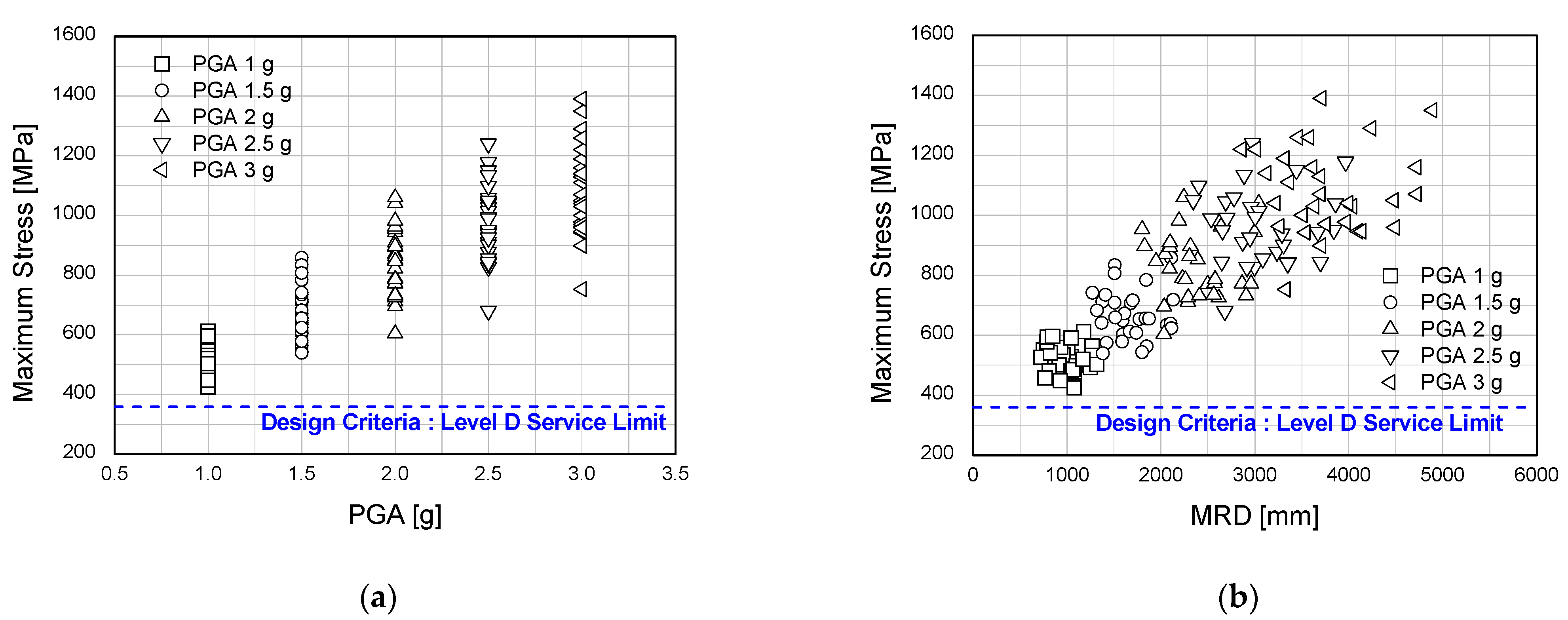
3.1. Maximum Stress and Strain
3.2. Damage Index
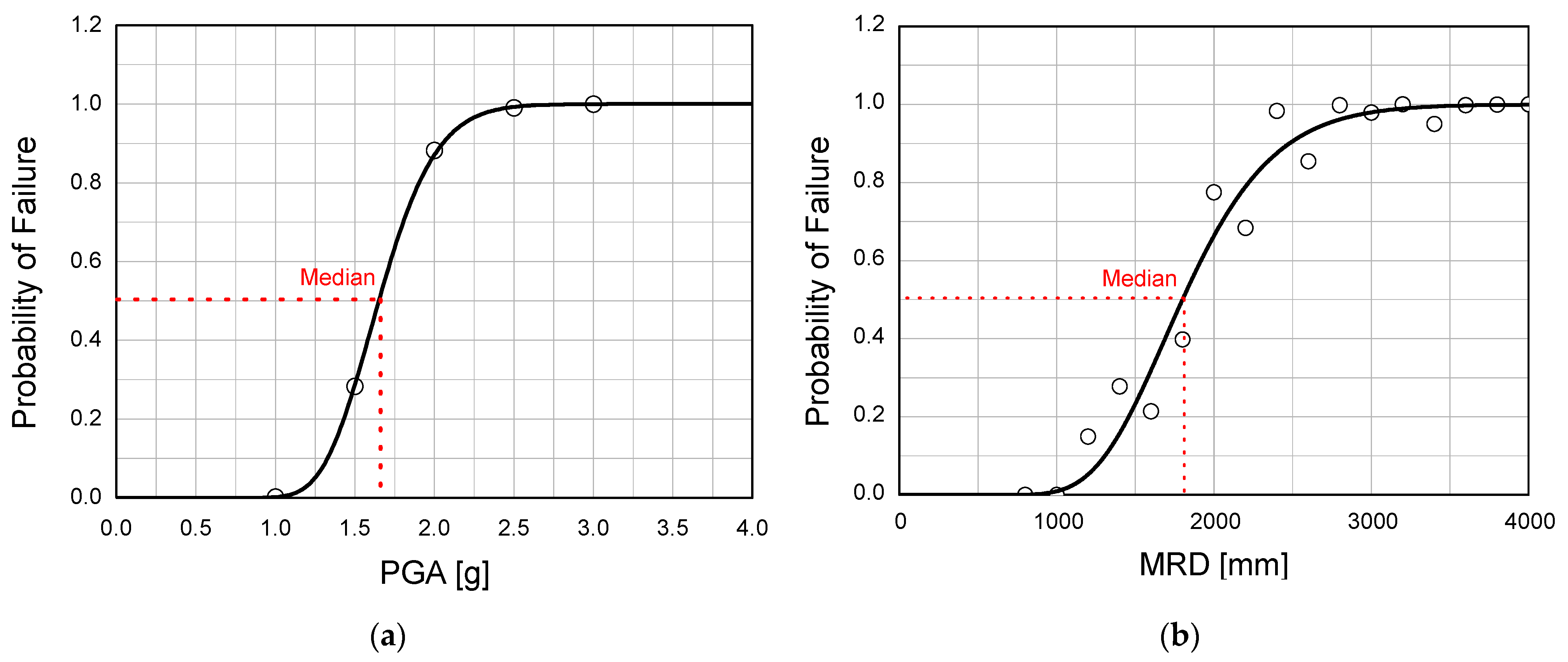
4. Seismic Fragility Analysis
5. Summaries and Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Conflicts of Interest
References
- Jang, K.S.; Chnag, H.P.; Lee, H.P. Influence evaluation of the multi-lead rubber bearing due to the compressive stress for nuclear power plant. J. Korean Soc. Adv. Compos. Struct. 2016, 7, 55–64. [Google Scholar] [CrossRef]
- Kammerer, A.M.; Whittaker, A.S.; Constantinou, M.C. Technical Considerations for Seismic Isolation of Nuclear Facilities (NUREG/CR- 7253); U.S. Nuclear Regulatory Commission: Washington, DC, USA, 2019.
- Vailati, M.; Monti, G.; Bianco, V. Integrated solution-base isolation and repositioning-for the seismic rehabilitation of a preserved strategic building. Buildings 2021, 11, 164. [Google Scholar] [CrossRef]
- Monti, G.; Vailati, M.; Marnetto, R. Base Isolation and Translation of a Strategic Building Under a Preservation Order. In Earthquakes and Their Impact on Society; Springer: Cham, Switzerland, 2016; pp. 433–447. [Google Scholar]
- Cheung, J.H.; Gae, M.S.; Seo, Y.D.; Choi, H.S.; Kim, M.K. Seismic capacity test of nuclear piping system using multi-platform shake table. J. Earthq. Eng. Soc. Korea 2013, 17, 21–31. [Google Scholar] [CrossRef] [Green Version]
- Hahm, D.G.; Park, J.H.; Choi, I.K. Seismic performance evaluation of piping system crossing the isolation interface in seismically isolated NPP. J. Earthq. Eng. Soc. Korea 2014, 18, 141–150. [Google Scholar] [CrossRef]
- Jeon, B.G.; Kim, S.W.; Choi, H.S.; Park, D.U.; Kim, N.S. A failure estimation method of steel pipe elbows under in-plane cyclic loading. Nucl. Eng. Technol. 2017, 49, 245–253. [Google Scholar] [CrossRef] [Green Version]
- Kim, S.W.; Chang, S.J.; Park, D.U.; Jeon, B.G. Failure criteria of a carbon steel pipe elbow for low-cycle fatigue using the damage index. Thin-Walled Struct. 2020, 153, 106800. [Google Scholar] [CrossRef]
- Kim, S.W.; Jeon, B.G.; Hahm, D.G.; Kim, M.K. Seismic fragility evaluation of the base-isolated nuclear power plant piping system using the failure criterion based on stress-strain. Nucl. Eng. Technol. 2019, 51, 561–572. [Google Scholar] [CrossRef]
- Xu, J.; DeGrassi, G.; Chokshi, N. A NRC-BNL benchmark evaluation of seismic analysis methods for non-classically damped coupled systems. Nucl. Eng. Des. 2004, 228, 345–366. [Google Scholar] [CrossRef]
- Eem, S.H.; Choi, I.K.; Cha, S.L.; Kwag, S.Y. Seismic response correlation coefficient for the structures, systems and components of the Korean nuclear power plant for seismic probabilistic safety assessment. Ann. Nucl. Energy 2021, 150, 107759. [Google Scholar] [CrossRef]
- Eem, S.H. Seismic Fragility Assessment of Isolated Structures Based on Stochastic Response Database. Ph. D. Thesis, Korean Advanced Institute for Science and Technology, Daejeon, Korea, 2014. [Google Scholar]
- Eem, S.H.; Jung, H.J. Seismic response distribution estimation for isolated structures using stochastic response database. Earthq. Struct. 2015, 9, 937–956. [Google Scholar] [CrossRef]
- Eem, S.H.; Jung, H.J. Seismic fragility assessment of isolated structures by using stochastic response database. Earthq. Struct. 2018, 14, 389–398. [Google Scholar]
- American Society of Civil Engineers. Minimum Design Loads for Buildings and Other Structures (ASCE/SEI 7-05); American Society of Civil Engineers: New York, NY, USA, 2005. [Google Scholar]
- Federal Emergency Management Agency. NEHRP Recommended Provisions: Design Examples (FEMA-451); Federal Emergency Management Agency: Washington, DC, USA, 2006.
- United States Nuclear Regulatory Commission. Design Response Spectra for Seismic Design of Nuclear Power Plants (Regulatory Guide 1.60); United States Nuclear Regulatory Commission: Washington, DC, USA, 2014.
- American Society of Civil Engineers. Seismic Analysis of Safety-Related Nuclear Structures (ASCE/SEI 4-16); American Society of Civil Engineers: New York, NY, USA, 2016. [Google Scholar]
- Ohno, S. Strong-motion characteristics during the 2011 Tohoku earthquake. J. Jpn. Landslide Soc. 2013, 50, 75–82. [Google Scholar] [CrossRef] [Green Version]
- The American Society of Mechanical Engineers. Welded and Seamless Wrought Steel Pipe (ASME B36.10M); The American Society of Mechanical Engineers: New York, NY, USA, 2015. [Google Scholar]
- Jeon, B.G.; Kim, S.W.; Yun, D.W.; Hahm, D.G. A Quantitative Limit State of the Carbon Steel Pipe Tee in the Nuclear Power Plants Under In-Plane Cyclic Loading. In Proceedings of the 25th International Conference in Structural Mechanics in Reactor Technology (SMiRT-25), Charlotte, NC, USA, 4–9 August 2019. [Google Scholar]
- Kwag, S.Y.; Eem, S.H.; Kwak, J.S.; Oh, J.H. Evaluation model of seismic response behavior and performance of nuclear plant piping systems. J. Korean Soc. Adv. Compos. Struct. 2020, 11, 54–62. [Google Scholar] [CrossRef]
- American Society of Mechanical Engineers. Section III, Rules for Construction of Nuclear Facility Components. In ASME Boiler and Pressure Vessel Code; American Society of Mechanical Engineers: New York, NY, USA, 2015. [Google Scholar]
- Korea Electric Power Corporation Engineering & Construction. SKN 3 & 4 Safety Related-Plant Manual-Main Stem System (MS); Korea Electric Power Corporation Engineering & Construction: Yongin, Korea, 2011. [Google Scholar]
- American Society of Mechanical Engineers. Section II, Part D, Properties (Customary). In ASME Boiler and Pressure Vessel Code; American Society of Mechanical Engineers: New York, NY, USA, 2015. [Google Scholar]
- Kim, J.H.; Kim, M.K.; Choi, I.K. Experimental study on seismic behavior of lead-rubber bearing considering bi-directional horizontal input motions. Eng. Struct. 2019, 198, 109529. [Google Scholar] [CrossRef]
- Zhang, T.; Brust, F.W.; Willkowski, G.; Shim, D.J.; Nie, J.; Hofmayer, C.H.; Ali, S.A. Analysis of JNES Seismic Tests on Degraded Piping. In Proceedings of the ASME 2010 Pressure Vessels & Piping Division/K-PVP Conference, Washington, DC, USA, 18–22 July 2010. [Google Scholar]
- Electric Power Research Institute. Piping and Fitting Dynamic Reliability Program (EPRI TR-102792-V1 through V5); Electric Power Research Institute: Palo Alto, CA, USA, 1994. [Google Scholar]
- Shinozuka, M.; Feng, M.Q.; Kim, H.K.; Kim, S.H. Nonlinear static procedure for fragility curve development. J. Eng. Mech. 2000, 126, 1287–1296. [Google Scholar] [CrossRef] [Green Version]





| Parameters | Values |
|---|---|
| 2939.72 MN/m | |
| 19,620.51 MN/m | |
| 1962.05 MN/m | |
| 329.43 MN |
| Location | D [mm] | t [mm] | D/t |
|---|---|---|---|
| Turbine building | 705.79 | 27.00 | 26.14 |
| Auxiliary building | 764.72 | 38.10 | 20.07 |
| 1458.11 | 59.54 | 24.49 |
| Density [N/mm3] | E [MPa] | Poisson’s Ratio |
|---|---|---|
| 7.85 10−9 | 205,000 | 0.3 |
| Support ID | Location | ||
|---|---|---|---|
| Building | Elevation [mm] | Constrained Directions | |
| A1~A7, A9, A17, A19, A21~A26 | auxiliary | 42,589 | X, Y |
| AP1~AP4 | pedestal | 42,589 | X, Y, Z |
| A13, A14 | auxiliary | 41,067 | X, Z |
| A8, A10, A18, A20 | auxiliary | 39,446 | Y |
| A11, A15 | auxiliary | 38,417 | Z |
| A12, A16 | auxiliary | 37,427 | X |
| M1, M2 | auxiliary | 32,309 | Y |
| TP1, TP2 | pedestal | 45,415 | X, Y, Z |
| TP3, TP4 | pedestal | 41,300 | X, Y, Z |
| T1~T4 | turbine | 32,181 | X, Z |
| T5~T8 | turbine | 35,929 | Y, Z |
| Model No. | Natural Frequency [Hz] | Participation Factors | Mass Participation Ratio | ||||
|---|---|---|---|---|---|---|---|
| X | Y | Z | X | Y | Z | ||
| 1 | 8.96 | 1.89800 | 0.08875 | 0.02998 | 1.00000 | 0.00219 | 0.00025 |
| 2 | 9.15 | 0.00343 | 0.98496 | 0.29788 | 0.00121 | 1.00000 | 0.09146 |
| 3 | 14.43 | −0.00173 | −0.67300 | 1.47700 | 0.00000 | 0.20792 | 1.00000 |
| PGA Level | Relative Displacement [mm] | ||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 g | 1.5 g | 2 g | 2.5 g | 3 g | |||||||||||
| EQ | Direction | MRD | Direction | MRD | Direction | MRD | Direction | MRD | Direction | MRD | |||||
| X | Y | X | Y | X | Y | X | Y | X | Y | ||||||
| 1 | 711 | 749 | 749 | 1376 | 1289 | 1376 | 2042 | 1838 | 2042 | 2704 | 2363 | 2704 | 3366 | 2888 | 3366 |
| 2 | 905 | 745 | 905 | 1595 | 1317 | 1595 | 2287 | 1888 | 2287 | 2996 | 2472 | 2996 | 3705 | 3056 | 3705 |
| 3 | 1268 | 638 | 1268 | 2132 | 1143 | 2132 | 2997 | 1648 | 2997 | 3859 | 2166 | 3859 | 4722 | 2684 | 4722 |
| 4 | 1042 | 696 | 1042 | 1770 | 1254 | 1770 | 2497 | 1812 | 2497 | 3234 | 2355 | 3234 | 3970 | 2898 | 3970 |
| 5 | 1266 | 677 | 1266 | 2064 | 1167 | 2064 | 2862 | 1656 | 2862 | 3672 | 2143 | 3672 | 4481 | 2652 | 4481 |
| 6 | 631 | 1046 | 1046 | 1027 | 1679 | 1679 | 1466 | 2315 | 2315 | 1983 | 2957 | 2957 | 2502 | 3612 | 3612 |
| 7 | 736 | 814 | 814 | 1269 | 1421 | 1421 | 1803 | 2032 | 2032 | 2328 | 2648 | 2648 | 2854 | 3263 | 3263 |
| 8 | 916 | 800 | 916 | 1506 | 1416 | 1506 | 2096 | 2037 | 2096 | 2691 | 2677 | 2691 | 3286 | 3318 | 3318 |
| 9 | 780 | 1009 | 1009 | 1427 | 1700 | 1700 | 2075 | 2392 | 2392 | 2726 | 3045 | 3045 | 3376 | 3698 | 3698 |
| 10 | 612 | 958 | 958 | 1098 | 1593 | 1593 | 1658 | 2230 | 2230 | 2219 | 2870 | 2870 | 2781 | 3510 | 3510 |
| 11 | 600 | 917 | 917 | 1064 | 1611 | 1611 | 1532 | 2305 | 2305 | 1990 | 3003 | 3003 | 2448 | 3701 | 3701 |
| 12 | 723 | 575 | 723 | 1409 | 1048 | 1409 | 2097 | 1525 | 2097 | 2778 | 2016 | 2778 | 3461 | 2508 | 3461 |
| 13 | 934 | 845 | 934 | 1514 | 1409 | 1514 | 2094 | 1978 | 2094 | 2656 | 2544 | 2656 | 3218 | 3109 | 3218 |
| 14 | 811 | 824 | 824 | 1319 | 1292 | 1319 | 1827 | 1766 | 1827 | 2343 | 2242 | 2343 | 2860 | 2733 | 2860 |
| 15 | 1098 | 726 | 1098 | 1835 | 1219 | 1835 | 2573 | 1779 | 2573 | 3305 | 2336 | 3305 | 4037 | 2893 | 4037 |
| 16 | 680 | 1081 | 1081 | 1259 | 1847 | 1847 | 1838 | 2614 | 2614 | 2423 | 3358 | 3358 | 3009 | 4102 | 4102 |
| 17 | 790 | 811 | 811 | 1369 | 1319 | 1369 | 1948 | 1827 | 1948 | 2535 | 2339 | 2535 | 3121 | 2851 | 3121 |
| 18 | 863 | 1045 | 1045 | 1416 | 1668 | 1668 | 1969 | 2291 | 2291 | 2520 | 2915 | 2915 | 3072 | 3540 | 3540 |
| 19 | 693 | 1079 | 1079 | 1171 | 1801 | 1801 | 1652 | 2563 | 2563 | 2125 | 3350 | 3350 | 2599 | 4138 | 4138 |
| 20 | 785 | 726 | 785 | 1271 | 1159 | 1271 | 1799 | 1669 | 1799 | 2405 | 2183 | 2405 | 3010 | 2697 | 3010 |
| 21 | 671 | 1065 | 1065 | 1113 | 1738 | 1738 | 1572 | 2411 | 2411 | 2051 | 3083 | 3083 | 2531 | 3756 | 3756 |
| 22 | 1179 | 524 | 1179 | 2110 | 900 | 2110 | 3042 | 1282 | 3042 | 3967 | 1660 | 3967 | 4892 | 2038 | 4892 |
| 23 | 607 | 1252 | 1252 | 1038 | 2103 | 2103 | 1468 | 2958 | 2958 | 1889 | 3841 | 3841 | 2310 | 4724 | 4724 |
| 24 | 654 | 766 | 766 | 1129 | 1383 | 1383 | 1607 | 2031 | 2031 | 2101 | 2680 | 2680 | 2595 | 3330 | 3330 |
| 25 | 1028 | 1169 | 1169 | 1654 | 1872 | 1872 | 2284 | 2575 | 2575 | 2902 | 3286 | 3286 | 3520 | 3998 | 3998 |
| 26 | 914 | 928 | 928 | 1587 | 1511 | 1587 | 2260 | 2094 | 2260 | 2948 | 2663 | 2948 | 3636 | 3237 | 3636 |
| 27 | 588 | 1316 | 1316 | 975 | 2111 | 2111 | 1362 | 2906 | 2906 | 1779 | 3699 | 3699 | 2210 | 4492 | 4492 |
| 28 | 1045 | 543 | 1045 | 1843 | 891 | 1843 | 2641 | 1305 | 2641 | 3442 | 1757 | 3442 | 4242 | 2211 | 4242 |
| 29 | 792 | 446 | 792 | 1510 | 873 | 1510 | 2243 | 1301 | 2243 | 2977 | 1737 | 2977 | 3711 | 2176 | 3711 |
| 30 | 846 | 635 | 846 | 1507 | 1171 | 1507 | 2192 | 1755 | 2192 | 2886 | 2314 | 2886 | 3580 | 2872 | 3580 |
| Avg. | 839 | 847 | 988 | 1445 | 1430 | 1675 | 2059 | 2026 | 2371 | 2681 | 2623 | 3071 | 3304 | 3223 | 3773 |
| EQ | PGA Level | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| 1 g | 1.5 g | 2 g | 2.5 g | 3 g | ||||||
[MPa] | [MPa] | [MPa] | [MPa] | [MPa] | ||||||
| 1 | 0.03 | 550.75 | 0.0664 | 711.48 | 0.0961 | 870.49 | 0.1134 | 991.02 | 0.1250 | 1110.00 |
| 2 | 0.0241 | 473.84 | 0.0476 | 603.62 | 0.0613 | 710.84 | 0.0725 | 827.94 | 0.0822 | 898.60 |
| 3 | 0.0390 | 564.21 | 0.0728 | 717.94 | 0.0986 | 943.65 | 0.1172 | 1039.39 | 0.1280 | 1160.00 |
| 4 | 0.0237 | 516.19 | 0.0495 | 653.65 | 0.0701 | 770.99 | 0.0844 | 878.13 | 0.0930 | 977.13 |
| 5 | 0.0328 | 532.61 | 0.0552 | 633.95 | 0.0733 | 772.27 | 0.0857 | 943.79 | 0.0984 | 1050.00 |
| 6 | 0.0235 | 528.60 | 0.0570 | 707.02 | 0.0834 | 896.99 | 0.0979 | 1026.97 | 0.1090 | 1160.00 |
| 7 | 0.0215 | 514.08 | 0.0444 | 575.31 | 0.0666 | 694.87 | 0.0854 | 845.66 | 0.0981 | 963.46 |
| 8 | 0.0272 | 545.96 | 0.0522 | 708.62 | 0.0708 | 893.28 | 0.0885 | 1045.78 | 0.1000 | 1190.00 |
| 9 | 0.0321 | 558.56 | 0.0566 | 716.42 | 0.0738 | 851.59 | 0.0847 | 1014.36 | 0.0931 | 1130.00 |
| 10 | 0.0214 | 534.42 | 0.0479 | 648.52 | 0.0706 | 790.21 | 0.0873 | 911.17 | 0.0977 | 1000.00 |
| 11 | 0.0179 | 500.82 | 0.0517 | 672.70 | 0.0832 | 862.86 | 0.1014 | 994.63 | 0.1140 | 1070.00 |
| 12 | 0.0326 | 525.93 | 0.0652 | 734.28 | 0.0884 | 909.07 | 0.1046 | 1058.89 | 0.1190 | 1260.00 |
| 13 | 0.0311 | 559.35 | 0.0554 | 658.96 | 0.0794 | 821.87 | 0.0941 | 949.25 | 0.1050 | 1040.00 |
| 14 | 0.0241 | 540.95 | 0.0523 | 682.40 | 0.0743 | 897.19 | 0.0899 | 1050.04 | 0.1030 | 1220.00 |
| 15 | 0.0280 | 497.82 | 0.0518 | 656.30 | 0.0690 | 772.71 | 0.0792 | 901.87 | 0.0873 | 1030.00 |
| 16 | 0.0231 | 476.43 | 0.0498 | 562.93 | 0.0732 | 725.00 | 0.0935 | 843.18 | 0.1090 | 946.92 |
| 17 | 0.0257 | 481.17 | 0.0522 | 641.04 | 0.0722 | 846.91 | 0.0857 | 989.36 | 0.0982 | 1140.00 |
| 18 | 0.0212 | 481.14 | 0.0442 | 613.06 | 0.0626 | 726.23 | 0.0740 | 826.34 | 0.0821 | 943.18 |
| 19 | 0.0175 | 424.61 | 0.0349 | 543.66 | 0.0461 | 735.27 | 0.0562 | 838.78 | 0.0664 | 947.06 |
| 20 | 0.0330 | 577.35 | 0.0632 | 741.93 | 0.0855 | 952.98 | 0.0992 | 1098.69 | 0.1110 | 1220.00 |
| 21 | 0.0190 | 485.54 | 0.0475 | 608.22 | 0.0673 | 731.17 | 0.0823 | 855.76 | 0.0941 | 970.46 |
| 22 | 0.0523 | 612.29 | 0.0779 | 857.98 | 0.0941 | 1040.00 | 0.1060 | 1177.69 | 0.1190 | 1350.00 |
| 23 | 0.0135 | 492.47 | 0.0424 | 638.73 | 0.0694 | 772.57 | 0.0931 | 951.04 | 0.1100 | 1070.00 |
| 24 | 0.0193 | 458.06 | 0.0341 | 539.53 | 0.0503 | 603.93 | 0.0629 | 680.28 | 0.0750 | 752.40 |
| 25 | 0.0215 | 520.17 | 0.0473 | 654.96 | 0.0712 | 786.30 | 0.0892 | 938.28 | 0.1030 | 1040.00 |
| 26 | 0.0291 | 447.91 | 0.0504 | 578.94 | 0.0693 | 785.87 | 0.0822 | 925.35 | 0.0929 | 1030.00 |
| 27 | 0.0180 | 502.63 | 0.0406 | 623.51 | 0.0612 | 731.84 | 0.0747 | 843.05 | 0.0838 | 959.56 |
| 28 | 0.0417 | 590.34 | 0.0666 | 784.37 | 0.0859 | 962.38 | 0.1032 | 1150.48 | 0.1150 | 1290.00 |
| 29 | 0.0332 | 593.92 | 0.0675 | 833.63 | 0.0922 | 1060.00 | 0.1084 | 1240.92 | 0.1240 | 1390.00 |
| 30 | 0.0317 | 595.84 | 0.0614 | 807.10 | 0.0831 | 982.21 | 0.0996 | 1133.77 | 0.112 | 1260.00 |
| Avg. | 0.0270 | 522.80 | 0.0535 | 670.36 | 0.0748 | 830.05 | 0.0899 | 965.73 | 0.1016 | 1085.63 |
| Median | 0.0249 | 523.05 | 0.0520 | 655.63 | 0.0727 | 806.04 | 0.0889 | 950.15 | 0.1015 | 1060.00 |
| Min. | 0.0135 | 424.61 | 0.0341 | 539.53 | 0.0461 | 603.93 | 0.0562 | 680.28 | 0.0664 | 752.40 |
| Max. | 0.0523 | 612.29 | 0.0779 | 857.98 | 0.0986 | 1060.00 | 0.1172 | 1240.92 | 0.1280 | 1390.00 |
| Stdev. | 0.0082 | 46.83 | 0.0105 | 81.41 | 0.0126 | 108.45 | 0.0140 | 124.17 | 0.0151 | 144.88 |
| EQ | PGA Level | ||||
|---|---|---|---|---|---|
| 1 g | 1.5 g | 2 g | 2.5 g | 3 g | |
| 1 | 19.94 | 38.43 | 54.67 | 64.72 | 71.35 |
| 2 | 15.68 | 28.42 | 36.41 | 42.32 | 47.44 |
| 3 | 24.35 | 41.91 | 56.04 | 66.55 | 72.57 |
| 4 | 15.10 | 29.61 | 40.86 | 48.65 | 53.67 |
| 5 | 20.15 | 31.94 | 41.91 | 48.89 | 55.71 |
| 6 | 16.90 | 34.01 | 48.55 | 56.76 | 63.05 |
| 7 | 15.11 | 27.19 | 38.84 | 48.94 | 56.08 |
| 8 | 17.81 | 31.02 | 41.52 | 51.40 | 57.81 |
| 9 | 19.49 | 32.55 | 42.47 | 48.53 | 53.42 |
| 10 | 14.69 | 28.51 | 40.81 | 50.43 | 56.41 |
| 11 | 14.17 | 31.40 | 47.71 | 58.01 | 65.31 |
| 12 | 20.13 | 38.32 | 51.27 | 59.81 | 67.41 |
| 13 | 18.98 | 32.31 | 45.41 | 53.63 | 59.80 |
| 14 | 14.58 | 30.64 | 42.96 | 51.75 | 58.80 |
| 15 | 17.63 | 30.59 | 39.89 | 45.74 | 50.78 |
| 16 | 15.54 | 29.74 | 42.44 | 53.35 | 61.69 |
| 17 | 15.29 | 29.69 | 40.85 | 48.98 | 56.05 |
| 18 | 11.98 | 25.07 | 35.88 | 42.12 | 46.54 |
| 19 | 10.68 | 20.44 | 27.28 | 33.24 | 38.66 |
| 20 | 18.82 | 36.14 | 48.12 | 56.47 | 63.07 |
| 21 | 14.32 | 29.07 | 39.83 | 48.19 | 54.75 |
| 22 | 30.44 | 45.12 | 54.67 | 61.05 | 67.83 |
| 23 | 12.50 | 27.00 | 41.15 | 53.80 | 63.10 |
| 24 | 12.01 | 20.00 | 28.75 | 35.74 | 42.27 |
| 25 | 15.71 | 29.21 | 41.54 | 51.43 | 59.33 |
| 26 | 17.58 | 29.47 | 39.75 | 46.95 | 52.80 |
| 27 | 13.55 | 25.74 | 36.55 | 43.59 | 48.66 |
| 28 | 24.86 | 38.72 | 49.55 | 59.02 | 65.56 |
| 29 | 21.45 | 39.99 | 53.82 | 62.73 | 71.43 |
| 30 | 20.65 | 36.08 | 48.26 | 57.66 | 64.67 |
| Avg. | 17.34 | 31.61 | 43.26 | 51.68 | 58.20 |
| Median | 16.31 | 30.62 | 41.73 | 51.42 | 58.31 |
| Max. | 30.44 | 45.12 | 56.04 | 66.55 | 72.57 |
| Min. | 10.68 | 20.00 | 27.28 | 33.24 | 38.66 |
| Stdev. | 4.29 | 5.80 | 7.04 | 7.90 | 8.52 |
| Probability of Failure | Seismic Intensity | |
|---|---|---|
| PGA [g] | MRD [mm] | |
| 5% | 1.25 | 1156 |
| 50% | 1.65 | 1800 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jeon, B.-G.; Kim, S.-W.; Yun, D.-W.; Hahm, D.; Eem, S. Seismic Fragility Evaluation of Main Steam Piping of Isolated APR1400 NPP Considering the Actual Failure Mode. Sustainability 2022, 14, 8315. https://doi.org/10.3390/su14148315
Jeon B-G, Kim S-W, Yun D-W, Hahm D, Eem S. Seismic Fragility Evaluation of Main Steam Piping of Isolated APR1400 NPP Considering the Actual Failure Mode. Sustainability. 2022; 14(14):8315. https://doi.org/10.3390/su14148315
Chicago/Turabian StyleJeon, Bub-Gyu, Sung-Wan Kim, Da-Woon Yun, Daegi Hahm, and Seunghyun Eem. 2022. "Seismic Fragility Evaluation of Main Steam Piping of Isolated APR1400 NPP Considering the Actual Failure Mode" Sustainability 14, no. 14: 8315. https://doi.org/10.3390/su14148315
APA StyleJeon, B.-G., Kim, S.-W., Yun, D.-W., Hahm, D., & Eem, S. (2022). Seismic Fragility Evaluation of Main Steam Piping of Isolated APR1400 NPP Considering the Actual Failure Mode. Sustainability, 14(14), 8315. https://doi.org/10.3390/su14148315