Study on the Characteristics of Water Jet Breaking Coal Rock in a Drilling Hole

Abstract

Water jet technology is an effective measure by which to improve the efficiency of deep coalbed methane mining. Nevertheless, the effect of a water jet impinging on coal rock remains unclear. In this study, numerical simulation is used to analyze a water jet impingement drill test block, after which experimental verification is carried out. Next, on the basis of the experimental verification that the simulation method is feasible, the influence factors of the water jet impingement in the drill hole are analyzed. It is concluded that the phase-field variables based on the fracture change method can effectively characterize the damage and destruction of coal rock. The water jet impact in the borehole has a central damage failure zone and two-side damage failure zone, and the damage failure ratio n is used to characterize the degree of damage to the coal rock. When the jet target distance is 70 mm, the damage ratio n is closest to 1, and the effect of water jet impact on coal-rock is the best. When the wall roughness is less than 10 mm, the blocking effect on the jet is dominant, resulting in a negative correlation between the damage size and the roughness. When the wall roughness exceeds 10 mm, the development of cracks and the connection effect exceed the blocking effect, resulting in larger damage. Therefore, it can be seen that the effect of a water jet impacting on coal rock is positively related to jet pressure. When the jet target distance is 70 mm, the damage range of 30 MPa jet pressure to the center and both sides of the coal rock reaches about 1.1 m, thus signifying a good coal rock breaking effect. The wall roughness has a significant effect on the coal rock breaking effect of the water jet.

1. Introduction

Coalbed methane is a form of clean fossil energy. The mining of coalbed methane has a great contribution to ensuring the safe production of coal mines, as well as to increasing the supply of natural gas resources and reducing greenhouse gas emissions [1,2]. Gas drainage is an effective means by which to develop coalbed methane resources. Today, with the continuous increase in coal mining depth, deep coalbed methane exhibits the characteristics of high reservoir pressure, high ground stress, and low permeability. This has resulted in the incidence of disasters such as gas explosions increasing significantly. Problems such as the difficulty of extraction continue to emerge [3,4,5], which urgently need to be solved by means of efficient and intelligent coal seam anti-reflection technology.

Water jet technology uses water as the working medium, adopts the principle of liquid pressurization, converts mechanical energy into pressure energy through a specific nozzle, and forms a jet with higher energy by the nozzle, so as to solve engineering problems [6,7]. In coal mines, the use of water jet technology to cut and erode the coal body within the borehole has become one of the mainstream measures by which to increase the permeability of the coal seam and improve the efficiency of coalbed methane extraction [8,9,10]. Through many scholars’ research and field tests, water jet technology has led to the formation of a complete set of hydraulic measures, among which are hydraulic punching technology, hydraulic slitting technology, and hydraulic cutting technology [11,12,13,14,15,16]. These hydraulic measures have been widely used in coal mines. For example, in 1969, the Fushun Coal Research Institute conducted a water jet slitting test in the Hebi No. 6 Mine and achieved a significant increase in the range of borehole pressure relief and permeability enhancement [17]. Prof. Lin Baiquan of the China University of Mining and Technology established the evolution model of stress relief in slotted coal bodies and analyzed the influence of the number, size, and opening of slots on stress relief [17]. Prof. Liu Mingju of Henan Polytechnic University conducted a hydraulic cutting test in the Jiaozuo mining area with serious outburst hazards, thereby effectively reducing the outburst hazard, greatly increasing the speed of coal tunnel excavation, and achieving good outburst prevention effects [17].

Water jet impact crushing coal rock exhibits the characteristics of high efficiency, dust-free, and low heat [17]. As coal mine enterprises grow more aware of safe production, water jet technology has become widely popular. Studies have shown that the impact of water jets in the borehole can alter the stress distribution of the surrounding coal, as well as promote the expansion of coal rock fissures, release the elastic energy of the coal, increase the permeability of the coal seam, and improve the efficiency of coalbed methane mining [18]. However, the mechanism of water jet impact breaking coal rock remains unclear. The process of water jet breaking coal rock in the borehole is rapid and difficult to observe, and there is no theoretical support for the mechanism of water jet impact drilling. Therefore, research on the characteristics of water jet impact breaking coal rock is still required.

This study carried out numerical simulation and experimental research on water jet impact drilling. First, the theory of a water jet breaking coal rock is introduced, and the numerical simulation and experimental research are mutually verified. Then, the impact factors of water jet impact in the borehole are studied. By adjusting different jet target distances, jet pressures and wall roughness, the jet impact effect was observed, and the optimal process parameters and effective impact range of drilling jets for breaking coal rock were determined. The results of this study provide an important basis for determining the reasonable jet parameters and improving the efficiency of coalbed methane extraction.

2. Materials and Methods

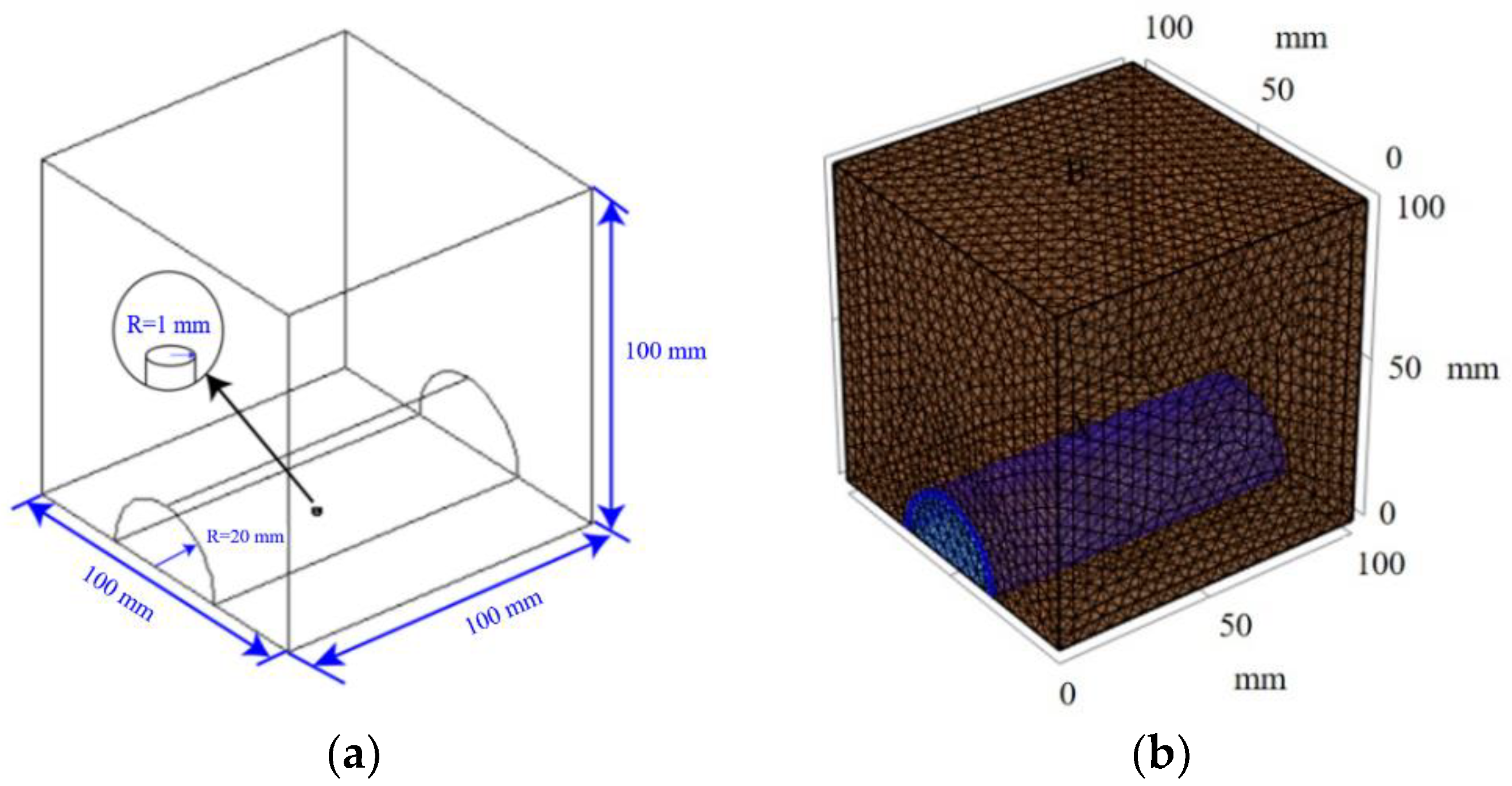
2.1. Description of Water Jet Impact Test Block

Figure 1 shows the model and grid division of the water jet percussion drilling. A semi-cylinder with a radius of 20 mm and a height of 100 mm at the bottom represents the drilling area, along with a cylindrical nozzle with a radius of 1 mm and a height of 1 mm.

The raw coal sample for simulation reference was taken from the 15th coal seam of the 12th Mine of Tian’an Coal Industry, Pingdingshan, Henan. This coal seam is a typical soft and high outburst coal seam, with a high incidence of disasters, such as gas explosions. Therefore, this area is suitable for the field application of water jet technology. The properties of the coal seam parameters are shown in

Table 1. Mechanical parameters table of forming the test block.

Density/(kg/m3)	Elastic Modulus/GPa	Compressive Strength/MPa	Tensile Strength/MPa	Angle of Internal Friction/°	Cohesion/MPa
1183	1.663	2.697	0.637	29.3	0.582

.

The simulation assumes that there is no loss of kinetic energy from the jet exit to the axis of the borehole. The water pressure is changed at the outlet of the water jet and set to 2~16 MPa (the interval is increased by 2 MPa), the drilling test block is impacted, and fixed constraints are set around the drilling test block. In this way, we can simulate and study the effects of the water jet percussive drilling on breaking the coal rock.

In order to verify the simulation results, a similar model is used for experimental research. Coal is a porous medium with a complex structure and obvious anisotropy. The application of similar models to conduct experiments is helpful in highlighting the main contradictions in complex experiments, and in facilitating the discovery of internal connections [19]. The similar test block should be similar to the mechanical properties of the raw coal, i.e., the shape of the full stress–strain curve, tensile and compressive strength, tensile–compression ratio, and Poisson’s ratio are similar to those of the actual coal [20]. The experimental materials are composed of coal powder, cement, gypsum, additives, and water. In addition, coal powder is used as aggregate, while cement and stone glue is used as cementing agents to provide a certain pore structure after the final setting. In the experiment, a 100 × 100 × 100 mm cube test block was produced. A semi-cylinder with a radius of 20 mm and height of 100 mm was opened at the bottom to represent the borehole. The center of the borehole was impacted with a high-pressure water jet to study the effects of the water jet breaking the coal rock. The experimental conditions and material parameters of the test block are shown to be consistent with the above model for calibration verification.

The water jet breaking coal rock experimental system mainly includes a high-pressure water supply device, water jet generating and regulating device, real-time monitoring device, and sample fixing device, as shown in Figure 2.

This study mainly focuses on the analysis of water jet impact drilling. Therefore, a core drill is used in the center of the test block to remove a semi-circular core from the test block, so as to create a simulated drilling test block, and the angles are arranged on the upper surface and the side of the test block. The 45° strain gauge is shown in Figure 2. In order to prevent the strain gauge from being short-circuited by splashing water, after the strain gauge has been bonded, hot glue is used to seal the surface and the connection terminals.

2.2. Characteristics of Water Jet Impact Test Block

During the impact process of the water jet in the borehole, the motion of the water jet follows the continuity equation, energy equation and turbulence $k-\epsilon$ equation.

(1)

The continuity equation is the specific expression form of the law of conservation of mass in fluid mechanics. The fluid adopts the continuum model, and the velocity and density are both continuous and differentiable functions of space coordinates and time, the formula for which is as follows:

$$\frac{\partial {\rho }_{\overline{ui}}}{\partial x_i^{}}=0$$

(1)

(2)

The energy equation refers to an equation that reflects the law of conservation of energy including internal energy when considering changes in density, temperature, and internal energy, the formula for which is as follows:

$$\rho \overline{u_j}\frac{\partial \overline{u_i}}{\partial x_j}=-\frac{\partial \overline{p}}{\partial x_i}+\frac{\partial }{\partial x_j}[\mu (\frac{\partial \overline{u_i}}{\partial x_j}+\frac{\partial \overline{u_j}}{\partial x_i})-\rho \overline{u_i}\overline{u_j}]$$

(2)

(3)

The velocity of the high-pressure water jet is very high, its Reynolds number being far beyond the range of laminar flow. Therefore, the turbulence model should first be selected. In order to make the simulation results closer to reality and more reliable, we select the standard $k-\epsilon$ equation, the formula for which is as follows:

$$\rho \left(\overline{u_j}\frac{\partial k}{\partial x_j}\right)=\frac{\partial }{\partial x_i}[(\mu +\frac{{\mu }_i}{{\sigma }_k})\frac{\partial k}{\partial x_i}]+{\mu }_i\frac{\partial }{\partial x_i}(\frac{\partial \overline{u_i}}{\partial x_j}+\frac{\partial \overline{u_j}}{\partial x_i})-\rho \epsilon$$

(3)

$$\rho \overline{u_j}\frac{{\partial }_{\epsilon }}{\partial x_j}=\frac{\partial }{\partial x_i}[(\mu +\frac{{\mu }_i}{{\sigma }_{\epsilon }})\frac{\partial \epsilon }{\partial x_i}]+C_1\frac{\epsilon }{k}\frac{\partial \overline{u_i}}{\partial x_j}(\frac{\partial \overline{u_i}}{\partial x_j}+\frac{\partial \overline{u_j}}{\partial x_j})-C_2\rho \frac{{\epsilon }^2}{k}$$

(4)

where $\rho$ is the density of the fluid, ${\mathrm{kg}/\mathrm{m}}^3$; $u_i,u_j$ is the component of the velocity, $\mathrm{m}/\mathrm{s}$; $p$ is pressure, $\mathrm{Pa}$; $\mu$ is the dynamic viscosity,$\mathrm{Pa}·\mathrm{s}$; k is the turbulent kinetic energy,$\mathrm{J}$; $\epsilon$ is the dissipation rate of the turbulent kinetic energy, $\%$, and $C_1$, $C_2$, ${\sigma }_k$ and ${\sigma }_{\epsilon }$ are the empirical constants, the respective values of which are $C_1$ = 1.44, $C_2$ = 1.92, ${\sigma }_k$ = 1.0 and ${\sigma }_{\epsilon }$ = 1.3.

The coal body area is expressed as a 100 × 100 × 100 mm cube structure with a half-cylindrical borehole in the center of the bottom. The high-pressure water jet impacts the borehole, which will result in a series of mechanical properties occurring inside the coal body. In this study, the coal body is regarded as a homogeneous and isotropic porous elastic material, which satisfies both the following strain–displacement relationship and stress balance equation [21]. The strain–displacement relationship can be expressed as follows:

$${\epsilon }_{i,j}=\frac{1}{2}(d_{i,j}+d_{j,i})$$

(5)

The coal body stress balance equation can be expressed as follows:

$${\sigma }_{ij,j}+f_i=0$$

(6)

where ${\epsilon }_{ij}$ is the component of the strain tensor; $d_{i,j},d_{j,i}$ is the displacement component, m; ${\sigma }_{ij,j}$ is the component of stress tensor, N/m², and $f_i$ is the body stress component, N/m³.

During the impact of the water jet in the borehole, the coal body breaks into particles under high-intensity load, and some of the particles are removed by the water, thereby forming cavities with some radial cracks [22], so as to achieve the purpose of increasing the coal seam’s permeability. The strength criterion is the basis for determining the failure of a rock mass under a certain stress state. Due to the different characteristics of the coal rock itself, great differences will appear in its failure mode. In this study, the Mohr–Coulomb yield criterion is used to characterize the damage and failure of the coal rock [19]. In addition, the theory of fracture mechanics is used to calculate the phase-field variables $\varphi$ of the damage characteristic parameters through the critical energy release rate. The relationship between the phase-field variables $\varphi$ and critical energy release rate G is expressed as follows:

$${\displaystyle {\int }_{\Gamma }^{}{G}_{}}dx\approx {\displaystyle \underset{\Omega }{\overset{}{\int }}{G}_{}}[\frac{{(\varphi -1)}^2}{2l_0}+\frac{l_0}{2}{\left|\nabla \varphi \right|}^2]dx$$

(7)

where G is the critical strain energy release rate, $\%$, and $\varphi$ is the phase-field variable with a value of 0~1. When the value is 0, there is no damage, while when the value is 1, complete damage is present. In addition, $l_0$ is the characteristic length parameter, which is used to control the width of the gradient region of the phase field.

The critical strain energy release rate G is expressed as follows:

$$G=\frac{\partial W}{\partial A}$$

(8)

where W is the strain energy, J, and A is the cross-sectional area, m². The strain energy W is the product of the strain energy density U and the volume of the object: W = U × V. The elastic strain energy density U in the coal rock is calculated by the following formula:

$$U=\frac{1}{2E}[{\sigma }_1{}^2+{\sigma }_2{}^2+{\sigma }_3{}^2-2u({\sigma }_1{\sigma }_2+{\sigma }_1{\sigma }_3+{\sigma }_2{\sigma }_3)]$$

(9)

where $U$ is the elastic strain energy density, J/m³; $E$ is the elastic modulus, MPa; $u$ is the Poisson’s ratio, and ${\sigma }_1$, ${\sigma }_2$ and ${\sigma }_3$ are the three-dimensional stress of the coal rock, N/m³.

The phase-field variables can be determined by calculating the strain energy density and critical energy release rate. The result effectively indicates the damage and destruction degree of the coal rock.

3. Results

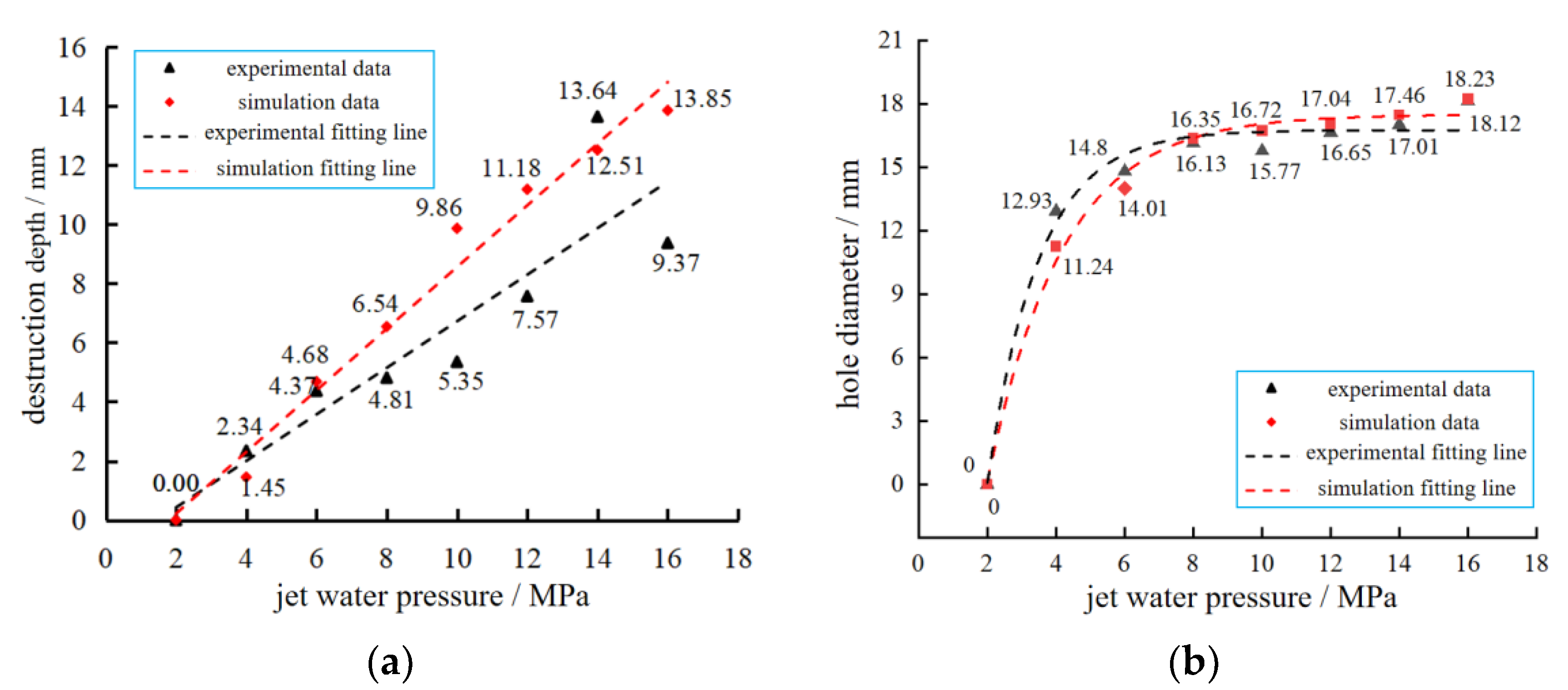
3.1. Model Verification

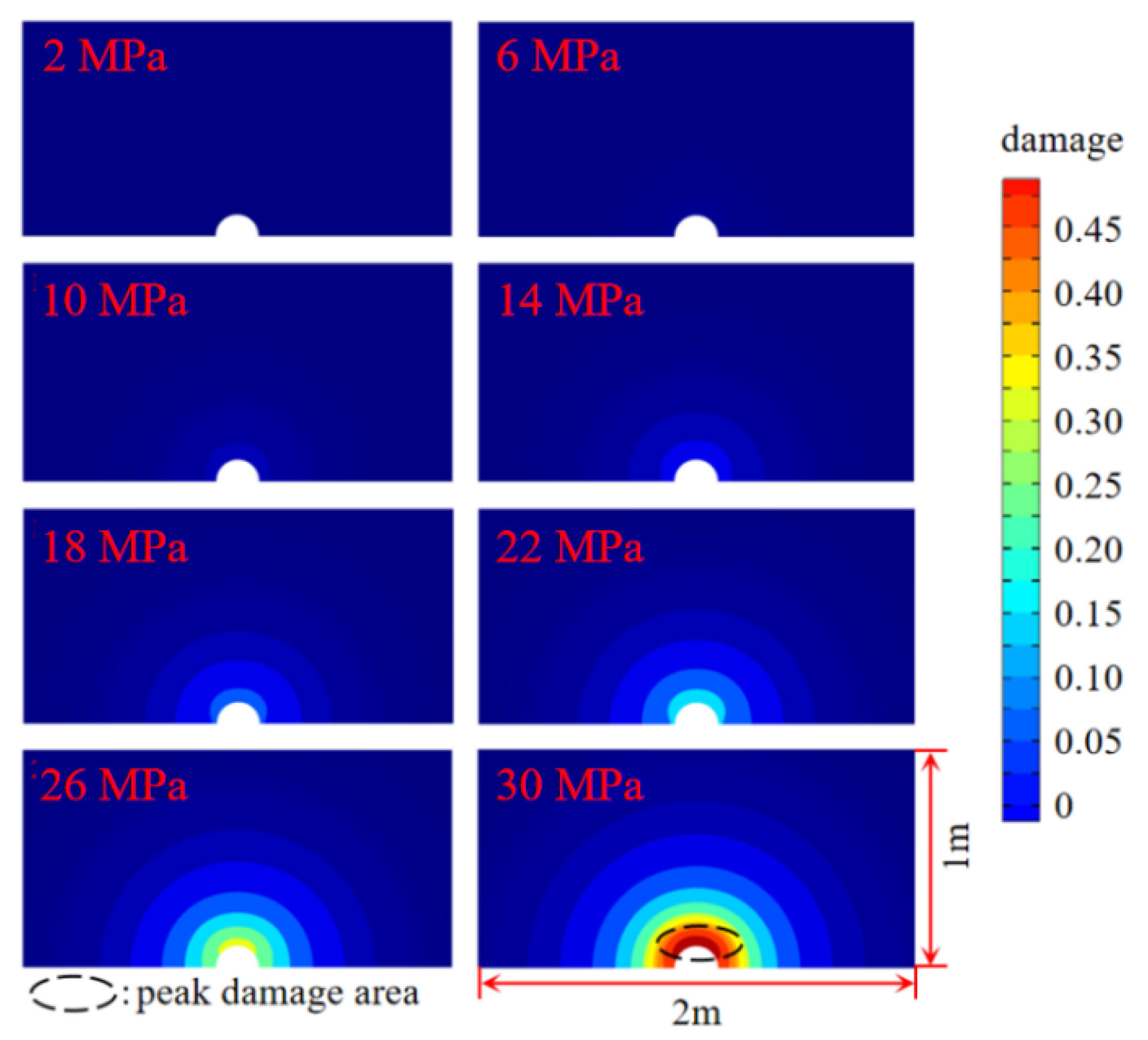
3.1.1. Damage Results of Different Jet Pressure Impacts

Figure 3 shows the damaging effect of different pressure water jets on the surface of the test block. The damage range is 0~1, where 0 signifies no damage, and 1 signifies complete damage. It can be seen from the figure that, when the water jet pressure is 2 MPa, no damage has been caused to the test block, and the water jet impact pressure is less than the critical pressure for crushing the coal sample block. In addition, when the water jet pressure is 4 MPa, then the test block on the surface of the borehole produces impact deformation. Then, when the jet pressure increases to 6 MPa, the damage and destruction can be clearly observed on the surface of the borehole, and the damaged area is in the shape of a round hole. With the increase in the water jet pressure, the surface is damaged, and the area expands. When the jet pressure is greater than 14 MPa, the surface of the coal sample test block exhibits a noticeable circular damaged area.

3.1.2. Feasibility of the Model

Figure 4 shows the surface fracture characteristics of the continuous impact of water jets at different pressures on the drilling test block. It can be seen from the figure that, when the pressure of the water jet is 2 MPa, then the surface of the drilling test block does not produce any cracks, and this is when the water jet impacts. The pressure is lower than the critical pressure for the failure of the drilled test block. However, when the water jet pressure is greater than 4 MPa, then obvious impact pits appear on the surface of the drilled test block, and the damage gradually increases with the increase in pressure. In addition, after the water jet pressure reaches 16 MPa, the test block exhibits longitudinal penetration fracture along the drill hole. The impact pits of the drilled test blocks appear in different shapes, the outlines can be clearly distinguished, and the pits are uneven. When the water jet pressure is greater than 4 MPa, obvious impact pits appear on the surface of the drilled test block, and the damage gradually increases with the increase in pressure.

It can be seen that when the jet pressure is 2 MPa, no impact damage is caused to the test block. However, when the jet pressure exceeds 4 MPa, pits begin to occur. As the jet pressure increases, the size of the impact pits continues to expand. The simulation results are fundamentally consistent with the experimental results. The following analysis and verification are performed using specific data.

Statistical simulation results and experimental results are used to obtain the data for the depth and diameter of the impact pit caused by the impact of the different jet pressures on the test block (the vernier caliper is used to measure the depth and diameter of the pit caused by water jet impinging on the drilling test block. The depth and diameter data are obtained through multiple measurements and taking the average value). Due to the fact that the impact of the 2 MPa outlet hydraulic water jet did not cause damage to the drilled test block, the depth and diameter parameters are both 0. The simulation and experimental data of the depth and diameter of the impact crater caused by different jet pressure impacts are plotted in the same plot group, and the results are shown in Figure 5.

Figure 5 shows the depth, diameter and area curves of the impact pit formed on the surface of the test block under different jet pressure impact conditions. Comparing the simulation and experimental data, the effective damage area is specified as being damage greater than 0.01. By comparing the depth data and fitting line in Figure 5, it can be seen that the simulation results of the depth of the water jet impact pit are fundamentally consistent with the experimental data. However, it also reflects from the side that the experiment is subject to many external factors, and the depth variation fluctuates greatly and is unstable. Under different jet pressure impact conditions, as the jet pressure increases, the depth of the impact pit basically continues to increase. Furthermore, when the water pressure is 16 MPa, then the depth of the impact pit of the experimental data curve drops significantly. This is due to the fact that the jet pressure impact of 16 MPa causes the test block to crack, causing the overall damage to the test block before the impact depth reaches the limit.

It can be seen that, under the simulation and experimental conditions, the jet pressure of 2 MPa did not damage the test block. However, when the pressure is 4 MPa, then the water jet impacts the borehole, and the test block undergoes obvious impact damage. As the jet pressure continues to rise, the diameter of the impact pit continues to increase, yet the rate of increase gradually decelerates. The simulation data are fundamentally consistent with the experimental results. Comparing the two graphs, it can be seen that the simulation results match the experimental results, thereby verifying the correctness of the simulation, and indicating that this method is feasible.

3.2. Simulation Result Analysis

Next, in order to explore the crushing mechanism of different pressure water jets impacting the test block, the section line AB is selected, and the stress curve and damage curve at the position of the section line are drawn, as shown in Figure 6. It can be seen that the stress distributions at the intercept line under different water pressure conditions are similar. As the depth from the wall continues to increase, the internal stress of the test block gradually decreases. In addition, when the jet pressure is below 10 MPa, then, as the pressure increases, the peak stress at the intercept line increases relatively slowly. However, when the jet pressure exceeds 10 MPa, then the increase in the peak stress at the intercept line gradually accelerates. The relationship between the jet pressure and peak stress of the intercept line can be expressed as follows:

$$y=0.978e^{\frac{x}{7.176}}+0.358$$

(10)

The fitting degree R² reaches 98.7%, which can well represent the relationship between pressure and stress peak under water jet impact test block.

The damage caused by the impact of water jets at different pressures on the test block is consistent, and the size of the damage gradually decreases as the depth from the wall increases. Similarly, when the jet pressure is lower than 10 MPa, then, as the jet pressure increases, the damage peak at the intercept line position increases at a relatively slow rate. Then, when the jet pressure exceeds 10 MPa, the damage size changes gradually. The relationship between the jet pressure and the peak value of the cutting damage can be expressed as follows:

$$y=0.04e^{\frac{x}{5.36}}-0.062$$

(11)

The fitting degree R² reaches 99.8%, which can well represent the relationship between the pressure and the failure peak value during the water jet impacting the test block.

It can be seen from the results that the higher the jet pressure is, the stronger the stress state change and damage caused by the impact of the water jet on the test block will be.

It is concluded that, in the process of the water jet impacting the test block, the impact force propagation must continuously overcome the internal stress of the test block itself, and the energy is constantly lost during the propagation process. In addition, the stress change and damage caused to the test block are gradually reduced. The greater the jet pressure is, the more energy will be carried by the impact, and the stronger the stress change effect on the test block, the wider the damage range, and the larger the corresponding stress peak and damage peak will be. However, due to the need to overcome more during the impact propagation process of the internal stress of the test block, the attenuation process of the impact force will be faster, and the stress distribution in the damaged area of the test block will be uneven. This is due to the damage and destruction of the test block caused by the impact of the water jet, which alters its original internal structure. In addition, there is a broken zone found within the impact area, and the stress distribution in the broken zone is uneven.

4. Discussion on Influencing Factors

Based on the feasibility of the aforementioned simulation method, the impact factors of real drilling water jet impact are studied, and the water jet impact drilling is simulated and analyzed under different target distances, pressure conditions and wall roughness. The impact factors and scope of the hole water jet impact provide a theoretical basis for determining reasonable parameters and optimizing operation technology at the actual site.

4.1. Water Jet Punching and Damage Evolution Model of Coal Rock

To study the characteristics of actual water jet impact breaking coal rock, the 15th coal seam of the Henan Pingdingshan Tian’an Coal Industry’s 12th mine is selected as the source of the field working condition data. This coal seam is a low-permeability and soft coal seam. The drilling water jet technology is the main pressure relief measure, and the design model geometry and mesh division are shown in Figure 7. The coal seam strikes 20 m, inclines 10 m, and has a thickness of 3.5 m. In addition, a borehole with a diameter of 200 mm is drilled at 10 m in the center of the strike, along the thickness direction of the coal seam, and the length of the borehole is 2.1 m. The high-pressure water jet impacts the coal rock. The diameter of the water jet nozzle is 2 mm, and the nozzle direction is perpendicular to the drilling direction. Based on this model, the impact of the water jet and the damage evolution of the coal rock are studied. The entire geometric grid contains 353,913 domain elements, 22,556 boundary elements and 1755 edge elements.

The coal seam material parameters are shown in

Table 2. Mechanical parameters of the coal seam.

Density/(kg/m3)	Elastic Modulus/GPa	Compressive Strength/MPa	Tensile Strength/MPa	Angle of Internal Friction/°	Cohesion/MPa
1467	1.455	2.208	0.580	26.3	0.625

.

The simulation must first balance the ground stress, then simulate the impact of the water jet. This section mainly studies the coal-breaking characteristics of the water jet impacting the coal under different jet target distances and jet pressure conditions. Under the jet pressure of 20 MPa, the jet target distance is set to 20~90 mm (increasing at intervals of 10 mm). Then, under the condition that the target distance is 70 mm, the water pressure is set to be 2 MPa to 30 MPa (increasing at intervals of 4 MPa), and under the conditions of jet pressure of 20 MPa and target distance of 70 mm, the wall roughness (equivalent sand grain roughness) is set to 0.1, 1, 5, 10, 20, 30, 40, and 50, respectively, to simulate the above three classifications.

4.2. Simulation Results and Analysis

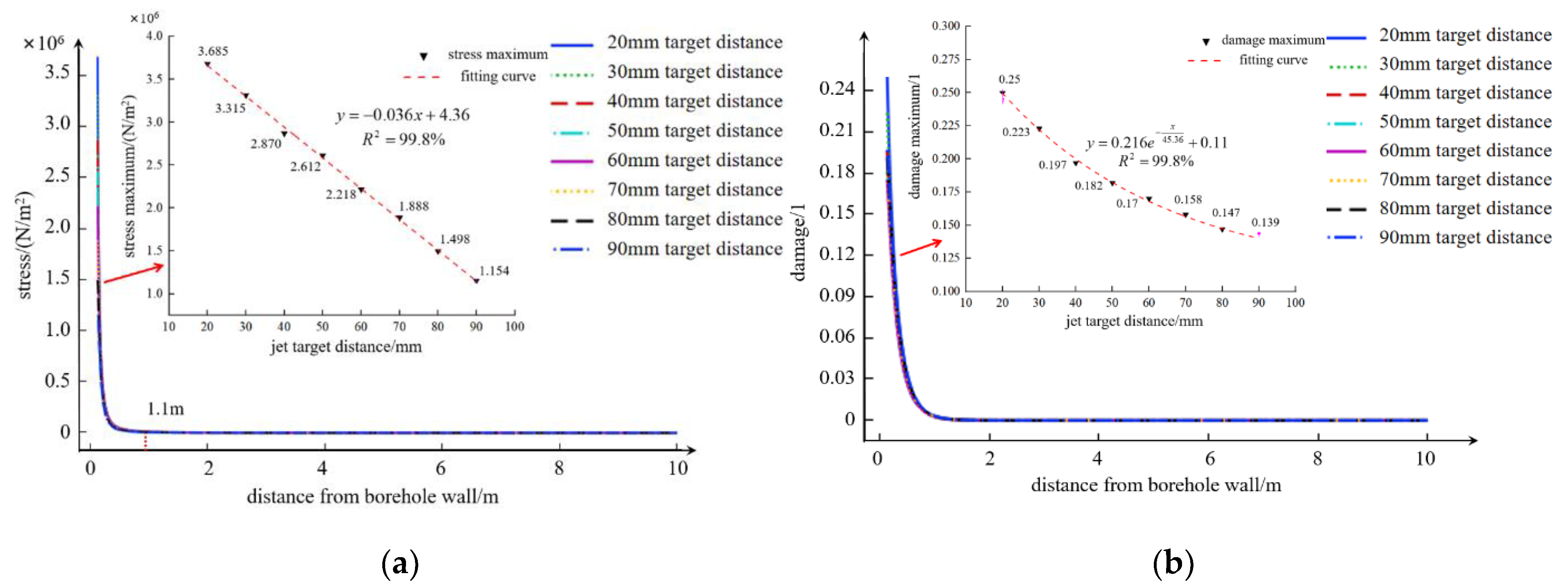
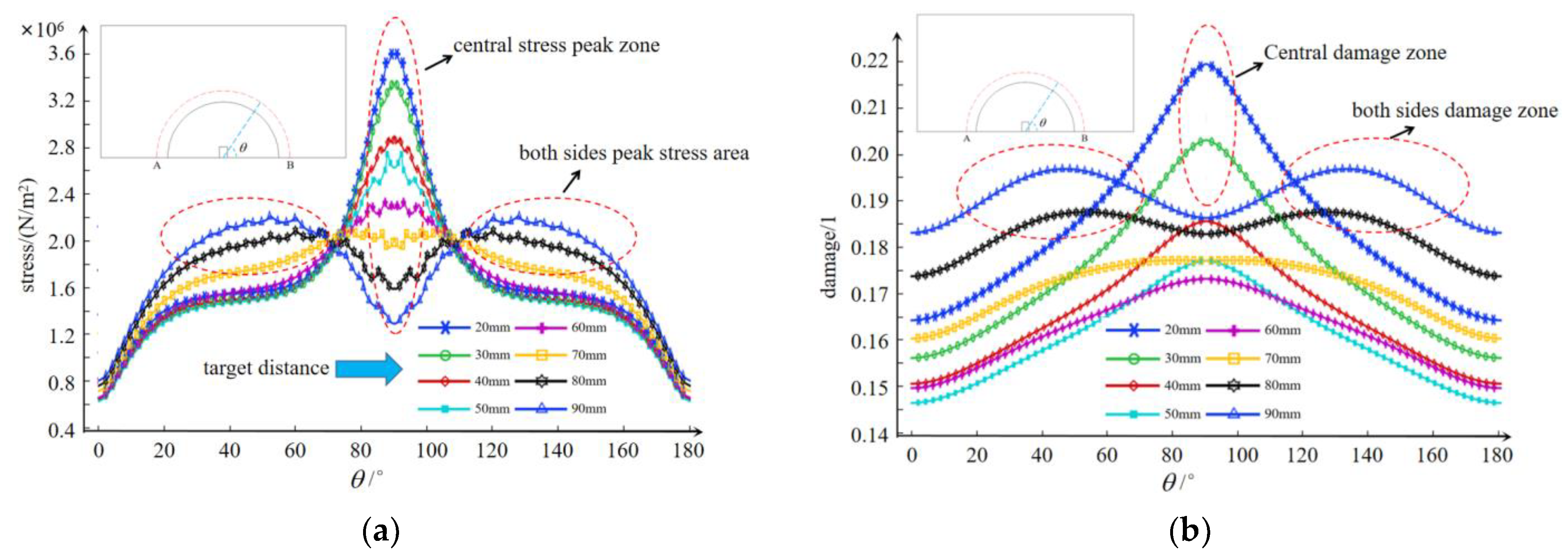
4.2.1. Damage Characteristics of the Coal Rock Impacted by the Target Distance

In order to reveal the characteristics of the water jets at different target distances for breaking the coal rock, section O shown in Figure 8 is selected (the height of section O is the same as the nozzle height). In addition, a rectangular area with a length of 2 m and a width of 1 m is intercepted near the borehole to observe the damage characteristics of the water jet impacting the coal rock in the rectangular area.

It can be seen that the damage distribution characteristics of water jets impacting the coal rock at different target distances are similar, and the damage to the wall of the hole is the strongest. As it penetrates deep into the coal seam, the degree of damage gradually decreases, and finally reaches 0. Meanwhile, in the process of water jet percussion drilling, there is a damage peak area, in which the damage value reaches the maximum, and the damage peak area continues to expand with the increase in the jet target distance.

It is worth noting that, when the jet target distance increases from 70 mm to 80 mm, the damage peak area begins to concentrate from the center to both sides. As shown in Figure 8, the damage peak area is divided into two. This phenomenon becomes more apparent when the jet target distance is 90 mm, which shows that the impact damage of the water jet impacting both sides of the borehole wall has exceeded the central area of the wall.

In order to further clarify the impact of the target distance on the impact of the water jet on the coal rock breaking effect, the analyzed section is shown in Figure 9. In the figure, MN and arc AB (the inner arc of the coal seam 20 mm deep from the borehole wall) are selected, and the stress and damage distributions at the cross-section position are drawn.

In Figure 10, the stress distribution characteristics of the MN cut-off line of the water jet impingement borehole with different target distances are shown to be consistent. With the deepening into the coal seam, the stress decreases sharply. This is due to the fact that the propagation of the impact stress of the water jet must continuously overcome the coal rock itself. This results in cohesion, thereby altering the initial stress state of the coal seam, and the stress peak value of water jet impacting coal rock at different target distances is different. The smaller the jet target distance is, the greater the stress peak value will be. When the jet target distance is 20 mm, then the stress peak value reaches 3.685 × 10⁶ N/m². The jet target distance and stress peak value of water jet impinging on coal rock can be fitted as follows:

y = −0.036x + 4.36

(12)

The fitting degree R² reaches 99.8%, which can well express the relationship between the impact target distance of the water jet and the stress peak under 20 MPa pressure.

Next, in order to accurately represent the stress and damage distribution curve at the arc AB position, using the analysis angle method, by changing the size of the analysis angle $\theta$, the stress damage data of different arc positions are drawn. Figure 11 shows the stress distribution and damage distribution at the arc AB. It can be seen that, in the central area of $\theta$ = 90°, the peak stress of the water jet impacting the coal rock reaches the extreme value. The stress distributions of the coal seams on both sides of the center are the same. The stress distribution includes a central stress peak zone and a two-side stress peak zone. With the continuous increase in the jet target distance, the central stress peak continues to decrease, while, on the contrary, the two-side stress peaks continue to increase. In addition, when the jet target distance is 30 mm, then the center stress peak value is fundamentally the same as the two-side stress peak value, while the jet target distance continues to increase, and the two-side stress peak value exceeds the center stress peak value. The movement of the central stress peak to both sides is due to the divergence effect of the water jet impact. With the increase in the target distance, the divergence effect becomes stronger, resulting in the movement of the stress peak to both sides.

Similar to the stress distribution, the arc AB position damage is based on the center position of $\theta$ = 90°, distributed symmetrically to both sides, and there is a central damage zone and a two-side damage zone. With the continuous increase in the jet target distance, the peak damage of the center damage gradually decreases, while, on the contrary, the peak damage of the two-side increases. When the jet target distance is 30 mm, the center damage is basically the same as the two-side damage. When the jet target distance exceeds 30 mm, then the two-side damage gradually exceeds the damage on the center. In practical engineering applications, in order to ensure the impact of the drilling water jet on breaking the coal rock, the impact range of the water jet must be enlarged, while ensuring the strongest impact on the center area of the nozzle.

Figure 12 shows the water jet with a pressure of 20 MPa, where, under different target distances, the damage-to-damage failure ratio n (n = the ratio of the peak damage at the center/the peak damage at both sides) caused by the impact drilling and target distance. From the above analysis, it can be seen that, when n = 1, the water jet has the best effect of breaking the coal rock. It can be intuitively seen from the figure that, when the jet target distance is 70 mm, the value of n is closest to 1, under which condition the water jet has the best impact on breaking the coal rock. Therefore, in actual engineering applications, in order to achieve a better drilling water jet impact on breaking coal rock, the jet target distance must be maintained near 70 mm.

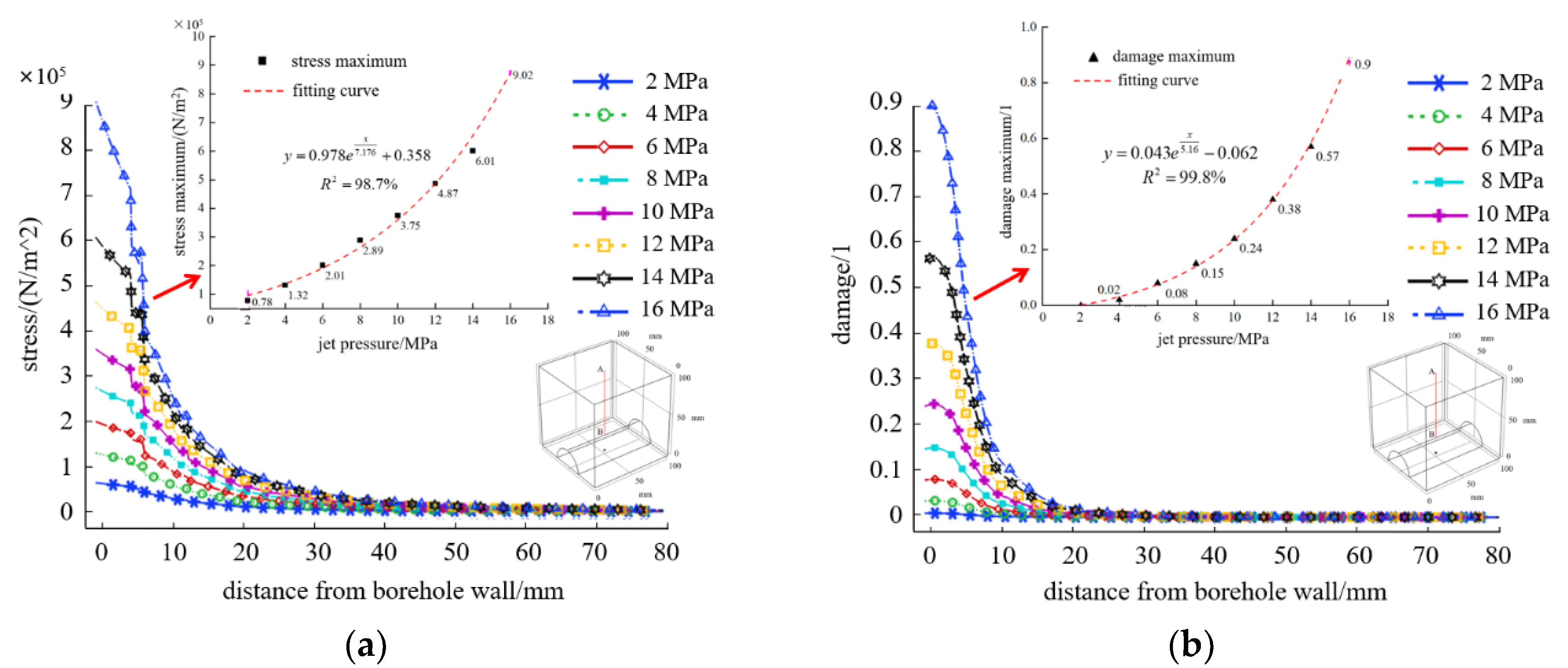
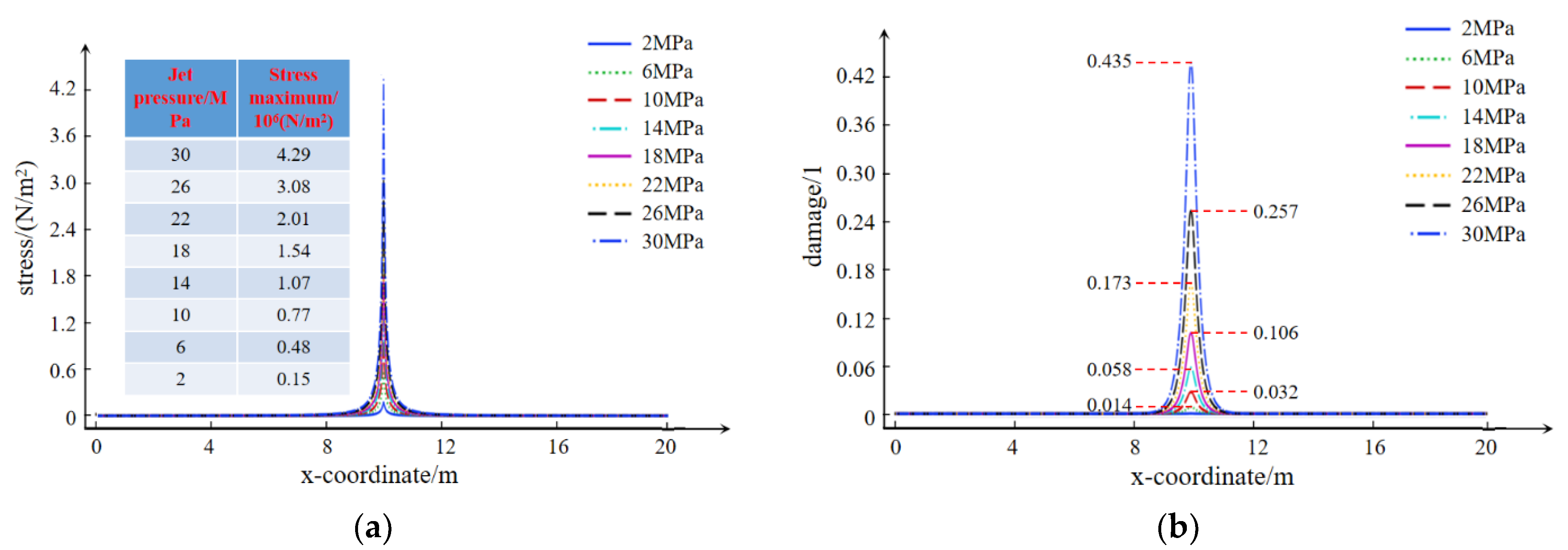
4.2.2. Damage Characteristics of Coal Rock Impacted by Different Water Jet Pressures

Based on the above research, in which, when the target distance of borehole water jet impact is about 70 mm, then the effect of coal rock breaking is good, the simulation analysis of water jet impact boreholes with different pressures is carried out. The rectangular area with a length of 2 m and width of 1 m on section O shown in Figure 8 is selected once again to observe the damage characteristics of the water jet impacting the coal rock in the rectangular area.

Figure 13 shows the damage characteristics of the water jets at different pressures impacting coal rock under the condition of a jet target distance of 70 mm. It can be seen that the impact of water jets causes damage to the center and both sides of the borehole. In addition, with the continuous increase in jet pressure, the impact of drilling water jets on breaking coal rock gradually becomes apparent, and the water jet impact does not cause damage to the borehole when the jet pressure is 2 MPa. However, when the jet pressure increases to 10 MPa, then the impact damage and destruction begin to appear. With the continuous increase in jet pressure, the damage and destruction range of coal rock gradually expands, the scope of the damage peak area continues to expand, and the greater the jet pressure is, the greater the impact energy of the drilling water jet and the stronger the coal rock breaking effect will be.

In order to further clarify the characteristics of the impact of water jets at different pressures on breaking coal rock, the analysis cut lines shown in Figure 14 are selected. The MN and SQ cut-off lines, along with the stress and damage distributions at the cut line positions, are, respectively, drawn.

Figure 15 shows the stress distribution curve and damage distribution curve at the MN section. It can be observed that the impact stress distribution characteristics of the water jets at different pressures are similar. In addition, with the deepening of the coal seam, the cohesive force of the coal rock must be continuously overcome during the stress transfer process, thus resulting in a sharp drop in stress. The larger the jet pressure is, the longer the stress propagation distance will be, and the greater the peak of the cross-line stress will be. The relationship between jet pressure and peak stress can be expressed as follows:

$$y=0.37e^{\frac{x}{11.758}}-0.993$$

(13)

The fitting degree R² reaches 99.1%, which shows that the relationship between water jet pressure and stress peak can be expressed by this formula when the jet target distance is 70 mm.

It can be seen that the damage to the coal rock caused by the water jet impact drilling gradually decreases with the deepening of the coal seam. With the increase in the jet pressure, the damage range at the cut line position gradually increases. In addition, when the jet pressure is 30 MPa, the damage range reaches 1.45 m. The relationship between the jet pressure and MN section position damage peak can be expressed as follows:

$$y=0.01e^{\frac{x}{9.25}}-0.023$$

(14)

The fitting degree R² reached 99.8%, indicating that the relationship between the water jet pressure and the damage peak can be expressed by this formula when the jet target distance is 70 mm.

The stress and damage distribution curves at the SQ section position are shown in Figure 16. It can be seen that the stress distribution of the water jet impacting the coal rock from different pressures is symmetrically distributed. With the impact of the water jet as the center, the stress in this area reaches the peak value to the two-side stress continuously decreasing, and the greater the jet pressure is, the wider the impact stress range will be. The same is true for the damage distribution, which gradually decreases from the central area to both sides. Finally, the damage range increases with the increase in the jet pressure.

Figure 17 shows the comparison of the damage range of the MN and SQ cut lines of the coal rock by the 30 MPa water jet with a jet target distance of 70 mm. It is not difficult to see that the damage range at the MN cut-off line position is approximately twice that of the SQ cut line position. The damage range increases with the increase in jet pressure. When the jet pressure is 30 MPa, the respective damage ranges of the MN and SQ cut line positions reach 1.09 m and 2.24 m, and the damage range of the center and two sides are basically the same. Once again it is shown that, at a target distance of 70 mm, the water jet has the best impact on breaking the coal rock. In actual engineering applications, in order to achieve a better effect of drilling water jet impacting the coal rock, the jet pressure must be increased while upholding the condition of ensuring construction safety, and it has been shown that a water jet pressure of about 30 MPa has a good impact on the coal rock breaking effect.

4.2.3. Damage Characteristics of Coal Rock Impacted by Different Wall Roughness

The roughness of the borehole wall is an important factor affecting the characteristics of water jets impacting coal rock. In the model, the jet pressure is 20MPa and the impact target distance is 70mm, By changing the value of wall roughness k_sep (equivalent sand grain roughness), the influence of wall roughness on coal and rock breaking characteristics of water jet was studied.

The wall roughness first affects the impact velocity of the jet. The jet velocity curve of the wall position under different roughness is drawn as shown in Figure 18. It can be seen that when the jet pressure and target distance are the same, with the increase in wall roughness, the wall velocity of the borehole gradually decreases. When the wall roughness is 0.1 mm, the peak wall velocity can reach 83.2 m/s. When the wall roughness increases to 50 mm, the peak velocity is only 17.5 m/s. This is because the existence of the wall roughness of the borehole will hinder the impact and flow of the water jet, and the movement of the water jet needs to continuously overcome the structure. Resistance, the kinetic energy of the fluid is continuously reduced, resulting in a reduction in velocity.

The damage characteristics of water jet impacting coal rock under different wall roughness as shown in Figure 19. It can be seen that under certain conditions of jet pressure and target distance, the damage and damage characteristics caused by water jet impact on boreholes with different wall roughnesses are similar, and the overall damage and damage degree remain at the same level. When the wall roughness is 0.1 mm, the damaged area in the center of the borehole is larger, and with the increase in roughness, the damaged area in the center gradually decreases. The larger the range, the larger the center damage range. As the roughness increases, the bulge of the wall structure hinders the movement of the jet and generates energy consumption, resulting in a smaller damaged area.

Figure 20 shows the damage curve of the borehole wall and the peak damage data under different roughness. It can be seen that the main damage area of the entire borehole wall is concentrated at the center of the jet, and the smaller the wall roughness, the more obvious this effect is. Under the conditions of constant pressure and target distance, the central damage caused by water jet impact takes the roughness of 10 mm as the dividing point. When the wall roughness is less than 10 mm, with the increase in roughness, the water jet impact damage gradually decreases. When the wall roughness is greater than 10 mm, the water jet impact damage value increases with the increase in roughness.

The water jet impacts the borehole wall with a certain roughness. During the impact process, on the one hand, the wall roughness will hinder the fluid movement and reduce the impact of the jet, resulting in less impact damage. On the other hand, the borehole wall has a certain roughness, the impact of the jet will promote the development and connection of cracks, resulting in an increase in the damage value. When the wall roughness is less than 10 mm, the blocking effect is dominant, resulting in a negative correlation between the damage size and the roughness. When the wall roughness exceeds 10 mm, the development of cracks and the connecting effect exceeds the blocking effect, resulting in a larger damage size.

5. Conclusions

This study analyzed the characteristics of the impact of the drilling water jet on breaking coal rock and carried out numerical simulation and experimental verification. On the basis of the feasible simulation method, the impact factors of the drilling water jet impact were studied, and the simulation analysis was carried out for different jet target distances and different jet pressures. The following major conclusions were drawn:

(1)

The phase-field model of the fracture variation method is used to calculate the phase-field variable $\varphi$ through the strain energy density and critical energy release rate, which can effectively indicate the damage and destruction of the coal rock, and the method is shown to be feasible through simulation and experiments. As for water jet impact, the test block must continuously overcome the stress in the coal rock, and the damage degree is positively related to the jet pressure.

(2)

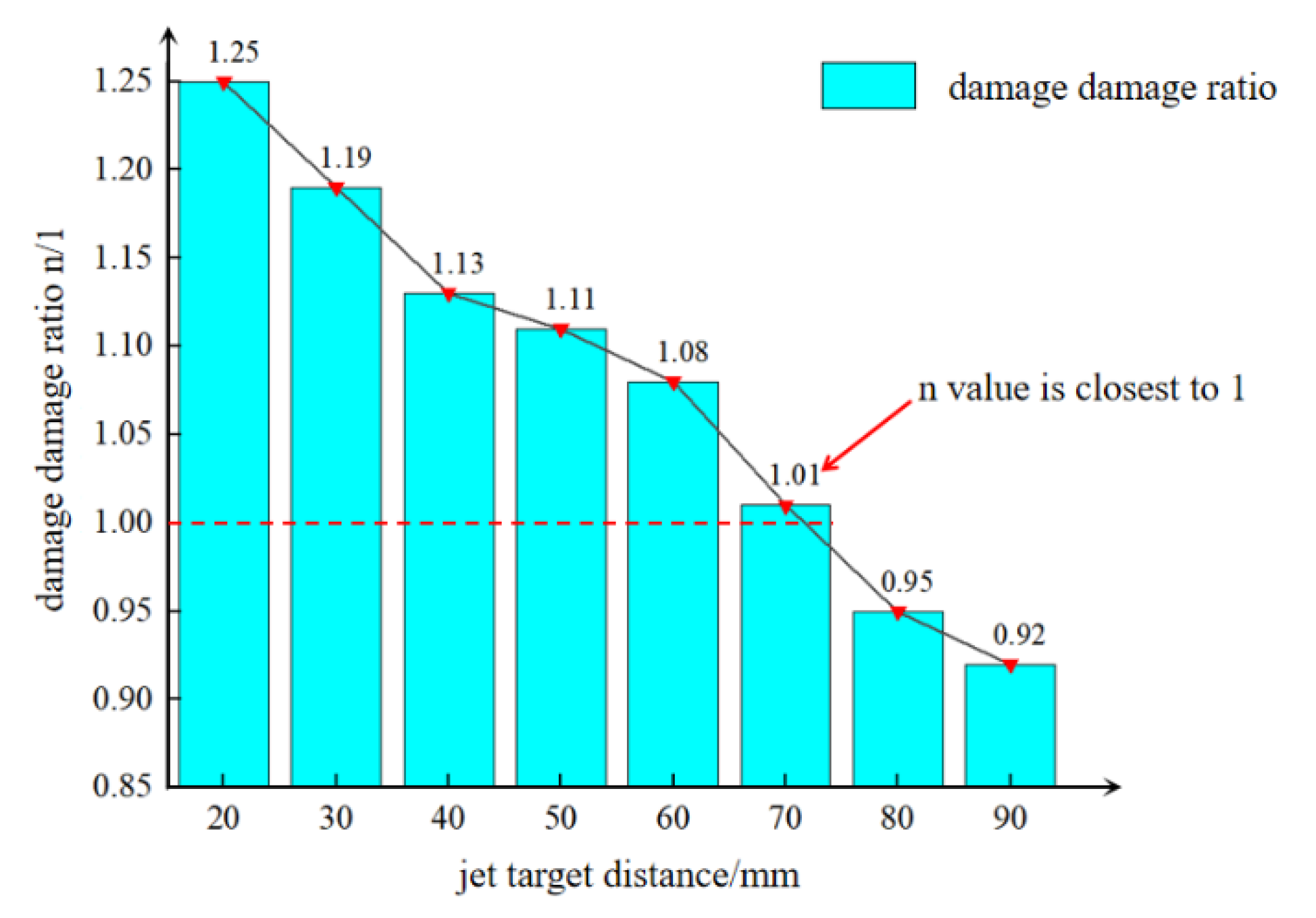
The impact of the water jet in the borehole will form a central damage destruction zone and two-side damage failure zone. The damage failure ratio n is proposed to characterize the damage degree of coal rock. When n < 1, the two-side damage threshold is greater than the damage threshold at the center. In addition, when the jet target distance is 70 mm, then the damage failure ratio n is closest to 1, and the water jet has the best impact on breaking the coal rock.

(3)

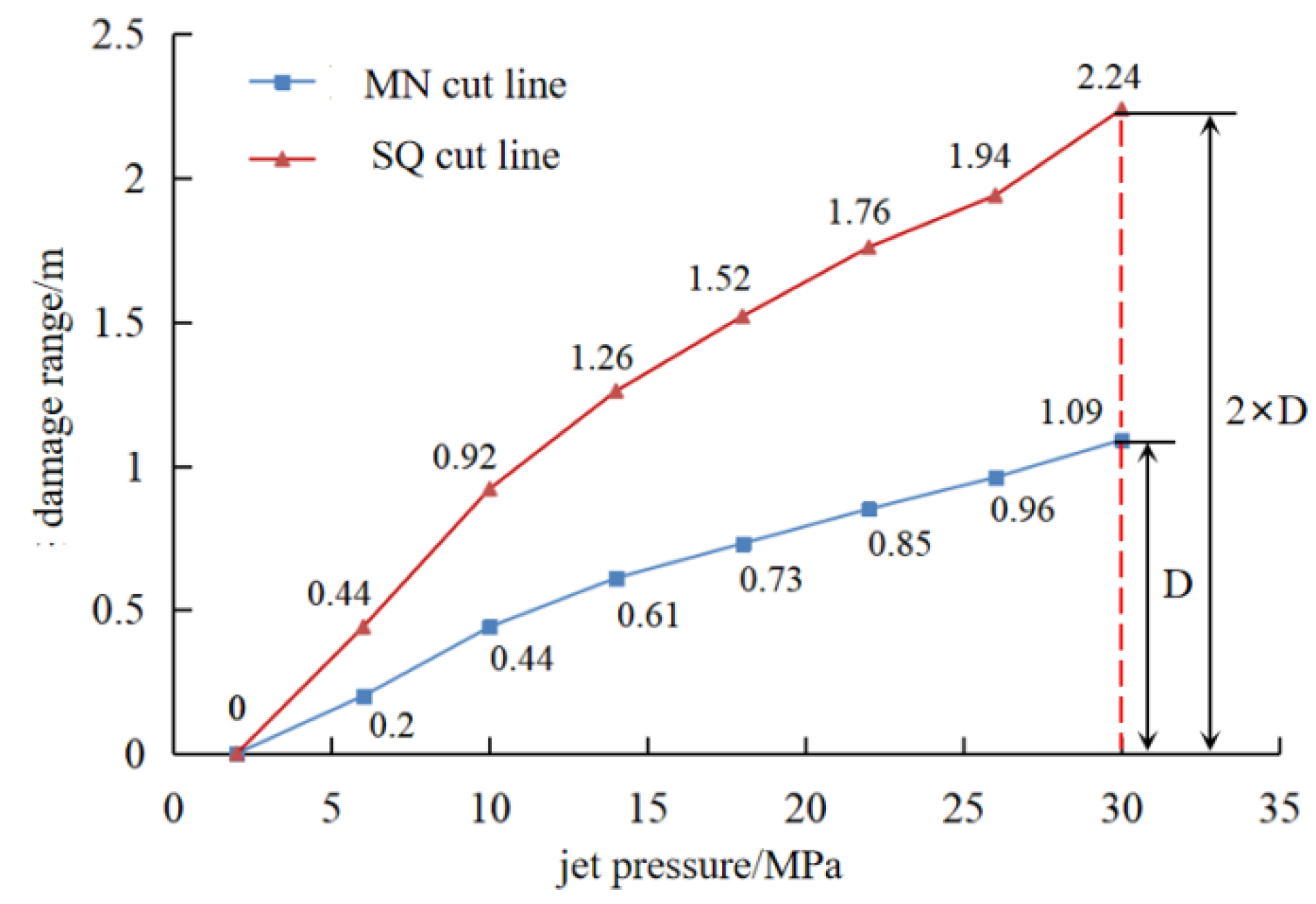
The effect of the water jet impacting the coal rock is positively correlated with the jet pressure. When the jet target distance is 70 mm, then the jet pressure of 30 MPa affects the center and both sides of the coal rock. The damage range of the body reaches approximately 1.1 m. In order to achieve a better effect of drilling water jet impacting coal rock, the jet pressure must be increased under the condition of ensuring construction safety, and the jet pressure of 30 MPa has a good impact and coal rock breaking effect.

(4)

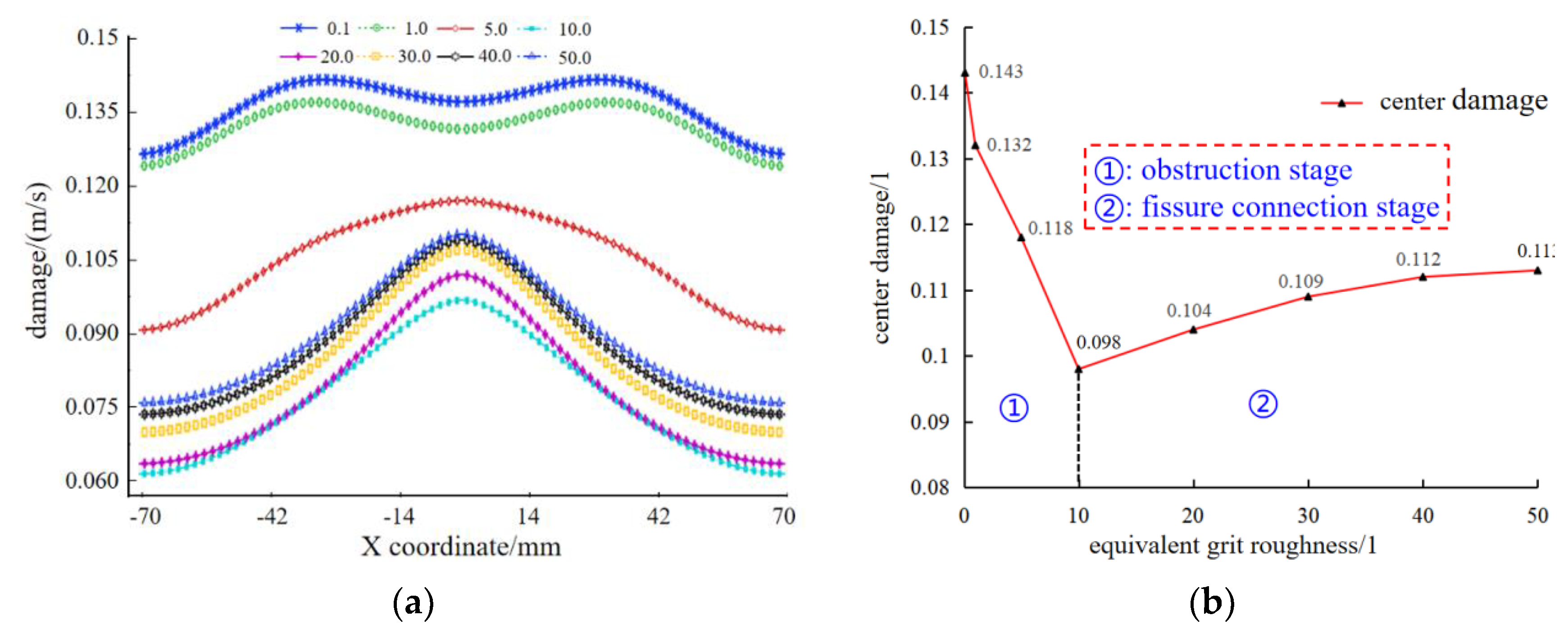
When a water jet impinges on the wall with roughness, there are two effects: the effect of hindering fluid movement and the effect of promoting fracture connectivity. When the wall roughness is less than 10 mm, the blocking effect is dominant, resulting in a negative correlation between the damage size and the roughness. When the wall roughness exceeds 10 mm, the development of cracks and the connecting effect exceeds the blocking effect, resulting in larger damage.