Modeling the Car-Following Behavior with Consideration of Driver, Vehicle, and Environment Factors: A Historical Review

Abstract

Car-following behavior is the result of the interaction of various elements in the specific driver-vehicle-environment aggregation. Under the intelligent and connected condition, the information perception ability of vehicles has been significantly enhanced, and abundant information about the driver-vehicle-environment factors can be obtained and utilized to study car-following behavior. Therefore, it is necessary to comprehensively take into account the driver-vehicle-environment factors when modeling car-following behavior under intelligent and connected conditions. While there are a considerable number of achievements in research on car-following behavior, a car-following model with comprehensive consideration of driver-vehicle-environment factors is still absent. To address this gap, the literature with a focus on car-following behavior research with consideration of the driver, vehicle, or environment were reviewed, the contributions and limitations of the previous studies were analyzed, and the future exploration needs and prospects were discussed in this paper. The results can help understand car-following behavior and the traffic flow characteristics affected by various factors and provide a reference for the development of traffic flow theory towards smart transportation systems and intelligent and connected driving.

1. Introduction

Car following refers to the vehicle behavior of maintaining the current lane and following its preceding vehicle(s). Modeling car-following behavior involves the longitudinal motion of vehicles in the lane, which is one of the core parts of traffic flow theory. The research on car-following behavior goes back nearly 70 years and covers hundreds of models; it is based on various theories, and different perspectives have been constructed in the developing process. According to the modeling idea, these models can be divided into six types: stimulus-response models, safety distance models, physiology-psychology models, artificial intelligence models, optimal velocity models, and intelligent driving models [1,2,3,4,5]. Among them, the representative models’ developing process is shown in Figure 1.

The models listed in Figure 1 are the cornerstone of the research on car-following behavior; they are referred to as “traditional models” in this paper. In early exploration, the car-following behavior research system was formed based on the traditional models and their extended (improved) models. However, there are many defects in these models, which are mainly reflected in that the set assumptions in the modeling process are too ideal. For instance, all vehicles and their drivers are homogeneous or the road (weather) conditions are perfect. These ideal assumptions cause the traditional models, along with their extended or improved models, to show poor performance when describing car-following behavior and the traffic flow characteristics, which are formed by the car-following behavior of vehicles in the traffic system in real, complex scenarios.

Figure 1. Development process of traditional car-following models.

Figure 1. Development process of traditional car-following models.

With the deepening of research, it has been found that the vehicle and its driver, as a whole unit, will present different characteristics of car-following behavior in various driver-vehicle-environment aggregations. It is necessary to carry out in-depth exploration of car-following behavior as affected by various driver, vehicle, and environment factors and to further study the traffic flow under different conditions. On the other side, intelligent and connected technology has been rapidly developing in the last few years. Supported by intelligent and connected technology, the transportation system is expected to be safer, more efficient, and more environmentally friendly, which is vital to the sustainability of our society. With the help of the applications of intelligent and connected technologies, represented by vehicle-to-everything (V2X) technology, the vehicle’s information perception ability has been significantly enhanced. Based on this, abundant information about factors in the driver-vehicle-environment aggregation can be obtained and utilized by the vehicle–driver unit in the car-following process. Thus, the comprehensive consideration of driver, vehicle, and environment factors is indispensable when modeling car-following behavior under the intelligent and connected condition. However, up to now, car-following models with comprehensive consideration of driver-vehicle-environment factors are still absent. A review is a very helpful tool to summarize the current research situation and discuss future study needs. There are several reviews of research on car-following behavior.

Helbing [6] reviewed the studies of car-following behavior and corresponding traffic flow based on the statistical physics and nonlinear dynamics methods. Chumsamutr and Fujioka [7] reviewed the previous car-following models used in simulation software to evaluate the vehicle longitudinal control system. In their review [8], Nagel et al. focused on the research on the nonlinear and phase transition characteristics of traffic flow. Kerner [9] reviewed the research on traffic flow characteristics under various penetration percentages of Autonomous Vehicles (AVs) using three-phase traffic theory and simulation. Kiran and Verm [10] reviewed the studies on the car-following behavior under the condition of mixed traffic composed of various types of vehicles. In the review [11], Li et al. focused on the research on the methods to calibrate parameters in car-following models. Datasets are vital for calibration. The methods to collect car-following trajectory data were reviewed by Shariff et al. [12]. Amini et al. [13] reviewed research on car-following behavior when vehicles interact with pedestrians. Do et al. [14] reviewed the studies on autonomous or connected vehicles’ car-following behavior and discussed the performance of the Intelligent Driver (ID) model and MICroscopic Model for Simulation of Intelligent Cruise Control (MIXIC) when describing the car-following behavior of such vehicles. Ahmed et al. [15] reviewed the car-following behavior models used to describe manual and autonomous vehicles in simulation software. In the same period, Al-Turki et al. [16] reviewed the research on traffic flow characteristics under different penetration percentages of AVs based on car-following behavior. Biswas et al. [17] reviewed the research on headway, a key indicator to describe car-following behavior.

These reviews contribute substantially to the research. Among the reviews, [7] involved the driver factor, and [9,10,14,15,16] involved the vehicle factor. To be specific, [9,14,15,16] reviewed the research involving intelligent and connected technology. However, these works are limited to AVs along with their impacts on traffic flow. To summarize, reviews that cover the driver, vehicle, and environment remain absent.

In this paper, the previous studies on car-following behavior with consideration of driver, vehicle, or environment factors from the perspectives of drivers’ external heterogeneity, driver’s internal heterogeneity, vehicle type, vehicle sort, road conditions, and weather conditions were reviewed; the shortcomings of previous works were summarized, and the further exploration prospects were discussed to provide a reference for the research on car-following behavior and traffic flow towards intelligent and connected driving and the new-generation smart transportation system. The paper is organized as follows: Section 2 includes a review of previous research; Section 3 contains a discussion of the shortcomings of previous research and the prospects of future exploration; and Section 4 contains the conclusion.

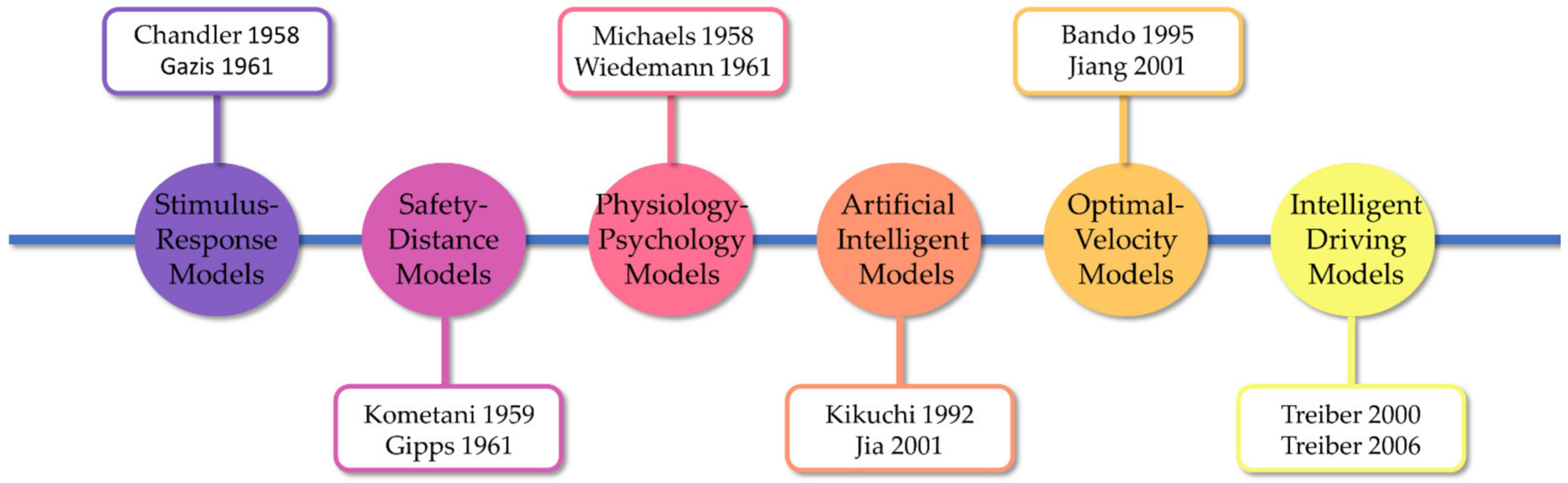
2. Literature Review

2.1. Driver

The impact of driver attributes cannot be ignored when modeling car-following behavior. However, these impacts are not comprehensively considered in the traditional car-following models. In these models, drivers in the system are assumed to be homogeneous, which is inconsistent with reality. Due to the differences in the driving experience, mental state, character, and other sociological characteristics, drivers will present different car-following characteristics. On the one hand, the car-following behavior of various drivers may be different under the same conditions (this is defined as “external heterogeneity” in this paper). On the other hand, the car-following behavior of the same driver could be different under the same conditions at different times (this is defined as “internal heterogeneity” in this paper).

2.1.1. External Heterogeneity

External heterogeneity describes the differences in the car-following behavior of different drivers. There are significant differences in car-following behavior among various drivers. These differences not only affect the motion state of vehicles at the micro level but also are the main factor affecting the nonlinear characteristics of traffic flow at the macro level [18]. These effects can be detected in the field data. According to this, many scholars have analyzed drivers’ external heterogeneity from the empirical analysis perspective. Brackstone et al. discussed the impacts of drivers’ characteristics on time headway in the car-following state [19]. The results reveal that the correlation between headway and driver age is the strongest one when following at high velocity. Ossen and Hoogendoorn first recognized drivers’ external heterogeneity along with its influence on micro and macro levels as pointed out in [18] from field data [20]. Later, other scholars analyzed and discussed the impact of driver heterogeneity on car-following behavior and even traffic flow operation characteristics based on different datasets. In recent years, with the development of mobile and high-performance computing technology, real vehicle driving experimental systems based on multi-sensor arrays and high-fidelity virtual driving systems are increasingly used in the research on car-following behavior, especially in the exploration of heterogeneity. Doroudgar et al. [21] analyzed the differences in car-following behavior between young and older drivers in terms of reaction time based on virtual driving experiments. The results suggest that the older drivers have a longer reaction time, have poorer ability to maintain headway, and maintain lower velocity (the distribution of velocity is more concentrated). Qi et al. [22] discussed the differences in discomfort degree in various scenarios between drivers using actual vehicle driving experiments and proposed a recognition model for this discomfort degree. The results reveal that the discomfort degree can be employed as the feature to identify the driver. Based on the extended curve Full Velocity Difference (FVD) model [23], An et al. [24] further introduced a reaction time item with a delay parameter to describe the differences in reacting to the same situation among drivers with different driving experiences and constructed a curve FVD model with consideration of driver heterogeneity. Later, the differences in the car-following characteristics of drivers with diverse cultural backgrounds were discussed by Cheng et al. [25] based on virtual driving experiments.

The above works are mainly based on the data collected from actual or virtual driving experiments. As another research emphasis, modeling the car-following behavior with consideration of external heterogeneity begins with incorporating the differences in time delay. As pointed out in [26], the time delay should be considered when modeling the car-following behavior. The reaction time mainly contains two parts: the cognition delay and the reaction delay. According to this, Meng et al. [27] introduced two probability parameters that adopted logarithmic normal distribution to describe the differences of various drivers in Perception–Response Time and constructed an extended Optimal Velocity (OV) model. Khodayari et al. [28] employed the data-driven method and constructed an Artificial Neural Network–based car-following model with consideration of the reaction delay. Due to the poor interpretation ability of data-driven methods, there is no explicit explanation of reaction delay in this Artificial Neural Network–based car-following model. Zheng et al. [29] proposed the instantaneous reaction delay model and combined this model with the multilayer feedforward network to establish a car-following model with consideration of the instantaneous reaction delay of diverse drivers. The results suggest that this model can better reproduce the nonlinear macro characteristic of traffic flow compared with the model without consideration of delay.

Drivers’ external heterogeneity is not only reflected in time delay but also in various aspects with different characteristics. It is difficult to analyze the car-following characteristics of each driver, one by one. However, there are certain rules that can be utilized. Some researchers divided drivers into several types and then analyzed the external heterogeneity of different types of drivers based on the division. Based on the car-following field trajectory data, Constantinescu et al. [30] proposed a model based on drivers’ risk preferences to identify the drivers’ type. Tang et al. [31] introduced a parameter $r$ to represent the driver’s type (aggressive, normal, and conservative type), rewrote the expression of the FVD model along with its optimal velocity function, proposed an extended model with consideration of drivers’ external heterogeneity, and analyzed the impacts of driver type on the characteristics of car-following behavior along with the energy consumption and exhaust emission. Wang et al. [32] introduced three new parameters to represent the three types of drivers, proposed an extended OV model, and derived the (non)linear characteristics of traffic flow. The results suggest that both aggressive and conservative drivers may contribute to traffic jams. Zhang et al. [33] introduced one parameter into the FVD model to describe the differences in velocity of three types of drivers to construct an extended model and discussed the impacts of the differences of three types of drivers on the desired velocity using the (non)linear characteristics of traffic flow. Based on Zhang’s model, Sun et al. [34] further incorporated the impacts of slope. To represent the differences in the ability to predict the changes in the traffic environment of the three types of drivers, Peng et al. [35] introduced two parameters into the FVD model and proposed an extended car-following model, named TAOVM. Later, Zhai and Wu [36] also proposed an extended FVD model, with consideration of driver types. Zhai and Wu’s model had a similar form to TAOVM. However, the introduced parameters represented different aspects. In Zhai and Wu’s model, the two parameters were employed to represent the differences in reaction delay to the changes in the traffic environment. The gray correlation analysis method was employed by Jiao et al. [37] to detect the correlation between the driver type and their optimal velocity. Based on the correlation analysis results, Jiao et al. improved the optimal velocity function and proposed an extended FVD model, named the RCF model. Based on the Big Five Factor model, Mian et al. [38] constructed a quantitative expression between driver type and parameters in the Intelligent Driver (ID) model and then proposed an extended ID model with consideration of drivers’ external heterogeneity. Based on the cluster analysis results of actual vehicle driving experimental data with 42 subjects, Zhou et al. [39] proposed a date-driven car-following model using the maximum entropy-based deep inverse reinforcement learning method.

The research results suggest that there are significant differences in car-following behavior among the different types of drivers. However, it was assumed in the frequently used traffic simulation programs and their embedded models that the drivers are the same, which leads to deviations in the simulation results at the micro and macro levels. Based on the analysis of highway car-following trajectory data, Ossen and Hoogendoorn [40] confirmed that the optimal car-following model is different for various drivers. To address this issue, Higgs et al. [41] detected that there are deviations between the simulation results and the field data of truck drivers’ car-following behavior and re-calibrated the parameters of the Wiedemann 74 model, which is at the core of the Vissim traffic flow simulation software. Utilizing the field data containing the three types of drivers, Soria et al. [42] re-calibrated the parameters in Gipps, Pitt, and MITSIM models and software. The results suggest that, of these three, the MITSIM has the best performance in describing the differences in car-following behavior of various types of drivers. Due to the avoidance of vehicle collision, the safe distance models, represented by the Gipps and Krauss models, are widely used as the vehicle longitudinal behavior control models in traffic simulation software. However, in the actual traffic system, not all drivers strictly abide by the safe car-following distance at all times. According to this, Tan et al. [43] proposed an extended safe distance car-following model, named ADM. Compared with the Krauss model, the safe distance in ADM consists of intervals rather than a constant, which better conforms to the car-following characteristics of human drivers. The above work effectively improves the ability of the simulation program to accurately reproduce the micro trajectory by further considering the heterogeneity outside the driver. The above achievements effectively improve the ability of the simulation program to accurately reproduce the micro trajectory by further considering the drivers’ external heterogeneity. In terms of the ability to reproduce macro traffic flow, previous studies have pointed out that driver heterogeneity is one of the causes of the “cavitation effect” in the free flow. However, in the previous works, the reproduction of the “cavitation effect” was carried out by adding noise in the car-following model. To address this, Makridis et al. [44] incorporated the impacts of vehicle dynamic characteristics and driver types into the Microsimulation Free-flow Acceleration (MFA) model. The results suggest that the extended MFA model can accurately describe the driver’s car-following behavior when the “cavitation effect” occurs.

2.1.2. Internal Heterogeneity

There are significant differences in car-following behavior among different drivers, which is defined as external heterogeneity. The car-following characteristics of the same driver under various conditions or even under the same condition will be different due to psychology, physiology, or physical influence, which is defined as internal heterogeneity. To explore the car-following behavior with consideration of internal heterogeneity, Hamdar et al. [45] incorporated the internal heterogeneity in the aspect of collision risk cognition and proposed a prospect theory-based car-following model. Zhu et al. [46] introduced two delay items, proposed an extended Newell model, and discussed the impacts of changes in the delay of the same driver on car-following behavior and traffic flow. Yu et al. [47] further discussed the impacts of drivers’ delay on the propagation and evolution of density waves. Utilizing the field data collected from a highway in Holland, Wang et al. [48] re-calibrated the Helly, Gipps, and ID models and, based on this, discussed the internal heterogeneity in reaction intensity during acceleration/deceleration. Under the condition of restricting lane-changing, traffic flow turbulence still occurs. Laval et al. [49] assumed that this phenomenon may be caused by the internal heterogeneity in the desired velocity; the authors added noise of the desired velocity into the Newell model and successfully reproduced the phenomenon. Saifuzzaman et al. [50] utilized the Task Capability Interface (TCI) to describe the correlation between the driving task requirements and driving ability, further incorporated this TCI-based model into the Gipps and ID models, and calibrated these extended models with virtual driving data. Later, Pekkanen et al. [51] confirmed that the TCI-based model can express the driver’s internal heterogeneity using virtual driving experiments. Based on the statistical analysis of car-following trajectory data collected from a highway, Huang et al. [52] identified the internal heterogeneity in car-following behavior. Based on this, Huang et al. [53] proposed an extended two-dimension ID model. Lindorfer et al. incorporated the time-varying reaction time affected by various scenarios into the ID and HD models and further modeled the errors in car-following behavior. The results suggest that there are errors in the driver’s cognition of headway, relative velocity, and acceleration, and these errors are not constant. Ou et al. [54] further utilized a random parameter subject to normal distribution to express the driver’s cognition errors of headway, relative velocity, and acceleration and constructed an extended FVD model. To address the driver’s cognition errors at different times, Ngoduy et al. [55] assumed that these errors will eventually present in adopted acceleration; they employed the Cox-Ingersoll-Ross model to describe the randomness in car-following behavior caused by cognition errors and proposed a Cox-Ingersoll-Ross–based car-following model. To address the impacts of the driver’s subjective state on car-following behavior, Paschalidis et al. [56] introduced a latent variable with consideration of the driver’s sociological characteristics into the stimulus-response framework, proposed an extended GM model, and calibrated the proposed model with virtual driving datasets that contained stress physiological data. The results reveal the significant impacts of a driver’s stress state on car-following behavior. Zhang et al. [57] incorporated the impacts of risk cognition, acceleration habits, and reaction characteristics on car-following behavior, proposed an extended Desired Safety Margin (DSM) car-following model, and calibrated the proposed model with the NGSIM dataset. The results suggest that the model with consideration of drivers’ internal heterogeneity can reproduce the density wave in traffic flow. With consideration of the differences in reaction time of the same driver at different times or under various conditions, Xie et al. [58] established a data-driven car-following model based on the Generative Adversarial Network (GAN). The results reveal that this GAN-based model can accurately describe the car-following behavior of the driver under the fatigue state.

It has been confirmed in the aforementioned studies that there is external and internal heterogeneity among driver(s) that significantly affects the car-following behavior at the micro level and the traffic flow at the macro level.

2.2. Vehicle

The vehicle is the specific tool for the driver to execute their car-following behavior. Due to this, the physical and dynamic characteristics of vehicles will affect the driver’s car-following behavior. First, when deciding which car-following behavior to take, the driver will consider whether the physical and dynamic characteristics of the vehicle he/she drives can meet the requirements of the car-following behavior he/she wants to take and, according to this, adjust his/her car-following behavior. For instance, when driving a heavy vehicle, considering the acceleration and deceleration performance, the driver will adopt relatively low speed and acceleration and relatively large headway to match the performance of the vehicle he/she is driving. Second, in addition to the vehicles driven, the physical and dynamic characteristics of other vehicles, especially the preceding vehicle, will also affect the driver’s car-following behavior. For example, when following a heavy vehicle rather than a normal vehicle, the driver will adopt relatively large headway and low speed. Third, with the development of intelligent vehicles, assisted driving, including automatic driving systems such as Adaptive Cruise Control (ACC) and Cooperative Adaptive Cruise Control (CACC), is applied. Autonomous lane-keeping and car-following have been realized. Compared with the human driver, the vehicle will show different car-following characteristics when controlled by these automatic controllers. According to these three points, the previous studies on car-following behavior with consideration of vehicle factors are reviewed from two aspects: vehicle types (representing vehicles with different physical and dynamic characteristics) and vehicle sorts (representing vehicles equipped with automatic controllers or not).

2.2.1. Types

• Dividing vehicles with different types into various car-following combinations

It has been widely acknowledged in the field of traffic flow theory that when there are multiple types of vehicles driving in the same road segment, especially when there are heavy vehicles, the operating and stability characteristics of traffic flow at both the micro and macro level will be significantly affected. In the previous studies on car-following behavior with consideration of impacts of vehicle types, the approach of dividing the mixed flow into various car-following combinations was widely employed. For instance, when the subject vehicle is a car, and its preceding vehicle is a truck, this car-following combination is Truck-Car (i.e., T-C). Similarly, there are C-T, H-C (Heavy-Car), C-H, B-C (Bus-Car), C-B, B-H, and so on. This approach, dividing vehicles with different types into various car-following combinations, was first utilized in the research on car-following behavior by Peeta et al. [59] studying differences in car-following behavior of the subject vehicle between the H-C and C-C. The results reveal that the driver tends to take larger headway when the preceding vehicle is a heavy one rather than a car. After this, many researchers explored the car-following characteristics with consideration of various combinations. In the research on driver’s car-following characteristics in different combinations, Aghabayk et al. made a significant contribution. In [60,61], Aghabayk et al. analyzed the headway characteristics of various combinations. The results suggest that the headway reaches a maximum in the H-H and a minimum in the C-C, and the headway in C-H is larger than that in H-C when the velocity is lower than 30 km/h. In these two works, it was detected that there were also differences in the reaction time and acceleration of the subject vehicle’s driver in different combinations. Based on the local linear model tree method, Aghabayk et al. [62] established a data-driven car-following model considering the impacts of vehicle type and trained this model with the utilization of the NGSIM dataset. The results suggest that the consideration of the vehicle type’s influence can improve the accuracy of the proposed model in describing the car-following behavior. Later, Aghabayk et al. [63] summarized their works along with other achievements in research on car-following behavior that considered the vehicle type’s impact. In [64], Aghabayk et al. further explored the impacts of heavy vehicles and their proportion on car-following behavior and traffic flow and, based on this, proposed a new car-following model, which is similar to the Wiedemann model. The results reveal that the perception threshold and action point vary with the self-vehicle’s and the preceding vehicle’s type, and the car-following behavior and traffic flow will be significantly affected by the penetration of heavy vehicles in the traffic system along with their proportion., Mathew et al. [65] studied the car-following behavior characteristics of the subject vehicle in C-C, C-H, H-C, and H-H combinations and the performance of several traditional car-following models when describing the car-following behavior under such conditions. The results confirmed that the traditional car-following models, without consideration of the vehicle type’s impacts, cannot achieve high performance, and the Gipps and Krauss models have better performance among these models. Using the NGSIM dataset and another dataset collected in Mumbai (India), Ravishankar et al. [66] re-calibrated the Gipps model to describe the subject vehicle’s car-following behavior in various combinations. The results reveal that the re-calibrated model can fit the car-following behavior and estimate the traffic flow volume with higher accuracy. Sarvi et al. [67] analyzed the headway in various combinations and discussed the car-following characteristics of a heavy vehicle compared with a normal vehicle using the field data collected from Tokyo (Japan) and Melbourne (Australia). The results revealed that when a car follows a heavy vehicle, it will adopt larger (time) headway, and when the preceding vehicle’s type is the same, the heavy vehicle will adopt larger (time) headway than other types of vehicles. Additionally, the traffic-carrying capacity will decrease when there are heavy vehicles in the lane. Yang et al. [68] proposed an extended OV model, with consideration of various combinations (C-C, C-T, T-C, and T-T), and analyzed the impacts of these combinations and their proportion on the traffic flow stability. In previous studies, in which the stability of mixed traffic flow (composed of various types of vehicles) was analyzed, the approach of setting different stability parameters for each type of vehicle and then calculating the weighted average of these parameters was widely employed. However, this approach cannot express the differences in stability of mixed traffic flow with diverse specific compositions. To address this, Ngoduy et al. [69] derived the linear stability of mixed traffic flow with diverse specific composition based on the combinations of C-C, C-T, T-C, and T-T. Liu et al. [70] set different desired headways for the combinations of C-C, C-T, T-C, and T-T, proposed an extended ID model, calibrated the proposed model with the NGSIM dataset, and derived the corresponding traffic flow fundamental diagram model. It was pointed out by Liu et al. that the impacts of trucks on the car-following behavior and traffic flow may be opposite under different conditions of car-following combinations and equilibrium velocity. To be specific, trucks can both stabilize and destabilize the traffic flow, depending on the aforementioned conditions. To deal with the combinations of C-C, C-B, B-B, and B-C, Shen et al. [71] proposed an extended GM model with consideration of acceleration/deceleration ability of the subject vehicle and its preceding vehicle and calibrated the proposed model with the data collected from Nanjing (China). The results reveal that the penetration of buses in the traffic system will cause the uneven distribution of vehicles in the lane and the decline of traffic-carrying capacity. Kong et al. [72] utilized the NGSIM dataset to construct an extended CA model to address the combinations of C-C, C-T, T-C, and T-T. In the model, the difference in acceleration and stable-state headway between the combinations was considered, and the results suggest that the extended CA model can fit the car-following trajectory data with higher accuracy. Utilizing the data collected from two road segments in India, Raju et al. [73] analyzed the characteristics of mixed traffic flow in India, introduced the “lateral distance” into the combinations of C-C, C-T, T-C, and T-T, and re-calibrated the Wiedemann model in Vissim software.

2.

Direct consideration of vehicle type impacts

In addition to the abovementioned approach (dividing vehicles with different types into various car-following combinations), there is another approach widely used to explore car-following behavior with consideration of vehicle type. In this approach, the car is set as the normal vehicle, and the truck, bus, heavy vehicle, and other types of vehicles are set as the non-normal vehicle. Based on this, the car-following model can be constructed by incorporating the dynamic and behavior characteristics of each type of vehicle. For instance, the specific power and deceleration ability of heavy vehicles are relatively lower than that of normal vehicles, and these dynamic characteristics will lead to differences in car-following and other driving behaviors. Considering this, Li et al. [74] proposed an improved car-following model based on the speed-dependent control gains, and the heavy vehicle’s dynamic characteristics were incorporated in this model. When the car-following model is regarded as an algorithm to control the longitudinal motion of the vehicle, the car-following process can be regarded as a typical Cyber Physical System (CPS). Based on this, Sun et al. [75] proposed a CPS-based extended car-following model and derived the stability conditions utilizing control theory. Based on the “discomfort level” proposed by Peeta et al. [59] to describe the impacts of trucks on car-following behavior, Zheng et al. [76] regraded the impacts of heavy preceding vehicles as a kind of uncomfortable visual stimulus and proposed an extended Visual Angle (VA) model, named the VIM model. The results suggest that the VIM model can better fit the field data when the preceding vehicle is a heavy one. In some traffic systems, the car-following combination is not limited to C, H, T, and B. For instance, in some cities (especially some European cities), vehicles have to share the road with trams and pedestrians. Most of the widely used traffic simulation software is not competent when simulating this kind of mixed traffic flow. To address this, Fujii et al. [77] constructed an agent-based mixed traffic flow framework. Considering that the preceding vehicle’s type and the driver’s own driving skills may make the driver adopt a different car-following strategy, Wang et al. [78] introduced a random coefficient of safe headway into the optimal velocity function and proposed an extended FVD model. The results suggest that this extended model can capture the traffic phenomenon and reproduce the stop-and-go wave, which is more likely to occur when there are heavy vehicles.

In the above studies, the car-following behavior was studied as affected by the type of vehicle from the perspective of theoretical analysis. In some studies, the car-following behavior as affected by the type of vehicle was discussed from the perspective of empirical analysis. The trajectory data containing the car-following behavior of various types of vehicles, such as mini, compact, medium, large, pickup, suburban utility, and heavy vehicles, were utilized by Rakha et al. to analyze the differences in desired velocity and acceleration of drivers when driving diverse types of vehicles [79]. Based on this, they re-calibrated the Gipps model to improve its performance when describing the car-following behavior as affected by the vehicle’s own type. Ossen and Hoogendoorn [20] employed aerial data to analyze the car-following characteristics of heavy vehicles. The results suggest that there is less randomness in the car-following behavior of heavy vehicles as compared with normal ones. Based on a questionnaire survey, Kong et al. [80] studied the changes in the car-following behavior of a car when the preceding vehicle is a truck compared with when it is also a car. The results suggest that the penetration of trucks in the traffic system will cause the decline of traffic flow volume along with the velocity, and these negative impacts will be enhanced with the increase of the trucks’ proportions. Aiming at the special mixed traffic flow in India, where diverse vehicles are of very different size and dynamics and lane discipline is usually ignored, Asaithambi et al. [81] tested five traditional car-following models’ performance when describing this kind of traffic flow. Nagahama et al. [82] utilized the decision tree method to analyze the field data and discussed the car-following characteristics of motorcycles, cars, and trucks in three car-following states: accelerating, stable following, and decelerating. The results reveal that there are differences in many indexes, such as acceleration, relative velocity, and headway, of car-following behavior in the aforementioned processes. It was also confirmed that the performance of the traditional car-following models to describe the car-following behavior of various types of vehicles can be improved to a satisfactory level by introducing new parameters that express the impacts of vehicle types. The identification of the preceding vehicle’s type is the basis of modeling car-following behavior with consideration of the vehicle’s type. Aiming at this, Wu et al. [83] proposed a hidden Markov-based method to identify the preceding vehicle’s type and, based on this, constructed a Gaussian mixture-based data-driven car-following behavior.

As pointed out in [5], the car-following models are the theoretical basis of many applications, such as energy consumption and exhaust emission estimation. However, the performance of the previous estimation method is unsatisfactory when describing a vehicle of abnormal type. To address this, Cattin et al. [84] adopted energy consumption estimation as one of the optimization objectives and proposed a car-following model calibration method based on a multi-objective particle swarm optimization algorithm. The results suggest that the Gipps model calibrated by this method can accurately estimate the fuel consumption of trucks in the car-following process.

2.2.2. Sorts

With the development of intelligent vehicles, a new sort of vehicles equipped with automatic controllers is now part of the traffic system. Up to now, the car-following characteristics of automatic controllers have been significantly different from that of human drivers. Thus, the vehicles equipped with automatic controllers should be regarded as a new sort, to distinguish them from manual vehicles (MVs) when modeling car-following behavior. Recently, the research on traffic flow composed of this new sort of vehicles and MVs has become the frontier and a hot topic in the field of traffic flow theory. Zhu et al. [85] employed basic and extended OV models to respectively describe the car-following behavior of the manual and new sort of vehicles and analyzed the impacts of sensitivity, the smooth factor, and new vehicles’ penetration rate on traffic flow. The results suggest that the traffic flow volume is positively related to the above three parameters before the critical point and negatively related to them after this point. Based on the model proposed in [86] to describe the car-following behavior of vehicles equipped with CACC systems, Qin et al. [87,88] derived the platoon stability of the new sort of vehicles and MVs utilizing the transfer function method. The results suggest that by altering the feedback coefficient, the platoon may reach the ideal stability condition, that is, the platoon can maintain a stable state under any condition. Seraj et al. [89] respectively employed the basic FVD model and an extended FVD model to describe the car-following behavior of connected automatic vehicles (CAVs) and MVs to construct a control strategy for the mixed platoon. The results reveal that adopting a small headway for each vehicle and a large total length for the platoon can improve the efficiency but damage the safety. Yao et al. [90] adopted the basic FVD model and PATH model, proposed in [91,92], to respectively describe the car-following behavior of CAVs and MVs and, based on this, constructed the analysis method for the stability and fundamental diagram of traffic flow composed of CAVs and MVs. Based on the perspective of the mass-spring-damper system, Jiang et al. [93] established a new concept car-following model for the mixed platoon. In this model, the errors of headway and velocity were set as the “total energy” of the system, and based on this, car-following safety constraints were constructed. Zhou et al. [94] adopted the approach to divide the mixed platoon into several sub-platoons, defined the system stability as equal to the stability of all sub-platoons, and proposed a distributed frequency domain-based car-following control method. Based on the FVD model, An et al. [95] constructed an improved model by incorporating the stable car-following state. In this model, when the relative velocity is higher than the preset threshold, vehicles’ velocity is controlled by the FVD model, and when the relative velocity is lower than the preset threshold, vehicles’ velocity is controlled by the extended FVD model. The results also suggest that the traffic flow volume is positively related to the above three parameters before the critical point and negatively related to them after this point, which is consistent with [85]. Utilizing the inverse reinforcement learning method, Ozkan et al. [96] proposed a data-driven car-following model based on the approach of dividing vehicles with different sorts into various car-following combinations. Yao et al. [97] employed the ID, ACC, and CACC models (the latter two were also proposed in [91,92]) to respectively describe the car-following behavior of manual, automatic, and connected and automatic vehicles and discussed the energy consumption and exhaust emission characteristics of the platoon with different proportions of the three sorts of vehicles or in the situation that the CACC-equipped CAV degenerates into an automatic vehicle. By introducing the nonlinear dynamic desired time headway to replace the time headway of the PATH model, which is linearly related to the velocity, Cao et al. [98] proposed an extended PATH model, employed this model and the ID model to respectively describe the car-following behavior of CAVs and MVs and discussed the traffic flow characteristics, including maximum volume, optimal density, and critical velocity, with different proportions of CAVs based on numerical simulation.

2.3. Environment

The research on car-following behavior cannot ignore the specific environment in which the object vehicle is located. There are differences in the car-following behavior when the vehicle is in various kinds of environments. In the traditional car-following models, the environmental factors are assumed to be ideal. To be specific, the road and weather conditions are assumed to be consistently good, and slope, curvature, or snow do not exist. These unrealistic assumptions lead to those models showing poor performance when used to describe the car-following behavior in realistic, complex traffic scenarios. To address this, studies on car-following behavior with consideration of environmental factors’ impacts have been carried out.

2.3.1. Road

• Road condition

Different from the traffic conditions that indicate traffic congestion on the road, road conditions are the technical conditions of the main body, surface, structure, and accessories of the road. In traffic flow theory, a good road condition is regarded as the normal road condition. According to driving experiences, when the road condition deviates from the normal condition, the car-following behavior will be affected and show different characteristics. Therefore, in the research on car-following behavior, the road condition refers to the damage to road surface or other components. Based on this, the characteristics of car-following behavior and traffic flow affected by road condition can be explored. The impacts of road conditions were considered in the study of car-following behavior for the first time by Delitala and Tosin in 2007 [99]. In this work, a dual-value parameter $\alpha$ was introduced to represent whether the road condition is good or bad, and a discrete velocity model based on the discrete dynamics and stochastic game theory was proposed. Soon after, the hyperbolic asymptotic limit of the model proposed in [99] was derived by Bellouquid and Delitala to obtain the corresponding macro traffic flow model [100]. In these two works, only two extreme road conditions, good or bad, were considered, and the equilibrium velocity of traffic flow when the road condition is bad was assumed to be zero, which is inconsistent with reality. To address this, further explorations were carried out. Tang et al. [101] proposed an extended FVD model to take into account the road conditions. In this model, a continuous function was constructed to represent various road conditions, from the worst to the best, and an adjustment item was constructed to represent the ability of a driver to adjust the car-following behavior according to the road conditions. Based on [101], Tang et al. [102] derived the corresponding macro traffic flow model. In [101,102], various road conditions, from the worst to the best, were considered and assumed to be stationary. However, the road condition is time-varying because of the vehicle’s movement. To deal with this, Tang et al. [103] introduced a random item $R$ to represent the road condition at the position and a certain range in front of where the vehicle was at the time $t$ and proposed an extended FVD model to take into account the real-time road condition. The items employed in previous studies to express the road condition and their explanation can be found in

Table 1. Items employed in previous studies to express the road condition and their explanation.

Literature	Item	Property	Explanation
Delitala and Tosin, 2007 [99]	$\alpha$	Dual-value parameter	$\alpha =+1$$\mathrm{means} \mathrm{the} \mathrm{road} \mathrm{condition} \mathrm{is} \mathrm{the} \mathrm{best} \mathrm{and} \alpha =-1$ means the road condition is the worst.
Tang et al. [101,102]	$g\left(x\right)$	Continuous function	$g\left(x\right)$$\mathrm{represents} \mathrm{the} \mathrm{road} \mathrm{condition} \mathrm{from} \mathrm{the} \mathrm{worst} \mathrm{to} \mathrm{the} \mathrm{best} \mathrm{in} \mathrm{its} \mathrm{value} \mathrm{range} \left[-1,1\right]$.
Tang et al. [103]	$R$	Random item	$R$$\mathrm{represents} \mathrm{the} \mathrm{road} \mathrm{condition} \mathrm{at} \mathrm{time} t$$\mathrm{and} \mathrm{vehicle} \mathrm{position} x$$\mathrm{in} \mathrm{its} \mathrm{value} \mathrm{range} \left[-1,1\right]$.

.

The results of the above research suggest that there are impacts of road condition on traffic flow at both the micro and macro levels.

(1)

Micro level. The vehicle’s acceleration/deceleration/velocity/headway/energy consumption/exhaust emissions in the starting, driving, and braking process are all affected by the road conditions. Specifically, the lasting time will enlarge, and the velocity along with acceleration/deceleration will decline in the starting and braking process. There will be a disturbance in the velocity and headway in the driving process, which will cause an increase of energy consumption and exhaust emissions.

(2)

Macro level. The stability of traffic flow will be enhanced, and the shock wave will be alleviated when the road condition is good. It is noteworthy that there are negative impacts of good road condition on stability when the traffic flow is evaluated for the stop-and-go state.

Although there are impacts of road condition on traffic flow at both the micro and macro levels, the road condition is one of several factors that will affect the car-following behavior. However, there are few studies that analyze car-following behavior as affected by the road condition and other factors. To address this shortcoming, Gao et al. [104] proposed an extended car-following model and derived the corresponding macro flow model to analyze the car-following behavior and traffic flow affected by the road condition and the traffic break that happens in the adjacent lane.

2.

Slope

On a road with slope, there will be a tendency for the vehicle to move towards a lower position due to gravity, and the driver will take measures to counteract this tendency to maintain a safe and desired driving state. To be specific, the vehicle needs to output more power to reach the same acceleration when going uphill than on a flat road, and the vehicle needs to output more brake force to reach the same deceleration when going downhill. These impacts of gravity will also make the driver correspondingly adjust the headway in the car-following process. Li et al. [105] first analyzed the maximum velocity and safety headway when car-following on roads with different slopes. In this work, Li et al. summarized a general expression of the optimal velocity function to describe the relationship between the optimal velocity function and position, slope, and safety headway. Based on this, Li et al. [106] proposed an extended OV model and analyzed the traffic flow utilizing numerical simulation. Different from the approaches that Li used to form the general expression of the optimal velocity function by analyzing the driver’s behavior characteristics, Komada et al. [107] proposed an extended OV model based on the force analysis of vehicles on roads with slope. The main deriving steps in [107] are as follows:

Step 1: Based on the well-known kinematic formula, one can obtain the force analysis equation of the vehicle on the road with slope:

$$m\frac{{\mathrm{d}}^2{x}_i(t)}{\mathrm{d}{t}^2}=F\left(\Delta x_i\right)-\gamma \frac{\mathrm{d}{x}_i(t)}{\mathrm{d}t}-mg\sin \theta B\left(\Delta x_i\right)$$

(1)

Step 2: Assuming that the driving force and break control are the functions of headway (when $\Delta x_i\to 0$, the vehicle will stop, i.e., the break control $B\left(\Delta x_i\right)\to 0$; when $\Delta x_i\to \infty$, the efforts of gravity on the vehicle are $mg\sin \theta$), Equation (1) can be rewritten as

$$\frac{{\mathrm{d}}^2{x}_i(t)}{\mathrm{d}{t}^2}=\frac{\gamma }{m}\left\{V\left(\Delta x_i\right)-\frac{\mathrm{d}{x}_i(t)}{\mathrm{d}t}\right\}$$

(2)

$$V\left(\Delta x_i\right)=\frac{F\left(\Delta x_i\right)-mg\sin \theta B\left(\Delta x_i\right)}{\gamma }$$

(3)

where $V\left(\Delta x_i\right)=\frac{F\left(\Delta x_i\right)-mg\sin \theta B\left(\Delta x_i\right)}{\gamma }$.

Step 3: Comparing the above two equations with the OV model, one can obtain

$$\frac{F\left(\Delta x_i\right)}{\gamma }=\frac{v_{f,\max }}{2}\left[\tanh \left(\Delta x_i-x_c\right)+\tanh \left(x_c\right)\right]$$

(4)

$$\frac{\gamma }{m}=a$$

(5)

Step 4: When $\Delta x_i\to \infty$, the efforts of gravity on the vehicle are a constant, which can derive

$$\frac{mg\sin \theta B\left(\Delta x_i\right)}{\gamma }=V_g\left(\Delta x_i\right)=\frac{v_{g,\max }}{2}\left[\tanh \left(\Delta x_i-x_b\right)+\tanh \left(x_b\right)\right]$$

(6)

Step 5: Based on the above equations, the slope OV model and its optimal velocity function can be obtained as

$$\frac{{\mathrm{d}}^2{x}_i(t)}{\mathrm{d}{t}^2}=a\left\{V\left(\Delta x_i\right)-\frac{\mathrm{d}{x}_i(t)}{\mathrm{d}t}\right\}$$

(7)

$$V\left(\Delta x_i\right)=\frac{v_{f,\max }}{2}\left[\tanh \left(\Delta x_i-x_c\right)+\tanh \left(x_c\right)\right]\hspace{1em}for no slope$$

(8)

$$V\left(\Delta x_i\right)=\frac{v_{f,\max }}{2}\left[\tanh \left(\Delta x_i-x_c\right)+\tanh \left(x_c\right)\right]-\frac{v_{g,up,\max }}{2}\left[\tanh \left(\Delta x_i-x_{up,b}\right)+\tanh \left(x_{up,b}\right)\right]\hspace{1em}for the uphill$$

(9)

$$V\left(\Delta x_i\right)=\frac{v_{f,\max }}{2}\left[\tanh \left(\Delta x_i-x_c\right)+\tanh \left(x_c\right)\right]+\frac{v_{g,down,\max }}{2}\left[\tanh \left(\Delta x_i-x_{down,b}\right)+\tanh \left(x_{down,b}\right)\right]\hspace{1em}for the downhill$$

(10)

The slope OV model has a similar structure to the basic OV model and two optimal velocity functions, which are suitable for the uphill and downhill. Based on this slope OV model, Komada et al. analyzed traffic flow with the help of numerical simulation and detected the congestion position on various slopes by adjusting the traffic flow density. However, theoretical analysis of the traffic flow on roads with slope is still absent. Aiming at this, Zhu and Yu [108] derived the neutral stability condition and the nonlinear characteristics near the critical point of the traffic flow based on Komada’s model. During the same period, Zhu and Yu [109] derived the Korteweg-de-Vries (KdV) equation and the solitary solutions in the metastable region based on Komada’s model. Soon after, Zhu [110] combined Komada’s model and the energy consumption and exhaust emission model proposed by Li et al. [106] to construct an energy consumption and exhaust emission estimation model for vehicles on roads with slope. Based on [108] and the energy consumption model for electric vehicles [111], Yang et al. [112] proposed an improved energy consumption model with consideration of the impacts of slopes and the kinetic energy recovery system. Two nondimensional parameters were introduced, which represent the impacts of fog on a driver’s misjudgment of the headway and the corresponding reduction of velocity, by Tan et al. into Komada’s model to form an extended model and to analyze car-following behavior as affected by the fog and slope [113]. Based on [108], Zhang et al. [114] further considered the two relative velocities (forward and backward), constructed an extended slope OV model, and derived the corresponding macro flow model.

The above works are all based on the OV model, which does not incorporate the relative velocity effect (the driver will not decelerate even if the headway is less than the safe value when the preceding vehicle is faster). The full velocity difference item in the FVD model can address this issue. Thus, Chen et al. [115] proposed the slope FVD model according to Komada’s approaches and derived the corresponding macro flow model. However, Chen et al. did not carry out nonlinear analysis of the traffic flow characteristics. According to this, Zhou et al. [116] derived the Burgers, KdV, and modified Korteweg-de-Vries equations (mKdV) of the slope FVD model. Based on Komada’s model and the proposed extended FVD model with consideration of dual lateral distance [117], Li et al. [118] proposed an extended FVD model to take into account the slope and dual lateral distance. In [118], the traffic flow characteristics in the non-lane-discipline-environment with a slope were analyzed. Based on the extended FVD model and considering the driver’s offensive characteristics [119], the slope FVD model [116], and the equation of vehicle movement and ETOA information [86], Jiao et al. [120] proposed a new extended slope FVD model considering a driver’s offensive characteristics and ETOA information and derived the corresponding macro flow model.

In addition to the above two series of studies, the OV-based and the FVD-based, there are several achievements that are based on other approaches to explore the characteristics of car-following behavior and traffic flow. Lan et al. [121] extended the LSK model [122] based on the force analysis and driving characteristics of the vehicle on roads with slope and formed a new slope CA model. The results suggest that the impacts of slope on traffic flow enhance with the increase of slope value. Based on the statistical analysis of NGSIM, Xu et al. [123] summarized drivers’ car-following characteristics when they are on roads with slope. The results reveal that the driver will operate the engine to output more power and to overcome the influence of gravity. For normal vehicles, the extra power will offset the impacts of gravity by about 50%; for heavy vehicles, the extra power will offset the impacts of gravity by only about 5%. These results point out that the influence of gravity on car-following behavior may be exaggerated, and this issue needs to be further studied with the help of a large-scale high-precision dataset. Moreover, the behavior that the driver operates the engine to output more power will cause extra energy consumption and exhaust emission, which is not considered in the previous studies on the characteristics of energy consumption and exhaust emission of vehicles on roads with slope.

To summarize, the aforementioned results suggest that there are significant impacts of gradient and length of the slope on the car-following behavior and traffic flow, which are represented in the aspects of acceleration/deceleration, headway, energy consumption, exhaust emission, volume, and density, and these impacts are related to the density of traffic flow.

3.

Curve

The curve refers to the section with a curvature on the road. When the vehicle is driving on a curve, on the one hand, the driver needs to adjust the direction to control the vehicle along the road curve; on the other hand, the velocity cannot be high due to the limitation of centrifugal force. The above-mentioned two points lead to the fact that the driving characteristics of vehicles on curves are different from those on straight roads. In 2010, Liang and Xue [124] first explored car-following behavior characteristics by constructing an extended CA model based on the force analysis of vehicles on the curve. In this work, it is assumed that the centripetal force required for the vehicle to safely turn is provided by the normal static friction force, and based on this, the maximum velocity for the vehicle to safely drive on the curve was derived. These relationships and limitation equations formed the basic theoretical system for modeling the car-following behavior of vehicles driving on curves. These vital equations are as follows:

$$s_n\left(t\right)=r·{\theta }_n\left(t\right)$$

(11)

$$\Delta s_n\left(t\right)=r·\Delta {\theta }_n\left(t\right)$$

(12)

$$m{\omega }_{\max }^{2}r=\mu mg$$

(13)

$${\omega }_{\max }=\sqrt{\frac{\mu g}{r}}$$

(14)

where $s_n\left(t\right)$ is the position of vehicle; ${\theta }_n\left(t\right)$ is radian; $r$ is radius; ${\omega }_{\max }$ is maximum angular velocity; $\mu$ is the friction coefficient; $m$ is the vehicle mass; and $g$ is the acceleration of gravity.

Based on the above equations, Zhang et al. [23] modified the vehicle motion parameters to be the curve geometric parameters, introduced reaction delay of the driver, and proposed the curve-extended FVD model. In the same period, Zhu and Zhang [125] modified the vehicle motion parameters in the OV model and its optimal velocity function to include the curve geometric parameters and constructed the extended curve OV model. Ref. [125] studied the impacts of curve curvature radius and friction coefficient on the maximum safety velocity and the stability of vehicles that are car-following at a curve with the utilization of numerical simulation and stability theoretical analysis. Soon after, based on the extended curve OV model, Zhu [126] derived a modified form of the energy consumption and exhaust emission estimation model, proposed in [127], to fit the application on vehicles that are car-following on a curve. The results suggest that the energy consumption is positively correlated with the curvature radius and friction coefficient of the curve. In [23], while the extended curve FVD model was proposed, the analysis of nonlinear characteristics of traffic flow near the critical point was absent. To address this, Jin et al. [128] derived the time-dependent Ginzburg–Landau (TDGL) equation, mKdV equation, and the correlation expression of these two equations. After this, the feedback control item based on the velocity difference between the subject vehicle and its preceding vehicle was designed and introduced into the extended curve OV model by Zheng et al. [29], and the impacts of this control item on the stability of car-following were discussed based on control theory. Different from [29], Tan et al. [129] constructed a feedback control item based on the preceding vehicle’s velocity and analyzed the impacts of feedback control based on the preceding vehicle’s velocity on the car-following stability of the subject vehicle. The results reveal that the negative feedback control of the preceding vehicle’s velocity can enhance the stability of traffic flow. In [23,128], the linear and nonlinear characteristics of traffic flow based on the micro behavior model were discussed. To comprehensively describe the characteristics of traffic flow on a curve, Liu et al. [130] derived a macro flow model corresponding to the aforementioned micro behavior model. The simulation results suggest that the continuous traffic flow on the curve will evolve into multiple local vehicle clusters. It was confirmed that the car-following velocity is affected by the curve. According to this, Sun et al. [131] introduced a velocity smoothing item based on the difference between the velocity of the stable car-following state and the velocity of the vehicle in the latest time with consideration of the smooth-driving expectation that most drivers are unwilling to alter their velocity frequently. In the same period, Sun et al. [132] introduced the delay feedback ETOA information of multiple preceding vehicles, modified the correlation between ETOA information and vehicle velocity into the curve-suitable form, and proposed a new curve FVD model with consideration of multiple preceding vehicles’ delay feedback ETOA information. The results show that the introduced information can enhance the stability of traffic flow and reduce the energy consumption of the car-following process on a curve.

In the above achievements, the characteristics of car-following behavior and the corresponding traffic flow were discussed based on the car-following model or the macro flow model derived from the car-following model. In addition to these works, there are also serval achievements in the research field of macro traffic flow [133,134,135,136,137,138,139,140], which are mainly based on the lattice hydrodynamic model. Limited by this research scope, they will not be discussed in this paper.

4.

Gyroidal road

The gyroidal road is a section with both slope and curvature. In the aforementioned studies, the impacts of curve and slope on car-following behavior and traffic flow have were analyzed. However, the curve and slope of roads in the actual traffic system are not independent of each other, and quite a number of roads are both curved and sloped. A typical gyroidal road is a ramp to elevated roads. However, there is no consideration of the gyroidal road, that is, the curve and slope are not considered at the same time. To address this, Zhu et al. [141] introduced the maximum angular velocity of the gyroidal road, velocity correction due to gradient, and the safety headway affected by slope to modify the optimal velocity function and, based on this, proposed an extended gyroidal OV model. The impacts of the gyroidal road were incorporated into the FVD model by Meng et al. [142], and they derived the stability conditions of traffic flow utilizing control theory. Considering that the $H_{\infty }$ norm can describe the traffic congestion with open boundary conditions and the OV model [143,144], Zhai et al. [145] proposed a delay feedback control method based on the extended gyroidal OV model constructed in [141] and discussed the impacts of controller gain coefficient and delay time on traffic flow on gyroidal roads under the Hulwitz criterion.

The car-following behavior and traffic flow affected by road condition, slope, curve, and gyroidal sections was explored in the studies reviewed in this section. With these works, we can better understand the characteristics of car-following behavior when a vehicle is driving on a road with slope, curve, or gyroidal section, and the traffic flow converges according to the vehicles’ behavior. However, there are some shortcomings in the above works.

(1)

Time-varying of the road condition is not considered. From the perspective of the driver, the vehicle is moving, and thus, the sections of the roads at different times are varying, which will cause the road conditions at the section where the vehicle is at a specific moment to be time-varying. However, this feature is not considered in the previous studies on car-following behavior.

(2)

The internal connection of road conditions was ignored. In the actual traffic system, the slope, curve, and bad road conditions can exist simultaneously and have a comprehensive impact on the car-following behavior. Although there are several works that considered the slope and curve (i.e., the gyroidal road), exploration with a comprehensive consideration of slope, curve, and bad road conditions are still absent.

(3)

The external connection between road conditions and other factors was ignored. There is no doubt that there are impacts of road factors on car-following behavior and traffic flow, but road factors are absolutely not the only factors affecting car-following behavior. The road factors are not the main influencing factors on car-following behavior. However, an exploration with a comprehensive consideration of road and other factors is still absent.

2.3.2. Weather

In addition to the road conditions, there are significant impacts of weather on car-following behavior. Good weather is generally regarded as normal weather in the research on car-following behavior. When the weather gets worse, it will increasingly affect the car-following behavior. The impacts of bad weather on driving behavior are significant and widely acknowledged. Because of this, traffic managers around the world will send alerts to drivers when they detect bad weather. The previous norm organized weather according to type, such as rain, snow, and fog. In fact, no matter what type of weather, its impacts on driving behavior can be divided into two aspects: visibility and adhesion. Compared with good weather, the presence of liquid and solid particles in the air in the rain, snow, fog, and other weather will lead to the decline of visibility, which will affect the driver’s perception of traffic conditions and then affect his/her car-following and other driving behaviors.

• Visibility

The research on car-following behavior affected by weather conditions in aspects of visibility began in 2007. Jiang et al. [146] constructed a partition optimal velocity function to describe the driver’s desired velocity under different visibility conditions and proposed an extended FVD model with consideration of the impacts of visibility. Based on virtual driving experiments, Kang et al. [147] discussed the car-following behavior of the subject vehicle utilizing the headway as an index under the condition that the preceding vehicle is driving at various velocity values and these vary in fog. Also based on virtual driving experiments, Gao et al. [148] discussed the impacts of fog on driver’s car-following behavior at different stages (stable driving, acceleration, or decelerating). Considering the “risk illusion” caused by visibility reduction in fog, Tan [149] proposed an extended FVD model to describe the car-following behavior in the low-visibility environment caused by bad weather. Later, based on the model in [149], Tan et al. [150] further incorporated the “velocity imitation” effect by introducing a function of the velocity of multiple vehicles in the adjacent lane and the subject vehicle. Utilizing “Time Exposed Time-to-collision” and “Time Integrated Time-to-collision” as indexes, Gao et al. [151] explored the impacts of low visibility on car-following behavior on aspects of headway, reaction time, and collision risk by employing virtual driving experiments. The results suggest that due to the reduction of visibility caused by fog, the headway along with time headway decrease, the reaction time increases, and the collision risks increase compared with driving under good weather conditions. Zhang et al. [152] utilized questionnaires to explore the impacts of visibility conditions on car-following behavior. The results reveal that drivers tend to undertake conservative driving behavior under low-visibility conditions. It is noteworthy that radical drivers are more likely to maintain a short headway and conduct aggressive driving behavior.

2.

Adhesion

In addition to reducing visibility, bad weather conditions may also reduce road adhesion. According to vehicle dynamics, the driving force and braking force of the vehicle need to be ultimately realized through the interaction between the tire and the ground. The change of adhesion will affect the effectiveness of vehicle driving force and braking force, which further affects the driving behavior of drivers. Considering this, based on the calculation model of driving resistance and Newton’s motion law, Li et al. [153] proposed an extended FVD model with consideration of driving resistance to describe car-following behavior under various adhesion conditions. The results suggest that there are significant impacts of driving resistance on car-following behavior on the aspects of headway, stability, and the start/brake wave. Employing the field data collected from icing and general roads in Hokkaido (Japan), Park et al. [154] calibrated the Van Aerde model to explore car-following behavior. The results reveal that the changes in adhesion significantly affect the driver’s car-following behavior, which is reflected in the significant statistical differences in the five indicators (response time, desired velocity, velocity, road capacity, and congestion density). Employing other field data, Asamer et al. [155] re-calibrated the Wiedemann model, which is at the core of VISSIM traffic flow simulation software, and discussed the impacts of adhesion on car-following behavior on snowy days. The results suggest that drivers will adopt lower acceleration, larger vehicle headway, and lower velocity. By uniformly expressing the adhesion and road surface damages as the impacts of road surface condition and modeling these impacts as an aspect of the tire attachment coefficient, Yang et al. [156] proposed an extended ID model to discuss the car-following behavior characteristics of a vehicle equipped with an ACC system under various road surface conditions.

Except for rain, snow, and other weather conditions, which obviously change the adhesion, strong wind will produce a “lifting force” that will indirectly change the equivalent adhesion of the road. To address this, Liu et al. [157] established a calculation model of the force of strong wind on vehicles in three-dimensional space and, based on this, proposed an extended FVD model with consideration of strong wind influence.

3. Discussion

Car-following behavior is essentially the implementation of the driver’s subjective driving intention, which is affected by internal and external factors. The previous achievements, which explored car-following behavior as affected by driver, vehicle, or environmental factors, were reviewed in the above section. The review results suggest that there are obvious differences in the characteristics of car-following behavior and traffic flow as affected by various drivers, vehicles, or environment factors, and the previous research can help us better understand the car-following behavior and traffic flow under the corresponding conditions. In this section, the shortcomings of the previous research will be summarized, and the needs and prospects of future works will be discussed.

3.1. Limitations of Previous Works

3.1.1. Driver

In the traditional car-following models, all drivers are assumed to be homogeneous, which is inconsistent with reality. In a realistic traffic system, due to the differences in the driving experience, gender, character, emotion, and other sociological, psychological, and physiological aspects, the drivers are heterogeneous. The results of previous studies, in which the heterogeneity of drivers was incorporated, confirm that there is external heterogeneity between different drivers and internal heterogeneity in one single driver, and the car-following behavior will be affected by the heterogeneity of the driver(s). In these studies, the approaches, dividing drivers into several groups, are universal. However, there are several shortcomings in these approaches. On the one hand, the so-called driver type is time-varying rather than static because of the impacts of various factors. To be specific, a conservative driver can transform into an aggressive driver due to an urgent driving task. On the other hand, the huge number of drivers is simply divided into three types (aggressive, normal, and conservative type), which ignores the richness of the drivers’ characteristics. For instance, as mentioned above, the conservative driver can transform into an aggressive driver. However, there will be differences in aggressiveness degree between an aggressive driver transformed from a conservative driver and an normally aggressive driver because of their own psychological and physiological characteristics. This requires a more detailed division of driver type according to the degree of aggressiveness (conservativeness).

Moreover, the previous works matched different parameters or even different model methods for different drivers with the utilization of datasets collected from actual or virtual driving experiments. With the development of computing technology, increasingly stronger computing power can satisfy the requirements of personalized calibration to a certain scale. However, the number of drivers is huge, and thus the characteristics of various drivers are extremely diverse and complex. As a result, the approaches that match different parameter values or even different models for various drivers are becoming more and more infeasible because of the surge in complexity and cost. To address this, it is necessary to explore and then employ online calibration methods to improve the flexibility of the calibration process and the adaptability of calibration results. More importantly, it is urgent to establish car-following models suitable for diverse drivers, from the perspective of the internal mechanism of the interaction between the drivers’ car-following behavior and their psychological, physiological, and other features.

3.1.2. Vehicle

It is very common that different types of vehicles drive in the traffic system and form a mixed traffic flow. The impacts of vehicle types on car-following behavior are caused by two core aspects: there are significant differences in the acceleration and deceleration ability of different types of vehicles; there are also significant differences in the overall size between different types of vehicles, which will affect the rear vehicle’s view. There are two main approaches, one of which is dividing the vehicles into various car-following combinations; the other directly considers the vehicle type impact. The approach of dividing the vehicles into various car-following combinations divides vehicles into limited groups according to the vehicle type of the subject vehicle and its preceding vehicle in the combination (for instance, Truck-Car). The approach of direct consideration of the vehicle type refers to the new item(s) or parameter(s) employed to express the impacts of vehicle type, introduced into the visual angle, FVD, or other traditional car-following models. Based on these two approaches, the car-following behavior affected by the factor of vehicle type was explored from empirical and theoretical perspectives. The results reveal that there are differences in car-following behavior when driving different types of vehicles, and there are also differences in car-following behavior when the type of the preceding vehicle is different. These differences are represented in the aspects of headway, velocity, acceleration, and response delay. In the studies employing these two approaches, the type of (preceding) vehicle is assumed to be constant. However, in the actual traffic system, although the subject vehicle in the car-following state will not execute the lane-changing behavior, the preceding vehicle may change to the adjacent lane, which may make the type of preceding vehicle change. The time-varying feature of the preceding vehicle type caused by this situation has not been considered.

The applications of automatic controllers represented by the ACC and CACC systems means that the car-following behavior of these emerging vehicles is different from that of the traditional MVs. Some scholars have discussed the car-following characteristics of vehicles equipped with automatic controllers, the impacts of the system key parameter(s) settings on the car-following characteristics, and the traffic flow characteristics affected by the penetration of vehicles equipped with automatic controllers. In these works, the ID model along with its extended models and the PATH model were widely employed. The research results can help us better understand the car-following and traffic flow characteristics as affected by the applications of automatic controllers. However, there are many imperfections in these achievements. On the one hand, many of the studies only utilize theoretical analysis without involving field data, and the adopted theoretical assumptions (virtual scenes) are too idealized and simplified, resulting in differences between the research results and the actual characteristics. On the other hand, part of the studies used field data, but most of these data were collected from a specialized test field, also resulting in differences between the research results and the actual characteristics. Therefore, the lack of large-scale datasets collected from actual traffic systems needs to be addressed in further research. Regarding the lack of datasets, we will discuss this issue in Section 3.2.

3.1.3. Environment

Various factors in the specific driving environment also have impacts on the car-following behavior. Among them, there are mainly two aspects: road conditions and weather conditions. For the road conditions, the condition, curve, slope, etc., of the road directly affect the dynamic characteristics of vehicles and then affect the driving behavior, such as car-following behavior. The research results suggest that when the road conditions are no longer ideal, which is assumed in the traditional car-following models, the car-following behavior of the subject vehicle will change. Bad road conditions will have a negative impact on vehicle operation, which is consistent with driving experience. However, it is noteworthy that in terms of macro traffic flow characteristics, when a disturbance has occurred, especially after the traffic flow has reached the stop-and-go state, bad road conditions may have a positive impact on the operation of traffic flow. The impacts of road curve and slope on car-following behavior are reflected in two aspects: on the one hand, curve and slope will increase the impacts of centrifugal force and gravity on vehicles, and measures must be taken to compensate for these impacts to ensure the vehicle normally maintains its current lane; on the other hand, curves and slopes, especially large ones, will have an impact on the driver’s psychology and make the driver change the car-following behavior. In the automatic car-following scenario, the impacts on the driver’s psychology disappear, and instead, the effective range of the sensors is shortened due to curve and slope, which will affect the car-following behavior.

There are still many shortcomings in the previous studies in terms of consideration of road conditions:

(1)

Time-varying of road conditions was not considered. The road conditions are relatively static for a certain period of time when observed from a systematic or macro perspective. However, when observing from the driver’s perspective, the road conditions are time-varying because the vehicle is in motion, and the specific road sections are different at different times. While the time variability was incorporated in [103], a random function of time was used to characterize the time-varying characteristics, which is quite different from the time-varying characteristics of actual road conditions. Thus, the aforementioned special time variability was not fully considered in previous studies.

(2)

The internal connections of road conditions were separated. In actual traffic systems, the road condition, slope, and curve exist simultaneously and have a comprehensive impact on the driver’s car-following behavior. However, in the previous research, the impacts of various road conditions on car-following behavior were not comprehensively considered, except that the slope and curve were considered at the same time as the gyroidal road.

(3)

The external connections between road conditions and other factors were separated. There is no doubt that car-following behavior is affected by various road conditions. However, as repeatedly mentioned above, road conditions are by no means the only factor affecting car-following behavior and are not even the major influential factor in many situations. However, up to now, there has been no car-following model in which the impacts of road conditions and other influencing factors are comprehensively considered. The differences in responses of diverse drivers and vehicles to the same road conditions have also not been considered.

3.2. Needs and Prospects of Future Works

3.2.1. Full Consideration of Driver–Vehicle Attributes

Car-following behavior is essentially the implementation of the driver’s subjective driving intention, and the carrier for the implementation is the vehicle. The differences in driver along with vehicle attributes have a profound impact on car-following behavior. Drivers with different attributes are likely to adopt different car-following behaviors under the same conditions, and the same driver’s car-following behavior can be different when driving different vehicles. More importantly, in most of the previous studies, it was assumed that the driver’s attributes were static and stable. However, in the actual driving process, the driver’s attributes are not static and stable; they are dynamic and time-varying due to the influence of psychological-physiological-sociological characteristics, life experiences, external environmental stimulus, and even the illegal use of alcohol, drugs, or other substances. Therefore, considering the time variability of driver attributes should be a focus of future research.

Moreover, the attributes of other vehicles and their drivers will also have a significant impact on the car-following behavior of the subject vehicle. With the application of intelligent and connected technology in traffic systems, it is possible to collect and exchange rich information about driver and vehicle attributes. In the foreseeable future, the automatic controller cannot completely replace the human driver. Therefore, it is necessary to carry out in-depth research on car-following behavior with comprehensive consideration of the attributes of vehicles and their drivers, and it may become the frontier of research on traffic flow theory.

3.2.2. General Modeling and Evaluation Methods

Most of the previous studies are improvements or expansions of the traditional car-following models. These studies can better describe the car-following behavior under specific conditions, and they reproduce some complex non-linear traffic flow phenomena. However, the factors considered in these studies are incomplete, resulting in poor performance of the corresponding models in describing car-following behavior under conditions other than assumptions. That is, the generalization ability is very poor. As summarized above, car-following behavior is the result of the combination and interaction of various elements, with very rich and diverse characteristics. Therefore, it is necessary to further promote the interdisciplinary integration of physics, psychology, traffic engineering, and other disciplines so as to promote a new round of development and innovation in car-following behavior research. Moreover, it is vital to establish the general modeling methods of car-following behavior. In addition, various models proposed in the past 70 years constitute the cornerstone of the research system of car-following behavior and traffic flow theory; they provide reference and guidance for the future research, including general modeling methods. How to effectively compare and evaluate the new works with the previous models and then form a system of general evaluation methods is another key issue that needs to be addressed.

3.2.3. Construction of Large-Scale Datasets Covering Different Scenarios

The trajectory data play an important role in the study of car-following behavior. On the one hand, the calibration of model parameters is a necessary prerequisite for the application of car-following models. On the other hand, the trajectory data comprise an indispensable research tool to explore the relationship between car-following behavior and various factors and analyze car-following characteristics. The promotion role of NGSIM and other similar datasets in the research of car-following and traffic flow theory has been widely acknowledged. However, the trajectory datasets can only present the car-following behavior characteristics in the specific environment in which the data were collected. It has been confirmed that there are differences in the car-following behavior of drivers from different countries or regions and with different cultural backgrounds [25]. It is of great significance for research on car-following behavior to organize natural driving experiments to collect rich trajectory data and accomplish the comprehensive coverage of different scenarios. The development of next-generation information technology (represented by big data, computing cloud, and edge computing) makes it possible to collect large-scale datasets containing rich attributes of drivers, vehicles, and other factors under various conditions. On the premise of protecting the privacy of subjects, how to construct large-scale, high-precision datasets, which can be supplemented in real time and contain rich attributes, and further sharing, utilizing, and analyzing the features expressed by the datasets is another major issue in the future exploration of car-following behavior. The development of computational vision and virtual reality technology also creates new opportunities for organizing high-fidelity virtual driving experiments to collect relevant data that are obtainable through actual road driving experiments or to collect large-scale datasets with considerable accuracy at a lower cost.

3.2.4. Combination of Theory-Driven and Data-Driven Models

The traditional car-following models take the theory-driven models as their main focus. There are sophisticated mathematical structures in these theory-driven models. Compared with the theory-driven models, the data-driven models can directly detect the car-following behavior laws from the field data and achieve high fitting precision, which has shown high performance in many research applications. However, the performance of the data-driven models is determined by the quality of the used dataset. When the dataset is incomplete, the segment is short, or the error is large, the established data-driven car-following model will not achieve satisfactory performance. In this situation, it is an effective approach to input the theory-driven model into the data-driven model as prior knowledge. This approach along with other approaches, such as integrating data-driven models with theory-driven models, can not only master the respective advantages of the theory-driven model and the data-driven model but also facilitates other research applications, including further research on the car-following behavior mechanism. Therefore, how to effectively utilize the previous theory-driven models, integrate new data acquisition, processing, and applicating technologies, and build the next generation of data- and theory-driven models is a major issue in future research on car-following behavior.

4. Conclusions

In this paper, the articles in which the car-following behavior was studied with consideration of one or multiple driver-vehicle-environment aggregations were systematically reviewed. The results reveal that there are differences in the car-following behavior when the vehicle is in various driver-vehicle-environment aggregations, which suggests that it is difficult to use one model to comprehensively and precisely describe the car-following behavior of a vehicle with enhanced information perception ability. Based on this, the limitations of previous works were summarized. Furthermore, the needs and prospects of future works were discussed. Generally speaking, (i) the reality that the car-following behavior is comprehensively affected by various driver-vehicle-environment factors has not been adequately considered, and (ii) the processing approaches of impacts of driver, vehicle, or environment on car-following behaviors were relatively simple in previous studies. Therefore, the comprehensive consideration of driver, vehicle, and environmental factors from a global perspective, fully incorporating the characteristics of various factors’ influence, the evolution of modeling and evaluation methods, and the construction of the new generation datasets are the more urgent needs for future works.