Performance Comparison of Predictive Methodologies for Carbon Emission Credit Price in the Korea Emission Trading System
Abstract
1. Introduction
2. Literature Reviews
2.1. Literature Reviews Relevant to the Prediction of Carbon Emission Credit
2.2. Search Queries-Based Prediction
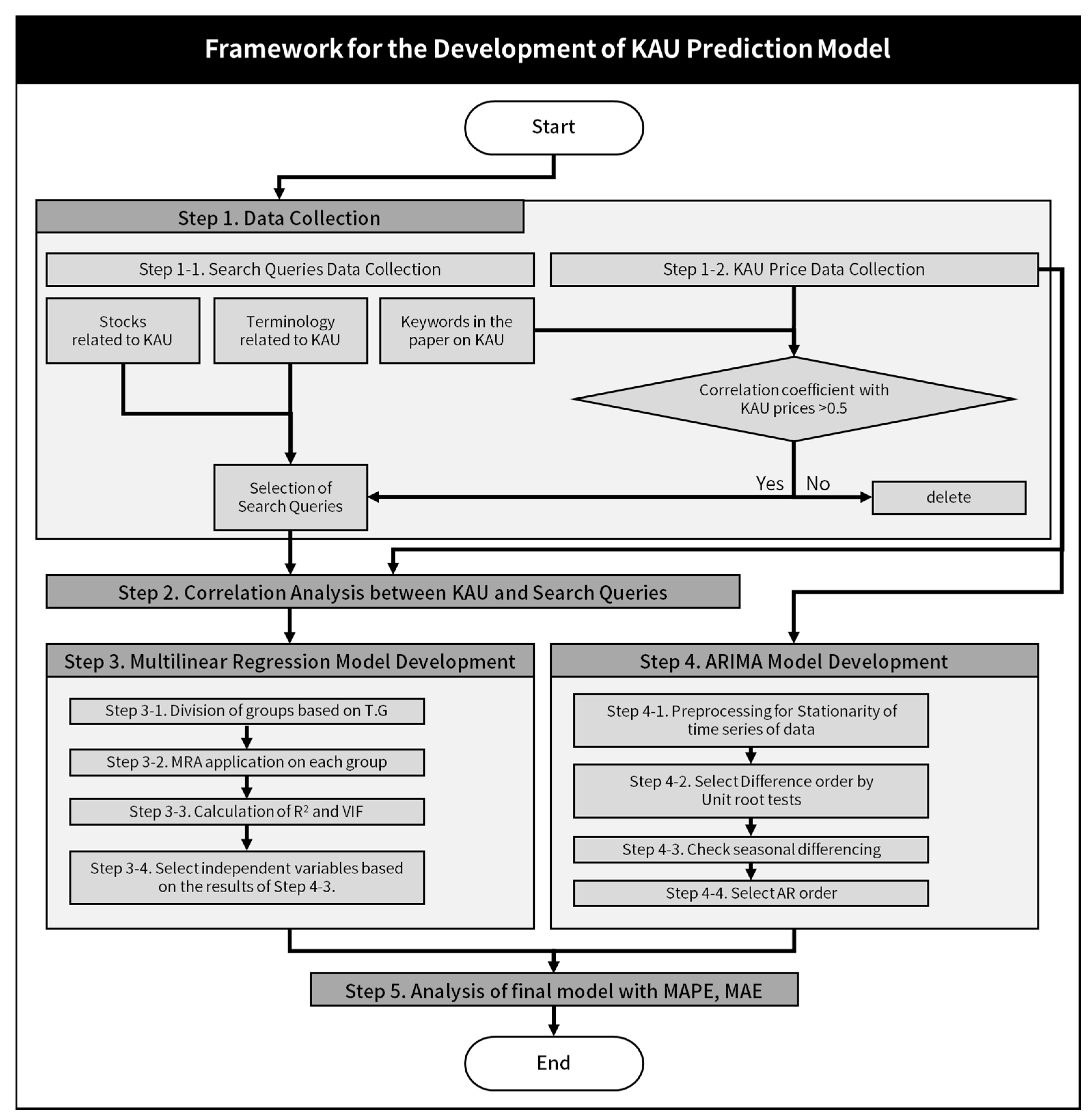
3. Analysis Method
3.1. Multiple Linear Regression Model
3.2. Auto Regressive Integrated Moving Average
4. Data Collection
4.1. Search Volume Data
4.2. Trading Price Data
5. ETS Prediction Model
5.1. ETS Multiple Linear Regression Model
5.1.1. Variables Selection
5.1.2. Model Derivation


5.2. Timeseries Analysis Using ARIMA
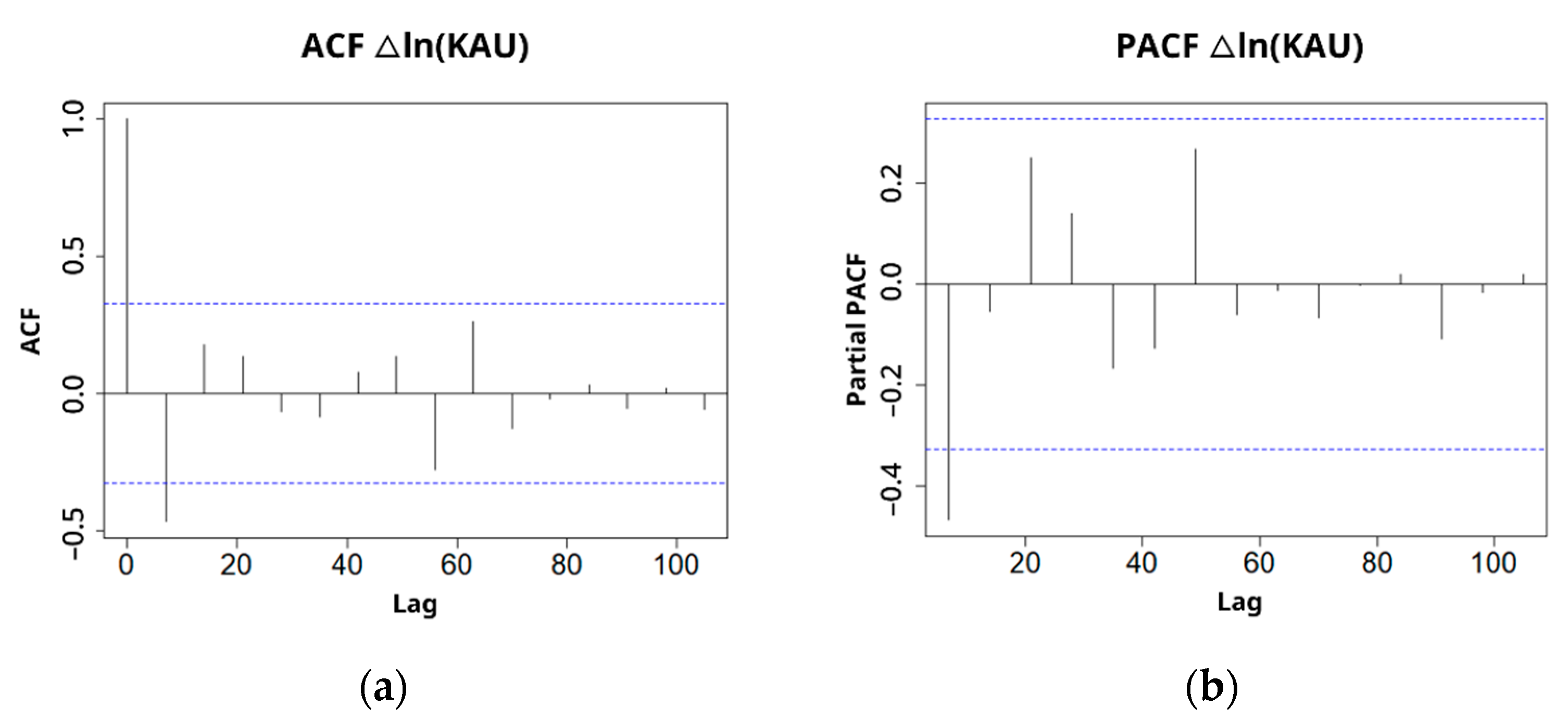
5.2.1. Data Pre-Processing
5.2.2. Time Lag for an Appropriate Prediction Model
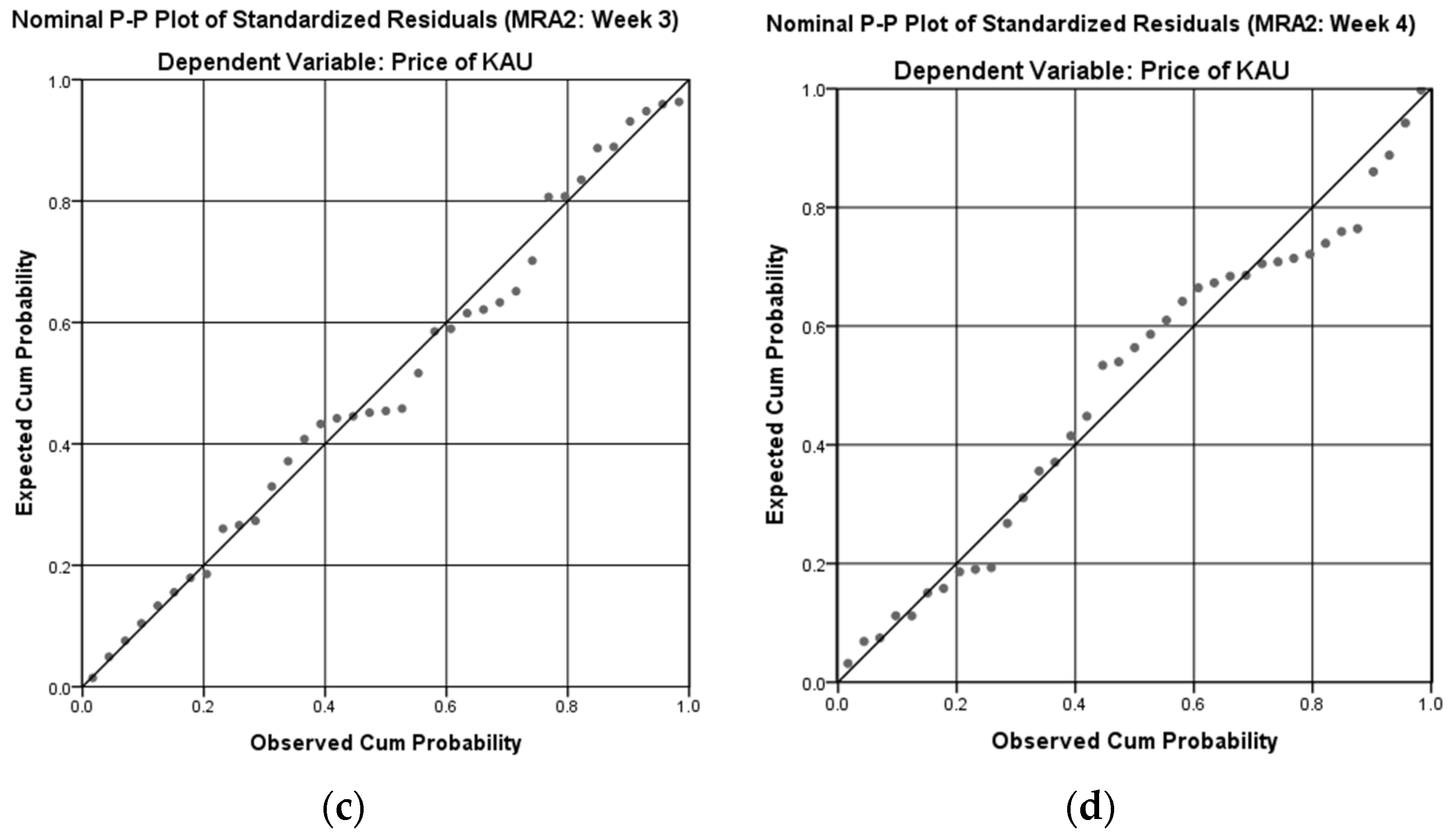
5.2.3. Model Derivation and Conformity Assessment
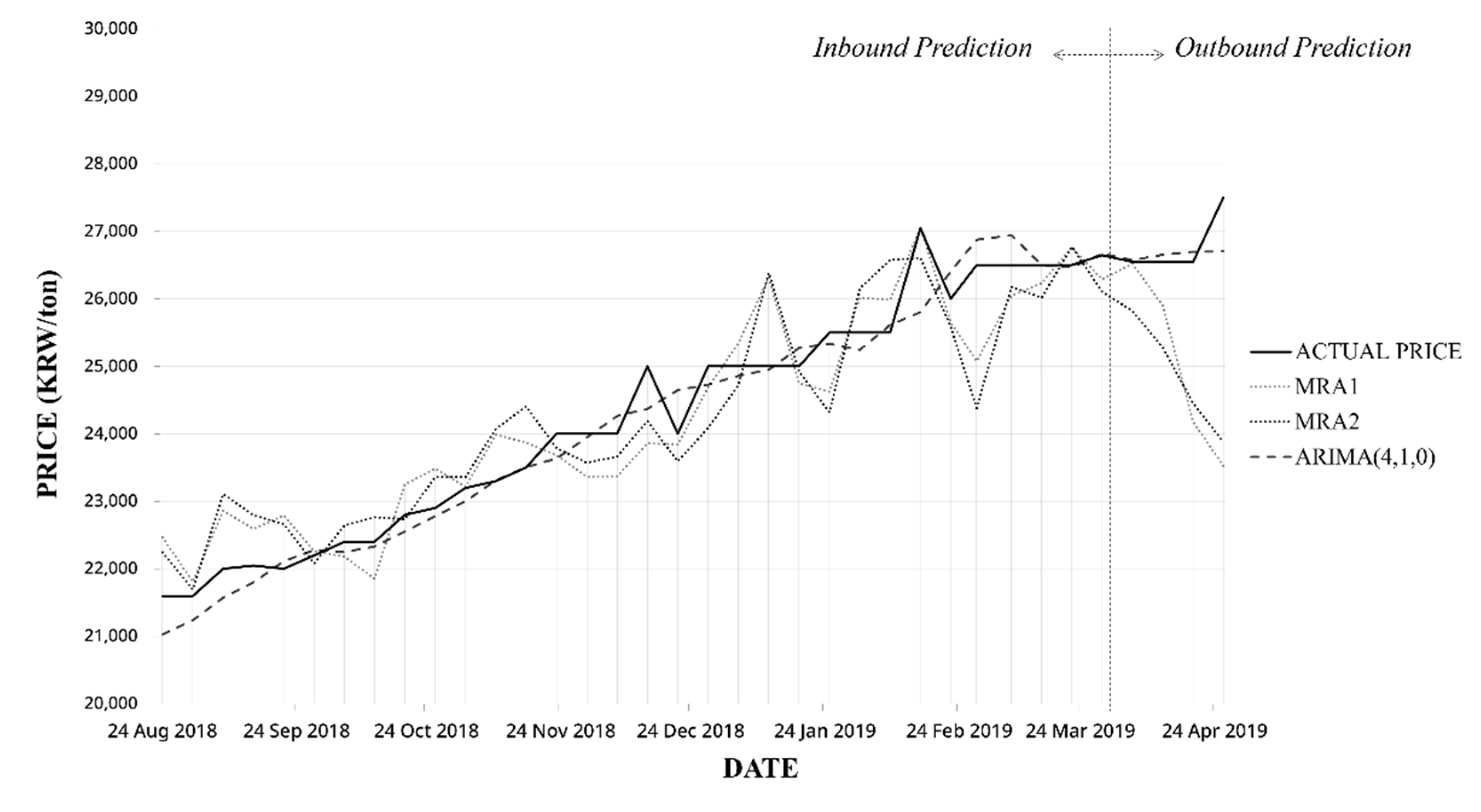
6. Results
7. Discussion
8. Conclusions
Author Contributions
Funding
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Stern, N.; Stern, N.H. The Economics of Climate Change: The Stern Review; Cambridge University: Cambridge, UK, 2007. [Google Scholar]
- European Commission. EU ETS Handbook; European Commission: Brussels, Belgium, 2015; pp. 3–138. [Google Scholar]
- Beck, U.; Kruse-Andersen, P.K. Endogenizing the Cap in a Cap-and-Trade System: Assessing the Agreement on EU ETS Phase 4. Environ. Resour. Econ. 2020, 77, 781–811. [Google Scholar] [CrossRef]
- European Commission. Questions and Answers on the Provisional Agreement to Revise the EU Emissions Trading System (EU ETS); European Commission: Brussels, Belgium, 2017; pp. 1–4. [Google Scholar]
- Song, H.S. Activation of the 2050 Carbon Neutral and Emission Trading System; Issue Report 21–23; KCMI Korea Capital Market Institute: Seoul, Korea, 2021; pp. 1–21. [Google Scholar]
- European Commission. The Paris Protocol–A Blueprint for Tackling Global Climate Change Beyond; European Commission: Brussels, Belgium, 2020. [Google Scholar]
- Son, D.; Jeon, Y. Learning-by-doing Effect on Price Determination System in Korea’s Emission Trading Scheme. Environ. Resour. Econ. Rev. 2018, 27, 667–694. [Google Scholar]
- Lee, S.; Kim, D. Domestic Greenhouse Gas Emission Trading System Analysis of enforcement effects. Korean Environ. Inst. Res. Rep. 2017, 1–115. [Google Scholar]
- Son, I.; Kim, D.K. Analysis of the Impact of Key Design Elements for the EU-ETS Phase 4 on the K-ETS in the Future. Environ. Resour. Econ. Rev. 2021, 30, 129–167. [Google Scholar]
- Yoo, I. Domestic Emission Trading Market Issues and Prospects for 2021. KONETIC, 2021; pp. 2–9. Available online: https://www.konetic.or.kr/user/P/PA/PA001_L01.do (accessed on 1 September 2021).
- K-eco (Korea Environment Corporation). GHG Reduction Policy Support. Available online: https://www.keco.or.kr/kr/business/climate/contentsid/1520/index.do (accessed on 1 February 2022).
- Lee, J.Y.; Seol, G.; Yoon, N.R.; Lee, M.K.; Lee, S.W.; Lee, S.Y.; Lee, J.H.; Jeong, Y.M. 2018 K-ETS Summary Report; President of the Greenhouse Gas Inventory and Research Center of Korea: Seoul, Korea, 2020; pp. 1–40. [Google Scholar]
- Benz, E.; Trück, S. Modeling the price dynamics of CO2 emission allowances. Energy Econ. 2009, 31, 4–15. [Google Scholar] [CrossRef]
- Chevallier, J. Carbon futures and macroeconomic risk factors: A view from the EU ETS. Energy Econ. 2009, 31, 614–625. [Google Scholar] [CrossRef]
- Zhu, B.; Chevallier, J. Carbon Price Forecasting with a Hybrid ARIMA and Least Squares Support Vector Machines Methodology. In Pricing and Forecasting Carbon Markets; Springer: Cham, Switzerland, 2017; pp. 87–107. [Google Scholar] [CrossRef]
- Sun, W.; Huang, C. A carbon price prediction model based on secondary decomposition algorithm and optimized back propagation neural network. J. Clean. Prod. 2020, 243, 118671. [Google Scholar] [CrossRef]
- Koop, G.; Tole, L. Forecasting the European carbon market. J. R. Stat. Soc. Ser. A 2013, 176, 723–741. [Google Scholar] [CrossRef]
- Zhang, J.; Li, D.; Hao, Y.; Tan, Z. A hybrid model using signal processing technology, econometric models and neural network for carbon spot price forecasting. J. Clean. Prod. 2018, 204, 958–964. [Google Scholar] [CrossRef]
- Ministry of Environment. 3rd Basic Plan for Emission Transaction System. 2019, pp. 1–35. Available online: https://www.gihoo.or.kr/portal/kr/community/data_view.do?p=1&idx=20483&column=&groupname=data&groupid=&f=1&q (accessed on 1 April 2020).
- Çanakoğlu, E.; Adıyeke, E.; Ağralı, S. Modeling of carbon credit prices using regime switching approach. J. Renew. Sustain. Energy 2018, 10, 035901. [Google Scholar] [CrossRef]
- Kim, Y.; Ahn, J. The Study on Development of Carbon Emission Price Forecasting Model Reflecting Emission Trading Market Characteristics. Entrue J. Inf. Technol. 2016, 15, 7–16. [Google Scholar]
- Kim, S. Analysis and Prospects of Price Determinants of Emissions Trading; Korea Energy Economics Institute: Seoul, Korea, 2007. [Google Scholar]
- Chevallier, J. EUAs and CERs: Vector autoregression, impulse response function and cointegration analysis. Econ. Bull. 2010, 30, 558–576. [Google Scholar]
- Chevallier, J. Nonparametric modeling of carbon prices. Energy Econ. 2011, 33, 1267–1282. [Google Scholar] [CrossRef]
- Conrad, C.; Rittler, D.; Rotfuß, W. Modeling and explaining the dynamics of European Union Allowance prices at high-frequency. Energy Econ. 2012, 34, 316–326. [Google Scholar] [CrossRef]
- Guðbrandsdóttir, H.N.; Haraldsson, H. Predicting the Price of EU ETS Carbon Credits. Syst. Eng. Procedia 2011, 1, 481–489. [Google Scholar] [CrossRef]
- Chevallier, J. Carbon price drivers: An updated literature review. Int. J. Appl. Logist. 2013, 4, 1–7. [Google Scholar] [CrossRef]
- Reboredo, J.C. Modeling EU allowances and oil market interdependence. Implications for portfolio management. Energy Econ. 2013, 36, 471–480. [Google Scholar] [CrossRef]
- Yahşi, M.; Çanakoğlu, E.; Ağralı, S. Carbon price forecasting models based on big data analytics. Carbon Manag. 2019, 10, 175–187. [Google Scholar] [CrossRef]
- Zhao, X.; Han, M.; Ding, L.; Kang, W. Usefulness of economic and energy data at different frequencies for carbon price forecasting in the EU ETS. Appl. Energy 2018, 216, 132–141. [Google Scholar] [CrossRef]
- Hao, Y.; Tian, C.; Wu, C. Modelling of carbon price in two real carbon trading markets. J. Clean. Prod. 2020, 244, 118556. [Google Scholar] [CrossRef]
- Kim, H.; Im, G.; Kim, Y.; Lee, M.; Han, S. The Comparison of Certified Emission Reductions Forecasting Model Using Price of Certified Emission Reductions and Related Search Keywords. In Proceedings of the Korean Institute of Building Construction Conference 2020, Seoul, Korea, 12 June 2020; pp. 44–45. [Google Scholar]
- Lamphiere, M.; Blackledge, J.; Kearney, D. Carbon Futures Trading and Short-Term Price Prediction: An Analysis Using the Fractal Market Hypothesis and Evolutionary Computing. Mathematics 2021, 9, 1005. [Google Scholar] [CrossRef]
- Zhang, Y.-J.; Sun, Y.-F. The dynamic volatility spillover between European carbon trading market and fossil energy market. J. Clean. Prod. 2016, 112, 2654–2663. [Google Scholar] [CrossRef]
- Wei, L.; Can, L. The research on setting a unified interval of carbon price benchmark in the national carbon trading market of China. Appl. Energy 2015, 155, 728–739. [Google Scholar]
- Zhibin, L.; Shan, H. Carbon option price forecasting based on modified fractional Brownian motion optimized by GARCH model in carbon emission trading. North Am. J. Econ. Financ. 2021, 55, 101307. [Google Scholar]
- Loperfido, N. Kurtosis-based projection pursuit for outlier detection in financial time series. Eur. J. Financ. 2019, 26, 142–164. [Google Scholar] [CrossRef]
- Yun, P.; Zhang, C.; Wu, Y.; Yang, Y. Forecasting Carbon Dioxide Price Using a Time-Varying High-Order Moment Hybrid Model of NAGARCHSK and Gated Recurrent Unit Network. Int. J. Environ. Res. Public Health 2022, 19, 899. [Google Scholar] [CrossRef] [PubMed]
- Ginsberg, J.; Mohebbi, M.H.; Patel, R.S.; Brammer, L.; Smolinski, M.S.; Brilliant, L. Detecting influenza epidemics using search engine query data. Nature 2009, 457, 1012–1014. [Google Scholar] [CrossRef]
- Da, Z.; Engelberg, J.; Gao, P. In search of attention. J. Financ. 2011, 66, 1461–1499. [Google Scholar] [CrossRef]
- Joseph, K.; Wintoki, M.B.; Zhang, Z. Forecasting abnormal stock returns and trading volume using investor sentiment: Evidence from online search. Int. J. Forecast. 2011, 27, 1116–1127. [Google Scholar] [CrossRef]
- Han, S.; Ko, Y.; Kim, J.-Y.; Shin, D.H. Enhancement of Prediction Accuracy for Home Sales Index Prediction Model based on Integration of Multiple Regression Analysis and Genetic Algorithm. KSCE J. Civ. Eng. 2018, 22, 2159–2166. [Google Scholar] [CrossRef]
- Beracha, E.; Wintoki, M.B. Forecasting Residential Real Estate Price Changes from Online Search Activity. J. Real Estate Res. 2013, 35, 283–312. [Google Scholar] [CrossRef]
- Goel, S.; Hofman, J.M.; Lahaie, S.; Pennock, D.M.; Watts, D.J. Predicting consumer behavior with Web search. Proc. Natl. Acad. Sci. USA 2010, 107, 17486–17490. [Google Scholar] [CrossRef] [PubMed]
- BizSpring Inc. Statistics. Available online: http://www.internettrend.co.kr/trendForward.tsp (accessed on 1 July 2019).
- Naver. Search Term Trend. Available online: http://datalab.naver.com/keyword/trendSearch.naver (accessed on 4 March 2022).
- Neter, J.; Kutner, M.H.; Nachtsheim, C.J.; Wasserman, W. Applied Linear Statistical Models; Irwin: Chicago, IL, USA, 1996. [Google Scholar]
- Nam, J.-O.; Noh, S.-G. A Study on Forecast of Oyster Production using Time Series Models. Ocean Polar Res. 2012, 34, 185–195. [Google Scholar] [CrossRef]
- Hyndman, R.J.; Athanasopoulos, G. Forecasting: Principles and Practice, 3rd ed.; OTexts: Melbourne, Australia, 2018. [Google Scholar]
- Han, S.; Ko, Y.; Kim, J.; Hong, T. Housing Market Trend Forecasts through Statistical Comparisons based on Big Data Analytic Methods. J. Manag. Eng. 2018, 34, 04017054. [Google Scholar] [CrossRef]
- Devore, J. Probability and Statistics for Engineering and Science, 8th ed.; Richard Stratton: New York, NY, USA, 2012; pp. 1–712. [Google Scholar]
- Ryu, N.; Kim, H.; Kang, P. Evaluating Variable Selection Techniques for Multivariate Linear Regression. J. Korean Inst. Ind. Eng. 2016, 42, 314–326. [Google Scholar] [CrossRef][Green Version]
- Asuero, A.G.; Sayago, A.; Gonzalez, A.G. The Correlation Coefficient: An Overview. Crit. Rev. Anal. Chem. 2006, 36, 41–59. [Google Scholar] [CrossRef]
- Im, C.Y.; Kim, H.C. A Study on the Analysis and Prediction of Housing Mortgage in Deposit Bank Using ARIMA Model. J. Korea Inst. Inf. Electron. Commun. Technol. 2019, 12, 265–272. [Google Scholar]
- Min, K.-C.; Jun, Y.-I.; Ha, H.-K. Forecasting the Air Cargo Demand with Seasonal ARIMA Model: Focusing on ICN to EU Route. J. Korean Soc. Transp. 2013, 31, 3–18. [Google Scholar] [CrossRef]




| Keywords | Mean | S.D | Minimum | Median | Maximum | Size |
|---|---|---|---|---|---|---|
| CET * | 108.7 | 41.0 | 38.5 | 109.1 | 198.9 | 37 |
| FOOSUNG | 23,663.7 | 7092.7 | 11,293.8 | 22,554.5 | 45,426.4 | 37 |
| CETS ** | 369.2 | 155.2 | 120.4 | 360.2 | 733.4 | 37 |
| EAGON | 11,542.5 | 8320.6 | 3555.1 | 9609.5 | 42,022.2 | 37 |
| Price of CERs | 54.0 | 44.5 | 0.0 | 43.8 | 213.6 | 37 |
| HH *** | 11,809.8 | 5206.7 | 5330.9 | 10,853.0 | 27,770.4 | 37 |
| UNISON | 16,969.4 | 4586.8 | 7856.3 | 16,120.1 | 34,258.3 | 37 |
| HOMEDECO | 1176.7 | 218.6 | 863.2 | 1155.3 | 1935.6 | 37 |
| HUCHEMS | 4862.7 | 1144.5 | 2336.9 | 4692.9 | 7703.0 | 37 |
| productive | 1675.0 | 520.4 | 973.7 | 1470.6 | 2869.6 | 37 |
| productivity | 1425.9 | 342.9 | 798.2 | 1370.5 | 2507.4 | 37 |
| compare | 1820.6 | 436.7 | 1285.7 | 1771.3 | 3289.3 | 37 |
| excavator | 855.6 | 80.4 | 709.1 | 861.1 | 1083.3 | 37 |
| emissions | 766.4 | 194.6 | 445.2 | 750.6 | 1201.0 | 37 |
| CO2 emissions | 14.0 | 13.5 | 0.0 | 9.6 | 55.7 | 37 |
| GW **** | 280.1 | 53.5 | 155.4 | 287.7 | 370.5 | 37 |
| NOx | 4087.3 | 755.7 | 3007.9 | 3991.2 | 6967.7 | 37 |
| PEMS | 168.9 | 163.1 | 0.0 | 122.3 | 914.0 | 37 |
| durable | 2100.4 | 475.3 | 1150.9 | 2075.8 | 3443.7 | 37 |
| furniture | 3026.7 | 536.9 | 1906.2 | 2902.2 | 4546.0 | 37 |
| wakefulness | 83.7 | 51.2 | 12.6 | 70.7 | 222.1 | 37 |
| Data | Mean | Standard Deviation | Minimum | Median | Maximum | Size |
|---|---|---|---|---|---|---|
| KAU | 23,931.081 | 1770.136 | 21,600 | 24,000 | 27,050 | 37 |
| Variable | Week 1 | Week 2 | Week 3 | Week 4 |
|---|---|---|---|---|
| CET * | −0.149 | −0.211 | −0.247 | −0.363 |
| FOOSUNG | −0.39 | −0.417 | −0.493 | −0.532 |
| CETS ** | −0.317 | −0.316 | −0.341 | −0.384 |
| EAGON | −0.368 | −0.346 | −0.359 | −0.374 |
| Price of CER | −0.313 | −0.356 | −0.465 | −0.507 |
| HANSOLHOMEDECO | −0.469 | −0.419 | −0.433 | −0.456 |
| UNISON | −0.191 | −0.146 | −0.213 | −0.223 |
| HOMEDECO | 0.578 | 0.623 | 0.666 | 0.702 |
| HUCHEMS | 0.166 | 0.183 | 0.066 | 0.075 |
| productive | 0.656 | 0.671 | 0.663 | 0.635 |
| productivity | 0.399 | 0.458 | 0.47 | 0.462 |
| Compare | 0.536 | 0.503 | 0.459 | 0.464 |
| Excavator | −0.444 | −0.218 | −0.215 | −0.319 |
| emissions | 0.468 | 0.537 | 0.529 | 0.548 |
| CO2 emissions | 0.14 | 0.112 | 0.097 | −0.022 |
| global warming | −0.161 | −0.101 | −0.067 | 0.02 |
| NOx | −0.08 | 0.025 | 0.102 | 0.168 |
| PEMS | −0.089 | −0.017 | −0.037 | −0.02 |
| durable | 0.513 | 0.499 | 0.464 | 0.387 |
| furniture | 0.285 | 0.314 | 0.334 | 0.348 |
| wakefulness | 0.582 | 0.543 | 0.5 | 0.482 |
| Time Gap | Search Queries |
|---|---|
| Week 1 | HOMEDECO, productive, compare, durable, wakefulness |
| Week 2 | HOMEDECO, productive, compare, emissions, wakefulness |
| Week 3 | HOMEDECO, productive, emissions, wakefulness |
| Week 4 | FOOSUNG, price of CER, HOMEDECO, productive, emissions |
| Variable | Coefficient | S.E | t | Pr | VIF | adj-R2 | D.W. | |
|---|---|---|---|---|---|---|---|---|
| U | S | |||||||
| HOMEDECO | 2.934 | 0.363 | 0.728 | 4.028 | 0.000 | 1.125 | 0.740 | 1.395 |
| productive | 2.113 | 0.622 | 0.418 | 5.057 | 0.000 | 2.092 | ||
| compare | 1.960 | 0.475 | 0.645 | 3.036 | 0.005 | 3.386 | ||
| durable | −1.693 | −0.453 | 0.688 | −2.461 | 0.020 | 4.687 | ||
| wakefulness | 8.256 | 0.233 | 3.892 | 2.121 | 0.042 | 1.671 | ||
| (Constant) | 16,306.254 | - | 1062.465 | 15.348 | 0.000 | - | ||
| Variable | Coefficient | S.E | t | Pr | VIF | adj-R2 | D.W. | |
|---|---|---|---|---|---|---|---|---|
| U | S | |||||||
| HOMEDECO | 3.505 | 0.435 | 0.832 | 4.211 | 0.000 | 1.271 | 0.698 | 1.281 |
| productive | 1.545 | 0.455 | 0.380 | 4.064 | 0.000 | 1.491 | ||
| emissions | −0.035 | −0.004 | 1.074 | −0.033 | 0.974 | 1.665 | ||
| compare | 0.821 | 0.184 | 0.491 | 1.672 | 0.105 | 1.446 | ||
| wakefulness | 5.259 | 0.135 | 4.412 | 1.192 | 0.242 | 1.522 | ||
| (Constant) | 15,428.686 | - | 1124.782 | 13.717 | 0.000 | - | ||
| Variable | Coefficient | S.E | t | Pr | VIF | adj-R2 | D.W. | |
|---|---|---|---|---|---|---|---|---|
| U | S | |||||||
| HOMEDECO | 3.958 | 0.492 | 0.854 | 4.635 | 0.000 | 1.306 | 0.698 | 1.281 |
| productive | 1.658 | 0.489 | 0.381 | 4.350 | 0.000 | 1.465 | ||
| emissions | 0.138 | 0.015 | 1.075 | 0.129 | 0.898 | 1.620 | ||
| wakefulness | 5.254 | 0.128 | 4.362 | 1.205 | 0.237 | 1.310 | ||
| (Constant) | 16,093.189 | - | 980.468 | 16.414 | 0.000 | - | ||
| Variable | Coefficient | S.E | t | Pr | VIF | adj-R2 | D.W. | |
|---|---|---|---|---|---|---|---|---|
| U | S | |||||||
| HOMEDECO | 2.415 | 0.302 | 4.068 | −0.797 | 0.434 | 2.322 | 0.822 | 1.561 |
| productive | 1.758 | 0.508 | 0.030 | −2.867 | 0.009 | 4.460 | ||
| emissions | 1.210 | 0.133 | 1.756 | −0.298 | 0.769 | 6.302 | ||
| FOOSUNG | −0.085 | −0.408 | 0.018 | 1.150 | 0.261 | 1.963 | ||
| price of CER | −1.441 | 0.043 | 4.353 | 0.194 | 0.848 | 3.613 | ||
| (Constant) | 19,590.524 | - | 1098.553 | 17.833 | 0.000 | - | ||
| Time Gap | Search Queries |
|---|---|
| Week 1 | productive, HOMEDECO, wakefulness |
| Week 2 | productive, HOMEDECO, compare |
| Week 3 | HOMDECO, productive |
| Week 4 | HOMEDECO, productive, FOOSUNG |
| Variable | Coefficient | S.E | t | Pr | VIF | D.W. | ||
|---|---|---|---|---|---|---|---|---|
| U | S | |||||||
| productive | 1.562 | 0.460 | 0.344 | 4.543 | 0.000 | 1.158 | 0.682 | 1.262 |
| HOMEDECO | 3.098 | 0.384 | 0.800 | 3.874 | 0.000 | 1.109 | ||
| wakefulness | 11.264 | 0.318 | 3.631 | 3.102 | 0.004 | 1.189 | ||
| (Constant) | 16,774.013 | - | 972.621 | 17.246 | 0.000 | - | ||
| Variable | Coefficient | S.E | t | Pr | VIF | D.W. | ||
|---|---|---|---|---|---|---|---|---|
| U | S | |||||||
| HOMEDECO | 2.658 | 0.333 | 0.689 | 3.861 | 0.000 | 1.499 | 0.703 | 1.281 |
| productive | 2.030 | 0.587 | 0.264 | 7.696 | 0.000 | 1.174 | ||
| FOOSUNG | −0.090 | −0.434 | 0.017 | −5.211 | 0.000 | 1.398 | ||
| (Constant) | 19,825.066 | - | 1023.652 | 19.367 | 0.000 | - | ||
| Variable | Coefficient | S.E | t | Pr | VIF | D.W | ||
|---|---|---|---|---|---|---|---|---|
| U | S | |||||||
| HOMEDECO | 4.318 | 0.537 | 0.765 | 5.643 | 0.000 | 1.063 | 0.694 | 1.064 |
| productive | 1.806 | 0.533 | 0.322 | 5.602 | 0.000 | 1.063 | ||
| (Constant) | 15,901.400 | - | 938.182 | 16.949 | 0.000 | - | ||
| Variable | Coefficient | S.E | t | Pr | VIF | D.W | ||
|---|---|---|---|---|---|---|---|---|
| U | S | |||||||
| HOMEDECO | 2.658 | 0.333 | 0.689 | 3.861 | 0.000 | 1.499 | 0.822 | 1.608 |
| productive | 2.030 | 0.587 | 0.264 | 7.696 | 0.000 | 1.174 | ||
| FOOSUNG | −0.090 | −0.434 | 0.017 | −5.211 | 0.000 | 1.398 | ||
| (Constant) | 19,825.066 | - | 1023.652 | 19.367 | 0.000 | - | ||
| Dependent Variable | Variable | First Difference | ||
|---|---|---|---|---|
| t-Statistic | Pr | t-Statistic | Pr | |
| KAU | –2.9167 | 0.2158 | –3.8459 | 0.02834 |
| Model | Week 1 | Week 2 | Week 3 | Week 4 |
|---|---|---|---|---|
| MRA 1 | 0.740 | 0.698 | 0.689 | 0.822 |
| MRA 2 | 0.682 | 0.703 | 0.694 | 0.822 |
| Model | ARIMA(1,1,0) | ARIMA(2,1,0) | ARIMA(3,1,0) | ARIMA(4,1,0) |
|---|---|---|---|---|
| AIC | −183.93 | −182.11 | −183.2 | −184.09 |
| Variable | Coefficient | Standard Error | z | Pr |
|---|---|---|---|---|
| (Constant) | 0.0007 | 0.0063 | 0.1144 | 0.9089 |
| AR(1) | −0.5192 | 0.1560 | −3.3269 | 0.0008 |
| AR(2) | 0.2080 | 0.1731 | 1.2018 | 0.2294 |
| AR(3) | 0.5824 | 0.1857 | 3.1358 | 0.0017 |
| AR(4) | 0.3191 | 0.1725 | 1.8498 | 0.0643 |
| AIC | −184.09 | |||
| Log-likelihood | 98.05 | |||
| Dependent Variable | MRA | Time Series | |
|---|---|---|---|
| Time Lag: Week 4 (MRA1) | Time Lag: Week 4 (MRA2) | ARIMA(4,1,0) | |
| Predicted Price (KRW/ton) | 25,702.69 | 25,819.75 | 26,579.88 |
| Actual Price (KRW/ton) | 26,550 | 26,550 | 26,550 |
| MAPE | 3.19 | 2.75 | 0.11 |
| MAE | 847.31 | 730.25 | 29.88 |
| Time Lag: Week 4 (MRA1) | Time Lag: Week 4 (MRA2) | ARIMA(4,1,0) | |
|---|---|---|---|
| MAPE | 7.31 | 7.14 | 0.99 |
| Inbound | Outbound | |||||
|---|---|---|---|---|---|---|
| MRA1 | MRA2 | ARIMA(4,1,0) | MRA1 | MRA2 | ARIMA(4,1,0) | |
| MAPE | 2.11 | 2.39 | 1.07 | 6.49 | 7.14 | 0.99 |
| MAE | 509.37 | 583.89 | 261.27 | 1756.25 | 1927.99 | 269.07 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kim, H.; Kim, Y.; Ko, Y.; Han, S. Performance Comparison of Predictive Methodologies for Carbon Emission Credit Price in the Korea Emission Trading System. Sustainability 2022, 14, 8177. https://doi.org/10.3390/su14138177
Kim H, Kim Y, Ko Y, Han S. Performance Comparison of Predictive Methodologies for Carbon Emission Credit Price in the Korea Emission Trading System. Sustainability. 2022; 14(13):8177. https://doi.org/10.3390/su14138177
Chicago/Turabian StyleKim, Hyeonho, Yujin Kim, Yongho Ko, and Seungwoo Han. 2022. "Performance Comparison of Predictive Methodologies for Carbon Emission Credit Price in the Korea Emission Trading System" Sustainability 14, no. 13: 8177. https://doi.org/10.3390/su14138177
APA StyleKim, H., Kim, Y., Ko, Y., & Han, S. (2022). Performance Comparison of Predictive Methodologies for Carbon Emission Credit Price in the Korea Emission Trading System. Sustainability, 14(13), 8177. https://doi.org/10.3390/su14138177






