Thermal Properties of Hydrated Lime-Modified Asphalt Concrete and Modelling Evaluation for Their Effect on the Constructed Pavements in Service
Abstract
:1. Introduction
2. Experiment
2.1. Raw Materials and Mixtures
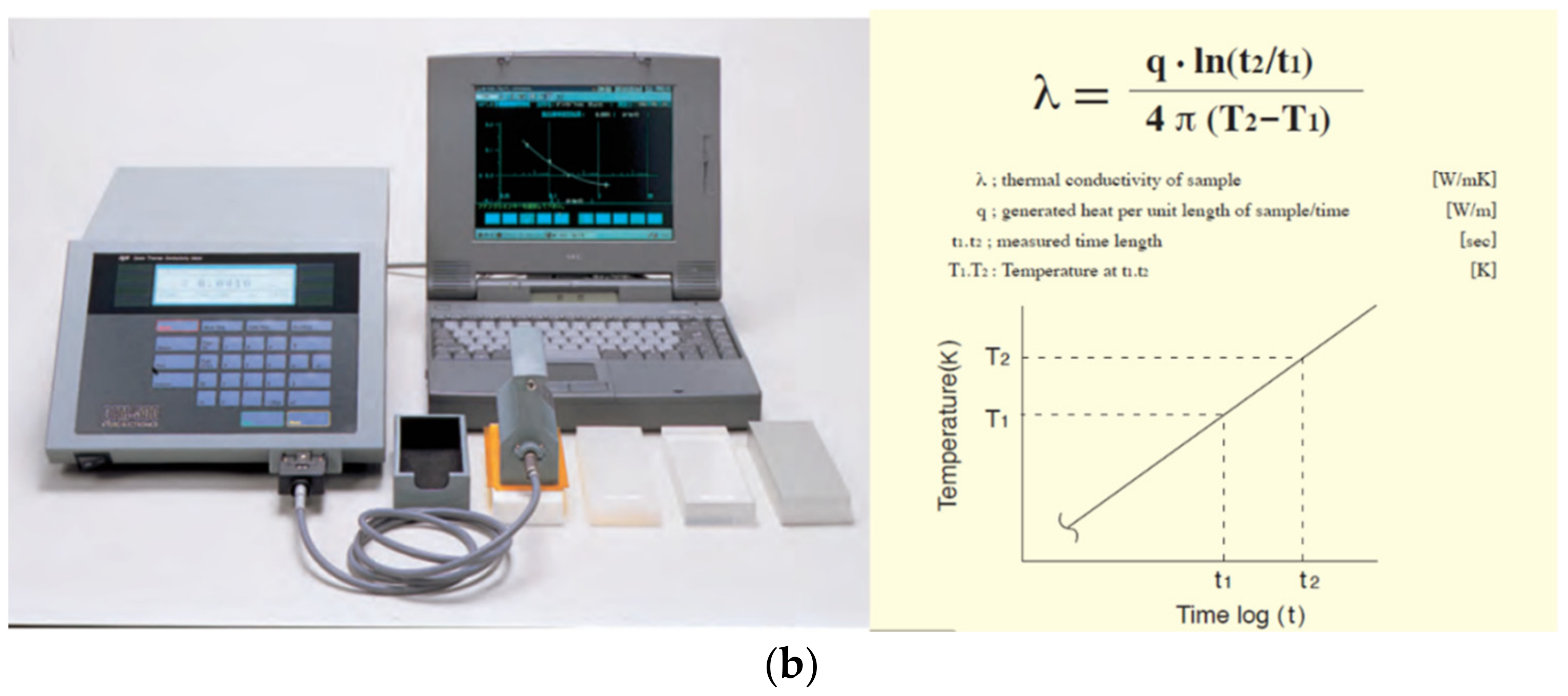
2.2. Specimen Preparation and Thermal Property Test
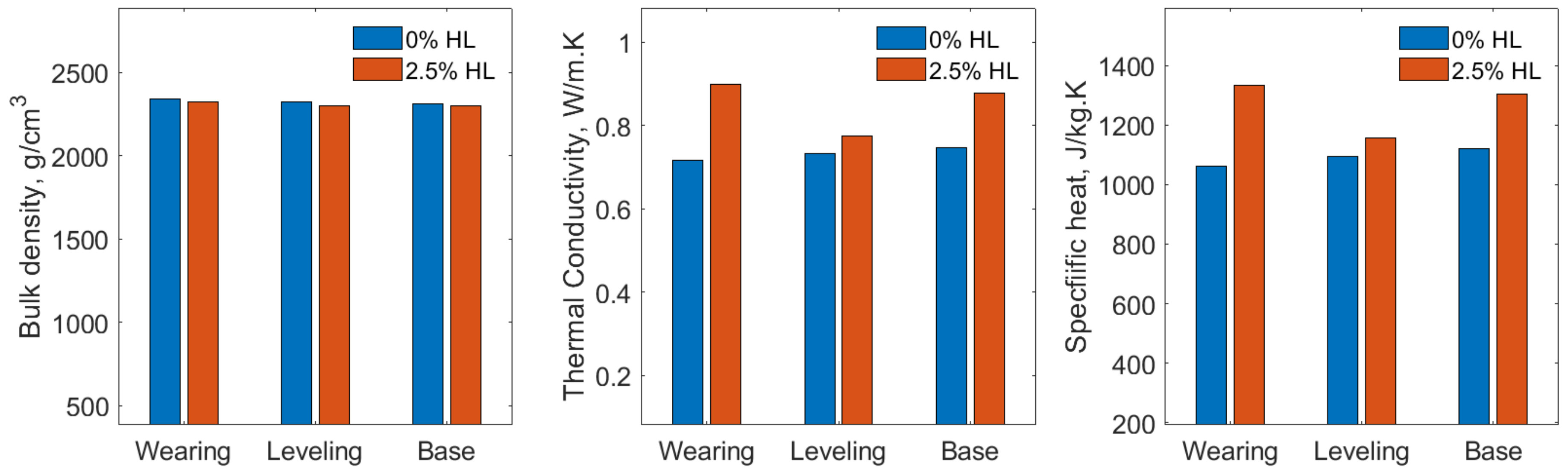
2.3. The Experimental Results
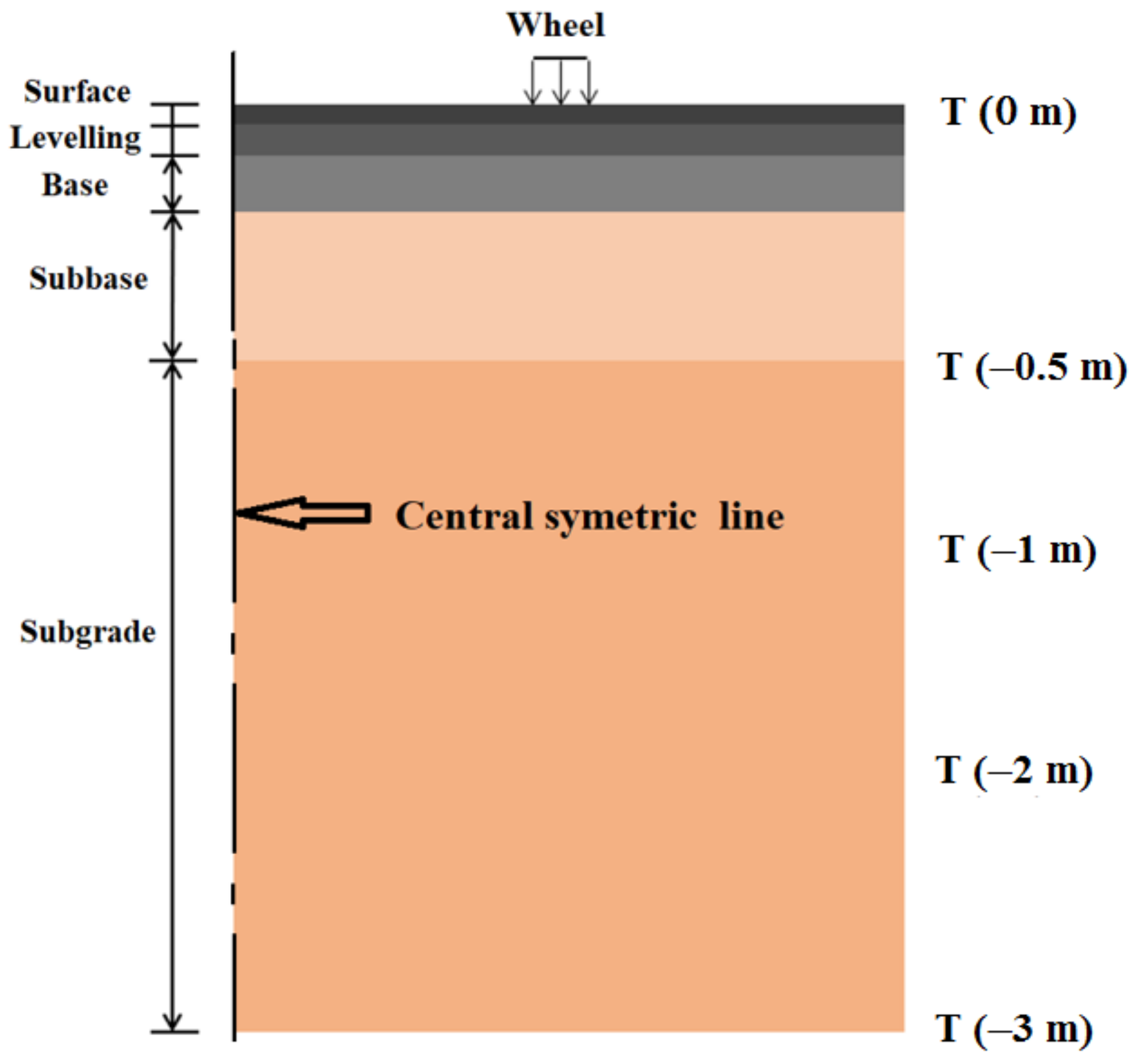
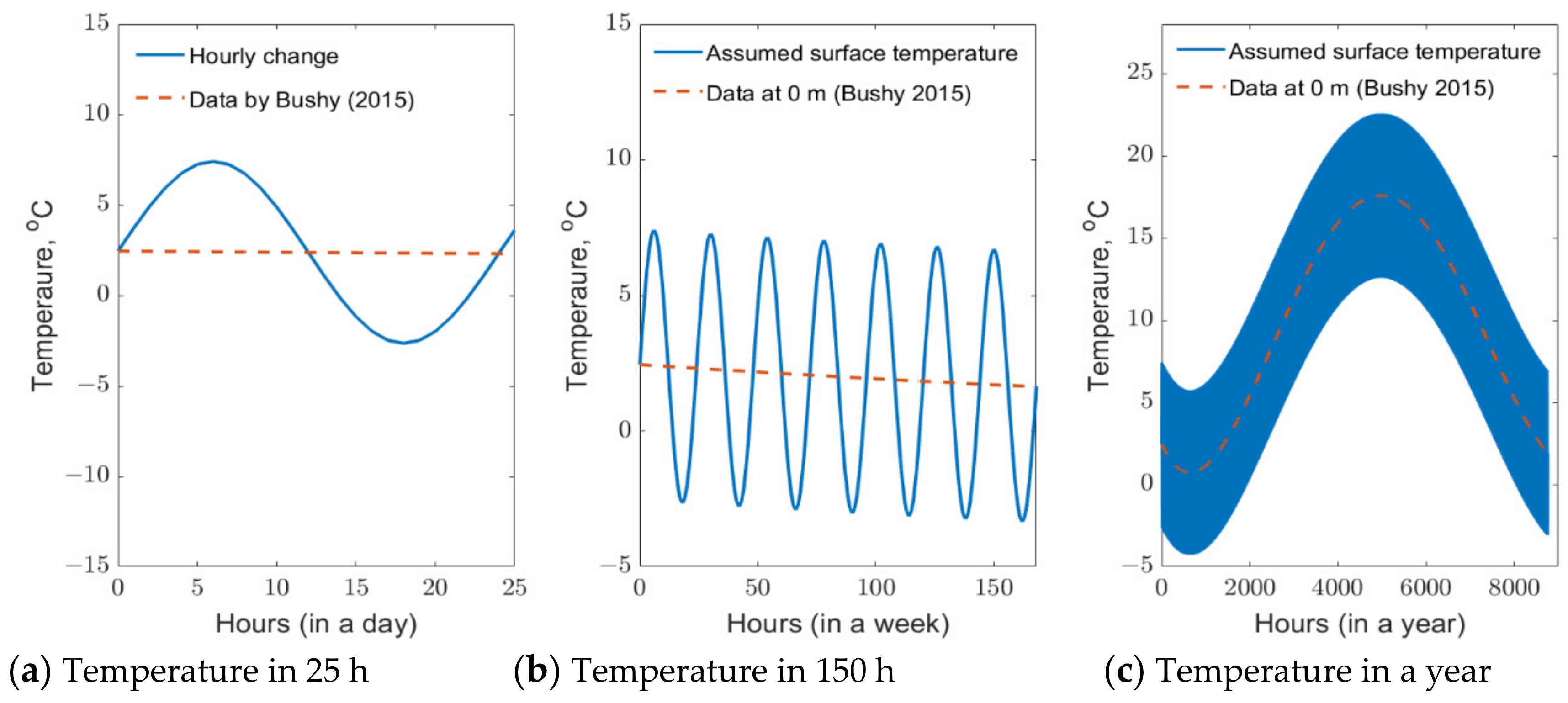
3. Modelling Evaluation for the Pavement Constructed Using HL Asphalt Concrete
- Motion equation
- Energy equation
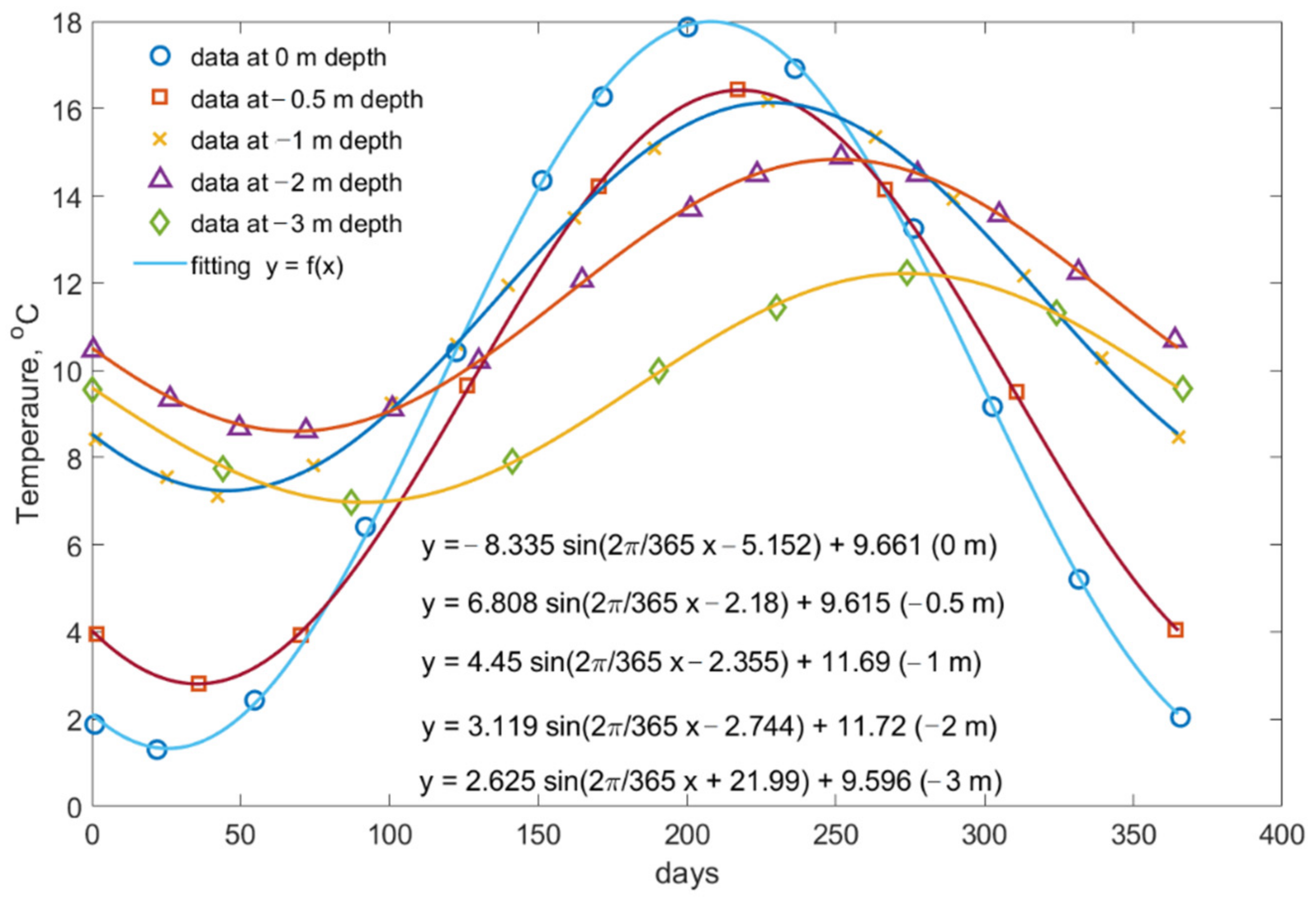
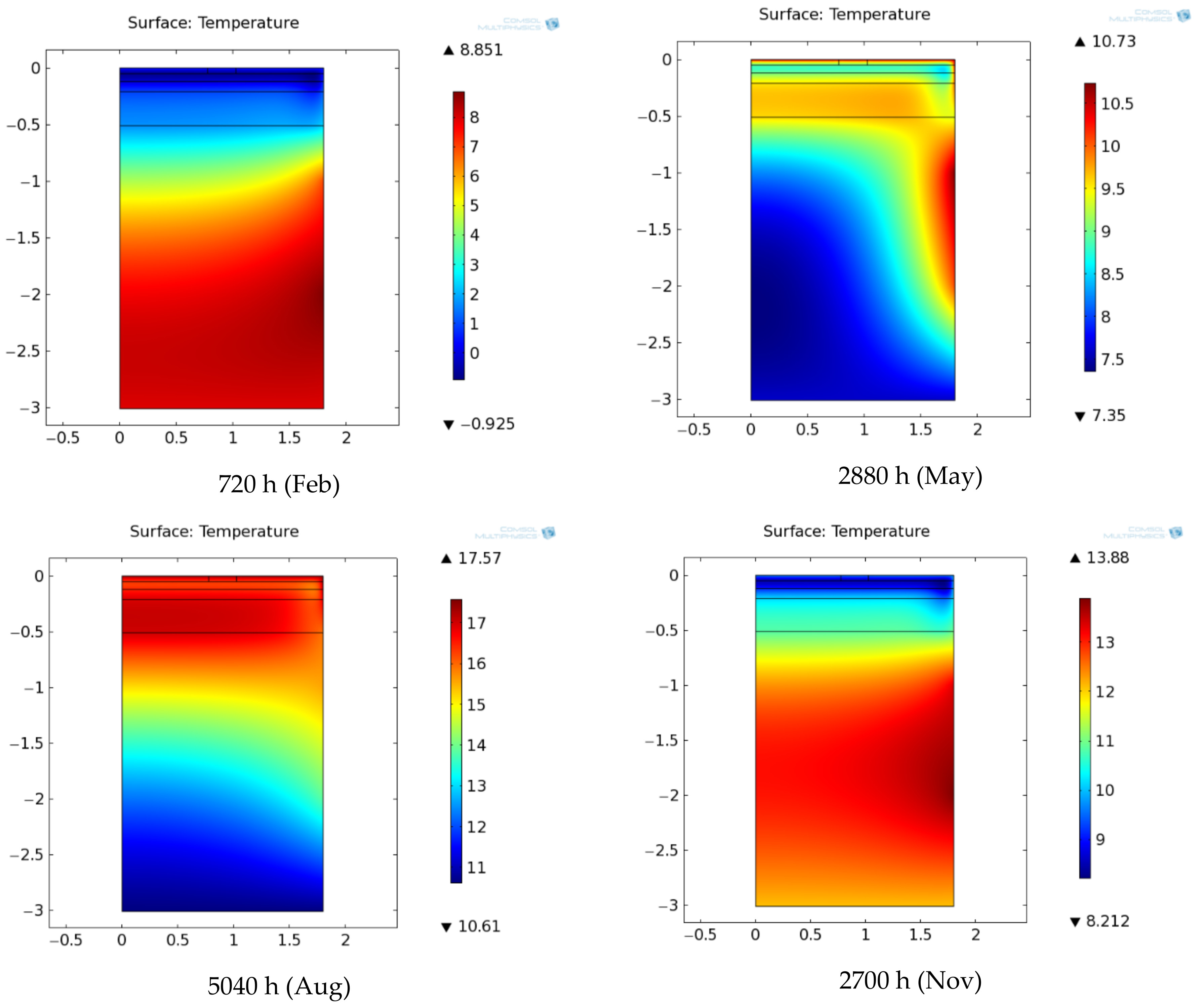
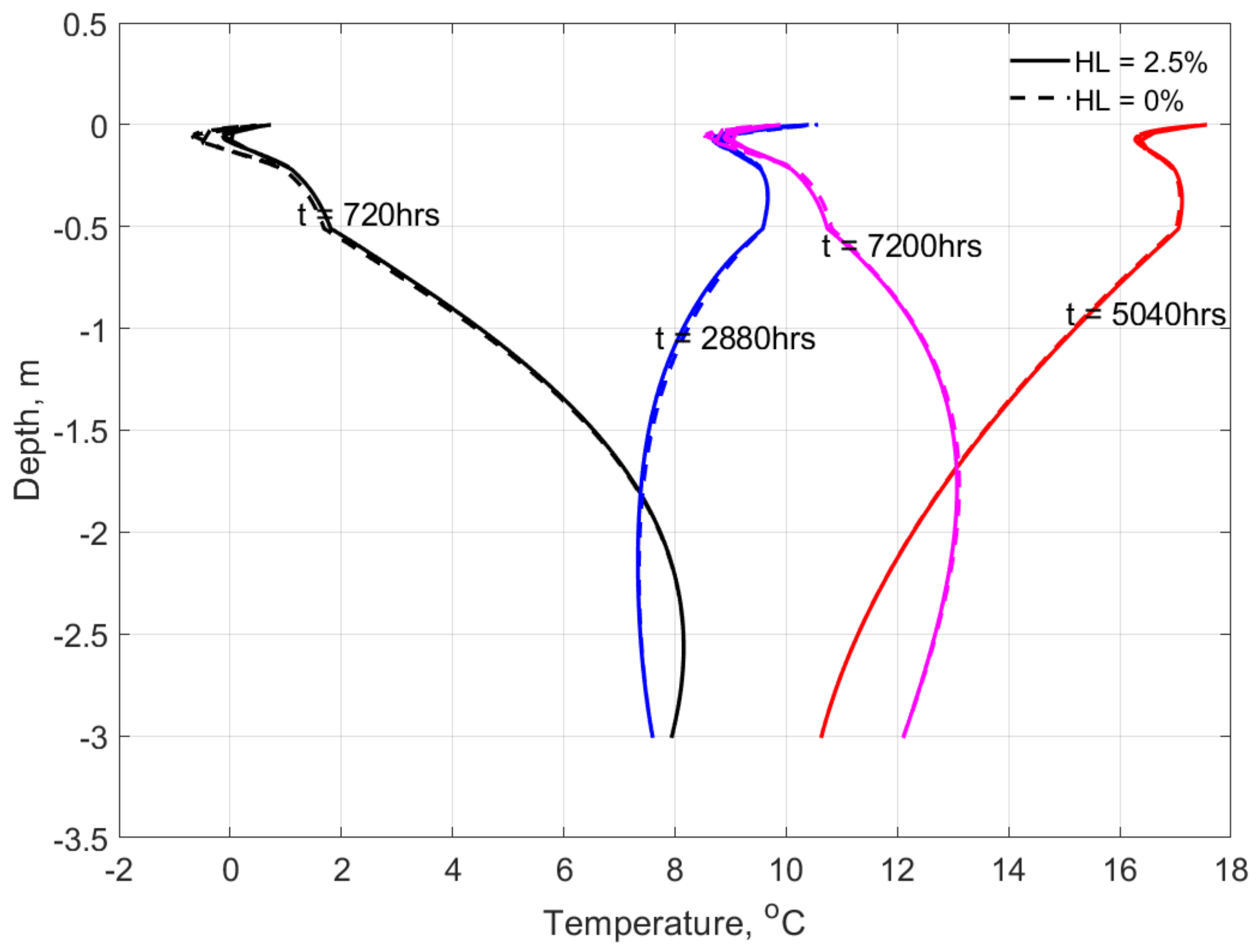
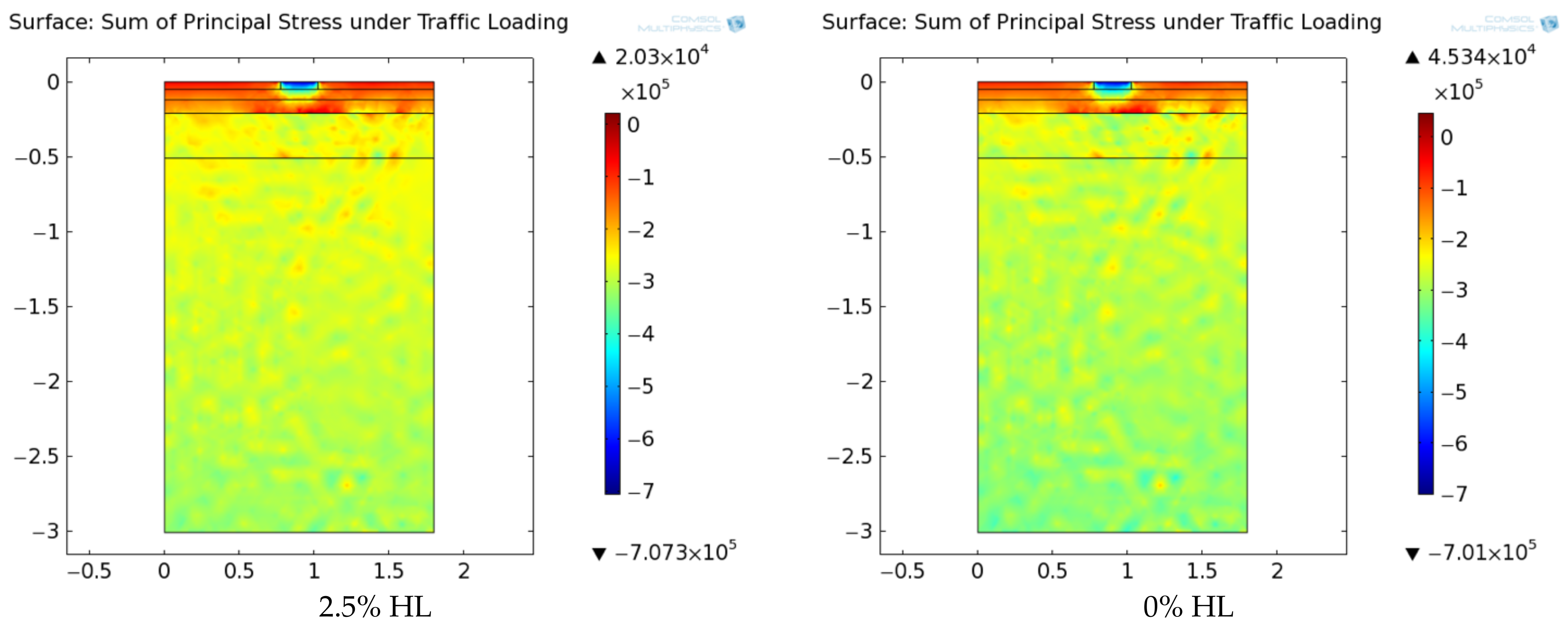
4. Modelling Results and Discussion
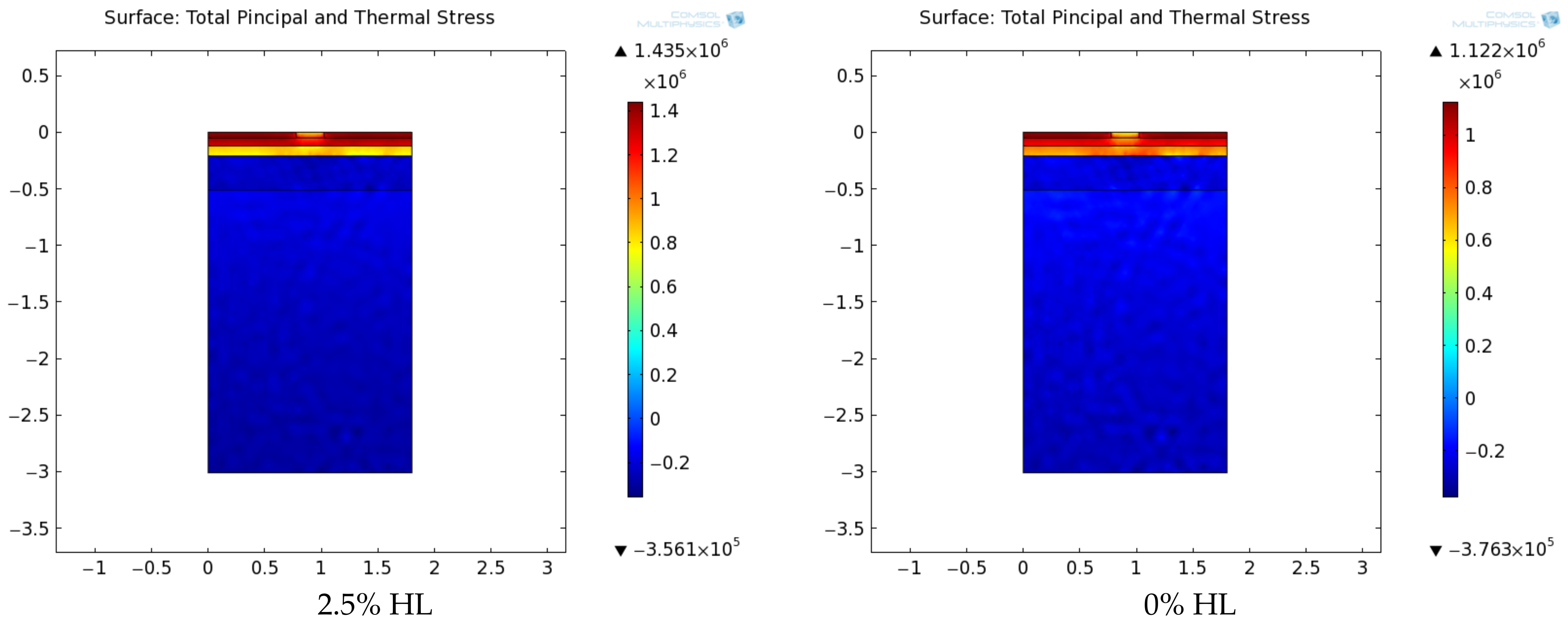
4.1. Temperature Profile and Thermal Strain & Stress Distribution
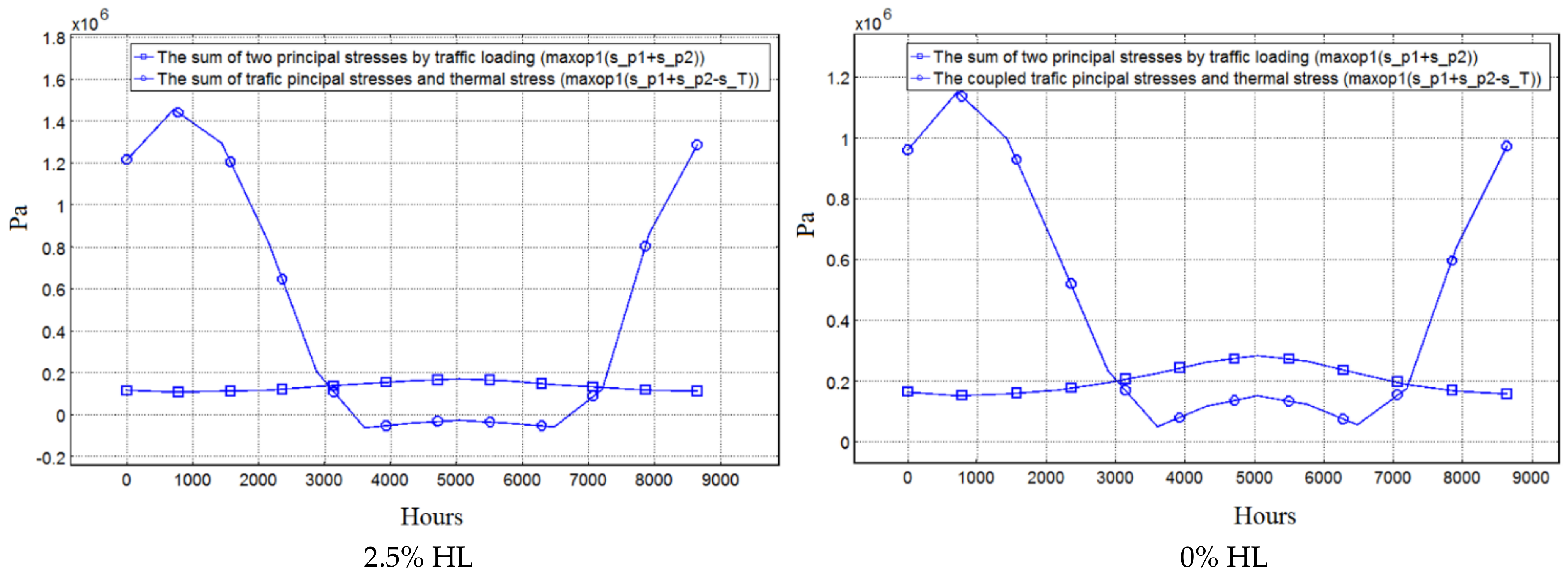
4.2. The Coupled Thermomechanical Effect
5. Conclusions
- 2.5% addition of HL to replace the equivalent weight of limestone dust filler enhances the thermal properties of the modified asphalt concrete of increased magnitudes of thermal conductivity (27% for wearing mix, 7% for leveling mix, 0.17% for base mix) and specific heat (25% for wearing mix, 6% for leveling mix, 0.16% for base mix). For the HL modified mix there is no correlation between the thermal properties and either the optimum asphalt cement or the mineral filler content.
- Between pavement using HL concrete and that not using HL concrete, there is a very small difference between the local temperature profiles within the structural layers. Correspondingly, the difference of the thermal strain and stress profiles with in the two pavements is very small as well.
- The thermal effect is pronounced under the coupled thermomechanical conditions for pavement exposed to both traffic and climatic impacts because of the temperature effect on the mechanical properties, such as the modulus and deformation coefficient, of the mixes.
- The modelling analysis shows that the HL pavement has about 1.5% less deformation than the control pavement at the place under the direct traffic loading. The result highlights the benefit of HL on long-term fatigue and rutting resistance.
- The modelling results indicate that the benefit of the HL on traffic-only stress reduction is about 39%, but the thermal effect increases that maximum total internal tensile stress level by 26% in the HL pavement in the winter season. It explains why there is an optimum HL content for asphalt concrete modification when exposed to temperature variation.
- The modelling results have showed that for HL pavement asphalt concrete, the local maximum tensile stress predominates in the surface region, i.e., wearing layer. It will help reduce the workload in crack repairing and in the long term help on saving costs and efforts of maintenance.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A
| Vehicle Type | Percentage of ith Vehicles Pi (%) | Number of Vehicles/Lane per Year Ni | Equivalent Axle Load Factor (EALF) | Growth Factor Gf | ESALs |
|---|---|---|---|---|---|
| Passenger car unit (PCU) | 55 | 250,937.50 | 0.0008 | 20.02 | 4019.02 |
| Single-unit trucks | |||||
| 2 axles, 4 tires | 10 | 45,625 | 0.003 | 20.02 | 2740.24 |
| 2 axles, 6 tires | 10 | 45,625 | 0.21 | 20.02 | 191,816.60 |
| 3 axles or more | 5 | 22,812.58 | 0.61 | 20.02 | 278,590.80 |
| Tractor semitrailers and combinations | |||||
| 4 axles or fewer | 5 | 22,812.50 | 0.62 | 20.02 | 283,157.90 |
| 5 axles | 10 | 45,625 | 1.09 | 20.02 | 995,619.60 |
| 6 axles or more | 5 | 22,812.50 | 1.23 | 20.02 | 561,748.70 |
| Total | 100 | 456,250 | 2,317,693 |
References
- Petersen, J.C. A Review of the Fundamentals of Asphalt Oxidation: Chemical, Physicochemical, Physical Property, and Durability Relationships; Transportation Research Circular; Transportation Research Board: Washington, DC, USA, 2009; 78p. [Google Scholar]
- Al-Marafi, M.N. Effects of Hydrated Lime on Moisture Susceptibility of Asphalt Concrete. Adv. Sci. Technol. Res. J. 2021, 15, 13–17. [Google Scholar] [CrossRef]
- Al-Tameemi, A.F.; Wang, Y.; Albayati, A. Experimental Study of the Performance Related Properties of Asphalt Concrete Modified with Hydrated Lime. J. Mater. Civ. Eng. 2016, 28, 04015185. [Google Scholar] [CrossRef]
- Iwanski, M.M. Effect of Hydrated Lime on Indirect Tensile Stiffness Modulus of Asphalt Concrete Produced in Half-Warm Mix Technology. Materials 2020, 13, 4731. [Google Scholar] [CrossRef] [PubMed]
- Bourona, S.; Hammouma, F.; Ruatb, H.; Métaisc, P.; Lesueurc, D. Improving the durability of asphalt mixtures with hydrated lime: Field results from highway A84. Case Stud. Constr. Mater. 2021, 14, e00551. [Google Scholar] [CrossRef]
- Al-Bayati, H.K.A.; Oyeyi, A.G.; Tighe, S.L. Experimental Assessment of Mineral Filler on the Volumetric Properties and Mechanical Performance of HMA Mixtures. Civ. Eng. J. 2020, 6, 2312–2331. [Google Scholar] [CrossRef]
- Al-Tameemi, A.F.; Wang, Y.; Albayati, A. Moisture Susceptibility and Fatigue Performance of Hydrated Lime–Modified Asphalt Concrete: Experiment and Design Application Case Study, Journal of Materials in Civil Engineering. Am. Soc. Civ. Eng. 2019, 31, 4019019. [Google Scholar]
- Albayati, A.; Wang, Y.; Haynes, J. Size effect of hydrated lime on the mechanical performance of asphalt concrete. Materials 2022, 15, 3715. [Google Scholar] [CrossRef] [PubMed]
- Mirzanamadi, R.; Johansson, P.; Grammatikos, S.A. Thermal properties of asphalt concrete: A numerical and experimental study. Constr. Build. Mater. 2018, 158, 774–785. [Google Scholar] [CrossRef]
- Han, D.G.; Zhu, H.; Li, L.L. Dynamic simulation analysis of the tire-pavement system considering temperature fields. Constr. Build. Mater. 2018, 171, 261–272. [Google Scholar] [CrossRef]
- Li, Y.; Liu, L.; Sun, L. Temperature predictions for asphalt pavement with thick asphalt layer. Constr. Build. Mater. 2017, 160, 802–809. [Google Scholar] [CrossRef]
- Albayati, A.H.; Mohammed, A.M. Effect of Lime Addition Methods on Performance Related Properties of Asphalt Concrete Mixture. J. Eng. 2016, 22, 1–20. [Google Scholar]
- SCRB/R9-State Corporation of Roads and Bridges. General Specification for Roads and Bridges; Ministry of Housing and Construction: Baghdad, Iraq, 2003.
- Little, D.N.; Allen, D.H.; Bhasin, A. Modeling and Design of Flexible Pavements and Materials; Springer International Publishing AG: Cham, Switzerland, 2018. [Google Scholar]
- Ishikawa, T.; Miura, S. Influence of moving wheel loads on mechanical behavior of submerged granular road bed. Soils Found. 2015, 55, 242–257. [Google Scholar] [CrossRef] [Green Version]
- Islam, R.; Tarefder, R.A. Coefficients of Thermal Contraction and Expansion of Asphalt Concrete in the Laboratory. J. Mater. Civ. Eng. 2015, 27, 04015020-1. [Google Scholar] [CrossRef]
- Chen, J.; Wang, H.; Xie, P.-Y. Pavement temperature prediction: Theoretical models and critical affecting factors. Appl. Therm. Eng. 2019, 158, 113755. [Google Scholar] [CrossRef]
- Qiao, Y.-N.; Dawson, A.R.; Parry, T.; Flintsch, G.; Wang, W.-S. Flexible Pavements and Climate Change: A Comprehensive Review and Implications. Sustainability 2020, 12, 1057. [Google Scholar] [CrossRef] [Green Version]
- Qin, Y.; Hiller, J.E. Modeling the temperature and stress distributions in rigid pavements: Impact of solar radiation absorption and heat history development. KSCE J. Civ. Eng. 2011, 15, 1361–1371. [Google Scholar] [CrossRef]
- Qin, Y.-H. Pavement surface maximum temperature increases linearly with solar absorption and reciprocal thermal inertial. Int. J. Heat Mass Transf. 2016, 97, 391–399. [Google Scholar] [CrossRef]
- Wu, H.; Sun, B.; Li, Z.; Yu, J. Characterizing thermal behaviors of various pavement materials and their thermal impacts on ambient environment. J. Clean. Prod. 2018, 172, 1358–1367. [Google Scholar] [CrossRef]
- Busby, J. UK shallow ground temperatures for ground coupled heat exchangers. Q. J. Eng. Geol. Hydrogeol. 2015, 48, 248–260. [Google Scholar] [CrossRef] [Green Version]




| Notation | Application | Hydrated Lime Content (%) | OAC% |
|---|---|---|---|
| CW | Wearing | 0 | 4.9 |
| CL | Levelling | 0 | 4.6 |
| CB | Base | 0 | 4.3 |
| HL2.5W | Wearing | 2.5 | 5.3 |
| HL2.5L | Levelling | 2.5 | 5 |
| HL2.5B | Base | 2.5 | 4.6 |
| Sieve Size | mm | Type I | Type II | Type IIIA |
|---|---|---|---|---|
| Base Course | Levelling Course | Wearing Course | ||
| % Passing by Weight of Total Aggregate and Filler | ||||
| 1.5 in | 37.5 | 100 | ||
| 1 in | 25.0 | 95 | 100 | |
| 0.75 in | 19.0 | 83 | 95 | 100 |
| 0.5 in | 12.5 | 68 | 80 | 95 |
| 3/8 in | 9.5 | 61 | 68 | 83 |
| No. 4 | 4.75 | 44 | 50 | 59 |
| No. 8 | 2.36 | 32 | 36 | 43 |
| No. 50 | 300 μm | 11 | 12 | 13 |
| No. 200 | 75 μm | 5 | 6 | 7 |
| Surface/Wearing | Binder/Levelling | Base | Subbase | Subgrade | Wheel | |
|---|---|---|---|---|---|---|
| Thickness (mm) | 50 | 70 | 90 | 300 | 2500 | - |
| Width (mm) | 1800 | 1800 | 1800 | 1800 | 1800 | 250 |
| Property | Mix | Wearing | Levelling | Base | Subbase | Subgrade |
|---|---|---|---|---|---|---|
| Modulus * E (MPa) | 0% HL | 0.28T2 − 41.53T + 2090 | 0.39T2 − 46.41T + 1929 | 0.34T2 − 40.41T + 1649 | 170 | 65 |
| 2.5% HL | 0.19T2 − 43.03T + 2623 | 0.52T2 − 63.3T + 2527 | 0.34T2 − 41.12T + 1803 | 170 | 65 | |
| Poisson ratio ν | 0% HL | 0.35 | 0.4 | |||
| 2.5% HL | ||||||
| Density ρ (g/cm3) | 0% HL | 2.34 | 2.32 | 2.31 | 1.76 | 1.29 |
| 2.5 HL | 2.32 | 2.30 | 2.3 | |||
| Thermal Conductivity k (W/m/K) | 0% HL | 0.71 | 0.73 | 0.75 | 1.3 | 0.28 |
| 2.5 HL | 0.90 | 0.78 | 0.88 | |||
| Thermal Capacity cp (J/kg/K) | 0% HL | 1062.6 | 1092.79 | 1121.12 | 837 | 800 |
| 2.5 HL | 1333.48 | 1155.49 | 1303.09 | |||
| Thermal deformation coefficient * α | 0% HL | CTC—Equation (5a) CTE—Equation (5b) | 3.32 × 10−6 | 3.4 × 10−5 | ||
| 2.5 HL | ||||||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Al Ashaibi, A.; Wang, Y.; Albayati, A.; Byzyka, J.; Scholz, M.; Weekes, L. Thermal Properties of Hydrated Lime-Modified Asphalt Concrete and Modelling Evaluation for Their Effect on the Constructed Pavements in Service. Sustainability 2022, 14, 7827. https://doi.org/10.3390/su14137827
Al Ashaibi A, Wang Y, Albayati A, Byzyka J, Scholz M, Weekes L. Thermal Properties of Hydrated Lime-Modified Asphalt Concrete and Modelling Evaluation for Their Effect on the Constructed Pavements in Service. Sustainability. 2022; 14(13):7827. https://doi.org/10.3390/su14137827
Chicago/Turabian StyleAl Ashaibi, Azedin, Yu Wang, Amjad Albayati, Juliana Byzyka, Miklas Scholz, and Laurence Weekes. 2022. "Thermal Properties of Hydrated Lime-Modified Asphalt Concrete and Modelling Evaluation for Their Effect on the Constructed Pavements in Service" Sustainability 14, no. 13: 7827. https://doi.org/10.3390/su14137827
APA StyleAl Ashaibi, A., Wang, Y., Albayati, A., Byzyka, J., Scholz, M., & Weekes, L. (2022). Thermal Properties of Hydrated Lime-Modified Asphalt Concrete and Modelling Evaluation for Their Effect on the Constructed Pavements in Service. Sustainability, 14(13), 7827. https://doi.org/10.3390/su14137827









