Research on Frequency Response Modeling and Frequency Modulation Parameters of the Power System Highly Penetrated by Wind Power
Abstract
:1. Introduction
1.1. Background and Literature Review
1.1.1. Background
1.1.2. The Impact of Strategies of DFIG on Frequency Response
1.1.3. The Research on System Frequency Response Model
1.2. Research Gap and Motivation
1.3. Contribution and Organization
1.3.1. Contribution of This Paper
- The frequency response model of the wind power highly penetrated system proposed this paper can fit the actual system better than TSFR.
- The calculation formulas of three indexes of system frequency stability are derived based on this model.
- The different effects of virtual inertia and virtual droop control strategies on the frequency response of the system are analyzed.
- The parameter setting of DFIG participating in frequency modulation is calculated according to the frequency stability requirements of the actual system.
1.3.2. Organization of This Paper
2. Frequency Response Model of the Wind Power Highly Penetrated System
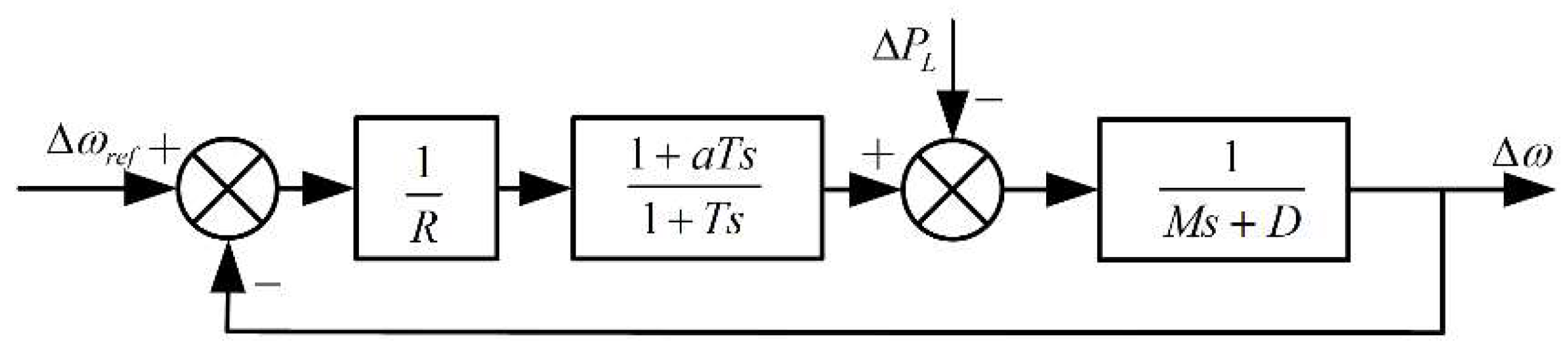
2.1. Frequency Response Model of Traditional Power System
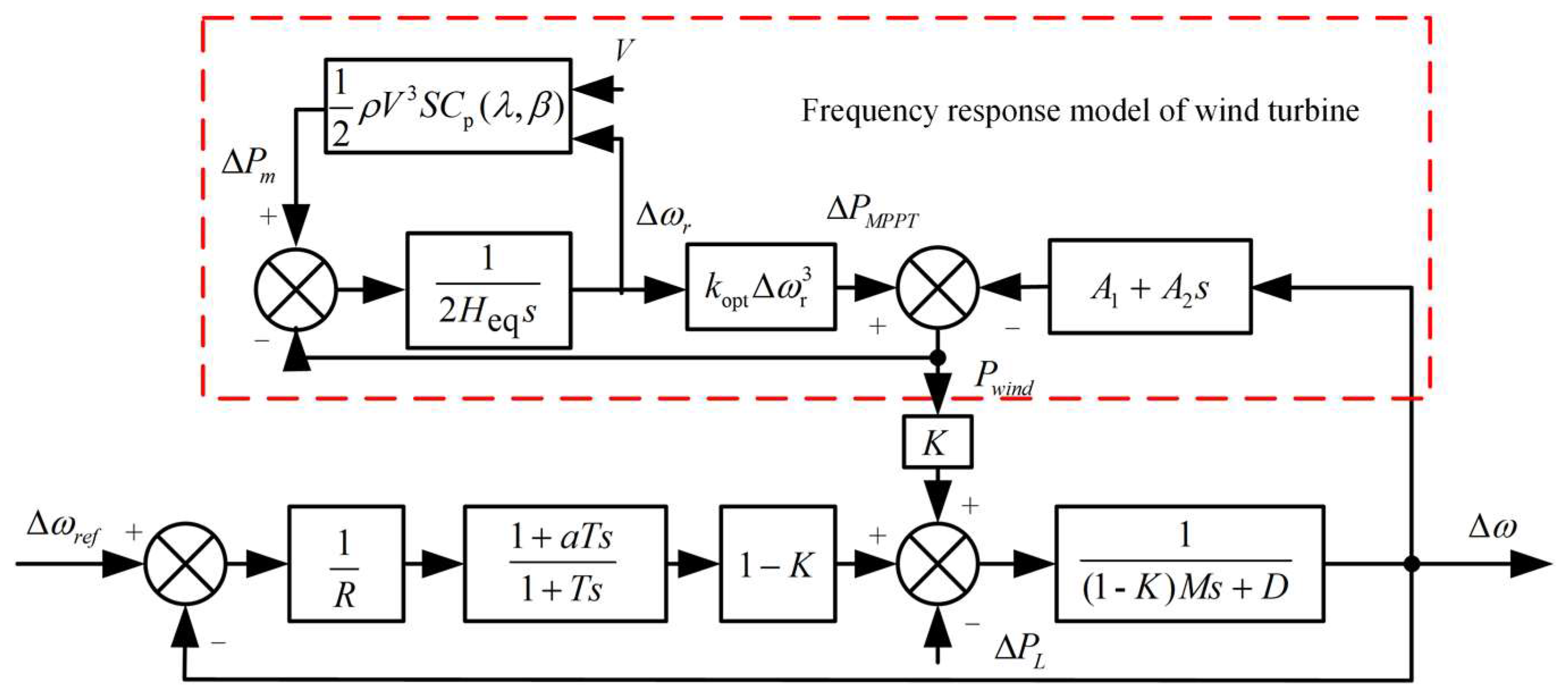
2.2. Wind Power System Modeling
2.3. Model Frequency Response Analysis
3. Frequency Stability Analysis of the Wind Power Highly Penetrated System
3.1. Steady-State Performance Analysis of Closed-Loop System
3.2. Analysis of the Maximum Rate of Change of Frequency of System Dynamic Frequency
3.3. Analysis of Lowest Point of System Dynamic Frequency
3.4. Analysis of Steady-State Frequency Deviation of the System
4. Case Study
4.1. Simulation Model Construction
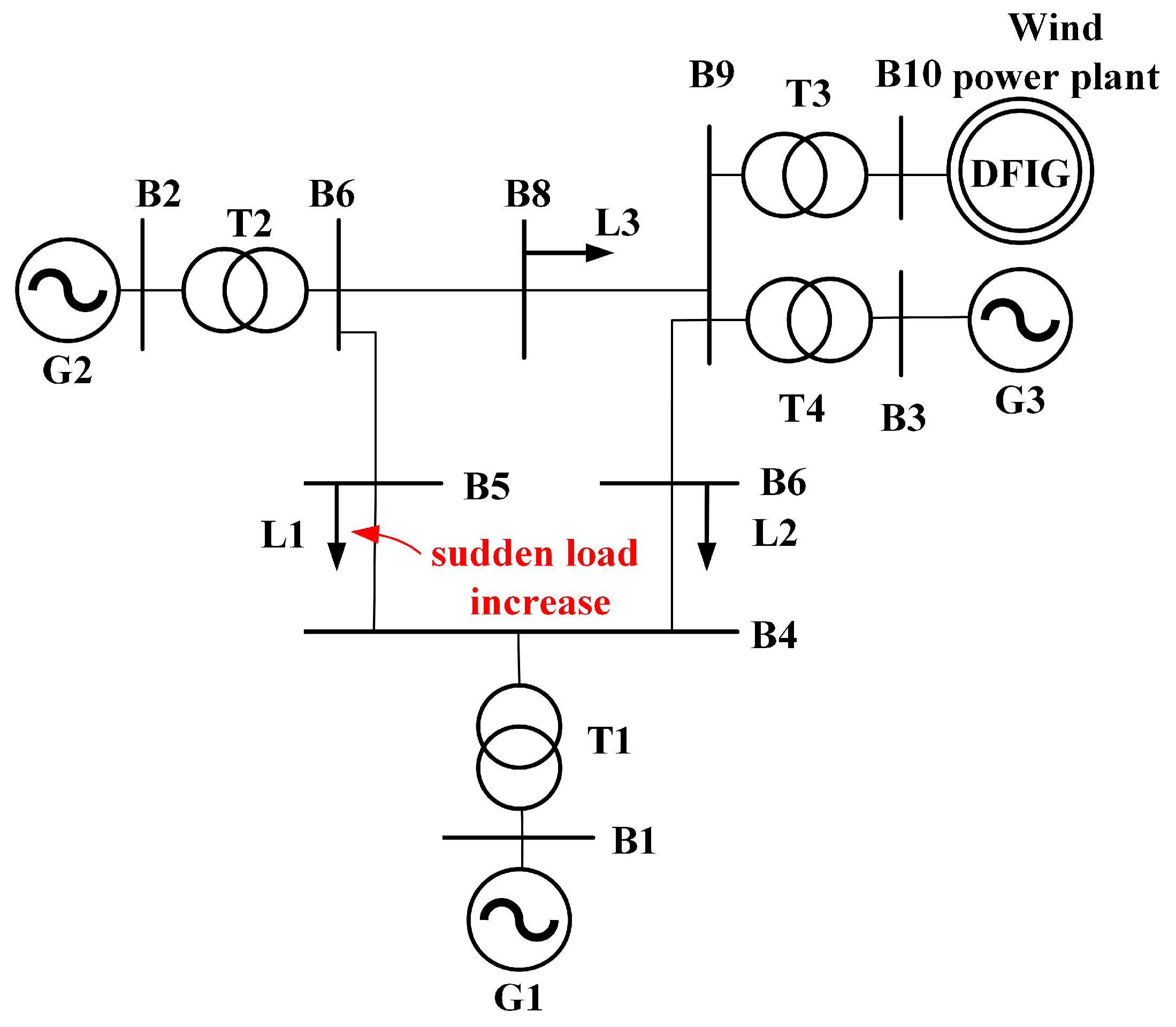
4.1.1. Small-Scale System
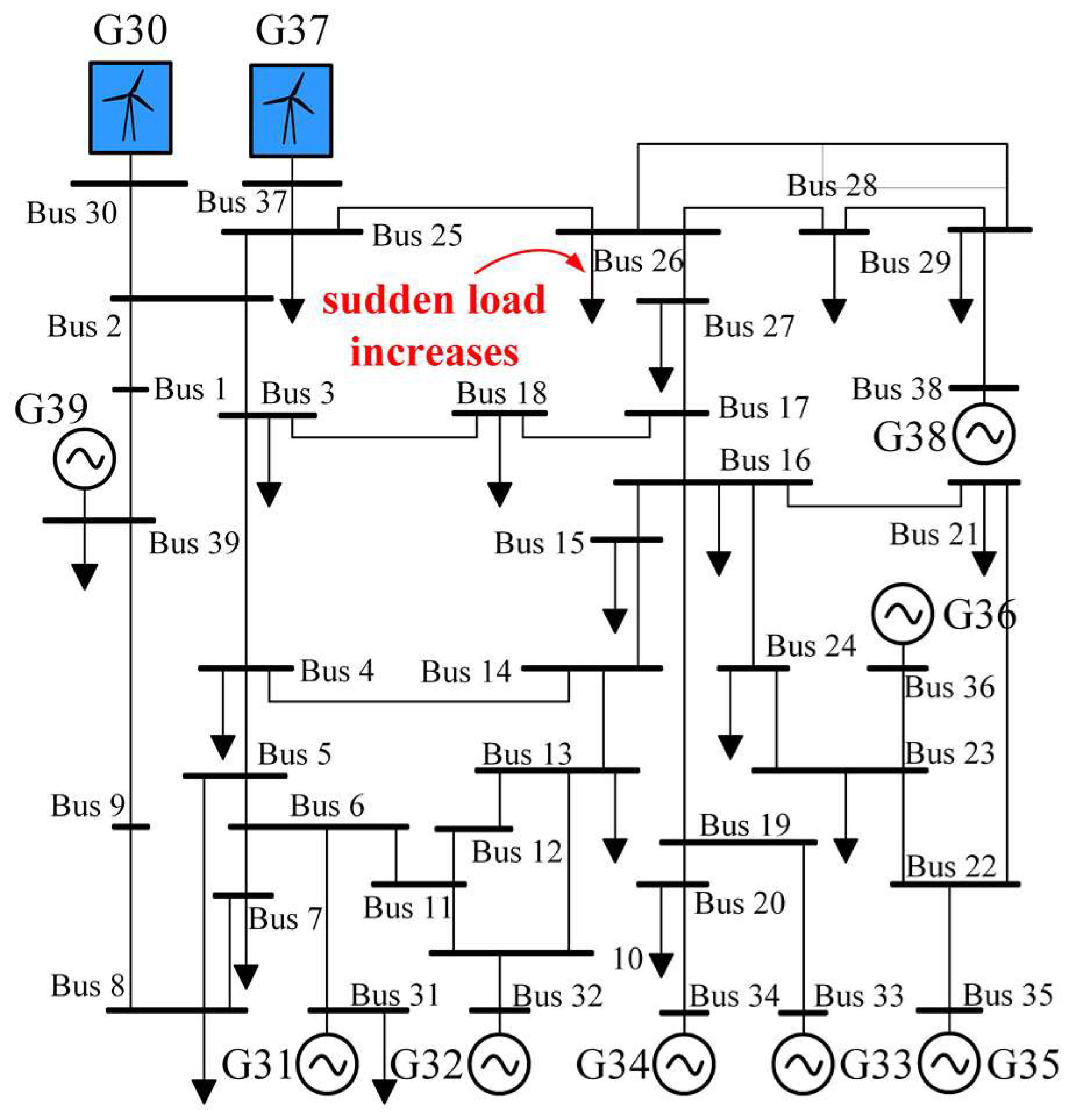
4.1.2. 39-Bus System
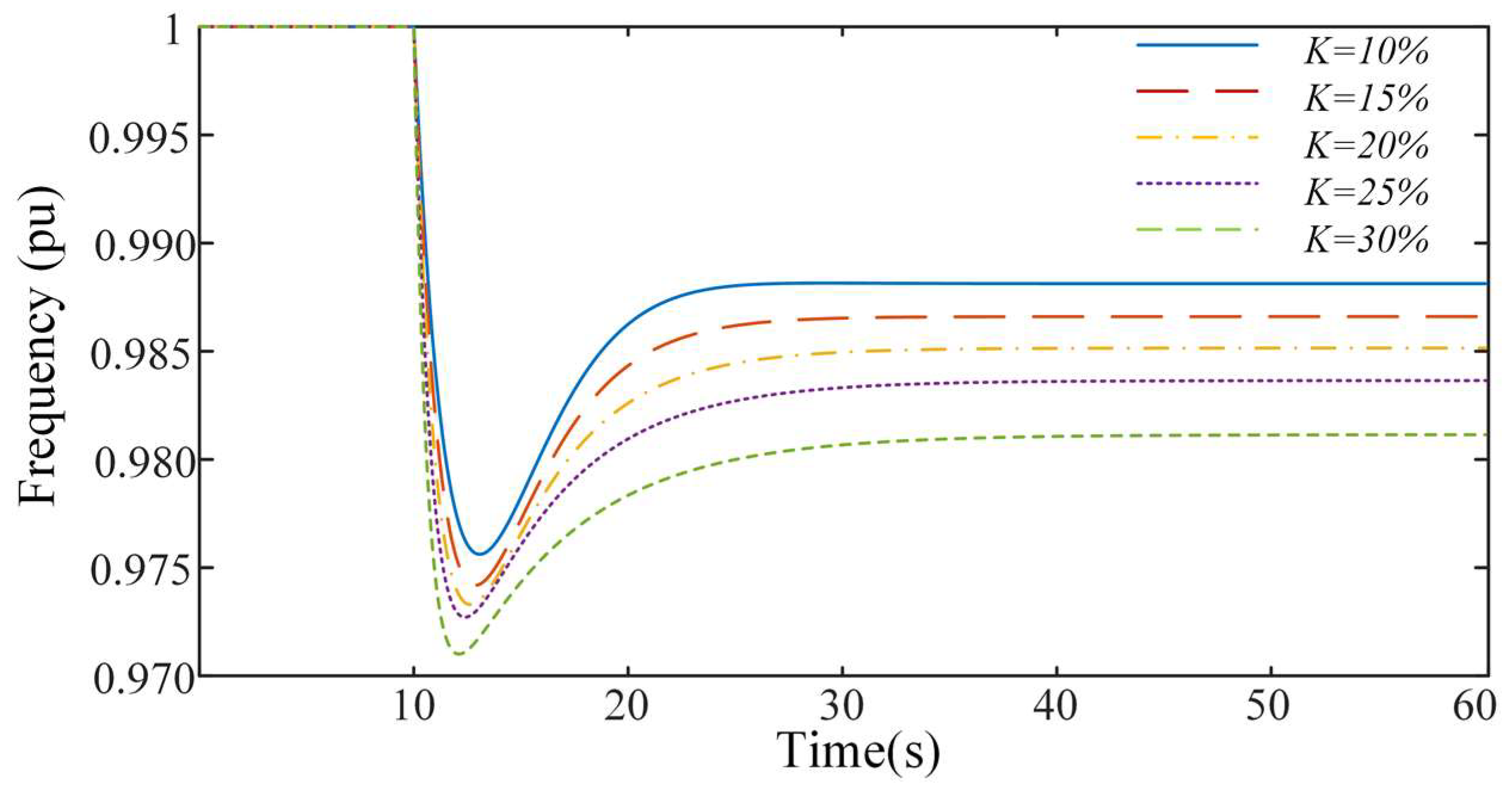
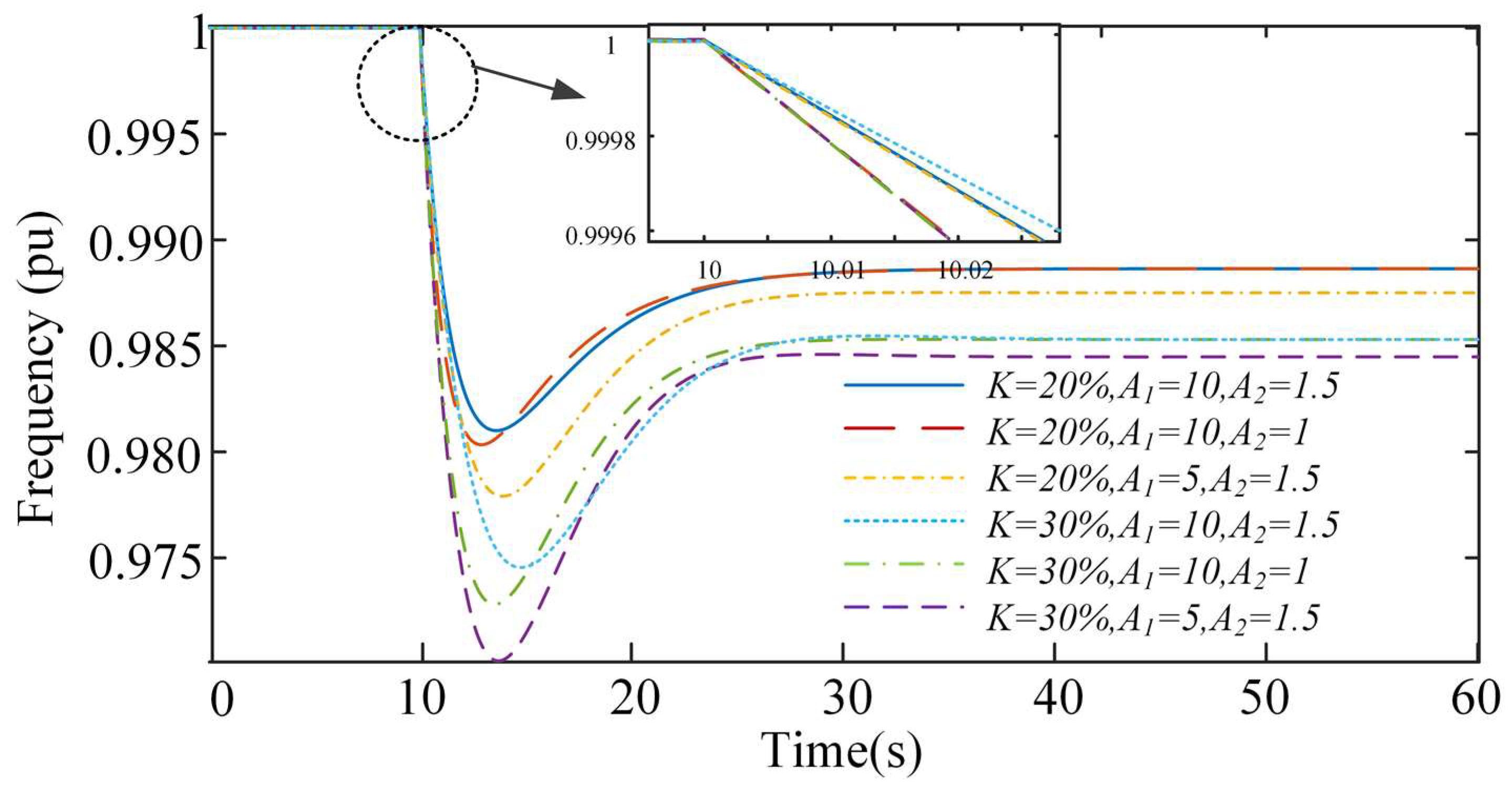
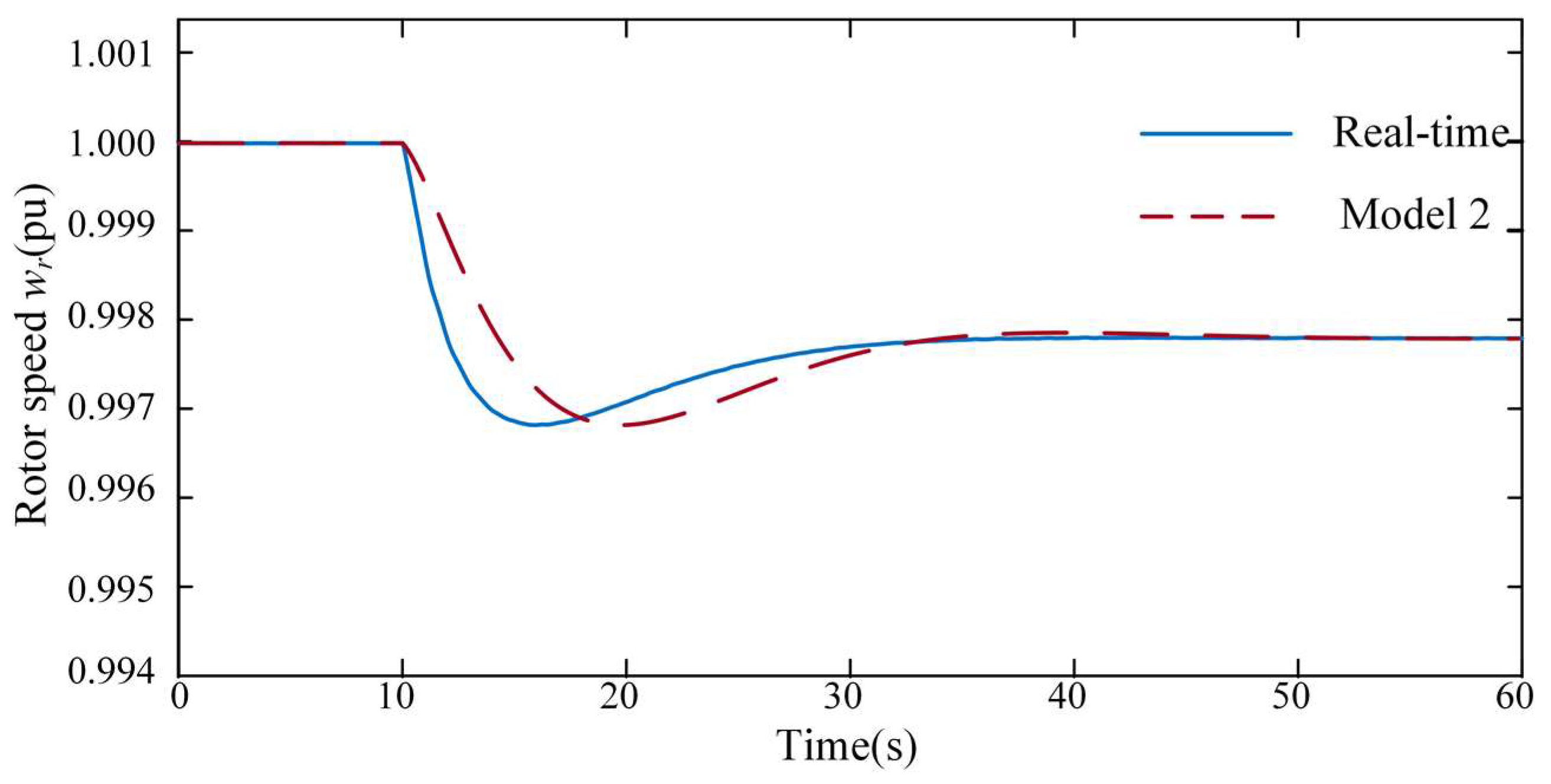
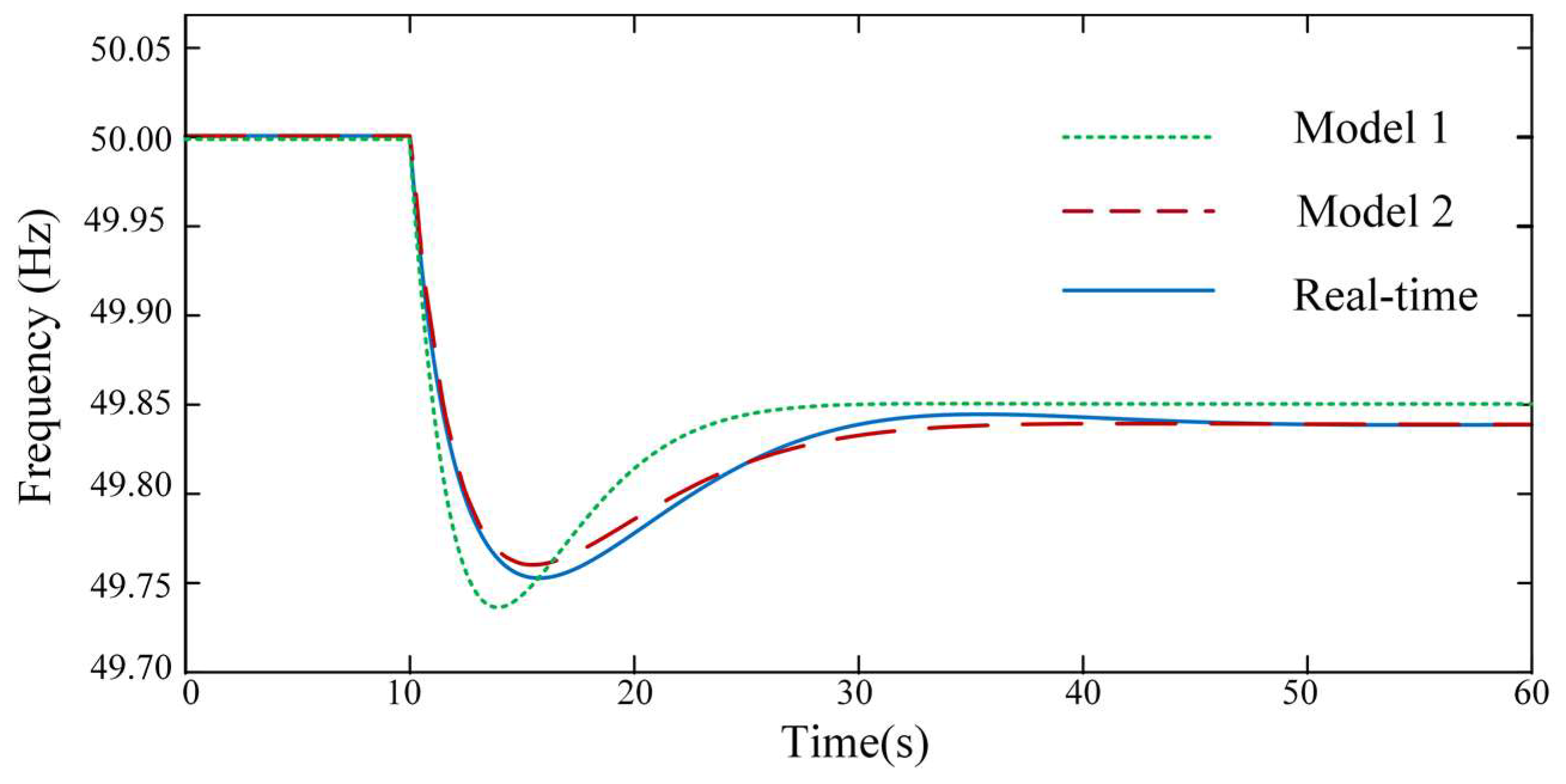
4.2. Case 1 Simulation Analysis
4.2.1. Scenario 1
4.2.2. Scenario 2
4.3. Case 2 Simulation Analysis
4.4. Case 3 Simulation Analysis
5. Conclusions and Research Prospect
5.1. Conclusions
5.2. Research Prospects
- Establishing DFIG frequency response models under different working states (the focus of the next work).
- Simplifying the calculation of the system frequency stable indexes when the SFR model considers the complex frequency response control strategies.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A
| Classification | Parameters | Values |
|---|---|---|
| Synchronous machine (G1, G2, G3) | Nominal power | 100 MW |
| Line-to-line voltage | 13.8 kV | |
| frequency | 50 Hz | |
| Reactance Xd | 1.3125 | |
| Reactance Xd′ | 0.1813 pu | |
| Reactance Xd″ | 0.107 pu | |
| Reactance Xq | 1.2578 pu | |
| Reactance Xq′ | 0.4 pu | |
| Reactance Xq″ | 0.107 pu | |
| Reactance Xl | 0.0742 pu | |
| Inertial time constant H | 6.4 s | |
| Transformer (T1, T2, T3) | Nominal power | 100 MW |
| Frequency | 50 Hz | |
| Winding 1 V1 (Ph-Ph) | 13.8 kV | |
| Winding 1 R1 | 0.002 pu | |
| Winding 1 L1 | 0 | |
| Winding 2 V2 (Ph-Ph) | 230 kV | |
| Winding 2 R2 | 0.002 pu | |
| Winding 2 L2 | 0.0586 | |
| Magnetization resistance | 500 pu | |
| Magnetization resistance | 500 pu | |
| Transformer (T4) | Nominal power | 100 MW |
| Frequency | 50 Hz | |
| Winding 1 V1 (Ph-Ph) | 575 V | |
| Winding 1 R1 | 0.002 pu | |
| Winding 1 L1 | 0 | |
| Winding 2 V2 (Ph-Ph) | 230 kV | |
| Winding 2 R2 | 0.002 pu | |
| Winding 2 L2 | 0.0586 | |
| Magnetization resistance | 500 pu | |
| Magnetization resistance | 500 pu | |
| DFIG | Nominal power | 1.5/0.9 MW |
| Line-to-line voltage | 575 V | |
| frequency | 50 Hz | |
| Stator Rs | 0.00706 pu | |
| Stator L1s | 0.171 pu | |
| Rotor Rr′ | 0.005 pu | |
| Rotor L1r′ | 0.156 pu | |
| Magnetizing inductance Lm | 2.9 pu | |
| Inertia constant H(s) | 5.04 s | |
| Power at point C | 0.73 pu | |
| Wind speed at point C | 12 m/s | |
| Power regulatorgains[kp ki] | [1 100] | |
| DC bus voltage regulator gains[kp ki] | [0.002 0.05] | |
| Grid-side converter current regulator gains[kp ki] | [1 100] | |
| Rotor-side converter current regulator gains[kp ki] | [0.3 8] |
References
- Fernández-Guillamón, A.; Gómez-Lázaro, E.; Muljadi, E.; Molina-García, Á. Power systems with high renewable energy sources: A review of inertia and frequency control strategies over time. Renew. Sustain. Energy Rev. 2019, 115, 109369. [Google Scholar] [CrossRef] [Green Version]
- Olujobi, O.J. The legal sustainability of energy substitution in Nigeria’s electric power sector: Renewable energy as alternative. Prot. Control Mod. Power Syst. 2020, 5, 32. [Google Scholar] [CrossRef]
- Tielens, P.; Van Hertem, D. The relevance of inertia in power systems. Renew. Sustain. Energy Rev. 2016, 55, 999–1009. [Google Scholar] [CrossRef]
- Arani, Z.D.; Taher, S.A.; Ghasemi, A.; Shahidehpour, M. Application of Multi-Resonator Notch Frequency Control for Tracking the Frequency in Low Inertia Microgrids Under Distorted Grid Conditions. IEEE Trans. Smart Grid 2019, 10, 337–349. [Google Scholar] [CrossRef]
- Qi, J.; Tang, F.; Xie, J.; Li, X. Effect of DFIG Under Droop Control on Center Migration of Out-of-Step Oscillation. In Proceedings of the 2021 IEEE 5th Conference on Energy Internet and Energy System Integration (EI2), Taiyuan, China, 22–24 October 2021; pp. 2970–2974. [Google Scholar]
- Dreidy, M.; Mokhlis, H.; Mekhilef, S. Inertia Response and Frequency Control Techniques for Renewable Energy Sources: A Review. Renew. Sustain. Energy Rev. 2017, 69, 144–155. [Google Scholar] [CrossRef]
- Josephine, R.; Suja, S. Estimating PMSG wind turbines by inertia and droop control schemes with intelligent fuzzy controller in Indian development. J. Electr. Eng. Technol. 2014, 9, 1196–1201. [Google Scholar] [CrossRef] [Green Version]
- Azizipanah-Abarghooee, R.; Malekpour, M.; Dragičević, T.; Blaabjerg, F.; Terzija, V. A Linear Inertial Response Emulation for Variable Speed Wind Turbines. IEEE Trans. Power Syst. 2020, 35, 1198–1208. [Google Scholar] [CrossRef]
- Pepiciello, A.; Vaccaro, A. An Optimization-based Method for Estimating Critical Inertia in Smart Grids. In Proceedings of the 2019 IEEE International Conference on Systems, Man and Cybernetics (SMC), Bari, Italy, 6–9 October 2019; pp. 2237–2241. [Google Scholar]
- Sun, M.; Xie, G.; Chen, L.; Liu, Y.; Li, X.; Min, Y. Study on the Necessity and Role of Inertia in Power System Frequency Response. In Proceedings of the 2020 IEEE 4th Conference on Energy Internet and Energy System Integration (EI2), Wuhan, China, 30 October–1 November 2020; pp. 155–159. [Google Scholar]
- Wang, S.; Tomsovic, K. Fast Frequency Support from Wind Turbine Generators with Auxiliary Dynamic Demand Control. IEEE Trans. Power Syst. 2019, 34, 3340–3348. [Google Scholar] [CrossRef]
- Jin, C.; Li, W.; Shen, J.; Li, P.; Liu, L.; Wen, K. Active Frequency Response Based on Model Predictive Control for Bulk Power System. IEEE Trans. Power Syst. 2019, 34, 3002–3013. [Google Scholar] [CrossRef]
- Abir, A.; Mehdi, D. Control of permanent-magnet generators applied to variable-speed wind-energy. In Proceedings of the 2017 International Conference on Green Energy & Conversion Systems (GECS), Hammamet, Tunisia, 23–25 March 2017; pp. 1–6. [Google Scholar]
- Liu, K.; Qu, Y.; Kim, H.M.; Song, H. Avoiding frequency second dip in power unreserved control during wind power rotational speed recovery. IEEE Trans. Power Syst. 2018, 33, 3097–3106. [Google Scholar] [CrossRef]
- Kayikci, M.; Milanovic, J.V. Dynamic contribution of DFIG-based wind plants to system frequency disturbances. IEEE Trans. Power Syst. 2009, 24, 859–867. [Google Scholar] [CrossRef]
- Wang, S.; Hu, J.; Yuan, X. Virtual synchronous control for grid-connected DFIG-based wind turbines. IEEE J. Emerg. Sel. Top. Power Electron. 2015, 3, 932–944. [Google Scholar] [CrossRef]
- Fazeli, M.; Asher, G.M.; Klumpner, C.; Yao, L.; Bazargan, M. Novel integration of wind generator-energy storage systems within microgrids. IEEE Trans. Smart Grid 2012, 3, 728–737. [Google Scholar] [CrossRef]
- Shi, Q.; Li, F.; Cui, H. Analytical Method to Aggregate Multi-Machine SFR Model with Applications in Power System Dynamic Studies. IEEE Trans. Power Syst. 2018, 33, 6355–6367. [Google Scholar] [CrossRef]
- Li, H.; Wang, J.; Du, Z.; Zhao, F.; Liang, H.; Zhou, B. Frequency control framework of power system with high wind penetration considering demand response and energy storage. J. Eng. 2017, 2017, 1153–1158. [Google Scholar] [CrossRef]
- Wu, Z.; Gao, W.; Gao, T.; Yan, W.; Zhang, H.; Yan, S.; Wang, X. State-of-the-art review on frequency response of wind power plants in power systems. J. Mod. Power Syst. Clean Energy 2018, 6, 1–16. [Google Scholar] [CrossRef] [Green Version]
- Golpîra, H.; Seifi, H.; Messina, A.R.; Haghifam, M. Maximum Penetration Level of Micro-Grids in Large-Scale Power Systems: Frequency Stability Viewpoint. IEEE Trans. Power Syst. 2016, 31, 5163–5171. [Google Scholar] [CrossRef]
- Zhang, J.; Li, M. Analysis of the Frequency Characteristic of the Power Systems Highly Penetrated by New Energy Generation. Proc. Chin. Soc. Electr. Eng. 2020, 9, 3498–3506. [Google Scholar]
- Li, D.; Sun, Y.; Xu, B.; Zhang, J. Minimum inertia and primary frequency capacity assessment for a new energy high permeability power system considering frequency stability. Power Syst. Prot. Control 2022, 3, 54–61. [Google Scholar]
- Garmroodi, M.; Verbic, G.; Hill, D.J. Frequency support from wind turbine generators with a time variable droop characteristic. IEEE Trans. Sustain. Energy 2017, 9, 676–684. [Google Scholar] [CrossRef]
- Ashton, P.; Saunders, C.; Taylor, G.; Carter, A.; Bradley, M. Inertia estimation of the GB power system using synchrophasor measurements. In Proceedings of the 2017 IEEE Power & Energy Society General Meeting, Chicago, IL, USA, 16–20 July 2017; pp. 701–709. [Google Scholar]
- Margaris, I.D.; Papathanassiou, S.A.; Hatziargyriou, N.D.; Hansen, A.D.; Sorensen, P. Frequency control in autonomous power systems with high wind power penetration. IEEE Trans. Sustain. Energy 2012, 3, 189–199. [Google Scholar] [CrossRef]
- Kundur, P. Power System Stability and Control; McGraw-Hill: New York, NY, USA, 1994; pp. 395–428. [Google Scholar]
- Krpan, M.; Kuzle, I. Introducing low-order system frequency response modelling of a future power system with high penetration of wind power plants with frequency support capabilities. IET Renew. Power Gener. 2018, 12, 1453–1461. [Google Scholar] [CrossRef]
- Hu, B.; Tang, F.; Liu, D.; Li, Y.; Wei, X. A Wind-Storage Combined Frequency Regulation Control Strategy Based on Improved Torque Limit Control. Sustainability 2021, 13, 3765. [Google Scholar] [CrossRef]
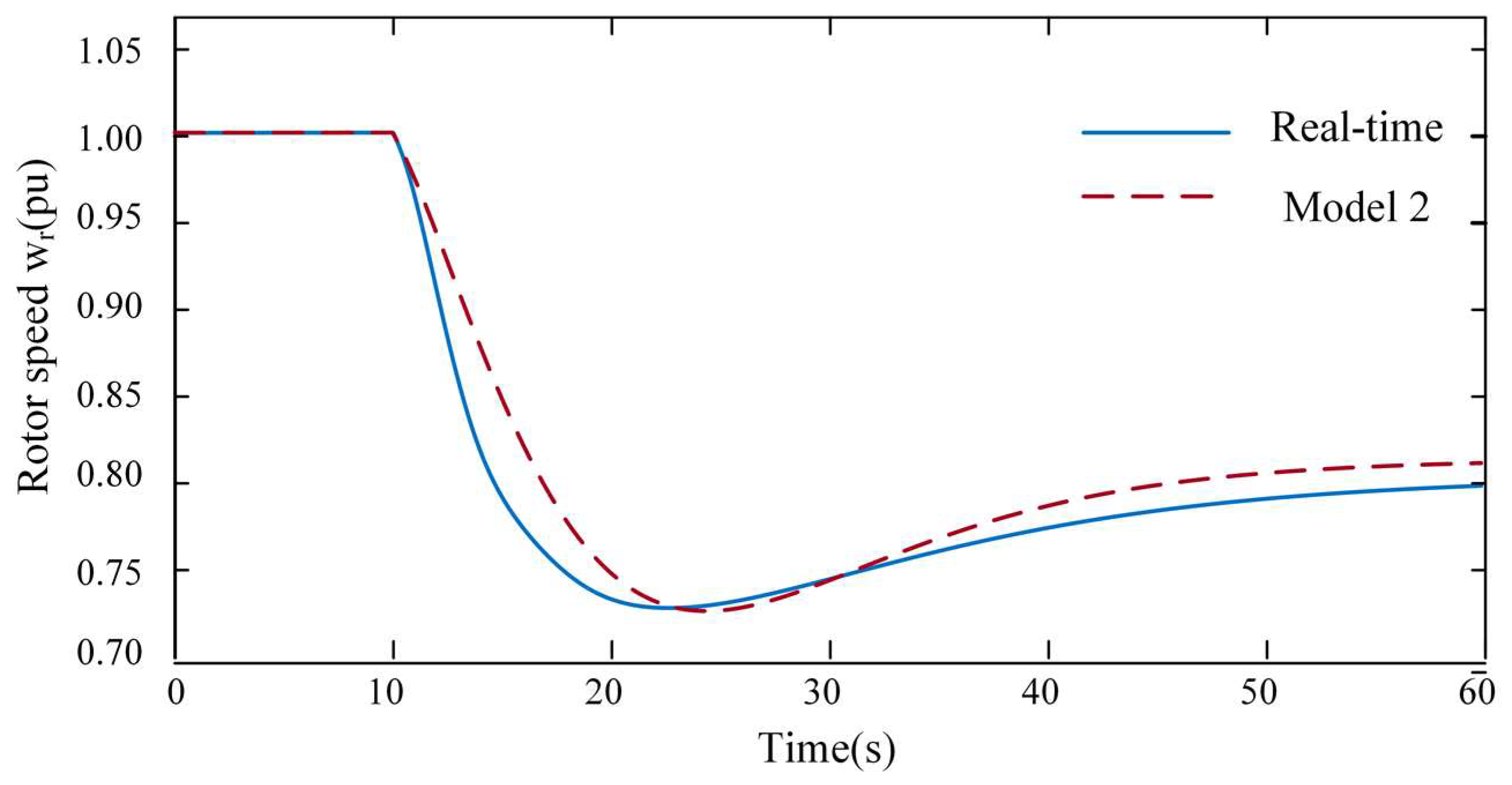
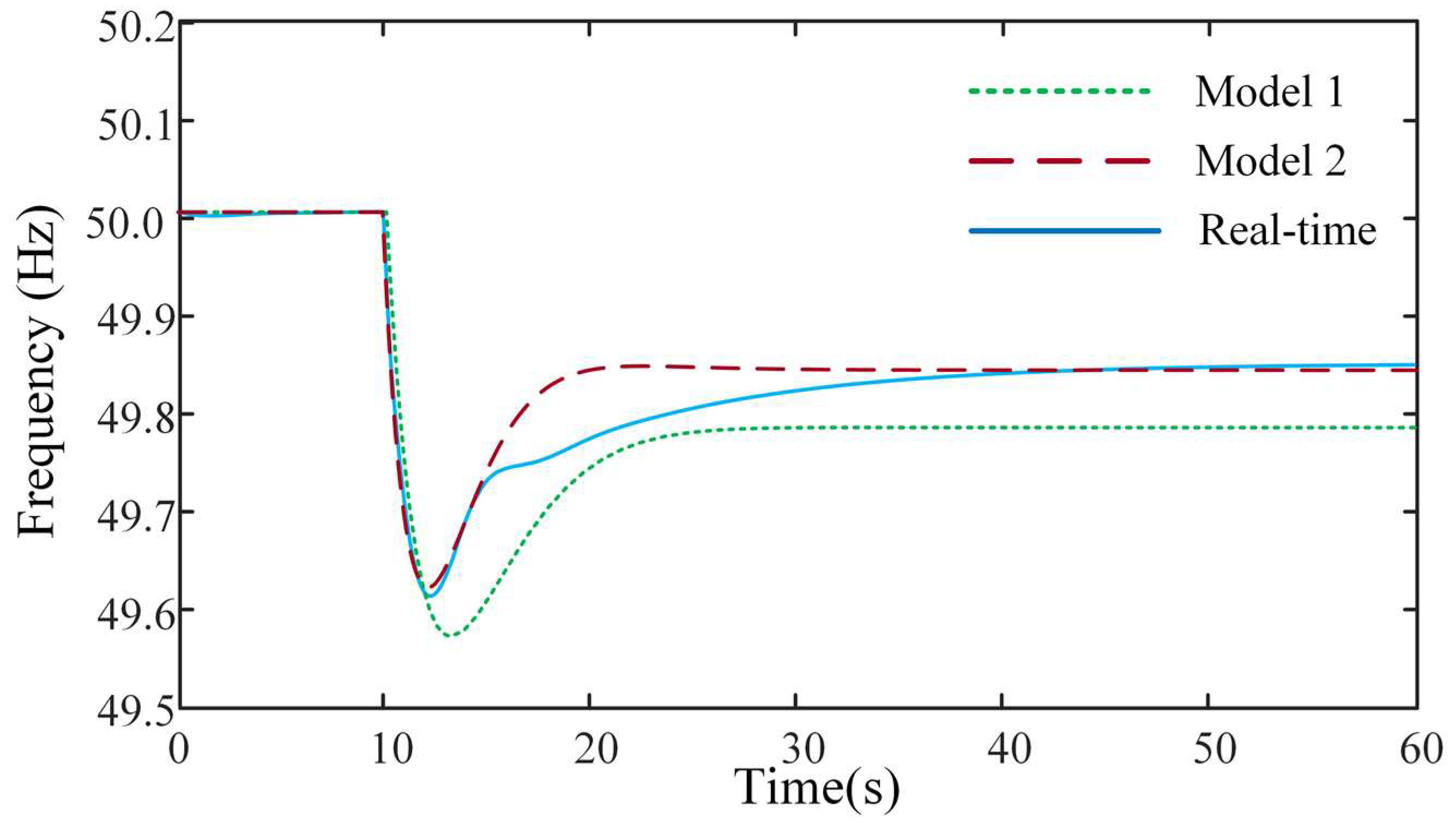
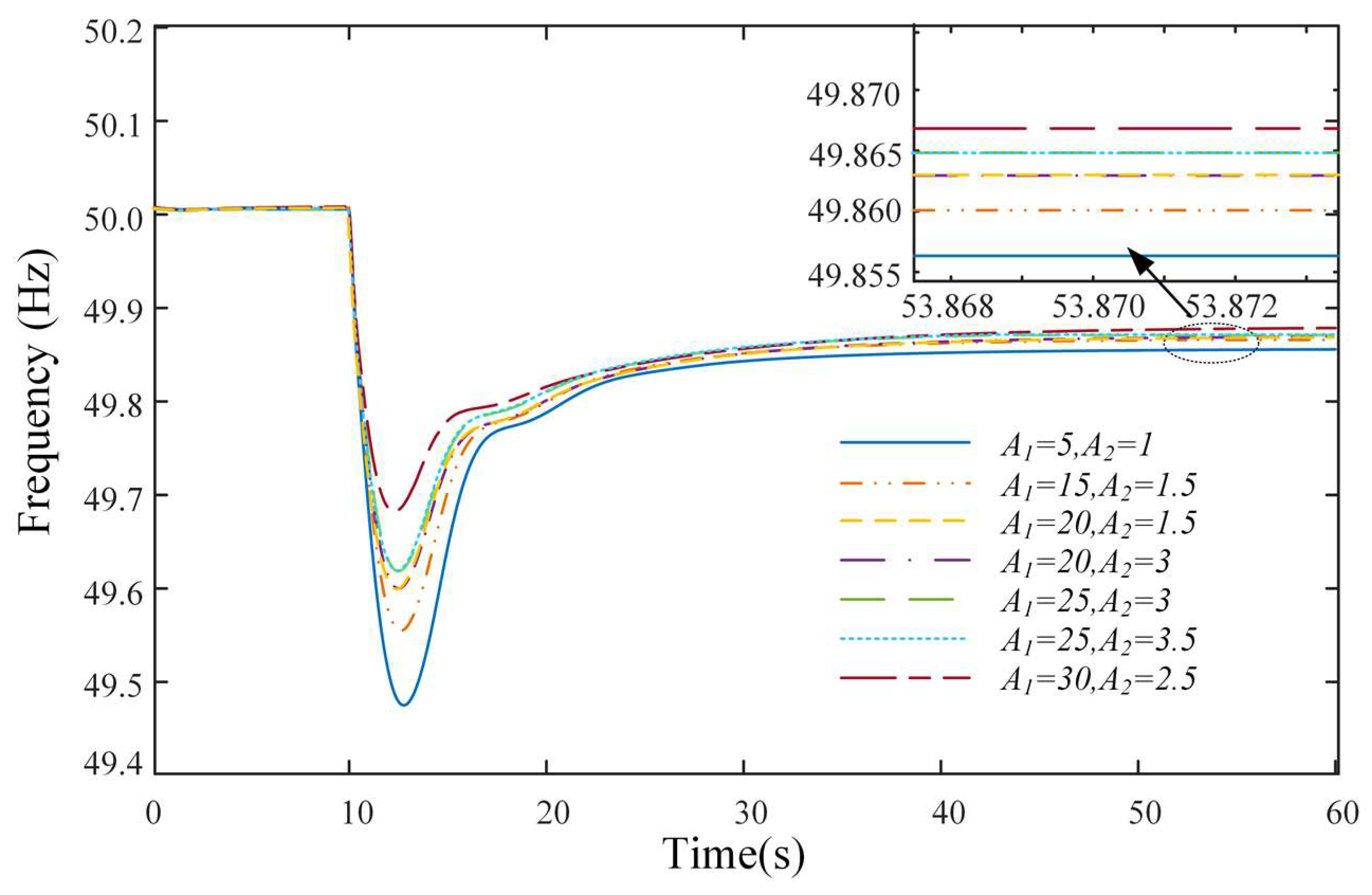
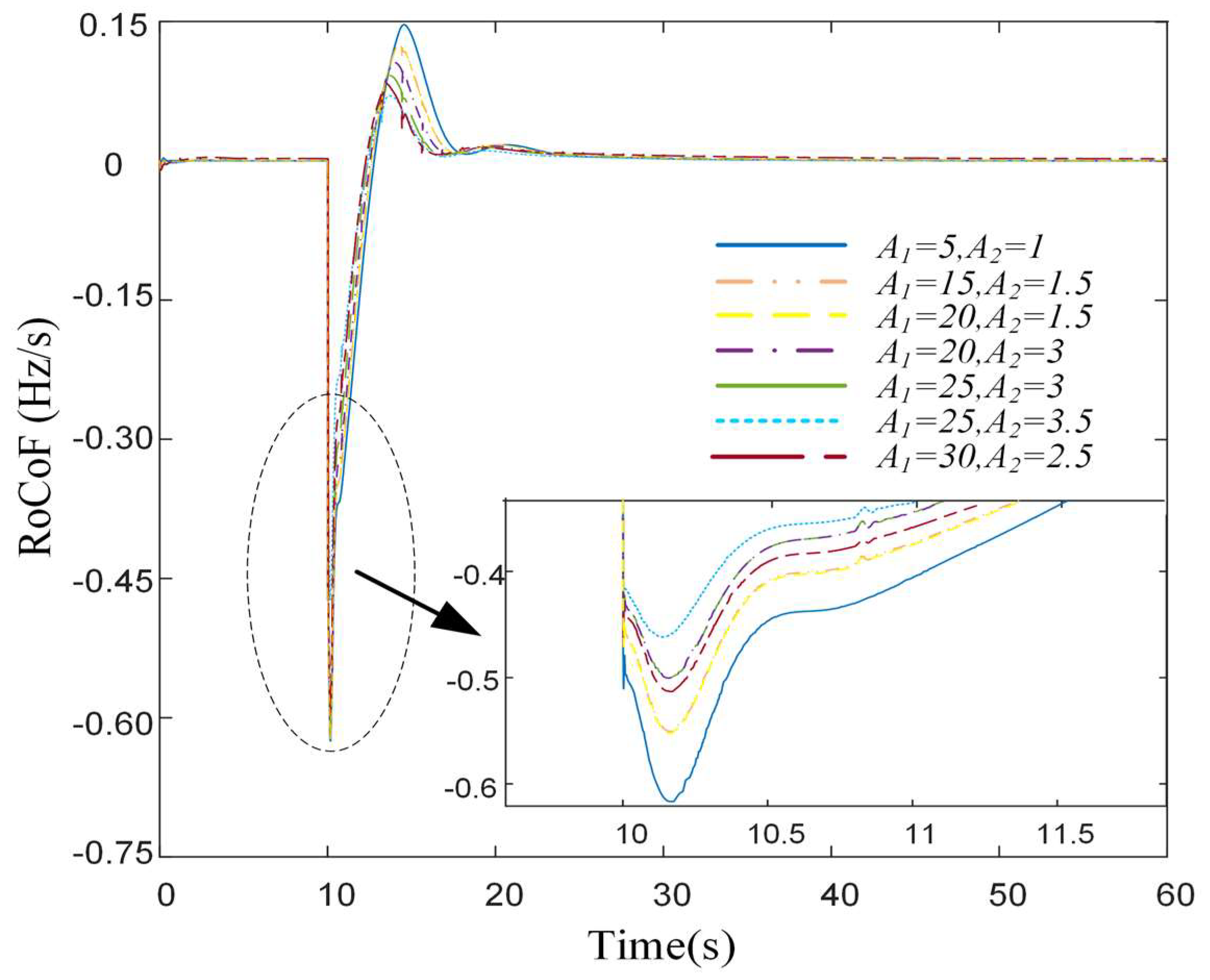
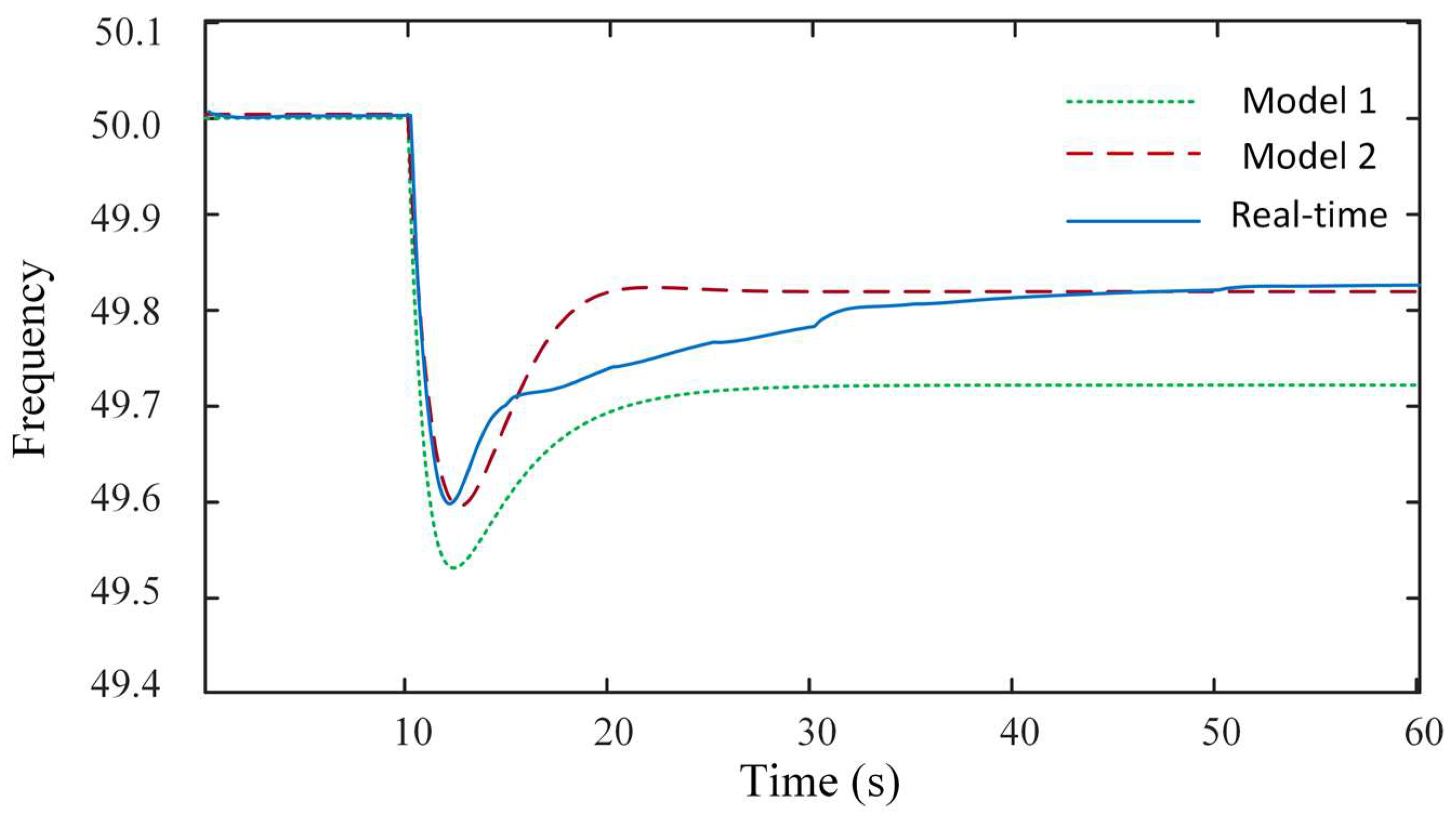
| Parameter Name | Parameter Value |
|---|---|
| 2 | |
| 12 s | |
| 0.0812 | |
| 12 s | |
| 0.0124 |
| Parameter Name | Parameter Value |
|---|---|
| 0.3 | |
| 8 s | |
| 0.3 | |
| 4 s | |
| 0.05 |
| Frequency Lowest Point Error | Steady-State Frequency Error | ||
|---|---|---|---|
| Scenario 1 | Model 1 | 0.03 Hz | 0.02 Hz |
| Model 2 | 0.01 Hz | 0 | |
| Scenario 2 | Model 1 | 0.05 Hz | 0.07 Hz |
| Model 2 | 0.01 Hz | 0 | |
| Frequency Lowest Point Error | Steady-State Frequency Error | ||
|---|---|---|---|
| Case 3 | Model 1 | 0.04 Hz | 0.05 Hz |
| Model 2 | 0.01 Hz | 0 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Qi, J.; Tang, F.; Xie, J.; Li, X.; Wei, X.; Liu, Z. Research on Frequency Response Modeling and Frequency Modulation Parameters of the Power System Highly Penetrated by Wind Power. Sustainability 2022, 14, 7798. https://doi.org/10.3390/su14137798
Qi J, Tang F, Xie J, Li X, Wei X, Liu Z. Research on Frequency Response Modeling and Frequency Modulation Parameters of the Power System Highly Penetrated by Wind Power. Sustainability. 2022; 14(13):7798. https://doi.org/10.3390/su14137798
Chicago/Turabian StyleQi, Junfeng, Fei Tang, Jiarui Xie, Xinang Li, Xiaoqing Wei, and Zhuo Liu. 2022. "Research on Frequency Response Modeling and Frequency Modulation Parameters of the Power System Highly Penetrated by Wind Power" Sustainability 14, no. 13: 7798. https://doi.org/10.3390/su14137798
APA StyleQi, J., Tang, F., Xie, J., Li, X., Wei, X., & Liu, Z. (2022). Research on Frequency Response Modeling and Frequency Modulation Parameters of the Power System Highly Penetrated by Wind Power. Sustainability, 14(13), 7798. https://doi.org/10.3390/su14137798






