In this section, the results of the machine learning regression analyses of the case study are presented and discussed. First, additional context regarding the case study particular situation is shown first. Next, the results of the model selection step are shown, and the resulting algorithms are applied to the case study.
5.1. Case Study Description
As previously mentioned, the proposed approach has been tested using the case of a Spanish wind turbine tower manufacturer. The data were collected from various databases of the company’s ERP; these different sources were merged so the resulting database would encompass the variables discussed above. The dataset includes information from the nearly 900 tower sections manufactured in the plant from March 2018 to February 2021, which are composed of over 7400 ferrules.
In this case, most of the information regarding lead times and machine use is entered by the plant workers in the midst of the operation. In order to ensure that the data accurately depict the functioning of the plant, the dataset has been preprocessed by removing outliers and infeasible values. Instances that show bending operations performed in less than 20 min or more than 5 h have been eliminated, since they are considered to be errors in the employees’ recording of the data; these instances represent only 2.23% of the dataset.
With regards to the input variables values, the following aspects must be noted:
The possible ferrule positions in the records of the plant operation range from the bottom position (1) to the highest ferrule position recorded (16).
As mentioned earlier, generally, towers have three sections (bottom, mid and top); however, the data contain examples of towers with up to six sections.
The studied plant has three different work shifts: morning, afternoon, or night. Additionally, it must be noted that employees periodically rotate their assigned shifts. As a result, the variability introduced by the workers and by the shifts is not expected to be confounded.
Eighteen different workers have performed the bending operation during the period analyzed.
There are two bending machines at the plant, of the same model.
Two values of the steel plate yield strength are found in this study, 355 N/mm2 and 455 N/mm2.
Regarding the steel plate toughness designation, the subgrades presented in
Table 1 have been found in the dataset:
Table 2 summarizes the distribution of the experience-related variables.
Table 3 summarizes the distribution of the thickness, length, width and lead time values of the instances of the dataset. Additionally, a histogram of the lead time distribution in shown in
Figure 4.
Table 3 and
Figure 4 provide insight into the lead times of the bending operation. Just under 75% of the recorded bending operations lasted between one and two hours. Of the remaining 25%, only 6.63% occur in less than an hour: 18.41% of the operations are performed in more than two hours, with some lasting up to 5 h; these are the instances in which the model should prove its predictive power in order to be used as an accurate forecasting tool for production planning and control. For this reason, as mentioned in
Section 4.3.1, the RMSE metric has been used as the deciding metric in the model selection step in order to minimize the prediction errors of these extreme values.
The potential correlations between the previously described input factors have been analyzed. The Pearson correlation coefficients for each pair of numeric variables are shown in
Table 4. Additionally, the correlation between each input variable and the output variable (bending lead time) is analyzed.
The Pearson correlation coefficients shown in
Table 4 are significant, with a 0.05 significance level, save for the coefficients written in italics. The coefficients higher than 0.3 (a standard threshold above which a correlation can be considered of moderate strength), are presented in bold. The correlations between the thickness and length variables and the thickness and width measures show the highest coefficients amongst the non-experience-related variables. Particularly, the thickness of the plate appears to be indirectly correlated with its width (ρ = −0.439). On the other hand, the thickness of the plate is directly correlated with its length (ρ = 0.342). Additionally, the thickness variable is strongly correlated to two experience-related variables. Thus, for the regression analyses presented later in this paper, the thickness variable has not been considered in order to avoid misinterpreting the outputs of the analyses, even if the predictive power of the model could have been increased with its inclusion.
Regarding the experience-related variables,
Table 4 shows considerably high values of the pairwise correlation coefficients; this was to be expected, given the definition of the variables, but should be taken into account in the design of the regression experiments. Thus, the following variables have also been discarded from the analyses: experience at the station, number of operations, global frequency, frequency in the previous 180 days, frequency in the previous 90 days and frequency in the previous 60 days.
Based on the results of this preliminary correlation analysis, two sets of input variables are considered for the regression analyses:
Without experience variables: includes the section position, ferrule position, length, width, shift, personnel, machine, yield strength, toughness and normalization variables.
With experience variables: includes the same variables as the previous set, plus the worker age, experience in the sector/plant and 30-day frequency variables.
Neither of the two variable configurations present conflicts regarding correlation: the correlation coefficients of all the pairs of input variables in each set are under 0.3.
5.3. Model Implementation Results
As explained in the previous section, the Linear Regression and M5P algorithms have been chosen for this study. The models are now tested using an 80/20 training-test split, as stated in the methodology section. In this case, there are over 1450 operations in the hold-out test set; these experiments have been conducted for the input variables set including the experience variables, and without them.
The Linear Regression algorithm is applied by selecting the LinearRegression module found in the Classifiers group. The WEKA workbench offers some parametrization options: the algorithm has been set to eliminate collinear attributes and to perform a selection, using the M5 method, of the attributes that are to be considered in the regression model.
Next, the M5P method has also been applied to the 80/20 split; this can be done in the Knowledge Flow models by substituting the LinearRegression module for the M5P module. The M5P algorithm constructs a decision tree where the leaves correspond to a set of Linear Regression models, also known as a model tree; this tree is capable of dealing with numeric attributes both on its decision nodes and on its leaves, thus using the traditional decision-model structure of classification algorithms but allowing numeric attributes to be predicted as the target variable, as required in a regression task. The model tree created by the M5P algorithm divides the dataset using a splitting method that minimizes the variation between the instances allocated to the same subset. Each leaf of the tree contains a Linear Regression model that uses the data in its subset to predict the target variable value for the evaluated instances that reach said leaf after going through the tree’s decision nodes; the algorithm also includes a pruning method that simplifies the branches of the decision tree as long as the expected adjusted error at the resulting leaves decreases. When an instance is fed to the trained model, it arrives at one of the tree’s leaves through attribute-based decisions at the tree’s nodes. Once there, the value of the target variable is predicted utilizing the corresponding leaf’s Linear Regression model.
The main performance statistics for the multivariate Linear Regression and M5P models are presented in
Table 6. Additionally, the predictions of the test set have been examined and the percentages of instances for which the models have produced predictions deviating in less than 10, 15 and 30 min are included.
Overall, the results show a better performance of the M5P method over the Linear Regression model, as expected in view of the cross-validation results. There are moderate correlations between the predicted and actual times for both methods and datasets, with the M5P coefficients being higher. The mean absolute error of the predictions is less than a minute lower for the M5P method than for the Linear Regression model when using the dataset without the experience-related variables. The inclusion of the experience-related variables does not cause a significant improvement in any of the metrics for the experiments carried out using the Linear Regression Model; however, the results show an increase of 10 percentage points of the correlation coefficient when adding the experience-related variables to the M5P model. Similarly, the mean absolute error is reduced in over 1.5 min if the complete dataset is used.
The relative absolute error represents the percentage error reduction of applying each method compared to predicting the lead time of every test instance as the mean lead time of the complete training dataset. Without the experience-related variables, the Linear Regression approach shows a 9.09% error reduction, while this value increases to 12.39% in the case of the M5P method. By adding the experience-related variables, these values are augmented to 11.3% and 17.62%, respectively.
Additionally, the M5P algorithm produces a higher percentage of “accurate” predictions than the Linear Regression approach in any of the proposed thresholds (10, 15, or 30 min). Once again, the use of the M5P method with the experience-related variables shows the highest accuracy in any of the thresholds. Nevertheless, it must be noted that the accuracy of each experiment can see changes in each threshold: for example, the M5P model without experience-related variables produces more accurate predictions with a margin of error of 10 and 15 min than the Linear Regression approach with any of the datasets; however, the latter proves more accurate than the former if the threshold is increased to 30 min.
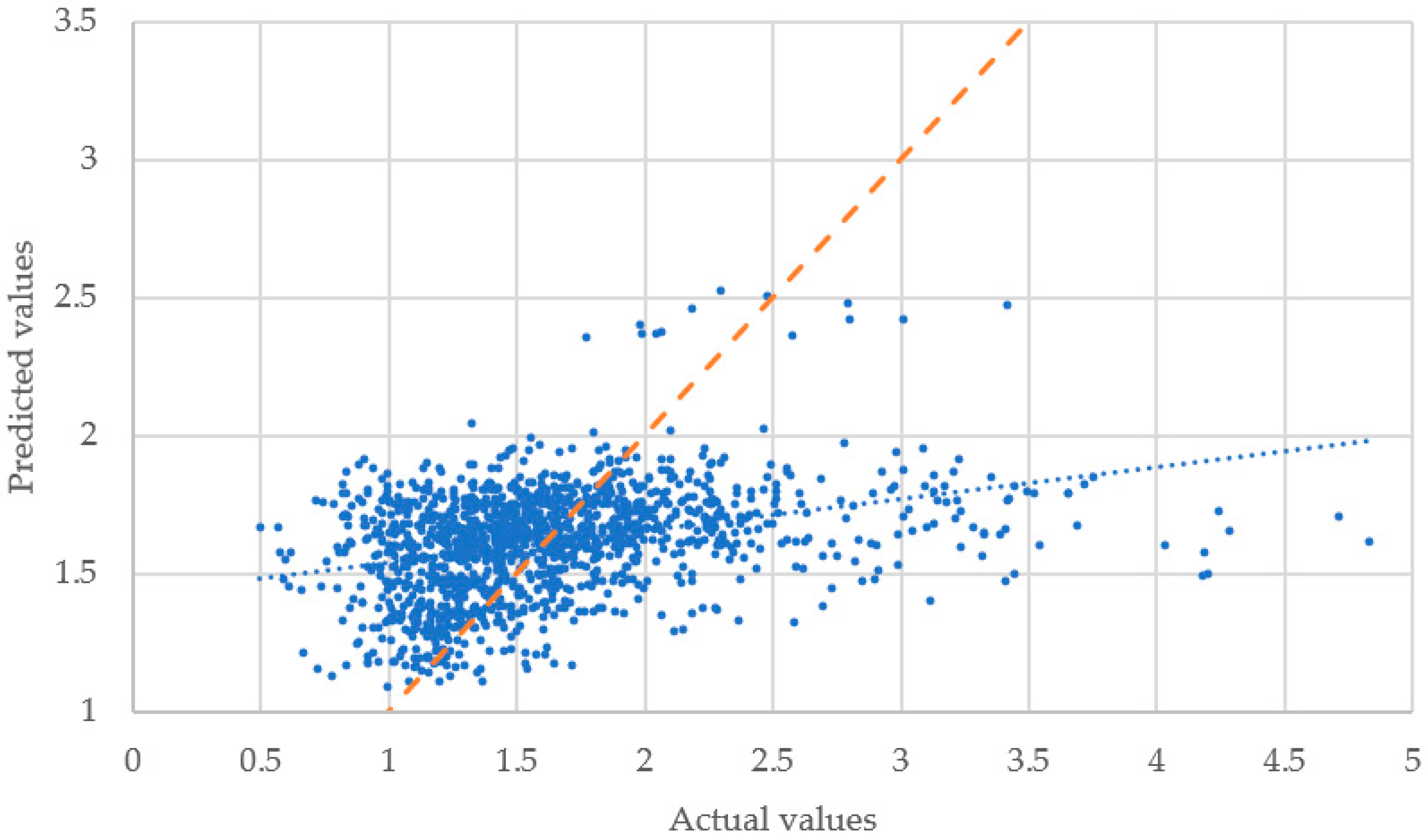
Finally, the RMSE value is lower for the M5P model than for the multivariate Linear Regression model, as expected given the cross-validation results, in the comparison with both datasets; this suggests that the M5P produces fewer large errors than the Linear Regression model, which was the main goal of the regression analysis. To delve deeper into the fitness of each model, the predicted and actual values of each experiment have been plotted in
Figure 5 (Linear Regression without experience-related variables), 6 (Linear Regression with experience-related variables), 7 (M5P without experience-related variables), and 8 (M5P with experience-related variables). The graphs plot the actual lead time values of the observation in the
x-axis, while the corresponding predicted values are shown in the
y-axis. The orange dashed line represents the line with slope 1, that is, where the perfect predictions would be located. The blue dotted line represents a linear trendline of the observations, showing the tendency of the predictions as the actual values change. By observing
Figure 5 and
Figure 6, just small changes can be found between the Linear Regression approach without the experience variables and with them.
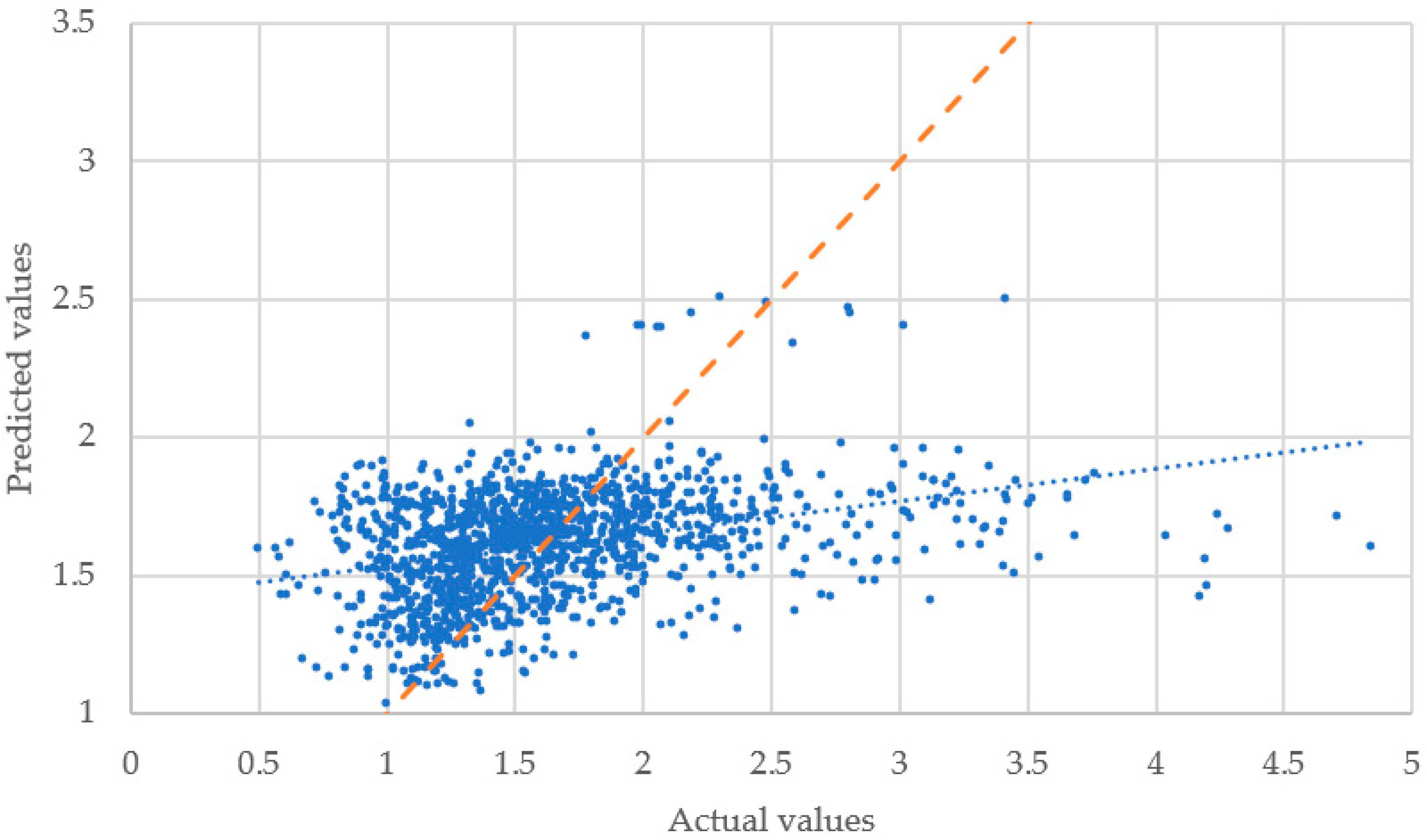
Figure 7 shows that the trend of the predictions moves closer to the line with slope 1, which, while not necessarily indicating a smaller error, suggests a better performance of the M5P model without experience-related variables. Furthermore,
Figure 8 reveals that the predictions of the M5P model without experience-related variables seem to be even more accurate, as indicated by the results shown in
Table 6.
Figure 5,
Figure 6 and
Figure 7 suggest that the corresponding models tend to underestimate the predicted values of the bending lead time as it increases; this can be observed in the right-most points, which are further away from the line with slope 1 than those with lower actual values. For lead times over three hours, the models’ predictions are significantly inferior to the actual values, with over two hours of difference in the most extreme cases; this effect seems to be diminished in
Figure 8, corresponding to the M5P model without experience-related variables. To further analyze the behavior of the models with this sort of instances,
Table 7 shows the percentage of instances exceeding 2 hours in actual lead time, for which its predictions differ in less than 10, 15 and 30 min of the actual value, respectively. There are 252 of the 1454 instances in the hold-out test set that present an actual lead time longer than two hours.
Once again, the M5P model with the experience variables shows superior performance when predicting the lead times of the extreme values; these results are encouraging, given that 41% of the instances over two hours can be predicted with less than 30 min of error. It must be remembered that almost 75% of the instances in the entire dataset range between 1 and 2 h, and thus the model should be able to predict the lead time for such instances with high accuracy; however, the critical aspect of the analysis is that the models accurately forecast the lead times for the more “uncommon” instances.
Figure 9 shows a plot of the predicted and actual values for the M5P model with experience-related variables for the instances with an actual lead time over 2 h.
After examining the performance of the models, the results of multivariate Linear Regression analysis with experience-related variables are interpreted, focusing on new-found correlations between input variables and lead time.
Table 8 shows the coefficients determined for each variable in this experiment, as well as their standard error and significance. WEKA does not provide the
p-values, but it performs a two-tailed Student’s
t-test. The
t-statistic values can be then converted into the significance
p-values.
It must be noted that there are both numeric and nominal input variables considered in the Linear Regression model. Coefficients for numeric variables represent the estimated growth in lead times when said numeric variable increases its value in one unit; however, when dealing with nominal variables, there is a coefficient for every level of the variable. For example, regarding the shift variable, which contains three levels (corresponding to the morning, afternoon, and night shifts), two resulting coefficients can be expected. If the night shift is taken as a reference, the coefficient for the morning shift level represents the expected variation in lead time for a morning-shift operation compared to when the instance corresponds to the night shift. Similarly, the model should produce a coefficient for the afternoon shift; however, the algorithm autonomously selects a reference level, and if the difference between the reference and a certain level is not significant, it does not produce its coefficient.
The results shown in
Table 8 provide interesting insight into the bending operation studied. Firstly, it must be noted that the variables included in the table are the ones chosen in the M5-based feature selection filter ran before executing the Linear Regression algorithm. The rest of the variables have not been found to provide additional information for the lead time prediction (save for the personnel variable, which will be discussed next). In particular, such input variables are the width, steel yield strength, steel normalization and worker age variables.
Secondly, it can be seen that most of the variable coefficients are significant at a 0.01 significance level; however, there are two exceptions: the shift variable coefficient, adding 0.0264 expected hours (less than two minutes) when the operation is performed in the morning shift, is only significant at a 0.1 level. Additionally, the toughness variable only has a level that is predicted to add a significant deviation, the NL toughness subgrade.
The intercept is a constant value that represents the estimated time when all the nominal variables are at their reference levels and the numeric variables are 0; this value is not of interest for this interpretation, since there are no plates with null length, width, or thickness, for example.
Regarding the nominal variables, the most noteworthy effects are those of the machine variable and, particularly, of the steel plate toughness variable. The operations performed in the bending station A are expected to take nearly 9 min more than those performed on station B. Furthermore, the steel plates with a toughness subgrade NL (the second toughest of the plates encountered in the dataset) are estimated to take 37 min longer than those with the lower subgrades JR and J0; these are significant time increases, especially when the mean bending time of all the operations in the dataset is of 1.62 h (97 min).
Regarding the numeric variables, the coefficients show slight increases as both the position of the section in the tower and the position of the ferrule in the section rise; this increase amounts to 11 min when comparing the lowest position of a ferrule (1) to the highest (16), and to 10 min when comparing ferrules from the bottom section to ferrules in the highest top section produced in the analyzed timespan (6).
As opposed to what was a priori expected, the length of the plate does not have a remarkable effect on the lead time of the process. The expected lead time increase per meter of length is only 1.08 min. The difference between processing the longest (24.953 m) and shortest (7.324 m) plates in the records is expected to be 19 min. It must be kept in mind that the steel plates are inserted through the bending machine rolls lengthwise and, therefore, it could be anticipated that a longer plate would take significantly more time to be bent, but the results suggest otherwise.
Regarding the experience variables, it can be seen that the age of the workers has been discarded from the model by the feature selection filter; however, the experience at the sector and the frequency at the station in the last 30 days pose significant effects on the bending lead time. For example, a worker with 4 and a half years of experience in the sector (the maximum value observed in the dataset) is expected to employ 9.8 min less to perform a bending operation than one with no experience, ceteris paribus. Furthermore, a worker that has performed 3.13 daily bending operations on average during the previous 30 days is predicted to take 8.7 min less to carry out a bending task than an employee with no operations performed in the previous 30 days, ceteris paribus.
It can be observed that the personnel variable has not been included in
Table 8, for the sake of conciseness. Conversely, the aggregate coefficients of each of the levels of the personnel variable are shown in
Table 9. There are 18 levels for the variable, representing each employee that has performed the bending operation in the recorded timespan: two of those workers are taken as the reference level (Q and R). Another two (A and B) are expected to perform the bending operations in nearly five fewer minutes than workers Q and R. The remaining 14 employees are estimated to produce an increase in the operation time ranging from 8 min up to 69 min over the expected bending time for employees Q and R. In fact, the highest difference found in expected lead time (O and P vs. A and B) amounts to 74 min, 76.19% of the average bending lead time, a testament to the relevance of personnel for the prediction of the bending lead time.