Assessment of the Landfill Barrier System through Numerical Analysis: Rehabilitation and Expansion of Belgrade Landfill Case Study

Abstract

There are still many unmanaged landfills around the world that pose significant potential environmental problems. One of the largest unmanaged landfills in Europe, which has been used for more than 40 years to deposit waste from Serbia’s capital, Belgrade, is the Vinča landfill. A revitalization and extension of this landfill was proposed that would allow its sustainable operation in the future. The revitalization project considered building a capping layer on the surface of the current landfill, which will close it and which will serve as a liner on the bottom of the new landfill. The use of a composite system including a HDPE geomembrane is considered in the project. New landfill settlements were predicted using the FEM method utilizing a Hardening-soil constitutive model for subgrade. Both immediate settlements of subgrade caused by waste deposition and primary consolidation settlement were calculated. The results show that a substantial increase in the settlement of the geomembrane subgrade can be expected during the primary consolidation period, due to the high rate of filling compared to the permeability of the subgrade. The total settlement of the new landfill in its crown is expected to be between 2.73 and 4.52 m. The axial force in the geomembrane will not exceed the tensile strength of the membrane at any time during or after the new landfill operation.

1. Introduction

The construction of engineered landfills is necessary for municipal solid waste (MSW) disposal [1]. By the end of the 1970s, landfill practice was generally unaffected by engineering, and there was little concern about the environmental effects of MSW disposal. Operation of the landfills typically consisted of the uncontrolled backfilling of natural valleys or abandoned open pit mines [2]. The spread of leachate (formed by the seepage of rainwater through the landfill body) into the subsoil was accepted as a common side effect of landfilling. It was assumed that the concentrations of all contaminants transported from the landfill to groundwater would be reduced to safe levels by dilution processes [3,4]. Nevertheless, the dilution processes do not alter the chemical nature of the contaminants or contaminated soil in any manner. Dilution simply decreases the concentrations of contaminants in the leachate [5]. Most landfills that operated with contaminant dilution were consequently declared to be potentially hazardous to the environment [6]. Vinča landfill, which began operation in 1977, is a typical example of the approach described above. The 130-hectare site (which is approximately the same size as 180 football fields) has never been officially operated as a landfill. Therefore, basic facilities, such as a drainage system, have never been developed there [7]. The MSW was dumped in the Vinča landfill area (see Figure 1), which consists of the natural valley of the Ošlian stream, without taking any technical measures at the bottom of the site to prevent the leachate from escaping and being transported through the Ošlian stream outside the landfill area. The risk of contamination of the nearby Danube River with leachate was increased after the 2014 earthquake, which initiated a series of landslides on the slopes of the landfill [8,9]. Millions of Belgrade’s citizens were endangered by a methane-stimulated fire in 2017 [10].

In the 1990s, the principles of landfilling shifted towards total containment, and waste disposal by landfilling incorporated far more highly engineered processes [6]. Currently, the progressive filling of 2 to 3 m high individual cells, formed by very low permeability soil, is preferred. It is not possible to make a landfill completely impermeable according to current knowledge, and so it is preferred to control possible leakages rather than trying to eliminate them completely [11]. Therefore, waste is deposited within pre-constructed containment areas equipped with the appropriate design measures, such as a low-permeability lining system, underdrainage/leachate detection system and leachate drainage and control system. Therefore, the construction and restoration of a landfill site is a major civil engineering project with a high level of geotechnical content [6].

1.1. Vinča Landfill Rehabilitation and Expansion Plans

The current condition of the Vinča landfill imposes a need for a planned rehabilitation solution, and for the expansion of the existing landfill in accordance with good international practice [12,13]. Due to the potential serious environmental hazards [14], the local authorities decided to redevelop the existing landfill. The project of landfill rehabilitation represents a fundamental change in the management of municipal waste in Belgrade [7]. The so-called Energy-From-Waste Facility project was designed as part of the Waste Management System for the City of Belgrade. It is a private–public partnership established to improve the current solid waste disposal practice [15]. It includes remediation of the existing landfill; the construction of a new sanitary landfill; the energy from a waste facility being used to produce electrical and thermal energy; a leachate collection system and treatment plant; a landfill gas collection system that will replace a portion of the imported natural gas [16,17] and be used in a cogeneration plant for the production of electricity and heat [18,19]; and the building of a construction and demolition waste processing plant [20].

1.2. Geotechnical Aspects of the New Vinča Landfill Project

An important detail of the proposed remediation works is the landfill containment system, which will separate the area of closed landfill horizontally from the area of new landfill. The landfill containment system should perform the following functions: (1) prevent leachate from seeping out of the landfill area and thus prevent groundwater contamination [21], (2) prevent landfill gases from leaking and collect them, so that they can be further effectively reused or rendered harmless, (3) remain stable and operate efficiently for the required design lifetime, (4) ensure that the completed landfill does not fill up with water, which would cause a leachate overflow. To achieve these objectives, landfill sites are lined with mineral layers or synthetic membranes, or with a combination of both. Clay liners are inherently more permeable than synthetic membranes. The use of clay liners can also be problematic, because the smectite components of bentonite liners interact chemically with leachate, which leads to a decrease in their swelling capacity and an increase in hydraulic conductivity. Therefore, they lose their sealing function over the course of their lifespans [22]. However, it is difficult to protect synthetic membranes from damage. This, together with uncertainty about the long-term durability [23,24] and degradation of synthetic lining systems in a harsh chemical environment at the base of the landfills [25,26], increases the possibility of liner failure at some stage in the future when the waste is still active, leading to groundwater pollution by landfill leachate [22,27]. There is no single ideal liner material. Composite mineral/geomembrane systems, including two separate barriers made of different materials, are thus combined to provide a synergistic effect. Such a composite system provides the highest degree of security against leakage [28].

The landfill containment will have two main functions in the Vinča landfill project. It will serve as the liner at the base of the new landfill, and simultaneously, as the final cover for the finished old landfill. This provides a major engineering challenge, as the barrier layer must be able to resist both the stresses caused by differential movements and settlements of the subgrade and loading by the MSW deposited on the new landfill. The planned rehabilitated and extended Vinča sanitary landfill will be located in part over the existing landfill (approximately 45% of the area), and on the ground surrounding the existing landfill (approximately 55% of the area). Among other factors, the design engineer must consider the subgrade bearing capacity required for landfill [29]. The bearing capacities of the two types of new landfill subgrade are different. The higher compressibility of the subgrade composed of untreated municipal waste, which is an extremely heterogeneous material with variable permeability and water retention properties, causes higher settlements when compared to the subgrade composed of naturally deposited soils. In the extreme case of settlement, an unwanted pooling of water may occur, or surface water may leak into the underlying waste through cracks in the liner [6]. Differential settlements in barrier systems can also induce strains in the geomembrane [30]. Great emphasis has to be placed on the design of the components and materials of the liner [31,32] to sustain deformations induced by differential settlement [33], and also by loading, traffic from filling vehicles, [34] etc. Deformation of the membrane is therefore affected by a number of variables, some of which are dependent on others. Thus, predicting, measuring, assessing, and determining acceptable limits of membrane strains poses a challenge for designers [30,35], and a number of studies tried to assess strain in geomembranes experimentally [36,37,38,39].

The settlement of MSW placed above the containment system also affects tensile stresses in the geomembrane significantly by down-drag effect. Hence, the geometry of the anchor trench to prevent the sliding of the membrane down a slope was designed according to Koerner and Soong [40] and was also modelled. Several researchers, e.g., [41,42,43,44], have formulated different constitutive models for the mathematical description of the MSW stress–strain relationship recently [45], with various level of accuracy of settlement prediction. Currently, new constitutive models are still being developed by researchers in response to advances in understanding the processes that occur over time in the decomposing MSW. Some researchers consider the effects of mechanical creep [46] and time-dependent biodegradation [47,48] to predict total landfill compression under incremental loading and with time. Machado et al. [47] introduced a mathematical concept based on two MSW components—fibers and organic paste. Machado’s model considered reduction of the ultimate tensile stress and the Young’s modulus of MSW and the mass loss caused by the organic component degradation over time. Models developed by Sivakumar Babu et al. [49] and upgraded later by Feng et al. [48] are based on the framework of critical state soil mechanics. The proposed constitutive model [49] incorporates increments in volumetric strains caused by elastic, plastic, time-dependent biodegradation, and mechanical creep effects, where the dependence of biodegradation is governed by an empirically determined exponential function. Feng et al. [48] followed up on the work of Sivakumar Babu et al. [49] by formulating the volumetric strain governed by the biodegradation-induced void change parameter. The most recent constitutive model by Wu Gao and Edward Kavazanjia Jr. [46], published in 2022, also utilizes the critical state soil mechanics framework to describe the stress–strain–time behavior of MSW over time. The hardening of the MSW in this model is considered to be a result of time-independent plastic volumetric strain, time-dependent volumetric mechanical creep strain and time-dependent volumetric strain resulting from the decomposition of MSW. Despite the theoretical precision of some of these models, the predicted stress–strain relationship can vary significantly depending on the model used and the parametric values selected, as was shown by Sivakumar Babu et al. [49]. They compared settlement predictions using 14 different models. The results varied between 0.8% and 67% of initial thickness of the MSW layer [49]. The MSW settlement levels caused by the mechanical compression and decay of biodegradable components were in the range of 25% to 50% of the initial thickness of the layer [50,51,52,53]. If no better alternative to the description of the stress–strain relationship for MSW is available, an interim quasi-geotechnical approach can be accepted [6]. For older landfills, most of the MSW settlement takes place in the first five years after waste is deposited. Total settlement values are then usually reached within thirty years [54,55]. The filling and closure of landfills is now much more rapid than in the past. Therefore, the time to reach total settlement can be expected to increase to about 100 years. Around 80% of the total settlement can be expected within 30 years [56].

Within the preliminary phases of the rehabilitation and expansion design of the Vinča landfill project, it was necessary to reasonably analyze the response of the geomembrane subjected to induced differential settlement of the subgrade progressively loaded with new layers of waste. This paper describes the mathematical modelling procedure performed for this purpose, including the determination of the input parameters of the material models (Hardening Soil and Mohr-Coulomb) used. The settlement in the plane of the new landfill ground zone and the axial force in the geomembrane were calculated and evaluated. (The axial force states for the force in the longitudinal (in-plane) direction of the geomembrane.) The consolidation processes in the subgrade and in the MSW were also modelled [35], with respect to the real planned filling stages of the new landfill.

The strength of the contact between the geomembrane and the adjacent layer was also analyzed, as it influences the resulting tensile forces in the geomembrane. Stronger contact results in lower calculated axial forces in the geomembrane. The strength of contact depends on the choice of geomembrane protection layer and the type of gravel aggregate used in the drainage layer. Although a uniform aggregate is preferred from a drainage perspective, it is undesirable in terms of geomembrane strain [30,57]. The significance of interface shear strength on the results can be seen in the many papers published on this subject. This phenomenon was analyzed by laboratory testing [58,59] mostly in direct shear apparatus and also numerically [60,61]. Discussions of many numerically and experimentally obtained results were published, e.g., by Palmeira [62] and by McCartney et al. [63]. The sensitivity of interface shear strength to the type of polymer used for geomembrane production, the geomembrane texturing and the type of clay liner was observed [63].

2. Geological and Geotechnical Conditions on the Site

The body of the planned new landfill will extend over both the existing landfill and over the areas adjacent to the existing landfill. For the design of the liner, it was therefore necessary to determine the mechanical and hydraulic parameters of both the original soil and the MSW deposited so far. The lithological boundaries of the subsoil layers of the landfill were modelled according to the description of the boreholes described in an engineering geological survey report [64]. The boreholes described in the report [65] and the description of the excavated probes and dynamic penetration probing result summarized in the survey [66] were also considered.

2.1. Natural Soil Description

After landscaping, the ground zone of the new landfill will be in contact with a layer of cohesive quaternary and tertiary soils. Quaternary soils are mainly represented by aeolian sediments, i.e., loess and silty clays (PRGd) deposited over the layer consisting of diluvial silty-sandy clays (Gj). These two types of soils have similar geotechnical properties: They are predominantly composed of silty particles and have variable admixtures of fine to medium sand. The soils have medium plasticity, or sometimes high plasticity. There is often a calcareous component present in the loess, either as concretions or as silty particles. Soils of both types of genesis are classified as F6-CI, and less often as F8-CH according to Unified Soil Classification System (USCS). An engineering geological map of the quaternary cover showing the main geotechnical types and the positions of the modelled sections is shown in Figure 2.

2.2. Hydrogeological Conditions at the Site

Groundwater level fluctuations were measured using exploratory probes over time. Below the surface of the existing landfill, it was detected at depths ranging from 1.7 to 14.9 m, most commonly 3 to 8 m. The differences may be due to the inhomogeneity of the deposited material, as a continuous aquifer is not formed, but isolated aquifers are allowed to form at different elevations. The groundwater level in the naturally deposited layers not affected by landfilling was found at a depth of 7.5 to 11.5 m below ground in the western and southern areas, and in the south-eastern part at a depth of 3.3 to 3.8 m. Based on the depths of the groundwater table, the requirement is met for it being 1.0 m or deeper underground of the landfill.

3. Numerical Calculation Assumptions

Numerical analysis was performed using the finite element method. Plane strain models were created using Plaxis 2D 2016.01 (Build 5460) [67]. Fifteen-noded triangular finite elements with the fourth-order interpolation of displacement were used. In this paper, we present two selected mathematical models: one cuts the area of interest longitudinally and the second one transversely. The dimensions of the mathematical models and the numbers of the of finite elements and nodes generated are summarized in

Table 1. Dimensions of the mathematical models.

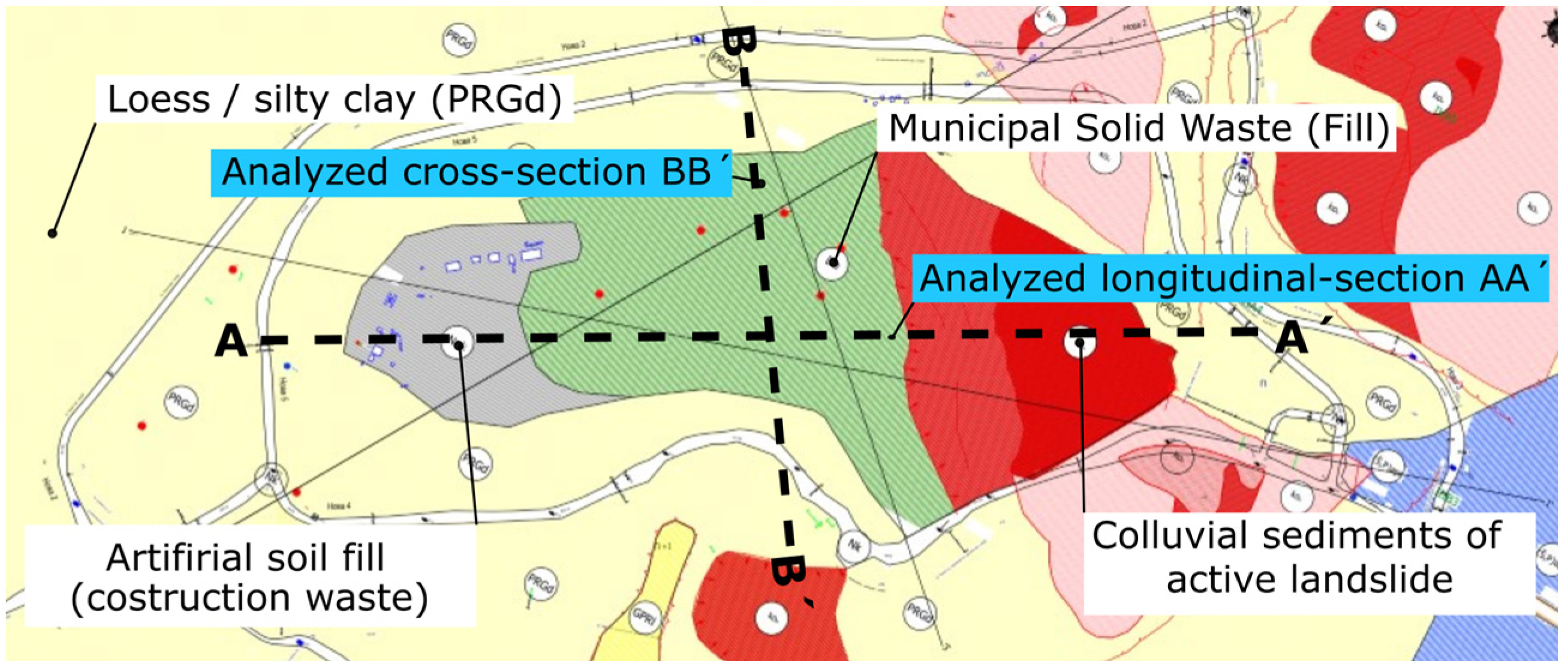
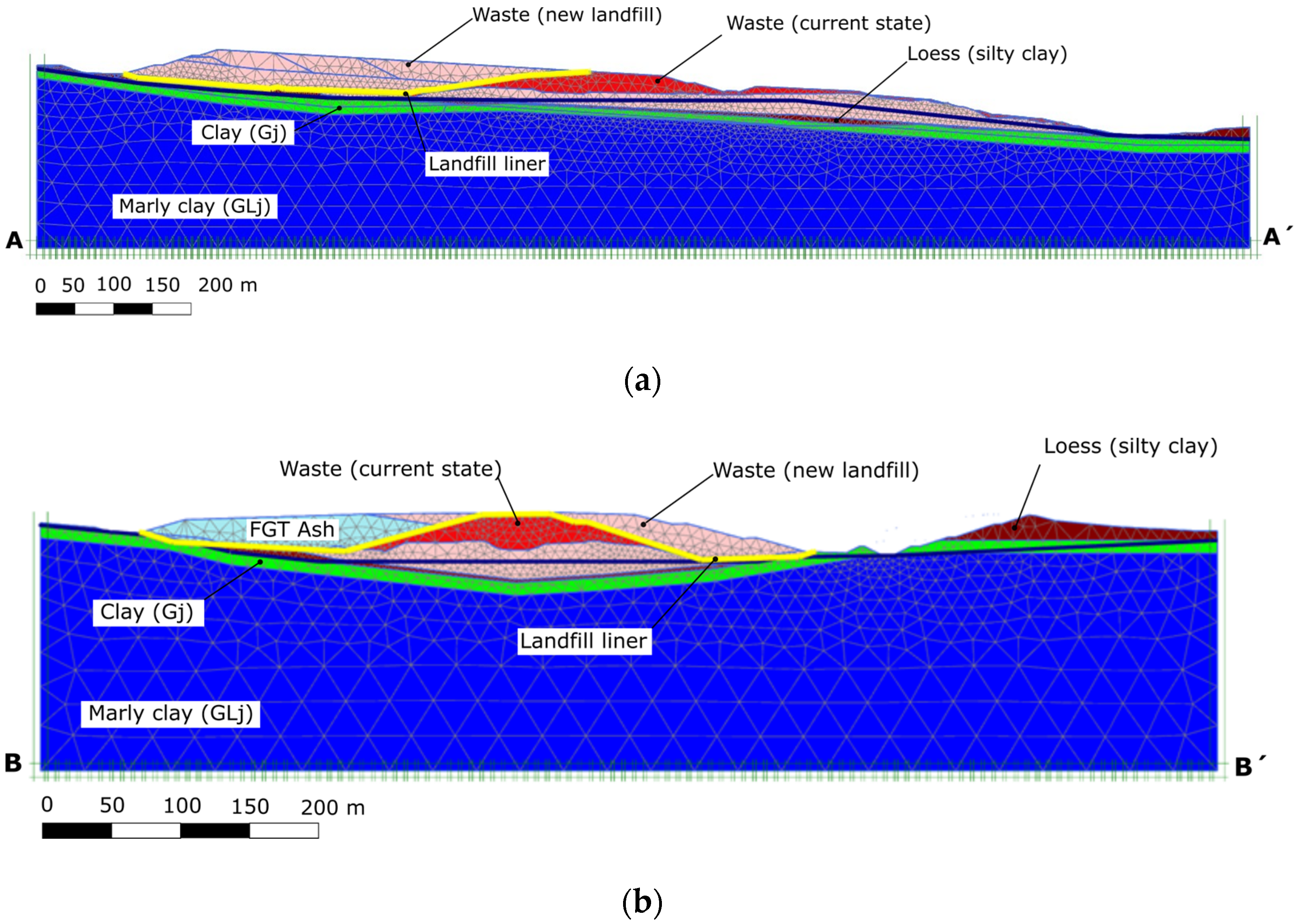
FE Model	Model Width [m]	Model Height [m]	Number of Finite Elements [-]	Number of Nodes [-]
Longitudinal section A–A′	1580	258	5081	41,143
Cross Section B–B′	920	202	3081	24,987

.

The mathematical models with indications of materials and with finite element mesh displayed are schematically shown in Figure 3.

The influence of the value of the strength reduction factor R_inter on the results was also studied. The composite liner was approximated by a geogrid type of finite element representing the geomembrane in the models. The reduction factor R_inter reduces the shear strength parameters of the linear elastic—perfectly plastic material model of the contact element. If relative movement occurs between the soil and geosynthetic layer (or between two geosynthetic layers), the shear strength in the soil–geosynthetic (geosynthetic–geosynthetic) interface is mobilized. In the cases of geomembranes and geotextiles, the interaction mechanism mobilized on the interface is the skin friction. When the shear strength of the interface is exceeded, the failure occurs by direct shear. The effective strength parameters of the interface elements (c_i, tan φ_i) are given by Equations (1) and (2), where c_i and tan φ_soil are the effective strength parameters of the soil surrounding the interface element. The same principle is applied when the soil strength is defined by the undrained shear strength s_u,soil (Equation (3)).

$$\tan {\mathsf{\phi }}_{\mathrm{i}}={\mathrm{R}}_{\mathrm{inter}}\tan {\mathsf{\phi }}_{\mathrm{soil}}$$

(1)

$${\mathrm{c}}_{\mathrm{i}}={\mathrm{R}}_{\mathrm{inter}}{\mathrm{c}}_{\mathrm{soil}}$$

(2)

$${\mathrm{s}}_{\mathrm{u},\mathrm{i}}={\mathrm{R}}_{\mathrm{inter} }{\mathrm{s}}_{\mathrm{u},\mathrm{soil}}$$

(3)

It must be noted that the R_inter factor also influences the interface stiffness, and consequently, the displacements parallel to the interface (u_t) and perpendicular to the interface (u_n):

$${\mathrm{u}}_{\mathrm{t}}=\frac{{\mathsf{\tau }\mathrm{t}}_{\mathrm{i}}}{{\mathrm{R}}_{\mathrm{inter}}^2{\mathrm{G}}_{\mathrm{soil}}}$$

(4)

$${\mathrm{u}}_{\mathrm{n}}=\frac{{\mathsf{\sigma }}_{\mathrm{n}}{\mathrm{t}}_{\mathrm{i}}}{2{\mathrm{R}}_{\mathrm{inter}}^2{\mathrm{G}}_{\mathrm{soil}}}\frac{1-2{\mathsf{\nu }}_{\mathrm{i}}}{1-{\mathsf{\nu }}_{\mathrm{i}}}$$

(5)

where τ and σ_n are the current shear and normal stress, respectively; G_i is the shear modulus of the interface; E_oed,i is the one-dimensional compression modulus of the interface; t_i is the virtual thickness of the interface; and ν_i is the Poisson ratio of the interface.

The numerical simulations were carried out in steps that relate to the planned waste disposal procedure in the new landfill area over the period of its operation. The sequences of calculation steps are summarized in

Table 2. Sequence of calculation phases of the model for longitudinal section A–A′.

No.	Description	Type of Calculation
01	Calculation of the original stress state before the current landfill began operation.	Gravity loading
02	Loading of the original valley by the weight of the waste deposited up to the moment before the landfill reconstruction.	Plastic
03	Ground zone of new landfill modification.	Plastic
04	Activation of geogrid finite elements simulating the installation of the liner system	Plastic
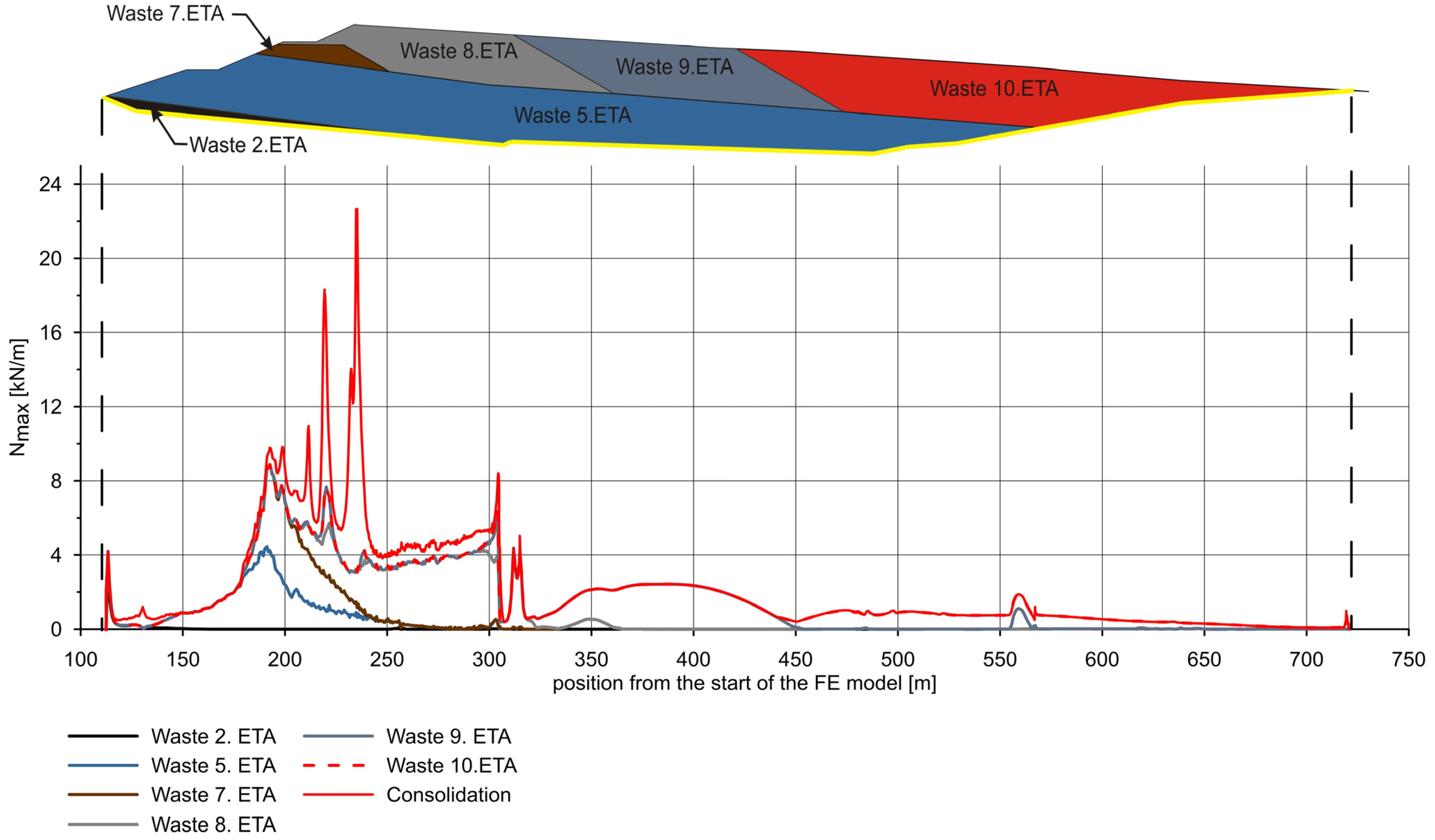
05	“Waste 2. ETA”—waste storage in the new landfill between the 2nd and 4th year of operation	Consolidation 2 years
06	“Waste 4 ETA”—waste storage in the new landfill between the 6th and 9th year of operation	Consolidation 3 years
07	“Waste 5. ETA”—waste storage in the new landfill between the 9th and 14th year of operation	Consolidation 5 years
08	“Waste 7. ETA”—waste storage in the new landfill between the 18th and 19th year of operation	Consolidation 1 year
09	“Waste 8. ETA”—waste storage in the new landfill between the 19th and 23rd year of operation	Consolidation 4 years
10	“Waste 9. ETA”—waste storage in the new landfill between the 23rd and 26th year of operation	Consolidation 3 years
11	“Waste 9. ETA”—waste storage in the new landfill between the 26th and 28th year of operation	Consolidation 2 years
12	Simulation of the consolidation process until the dissipation of pore pressures	Consolidation

and

Table 3. Sequence of calculation phases of the model for cross-section B–B′.

No.	Description	Type of Calculation
01	Calculation of the original stress state before the current landfill began operation.	Gravity loading
02	Loading of the original valley by the weight of the waste deposited up to the moment before the landfill reconstruction.	Plastic
03	Ground zone of new landfill modification.	Plastic
04	Activation of geogrid finite elements simulating the installation of the liner system	Plastic
05	“Waste FGT Ash”—deposition of solidified FGT fly ash	Plastic
06	“Waste 01. ETA”—storage of waste in the new landfill between the 1st and 2nd year of operation	Consolidation 2 years
07	“Waste 10. ETA”—waste storage in the new landfill between the 26th and 28th year of operation	Consolidation 2 years
08	Simulation of the consolidation process until the dissipation of pore pressures	Consolidation

.

The minimum excess pore water pressure value of 1 kPa was chosen as the criterion for the end of consolidation in the last calculation phase for both models.

3.1. Material Models Used in Simulation

The constitutive model, or material model generally, shows the relation between two physical quantities that is specific to a material. The material model in the mathematical analyses in this paper describes the relation between stress increment and strain increment. Two material models were utilized throughout the analyses to describe soils and MSW:

• The linear elastic—perfectly plastic Mohr–Coulomb MC model (MC);
• The Hardening Soil Model (HS)—an elastoplastic model with shear and volumetric hardening [68].

The MC model was used to describe the MSW and a soil used to modify the terrain before the liner installation. The HS model was used to simulate the behavior of the subgrade layers. The definition of HS model was based on the non-linear (hyperbolic) relationship between axial strain and the deviatoric strain in pioneering works [69,70]. These non-linear elastic constitutive models were later complemented by shear and compression yield surfaces. Non-associated plasticity was adopted in the case of shear hardening. The associated plasticity was utilized to predict plastic volumetric changes during compression hardening. The basic features of both material models are graphically compared in Figure 4 and Figure 5 for isotropic and deviatoric loading, respectively.

NCL and URL stand for the normally consolidated line and the unloading–reloading line. E is the modulus of elasticity adopted in the MC model. The response of the HS model is governed by three stiffness parameters: E₅₀ is the secant stiffness in the standard drained triaxial test, E_ur is the unloading/reloading stiffness, and E_oed is the tangent stiffness for the primary oedometer loading. All stiffness modules are stress-dependent; thus, their values for the reference stress level p_ref present inputs for the material model.

E_oed is important in the displacement analysis of large embankments, and therefore, the adopted stress–stiffness formulation is stated below. The friction angle $\mathsf{\phi }$ and cohesion c are the shear strength parameters, m is the power for the stress-level dependence of stiffness, and K₀^nc is the K₀ value for normal consolidation (K₀^nc = 1 – $\sin \mathsf{\phi }$):

$${\mathrm{E}}_{\mathrm{oed}}={\mathrm{E}}_{\mathrm{oed}}^{\mathrm{ref}}{\left(\frac{\mathrm{c}´\cos \mathsf{\phi }´-\frac{\mathsf{\sigma }{´}_3}{{\mathrm{K}}_0^{\mathrm{nc}}}\sin \mathsf{\phi }}{\mathrm{c}´\cos \mathsf{\phi }´+{\mathrm{p}}^{\mathrm{ref}}\sin \mathsf{\phi }}\right)}^{\mathrm{m}}$$

(6)

The performed analyses account for not only the plastic deformations inferred by waste disposal loading, but also for the consolidation processes associated with the dissipation of excess pore pressures in the geological layers underlying the landfill. The consolidation is a coupled hydro–mechanical problem. The change in porosity is influenced by the change in the effective stress state, which means that a hydraulic problem is influenced by a mechanical problem. On the contrary, the change in pore pressures, and hence the effective stresses, is controlled by the hydraulic model, which means that the mechanical model depends on the hydraulic one. Both the equilibrium conditions and continuity equations are linked and solved simultaneously:

$$\left[\begin{array}{cc}\mathrm{K}& \mathrm{L}\\ {\mathrm{L}}^{\mathrm{T}}& -\mathrm{S}\end{array}\right]\left[\begin{array}{c}\frac{\mathrm{dv}}{\mathrm{dt}}\\ \frac{{\mathrm{dp}}_{\mathrm{n}}}{\mathrm{dt}}\end{array}\right]=\left[\begin{array}{cc}0& 0\\ 0& \mathrm{H}\end{array}\right]\left[\begin{array}{c}\mathrm{v}\\ {\mathrm{p}}_{\mathrm{n}}\end{array}\right]+\left[\begin{array}{c}\frac{{\mathrm{df}}_{\mathrm{n}}}{\mathrm{dt}}\\ {\mathrm{q}}_{\mathrm{n}}\end{array}\right]$$

(7)

where K is the stiffness matrix, L is the coupling matrix, S is the compressibility matrix, H is the permeability matrix, ν is the nodal displacements vector, p_n is the nodal excess pore pressure vector, f_n is the incremental load vector, and q_n is the vector due to the prescribed flow at the boundary.

An elastoplastic material model [71] was used for the description of the stress–strain dependence in the geogrid element simulating the liner. The axial stiffness of the geogrid element EA₁ = 309 kN/m and the characteristic tensile strength N_p,1k = 34 kN/m were determined according to [72]. The characteristic value was decreased by a reduction coefficient R_FCR = 1.5, which considers the creep behavior of the material. The design value of the tensile strength after this adjustment is N_p,1d = 22.6 kN/m.

3.2. Input Values of Soil and Waste Material Parameters

A summary of the key engineering parameters of MSW can be found in the literature [73]. MSW consists of different types of materials that are different in their mechanical and chemical properties. Some of these materials decompose over time through ongoing chemical and biological processes, while the properties of others do not change. The classical concepts of soil mechanics themselves have limitations in the modeling of such a complex material as MSW [74]. However, many studies show that, despite the heterogeneous nature of the waste, its mechanical properties change predictably depending on the stress state [73]. This can be observed, for example, in the increasing stiffness of MSW confirmed by dynamic probing performed during surveying of the landfill. (Note: in situ methods can generally be considered very suitable tools for the investigation of landfills [75], whose characteristics can vary considerably in space). The results of probing are mentioned in the following paragraph.

The thickness of MSW was determined by the heavy dynamic probing to be between 3.9 and 29.6 m. The stiffness was also determined based on the above-mentioned penetration tests. In the upper layer of the deposited MSW, which is up to 5 m thick where the waste has not yet been homogenized by biochemical processes and its subsequent consolidation, the ${\mathrm{E}}_{\mathrm{oed}}^{\mathrm{ref}}$ values vary in the range of 5 to 15 MPa (with one outlier ${\mathrm{E}}_{\mathrm{oed}}^{\mathrm{ref}}$= 64 MPa probably caused by the presence of a locally buried obstacle composed of material of relatively higher stiffness). In the deeper part of the landfill, the ${\mathrm{E}}_{\mathrm{oed}}^{\mathrm{ref}}$ values range between 10 and 20 MPa. The single value ${\mathrm{E}}_{\mathrm{oed}}^{\mathrm{ref}}$ = 10 MPa was considered in calculations, which seems to be reasonable in terms of fitting within the intervals of the measured values and which is also on the safe side in terms of calculating the MSW settlements. The unit weight of municipal solid waste is also an important parameter in engineering analyses of landfill performance, but there is currently significant uncertainty about its value. The data show that individual landfills have characteristic unit weight profiles [76,77]. The bulk density of MSW depends on its specific gravity [78] and the degrees of decomposition and compaction. The values of 1000 to 1200 kg/m³ were considered in the present case according to the relationship based on the critical review of published field research data [76]. It is possible to find the results of shear box tests [6] in the literature aimed at determining the shear parameters of waste [6], e.g., [79,80]. Although MSW is an inherently variable substance, the published values of the shear strength parameters appear to be relatively consistent. Values between 0 to 30 kN/m² for cohesion and the range of 20 to 35 degrees for a friction angle can be considered reasonable for design purposes according to [6]. The values of effective strength parameters of the MSW determined according to the results of the undrained full-scale shear test published in [81] were considered in the presented analysis and are summarized in

Table 4. Values of input parameters: index, strength and permeability parameters.

Material	Mass Unit Weight		Cohesion/Angle of Internal Friction		Hydraulic Conductivity Coefficient
	γunsat [kN/m3]	γsat [kN/m3]	C′ [kPa]	φ′ [°]	kx,y sat [m/day]
Modified terrain	11.0	12.0	13.5	33.0	0.864
MSW	11.0	12.0	13.5	33.0	0.864
FGT Ash	15.0	15.0	34.0	29.0	0.864
Clay; Gj	19.4	21.0	24.3	21.6	1.36 × 10−6
Marly clay; GLj	19.6	21.0	26.0	20.5	1.36 × 10−6
Loess (silty clay); PRGd	19.75	21.0	25.0	21.0	1.36 × 10−6

. Determining the filtration coefficient of MSW also poses a major challenge, as it is largely dependent on pore structure, which is directly affected by compression stress and degradation [82,83,84,85]. Based on the published results of an extensive review of the characteristics of landfilled MSW in several countries [86], the values of the permeability coefficient range from k = 3.5 × 10⁻⁴ to 5.0 × 10⁻¹⁰ m/s, which is also consistent with the results of other researchers [87,88]. The value of the permeability coefficient k = 1.0 × 10⁻⁵ m/s was considered in the presented analyses, which is in accordance with the above referenced studies. In addition to MSW, the disposal of flue gas residues, namely, solidified fly ash (FGT), is also planned in an area of the newly constructed landfill. The mechanical and hydraulic parameters of solidified fly ash FGT used in the presented paper were taken from [89]. The values of strength, hydraulic and index parameters of materials used in analyses are summarized in Table 4.

The reference value of tangent stiffness for primary oedometer loading ${\mathrm{E}}_{\mathrm{oed}}^{\mathrm{ref}}$ and the m parameters that govern the stress-level dependency of stiffness according to Equation (6) were determined based on available 1D compression tests. Graphs of the increase in stiffness with the effective normal stress based on the laboratory test results for natural soils are shown in Figure 6. The results of odometric tests [64] do not show an overconsolidation of the soils tested. Therefore, the values OCR = 1 and POP = 0 kPa were considered in the analysis. The input values of the stiffness parameters of the materials used in the model are summarized in

Table 5. Values of input parameters: index, strength and permeability parameters.

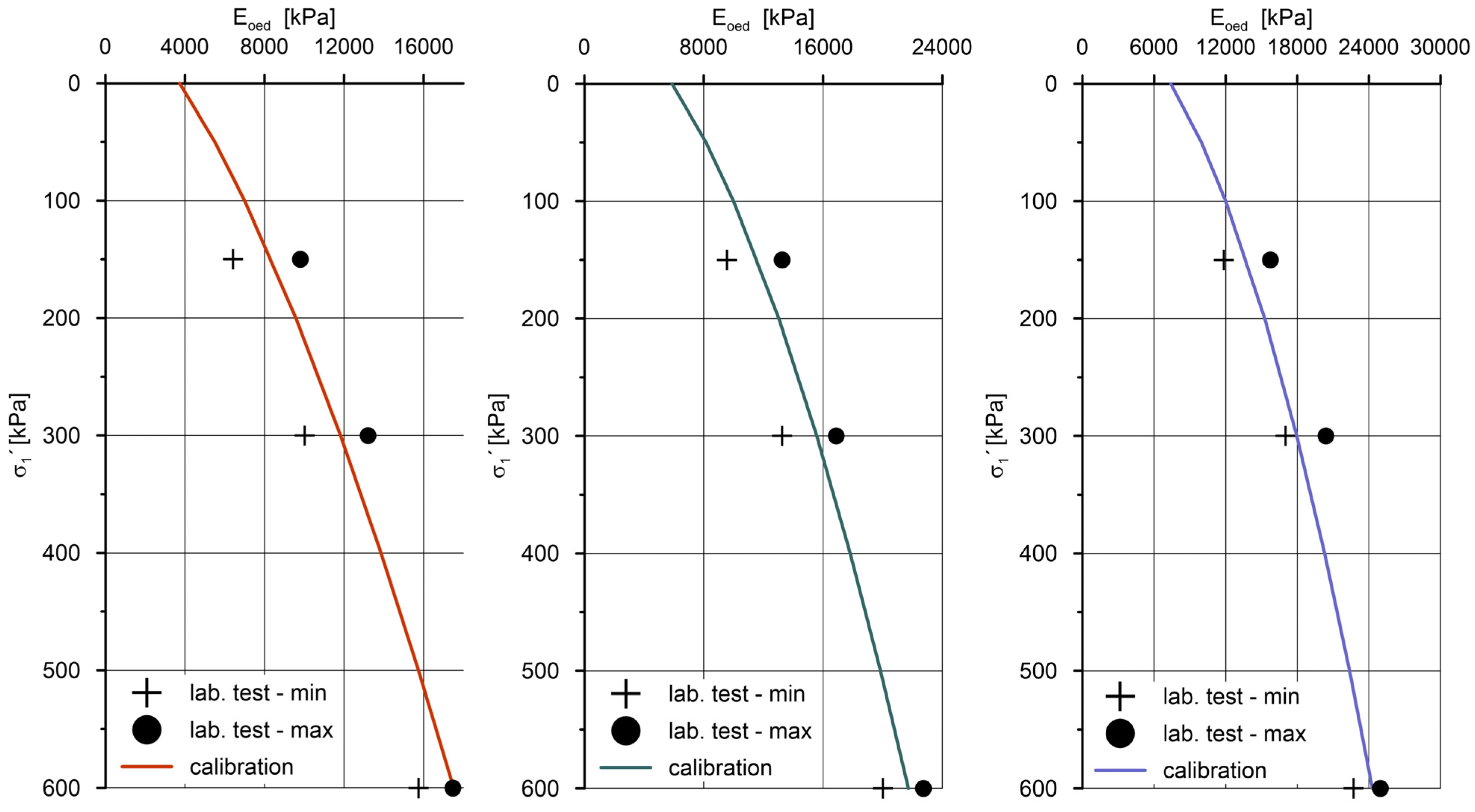
Material	MC		HS
	E′ [MPa]	ν′ [-]	Eoed,ref [MPa]	E50,ref [MPa]	Eur,ref [MPa]	m [-]
Modified terrain	10.0	0.35
MSW	10.0	0.35
FGT Ash	15.0	0.35
Clay; Gj			10.0	10.0	30.0	0.55
Marly clay; GLj			12.0	12.0	36.0	0.50
Loess (silty clay); PRGd			7.0	7.0	21.0	0.65

.

4. Results

The axial force in the geomembrane and the settlement measured at the level of the liner were calculated for each phase. Graphs with the values of these variables plotted along the length of the analyzed individual section are shown in Figure 7, Figure 8, Figure 9, Figure 10 and Figure 11. Only the settlement of the subgrade induced by the load of the newly deposited waste is relevant for the evaluation of the new landfill liner. Therefore, the settlement graphs show only the sum of vertical deformations starting from phase 4, which simulates the installation of the liner in the analyses.

Reducing the shear strength of the geomembrane–soil interface R_inter = 0.5 caused the shear strength of that interface to be reached in the section between 170 and 250 m from the start of the model. This was reflected in the occurrence of unrealistic axial force oscillations during the consolidation stage (Figure 8).

Figure 9 shows that the rate of filling is significantly higher than the permeability of the underlaying layers would allow. Therefore, a substantial increase in settlement during the period of primary consolidation can be expected. The increase in axial forces in the geomembrane is mainly due to a non-uniform layering of a waste material. According to the Figure 7, the change in the axial forces during consolidation is small when compared to the phase of waste deposition.

The settlement of the crown of the newly built landfill u_tot = 4.52 m in the case of the model of longitudinal section A–A′ and u_tot = 2.73 m in the case of the cross-sectional model B–B′ were calculated at the time after the minimum excess pore pressure 1 kPa was reached.

5. Discussion

Settlement is one of the main factors for the development of tensile stresses in the geomembrane in landfill applications. Recently, studies have been published that investigate the development of tensile strains in the geomembrane using the FEM method [46,90]. The landfills modelled in these studies simulated ideal conditions for the setting and filling of new landfill. This means that the subsoil of the modelled landfills is made of competent rock and the waste is deposited in a controlled manner in evenly distributed layers. In some areas, it is sometimes inevitable to build landfills on soft subgrade settlement. In Xu et al.’s paper [91], such a landfill with a flat bottom was analyzed. If a new landfill project is being developed, a suitable site is selected for its construction and filling is properly managed further. However, this may not always be the case for existing landfills. Some case studies regarding the redevelopment of MSW landfills were published, e.g., [92,93], but they are not based on numerical modeling. The purpose of this paper was to numerically analyze a real-life case with initial geological and geometrical conditions predetermined by the previous development of an originally unmanaged and subsequently rehabilitated landfill site considering the realistic filling plan and to analyze results influenced by these conditions.

The results of the numerical analyses showed that the expected axial force does not exceed the design strength N_p,1d = 22.6 kN/m of the geomembrane planned to be incorporated into the composite liner. A significant increase in the axial force can be observed where the liner transitions from the area of the current landfill to the area of the extended landfill (see, e.g., the section between 175 and 250 m from the start in the mathematical model B–B′ in Figure 8). In other words, the peak values in the axial force are observed in the sections where the subsurface properties change abruptly. The increases in axial forces in the geomembrane are also due to non-uniform layering of MSW given by the filling plan prescribed by the landfill operator.

The influence of the value of the strength reduction factor R_inter on the results was also evaluated. Without the strength reduction (R_inter = 1.0), the maximum axial force 7.2 kN/m was calculated in the model of longitudinal section A–A′. Reducing the shear strength of the geomembrane-soil interface caused the shear strength to be reached in the section between 170 and 250 m in the mathematical model of cross-section A–A′. This was reflected in the occurrence of unrealistic axial force oscillations during the consolidation stage of calculation. The actual R_inter value selection considers the weakest interface in the geomembrane–geotextile–drainage layer system. From these three interfaces, the geomembrane–geotextile contact is usually the weakest one. As the final choice of the composition of the sealing layer was not made in the initial phase of the project, it was not possible to perform an analysis with a particular value of R_inter. Since the value of R_inter affects the stresses induced in the geomembrane, further research regarding the modeling of this detail is still required.

As part of the preliminary considerations for the use of the area of the planned landfill after it has finished operation in the future, it should be considered that settlement at the level of the future landfill crown will be in the order of meters (u_tot = 2.7 m to u_tot = 4.5 m in the cross-sections presented). Most studies are concerned with the settlement of the MSW layer itself, but not with the settlement of a subgrade. As the results of the analyses conducted show, subgrade settlement can be a non-negligible component of total settlement. The settlement of only subgrade u_y = 3.75 m in the case of longitudinal section A–A′ represents 83% of the total settlement u_tot = 4.52 m, including the settlement of a 47 m thick MSW layer. This value is dependent on the constitutive model used for the description of the MSW behavior within the analysis. If the settlement of the MSW layer to the order of 25% to 50% of the initial thickness was theoretically considered, as reported by the results of referenced studies [49,50,51,52,53], the settlement of the originally 47 m thick layer would be u_MSW = 11.75 m or u_MSW = 23.5 m, respectively. Still, the total settlement of subgrade u_y = 3.75 m would represent 32% of theoretical total settlement or 16%, respectively. Moreover, the settlement distribution is highly non-uniform along the cross-sections, due to the non-evenly deposited MSW layers.

According to the referenced literature, 80% of the settlement of MSW layer should take place within the first 30 years after its deposition. Compared to the time needed for the settlement of the MSW, the time for reaching the final primary consolidation settlement of subgrade is longer. Only 25% of primary consolidation settlement of subsoil is expected to be reached during the 28 years of operation of the new landfill in the case of cross-section B–B′, and 27% in the case of cross-section A–A′.

Deformations of the subgrade beneath the landfill body also result in uplifting of the terrain at the landfill perimeter during the filling and in a settlement during the consolidation phase. Thus, a fixed position of the anchor trench in the space that is assumed in analytical methods for the design of anchor trenches is not guaranteed.

The synergistic effect of MSW settlement and the settlement of the landfill subgrade on membrane stresses requires further studies, adopting eventually different constitutive models for MSW and different strength reductions of the interface between the geomembrane and adjacent materials.