Development of a Cost-Based Design Model for Spread Footings in Cohesive Soils
Abstract
:1. Introduction
2. Literature Review
2.1. Research Gap
2.2. Aim and Objectives of the Study
- To present an optimized model comprising of cost-based foundation design charts which consider safety requirements, i.e., ultimate limit state (ULS) and serviceability limit state (SLS), along with the economy of the design project.
- To clarify the flaws in usual practices adopted to estimate bearing capacity by analyzing different case studies.
- To analyze cost estimation and to compare the economic effect while considering the variability of BC values.
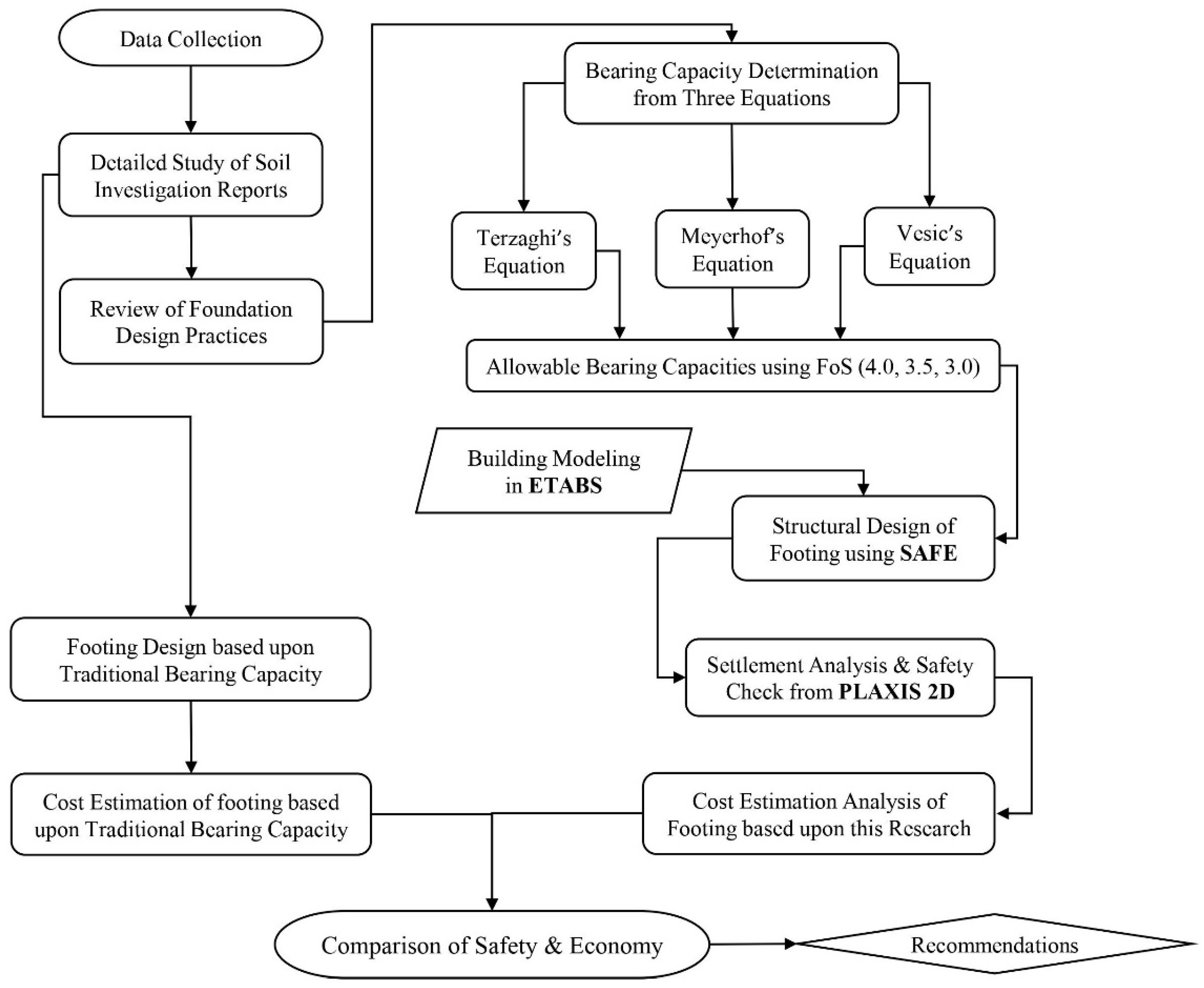
3. Development of Conceptual Framework
3.1. Data Collection
3.2. Bearing Capacity Calculations and Foundation Design
3.2.1. Correlations between N-Value and Su
3.2.2. Bearing Capacity Equations
3.3. Calibration of Factor of Safety for Design
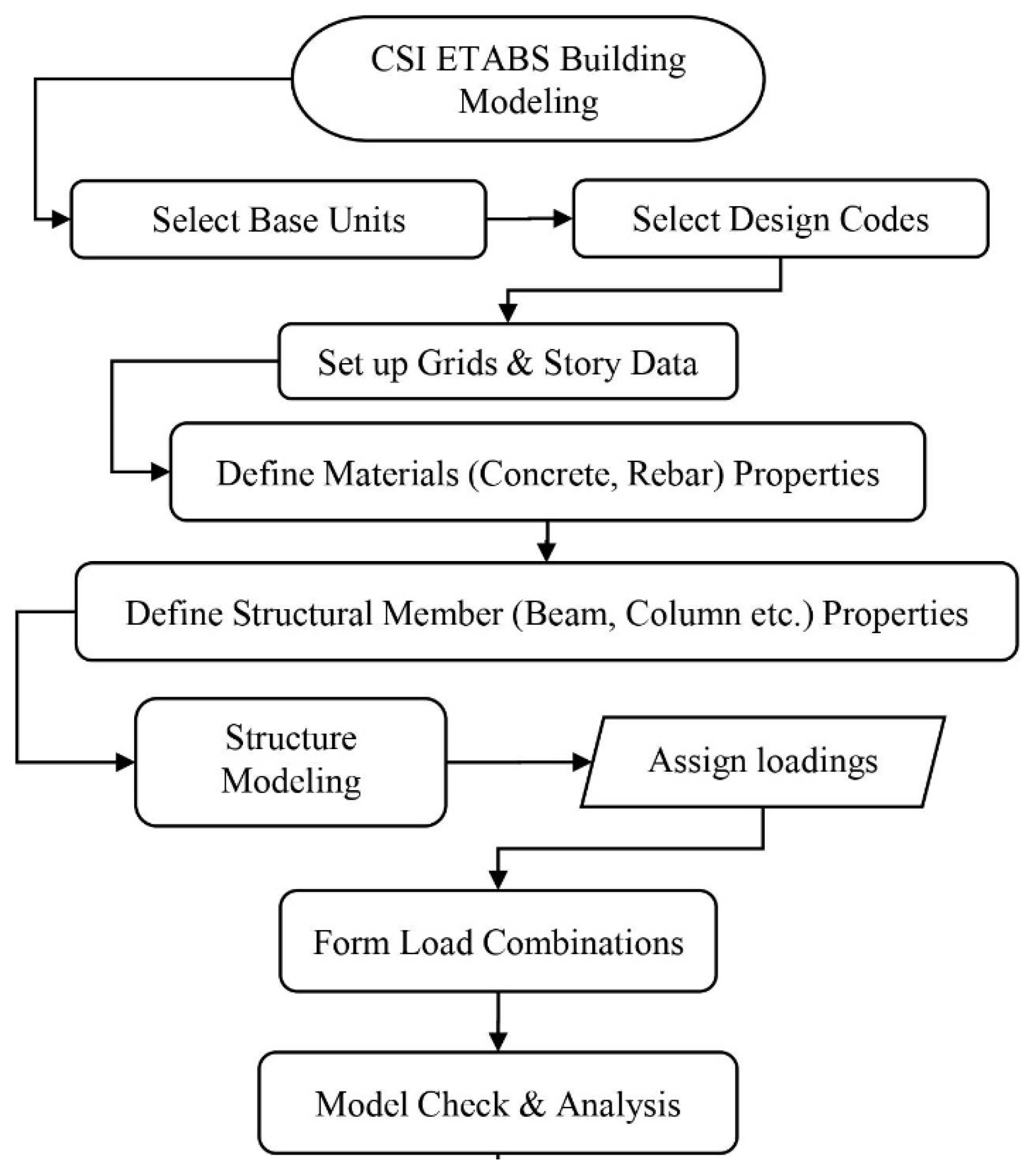
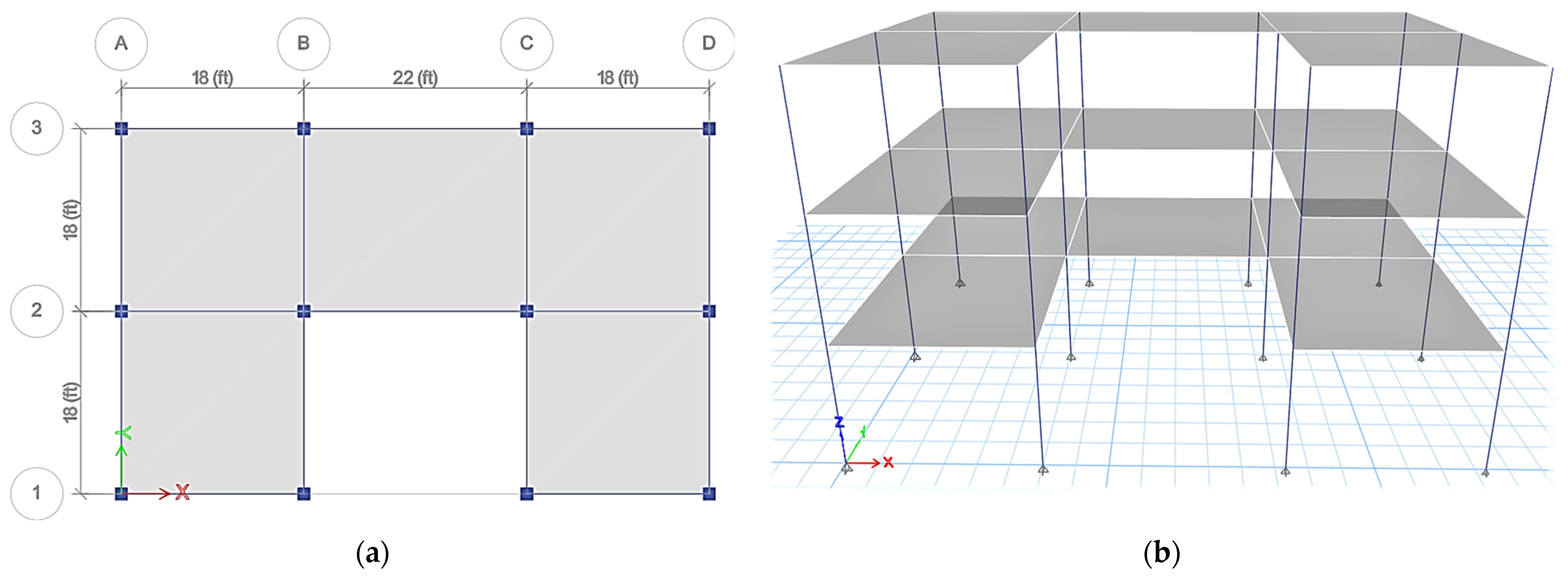
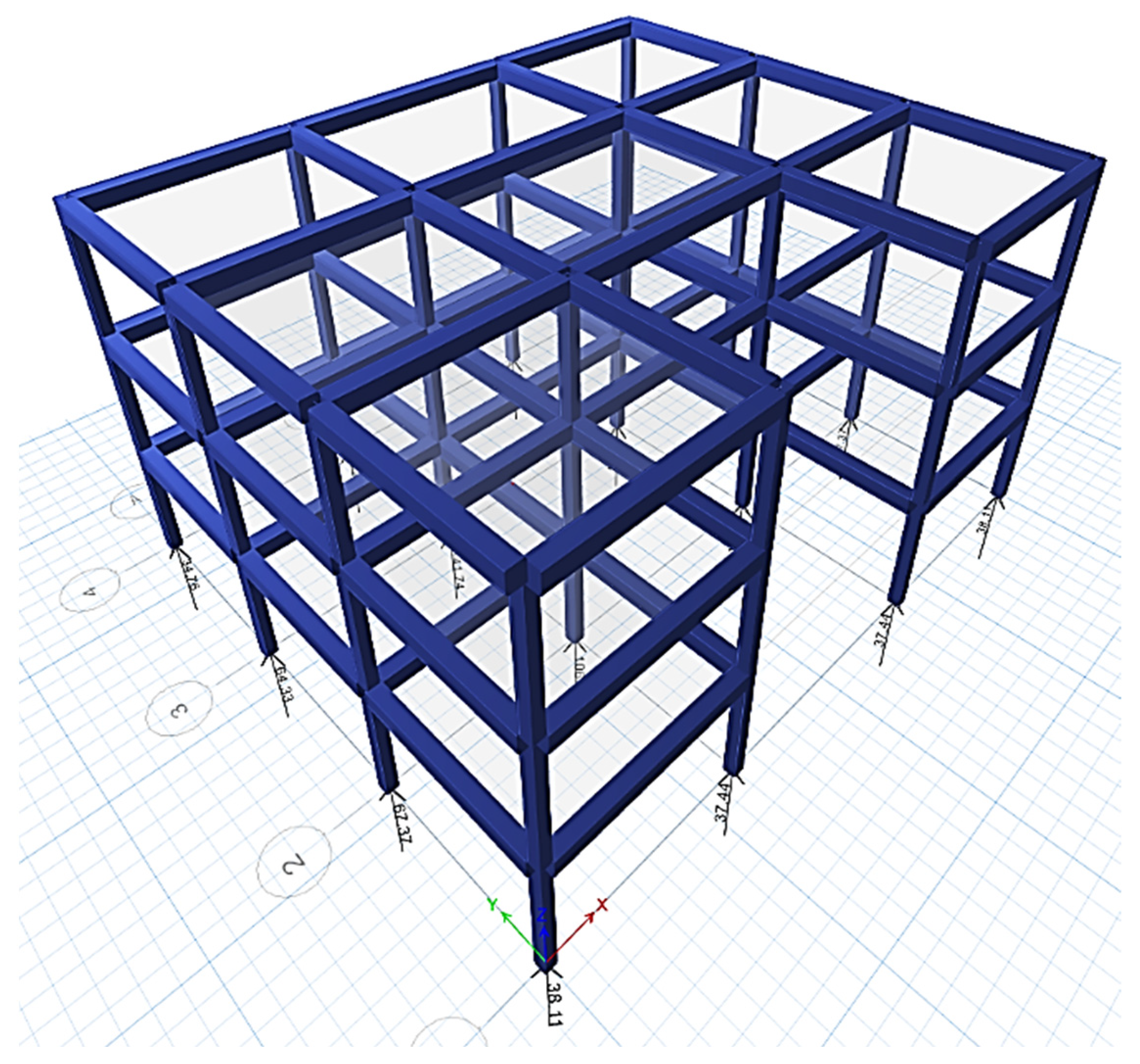
3.4. CSI ETABS Modeling
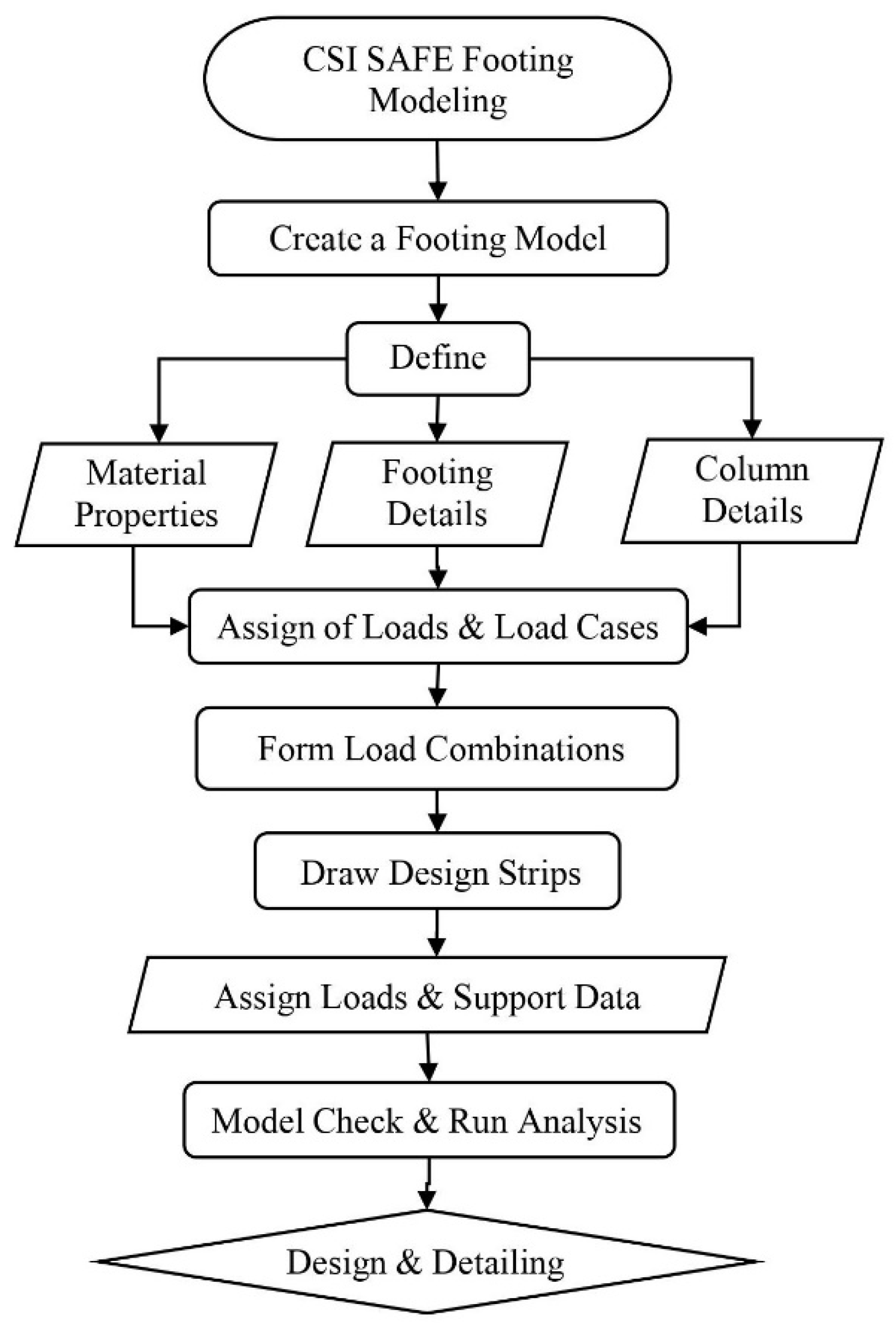
3.5. CSI SAFE Modeling
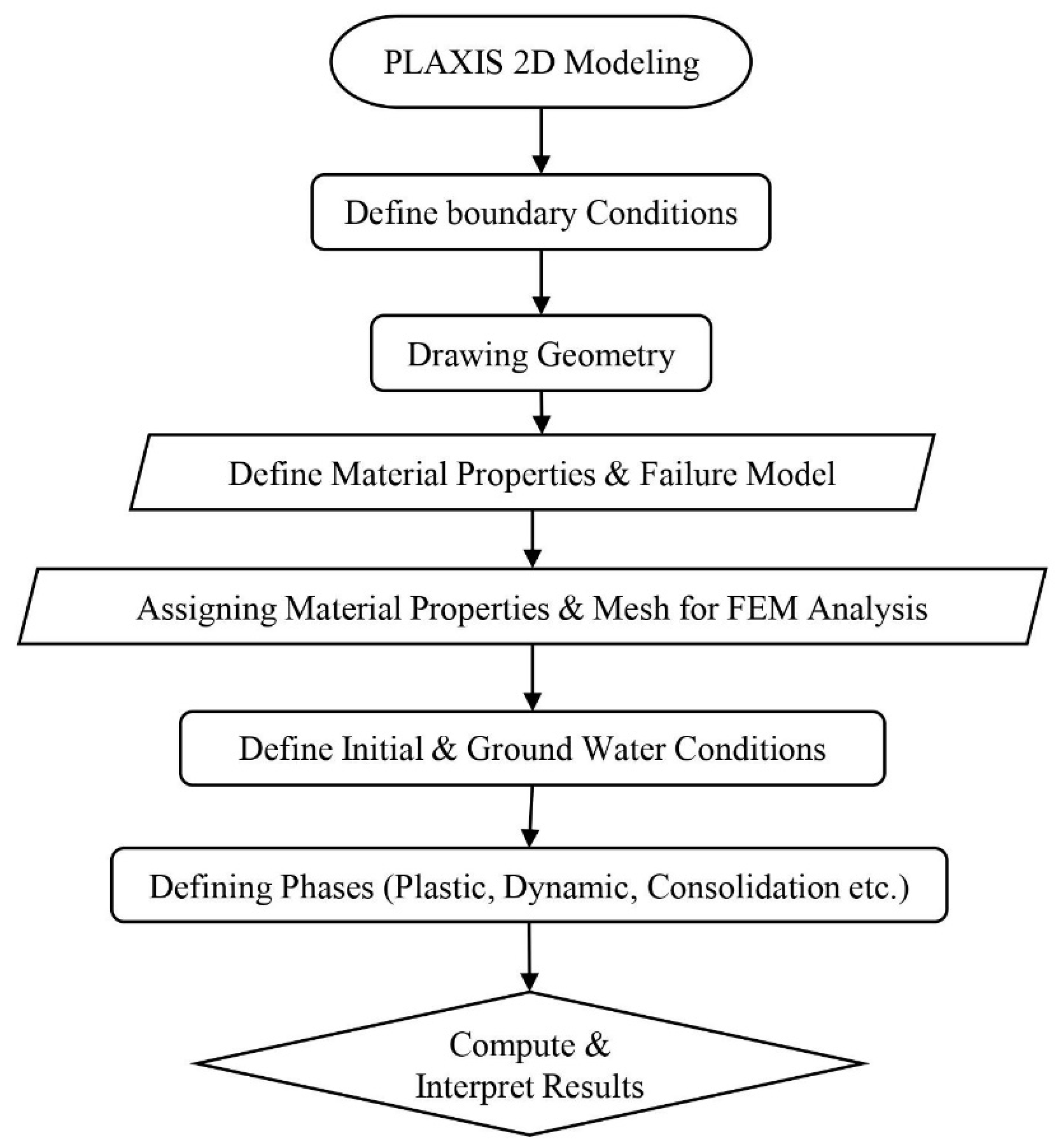
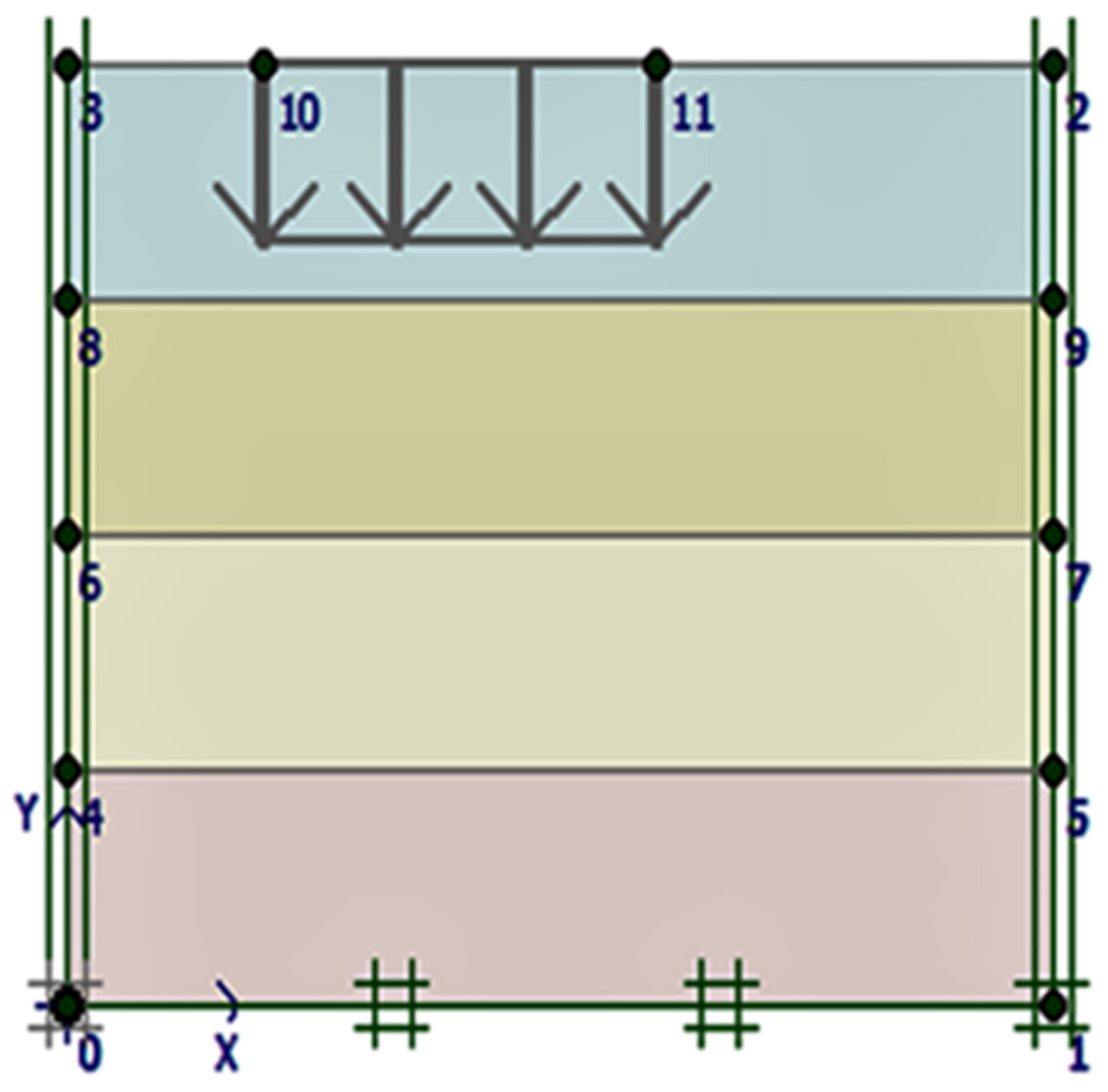
3.6. PLAXIS 2D Modeling
3.7. Cost Estimation Analysis
4. Results
4.1. Results from CSI ETABS
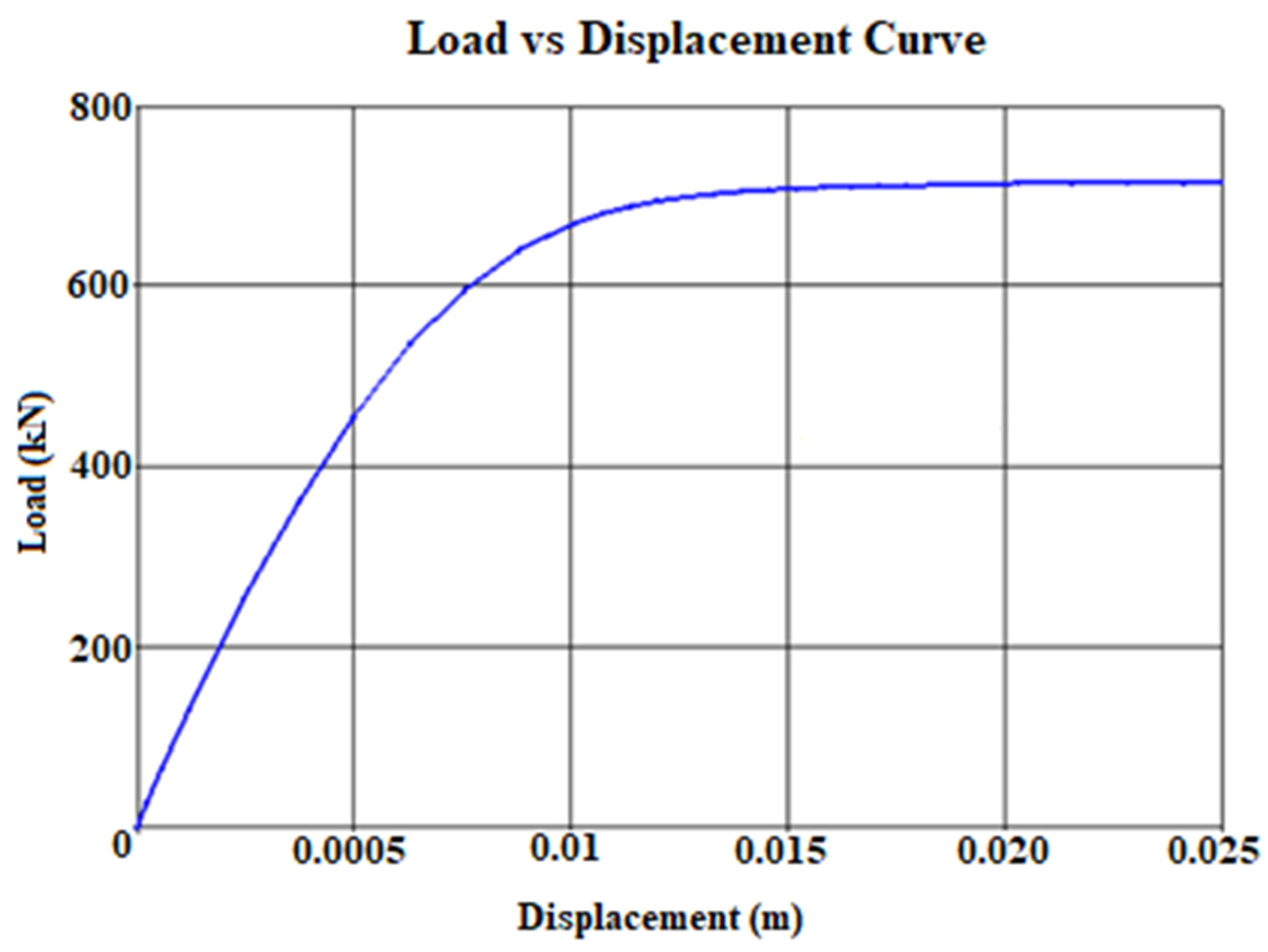
4.2. Results from CSI SAFE
4.3. Results from PLAXIS-2D
4.4. Bearing Capacities of Selected Sites
4.5. Design Charts
4.5.1. Design Charts Based upon Terzaghi’s Equation
4.5.2. Design Charts Based upon Meyerhof’s Equation
4.5.3. Design Charts Based upon Vesic’s Equation
5. Discussion
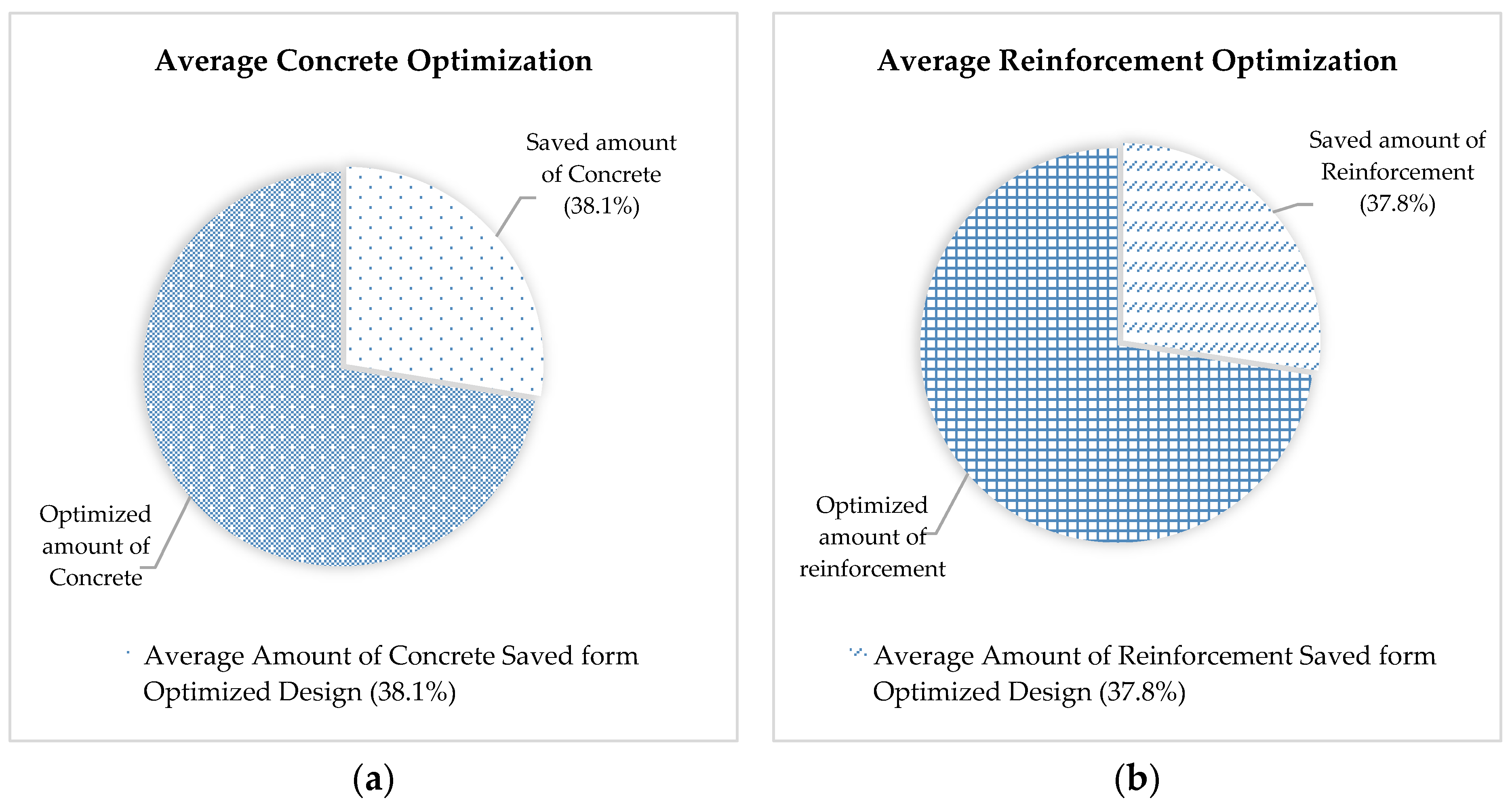
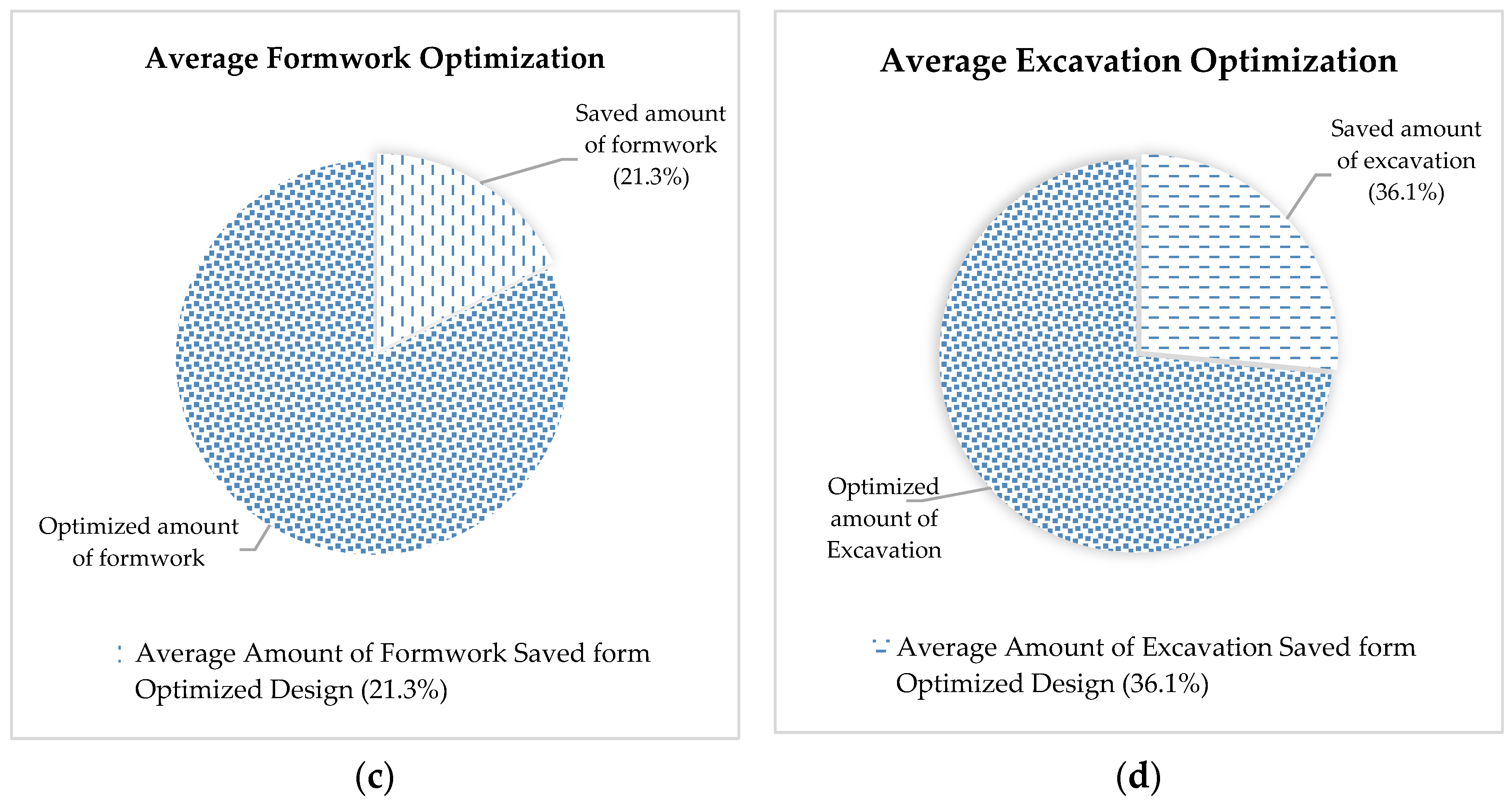
5.1. Optimization of Foundation Material
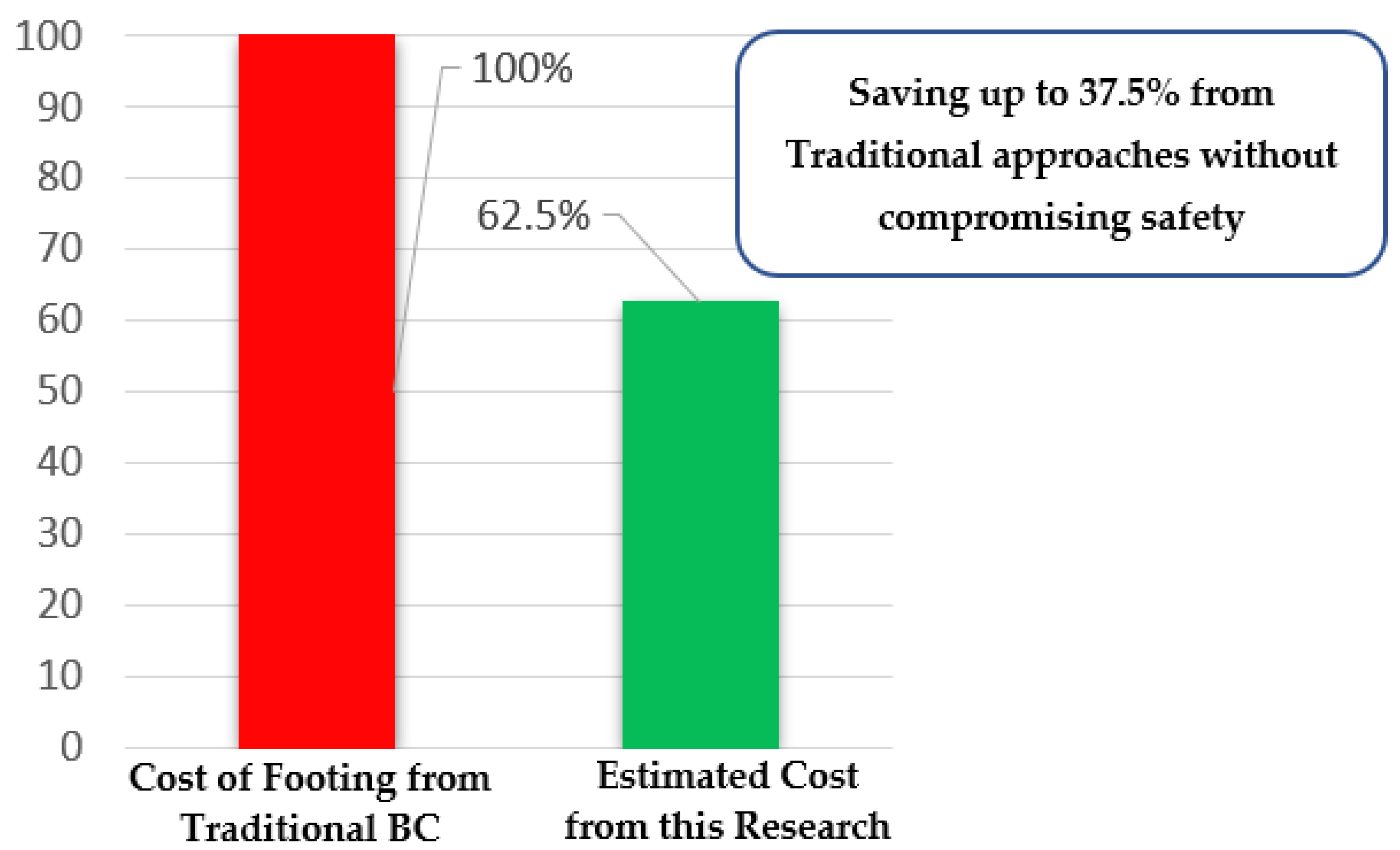
5.2. Comparison between Traditional and Optimized Foundation Design
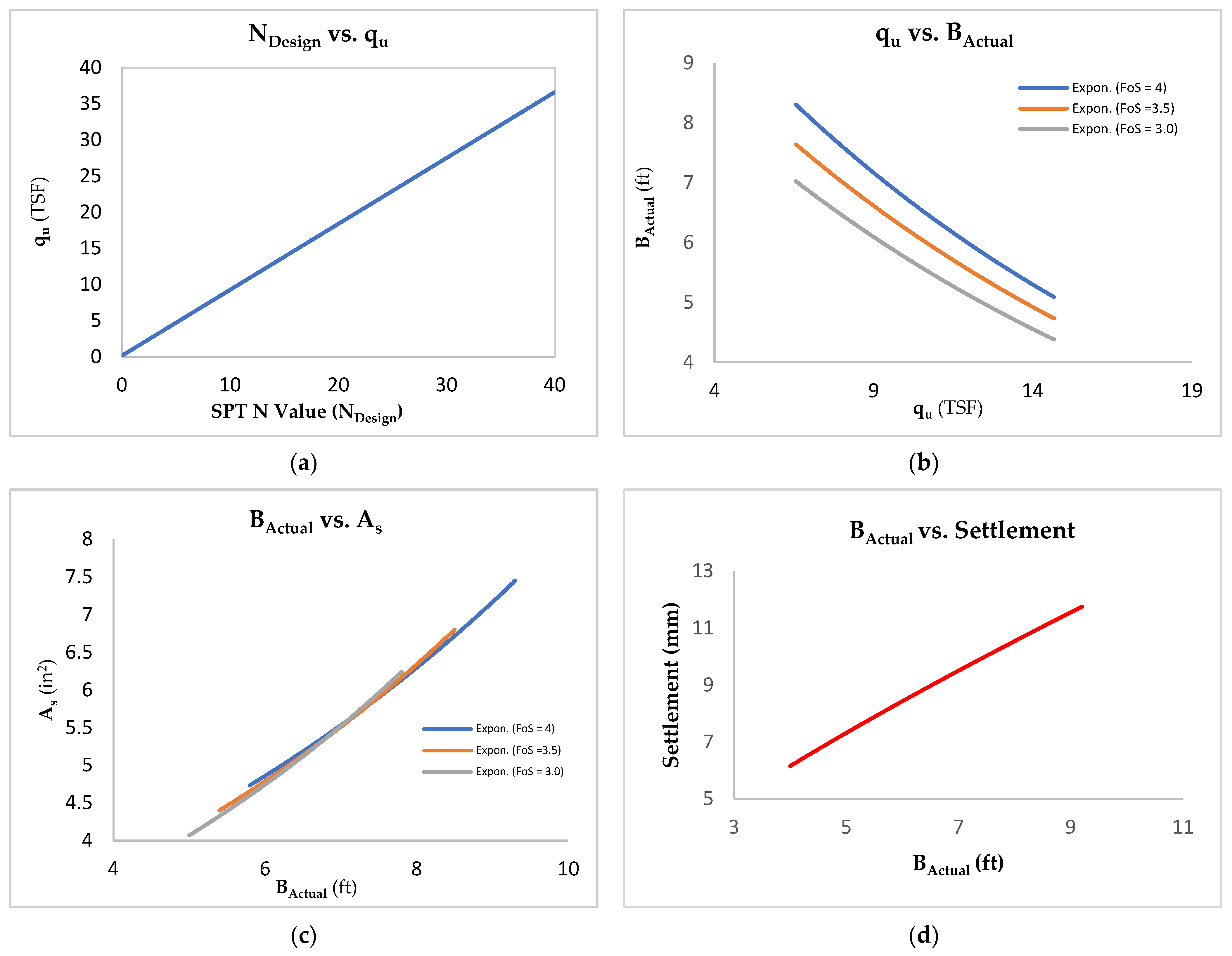
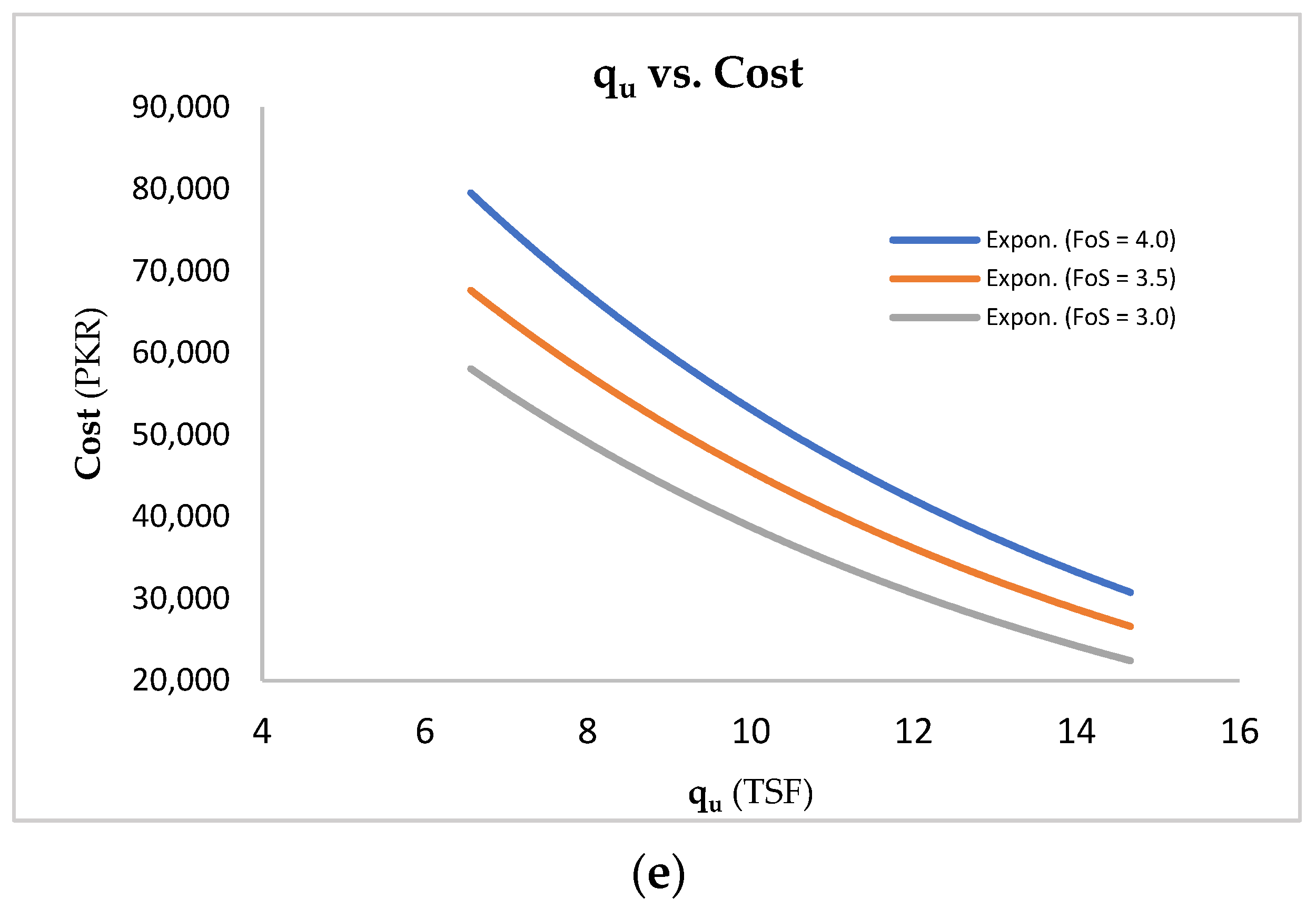
5.3. Proposed Framework
- Step One: In the first step, NDesign will be selected using Equation (25). Then, the ultimate bearing capacity will be determined using Figure 12a based on NDesign value.
- Step Two: In the second step, qu computed in the first step will be utilized to estimate the actual width of footing corresponding to desired FoS value using Figure 12b.
- Step Three: The value of BActual computed in step two will be used to estimate the area of reinforcement from Figure 12c.
- Step Four: The value of BActual will be used to assess the settlement of the footing in quantitative terms using Figure 12d.
- Step Five: The value of qu will be used to assess the construction cost of footing in quantitative terms using Figure 12e.
6. Conclusions
- This study presents an optimized model of foundation design comprising cost-based design charts which consider safety requirements, i.e., ULS, SLS, and economy at once. This developed optimized design approach provides a speedy method for foundation design for Silty Clay soils. The developed design charts can be used for an efficient economical design of shallow foundations considering safety requirements.
- This study concludes that the conventional design practices inculcate the use of a higher FoS to compensate for the uncertainties, inaccuracies, and unavailability of enough soil investigation data. Contrary to that, this study provides the design charts to estimate the design of shallow foundations with the use of an appropriate FoS, even with the non-availability of enough data. The design charts are also useful in designing a cost-effective shallow foundation considering safety requirements.
- Overconservative approaches may lead to an uneconomical situation. Therefore, it was observed that even the highest bearing capacity values, obtained from the utilized (Terzaghi, Meyerhof, Vesic) equations, can be recommended if they satisfy safety requirements. Thus, the highest bearing capacity computed can be recommended for the foundation design.
- The results show that savings could be as much as 37.5% in comparison with the cost obtained from conventional foundation design. The optimized construction cost may change depending upon the subsurface soil conditions, design requirements, and groundwater conditions.
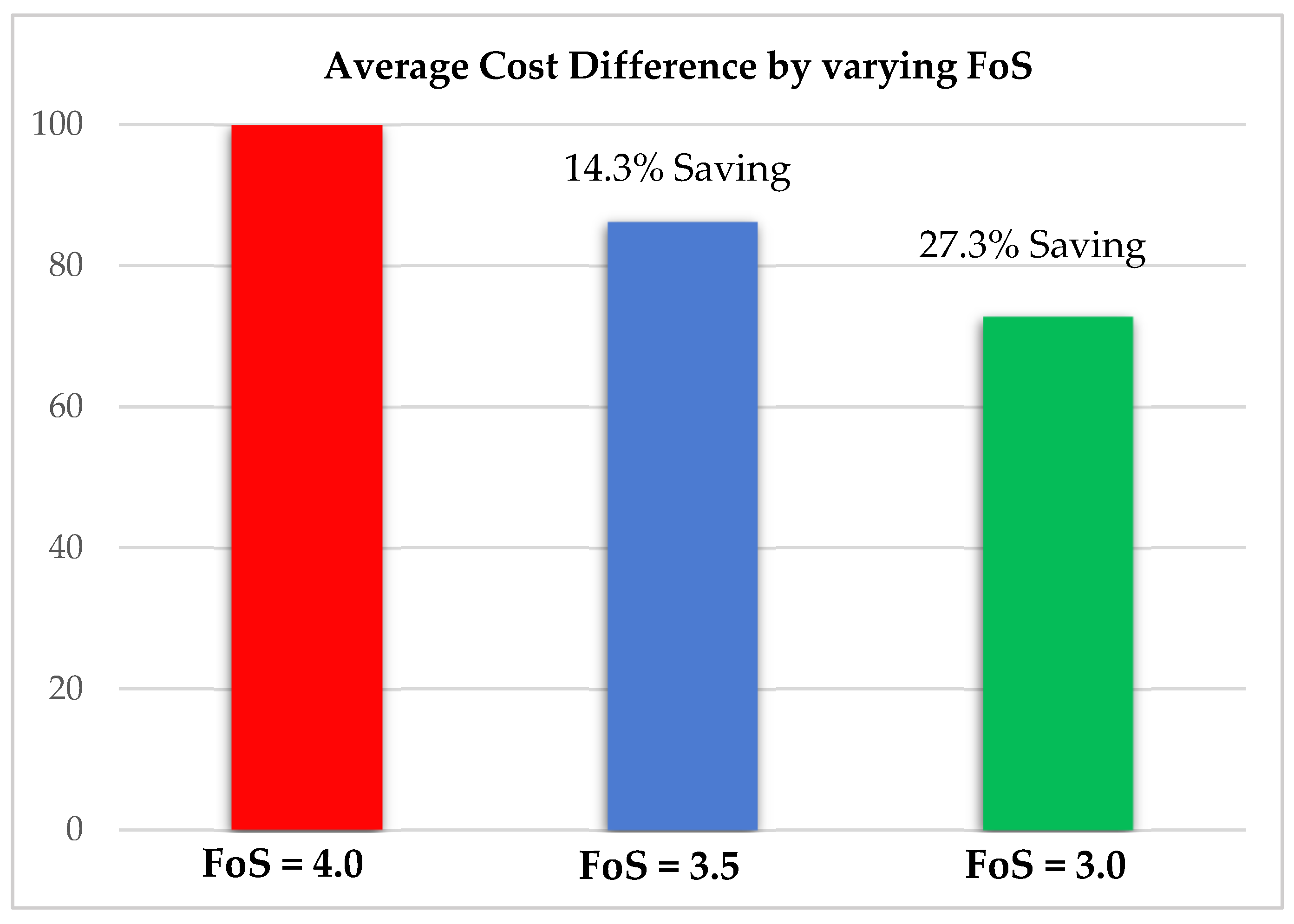
- Statistical analysis shows there is a 0% probability of failure for low-rise buildings against the highest bearing capacity value and FoS equal to three or lesser can be used in general as the optimal value for design purposes to determine allowable bearing capacity. Since the average savings by changing FoS from 4.0 to 3.5 are 14.3% while changing FoS from 4.0 to 3.0 can be 27.3% can be achieved.
- It is observed that even the most conservative approaches for the foundation yield more than 2 Tsf bearing capacity for the silty clayey soil.
- Hence, future research may address other aspects of foundation design, such as seismic design parameters, variation of design loads, and validation of design charts through large-scale in-situ testing.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Kuhlman, T.; Farrington, J. What is sustainability? Sustainability 2010, 2, 3436–3448. [Google Scholar] [CrossRef] [Green Version]
- Al-Taie, E. Analysis of Shallow Foundations in Three Different Regions in Iraq. Ph.D. Thesis, Luleå Tekniska Universitet, Luleå, Sweden, 2016. [Google Scholar]
- Wellington, A.M. The Economic Theory of the Location of Railways: An Analysis of the Conditions Controlling the Laying Out of Railways in Effect this Most Judicious Expenditure of Capital; John Wiley & Sons: Hoboken, NJ, USA, 1887. [Google Scholar]
- Coduto, D.P.; Kitch, W.A.; Yeung, M.R. Foundation Design: Principles and Practices; Prentice Hall: Hoboken, NJ, USA, 2001; Volume 2. [Google Scholar]
- Shahin, M.A.; Cheung, E.M. Probabilistic Analysis of Bearing Capacity of Strip Footings; Department of Civil Engineering, Curtin University: Perth, Australia, 2011; pp. 225–230. [Google Scholar]
- Azhim, A.; Prakoso, W.A. Construction cost optimization of shallow foundation for sand soil in Indonesia. MATEC Web Conf. 2019, 270, 05005. [Google Scholar] [CrossRef]
- Chaudhuri, P.; Maity, D. Cost optimization of rectangular RC footing using GA and UPSO. Soft Comput. 2020, 24, 709–721. [Google Scholar] [CrossRef]
- Juang, C.H.; Wang, L. Reliability-based robust geotechnical design of spread foundations using multi-objective genetic algorithm. Comput. Geotech. 2013, 48, 96–106. [Google Scholar] [CrossRef]
- Rawat, S.; Kant Mittal, R. Optimization of eccentrically loaded reinforced-concrete isolated footings. Pract. Period. Struct. Des. Constr. 2018, 23, 6018002. [Google Scholar] [CrossRef]
- Islam, M.S.; Rokonuzzaman, M. Optimized design of foundations: An application of genetic algorithms. Aust. J. Civ. Eng. 2018, 16, 46–52. [Google Scholar] [CrossRef]
- Wang, Y. Reliability-based economic design optimization of spread foundations. J. Geotech. Geoenviron. Eng. 2009, 135, 954–959. [Google Scholar] [CrossRef]
- Wang, Y.; Kulhawy, F.H. Economic design optimization of foundations. J. Geotech. Geoenviron. Eng. 2008, 134, 1097–1105. [Google Scholar] [CrossRef]
- Kashani, A.R.; Gandomi, M.; Camp, C.V.; Gandomi, A.H. Optimum design of shallow foundation using evolutionary algorithms. Soft Comput. 2020, 24, 6809–6833. [Google Scholar] [CrossRef]
- Khalid, M.H.; Alshameri, B.; Abid, U. Application of Kriging for development of SPT N value contour maps and USCS-based soil type qualitative contour maps for Islamabad, Pakistan. Environ. Earth Sci. 2021, 80, 413. [Google Scholar] [CrossRef]
- Luat, N.-V.; Nguyen, V.-Q.; Lee, S.; Woo, S.; Lee, K. An evolutionary hybrid optimization of MARS model in predicting settlement of shallow foundations on sandy soils. Geomech. Eng. 2020, 21, 583–598. [Google Scholar]
- Rabiei, M.; Choobbasti, A.J. Economic design optimization of piled raft foundations. Innov. Infrastruct. Solut. 2018, 3, 65. [Google Scholar] [CrossRef]
- Fathima Sana, V.K.; Nazeeh, K.M.; Dilip, D.M.; Sivakumar Babu, G.L. Reliability-Based Design Optimization of Shallow Foundation on Cohesionless Soil Based on Surrogate-Based Numerical Modeling. Int. J. Geomech. 2022, 22, 4021283. [Google Scholar] [CrossRef]
- Zhong, Z.; Zhang, S.; Zhao, M.; Hou, B.; Gong, W. Reliability-based robust geotechnical design of spread foundations considering multiple failure modes. Comput. Geotech. 2020, 119, 103292. [Google Scholar] [CrossRef]
- Moayedi, H.; Mosavi, A. A water cycle-based error minimization technique in predicting the bearing capacity of shallow foundation. Eng. Comput. 2021, 1–14. [Google Scholar] [CrossRef]
- Jaafar, K.; El-Halawani, L.I. Simulation-based multi-objective optimization model for machinery allocation in shallow foundation. Int. J. Constr. Manag. 2020, 20, 1–10. [Google Scholar] [CrossRef]
- Abdul-husain, H.A. Comparison of Theoretical Ultimate Bearing Capacity of Cohesionless Soils with Experimental And Field Data. J. Babylon Univ. Eng. Sci. 2016, 24, 596–603. [Google Scholar]
- ACI Committee 318. Building Code Requirements for Structural Concrete; American Concrete Institute: Indianapolis, IN, USA, 2014; ISBN 9780870317446. [Google Scholar]
- Pereira, C.; Caldeira, L. Shallow Foundation Design through Probabilistic and Deterministic Methods. In Proceedings of the 3rd International Symposium on Geotechnical Safety and Risk (ISGSR 2011), Munich, Germany, 2–3 June 2011. [Google Scholar]
- Terzaghi, K. Theoretical Soil Mechanics; John Wiley & Sons: Hoboken, NJ, USA, 1943. [Google Scholar]
- Meyerhof, G.G. The ultimate bearing capacity of foudations. Geotechnique 1951, 2, 301–332. [Google Scholar] [CrossRef]
- Vesic, A.S. Bearing Capacity of Shallow Foundations. In Foundation Engineering Handbook; Winterkorn, F.S., Fand, H.Y., Eds.; Springer: Boston, MA, USA, 1975. [Google Scholar]
- Hettiarachchi, H.; Brown, T. Use of SPT blow counts to estimate shear strength properties of soils: Energy balance approach. J. Geotech. Geoenviron. Eng. 2009, 135, 830–834. [Google Scholar] [CrossRef]
- Rahman, M. Foundation Design using Standard Penetration Test (SPT) N-value. Researchgate 2019, 5, 1–39. [Google Scholar] [CrossRef]
- Das, B.M. Principles of Foundation Engineering, 8th ed.; Cengage Learning: Boston, MA, USA, 2015; ISBN 1305537890. [Google Scholar]
- Budhu, M. Soil Mechanics and Foundations; John Wiley & Sons: Hoboken, NJ, USA, 2010; ISBN 0470556846. [Google Scholar]
- Bowles, J.E. Foundation Engineering; McGraw Hills: Singapore, 1997. [Google Scholar]
- Sivakumar Babu, G.L.; Srivastava, A.; Murthy, D.S.N. Reliability analysis of the bearing capacity of a shallow foundation resting on cohesive soil. Can. Geotech. J. 2006, 43, 217–223. [Google Scholar] [CrossRef]
- Foye, K.C.; Salgado, R.; Scott, B. Resistance factors for use in shallow foundation LRFD. J. Geotech. Geoenviron. Eng. 2006, 132, 1208–1218. [Google Scholar] [CrossRef]
- Cheng, L. Soils and Foundations; Food and Agriculture Organization of the United Nations: Rome, Italy, 1992. [Google Scholar]
- Guleria, A. Structural analysis of a multi-storeyed building using ETABS for different plan configurations. Int. J. Eng. Res. Technol. 2014, 3, 1481–1485. [Google Scholar]
- Mirmohammad, S.S.J.; Babaei, A.L.I.R. Structural optimization of B70 railway prestressed concrete sleepers. Iran. J. Sci. Technol. Trans. B Eng. 2006, 30, 461–473. [Google Scholar]
- Teli, S.; Kundhani, P.; Choksi, V.; Sinha, P.; Iyer, K.K.R. Influence of Loading and Soil Modeling Approach on Soil-Shallow Foundation Interaction. In Lecture Notes in Civil Engineering, Proceedings of the Indian Geotechnical Conference 2019; Springer: Singapore, 2021; pp. 505–514. [Google Scholar]
- Sherazi, S.M.A.; Hassan, S.; Sherazi, A. (Eds.) National Highway Authority Composite Schedule of Rates (Punjab); SAMPAK International (Pvt.) Ltd.: Punjab, Pakistan, 2014. [Google Scholar]
- Bledsoe, J.D. From Concept to Bid: Successful Estimating Methods; RS Means Company: Rockland, MA, USA, 1992; ISBN 0876292163. [Google Scholar]
- Das, B.M. Principles of Foundation Engineering, 7th ed.; Cengage Learning: Boston, MA, USA, 2002; ISBN 0534030521. [Google Scholar]




| Material | Strength of Material | Usage |
|---|---|---|
| Concrete | 3000 Psi | For beams and slabs |
| Concrete | 4000 Psi | For columns and footings |
| Rebar | Grade 60 | Longitudinal (main) reinforcement |
| Rebar | Grade 40 | Confinement bars (ties) |
| Section | Size | Section | Size | Section | Size |
|---|---|---|---|---|---|
| Columns | 15″ × 15″ | Beams | 18″ × 15″ | Slab | 6″ Thick |
| Materials | Labor | Material | Unit |
|---|---|---|---|
| Concrete | PKR 4714 | PKR 5600 | Cubic Yard |
| Reinforcement | PKR 12 | PKR 112 | Kilogram |
| Formwork | PKR 18 | PKR 14 | Sq. ft/contact area |
| Excavation | PKR 216 | PKR 0 | Cubic Yard |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nawaz, M.M.; Khan, S.R.; Farooq, R.; Nawaz, M.N.; Khan, J.; Tariq, M.A.U.R.; Tufail, R.F.; Farooq, D.; Ng, A.W.M. Development of a Cost-Based Design Model for Spread Footings in Cohesive Soils. Sustainability 2022, 14, 5699. https://doi.org/10.3390/su14095699
Nawaz MM, Khan SR, Farooq R, Nawaz MN, Khan J, Tariq MAUR, Tufail RF, Farooq D, Ng AWM. Development of a Cost-Based Design Model for Spread Footings in Cohesive Soils. Sustainability. 2022; 14(9):5699. https://doi.org/10.3390/su14095699
Chicago/Turabian StyleNawaz, Muhammad Muneeb, Shah Rukh Khan, Rashid Farooq, Muhammad Naqeeb Nawaz, Jamil Khan, Muhammad Atiq Ur Rehman Tariq, Rana Faisal Tufail, Danish Farooq, and Anne W. M. Ng. 2022. "Development of a Cost-Based Design Model for Spread Footings in Cohesive Soils" Sustainability 14, no. 9: 5699. https://doi.org/10.3390/su14095699
APA StyleNawaz, M. M., Khan, S. R., Farooq, R., Nawaz, M. N., Khan, J., Tariq, M. A. U. R., Tufail, R. F., Farooq, D., & Ng, A. W. M. (2022). Development of a Cost-Based Design Model for Spread Footings in Cohesive Soils. Sustainability, 14(9), 5699. https://doi.org/10.3390/su14095699









