Stabilization Strategy of a Novel Car-Following Model with Time Delay and Memory Effect of the Driver
Abstract
:1. Introduction
- (1)
- Driver memory is considered on the basis of OVM, and it is pointed out that drivers’ memory of previous traffic will have a significant impact on subsequent follow-up behavior.
- (2)
- This study comprehensively designs control term parameters to mitigate delay-induced unstable traffic flow.
- (3)
- The control strategy of this study considers the influence of multiple time delays on the traffic flow, which is closer to the actual traffic situation.
- (4)
- The IDISM and Hopf bifurcation analysis methods are used to determine the stability interval of the system. Thus, an appropriate combination of parameters for a drivers’ memory model with time delay feedback control is determined.
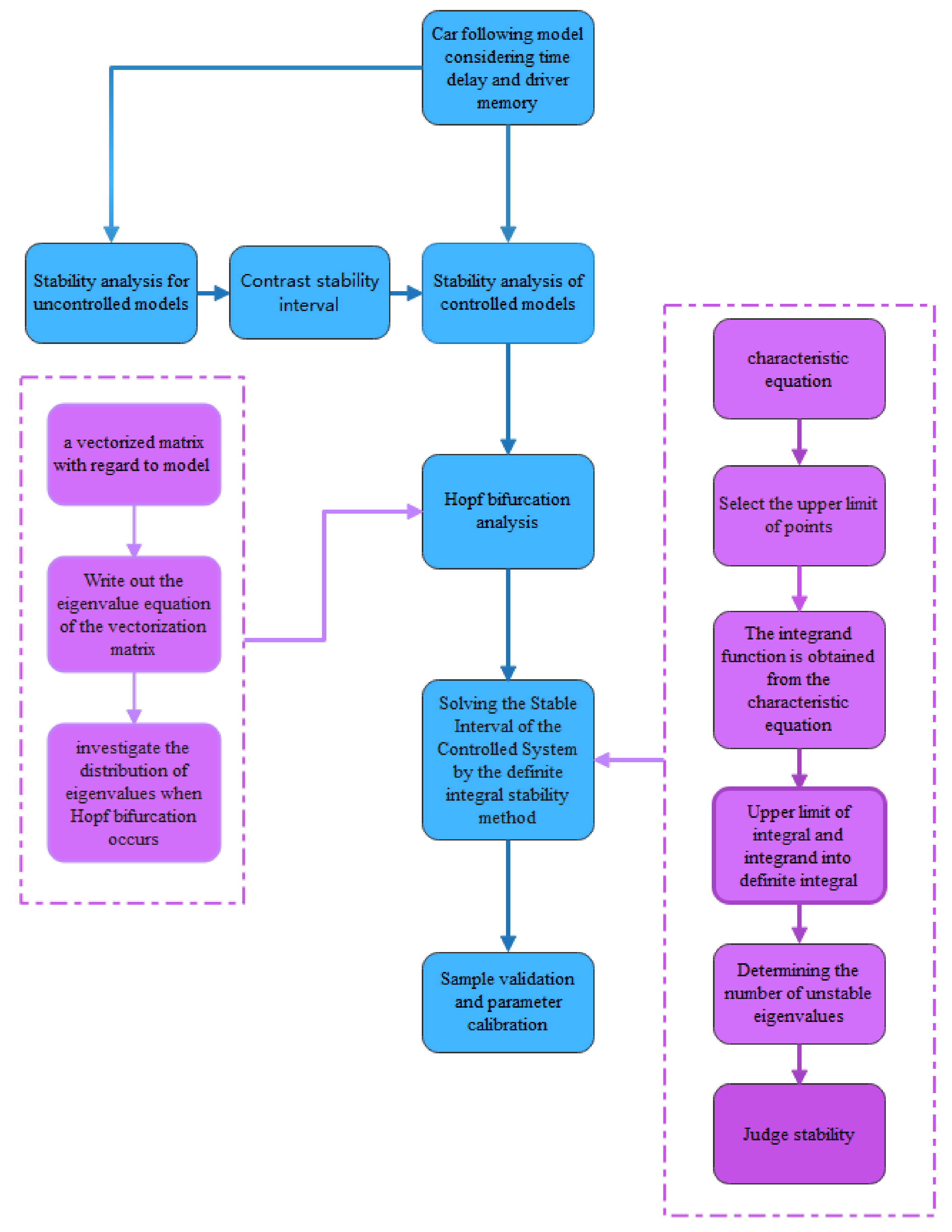
2. A Novel Time Delayed Car-Following Model
3. Stability Analysis
4. The Design of Control Parameters in the Car-Following Model
4.1. Control Strategy for Stability
4.2. Design of Delay Feedback Control Strategy
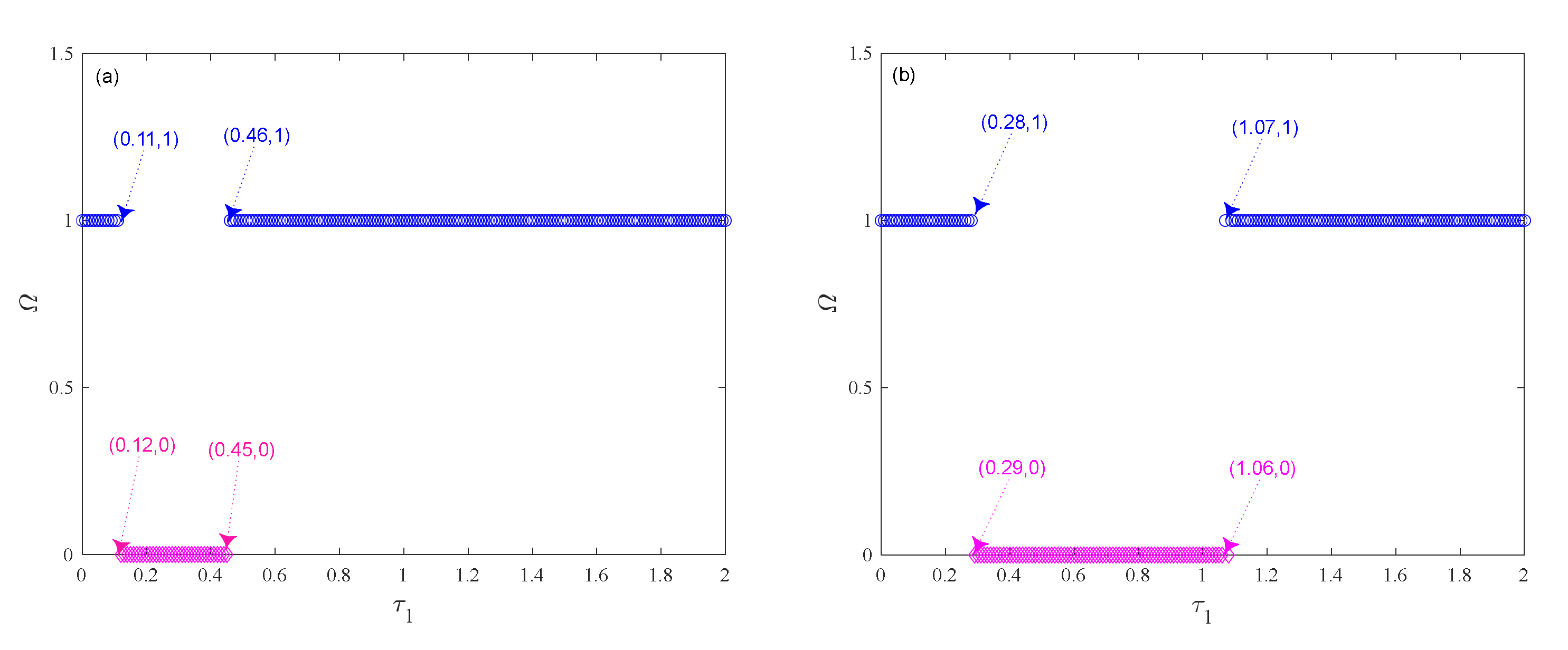
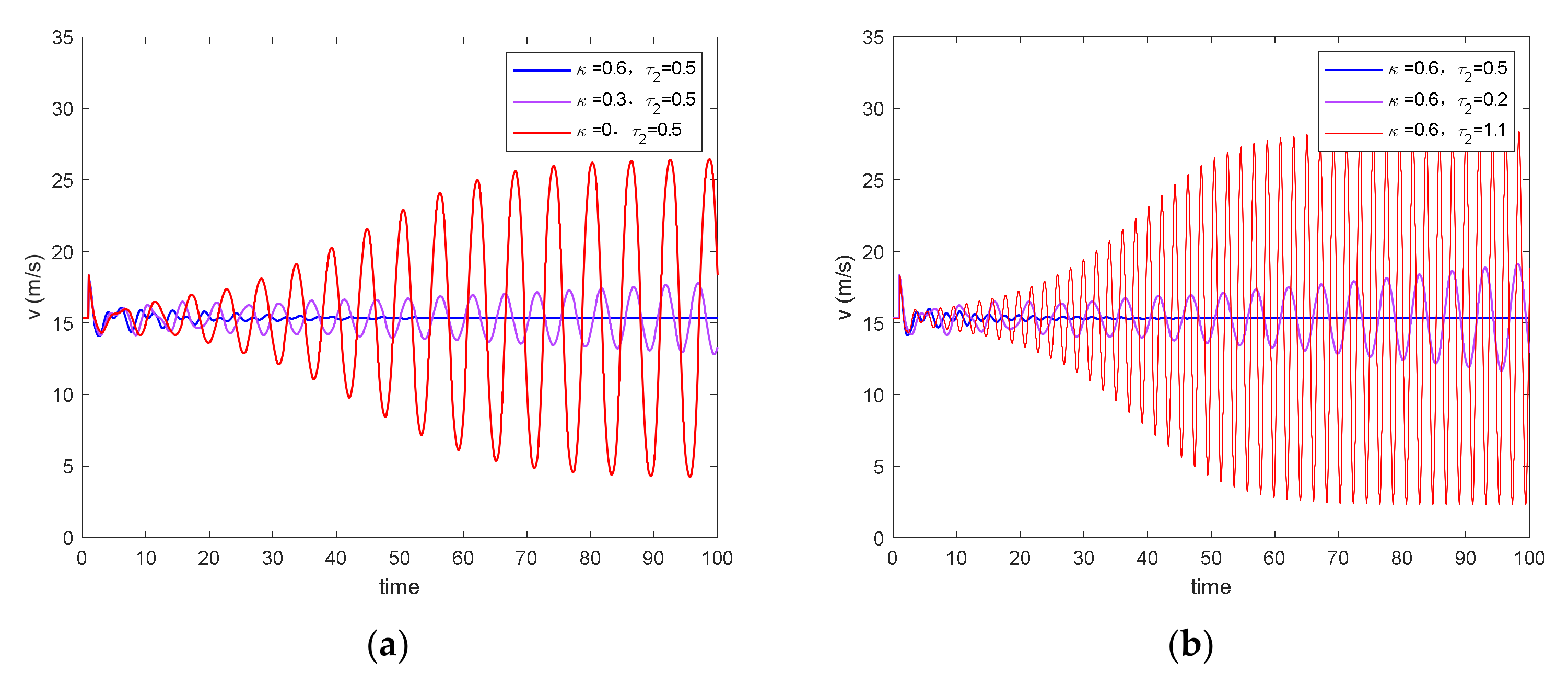
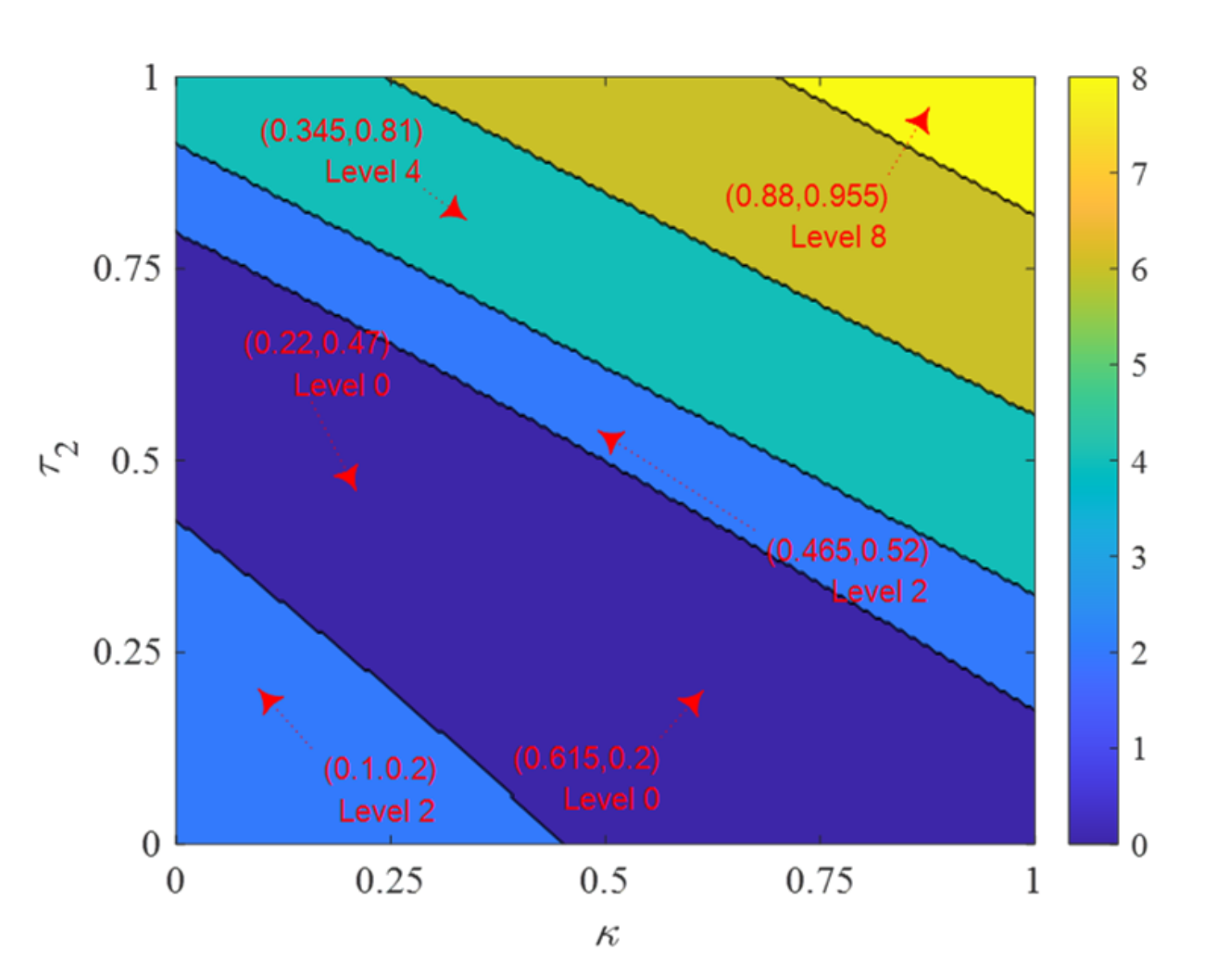
5. Case Studies
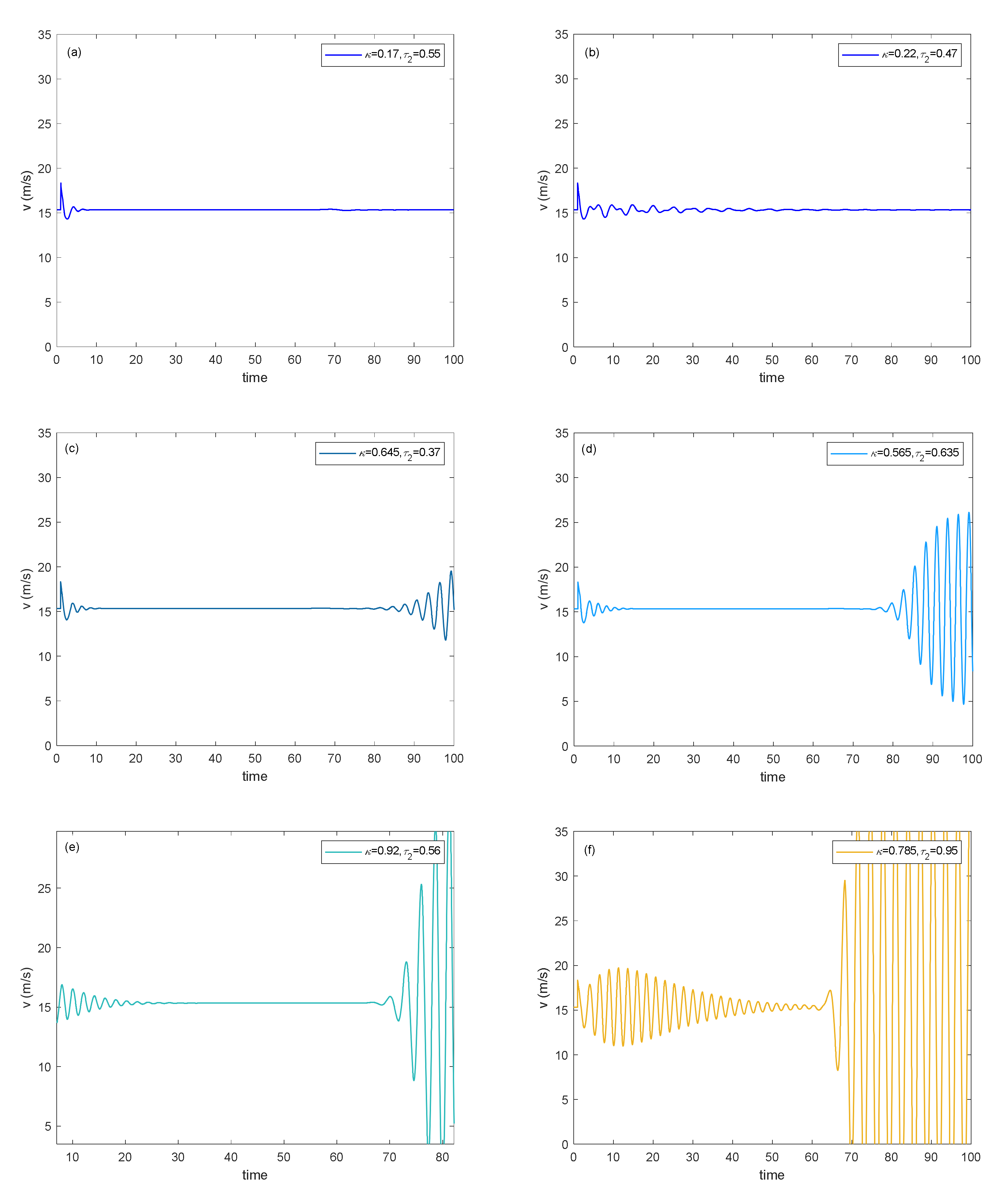
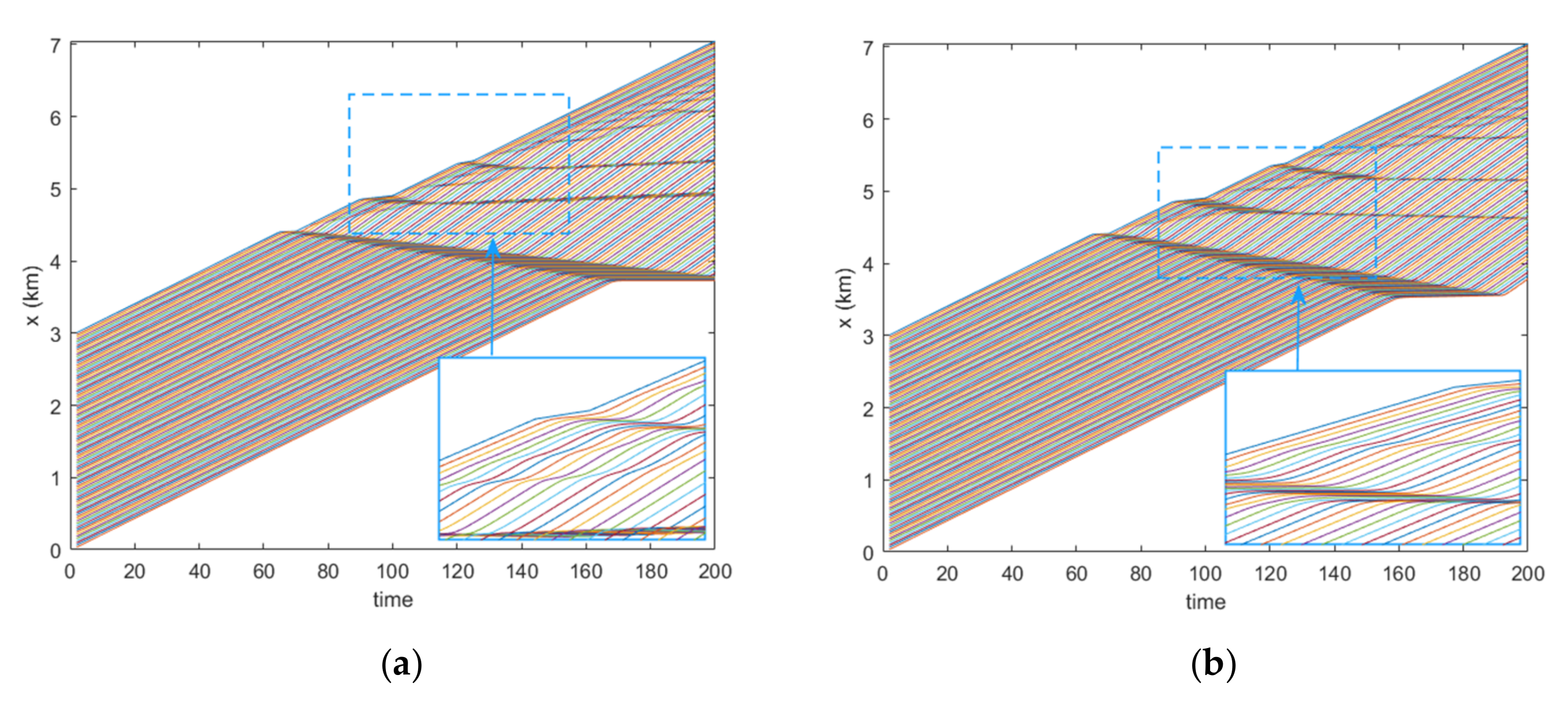
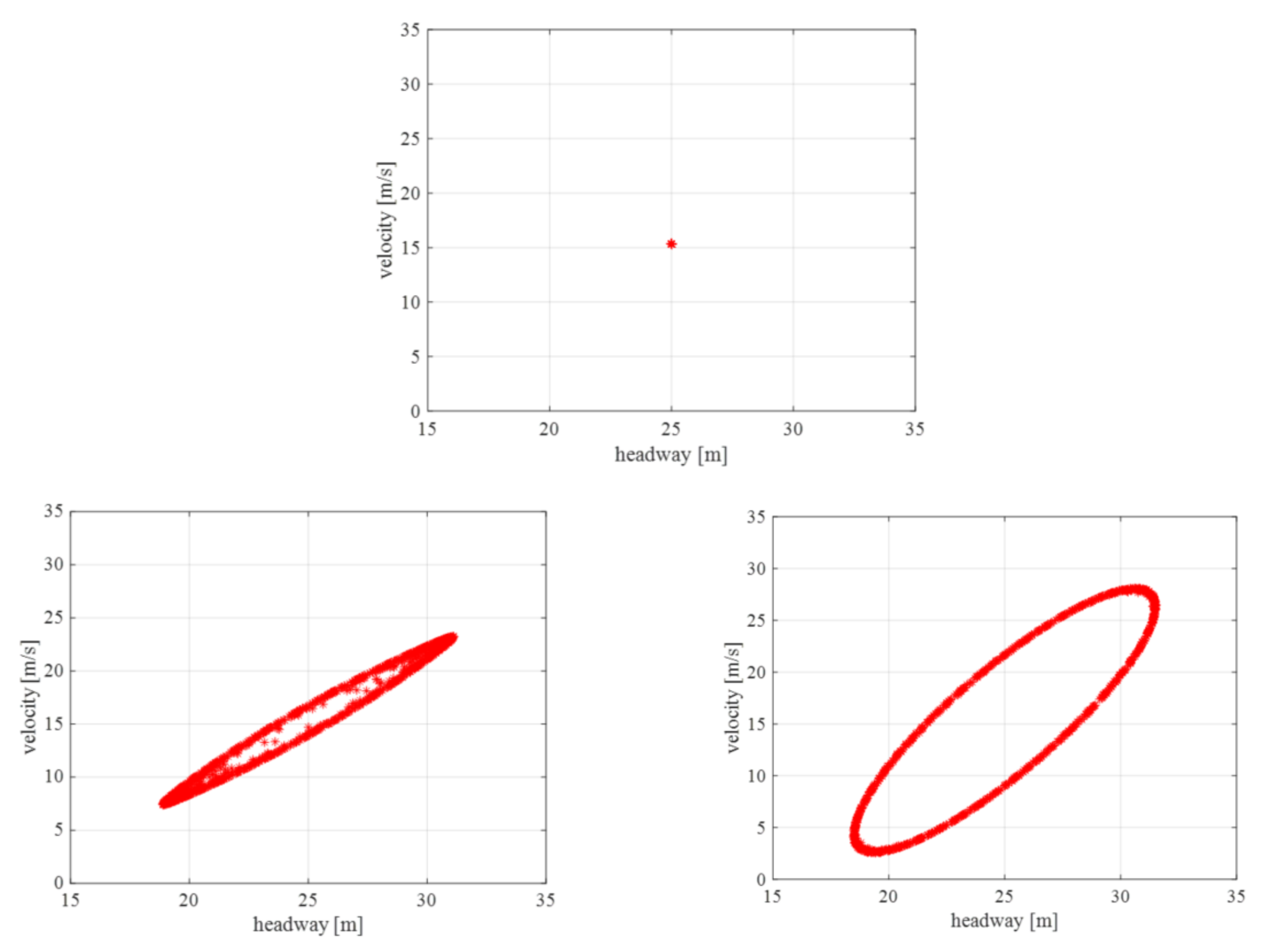
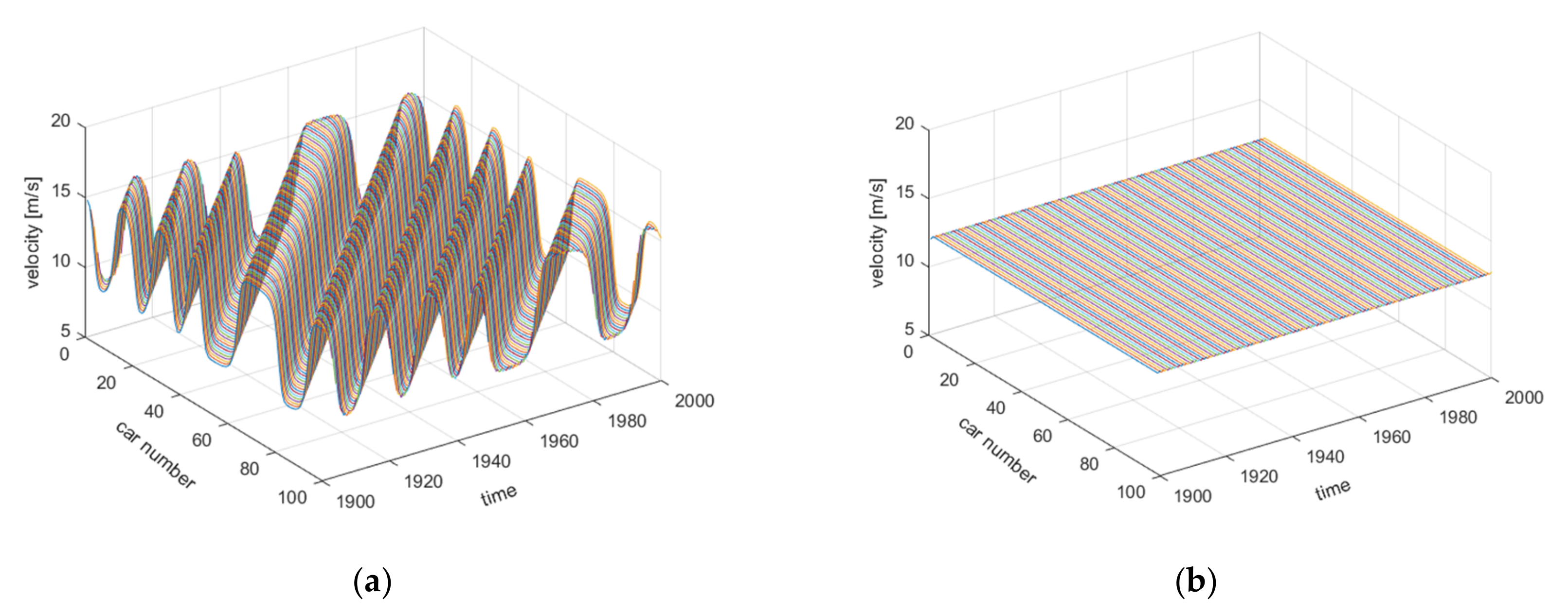
5.1. Verification of Control Strategy
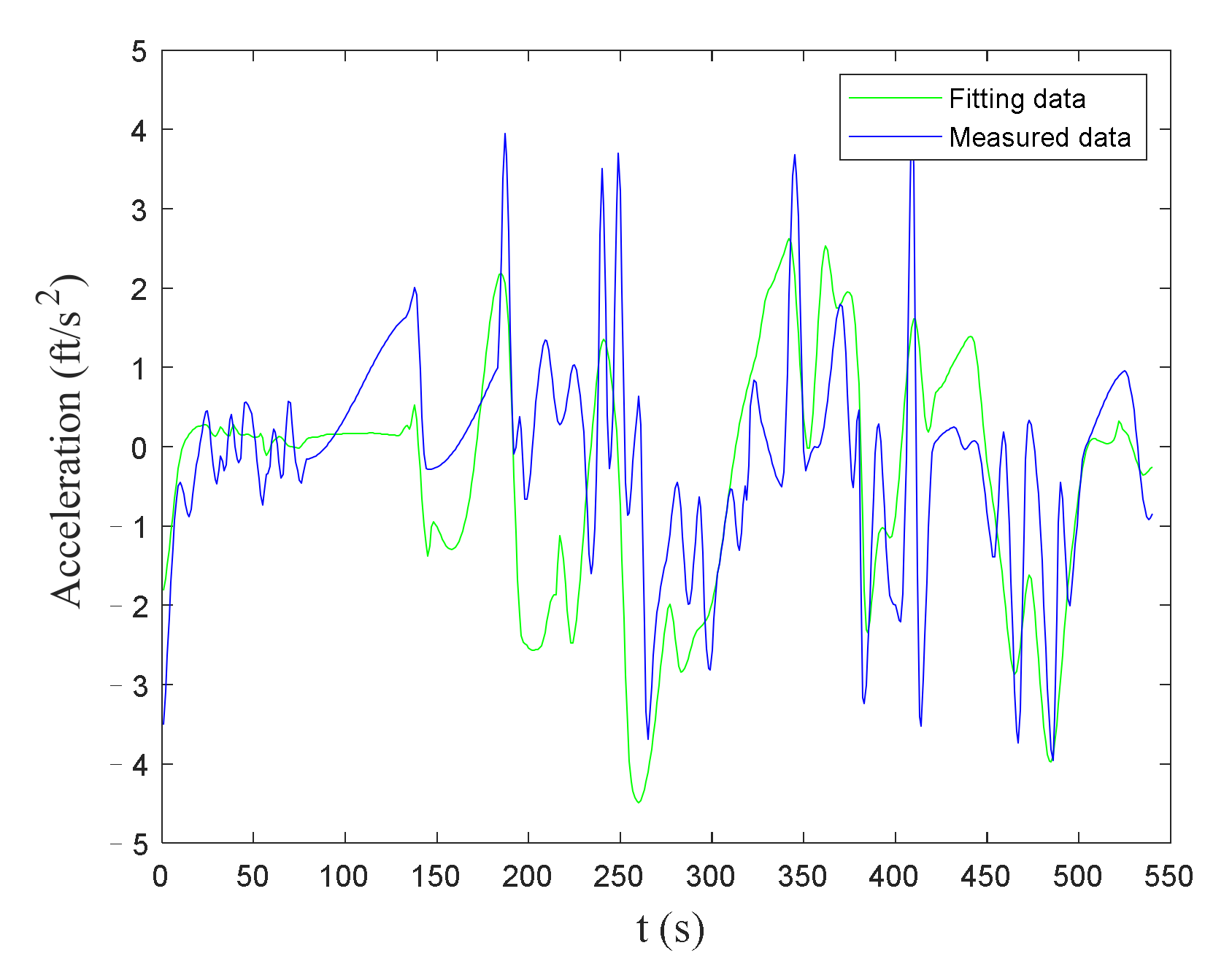
5.2. Parameter Calibration
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Sun, Y.; Ge, H.; Cheng, R. An extended car-following model considering driver’s memory and average speed of preceding vehicles with control strategy. Physica A 2019, 521, 752–761. [Google Scholar] [CrossRef]
- Li, X.M.; Oscar, T.; Andry, R.; Yan, X.D. Collision risk management of cognitively distracted drivers in a car-following situation. Transp. Res. Part F 2019, 60, 288–298. [Google Scholar] [CrossRef]
- Li, S.; Wang, T.; Cheng, R.; Ge, H. An Extended Car-Following Model considering the Driver’s Desire for Smooth Driving and Self-Stabilizing Control with Velocity Uncertainty. Math. Probl. Eng. 2020, 2020, 9546012. [Google Scholar] [CrossRef]
- Ge, H.-X.; Cui, Y.; Zhu, K.-Q.; Cheng, R.-J. The control method for the lattice hydrodynamic model. Commun. Nonlinear Sci. Numer. Simul. 2015, 22, 903–908. [Google Scholar] [CrossRef]
- Wang, Q.; Cheng, R.; Ge, H. A novel lattice hydrodynamic model accounting for driver’s memory effect and the difference of optimal velocity on curved road. Physica A 2020, 559, 125023. [Google Scholar] [CrossRef]
- Cheng, R.; Ge, H.; Wang, J. An extended continuum model accounting for the driver’s timid and aggressive attributions. Phys. Lett. A 2017, 381, 1302–1312. [Google Scholar] [CrossRef]
- Huang, K.; Di, X.; Du, Q.; Chen, X. Scalable traffic stability analysis in mixed-autonomy using continuum models. Transp. Res. Part C: Emerg. Technol. 2020, 111, 616–630. [Google Scholar] [CrossRef]
- Ren, W.; Cheng, R.; Ge, H. Bifurcation analysis for a novel heterogeneous continuum model considering electronic throttle angle changes with memory. Appl. Math. Comput. 2021, 401, 126079. [Google Scholar] [CrossRef]
- Pipes, L.A. An Operational Analysis of Traffic Dynamics. J. Appl. Phys. 1953, 24, 274–281. [Google Scholar] [CrossRef]
- Newell, G.F. Nonlinear Effects in the Dynamics of Car Following. Oper. Res. 1961, 9, 209–229. [Google Scholar] [CrossRef]
- Bando, M.; Hasebe, K.; Nakayama, A.; Shibata, A.; Sugiyama, Y. Dynamical model of traffic congestion and numerical simulation. Phys. Rev. E 1995, 51, 1035–1042. [Google Scholar] [CrossRef] [PubMed]
- Zhang, H. Driver memory, traffic viscosity and a viscous vehicular traffic flow model. Transp. Res. Part B Methodol. 2003, 37, 27–41. [Google Scholar] [CrossRef]
- Yu, S.; Shi, Z. An improved car-following model considering relative velocity fluctuation. Commun. Nonlinear Sci. Numer. Simul. 2016, 36, 319–326. [Google Scholar] [CrossRef]
- Treiber, M.; Kesting, A.; Helbing, D. Delays, inaccuracies and anticipation in microscopic traffic models. Physica A 2006, 360, 71–88. [Google Scholar] [CrossRef]
- Pan, D.B.; Zhang, G.; Jiang, S.; Zhang, Y.; Yuan, B. Delay-independent traffic flux control for a discrete-time lattice hydrodynamic model with time-delay. Physica A 2021, 563, 125440. [Google Scholar] [CrossRef]
- Liu, B.; Zhang, G. A double velocity control method for a discrete-time cooperative driving system with varying time-delay. Phys. A 2020, 565, 125579. [Google Scholar] [CrossRef]
- Chandler, R.E.; Herman, R.; Montroll, E.W. Traffic Dynamics: Studies in Car Following. Oper. Res. 1958, 6, 165–184. [Google Scholar] [CrossRef] [Green Version]
- Gazis, D.C.; Herman, R.; Rothery, W. Nonlinear Follow-the-Leader Models of Traffic Flow. Oper. Res. 1961, 9, 545–567. [Google Scholar] [CrossRef]
- Zhang, G. Study on varying time delay on traffic stability in a novel lattice hydrodynamic model. Physica A 2018, 505, 1103–1112. [Google Scholar] [CrossRef]
- Sun, D.; Chen, D.; Zhao, M.; Liu, W.; Zheng, L. Linear stability and nonlinear analyses of traffic waves for the general nonlinear car-following model with multi-time delays. Physica A 2018, 501, 293–307. [Google Scholar] [CrossRef]
- Gasser, I.; Sirito, G.; Werner, B. Bifurcation analysis of a class of ‘car following’ traffic models. Physica D 2004, 197, 222–241. [Google Scholar] [CrossRef]
- Orosz, G.; Krauskopf, B.; Wilson, R. Bifurcations and multiple traffic jams in a car-following model with reaction-time delay. Physica D 2005, 211, 277–293. [Google Scholar] [CrossRef] [Green Version]
- Jin, Y.; Meng, J. Dynamical analysis of an optimal velocity model with time-delayed feedback control. Commun. Nonlinear Sci. Numer. Simul. 2020, 90, 105333. [Google Scholar] [CrossRef]
- Jin, Y.F.; Xu, M. Bifurcation Analysis of the Full Velocity Difference Model. Chin. Phys. Lett. 2010, 27, 040501. [Google Scholar]
- Zhang, Y.; Xue, Y.; Zhang, P.; Fan, D.; di He, H. Bifurcation analysis of traffic flow through an improved car-following model considering the time-delayed velocity difference. Physica A 2018, 514, 133–140. [Google Scholar] [CrossRef]
- Wang, X.; Liu, J.; Zhang, Y.; Shi, B.; Jiang, D.; Peng, H. A unified symplectic pseudospectral method for motion planning and tracking control of 3D underactuated overhead cranes. Int. J. Robust Nonlinear Control 2019, 29, 2236–2253. [Google Scholar] [CrossRef]
- Peng, H.; Li, F.; Liu, J.G.; Ju, Z. A Symplectic Instantaneous Optimal Control for Robot T rajectory T racking With Differential-Algebraic Equation Models. IEEE Trans. Ind. Electron. 2020, 69, 3819–3828. [Google Scholar] [CrossRef] [Green Version]
- Shi, B.; Peng, H.; Wang, X.; Zhong, W. A symplectic direct method for motion-driven optimal control of mechanical systems. Commun. Nonlinear Sci. Numer. Simul. 2022, 111, 106501. [Google Scholar] [CrossRef]
- Li, S.; Yang, L.; Gao, Z.; Li, K. Stabilization strategies of a general nonlinear car-following model with varying reaction-time delay of the drivers. ISA Trans. 2014, 53, 1739–1745. [Google Scholar] [CrossRef]
- Zhou, T.; Chen, D.; Zheng, L.; Liu, W.; He, Y.; Liu, Z. Feedback-based control for coupled map car-following model with time delays on basis of linear discrete-time system. Physica A 2018, 512, 174–185. [Google Scholar] [CrossRef]
- Chai, C.; Zeng, X.; Wu, X.; Wang, X. Evaluation and Optimization of Responsibility-Sensitive Safety Models on Autonomous Car-Following Maneuvers. Transp. Res. Rec. J. Transp. Res. Board 2020, 2674, 662–673. [Google Scholar] [CrossRef]
- Bando, M.; Hasebe, K.; Nakanishi, K. Phenomenological Study of Dynamical Model of Traffic Flow. J. De Phys. I 1995, 5, 1389–1399. [Google Scholar] [CrossRef] [Green Version]
- Xu, Q.; Stepan, G.; Wang, Z. Delay-dependent stability analysis by using delay-independent integral evaluation. Automatica 2016, 70, 153–157. [Google Scholar] [CrossRef]
- Davis, L. Modifications of the optimal velocity traffic model to include delay due to driver reaction time. Physica A 2003, 319, 557–567. [Google Scholar] [CrossRef]

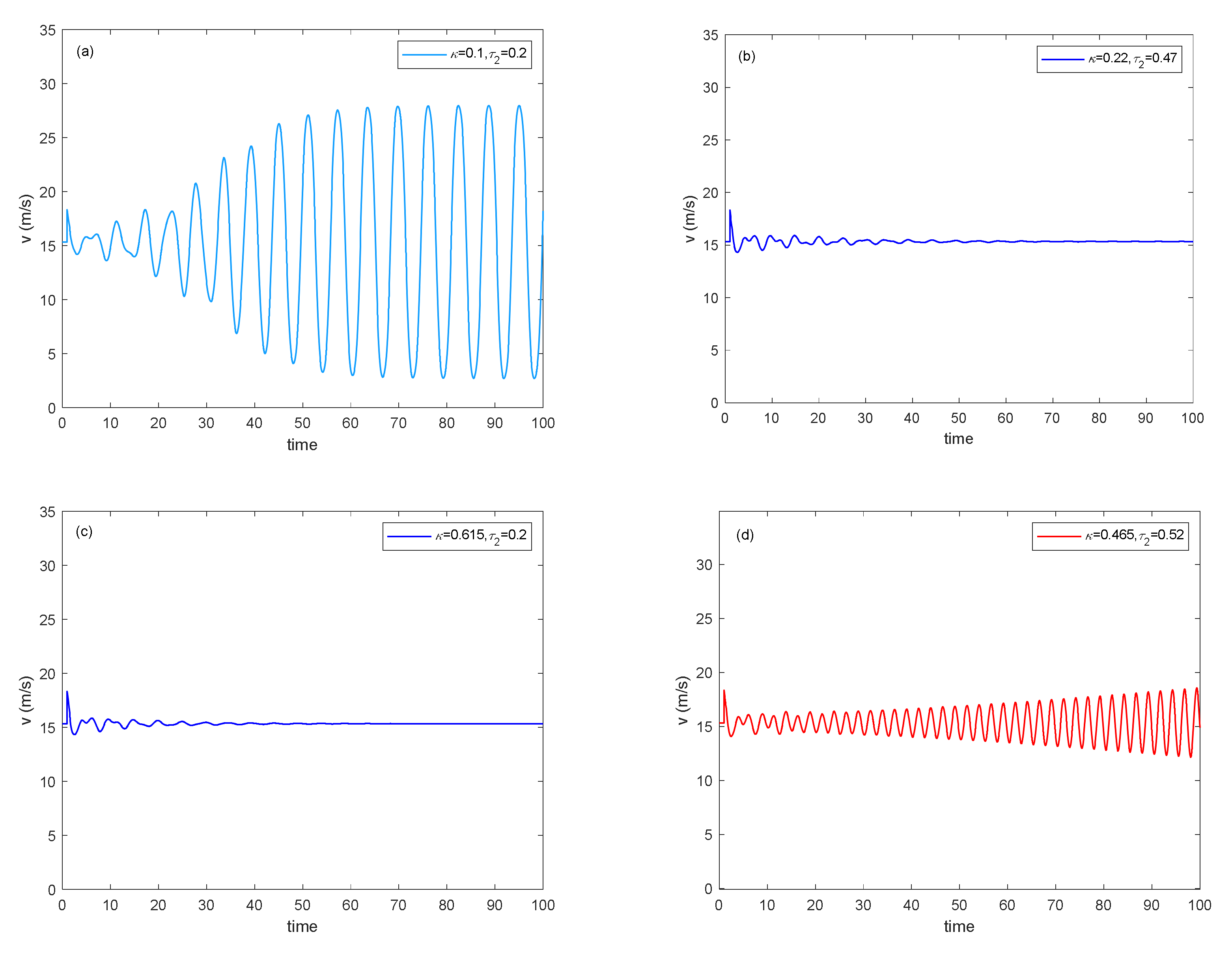
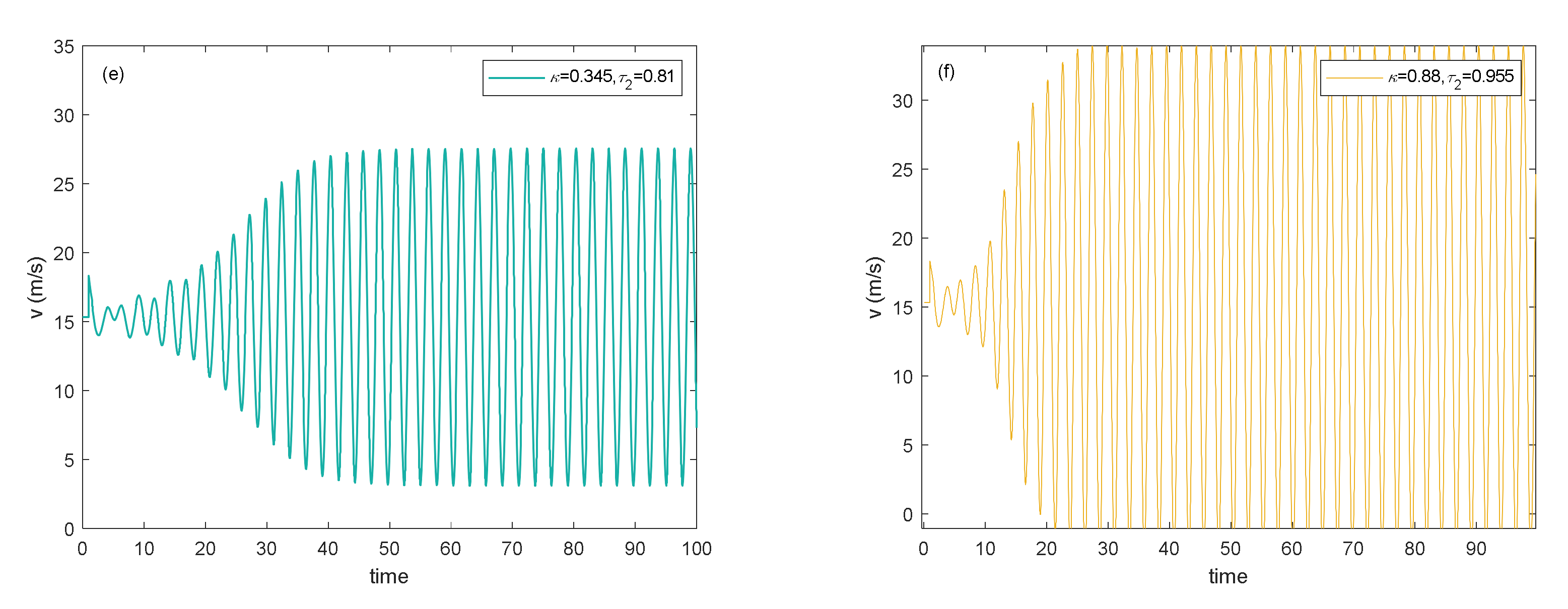
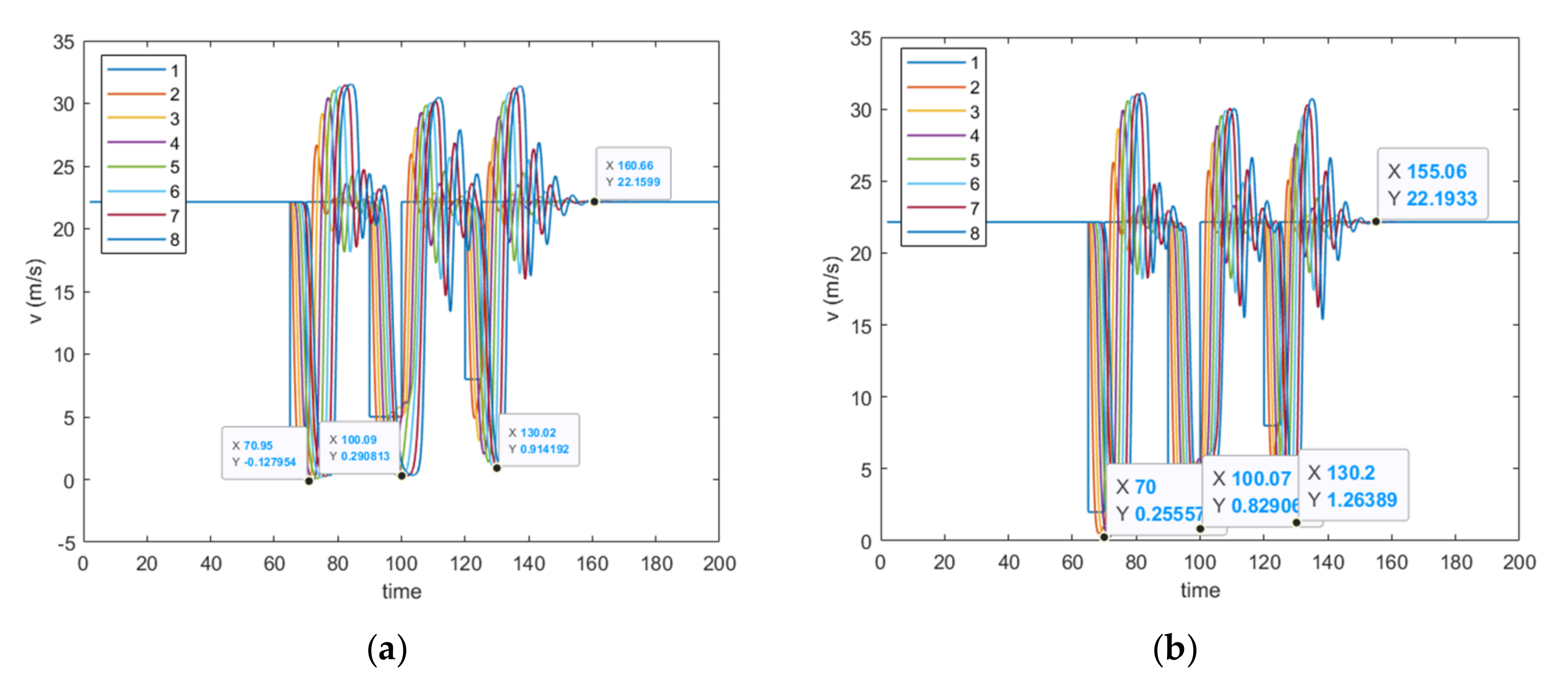

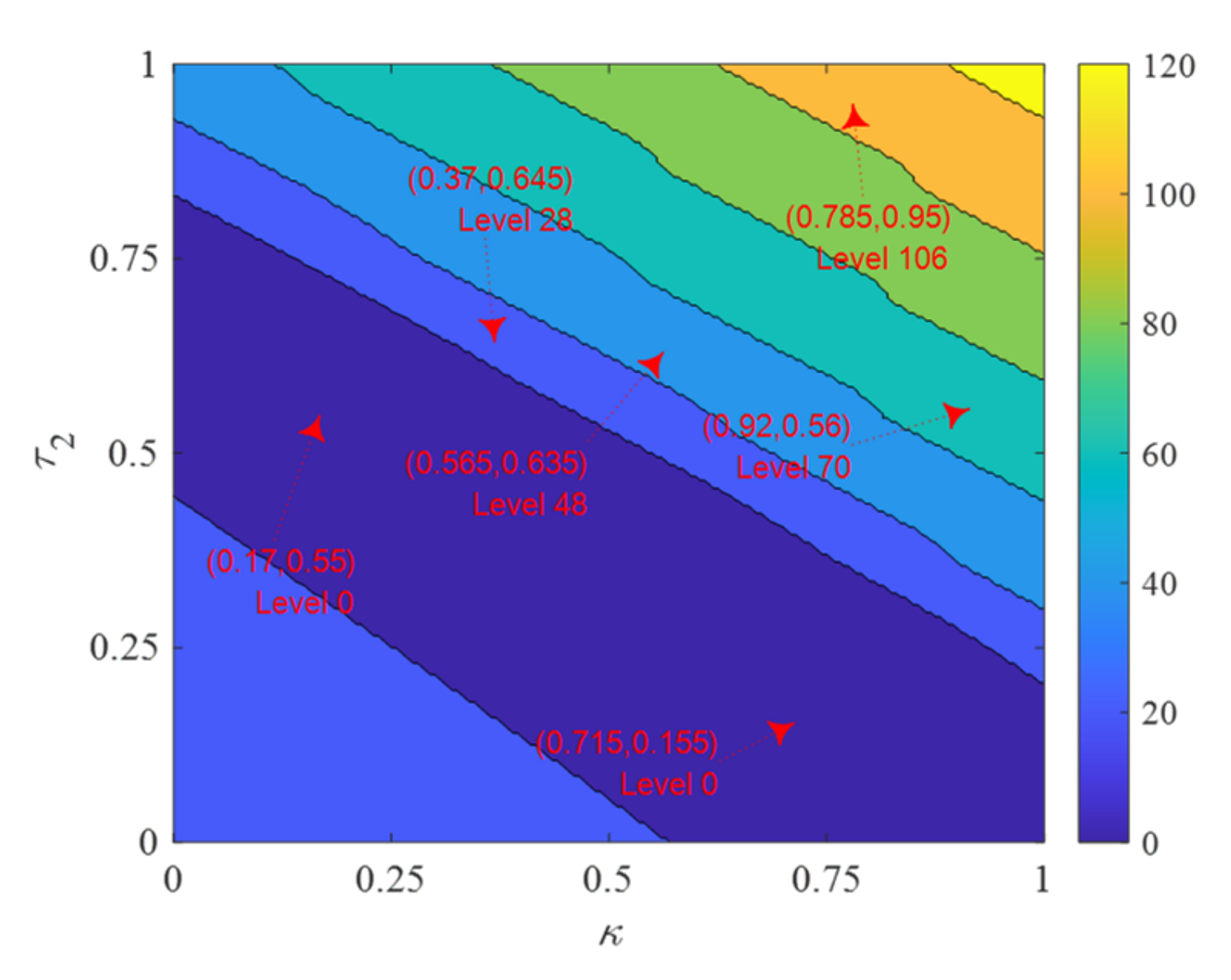

| Options | Values |
|---|---|
| Population Size | 100 |
| Mutation Rate | 0.1 |
| Crossover Rate | 0.95 |
| Generations | 1000 |
| Parameters | Value |
|---|---|
| 0.8334 | |
| 0.9105 | |
| 21.9235 | |
| 32.6472 | |
| 0.0746 | |
| 0.5983 | |
| 0.5007 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pan, Y.; Wang, Y.; Miao, B.; Cheng, R. Stabilization Strategy of a Novel Car-Following Model with Time Delay and Memory Effect of the Driver. Sustainability 2022, 14, 7281. https://doi.org/10.3390/su14127281
Pan Y, Wang Y, Miao B, Cheng R. Stabilization Strategy of a Novel Car-Following Model with Time Delay and Memory Effect of the Driver. Sustainability. 2022; 14(12):7281. https://doi.org/10.3390/su14127281
Chicago/Turabian StylePan, Yifan, Yongjiang Wang, Baobin Miao, and Rongjun Cheng. 2022. "Stabilization Strategy of a Novel Car-Following Model with Time Delay and Memory Effect of the Driver" Sustainability 14, no. 12: 7281. https://doi.org/10.3390/su14127281
APA StylePan, Y., Wang, Y., Miao, B., & Cheng, R. (2022). Stabilization Strategy of a Novel Car-Following Model with Time Delay and Memory Effect of the Driver. Sustainability, 14(12), 7281. https://doi.org/10.3390/su14127281





