A Data-Driven Method for Identifying Drought-Induced Crack-Prone Levees Based on Decision Trees
Abstract
:1. Introduction
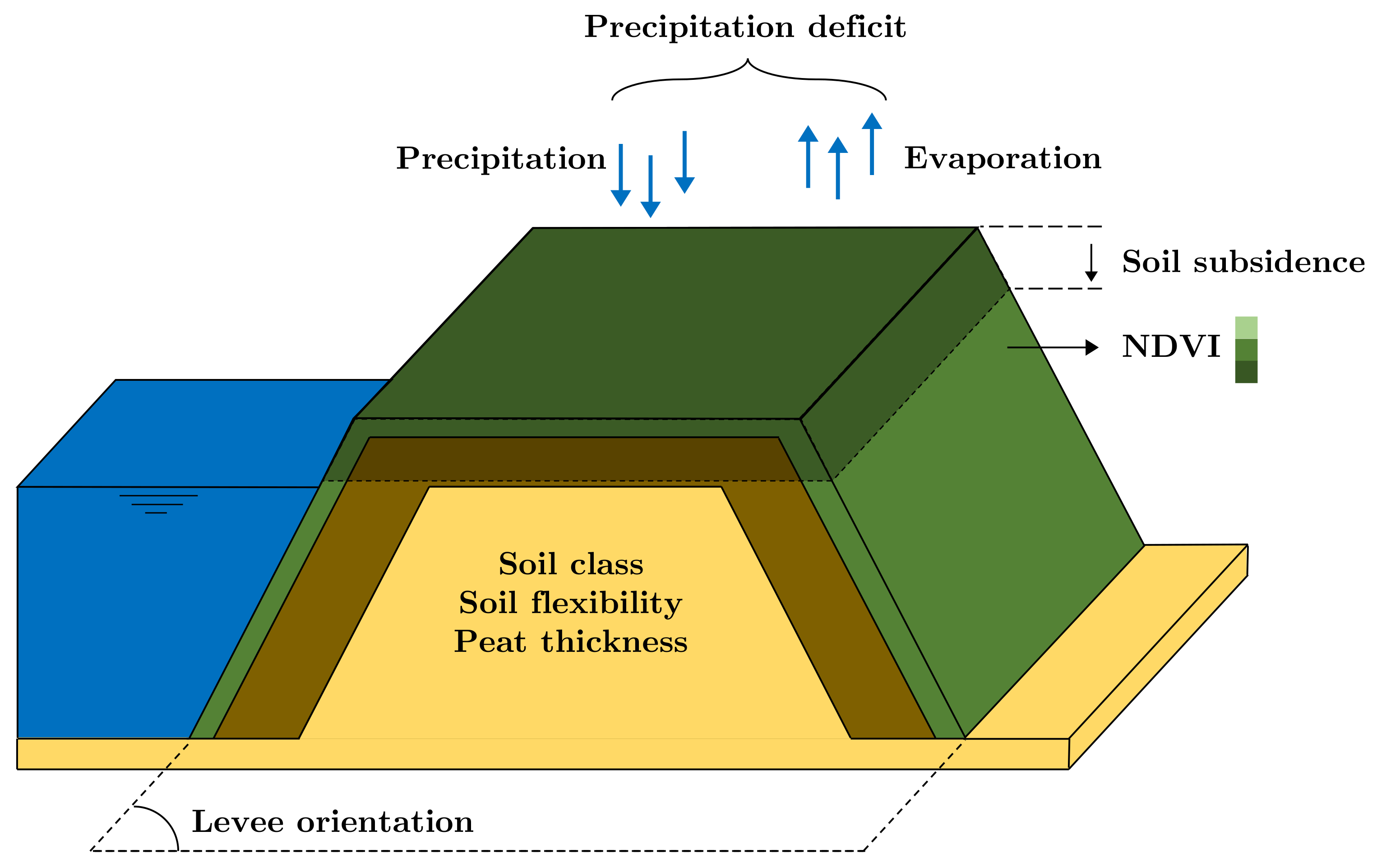
2. Factors Affecting Susceptibility to Cracking
2.1. Precipitation Deficit
2.2. Soil Subsidence Rate
2.3. NDVI
2.4. Soil Class/Type
2.5. Peat Layer Thickness
2.6. Soil Stiffness/Flexibility
2.7. Levee Orientation with Respect to the Sun
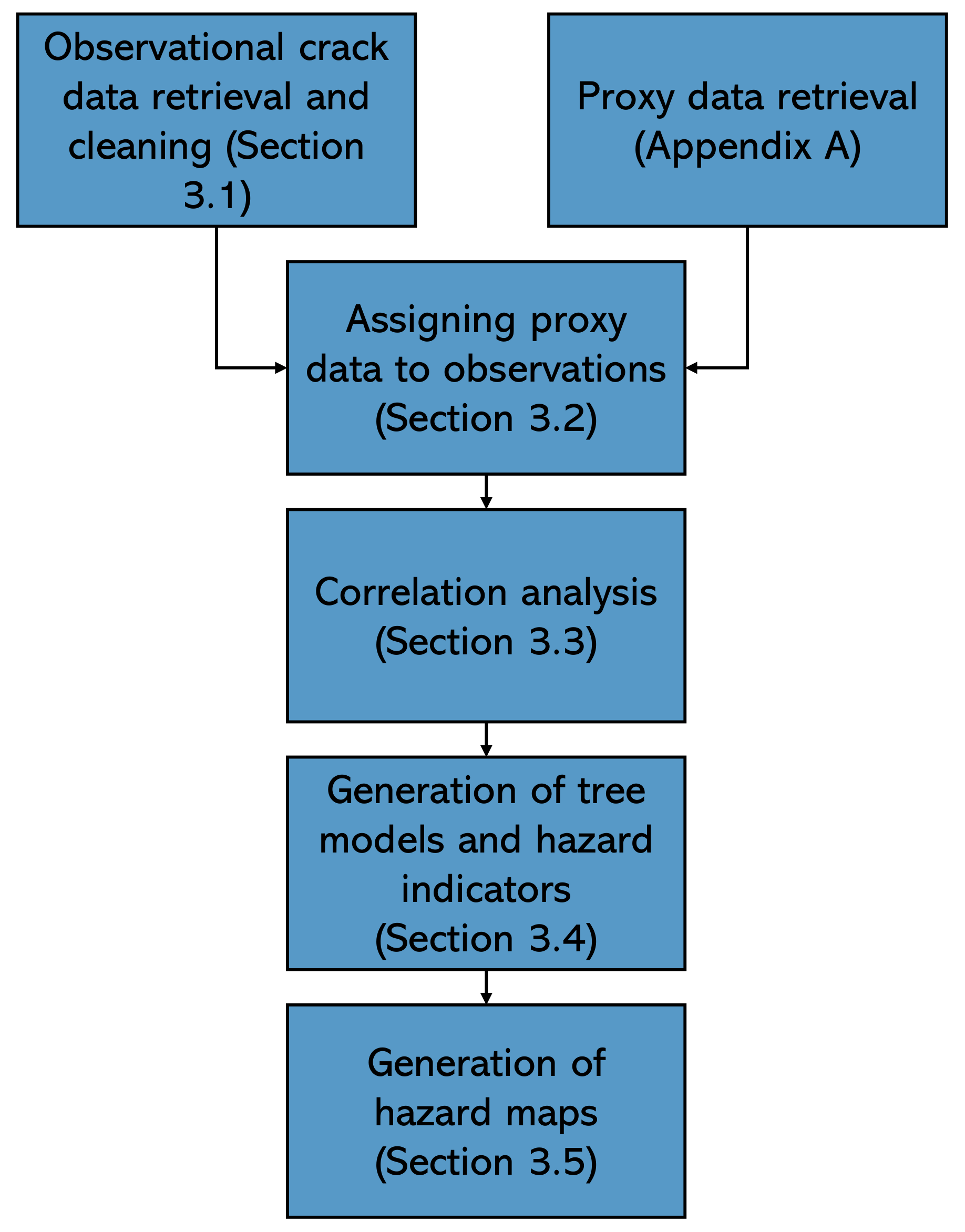
3. Method
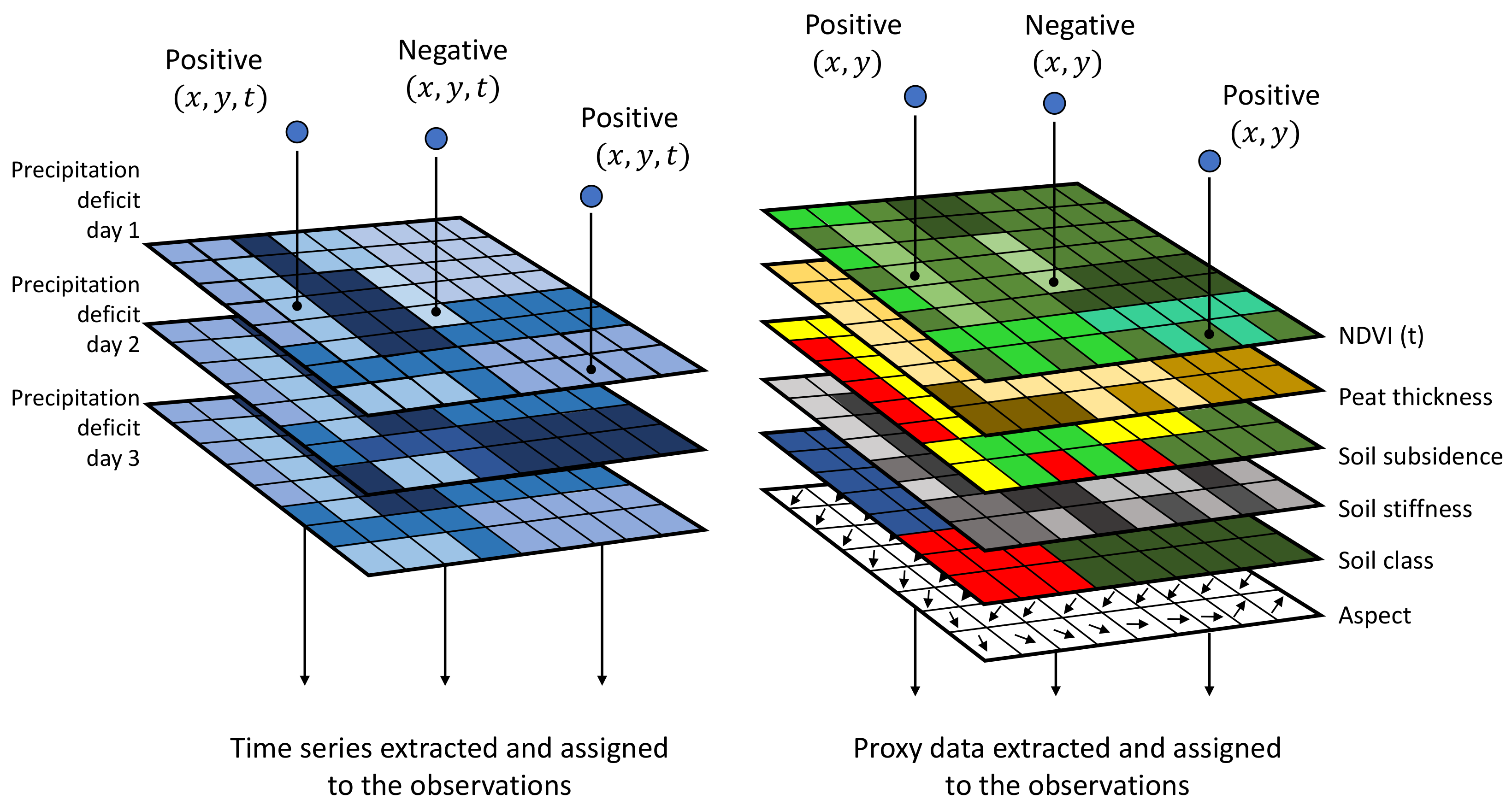
3.1. Observational Data Retrieval on Cracks and Proxies
3.2. Correlation Analysis
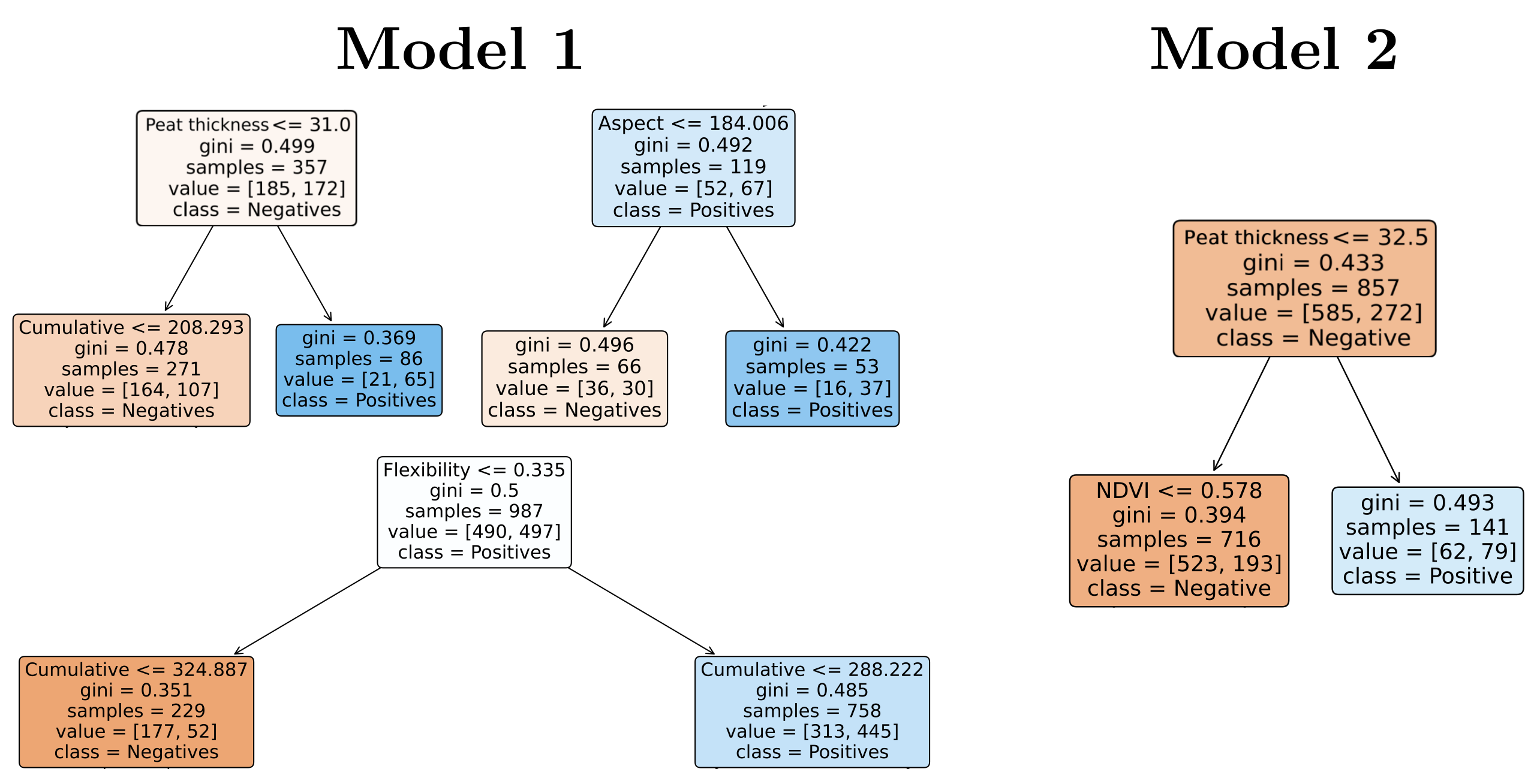
3.3. Generation of Tree Models
3.4. Generation of Hazard Maps
4. Case Study
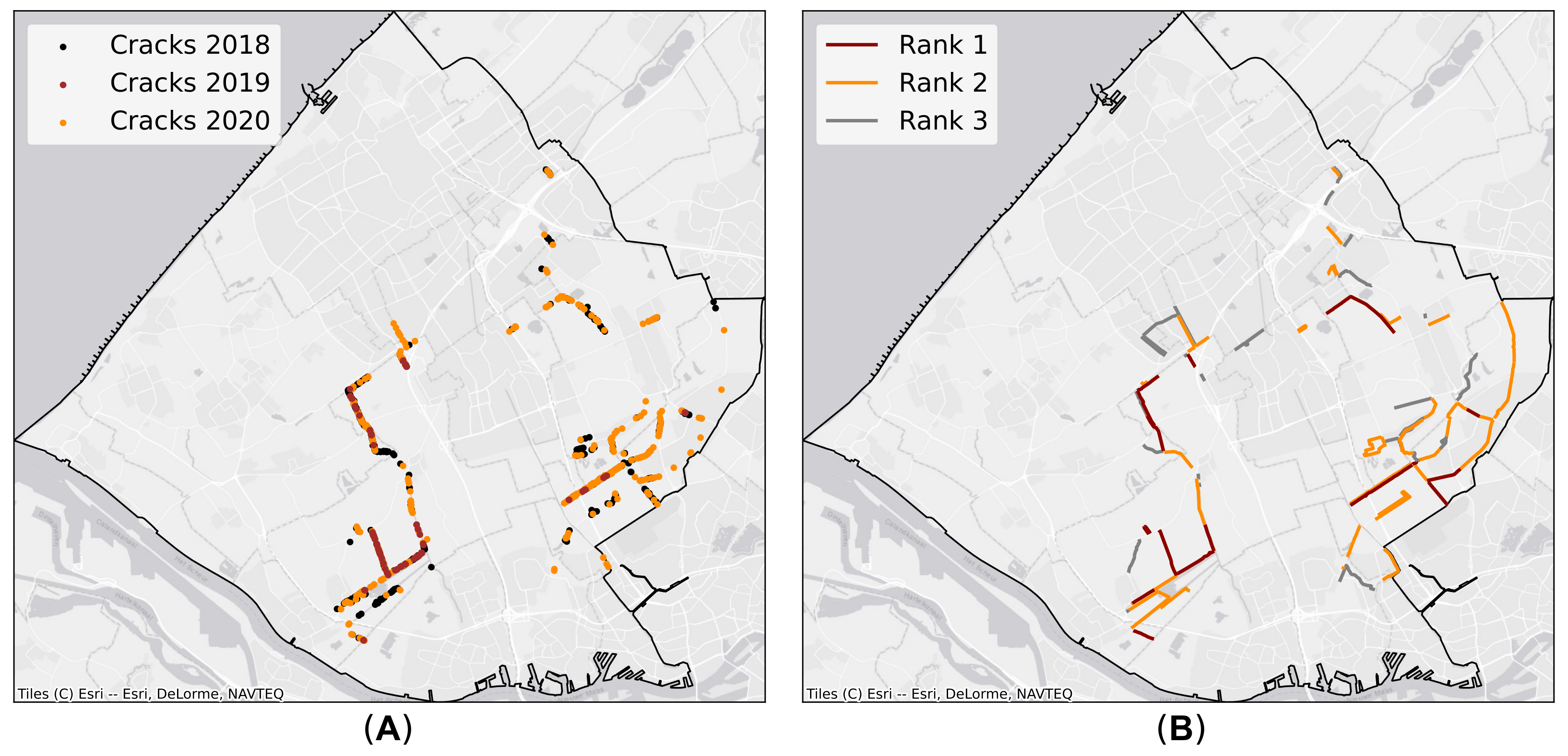
4.1. Inspection Database
4.2. Generation of Negative Observations
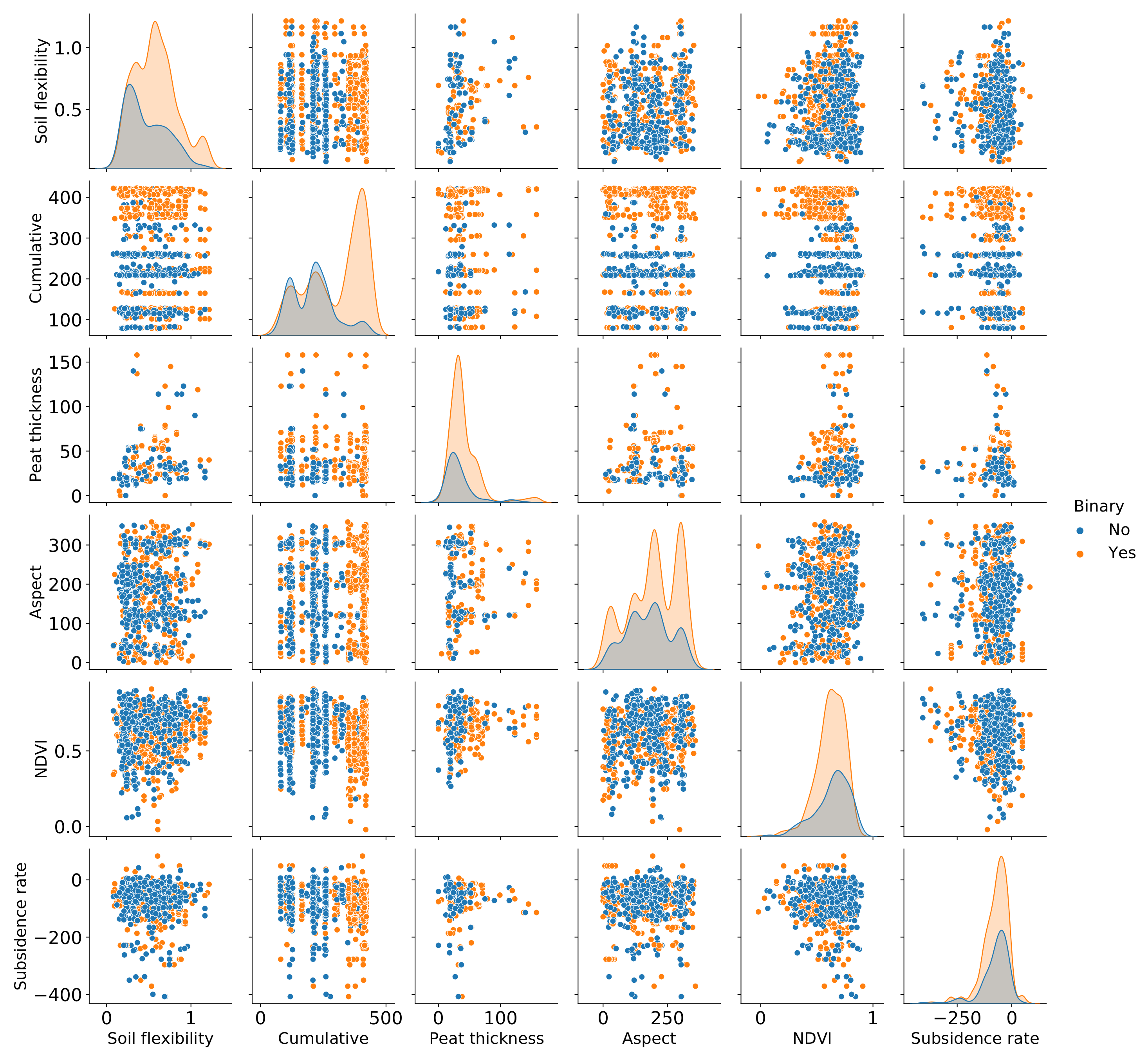
4.3. Database with Proxies
5. Results
5.1. Time Lag Correlation Analysis of the Precipitation Deficit
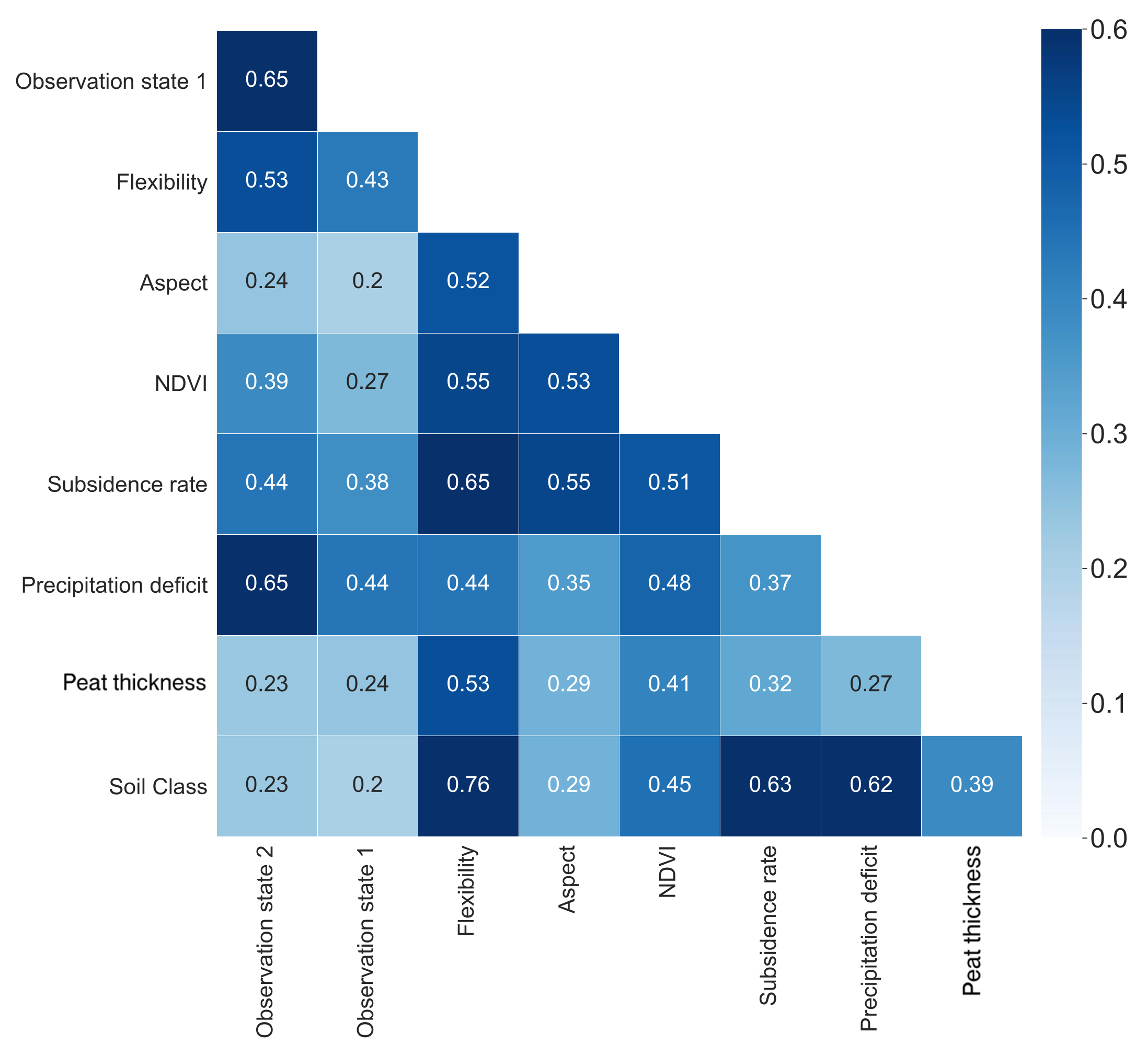
5.2. Correlation Matrix
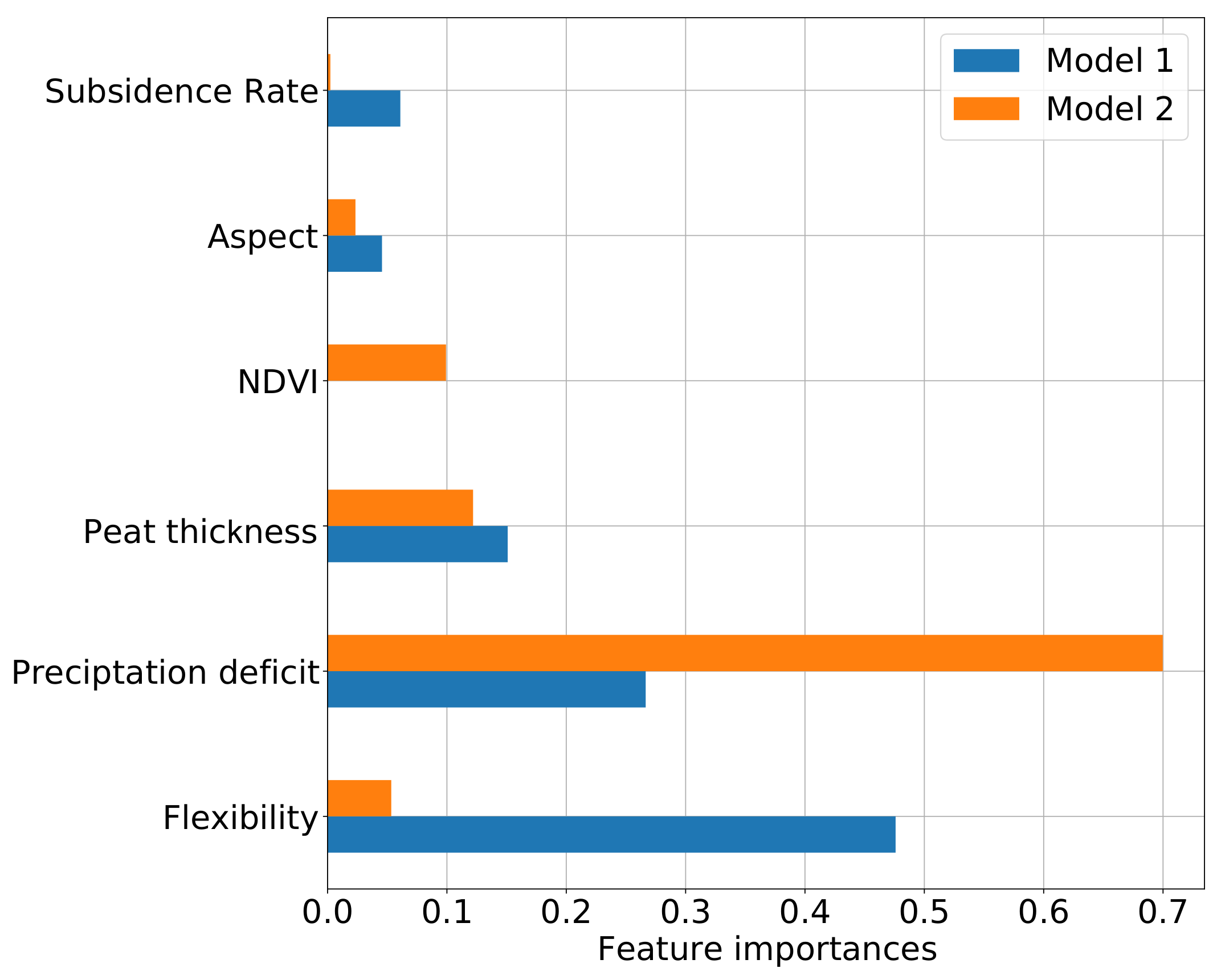
5.3. Hazard Indicators
5.4. Hazard Maps
6. Discussion
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| FN | False Negative |
| FP | False Positive |
| HHD | Hoogheemraadschap Delft |
| KNMI | Koninlijk Nederlands Meteorologisch Instituut |
| MCC | Matthews Correlation Coefficient |
| NDVI | Normalized Difference Vegetation Index |
| SPEI | Standardized Precipitation Evaporation Index |
| TN | True Negative |
| TP | True Positive |
Appendix A. Data Retrieval
Appendix A.1. Precipitation Deficit
Appendix A.2. Digital Elevation Model
Appendix A.3. Soil Flexibility, Soil Class and Peat Thickness
Appendix A.4. Soil Subsidence
Appendix A.5. NDVI
References
- Attema, J.; Bakker, A.; Beersma, J.; Bessembinder, J.; Boers, J.; Brandsma, T.; van den Brink, H.; Drijfhout, S.; Eskes, H.; Haarsma, R.; et al. KNMI’14: Climate Change Scenarios for the 21st Century–A Netherlands Perspective; Technical Report WR-2014-01; KNMI: De Bilt, The Netherlands, 2014. [Google Scholar]
- Vardon, P.J. Climatic influence on geotechnical infrastructure: A review. Environ. Geotech. 2015, 2, 166–174. [Google Scholar] [CrossRef]
- Jamalinia, E.; Vardon, P.J.; Steele-Dunne, S. The impact of evaporation induced cracks and precipitation on temporal slope stability. Comput. Geotech. 2020, 122, 103506. [Google Scholar] [CrossRef]
- Van Baars, S. The horizontal failure mechanism of the Wilnis peat dyke. Géotechnique 2005, 55, 319–323. [Google Scholar] [CrossRef]
- Vahedifard, F.; Robinson, J.; AghaKouchak, A. Can protracted drought undermine the structural integrity of California’s earthen levees? J. Geotech. Geoenviron. Eng. 2016, 142, 02516001. [Google Scholar] [CrossRef] [Green Version]
- van den Akker, J.; Hendriks, R.; Frissel, J.; Oostindie, K.; Wesseling, J. Gedrag van Verdroogde Kades: Fase B, C, D: Onstaan en Gevaar van Krimpscheuren in Klei- en Veenkades; Number 2473 in Alterra-Rapport; Alterra: Wageningen, The Netherlands, 2014. [Google Scholar]
- Yang, R.; Huang, J.; Griffiths, D.; Sheng, D. Effects of desiccation cracks on slope reliability. In Proceedings of the 7th International Symposium on Geotechnical Safety and Risk (ISGSR), Taipei, Taiwan, 11–13 December 2019; pp. 261–266. [Google Scholar] [CrossRef]
- Aguilar-López, J.P.; Bogaard, T.; Gerke, H.H. Dual-permeability model improvements for representation of preferential flow in fractured clays. Water Resour. Res. 2020, 56, e2020WR027304. [Google Scholar] [CrossRef]
- Wang, Z.F.; Li, J.H.; Zhang, L.M. Influence of cracks on the stability of a cracked soil slope. In Proceedings of the 5th Asia-Pacific Conference on Unsaturated Soils, Pattaya, Thailand, 14–16 November 2011; Volume 2, pp. 721–728. [Google Scholar]
- Hallett, P.D.; Newson, T.A. Describing soil crack formation using elastic–plastic fracture mechanics. Eur. J. Soil Sci. 2005, 56, 31–38. [Google Scholar] [CrossRef]
- Hoang, N.D.; Nguyen, Q.L. A novel method for asphalt pavement crack classification based on image processing and machine learning. Eng. Comput. 2019, 35, 487–498. [Google Scholar] [CrossRef]
- Al-Ruzouq, R.; Shanableh, A.; Yilmaz, A.G.; Idris, A.; Mukherjee, S.; Khalil, M.A.; Gibril, M.B.A. Dam site suitability mapping and analysis using an integrated GIS and machine learning approach. Water 2019, 11, 1880. [Google Scholar] [CrossRef] [Green Version]
- Jamalinia, E.; Tehrani, F.S.; Steele-Dunne, S.C.; Vardon, P.J. A Data-Driven Surrogate Approach for the Temporal Stability Forecasting of Vegetation Covered Dikes. Water 2021, 13, 107. [Google Scholar] [CrossRef]
- Zhu, M.; Li, S.; Wei, X.; Wang, P. Prediction and Stability Assessment of Soft Foundation Settlement of the Fishbone-Shaped Dike Near the Estuary of the Yangtze River Using Machine Learning Methods. Sustainability 2021, 13, 3744. [Google Scholar] [CrossRef]
- Stark, T.; Jafari, N.; Leopold, A.; Brandon, T. Soil Compressibility in Transient Unsaturated Seepage Analyses. Can. Geotech. J. 2014, 51, 858–868. [Google Scholar] [CrossRef]
- Camporese, M.; Ferraris, S.; Putti, M.; Salandin, P.; Teatini, P. Hydrological modeling in swelling/shrinking peat soils. Water Resour. Res. 2006, 42, W06420. [Google Scholar] [CrossRef] [Green Version]
- Pyatt, D.G.; John, A.L. Modelling volume changes in peat under conifer plantations. J. Soil Sci. 1989, 40, 695–706. [Google Scholar] [CrossRef]
- Fredlund, D.G. Consolidation and swelling processes in unsaturated soils. In Unsaturated Soil Mechanics in Engineering Practice; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2012; Chapter 16; pp. 809–857. [Google Scholar] [CrossRef]
- World Meteorological Organization (WMO); Global Water Partnership (GWP). Handbook of Drought Indicators and Indices; Technical Report; Integrated Drought Management Programme (IDMP), Integrated Drought Management Tools and Guidelines Series 2; WMO: Geneva, Switzerland; GWP: Geneva, Switzerland, 2016. [Google Scholar]
- Makkink, G.F.; Van Heemst, H.D.J. Potential evaporation. In Mededelingen; Instituut voor Biologisch en Scheikundig Onderzoek van Landbouwgewassen: Wageningen, The Netherlands, 1970. [Google Scholar]
- Lu, J.; Sun, G.; McNulty, S.G.; Amatya, D.M. A Comparison of Six Potential Evapotranspiration Methods for Regional Use in the Southeastern United States. JAWRA J. Am. Water Resour. Assoc. 2005, 41, 621–633. [Google Scholar] [CrossRef]
- Gerten, D.; Schaphoff, S.; Haberlandt, U.; Lucht, W.; Sitch, S. Terrestrial vegetation and water balance—Hydrological evaluation of a dynamic global vegetation model. J. Hydrol. 2004, 286, 249–270. [Google Scholar] [CrossRef]
- Peters, A.J.; Walter-Shea, E.A.; Ji, L.; Viña, A.; Hayes, M.; Svoboda, M.D. Drought Monitoring with NDVI-Based Standardized Vegetation Index. Photogramm. Eng. Remote Sens. 2002, 68, 71–75. [Google Scholar]
- Peng, X.; Horn, R. Identifying Six Types of Soil Shrinkage Curves from a Large Set of Experimental Data. Soil Sci. Soc. Am. J. 2013, 77, 372–381. [Google Scholar] [CrossRef]
- Erkens, G. Draagkracht-Zettingsgevoeligheid, 2010, Deltares-1208234-DANK-024a. Available online: https://data.overheid.nl/en/dataset/26216-draagkracht—zettingsgevoeligheid (accessed on 30 September 2019).
- Cramér, H. Mathematical Methods of Statistics (PMS-9); Princeton University Press: Princeton, NJ, USA, 2016. [Google Scholar] [CrossRef]
- Rutkowski, L.; Jaworski, M.; Pietruczuk, L.; Duda, P. The CART decision tree for mining data streams. Inf. Sci. 2014, 266, 1–15. [Google Scholar] [CrossRef]
- Zhi, T.; Luo, H.; Liu, Y. A Gini impurity-based interest flooding attack defence mechanism in NDN. IEEE Commun. Lett. 2018, 22, 538–541. [Google Scholar] [CrossRef]
- Pedregosa, F.; Varoquaux, G.; Gramfort, A.; Michel, V.; Thirion, B.; Grisel, O.; Blondel, M.; Prettenhofer, P.; Weiss, R.; Dubourg, V.; et al. Scikit-learn: Machine Learning in Python. J. Mach. Learn. Res. 2011, 12, 2825–2830. [Google Scholar]
- Boughorbel, S.; Jarray, F.; El-Anbari, M. Optimal classifier for imbalanced data using Matthews Correlation Coefficient metric. PLoS ONE 2017, 12, e0177678. [Google Scholar] [CrossRef] [PubMed]
- Chicco, D.; Jurman, G. The advantages of the Matthews correlation coefficient (MCC) over F1 score and accuracy in binary classification evaluation. BMC Genom. 2020, 21, 1–13. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Beguería, S.; Vicente-Serrano, S.M.; Reig, F.; Latorre, B. Standardized precipitation evapotranspiration index (SPEI) revisited: Parameter fitting, evapotranspiration models, tools, datasets and drought monitoring. Int. J. Climatol. 2014, 34, 3001–3023. [Google Scholar] [CrossRef] [Green Version]
- Cateni, S.; Colla, V.; Vannucci, M. A method for resampling imbalanced datasets in binary classification tasks for real-world problems. Neurocomputing 2014, 135, 32–41. [Google Scholar] [CrossRef]
- Wolters, E.; Hakvoort, H.; Bosch, S.; Versteeg, R.; Bakker, M.; Heijkers, J.; Talsme, M.; Peerdeman, K. Meteobase: Online neerslag-en referentiegewasver-dampingsdatabase voor het Nederlandse waterbeheer. Meteorologica 2013, 1, 15–18. [Google Scholar]
- De Bruin, H. Over referentiegewasverdamping. Meteorologica 2014, 1, 15–20. [Google Scholar]
- GDAL/OGR Contributors. GDAL/OGR Geospatial Data Abstraction Software Library; Open Source Geospatial Foundation: Chicago, IL, USA, 2021. [Google Scholar]
- Brouwer, F. BRO—Bodemkaart van Nederland, uri:0e4c899b-42b1-4654-906e-4ad2a8d838cb. 2018. Available online: https://www.dinoloket.nl (accessed on 30 September 2019).
- Provincie Zuid-Holland. Veendikte 2014, uri:098B74D3-D49B-422A-BCA4-6C11A3FA7D2A. 2014. Available online: https://atlas.zuid-holland.nl/GeoWeb56/index.html?viewer=Bodematlas (accessed on 30 September 2019).
- Jeevalakshmi, D.; Reddy, S.N.; Manikiam, B. Land cover classification based on NDVI using LANDSAT8 time series: A case study Tirupati region. In Proceedings of the 2016 International Conference on Communication and Signal Processing (ICCSP), Melmaruvathur, India, 6–8 April 2016; pp. 1332–1335. [Google Scholar] [CrossRef]









| Proxy | Definition |
|---|---|
| Precipitation deficit | Cumulative precipitation deficit over computed period |
| Aspect | Anticlockwise angle of the levee with respect to the west |
| Soil flexibility | Deformation of the soil when loaded mechanically |
| Soil class | Nature and constitution of topsoil |
| Peat thickness | Thickness of the upper peat layer of a levee |
| Soil subsidence | Average annual subsidence between 2015 and 2019 |
| NDVI | Difference between near-infrared and red light |
| Model 1 | Model 2 | |
|---|---|---|
| Train set accuracy | 0.64 | 0.77 |
| Test set accuracy | 0.68 | 0.73 |
| Precision | 0.82 | 0.89 |
| Recall | 0.68 | 0.60 |
| MCC | 0.31 | 0.51 |
| Cross validation accuracy | 0.59 | 0.67 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chotkan, S.; van der Meij, R.; Klerk, W.J.; Vardon, P.J.; Aguilar-López, J.P. A Data-Driven Method for Identifying Drought-Induced Crack-Prone Levees Based on Decision Trees. Sustainability 2022, 14, 6820. https://doi.org/10.3390/su14116820
Chotkan S, van der Meij R, Klerk WJ, Vardon PJ, Aguilar-López JP. A Data-Driven Method for Identifying Drought-Induced Crack-Prone Levees Based on Decision Trees. Sustainability. 2022; 14(11):6820. https://doi.org/10.3390/su14116820
Chicago/Turabian StyleChotkan, Shaniel, Raymond van der Meij, Wouter Jan Klerk, Phil J. Vardon, and Juan Pablo Aguilar-López. 2022. "A Data-Driven Method for Identifying Drought-Induced Crack-Prone Levees Based on Decision Trees" Sustainability 14, no. 11: 6820. https://doi.org/10.3390/su14116820
APA StyleChotkan, S., van der Meij, R., Klerk, W. J., Vardon, P. J., & Aguilar-López, J. P. (2022). A Data-Driven Method for Identifying Drought-Induced Crack-Prone Levees Based on Decision Trees. Sustainability, 14(11), 6820. https://doi.org/10.3390/su14116820






