Characterization and Prediction of Water Stress Using Time Series and Artificial Intelligence Models
Abstract
:1. Introduction
2. Materials and Methods
2.1. Description of the Data and Study Area
2.2. Standardized Precipitation Index (SPI)
2.3. ARIMA Model
2.4. Artificial Neural Network (ANN)
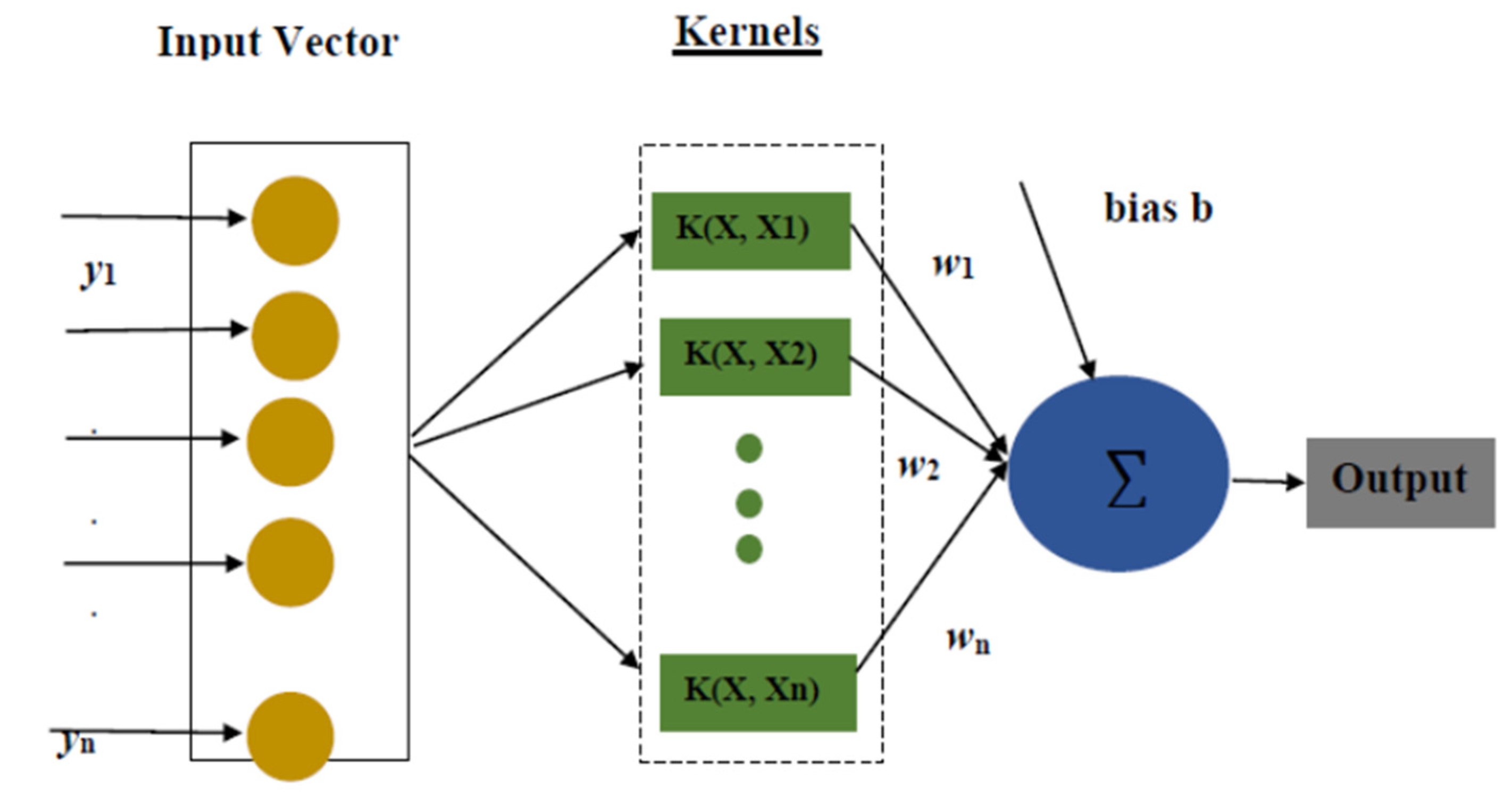
2.5. Support Vector Regression (SVR)
3. Results
3.1. Calculated SPI
3.2. ARIMA Model
3.3. ANN Model
3.4. SVR Model
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Markulj Kulundžić, A.; ViljevacVuletić, M.; MatošaKočar, M.; Mijić, A.; Varga, I.; Sudarić, A.; Cesar, V.; Lepeduš, H. The Combination of Increased Temperatures and High Irradiation Causes Changes in Photosynthetic Efficiency. Plants 2021, 10, 2076. [Google Scholar] [CrossRef] [PubMed]
- Heim, R.R., Jr. A comparison of the early twenty-first century drought in the United States to the 1930s and 1950s drought episodes. Bull. Am. Meteorol. Soc. 2017, 98, 2579–2592. [Google Scholar] [CrossRef]
- Seleiman, M.F.; Al-Suhaibani, N.; Ali, N.; Akmal, M.; Alotaibi, M.; Refay, Y.; Dindaroglu, T.; Abdul-Wajid, H.H.; Battaglia, M.L. Drought Stress Impacts on Plants and Different Approaches to Alleviate Its Adverse Effects. Plants 2021, 10, 259. [Google Scholar] [CrossRef] [PubMed]
- Raza, A.; Razzaq, A.; Mehmood, S.S.; Zou, X.; Zhang, X.; Lv, Y.; Xu, J. Impact of Climate Change on Crops Adaptation and Strategies to Tackle Its Outcome: A Review. Plants 2019, 8, 34. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Raihan, F.; Ondrasek, G.; Islam, M.S.; Maina, J.M.; Beaumont, L.J. Combined Impacts of Climate and Land Use Changes on Long-Term Streamflow in the Upper Halda Basin, Bangladesh. Sustainability 2021, 13, 12067. [Google Scholar] [CrossRef]
- Ondrasek, G.; Rathod, S.; Manohara, K.K.; Gireesh, C.; Anantha, M.S.; Sakhare, A.S.; Parmar, B.; Yadav, B.K.; Bandumula, N.; Raihan, F.; et al. Salt Stress in Plants and Mitigation Approaches. Plants 2022, 11, 717. [Google Scholar] [CrossRef]
- Ondrasek, G. Water Scarcity and Water Stress in Agriculture. In Physiological Mechanisms and Adaptation Strategies in Plants under Changing Environment; Ahmad, P., Wani, M., Eds.; Springer: New York, NY, USA, 2014. [Google Scholar] [CrossRef]
- The State of Food and Agriculture: Climate Change, Agriculture and Food Security. Available online: https://www.fao.org/3/i6030e/i6030e.pdf (accessed on 4 March 2022).
- Mishra, A.K.; Singh, V.P. Drought Modeling—A Review. J. Hydrol. 2011, 403, 157–175. [Google Scholar] [CrossRef]
- McKee, T.B.; Doesken, N.J.; Kleist, J. The relationship of drought frequency and duration to time scales. In Proceedings of the 8th Conference on Applied Climatology, Anaheim, CA, USA, 17–22 January 1993; American Meteorological Society: Boston, MA, USA, 1993; Volume 17, pp. 179–183. [Google Scholar]
- Thom, H.C.S. Some Methods of Climatological Analysis; Secretariat of the World Meteorological Organization: Geneva, Switzerland, 1966. [Google Scholar]
- Jaber, A. Drought Analysis for Kuwait Using Standardized Precipitation Index. Sci. World J. 2014, 2014, 1–9. [Google Scholar] [CrossRef]
- Musonda, B.; Jing, Y.; Iyakaremye, V.; Ojara, M. Analysis of Long-Term Variations of Drought Characteristics Using Standardized Precipitation Index over Zambia. Atmosphere 2020, 11, 1268. [Google Scholar] [CrossRef]
- Jobin, T.; Prasannakumar, V. Temporal analysis of rainfall (1871–2012) and drought characteristics over a tropical monsoon-dominated State (Kerala) of India. J. Hydrol. 2016, 534, 266–280. [Google Scholar] [CrossRef]
- Caloiero, T.; Caroletti, G.N.; Coscarelli, R. IMERG-Based Meteorological Drought Analysis over Italy. Climate 2021, 9, 65. [Google Scholar] [CrossRef]
- Tien Thanh, N. A Proposal to Evaluate Drought Characteristics Using Multiple Climate Models for Multiple Timescales. Climate 2018, 6, 79. [Google Scholar] [CrossRef] [Green Version]
- Zhao, Q.; Chen, Q.; Jiao, M.; Wu, P.; Gao, X.; Ma, M.; Hong, Y. The Temporal-Spatial Characteristics of Drought in the Loess Plateau Using the Remote-Sensed TRMM Precipitation Data from 1998 to 2014. Remote Sens. 2018, 10, 838. [Google Scholar] [CrossRef] [Green Version]
- Pandey, V.; Srivastava, P.K.; Singh, S.K.; Petropoulos, G.P.; Mall, R.K. Drought Identification and Trend Analysis Using Long-Term CHIRPS Satellite Precipitation Product in Bundelkhand, India. Sustainability 2021, 13, 1042. [Google Scholar] [CrossRef]
- Guo, H.; Bao, A.; Liu, T.; Ndayisaba, F.; He, D.; Kurban, A.; Maeyer, P.D. Meteorological drought analysis in the Lower Mekong Basin using satellite based Long term CHIRPS product. Sustainability 2017, 9, 901. [Google Scholar] [CrossRef] [Green Version]
- Roman, R.; Ali, Y.; Joanna, K.; Atilgan, A.; Monika, M.; Daniel, L. Analysis of SPI as a drought indicator during the maize growing period in the cukurova region (Turkey). Sustainability 2022, 14, 3697. [Google Scholar] [CrossRef]
- Li, K.; Wang, M.; Liu, K. The study on compound heatwave events in china using complex networks. Sustainability 2021, 13, 12774. [Google Scholar] [CrossRef]
- Box, G.; Jenkins, G. Time Series Analysis: Forecasting and Control; Holden-Day: San Francisco, CA, USA, 1970. [Google Scholar]
- Morid, S.; Smakhtin, V.; Bagherzadeh, K. Drought forecasting using artificial neural networks and time series of drought indices. Int. J. Climatol. 2007, 27, 2103–2111. [Google Scholar] [CrossRef]
- Patil, R.; Polisgowdar, B.S.; Rathod, S.; Satish, K.U.; Srinivasa Reddy, G.V.; Vijaya, W.; Satyanarayana, R. Drought Modelling and Forecasting using Arima and Neural Networks for Ballari District, Karnataka. J. Indian Soc. Agric. Stat. 2020, 74, 149–157. [Google Scholar]
- Rathod, S.; Singh, K.N.; Arya, P.; Ray, M.; Mukherjee, A.; Sinha, K.; Kumar, P.; Shekhawat, R.S. Forecasting maize yield using ARIMA-Genetic Algorithm approach. J. Outlook Agr. 2017, 46, 265–271. [Google Scholar] [CrossRef]
- Rathod, S.; Mishra, G.C. Statistical Models for Forecasting Mango and Banana Yield of Karnataka, India. J. Agric. Sci. Technol. 2018, 20, 803–816. [Google Scholar]
- Patil, R.; Nagaraj, D.M.; Polisgowdar, B.S.; Rathod, S. Forecasting potential evapotranspiration for Raichur district using seasonal ARIMA model. Mausam 2022, 73, 433–440. [Google Scholar] [CrossRef]
- Rathod, S.; Saha, A.; Patil, R.; Ondrasek, G.; Gireesh, C.; Anantha, M.S.; Rao, D.V.K.N.; Nirmala, B.; Senguttuvel, P.; Arun, K.S.; et al. Two-Stage Spatiotemporal Time Series Modelling Approach for Rice Yield Prediction & Advanced Agroecosystem Management. Agronomy 2021, 11, 2502. [Google Scholar] [CrossRef]
- Naveena, K.; Singh, S.; Rathod, S.; Singh, A. Hybrid ARIMA-ANN Modelling for forecasting the price of Robusta Coffee in India. Int. J. Curr. Microbiol. App. Sci. 2017, 6, 1721–1726. [Google Scholar] [CrossRef]
- Saha, A.; Singh, K.N.; Ray, M.; Rathod, S. A hybrid spatio-temporal modelling: An application to space-time rainfall forecasting. Theor. App. Climat. 2020, 142, 1271–1282. [Google Scholar] [CrossRef]
- Zhu, Q.; Luo, Y.; Zhou, D.; Xu, Y.; Wang, G.; Tian, Y. Drought prediction using in situ and remote sensing products with SVM over the Xiang River Basin, China. Nat. Hazards 2020, 105, 2161–2185. [Google Scholar] [CrossRef]
- Alam, W.; Ray, M.; Kumar, R.R.; Sinha, K.S.; Rathod, S.; Singh, K.N. Improved ARIMAX modal based on ANN and SVM approaches for forecasting rice yield using weather variables. Indian J. Agric. Sci. 2018, 88, 1909–1913. [Google Scholar]
- Alam, W.; Sinha, K.; Kumar, R.R.; Ray, M.; Rathod, S.; Singh, K.N.; Arya, P. Hybrid linear time series approach for long term forecasting of crop yield. Indian J. Agric. Sci. 2018, 88, 1275–1279. [Google Scholar]
- Zhang, Y.; Yang, H.; Cui, H.; Chen, Q. Comparison of the Ability of ARIMA, WNN and SVM Models for Drought Forecasting in the Sanjiang Plain, China. Nat. Reso. Rese. 2019, 29, 1447–1464. [Google Scholar] [CrossRef]
- Saha, A.; Singh, K.N.; Ray, M.; Rathod, S.; Choudhury, S. Modelling and forecasting cotton production using tuned-support vector regression. Curr. Sci. 2021, 121, 1090. [Google Scholar] [CrossRef]
- Chakraborty, S.; Goyal, M.; Rao, A.; Sen, S.; Jain, S.; Manoj, J. Drought Preparedness of Vulnerable Sections in Rural Telangana; South Asia Consortium for Interdisciplinary Water Resources Studies: Secunderabad, India, 2018; Available online: http://www.saciwaters.org/pdfs/DPVSRT.pdf (accessed on 6 March 2022).
- Diebold, F.X.; Mariano, R.S. Comparing predictive accuracy. J. Bus. Econ. Stat. 1995, 13, 253–263. [Google Scholar]
- Abramowitz, M.; Stegun, I.A. Handbook of Mathematical Functions with Formulas, Graphs and Mathematical Table; Courier Dover Publications: New York, NY, USA, 1965. [Google Scholar]
- Zhang, G.P. Time series forecasting using a hybrid ARIMA and neural network model. Neurocomputing 2003, 50, 159–175. [Google Scholar] [CrossRef]
- Zhang, G.; Eddy Patuwo, B.; Hu, Y.M. Forecasting with artificial neural networks: The state of the art. Int. J. Forecast. 1998, 14, 35–62. [Google Scholar] [CrossRef]
- Rathod, S.; Singh, K.N.; Patil, S.G.; Naik, R.H.; Ray, M.; Meena, V.S. Modelling and forecasting of oilseed production of India through artificial intelligence techniques. Indian J. Agric. Sci. 2018, 88, 22–27. [Google Scholar]
- Vapnik, V.N. The Nature of Statistical Learning Theory; Springer: New York, NY, USA, 1995. [Google Scholar]
- Brock, W.; Scheinkman, J.A.; Dechert, W.D.; LeBaron, B. A Test for Independence Based on the Correlation Dimension. Eco. Rev. 1996, 15, 197–235. [Google Scholar] [CrossRef]
- Leszek, L. Estimation of local drought frequency in central Poland using the standardized precipitation index SPI. Irrig. Drain. 2007, 56, 67–77. [Google Scholar] [CrossRef]
- Thomas, T.; Jaiswal, R.K.; Nayak, P.C.; Ghosh, N.C. Comprehensive evaluation of the changing drought characteristics in Bundelkhand region of Central India. Meteor. Atmos. Phys. 2015, 127, 163–182. [Google Scholar] [CrossRef]
- Botai, C.; Botai, J.; de Wit, J.; Ncongwane, K.; Adeola, A. Drought Characteristics over the Western Cape Province, South Africa. Water 2017, 9, 876. [Google Scholar] [CrossRef] [Green Version]
- Caloiero, T.; Veltri, S.; Caloiero, P.; Frustaci, F. Drought Analysis in Europe and in the Mediterranean Basin Using the Standardized Precipitation Index. Water 2018, 10, 1043. [Google Scholar] [CrossRef] [Green Version]
- Xia, L.; Zhao, F.; Mao, K.; Yuan, Z.; Zuo, Z.; Xu, T. SPI-Based Analyses of Drought Changes over the Past 60 Years in China’s Major Crop-Growing Areas. Remote Sens. 2018, 10, 171. [Google Scholar] [CrossRef] [Green Version]
- Sobral, B.S.; de Oliveira-Junior, J.S.; de Gois, G.; Pereira-Junior, E.R.; de BodasTerassi, P.M.; Muniz-Junior, J.G.R.; Lyra, G.B.; Zeri, M. Drought characterization for the state of Rio de Janeiro based on the annual SPI index: Trends, statistical tests and its relation with ENSO. Atmos. Res. 2019, 220, 141–154. [Google Scholar] [CrossRef]
- Pei, Z.; Fang, S.; Wang, L.; Yang, W. Comparative Analysis of Drought Indicated by the SPI and SPEI at Various Timescales in Inner Mongolia, China. Water 2020, 12, 1925. [Google Scholar] [CrossRef]
- Falak, N.; Dars, G.H.; Ansari, K.; Jamro, S.; Nir, Y.K. Drought trends in Balochistan. Water 2020, 12, 470. [Google Scholar] [CrossRef] [Green Version]
- Borji, M.; Malekian, A.; Salajegheh, A.; Ghadimi, M. Multi-time-scale analysis of hydrological drought forecasting using support vector regression (SVR) and artificial neural networks (ANN). Arab. J. Geosci. 2016, 9, 725. [Google Scholar] [CrossRef]
- Mokhtarzad, M.; Eskandari, F.; Jamshidi, V.N.; Arabasadi, A. Drought forecasting by ANN, ANFIS, and SVM and comparison of the models. Environ. Earth Sci. 2017, 76, 729. [Google Scholar] [CrossRef]
- Rathod, S.; Mishra, G.; Singh, K.N. Hybrid time series models for forecasting banana production in Karnataka state, India. J. Indian Soc. Agric. Stat. 2017, 71, 193–200. [Google Scholar]
- Khan, N.; Sachindra, D.A.; Shahid, S.; Ahmed, K.; Shiru, M.S.; Nawaz, N. Prediction of droughts over Pakistan using machine learning algorithms. Adva. Water Reso. 2020, 139, 103562. [Google Scholar] [CrossRef]
- Rathod, S.; Yerram, S.; Arya, P.; Katti, G.; Rani, J.; Padmakumari, A.P.; Somasekhar, N.; Padmavathi, C.; Ondrasek, G.; Amdan, S.; et al. Climate-Based Modeling and Prediction of Rice Gall Midge Populations Using Count Time Series and Machine Learning pproaches. Agronomy 2022, 12, 22. [Google Scholar] [CrossRef]
- Chitikela, G.; Meena, A.; Vijaya, K.R.; Nirmala, B.; Gabrijel, O.; Raman, M.S.; Rathod, S. Artificial-Intelligence-Based Time-Series Intervention Models to Assess the Impact of the COVID-19 Pandemic on Tomato Supply and Prices in Hyderabad, India. Agronomy 2020, 11, 1878. [Google Scholar] [CrossRef]




| SPI Range | Category |
|---|---|
| +2 to more | Extremely wet |
| 1.5 to1.99 | Very wet |
| 1.0 to 1.49 | Moderately wet |
| −0.99 to 0.99 | Near normal |
| −1.0 to −1.49 | Moderately dry |
| −1.5 to −1.99 | Severely dry |
| −2 to less | Extremely dry |
| Year | Jan | Feb | Mar | Apr | May | Jun | Jul | Aug | Sep | Oct | Nov | Dec |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1982 | −1.21 | |||||||||||
| 1983 | −1.56 | −2.04 | −2.25 | −3.15 | −2.13 | −1.30 | −1.48 | |||||
| 1984 | −1.56 | −1.23 | −1.89 | |||||||||
| 1985 | −1.15 | |||||||||||
| 1988 | −1.30 | |||||||||||
| 1989 | −1.19 | −1.43 | −1.22 | −1.08 | −1.34 | |||||||
| 1990 | −1.34 | −1.64 | −1.78 | −1.17 | ||||||||
| 1991 | −1.51 | |||||||||||
| 1992 | −2.06 | −1.11 | −1.49 | |||||||||
| 1993 | −2.04 | −1.12 | −1.71 | |||||||||
| 1994 | −1.21 | |||||||||||
| 1997 | −1.30 | −1.48 | ||||||||||
| 1998 | −1.60 | −1.00 | −1.92 | |||||||||
| 1999 | −1.14 | |||||||||||
| 2002 | −1.26 | |||||||||||
| 2003 | −1.37 | −1.48 | −1.67 | |||||||||
| 2004 | −1.15 | −1.13 | ||||||||||
| 2007 | −2.08 | |||||||||||
| 2010 | −1.32 | −1.67 | ||||||||||
| 2015 | −2.25 | |||||||||||
| 2018 | −2.08 | −2.49 | −1.27 | −1.97 | −1.11 | −1.80 | ||||||
| 2019 | −1.12 | −1.82 | −1.66 |
| Year | Jan | Feb | Mar | Apr | May | Jun | Jul | Aug | Sep | Oct | Nov | Dec |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1983 | −1.18 | −1.08 | −2.66 | |||||||||
| 1985 | −1.37 | −1.33 | −1.36 | |||||||||
| 1986 | −1.86 | −1.53 | ||||||||||
| 1989 | −1.27 | −1.35 | −1.19 | |||||||||
| 1990 | −1.11 | −1.18 | ||||||||||
| 1991 | −2.42 | |||||||||||
| 1996 | −1.37 | −1.28 | −1.07 | |||||||||
| 2000 | −1.08 | −1.02 | −1.04 | |||||||||
| 2002 | −1.21 | −1.86 | −1.56 | −1.98 | ||||||||
| 2003 | −1.72 | −1.24 | ||||||||||
| 2007 | −1.53 | |||||||||||
| 2011 | −2.20 | −1.85 | ||||||||||
| 2016 | −2.66 | |||||||||||
| 2018 | −1.95 | −1.62 | ||||||||||
| 2019 | −1.66 |
| Time Scales | Model | Parameters | Estimation | S. E | Z Value | Prob. | Model Fitting | Box–Pierce Non-Correlation Test | ||
|---|---|---|---|---|---|---|---|---|---|---|
| SPI3 | ARIMA (1,0,2) | AR1 | −0.018 | 0.130 | −0.143 | p < 0.0001 | Log likelihood | −544.14 | Original | Residuals |
| MA1 | 0.674 | 0.121 | 5.559 | p < 0.0001 | BIC | 1112.79 | Chi-square = 148.39 (p < 0.001) | Chi-square = 0.005 (p = 0.938) | ||
| MA2 | 0.393 | 0.066 | 5.956 | p < 0.0001 | AIC | 1096.27 | ||||
| SPI6 | ARIMA (1,0,0) | AR1 | 0.717 | 0.032 | 22.03 | p < 0.0001 | Log likelihood | −479.53 | Chi-square = 233.19 (p < 0.001) | Chi-square = 0.078 (p = 0.779) |
| AIC | 963.07 | |||||||||
| BIC | 971.31 | |||||||||
| Sample | Dimension | SPI3 | SPI6 | ||
|---|---|---|---|---|---|
| Statistics | Probability | Statistics | Probability | ||
| eps(1) | m = 2 | 15.63 | p < 0.0001 | 15.68 | p < 0.0001 |
| m = 3 | 15.37 | p < 0.0001 | 18.09 | p < 0.0001 | |
| eps(2) | m = 2 | 14.23 | p < 0.0001 | 12.72 | p < 0.0001 |
| m = 3 | 13.11 | p < 0.0001 | 12.09 | p < 0.0001 | |
| eps(3) | m = 2 | 13.90 | p < 0.0001 | 12.51 | p < 0.0001 |
| m = 3 | 12.34 | p < 0.0001 | 11.18 | p < 0.0001 | |
| eps(4) | m = 2 | 15.40 | p < 0.0001 | 13.92 | p < 0.0001 |
| m = 3 | 13.76 | p < 0.0001 | 12.43 | p < 0.0001 | |
| Parameters | SPI3 | SPI6 |
|---|---|---|
| Input lag | 5 | 4 |
| Output variable/dependent | 1 | 1 |
| Hidden nodes | 1 | 1 |
| Hidden layers | 2 | 4 |
| Model | (5:2S:1L) | (4:4S:1L) |
| Total number of parameters | 15 | 25 |
| Network type | Feed forward | Feed forward |
| Activation function (I:H) | Sigmoidal | Sigmoidal |
| Activation function (H:O) | Identity | Identity |
| Box–pierce non-correlation test for residuals | 0.018 | 0.124 |
| p-value | 0.873 | 0.724 |
| Model | SPI3 | SPI6 |
|---|---|---|
| Parameters | Values | Values |
| Kernel function | RBF | RBF |
| No. of S. V’s | 451 | 337 |
| Cost | 7.9 | 7.7 |
| Gamma | 0.16 | 0.16 |
| Epsilon | 0.01 | 0.1 |
| Cross validation error | 0.043 | 0.029 |
| Box–Pierce non-correlation test for residuals | 0.19 | 0.31 |
| p-value | 0.27 | 0.57 |
| Category | SPI3 | SPI6 |
|---|---|---|
| Extremely wet | - | - |
| Very wet | - | - |
| Moderately wet | - | - |
| Near normal | - | - |
| Moderately dry | Oct-1982, Sep-1983, Oct-1983, Jul-1984, Dec-1985, Dec-1988, Jan-1989, Feb-1989, Apr-1989, Nov-1989, Dec-1989, Jan-1990, Apr-1990, Jun-1992, Jul-1992, Jun-1993, Oct-1994, Aug-1997, Sep-1997, Jun-1998, Nov-1999, Oct-2002, Mar-2003, Jun-2003, Sep-2004, Nov-2004, Apr-2010, Sep-2018, Nov-2018, Jan-2019 | Jan-1983, Feb-1983, Jun-1985, Jul-1985, Aug-1985, Jan-1989, Feb-1989, Mar-1989, Jan-1990, Feb-1990, Jul-1996, Aug-1996, Sep-1996, Fep-2000, Nov-2000, Dec-2000, Aug-2002, Feb-2003 |
| Severely dry | Jan-1983, Jun-1984, Aug-1984, Feb-1990, Mar-1990, Mar-1991, May-1998, Jul-1998, Jul-2003, May-2010, Oct-2018, Dec-2018, May-2019, Jun-2019 | Oct-1986, Nov-1986, Sep-2002, Oct-2002, Dec-2002, Jan-2003, Jun-2007, Mar-2011, Nov-2018, Dec-2018, Jan-2019 |
| Extremely dry | Feb-1983, Mar-1983, May-1983, Mar-1992, Mar-1993, Jul-1993, Mar-2007, Jul-2015, Jan-2018, Feb-2018 | May-1983, May-1991, Feb-2011, Mar-2016 |
| Model | Parameter | ARIMA | ANN | SVR |
|---|---|---|---|---|
| SPI3 | MSE | 0.438 | 0.418 | 0.378 |
| RMSE | 0.496 | 0.459 | 0.413 | |
| SPI6 | MSE | 0.328 | 0.275 | 0.237 |
| RMSE | 0.363 | 0.317 | 0.289 |
| Period | Actual | Forecasted | ||||||
|---|---|---|---|---|---|---|---|---|
| ARIMA | ANN | SVR | ||||||
| SPI3 | SPI6 | SPI3 | SPI6 | SPI3 | SPI6 | SPI3 | SPI6 | |
| Jun-20 | 0.917 | 0.851 | 0.241 | 0.083 | 0.132 | 0.254 | 0.197 | 0.064 |
| Jul-20 | 1.477 | 1.418 | 0.194 | 0.11 | 0.07 | 0.182 | 0.713 | 0.669 |
| Aug-20 | 0.133 | 0.12 | −0.004 | 0.082 | −0.089 | 0.131 | 0.554 | 0.83 |
| Sep-20 | 0.226 | 0.262 | −0.689 | 0.085 | −0.068 | 0.094 | −0.085 | 0.352 |
| Oct-20 | 0.279 | 0.400 | −0.812 | 0.059 | −0.083 | 0.067 | −0.186 | −0.501 |
| Nov-20 | 1.734 | 0.369 | −0.987 | 0.433 | 0.357 | 0.048 | 0.403 | 0.338 |
| Dec-20 | 1.142 | 0.322 | −0.988 | 0.025 | −0.072 | 0.035 | 0.87 | 0.294 |
| Jan-21 | −0.342 | 0.23 | −0.567 | 0.096 | −0.069 | 0.025 | −0.549 | 0.25 |
| Feb-21 | −0.636 | 1.646 | −0.288 | −0.028 | −0.074 | 0.018 | −0.804 | 0.839 |
| Mar-21 | −0.853 | 0.84 | −0.755 | −0.013 | −0.07 | 0.013 | −0.025 | 1.416 |
| Apr-21 | −0.138 | −0.526 | 1.988 | −0.02 | −0.072 | 0.009 | −0.994 | 0.399 |
| May-21 | 1.709 | 1.491 | 1.832 | −0.025 | −0.07 | 0.007 | −0.111 | 0.227 |
| MSE | 1.317 | 0.72 | 0.867 | 0.672 | 0.686 | 0.495 | ||
| RMSE | 1.734 | 0.848 | 0.931 | 0.82 | 0.828 | 0.703 | ||
| Model | Data Type | M1, M2 | M1, M3 | M2, M3 |
|---|---|---|---|---|
| SPI3 | Training set | 5.62 (p < 0.0001) | 5.05 (p < 0.0001) | −0.38 (p < 0.0001) |
| Testing set | 3.67 (p < 0.0001) | 2.57 (p < 0.0001) | −0.12 (p < 0.0001) | |
| SPI6 | Training set | 7.77 (p < 0.0001) | 6.24 (p < 0.0001) | 4.07 (p < 0.0001) |
| Testing set | 0.75 (p < 0.0001) | 0.62 (p < 0.0001) | 0.52 (p < 0.0001) |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gorlapalli, A.; Kallakuri, S.; Sreekanth, P.D.; Patil, R.; Bandumula, N.; Ondrasek, G.; Admala, M.; Gireesh, C.; Anantha, M.S.; Parmar, B.; et al. Characterization and Prediction of Water Stress Using Time Series and Artificial Intelligence Models. Sustainability 2022, 14, 6690. https://doi.org/10.3390/su14116690
Gorlapalli A, Kallakuri S, Sreekanth PD, Patil R, Bandumula N, Ondrasek G, Admala M, Gireesh C, Anantha MS, Parmar B, et al. Characterization and Prediction of Water Stress Using Time Series and Artificial Intelligence Models. Sustainability. 2022; 14(11):6690. https://doi.org/10.3390/su14116690
Chicago/Turabian StyleGorlapalli, Amuktamalyada, Supriya Kallakuri, Pagadala Damodaram Sreekanth, Rahul Patil, Nirmala Bandumula, Gabrijel Ondrasek, Meena Admala, Channappa Gireesh, Madhyavenkatapura Siddaiah Anantha, Brajendra Parmar, and et al. 2022. "Characterization and Prediction of Water Stress Using Time Series and Artificial Intelligence Models" Sustainability 14, no. 11: 6690. https://doi.org/10.3390/su14116690
APA StyleGorlapalli, A., Kallakuri, S., Sreekanth, P. D., Patil, R., Bandumula, N., Ondrasek, G., Admala, M., Gireesh, C., Anantha, M. S., Parmar, B., Yadav, B. K., Sundaram, R. M., & Rathod, S. (2022). Characterization and Prediction of Water Stress Using Time Series and Artificial Intelligence Models. Sustainability, 14(11), 6690. https://doi.org/10.3390/su14116690







