Repositioning and Optimal Re-Allocation of Empty Containers: A Review of Methods, Models, and Applications
Abstract
1. Introduction
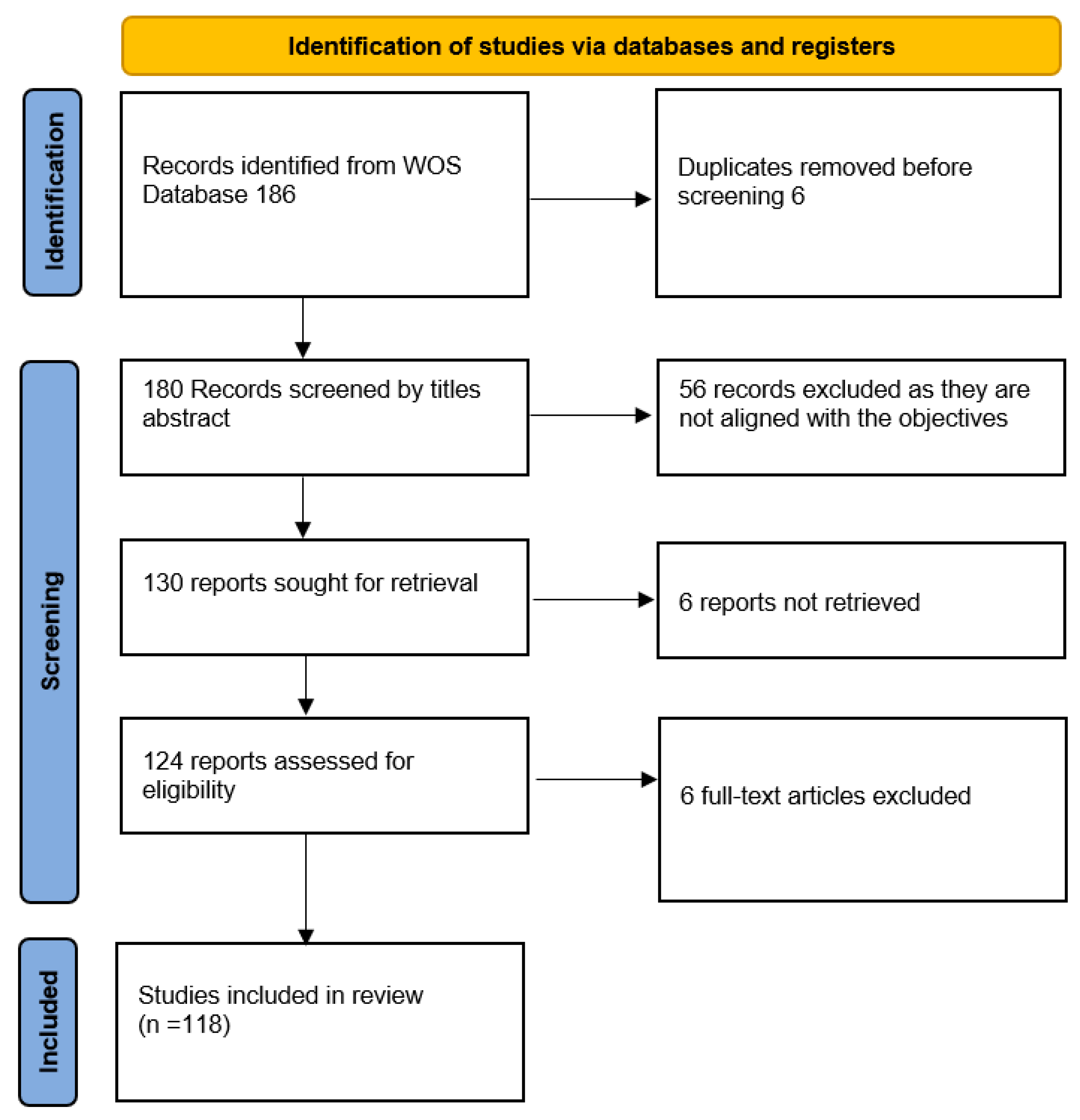
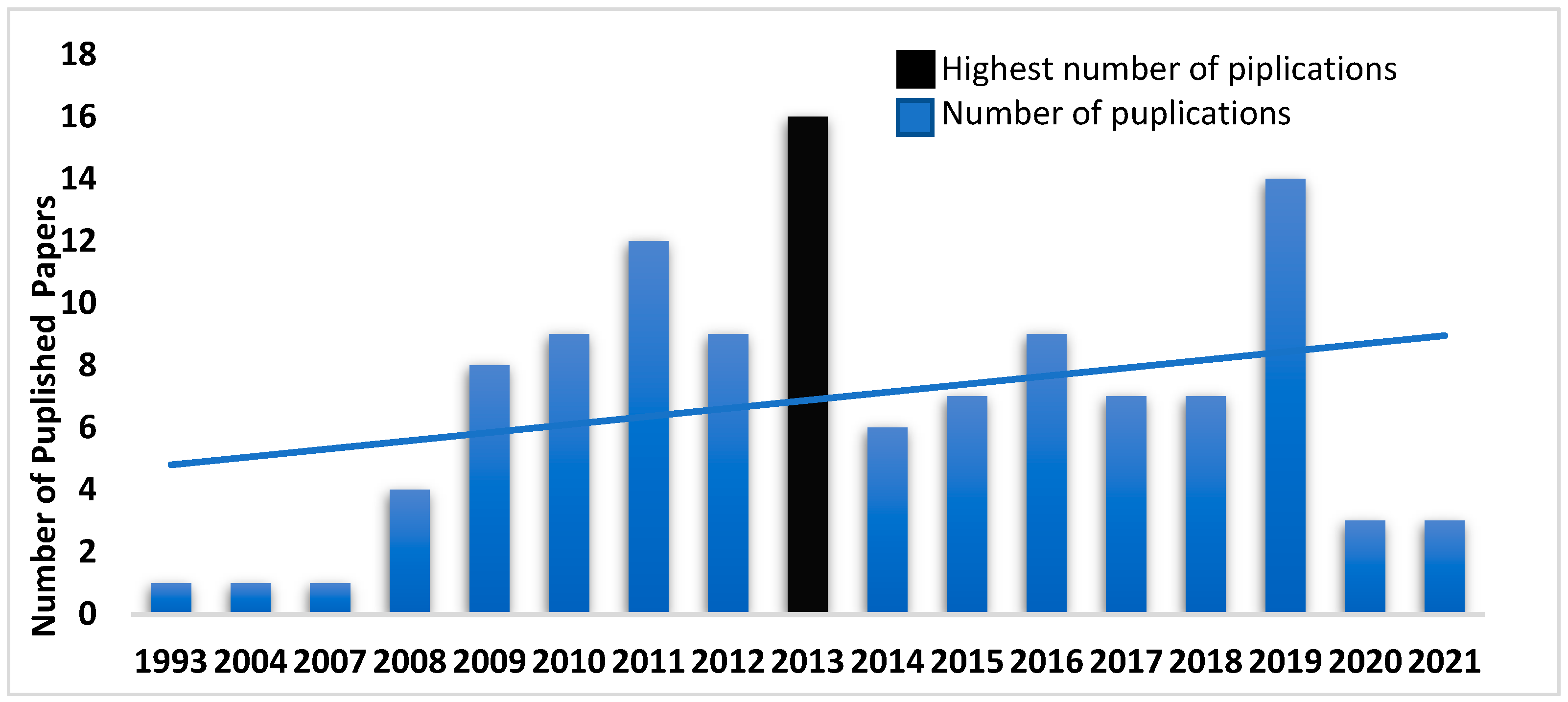
2. Research Methodology
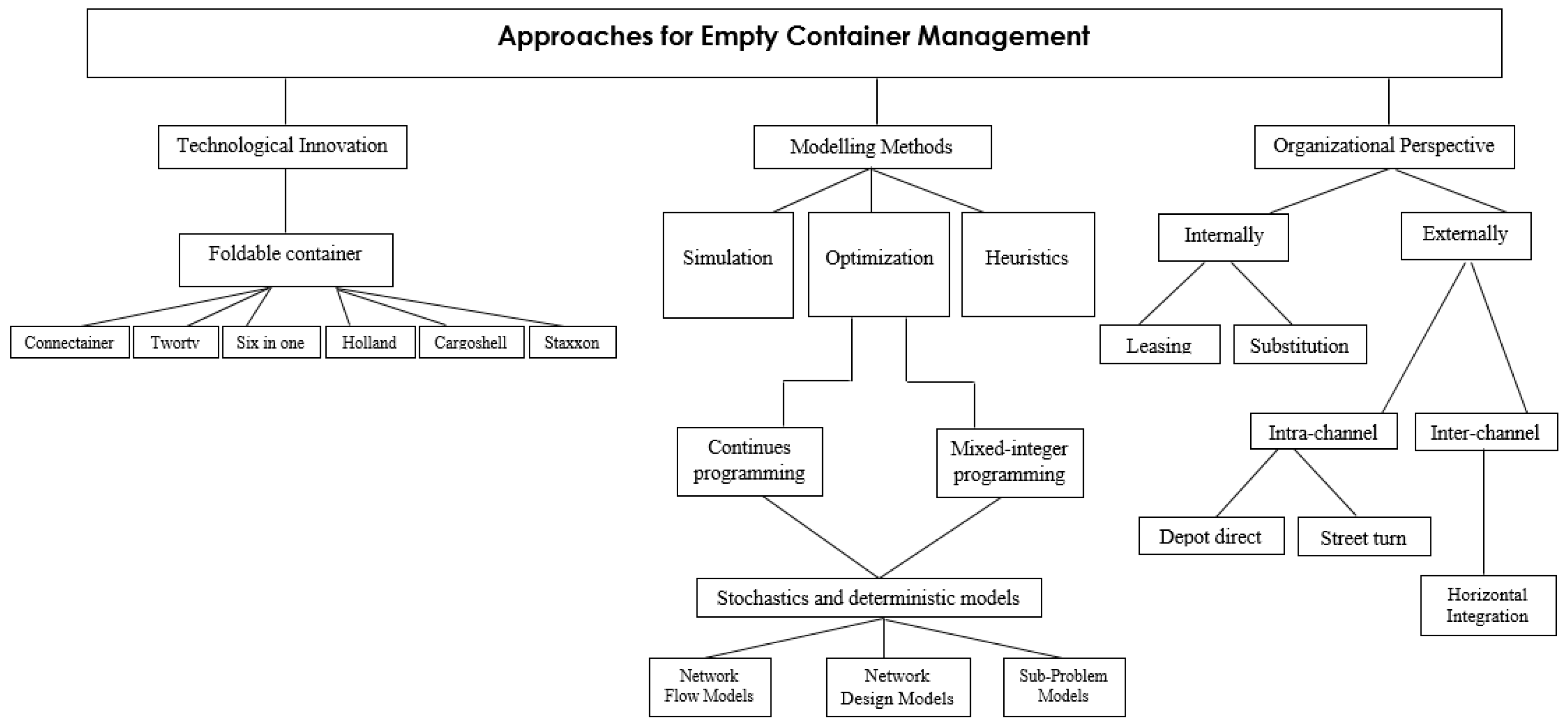
3. Empty-Container Management
3.1. Organizational Logistics Perspective
3.1.1. Internal Solutions
- Container leasing has seen more attention in the past few years, as an approach for managing empty-container traffic. According to Theofanis and Boile [7], leasing arrangements come into three major types: master lease, long-term lease, and short-term lease. The master lease is the type that is most related to the repositioning issue, by hiring containers at places with a shortage and to off-hire containers at surplus points. On the contrary, long- and short-term leases aim to invest their equipment, without any management services provided to the lessee. However, the opportunity for shipping lines to save costs by leasing containers remains linked to the terms and conditions of leasing contracts [12].
- Container substitution is the second internal approach to deal with container fleet imbalance [13]. Due to containers having different types and sizes, the demand for a particular container can be fulfilled by supplying another one [14]. Regarding the size substitution, the demand for two 20 ft empty containers may be replaced by supplying a 40 ft empty container [15]. Additionally, shipping lines can apply type substitution, by exchanging the demand for dry containers by providing a reefer container, without operating the refrigerator. Braekers et al. [16] explained that this strategy is challenging and cannot be a common practice, especially if the customer demand is subjected to some rules and conditions.
3.1.2. External Solutions
- Intra-channel solutions focus on vertical coordination among the different players in the container-transport chain. There are two proposed strategies for allocating empty containers: depot-direct and street-turn [17]. The idea of depot-direct is to establish a neutral supply point for empty containers to be stored, instead of moving them back to the port. Furthermore, the exporter can get the empty container faster, and the travel time and the repositioning cost will decrease [18]. Street-turn means that shipping companies can use imported containers directly for exporting purposes at the consignee’s location [17,19]. Although a street-turn strategy can reduce the total cost and congestion, it needs changing regarding some contract regulations with customers to deal with such reuse, tracking, and tracing of the empties’s interchange [20].
- Inter-channel solutions depends on horizontal cooperation [21]. Shipping lines can cooperate in several formats, such as slot exchange, alliances, and resource pooling, while competing in providing shipping services [22,23]. Pool-sharing containers is one of the critical strategies discussed by Theofanis and Boile [7]. They refer to the box-pool attempt, called Grey-Boxes, also known as free-label containers, which aims to reduce shareholders’s expenses by cooperating in providing empty containers without possession consideration. Vojdani et al. [24] ensured that such a strategy could decrease the movements of the empty container, store operations and subsequently, the total costs. This strategy did not receive the expected commercial acceptance due to competitiveness and confidentiality.
3.2. Technological Innovation
3.3. Modelling Approaches
4. Review on the Optimization of Empty-Container-Repositioning Techniques
4.1. Repositioning by Network Flow Model
4.2. Repositioning by Network Design
4.3. Repositioning under Resource Constraints
4.4. The Use of Metaheuristic Algorithms
4.4.1. Genetic Algorithm
4.4.2. Tabu Search
5. Discussion
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Elmi, Z.; Singh, P.; Meriga, V.K.; Goniewicz, K.; Borowska-Stefańska, M.; Wiśniewski, S.; Dulebenets, M.A. Uncertainties in Liner Shipping and Ship Schedule Recovery: A State-of-the-Art Review. J. Mar. Sci. Eng. 2022, 10, 563. [Google Scholar] [CrossRef]
- Meng, Q.; Zhao, H.; Wang, Y. Revenue management for container liner shipping services: Critical review and future research directions. Transp. Res. Part E Logist. Transp. Rev. 2019, 128, 280–292. [Google Scholar] [CrossRef]
- Song, D.-P.; Dong, J.-X. Empty container repositioning. In Handbook of Ocean Container Transport Logistics; Springer: Cham, Switzerland, 2015; pp. 163–208. [Google Scholar]
- Review of Maritime Transport 2020|UNCTAD. 2020. Available online: https://unctad.org/webflyer/review-maritime-transport-2020 (accessed on 31 January 2021).
- Kuzmicz, K.A.; Pesch, E. Approaches to empty container repositioning problems in the context of Eurasian intermodal transportation. Omega 2019, 85, 194–213. [Google Scholar] [CrossRef]
- Rodrigue, J.-P. The Geography of Transport Systems; Routledge: London, UK, 2020. [Google Scholar]
- Theofanis, S.; Boile, M. Empty marine container logistics: Facts, issues and management strategies. GeoJournal 2009, 74, 51. [Google Scholar] [CrossRef]
- Epstein, R.; Neely, A.; Weintraub, A.; Valenzuela, F.; Hurtado, S.; Gonzalez, G.; Beiza, A.; Naveas, M.; Infante, F.; Alarcon, F.; et al. A Strategic Empty Container Logistics Optimization in a Major Shipping Company. Interfaces 2012, 42, 5–16. [Google Scholar] [CrossRef]
- Dulebenets, M.A.; Pasha, J.; Abioye, O.F.; Kavoosi, M. Vessel scheduling in liner shipping: A critical literature review and future research needs. Flex. Serv. Manuf. J. 2021, 33, 43–106. [Google Scholar] [CrossRef]
- Moher, D.; Liberati, A.; Tetzlaff, J.; Altman, D.G.; The PRISMA Group. Preferred reporting items for systematic reviews and meta-analyses: The PRISMA statement. Int. J. Surg. 2010, 8, 336–341. [Google Scholar] [CrossRef]
- Song, D.; Dong, J.-X. Cargo routing and empty container repositioning in multiple shipping service routes. Transp. Res. Part B Methodol. 2012, 46, 1556–1575. [Google Scholar] [CrossRef]
- Di Francesco, M. New Optimization Models for Empty Container Management. Ph.D. Thesis, University of Cagliari, Cagliari, Italy, 2007. [Google Scholar]
- Chang, H.; Jula, H.; Chassiakos, A.; Ioannou, P. A heuristic solution for the empty container substitution problem. Transp. Res. Part E Logist. Transp. Rev. 2008, 44, 203–216. [Google Scholar] [CrossRef]
- Olivo, A.; di Francesco, M.; Zuddas, P. An optimization model for the inland repositioning of empty containers. In Port Management; Palgrave Macmillan: London, UK, 2015; pp. 84–108. [Google Scholar]
- Konings, R.; Thijs, R. Foldable containers: A new perspective on reducing container-repositioning costs. Eur. J. Transp. Infrastruct. Res. 2001, 1, 333–352. [Google Scholar] [CrossRef]
- Braekers, K.; Caris, A.; Janssens, G.K. Integrated planning of loaded and empty container movements. OR Spektrum 2013, 35, 457–478. [Google Scholar] [CrossRef]
- Jula, H.; Chassiakos, A.; Ioannou, P. Port dynamic empty container reuse. Transp. Res. Part E Logist. Transp. Rev. 2006, 42, 43–60. [Google Scholar] [CrossRef]
- Boile, M.; Theofanis, S.; Baveja, A.; Mittal, N. Regional repositioning of empty containers: Case for inland depots. Transp. Res. Rec. 2008, 2066, 31–40. [Google Scholar] [CrossRef]
- Braekers, K. Optimization of empty container movements in intermodal transport. 4OR 2013, 11, 299–300. [Google Scholar] [CrossRef]
- Smilowitz, K. Multi-resource routing with flexible tasks: An application in drayage operations. IIE Trans. 2006, 38, 577–590. [Google Scholar] [CrossRef]
- Jeong, Y.; Saha, S.; Chatterjee, D.; Moon, I. Direct shipping service routes with an empty container management strategy. Transp. Res. Part E Logist. Transp. Rev. 2018, 118, 123–142. [Google Scholar] [CrossRef]
- Song, D.; Zhang, J.; Carter, J.; Field, T.; Marshall, J.; Polak, J.; Schumacher, K.; Sinha-Ray, P.; Woods, J. On cost-efficiency of the global container shipping network. Marit. Policy Manag. 2005, 32, 15–30. [Google Scholar] [CrossRef]
- Varamäki, E.; Vesalainen, J. Modelling different types of multilateral co-operation between SMEs. Entrep. Reg. Dev. 2003, 15, 27–47. [Google Scholar] [CrossRef]
- Vojdani, N.; Lootz, F.; Rösner, R. Optimizing empty container logistics based on a collaborative network approach. Marit. Econ. Logist. 2013, 15, 467–493. [Google Scholar] [CrossRef]
- Moon, I.; Ngoc, A.-D.D.; Konings, R. Foldable and standard containers in empty container repositioning. Transp. Res. Part E Logist. Transp. Rev. 2013, 49, 107–124. [Google Scholar] [CrossRef]
- Shintani, K.; Konings, R.; Imai, A. Combinable containers: A container innovation to save container fleet and empty container repositioning costs. Transp. Res. Part E Logist. Transp. Rev. 2019, 130, 248–272. [Google Scholar] [CrossRef]
- Ivanov, D.; Sokolov, B. Adaptive Supply Chain Management; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2009. [Google Scholar]
- Cheung, R.K.; Chen, C.-Y. A Two-Stage Stochastic Network Model and Solution Methods for the Dynamic Empty Container Allocation Problem. Transp. Sci. 1998, 32, 142–162. [Google Scholar] [CrossRef]
- Choong, T.S.; Cole, M.H.; Kutanoglu, E. Empty container management for intermodal transportation networks. Transp. Res. Part E Logist. Transp. Rev. 2002, 38, 423–438. [Google Scholar] [CrossRef]
- Olivo, A.; Zuddas, P.; Di Francesco, M.; Manca, A. An Operational Model for Empty Container Management. Marit. Econ. Logist. 2005, 7, 199–222. [Google Scholar] [CrossRef]
- Shintani, K.; Imai, A.; Nishimura, E.; Papadimitriou, S. The container shipping network design problem with empty container repositioning. Transp. Res. Part E Logist. Transp. Rev. 2007, 43, 39–59. [Google Scholar] [CrossRef]
- Lam, S.-W.; Lee, L.-H.; Tang, L.-C. An approximate dynamic programming approach for the empty container allocation problem. Transp. Res. Part C Emerg. Technol. 2007, 15, 265–277. [Google Scholar] [CrossRef]
- Bin, W.; Zhongchen, W. Research on the optimization of intermodal empty container reposition of land-carriage. J. Transp. Syst. Eng. Inf. Technol. 2007, 7, 29–33. [Google Scholar] [CrossRef]
- Bandeira, D.L.; Becker, J.L.; Borenstein, D. A DSS for integrated distribution of empty and full containers. Decis. Support Syst. 2009, 47, 383–397. [Google Scholar] [CrossRef]
- Di Francesco, M.; Crainic, T.G.; Zuddas, P. The effect of multi-scenario policies on empty container repositioning. Transp. Res. Part E Logist. Transp. Rev. 2009, 45, 758–770. [Google Scholar] [CrossRef]
- Dong, J.-X.; Song, D. Container fleet sizing and empty repositioning in liner shipping systems. Transp. Res. Part E Logist. Transp. Rev. 2009, 45, 860–877. [Google Scholar] [CrossRef]
- Shintani, K.; Konings, R.; Imai, A. The impact of foldable containers on container fleet management costs in hinterland transport. Transp. Res. Part E Logist. Transp. Rev. 2010, 46, 750–763. [Google Scholar] [CrossRef]
- Brouer, D.B.; Pisinger, D.; Spoorendonk, S. Liner shipping cargo allocation with repositioning of empty containers. INFOR Inf. Syst. Oper. Res. 2011, 49, 109–124. [Google Scholar] [CrossRef]
- Meng, Q.; Wang, S. Liner shipping service network design with empty container repositioning. Transp. Res. Part E Logist. Transp. Rev. 2011, 47, 695–708. [Google Scholar] [CrossRef]
- Choi, S.-H.; Kim, H.-J.; Kim, G.-T. Optimizing Empty Container Repositioning at a Global Maritime Company. IE Interfaces 2011, 24, 164–172. [Google Scholar] [CrossRef][Green Version]
- Long, Y.; Lee, L.H.; Chew, E.P. The sample average approximation method for empty container repositioning with uncertainties. Eur. J. Oper. Res. 2012, 222, 65–75. [Google Scholar] [CrossRef]
- Dang, Q.-V.; Yun, W.-Y.; Kopfer, H. Positioning empty containers under dependent demand process. Comput. Ind. Eng. 2012, 62, 708–715. [Google Scholar] [CrossRef]
- Di Francesco, M.; Lai, M.; Zuddas, P. Maritime repositioning of empty containers under uncertain port disruptions. Comput. Ind. Eng. 2013, 64, 827–837. [Google Scholar] [CrossRef]
- Lai, M. Models and Algorithms for the Empty Container Repositioning and Its Integration with Routing Problems. Ph.D. Thesis, University of Cagliari, Cagliari, Italy, 2013. [Google Scholar]
- Furió, S.; Andrés, C.; Adenso-Díaz, B.; Lozano, S. Optimization of empty container movements using street-turn: Application to Valencia hinterland. Comput. Ind. Eng. 2013, 66, 909–917. [Google Scholar] [CrossRef]
- Mittal, N.; Boile, M.; Baveja, A.; Theofanis, S. Determining optimal inland-empty-container depot locations under stochastic demand. Res. Transp. Econ. 2013, 42, 50–60. [Google Scholar] [CrossRef]
- Dong, J.; Xu, J.; Song, D. Assessment of empty container repositioning policies in maritime transport. Int. J. Logist. Manag. 2013, 24, 49–72. [Google Scholar] [CrossRef]
- Jansen, E. Empty Tank Container Repositioning: Including a Forecast. Master’s Thesis, Tilburg University, Tilburg, The Netherlands, 2014. [Google Scholar]
- Huang, Y.-F.; Hu, J.-K.; Yang, B. Liner services network design and fleet deployment with empty container repositioning. Comput. Ind. Eng. 2015, 89, 116–124. [Google Scholar] [CrossRef]
- Wong, E.Y.; Tai, A.H.; Raman, M. A maritime container repositioning yield-based optimization model with uncertain upsurge demand. Transp. Res. Part E Logist. Transp. Rev. 2015, 82, 147–161. [Google Scholar] [CrossRef]
- Zheng, J.; Sun, Z.; Gao, Z. Empty container exchange among liner carriers. Transp. Res. Part E Logist. Transp. Rev. 2015, 83, 158–169. [Google Scholar] [CrossRef]
- Zheng, J.; Sun, Z.; Zhang, F. Measuring the perceived container leasing prices in liner shipping network design with empty container repositioning. Transp. Res. Part E Logist. Transp. Rev. 2016, 94, 123–140. [Google Scholar] [CrossRef]
- Sainz Bernat, N.; Schulte, F.; Voß, S.; Boße, J. Empty Container Management at Ports Considering Pollution, Repair Options, and Street-Turns. Math. Probl. Eng. 2016, 2016, 3847163. [Google Scholar] [CrossRef]
- Akyüz, M.H.; Lee, C.-Y. Service type assignment and container routing with transit time constraints and empty container repositioning for liner shipping service networks. Transp. Res. Part B Methodol. 2016, 88, 46–71. [Google Scholar] [CrossRef]
- Monemi, N.R.; Gelareh, S. Network design, fleet deployment and empty repositioning in liner shipping. Transp. Res. Part E Logist. Transp. Rev. 2017, 108, 60–79. [Google Scholar] [CrossRef]
- Wang, K.; Wang, S.; Zhen, L.; Qu, X. Ship type decision considering empty container repositioning and foldable containers. Transp. Res. Part E Logist. Transp. Rev. 2017, 108, 97–121. [Google Scholar] [CrossRef]
- Xie, Y.; Liang, X.; Ma, L.; Yan, H. Empty container management and coordination in intermodal transport. Eur. J. Oper. Res. 2017, 257, 223–232. [Google Scholar] [CrossRef]
- Razouk, C.; Benadada, Y. Optimization and Simulation Approach for Empty Containers Handling. Int. J. Adv. Comput. Sci. Appl. 2017, 8, 520–525. [Google Scholar] [CrossRef][Green Version]
- Belayachi, N.; Amrani, F.; Bouamrane, K. A Decision-Making Tool for the Optimization of Empty Containers’ Return in the Liner Shipping: Optimization by Using the Genetic Algorithm. Int. J. Decis. Support Syst. Technol. 2018, 10, 39–56. [Google Scholar] [CrossRef]
- Zhang, H.; Lu, L.; Wang, X. Tactical and Operational Cooperative Empty Container Repositioning Optimization Model Based on Business Flow and Initial Solutions Generation Rules. Symmetry 2019, 11, 300. [Google Scholar] [CrossRef]
- Xing, X.; Drake, P.R.; Song, D.; Zhou, Y. Tank Container Operators’ profit maximization through dynamic operations planning integrated with the quotation-booking process under multiple uncertainties. Eur. J. Oper. Res. 2019, 274, 924–946. [Google Scholar] [CrossRef]
- Hosseini, A.; Sahlin, T. An optimization model for management of empty containers in distribution network of a logistics company under uncertainty. J. Ind. Eng. Int. 2018, 15, 585–602. [Google Scholar] [CrossRef]
- Gusah, L.; Cameron-Rogers, R.; Thompson, R.G. A systems analysis of empty container logistics–A case study of Melbourne, Australia. Transp. Res. Procedia 2019, 39, 92–103. [Google Scholar] [CrossRef]
- Göçen, M.Y.; Çağlar, Ö.; Ercan, E.; Kizilay, D. Optimization of Costs in Empty Container Repositioning. In Proceedings of the International Symposium for Production Research 2019, ISPR 2019, Vienna, Austria, 28–30 August 2019; Springer: Cham, Switzerland, 2020; pp. 732–747. [Google Scholar] [CrossRef]
- Florez, H. Empty-Container Repositioning and Leasing: An Optimization Model. Ph.D. Thesis, Polytechnic Institute of New York, New York, NY, USA, 1986. [Google Scholar]
- Erera, A.L.; Morales, J.C.; Savelsbergh, M. Robust Optimization for Empty Repositioning Problems. Oper. Res. 2009, 57, 468–483. [Google Scholar] [CrossRef]
- Crainic, T.G.; Gendreau, M.; Dejax, P. Dynamic and Stochastic Models for the Allocation of Empty Containers. Oper. Res. 1993, 41, 102–126. [Google Scholar] [CrossRef]
- Li, J.-A.; Liu, K.; Leung, S.C.; Lai, K.K. Empty container management in a port with long-run average criterion. Math. Comput. Model. 2004, 40, 85–100. [Google Scholar] [CrossRef]
- Song, D.; Dong, J.-X. Empty Container Management in Cyclic Shipping Routes. Marit. Econ. Logist. 2008, 10, 335–361. [Google Scholar] [CrossRef]
- Chou, C.-C.; Kuo, F.-T.; Gou, R.-H.; Tsai, C.-L.; Wong, C.-P.; Tsou, M.-C. Application of a combined fuzzy multiple criteria decision making and optimization programming model to the container transportation demand split. Appl. Soft Comput. 2010, 10, 1080–1086. [Google Scholar] [CrossRef]
- Chou, C.-C.; Gou, R.-H.; Tsai, C.-L.; Tsou, M.-C.; Wong, C.-P.; Yu, H.-L. Application of a mixed fuzzy decision making and optimization programming model to the empty container allocation. Appl. Soft Comput. 2010, 10, 1071–1079. [Google Scholar] [CrossRef]
- Álvarez, J.F. Jos Joint Routing and Deployment of a Fleet of Container Vessels. Marit. Econ. Logist. 2009, 11, 186–208. [Google Scholar] [CrossRef]
- Wang, S.; Meng, Q. Liner ship fleet deployment with container transshipment operations. Transp. Res. Part E Logist. Transp. Rev. 2012, 48, 470–484. [Google Scholar] [CrossRef]
- Wang, S. A novel hybrid-link-based container routing model. Transp. Res. Part E Logist. Transp. Rev. 2014, 61, 165–175. [Google Scholar] [CrossRef][Green Version]
- Alfandari, L.; Davidović, T.; Furini, F.; Ljubic, I.; Maraš, V.; Martin, S. Tighter MIP models for Barge Container Ship Routing. Omega 2019, 82, 38–54. [Google Scholar] [CrossRef]
- Imai, A.; Rivera, F.I.V. Strategic fleet size planning for maritime refrigerated containers. Marit. Policy Manag. 2001, 28, 361–374. [Google Scholar] [CrossRef]
- Moon, I.-K.; Ngoc, A.-D.D.; Hur, Y.-S. Positioning empty containers among multiple ports with leasing and purchasing considerations. OR Spektrum 2010, 32, 765–786. [Google Scholar] [CrossRef]
- Jami, N.; Schröder, M.; Küfer, K.-H. A model and polynomial algorithm for purchasing and repositioning containers. IFAC-PapersOnLine 2016, 49, 48–53. [Google Scholar] [CrossRef]
- Chandoul, A.; Cung, V.-D.; Mangione, F. Optimal repositioning and purchasing policies in returnable container management. In Proceedings of the 2009 IEEE International Conference on Industrial Engineering and Engineering Management, Hong Kong, China, 8–11 December 2009. [Google Scholar]
- Zhou, W.-H.; Lee, C.-Y. Pricing and competition in a transportation market with empty equipment repositioning. Transp. Res. Part B Methodol. 2009, 43, 677–691. [Google Scholar] [CrossRef]
- Roso, V.; Woxenius, J.; Lumsden, K. The dry port concept: Connecting container seaports with the hinterland. J. Transp. Geogr. 2009, 17, 338–345. [Google Scholar] [CrossRef]
- Song, D.; Dong, J.-X. Long-haul liner service route design with ship deployment and empty container repositioning. Transp. Res. Part B Methodol. 2013, 55, 188–211. [Google Scholar] [CrossRef]
- Braekers, K.; Caris, A.; Janssens, G.K. Optimal shipping routes and vessel size for intermodal barge transport with empty container repositioning. Comput. Ind. 2013, 64, 155–164. [Google Scholar] [CrossRef]
- Wang, S. Essential elements in tactical planning models for container liner shipping. Transp. Res. Part B Methodol. 2013, 54, 84–99. [Google Scholar] [CrossRef]
- Chao, S.-L.; Chen, C.-C. Applying a time–space network to reposition reefer containers among major Asian ports. Res. Transp. Bus. Manag. 2015, 17, 65–72. [Google Scholar] [CrossRef]
- Zhao, H.; Zhang, C. An online-learning-based evolutionary many-objective algorithm. Inf. Sci. 2020, 509, 1–21. [Google Scholar] [CrossRef]
- Gholizadeh, H.; Fazlollahtabar, H.; Fathollahi-Fard, A.M.; Dulebenets, M.A. Preventive maintenance for the flexible flowshop scheduling under uncertainty: A waste-to-energy system. Environ. Sci. Pollut. Res. 2021, 28, 1–20. [Google Scholar] [CrossRef]
- Pasha, J.; Nwodu, A.L.; Fathollahi-Fard, A.M.; Tian, G.; Li, Z.; Wang, H.; Dulebenets, M.A. Exact and metaheuristic algorithms for the vehicle routing problem with a factory-in-a-box in multi-objective settings. Adv. Eng. Inform. 2022, 52, 101623. [Google Scholar] [CrossRef]
- Dulebenets, M.A. An Adaptive Polyploid Memetic Algorithm for scheduling trucks at a cross-docking terminal. Inf. Sci. 2021, 565, 390–421. [Google Scholar] [CrossRef]
- Rabbani, M.; Oladzad-Abbasabady, N.; Akbarian-Saravi, N. Ambulance routing in disaster response considering variable patient condition: NSGA-II and MOPSO algorithms. J. Ind. Manag. Optim. 2022, 18, 1035. [Google Scholar] [CrossRef]
- Holland, J. Adaptation in Natural and Artificial Systems: An Introductory Analysis with Application to Biology, Control and Artificial Intelligence; MIT Press: Cambridge, MA, USA, 1975. [Google Scholar]
- Radcliffe, N.J. Equivalence class analysis of genetic algorithms. Complex Syst. 1991, 5, 183–205. [Google Scholar]
- Inagaki, J.; Haseyama, M.; Kitajima, H. A genetic algorithm for determining multiple routes and its applications. In Proceedings of the 1999 IEEE International Symposium on Circuits and Systems (ISCAS), Orlando, FL, USA, 30 May–2 June 1999. [Google Scholar] [CrossRef]
- Glover, F. Future paths for integer programming and links to artificial intelligence. Comput. Oper. Res. 1986, 13, 533–549. [Google Scholar] [CrossRef]
- Sterzik, S.; Kopfer, H.; Yun, W.-Y. Reducing hinterland transportation costs through container sharing. Flex. Serv. Manuf. J. 2015, 27, 382–402. [Google Scholar] [CrossRef]
- Belayachi, N.; Gelareh, S.; Yachba, K.; Bouamrane, K. The Logistic of Empty Containers′ Return in the Liner-Shipping Network. Transp. Telecommun. J. 2017, 18, 207–219. [Google Scholar] [CrossRef][Green Version]
| Transpacific | Europe to Asia | Transatlantic | ||||
|---|---|---|---|---|---|---|
| Year | Asia–North America | North America–Asia | Europe–Asia | Asia–Europe | North America–Europe | Europe–America |
| 2019 | 19.9 | 6.8 | 7.2 | 17.5 | 2.9 | 4.9 |
| 2020 | 20.6 | 6.9 | 7.2 | 16.9 | 2.8 | 4.8 |
| 2021 | 24.1 | 7.1 | 7.8 | 18.5 | 2.8 | 5.2 |
| Percentage change 2020–2021 | 17.1 | 2.7 | 8.0 | 9.5 | 1.4 | 9.0 |
| Selection Criteria | Scientific Database | |
|---|---|---|
| Inclusion | Peer-reviewed research articles, conference proceedings papers, books, book chapters, review papers, short surveys, and serials mainly discuss the models and methods to solve the empty-container-movements problem. | |
| Exclusion | Before importation to a bibliographic manager | Non-English publications, articles with missing abstracts, notes, editorials |
| During title screening | Generic articles about empty-container movements are used as examples and/or future recommendations. | |
| During abstract screening | -Not related to the transportation field, e.g., safety management. -Articles address the new technologies of reusing empty containers. -Industry publications where outcomes are not relevant for analysis. | |
| During full-text screening | -Articles related to the environmental responsibilities and emissions measurement of empty-container movements. -Articles discussed the empty-container repositioning without describing specific applications. | |
| Year | Authors | Model | Solution Approach | Description |
|---|---|---|---|---|
| 1998 | Cheung and Chen [28] | A two-stage stochastic network | Quasi-gradient method | Evaluating the model over a rolling horizon environment |
| 2002 | Choong et al. [29] | Integer programming | Deterministic Dynamic Optimization | A case study of potential container-on-barge operations within the Mississippi River |
| 2005 | Olivo et al. [30] | Integer programming | A minimum cost flow problem | A Mediterranean region was examined as a case study by different modes of transportation. |
| 2007 | Shintani et al. [31] | Knapsack problem, then network flow problem | Genetic algorithm | Both port and ship-related cost factors were used in a non-linear cost function |
| 2007 | Lam et al. [32] | Dynamic stochastic programming | Approximate Dynamic Programming | The cost function is based on multi-port and multi-service system |
| 2007 | Wang and Wang [33] | Integer linear programming | LINGO | Inland transportation considers the container shortage and leasing costs |
| 2008 | Chang et al. [13] | Container substitution flow problem | Rounding LP-solution, branch and bound and CPLEX | Container substitution allows street turns |
| 2009 | Bandeira et al. [34] | Decision support system | LINDO | Mathematical programming techniques, stochastic models, simulation, and heuristic technique was integrated |
| 2009 | Di Francesco et al. [35] | Multi-commodity flow problems | Time-extended multi-scenario optimization model | A shipping company located in the Mediterranean region was examined |
| 2009 | Dong and Song [36] | Simulation-based Optimization | Genetic Algorithms and Evolutionary Strategies | The model includes multi-vessel, multi-port and multi-voyage shipping systems |
| 2010 | Shintani et al. [37] | An integer linear programming model | container flow mode | Foldable containers were considered |
| 2011 | Brouer et al. [38] | Relaxed linear multi-commodity flow model | Column generation algorithm | Real-life data from the largest liner shipping company, Maersk |
| 2011 | Meng and Wang [39] | Network design problem: mixed-integer linear programming model | CPLEX | Hub and spoke and multi-port-calling operations based on Asia–Europe–Oceania shipping network |
| 2011 | Choi et al. [40] | linear programming model | Time-expanded minimum-cost flow problem | Global shipping company in Korea used as a case study |
| 2012 | Long et al. [41] | A two-stage stochastic programming model | Sample Average Approximation | Scenario decomposition as considered |
| 2012 | Dang et al. [42] | Inventory control problem by the simulation model | Heuristics with genetic algorithm | The perspective of a container depot |
| 2012 | Dong and Song [11] | Cargo routing problem: Integer programming | Two-stage of shortest path and heuristics for an integer programming | An Asian shipping company with multiple service routes was examined as a case study |
| 2012 | Epstein et al. [8] | An inventory model and a multi-commodity network flow model | CPLEX | Consider multiple container types |
| 2013 | Moon et al. [25] | Three mathematical models and Two heuristics | A heuristic for an initial solution of small instances by using Lingo and using local search for improvement | Comparing standard and foldable containers based on costs |
| 2013 | Di Francesco et al. [43] | A stochastic programming approach | Time-extended multi-scenario/CPLEX | Non-anticipatively conditions were used to link scenarios |
| 2013 | Lai [44] | Time-space network | Integrating Branch and Bound with CPLEX for the multiple-scenarios situation | Data uncertainties for empty containers were used, such as capacity, handling, storage and transport |
| 2013 | Furio et al. [45] | Min-cost network flow optimization model | Decision Support System (DSS) | The model considered street-turn applications in the hinterland of Valencia |
| 2013 | Mittal et al. [46] | A two-stage stochastic programming model | Depot location problem in time horizon/CPLEX | New York/New Jersey port was selected as a case study for the model |
| 2013 | Dong et al. [47] | OD-based matrix solutions | Genetic algorithm | Experiments on three shipping service routes operated by three shipping companies |
| 2014 | Jansen [48] | Integer programming formulation/The flow network | CPLEX | Solving problems with planning horizons and forecast |
| 2015 | Huang et al. [49] | Mixed-integer programming model | CPLEX | A case study: Asia-Europe-Oceania shipping network |
| 2015 | Wong et al. [50] | Constrained linear programming | Shipment yield network driven-based model | A case study of service routes of Trans-Pacific trade operated in the G6 alliance |
| 2015 | Zheng et al. [51] | Two-stage optimization method | Centralised Optimization then Inverse Optimization | Experiments on an Asia–Europe–Oceania shipping service network |
| 2016 | Zheng et al. [52] | Network design: mixed-integer non-linear model | CPLEX | Considered perceived container and leasing prices |
| 2016 | Sainz Bernat et al. [53] | Simulation models with metaheuristic | Discrete-event simulation and genetic algorithm | Pollution, repair, and street turns are in the context of model |
| 2016 | Akyüz and Lee [54] | Mixed-integer linear programming model | b-column generation and ranch and bound algorithm | Simultaneous service type assignment and container routing problem were solved |
| 2017 | Monemi and Gelareh [55] | Integrated modelling framework: mixed-integer linear programming | Branch, Cut and Benders Algorithm (BCB) | The transhipment decision was considered |
| 2017 | Wang et al. [56] | A revised simplex algorithm | Network flow model | Foldable containers were included |
| 2017 | Xie at al. [57] | A game-theoretical: Inventory sharing game | Nash equilibrium | Intermodal transportation system consists of one rail firm and one-liner carrier |
| 2017 | Benadada and Razouk [58] | Optimization-simulation | Arena software | A real case study of the container terminal at Tanger Med port was applied |
| 2018 | Belayachi et al. [59] | A heuristic method by neighbourhood. | A decision-making/Taboo Search method. | Reverse logistics of containers |
| 2019 | Zhang et al. [60] | Two-layer collaborative optimization model | CPLEX and Genetic Algorithm | Combined tactical and operational levels based on business flow |
| 2019 | Xing et al. [61] | Simulation-based two-stage Optimization | Dynamic planning horizon and Genetic Algorithm | The quotation-booking process is included in operations decisions |
| 2019 | Hosseini and Sahlin [62] | A multi-period uncertainty optimization model | Chance constrained programming | A case study of European logistic service provider |
| 2019 | Gusah et al. [63] | Simulation modelling by agent-based modelling | AnyLogic | A case study of Melbourne, Australia |
| 2020 | Göçen et al. [64] | Two mathematical programming models | Mixed-integer linear programming and scenario-based stochastic programming | Real data taken from a liner carrier company include different types of containers |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Abdelshafie, A.; Salah, M.; Kramberger, T.; Dragan, D. Repositioning and Optimal Re-Allocation of Empty Containers: A Review of Methods, Models, and Applications. Sustainability 2022, 14, 6655. https://doi.org/10.3390/su14116655
Abdelshafie A, Salah M, Kramberger T, Dragan D. Repositioning and Optimal Re-Allocation of Empty Containers: A Review of Methods, Models, and Applications. Sustainability. 2022; 14(11):6655. https://doi.org/10.3390/su14116655
Chicago/Turabian StyleAbdelshafie, Alaa, May Salah, Tomaž Kramberger, and Dejan Dragan. 2022. "Repositioning and Optimal Re-Allocation of Empty Containers: A Review of Methods, Models, and Applications" Sustainability 14, no. 11: 6655. https://doi.org/10.3390/su14116655
APA StyleAbdelshafie, A., Salah, M., Kramberger, T., & Dragan, D. (2022). Repositioning and Optimal Re-Allocation of Empty Containers: A Review of Methods, Models, and Applications. Sustainability, 14(11), 6655. https://doi.org/10.3390/su14116655






