Bi-Level Planning Model for Urban Energy Steady-State Optimal Configuration Based on Nonlinear Dynamics
Abstract
1. Introduction
2. Literature Review
- (1)
- The basic structure of an urban energy system is built. Considering the substitution relationship between different energy forms, a bi-level optimization model of multi- energy comprehensive planning and steady-state configuration of urban energy system is proposed.
- (2)
- A four-dimensional nonlinear urban energy system model with coal as the main source and diversified development of natural gas, petroleum, and renewable energy is established, and the stability of nonlinear system solutions and Lyapunov’s theorem are applied to analyze the steady-state relationship of multiple energy sources and find out the demand for each energy source in the steady state of the urban energy system.
- (3)
- An urban energy system planning model is developed. Based on the steady-state relationship of multiple energy sources, the second-level planning model focuses on the energy planning configuration of the urban energy system in the steady state, to achieve the minimization of the construction and operation costs of the urban energy system, and as pollutant emissions petroleum.
3. Model of Bi-Level Programming
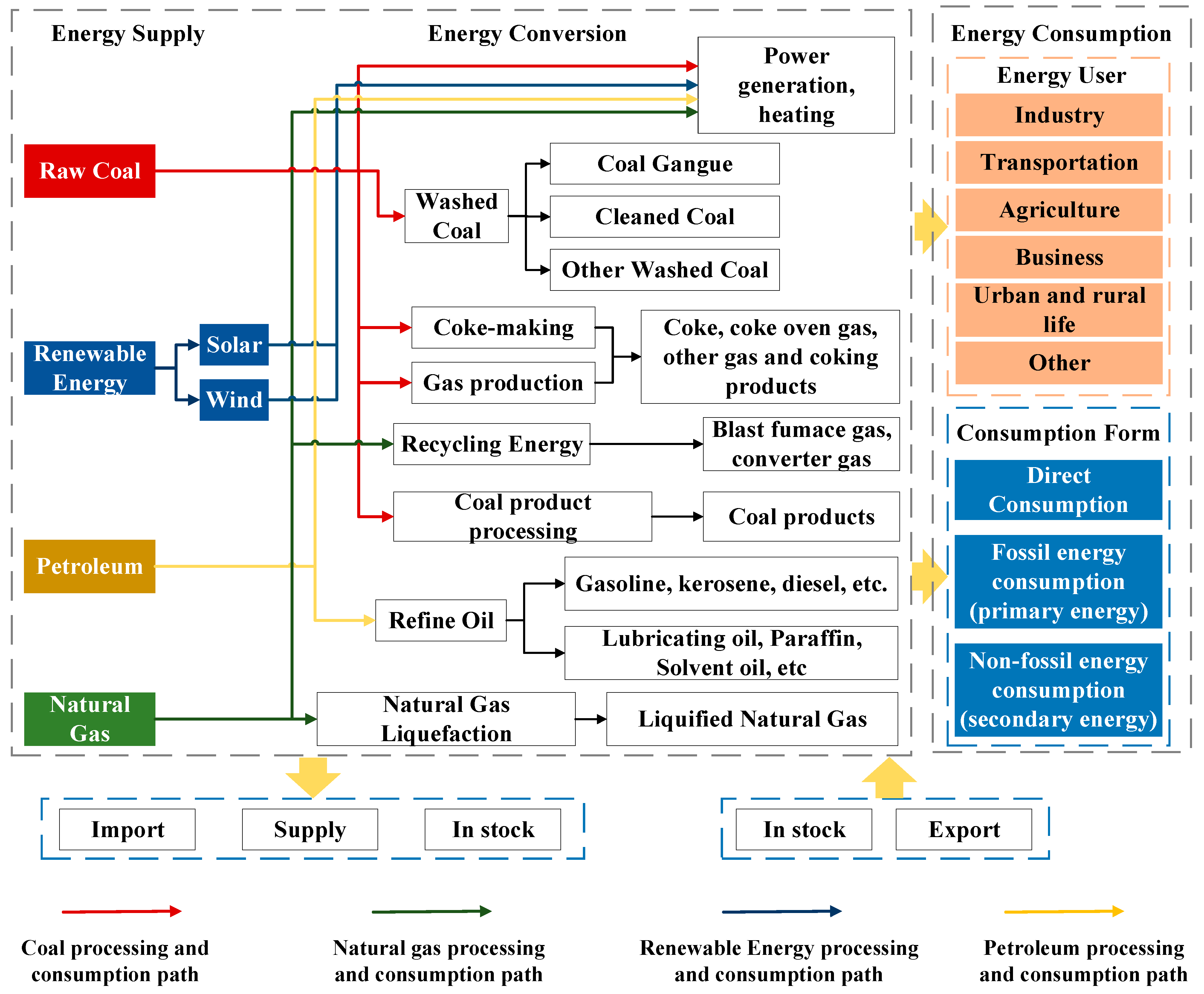
3.1. Four-Dimensional Nonlinear Urban Energy System Model of the First Level
3.2. Urban Energy System Planning Model of the Second Level
3.2.1. Objective Function
- Economic model
- 2.
- Environmental model
3.2.2. Constraint Conditions
- Energy supply and demand balance constraint
- 2.
- Energy exploitation capacity constraint
- 3.
- Technical capacity constraint
- 4.
- Energy planning policy constraint
- 5.
- Environmental constraint
3.3. Model Solving Method
3.3.1. Solution of the First Level Based on Nonlinear System Dynamics
- Dissipative analysis
- 2.
- Balance point stability
- (1)
- For the balance point S1(0, 0, 0), the coefficient matrix of the linear approximation system is
- (2)
- For the balance point S2 (x2, y2, z2)
- (3)
- For the balance point S3(x3, y3, z3)
3.3.2. Solution of the Second Level Based on IMFO
- Dynamic inertia weights [30]
- 2.
- Gaussian variation mechanism [31]
- 3.
- Corsi variant strategy [32]
- (1)
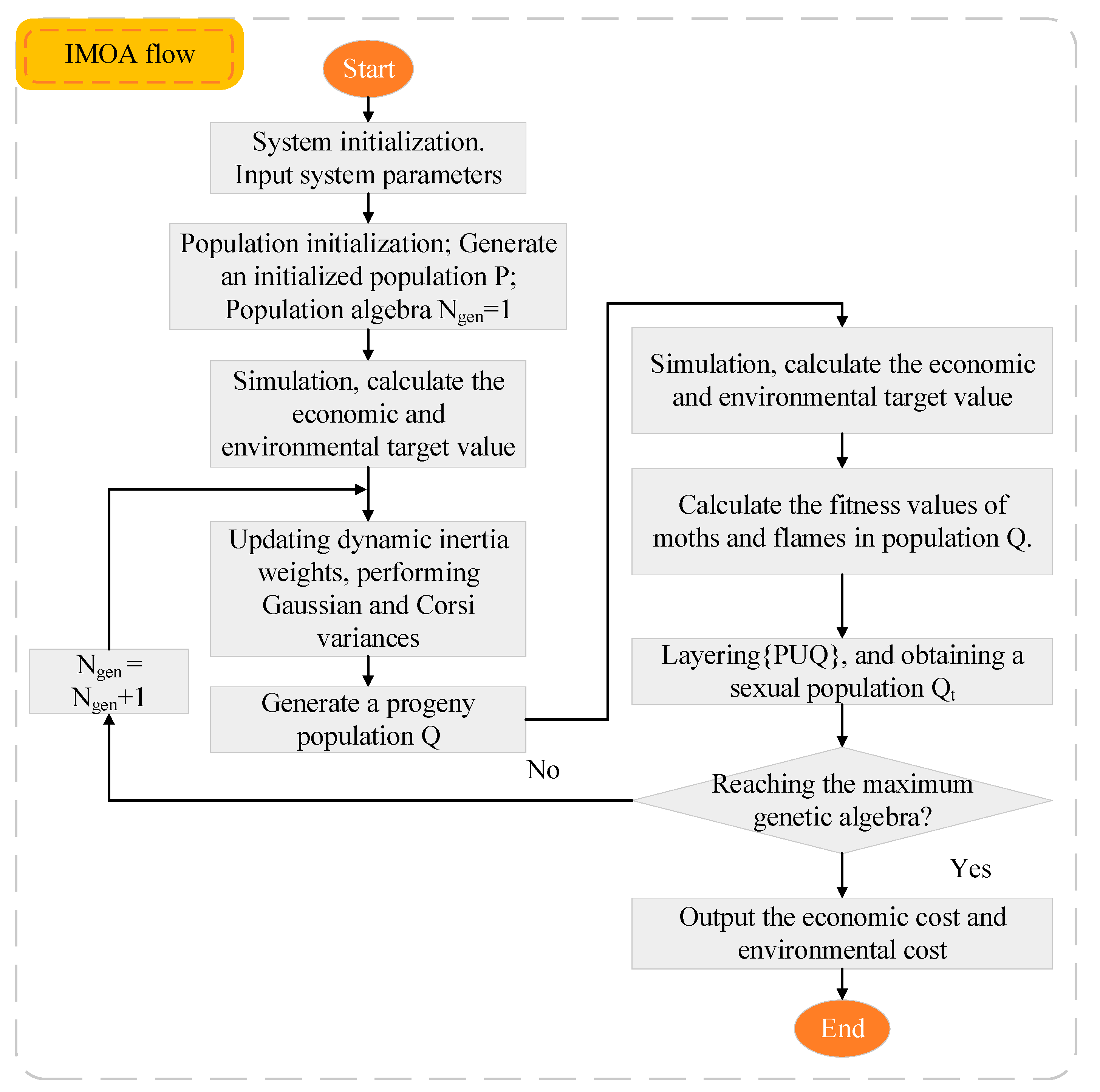
- System initialization. Input system parameters: energy system steady-state coefficients, energy demand, energy prices, pollutant emissions, and environmental cost factors, etc.
- (2)
- Population initialization. Generate the initialized population P; population algebra , t = 1.
- (3)
- Simulation. Calculation of economic and environmental target values.
- (4)
- Location update. Updating dynamic inertia weights, performing Gaussian and Corsi variances, and generating offspring population Q.
- (5)
- Simulation calculation. Calculating the economic environmental target, artificial moth and artificial flame fitness values for population Q, and ranking them by fitness value.
- (6)
- Combination. Combining the current population P with the offspring population Q to obtain a population, calculating the dominance relationship and aggregation distance of each individual according to the fitness function, and Pareto ranking the individuals.
- (7)
- Termination condition. Judge the termination condition; if the termination condition is satisfied, output the optimal solution, economic cost, and environmental cost, otherwise, return to step 4.
4. Simulation
4.1. Parameters
- Input parameters of the first level
- 2.
- Input parameters of the second level
4.2. The First Level Simulation
- Determination of parameters of the nonlinear system a1 and M
- 2.
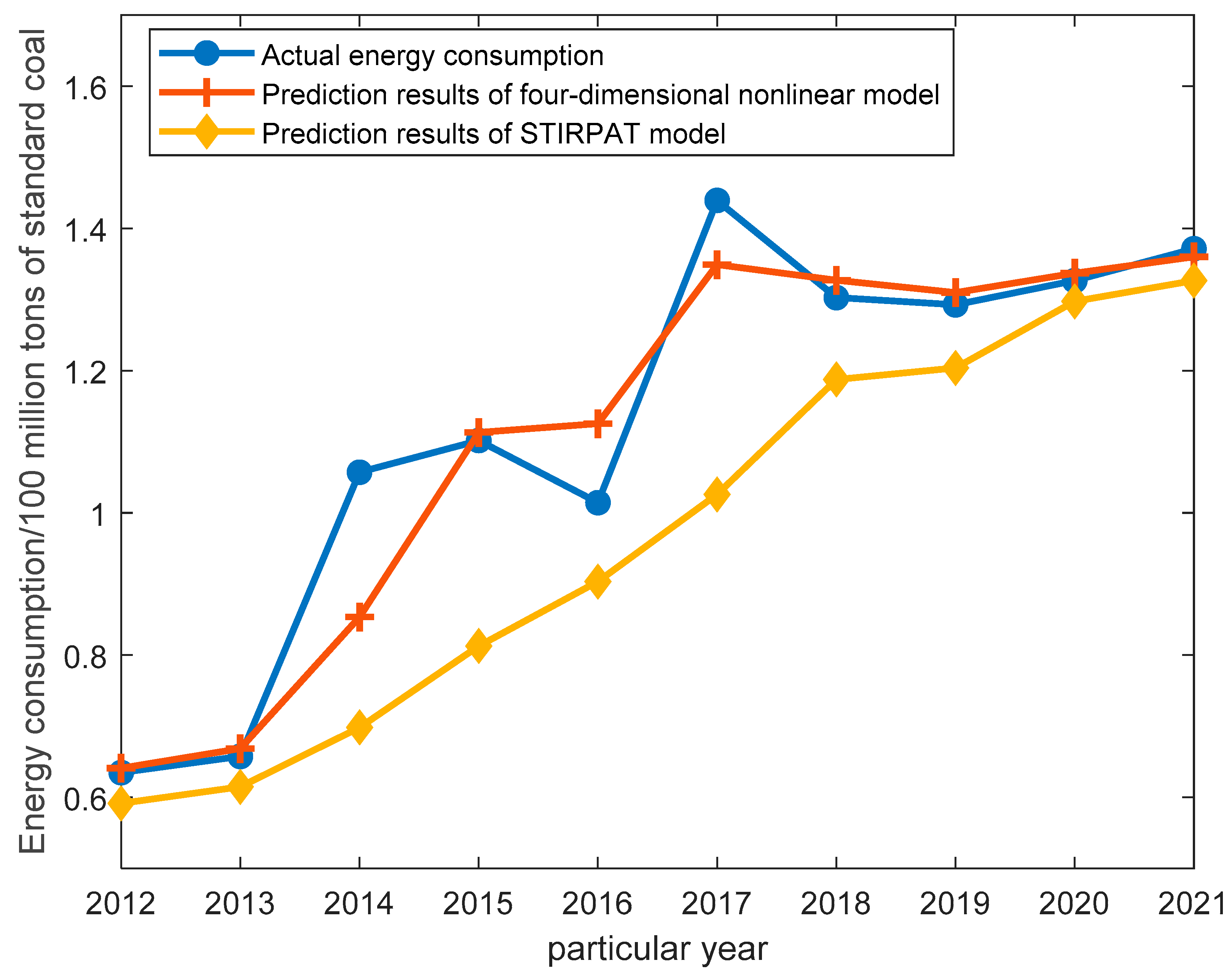
- Identification and determination of other nonlinear system parameters
4.3. The Second Level Simulation
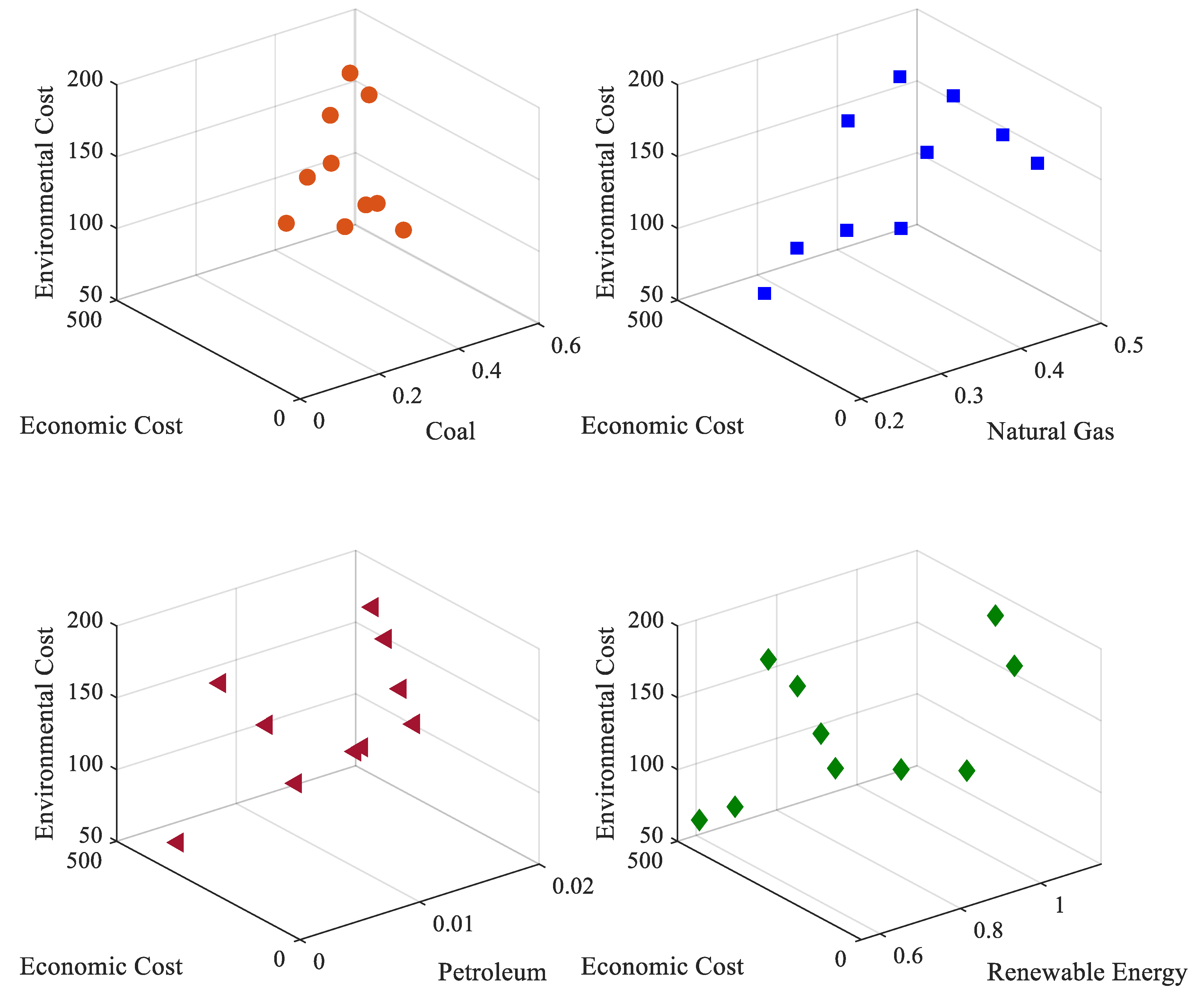
4.4. Analysis Results and Discussion
4.4.1. The First Type of Planning Schemes
4.4.2. The Second Type of Planning Schemes
4.4.3. Sub-Scenario Discussion
- Scenario Ⅰ: 10% increase in coal planning
- 2.
- Scenario II: 10–20% reduction in coal planning
- 3.
- Scenario Ⅲ: 20% reduction in coal planning
4.4.4. Recommendation
5. Conclusions
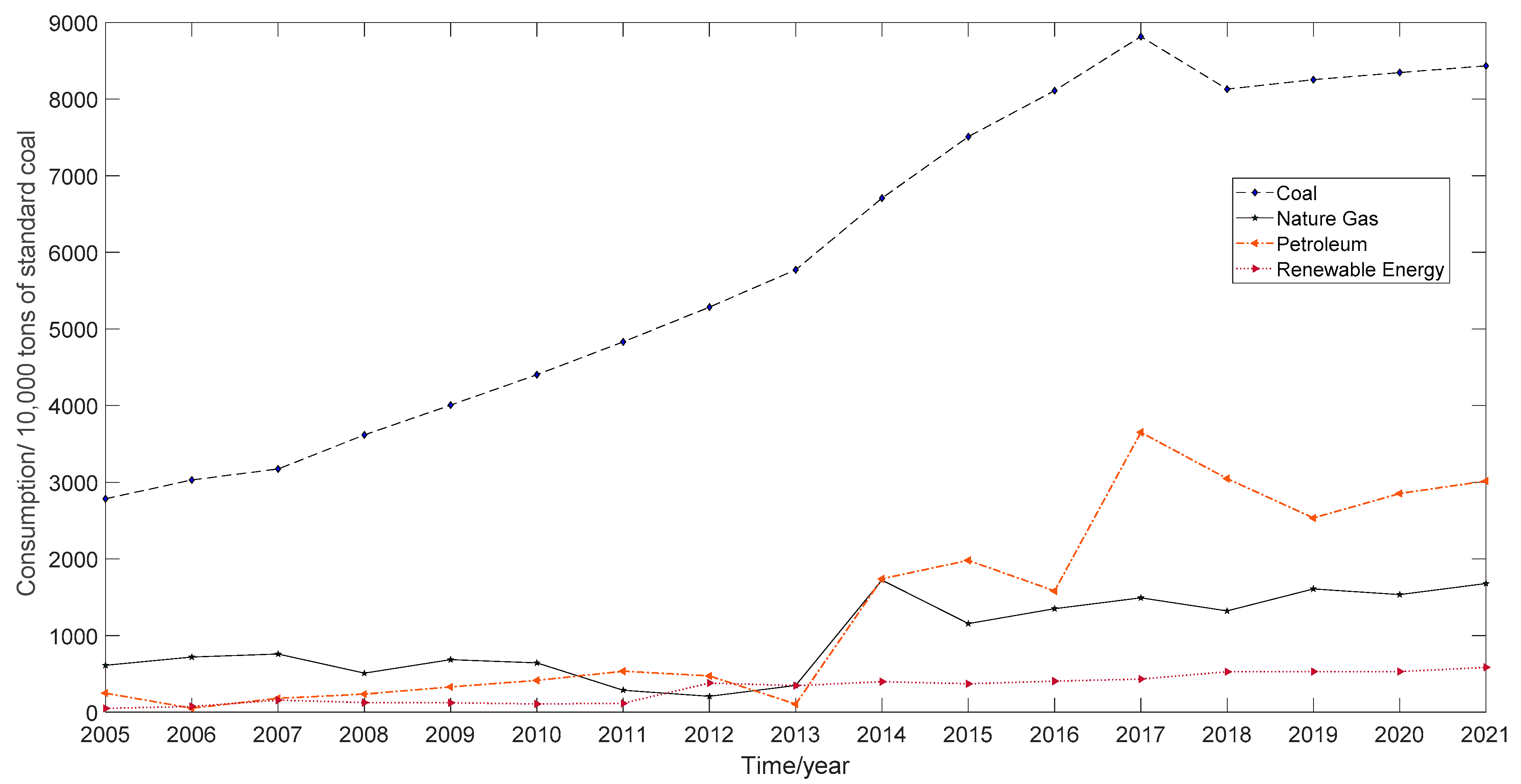
- In order to reduce energy consumption and optimize the urban energy structure, an urban energy steady-state model based on nonlinear system dynamics was developed on the basis of competing systems, and the relationship between coal, natural gas, petroleum, and renewable energy was studied. We used the consumption of coal, petroleum, natural gas, and renewable energy in certain region of China during 2005–2021 as the base data. It was found that the urban energy system could maintain a steady state when the parameters were as shown in Table 5. Compared with the method used in literature [24] to solve for the stability of urban energy systems, literature [24] considers more external factors related to energy usage (population size, affluence, etc.), while the method proposed in this paper is directly related to the endogenous factors of each type of energy (usage, elasticity coefficient, etc.), and the error with the actual data is 61.68% lower than that of literature [24].
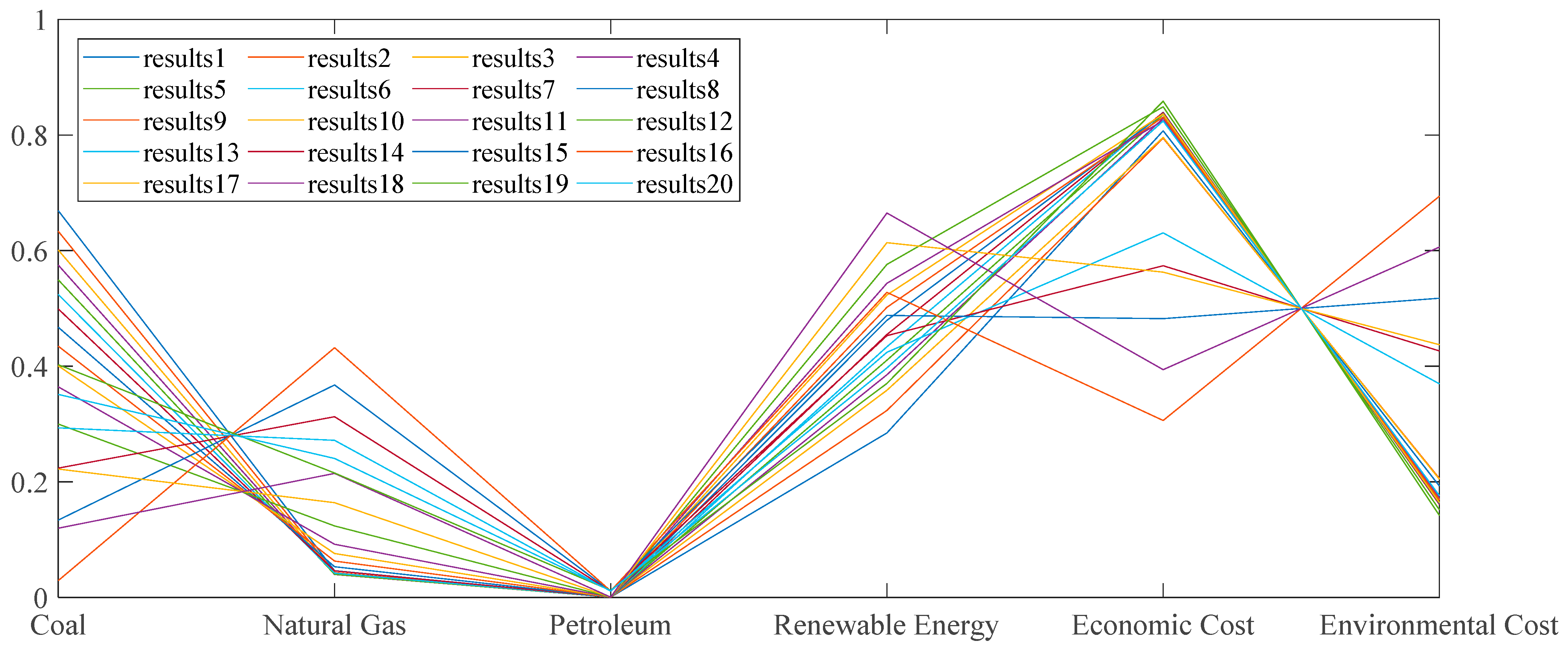
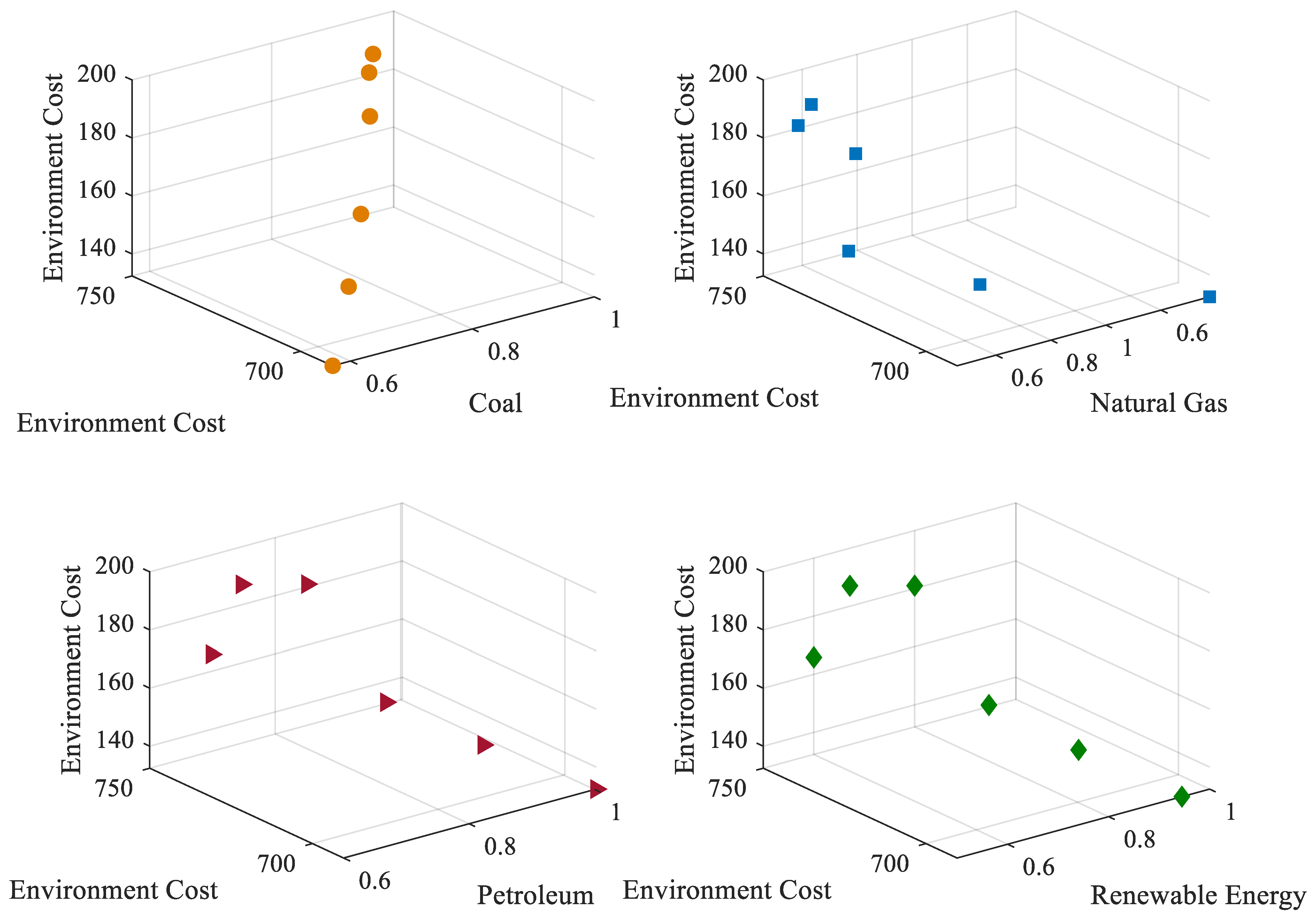
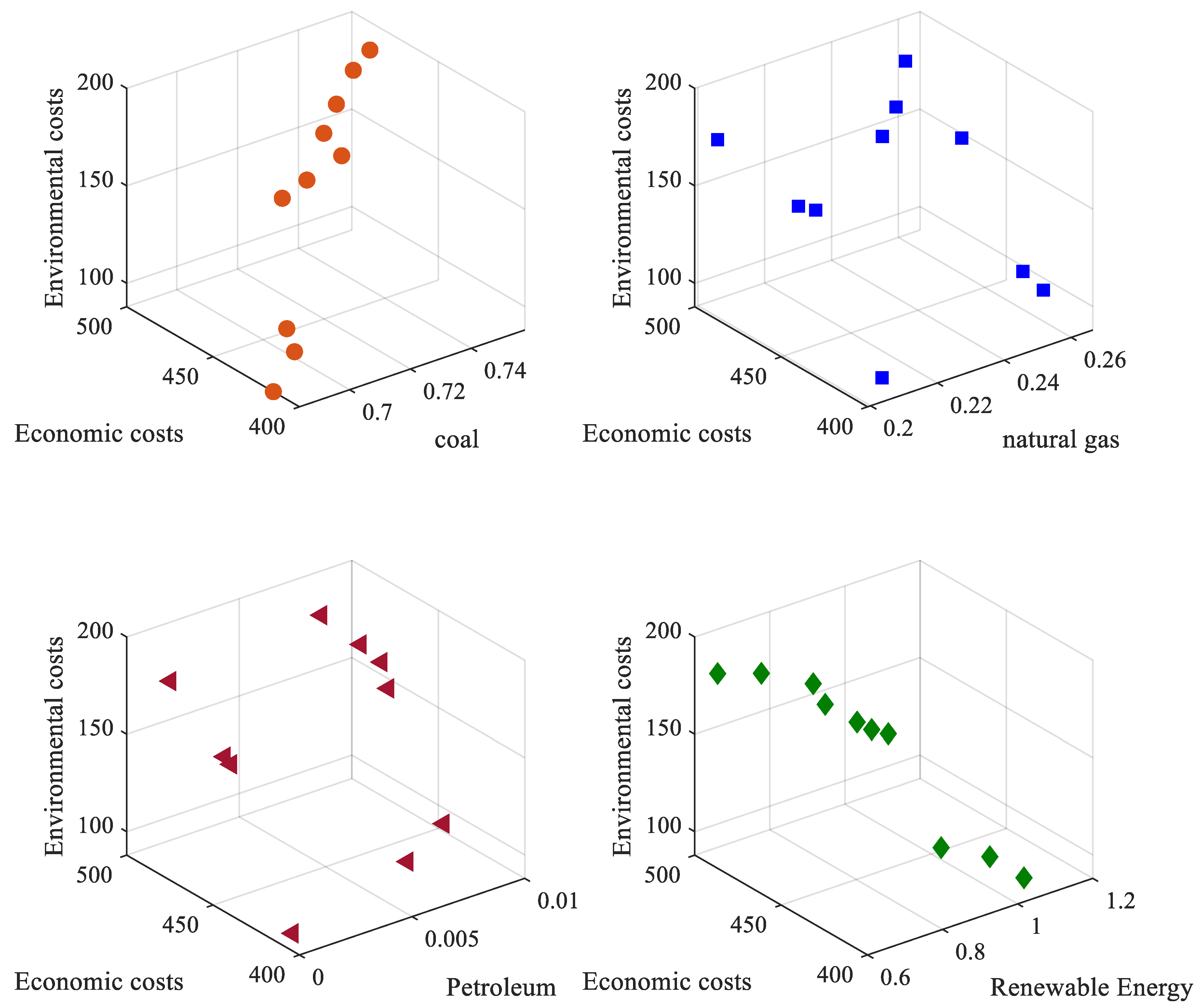
- An optimization model for urban energy planning is proposed and solved using the IMFO algorithm. A comparison of the algorithms revealed that the improved algorithm in this paper finds the optimal solution faster than the original method, and that the feasible solutions are found to fall into two categories, coal-based and high- quality energy. The research found that in the coal-based scheme, petroleum and natural gas are the most sensitive factors related to the target cost. In the high-quality energy-based scheme, the relationship between the planned amount of natural gas and the target cost is not sensitive, and there is no strong correlation between renewable energy and target cost. Overall, without adding the constraint of coal energy consumption, where the smaller the share of coal is, the lower the cost.
- On the basis of the two-layer planning model for the optimal allocation of urban energy steady-state, the constraints of 10% increase, 10–20% reduction, and more than 20% reduction in the future planned coal volume were added, respectively, and the energy system of the region was carried out. In Scenario Ⅰ, we found that the results were basically consistent with the results of the coal-based scheme, but when the natural gas consumption exceeded 10,000 tons, the natural gas consumption was not a sensitive factor. In Scenario II, we found that coal had a strong substitution relationship with renewable energy. In Scenario Ⅲ, we found that only coal consumption maintained a relatively consistent linear relationship with the total target cost, however, the consumption of other energy sources could not fit a strong correlation with the total cost target. Through planning and simulation, it was found that the reduction of coal consumption should be carried out gradually (within 10%). If the coal consumption is suddenly reduced, the correlation between various energy sources and the target cost cannot be fitted, which will affect the urban energy stability to a certain extent.
- Although the above research results are presented in this paper, there are still some limitations. For example, in terms of modeling, the first-level model proposed in this paper is applicable to energy system stability prediction, and the solutions in this paper can actually find rigorous solutions mathematically, but there are also elements of trial, so the solutions obtained may only reflect part of the situation. However, they are still strictly analytical solutions and have their important theoretical value. At the same time, the second-level planning model can only solve planning usage problems for petroleum, coal, natural gas, and renewable energy, not practical operational problems. In terms of practical applications: this paper only examined the steady-state results and planning scenarios for urban energy systems. However, if planners want to achieve an optimal planning state for urban energy, city managers need to manage it through various macro-regulation means (e.g., giving clean energy subsidies through economic means, limiting coal consumption through policies, etc.), which requires follow-up research by scholars.
Author Contributions
Funding
Conflicts of Interest
Nomenclature
| A. Acronyms | |
| IMFO | Improved Moth–Flame Optimization Algorithm |
| MINLP | Mixed integer nonlinear programming |
| GAMS | General algebraic modeling system |
| BP neural network | Back propagation neural network |
| EDFS | Energy demand forecasting system |
| ENA | Ecological network analysis |
| LCA | Life cycle assessment |
| MFO | Moth–Flame Optimization |
| PSO-LSSVR | Least-squares support-vector regression optimized by particle swarm optimization |
| CCHP | Combined cooling, heating, and power |
| B. Parameters | |
| the consumption of coal, petroleum, natural gas, and renewable energy under the constraints of each indicator when the urban energy system is in a stable state | |
| the coal consumption | |
| the coal consumption | |
| the petroleum consumption | |
| the consumption of renewable energy (mainly including wind and photovoltaic) | |
| the consumption elasticity coefficient of coal | |
| the consumption elasticity coefficient of natural gas | |
| the consumption elasticity coefficient of petroleum | |
| the consumption elasticity coefficient of renewable energy | |
| the influence coefficient of petroleum and natural gas on coal | |
| the influence coefficient of coal on natural gas in the energy system | |
| the price per unit of coal in the energy system | |
| the influence coefficient of coal, petroleum, and natural gas on renewable energy in the energy system | |
| the clean coal technology cost in the energy system | |
| the influence coefficient of renewable energy on coal in the energy system | |
| the maximum energy gap | |
| the threshold of environmental pollution in the energy system | |
| the total cost of the urban energy system | |
| the energy supply cost | |
| the energy conversion cost | |
| the different period of the planning period | |
| the price of coal during the period t | |
| the price of natural gas during the period t | |
| the price of petroleum during the period t | |
| the price of renewable energy during the period t | |
| the supply of coal during the period t | |
| the supply of natural gas during the period t | |
| the supply of petroleum during the period t | |
| the supply of renewable energy during the period t | |
| local power generation technology (power generation technology includes coal power, gas power generation, wind power, solar power generation, etc.) | |
| the operating cost of local power generation technology k during the period t | |
| the power generation capacity of local power generation technology k during the period t | |
| the new capacity of local power generation technology k during the period t | |
| the unit investment cost of the new capacity of local power generation technology k during the period t | |
| the environmental cost | |
| the environmental value of the pollutant | |
| the pollutant emissions | |
| the penalty cost due to excessive emissions | |
| the cost of ecological restoration | |
| the amount of production for energy n during the period t | |
| the amount of purchase for energy n during the period t | |
| the amount of consumption for energy n during the period t | |
| the amount of forecast demand for energy n during the period t | |
| the upper limit of the production capacity of energy n during the period t | |
| the upper limit of the installed capacity of local power generation technology k during the period t | |
| the average annual running time of local power generation technology k during the period t | |
| energy conversion technology update rate | |
| the upper limit of the supply capacity of energy n controlled in the government energy planning document during the period t | |
| the maximum allowable emissions specified by environmental policy | |
References
- Webb, J.; Hawkey, D.; Tingey, M. Governing cities for sustainable energy: The UK case. Cities 2016, 54, 28–35. [Google Scholar] [CrossRef]
- Teng, Z.Y.; Zhang, Y.; Li, X. Energy Internet—Integration of Information and Energy Infrastructure. Inf. Commun. 2018, 10, 265–266. [Google Scholar]
- Mi, Z.F.; Guan, D.B.; Liu, Z.; Liu, J.R.; Vincent, V.; Neil, F.; Wang, Y.T. Cities: The core of climate change mitigation. J. Clean. Prod. 2019, 207, 582–589. [Google Scholar] [CrossRef]
- Yu, S.H.; Sun, Y.; Niu, X.N.; Zhao, C.H. Energy internet system based on distributed renew able energy generation. Electr. Power Autom. Equip. 2010, 30, 104–108. [Google Scholar]
- Grossman, G.M.; Krueger, A.B. Economic growth and the environment. Q. J. Econ. 1995, 110, 353–377. [Google Scholar] [CrossRef]
- Ji, P.; Zhou, X.X.; Song, Y.T.; Ma, S.Y.; Li, B.Q. Review and prospect of regional renew able energy planning models. Power Syst. Technol. 2013, 37, 2071–2079. [Google Scholar]
- Bo, P.; Xu, C.; Xu, Q.Y.; Zhang, N.; Kang, C.Q. Preliminary research on power grid planning method aiming at accommodating new energy. Power Syst. Technol. 2013, 37, 3386–3391. [Google Scholar]
- Liang, H.; Long, W.D. Research and Application of Urban Energy System Comprehensive Planning Model. J. Shandong Jianzhu Univ. 2010, 25, 524–528 +557. [Google Scholar]
- Yeo, I.A.; Yoon, S.H.; Yee, J.J. Development of an urban energy demand forecasting system to support environmentally friendly urban planning. Appl. Energy 2013, 110, 304–317. [Google Scholar] [CrossRef]
- Yang, Y.F.; Han, L.; Wang, Y.R.; Wang, J.Z.; Jafari, N.N. China’s Energy Demand Forecasting Based on the Hybrid PSO-LSSVR Model. Wirel. Commun. Mob. Comput. 2022, 2022, 1–12. [Google Scholar] [CrossRef]
- Xie, N.M.; Yuan, C.Q.; Yang, Y.J. Forecasting China’s energy demand and self-sufficiency rate by grey forecasting model and Markov model. Electr. Power Energy Syst. 2015, 66, 1–8. [Google Scholar] [CrossRef]
- Filippov, S.P.; Malakhov, V.A.; Veselov, F.V. Long-Term Energy Demand Forecasting Based on a Systems Analysis. Therm. Eng. 2021, 68, 881–894. [Google Scholar] [CrossRef]
- Wu, W.J.; Wu, J.K.; Lei, Z.; Zheng, M.J.; Zhang, Y.N.; Li, M.; Huang, X.; Li, Y.X. Energy demand prediction based on PSO Optimized BP neural network. Electr. Appl. 2021, 40, 49–58. [Google Scholar]
- Zhang, Y.M. Research on China’s Energy Demand Forecasting Based on Combination Model. Master’s Thesis, Yan’an University, Yan’an, China, 2021. [Google Scholar]
- Jing, R.; Kuriyan, K.; Lin, J.; Shah, N.; Zhao, Y.R. Quantifying the contribution of individual technologies in integrated urban energy systems—A system value approach. Appl. Energy 2020, 266, 1–15. [Google Scholar] [CrossRef]
- Chen, C.; Su, M.R.; Yang, Z.F.; Liu, G.Y. Evaluation of the environmental impact of the urban energy lifecycle based on lifecycle assessment. Front. Earth Sci. 2014, 8, 123–130. [Google Scholar] [CrossRef]
- Kagaya, S.; Ueda, M. An Evaluation on Improvement of the Urban Energy System in a Snowy Cold Region. Environ. Syst. Res. 2010, 23, 204–213. [Google Scholar] [CrossRef][Green Version]
- Xie, S.; Jia, Y.L.; Bai, X.T.; Zhang, Z.H.; Wang, S.Y.; Zheng, X.Y.; Zhao, Y.R. A review of urban energy system planning and design and energy consumption analysis tools. Glob. Energy Internet 2021, 4, 163–177. [Google Scholar]
- Zheng, X.Y.; Qiu, Y.W.; Zhan, X.Y.; Zhu, X.Y.; Keirstead, J.; Shah, N.; Zhao, Y.R. Optimization based planning of urban energy systems: Retrofitting a Chinese industrial park as a case-study. Energy 2017, 139, 31–41. [Google Scholar] [CrossRef]
- Neshat, N.; Hadian, H.; Alangi, S.R. Technological learning modelling towards sustainable energy planning. J. Eng. Des. Technol. 2020, 18, 84–101. [Google Scholar] [CrossRef]
- Yazdanie, M.; Orehounig, K. Advancing urban energy system planning and modeling approaches: Gaps and solutions in perspective. Renew. Sustain. Energy Rev. 2021, 137, 110607. [Google Scholar] [CrossRef]
- Su, M.R.; Chen, C.; Yang, Z.F. Urban energy structure optimization at the sector scale: Considering environmental impact based on life cycle assessment. J. Clean. Prod. 2016, 112, 1464–1474. [Google Scholar] [CrossRef]
- Wang, R.X.; Li, H.; Xing, M.B.; Xue, R.J. An approach to urban energy planning from the perspective of all-energy flow. Sci. Technol. Eng. 2019, 19, 365–370. [Google Scholar]
- Shen, M.; Shen, L.; Zhang, Y.; Liu, L.T.; Xue, J.J.; Chen, F.N. Analysis on stability and influencing factors of energy supply system in Shaanxi Province. Econ. Geogr. 2015, 35, 39–46. [Google Scholar]
- Li, A.M.; Zheng, H.M. Energy security and sustainable design of urban systems based on eco-logical network analysis. Ecol. Indic. 2021, 129, 1–10. [Google Scholar] [CrossRef]
- Zhu, X.T.; Mu, X.Z.; Hu, G.W. Ecological network analysis of urban energy metabolic system—A case study of Beijing. Ecol. Model. 2019, 404, 36–45. [Google Scholar] [CrossRef]
- Kazaoka, R. Nonlinear dynamics and stability of an electric power system with multiple homes. Ieice Tech. Rep. Non-Linear Probl. 2011, 111, 67–72. [Google Scholar]
- Zhao, H.S.; Xue, N.; Shi, N. Nonlinear Dynamic Power System Model Reduction Analysis Using Balanced Empirical Gramian. Appl. Mech. Mater. 2013, 448–453, 2368–2374. [Google Scholar] [CrossRef]
- Du, T.; Zeng, G.H.; Huang, B.; Wei, Y. PMSM vector control optimization based on improved moth-to-fire optimization algorithm. Sens. Microsyst. 2021, 40, 52–55. [Google Scholar]
- Long, W.; Jiao, J.J.; Zhang, W.Z.; Xu, M.; Cai, S.H. An Improved Moth Flame Optimization Algorithm for Solving High-Dimensional Global Optimization Problems. Pract. Underst. Math. 2020, 50, 153–163. [Google Scholar]
- Zhao, Q.; Mao, Q.H.; Liang, P. Research on location selection of electric vehicle charging station based on improved moth algorithm. J. Hunan Univ. Arts Sci. 2021, 33, 12–19. [Google Scholar]
- Qin, T.; Xiang, T.M.; Li, B.B. Optimization of Microstrip Antenna Design Based on Improved Moth to Fire Algorithm. J. Hangzhou Dianzi Univ. 2020, 40, 13–18. [Google Scholar]
- Ministry of Ecology and Environment of the People’s Republic of China. Measures for the Administration of Emission Fee Collection Standards. 2003. Available online: https://www.mee.gov.cn/ywgz/fgbz/gz/200302/t20030228_86250.shtml (accessed on 1 March 2022).
- Liu, F.; Guo, L.F.; Zhao, L.Z. Coal safety zone and green low-carbon technology path under the background of double carbon. J. Coal 2022, 47, 1–15. [Google Scholar]








| Ref. | Research Object | Bi-Level | Objectives | Solving Algorithm | Qualitative/Quantitative |
|---|---|---|---|---|---|
| [9] | Electricity, heat | No | Minimum urban electricity demand | Urban energy demand forecasting algorithm | Quantitative |
| [10] | Influencing factors of energy demand | No | Minimum system cost | PSO-LSSVR | Quantitative |
| [11] | Natural gas, crude petroleum | No | Minimum system cost | A novel Markov approach based on quadratic programming model | Quantitative |
| [12] | Electric demand | No | Minimum annual total cost | EDFS computing system | Quantitative |
| [13] | Coal, petroleum, gas, and electricity | No | Minimum system cost | Improved particle swarm optimization | Quantitative |
| [14] | Coal, petroleum, natural gas, and renewable energy | No | Minimum system cost | Multiple linear regression, BP neural network | Qualitative and quantitative |
| [15] | Urban energy value system | No | Minimum system cost | Mixed integer linear programming | Quantitative |
| [16] | Coal, petroleum, natural gas, electricity, renewable energy | No | Minimum system cost | Life cycle assessment | Quantitative |
| [17] | Urban energy system | No | Minimum system cost | Fuzzy utility function | Qualitative |
| [18] | urban energy system planning and design tools | No | / | / | Qualitative |
| [19] | Urban energy equipment configuration planning | No | Minimum system cost | MINLP model and GAMS | Quantitative |
| [20] | Electricity | No | Maximum economic benefits | Technology learning mechanism | Quantitative |
| [21] | Urban energy system planning and modeling approaches | No | / | / | Qualitative |
| [22] | Coal, petroleum, natural gas, and electricity, | No | Minimum total energy cost, environmental impact, and total energy use | Life cycle assessment | Quantitative |
| [23] | Urban energy system | No | Maximum economic benefits | Hamiltonian directed graph | Qualitative and quantitative |
| [24] | Energy supply stability | No | Maximum urban energy system stability | Ridge regression analysis | Qualitative and quantitative |
| [25] | Urban energy system | No | / | Ecological network analysis | Qualitative and quantitative |
| [26] | Raw coal, coal products, and natural gas | No | / | Improved ecological network analysis framework | Qualitative and quantitative |
| [27] | Electric power system | No | / | Nonlinear dynamics | Qualitative |
| [28] | Power systems | No | / | Balanced empirical Gramian | Qualitative |
| This paper | Coal, petroleum, natural gas, and renewable energy | Yes | Minimum economic costs and environmental cost | Nonlinear system dynamics and IMFO | Qualitative and quantitative |
| Energy | Price |
|---|---|
| Coal (yuan/t standard coal) | 839.98 |
| Petroleum (yuan/t standard coal) | 3009.04 |
| Natural Gas (yuan/t standard coal) | 2701.15 |
| Renewable Energy (yuan/t standard coal) | Wind: 1410.89 Solar: 1856.44 |
| Pollutants | SO2 | NOx | CO2 | CO | |
|---|---|---|---|---|---|
| Emission | Coal (kg/t) | 18 | 8 | 1731 | 0.26 |
| Natural Gas (kg/106m3) | 11.6 | 0.0062 | 2.01 | 0 | |
| Petroleum (kg/t) | 12 | 10.1 | 1592 | 0.33 | |
| Environmental value (yuan/kg) | 6.00 | 8.00 | 0.023 | 1.00 | |
| M | 1.1 | 1.2 | 1.3 | 1.4 | 1.5 | 1.6 | 1.7 | 1.8 |
|---|---|---|---|---|---|---|---|---|
| R2 | 0.81503 | 0.845683 | 0.916619 | 0.855389 | 0.993331 | 0.995554 | 0.99678 | 0.996837 |
| −1.174 | −0.791 | −0.5343 | −0.9564 | −0.1711 | −0.0312 | 0.0911 | 0.1253 | |
| 0.1081 | 0.0778 | 0.0636 | 0.1333 | 0.0496 | 0.0456 | 0.0426 | 0.0466 |
| 0.0466 | 0.15 | 0.06 | 0.082 | 0.06 | 0.2 | 0.5 | 0.4 | 0.1 | 0.06 | 0.13 | 1.8 | 1 |
| No. | Coal (10,000 Tons of Standard Coal) | Natural Gas (10,000 Tons of Standard Coal) | Petroleum (10,000 Tons of Standard Coal) | Renewable Energy (10,000 Tons of Standard Coal) | Economic Cost (Billion Yuan) | Environmental Cost (Billion Yuan) |
|---|---|---|---|---|---|---|
| 1 | 0.602982133 | 0.322441807 | 0.018182392 | 0.554282462 | 441.3970003 | 72.76593041 |
| 2 | 0.531510779 | 0.363596454 | 0.017329108 | 0.600545082 | 395.0105866 | 84.32441609 |
| 3 | 1.223222143 | 0.084486551 | 0.000717157 | 0.520514905 | 737.6377162 | 176.0332609 |
| 4 | 1.23253118 | 0.083563165 | 0.000756146 | 0.629394813 | 743.4596253 | 192.4520151 |
| 5 | 1.225144883 | 0.082584003 | 0.000797321 | 0.730605559 | 739.2684847 | 189.8653556 |
| 6 | 1.207153448 | 0.083162826 | 0.000832799 | 0.809391871 | 728.6800754 | 150.5531197 |
| 7 | 1.179411369 | 0.086001846 | 0.000867776 | 0.881071872 | 712.2418522 | 140.2292337 |
| 8 | 1.142718874 | 0.091766228 | 0.000901193 | 0.945140393 | 690.4312409 | 132.3944984 |
| 9 | 1.097732662 | 0.100890899 | 0.000931912 | 1.001174452 | 663.6385144 | 127.3137253 |
| 10 | 1.031886602 | 0.11698691 | 0.000964226 | 1.058524505 | 624.3604742 | 121.5998734 |
| 11 | 0.955122458 | 0.138414925 | 0.00098856 | 1.102813626 | 578.5061408 | 117.4752378 |
| 12 | 0.431885409 | 0.400346589 | 0.016227261 | 0.624552446 | 330.6338092 | 193.6766361 |
| 13 | 0.307915537 | 0.430287245 | 0.014855649 | 0.623654008 | 250.4515677 | 186.1370679 |
| 14 | 0.030632606 | 0.452986089 | 0.011700065 | 0.553422303 | 70.5408957 | 159.933346 |
| 15 | 0.163769308 | 0.449337899 | 0.013225338 | 0.59653623 | 156.9980795 | 168.4352068 |
| 16 | 0.187650579 | 0.336434923 | 0.000835972 | 1.042430204 | 117.9765388 | 181.4745739 |
| 17 | 0.771152721 | 0.194787951 | 0.001005602 | 1.150942565 | 468.4142455 | 99.45308016 |
| 18 | 0.598403545 | 0.246772582 | 0.00098234 | 1.150005826 | 364.8346072 | 65.09821296 |
| 19 | 0.868065361 | 0.16467288 | 0.001002937 | 1.133707255 | 526.4402196 | 103.1215876 |
| 20 | 0.403222837 | 0.297291733 | 0.0009248 | 1.113912957 | 247.6206412 | 192.4216718 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, Y.; Liu, C.; Cai, C.; Ma, Z.; Zhou, M.; Dong, H.; Li, F. Bi-Level Planning Model for Urban Energy Steady-State Optimal Configuration Based on Nonlinear Dynamics. Sustainability 2022, 14, 6485. https://doi.org/10.3390/su14116485
Wang Y, Liu C, Cai C, Ma Z, Zhou M, Dong H, Li F. Bi-Level Planning Model for Urban Energy Steady-State Optimal Configuration Based on Nonlinear Dynamics. Sustainability. 2022; 14(11):6485. https://doi.org/10.3390/su14116485
Chicago/Turabian StyleWang, Yongli, Chen Liu, Chengcong Cai, Ziben Ma, Minhan Zhou, Huanran Dong, and Fang Li. 2022. "Bi-Level Planning Model for Urban Energy Steady-State Optimal Configuration Based on Nonlinear Dynamics" Sustainability 14, no. 11: 6485. https://doi.org/10.3390/su14116485
APA StyleWang, Y., Liu, C., Cai, C., Ma, Z., Zhou, M., Dong, H., & Li, F. (2022). Bi-Level Planning Model for Urban Energy Steady-State Optimal Configuration Based on Nonlinear Dynamics. Sustainability, 14(11), 6485. https://doi.org/10.3390/su14116485






