Green Construction Grade Evaluation of Large Channels Based on Uncertain AHP-Multidimensional Cloud Model
Abstract
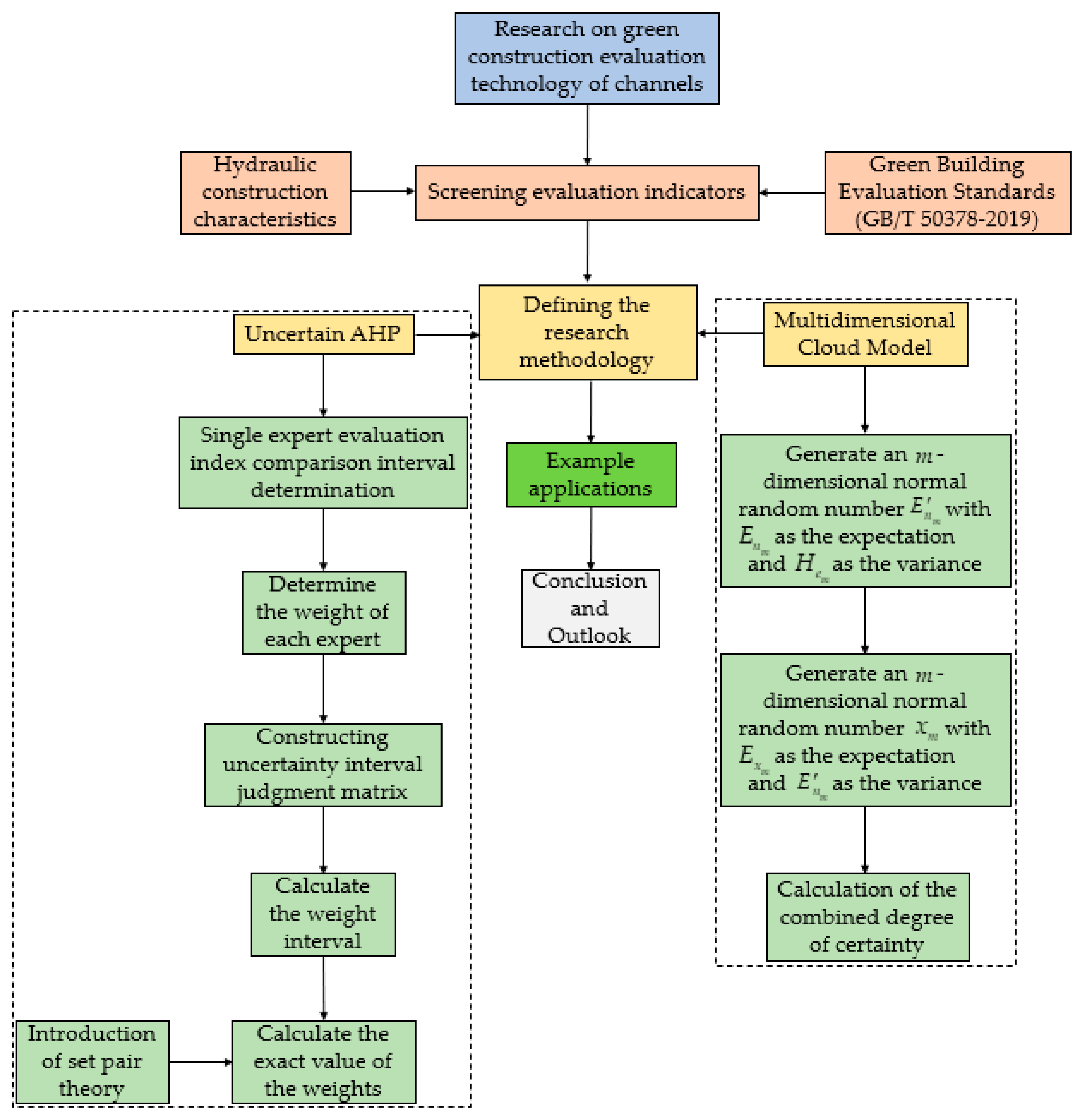
:1. Introduction
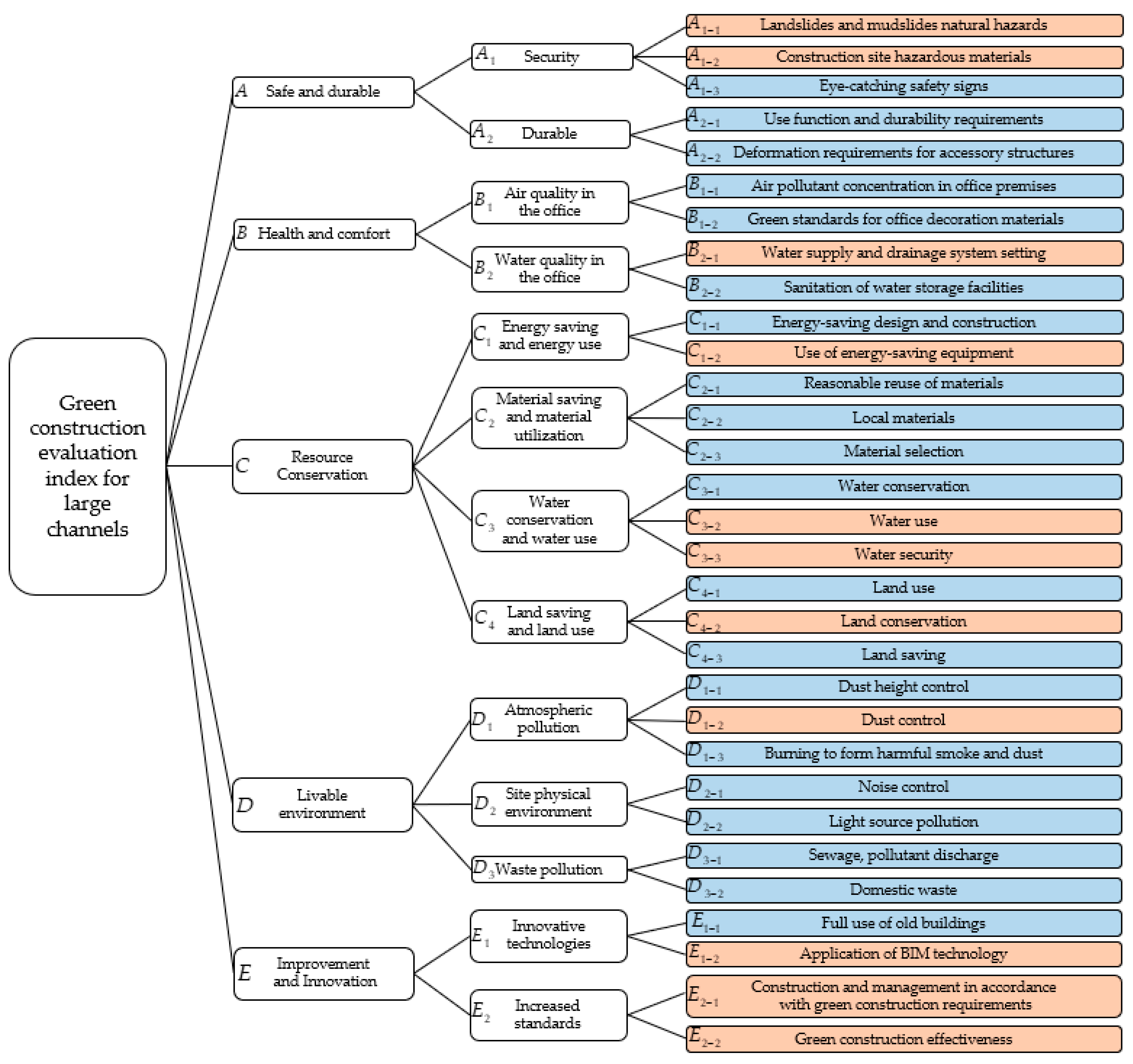
2. Selection of Evaluation Indicators
3. Rating Method
3.1. Uncertain AHP
- (1)
- Determine the comparison interval of evaluation indicators for individual experts
- (2)
- Determination of expert weights
- (3)
- Construction of uncertainty interval judgment matrix
- (4)
- Calculation of the weight interval
- (5)
- Calculate the weight value
3.2. Multidimensional Linked Normal Cloud Model
- (1)
- Concept of multidimensional cloud model
- (2)
- Determination of numerical features of multidimensional cloud models
- (3)
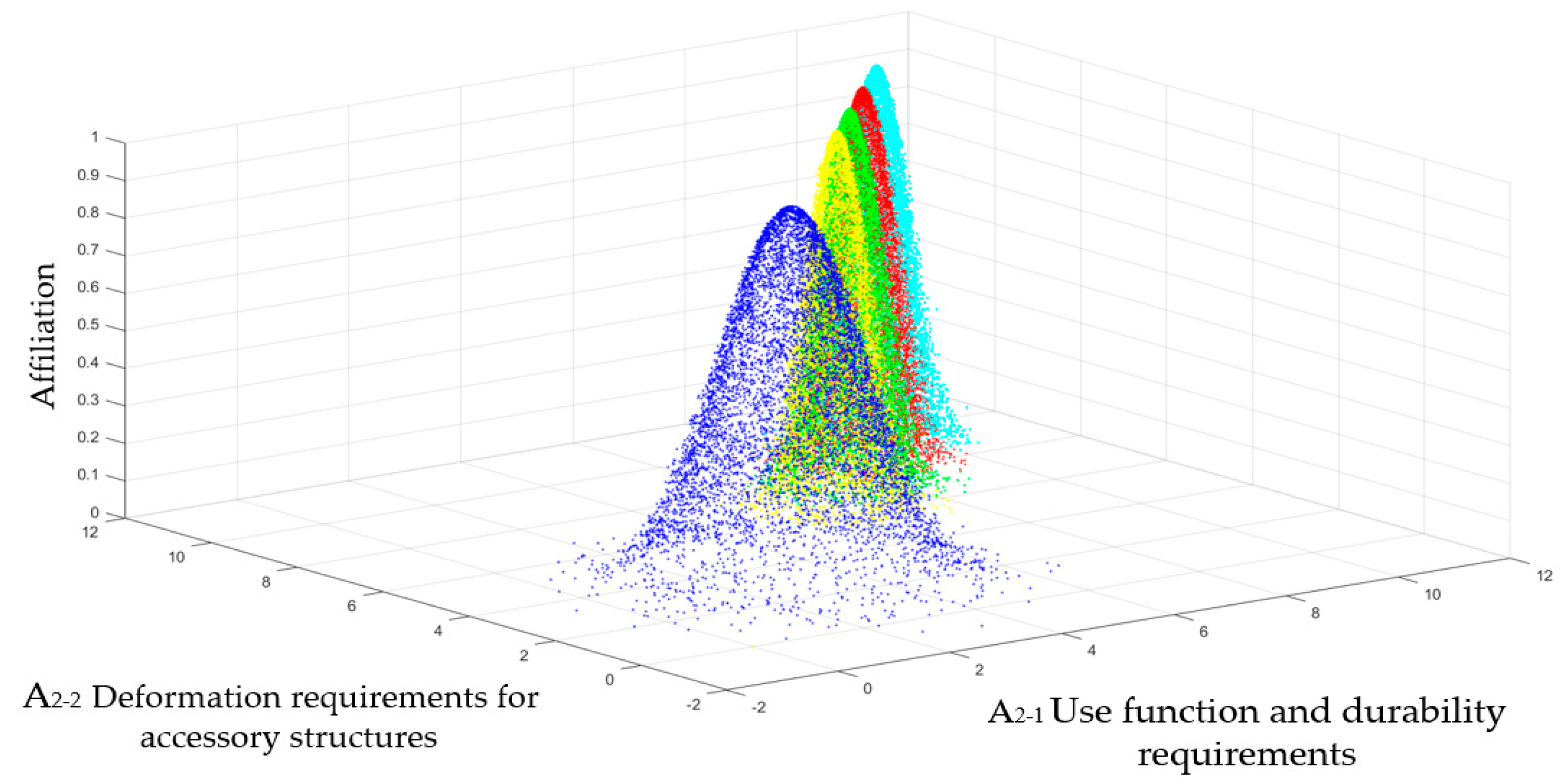
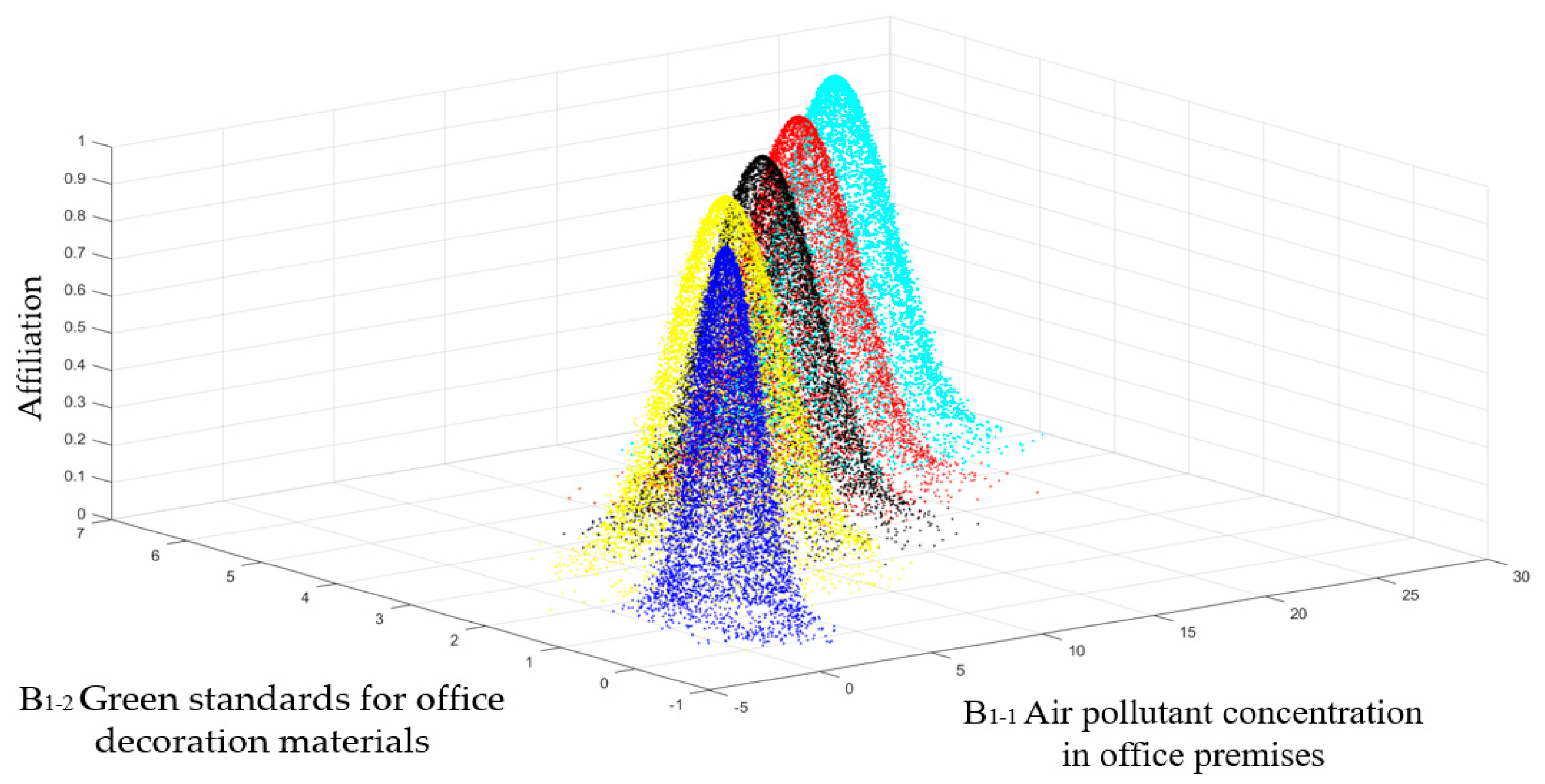
- Multidimensional normal cloud model generated by multidimensional forward cloud generator
- Generate a -dimensional normal random number with as the expectation and as the variance.
- Generate a -dimensional normal random number with as the expectation and as the variance.
- Calculate the degree of certainty by means of Equation (15).
- denotes a cloud drop. where denotes the primary counterpart of the qualitative concept in and is a measure of the qualitative concept to which is subordinate.Repeat steps 1 to 4 until a cloud droplet is generated.
3.3. Evaluation of Results
4. Large-Scale Channel Green Construction Example Application
- (1)
- Determination of expert weights
- (2)
- Determine the comparison interval of evaluation indicators for individual experts
- (3)
- Constructing uncertainty interval judgment matrix
- (4)
- Calculation of the weight interval
- (5)
- Calculate the exact weight value
- (6)
- Green construction index evaluation level classification
- (7)
- Multidimensional cloud model digital features
- (8)
- Multi-dimensional evaluation cloud model
- (9)
- Project evaluation results
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- 4GB/T 50378-2019; Green Building Evaluation Standard. China Construction Industry Press: Beijing, China, 2019.
- Xu, J. Evaluation Model and Empirical Research on the Green Innovation Capability of Manufacturing Enterprises from the Perspective of Ecological Niche. Sustainability 2021, 13, 11710. [Google Scholar] [CrossRef]
- Gao, Z.G.; Chen, W.G.; Yang, H.Y. Research on green construction level evaluation of deep foundation pit based on cloud material element model. J. Qingdao Univ. Technol. 2021, 42, 1–11. [Google Scholar]
- Hong, W.X.; Lu, C.; Zhao, D.F.; Li, B.B. Research on micro risk evaluation of green building based on combined empowerment-cloud model. J. Xi’an Univ. Archit. Technol. 2021, 40, 72–79. [Google Scholar] [CrossRef]
- Guo, R.X.; Xia, J.B.; Dong, S.F.; Long, M. A multi-attribute comprehensive evaluation method based on multi-dimensional cloud model. Comput. Sci. 2010, 37, 3. [Google Scholar]
- Zhang, Q.; Chen, J.; Lu, L.S.; Cao, Z.Z.; Duan, W.P. Multidimensional cloud model for rock slope stability assessment. Mod. Min. 2020, 36, 6. [Google Scholar]
- Li, X.; Li, W.; Lei, W.; Wang, Y.H.; Luo, N.; Fan, H.Y. Research on green construction evaluation of urban water environment management based on AHP-artificial neural network. Water Sci. Technol. Econ. 2021, 27, 18–23. [Google Scholar]
- Ren, Y.L.; Bao, X.Y. Comprehensive evaluation of environmental impact of railroad green construction based on game-theory-cloud model. Highw. Eng. 2021, 1–14. Available online: http://kns.cnki.net/kcms/detail/43.1481.U.20210408.1153.028.html (accessed on 23 April 2022).
- Zhu, W.H.; Zou, T. Green railroad construction phase scheme selection based on AHM and improved TOPSIS. J. Civ. Eng. Manag. 2018, 35, 187–191. [Google Scholar] [CrossRef]
- Wang, J.Y.; Wang, H.T. Fuzzy comprehensive evaluation of construction project risk based on uncertain AHP. J. Shenzhen Univ. 2006, 48–53. [Google Scholar] [CrossRef]
- Guo, R.C.; Chen, G.W.; Zhao, X.J.; Huo, J.Y.; Fan, D.W. Safety assessment of column control operation based on cloud model and uncertain AHP. J. Railw. 2016, 38, 69–74. [Google Scholar]
- Li, L. Research on Green Construction Organization and Management Technology of Large Bridges. Master’s Thesis, Zhengzhou University, Zhengzhou, China, 2017. [Google Scholar]
- Xie, S.J. Construction evaluation of water conservancy and hydropower projects based on green construction evaluation index system. Heilongjiang Water Conserv. Sci. Technol. 2018, 46, 219–223. [Google Scholar] [CrossRef]
- Li, H.W.; Bao, X.Y. Comprehensive evaluation of green construction level of railroad tunnel in Qinghai-Tibet plateau region. J. Railw. Sci. Eng. 2021, 18, 524–532. [Google Scholar] [CrossRef]
- Li, B.W.; Yang, M.R.; Wang, X.L.; Chen, T.J. Research on the evaluation index system of green road construction stage in Hainan Province. Highway 2020, 65, 265–272. [Google Scholar]
- Shi, Z.J.; Wang, H.W.; Wang, X. Aviation maintenance risk posture assessment based on multivariate linkage set-pair analysis. Syst. Eng. Electron. Technol. 2016, 38, 588–594. [Google Scholar]
- Li, D.S. Research on System Hazard Evaluation Based on Generalized Set-Pair Analysis. Ph.D. Thesis, Northeastern University, Boston, MA, USA, 2010. [Google Scholar]
- Zhou, T.; Hu, J.H.; Kuang, Y. Method and application of rock quality evaluation based on fuzzy RES-multidimensional cloud model. Chin. J. Nonferr. Met. 2019, 29, 1771–1780. [Google Scholar] [CrossRef]
- Yue, K.W. Comprehensive Evaluation of Power Quality Based on Cloud Object Element and Its Application Research. Master’s Thesis, Beijing Jiaotong University, Beijing, China, 2012. [Google Scholar]
- Wang, M.W.; Wang, X.; Long, J.Y.; Jin, J.L. Evaluation of debris flow hazard based on multidimensional linked normal cloud model. J. Appl. Basic Eng. Sci. 2021, 29, 368–375. [Google Scholar] [CrossRef]
- Liu, X.Y.; Yang, W.; Zhang, X.M. Rockburst prediction by multidimensional cloud model based on improved hierarchical method and CRITIC method. J. Hunan Univ. 2021, 48, 118–124. [Google Scholar] [CrossRef]
- Guo, J.; Zhang, W.X.; Zhao, Y. A comprehensive evaluation method of multidimensional cloud model for rockburst prediction. J. Rock Mech. Eng. 2018, 37, 1199–1206. [Google Scholar] [CrossRef]
- Luo, C.H.; Qu, G.J.; Zou, T.H.; Tang, T.; Xie, J.; Luo, Q. A multidimensional evaluation model of wind farm operation performance based on hierarchical analysis and cloud model. Mod. Electr. 2021, 38, 601–612. [Google Scholar] [CrossRef]

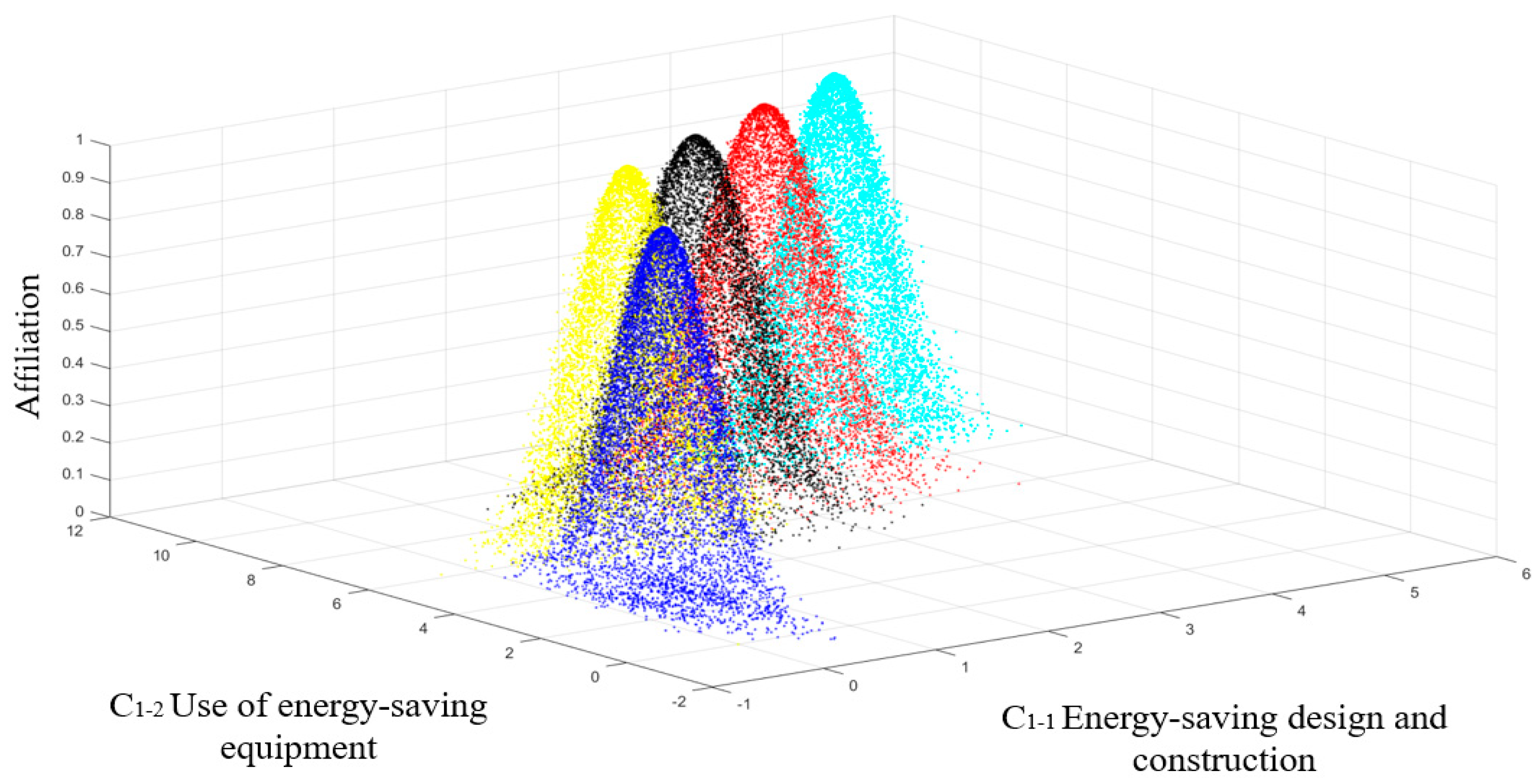
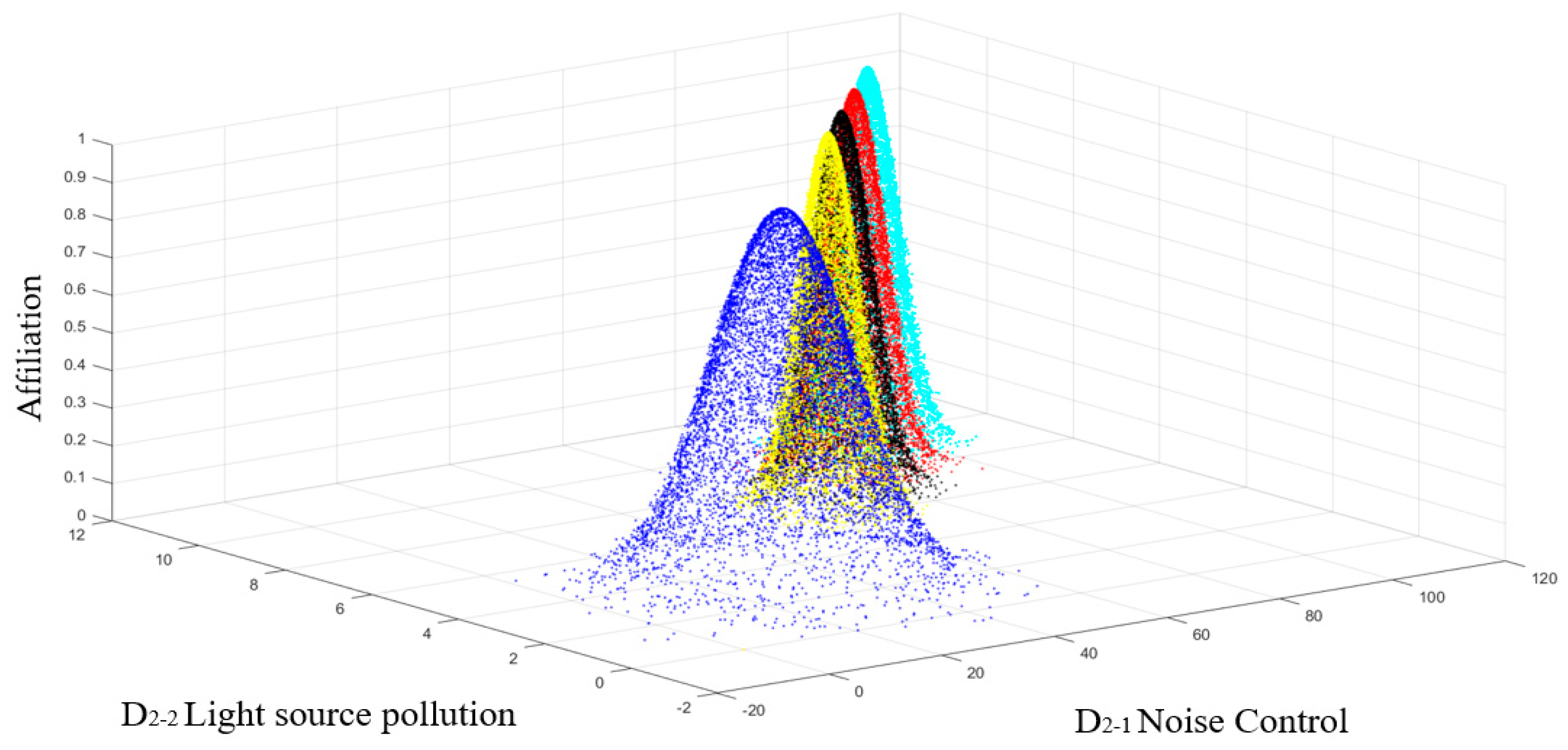

| Notation | Explanation |
|---|---|
| Cloud model structure | |
| Comparison interval of evaluation indicators | |
| Lower limit of interval importance | |
| Upper limit of interval importance | |
| Expert Weights | |
| Weight interval matrix | |
| Uncertainty interval judgment matrix | |
| Consistent approximation matrix satisfying mutual inverse | |
| Weights of the consistency approximation matrix | |
| Polar difference matrix | |
| The weight interval of the interval number judgment matrix | |
| Set to contact degree | |
| Interval Difference | |
| Coefficient of variance | |
| Contrast coefficient | |
| Relative weights of deterministic intervals | |
| Relative weights of uncertainty intervals | |
| Precise weighting values of evaluation indicators | |
| Expected Value | |
| Entropy value | |
| Hyperentropy value | |
| Measured value | |
| Degree of certainty | |
| Constraint interval small value | |
| Constraint interval large value | |
| rule | |
| Cloud entropy based on “50% association degree” rule |
| Sub-Indicators | Expert Title | Years in Channel Construction and Management (Years) | Familiarity with Engineering Green Construction | Understanding of This Channel Project | Sub-Index Score | Relative Weighting Values of Sub-Indicators |
| Positive senior | >20 | Very familiar | Very familiar | 10 | 0.323 | |
| Associate senior | 10~20 | Familiarity | Familiarity | 8 | 0.258 | |
| Intermediate | 5~10 | More familiar | More familiar | 6 | 0.193 | |
| Primary | 2~5 | Understanding | Understanding | 4 | 0.129 | |
| Other | <2 | Better understanding | Better understanding | 3 | 0.097 |
| Experts | Title | Number of Years Engaged in Channel Construction (Years) | Familiarity with Engineering Green Construction | Understanding of This Channel Project | Cumulative Weighting | Normalized Weights |
|---|---|---|---|---|---|---|
| 1 | Positive senior (0.323) | 22 (0.323) | Very familiar (0.323) | Familiarity (0.258) | 1.227 | 0.284 |
| 2 | Associate senior (0.258) | 18 (0.258) | Very familiar (0.323) | Familiarity (0.258) | 1.097 | 0.254 |
| 3 | Intermediate (0.193) | 9 (0.193) | Familiarity (0.258) | More familiar (0.193) | 0.837 | 0.194 |
| 4 | Positive senior (0.258) | 19 (0.258) | Very familiar (0.323) | Very familiar (0.323) | 1.162 | 0.268 |
| Primary Indexes | Single Weighting | Secondary Indexes | Single Weighting | Total Weighting | Tertiary Indexes | Single Weighting | Total Weighting |
|---|---|---|---|---|---|---|---|
| 0.2660 | 0.6014 | 0.1600 | 0.5570 | 0.0891 | |||
| 0.2705 | 0.0433 | ||||||
| 0.1725 | 0.0276 | ||||||
| 0.3986 | 0.1060 | 0.7942 | 0.0842 | ||||
| 0.2058 | 0.0218 | ||||||
| 0.0650 | 0.3795 | 0.0247 | 0.3573 | 0.0088 | |||
| 0.6427 | 0.0159 | ||||||
| 0.6205 | 0.0403 | 0.3993 | 0.0161 | ||||
| 0.6007 | 0.0242 | ||||||
| 0.2207 | 0.2822 | 0.0623 | 0.6725 | 0.0419 | |||
| 0.3275 | 0.0204 | ||||||
| 0.4253 | 0.0939 | 0.1924 | 0.0181 | ||||
| 0.3058 | 0.0287 | ||||||
| 0.5018 | 0.0471 | ||||||
| 0.2241 | 0.0495 | 0.6047 | 0.0299 | ||||
| 0.2548 | 0.0126 | ||||||
| 0.1405 | 0.0070 | ||||||
| 0.0684 | 0.0151 | 0.6061 | 0.0091 | ||||
| 0.2399 | 0.0036 | ||||||
| 0.1540 | 0.0023 | ||||||
| 0.3624 | 0.6063 | 0.2197 | 0.2306 | 0.0508 | |||
| 0.2635 | 0.0579 | ||||||
| 0.5059 | 0.1111 | ||||||
| 0.2402 | 0.0870 | 0.7330 | 0.0638 | ||||
| 0.2670 | 0.0232 | ||||||
| 0.1535 | 0.0556 | 0.6616 | 0.0368 | ||||
| 0.3384 | 0.0188 | ||||||
| 0.0859 | 0.3573 | 0.0307 | 0.3617 | 0.0111 | |||
| 0.6383 | 0.0196 | ||||||
| 0.6427 | 0.0552 | 0.7149 | 0.0395 | ||||
| 0.2851 | 0.0157 |
| Indicators | Green Level | ||||
|---|---|---|---|---|---|
| Failure | Basic Level | One-Star | Two-Star | Three-Star | |
| [0,6) | [6,7) | [7,8) | [8,9) | [9,10] | |
| [0,6) | [6,7) | [7,8) | [8,9) | [9,10] | |
| [0,6) | [6,7) | [7,8) | [8,9) | [9,10] | |
| [0,6) | [6,7) | [7,8) | [8,9) | [9,10] | |
| [0,6) | [6,7) | [7,8) | [8,9) | [9,10] | |
| [0,5) | [5,10) | [10,15) | [15,20) | [20,25] | |
| [0,2) | [2,3) | [3,4) | [4,5) | [5,6] | |
| [0,6) | [6,7) | [7,8) | [8,9) | [9,10] | |
| [0,4) | [4,5) | [5,7) | [7,9) | [9,10] | |
| [0,1) | [1,2) | [2,3) | [3,4) | [4,5] | |
| [0,6) | [6,7) | [7,8) | [8,9) | [9,10] | |
| [0,60) | [60,70) | [70,80) | [80,90) | [90,100] | |
| [0,6) | [6,7) | [7,8) | [8,9) | [9,10] | |
| [0,6) | [6,7) | [7,8) | [8,9) | [9,10] | |
| [0,5) | [5,10) | [10,15) | [15,20) | [20,25] | |
| [0,6) | [6,7) | [7,8) | [8,9) | [9,10] | |
| [0,6) | [6,7) | [7,8) | [8,9) | [9,10] | |
| [0,60) | [60,70) | [70,80) | [80,90) | [90,100] | |
| [0,6) | [6,7) | [7,8) | [8,9) | [9,10] | |
| [0,6) | [6,7) | [7,8) | [8,9) | [9,10] | |
| [0,6) | [6,7) | [7,8) | [8,9) | [9,10] | |
| [0,6) | [6,7) | [7,8) | [8,9) | [9,10] | |
| [0,6) | [6,7) | [7,8) | [8,9) | [9,10] | |
| [0,60) | [60,70) | [70,80) | [80,90) | [90,100] | |
| [0,6) | [6,7) | [7,8) | [8,9) | [9,10] | |
| [0,300) | [300,350) | [350,400) | [400,450) | [450,600] | |
| [0,6) | [6,7) | [7,8) | [8,9) | [9,10] | |
| [0,60) | [60,70) | [70,80) | [80,90) | [90,100] | |
| [0,6) | [6,7) | [7,8) | [8,9) | [9,10] | |
| [0,6) | [6,7) | [7,8) | [8,9) | [9,10] | |
| [0,6) | [6,7) | [7,8) | [8,9) | [9,10] | |
| Indicators | Green Level | ||||
|---|---|---|---|---|---|
| Failure | Basic Level | One-Star | Two-Star | Three-Star | |
| (3,1,0.08) | (6.5,0.42,0.08) | (7.5,0.42,0.08) | (8.5,0.42,0.08) | (9.5,0.42,0.08) | |
| (3,1,0.08) | (6.5,0.42,0.08) | (7.5,0.42,0.08) | (8.5,0.42,0.08) | (9.5,0.42,0.08) | |
| (3,1,0.08) | (6.5,0.42,0.08) | (7.5,0.42,0.08) | (8.5,0.42,0.08) | (9.5,0.42,0.08) | |
| (3,1,0.08) | (6.5,0.42,0.08) | (7.5,0.42,0.08) | (8.5,0.42,0.08) | (9.5,0.42,0.08) | |
| (3,1,0.08) | (6.5,0.42,0.08) | (7.5,0.42,0.08) | (8.5,0.42,0.08) | (9.5,0.42,0.08) | |
| (2.5,0.83,0.08) | (7.5,2.12,0.08) | (12.5,2.12,0.08) | (17.5,2.12,0.08) | (22.5,2.12,0.08) | |
| (1,0.33,0.08) | (2.5,0.42,0.08) | (3.5,0.42,0.08) | (4.5,0.42,0.08) | (5.5,0.42,0.08) | |
| (3,1,0.08) | (6.5,0.42,0.08) | (7.5,0.42,0.08) | (8.5,0.42,0.08) | (9.5,0.42,0.08) | |
| (2,0.67,0.08) | (4.5,0.42,0.08) | (6,0.85,0.08) | (8,0.85,0.08) | (9.5,0.42,0.08) | |
| (0.5,0.17,0.08) | (1.5,0.42,0.08) | (2.5,0.42,0.08) | (3.5,0.42,0.08) | (4.5,0.42,0.08) | |
| (3,1,0.08) | (6.5,0.42,0.08) | (7.5,0.42,0.08) | (8.5,0.42,0.08) | (9.5,0.42,0.08) | |
| (30,10,0.08) | (65,4.25,0.08) | (75,4.25,0.08) | (85,4.25,0.08) | (95,4.25,0.08) | |
| (3,1,0.08) | (6.5,0.42,0.08) | (7.5,0.42,0.08) | (8.5,0.42,0.08) | (9.5,0.42,0.08) | |
| (3,1,0.08) | (6.5,0.42,0.08) | (7.5,0.42,0.08) | (8.5,0.42,0.08) | (9.5,0.42,0.08) | |
| (2.5,0.83,0.08) | (7.5,2.12,0.08) | (12.5,2.12,0.08) | (17.5,2.12,0.08) | (22.5,2.12,0.08) | |
| (3,1,0.08) | (6.5,0.42,0.08) | (7.5,0.42,0.08) | (8.5,0.42,0.08) | (9.5,0.42,0.08) | |
| (3,1,0.08) | (6.5,0.42,0.08) | (7.5,0.42,0.08) | (8.5,0.42,0.08) | (9.5,0.42,0.08) | |
| (30,10,0.08) | (65,4.25,0.08) | (75,4.25,0.08) | (85,4.25,0.08) | (95,4.25,0.08) | |
| (3,1,0.08) | (6.5,0.42,0.08) | (7.5,0.42,0.08) | (8.5,0.42,0.08) | (9.5,0.42,0.08) | |
| (3,1,0.08) | (6.5,0.42,0.08) | (7.5,0.42,0.08) | (8.5,0.42,0.08) | (9.5,0.42,0.08) | |
| (3,1,0.08) | (6.5,0.42,0.08) | (7.5,0.42,0.08) | (8.5,0.42,0.08) | (9.5,0.42,0.08) | |
| (3,1,0.08) | (6.5,0.42,0.08) | (7.5,0.42,0.08) | (8.5,0.42,0.08) | (9.5,0.42,0.08) | |
| (3,1,0.08) | (6.5,0.42,0.08) | (7.5,0.42,0.08) | (8.5,0.42,0.08) | (9.5,0.42,0.08) | |
| (30,10,0.08) | (65,4.25,0.08) | (75,4.25,0.08) | (85,4.25,0.08) | (95,4.25,0.08) | |
| (3,1,0.08) | (6.5,0.42,0.08) | (7.5,0.42,0.08) | (8.5,0.42,0.08) | (9.5,0.42,0.08) | |
| (150,50,0.08) | (325,21.23,0.08) | (375,21.23,0.08) | (425,21.23,0.08) | (525,63.7,0.08) | |
| (3,1,0.08) | (6.5,0.42,0.08) | (7.5,0.42,0.08) | (8.5,0.42,0.08) | (9.5,0.42,0.08) | |
| (30,10,0.08) | (65,4.25,0.08) | (75,4.25,0.08) | (85,4.25,0.08) | (95,4.25,0.08) | |
| (3,1,0.08) | (6.5,0.42,0.08) | (7.5,0.42,0.08) | (8.5,0.42,0.08) | (9.5,0.42,0.08) | |
| (3,1,0.08) | (6.5,0.42,0.08) | (7.5,0.42,0.08) | (8.5,0.42,0.08) | (9.5,0.42,0.08) | |
| (3,1,0.08) | (6.5,0.42,0.08) | (7.5,0.42,0.08) | (8.5,0.42,0.08) | (9.5,0.42,0.08) | |
| Green evaluation indicators | ||||||||
| Actual value | 8.732 | 9.347 | 9.635 | 9.986 | 9.451 | 17.845 | 5.298 | 9.171 |
| Green evaluation indicators | ||||||||
| Actual value | 9.617 | 3.687 | 8.947 | 98.199 | 9.491 | 9.249 | 18.267 | 8.115 |
| Green evaluation indicators | ||||||||
| Actual value | 9.333 | 97.442 | 9.777 | 9.713 | 9.911 | 8.336 | 9.633 | 93.147 |
| Green evaluation indicators | ||||||||
| Actual value | 10.000 | 437.116 | 9.525 | 91.478 | 7.663 | 8.797 | 9.211 |
| Affiliation | Evaluation Results of This Paper | AHP-Cloud Model | ||||
|---|---|---|---|---|---|---|
| I | II | III | IV | V | ||
| V | V | |||||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ma, Q.; Lu, L.; Li, Q.; Wang, Z. Green Construction Grade Evaluation of Large Channels Based on Uncertain AHP-Multidimensional Cloud Model. Sustainability 2022, 14, 6143. https://doi.org/10.3390/su14106143
Ma Q, Lu L, Li Q, Wang Z. Green Construction Grade Evaluation of Large Channels Based on Uncertain AHP-Multidimensional Cloud Model. Sustainability. 2022; 14(10):6143. https://doi.org/10.3390/su14106143
Chicago/Turabian StyleMa, Qiang, Linfang Lu, Qingfu Li, and Zhipeng Wang. 2022. "Green Construction Grade Evaluation of Large Channels Based on Uncertain AHP-Multidimensional Cloud Model" Sustainability 14, no. 10: 6143. https://doi.org/10.3390/su14106143
APA StyleMa, Q., Lu, L., Li, Q., & Wang, Z. (2022). Green Construction Grade Evaluation of Large Channels Based on Uncertain AHP-Multidimensional Cloud Model. Sustainability, 14(10), 6143. https://doi.org/10.3390/su14106143





