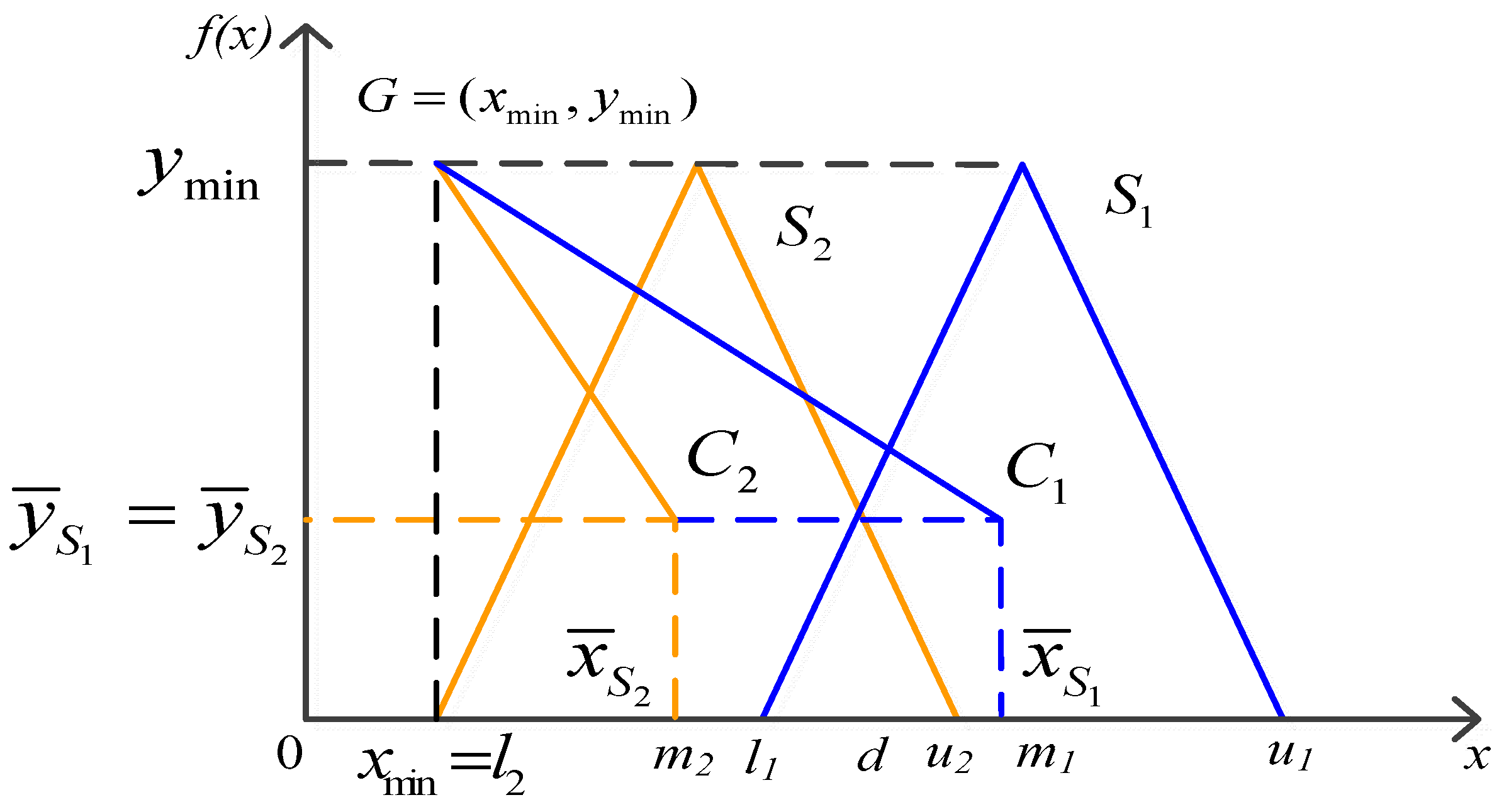1. Introduction
In recent years, administrators and universities all over the world have been increasingly interested in improving lecturers’ research productivity, which is a key criterion for university rankings and one of the most important factors to consider when evaluating a university’s research performance [
1,
2]. Many scholars have conducted research on individual and organizational factors that influence university lecturers’ research productivity and research outcomes [
3,
4,
5]. According to Nafukho et al. [
3], the research productivity of lecturers at top Kenyan universities varies with gender, subject major, number of years of experience, terminal degree, number of students enrolled, proportion of students pursuing a doctoral degree, and research funding. These authors also point out that at top Kenyan universities, lecturers’ experience is not a determining factor in their research productivity. Abramo et al. [
4] investigated how individual and organizational factors interact to influence lecturer collaboration and research productivity in Italy. According to their findings, academic rank has an impact on cooperation but not on lecturers’ research productivity. The authors further show that research productivity has a positive impact on national and international collaboration, but only domestic collaboration has a positive impact on research productivity. Tafreshi et al. [
5] investigated the factors that influence lecturers’ research productivity at Islamic Azad University. Their results show that individual factors such as job satisfaction, learning and teaching processes, and the desire to specialize have an impact on lecturers’ scientific research productivity, but organizational factors such as organizational support, organizational culture, organizational objectives, motivational factors, student characteristics, and industrial relationships have no direct impact.
In addition, there have been a number of studies addressing factors related to university governance that affect lecturers’ research productivity. Typical factors include research objectives and strategies [
2,
6,
7], the autonomy and decentralization of academic institutions and lecturers [
1,
8,
9], leadership [
6,
10,
11], support for scientific research activities [
4,
12], policy regimes affecting lecturers [
13,
14] and resources [
15,
16]. Jung [
1] indicated that the research productivity of Hong Kong academics was influenced by personal characteristics, workload, differences in research styles, and institutional characteristics. Hedjazi and Jaleh [
2] found that network of communication with colleagues, resources of facilities, corporate management, and clear research objectives were significant predictors for agricultural faculty members’ research product all over Tehran Province. Abramo et al. [
4] applied different cross-lagged panel models to analyze the relationship between research productivity, collaboration, and their determinants. Their results showed that only collaboration at the intramural and domestic level has a positive effect on research productivity. Jahan et al. [
6] indicated that research training and skill, financial support, technical and logistic support, mentorship, and teamwork were the main factors affecting quality academic research at Oman Medical College. Bland [
7] found that faculty productivity was influenced more by individual and institutional characteristics; group productivity was more affected by institutional and leadership characteristics. Ryu [
9] showed that leadership was the most important factor affecting basic research performance. Knowledge sharing, autonomy, collaboration, and creativity in sequence were also statistically valuable factors that impact the performance of basic research in South Korea. Kok and McDonal [
10] revealed a thematic framework of eight broad themes that contribute to excellence in academic departments. These were in the areas of change management, research and teaching, communication, strategy, and shared values, leadership, departmental culture, rewards, and staffing. Salman [
13] found that teaching responsibilities and conferences play a significant role in determining research productivity in universities. Hoffmann et al. [
14] indicated that the research productivity of academic librarians was significantly impacted by individual attributes, peers and community, and institutional structures and supports. Yang [
15] mentioned that university professors in Taiwan generally considered governmental research funding to be the most important indicator, followed by students’ academic ability and digital library resources. However, there seems to have been no research examining the overall impact of university governance factors on lecturers’ scientific research productivity. The research methods frequently applied in previous studies include regression analysis [
1,
3,
17], analysis of variance [
10,
18], structural equation modeling [
4,
5,
19], descriptive statistics and qualitative analysis [
11,
20], and analytic hierarchy process methods [
15].
Currently, the extent analysis method for fuzzy AHP, as proposed by Chang [
21], has become one of the most widely used tools for multiple criteria decision-making (MCDM). Fuzzy AHP methodology is used to demonstrate a hierarchical structure and to examine the weights of the decision elements reviewed and evaluated by experts in a vague environment. The literature has proposed numerous fuzzy AHP approaches for solving various types of problems, including renewable energy resources selection [
22,
23], urban green evaluation [
24], operational efficiencies of airports [
25], digital transformation strategy analysis [
26], land suitability assessment [
27], diagnosis of heart diseases [
28], supplier selection [
29,
30], and teaching performance evaluation [
31]. Despite its merits, there are some shortcomings associated with Chang’s [
21] approach. Wang et al. [
32] indicated that Chang’s [
21] approach may assign an irrational zero weight to some useful decision criteria and sub-criteria. In addition, Chang’s [
21] approach may make a wrong decision and select the worst decision alternative as the best one. Furthermore, the application of the approach is limited in normalized triangular fuzzy numbers. To overcome all the aforementioned shortcomings with Chang’s [
21] approach, this paper proposes an improved fuzzy AHP approach for generalized triangular fuzzy numbers. In the proposed approach, a centroid index is used to determine the priority of the weight vectors. The proposed approach is further applied to define the prioritization of factors impacting lecturer research productivity at Vietnam National University, Hanoi, Vietnam (VNU).
The rest of the paper is organized as follows.
Section 2 presents the concepts and definitions of generalized fuzzy numbers.
Section 3 briefly reviews Chang’s extent analysis method for fuzzy AHP.
Section 4 presents the shortcomings of Chang’s method and the proposed and improved generalized fuzzy AHP method. An application of the proposed method is given in
Section 5 to demonstrate its suitability. Finally, conclusions are drawn in
Section 6.
4. Shortcomings of Chang’s Approach and the Proposed Improved Generalized Fuzzy AHP Method
Wang et al. [
32] indicated that using Chang’s [
21] approach may assign an irrational zero weight to some useful decision criteria and alternatives, leading to them not being considered in decision analysis. This problem is shown in Example 1.
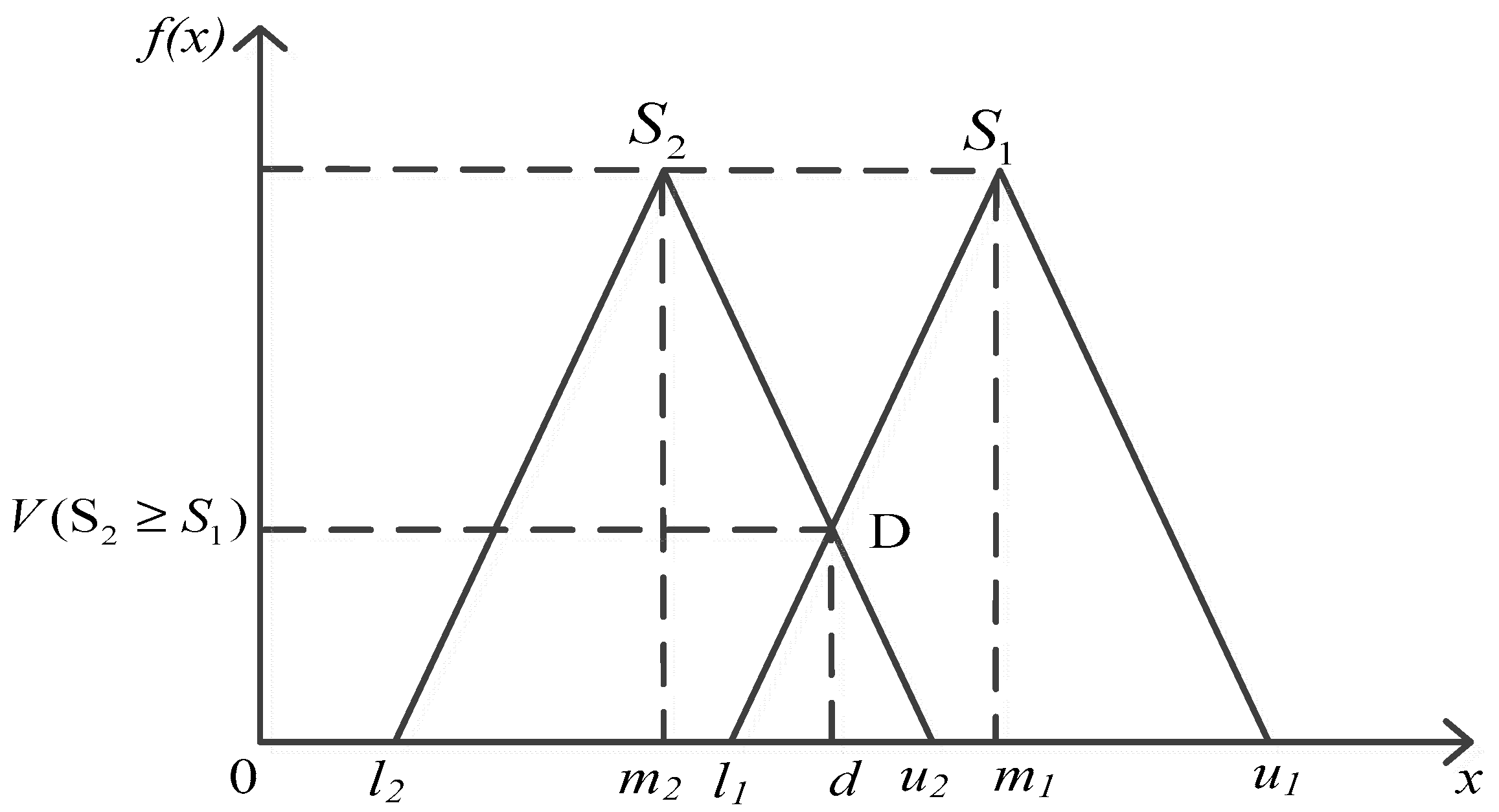
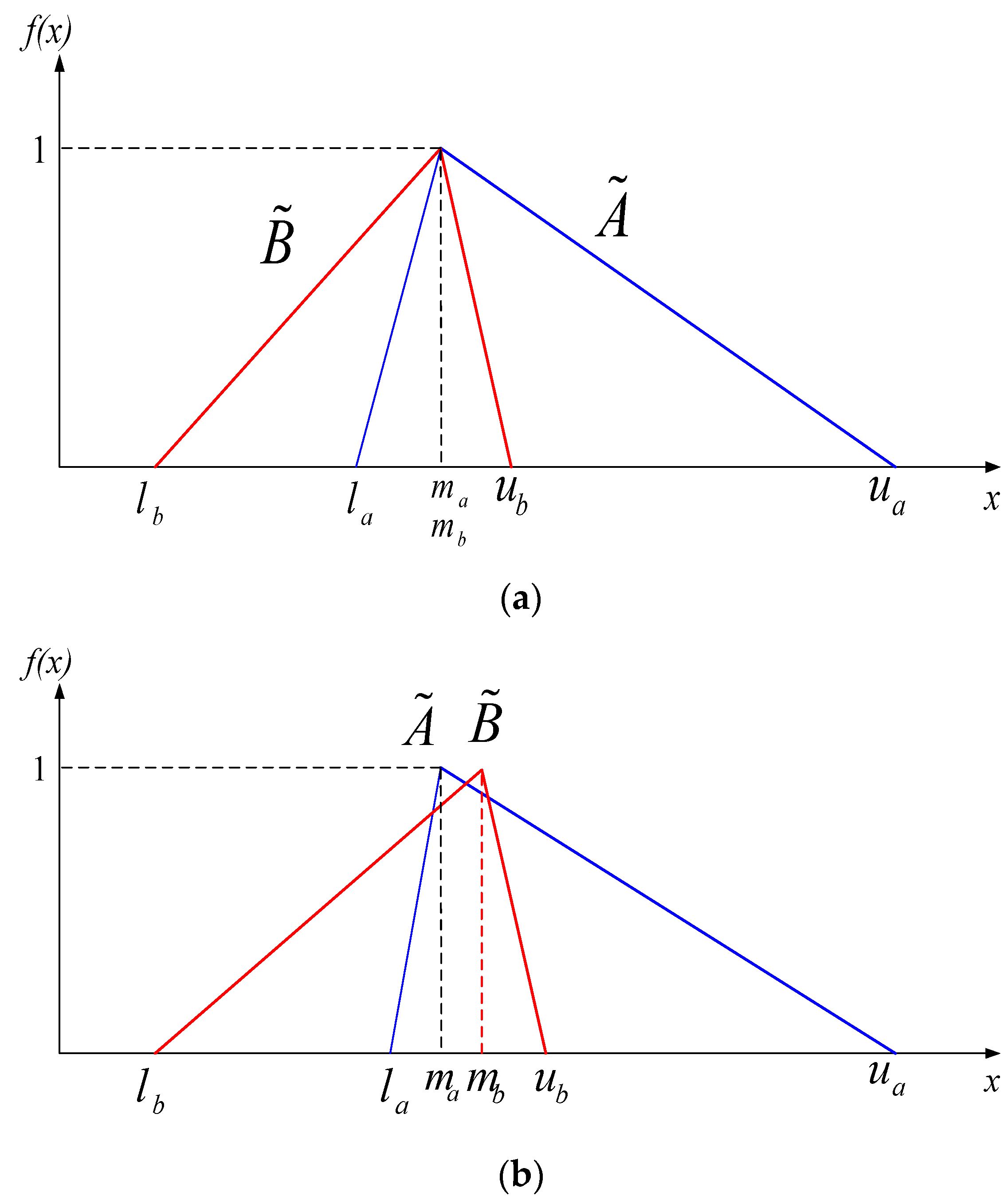
Example 1. Assume that a university wishes to evaluate its lecturers’ performance. Three decision makers, D1, D2, and D3, are responsible for the evaluation of three candidates, A1, A2, and A3. Five criteria are chosen for evaluating the lecturers: publication (C1), classroom teaching (C2), student advising (C3), personality factors (C4), and fluency in a foreign language (C5). Table 1 shows the fuzzy comparison matrix of the five criteria based on three decision makers. Accordingly, the priority vector of the five criteria is estimated by Chang’s approach as W = (1, 0, 0, 0.008, 0), which means that the criteria C2, C3, and C5 are given a zero weight and are not considered in decision analysis. In addition, Liu et al. [
34] found that Chang’s [
21] approach is inappropriate for determining the relative importance in some cases. Consider two TFNs, i.e.,
and
. In the case that
but
and
one can logically infer that
should have priority over
(
Figure 2a). However, according to Equation (4), when
the priorities of
and
are the same. In the case that
where
is a very small positive number close to 0 and
is a large positive number (as shown in
Figure 2b), intuitively, the TFN
should be preferred over
. However, using Equation (4), we have
, which indicates that the TFN
has a higher priority. Chang’s approach, therefore, fails to correctly determine the relative importance of fuzzy numbers.
Furthermore, Chang’s [
21] approach only can apply to normal fuzzy numbers. However, in the real world, it is impossible to restrict the membership function to the normal form in some cases. In order to overcome the shortcomings of Chang’s [
21] approach, this paper proposes a revised fuzzy AHP based on the centroid index ranking approach as follows.
The first step defines the generalized triangular fuzzy comparison matrix. The matrix is expressed by:
where
,
for
and
.
The second step determines the values of the fuzzy synthetic extents. In this paper, the values of fuzzy synthetic extents
are defined using the correct normalization formula presented by Wang et al. [
32] in the following equation:
where
The third step is to calculate the centroid indices of the fuzzy synthetic extent,
by using Dat et al.’s [
35] approach.
Suppose
are the values of the fuzzy synthetic extents. The centroid point of all fuzzy numbers
can be calculated by:
The distance between the centroid point
and the minimum point
, is determined by Equation (12) and
Figure 3:
where
The fourth step defines the weight vector
of the fuzzy comparison matrix as:
Example 2. This re-considers the data in Example 1. Using Equations (9)–(11), the new fuzzy synthetic extents and the centroid point of five criteria are obtained, respectively (as shown in Table 2). The minimum point of the five criteria is. By using Equation (12), the distances between the centroid point and minimize point of five criteria are calculated. Finally, the priority vector of five criteria is obtained using Equation (13). Evidently, the priority vector obtained by the proposed fuzzy AHP approach is more reasonable than the outcome obtained using Chang’s [21] approach. Example 3. This considers two fuzzy numbers in Figure 2a, i.e.,andUsing Equation (9), thefuzzy synthetic extent values of fuzzy numbersand are 0.375, 0.500, and 0.875 and 0.125, 0.500, and 0.625, respectively. Then, the centroid points of fuzzy numbersandare obtained by using Equations (10) and (11), i.e.,and. By using Equation (12), the relative importance measures ofandare 0.611 and 0.389, respectively, and thusNote that the priorityobtained using Chang’s approach is seen as unreasonable and not consistent with human intuition. Clearly, the revised approach can overcome the shortcomings of the inconsistency of Chang’s [
21]
approach. Example 4. This considers two fuzzy numbers in Figure 2b, i.e.,andUsing Equation (9), thefuzzy synthetic extent values of fuzzy numbersand are 0.476, 0.492, and 0.921 and 0.079, 0.508, and 0.524, respectively. Then, the centroid points of fuzzy numbersand are obtained by using Equations (10) and (11), i.e.,and. By using Equation (12), the relative importance ofandis 0.654 and 0.346, respectively, and thusNote that the priorityobtained using Chang’s [
21]
approach is not consistent with human intuition. Again, this example shows that the proposed approach can overcome the shortcomings of Chang’s [
21]
approach. 5. Application of the Proposed Fuzzy AHP Approach
In this section, the improved fuzzy AHP approach is applied to define the priority of the university’s governance factors that affect lecturers’ scientific research productivity at Vietnam National University, Hanoi, Vietnam (VNU). VNU is one of two leading multi-disciplinary and multi-sectoral national universities in Vietnam. VNU is entrusted with the task of producing highly qualified human resources for the industrialization and modernization of the country. VNU holds a special position in Vietnam’s higher education system, operating according to a special regulation promulgated by the Prime Minister. Currently, this university has 35 members (including 8 affiliated universities, 4 affiliated schools, 7 research institutes, 2 training and research centers, and 13 support/service units), 33 research groups, 216 laboratories, and 4.326 staff members. As of the end of 2020, VNU had 488 training programs (including 185 undergraduate programs, 187 master’s programs, and 116 doctoral programs), with 40.038 undergraduate students, 7500 graduate students, and 819 international students.
In this study, data were collected by conducting semi-structured interviews with the director of VNU’s Organization-Personnel Department, University of economics and Business -VNU’s Office of Human resources and department head, University of economics and Business-VNU’s faculty head. A committee of three decision makers (D1, D2, and D3) conducted the evaluation of the university’s governance factors.
The entire the evaluation of university’s governance factors was characterized by the following steps:
Step 1: Defining the university’s governance factors.
Step 2: Determining fuzzy judgment matrices of factors and sub-factors.
Step 3: Aggregating decisions from decision makers based on geometric means.
Step 4: Calculating fuzzy synthetic extent values of factors and sub-factors.
Step 5: Determining the weight vector of factors and sub-factors impacting lecturer research productivity.
Steps 1 and 2 were performed by the committee (three decision makers, i.e., D1, D2, and D3) without any intervention from the authors. Steps 3–5 were calculated using the improved fuzzy AHP approach on a spreadsheet.
5.1. Defining the University’s Governance Factors
Following a survey of the literature and discussions with the committee, six factors and twenty-two sub-factors affecting lecturers’ scientific research productivity were chosen.
Table 3 shows the factors and sub-factors used in this study.
5.2. Determining Fuzzy Judgment Matrices of Factors and Sub-Factors
In this study, the committee was requested to separately proceed to their own fuzzy judgment matrices for the evaluation of the university’s governance factors. This study adopts an intensity scale for fuzzy numbers to transform the linguistic values into TFNs, as shown in
Table 4.
5.3. Aggregating Decisions from Decision Makers Based on Geometric Means
5.4. Calculating Fuzzy Synthetic Extent Values of Factors and Sub-Factors
5.5. Determining the Weight Vector of Factors and Sub-Factors Impacting on Lecturer Research Productivity
Using Equations (10)–(13), the weight vectors of the factors and sub-factors affecting lecturer research productivity are shown in
Table 13. The result indicates that “resources for research activities” is the most important factor affecting the research productivity of lecturers at VNU. This result is similar to other studies in which it has been found that the quality of human resources, investment in facilities, equipment, and investment funds for research activities have a strong impact on the research productivity of lecturers. VNU is a multi-disciplinary university with a higher percentage of lecturers with doctoral degrees than many other universities in Vietnam. This has been used by VNU in the establishment of interdisciplinary research groups and has resulted in many important achievements through the implementation of national and international research missions. However, at present, the facilities of many universities under VNU are quite limited, scattered, and not synchronized. The financial resources invested in science and technology activities are not commensurate with the potential or the need to improve the research capacity of the teaching staff to meet international standards.