Abstract
This paper considers a dynamic platform-based, closed-loop supply chain consisting of a manufacturer and an online platform. As an online distributor of the manufacturer, the platform expands the market scale by exerting the platform power. At the same time, to solve the problem of inconsistency between the actual recycling amount and the theoretical recycling amount in the recycling process of waste electronic products, the whole-process supervision of waste products is carried out with the help of blockchain technology, which is difficult to tamper with and is traceable. With the help of differential game theory, four differential game models of manufacturer recycling and platform recycling with and without blockchain are established. The state feedback strategies are derived from Bellman’s continuous dynamic programming theory. Through analytical results and comparative analysis, the adoption conditions of blockchain and the impact of blockchain on the selection of recycling models are obtained. The results illustrated that the introduction of blockchain technology effectively improves the real recycling rate of waste electronics, building trust in consumers, which benefits corporations in certain conditions. However, it amplifies the double marginal effect of the CLSC. Nevertheless, the implementation of blockchain is still beneficial to consumers, as the adverse impact of the double marginal effect is compensated by the improvement in consumer surplus. In addition, the study shows that the implementation of the blockchain incentivizes members, who benefit on the same recycling model when the fixed cost of the blockchain and the share ratio of the residual value of waste electronics are between certain thresholds. That is, both the manufacturer and the platform are better off in a manufacturer recycling model enabled by blockchain. Moreover, in this model, the social welfare and the recycling rate of waste electronics are increased, which enable the CLSC to achieve benefits related to economy, environment, and society.
1. Introduction
With the rapid development of information technology and e-commerce, online sales have become a mainstream sales trend. According to the 2020 Suning Annual Report, Suning merchandise sales scale was 416.315 billion yuan, of which the online platform merchandise sales scale reached 290.335 billion yuan, an increase of 21.60% year-on-year, with the online sales scale accounting for nearly 70%. Online platforms are increasingly becoming the mainstream sales channels for electronic products. During the 2020 Tmall “Double Eleven” global shopping event, more than 70 electronic brands, including Apple, Huawei, Xiaomi, Haier, Gree, and so on, had a turnover of over 100 million. After 10 min at zero on “Double Eleven”, the turnover of Huawei phones on JD.com increased by more than 100% year-on-year. In addition to the cell phone category, other digital electronic products such as high-end HiFi headphones, routers, and high-end thin and light notebooks all saw a multi-fold growth in sales.
Today, more and more consumers are switching from offline shopping to online, and more and more manufacturers are relying on online platforms to sell their products. The advantages of platform sales over traditional offline sales are obvious, as consumers can purchase products without being bound by time and place. In addition, online platforms can use the network effect of their own channels or adopt online marketing to expand the potential demand of the consumer market, which is the unique “platform power” of platform sales [1]. For example, Tmall and Taobao hired influential celebrities and weblebrities to broadcast live to promote their products. There is the augmented reality (AR) experience function launched by Dewu APP, which reduces the uncertainty of consumers when purchasing products online. “Platform power” enables online retail platforms to create more demand through their online channels and attract more manufacturers to sell products through the platform [2].
There are mainly two modes of cooperative sales between the manufacturer and platforms, namely the platform reselling model (by purchasing products from the manufacturer and selling them to buyers) and the platform agent selling model (in which the manufacturer sells their products directly to buyers). Platform agent reselling is where the platform receives a commission or a portion of sales from the manufacturer, who sells directly to the consumer [3]. In the case of electronics, consumers demand electronics more frequently. Therefore, most platforms use a reselling model when selling electronics in order to gain pricing power over them and thus have better control over price as a marketing lever [4]. For example, Amazon resells high-demand products such as electronics produced by upstream manufacturers, while it adopts the agent reselling model for non-mainstream, long-tail products [5].
Electronics are different from general durable products. With the rapid development of electronic technology, the replacement of electronic products is extremely fast. Although it can bring us an improvement in the quality of life, the frequency of elimination is higher than that of other products. If the discarded electronic products cannot be disposed of in time, it will bring serious pollutive damage to the ecological environment. For example, lead in televisions, and arsenic, mercury, and other harmful substances contained in computers, are extremely harmful to the environment. However, there are many reusable and even non-renewable resources in waste electronic products, such as aluminum alloys in computer hard drives, and lithium or nickel-metal hydride batteries in communication tools, which can be recycled and reused. Electronic products are products with high recycling value, which have three attributes of fast replacement, environmental pollution, and resource reuse. Therefore, in order to reduce the impact of waste electronics on the environment, it is very important to properly recycle waste electronics [6]. Now, many companies have started to recycle these reusable waste electronic products. The recycling of waste electronic products is a problem to be solved in practice and theory. The first and foremost problem to be solved for waste electronic products is the choice of recycling model for the manufacturer. There are two main types of manufacturer recycling: one is self-recycling by the manufacturer, and the other is with the help of online platforms or third-party recycling. The manufacturer’s independent recycling is in direct contact with consumers and can keep up with the latest product trends and retain accurate information feedback, thus making the production and sale of products and reverse recycling more efficient while also maximizing residual value profits. For example, BYD independently recycles lithium power batteries in electric vehicles. There are also many cases of the manufacturer using online platforms or third parties for recycling. For example, Aihuishou, as one of the electronic product-recycling platforms, cooperates with Huawei, Xiaomi, Apple, oppo, and other mobile phone manufacturers to recycle waste electronic products. Haier, TCL, Skyworth, and other home appliance companies use third-party recycling service platforms, combined with their own sales channels and networks, to carry out used-product recycling and trade-in services across the country with the operation idea of “Internet + recycling”. Unlike traditional offline recycling, online recycling is becoming an important recycling method for the manufacturer because it reaches a wider range of consumers and is more convenient for them. For the manufacturer, both recycling models have their advantages. At present, however, the incentive for the manufacturer to recycle themselves or through platforms remains unclear, especially for electronic products with environmental pollution and high recycling value. Therefore, the selection of a recycling model of waste electronic products is one of the key points discussed in this paper.
In addition to the choice of recycling model, the opaque recycling process, lax supervision, and other problems easily affect consumers’ trust in the recycling of waste products. Consumers returned used products, but not all of them reached the manufacturer, and the actual recycling of waste products was far less than the theoretical recycling. It is reported that, in 2020, the theoretical recycling amount of lithium ion batteries in the Chinese market reached 478,000 tons, but that the actual recycling amount was only 196,000 tons, accounting for only 41% of the theoretical recycling amount. Such false recycling problems will cause consumers to no longer trust the product, which can affect the brand goodwill of the product and reduce consumers’ willingness to recycle.
In fact, the effective recycling of waste electronic products restricts the key bottleneck of recycling waste electronic products. As a distributed accounting technology, blockchain has the characteristics of visibility, tamper-proof, traceability, decentralization, and the high reliability of the system, which can verify transactions on peer-to-peer networks and achieve security, transparency, low transaction costs, and the automation of transactions [7,8,9]. We can increase the trust of consumers by using the visibility and traceability features of blockchain technology to enable the real and effective recycling of waste products. At present, some enterprises have applied blockchain technology in the recycling process of waste products. For example, BASF ag in Canada has increased the recycling utilization of plastic products and improved the circularity of its supply chain through reciChain, a distributed ledger blockchain platform. Moreover, because of reciChain’s transparency, the platform can better assure brand owners that their recycling certificates are valid, thereby increasing consumer trust. The recycling and treatment of waste electronic products mainly involve two fields of renewable resources and environmental protection. A relatively perfect management system has been formed for green design and the manufacturing, recycling, treatment, remanufacturing, and disposal of the resources of electronic products, with strict reference standards. Therefore, waste electronic products are easier to “record on the chain” than other products, and the process of “recording to the chain” will be more standardized and standard.
Considering the successful application of blockchain in the recycling of waste products in practice, this paper introduces blockchain technology into the closed-loop supply chain as an important technical tool to regulate the recycling of waste products and improve consumer trust. However, considering the excessive cost of introducing blockchain, the circumstances under which enterprises introduce blockchain is also one of the focuses of this paper.
As a result, this paper explores the following three questions:
- RQ1:
- Under what conditions does the recycler choose to implement blockchain technology to increase the amount of real recycling of waste products?
- RQ2:
- What are the impacts of the implementation of blockchain technology on pricing and marketing strategies as well as the recycling model selection?
- RQ3:
- How to take advantage of the combination of blockchain and recycling model to enhance the triple benefits of economy, environment, and society in the CLSC?
In order to solve the above three problems, this paper considers four strategies for choosing the reverse recycling model of used electronics: (1) manufacturer recycling model without blockchain technology (); (2) platform recycling model without blockchain technology (); (3) manufacturer recycling model with blockchain empowerment (); (4) platform recycling model with blockchain empowerment (). In this paper, we assume that the introduced blockchain is a recycler-built permission blockchain and study the impact of permission blockchain on the recycling options of waste electronics in a platform-based, closed-loop supply chain. In terms of economic, social, and environmental considerations, a recycling model is the optimal choice. In addition, we consider that the recycler does not have the ability to build the blockchain by themself. The recycler can introduce blockchain technology through cooperation with a third party to influence the choice of recycling model of waste electronics.
Our paper contributes to both practical operation and theoretical research. In terms of theoretical research, it helps to further sublimate the research of a closed-loop supply chain under new technology (platform) and fills the research gap of platforms having both sales and recycling functions in a platform-based closed-loop supply chain. In terms of practical operation, when the cost of introducing blockchain is between two thresholds and the manufacturer choose the manufacturer recycling model, the platform can benefit from it, the supply chain can reach coordination, and the benefits related to the economy, environment, and society can be improved. It provides some reference for how enterprises can better improve their economic efficiency and fulfill their social responsibility with the help of blockchain technology.
The remainder of this paper is organized as follows. In Section 2, we summarize the relevant literature. Section 3 and Section 4 introduce the relevant models and analyze the optimal equilibrium strategy under each recycling model. Section 5 introduces the implementation conditions and implementation value of blockchain technology. Section 6 assigns exogenous parameters to introduce the influence of blockchain on the choice of recycling model from the perspective of economy, environment, and society. We expand the model by assuming that the recycler cooperates with third parties, and the optimal equilibrium strategy under each recycling model when renting the blockchain technology is discussed in Section 7. In Section 8, the conclusions drawn in this paper are summarized and the important implications are discussed.
2. Literature Review
The main studies related to this paper can be divided into three categories: electronic products’ supply chain, the choice of recycling models for used products, and the application of blockchain in the supply chain.
2.1. Electronic Products Supply Chain
Unlike other durable goods, electronic products tend to have a short life cycle, fast response time, high pollution, and high recycling value. With low recycling rates and a lack of government and consumer involvement [10], waste electronics have become one of the fastest growing waste streams in the world, with a significant impact on the earth’s environment. Therefore, the research on the recycling of waste electronics has high theoretical and practical value.
Due to the above characteristics of electronic products, Yang et al. [11] argued that electronics will face the risk of rapidly increasing technological innovation, which will lead to a significant decrease in parts cost, sales price, and demand. Tansel [12] also pointed out the challenges associated with the increase in the amount of waste electronics. Wang et al. [13] studied how high-tech electronics companies can coordinate environmental protection and social responsibility while gaining profits in order to promote the sustainable development of the electronics supply chain in response to the problems of the rapid replacement of electronic products and high obsolescence rates, considering that precious metals in waste electronics can bring huge economic benefits to the recycling industry. Kumar et al. [14] highlighted the importance and benefits of recycling waste electronics and emphasized the importance of recycling facilities. Wang et al. [15] pointed out that the recycling of waste electronics has become a key bottleneck for the proper disposal of waste electronics for reuse and recycling and analyzed the barriers to waste electronics enterprises by various stakeholders in China. They showed that it is important for the government to provide some subsidies, tax breaks, and other support to formal recycling enterprises. Zlamparet et al. [16] confirmed various views on the feasibility of remanufacturing in the waste electronics industry and showed that the potential for buyback can be increased by implementing good management, eco-design, and the reuse of waste electronics, thus avoiding major barriers such as environmental concerns and consumer acceptance.
In summary, research on the recycling of waste electronic products is crucial due to their rapid renewal, high pollution, and high recycling value attributes. Moreover, electronic products such as high demand products and the platform adhere to “no time, no space” restrictions on the sales characteristics, so most of the electronic products will be sold on the platform. We expand on the advantages of platform sales and further consider the platform as a recycler to explore the issue of recycling model options for waste electronics.
2.2. Selection of Recycling Model for Waste Products
In recent years, with the proposal of sustainable development, many the manufacturer save costs by recycling and remanufacturing activities. At present, there are many literatures on the analysis of the reverse recycling of waste products, and some results have been achieved on the issue of reverse recycling model selection.
Around this theme, scholars have considered factors affecting the choice of recycling model, such as competition in recycling channels, the costs and benefits of remanufacturing, and the adoption of new recycling technology (platform). In terms of considering recycling channel competition. Savaskan et al. [17] explored the issue of recycling channel selection for waste products and found that retailers recycled at a higher rate than the manufacturer and third parties when other conditions are the same. Wu and Zhou [18] extended the model of Savaskan et al. (2004) to examine the influence of supply chain competition on the manufacturer’s choice of optimal recycling channels. The results showed that the manufacturer adopted a manufacturer-managed recycling strategy. Liu et al. [19] showed that the dual manufacturer-retailer recycling model is the best recycling choice model for the manufacturer, regardless of the intensity of competition. Huang et al. [20] showed that, in the forward supply chain, the manufacturers sell products through retailers, while, in the reverse supply chain, retailers compete with third parties to recycle waste products. The results showed that a single recycling channel model for retailers is always better than the third party model. In terms of considering the costs and benefits of remanufacturing. Hong et al. [21] considered the effect of advertising on consumers’ acceptance of re-products and compared the performance of a closed-loop supply chain under the mode of manufacturer, retailer, and third party recycling. He et al. [22] showed that retailers’ participation in recycling competition leads to an increase in the manufacturers’ remanufacturing costs, which is not conducive to improving recycling efficiency. In considering new recycling technology (platform). Wang et al. [23] pointed out that platforms can increase consumers’ willingness to recycle online by publishing green information such as environmental knowledge about product recycling and corporate social responsibility online. Liu and Huang [24] considered the option of e-commerce platform recycling in the reverse recycling process and showed that the best strategy for the manufacturer and the platform is a separate recycling model for e-commerce platforms when the recycling price sensitivity is low.
The research on the selection of a recycling model for waste electronics is as follows. Liu et al. [25] in the context of recycling waste batteries from new energy vehicles found that manufacturer recycling models can generate higher profits for closed-loop supply chain systems, though may create environmental burdens. Chuang et al. [26] studied the problem of recycling model selection for high-tech electronics, which are characterized by short life cycles and fluctuating demand. It was found that manufacturer recycling is optimal when recycling costs exhibit diseconomies of scale, and that retailer recycling outperforms manufacturer and third-party recycling when recycling costs exhibit economies of scale. Xue et al. [27], aiming at the inefficiency of recycling and management of electronics in China, examined and compared the impact of closed-loop supply chain recycling and remanufacturing strategies on total supply chain revenue and the market share of two manufacturers, combined with the implementation of the Gree and Haier renewable energy projects. It was found that optimizing the incentive strategy between the manufacturer and retailers can effectively improve retailers’ motivation to recycle. Moreover, retailers can improve recycling efficiency by increasing recycling channels.
Most of the above studies are related to the offline recycling of waste products, and the recycling channels are mainly focused on the manufacturer, retailers, third parties, or online platforms for recycling; however, there are relatively few studies on recycling by the manufacturer with the help of online platforms. Particularly in the recycling of waste electronics, there is little research that considers both platform sales and recycling functions. This paper studies the selection of the recycling model of waste electronic products empowered by blockchain in a closed-loop supply chain on the basis of platform resale. This study aims to fill the gap of such research.
2.3. Application of Blockchain Technology in Supply Chain
Blockchain is a unique information technology with decentralized structure, distributed storage mechanism, consensus algorithm, smart contract, asymmetric encryption, and other functions. It has the “4T” technology features of traceability, transparency, trust, and transaction, ensuring the security and transparency of network information [28]. Although the development and application of blockchain technology is still in its infancy, it has been accepted by more and more groups and organizations in recent years, and its application potential has been recognized by more and more industries. We review the relevant literature on the application of blockchain technology in the supply chain in recent years and analyze and summarize the benefits and challenges brought by the application of blockchain technology in the supply chain combined with the technical characteristics of blockchain.
Babich and Hilary [29] summarized five key advantages and five major weaknesses of blockchain technology in operations management. They also pointed out that blockchain technology improves supply chain operations through its advantages of transparency, information aggregation, information verification, automation, and system resilience, thereby creating a more stable, secure, efficient, ethical, and robust supply chain system. Lim et al. [30] pointed out that blockchain enables supply chain information sharing, maintains traceability throughout the process, and improves the efficiency of supply chain operations. Moreover, blockchain technology will bring disruptive changes to supply chain operations. Wang et al. [7] stated that blockchain overcomes the barriers of distrust, privacy issues, data misuse, and information asymmetry in information sharing between upstream and downstream of the supply chain by creating a transparent, trustworthy, and fair mechanism for sharing supply chain information. With the transparent and trustworthy nature of blockchain technology, Yu et al. [31] showed that small- and medium-sized enterprises (SMEs) can use self-guarantees to obtain loans from financial institutions and showed that platform guarantees with the help of blockchain are more efficient and market-effective compared to traditional platform guarantees. Shen et al. [32] categorized consumers into professional and novice types and explored the market conditions for brands and manufacturers to effectively combat counterfeit products by using blockchain technology. Cai and Choi [33] analyzed a supply chain model with the presence of a platform and found that the presence of a platform leads to a “triple marginal effect”, particularly that labeling contracts can coordinate the supply chain but may lead to moral hazard problems for retailers. The introduction of blockchain can effectively avoid moral hazard while coordinating the supply chain. Chod et al. [34] investigated the problem of asymmetric information from lenders to borrowers, specifically their operational capabilities, and studied the impact of two types of information reflecting borrowers’ operational capabilities: lenders’ application information and blockchain-recorded inventory transaction information on financing. The study found that transparent inventory transaction information will produce less distortion in business financing. With the traceable characteristics of blockchain technology, Hastig and Sodhi [35] addressed the need for traceability systems in cobalt mining and pharmaceuticals industries, and presented the industry needs and critical success factors for blockchain implementation, laying the foundation for blockchain applications in the supply chain. Wu et al. [36] investigated the optimal strategy for different member-led blockchain construction in a fresh produce supply chain consisting of suppliers, third-party logistics service providers, and e-retailers, aiming at issues such as perishability and difficulty in the traceability of fresh produce. The study found that blockchain implementation was related to the consumer acceptance of products without blockchain technology, product spoilage rate, and the proportion of traceability costs borne by members when adopting blockchain. Liu et al. [37] proposed a five-layer smart traceability platform based on blockchain and the Internet of Things (IoT) to provide drug traceability and visibility solutions for the drug supply chain in response to the inability of pharmaceutical companies to address potential data manipulation and conflicts of interest by using traditional traceability platforms for controlling drug quality and improving transparency.
In summary, the application of blockchain in supply chain management mainly focuses on the forward sales process of products, mostly relying on the trust, traceability, visibility, and other characteristics of blockchain technology, focusing on the research of product traceability and anti-counterfeiting. The theoretical research results of blockchain in the reverse recycling of waste products are rarely reported, especially in the electronics industry. This paper mainly relies on the transparency and traceability of blockchain technology to strengthen the supervision of the reverse recycling process and promote the real and effective recycling of waste electronic products in the closed-loop supply chain.
In order to sort out the studies related to this paper and highlight the contributions of this paper, some representative articles are listed, compared, and analyzed in Table 1, as follows.

Table 1.
Comparison of some important studies in the literature.
3. Model Description and Assumptions
A two-level, closed-loop supply chain system consists of a manufacturer and a retailer platform , in which the manufacturer is responsible for the remanufacturing activities of waste electronics. Assume that the quality of the remanufactured product is the same as that of the new product. In the forward selling process of electronic products, the manufacturer decides the wholesale price of the product, and the platform purchases the product from the manufacturer and sells it to consumers and determines the retail price of the product. The platform promotes the demand of the consumer market through certain marketing efforts . In the reverse recycling process, whoever does the recycling invests in the corresponding recycling effort . The Stackelberg differential game is played in a power structure where the manufacturer is the channel leader and the platform is the channel follower. The relevant assumptions of this paper are as follows.
We considered four different recycling models, i.e., the manufacturer recycling model NM and the platform recycling model NP without blockchain technology, and the manufacturer recycling model BM and the platform recycling model BP with blockchain empowerment, as shown in the Table 2.

Table 2.
Recycling mode type.
Marketing investment can improve the visibility of the product and win consumers’ good impression of the product so as to improve the brand goodwill of the product. In this paper, brand goodwill of the product is taken as the state variable of the model, and the Nerlove–Arrow (1962) [38] model is used to portray the impact of marketing efforts on brand goodwill. The dynamics of brand goodwill change is modeled without blockchain technology as follows:
where represents the marketing efforts of the platform, is the influence coefficient of marketing efforts on brand goodwill, and represents the normal decay rate of goodwill caused by the consumer forgetting effect. represents initial goodwill. When the recycler does not implement the blockchain, represents the ratio of the actual recycling volume of waste electronic products to the theoretical recycling volume, namely, the real recycling rate. represents a false ratio. This false recycling will make consumers who return waste products distrust the recycling party, thereby dampening the goodwill of the product brand.
When the recycler implements the blockchain, the recycling process of waste electronic products is made more transparent by utilizing the visibility and traceability of the blockchain technology. It can effectively supervise the recycling process of waste electronic products, so that the actual recycling amount is consistent with the theoretical recycling amount, that is, . Therefore, in the case of the introduction of blockchain, the dynamic equation of brand goodwill can be expressed as:
Positive consumer market demand is always positively related to the product’s brand goodwill , that is, the higher the brand’s goodwill, the more trust it will gain from consumers, thereby increasing market demand. The demand of the consumer market and the retail price of the product is always negatively correlated, that is, the higher the price of the product, consumers may choose to give up buying the brand product or switch to other brands, which will lead to a lower demand for the brand’s product in the consumer market. Therefore, the demand function of the consumer market can be expressed as:
where represents the coefficient of goodwill’s influence on the basic size of market demand, and reflects the market demand due to the brand’s own influence. represents the expansion of the potential market size due to “platform power” when the manufacturer sells products at the platform, and reflects the size of this “platform power”. The square root of brand goodwill’s influence on demand reflects the saturation effect of brand goodwill’s influence on market demand. is the price sensitivity of consumers.
The recycling amount of waste electronics is affected by the recycling effort , assuming that the theoretical recycling amount of waste electronics is:
where is the basic recycling amount of waste electronics, and represents the impact of the recycling efforts of the recycling party on the theoretical recycling amount of waste products. When blockchain is not implemented for recycling, there is always the possibility of false recycling, and the real recycling volume is lower than the theoretical recycling volume because the recycling process is not transparent and cannot be effectively monitored. Suppose the real recycling volume of waste electronics is . When the recycler implements the blockchain, the real recycling volume is equal to the theoretical recycling volume, that is, .
In order to conform to the actual operation rules of the market, , namely , should be guaranteed. In addition, according to the research of Giovanni [39] and Liu et al. [40], it is assumed that the recycling cost of the waste electronic products of the recycler and the online marketing cost of the platform are:
where represents the recycling cost coefficient and online marketing cost coefficient, respectively. The marginal revenue of the manufacturer mainly comes from the wholesale price of electronic products and the recycling and remanufacturing , where is the marginal residual value of waste electronic products, which is also expressed as the marginal cost that can be saved by remanufacturing waste electronic products [41]. The marginal revenue of the platform mainly comes from the sales activities of products. The implementation cost of blockchain technology is , which is an exogenous variable [32]. In the extended model, we further consider the assumption that the blockchain implementation cost is a unit cost scenario to test the robustness of the model results. The manufacturer and the platform have the same time discount rate , and each seeks to maximize its own profit within the planning period . In the manufacturer recycling model, the present value of the manufacturer’s profit and the platform’s profit before and after blockchain technology is used are:
In the platform recycling model, the manufacturer enters into revenue sharing contracts with the platform for the residual value of waste electronics to incentivize the platform to recycle waste electronics. In this case, the residual value obtained by the platform is , . The residual value benefits obtained by the manufacturer and the platform under different recycling modes are shown in Table 3. Where denotes the residual value sharing ratio of waste electronics, also known as the revenue sharing coefficient. Thus, in the platform recycling model, the present value of the manufacturer’s profit and the present value of the platform’s profit without and with the blockchain technology are:

Table 3.
Residual value benefits under different recovery modes.
For the sake of clarity of the model formulation, the notations used in this paper and their meanings are listed in Table 4.

Table 4.
Notation and definitions.
4. Model Analysis
Based on the problem description and decision assumptions in the previous section, this section first discusses and in the benchmark model. Secondly, we explore and . The optimal steady-state strategies and profits of supply chain participants and brand goodwill under four different recycling models are obtained. In addition, we also analyze consumer surplus and social welfare under each model.
4.1. Manufacturer Recycling Model without Blockchain Technology ()
In the benchmark model without the use of blockchain technology, the manufacturer and the platform take the maximization of their own profits as the business objective and carry out Stackelberg differential game, dominated by the manufacturer in the planning period. In the recycling model dominated by manufacturer channels, the game order is as follows: the manufacturer first determines the wholesale price of the product. In the recycling process, in order to increase the recycling volume of waste electronics, the manufacturer needs to determine its recycling effort . The platform purchases products from the manufacturer and resells them to consumers and determines the retail price . In the sales process, in order to expand consumer market demand, the platform needs to conduct marketing activities and determine its marketing effort . The goal of the manufacturer and the platform is to maximize their respective profits by offering the optimal price. When waste electronics are recycled through the manufacturer, the optimization problems are as follows:
Proposition 1.
In the benchmark model, the optimal time evolution trajectory of brand goodwill under the manufacturer recycling model is:, the steady-state value of brand goodwill is, and the corresponding optimal steady-state strategy and optimal steady-state profit are:
Proof.
See the Appendix A. □
Proposition 1 states that all optimal policies are invariant over time. From a management point of view, it is easier to implement a constant price, effort decision, and marketing decision. We can more intuitively see that these decision variables are relatively static. The greater the impact of brand goodwill on consumer market demand (i.e., the greater the ), the more the platform will invest in marketing efforts. In addition, cost parameters, decay rate, and discount factor have a negative impact on the corresponding decisions.
The consumer surplus and social welfare under the manufacturer’s recycling model are calculated as shown in the Appendix A.
4.2. Platform Recycling Model without Blockchain Technology ()
In the benchmark model without blockchain technology, the platform recycling model is the same, wherein the manufacturer prioritizes the wholesale price of the product. The platform determines the retail price of the product and the marketing effort . The difference is that, in order to increase the recycling volume of waste electronics, its recycling effort is determined by the platform. The manufacturer and the platform take profit maximization as the decision-making goal, respectively, and their differential game model is as follows:
Proposition 2.
The optimal time trajectory of brand goodwill at platform recycling is:, where is brand goodwill steady-state, and the corresponding optimal steady-state strategy and profit are:
Proof.
See the Appendix A. □
Proposition 2 is very similar to Proposition 1. The wholesale price and the retail price of electronics and the marketing effort of the platform are the same; the difference is that, in the platform recycling model, the amount of recycling effort invested is determined by the platform, therefore the profit of the manufacturer and the platform varies slightly. In the manufacturer recycling model, the residual value of recycled waste electronics belongs to the manufacturer, that is, . During platform recycling, the residual value of recycled waste electronics will be divided into the platform part (), namely . The residual value obtained by the manufacturer is , and the share ratio is going to be between 0 and 1. The manufacturer encourages the platform to recycle by increasing the profits of the platform.
For consumer surplus and social welfare in platform recycling model, see Appendix A for specific calculation steps.
4.3. Manufacturer Recycling Model Empowered by Blockchain ()
In the manufacturer recycling model empowered by blockchain, the marginal revenue of the manufacturer will add a fixed cost of using blockchain in addition to the marginal revenue of product wholesale, of recycling and remanufacturing, and the marketing effort to increase recycling. The blockchain technology used here is self-built by the recycler, therefore there is only a fixed cost , assuming that the cost per unit of blockchain consumed per recycling is zero (as discussed in Section 7, when recyclers introduce blockchain technology in partnership with third parties). Therefore, when waste electronic products are recycled by the manufacturer empowered by blockchain, the optimization problems are as follows:
Proposition 3.
When using blockchain technology, the optimal time evolution trajectory of brand goodwill at manufacturer recycling is, the steady state of brand goodwill is, and the corresponding optimal steady state strategies and profits are:
Proof.
See the Appendix A. □
Proposition 3 is basically similar to Proposition 1, albeit with three main differences. First, the real recycling rate is 1 when using blockchain technology, which ensures that no loss and malicious damage to goods will occur during the recycling process. A false recycling rate of 0 will not have a negative impact on brand goodwill. As a result, the brand goodwill of the product is also improved. Second, when the true recycling rate equals 1, the investment of the recycling effort will increase, thus increasing the recycling amount of reverse waste electronics. Third, the introduction of blockchain technology incurs a fixed cost , and the manufacturers are likely to introduce blockchain technology only if . Conversely, a manufacturer with a profit less than zero will not introduce blockchain technology.
In the manufacturer recycling model empowered by blockchain, consumer surplus and social welfare are as follows. See Appendix A for specific calculation steps.
4.4. Platform Recycling Model Empowered by Blockchain ()
In the blockchain-enabled platform recycling model, the platform will introduce blockchain technology to generating a fixed cost . Thus, the main sources of marginal revenue for the platform are the sales activity of the product (namely, ), the marketing effort invested by the platform, and the fixed cost of the blockchain. Therefore, when blockchain-enabled waste electronics are recycled through the platform, and the manufacturer and the platform maximize their respective profits by offering the optimal price, and the optimization problem is as follows:
Proposition 4.
In the case of blockchain empowerment, the optimal time evolution trajectory of brand goodwill during platform recycling is , the steady-state of brand goodwill is, and the corresponding optimal steady-state strategy and profit are:
Proof.
See the Appendix A. □
Proposition 4 is essentially similar to Proposition 3 in that the wholesale price and the retail price of the electronics and the marketing investment in the platform are the same, as is the brand goodwill of the product. The difference is that the platform gains a percentage of the salvage value of the waste electronics, but the fixed cost of the blockchain is spent by the platform, and the platform may introduce blockchain technology only when .
In the platform recycling model empowered by blockchain, consumer surplus and social welfare are as follows. See Appendix A for specific calculation steps.
5. Implementation Conditions and Value of Blockchain Technology
In this section, we first compare the optimal steady-state profit under the four recycling models, and then we analyze the manufacturer and platform preferences in the scenarios of the four recycling models. Finally, the consumer surplus and social welfare in different recycling models are analyzed, and it is concluded that the profit (economics) and social welfare (society) of each participant we are concerned about are improved when using blockchain technology. (In the numerical example in Section 6, it is concluded that the recycling rate of waste electronic products is also significantly improved with the use of blockchain technology.)
5.1. Implementation Conditions of Blockchain
In the manufacturer recycling model, the manufacturer’s profit and platform profit are compared respectively when blockchain technology is used and not used, and the following propositions are obtained.
Proposition 5.
In the manufacturer recycling model, both the manufacturer and the platform prefer to use blockchain technology when the self-constructed cost of the blockchain satisfies
In the manufacturer recycling model, we first compare manufacturer profits with and without blockchain technology.
It is found that when
the manufacturer’s profit when using blockchain technology is greater than when not using it in the manufacturer recycling model, i.e.,. That is, using blockchain technology is better than not using blockchain technology for the manufacturer.
Secondly, the impact of the presence or absence of blockchain technology on their profits was compared from the perspective of the platform..
Finding that the profits of the platform using blockchain technology are constantly greater than those of the platform not using blockchain in the manufacturer recycling model,. That is, it is always better for the platform to use blockchain technology in the manufacturer recycling model than non-blockchain technology.
Overall, in the manufacturer recycling model, when the fixed cost of using blockchain technology satisfies
the manufacturer and platform are aligned in choosing whether to use blockchain technology, and both are willing to use blockchain technology.
In the platform recycling model, the manufacturer’s profit and platform’s profit are also compared respectively with and without blockchain technology, and the following propositions are obtained.
Proposition 6.
In the platform recycling model, both the manufacturer and platform prefer to use blockchain technology when the self-constructed cost of the blockchain is
In platform mode recycling, the impact of blockchain on manufacturer’s profits is first compared:
It is found that the manufacturer profit, when blockchain technology is used, is greater than when not used, that is, . For the manufacturer, using blockchain technology is always better than not using blockchain technology in platform mode recycling.
Secondly, we analyze and compare the profits of the platform with and without blockchain technology:
It can be concluded that, when
the profit of the platform with blockchain technology is greater than that without blockchain technology, ; that is, for the platform, using blockchain technology is better than not using.
In general, in the platform recycling model, both the manufacturer and the platform prefer to use blockchain technology when the fixed cost of using blockchain
Combining Propositions 5 and 6, we arrive at Proposition 7, as follows:
Proposition 7.
When the self-constructed cost of blockchain
the manufacturer and platform prefer to use blockchain technology, whether in the manufacturer recycling model or the platform recycling model.
In the manufacturer recycling model, the condition that both the manufacturer and the platform will choose to use blockchain technology from their own profit maximization is:
In the platform recycling model, the condition that both the manufacturer and the platform will choose to use blockchain technology from their own profit maximization is:
We take an intersection ofhere; that is,, where
When the fixed cost of blockchain is , in both recycling models, the economic benefit of using blockchain technology is better than that of not using blockchain technology, both for the manufacturer and the platform.
5.2. Implementation Value of Blockchain
In the absence of blockchain technology, we will compare the profits of the manufacturer and the platform under the manufacturer recycling model and platform recycling model, respectively, and arrive at the following proposition.
Proposition 8.
Without the use of blockchain technology, the manufacturer will choose the manufacturer recycling model; however, the platform does not benefit more from it, and the supply chain cannot reach coordination.
In the absence of blockchain technology, we first compare manufacturer profits under the manufacturer recycling model versus the platform recycling model. From Propositions 1 and 2, we can conclude that ; there is always . Therefore, when blockchain technology is not used, it is always better for the manufacturer to choose the manufacturer recycling model than the platform recycling model. Then, we compare the profit of the platform in both models analytically; again, by Propositions 1 and 2, we can conclude that ; there is always . Therefore, the platform recycling model is always better than the manufacturer recycling model for the platform when blockchain technology is not used. Overall, without blockchain, the manufacturer will opt for the manufacturer recycling model without the platform gaining more revenue from it, thus the supply chain cannot be coordinated.
With the introduction of blockchain technology, the profits of the manufacturer and the platform under the manufacturer recycling model and platform recycling model are analyzed and compared, resulting in Proposition 9, as follows.
Proposition 9.
When the self-built cost of blockchain, the manufacturer chooses the manufacturer recycling model, and the platform can also gain more revenue from it, and the supply chain reaches coordination.
With the introduction of blockchain technology, we first analyze and compare the manufacturer’s profit under the manufacturer recycling model and the platform recycling model. From Propositions 3 and 4, we can derive , when the fixed cost of introducing blockchain technology , the manufacturer’s profit under the manufacturer recycling model is greater than that under the platform recycling model, , namely, the manufacturer recycling model is superior to the platform recycling model for the manufacturer. Secondly, we analyze and compare the profit of the platform under the two recycling models, . When the fixed cost of blockchain , the profit of the platform under the manufacturer recycling model is smaller than those under the platform recycling model, . That is, the platform recycling model is better than the manufacturer recycling model from the perspective of the platform.
From the above comparative analysis, it is clear that, when the manufacturer and the platform have the ability to build their own blockchain technology, the manufacturer will gain more from the manufacturer recycling model, while platforms will gain more from the platform recycling model. For the above two ranges, we take an intersection of the fixed cost of blockchain, that is, . When is within this interval, the manufacturer recycling model outperforms the platform recycling model from the perspective of both platform and manufacturer. In general, when the fixed cost for self-built blockchain, the manufacturer recycling model is better than the platform recycling model for the manufacturer and the platform, and the supply chain achieves coordination. From Propositions 8 and 9, it is clear that the use of blockchain technology enables supply chain coordination from an economic perspective. That is, when the fixed cost of blockchain self-construction , the manufacturer and the platform will both gain more benefits when the manufacturer chooses the manufacturer recycling model.
We analyze how blockchain technology affects consumer surplus and social welfare from a social perspective. We first analyze by comparing consumer surplus and social welfare under two recycling models without blockchain technology.
Proposition 10.
From the consumer surplus and social welfare in Propositions 1 and 2, it is clear that the consumer surplus in the manufacturer recycling model and in the platform recycling model are equal when blockchain technology is not used. The comparison of social welfare under the two recycling models,, indicates that social welfare under the manufacturer recycling model is superior to that under the platform recycling model when blockchain technology is not used.
Secondly, we compare consumer surplus and social welfare in the two recycling models using blockchain technology, resulting in Proposition 11, as follows.
Proposition 11.
The social welfare under the manufacturer recycling model is always better than that under the platform recycling model, regardless of whether blockchain technology is used. Consumer surplus under blockchain empowerment is better than that without blockchain technology.
From the consumer surplus and social welfare in Propositions 3 and 4, it is clear that the consumer surplus in the manufacturer recycling model and that in the platform recycling model are equal when using blockchain technology. The comparison of social welfare under the two recycling models, , found that the social welfare under the manufacturer recycling model is always better than that under the platform recycling model when using the blockchain. Combining Proposition 10, an analysis comparing social welfare under the two models without blockchain technology, we conclude that social welfare under the manufacturer recycling model is always better than that under the platform recycling model, regardless of whether blockchain technology is used. For the longitudinal comparison, i.e., the impact of whether or not to use blockchain on the social welfare of the manufacturer recycling model and the platform recycling model, respectively, we assign values to them in the numerical algorithm in Section 6 and then compare them analytically.
To sum up, we find that consumer surplus in the manufacturer recycling model is the same as that in platform recycling model regardless of whether blockchain technology is used. Not only is the consumer surplus the same, but we can see from Propositions 1, 2, 3, and 4 that the wholesale price of electronics, the retail price, and the marketing effort of the platform are the same for both recycling models, meaning that the optimal pricing of electronics and the marketing strategy of the platform are independent of the recycling model is chosen. Therefore, we use the superscript B to denote the consumer surplus under both recycling models when using blockchain technology and the superscript N to denote the consumer surplus under both recycling models when not using blockchain technology, and then analyze and compare the effect of blockchain technology on the consumer surplus again, finding that , that is to say, the consumer surplus with blockchain technology is better than that without blockchain technology.
Proposition 12.

Considering the impact of a relevant parameter on brand goodwill, retail and wholesale prices of electronics, marketing efforts of the platform, and recycling efforts of the recycler, this paper analyzes the key parameters in the manufacturer recycling model and the platform recycling model in both cases with and without the use of blockchain technology, as shown in Table 5.

Table 5.
Sensitivity analysis of relevant parameters.
Since the wholesale price, retail price, marketing effort of the platform, and brand goodwill of the electronics are independent of which recycling model is used, we directly use , , , to denote the wholesale price, retail price, marketing effort of the platform, and brand goodwill, respectively, when blockchain technology is not used, and use , , , to denote them when blockchain technology is used, respectively.
As can be seen from the above table, brand goodwill , retail price , wholesale price , and marketing effort under the two recycling models with or without blockchain technology increase with the increase in the influence coefficient of goodwill on basic market demand, platform power , and the influence coefficient of marketing effort input on brand goodwill. All decrease with the increase in the coefficient of platform marketing cost , price sensitivity of consumers, the discount rate , and the coefficient of the decay of brand goodwill . In the absence of blockchain technology, if the real recycling is increased, the impact of the false recycling rate on the brand goodwill of the product will be reduced, thus improving the brand goodwill of the product. Based on the expressions for each control variable that we derived in Section 4 and Section 5, we can find that the wholesale price of the product, the retail price, the marketing effort, and the recycling effort of the platform in both recycling model strategies increase as the real recycling rate increases.
In the platform recycling model, the platform delivers the recovered electronics to the manufacturer, and gains a share of the residual value of . The higher the share ratio is, the more the platform will invest in recycling efforts and increase the recycling amount, thus increasing the total profit of the platform. In other words, in the platform recycling model, regardless of whether blockchain technology is adopted, the platform’s recycling effort will increase with the increase in the residual value ratio . We also find that the recycling effort in both recycling models increases with the marginal residual value of the recycled scrap product and the coefficient of the impact of the recycling effort on the amount of waste electronics recycled, and decreases with the increase in the recycling effort cost coefficient , regardless of whether blockchain technology is used. It is easy to explain that, when the cost coefficient of recycling effort increases, the recycler will certainly reduce the recycling effort accordingly unless there is sufficient funding available to support it. When the marginal residual value of waste electronics increases, it will directly improve the profit of the recycler, therefore the recycler will continue to increase the recycling efforts to improve the recycling amount. When the coefficient of the impact of the input of recycling effort on the amount of waste electronics recovered increases, the improvement of recycling efforts will directly increase the recycling amount of waste electronics, improve the total residual value, and thus improve the profit of the recycler, which is in line with practical significance.
6. Numerical Analysis
In this section, we perform numerical analysis to gain more management insights by examining the following questions:
- (1)
- The effect of the change in the share ratio on the growth rate of recycling rate, the growth rate of supply chain profit, and the growth rate of social welfare;
- (2)
- The impact of the ratio of real to theoretical recycling volume on profit of manufacturer, platform and supply chain, and social welfare under two recycling models;
- (3)
- The impact of platform power on profit of manufacturer, platform and supply chain, and social welfare under two recycling models;
- (4)
- Proposition 7 shows that, when , both the manufacturer and the platform prefer to use blockchain technology in both recycling models. Proposition 9 shows that, when the self-built cost of the blockchain is , the manufacturer chooses the manufacturer recycling model and the platform can also gain more revenue from it. Then, whether there is an intersection between the two, both the manufacturer and the platform will choose the manufacturer recycling model empowered by blockchain from their own interests. If so, what is the range of as well as , and are the economic, environmental, and social aspects of choosing the manufacturer recycling model enabled by blockchain better than other modes?
In this section, based on the actual situation, basic parameters are set as follows:
6.1. Brand Goodwill Time Trajectory Chart
The initial goodwill of the electronics brand is and , respectively, with and . The time trajectory of product brand goodwill and the time trajectory of product retail price under the four recycling models of manufacturer recycling and platform recycling without blockchain empowerment, and manufacturer recycling and platform recycling with blockchain empowerment, are shown below.
As can be seen from Figure 1, the time trajectory of brand goodwill under the four recycling models has nothing to do with the initial goodwill. A higher initial goodwill will decay with an increase in time, while a lower initial goodwill will improve with an increase in time; however, both will eventually converge to a steady state. Brand goodwill in both recycling models is the same regardless of whether blockchain is used, though brand goodwill with blockchain enabled is higher than that without blockchain. When brand goodwill is high, that is, in the recycling model enabled by blockchain, consumer market demand and the wholesale and retail prices of products are increased, and the profits of the manufacturer and the platform are also increased. However, the use of blockchain technology leads to a double marginalization effect. The retail price of electronic products changes with the change of goodwill, thus the time trajectory of the retail price of products under the four recycling models in Figure 2 is similar to that in Figure 1.
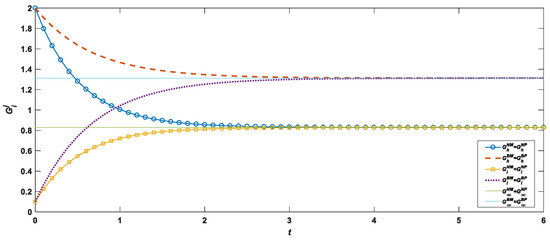
Figure 1.
Time trajectory diagram of brand goodwill under four recycling models.
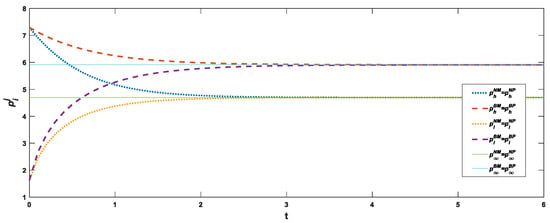
Figure 2.
Time trajectory of product retail price under four decision modes.
6.2. Influence of the Ratio of Real to Theoretical Recycling (Real Recycling Rate) on Profits of Supply Chain Participants and Supply Chain, and Social Welfare
In the absence of blockchain empowerment, we conduct a comparative analysis of the impact of the true recycling rates on manufacturer profits, platform profits, supply chain profit, and social welfare under the two recycling models. The supply chain profit is the sum of manufacturer profit and platform profit, and the supply chain profit under the manufacturer and the platform recycling model, are and .
From Figure 3, Figure 4 and Figure 5, it can be clearly seen that the real recycling rate has a positive impact on profits of the manufacturer, the platform and overall supply chain, and social welfare under the two recycling models. With the gradual increase in the real recycling rate, it has a greater impact on supply chain profits and social welfare in the manufacturer recycling model than in the platform recycling model. As can be seen from Figure 3, the effect of the real recycling rate on the manufacturer’s profit and platform profit under two recycling models is that the manufacturer’s profit under the manufacturer’s recycling model is greater than the platform profit under the platform recycling model, and greater than the manufacturer’s profit under the platform recycling model and greater than the platform profit under the manufacturer recycling model. As can be seen from Table 5, with an increase in the real recycling rate, the wholesale price, retail price, brand goodwill and recycling efforts of the recycler all increase accordingly. The increase in recycling efforts increases the recycling amount of reverse waste electronic products. Moreover, an increase in the real recycling rate will increase the total residual value of waste electronic products. Therefore, under the influence of the above factors, regarding the manufacturer’s mode recycling, the manufacturer’s profit will increase more with an increase in the real recycling rate, and the residual value of the waste products’ recycling all belong to the manufacturer; the profit of the platform will not be affected by the residual value, therefore the real recycling rate has a smaller image of the platform profit under the manufacturer recycling model. In the platform recycling model, the manufacturer signs a revenue-sharing contract with the platform for the residual value of waste electronics, therefore the platform will have a residual value share ratio of . Therefore, as the real recycling rate increases, its impact on the platform profit under the platform recycling model is greater than that under the manufacturer recycling model.
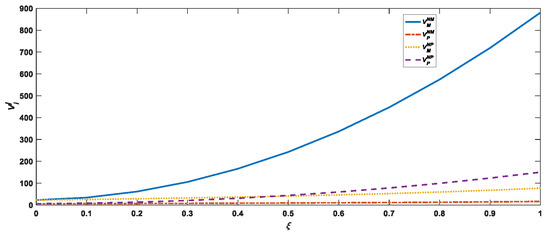
Figure 3.
Impact of real recycling rate on profits of participants in the supply chain.
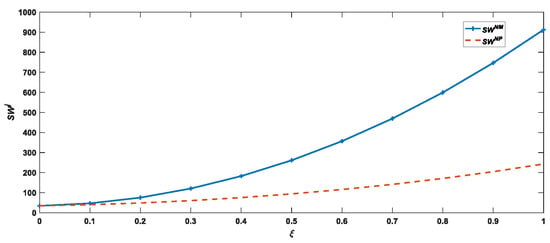
Figure 4.
Impact of real recycling rate on social welfare.
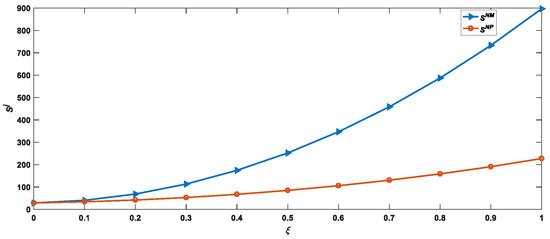
Figure 5.
Impact of true recycling rate on supply chain profit.
6.3. Impact of Platform Power on Profits of Supply Chain Participants and Supply Chain and Social Welfare
A comparative analysis of the impact of platform power on manufacturer profit, platform profit, supply chain profit, and on social welfare under two recycling models.
As seen in Figure 6, the impact of platform force on manufacturer profit is positively and essentially the same in both recycling models (manufacturer recycling and platform recycling) without the use of blockchain technology, that is, . The impact of platform power on manufacturer profits when using blockchain technology is also positively correlated and essentially the same in both recycling models, that is, . Similarly, the impact of platform power on platform profit is positively and identically correlated in both recycling models, that is, , regardless of whether blockchain technology is used. In both recycling models, the impact of using blockchain technology on the profitability of each participant is more pronounced than the platform power without blockchain technology.
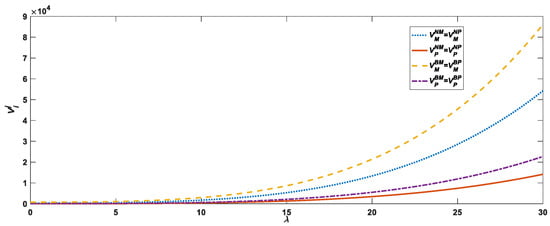
Figure 6.
Impact of platform power on profit of each participant in the supply chain.
From Figure 7 and Figure 8, it can be seen that the impact of platform power on supply chain profit and social welfare is the same in the manufacturer recycling and platform recycling models without the use of blockchain technology, namely, and . Similarly, the impact of platform power on supply chain profit and social welfare is the same in the manufacturer recycling and platform recycling models with the use of blockchain technology, namely, and . Compared with the case without blockchain technology, the impact of platform power on supply chain profit and social welfare is more obvious when using blockchain technology, and the platform power is always positively correlated with supply chain profit and social welfare regardless of whether blockchain technology is used or not and regardless of which recycling model is adopted.
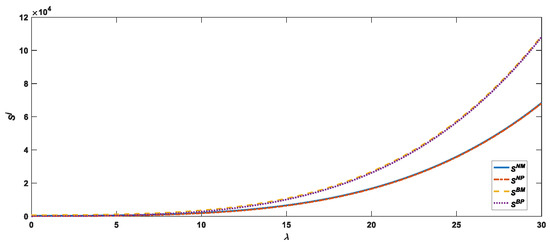
Figure 7.
Impact of platform power on supply chain profit.
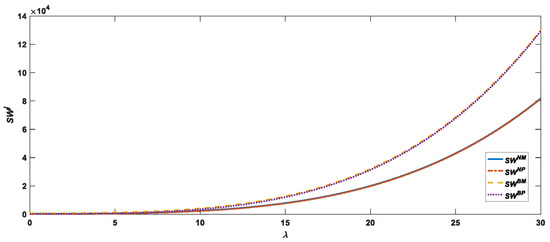
Figure 8.
Impact of platform power on social welfare.
From the analysis of Figure 6, Figure 7 and Figure 8, we can conclude that the impact of platform power on the profits of the manufacturer and the platform, supply chain profits, and social welfare is more pronounced when using blockchain technology as opposed to not using blockchain technology. In other words, for every unit of increased platform power, the profits of the manufacturer, the platform and the CLSC, as well as the social welfare, increase more in each of the two recycling models under blockchain empowerment than they would have without it. As shown in Table 5, platform power is positively related to the wholesale price of the product, retail price, marketing effort of the platform, and brand goodwill, therefore the impact of platform power on the profitability of each supply chain participant as well as social welfare is also positive. The introduction of blockchain technology will increase the real recycling rate and brand goodwill and increase the profit of each participant in the supply chain as well as social welfare. Therefore, under the dual role of platform power and blockchain technology, its impact on the profit of each participant in the supply chain, supply chain profits, and the social welfare will increase even more.
6.4. Impact of Residual Value Share Ratio and Blockchain Fixed Cost of Waste Electronics on Recycling Model Selection
From Proposition 9, when the fixed cost of the blockchain satisfies a certain range, the benefits of both the manufacturer and the platform will be better than the platform recycling model when the manufacturer chooses the manufacturer recycling model. The impact of the residual value share ratio and blockchain fixed cost on the choice of recycling model is verified and reflected by numerical arithmetic examples from the economic perspective of the manufacturer and the platform, as shown in Figure 6, Figure 7, Figure 8 and Figure 9.
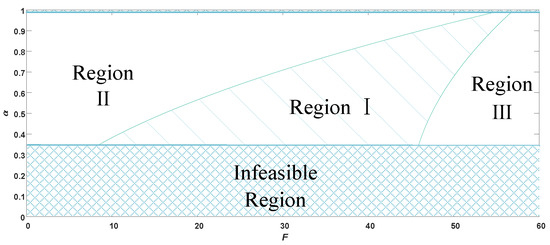
Figure 9.
Optimal recycling model selection from an economic perspective under blockchain empowerment.
From Figure 9, it can be seen that, when the residual value share ratio , the manufacturer chooses the manufacturer recycling model in the case of using blockchain, and the platform will also gain more revenue from it. Region I and Region II are the ranges from which the platform can also gain more revenue when the manufacturer chooses the manufacturer recycling model. However, with a residual value share ratio of almost 1, why does the platform still obtain more from the manufacturer recycling model?
This is easy to explain. We can see clearly in the figure above that, when the share ratio reaches a maximum value of 0.98, the fixed cost of self-built blockchain technology is also high. The cost of introducing a blockchain technology alone is expensive, and even if all the residual value of the waste electronics goes to the platform, it may not offset the cost of the self-built blockchain. Region I and Region III are the range of conditions for the manufacturer to choose the manufacturer recycling model based on their maximization of benefits. When the share ratio and the fixed cost of blockchain are in Region I, both the manufacturer and the platform will prefer the blockchain-enabled manufacturer recycling model.
Figure 10 reflects the impact of the residual share ratio and blockchain fixed cost on the choice of recycling model from a social perspective when using blockchain technology.
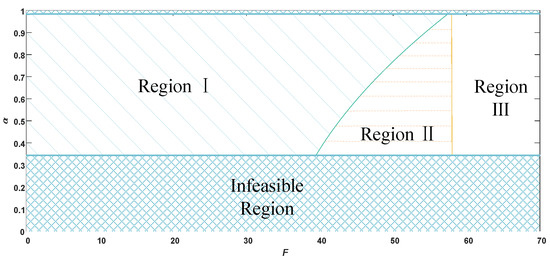
Figure 10.
Optimal recycling model selection from a social perspective under blockchain empowerment.
From Figure 10, when the share ratio and the fixed cost of blockchain are within Region I, the social welfare under blockchain empowerment is superior to that without the use of blockchain technology in the platform recycling model. In the manufacturer recycling model, social welfare is better with blockchain technology than without it when the share ratio and the fixed cost of blockchain are within Region I and Region II. It can be clearly seen that, within Region I, the social welfare with blockchain empowerment is better than that without blockchain technology in both the manufacturer and platform recycling models. This is also the result of the longitudinal comparison of the impact of using or not using blockchain on the social welfare in the manufacturer recycling model and the platform recycling model, respectively, in Section 5. However, in Region III, manufacturers and platforms are not inclined to use blockchain technology due to the high fixed cost of blockchain. As seen in Proposition 11, the manufacturer recycling model is superior to the platform recycling model from a social welfare perspective, regardless of whether blockchain technology is used. Therefore, we conclude that the use of blockchain technology and the choice of the manufacturer recycling model is superior in terms of social welfare when the share ratio and the fixed cost of blockchain are within Region I. In Region III, it is preferable not to use blockchain technology and to choose the manufacturer recycling model.
Make the share ratio of the residual value to compare the impact of the blockchain technology on the recycling rate in different recycling models.
As shown in Table 6, the recycling rate is higher when using blockchain technology than when not using it, regardless of whether the manufacturer recycles or the platform recycles. When using blockchain technology, the manufacturer recycling model has a higher recycling rate than the platform recycling model. Therefore, from the perspective of the recycling rate (environment), it is optimal to choose the manufacturer recycling model under blockchain empowerment.

Table 6.
Effect of the presence or absence of blockchain on the recycling rate under the two recycling models.
Next, we analyze the impact of the residual value share ratio and the blockchain fixed cost on the choice of recycling model from the joint perspective of economic, environmental, and social effects under the premise that the choice of a blockchain-enabled recycling model for the manufacturer is known to be the best for the environment, as shown in Figure 11.
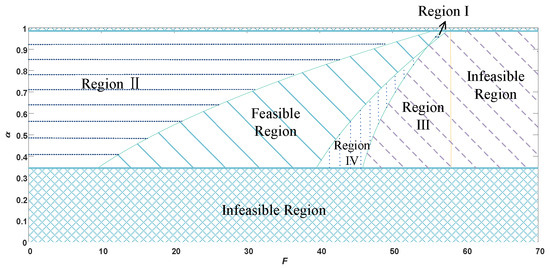
Figure 11.
Optimal recycling model selection from a triple benefit perspective under blockchain empowerment.
As can be seen from Figure 11, Region I, Region II, and Feasible Region are preferable from the perspective of social welfare to use blockchain technology and select the manufacturer recycling model. From a manufacturer and platform profit (economic) point of view, it is preferable to choose a manufacturer recycling model within the Feasible Region. It is found that, when the share ratio and the fixed cost of blockchain are within the Feasible Region, the introduction of blockchain technology and the choice of manufacturer recycling model are better for economic, social, and environmental benefits compared to the choice of other models. In other scopes and other recycling models, the common improvement of the benefits of economy, environment, and society cannot be achieved.
6.5. Influence of the Change of Revenue Sharing Coefficient on Economy, Society, and Environment
In the platform recycling model empowered by block chain, the influence of changes in the revenue sharing coefficient on supply chain profit growth rate (economy), recycling growth rate (environment), and social welfare growth rate (society) is further analyzed, as shown in Table 7.

Table 7.
Impact of changes in share ratio on economy, society, and environment.
As seen in Table 7, the supply chain profit growth rate (economic), social welfare growth rate (social), and recycling rate growth rate (environmental) all increase as the share ratio increases. When , the growth rate of the three types of benefits have been increasing, although it is negative. Moreover, it can be seen from Figure 11 that, when , the choice of manufacturer recycling model is optimal from both economic and social perspectives. In the above table, the growth rate of the triple benefits is positive when , which means that it is better with blockchain technology than without it. This reinforces our conclusion above that economic, environmental, and societal improvement can be achieved when and are within the Feasible Region in Figure 11 through the introduction of blockchain technology and the choice of manufacturer recycling model.
7. Extension with Unit Cost of Blockchain
In the main model, we explored how blockchain technology affects the choice of recycling model from the perspective of the triple benefits, and concluded that, when and are within the Feasible Region in Figure 11, the introduction of blockchain technology and the choice of the manufacturer recycling model can result in better economic, social, and environmental outcomes. In this section, we consider another form of introducing blockchain technology, assuming that the recycler partners with a third party to rent the blockchain technology, that is, for each use of the blockchain technology, the recycler pays a fee to the third party (the owner of the blockchain technology), being the unit cost of using the blockchain technology. In this case, we will only discuss manufacturer recycling and platform recycling when using blockchain technology.
The Stackelberg differential game model for the choice of two recycling models by the manufacturer and the platform to maximize their respective interests is as follows.
Manufacturer recycling model empowered by blockchain:
Platform recycling model empowered by blockchain:
In both recycling models, the Hamilton–Jacobi–Bellman (HJB) equations are constructed for the platform and the manufacturer successively, and their marketing strategies and recycling effort strategies satisfy the respective HJB equations. The equilibrium solution of the strategy is solved by using the inverse induction method.
Proposition 13.
Balance strategy in manufacturer recycling model:,,,, where.
Proposition 14.
Balance strategy in platform reclamation mode:,,,,where.
Proof.
See the Appendix A. □
It can be found that the balance strategy of wholesale price, retail price, and marketing effort of the platform remains unchanged when renting blockchain technology from a third party compared with self-built blockchain technology. The only difference is that the recycling effort is reduced in both recycling models.
We still make to analyze the influence of the unit cost of the blockchain on the choice of recycling model when using blockchain technology.
As shown in Figure 12, the range of the residual value share ratio of waste electronics is the same as in Section 6, which is unchanged. When the unit cost of using blockchain lies within Region (P), it is better for the manufacturer to choose the platform recycling model than the manufacturer recycling model; however, when the manufacturer chooses the platform recycling, the cost of the platform using blockchain technology is greater than the residual value, therefore this range is not desirable. When the unit cost of using the blockchain is within Region M, the manufacturer chooses the manufacturer recycling model. In Figure 13, we can see that the platform prefers the manufacturer recycling model when the residual value share ratio and the unit cost of the blockchain are within Region M. From the perspective of maximizing platform profits, the platform will prefer the platform recycling model only when the residual value sharing ratio and unit cost of blockchain are within Region P, under the condition that the recycling effort of the recycler is positive. When lies within Region (P), that is, when the manufacturer chooses the platform to recycle, the platform will gain more revenue; however, within this range, the cost of using blockchain technology is greater than the residual value, and the platform will not use the blockchain to recycle, therefore it is contradictory in Region (P) region.
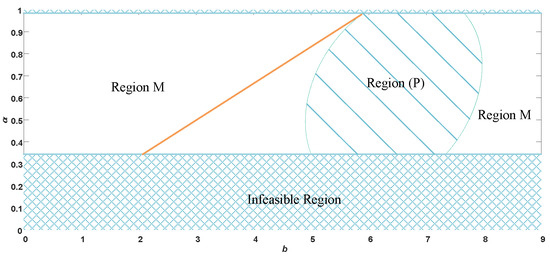
Figure 12.
Impact of blockchain’s unit cost on the manufacturers’ choice of recycling model.
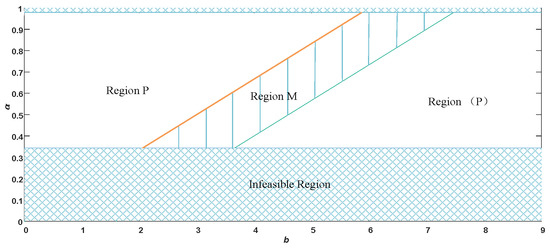
Figure 13.
Influence of platform benefits on the choice of recycling model under the unit cost of blockchain.
In the light of the above analysis, when introducing blockchain technology in the form of third-party cooperation, do the manufacturer and the platform models respectively start from maximizing their own interests, and is there a certain range of unit cost of blockchain technology so that, when the manufacturer chooses a certain recycling model, both the manufacturer and platform can gain more from it?
We aggregate the impact of blockchain’s unit cost on the manufacturers’ and platform’s preferences for recycling models, as shown in Figure 14. It is found that both the manufacturer and the platform prefer the manufacturer recycling model when the unit cost of the blockchain lies within Region I. When the platform introduces blockchain technology as the recycler, the platform not only needs to pay the cost of using the blockchain per unit, but also needs to invest some recycling effort, and the platform is charging a percentage of the total residual value of the waste electronics, therefore the cost of the blockchain that is acceptable to the platform is lower, while, when the manufacturer is the recycler, the total residual value of the waste electronics goes to the manufacturer, thus both the manufacturer and the platform will prefer the manufacturer recycling model when is located within Region II. Moreover, when the unit cost of the blockchain is low, namely, within Region I, the manufacturer will prefer the manufacturer recycling model and the platform will prefer the platform recycling model. The use of blockchain can both enhance product brand goodwill and improve the recycling rate of waste products, increasing the recycling volume and thus the profitability of the recycler, therefore both the manufacturer and the platform will each prefer to recycle.
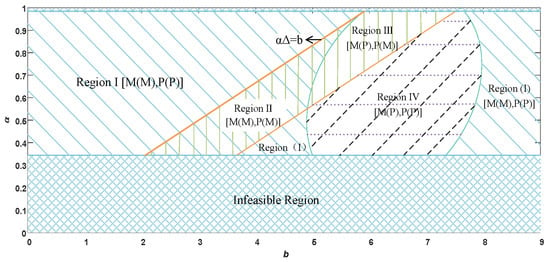
Figure 14.
Impact of unit cost of blockchain on recycling model selection.
Within Region IV, both the manufacturer and the platform will prefer the platform model recycling; however, when choosing the platform recycling model, it is necessary to ensure that the unit residual value obtained by the platform is greater than the unit cost of the blockchain, namely, , therefore it is undesirable within Region IV. Moreover, all the ranges on the right side of restriction are undesirable when choosing the platform recycling model, that is, within Region III, Region IV, and Region (I).
In this case, essentially the same trade-offs as in the main model can be found. When the cost of using blockchain technology is between two thresholds, the optimal decision for the manufacturer and the platform can be unified, that is, the blockchain-enabled manufacturer recycling model. That said, the same conclusions we draw apply when replacing the self-constructed cost of using blockchain technology with the unit cost of working with a third party.
8. Discussion and Conclusions
The final discussion and conclusions mainly highlight the contributions related to the study results. This study has important implications for the sustainability of platform-based, closed-loop supply chains, especially for companies in the electronics category that can better develop recycling strategies to increase environmental benefits and play an important role in promoting long-term sustainable development.
8.1. Discussion
The main objective of this paper is to explore how electronics manufacturers can develop recycling strategies and consider the inclusion of online platforms as recyclers and consider the recycling function of platforms on the basis of platform resell. Therefore, the impact of blockchain technology on the selection of recycling models for electronics manufacturers is considered on the basis of a platform-based, closed-loop supply chain.
It is different from the static game of enterprises considering immediate interests found in previous studies. With the help of differential game theory and Bellman’s continuous dynamic programming method, this paper explores the optimal operational decisions of enterprises with the goal of long-term profits and integrates the impact of current decisions on current profits and future performance, which is more in line with the actual decision-making environment of enterprises.
In addition, we have innovated the recycling model. Most of the research on recycling models are about offline recycling, with recycling channels focused on manufacturers, retailers, and third parties [17,18,19,20,21,22,23]. We further considered the online platform as a recycling channel and added blockchain technology to the recycling process. The use of blockchain technology can not only expand the market scale in the forward sales process, but also increase the actual recycling amount in the reverse recycling process, which has a positive impact on the whole closed-loop supply chain process.
8.2. Conclusions
This paper studies the selection of recycling models for waste electronics in a platform-based, closed-loop supply chain empowered by blockchain. Specifically, we considered a dynamic closed-loop supply chain consisting of an electronics manufacturer and an online platform. In the forward selling process, electronics manufacturers resell their products through the platform. In the reverse recycling process, manufacturers can either recycle by themselves or use online platforms to recycle waste electronics. In this paper, we study the strategies of four recycling models, namely, the manufacturer recycling model () and platform recycling model () without blockchain technology, and the manufacturer recycling model () and platform recycling model () with blockchain enabled. This paper focuses on the impact of blockchain technology on the selection of recycling models for waste electronics from the perspective of profit maximization for the manufacturer and the platform. Next, we analyze the consumer surplus and social welfare under each recycling model, and further consider the possibility that blockchain technology can improve the “triple benefits”. Finally, the model for unit cost used by blockchain technology is expanded and several main findings are made.
We found that blockchain technology can solve the challenge of uncoordinated supply chain in the reverse recycling process. In the absence of the introduction of blockchain technology, the manufacturers prefer to recycle waste electronics themselves, however the platform cannot gain more revenue from it and the supply chain is difficult to coordinate. The introduction of blockchain technology can effectively solve this problem. When the fixed cost of the blockchain and the share ratio of the residual value of waste electronics are between two thresholds, both the manufacturer and the platform prefer the manufacturer to recycle the waste electronics. This means that both receive more out of it and the supply chain is coordinated.
The blockchain-enabled manufacturer recycling model can improve profits for participants in the supply chain. Blockchain technology makes the reverse recycling process of the closed-loop supply chain more transparent and easier to supervise, therefore the true recycling rate of waste electronics can be significantly improved. When the real recycling rate increases, the total residual value of waste products will also increase. Therefore, the recycler will increase the investment in recycling efforts, thus improving the recycling amount of waste electronics and further increasing the profit of the recycler. However, using blockchain technology by the recycler is not a small expense. For platforms, when the fixed cost of the blockchain is too high, the higher residual value share will not offset the cost of using blockchain technology for the platform. As a result, platforms will then abandon the use of blockchain technology or abandon recycling. However, the use of blockchain technology will increase the brand goodwill of the product and thus its profits, therefore the platform continues to prefer blockchain technology. Moreover, for manufacturers, the use of blockchain technology will also increase their profits. When the manufacturer recycles, all of the residual value of the waste electronics goes to the manufacturer, thus making it more profitable. Although the cost of using blockchain is higher, using blockchain technology can be more profitable for manufacturers. In the numerical analysis, we concluded that, in the problem of choosing the recycling model, when the ratio of the fixed cost of blockchain technology and the share of the residual value of waste electronics is in a certain interval, the model in which both the manufacturer and the platform can gain more revenue is the blockchain-enabled manufacturer recycling model. Moreover, the same applies when the fixed cost of a blockchain input becomes a marginal cost of use.
The blockchain-enabled manufacturer recycling model can achieve economic, environmental, and social “triple benefits”. This means that, in this model, the profit of supply chain, the recycling rate of waste electronics, and social welfare are significantly improved. Specifically, blockchain technology can improve the real recycling rate of waste electronics, so that all recycled products can be truly and effectively recycled, thus increasing the real recycling volume. Thus, the recycling rate is higher with blockchain than it is without blockchain. Blockchain technology further improves the consumer trust effect by increasing the amount of real recycling and reduces the impact of false recycling rates on goodwill, thus improving the brand goodwill of electronic products. When the brand goodwill of a product increases, the retail and wholesale prices of electronics also increase, which leads to a double marginal effect and indirectly affects the demand in the consumer market. However, the use of blockchain technology will also increase consumer surplus, and the increased consumer surplus will compensate for the loss due to the double marginal effect. Moreover, as the profits of supply chain increase with blockchain empowerment, social welfare increases as well. Based on the numerical analysis, we obtain an interesting finding that the recycling rate and social welfare are always higher in the manufacturer recycling model than in the platform recycling model. Therefore, we conclude that, in the closed-loop supply chain, the blockchain-enabled recycling model for manufacturers can achieve the improvement of the “triple benefits”. The numerical analysis also verifies our conclusion that, in the problem of the selection of a recycling model, when the fixed cost of blockchain and the share ratio of the residual value of waste electronics are between two thresholds, the condition to meet the common improvement of the “triple benefit” is the blockchain-enabled manufacturer recycling model.
This paper highlights the important role of blockchain technology for the recycling of waste electronics. It considers the recycling function of the platform on the basis of platform resell and analyzes the impact of blockchain technology on the selection of recycling model (manufacturer recycling/platform recycling) for waste electronics in a platform-based, closed-loop supply chain, filling in this aspect of the study and providing some valuable management insights for relevant enterprises and personnel, as follows.
For electronics manufacturers, the recycling of waste electronics will reduce the waste of resources and environmental pollution and other conditions, which is the specific performance of enterprises to fulfill their social responsibility. It has a high economic and social value and plays an important role in promoting long-term sustainable development. Blockchain technology can make the whole process of the supply chain more transparent through its visibility and traceability features. Manufacturers can leverage blockchain technology in the process of reverse recycling electronics for better regulation and recycling. However, manufacturers have to consider its construction costs when using blockchain technology to further achieve the improvement of “triple benefits” while increasing profits.
For online platforms, blockchain technology can increase the real recycling rate of waste electronics, increase consumer trust, and reduce the impact of false recycling rates on brand goodwill, thereby expanding the market scale. However, the platform only receives a portion of the residual value of the recycled waste electronics, therefore it can barely make up for the higher cost of blockchain self-construction. Therefore, in the closed-loop supply chain using blockchain technology, the platform is not involved in the reverse recycling process, and the platform will benefit from the manufacturer’s recycling. In the positive sales process, the platform should give full play to its unique “platform power”, leveraging the network effect of its own channels or adopting online marketing to expand the potential demand of the consumer market, increase the sales volume of products, and increase the profits of manufacturers and platforms.
In short, the research in this paper is based on a one-to-one, two-stage, platform-based, closed-loop supply chain, and solves the problems of low recycling rates of waste electronics and consumer trust with the help of the visibility and traceability of blockchain. This study is also applicable to the recycling of waste products in other industries, which can solve the problems of resource waste and environmental pollution and contribute to long-term sustainable development. In the future, it can be considered to increase the competitive relationship of supply chain members and expand the complex closed-loop supply chain network system. In addition, the assumptions in this study are based on information symmetry; however, in practice, enterprises tend to be more reluctant to disclose their private information. Further research can consider how blockchain technology impacts platform-based, closed-loop supply chains in the presence of information asymmetry. The future research can consider the impact of using blockchain technology on forward selling and reverse recycling processes when remanufactured products are unequal to new products.
Author Contributions
Formal analysis, X.W.; methodology, D.M.; supervision, J.H.; writing—original draft, X.W.; writing—review and editing, D.M. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the National Natural Science Foundation of China with Grants Nos. 71771129.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Informed consent was obtained from all subjects involved in the study.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A
Proof of Proposition 1.
where
is the first-order partial derivative of the platform optimal value function with respect to goodwill . By the first-order optimality condition, the equilibrium retail price
and marketing effort are obtained as , , respectively. Substituting them into the manufacturer’s objective generalized function, we obtain the Hamilton–Jacobi–Bellman (HJB) equation that the manufacturer should satisfy.
where
is the first-order partial derivative of the manufacturer’s optimal value function with respect to goodwill . According to the first-order optimality condition, the wholesale price
and the recycling effort
of electronic products are obtained as , , respectively. Bringing
into the HJB equation for the manufacturer and the platform yields:
□
We use inverse induction to solve this strategy, and, according to the theory of continuum dynamics, the continuously differentiable value function satisfies the Hamilton–Jacobi–Bellman (HJB) equation as:
The optimal value function of manufacturer and platform is assumed to be
.
where
, and , are the corresponding constant coefficients to be determined, respectively, which are substituted into (A3) to obtain the set of equations to be determined as
According to the system of equations to be solved, we can obtain:
Substituting and in (A5) into the state equation for product brand goodwill yields:
The differential equation can be solved to obtain the brand goodwill as:
The corresponding optimal strategic steady-state strategies and optimal steady-state profits can therefore be derived as follows.
Proof of Proposition 2.
where is the optimal value function of the platform that is the first-order partial derivative of the platform optimal value function with respect to goodwill . By the first-order optimality condition, the equilibrium retail price , marketing effort , and recycling efforts . Substituting them into the manufacturer’s objective generalized function, we obtain the Hamilton–Jacobi–Bellman (HJB) equation that the manufacturer should satisfy.
where is the first-order partial derivative of the manufacturer’s optimal value function with respect to goodwill . According to the first-order optimality condition, the wholesale price of electronic products. Bringing , , , into the HJB equation for the manufacturer and the platform yields:
□
The HJB equation for the platform is first constructed according to the inverse induction method.
The optimal value function of manufacturer and platform is assumed to be .
where , and , are the corresponding constant coefficients to be determined, respectively, which are substituted into (A12) to obtain the set of equations to be determined as
According to the system of equations to be solved, we can obtain:
Substituting and in (A14) into the state equation for product brand goodwill yields:
The differential equation can be solved to obtain the brand goodwill as:
The corresponding optimal strategic steady-state strategies and optimal steady-state profits can therefore be derived as follows.
Proof of Proposition 3.
where is the first-order partial derivative of the platform optimal value function with respect to goodwill . By the first-order optimality condition, the equilibrium retail price and marketing effort are obtained as , , respectively. Substituting them into the manufacturer’s objective generalized function, we obtain the Hamilton–Jacobi–Bellman (HJB) equation that the manufacturer should satisfy.
where is the first-order partial derivative of the manufacturer’s optimal value function with respect to goodwill . According to the first-order optimality condition, the wholesale price and the recycling effort of electronic products are obtained as , , respectively. Bringing into the HJB equation for the manufacturer and the platform yields:
□
We use inverse induction to solve this strategy, and, according to the theory of continuum dynamics, the continuously differentiable value function satisfies the Hamilton–Jacobi–Bellman (HJB) equation as:
The optimal value function of the manufacturer and platform models is assumed to be , where , and , are the corresponding constant coefficients to be determined, respectively, which are substituted into (A21) to obtain the set of equations to be determined as
It can be obtained from (A22):
Substituting and in (A23) into the state equation for product brand goodwill yields:
The differential equation can be solved to obtain the brand goodwill as:
The corresponding optimal strategic steady-state strategies and optimal steady-state profits can therefore be derived as follows.
Proof of Proposition 4.
where is the optimal value function of the platform, is the first-order partial derivative of the platform optimal value function with respect to goodwill . By the first-order optimality condition, the equilibrium retail price , marketing effort , and recycling efforts . Substituting them into the manufacturer’s objective generalized function, we obtain the Hamilton–Jacobi–Bellman (HJB) equation that the manufacturer should satisfy.
where is the first-order partial derivative of the manufacturer’s optimal value function with respect to goodwill . According to the first-order optimality condition, the wholesale price of electronic products. Bringing , , , into the HJB equation for the manufacturer and the platform yields:
□
The HJB equation for the platform is first constructed according to the inverse induction method.
The optimal value function of manufacturer and platform is assumed to be .
where , and , are the corresponding constant coefficients to be determined, respectively, which are substituted into (A30) to obtain the set of equations to be determined as
According to the system of equations to be solved, we can obtain:
Substituting and in (A32) into the state equation for product brand goodwill yields:
The differential equation can be solved to obtain the brand goodwill as:
The corresponding optimal strategic steady-state strategies and optimal steady-state profits can therefore be derived as follows.
Proof of Proposition 12.
Since the wholesale price of the product, the retail price, the marketing effort of the platform, and the brand goodwill of the electronic product are independent of which recycling model is used, we directly use , , , to denote the wholesale price of the product, the retail price, the marketing effort of the platform, and the brand goodwill, respectively, when blockchain technology is not used, and use , , , to denote the wholesale price of the product, the retail price, the marketing effort of the platform, and the brand goodwill, respectively, when blockchain technology is used.
- Effect of the correlation parameter on the steady-state value of brand goodwill. (If the partial derivative is greater than 0, the two are positively correlated; the partial derivative is less than 0, indicating negative correlation).
- Influence of related parameters on the steady-state value of electronic product retail price. (If the partial derivative is greater than 0, the two are positively correlated; the partial derivative is less than 0, indicating negative correlation.)
- Influence of related parameters on steady-state value of wholesale price of electronic products. (If the partial derivative is greater than 0, the two are positively correlated; the partial derivative is less than 0, indicating negative correlation).
- Influence of relevant parameters on steady-state value of marketing effort. (If the partial derivative is greater than 0, the two are positively correlated; the partial derivative is less than 0, indicating negative correlation.)
- Influence of related parameters on steady-state value of recycling effort. represents the recycling effort when the manufacturer recycling model and platform recycling model without blockchain technology and the recycling effort when the manufacturer recycling model and platform recycling model with blockchain technology, respectively. (If the partial derivative is greater than 0, the two are positively correlated; the partial derivative is less than 0, indicating negative correlation.)Manufacturer recycling model:Platform recycling model:
□
Proof of Proposition 13.
We use inverse induction to solve this strategy, and according to the theory of continuum dynamics, the continuously differentiable value function satisfies the Hamilton–Jacobi–Bellman (HJB) equation as:
where is the first-order partial derivative of the platform optimal value function with respect to goodwill . By the first-order optimality condition, the equilibrium retail price and marketing effort are obtained as , , respectively. Substituting them into the manufacturer’s objective generalized function, we obtain the Hamilton–Jacobi–Bellman (HJB) equation that the manufacturer should satisfy.
where is the first-order partial derivative of the manufacturer’s optimal value function with respect to goodwill . According to the first-order optimality condition, the wholesale price and the recycling effort of electronic products are obtained as , , respectively. Bringing , , , and into the HJB equation for the manufacturer and the platform yields:
The optimal value function of manufacturer and platform is assumed to be .
where , and , are the corresponding constant coefficients to be determined, respectively, which are substituted into (A21) to obtain the set of equations to be determined as
It can be obtained from (A40):
Thus, the brand goodwill in equilibrium state is .
The corresponding optimal strategic steady-state strategies and optimal steady-state profits can therefore be derived as follows.
□
Proof of Proposition 14.
The HJB equation for the platform is first constructed according to the inverse induction method.
where is the optimal value function of the platform, is the first-order partial derivative of the platform optimal value function with respect to goodwill . By the first-order optimality condition, the equilibrium retail price , marketing effort , and recycling efforts . Substituting them into the manufacturer’s objective generalized function, we obtain the Hamilton–Jacobi–Bellman (HJB) equation that the manufacturer should satisfy.
where is the first-order partial derivative of the manufacturer’s optimal value function with respect to goodwill . According to the first-order optimality condition, the wholesale price of electronic products. Bringing , , , into the HJB equation for the manufacturer and the platform yields:
The optimal value function of manufacturer and platform is assumed to be .
where , and , are the corresponding constant coefficients to be determined, respectively, which are substituted into (A46) to obtain the set of equations to be determined as
According to the system of equations to be solved, we can obtain:
Thus, the brand goodwill in equilibrium state is .
The corresponding optimal strategic steady-state strategies and optimal steady-state profits can therefore be derived as follows.
□
References
- Xu, X.; Choi, T.M. Supply chain operations with online platforms under the cap-and-trade regulation: Impacts of using blockchain technology. Transp. Res. Part E 2021, 155, 102491. [Google Scholar] [CrossRef]
- Ha, A.Y.; Tong, S.; Wang, Y. Channel structures of online retail platforms. Manuf. Serv. Oper. Manag. 2021. [CrossRef]
- Tian, L.; Vakharia, A.J.; Tan, Y.; Xu, Y. Marketplace, reseller, or hybrid: Strategic analysis of an emerging e-commerce model. Prod. Oper. Manag. 2018, 27, 1595–1610. [Google Scholar] [CrossRef]
- Hagiu, A.; Wright, J. Marketplace or reseller? Manag. Sci. 2015, 61, 184–203. [Google Scholar] [CrossRef] [Green Version]
- Jiang, B.; Jerath, K.; Srinivasan, K. Firm strategies in the “mid tail” of platform-based retailing. Mark Sci. 2011, 30, 757–775. [Google Scholar] [CrossRef] [Green Version]
- Marinello, S.; Gamberini, R. Multi-criteria decision making approaches applied to waste electrical and electronic equipment (WEEE): A comprehensive literature review. Toxics 2021, 9, 13. [Google Scholar] [CrossRef]
- Wang, Z.; Zheng, Z.; Jiang, W.; Tang, S. Blockchain-enabled data sharing in supply chains: Model, operationalization, and tutorial. Prod. Oper. Manag. 2021, 30, 1965–1985. [Google Scholar] [CrossRef]
- Hussien, H.M.; Yasin, S.M.; Udzir, N.I.; Ninggal, M.I.H.; Salman, S. Blockchain technology in the healthcare industry: Trends and opportunities. J. Ind. Inf. Integr. 2021, 22, 100217. [Google Scholar] [CrossRef]
- Centobelli, P.; Cerchione, R.; Del, V.P.; Oropallo, E.; Secundo, G. Blockchain technology for bridging trust, traceability and transparency in circular supply chain. Inform. Manage-Amster. 2021, 103508. [Google Scholar] [CrossRef]
- Bahers, J.B.; Kim, J. Regional approach of waste electrical and electronic equipment (WEEE) management in France. Resour. Conserv. Recycl. 2018, 129, 45–55. [Google Scholar] [CrossRef]
- Yang, P.C.; Wee, H.M.; Liu, B.S.; Fong, O.K. Mitigating hi-tech products risks due to rapid technological innovation. Omega 2011, 39, 456–463. [Google Scholar] [CrossRef]
- Tansel, B. From electronic consumer products to e-wastes: Global outlook, waste quantities, recycling challenges. Environ. Int. 2017, 98, 35–45. [Google Scholar] [CrossRef] [PubMed]
- Wang, M.; Luan, J.; Li, X.; Zhu, X. Sustainable decisions in a high-tech electronic product supply chain considering environmental effort and social responsibility: A hierarchical bi-level intelligent approach. IAENG Inter. J. Appl. Math. 2021, 51, 1–16. [Google Scholar]
- Kumar, A.; Holuszko, M.; Espinosa, D.C.R. E-waste: An overview on generation, collection, legislation and recycling practices. Resour. Conserv. Recycl. 2017, 122, 32–42. [Google Scholar] [CrossRef]
- Wang, W.; Tian, Y.; Zhu, Q.; Zhong, Y. Barriers for household e-waste collection in China: Perspectives from formal collecting enterprises in Liaoning Province. J. Clean. Prod. 2017, 153, 299–308. [Google Scholar] [CrossRef]
- Zlamparet, G.I.; Ijomah, W.; Miao, Y.; Awasthi, A.K.; Zeng, X.; Li, J. Remanufacturing strategies: A solution for WEEE problem. J. Clean. Prod. 2017, 149, 126–136. [Google Scholar] [CrossRef] [Green Version]
- Savaskan, R.C.; Bhattacharya, S.; Wassenhove, L. Closed-loop supply chain models with product remanufacturing. Manag. Sci. 2004, 50, 239–252. [Google Scholar] [CrossRef] [Green Version]
- Wu, X.; Zhou, Y. The optimal reverse channel choice under supply chain competition. Eur. J. Oper. Res. 2017, 259, 63–66. [Google Scholar] [CrossRef]
- Liu, L.; Wang, Z.; Xu, L.; Hong, X.; Govindan, K. Collection effort and reverse channel choices in a closed-loop supply chain. J. Clean. Prod. 2017, 144, 492–500. [Google Scholar] [CrossRef]
- Huang, M.; Song, M.; Lee, L.H.; Ching, W.K. Analysis for strategy of closed-loop supply chain with dual recycling channel. Inter. J. Prod. Econ. 2013, 144, 510–520. [Google Scholar] [CrossRef]
- Hong, X.; Xu, L.; Du, P.; Wang, W. Joint advertising, pricing and collection decisions in a closed-loop supply chain. Inter. J. Prod. Econ. 2015, 167, 12–22. [Google Scholar] [CrossRef]
- He, Q.; Wang, N.; Yang, Z.; He, Z.; Jiang, B. Competitive collection under channel inconvenience in closed-loop supply chain. Eur. J. Oper. Res. 2019, 275, 155–166. [Google Scholar] [CrossRef]
- Wang, B.; Ren, C.; Dong, X.; Zhang, B.; Wang, Z. Determinants shaping willingness towards on-line recycling behaviour: An empirical study of household e-waste recycling in China. Resour. Conserv. Recycl. 2019, 143, 218–225. [Google Scholar] [CrossRef]
- Liu, S.; Huang, Y. Decision Analysis of E-commerce Closed-loop Supply Chain with Different Recycling models. E3S Web of Conferences. EDP Sci. 2021, 257, 02019. [Google Scholar]
- Liu, C.Y.; Wang, H.; Tang, J.; Chang, C.T.; Liu, Z. Optimal recycling model in a used batteries closed-loop supply chain considering uncertain residual capacity. Transp. Res. Part E 2021, 156, 102516. [Google Scholar] [CrossRef]
- Chuang, C.H.; Wang, C.X.; Zhao, Y. Closed-loop supply chain models for a high-tech product under alternative reverse channel and collection cost structures. Inter. J. Prod. Econ. 2014, 156, 108–123. [Google Scholar] [CrossRef]
- Xue, R.; Zhang, F.; Tian, F.; Oloruntoba, R.; Miao, S. Dual chains competition under two recycling models based on system dynamics method. Sustainability 2018, 10, 2382. [Google Scholar] [CrossRef] [Green Version]
- Dutta, P.; Choi, T.M.; Somani, S.; Butala, R. Blockchain technology in supply chain operations: Applications, challenges and research opportunities. Transp. Res. Part E 2020, 142, 102067. [Google Scholar] [CrossRef]
- Babich, V.; Hilary, G. OM Forum—Distributed ledgers and operations: What operations management researchers should know about blockchain technology. Manuf. Serv. Oper. Manag. 2020, 22, 223–240. [Google Scholar] [CrossRef] [Green Version]
- Lim, M.K.; Li, Y.; Wang, C.; Tseng, M.L. A literature review of blockchain technology applications in supply chains: A comprehensive analysis of themes, methodologies and industries. Comput. Ind. Eng. 2021, 154, 107133. [Google Scholar] [CrossRef]
- Yu, Y.; Huang, G.; Guo, X. Financing strategy analysis for a multi-sided platform with blockchain technology. Eur. J. Oper Res. 2021, 59, 4513–4532. [Google Scholar] [CrossRef]
- Shen, B.; Dong, C.; Minner, S. Combating copycats in the supply chain with permissioned blockchain technology. Prod. Oper. Manag. 2022, 31, 138–154. [Google Scholar] [CrossRef]
- Cai, Y.J.; Choi, T.M.; Zhang, J. Platform supported supply chain operations in the blockchain era: Supply contracting and moral hazards. Decis. Sci. 2021, 52, 866–892. [Google Scholar] [CrossRef]
- Chod, J.; Trichakis, N.; Tsoukalas, G.; Aspegren, H.; Weber, M. On the financing benefits of supply chain transparency and blockchain adoption. Manag. Sci. 2020, 66, 4378–4396. [Google Scholar] [CrossRef]
- Hastig, G.M.; Sodhi, M. Blockchain for supply chain traceability: Business requirements and critical success factors. Prod. Oper. Manag. 2020, 29, 935–954. [Google Scholar] [CrossRef]
- Wu, X.Y.; Fan, Z.P.; Cao, B.B. An analysis of strategies for adopting blockchain technology in the fresh product supply chain. Inter. J. Prod. Ees. 2021, 1–18. [Google Scholar] [CrossRef]
- Liu, X.; Barenji, A.V.; Li, Z.; Montreuil, B.; Huang, G.Q. Blockchain-based smart tracking and tracing platform for drug supply chain. Comput. Ind. Eng. 2021, 161, 107669. [Google Scholar] [CrossRef]
- Nerlove, M.; Arrow, K.J. Optimal advertising policy under dynamic conditions. Economica 1962, 29, 129–142. [Google Scholar] [CrossRef]
- Giovanni, D.P. Smart Supply Chains with vendor managed inventory, coordination, and environmental performance. Eur. J. Oper. Res. 2021, 292, 515–531. [Google Scholar] [CrossRef]
- Liu, G.; Zhang, J.; Tang, W. Strategic transfer pricing in a marketing–operations interface with quality level and advertising dependent goodwill. Omega 2015, 56, 1–15. [Google Scholar] [CrossRef]
- Giovanni, D.P. A joint maximization incentive in closed-loop supply chains with competing retailers: The case of spent-battery recycling. Eur. J. Oper. Res. 2018, 268, 128–147. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).