Planning, Optimisation and Evaluation of Small Power-to-Gas-to-Power Systems: Case Study of a German Dairy
Abstract
:1. Introduction
- Identification of the relevant current economic and regulatory market conditions in Germany;
- Technical modelling of a PtGtP plant based on data sheets of different manufacturers;
- Linking of all relevant technical components in an established open-source energy system modelling tool (oemof.solph);
- Development of a multi-criteria and objective evaluation metric for assessing the use of PtGtP in existing HES;
- Optimal sizing of all relevant technologies for a case study with a brute force approach;
- Analysis of future viability using a sensitivity analysis.
2. Related Work
3. Methodology
3.1. Targeting
3.1.1. Economic Evaluation
3.1.2. Ecological Evaluation
3.2. Synthesis
3.2.1. Scenario 1
3.2.2. Scenario 2
3.3. Design
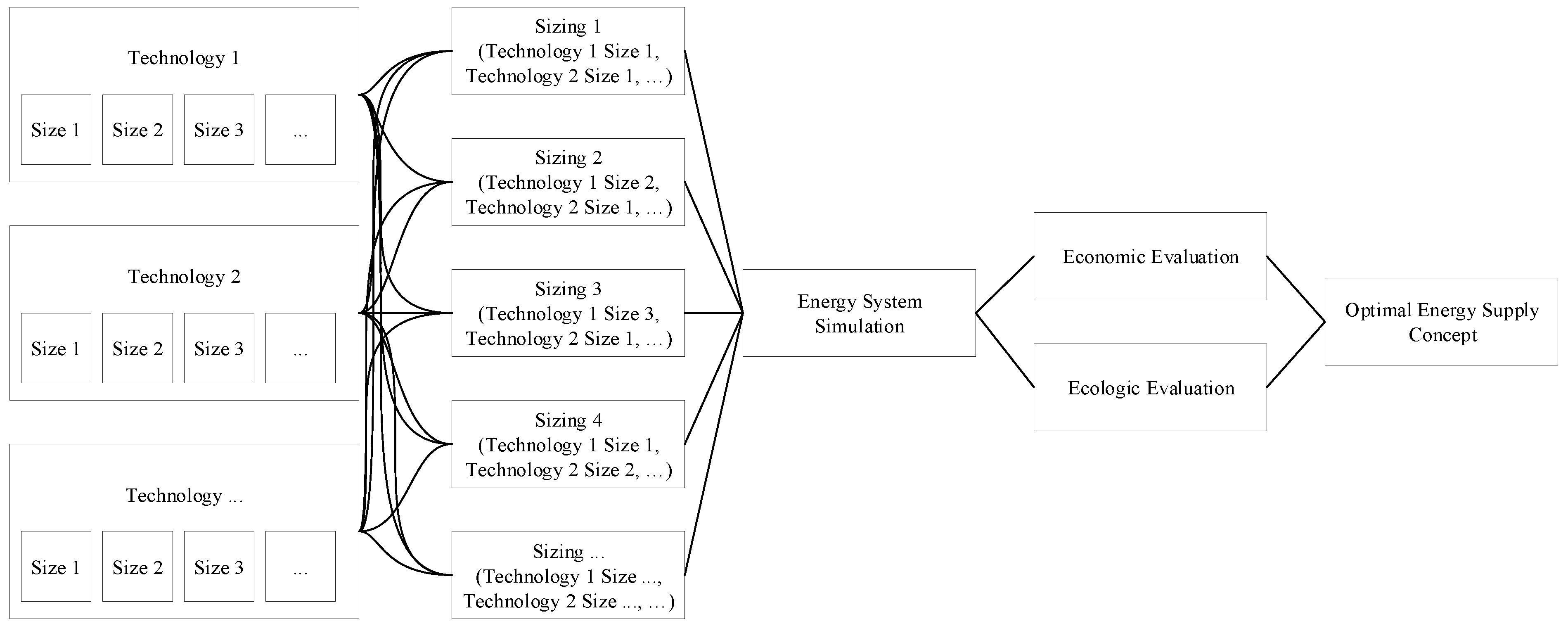
3.3.1. Optimal Sizing
3.3.2. Energy System Simulation
3.3.3. Modelling the Hydrogen Technologies
4. Case Study
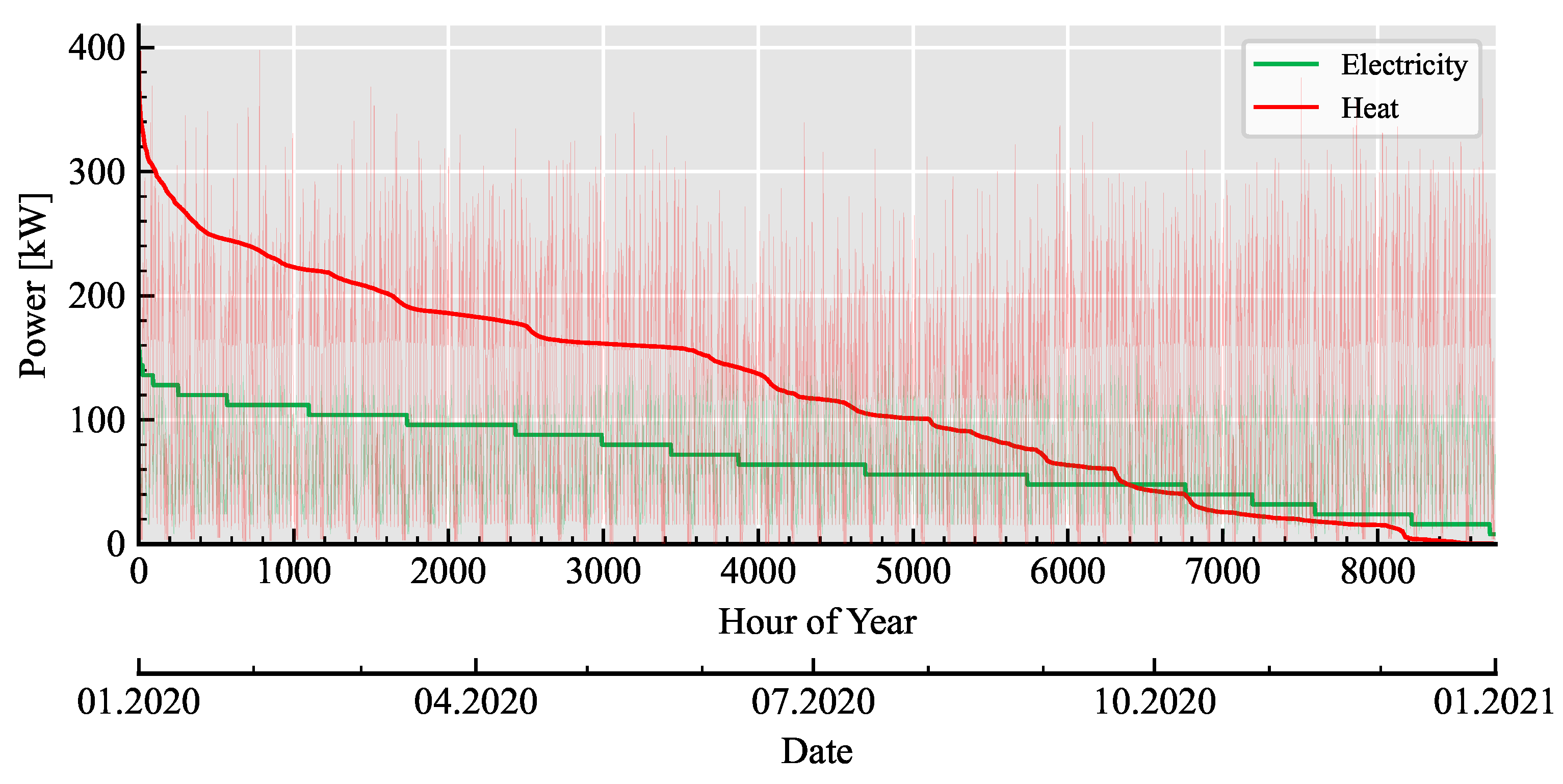
4.1. Energy Supply Object
4.2. Energy Prices, Taxes, and Allowances
5. Results
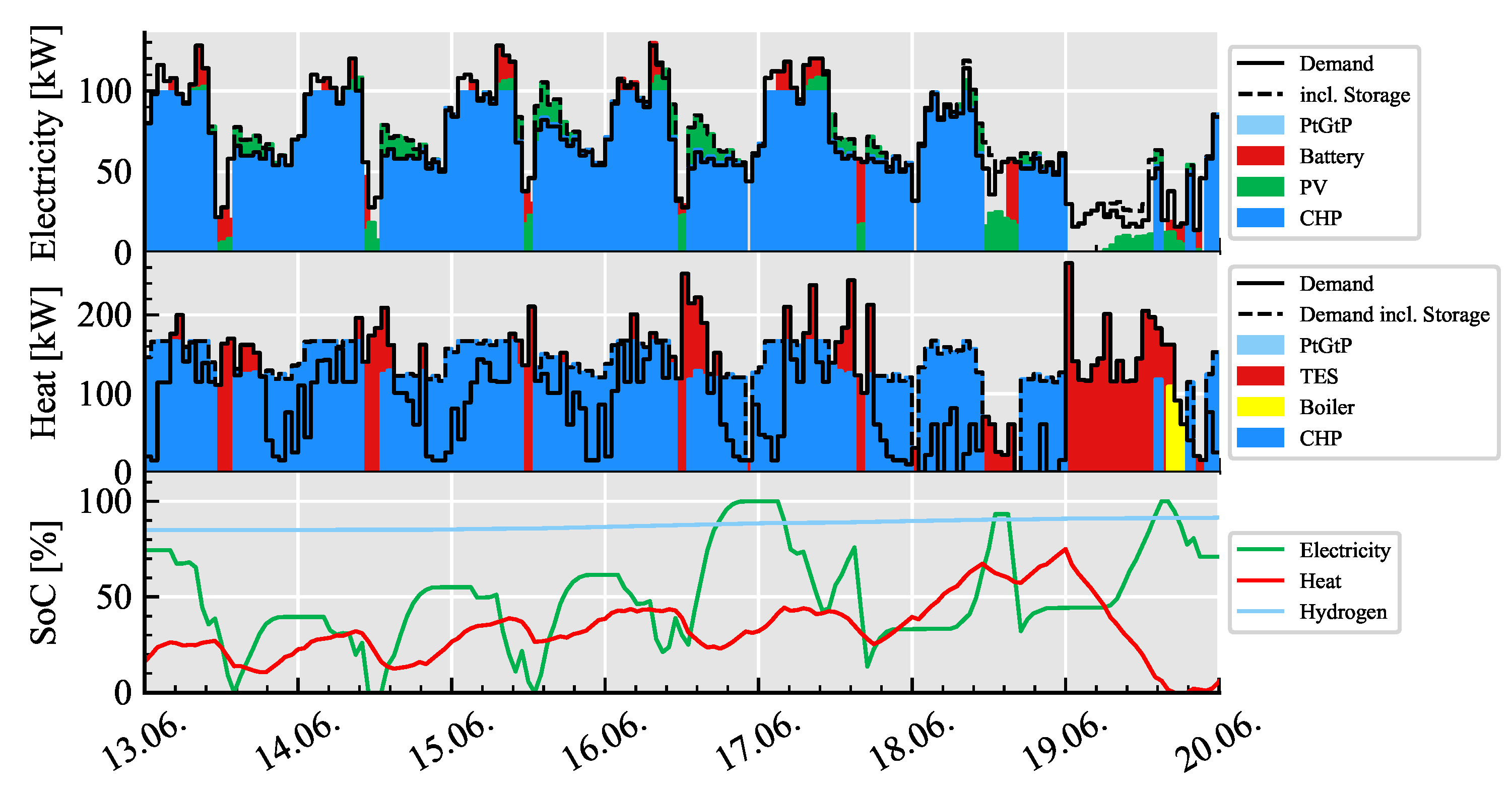
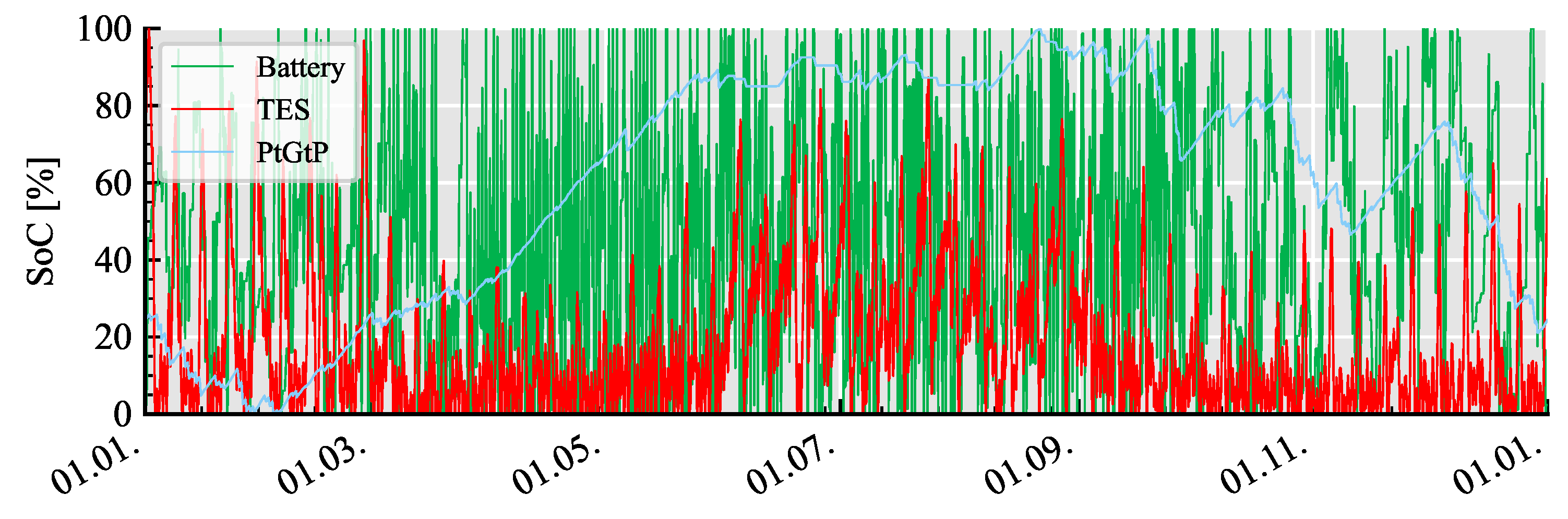
5.1. Optimal Dispatch
5.2. Multiobjective Optimal Sizing
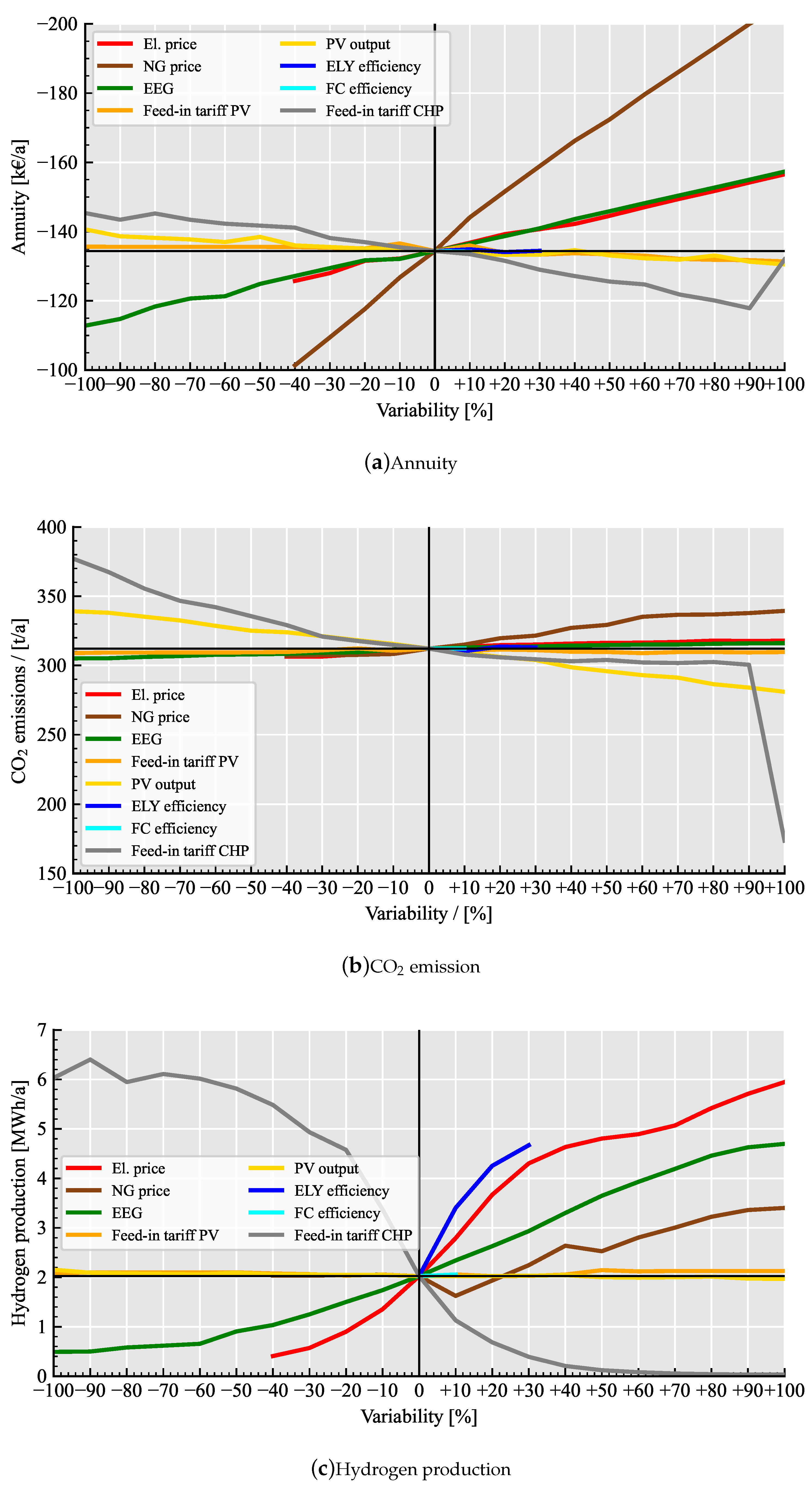
5.3. Sensitivity Analysis
6. Discussion and Outlook
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| CHP | combined heat and power |
| EEG | German renewable energy sources act |
| ELY | electrolyzer |
| FC | fuel cell |
| HES | hybrid energy system |
| HS | hydrogen storage |
| MILP | mixed integer linear programming |
| MO | multi-objective optimisation |
| NG | natural gas |
| PEM | proton exchange membrane |
| PtGtP | power-to-gas-to-power |
| PV | photovoltaic |
| SOC | state of charge |
| TES | thermal energy storage |
References
- Manwell, J.F. Hybrid Energy Systems. Encycl. Energy 2004, 3, 215–229. [Google Scholar] [CrossRef]
- Sterner, M.; Stadler, I. Energiespeicher—Bedarf, Technologien, Integration; Springer: Berlin/Heidelberg, Germany, 2017. [Google Scholar] [CrossRef]
- Zapf, M. Stromspeicher und Power-to-Gas im Deutschen Energiesystem: Rahmenbedingungen, Bedarf und Einsatzmöglichkeiten; Springer: Berlin/Heidelberg, Germany, 2017. [Google Scholar] [CrossRef]
- International Energy Agency (IEA). The Future of Hydrogen: Seizing Today’s Opportunities; OECD: Paris, France, 2019. [Google Scholar]
- Floristran, A.; Brahy, N.; Kraus, N.; Skiker, S.; Damman, S.; Hayter, D.; Nozharova, D. HyLaw—EU Policy Paper; European Commission: Brussels, Belgium, 2019. [Google Scholar]
- Fuel Cells and Hydrogen 2 Joint Undertaking. Hydrogen Roadmap Europe: A Sustainable Pathway for the European Energy Transition; Publications Office of the European Union: Luxembourg, 2019. [Google Scholar]
- FuelCellsWorks. Germany: Hydrogen Partnership with Africa Begins. 2020. Available online: https://fuelcellsworks.com/news/germany-hydrogen-partnership-with-africa-begins/ (accessed on 16 March 2022).
- Liu, Z.; Kendall, K.; Yan, X. China Progress on Renewable Energy Vehicles: Fuel Cells, Hydrogen and Battery Hybrid Vehicles. Energies 2019, 12, 54. [Google Scholar] [CrossRef] [Green Version]
- The Energy and Resources Institute; National Centre for Climate Change Strategy and International Cooperation; Central University of Finance and Economics; Zhejiang University; United Nations Development Programme; Shakti Sustainable Energy Foundation. Low Carbon Development in China and India; The Energy and Resources Institute: New Delhi, India, 2016. [Google Scholar]
- Vosen, S.; Keller, J. Hybrid energy storage systems for stand-alone electric power systems: Optimization of system performance and cost through control strategies. Int. J. Hydrogen Energy 1999, 24, 1139–1156. [Google Scholar] [CrossRef]
- Bocci, E.; Zuccari, F.; Dell’Era, A. Renewable and hydrogen energy integrated house. Int. J. Hydrogen Energy 2011, 36, 7963–7968. [Google Scholar] [CrossRef]
- Gillessen, B.; Heinrichs, H.U.; Stenzel, P.; Linssen, J. Hybridization strategies of power-to-gas systems and battery storage using renewable energy. Int. J. Hydrogen Energy 2017, 42, 13554–13567. [Google Scholar] [CrossRef]
- Nguyen, H.T.; Safder, U.; Nhu Nguyen, X.Q.; Yoo, C. Multi-objective decision-making and optimal sizing of a hybrid renewable energy system to meet the dynamic energy demands of a wastewater treatment plant. Energy 2020, 191, 116570. [Google Scholar] [CrossRef]
- Luta, D.N.; Raji, A.K. Optimal sizing of hybrid fuel cell-supercapacitor storage system for off-grid renewable applications. Energy 2019, 166, 530–540. [Google Scholar] [CrossRef]
- Yazdani, S.; Deymi-Dashtebayaz, M.; Salimipour, E. Comprehensive comparison on the ecological performance and environmental sustainability of three energy storage systems employed for a wind farm by using an emergy analysis. Energy Convers. Manag. 2019, 191, 1–11. [Google Scholar] [CrossRef]
- Cilogulları, M.; Erden, M.; Karakilcik, M.; Dincer, I. Investigation of hydrogen production performance of a Photovoltaic and Thermal System. Int. J. Hydrogen Energy 2017, 42, 2547–2552. [Google Scholar] [CrossRef]
- Guinot, B.; Champel, B.; Montignac, F.; Lemaire, E.; Vannucci, D.; Sailler, S.; Bultel, Y. Techno-economic study of a PV-hydrogen-battery hybrid system for off-grid power supply: Impact of performances’ ageing on optimal system sizing and competitiveness. Int. J. Hydrogen Energy 2015, 40, 623–632. [Google Scholar] [CrossRef]
- Eriksson, E.; Gray, E. Optimization and integration of hybrid renewable energy hydrogen fuel cell energy systems—A critical review. Appl. Energy 2017, 202, 348–364. [Google Scholar] [CrossRef]
- Firtina-Ertis, I.; Acar, C.; Erturk, E. Optimal sizing design of an isolated stand-alone hybrid wind-hydrogen system for a zero-energy house. Appl. Energy 2020, 274, 115244. [Google Scholar] [CrossRef]
- Bakhtiari, H.; Naghizadeh, R.A. Multi–criteria optimal sizing of hybrid renewable energy systems including wind, photovoltaic, battery, and hydrogen storage with ε–constraint method. IET Renew. Power Gener. 2018, 12, 883–892. [Google Scholar] [CrossRef]
- Pfenninger, S.; Hawkes, A.; Keirstead, J. Energy systems modeling for twenty-first century energy challenges. Renew. Sustain. Energy Rev. 2014, 33, 74–86. [Google Scholar] [CrossRef]
- Schmeling, L.; Schönfeldt, P.; Klement, P.; Wehkamp, S.; Hanke, B.; Agert, C. Development of a Decision-Making Framework for Distributed Energy Systems in a German District. Energies 2020, 13, 552. [Google Scholar] [CrossRef] [Green Version]
- Løken, E. Use of multicriteria decision analysis methods for energy planning problems. Renew. Sustain. Energy Rev. 2005, 11, 1584–1595. [Google Scholar] [CrossRef]
- Wang, Y.; Wang, X.; Yu, H.; Huang, Y.; Dong, H.; Qi, C.; Baptiste, N. Optimal design of integrated energy system considering economics, autonomy and carbon emissions. J. Clean. Prod. 2019, 225, 563–578. [Google Scholar] [CrossRef]
- Di Somma, M.; Yan, B.; Bianco, N.; Graditi, G.; Luh, P.B.; Mongibello, L.; Naso, V. Operation optimization of a distributed energy system considering energy costs and exergy efficiency. Energy Convers. Manag. 2015, 103, 739–751. [Google Scholar] [CrossRef]
- Ngatchou, P.N.; Zarei, A.; Fox, W.L.J.; El-Sharkawi, M.A. Pareto Multiobjective Optimization. In Modern Heuristic Optimization Techniques; Lee, K.Y., El-Sharkawi, M.A., Eds.; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2008; pp. 189–207. [Google Scholar] [CrossRef]
- Orner, M. Nutzungsorientierte Auslegung des Antriebsstrangs und der Reichweite von Elektrofahrzeugen; Springer Fachmedien: Wiesbaden, Germany, 2018. [Google Scholar] [CrossRef]
- Verein Deutscher Ingenieure. VDI 2067—Economic Efficiency of Building Installations: Fundamentals and Economic Calculation; Beuth-Verlag: Berlin, Germany, 2012. [Google Scholar]
- Brealey, R.A.; Myers, S.C.; Allen, F. Principles of Corporate Finance; The McGraw-Hill Irwin Series in Finance, Insurance, and Real Estate; McGraw-Hill Education: Maidenhead, UK, 2014. [Google Scholar]
- Heuck, K.; Dettmann, K.D.; Schulz, D. Elektrische Energieversorgung: Erzeugung, Übertragung und Verteilung Elektrischer Energie für Studium und Praxis; Springer Vieweg: Wiesbaden, Germany, 2013. [Google Scholar] [CrossRef]
- Rubik, F.; Müller, R.; Harnisch, R.; Holzhauer, B.; Schipperges, M.; Geiger, S. Umweltbewusstsein in Deutschland 2018: Ergebnisse Einer Repräsentativen Bevölkerungsumfrage; Bundesministerium für Umwelt, Naturschutz und Nukleare Sicherheit/Umweltbundesamt: Berlin/Dessau-Roßlau, Germany, 2019. [Google Scholar]
- Peters, G.P. Carbon footprints and embodied carbon at multiple scales. Curr. Opin. Environ. Sustain. 2010, 2, 245–250. [Google Scholar] [CrossRef]
- Wehkamp, S.; Schmeling, L.; Vorspel, L.; Roelcke, F.; Windmeier, K.L. District Energy Systems: Challenges and New Tools for Planning and Evaluation. Energies 2020, 13, 2967. [Google Scholar] [CrossRef]
- Bundesamt für Wirtschaft und Ausfuhrkontrolle. Merkblatt zu den CO2-Faktoren: Energieeffizienz in der Wirtschaft—Zuschuss und Kredit; Bundesamt für Wirtschaft und Ausfuhrkontrolle: Eschborn, Germany, 2019. [Google Scholar]
- Tranberg, B.; Corradi, O.; Lajoie, B.; Gibon, T.; Staffell, I.; Andresen, G.B. Real-time carbon accounting method for the European electricity markets. Energy Strategy Rev. 2019, 26, 100367. [Google Scholar] [CrossRef]
- Windmeier, K.L. Länderspezifische Berechnung der Spezifischen C02-Emissionen des Stromverbrauchs im Europäischen Verbundnetz; Internship Report; University of Bremen and KEHAG Energiehandel: Bremen/Oldenburg, Germany, 2019. [Google Scholar]
- Gröger, M.; Berking, D.; Ludwig, A.; Bruckner, T. Kraft-Wärme-Kopplung und Solarthermie: Konkurrenzeffekte beim integrierten Einsatz. In Proceedings of the 8th Internationale Energiewirtschaftstagung der TU Wien, Vienna, Austria, 13–15 February 2013. [Google Scholar]
- Von Roon, S.; Huck, M. Merit Order des Kraftwerkparks; Forschungsstelle für Energiewirtschaft: Munich, Germany, 2010. [Google Scholar]
- Klotz, E.M.; Koepp, M.; Peter, F.; Thamling, N.; Wünsch, M.; Ziegenhagen, I.; Eikmeier, B.; Fette, M.; Janßen, K.; Jochem, E.; et al. Potenzial- und Kosten-Nutzen-Analyse zu den Einsatzmöglichkeiten von Kraft-Wärme-Kopplung (Umsetzung der EU-Energieeffizienzrichtlinie) Sowie Evaluierung des KWKG im Jahr 2014; Bundesministerium für Wirtschaft und Energie: Berlin, Germany, 2014. [Google Scholar]
- Kneiske, T.M.; Braun, M. Flexibility potentials of a combined use of heat storages and batteries in PV-CHP hybrid systems. Energy Procedia 2017, 135, 482–495. [Google Scholar] [CrossRef]
- Shah, K.K.; Mundada, A.S.; Pearce, J.M. Performance of U.S. hybrid distributed energy systems: Solar photovoltaic, battery and combined heat and power. Energy Convers. Manag. 2015, 105, 71–80. [Google Scholar] [CrossRef] [Green Version]
- Prakash, P.; Khatod, D.K. Optimal sizing and siting techniques for distributed generation in distribution systems: A review. Renew. Sustain. Energy Rev. 2016, 57, 111–130. [Google Scholar] [CrossRef]
- Schmeling, L.; Schönfeldt, P.; Klement, P.; Vorspel, L.; Hanke, B.; von Maydell, K.; Agert, C. A generalised optimal design methodology for distributed energy systems. TexhRxiv 2022. Preprint. [Google Scholar] [CrossRef]
- Miettinen, K. Nonlinear Multiobjective Optimization; Springer: New York, NY, USA, 1998. [Google Scholar] [CrossRef]
- Connolly, D.; Lund, H.; Mathiesen, B.V.; Leahy, M. A review of computer tools for analysing the integration of renewable energy into various energy systems. Appl. Energy 2010, 87, 1059–1082. [Google Scholar] [CrossRef]
- Sinha, S.; Chandel, S.S. Review of software tools for hybrid renewable energy systems. Renew. Sustain. Energy Rev. 2014, 32, 192–205. [Google Scholar] [CrossRef]
- Schmeling, L.; Klement, P.; Erfurth, T.; Kästner, J.; Hanke, B.; von Maydell, K.; Agert, C. Review of different Software Solutions for the holistic Simulation of distributed hybrid Energy Systems for the commercial Energy Supply. In Proceedings of the 33rd European Photovoltaic Solar Energy Conference and Exhibition, Amsterdam, The Netherlands, 25–29 September 2017; Smets, A., Taylor, N., Helm, P., Eds.; 2017; pp. 1994–1998. [Google Scholar] [CrossRef]
- Krien, U.; Schönfeldt, P.; Launer, J.; Hilpert, S.; Kaldemeyer, C.; Pleßmann, G. oemof.solph—A model generator for linear and mixed-integer linear optimisation of energy systems. Softw. Impacts 2020, 6, 100028. [Google Scholar] [CrossRef]
- Hilpert, S. Effects of Decentral Heat Pump Operation on Electricity Storage Requirements in Germany. Energies 2020, 13, 2878. [Google Scholar] [CrossRef]
- Boysen, C.; Kaldemeyer, C.; Hilpert, S.; Tuschy, I. Integration of Flow Temperatures in Unit Commitment Models of Future District Heating Systems. Energies 2019, 12, 1061. [Google Scholar] [CrossRef] [Green Version]
- Hart, W.E.; Laird, C.; Watson, J.P.; Woodruff, D.L. Pyomo—Optimization Modeling in Python; Springer Optimization and Its Applications; Springer: Boston, MA, USA, 2012; Volume 67. [Google Scholar] [CrossRef]
- Hilpert, S.; Kaldemeyer, C.; Krien, U.; Günther, S.; Wingenbach, C.; Plessmann, G. The Open Energy Modelling Framework (oemof)—A new approach to facilitate open science in energy system modelling. Energy Strategy Rev. 2018, 22, 16–25. [Google Scholar] [CrossRef] [Green Version]
- Töpler, J.; Lehmann, J. Wasserstoff und Brennstoffzelle; Springer: Berlin/Heidelberg, Germany, 2017. [Google Scholar] [CrossRef]
- Mollenhauer, E.; Christidis, A.; Tsatsaronis, G. Evaluation of an energy- and exergy-based generic modeling approach of combined heat and power plants. Int. J. Energy Environ. Eng. 2016, 7, 167–176. [Google Scholar] [CrossRef] [Green Version]
- Salgado, F.; Pedrero, P. Short-term operation planning on cogeneration systems: A survey. Electr. Power Syst. Res. 2008, 78, 835–848. [Google Scholar] [CrossRef]
- Kurzweil, P.; Dietlmeier, O.K. Elektrochemische Speicher; Springer Fachmedien: Wiesbaden, Germany, 2018. [Google Scholar] [CrossRef]
- Matthey, A.; Bünger, B. Methodenkonvention 3.0 zur Ermittlung von Umweltkosten: Kostensätze; Umweltbundesamt: Dessau-Rosslau, Germany, 2018. [Google Scholar]
- Gleißner, W. Grundlagen des Risikomanagements im Unternehmen: Controlling, Unternehmensstrategie und wertorientiertes Management; Management Competence, Vahlen: Munich, Germany, 2011. [Google Scholar] [CrossRef]
- Saltelli, A.; Tarantola, S.; Campolongo, F.; Ratto, M. Sensitivity Analysis in Practice: A Guide to Assessing Scientific Models, reprinted, ed.; Wiley: Chichester, UK; Weinheim, Germany, 2007. [Google Scholar] [CrossRef]
- Abdollahi, G.; Sayyaadi, H. Application of the multi-objective optimization and risk analysis for the sizing of a residential small-scale CCHP system. Energy Build. 2013, 60, 330–344. [Google Scholar] [CrossRef]
- Arnold, U.; Yildiz, Ö. Economic risk analysis of decentralized renewable energy infrastructures—A Monte Carlo Simulation approach. Renew. Energy 2015, 77, 227–239. [Google Scholar] [CrossRef]
- Ristimäki, M.; Säynäjoki, A.; Heinonen, J.; Junnila, S. Combining life cycle costing and life cycle assessment for an analysis of a new residential district energy system design. Energy 2013, 63, 168–179. [Google Scholar] [CrossRef]
- Urbanucci, L.; Testi, D. Optimal integrated sizing and operation of a CHP system with Monte Carlo risk analysis for long-term uncertainty in energy demands. Energy Convers. Manag. 2018, 157, 307–316. [Google Scholar] [CrossRef]
- Giannakoudis, G.; Papadopoulos, A.I.; Seferlis, P.; Voutetakis, S. Optimum design and operation under uncertainty of power systems using renewable energy sources and hydrogen storage. Int. J. Hydrogen Energy 2010, 35, 872–891. [Google Scholar] [CrossRef]
- Coppitters, D.; De Paepe, W.; Contino, F. Robust design optimization and stochastic performance analysis of a grid-connected photovoltaic system with battery storage and hydrogen storage. Energy 2020, 213, 118798. [Google Scholar] [CrossRef]
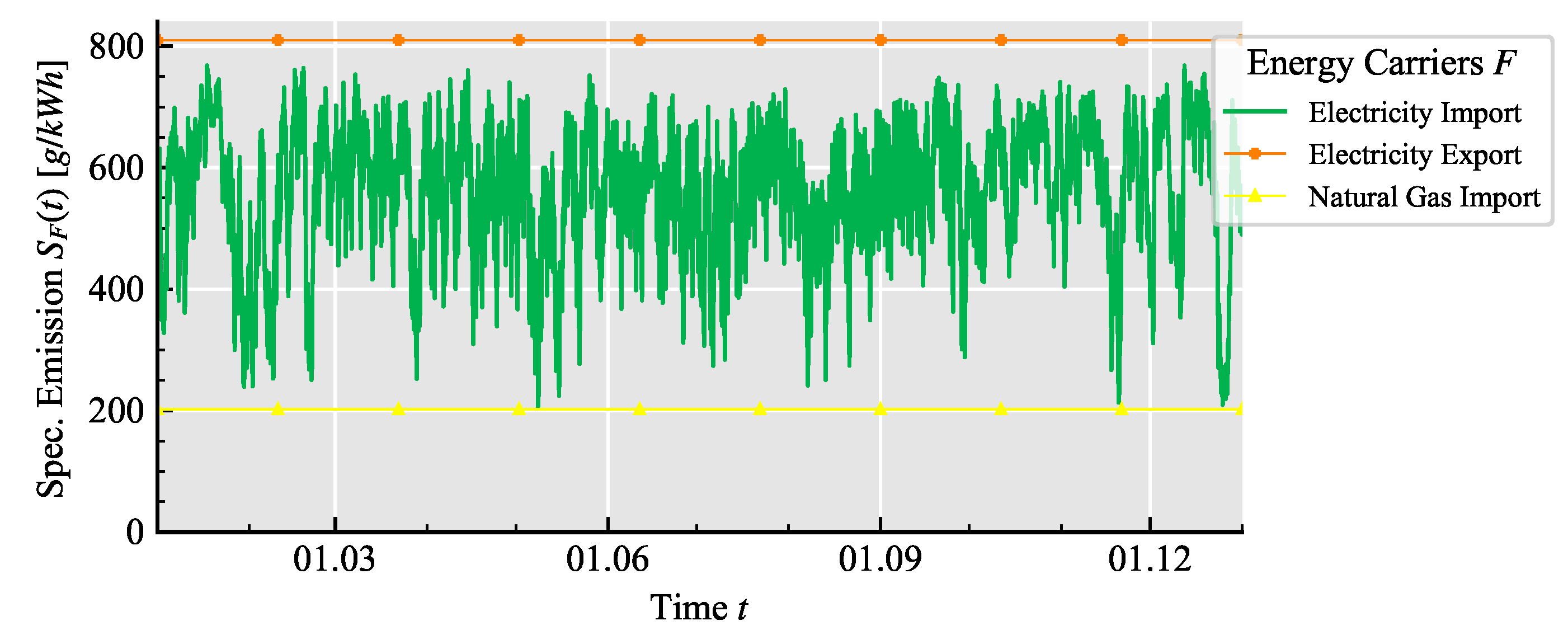
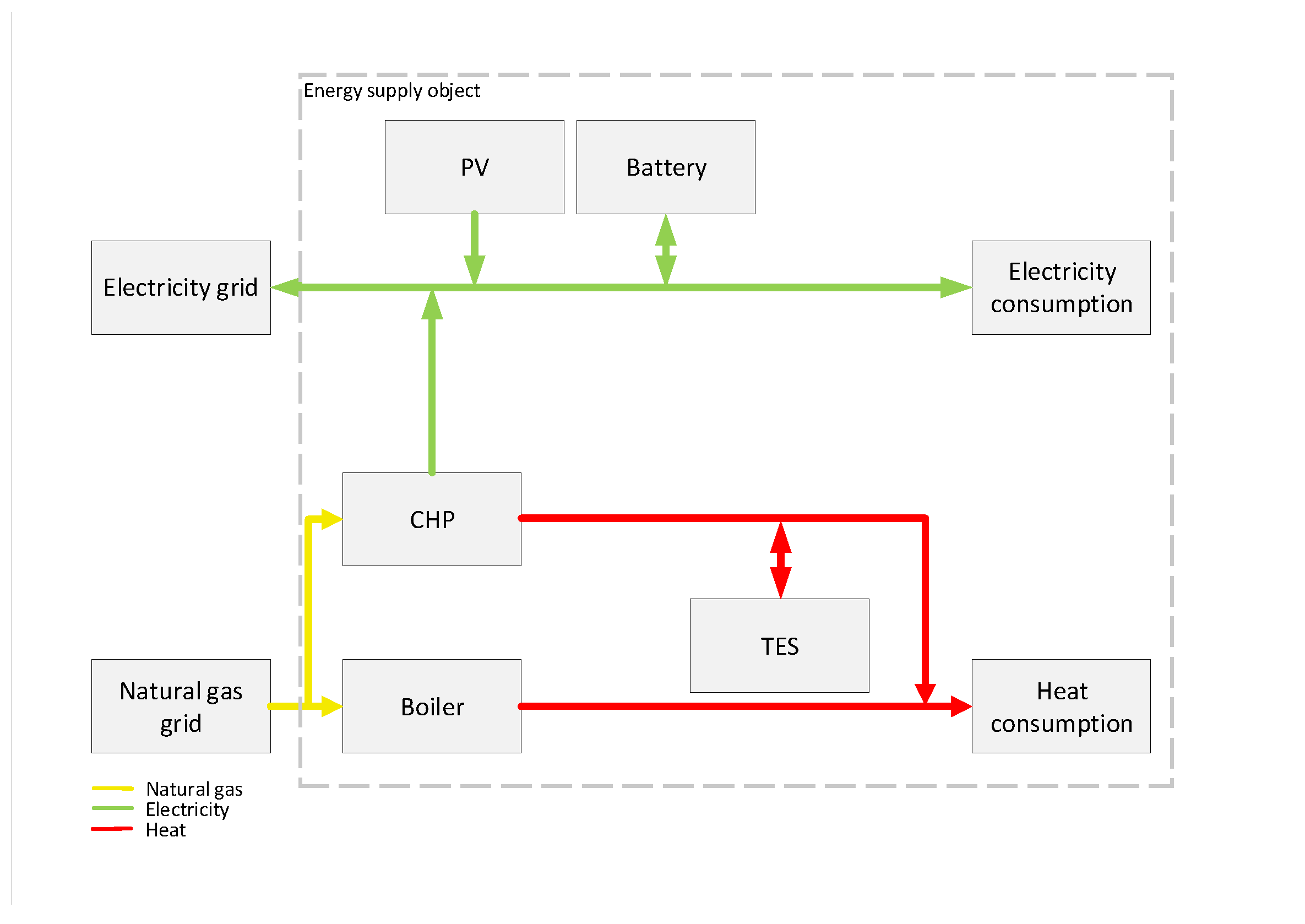
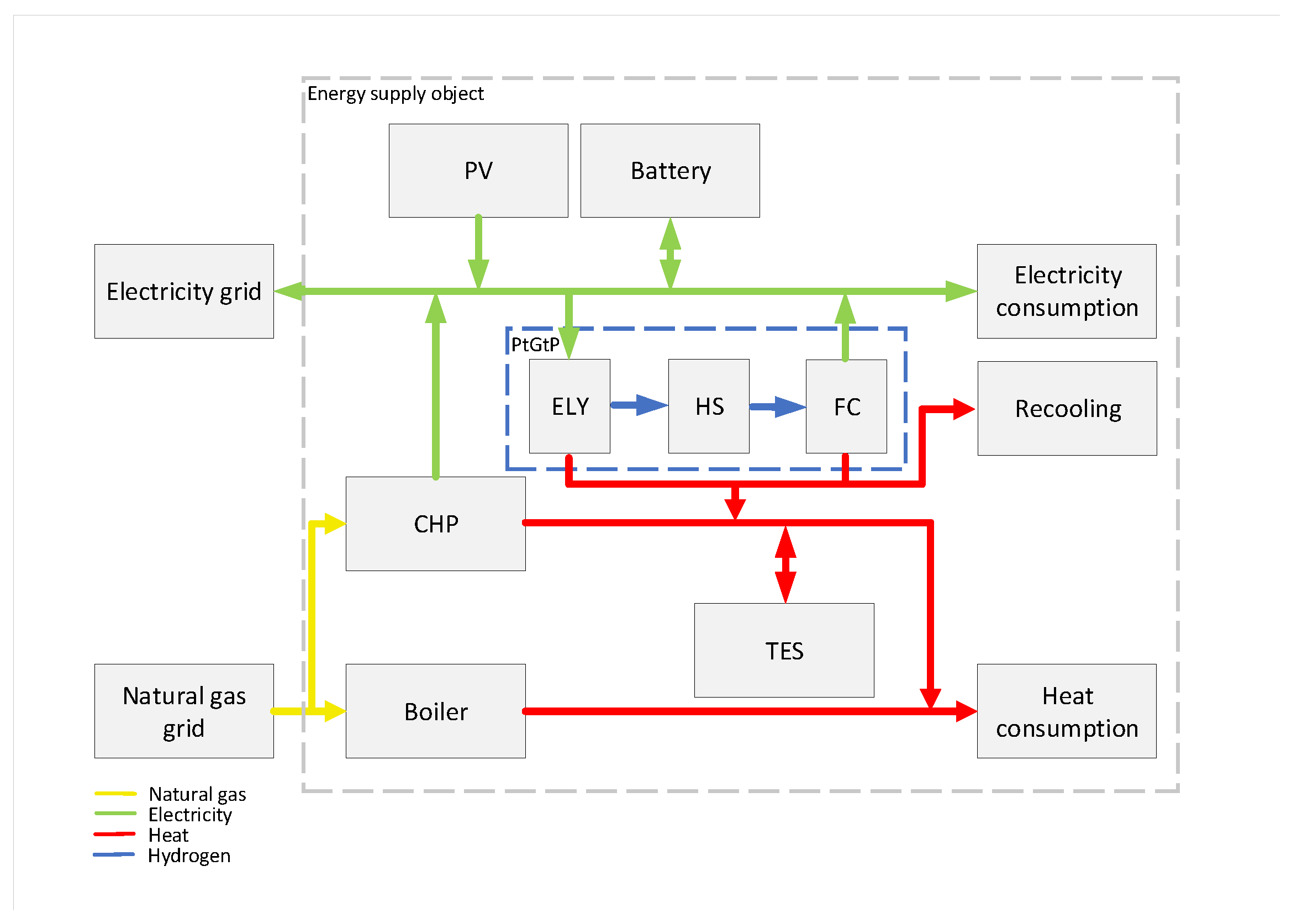

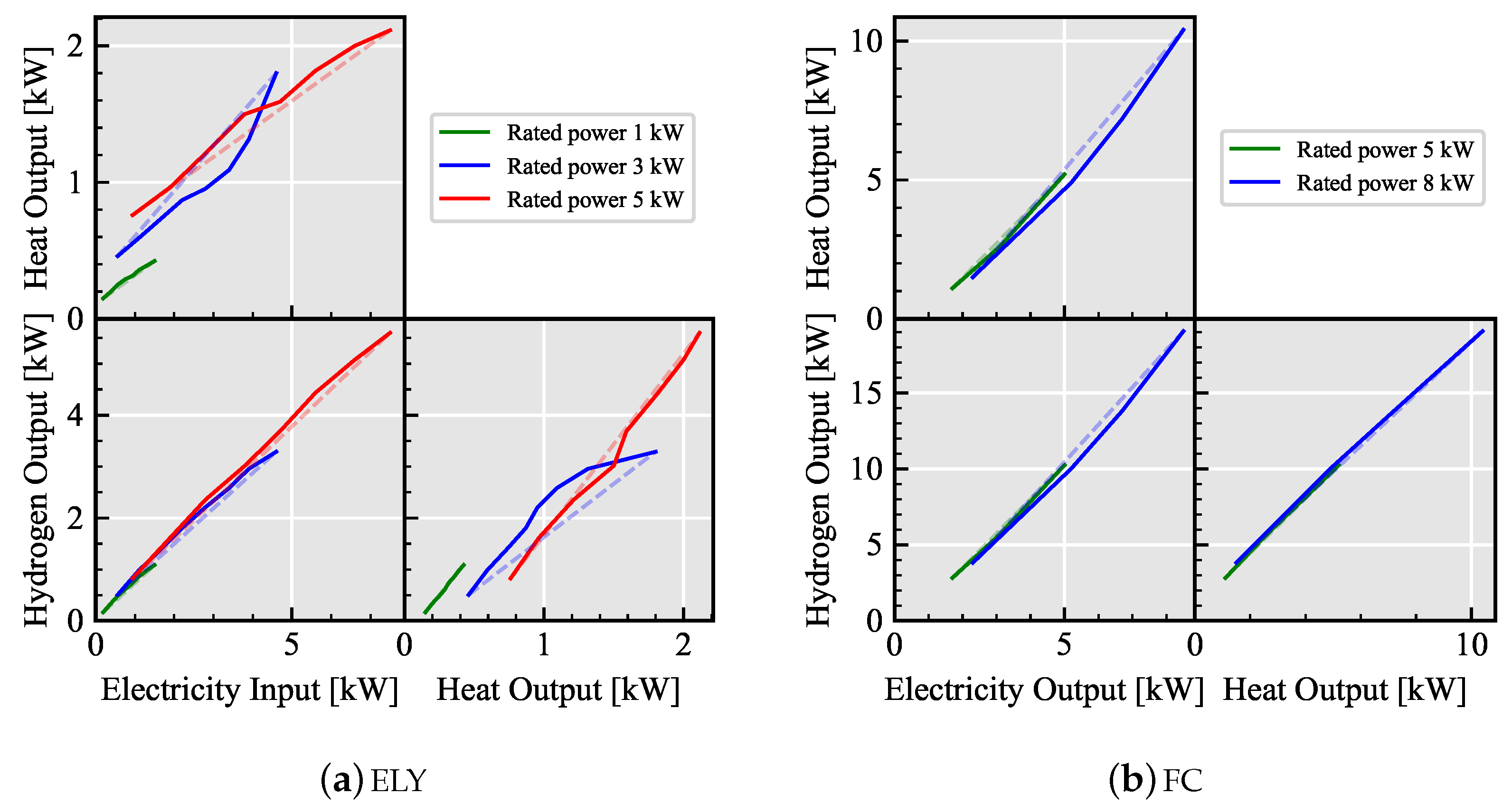


| Technology | Performance Spectrum |
|---|---|
| Boiler/ | 500 |
| CHP/ | 0, 50, 70, 99, 134, 190 |
| PV/ | 0, 10, 20, 30, 40 |
| TES/ | 0, 10, 30, 50 |
| Battery/ | 0, 30, 70, 131, 233 |
| ELY/ | 1, 3, 5 |
| HS/ | 670, 1340 |
| FC/ | 5, 8 |
| Sink | Elec. grid | Battery | PtGtP | El. cons. | CHP | Boiler | Th. cons. | |
|---|---|---|---|---|---|---|---|---|
| Source | ||||||||
| Elec. grid | X | −21.43 to 3.97 | −23.48 to 1.92 | |||||
| PV | 10.06 to 10.27 | 0 | 0 | −2.70 | ||||
| Battery | X | X | −2.70 | |||||
| PtGtP | −10.49 to 13.01 | X | −2.70 | - | ||||
| NG grid | −5.95 to −4.59 | −5.95 to −4.59 | ||||||
| CHP | −9.83 to 21.01 | 0 to 4.00 | −2.70 to 1.30 | 0 | ||||
| Boiler | 0 | |||||||
| CHP | PV | TES | Battery | ELY | HS | FC | Annuity | CO2 Emission | |
|---|---|---|---|---|---|---|---|---|---|
| Scenario 1 | 99 | 40 | 50 | 0 | - | - | - | −121,263 | 312 |
| 134 | 20 | 50 | 0 | - | - | - | −152,043 | 283 | |
| 134 | 40 | 50 | 30 | - | - | - | −154,122 | 272 | |
| 190 | 40 | 50 | 0 | - | - | - | −174,683 | 239 | |
| Scenario 2 | 99 | 40 | 50 | 0 | 1 | 670 | 5 | −134,384 | 312 |
| 99 | 40 | 50 | 0 | 1 | 1340 | 5 | −138,463 | 311 | |
| 134 | 30 | 30 | 0 | 1 | 670 | 5 | −166,177 | 286 | |
| 134 | 40 | 30 | 0 | 1 | 670 | 5 | −166,628 | 279 | |
| 134 | 40 | 50 | 30 | 1 | 670 | 5 | −167,556 | 271 | |
| 134 | 40 | 50 | 0 | 3 | 670 | 5 | −170,751 | 271 | |
| 134 | 40 | 50 | 0 | 1 | 1340 | 8 | −172,152 | 271 | |
| 190 | 40 | 50 | 0 | 1 | 670 | 5 | −188,228 | 239 | |
| 190 | 40 | 50 | 0 | 3 | 670 | 5 | −190,295 | 235 | |
| 190 | 40 | 50 | 0 | 1 | 670 | 8 | −192,218 | 235 | |
| 190 | 40 | 50 | 0 | 5 | 670 | 5 | −192,457 | 235 | |
| 190 | 40 | 50 | 0 | 5 | 1340 | 8 | −196,565 | 235 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Schmeling, L.; Buchholz, A.A.I.; Heineke, H.; Klement, P.; Hanke, B.; von Maydell, K. Planning, Optimisation and Evaluation of Small Power-to-Gas-to-Power Systems: Case Study of a German Dairy. Sustainability 2022, 14, 6050. https://doi.org/10.3390/su14106050
Schmeling L, Buchholz AAI, Heineke H, Klement P, Hanke B, von Maydell K. Planning, Optimisation and Evaluation of Small Power-to-Gas-to-Power Systems: Case Study of a German Dairy. Sustainability. 2022; 14(10):6050. https://doi.org/10.3390/su14106050
Chicago/Turabian StyleSchmeling, Lucas, Alexander August Ionnis Buchholz, Hilmer Heineke, Peter Klement, Benedikt Hanke, and Karsten von Maydell. 2022. "Planning, Optimisation and Evaluation of Small Power-to-Gas-to-Power Systems: Case Study of a German Dairy" Sustainability 14, no. 10: 6050. https://doi.org/10.3390/su14106050
APA StyleSchmeling, L., Buchholz, A. A. I., Heineke, H., Klement, P., Hanke, B., & von Maydell, K. (2022). Planning, Optimisation and Evaluation of Small Power-to-Gas-to-Power Systems: Case Study of a German Dairy. Sustainability, 14(10), 6050. https://doi.org/10.3390/su14106050






