Optimal Power Flow Solution of Power Systems with Renewable Energy Sources Using White Sharks Algorithm
Abstract
:1. Introduction
- The white shark optimizer (WSO), a novel meta-heuristic algorithm proposed in [25], is employed to efficiently solve the OPF issue in this study;
- The proposed algorithm is developed to test an IEEE-30 bus system with double wind farms and a single solar photovoltaic to determine if it can discover the best results for the OPF problem using renewable power in both unpractical and real scenarios;
- The four algorithms were prepared to find the optimal solution after 10 runs and 300 iterations. The best three solutions are selected among the ten to be presented in the results and used to study the convergence for each case in terms of reaching the optimal solution for scheduling and using power from different power plants;
- In addition, the solutions of the proposed method are compared with the method (ESMAOPF) that the authors used in [18], where the enhanced slime mold algorithm was used instead of conventional SMA, for solving the optimal power flow problem. The comparison showed the success of WSO over ESMAOPF in terms of achieving a lower total generating cost.
2. Optimal Power Flow Mathematical Models
2.1. Thermal Power Generation Cost
2.2. Direct Cost of Wind and Solar Photovoltaic
2.3. Cost Estimation for Wind Power with Uncertain Output
2.4. Cost Estimation for Solar Power with Uncertain Output
2.5. Emission
2.6. Equality Constraints
2.7. Inequality Constraints
2.7.1. Generator’s Constraints
2.7.2. Safety Constraints
3. Estimation of the Uncertain Power of Renewable Energy Sources
3.1. Renewable Energy Source Probability Distribution
3.2. Power Models for Wind Generator and Solar Photovoltaic
4. The Basis of the Proposed Method’s Development
4.1. White Shark Optimizer (WSO)
4.2. Initialization of WSO
4.3. Speed of Movement towards Prey
4.4. Movement in the Direction of the Optimal Prey
4.5. Movement in the Direction of the Optimal Shark
| Algorithm 1: Code summarizing the iterative optimization process of WSO. | |
| 1: | Initialize the parameters of the problem |
| 2: | Initialize the parameters of WSO |
| 3: | Randomly generate the initial positions of WSO |
| 4: | Initialize the velocity of the initial population |
| 5: | Evaluate the position of the initial population |
| 6: | while (k < K) do |
| 7: | Update the parameters ν, p1, p2, µ, a, b, w0, f, mv and Ss using Equations (40)–(43), (45)–(49) and (52), respectively. |
| 8: | fori = 1 to n do |
| 9: | vik+1= µ [vik + p1 (wgbestk − wik) × c1 + p2(w′vkbest − wik) × c2] |
| 10: | end for |
| 11: | fori = 1 to n do |
| 12: | if rand < mv then |
| 13: | wik+1 = wik·− ⊕ w0 + u·a + l·b |
| 14: | else |
| 15: | wik+1 = wik + vik/f |
| 16: | end if |
| 17: | end for |
| 18: | fori = 1 to n do |
| 19: | if rand ≤ Ss then |
| 20: | |
| 21: | if i == 1 then |
| 22: | |
| 23: | else |
| 24: | |
| 25: | |
| 26: | end if |
| 27: | end if |
| 28: | end for |
| 29: | Adjust the position of the white sharks that proceed beyond the boundary |
| 30: | Evaluate and update the new positions |
| 31: | k = k + 1 |
| 32: | end while |
| 33: | Return the optimal solution obtained so far |
4.6. Fish School Behavior
4.7. Implementation and Analysis of WSO
5. Simulation Results and Comparison
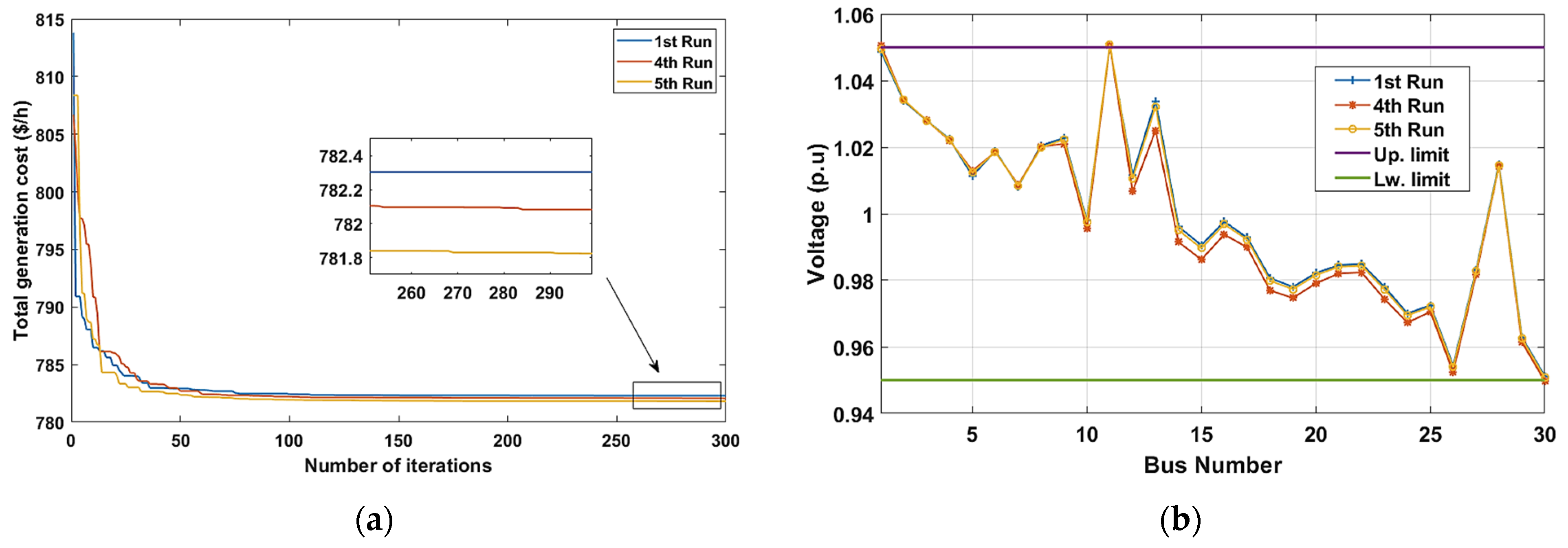
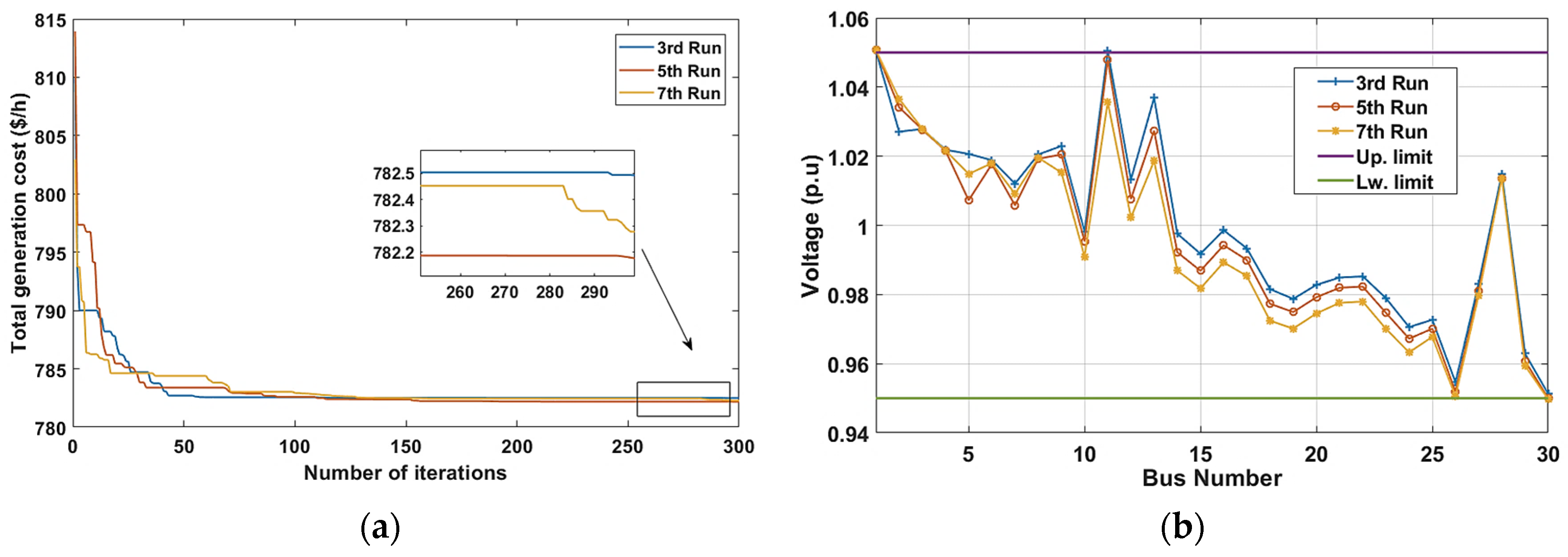
5.1. White Shark Optimizer (WSO)
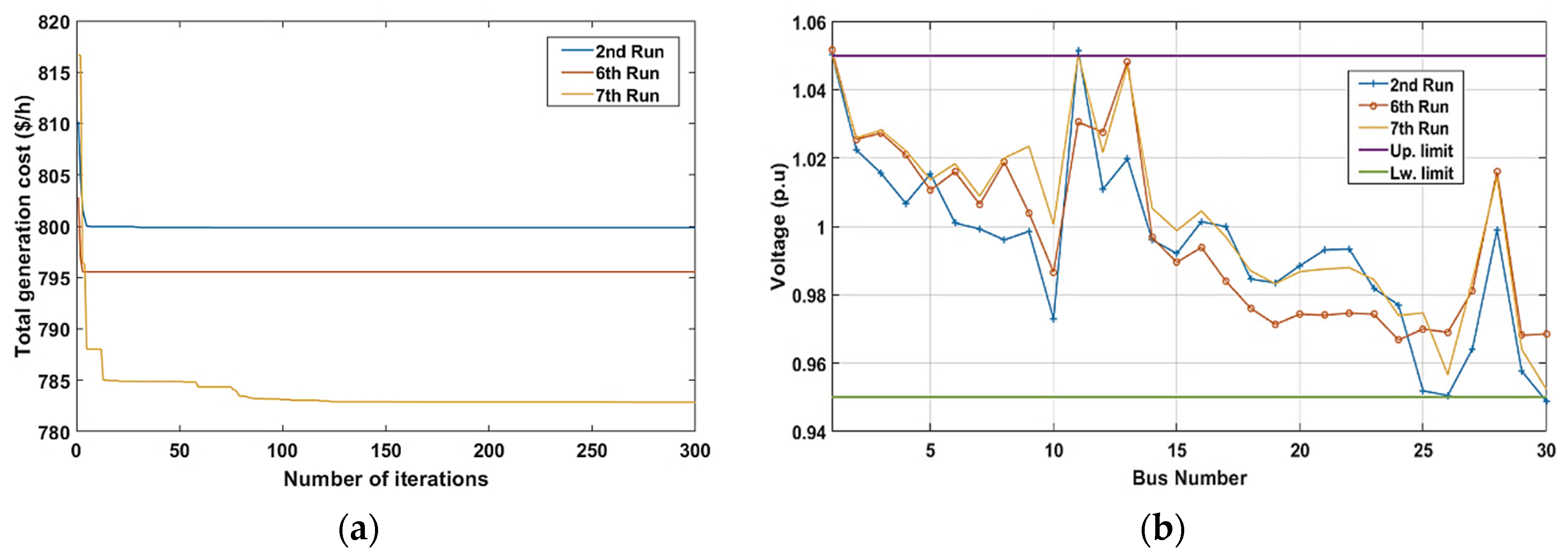
5.2. Northern Goshawk Optimization (NGO)
5.3. Pelican Optimization Algorithm (POA)
5.4. Smell Agent Optimization (SAO)
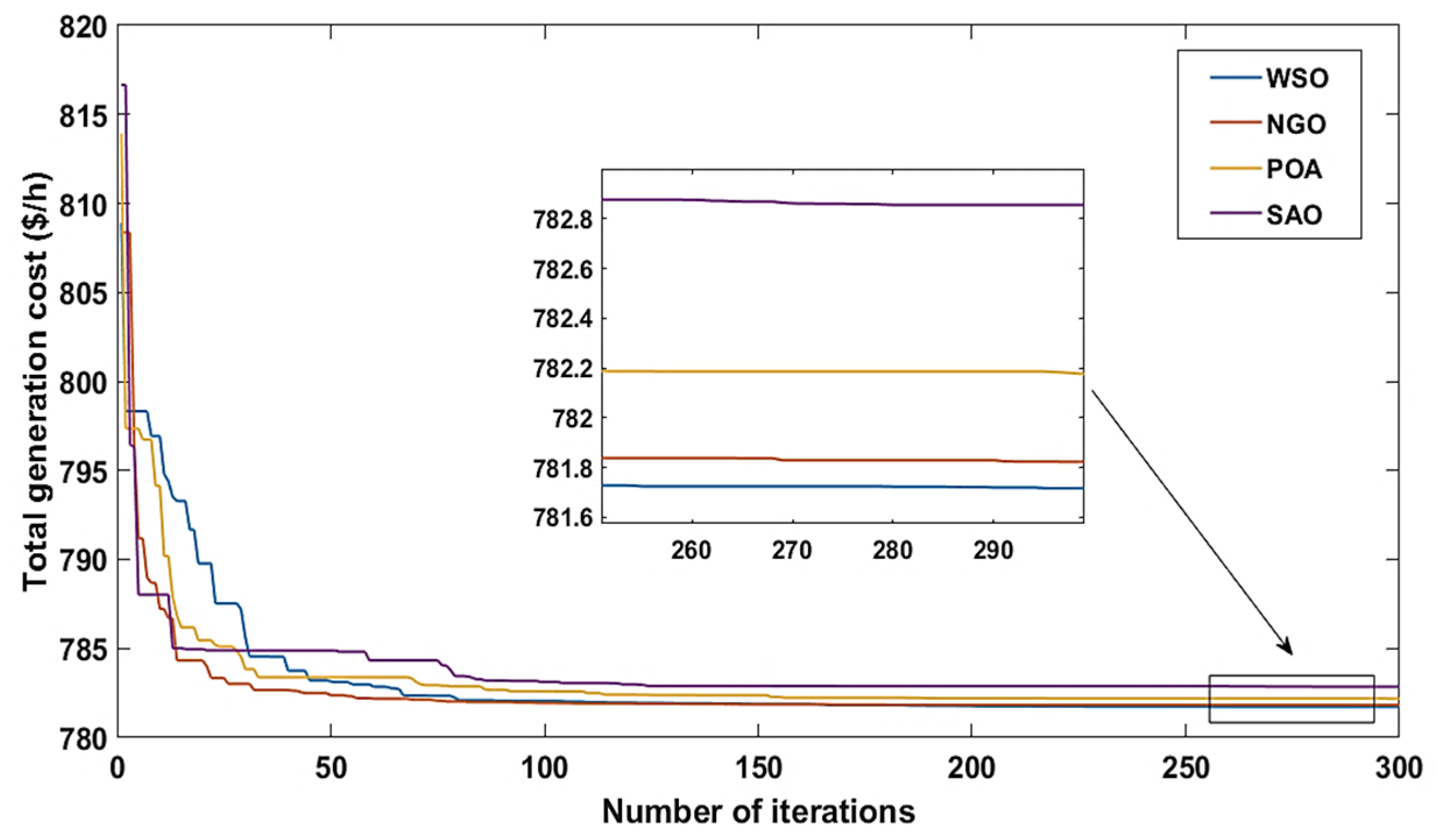
5.5. Comparison of the Results of Different Optimization Techniques and Discussion
6. Conclusions
7. Future Work
- Apply the proposed methods to solve optimal power flow in a larger power system;
- Incorporate more renewable energy sources (such as hydropower plants) into the larger power system;
- Apply of more than one case study that takes into account factors other than the minimization of generation cost, such as emissions, carbon tax, reserve cost, penalty cost, and the dynamic nature of generating facilities’ control;
- Studying multi-objective optimal power flow in a power system with renewable energy sources.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Farhat, M.; Kamel, S.; Atallah, A.M.; Khan, B. Optimal Power Flow Solution Based on Jellyfish Search Optimization Considering Uncertainty of Renewable Energy Sources. IEEE Access 2021, 9, 100911–100933. Available online: https://ieeexplore.ieee.org/document/9481886 (accessed on 22 July 2021). [CrossRef]
- Carpentier, J. Contribution to the economic dispatch problem. Bull. Soc. Fr. Electr. 1962, 3, 431–447. [Google Scholar]
- Nguyen, T.T. A high performance social spider optimization algorithm for optimal power flow solution with single objective optimization. Energy 2019, 171, 218–240. [Google Scholar] [CrossRef]
- Momoh, J.A.; Adapa, R.; El-Hawary, M.E. A review of selected optimal power flow literature to 1993. I. Nonlinear and quadratic programming approaches. IEEE Trans. Power Syst. 1993, 14, 96–104. [Google Scholar]
- Roy, R.; Jadhav, H.T. Optimal power flow solution of power system incorporating stochastic wind power using Gbest guided artificial bee colony algorithm. Int. J. Electr. Power Energy Syst. 2015, 64, 562–578. [Google Scholar] [CrossRef]
- Panda, A.; Tripathy, M. Security constrained optimal power flow solution of wind-thermal generation system using modified bacteria foraging algorithm. Energy 2015, 93, 816–827. [Google Scholar] [CrossRef]
- Ravi, K. Optimal power flow considering intermittent wind power using particle swarm optimization. Int. J. Renew. Energy Res. 2016, 6, 504–509. [Google Scholar]
- Abido, M.A. Optimal power flow using tabu search algorithm. Electr. Power Compon. Syst. 2002, 30, 469–483. [Google Scholar] [CrossRef] [Green Version]
- Niknam, T.; Narimani, M.R.; Aghaei, J.; Tabatabaei, S.; Nayeripour, M. Modified honeybee mating optimisation to solve dynamic optimal power flow considering generator constraints. IET Gener. Transm. Distrib. 2011, 5, 989–1002. [Google Scholar] [CrossRef]
- Ara, A.L.; Kazemi, A.; Gahramani, S.; Behshad, M. Optimal reactive power flow using multi-objective mathematical programming. Sci. Iran. 2012, 19, 1829–1836. [Google Scholar]
- Duman, S.; Güvenç, U.; Sonmez, Y.; Yörükeren, N. Optimal power flow using gravitational search algorithm. Energy Convers. Manag. 2012, 59, 86–95. [Google Scholar] [CrossRef]
- Adaryani, M.R.; Karami, A. Artificial bee colony algorithm for solving multiobjective optimal power flow problem. Int. J. Electr. Power Energy Syst. 2013, 53, 219–230. [Google Scholar] [CrossRef]
- Ghasemi, M.; Ghavidel, S.; Ghanbarian, M.M.; Gharibzadeh, M.; Vahed, A.A. Multiobjective optimal power flow considering the cost, emission, voltage deviation and power losses using multi-objective modified imperialist competitive algorithm. Energy 2014, 78, 276–289. [Google Scholar] [CrossRef]
- Le Anh, T.N.; Vo, D.N.; Ongsakul, W.; Vasant, P.; Ganesan, T. Cuckoo optimization algorithm for optimal power flow. In Proceedings of the 18th Asia Pacific Symposium on Intelligent and Evolutionary Systems, Singapore, 10–12 November 2014; Volume 479, p. 4931. [Google Scholar]
- Ladumor, D.P.; Trivedi, I.N.; Bhesdadiya, R.H.; Jangir, P. A grey wolf optimizer algorithm for voltage stability enhancement. In Proceedings of the Third International Conference on Advances in Electrical, Electronics, Information, Communication and Bio-Informatics (AEEICB), Chennai, India, 27–28 February 2017; pp. 278–282. [Google Scholar]
- Biswas, P.P.; Suganthan, P.N.; Amaratunga, G.A. Optimal power flow solutions incorporating stochastic wind and solar power. Energy Convers. Manag. 2017, 148, 1194–1207. [Google Scholar] [CrossRef]
- Khan, B.; Singh, P. Optimal power flow techniques under characterization of conventional and renewable energy sources: A comprehensive analysis. J. Eng. 2017, 2017, 9539506. [Google Scholar] [CrossRef] [Green Version]
- Farhat, M.; Kamel, S.; Atallah, A.M.; Hassan, M.H.; Agwa, A.M. ESMA-OPF: Enhanced Slime Mould Algorithm for Solving Optimal Power Flow Problem. Sustainability 2022, 14, 2305. [Google Scholar] [CrossRef]
- Ghasemi, M.; Ghavidel, S.; Ghanbarian, M.M.; Gitizadeh, M. Multi-objective optimal electric power planning in the power system using Gaussian barebones imperialist competitive algorithm. Inf. Sci. 2015, 294, 286–304. [Google Scholar]
- El-Hana Bouchekara, H.R.; Abido, M.A.; Chaib, A.E. Optimal power flow using an improved electromagnetism-like mechanism method. Electr. Power Compon. Syst. 2016, 44, 434–449. [Google Scholar] [CrossRef]
- Bouchekara, H.R.E.H.; Chaib, A.E.; Abido, M.A.; El-Sehiemy, R.A. Optimal power flow using an improved colliding Bodies optimization algorithm. Appl. Soft Comput. 2016, 42, 119–131. [Google Scholar] [CrossRef]
- Abaci, K.; Yamacli, V. Differential search algorithm for solving multi-objective optimal power flow problem. Int. J. Electr. Power Energy Syst. 2016, 1, 10–79. [Google Scholar] [CrossRef]
- Pulluri, H.; Naresh, R.; Sharma, V. A solution network based on stud krill herd algorithm for optimal power flow problems. Soft Comput. 2018, 22, 159–176. [Google Scholar] [CrossRef]
- Niknam, T.; Rasoul Narimani, M.; Jabbari, M.; Malekpour, A.R. A modified shuffle frog leaping algorithm for multi-objective optimal power flow. Energy 2011, 36, 6420–6432. [Google Scholar] [CrossRef]
- Braik, M.; Hammouri, A.; Atwan, J.; Al-Betar, M.A.; Awadallah, M.A. White Shark Optimizer: A novel bio-inspired meta-heuristic algorithm for global optimization problems. Knowl. Based Syst. 2022, 243, 108457. Available online: www.elsevier.com/locate/knosys (accessed on 22 February 2022). [CrossRef]
- Salawudeen, A.T.; Mu’azu, M.B.; Sha’aban, Y.A.; Adedokun, E.A. A Novel Smell Agent Optimization: An Extensive CEC Study and Engineering Application. Knowl. Based Syst. 2021, 232, 107486. [Google Scholar] [CrossRef]
- Dehghani, M.; Hubálovský, Š.; Trojovský, P. Northern Goshawk Optimization: A New Swarm-Based Algorithm for Solving Optimization Problems. IEEE Access 2021, 9, 162059–162080. [Google Scholar] [CrossRef]
- Trojovský, P.; Dehghani, M. Pelican Optimization Algorithm: A Novel Nature-Inspired Algorithm for Engineering Applications. Sensors 2022, 22, 855. [Google Scholar] [CrossRef]
- Alsac, O.; Stott, B. Optimal load flow with steady-state security. IEEE Trans. Power Appar. Syst. 1974, 93, 745–751. [Google Scholar] [CrossRef] [Green Version]
- Chaib, A.E.; Bouchekara, H.R.; Mehasni, R.; Abido, M.A. Optimal power flow with emission and non-smooth cost functions using backtracking search optimization algorithm. Int. J. Electr. Power Energy Syst. 2016, 81, 64–77. [Google Scholar] [CrossRef]
- Shi, L.; Wang, C.; Yao, L.; Ni, Y.; Bazargan, M. Optimal power flow solution incorporating wind power. IEEE Syst. J. 2012, 6, 233–241. [Google Scholar] [CrossRef]
- Tian-Pau, C. Investigation on frequency distribution of global radiation using different probability density functions. Int. J. Appl. Sci. Eng. 2010, 8, 99–107. [Google Scholar]
- Reddy, S.S.; Bijwe, P.R.; Abhyankar, A.R. Real-time economic dispatch considering renewable power generation variability and uncertainty over scheduling period. IEEE Syst. J. 2014, 9, 1440–1451. [Google Scholar] [CrossRef]
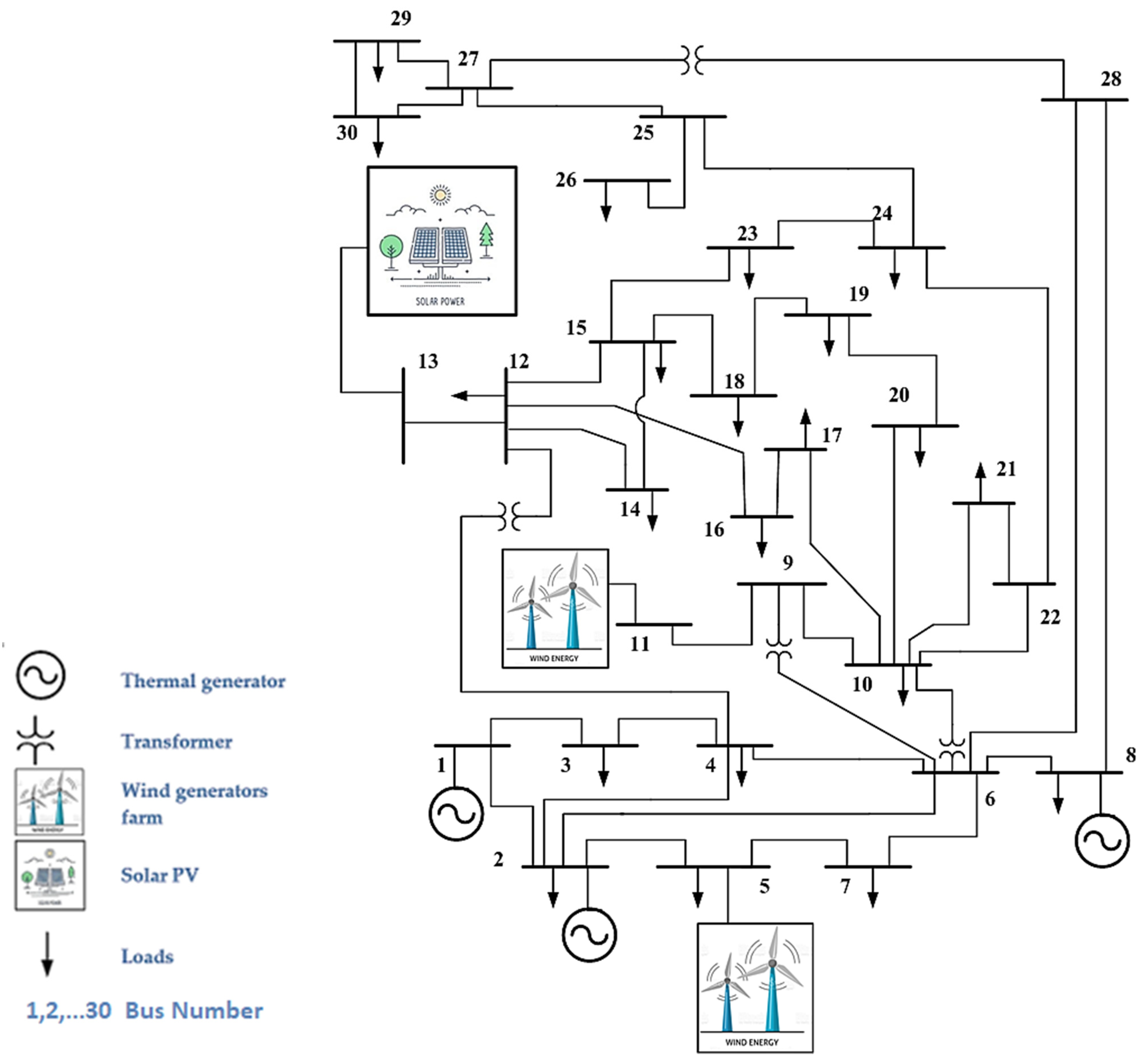



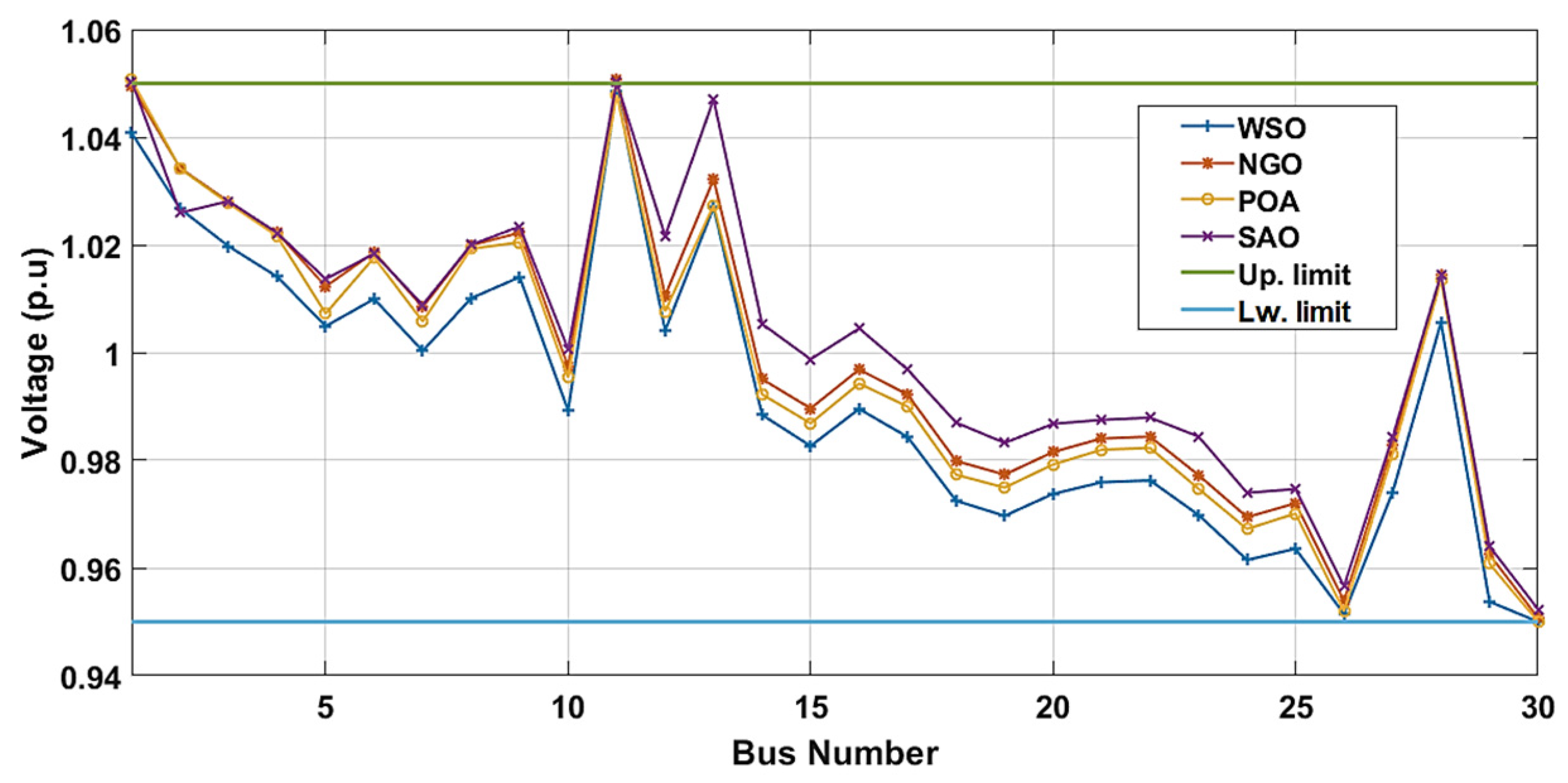
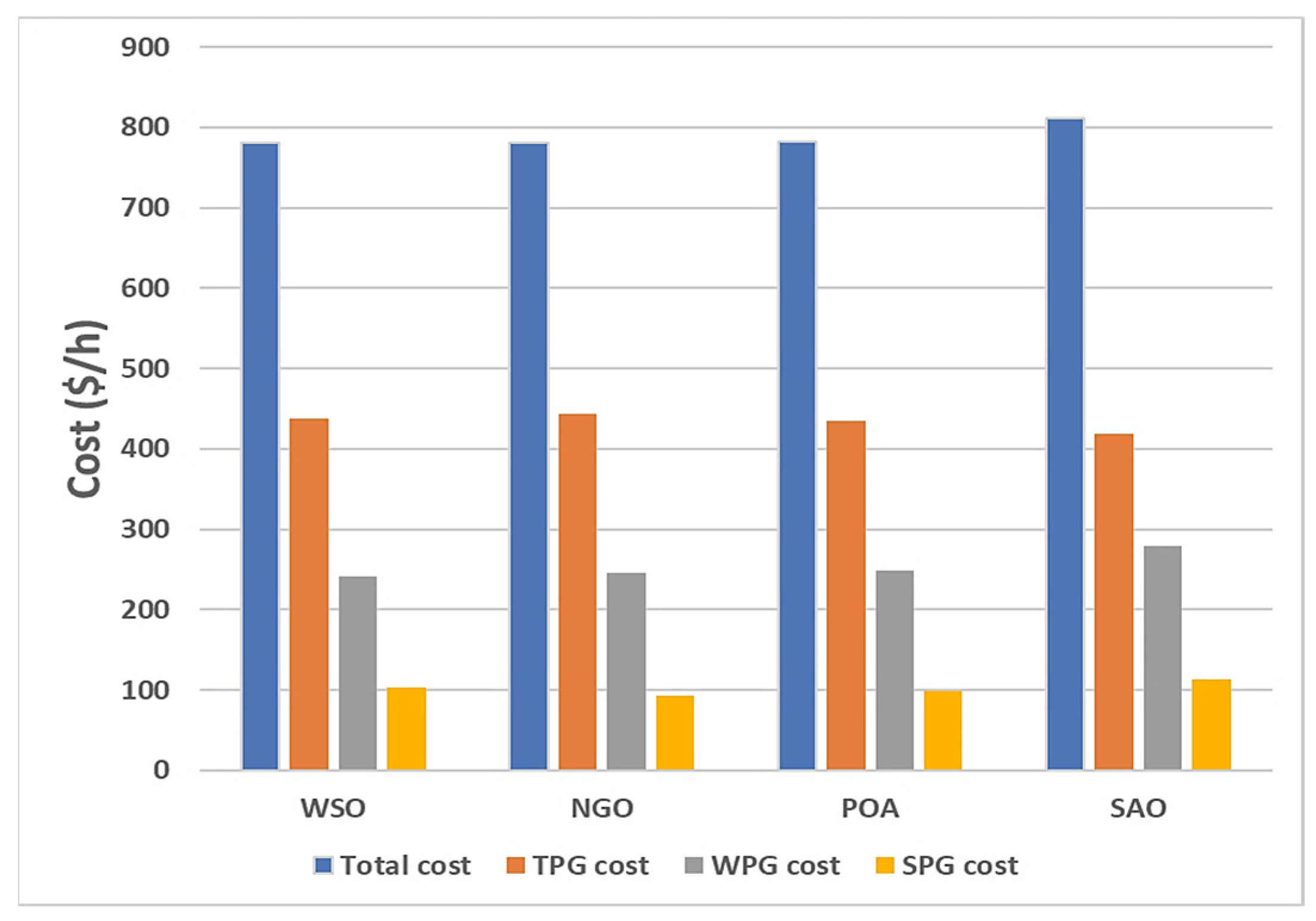
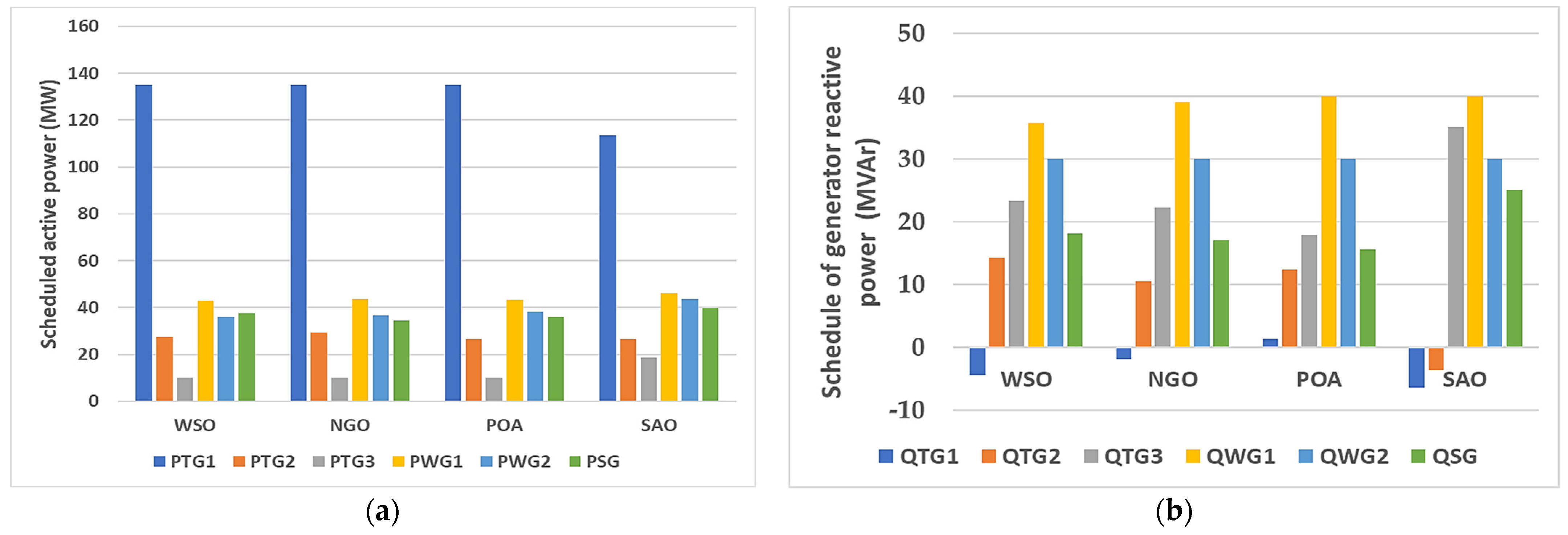
| Items | Quantity | Details |
|---|---|---|
| Buses | 30 | [29] |
| Branches | 41 | [29] |
| Thermal Generators (TG1, TG2, TG3) | 3 | Bus 1 (Swing), Bus 2, and Bus 8. |
| Wind Generators (WPG1, WPG2) | 2 | Bus 5 and bus 11. |
| Solar PV (SPG) | 1 | Bus 13. |
| Control variables | 11 | The planned power of five generators (TG2, TG3, WPG1, WPG2, and SPG), as well as six generating bus voltages. |
| Connected load | - | 283.4 MW, 126.2 MVAR |
| Allowable voltage range for load buses | 24 | [0.95–1.05] p.u. |
| Gen. | Bus | a | b | c | l | m | α | β | γ | ω | μ | P0TGi (MW) | DRi (MW) | URi (MW) |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| TG1 | 1 | 0 | 2 | 0.00375 | 18 | 0.037 | 4.091 | −5.554 | 6.49 | 0.0002 | 6.667 | 99.211 | 20 | 15 |
| TG2 | 2 | 0 | 1.75 | 0.0175 | 16 | 0.038 | 2.543 | −6.047 | 5.638 | 0.0005 | 3.333 | 80 | 15 | 10 |
| TG3 | 8 | 0 | 3.25 | 0.00834 | 12 | 0.045 | 5.326 | −3.55 | 3.38 | 0.002 | 2 | 20 | 8 | 4 |
| Wind Power Farm | Solar Power Plant | ||||||
|---|---|---|---|---|---|---|---|
| Wind Power Generator | No. of Turbines | Rated Power (MW) | Weibull PDF Parameters | Weibull Mean, Mwbl | Rated Power (MW) | Lognormal PDF Parameters | Lognormal |
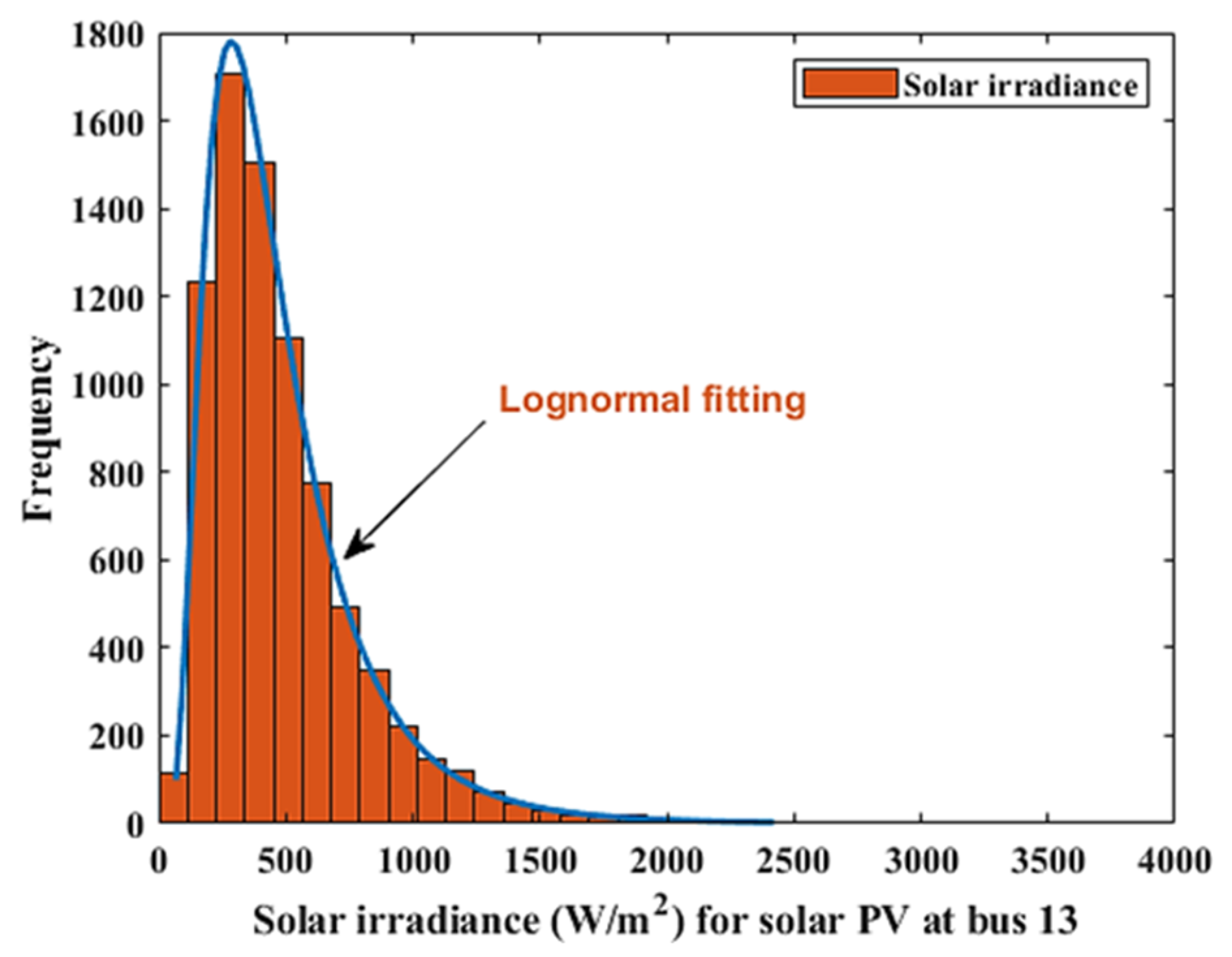
| 1 (at bus 5) | 25 | 75 | K = 2, c = 9 | v = 7.976 (m/s) | 50 (at bus 13) | μ = 6, δ = 0.6 | R = 483 W/m2 |
| 2 (at bus 11) | 20 | 60 | K = 2, c = 10 | v = 8.862 (m/s) | |||
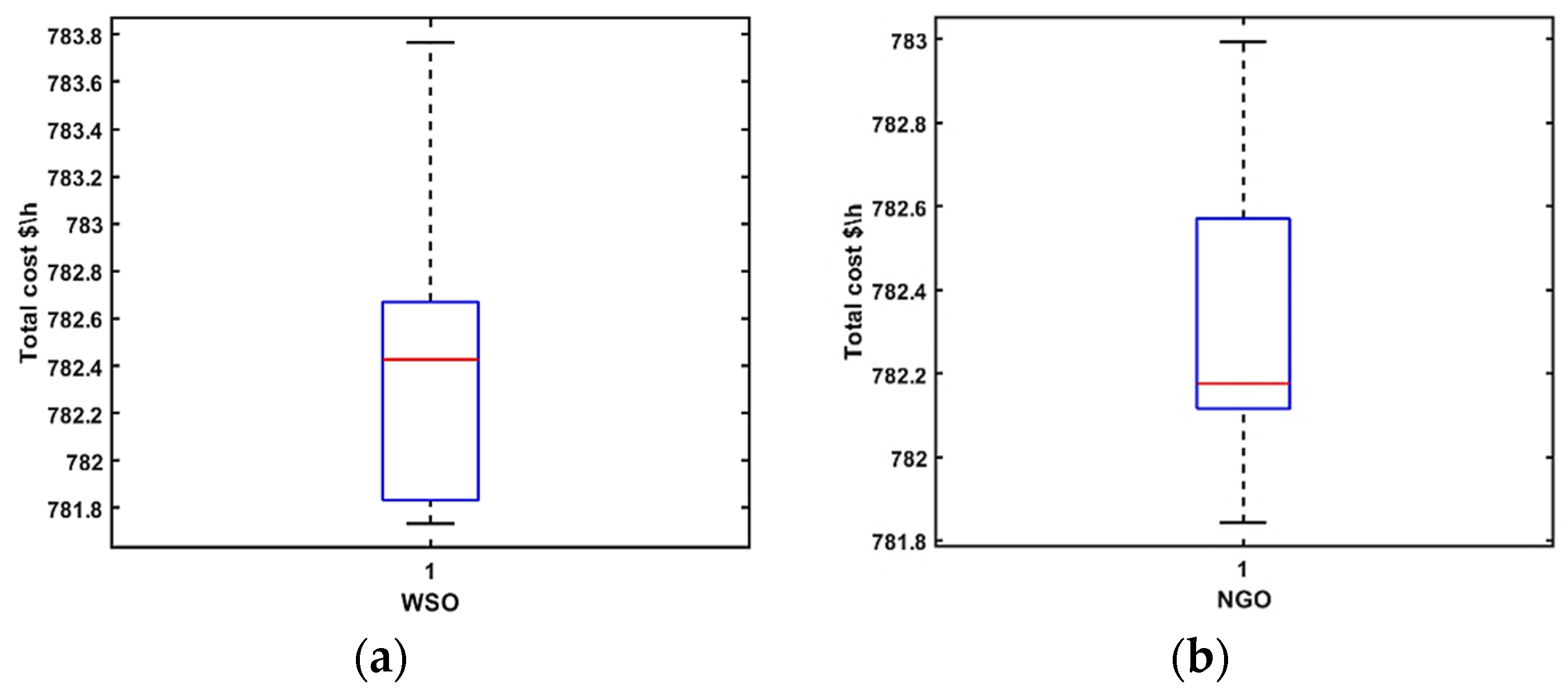
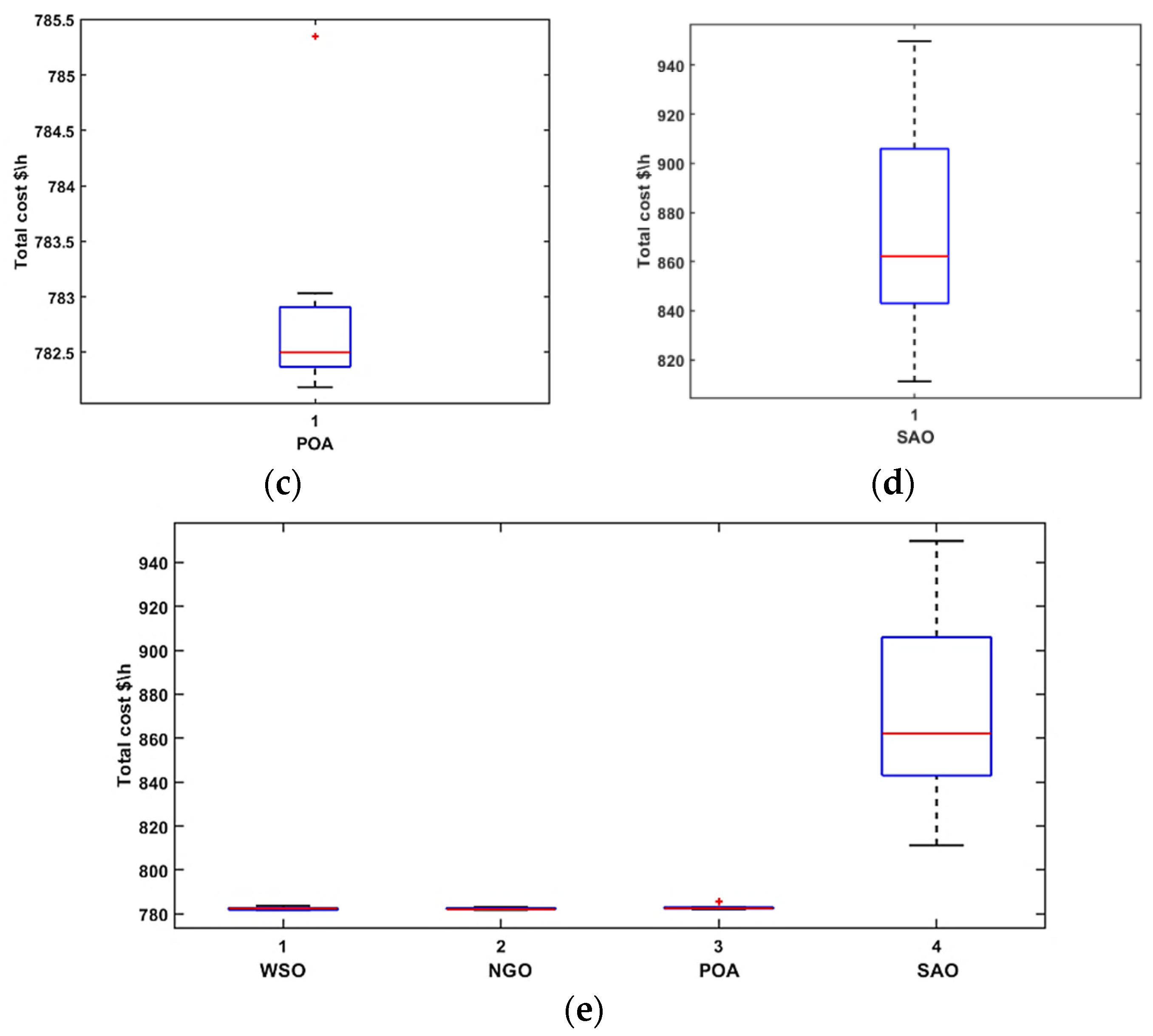
| The Results of Total Generation Cost for 10 Runs and 300 Iterations | ||||
| WSO | NGO | POA | SAO | |
| 1st Run | 782.6698 | 782.313 | 782.8485 | 907.0226 |
| 2nd Run | 783.7659 | 782.9944 | 785.3441 | 846.683 |
| 3rd Run | 782.5018 | 782.5711 | 782.5089 | 843.0099 |
| 4th Run | 781.8318 | 782.1243 | 782.4893 | 905.917 |
| 5th Run | 781.7552 | 781.8438 | 782.1865 | 872.6064 |
| 6th Run | 782.3621 | 782.2253 | 782.3702 | 851.711 |
| 7th Run | 781.733 | 782.9235 | 782.2994 | 811.187 |
| 8th Run | 783.3357 | 782.1109 | 782.4652 | 887.9602 |
| 9th Run | 782.4915 | 782.1162 | 782.9073 | 949.768 |
| 10th Run | 782.1152 | 782.1276 | 783.033 | 823.5738 |
| The Statistical Results of Total Generation Cost for 10 Runs and 300 Iterations | ||||
| WSO | NGO | POA | SAO | |
| Best | 781.733 | 781.8438 | 782.1865 | 811.187 |
| Worst | 783.7659 | 782.9944 | 785.3441 | 949.768 |
| Mean | 782.4562 | 782.335 | 782.8452 | 869.9439 |
| Std | 0.6722 | 0.3766 | 0.9205 | 42.9133 |
| Average time of one run (s) | 524 | 1024 | 1610 | 1790 |
| Control Variables | Min | Max | WSO | NGO | POA | SAO | ESMA [18] |
| PTG1 (MW) | 50 | 140 | 134.9165 | 134.9041 | 134.9076 | 113.404 | 134.9143 |
| PTG2 (MW) | 20 | 80 | 27.57455 | 29.36321 | 26.6666 | 26.64171 | 27.688 |
| PTG3 (MW) | 10 | 35 | 10.00492 | 10.0109 | 10.02834 | 18.70488 | 10.0125 |
| PwG1 (MW) | 0 | 75 | 43.05681 | 43.73514 | 43.27867 | 46.21081 | 43.5782 |
| PwG2 (MW) | 0 | 60 | 36.12732 | 36.71591 | 38.29961 | 43.67977 | 37.4508 |
| PsG1 (MW) | 0 | 50 | 37.52105 | 34.45914 | 35.97858 | 39.90458 | 35.5275 |
| V1 (p.u) | 0.95 | 1.1 | 1.070752 | 1.071513 | 1.072656 | 1.017665 | 1.0699 |
| V2 (p.u) | 0.95 | 1.1 | 1.056697 | 1.056241 | 1.056156 | 1.004626 | 1.0568 |
| V5 (p.u) | 0.95 | 1.1 | 1.034903 | 1.034296 | 1.029249 | 1.095148 | 1.0334 |
| V8 (p.u) | 0.95 | 1.1 | 1.0401 | 1.041903 | 1.043762 | 1.105398 | 1.088 |
| V11 (p.u) | 0.95 | 1.1 | 1.099687 | 1.099531 | 1.099998 | 1.084872 | 1.097 |
| V13 (p.u) | 0.95 | 1.1 | 1.056971 | 1.054164 | 1.049375 | 1.109471 | 1.052 |
| Parameters | Min | Max | WSO | NGO | POA | SAO | ESMA [18] |
| QTG1 (MVAr) | −20 | 150 | −4.43953 | −1.8199 | 1.326721 | −6.41329 | −6.588 |
| QTG2 (MVAr) | −20 | 60 | 14.28056 | 10.49797 | 12.42993 | −3.53766 | 16.436 |
| QTG3 (MVAr) | −15 | 40 | 23.31959 | 22.32038 | 17.85702 | 35 | 40 |
| QwG1 (MVAr) | −30 | 35 | 35.7025 | 39.00757 | 40 | 40 | 21.181 |
| QwG2 (MVAr) | −25 | 30 | 30 | 30 | 30 | 30 | 29.548 |
| QwG1 (MVAr) | −20 | 25 | 18.19068 | 17.01745 | 15.63321 | 25 | 16.472 |
| Total power cost (USD/h) | 781.733 | 781.8438 | 782.1865 | 811.1871 | 781.9375 | ||
| Emissions (t/h) | 1.763241 | 1.761466 | 1.7625 | 0.510854 | 1.7629 | ||
| Ploss (MW) | 5.80114 | 5.788415 | 5.759369 | 5.145789 | 5.7715 | ||
| Vd (p.u) | 0.468569 | 0.465172 | 0.44752 | 0.68291 | 0.45868 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ali, M.A.; Kamel, S.; Hassan, M.H.; Ahmed, E.M.; Alanazi, M. Optimal Power Flow Solution of Power Systems with Renewable Energy Sources Using White Sharks Algorithm. Sustainability 2022, 14, 6049. https://doi.org/10.3390/su14106049
Ali MA, Kamel S, Hassan MH, Ahmed EM, Alanazi M. Optimal Power Flow Solution of Power Systems with Renewable Energy Sources Using White Sharks Algorithm. Sustainability. 2022; 14(10):6049. https://doi.org/10.3390/su14106049
Chicago/Turabian StyleAli, Mahmoud A., Salah Kamel, Mohamed H. Hassan, Emad M. Ahmed, and Mohana Alanazi. 2022. "Optimal Power Flow Solution of Power Systems with Renewable Energy Sources Using White Sharks Algorithm" Sustainability 14, no. 10: 6049. https://doi.org/10.3390/su14106049
APA StyleAli, M. A., Kamel, S., Hassan, M. H., Ahmed, E. M., & Alanazi, M. (2022). Optimal Power Flow Solution of Power Systems with Renewable Energy Sources Using White Sharks Algorithm. Sustainability, 14(10), 6049. https://doi.org/10.3390/su14106049









