Extracting Optimal Operation Rule Curves of Multi-Reservoir System Using Atom Search Optimization, Genetic Programming and Wind Driven Optimization
Abstract
1. Introduction
2. Materials and Methods
2.1. Study Area and Data Collection
2.2. The Proposed Computational Approach
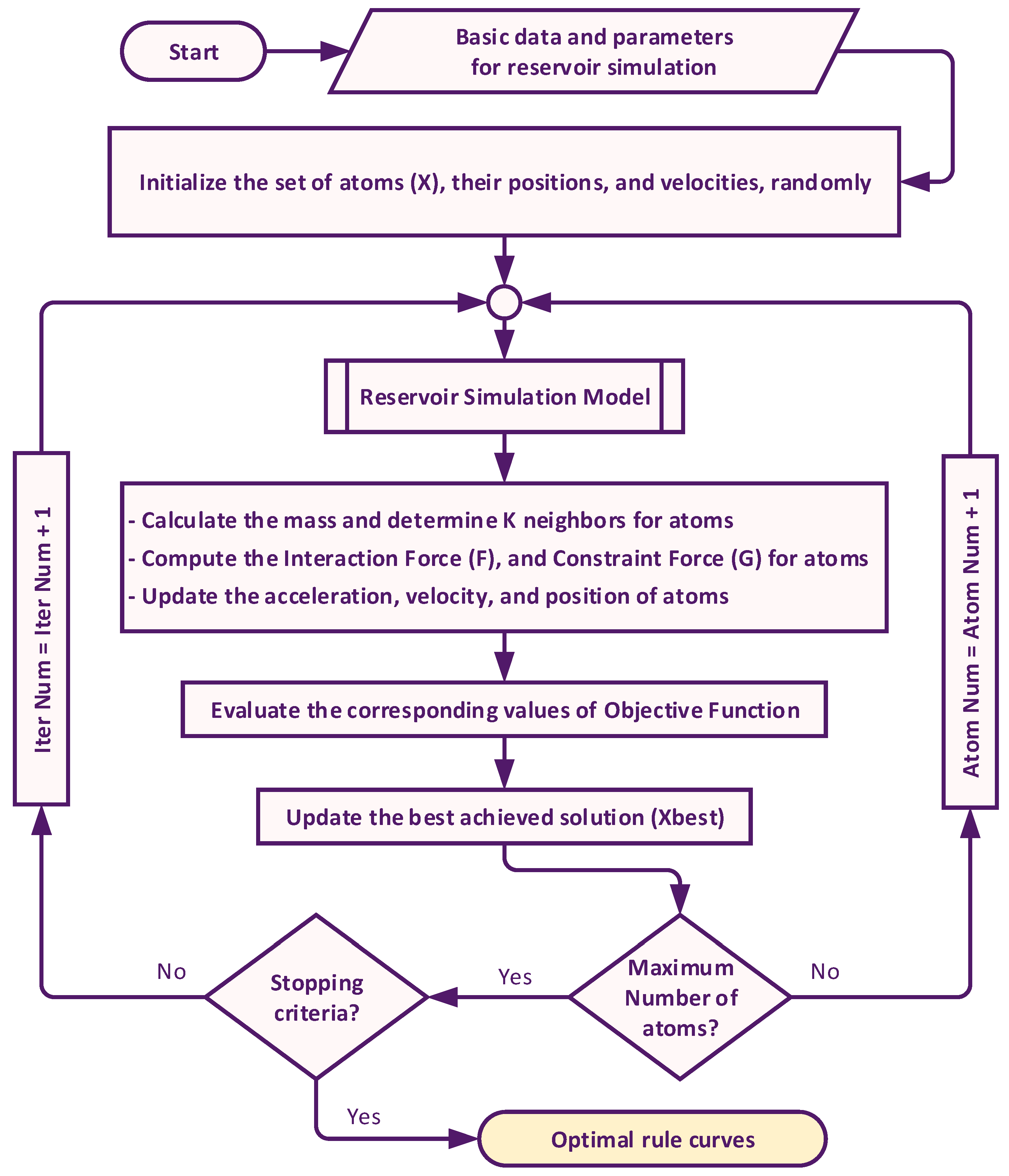
2.3. Atom Search Optimization Algorithm for Finding Operation Rule Curves
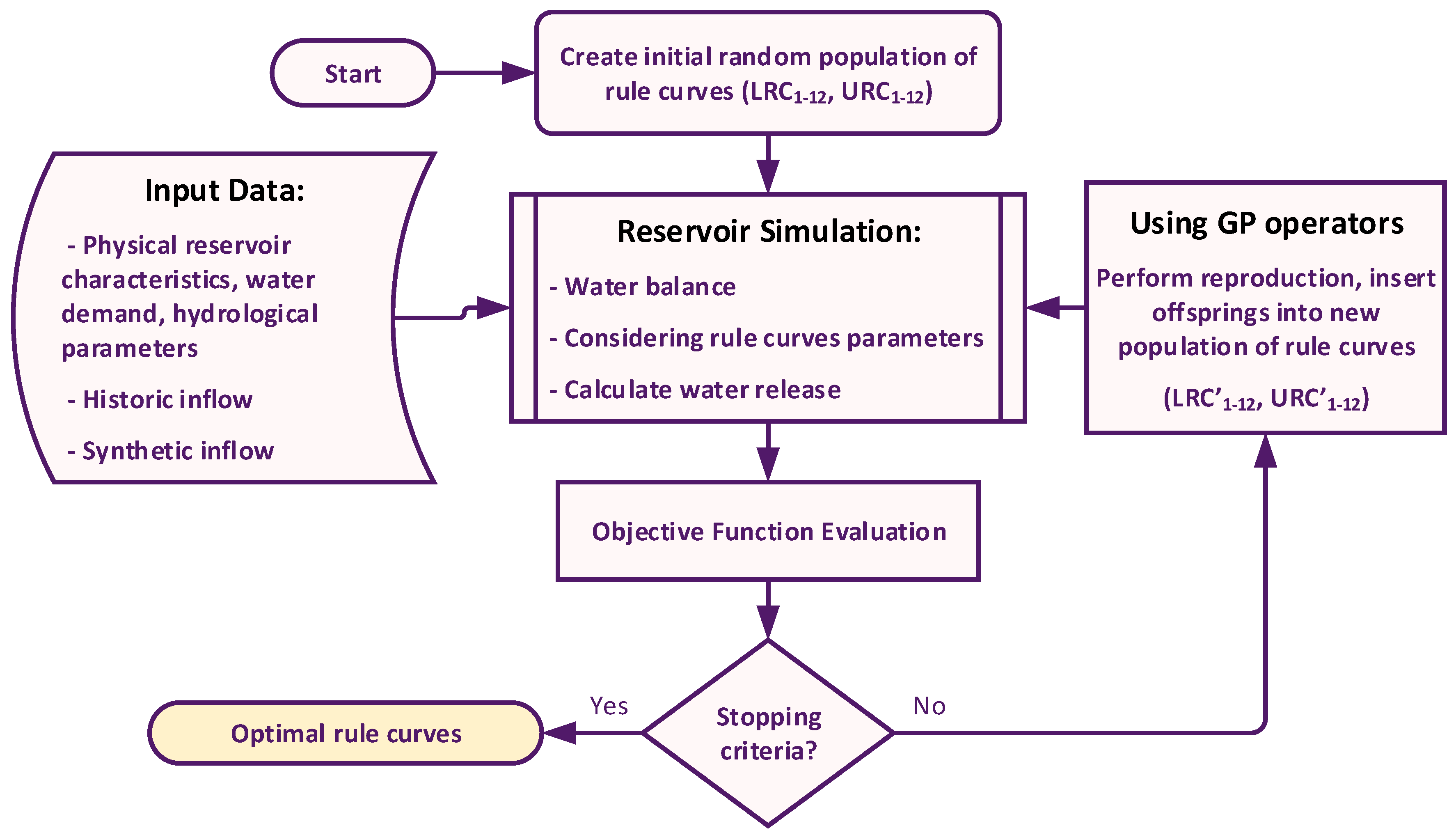
2.4. Genetic Programming for Finding Operation Rule Curves
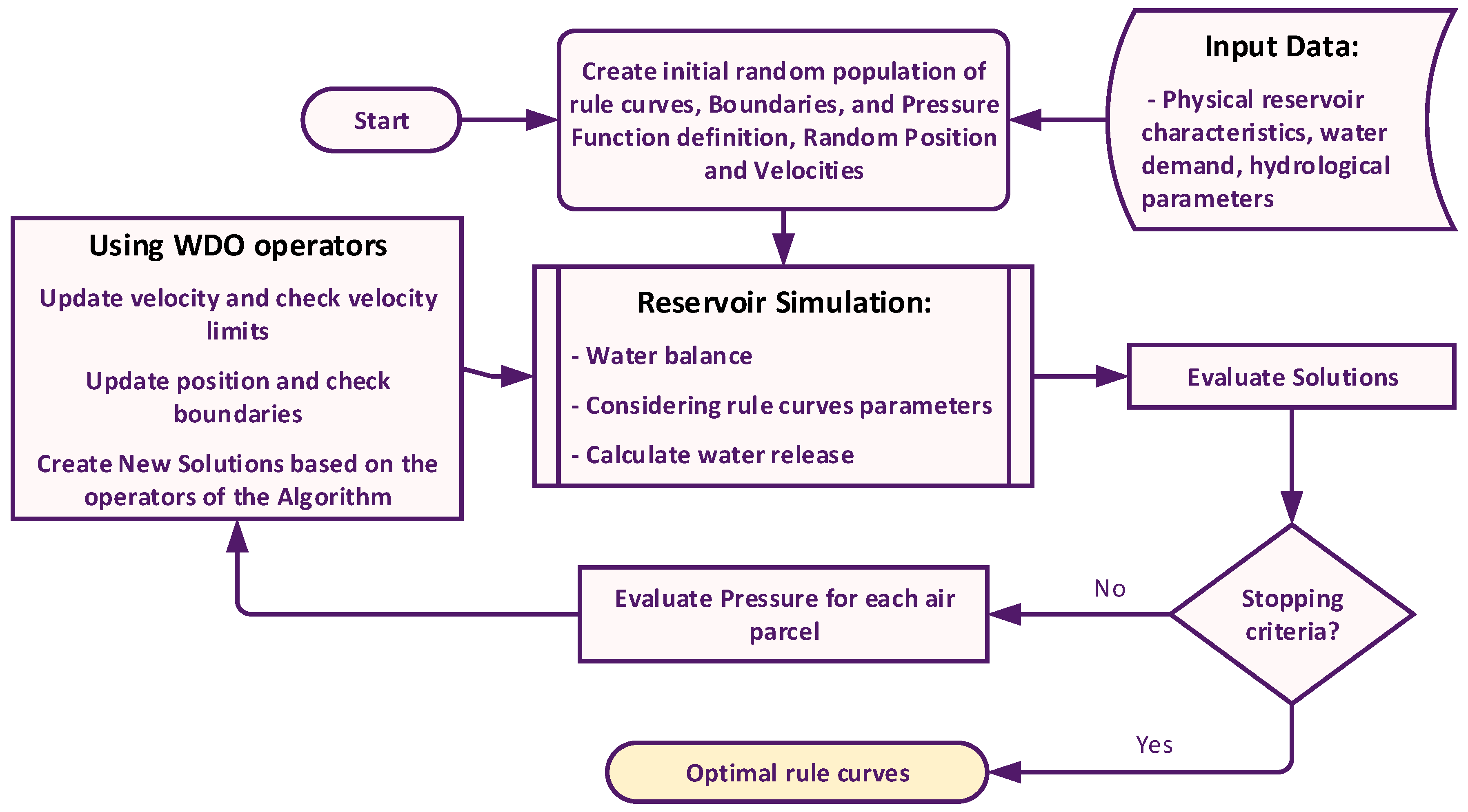
2.5. Wind-Driven Optimization for Finding Operation Rule Curves
2.6. Rule Curve Performance Assessment
- The performance of the proposed model was evaluated with historical inflow data for 2005–2020 and monthly synthetic inflow data across 1000 incident sets with the standard operating rule of release criteria.
- A comparison of the performance of the rule curve obtained by the ASO with the current rule curves, genetic programming (GP) and wind-driven optimization (WDO) using the least mean excess water content.
- The water situation when considering the amount of water discharged from the Upper Huai Sai-1 reservoir, the Upper Huai Sai-2 reservoir and the Upper Huai Sai-3 reservoir when combined flows are limited by the capacity of the Huai Sai Weir (that can drain the maximum 3.5 MCM/months) before flowing into the Huai Sai Kamin reservoir was evaluated.
3. Results
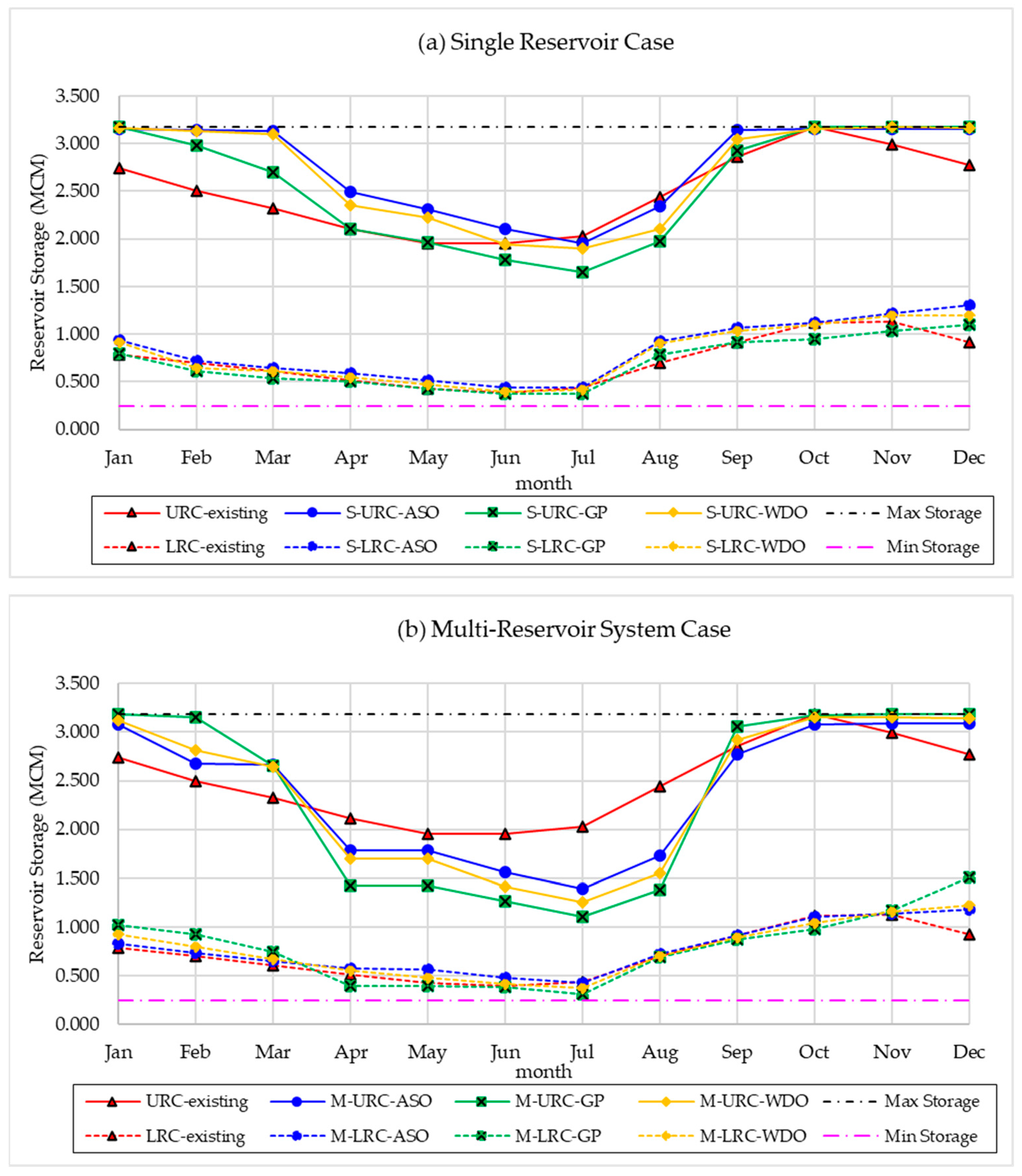
3.1. The Multi-Reservoir Rule Curves Search
3.2. Assessment of the Amount of Inflow into the Huai Sai Kamin Reservoir Obtained from the Newly Obtained Rule Curves
3.3. Performance of Optimal Rule Curves in Monthly Historical and Synthetic Inflow Data across 1000 Incident Sets
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Deb, D.; Tuppad, P.; Daggupati, P.; Srinivasan, R.; Varma, D. Spatio-Temporal Impacts of Biofuel Production and Climate Variability on Water Quantity and Quality in Upper Mississippi River Basin. Water 2015, 7, 3283–3305. [Google Scholar] [CrossRef]
- Ngene, B.U.; Nwafor, C.O.; Bamigboye, G.O.; Ogbiye, A.S.; Ogundare, J.O.; Akpan, V.E. Assessment of Water Resources Development and Exploitation in Nigeria: A Review of Integrated Water Resources Management Approach. Heliyon 2021, 7, e05955. [Google Scholar] [CrossRef] [PubMed]
- Jonoski, A.; Popescu, I. Distance Learning in Support of Water Resources Management: An Online Course on Decision Support Systems in River Basin Management. Water Resour. Manag. 2012, 26, 1287–1305. [Google Scholar] [CrossRef]
- Phumiphan, A.; Kangrang, A. Development of decision-making support tools for future reservoir management under climate and land cover variability: A case study. Int. Rev. Civ. Eng. 2021, 12, 271. [Google Scholar] [CrossRef]
- Soundharajan, B.-S.; Adeloye, A.J.; Remesan, R. Evaluating the variability in surface water reservoir planning characteristics during climate change impacts assessment. J. Hydrol. 2016, 538, 625–639. [Google Scholar] [CrossRef]
- Xu, D.; Lyon, S.W.; Mao, J.; Dai, H.; Jarsjö, J. Impacts of multi-purpose reservoir construction, land-use change and climate change on runoff characteristics in the Poyang Lake basin, China. J. Hydrol. Reg. Stud. 2020, 29, 100694. [Google Scholar] [CrossRef]
- Kangrang, A.; Prasanchum, H.; Hormwichian, R. Active future rule curves for multi-purpose reservoir operation on the impact of climate and land use changes. J. Hydro-Environ. Res. 2019, 24, 1–13. [Google Scholar] [CrossRef]
- Shaikh, S.A.; Pattanayek, T. Implicit stochastic optimization for deriving operating rules for a multi-purpose multi-reservoir system. Sustain. Water Resour. Manag. 2022, 8, 1–13. [Google Scholar] [CrossRef]
- Ashrafi, S.M.; Dariane, A.B. Coupled operating rules for optimal operation of multi-reservoir systems. Water Resour. Manag. 2017, 31, 4505–4520. [Google Scholar] [CrossRef]
- Wan, W.; Guo, X.; Lei, X.; Jiang, Y.; Wang, H. A Novel Optimization Method for Multi-Reservoir Operation Policy Derivation in Complex Inter-Basin Water Transfer System. Water Resour. Manag. 2018, 32, 31–51. [Google Scholar] [CrossRef]
- Choi, Y.; Lee, E.; Ji, J.; Ahn, J.; Kim, T.; Yi, J. Development and Evaluation of the Hydropower Reservoir Rule Curve for a Sustainable Water Supply. Sustainability 2020, 12, 9641. [Google Scholar] [CrossRef]
- Fayaed, S.S.; Fiyadh, S.S.; Khai, W.J.; Ahmed, A.N.; Afan, H.A.; Ibrahim, R.K.; Fai, C.M.; Koting, S.; Mohd, N.S.; Binti Jaafar, W.Z.; et al. Improving Dam and Reservoir Operation Rules Using Stochastic Dynamic Programming and Artificial Neural Network Integration Model. Sustainability 2019, 11, 5367. [Google Scholar] [CrossRef]
- Songsaengrit, S.; Kangrang, A. Dynamic Rule Curves and Streamflow under Climate Change for Multipurpose Reservoir Operation Using Honey-Bee Mating Optimization. Sustainability 2022, 14, 8599. [Google Scholar] [CrossRef]
- Connaughton, J.; King, N.; Dong, L.; Ji, P.; Lund, J. Comparing Simple Flood Reservoir Operation Rules. Water 2014, 6, 2717–2731. [Google Scholar] [CrossRef]
- Ahmadi, M.; Haddad, O.B.; Loáiciga, H.A. Adaptive reservoir operation rules under climatic change. Water Resour. Manag. 2015, 29, 1247–1266. [Google Scholar] [CrossRef]
- Diao, Y.; Wang, C.; Wang, H.; Liu, Y. Construction and Application of Reservoir Flood Control Operation Rules Using the Decision Tree Algorithm. Water 2021, 13, 3654. [Google Scholar] [CrossRef]
- Vudhivanich, V.; Rittima, A. Development of Probability Based Rule Curves for a Reservoir. Agric. Nat. Resour. 2003, 37, 234–242. [Google Scholar]
- Chang, Y.T.; Chang, L.C.; Chang, F.J. Intelligent control for modeling of real-time reservoir operation, part II: Artificial neural network with operating rule curves. Hydrol. Process. Int. J. 2005, 19, 1431–1444. [Google Scholar] [CrossRef]
- Chen, L.; McPhee, J.; Yeh, W.W.G. A diversified multiobjective GA for optimizing reservoir rule curves. Adv. Water Resour. 2007, 30, 1082–1093. [Google Scholar] [CrossRef]
- Karami, H.; Farzin, S.; Jahangiri, A.; Ehteram, M.; Kisi, O.; El-Shafie, A. Multi-Reservoir System Optimization Based on Hybrid Gravitational Algorithm to Minimize Water-Supply Deficiencies. Water Resour. Manag. 2019, 33, 2741–2760. [Google Scholar] [CrossRef]
- Al-Aqeeli, Y.H.; Mahmood Agha, O.M.A. Optimal Operation of Multi-reservoir System for Hydropower Production Using Particle Swarm Optimization Algorithm. Water Resour. Manag. 2020, 34, 3099–3112. [Google Scholar] [CrossRef]
- Kangrang, A.; Chaleeraktrakoon, C. Suitable conditions of reservoir simulation for searching rule curves. J. Appl. Sci. 2008, 8, 1274–1279. [Google Scholar] [CrossRef][Green Version]
- Adeloye, A.J.; Soundharajan, B.-S.; Ojha, C.S.; Remesan, R. Effect of hedging-integrated rule curves on the performance of the Pong reservoir (India) during scenario-neutral climate change perturbations. Water Resour. Manag. 2016, 30, 445–470. [Google Scholar] [CrossRef]
- Mohanavelu, A.; Soundharajan, B.-S.; Kisi, O. Modeling Multi-objective Pareto-optimal Reservoir Operation Policies Using State-of-the-art Modeling Techniques. Water Resour. Manag. 2022, 36, 3107–3128. [Google Scholar] [CrossRef]
- Chang, F.J.; Chen, L.; Chang, L.C. Optimizing the reservoir operating rule curves by genetic algorithms. Hydrol. Process. 2005, 19, 2277–2289. [Google Scholar] [CrossRef]
- Darakantong, T.; Kangrang, A. Improvement of Reservoir Rule Curve using Flower Pollination Algorithm. Master’s Thesis, Mahasarakham University, Mahasarakham, Thailand, 2019. [Google Scholar]
- Kangrang, A.; Prasanchum, H.; Hormwichian, R. Development of future rule curves for multipurpose reservoir operation using conditional genetic and tabu search algorithms. Adv. Civ. Eng. 2018, 2018, 6474870. [Google Scholar] [CrossRef]
- Marchand, A.; Gendreau, M.; Blais, M.; Guidi, J. Optimized operating rules for short-term hydropower planning in a stochastic environment. Comput. Manag. Sci. 2019, 16, 501–519. [Google Scholar] [CrossRef]
- Haddad, O.B.; Afshar, A.; Mariño, M. Honey-bee mating optimization (HBMO) algorithm in deriving optimal operation rules for reservoirs. J. Hydroinformatics 2008, 10, 257–264. [Google Scholar] [CrossRef]
- Techarungruengsakul, R.; Kangrang, A. Application of Harris Hawks Optimization with Reservoir Simulation Model Considering Hedging Rule for Network Reservoir System. Sustainability 2022, 14, 4913. [Google Scholar] [CrossRef]
- Pandey, A.; Parhi, D.R. Optimum path planning of mobile robot in unknown static and dynamic environments using Fuzzy-Wind Driven Optimization algorithm. Def. Technol. 2017, 13, 47–58. [Google Scholar] [CrossRef]
- Assimi, H.; Jamali, A.; Nariman-Zadeh, N. Sizing and topology optimization of truss structures using genetic programming. Swarm Evol. Comput. 2017, 37, 90–103. [Google Scholar] [CrossRef]
- Zhao, W.; Wang, L.; Zhang, Z. Atom search optimization and its application to solve a hydrogeologic parameter estimation problem. Knowl.-Based Syst. 2019, 163, 283–304. [Google Scholar] [CrossRef]
- Almagboul, M.A.; Shu, F.; Qian, Y.; Zhou, X.; Wang, J.; Hu, J. Atom search optimization algorithm based hybrid antenna array receive beamforming to control sidelobe level and steering the null. AEU Int. J. Electron. Commun. 2019, 111, 152854. [Google Scholar] [CrossRef]
- Kamel, S.; Hamour, H.; Ahmed, M.H.; Nasrat, L. Atom search optimization algorithm for optimal radial distribution system reconfiguration. In Proceedings of the 2019 International Conference on Computer, Control, Electrical, and Electronics Engineering (ICCCEEE), Khartoum, Sudan, 21–23 September 2019. [Google Scholar] [CrossRef]
- Barshandeh, S.; Haghzadeh, M. A new hybrid chaotic atom search optimization based on tree-seed algorithm and Levy flight for solving optimization problems. Eng. Comput. 2021, 37, 3079–3122. [Google Scholar] [CrossRef]
- Sun, P.; Liu, H.; Zhang, Y.; Tu, L.; Meng, Q. An intensify atom search optimization for engineering design problems. Appl. Math. Model. 2021, 89, 837–859. [Google Scholar] [CrossRef]
- Loucks, D.P.; van Beek, E. Water resources planning and management: An overview. In Water Resource Systems Planning and Management; Springer: Cham, Switzerland, 2017; pp. 1–49. [Google Scholar]
- Petvirojchai, P.; Sarpa, S. Current Technology for Alerting and Warning Tropical Cyclones in Thailand. Trop. Cyclone Res. Rev. 2018, 7, 193–200. [Google Scholar]
- Hormwichian, R.; Kangrang, A.; Lamom, A. A conditional genetic algorithm model for searching optimal reservoir rule curves. J. Appl. Sci. 2009, 9, 3575–3580. [Google Scholar] [CrossRef]
- Thongwan, T.; Kangrang, A.; Prasanchum, H. Multi-objective future rule curves using conditional tabu search algorithm and conditional genetic algorithm for reservoir operation. Heliyon 2019, 5, e02401. [Google Scholar] [CrossRef]
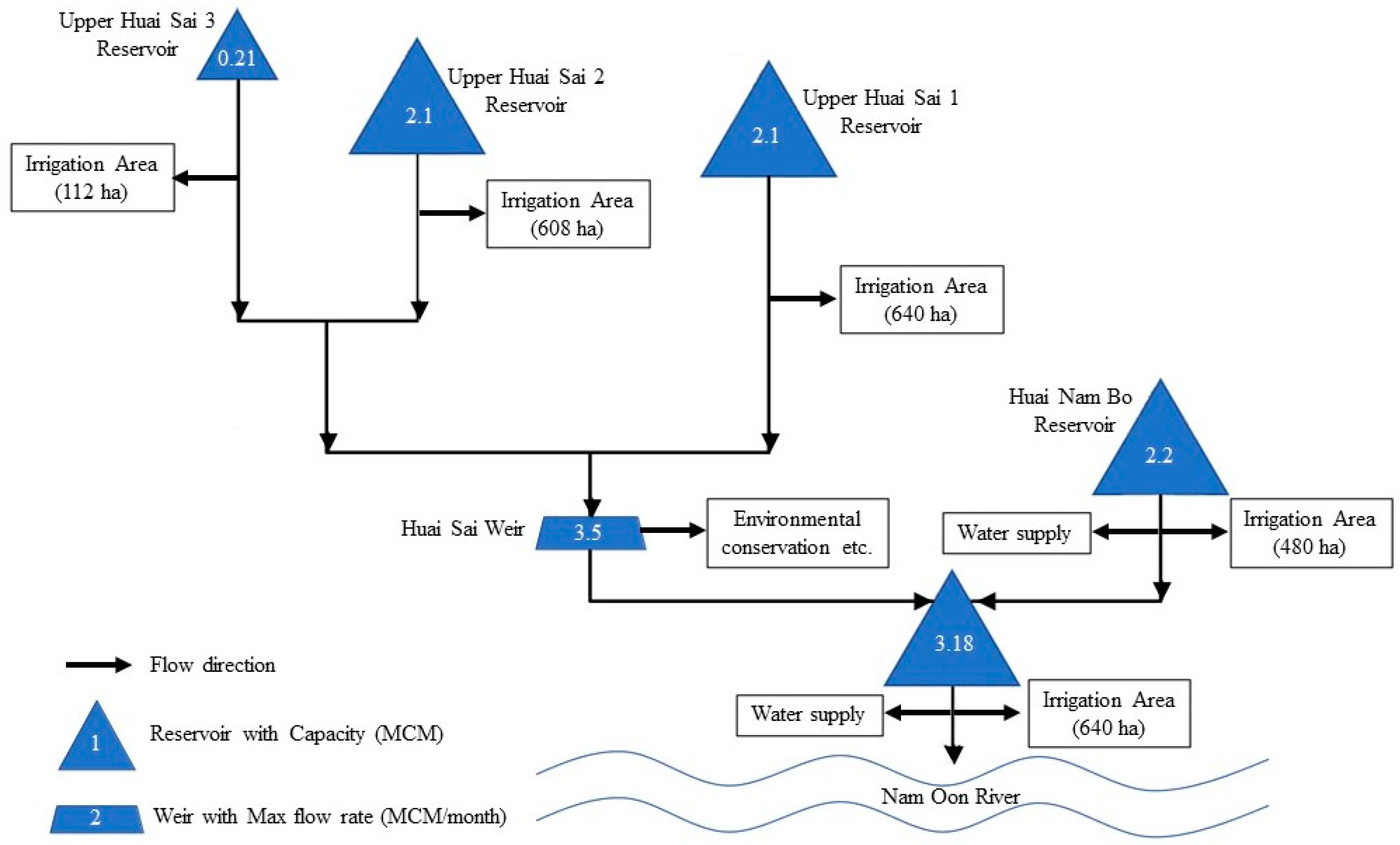

| Characteristics | Huai Nam Bo | Upper Huai Sai-1 | Upper Huai Sai-2 | Upper Huai Sai-3 | Huai Sai Kamin |
|---|---|---|---|---|---|
| Type of dam | Earth dam | Earth dam | Earth dam | Earth dam | Earth dam |
| First year of operation | 1964 | 1991 | 1986 | 1985 | 1956 |
| Catchment area (km2) | 9.87 | 6.63 | 5.6 | 0.6 | 29.00 |
| Height from foundation (m) | 17 | 13.5 | 12.9 | 8 | 8.30 |
| Crest length (m) | 950 | 575 | 690 | 450 | 1300 |
| Normal storage capacity (MCM) | 2.2 | 2.1 | 2.1 | 0.21 | 3.18 |
| Irrigation area (km2) | 4.8 | 6.4 | 6.08 | 1.12 | 6.40 |
| Spillway discharge capacity (m3/s) | 15 | 25 | 21.3 | 1.9 | 85.50 |
| Average annual inflow (MCM) | 9.04 | 2.38 | 1.54 | 0.40 | 45.77 |
| Reservoir | Average Monthly Inflow (MCM/Month) | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| January | February | March | April | May | June | July | August | September | October | November | December | |
| Huai Nam Bo | 0.130 | 0.128 | 0.215 | 0.151 | 0.282 | 1.008 | 1.777 | 1.643 | 1.857 | 1.452 | 0.266 | 0.137 |
| Upper Huaisai-1 | 0.044 | 0.047 | 0.052 | 0.047 | 0.147 | 0.250 | 0.360 | 0.425 | 0.479 | 0.408 | 0.074 | 0.051 |
| Upper Huaisai-2 | 0.087 | 0.038 | 0.045 | 0.038 | 0.086 | 0.167 | 0.315 | 0.286 | 0.197 | 0.159 | 0.083 | 0.043 |
| Upper Huaisai-3 | 0.002 | 0.002 | 0.004 | 0.006 | 0.075 | 0.124 | 0.055 | 0.070 | 0.060 | 0.182 | 0.008 | 0.005 |
| Huai Sai Kamin | 0.878 | 0.683 | 0.779 | 0.374 | 0.555 | 2.415 | 8.161 | 11.654 | 12.053 | 6.321 | 1.401 | 0.499 |
| Rule Curves | Volume of Inflow through Huai Sai Weir (MCM/Month) | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| January | February | March | April | May | June | July | August | September | October | November | December | ||
| Single Reservoir | RC-Existing | 0.000 | 0.000 | 0.392 | 0.626 | 0.959 | 1.962 | 2.668 | 4.175 | 4.741 | 1.342 | 0.559 | 0.223 |
| S-RC-ASO | 0.005 | 0.004 | 0.238 | 0.383 | 0.585 | 1.862 | 2.806 | 3.835 | 4.716 | 1.332 | 0.509 | 0.135 | |
| S-RC-GP | 0.005 | 0.000 | 0.238 | 0.395 | 0.747 | 1.712 | 2.766 | 3.759 | 4.866 | 1.202 | 0.559 | 0.135 | |
| S-RC-WDO | 0.005 | 0.004 | 0.238 | 0.380 | 0.590 | 1.860 | 2.786 | 3.840 | 4.816 | 1.232 | 0.539 | 0.135 | |
| Multi Reservoir | M-RC-ASO | 0.005 | 0.000 | 0.238 | 0.383 | 0.581 | 1.192 | 2.026 | 3.409 | 4.726 | 1.572 | 0.619 | 0.135 |
| M-RC-GP | 0.005 | 0.000 | 0.238 | 0.395 | 0.581 | 1.192 | 2.066 | 3.445 | 4.751 | 1.512 | 0.579 | 0.135 | |
| M-RC-WDO | 0.005 | 0.000 | 0.238 | 0.385 | 0.581 | 1.162 | 2.03 | 3.412 | 4.732 | 1.552 | 0.609 | 0.135 | |
| Criteria for Consideration | Rule Curves | Frequency | Magnitude of Excess Release Water (MCM/Year) | Duration (Year) | ||
|---|---|---|---|---|---|---|
| (Times/Year) | Average | Maximum | Average | Maximum | ||
| Single Reservoir | RC-existing | 1 | 45.788 | 90.945 | 16 | 16 |
| S-RC-ASO | 1 | 45.602 | 90.550 | 16 | 16 | |
| S-RC-GP | 1 | 45.562 | 90.408 | 16 | 16 | |
| S-RC-WDO | 1 | 45.588 | 90.502 | 16 | 16 | |
| Multi Reservoir | RC-existing | 1 | 45.788 | 90.945 | 16 | 16 |
| M-RC-ASO | 1 | 43.828 | 88.345 | 16 | 16 | |
| M-RC-GP | 1 | 43.722 | 88.794 | 16 | 16 | |
| M-RC-WDO | 1 | 43.822 | 88.455 | 16 | 16 | |
| Criteria for Consideration | Rule Curves | Frequency | Magnitude of Excess Release Water (MCM/Year) | Duration (Year) | |||
|---|---|---|---|---|---|---|---|
| (Times/Year) | Average | Maximum | Average | Maximum | |||
| Single Reservoir | RC-existing | µ | 1 | 45.639 | 75.388 | 16 | 16 |
| σ | 0 | 3.769 | 10.006 | 0 | 0 | ||
| S-RC-ASO | µ | 1 | 45.536 | 74.834 | 16 | 16 | |
| σ | 0 | 3.869 | 9.569 | 0 | 0 | ||
| S-RC-GP | µ | 1 | 45.495 | 74.793 | 16 | 16 | |
| σ | 0 | 3.868 | 9.569 | 0 | 0 | ||
| S-RC-WDO | µ | 1 | 45.533 | 74.828 | 16 | 16 | |
| σ | 0 | 3.869 | 9.569 | 0 | 0 | ||
| Multi Reservoir | RC-existing | µ | 1 | 45.639 | 75.388 | 16 | 16 |
| σ | 0 | 3.769 | 10.006 | 0 | 0 | ||
| M-RC-ASO | µ | 1 | 43.833 | 72.389 | 16 | 16 | |
| σ | 0 | 3.697 | 9.286 | 0 | 0 | ||
| M-RC-GP | µ | 1 | 43.673 | 72.893 | 16 | 16 | |
| σ | 0 | 3.798 | 9.939 | 0 | 0 | ||
| M-RC-WDO | µ | 1 | 43.734 | 72.445 | 16 | 16 | |
| σ | 0 | 3.705 | 9.546 | 0 | 0 | ||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kosasaeng, S.; Yamoat, N.; Ashrafi, S.M.; Kangrang, A. Extracting Optimal Operation Rule Curves of Multi-Reservoir System Using Atom Search Optimization, Genetic Programming and Wind Driven Optimization. Sustainability 2022, 14, 16205. https://doi.org/10.3390/su142316205
Kosasaeng S, Yamoat N, Ashrafi SM, Kangrang A. Extracting Optimal Operation Rule Curves of Multi-Reservoir System Using Atom Search Optimization, Genetic Programming and Wind Driven Optimization. Sustainability. 2022; 14(23):16205. https://doi.org/10.3390/su142316205
Chicago/Turabian StyleKosasaeng, Suwapat, Nirat Yamoat, Seyed Mohammad Ashrafi, and Anongrit Kangrang. 2022. "Extracting Optimal Operation Rule Curves of Multi-Reservoir System Using Atom Search Optimization, Genetic Programming and Wind Driven Optimization" Sustainability 14, no. 23: 16205. https://doi.org/10.3390/su142316205
APA StyleKosasaeng, S., Yamoat, N., Ashrafi, S. M., & Kangrang, A. (2022). Extracting Optimal Operation Rule Curves of Multi-Reservoir System Using Atom Search Optimization, Genetic Programming and Wind Driven Optimization. Sustainability, 14(23), 16205. https://doi.org/10.3390/su142316205










