1. Introduction
In agricultural landscapes, the continuous and complex coevolutionary process among natural and agricultural production systems has led to the formation of traditional agroecosystems [
1]. These are considered essential sanctuaries of agrobiodiversity [
2,
3] of a high conservation value [
4]. The values of traditional agroecosystems, along with the great variety of traditional practices implemented in these areas, are gradually recognized in the context of the European agroenvironmental policies; they are referred to as “High Nature Value farmland areas” (hereafter HNVf) [
5,
6], and have contributed to enhancing the implementation and effectiveness of conservation actions [
7].
In the Mediterranean basin, a variety of traditional agroecosystems can be found, including traditional olive groves [
8,
9,
10], which are considered a type of HNVf in Europe [
11]. Traditional olive groves are characterized by the presence of old trees growing at low densities, absence of irrigation, nonregular pruning, grazing of seminatural vegetation under and between the olive trees, low or no input of fertilizers and biocides [
12,
13], and infrastructures such as terraces and dry stone walls [
14] that contribute to preserving natural habitats and viable animal diversity populations of the highest conservation value [
6,
15], supporting conservation and/or creating a stable and high-value agricultural ecosystem. In parallel, the ineffective European Union regulations and policies towards the intensification of olive and olive oil production of the past [
16,
17,
18] have changed and shifted towards sustainable practices, supporting traditional olive grove conservation and acknowledging the importance of traditional practices for alleviating biodiversity loss, soil erosion, and land degradation [
19,
20,
21].
Despite these positive steps, traditional olive groves of the Mediterranean basin, especially terraced ones, are progressively deteriorating due to the continuous intensification of agriculture [
22,
23,
24], as well as land depopulation and abandonment [
20,
25,
26]. Land abandonment, in particular, exerts additional indirect abiotic (e.g., hydrogeological instability, water stress, loss of soil organic matter, soil erosion) [
27,
28] and pathogenic (fungi, bacteria, viruses) pressures on terraced olive trees. At the same time, gradual renaturalization processes are an added factor directly influencing the dynamics of these ecosystems and can lead to terrace collapse [
29] and microclimate alterations (e.g., humidity), resulting in increased incidence of airborne fungi, such as the olive leaf spot [
30], and a combined further degradation of these HNVf areas.
In order to sustain the conservation of terraced olive groves, European countries should (a) identify, characterize, and map the HNVf olive groves in their territory, (b) support their maintenance and their socioecological values, and (c) monitor the pressures and their overall state [
31,
32]. In this regard, despite the effort that has been made both through legal instruments and through targeted research, monitoring the state and pressures exerted on traditional olive groves is still a challenge.
Recent advances in monitoring methodologies combine field data and multispectral sensors of various spatial resolutions [
33], enabling the rapid detection of land-use changes and ecosystem degradation [
34,
35]. This set of rapid and noninvasive plant phenotypic techniques [
36] is mainly used towards agricultural productivity increase and disease detection [
37,
38,
39], while it can also adequately support effective conservation strategies [
40,
41,
42]. At individual tree level, a relevant nondestructive technique is infrared thermography (IRT) [
43], a fast-growing type of aerial and/or ground optical remote sensing technique [
44,
45,
46]. To date, IRT is widely used in various agroecological systems [
44,
47], in monitoring crop vegetation [
48,
49,
50], in detecting water stress [
51,
52,
53] and fungal infestation [
54,
55], and in assessing the health state of various woody vegetation species [
56].
Along with IRT, plant phenotyping spectral reflectance indices related to plant photosynthetic status such as leaf and crown chlorophyll concentration [
57,
58,
59,
60], obtained in situ and noninvasively, can reflect the health state of plants. After all, chlorophyll as a pivotal photosynthetic pigment on which plant growth and productivity depend [
60,
61], is considered a hallmark index to plant health estimation [
62,
63,
64]. Low chlorophyll content may mean exposure to biotic and/or abiotic stresses, diseases, and senescence [
65,
66,
67], and provides significant information about plant photosynthetic potential and primary production.
The above noninvasive monitoring techniques can be further enhanced with the support of traditional methods of measuring plant structural and functional traits, such as height, diameter, leaf area and its related indices (e.g., leaf area index—LAI), and canopy architecture. Specifically, in terraced olive groves, as in any other agroecosystem, LAI is considered one of the fundamental biophysical traits and is directly associated, among others, with olive growth and productivity [
68,
69]. A combination of these traits can provide a variety of different composite indices and equations that describe the overall condition of trees in traditional olive groves.
Thus, the main aim of our research was to assess traditional olive grove health state, with the emphasis on estimating productivity, using nondestructive phenotypic techniques, in a typical Mediterranean environment. We obtained phenotypic information from olive trees on the Greek island of Lesvos by combining this with in situ measurement of spectral reflectance indices and collection of IRT images to investigate the following objectives: (a) to quantify the effect of the olive tree phenotypic traits and indices on productivity, (b) to examine if olive tree phenotypic parameters can explain the presence of one of the most common biotic stressors, the olive leaf spot disease (OLS), and (c) to examine whether olive trees can be classified into groups of different health state, based on the above information.
4. Discussion
Our study represents the first attempt to monitor the pressures and the overall state of trees in traditional olive groves which are located on the island of Lesvos, within a part of the recognized European HNVf. For this, a crucial step was to separate the island’s extensive olive groves into traditional and nontraditional. However, their identification was challenging, as their exact boundaries were not mapped, and there was no accompanying information on the individual cultivation methods used at the grove level nor any information on criteria used to define each olive grove as a traditional one. Having determined the boundaries of the traditional olive groves, our analysis focused on areas with a clear long-term absence of cultivation practices so that we have the unequivocal image of the island’s traditionally grown olive tree state. After all, the agricultural landscape of the island of Lesvos has changed since the 1990s due to land abandonment [
26] and, with it, cultivation practices have differentiated; nowadays, “cultivation” is often restricted to the mere harvest of olives. In some cases, pruning is also carried out, which abruptly modifies the vegetative–productive balance of the tree (pers. obs.). Therefore, an attempt was made to find traditional olive groves with clear features of cultivation practices of the past, obtaining a glimpse into the state of olive groves in the Mediterranean basin, as well as of Lesvos terraced groves, of previous decades [
92]. These practices involved forming the trees’ shape to a great height and crown area, in order to overcome environmental stress and to produce larger biennial crops, by being able to accumulate water and nutrients in their large trunk and branches, and their extensive canopy and root system. Modern cultivation practices are substantially differentiated in terms of techniques (irrigation, fertilization, mechanical harvesting, pruning) [
92] and shape of trees, aiming at low-growing irrigated trees, with a specific leaf area that produces a constant crop annually [
30].
Having identified and located traditional olive groves, we introduced a comprehensive methodological framework for traditional olive grove productivity prediction, including both easily obtainable tree trait information, which can be recorded with simple tools even with the knowledge and experience of an average olive grower, and additional information obtained with more specialized, but noninvasive, tools and techniques. Contrary to intensive agricultural systems, assessing productivity in traditional olive groves is acceptable without continual monitoring of a large set of physiological and environmental variables because immediate interventions are not possible and, occasionally, even not desirable. It should be noted that traditional olive groves tend to be less easily accessible than more intensively grown olive groves, thus, minimizing the number of necessary field visits is important. We selected techniques that can be used to collect field data in one or a few sessions, at the correct time of year, to increase the applicability of our results by both growers and cooperatives as well as by land management and nature conservation authorities.
As the main concern of all those involved in olive growing is tree productivity, we placed particular emphasis on this parameter, bearing in mind that a typical olive tree in favorable environmental conditions and with the proper management practices (regular pruning, fertilization, soil management, pest and disease control) can be productively efficient for more than 100 years [
93]. However, in traditional olive groves, in which the trees are much older, the absence of effective cultivation practices, in conjunction with biotic and abiotic pressures (e.g., phloem shoot-to-root flow depression due to wood decay), leads to inner crown leaf drop and retention of foliage on the outer part of the crown. Simultaneously, the inner branches start to be replaced by others on the outside and, thus, the available resources are invested in nonproductive structures [
94,
95], resulting in decreased productivity as trees trade reproductive for vegetative activity [
30,
95]. Thus, in contrast with other studies [
96,
97], we took into account four consecutive years for estimating average annual productivity as well as the average renewal of productive shoots. Theoretically, we should be able to consider only two productivity years, due to biennial fruiting, but we noticed that, in our case, the alternate bearing was not very clear (
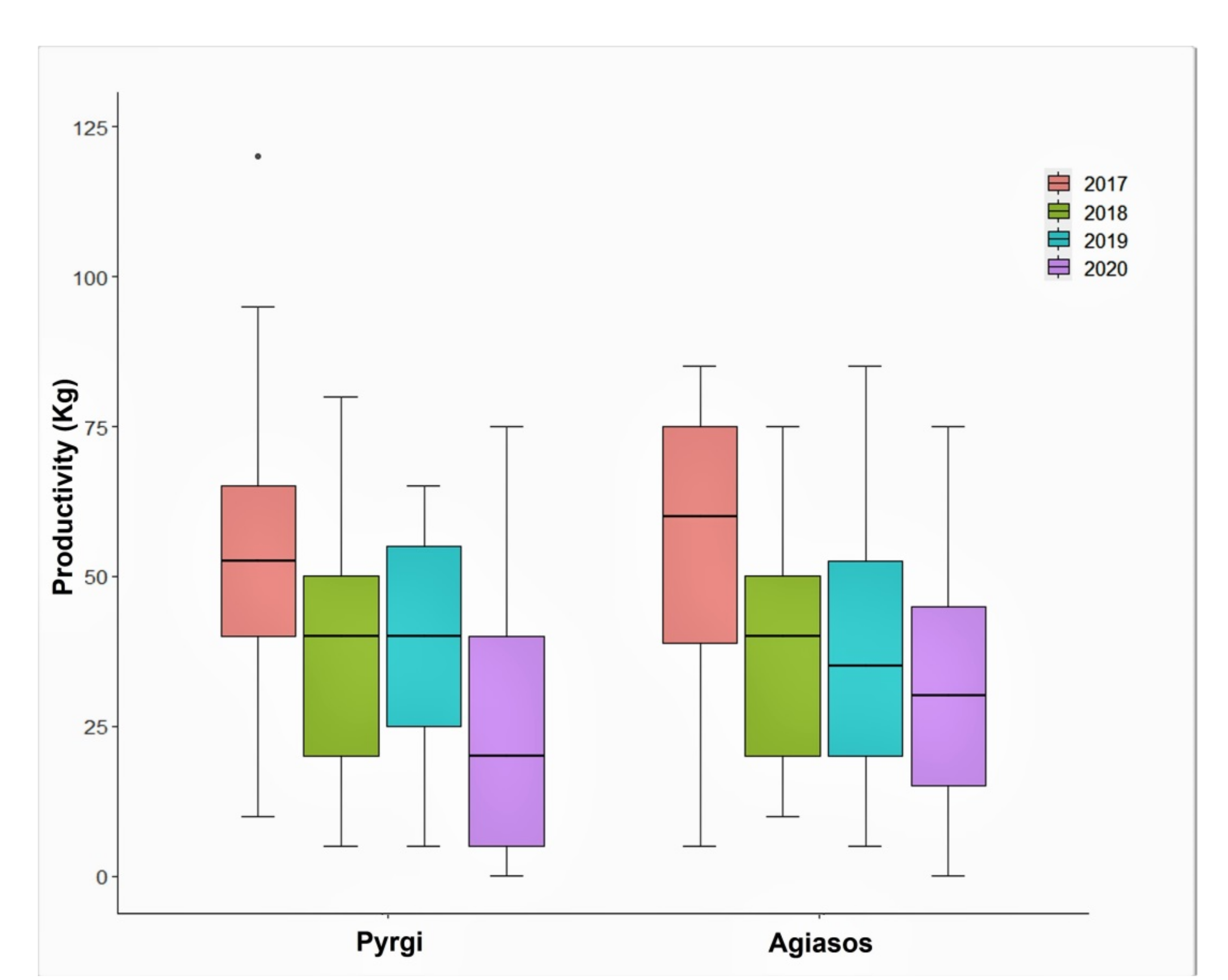
Figure 4), so we chose to include all four years. Moreover, the activation of metabolic pathways related to the expression of alternate bearing is affected by a wide range of climatic events which influence the vegetative and reproductive development of olives [
98], especially traditional ones, which we could not control.
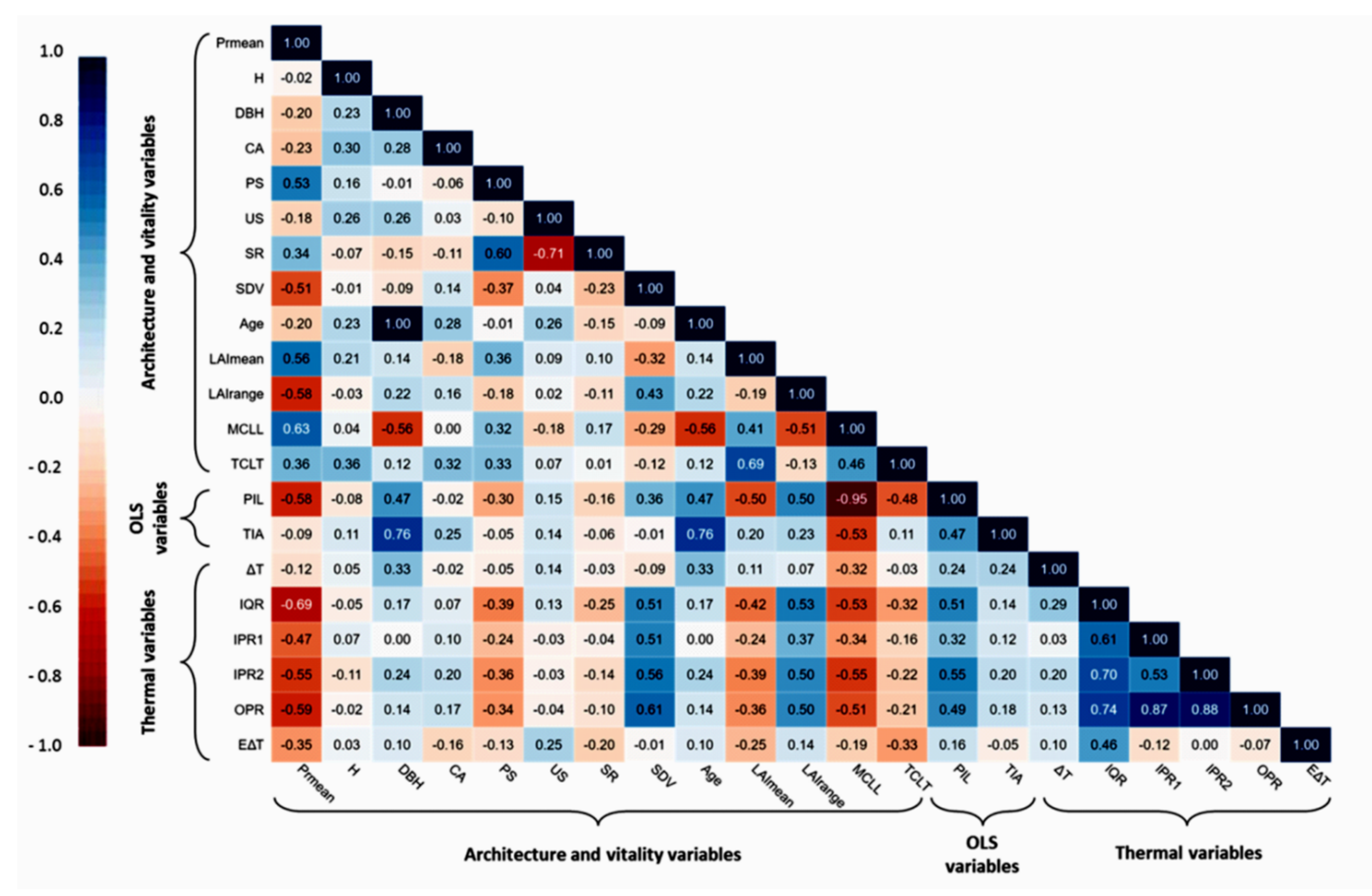
The investigation of the relationship between productivity and the architecture and vitality traits of the olive trees revealed significant evidence in linking these traits and with traditional olive grove functioning as a productive system. Of the twelve distinct traits that were either measured or calculated (e.g., MCL
L, TCL
T), five were found to be positively related (PS, SR, LAI
mean, MCL
L, TCL
T) and two negatively related (SDV, LAI
range) to productivity (
Figure 5). Resistance mechanisms against biotic and abiotic stressors are reduced in aged olive trees [
99], such as ours, and physiological adaptation mechanisms (e.g., high photosynthetic rate with low stomatal conductance) are affected by reduced vegetative activity [
100,
101]; these effects are compatible with the negative productivity relationships with OLS variables.
On the one hand, the highest positive correlations which were observed between productivity and MCL
L and LAI
mean confirmed the already established view that these traits are considered ideal biophysical indices for the description of these relationships [
102]. Regarding MCL
L, it is well known that, despite being the essential driver of photosynthesis, and consequently olive productivity, it should be used in combination with LAI [
103], which is an important criterion in evaluating olive trees’ state, as it shows the degree to which a tree can photosynthesize. In our case, the LAI
mean for the 80 olive trees was particularly low (2.11 ± 0.75), compared with the optimal value of 6 for achieving high olive yields [
30]. Apart from this, we consider that the LAI values that we found are more representative of old, rather than young, olive groves, as similar studies for measuring LAI in an old olive grove in Italy found a value of 3.5 [
104] and, in an intensive mature grove in Tunisia, a value of 2.8 [
105].
On the other hand, the negative correlations between productivity and SDV and LAI
range, and both the relationship between them (r = 0.427;
p < 0.0001) and their relationship with other significant traits (e.g., MCL
L, PIL), identify two very important parameters for estimating olive tree health. To the best of our knowledge, there is no other relevant study to use both of these traits as estimators of olive tree health. Nevertheless, we consider that it is of great importance, as LAI
range highlighted the deviation of olive trees from a healthy state, with extreme differences in LAI values taken into account, while SDV estimated the possible extent of the trees’ phloem shoot-to-root flow depression, by quantifying its structural abnormalities. In parallel, SDV is a crucial connecting link between olive tree vitality metrics and infrared thermography; it describes trunk growth patterns, which may exhibit cracks, wounds, detached bark, and cankers, and it shows a positive correlation with almost all the thermal statistical variables which describe the thermal profile of olive trees (
Figure 5).
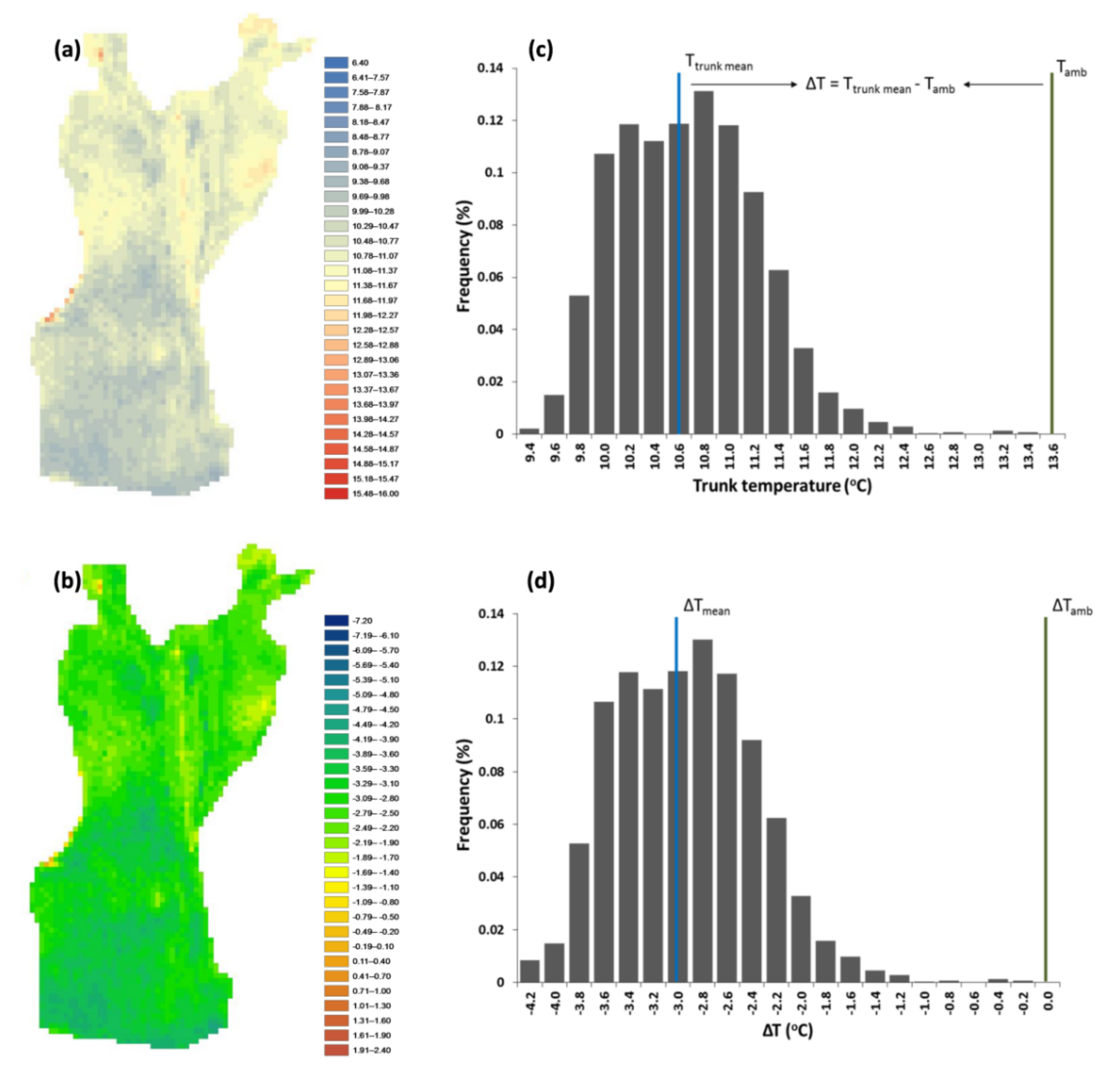
These relationships result from olive tree hydraulic physiology, as olive trees have developed different strategies to sustain a balance between water supply and water loss [
106], by either adapting their leaf and root distribution [
107] or by entire branch failure [
108]. Regarding their trunks, the alteration of their hydraulic properties due to less plasticity leads to interrupting the water supply to all trunks’ neighboring segments [
109]. Thus, possible hydraulic failure in conductive tissues, related to both water supply conditions and xylem anatomical characteristics [
110], causes the surface temperature of the tree trunk to fluctuate [
111] and reflects tree health. IRT can detect these fluctuations, indicating potential disturbances, when temperature distribution is uneven, or a healthy state when surface temperature is homogenous [
56,
112]. In our case, the exported thermal variables allowed the reliable detection of SDV, while their association with other significant phenotypic traits provided critical insights into the conservation state of traditional olive groves.
Given the prominence of traditional olive groves both on the island of Lesvos and in other parts of Greece [
113], a detailed analysis regarding their productivity estimation based on both trees’ phenotypic traits and their thermal properties is required. However, for productivity assessment, it is important to take into account the possible susceptibility of traditionally grown olive trees to disease infestations. In this context, we have created a suite of important features, derived from the linear and the logistic models, which can satisfactorily explain traditional olive grove dynamics.
The high explanatory nature of the four linear models, using different predictor groups, showed that the four-year average productivity of the traditional olive trees can be explained to a very high degree. This high explanatory power, as indicated by the coefficient of determination values, especially in the “architecture and vitality traits” model (R
2 = 0.610) and in the “combination” model (R
2 = 0.702), showed that there are specific features of olive trees that can disclose the variation levels of their productivity (
Table 2). We consider this to be extremely important if one considers that parameters that would potentially enhance our models, such as slope and aspect at individual tree level, slope and aspect of terraced sites, soil nutrient content, and trees’ competition levels, which were essential in other predictive models for olive tree productivity [
97], were not taken into account. The separate examination of each harvest season, although with a lower explanatory power in three out of four years, followed a similar pattern: the “architecture and vitality traits” and the “combination” models showed an explanatory power ranging from 41.5% to 60.2% (
Table A2,
Table A3,
Table A4 and
Table A5).
It is noteworthy that, even though the model based on thermal variables showed moderate interpretive power in estimating of Pr
mean (R
2 = 0.463) (
Table 2), lower still for individual years (24.5–35.4%) (
Table A2,
Table A3,
Table A4 and
Table A5), infrared thermography appears to be a valuable method for obtaining precise data for productivity estimation. Among the extracted thermal variables, only IQR had an important contribution to Pr
mean in the “thermal” model, while in the “combination” model, IQR showed the third-largest unique contribution (5.4%) out of the six predictive factors. Additionally, the negative coefficient of IQR demonstrates an inverse relationship of IQR with productivity, supporting the view that a uniform tree trunk surface temperature distribution is associated with a healthy tree state and higher productivity.
The dependence of productivity from OLS severity metrics indicated a moderate to low inverse effect (R
2 = 0.368;
Table 2), which strengthens the argument, also reported by MacDonald et al. [
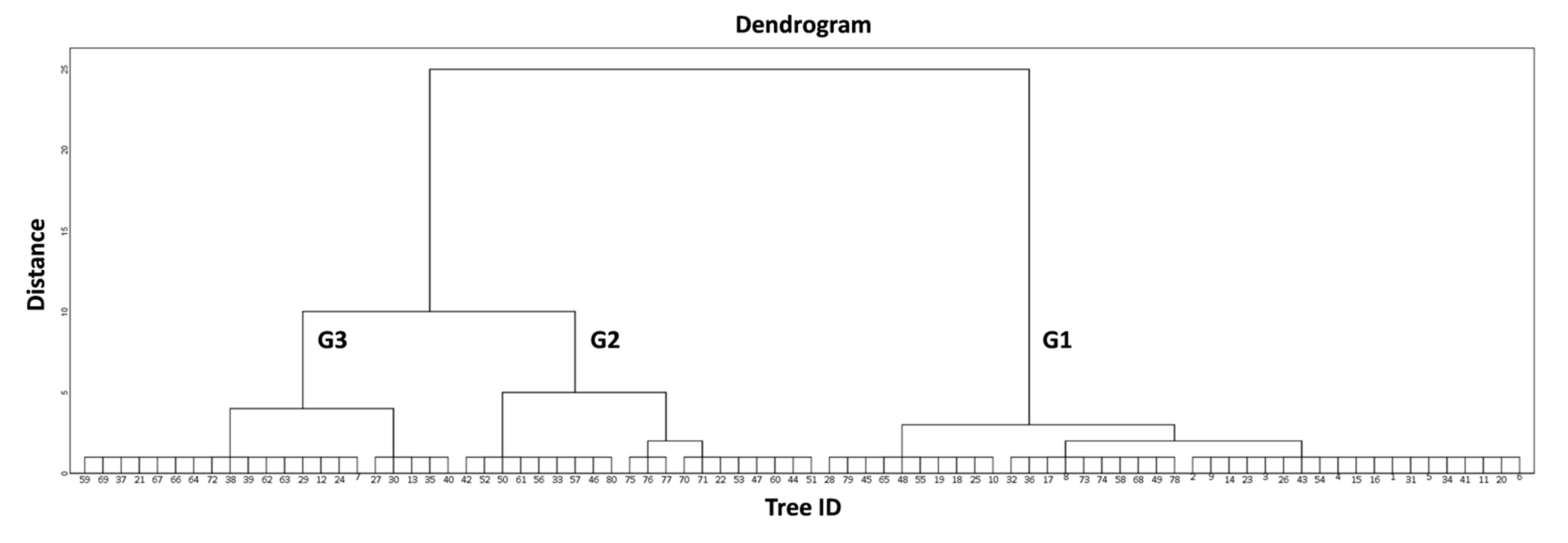
114], that this fungal disease is probably responsible for the reported low productivity of the infected olive trees. Indeed, by repeating the multiple linear regression with the poor condition group of trees (G3), the explanatory power of the model rises to 46.5% (F (2, 19) = 18.41,
p < 0.001, R
2 = 0.465), having TIA as the only statistically significant explanatory variable in the final model. Following the same procedure for the G1 and G2 groups did not yield any significant results. The age of the G3 olive trees (300.60 ± 84.62 years) also played an important role; controlling for the effect of age, the correlation of Pr
mean with PIL had a negative nonsignificant coefficient (r = −0.44;
p = 0.053) and a positive nonsignificant coefficient with TIA (r = 0.26;
p = 0.254).
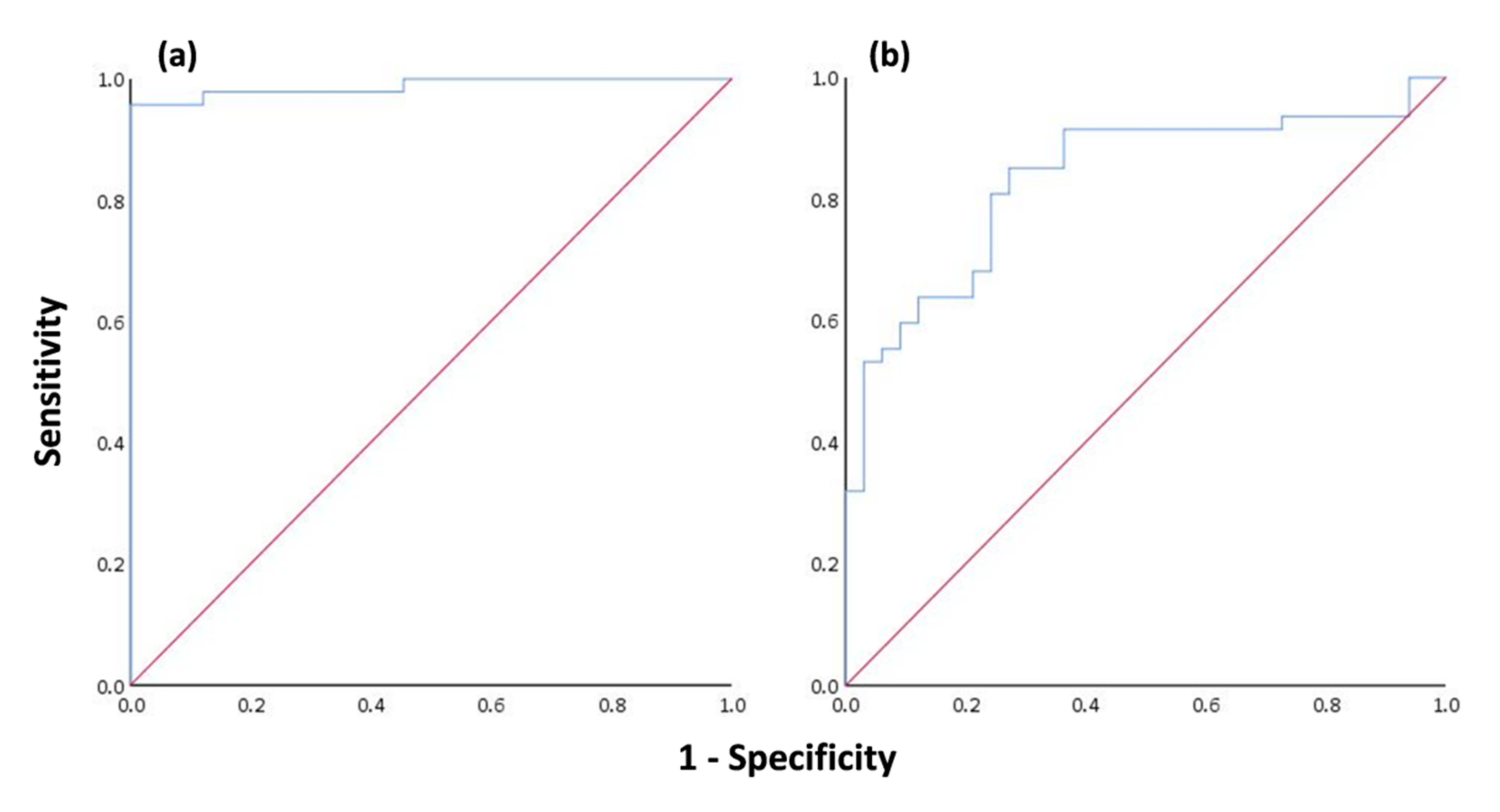
Assessing the olive tree infection by OLS indicated that 58.75% of the studied trees were infected. The presence of fungal pathogens is difficult to control as their populations show spatiotemporal and genetic variability, depending, to a large extent, on humidity and ambient temperature, while climate change increases the risk of infection in trees [
115]. The logistic regression models had a high discriminatory performance and were quite informative regarding the predictors of both architecture and vitality traits and thermal variables groups, indicating that the probability of OLS infection could be predicted accurately by MCL
L and IQR. On the extremely high predicted classification accuracy of MCL
L (95.7%), trees with no symptoms presented a mean MCL
L of 0.98 ± 0.03 g/m
2, while those classified as infected had a much lower value of MCL
L (0.73 ± 0.14 g/m
2). This differentiation occurs as the infected leaves undertake a gradual deterioration of their cytoplasmic contents, resulting in the degradation of chloroplasts and the progressive disappearance of chlorophyll [
116]. From the standpoint of assessing OLS presence using thermal variables, it is understood that both the classification accuracy (80%) and the degree of explanatory power of the model (39%) are not ideal to suggest the use of IRT for detecting infection in olive trees. However, we must keep in mind that the examined thermal variables (IQR) (a) had a substantial difference between infected (0.85 ± 0.38) and noninfected trees (0.55 ± 0.13), and (b) were calculated from infrared images of the tree trunk and not from the leaves, which is the main organ that this disease affects. In addition, IRT has been proved to be a valuable method for identifying biotic stresses by analyzing temperature alterations in plant leaves [
44].
The classification of the 80 trees in three classes (G1, G2, G3) enabled tree health state categorization at a population level, as the group G1 includes olive trees that are in a good condition, G2 includes trees in an intermediate state, and group G3 contains trees which are in poor condition. Moreover, specific traits of the olive trees’ groups can be adequately described, to some extent, by the extracted thermal variables, as shown by the initial examination of the relationships between them (
Figure 5). In particular, it is noted that G1 and G3 display the lowest and highest values in all thermal variables, respectively, while G2 lies somewhere in between, except for ΔT (
Table 4).
The high ΔT value of the G3 trees indicated their low temperature distance from Tamb; this means that the tree trunk has a faster response to ambient temperature indicative of hollows within the trunk where the air enters and heats the trunk surface faster. Paradoxically, regarding a particularly important thermal variable describing the actual extent of defect patches (ΕΔΤ), we did not find any statistically significant differences between the examined groups (F (2, 77) = 2.97, p = 0.057); this suggests that the area of any abnormalities is not as important, at least for traditional olive groves, as their intensity, described by the IQR for the whole tree and by the OPR for individual elements of the trunk. Hence, the three classes that describe the health state of olive trees (good, intermediate, poor) correspond to specific value ranges of these thermal variables. Poor condition corresponds to the highest values of the extracted thermal variables, while good condition corresponds to the lowest values.
Thus, combining the results of productivity assessment, infected trees’ identification, and hierarchical classification, we can conclude that mainly IQR and secondarily OPR can be considered as indicators of olive trees’ health state. The low value of these indices confirms the homogeneous temperature distribution on the tree trunk, as originally described by Catena and Catena [
56], and identifies high values of vitality traits simultaneously with the absence of the OLS disease. Therefore, these indices are appropriate for measuring the thermal profile of each olive tree and for assessing its health state.
In conclusion, our results provide evidence for a combinatory methodological framework for traditional olive grove productivity prediction, taking into account typical phenotypic, spectral, and thermal tree traits. We further demonstrate that it is possible to detect the incidence of OLS in traditional olive groves and to classify olive trees into different health state categories using the same variables. Although infrared images did not provide the best prediction of tree productivity, nor the optimal classification for OLS incidence, nonetheless, they could give satisfactory information for a rapid first assessment of the health and productivity of a traditional olive grove noninvasively. Combined with long-established methods and tools of assessing health and productivity, such as LAI and chlorophyll concentration, they can further improve the predictive power to a very high level. Overall, this study establishes a foundation for the design and application of appropriate management measures of traditional olive groves using a relatively simple and time-saving, but sufficiently accurate, methodology.