System Dynamics Approach to TALC Modeling
Abstract
1. Introduction
2. Tourist Destination as a Complex System—Theoretical Background
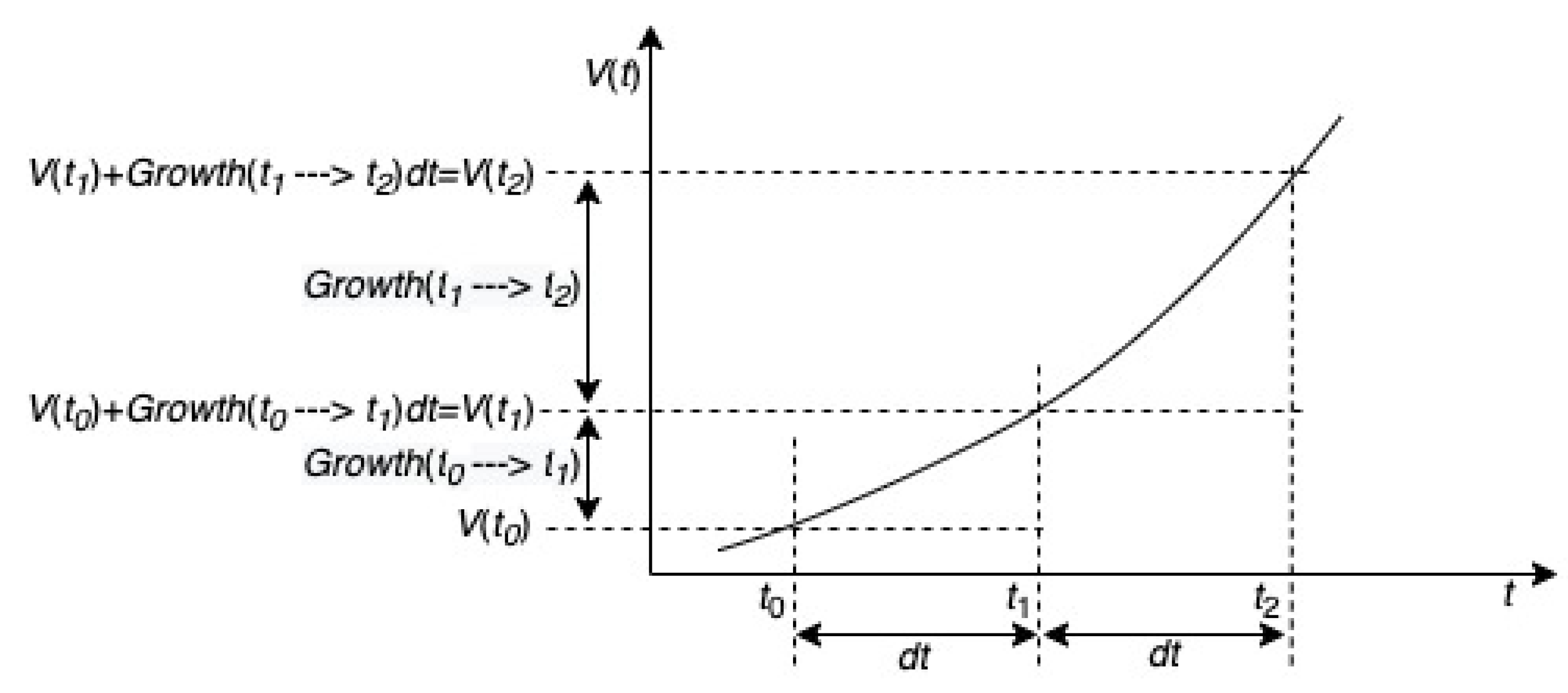
3. Tourist Destination Life Cycle Behavior from the System Dynamics Perspective
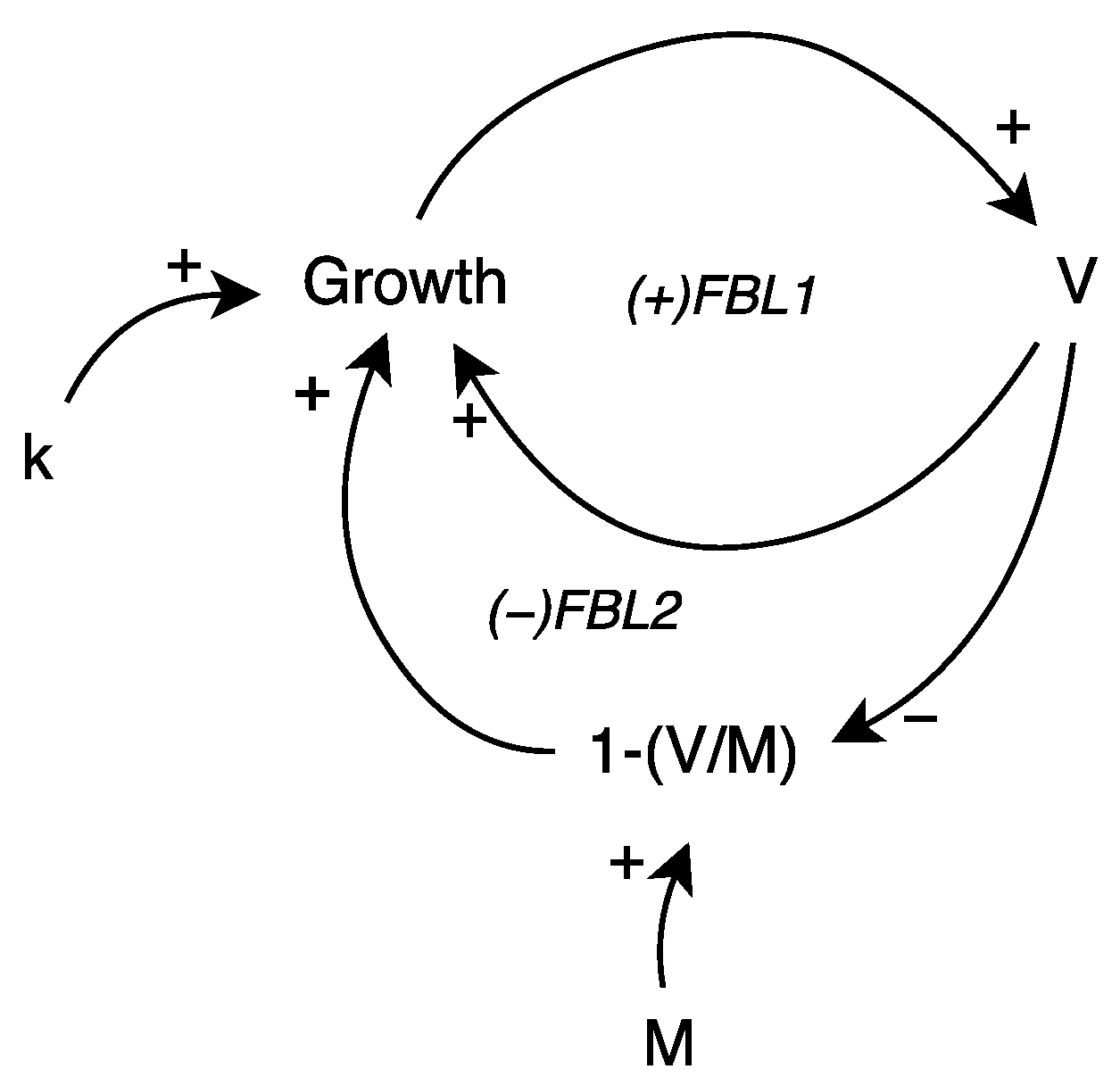
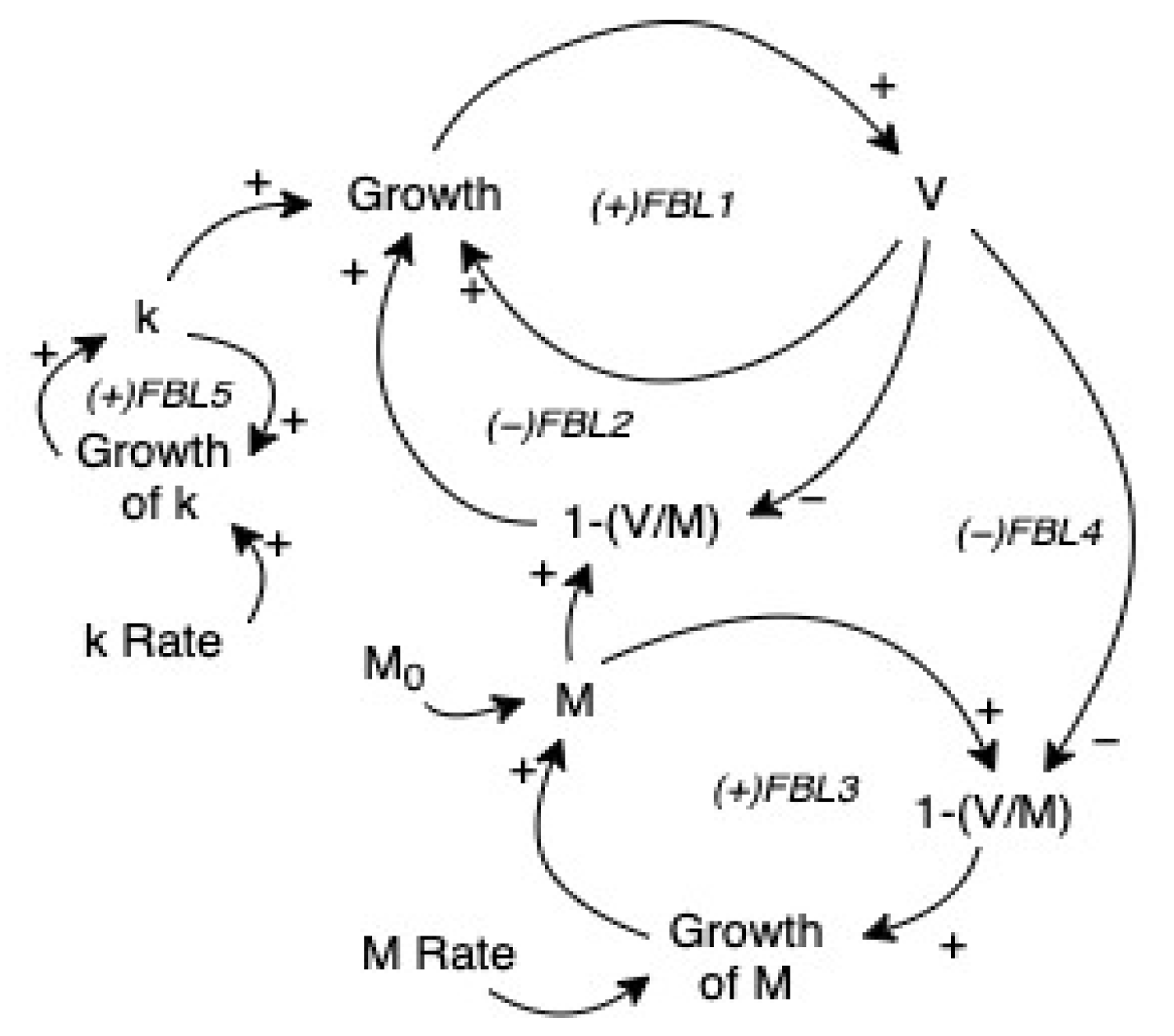
4. The TALC Model Development Based on Causal Loop Diagram
5. Results
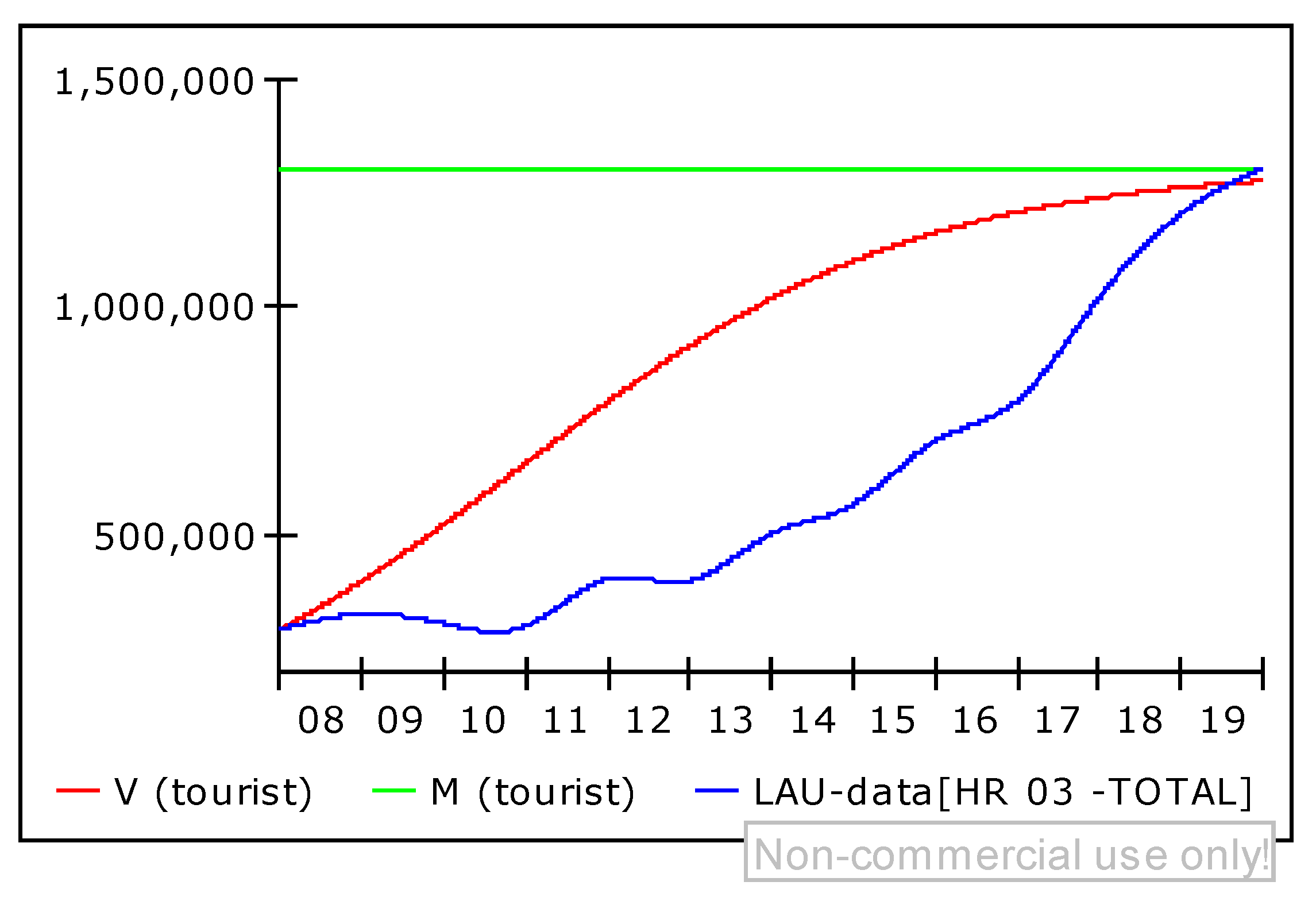
5.1. The TALC Model Verification
- The supply-dominance stage;
- The demand-dominance stage;
- The restructuring stage.
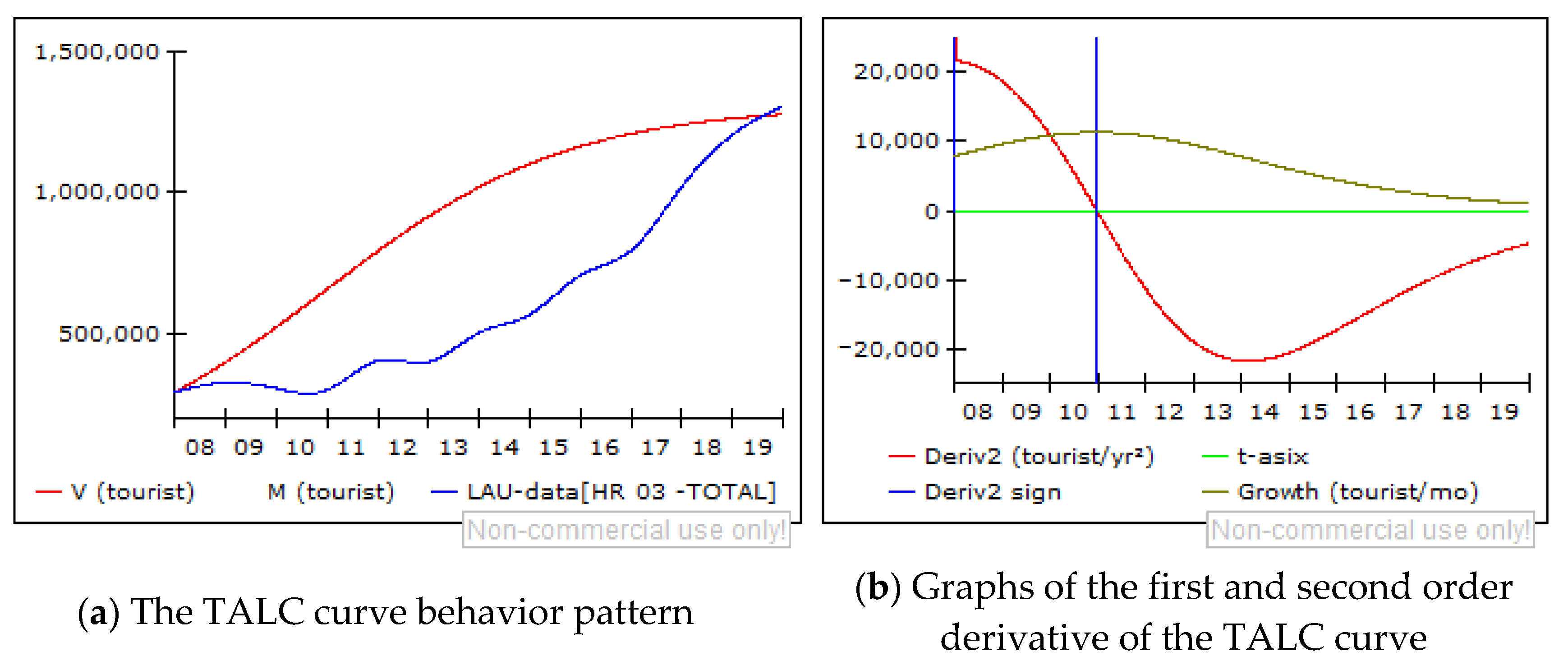
5.2. Generic Structures of the TALC Model Behavior
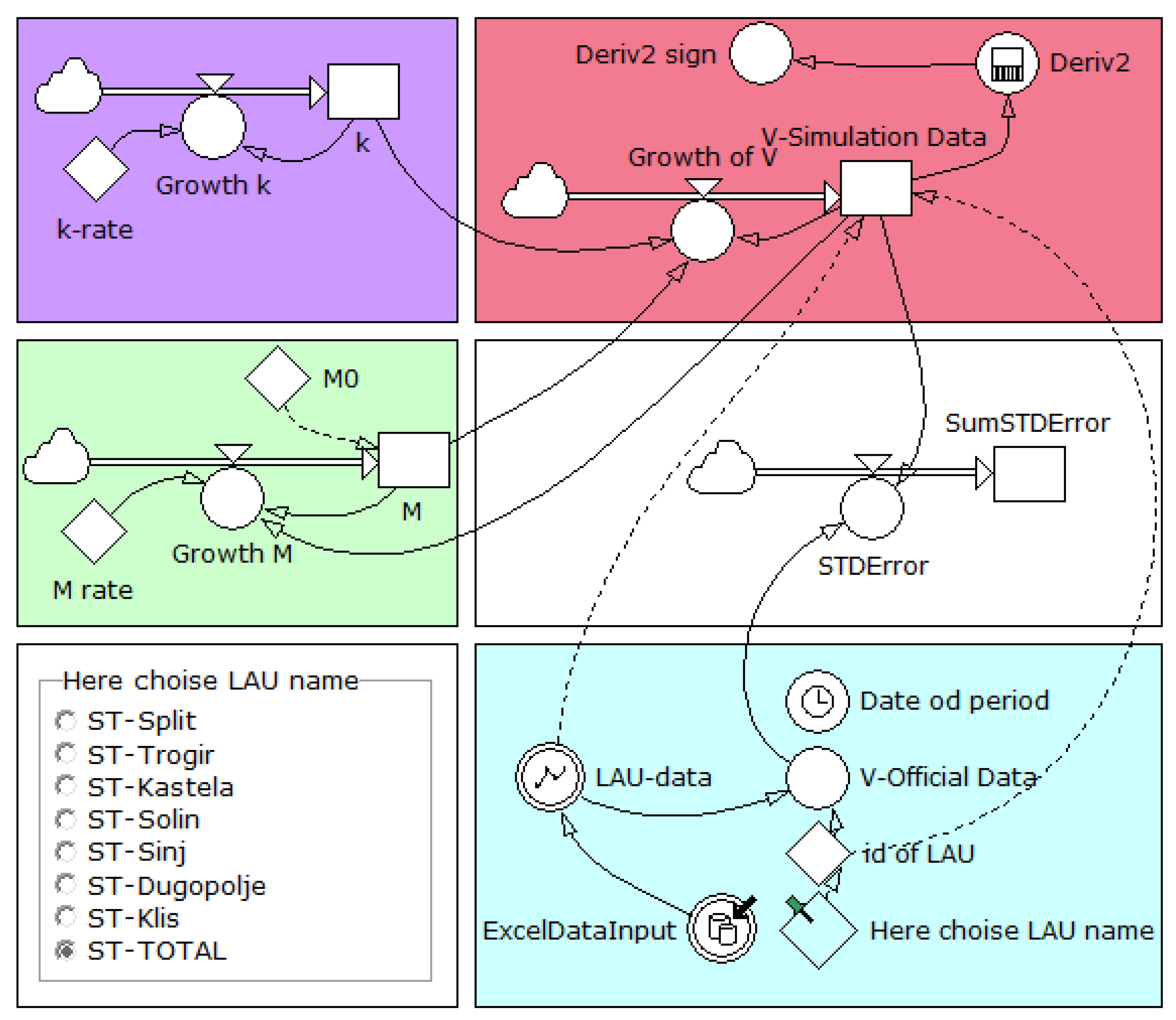
5.3. The TALC System Dynamics Model in Powersim Studio
- State variables—which accumulate change. It takes one moment to read them. These variables remember values and are denoted by the rectangle symbol (in Figure 9, these are k, M, SumSTDError and V-simulation Data).
- Rate variables—which indicate change, i.e., speed (first-order derivative). It takes two time moments to calculate their values. They are marked with a picture of the valve and flow. A bubble at the beginning or end indicates the source and abyss of the stream. Input or output presents a parameter for state variables. In Figure 9, these are Growth k, Growth M, Growth V, STDError.
- Auxiliary variables—which are used to clarify calculations and flow within the model. Linking them to/from rate variables enables a partial calculus. Constants are permanent identifiers throughout the simulation period. They are denoted by a rhombus (in Figure 9, k-rate, M-rate, M0, id-LAU-whose value in the model is selected based on the radio-button and the variable).
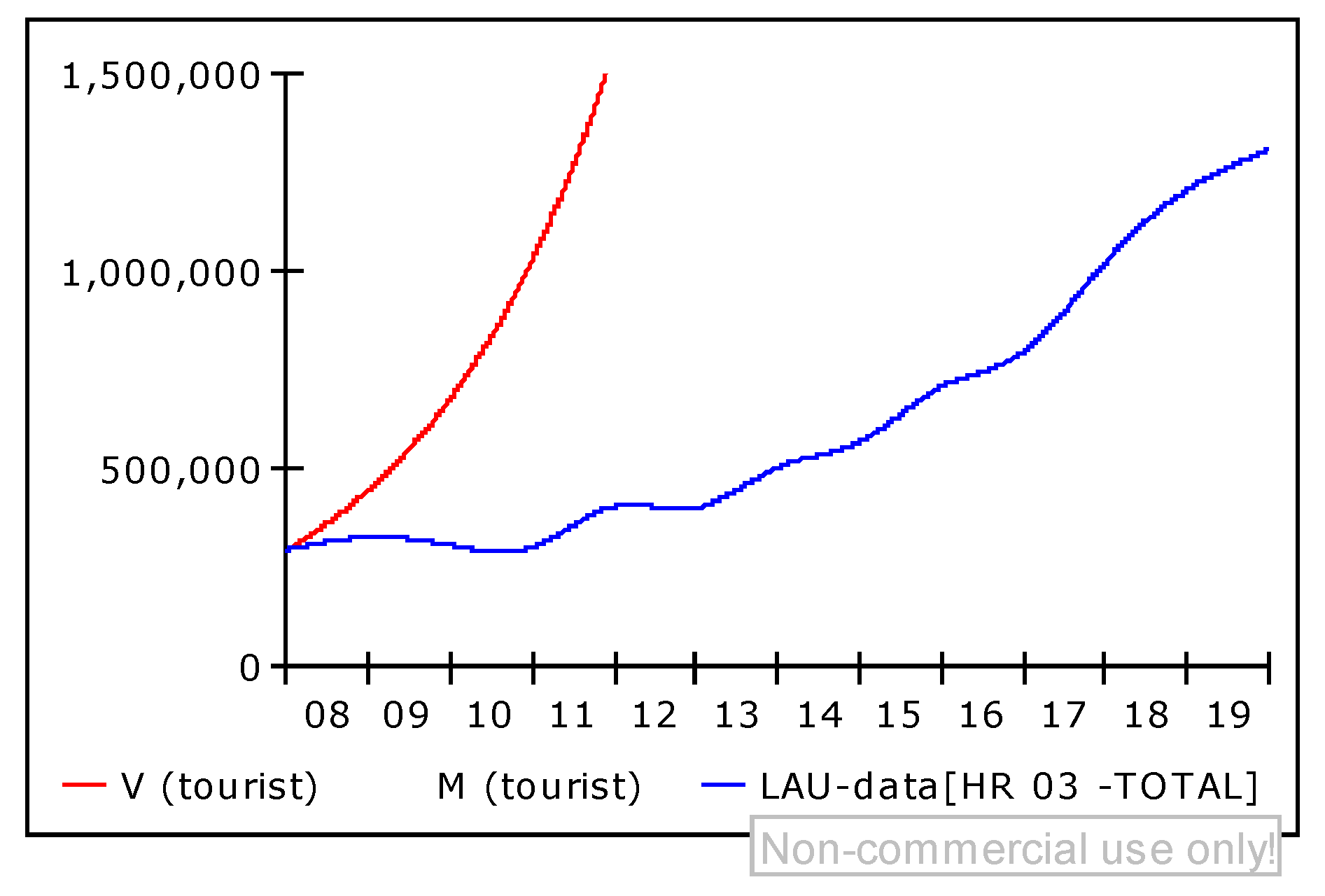
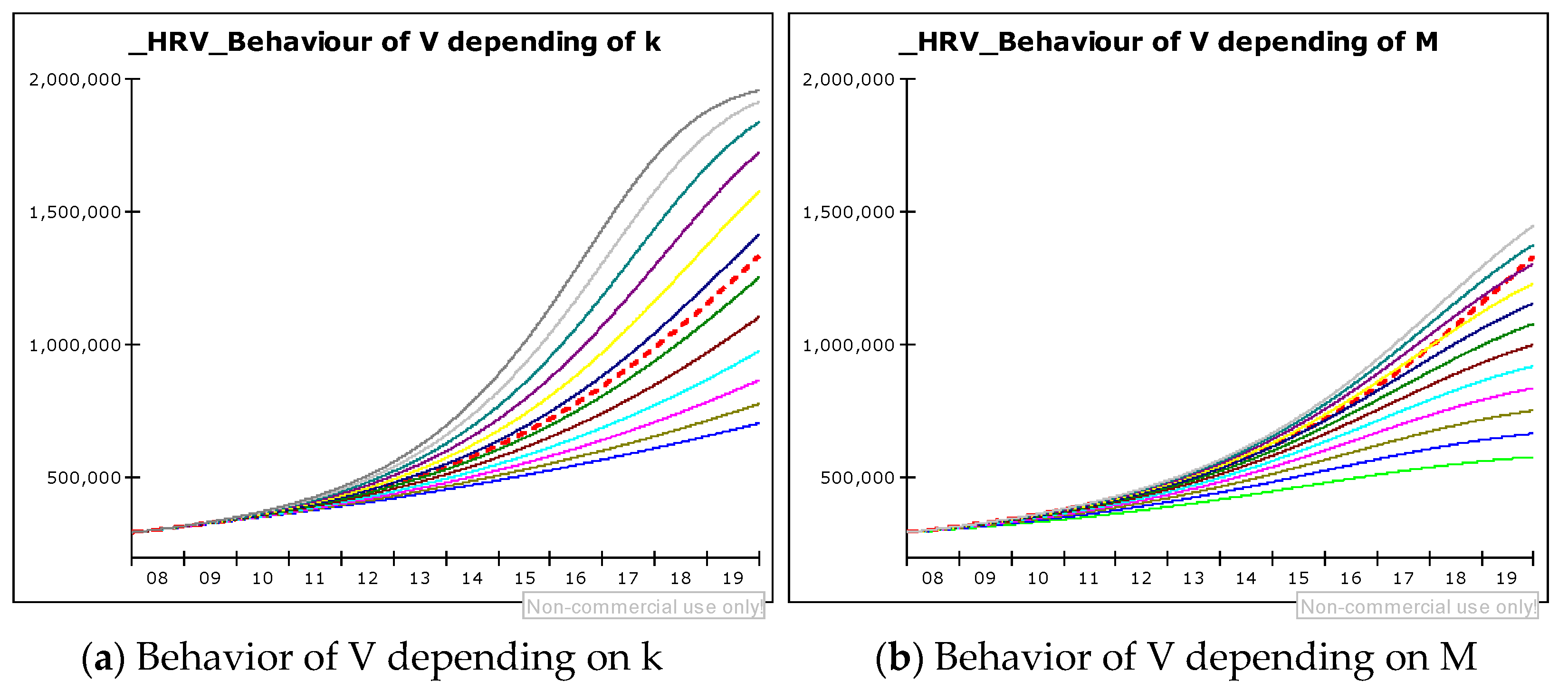
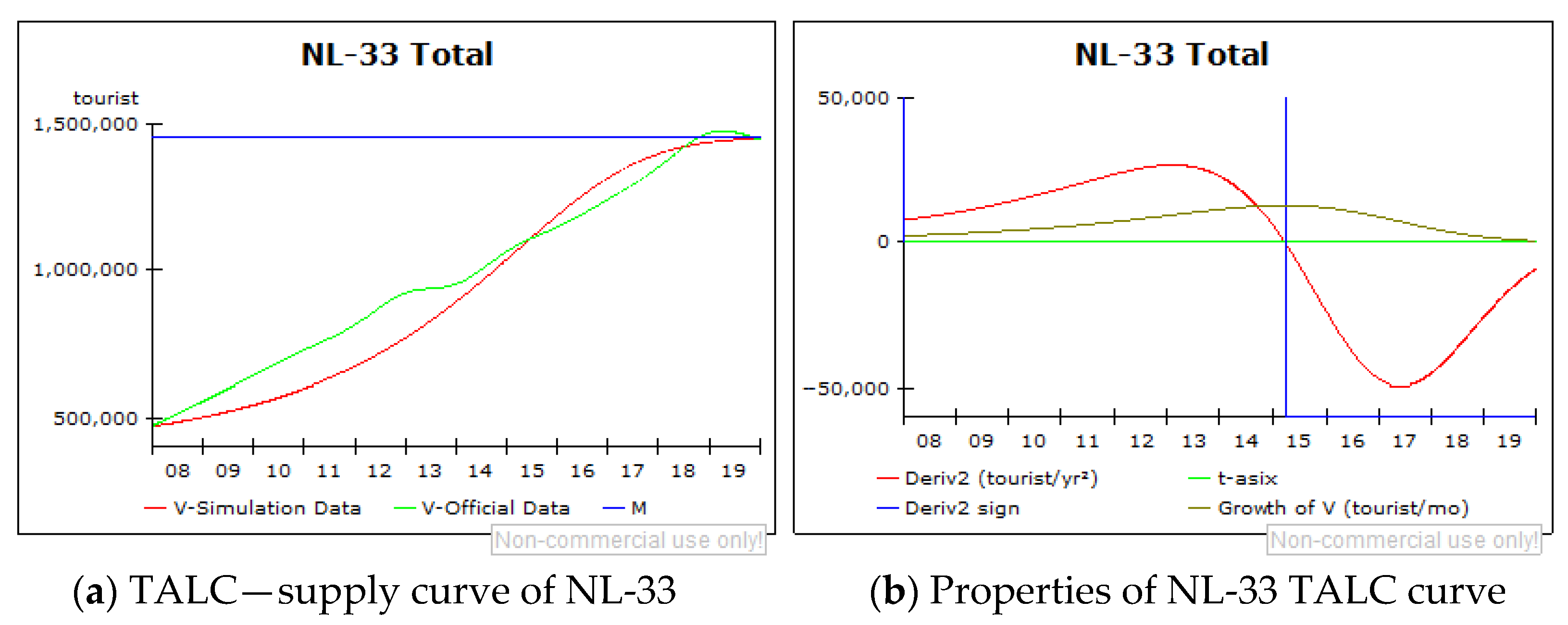
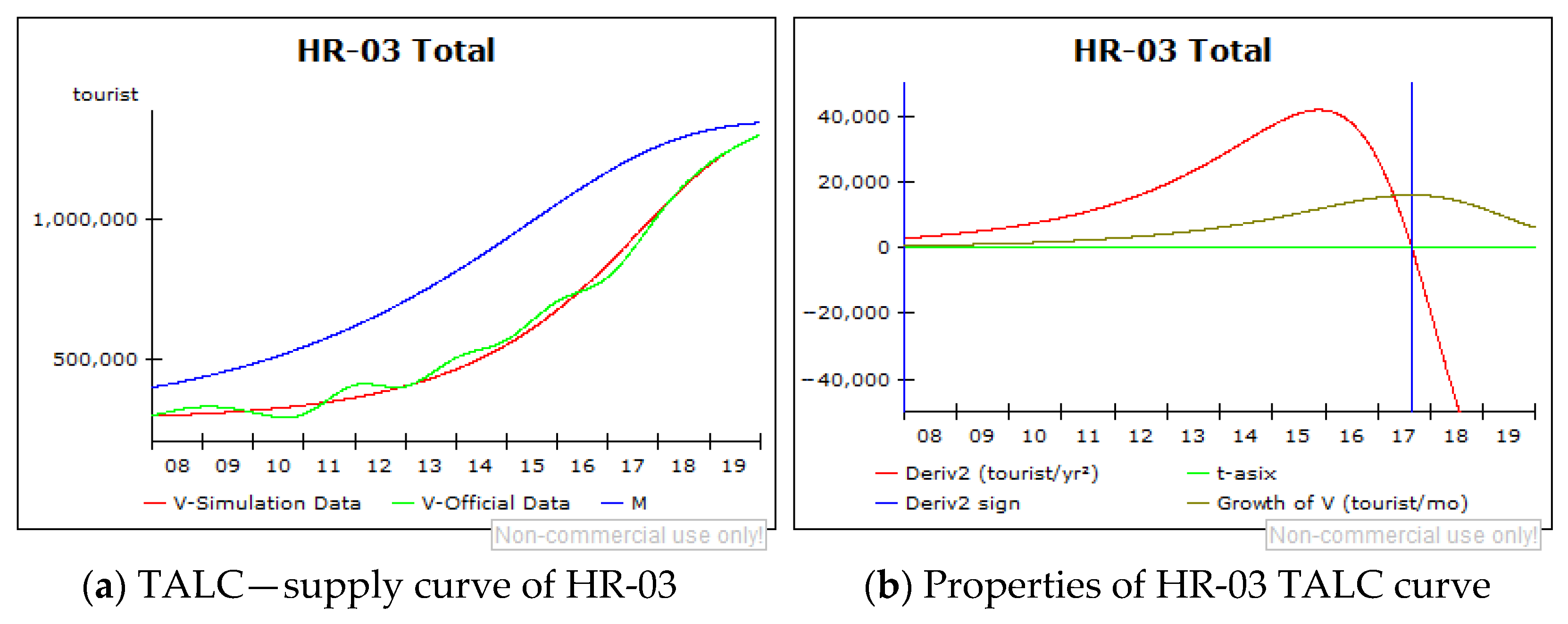
5.4. Scenario Analysis Based on the TALC System Dynamics Model
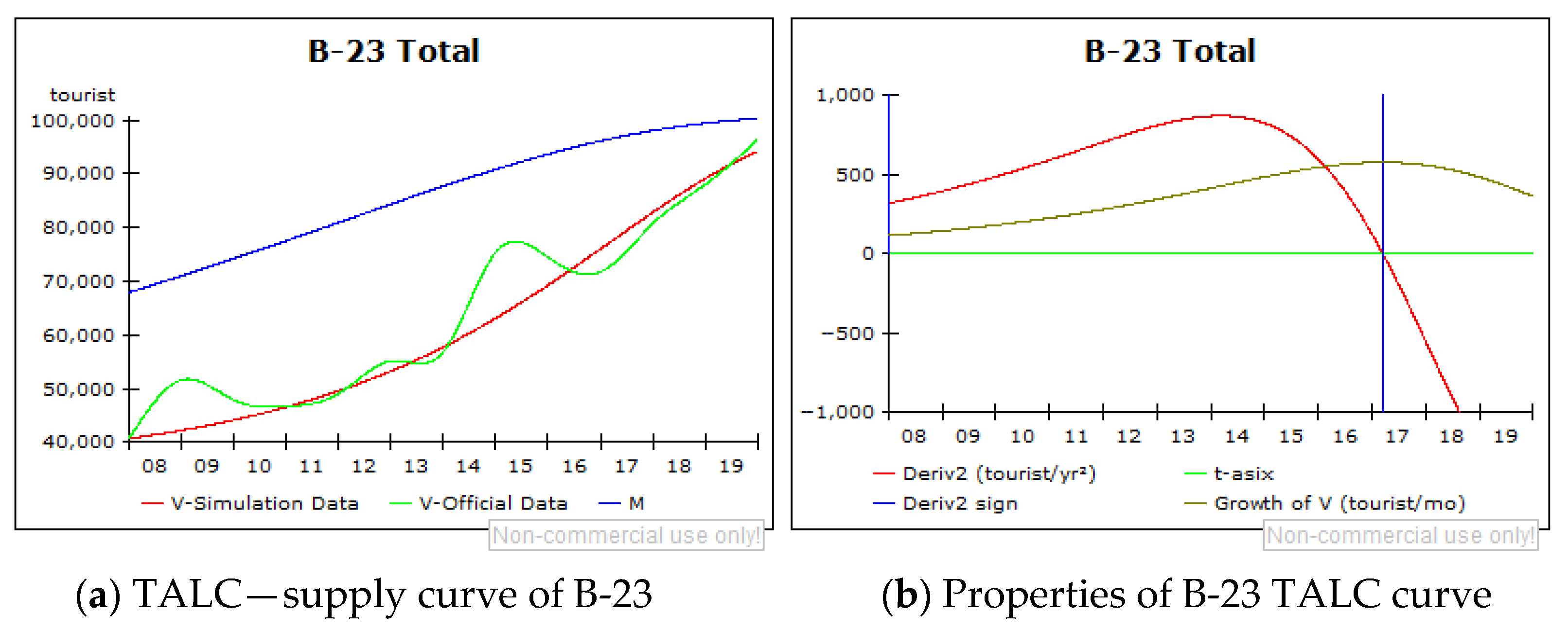
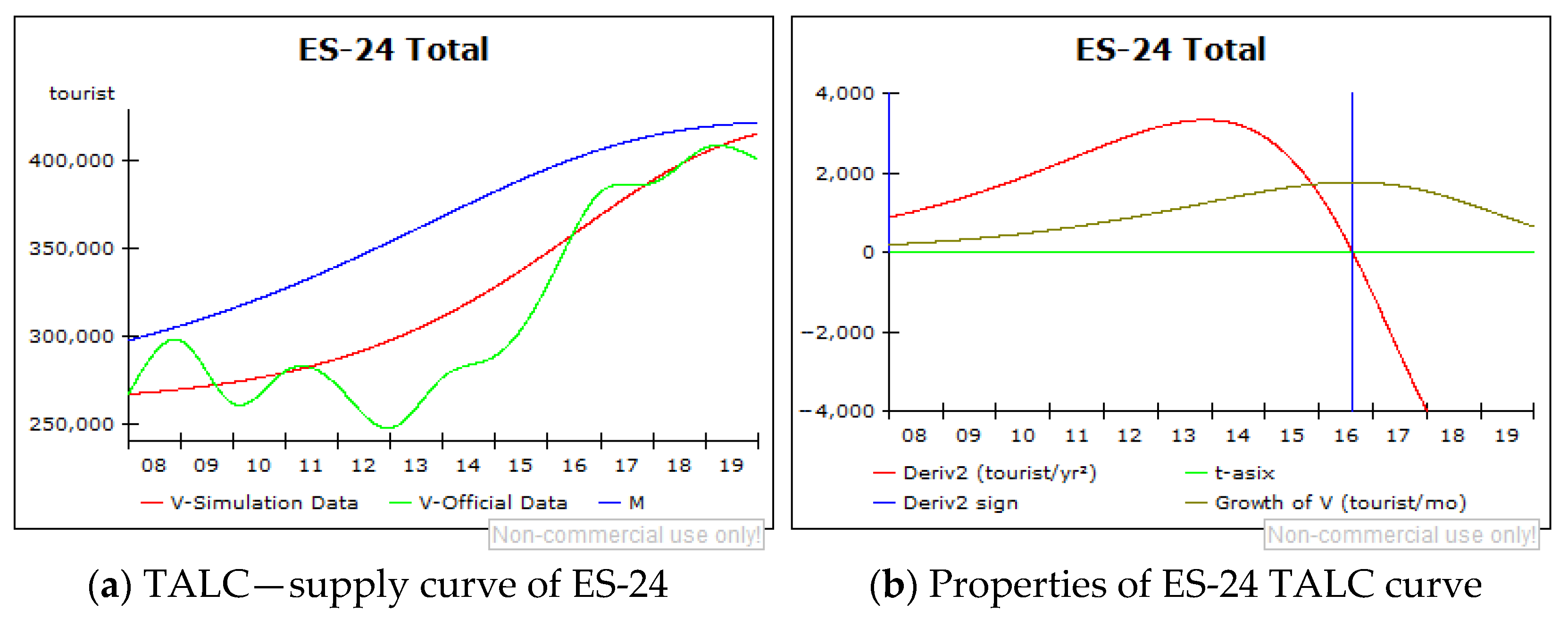
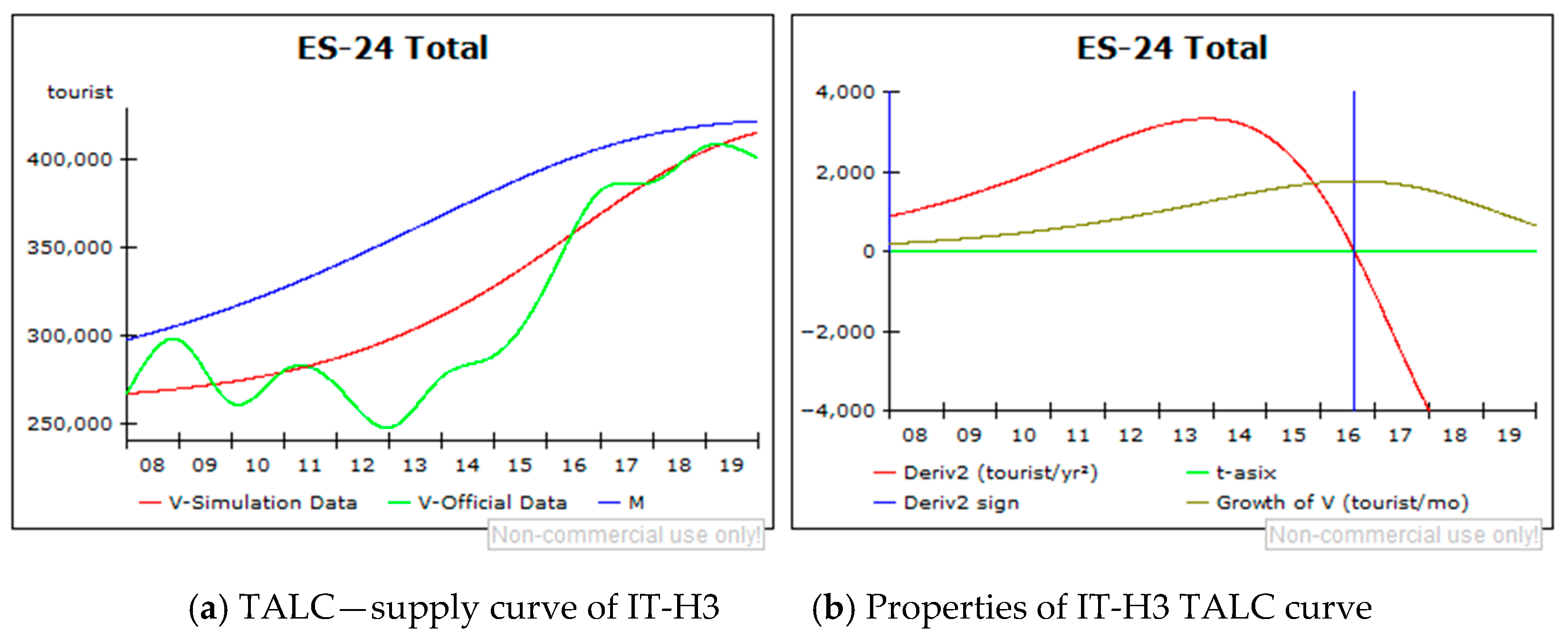
- V-simulation data (red graph)—representing the number of arrivals per year, representing the trend of the observed period;
- V-Official Data (light green graph)—representing the number of arrivals per year, based on the interpolated data;
- Maximum expected number of visitors (M) (blue graph) equals total supply.
- Growth of V (dark green graph)—the first-order derivative of the V-simulation function;
- Derivative2 (red graph)—the second-order derivative of the V-simulation function;
- Derivative2 sign (blue graph)—a sign of the second-order derivative indicating moment when a destination passes from one stage to another;
- t-asix (light green graph)—drawn to enable monitoring of the first and second-order derivative functions flow.
6. Discussion and Conclusive Remarks
- To reduce the number of arrivals;
- To remain in the steady-state (the same number of arrivals each year), or
- To initiate a new lifecycle by introducing innovative and sustainable tourism products to enhance offer (M) and to rejuvenate destination.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- McDonald, J.R. Complexity science: An alternative world view for understanding sustainable tourism development. J. Sustain. Tour. 2009, 17, 455–471. [Google Scholar] [CrossRef]
- Farrell, B.H.; Twining-Ward, L. Reconceptualizing tourism. Ann. Tour. Res. 2004, 31, 274–295. [Google Scholar] [CrossRef]
- Baggio, R. Symptoms of Complexity in a Tourism System. Tour. Anal. 2008, 13, 1–20. [Google Scholar] [CrossRef]
- Olmedo, E.; Mateos, R. Quantitative characterization of chaordic tourist destination. Tour. Man. 2015, 47, 115–126. [Google Scholar] [CrossRef]
- Faulkner, B.; Valerio, P. Towards an integrative approach to tourism demand forecasting. Tour. Man. 1995, 16, 29–37. [Google Scholar]
- Parry, B.; Drost, R. Is chaos good for your profits? Int. J. Cont. Hosp. Man. 1995, 7, 1–3. [Google Scholar]
- Sedarati, P.; Santos, S.; Pintassilgo, P. System Dynamics in Tourism Planning and Development. Tour. Plan. Dev. 2019, 16, 256–280. [Google Scholar] [CrossRef]
- Zhang, Z.; Ding, Z.J. The Systematic Spatial Characteristics of Sports Tourism Destinations in the Core Area of Marine Economy. J. Coast. Res. 2020, 112, 109–111. [Google Scholar] [CrossRef]
- Valeri, M.; Baggio, R. Social network analysis: Organizational implications in tourism management. Int. J. Org. Anal. 2020, 29, 342–353. [Google Scholar] [CrossRef]
- Rodriguez-Giron, S.; Vanneste, D. Tourism systems thinking: Towards an integrated framework to guide the study of the tourism culture & communication. Tour. Tour. Cult. Commun. Comm. 2019, 19, 1–16. [Google Scholar] [CrossRef]
- Yang, Z.Y.; Yin, M.; Xu, J.G.; Lin, W. Spatial evolution model of tourist destinations based on complex adaptive system theory: A case study of Southern Anhui, China. J. Geogr. Sci. 2019, 29, 1411–1434. [Google Scholar] [CrossRef]
- Iandolo, F.; Fulco, I.; Bassano, C.; D’Amore, R. Managing a tourism destination as a viable complex system. The case of Arbatax Park. Land Use Policy 2019, 84, 21–30. [Google Scholar] [CrossRef]
- Speakman, M. Paradigm for the Twenty-first Century or Metaphorical Nonsense? The Enigma of Complexity Theory and Tourism Research. Tour. Plan. Dev. 2017, 14, 282–296. [Google Scholar] [CrossRef]
- Pizzitutti, F.; Walsh, S.J.; Rindfuss, R.R.; Gunter, R.; Quiroga, D.; Tippett, R.; Mena, C.F. Scenario planning for tourism mana-gement: A participatory and system dynamics model applied to the Galapagos Islands of Ecuador. J. Sustain. Tour. 2017, 25, 1117–1137. [Google Scholar] [CrossRef]
- Butler, R. The concept of a tourist area cycle of evolution: Implications for management of resources. Can. Geogr. 1980, 24, 5–12. [Google Scholar] [CrossRef]
- United Nations World Tourism Organization (UNWTO). Report of the Secretary General of the General Programme of Work for the Period 1980–1981: Tourist Markets, Promotion and Marketing-Saturation of Tourist Destinations; UNWTO: Madrid, Spain, 1981. [Google Scholar]
- Jere Lazanski, T.; Kljajić, M. Systems approach to complex systems modelling with special regards to tourism. Kybernetes 2006, 35, 1048–1058. [Google Scholar] [CrossRef]
- Bui, H.L.; Jones, T.E.; Weaver, D.B.; Le, A. The adaptive resilience of living cultural heritage in a tourism destination. J. Sustain. Tour. 2020, 28, 1022–1040. [Google Scholar] [CrossRef]
- Jere Jakulin, T. Systems Approach to Tourism: A Methodology for Defining Complex Tourism System. Organizacija 2017, 50, 208–215. [Google Scholar] [CrossRef]
- Baggio, R.; Sainaghi, R. Complex and chaotic tourism systems: Towards a quantitative approach. Int. J. Contemp. Hosp. Manag. 2011, 23, 840–861. [Google Scholar] [CrossRef]
- Baranger, M. Chaos, Complexity, and Entropy—A Physics Talk for Non-Physicists. Center for Theoretical Physics, Laboratory for Nuclear Science and Department of Physics Massachusetts Institute of Technology, Cambridge and New England Complex Systems Institute. 2010. Available online: http://grex.cyberspace.org/~jayk/ChaosComplexityAndEntropy.pdf (accessed on 15 January 2021).
- Berkes, F.; Ross, H. Panarchy and community resilience: Sustainability science and policy implications. Environ. Sci. Policy 2016, 61, 185–193. [Google Scholar] [CrossRef]
- Faulkner, B.; Russell, R. Chaos and complexity in tourism: In search of a new perspective. Pac. Tour. Rev. 1997, 1, 93–102. [Google Scholar]
- Russell, R.; Faulkner, B. Entrepreneurship, Chaos and the Tourism Area Lifecycle. Ann. Tour. Res. 2004, 31, 556–579. [Google Scholar] [CrossRef]
- Petrić, L. Has the myth of tourist destination sustainability faded? Behind the curtains of the global crises. In Proceedings of the 2nd International Scientific Conference “Tourism in Southern and Eastern Europe”, Opatija, Croatia, 15–18 May 2013; Janković, S., Smolčić Jurdana, D., Eds.; Faculty of Tourism and Hospitality Management: Opatija, Croatia, 2013; pp. 19–23. [Google Scholar]
- McKercher, B. A Chaos Approach to Tourism. Tour. Manag. 1999, 20, 425–434. [Google Scholar] [CrossRef]
- Williams, B.K.; Szaro, R.C.; Shapiro, C.D. Adaptive Management: The US Department of the Interior Technical Guide; Adaptive Management Working Group, US Department of the Interior: Washington, DC, USA, 2007. Available online: https://www.doi.gov/sites/doi.gov/files/migrated/ppa/upload/TechGuide.pdf (accessed on 7 April 2021).
- Murphy, P. Tourism: A Community Approach; Methuen: New York, NY, USA, 1985. [Google Scholar]
- Tosun, C. Limits to community participation in the tourism development process in developing countries. Tour. Manag. 2000, 21, 613–633. [Google Scholar] [CrossRef]
- Tosun, C.; Timothy, D.J. Arguments for community participation in tourism development. Tour. Stud. 2003, 14, 2–11. [Google Scholar]
- Beeton, S. Community Development through Tourism; Landlink Press: Collingwood, Australia, 2006. [Google Scholar]
- Eyisi, A.; Lee, D.; Trees, K. Facilitating collaboration and community participation in tourism development: The case of South-Eastern Nigeria. Tour. Hosp. Res. 2020. [Google Scholar] [CrossRef]
- Rasoolimanesh, S.M.; Jaafar, M.; Kock, N.; Ahmad, A.G. The effects of community factors on residents’ perceptions toward World Heritage Site inscription and sustainable tourism development. J. Sustain. Tour. 2017, 25, 198–216. [Google Scholar] [CrossRef]
- Higgins-Desbiolles, F.; Carnicelli, S.; Krolikowski, C.; Wijesinghe, G.; Boluk, K. Degrowing tourism: Rethinking tourism. J. Sustain. Tour. 2019, 27, 1926–1944. [Google Scholar] [CrossRef]
- Butowski, L. Sustainable Tourism: A Human-Centered Approach. Sustainability 2021, 13, 1835. [Google Scholar] [CrossRef]
- Miller, D.S.; Gonzalez, C.; Hutter, M. Phoenix tourism within dark tourism. Worldw. Hosp. Tour. Themes 2017, 9, 196–215. [Google Scholar] [CrossRef]
- Butler, R. The Origins of the Tourism Area Life Cycle. In The Tourism Area Life Cycle, Applications and Modifications; Butler, R., Ed.; Channel View Publications: Clevedon, UK, 2006; Volume 1, pp. 13–26. [Google Scholar]
- Coyle, G. System Dynamics Modelling: A Practical Approach; Springer-Science+Business Media: Berlin, Germany, 1996. [Google Scholar]
- Ogata, K. Modern Control Engineering Systems, 3rd ed.; Prentice Hall: Hoboken, NJ, USA, 1997. [Google Scholar]
- Forrester, J.W. Urban Dynamics; M.I.T. Press: Cambridge, MA, USA, 1969; p. xiv + 290. [Google Scholar]
- Sterman, J.D. System Dynamics: Systems Thinking and Modelling for a Complex World; Engineering Systems Division Working Paper Series; Massachusetts Institute of Technology: Cambridge, MA, USA, 2002; Available online: https://dspace.mit.edu/bitstream/handle/1721.1/102741/esd-wp-2003-01.13.pdf?sequence=1&isAllowed=y (accessed on 3 February 2021).
- Davidsen, P. The structure±behavior diagram: Understanding the relationship between structure and behavior in complex dynamic systems. In Proceedings of the System Dynamics Conference, Utrecht, The Netherlands, 14–17 July 1992; Vennis, J.A.M., Ed.; The Systems Dynamics Society: Albany, NY, USA, 1992; pp. 127–140. [Google Scholar]
- Forrester, J.W. Industrial Dynamics; The Massachusetts Institute of Technology: Cambridge, MA, USA, 1961. [Google Scholar]
- Rahmandad, H.; Repenning, N.; Sterman, J. Effects of feedback delay on learning. Syst. Dyn. Rev. 2009, 25, 309–338. [Google Scholar] [CrossRef]
- Huang, J.B. Analytical and Computational Methods for Analyzing Feedback Structure in System Dynamics Models. Ph.D. Thesis, School of Engineering & Informatics, National University of Ireland, Galway, Ireland, 7 October 2012. [Google Scholar]
- Richardson, G.P. Feedback Thought in Social Science and Systems Theory; University of Pennsylvania Press: Philadelphia, PA, USA, 1991. [Google Scholar]
- Richardson, G.P. Loop polarity, loop dominance, and the concept of dominant polarity. Syst. Dyn. Rev. 1995, 11, 67–88. [Google Scholar] [CrossRef]
- Ford, F.A. Modeling the Environment: An Introduction to System Dynamics Models of Environmental Systems; Island Press: Washington, DC, USA, 1999. [Google Scholar]
- Pejić-Bach, M.; Čerić, V. Developing System Dynamics Models with Step by Step approach. J. Inf. Organ. Sci. 2007, 31, 171–185. [Google Scholar]
- Cole, S. Synergy and congestion in the tourist destination life cycle. Tour. Manag. 2012, 33, 1128–1140. [Google Scholar] [CrossRef]
- Petrić, L.; Škrabić Perić, B.; Hell, M.; Kuliš, Z.; Mandić, A.; Pivčević, S.; Šimundić, B.; Muštra, V.; Grgić, J.; Mikulić, D. Report outlining the SRT framework. Deliverable 4.2. of the Horizon 2020 project SmartCulTour (GA number 870708). Published on the Project Web Site on February 2021. Available online: http://www.smartcultour.eu/deliverables/ (accessed on 3 March 2021).
- Haywood, K.M. Can the tourist area life-cycle be made operational? Tour. Manag. 1986, 7, 154–167. [Google Scholar] [CrossRef]
- Dealbuquerque, K.; Mcelroy, J.L. Caribbean small-island tourism styles and sustainable strategies. Environ. Manag. 1992, 16, 619–632. [Google Scholar] [CrossRef]
- Prideaux, B. The resort development spectrum—A new approach to modelling resort development. Tour. Manag. 2000, 21, 225–240. [Google Scholar] [CrossRef]
- Romao, J.; Guerreiro, J.; Rodrigues, P. Regional tourism development: Culture, nature, life cycle and attractiveness. Curr. Issues Tour. 2013, 16, 517–534. [Google Scholar] [CrossRef]
- Fletcher, R. Sustaining Tourism, Sustaining Capitalism? The Tourism Industry’s Role in Global Capitalist Expansion. Tour. Geogr. 2011, 13, 443–461. [Google Scholar] [CrossRef]
- Fletcher, R.; Murray Mas, I.; Blanco-Romero, A.; Blázquez-Salomet, M. Tourism and de-growth: An emerging agenda for research and praxis. J. Sustain. Tour. 2019, 10, 1–19. [Google Scholar] [CrossRef]
- Seyfi, S.; Hall, C.M. COVID-19 pandemic, tourism and de-growth. In De-Growth and Tourism: New Perspectives on Tourism Entrepreneurship, Destinations and Policy; Hall, C.M., Lundmark, L., Zhang, J., Eds.; Routledge: London, UK, 2021; pp. 287–313. [Google Scholar]
- Faulkner, B. Rejuvenating a Maturing Tourist Destination: The Case of the Gold Coast; Common Ground Publishing Pty Ltd.: Melbourne, Australia, 2002; Available online: https://citeseerx.ist.psu.edu/viewdoc/download?doi=10.1.1.505.3592&rep=rep1&type=pdf (accessed on 7 April 2021).
- Faulkner, B.; Tideswell, C. Rejuvenation a Maturing Tourist Destination; The case of the Gold Coast, Australia. In The Tourism Area Life Cycle, Applications and Modifications; Butler, R., Ed.; Channel View Publications: Clevedon, UK, 2006; Volume 1, pp. 306–335. [Google Scholar]
- Hovinen, G.R. Lancaster County, the TALC and the search for sustainable tourism. In The Tourism Area Life Cycle, Applications and Modifications; Butler, R., Ed.; Channel View Publications: Clevedon, UK, 2006; Volume 1, pp. 73–90. [Google Scholar]
- Albaladejo, I.; Martinez Garcia, M.P. The post-stagnation stage for mature tourism areas: A mathematical modelling process. Tour. Econ. 2017, 2, 387–402. [Google Scholar] [CrossRef]
- Ferreira, S.L.A.; Hunter, C.A. Wine tourism development in South Africa: A geographical analysis. Tour. Geogr. 2017, 19, 676–698. [Google Scholar] [CrossRef]
- Malcom-Davies, J. The TALC for Heritage Sites. In The Tourism Area Life Cycle, Applications and Modifications; Butler, R., Ed.; Channel View Publications: Clevedon, UK, 2006; Volume 1, pp. 162–180. [Google Scholar]
- Lundtorp, S.; Wanhill, S. The resort lifecycle theory. Generating Processes and Estimation. Ann. Tour. Res. 2001, 28, 947–964. [Google Scholar] [CrossRef]
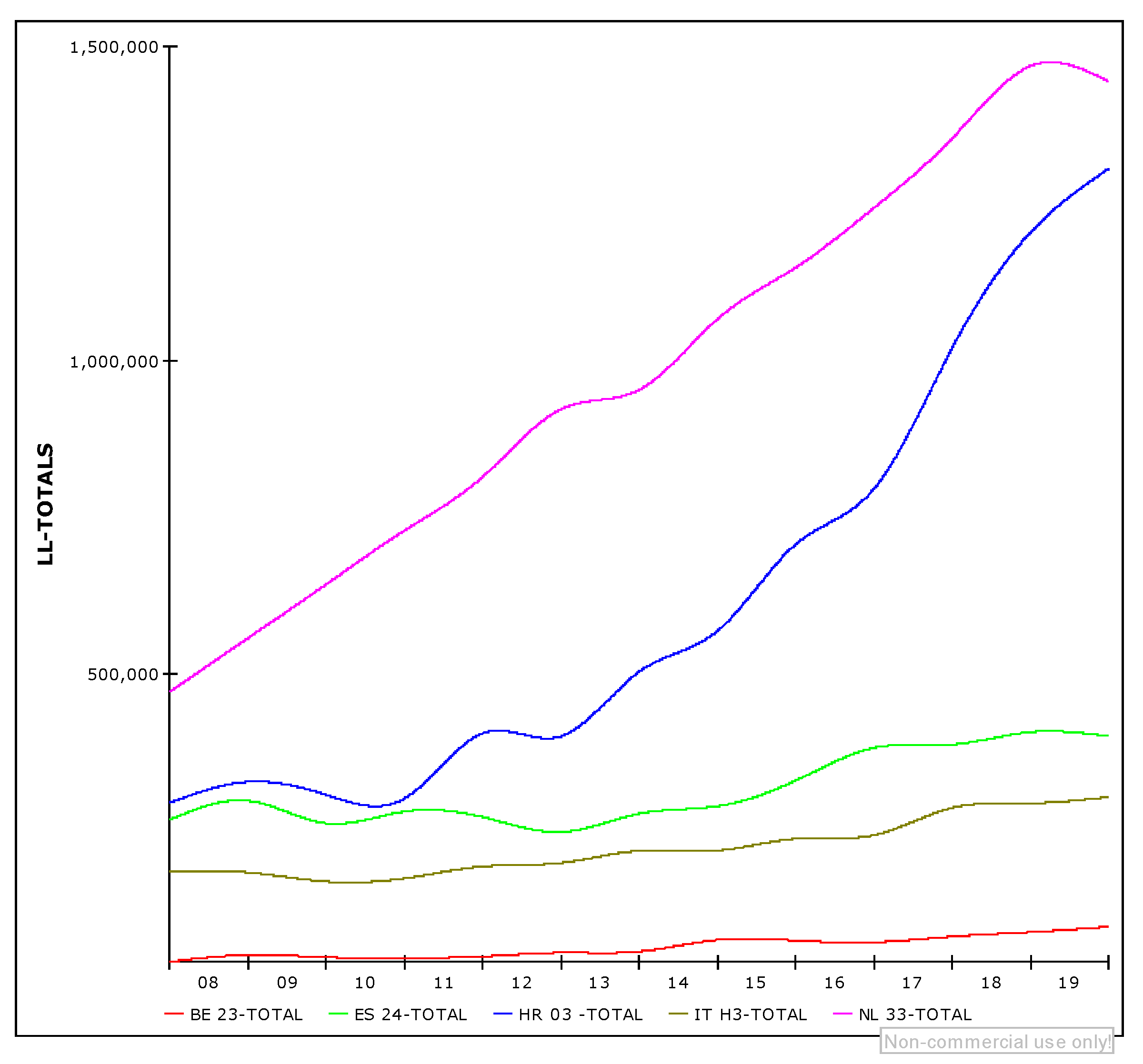
| 2007 | 2008 | 2009 | 2010 | 2011 | 2012 | 2013 | 2014 | 2015 | 2016 | 2017 | 2018 | 2019 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| BE 23-TOTAL | 40,727 | 51,614 | 47,882 | 46,696 | 49,077 | 55,170 | 56,907 | 75,382 | 74,473 | 71,756 | 80,759 | 88,008 | 96,358 |
| Bornem | 12,020 | 12,105 | 11,889 | 12,146 | 12,543 | 12,325 | 12,003 | 13,315 | 13,700 | 13,356 | 13,876 | 13,601 | 15,660 |
| Pu.-Si.-Am. | 2638 | 2996 | 3354 | 3713 | 4071 | 4429 | 4787 | 5442 | 5395 | 6144 | 5276 | 6570 | 7418 |
| Aalst | 18,759 | 28,618 | 25,143 | 23,230 | 25,405 | 29,688 | 31,119 | 48,224 | 47,814 | 44,537 | 52,851 | 58,623 | 62,628 |
| Berlare | 2838 | 2839 | 2487 | 2797 | 2606 | 3151 | 2482 | 2100 | 2862 | 2732 | 2921 | 3109 | 4020 |
| Dendermonde | 4472 | 5056 | 5009 | 4810 | 4452 | 5577 | 6516 | 6301 | 4702 | 4987 | 5835 | 6105 | 6632 |
| ES 24-TOTAL | 267,090 | 297,506 | 261,463 | 280,208 | 271,409 | 247,693 | 276,771 | 288,902 | 329,622 | 381,897 | 387,165 | 407,220 | 400,611 |
| Ainsa | 3439 | 6356 | 9273 | 12,190 | 15,107 | 18,024 | 19,426 | 26,888 | 25,260 | 29,692 | 32,609 | 55,503 | 35,258 |
| Benasque | 70,753 | 68,201 | 63,243 | 72,698 | 67,585 | 49,759 | 56,079 | 57,041 | 59,285 | 71,142 | 81,818 | 78,271 | 79,695 |
| Huesca | 77,565 | 92,458 | 71,568 | 69,988 | 66,990 | 65,409 | 72,650 | 78,374 | 90,168 | 92,857 | 90,091 | 90,091 | 90,168 |
| Jaca | 115,333 | 130,491 | 117,379 | 125,332 | 121,727 | 114,501 | 128,616 | 126,599 | 154,909 | 188,206 | 182,647 | 183,355 | 195,490 |
| HR 03-TOTAL | 294,370 | 327,557 | 306,968 | 301,086 | 405,275 | 400,456 | 503,400 | 568,271 | 706,592 | 794,964 | 1,019,852 | 1,204,130 | 1,305,993 |
| Dugopolje | 3000 | 4000 | 9000 | 10,282 | 29,676 | 32,258 | 61,193 | 46,726 | 53,960 | 25,927 | 51,299 | 49,159 | 45,779 |
| Kaštela | 28,501 | 29,987 | 26,893 | 25,509 | 54,880 | 32,670 | 41,016 | 42,406 | 50,191 | 60,364 | 83,605 | 100,530 | 114,990 |
| Klis | 100 | 100 | 100 | 100 | 100 | 300 | 300 | 300 | 500 | 877 | 1909 | 2931 | 4085 |
| Sinj | 8689 | 9645 | 7649 | 7179 | 7694 | 7110 | 9035 | 10,691 | 10,266 | 9633 | 11,317 | 13,116 | 11,620 |
| Solin | 2500 | 4000 | 5500 | 7530 | 14,590 | 11,118 | 6915 | 10,422 | 14,449 | 15,693 | 22,139 | 32,042 | 41,322 |
| Split | 185,718 | 211,299 | 176,185 | 203,539 | 252,287 | 265,630 | 318,057 | 381,227 | 487,474 | 583,041 | 720,325 | 859,224 | 941,185 |
| Trogir | 65,862 | 68,526 | 81,641 | 46,947 | 46,048 | 51,370 | 66,884 | 76,499 | 89,752 | 99,429 | 129,258 | 147,128 | 147,012 |
| IT H3-TOTAL | 183,858 | 183,119 | 168,631 | 173,731 | 192,618 | 198,268 | 217,598 | 218,073 | 236,852 | 242,609 | 286,103 | 293,648 | 303,550 |
| Caldogno | 1833 | 2029 | 1742 | 1651 | 1838 | 2121 | 1131 | 842 | 842 | 842 | 842 | 842 | 842 |
| Gr. delle Abb. | 1769 | 3146 | 5642 | 3663 | 8396 | 9622 | 11,115 | 11,038 | 11,748 | 12,458 | 13,168 | 13,878 | 14,588 |
| Lonigo | 7403 | 8013 | 7154 | 7136 | 6718 | 6949 | 6913 | 7130 | 7717 | 8304 | 8891 | 9478 | 10,065 |
| Montagnana | 6121 | 6369 | 4636 | 4681 | 4667 | 3700 | 4055 | 4514 | 3248 | 1982 | 716 | 0 | 0 |
| Vicenza | 166,732 | 163,562 | 149,457 | 156,600 | 170,999 | 175,876 | 194,384 | 194,549 | 213,297 | 219,023 | 262,486 | 270,000 | 279,871 |
| NL 33-TOTAL | 471,342 | 557,097 | 642,852 | 728,607 | 814,361 | 922,282 | 953,188 | 1,065,836 | 1,148,228 | 1,243,377 | 1,354,261 | 1,469,674 | 1,445,218 |
| Barendrecht | 12,801 | 14,187 | 15,573 | 16,959 | 18,345 | 19,260 | 20,924 | 22,601 | 24,012 | 25,013 | 28,755 | 28,106 | 27,980 |
| Delft | 26,527 | 29,515 | 32,503 | 35,490 | 38,478 | 40,290 | 44,185 | 48,050 | 50,688 | 52,455 | 60,653 | 59,572 | 59,501 |
| Dordrecht | 33,779 | 36,944 | 40,109 | 43,274 | 46,439 | 48,165 | 52,419 | 56,548 | 59,602 | 61,432 | 70,246 | 68,517 | 68,513 |
| Ridderkerk | 12,350 | 13,638 | 14,927 | 16,215 | 17,503 | 18,430 | 19,986 | 21,473 | 22,625 | 23,494 | 27,160 | 26,702 | 26,529 |
| Rotterdam | 373,226 | 448,964 | 524,702 | 600,440 | 676,179 | 778,000 | 796,000 | 896,000 | 969,000 | 1,058,000 | 1,141,000 | 1,261,000 | 1,237,000 |
| Zwijndrecht | 12,659 | 13,848 | 15,038 | 16,228 | 17,418 | 18,137 | 19,674 | 21,165 | 22,302 | 22,982 | 26,447 | 25,777 | 25,695 |
| Living Lab | The Year When the Maximum Acceleration of the Visitor Growth Rate Was Reached | The Year When the Maximum Growth Rate of Arrivals Is Reached (Carrying Capacities Threshold) | Lifecycle Stage |
|---|---|---|---|
| BE-23; BELGIUM, Prov. Oost-Vlaanderen and Antwerpen, the Scheldeland region | 2014 | 2017 | The second lifecycle stage-the demand dominance stage |
| ES 24: SPAIN, Aragón, Huesca | 2014 | 2016 | The second lifecycle stage- the demand dominance stage |
| HR-03; CROATIA, City of Split metropolitan area | 2016 | 2017 | The second lifecycle stage- the demand dominance stage |
| IT H3; ITALY, Veneto, Vicenza | 2015 | 2018 | The second lifecycle stage- the demand dominance stage |
| NL 33; NETHERLANDS, Zuid-Holland, The Rotterdam Metropolitan Region | 2015 | 2015 | The end of the second lifecycle stage |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hell, M.; Petrić, L. System Dynamics Approach to TALC Modeling. Sustainability 2021, 13, 4803. https://doi.org/10.3390/su13094803
Hell M, Petrić L. System Dynamics Approach to TALC Modeling. Sustainability. 2021; 13(9):4803. https://doi.org/10.3390/su13094803
Chicago/Turabian StyleHell, Marko, and Lidija Petrić. 2021. "System Dynamics Approach to TALC Modeling" Sustainability 13, no. 9: 4803. https://doi.org/10.3390/su13094803
APA StyleHell, M., & Petrić, L. (2021). System Dynamics Approach to TALC Modeling. Sustainability, 13(9), 4803. https://doi.org/10.3390/su13094803






