A Trial-and-Error Toll Design Method for Traffic Congestion Mitigation on Large River-Crossing Channels in a Megacity
Abstract
1. Introduction
2. Literature Review
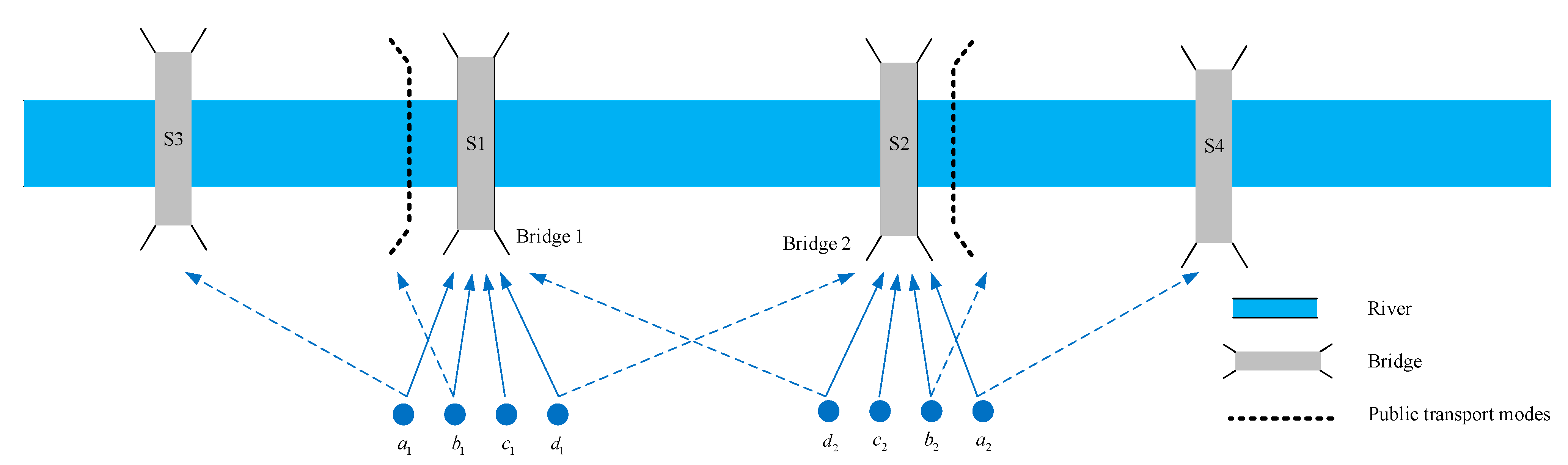
3. Problem Statement
3.1. Demand Function
3.2. Mathematical Model
4. The Trial-and-Error Toll Design Method
| Algorithm 1: A trial-and-error algorithm | |
| 1 | Set the iteration counter . Set the initial upper |
| bound of and , i.e., and . Let and denote the adjusted lower and upper bound of in th iteration. Let and denote the adjusted lower and upper bound of in th iteration. Set , , , . Set the error gap . | |
| 2 | Adjust the tolls with the following formula: |
| 3 | Observe the and . If , , the Pareto-optimal solution has obtained. |
| 4 | Remove the infeasible region according to the observed and and update the lower and upper bound , , , of and , respectively. |
| 5 | Let . Go back to Step 2. |
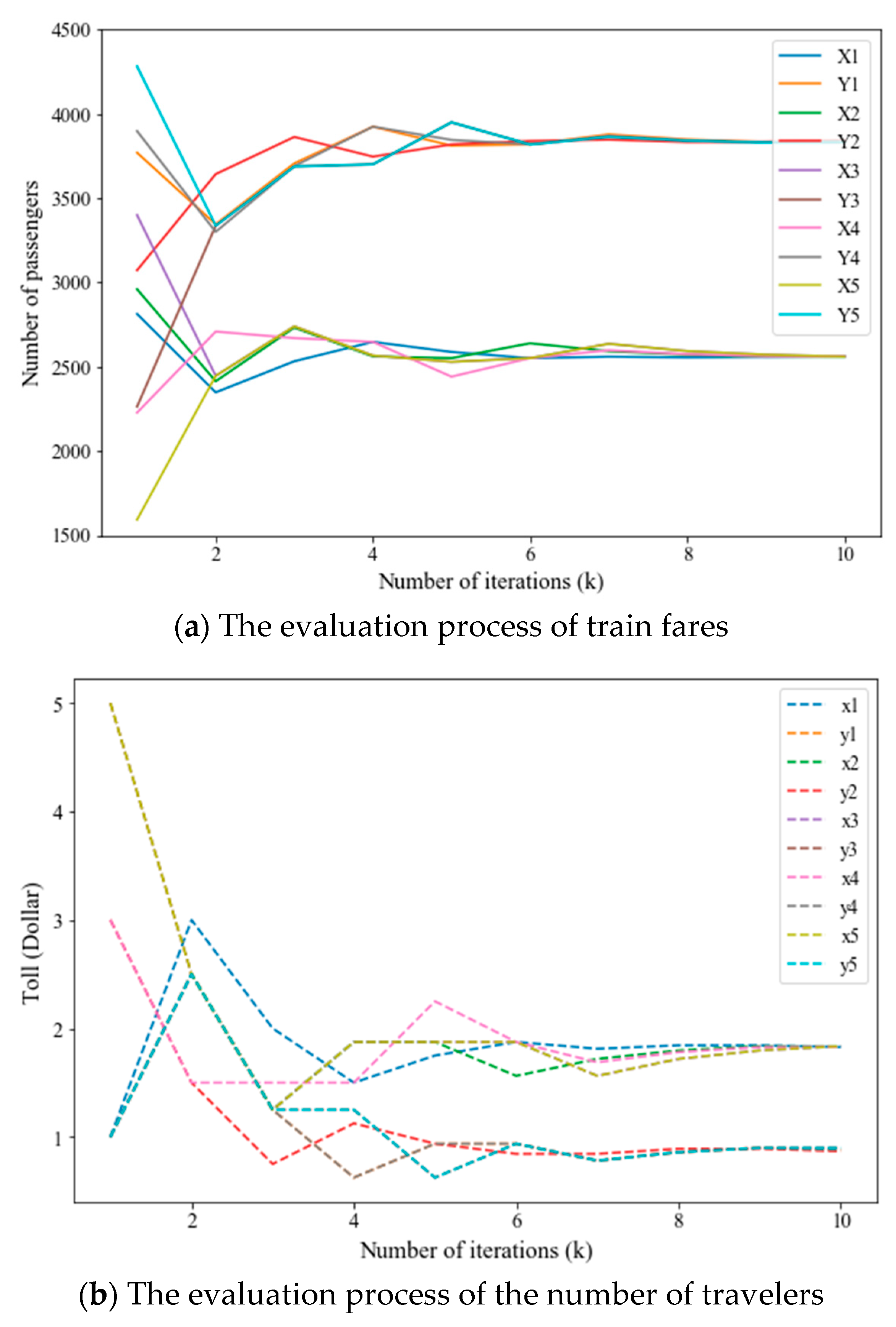
5. Numerical Experiments
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Gu, W. A Sustainable Strategy to Address Traffic Congestion on Nanjing River-Crossing Channels. Available online: http://news.xhby.net/nj/zx/202004/t20200413_6598720.shtml (accessed on 17 January 2021).
- Chen, M. Some Thought of the Traffic Congestion on Nanjing Yangtze River Bridge. Available online: http://m.xinhuanet.com/js/2019-01/07/c_1123953980.htm (accessed on 17 January 2021).
- Wang, S.; Zhang, W.; Qu, X. Trial-and-error train fare design scheme for addressing boarding/alighting congestion at CBD stations. Transp. Res. Part B Methodol. 2018, 118, 318–335. [Google Scholar] [CrossRef]
- Liu, J.; Wang, R. Daily Traffic Volume is Keeping Increasing on the Nanjing Yangtze River Bridge. Available online: http://js.people.com.cn/n2/2020/0930/c360302-34327756.html (accessed on 17 January 2021).
- Chen, X.; Kim, I. Modelling rail-based park and ride with environmental constraints in a multimodal transport network. J. Adv. Transp. 2018, 2018, 15. [Google Scholar] [CrossRef]
- Chen, X.; Liu, Z.; Currie, G. Optimizing location and capacity of rail-based Park-and-Ride sites to increase public transport usage. Transp. Plan. Technol. 2016, 39, 507–526. [Google Scholar] [CrossRef]
- Liu, Z.; Chen, X.; Meng, Q.; Kim, I. Remote park-and-ride network equilibrium model and its applications. Transp. Res. Part B Methodol. 2018, 117, 37–62. [Google Scholar] [CrossRef]
- Huang, D.; Chen, X.; Liu, Z.; Lyu, C.; Wang, S.; Chen, X. A static bike repositioning model in a hub-and-spoke network framework. Transp. Res. Part E Logist. Transp. Rev. 2020, 141, 102031. [Google Scholar] [CrossRef]
- Huang, D.; Gu, Y.; Wang, S.; Liu, Z.; Zhang, W. A two-phase optimization model for the demand-responsive customized bus network design. Transp. Res. Part C Emerg. Technol. 2020, 111, 1–21. [Google Scholar] [CrossRef]
- Cheng, Q.; Liu, Z.; Szeto, W.Y. A cell-based dynamic congestion pricing scheme considering travel distance and time delay. Transp. B Transp. Dyn. 2019, 7, 1286–1304. [Google Scholar] [CrossRef]
- Liu, Z.; Meng, Q. Bus-based park-and-ride system: A stochastic model on multimodal network with congestion pricing schemes. Int. J. Syst. Sci. 2014, 45, 994–1006. [Google Scholar] [CrossRef]
- Liu, Z.; Meng, Q.; Wang, S. Speed-based toll design for cordon-based congestion pricing scheme. Transp. Res. Part C Emerg. Technol. 2013, 31, 83–98. [Google Scholar] [CrossRef]
- Liu, Z.; Meng, Q.; Wang, S. Variational inequality model for cordon-based congestion pricing under side constrained stochastic user equilibrium conditions. Transp. A Transp. Sci. 2014, 10, 693–704. [Google Scholar] [CrossRef]
- Liu, Z.; Wang, S.; Meng, Q. Optimal joint distance and time toll for cordon-based congestion pricing. Transp. Res. Part B Methodol. 2014, 69, 81–97. [Google Scholar] [CrossRef]
- Liu, Z.; Wang, S.; Zhou, B.; Cheng, Q. Robust optimization of distance-based tolls in a network considering stochastic day to day dynamics. Transp. Res. Part C Emerg. Technol. 2017, 79, 58–72. [Google Scholar] [CrossRef]
- Liu, Z.; Zhang, Y.; Wang, S.; Li, Z. A trial-and-error method with autonomous vehicle-to-infrastructure traffic counts for cordon-based congestion pricing. J. Adv. Transp. 2017, 2017, 9243039. [Google Scholar] [CrossRef]
- Meng, Q.; Liu, Z. Impact analysis of cordon-based congestion pricing on mode-split for a bimodal transportation network. Transp. Res. Part C Emerg. Technol. 2012, 21, 134–147. [Google Scholar] [CrossRef]
- Meng, Q.; Liu, Z. Trial-and-error method for congestion pricing scheme under side-constrained probit-based stochastic user equilibrium conditions. Transportation 2011, 38, 819–843. [Google Scholar] [CrossRef]
- Meng, Q.; Liu, Z.; Wang, S. Optimal distance tolls under congestion pricing and continuously distributed value of time. Transp. Res. Part E Logist. Transp. Rev. 2012, 48, 937–957. [Google Scholar] [CrossRef]
- Vickrey, W.S. Point of view: Principles and applications of congestion pricing. TR News 1993, 167, 4–5. [Google Scholar]
- Downs, A. Point of view: Implementing peak-hour road pricing at fullscale: Finding solutions to practical problems. TR News 1993, 167, 7–9. [Google Scholar]
- Li, M.Z.F. The role of speed-flow relationship in congestion pricing implementation with an application to Singapore. Transp. Res. Part B Methodol. 2002, 36, 731–754. [Google Scholar] [CrossRef]
- Yang, H.; Meng, Q.; Lee, D. Trial-and-error implementation of marginal-cost pricing on networks in the absence of demand functions. Transp. Res. Part B Methodol. 2004, 38, 477–493. [Google Scholar] [CrossRef]
- Yang, H.; Xu, W.; Meng, Q. A sequential experimental approach for analyzing second-best road pricing with unknown demand functions. In Proceedings of the 16th International Symposium on Transportation and Traffic Theory, College Park, MD, USA, 19–21 July 2005. [Google Scholar]
- Zhao, Y.; Kockelman, K.M. On-line marginal-cost pricing across networks: Incorporating heterogeneous users and stochastic equilibria. Transp. Res. Part B Methodol. 2006, 40, 424–435. [Google Scholar] [CrossRef]
- Han, D.; Yang, H. Congestion pricing in the absence of demand functions. Transp. Res. Part E Logist. Transp. Rev. 2009, 45, 159–171. [Google Scholar] [CrossRef]
- Xu, W.; Yang, H.; Han, D. Sequential experimental approach for congestion pricing with multiple vehicle types and multiple time periods. Transp. B Transp. Dyn. 2013, 1, 136–152. [Google Scholar] [CrossRef]
- Meng, Q.; Xu, W.; Yang, H. Trial-and-error procedure for implementing a road-pricing scheme. Transp. Res. Rec. 2005, 1923, 103–109. [Google Scholar] [CrossRef]
- Yang, H.; Xu, W.; He, B.S.; Meng, Q. Road pricing for congestion control with unknown demand and cost functions. Transp. Res. Part C Emerg. Technol. 2010, 18, 157–175. [Google Scholar] [CrossRef]
- Han, D.; Xu, W.; Yang, H. Solving a class of variational inequalities with inexact oracle operators. Math. Methods Oper. Res. 2010, 71, 427–452. [Google Scholar] [CrossRef]
- Zhou, B.; Bliemer, M.; Yang, H.; He, J. A trial-and-error congestion pricing scheme for networks with elastic demand and link capacity constraints. Transp. Res. Part B Methodol. 2015, 72, 77–92. [Google Scholar] [CrossRef]
- Ye, H.; Yang, H.; Tan, Z. Learning marginal-cost pricing via a trial-and-error procedure with day-to-day flow dynamics. Transp. Res. Part B Methodol. 2015, 81, 794–807. [Google Scholar] [CrossRef]
- Guo, R.Y.; Yang, H.; Huang, H.J.; Tan, Z. Link-based day-to-day network traffic dynamics and equilibria. Transp. Res. Part B Methodol. 2015, 71, 248–260. [Google Scholar] [CrossRef]
- Xu, M.; Meng, Q.; Huang, Z. Global convergence of the trial-and-error method for the traffic-restraint congestion-pricing scheme with day-to-day flow dynamics. Transp. Res. Part C Emerg. Technol. 2016, 69, 276–290. [Google Scholar] [CrossRef]
- Zhou, B.; Xu, M.; Zhang, Y. A trial-and-error congestion pricing method for day-to-day dynamic network flows considering travelers’ heterogeneous inertia patterns. Math. Probl. Eng. 2019, 2019, 8514765. [Google Scholar] [CrossRef]
| Potential Cases (Infeasible Regions Are Indicated by the Shadow Segment) | |
|---|---|
(i) , , .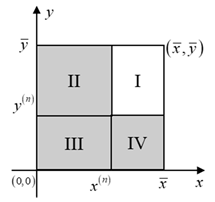 | (ii) , , .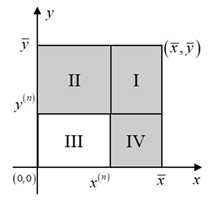 |
(iii) , , .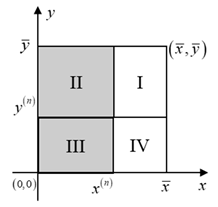 | (iv) , , .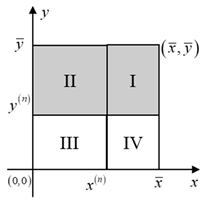 |
(v) , , . | (vi) , , .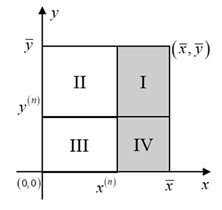 |
| Unknown Demand Functions: |
|---|
| , . , . , . , . |
| Case | |||||||||
|---|---|---|---|---|---|---|---|---|---|
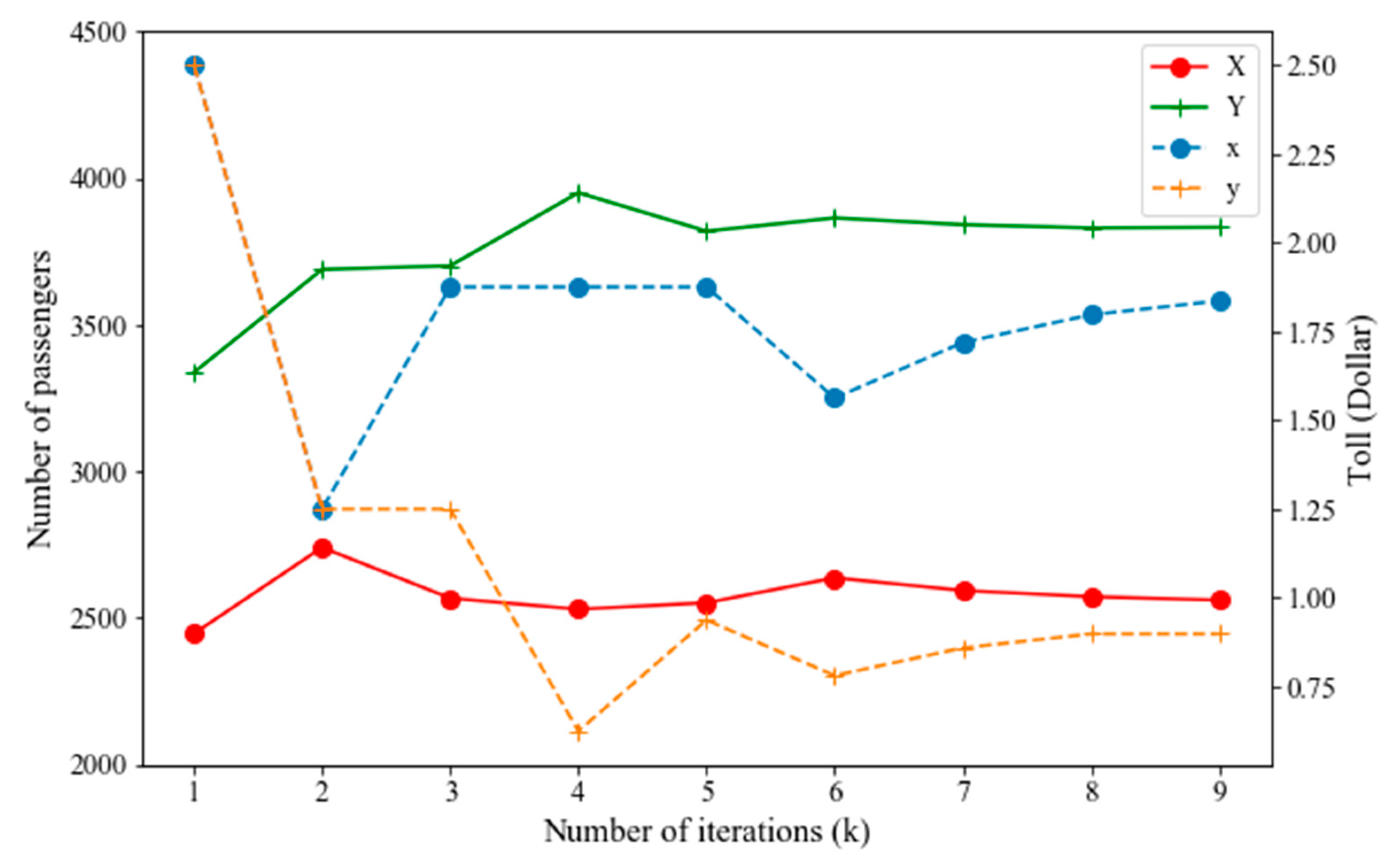
| 1 | 2.5 | 2.5 | 2446.19 | 3337.32 | 0.0 | 2.5 | 0.0 | 2.0 | (ii) |
| 2 | 1.25 | 1.25 | 2740.21 | 3688.75 | 1.25 | 2.5 | 0.0 | 2.5 | (iii) |
| 3 | 1.25 | 1.25 | 2566.96 | 3701.25 | 1.25 | 2.5 | 0.0 | 1.25 | (vi) |
| 4 | 1.875 | 0.625 | 2529.46 | 3950.29 | 1.25 | 2.5 | 0.625 | 1.25 | (v) |
| 5 | 1.875 | 0.9375 | 2551.33 | 3819.34 | 1.25 | 1.875 | 0.625 | 0.9375 | (ii) |
| 6 | 1.875 | 0.78125 | 2636.54 | 3864.43 | 1.5625 | 1.875 | 0.78125 | 0.9375 | (i) |
| 7 | 1.5625 | 0.859375 | 2593.23 | 3841.48 | 1.71785 | 1.875 | 0.859275 | 0.9375 | (i) |
| 8 | 1.71875 | 0.8984375 | 2572.11 | 3830.31 | 1.796875 | 1.875 | 0.859375 | 0.9375 | (iii) |
| 9 | 1.796875 | 0.8984375 | 2560.52 | 3832.60 | 1.796875 | 1.875 | 0.859375 | 0.8984375 | (vi) |
| Case | |||||||||
|---|---|---|---|---|---|---|---|---|---|
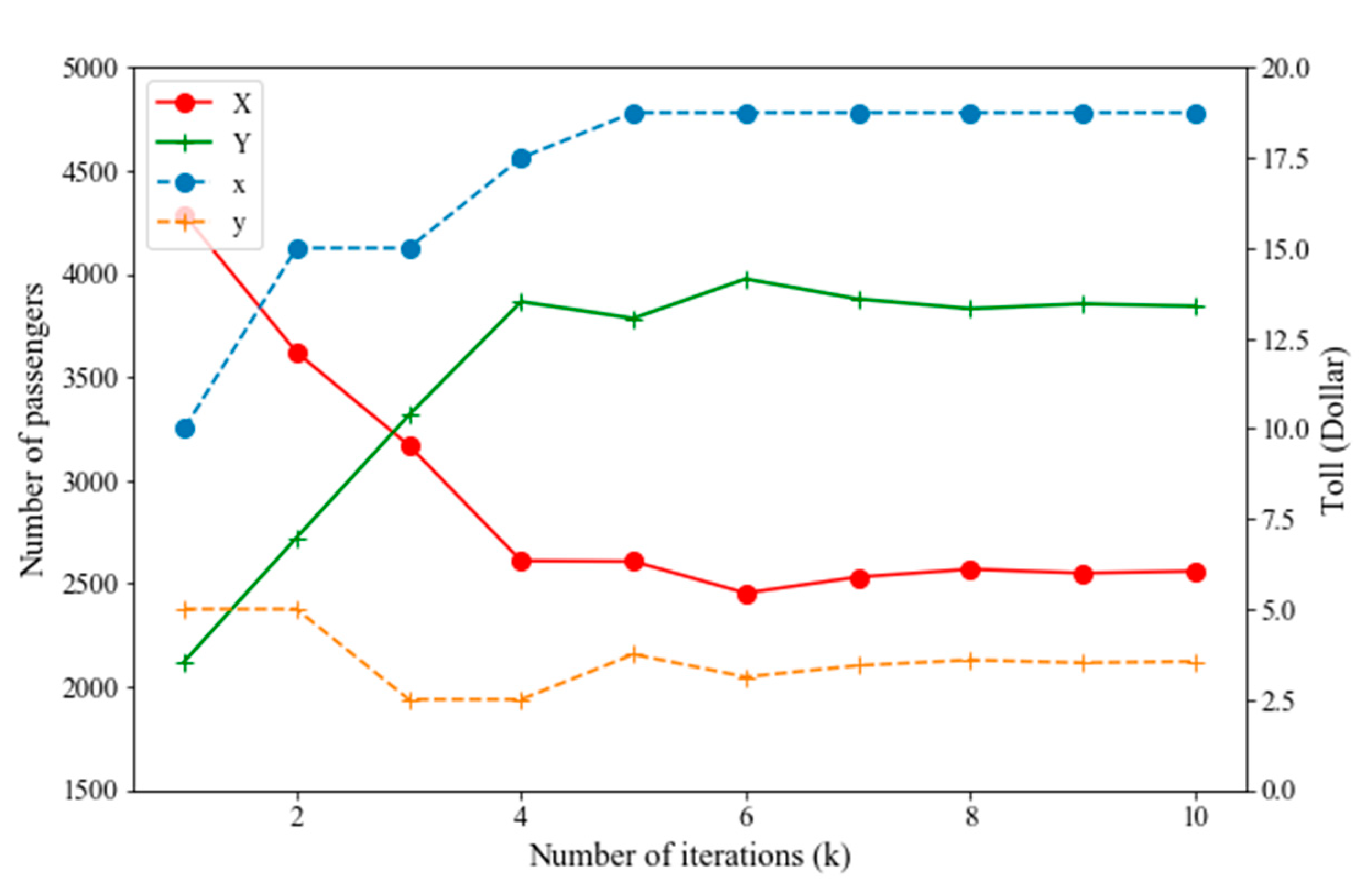
| 1 | 10 | 5 | 4286.62 | 2121.46 | 10.0 | 20.0 | 0.0 | 10.0 | (iii) |
| 2 | 15 | 5 | 3619.32 | 2721.46 | 10.0 | 20.0 | 0.0 | 5.0 | (vi) |
| 3 | 15 | 2.5 | 3169.32 | 3315.13 | 15.0 | 20.0 | 0.0 | 5.0 | (iii) |
| 4 | 17.5 | 2.5 | 2609.13 | 3865.13 | 17.5 | 20.0 | 2.5 | 5.0 | (i) |
| 5 | 18.75 | 3.75 | 2606.27 | 3784.36 | 17.5 | 20.0 | 2.5 | 3.125 | (vi) |
| 6 | 18.75 | 3.125 | 2453.15 | 3975.35 | 17.5 | 20.0 | 3.125 | 3.75 | (v) |
| 7 | 18.75 | 3.4375 | 2530.49 | 3875.48 | 17.5 | 20.0 | 3.4375 | 3.75 | (v) |
| 8 | 18.75 | 3.59375 | 2568.58 | 3831.08 | 17.5 | 20.0 | 3.4375 | 3.59375 | (vi) |
| 9 | 18.75 | 3.515625 | 2549.58 | 3854.70 | 17.5 | 20.0 | 3.515625 | 3.59375 | (v) |
| 10 | 18.75 | 3.5546875 | 2559.09 | 3842.87 | 17.5 | 20.0 | 3.5546875 | 3.59375 | (v) |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, X.; Wang, Y.; Zhang, Y. A Trial-and-Error Toll Design Method for Traffic Congestion Mitigation on Large River-Crossing Channels in a Megacity. Sustainability 2021, 13, 2749. https://doi.org/10.3390/su13052749
Chen X, Wang Y, Zhang Y. A Trial-and-Error Toll Design Method for Traffic Congestion Mitigation on Large River-Crossing Channels in a Megacity. Sustainability. 2021; 13(5):2749. https://doi.org/10.3390/su13052749
Chicago/Turabian StyleChen, Xinyuan, Yiran Wang, and Yuan Zhang. 2021. "A Trial-and-Error Toll Design Method for Traffic Congestion Mitigation on Large River-Crossing Channels in a Megacity" Sustainability 13, no. 5: 2749. https://doi.org/10.3390/su13052749
APA StyleChen, X., Wang, Y., & Zhang, Y. (2021). A Trial-and-Error Toll Design Method for Traffic Congestion Mitigation on Large River-Crossing Channels in a Megacity. Sustainability, 13(5), 2749. https://doi.org/10.3390/su13052749





