Latent Heat Thermal Storage in Non-Uniform Metal Foam Filled with Nano-Enhanced Phase Change Material
Abstract
:1. Introduction
2. Mathematical Model
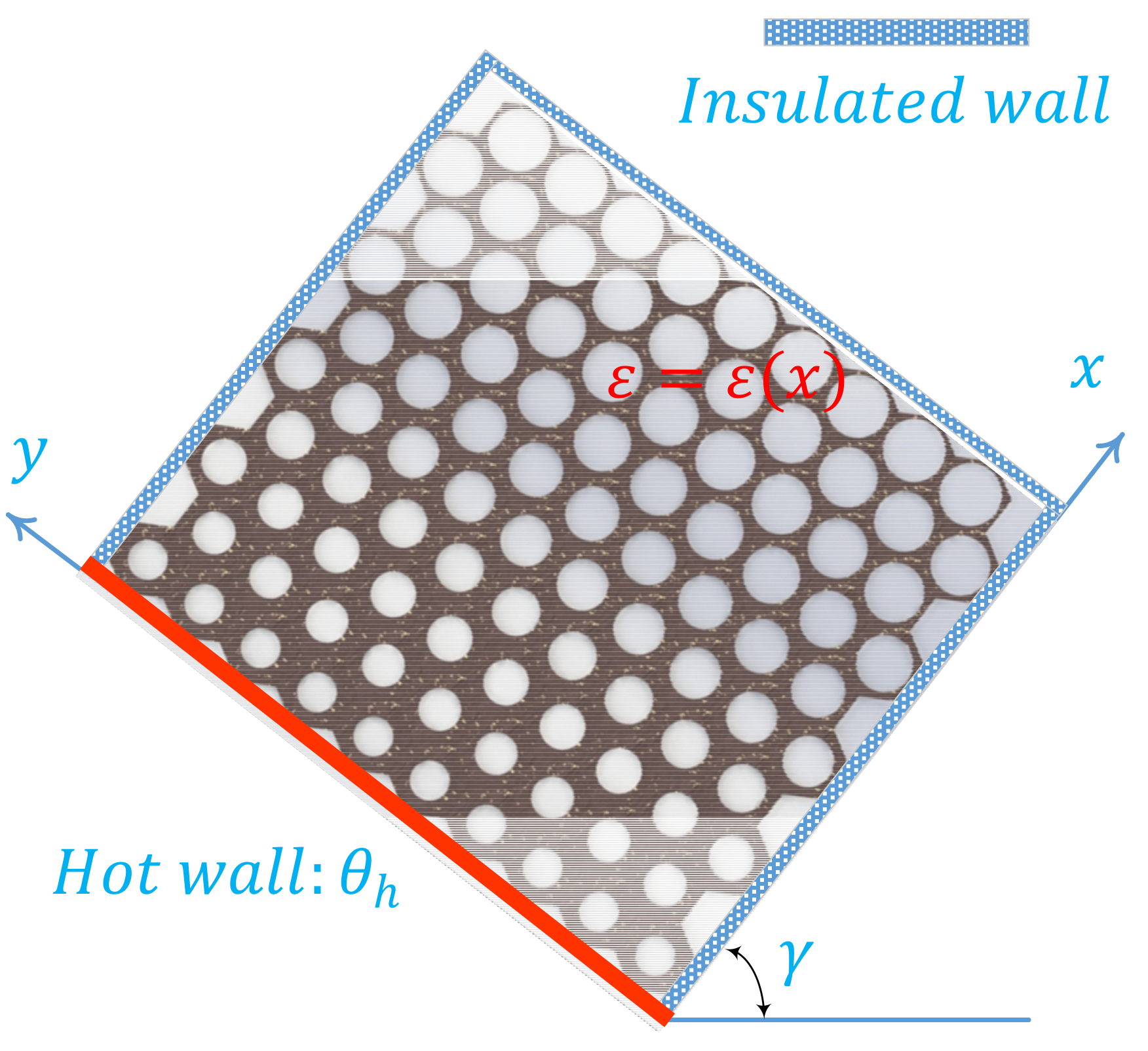
2.1. Physical Model
2.2. Convective Phase Change Heat Transfer in NePCM
2.3. NePCM Thermo-Physical Properties
2.4. Model Conditions
2.5. Characteristics Parameters
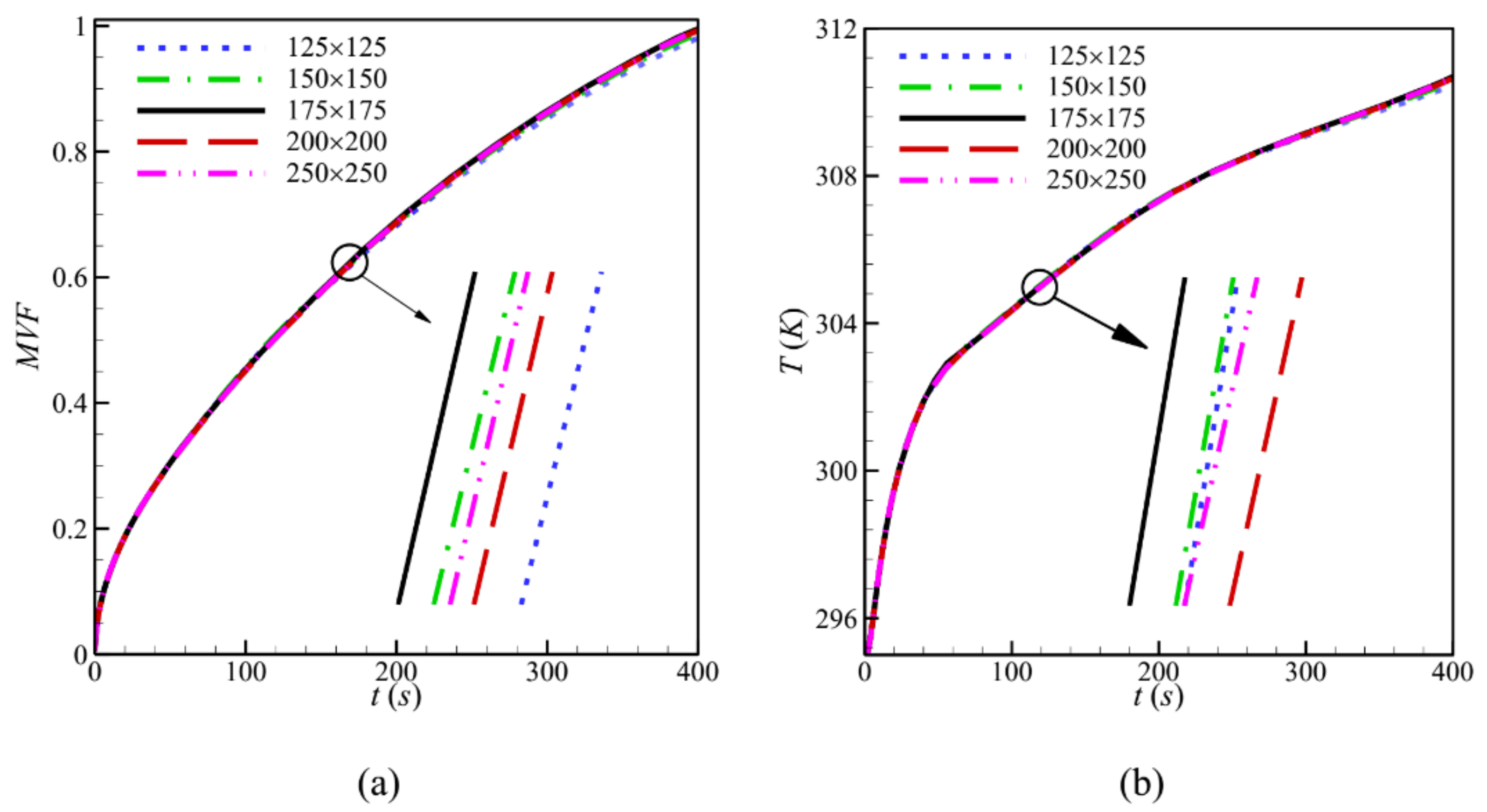
3. Numerical Approach and Grid Dependency
4. Results and Discussion
5. Conclusions
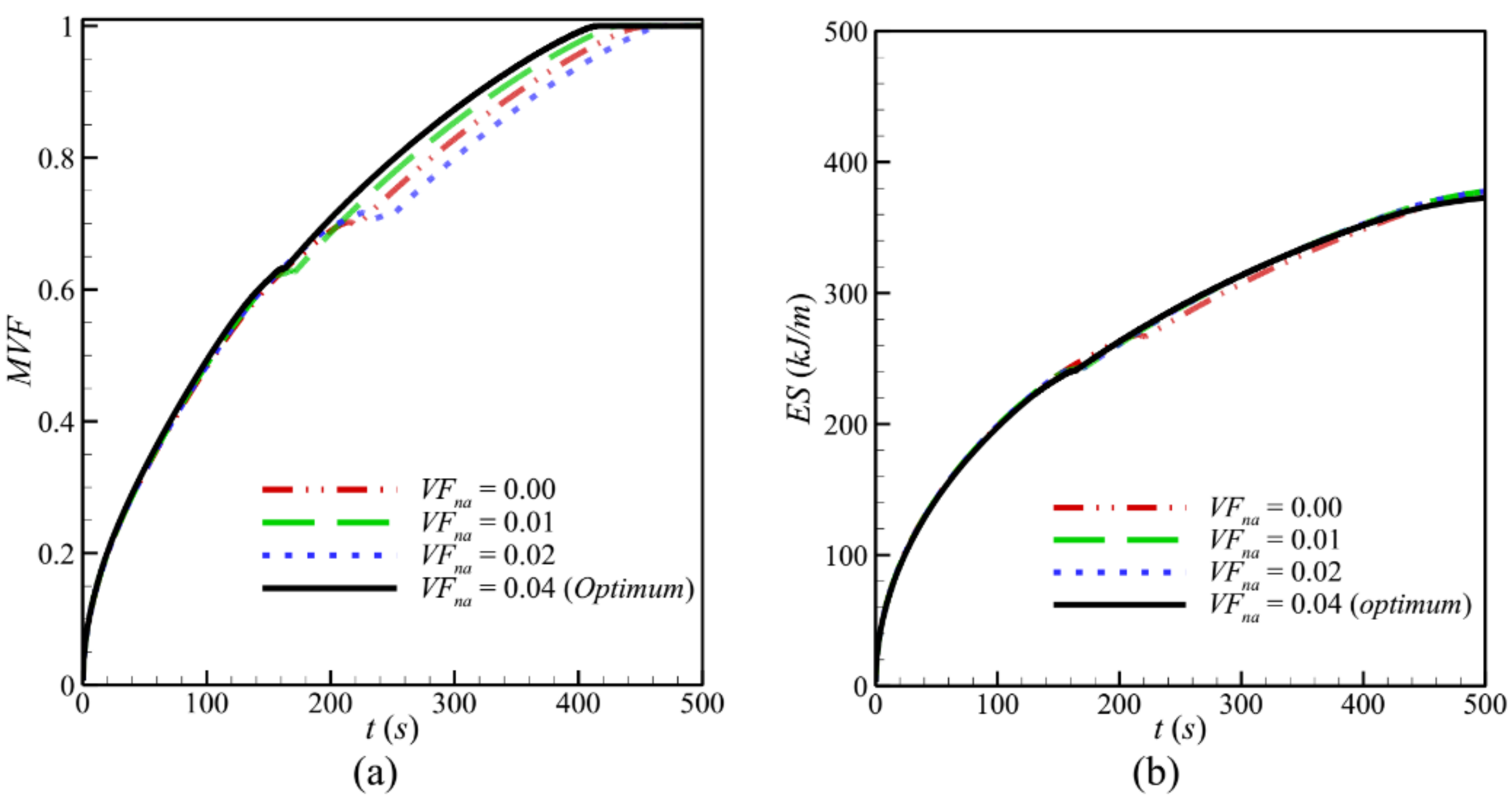
- Increasing the volume fraction of the nanoparticles improves the effective thermal conductivity of PCM, which enhances heat transfer and accelerates PCM melting. The value that leads to the fastest melting and maximum charging power P is VFna = 0.04.
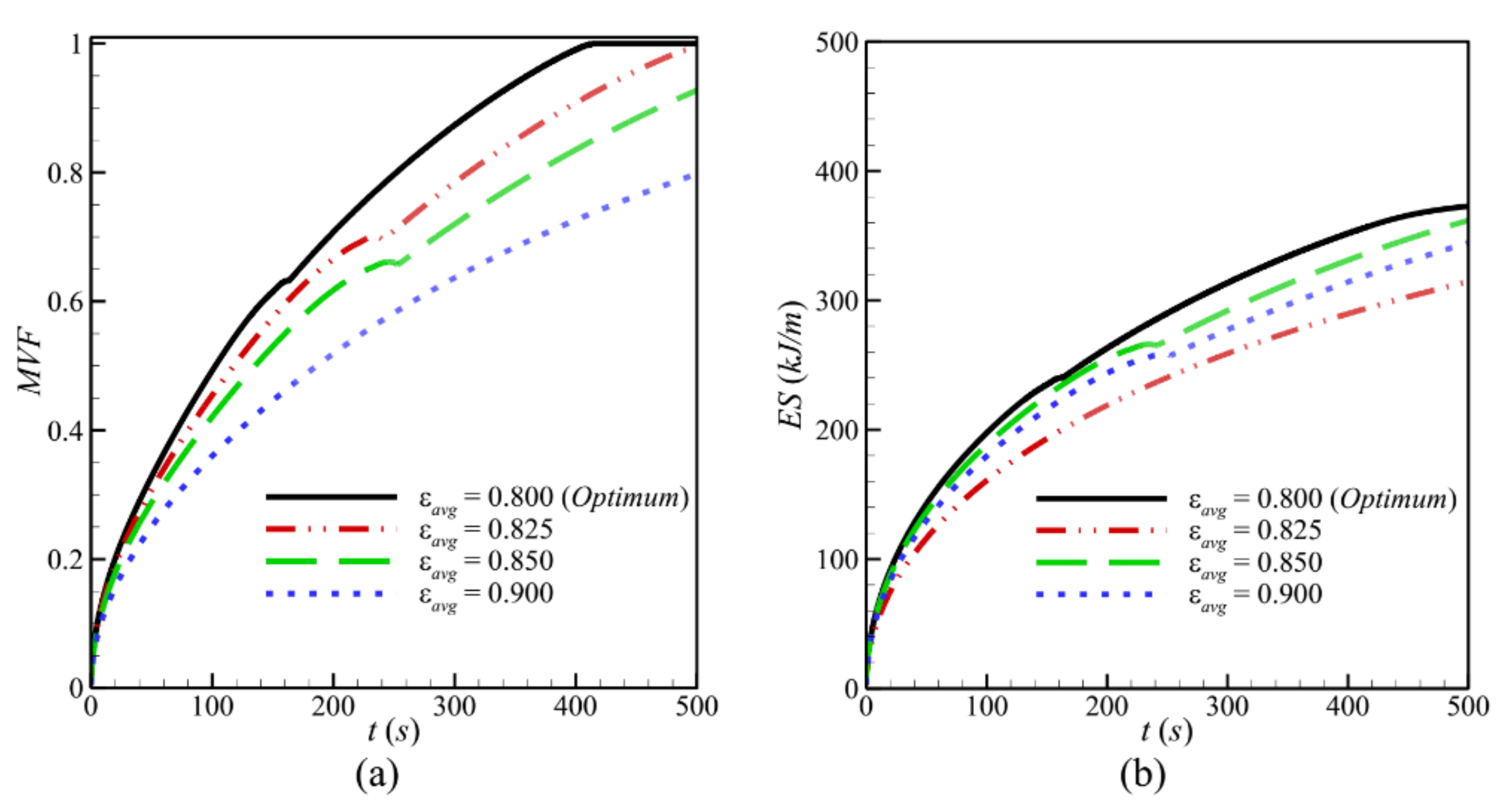
- Reducing the average porosity εavg of metal foam increased the volume of the metallic matrix and resulted in higher thermal conductivity. This led to faster PCM melting and higher stored energy and charging power. The lowest melting duration was obtained for εavg = 0.8.
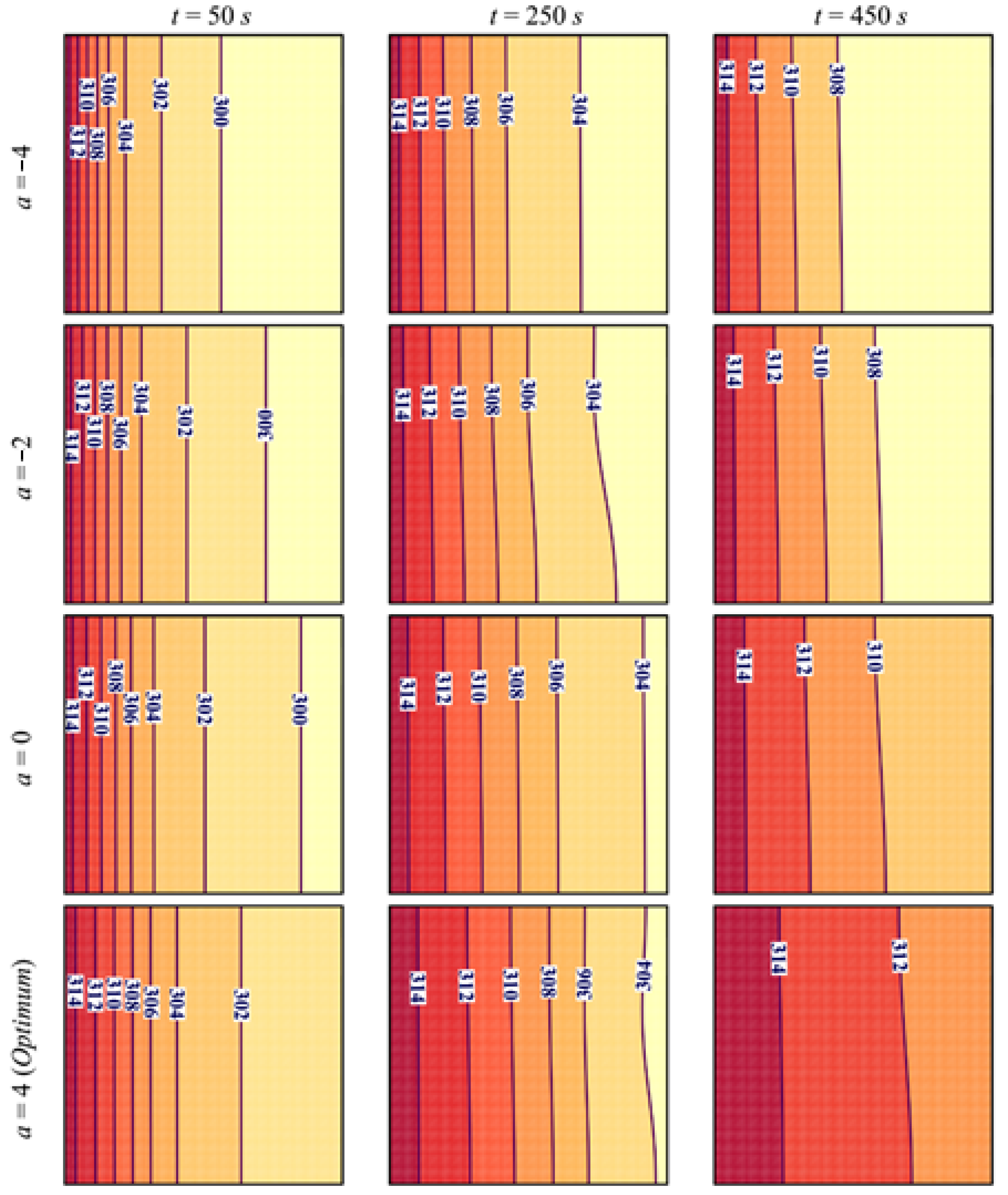
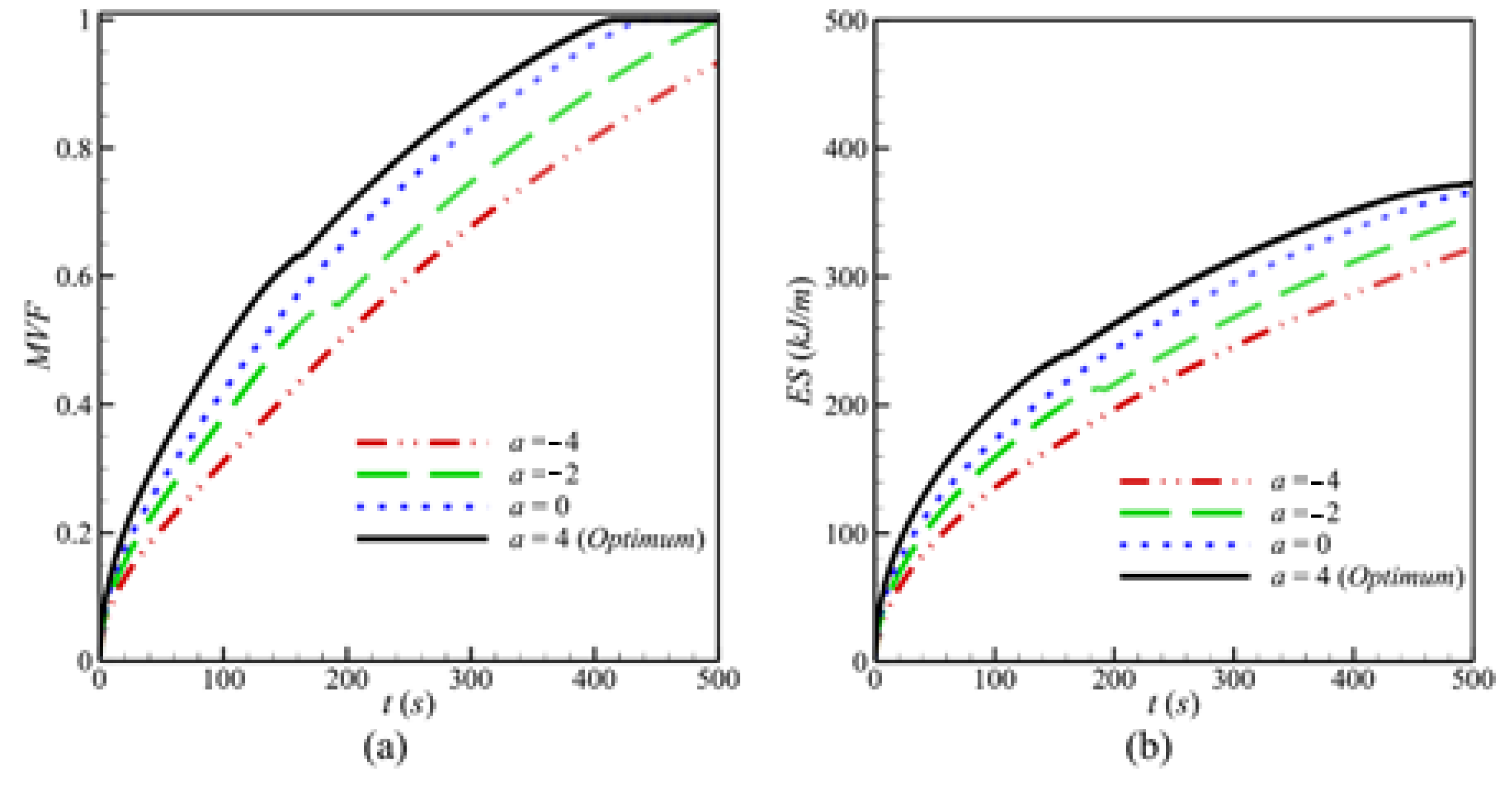
- At a constant average porosity, using a higher positive porosity gradient a, defined from the left hot wall toward the right, enhances conductive heat transfer near the left region with low porosity in initial stages and the convective heat transfer in the right side of the cavity in the final stages. The opposite occurs when lower and negative values of a are used. Melting duration is minimized for a = 4.
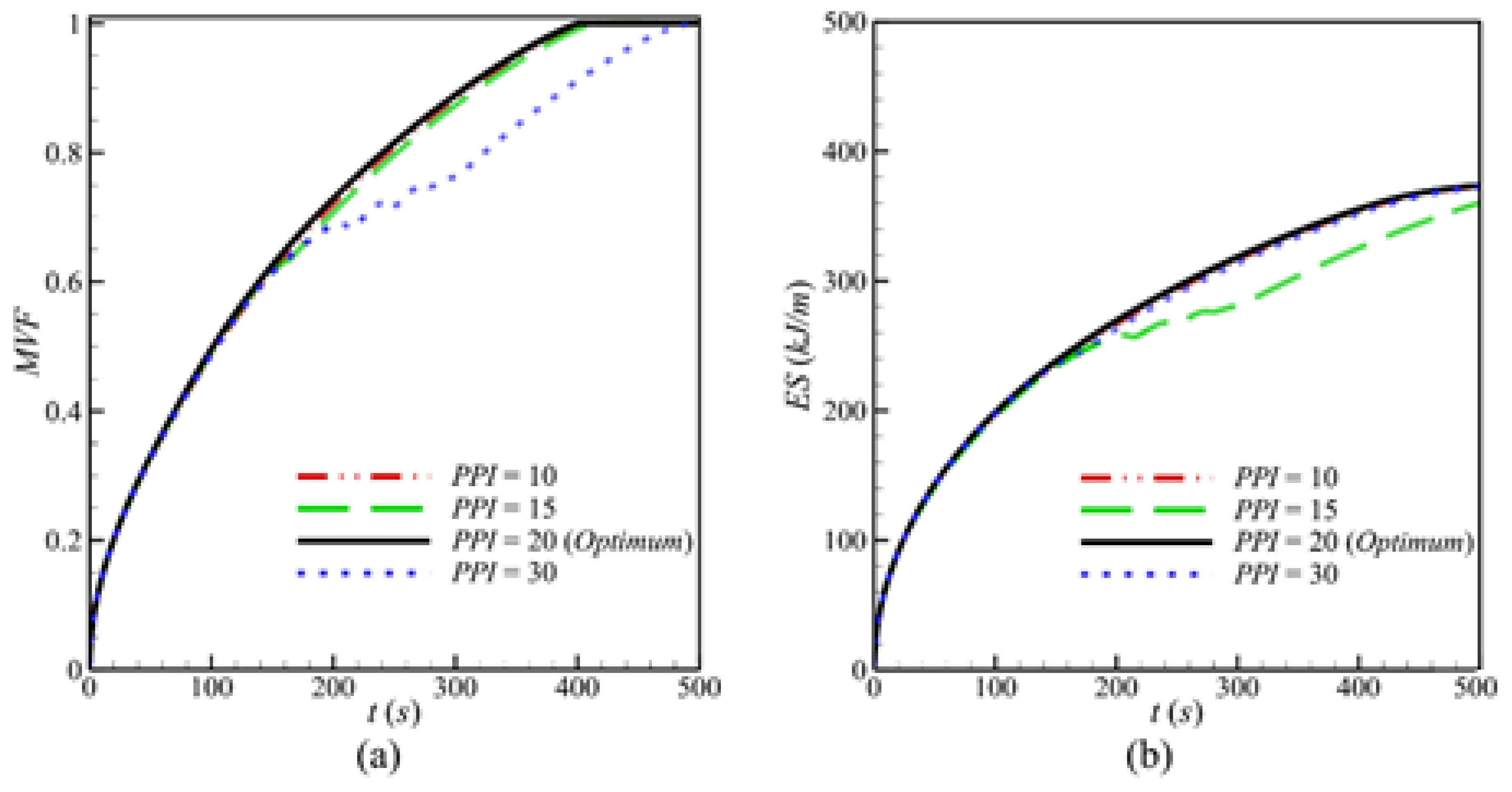
- Raising the PPI presents two effects. First, it reduces the thickness of the solid matrix, which diminishes effective thermal conductivity. Second, it increases surface contact and improves the heat transfer between metal foam and PCM. The balance between these two effects leads to a slight overall impact of PPI on the charging power.
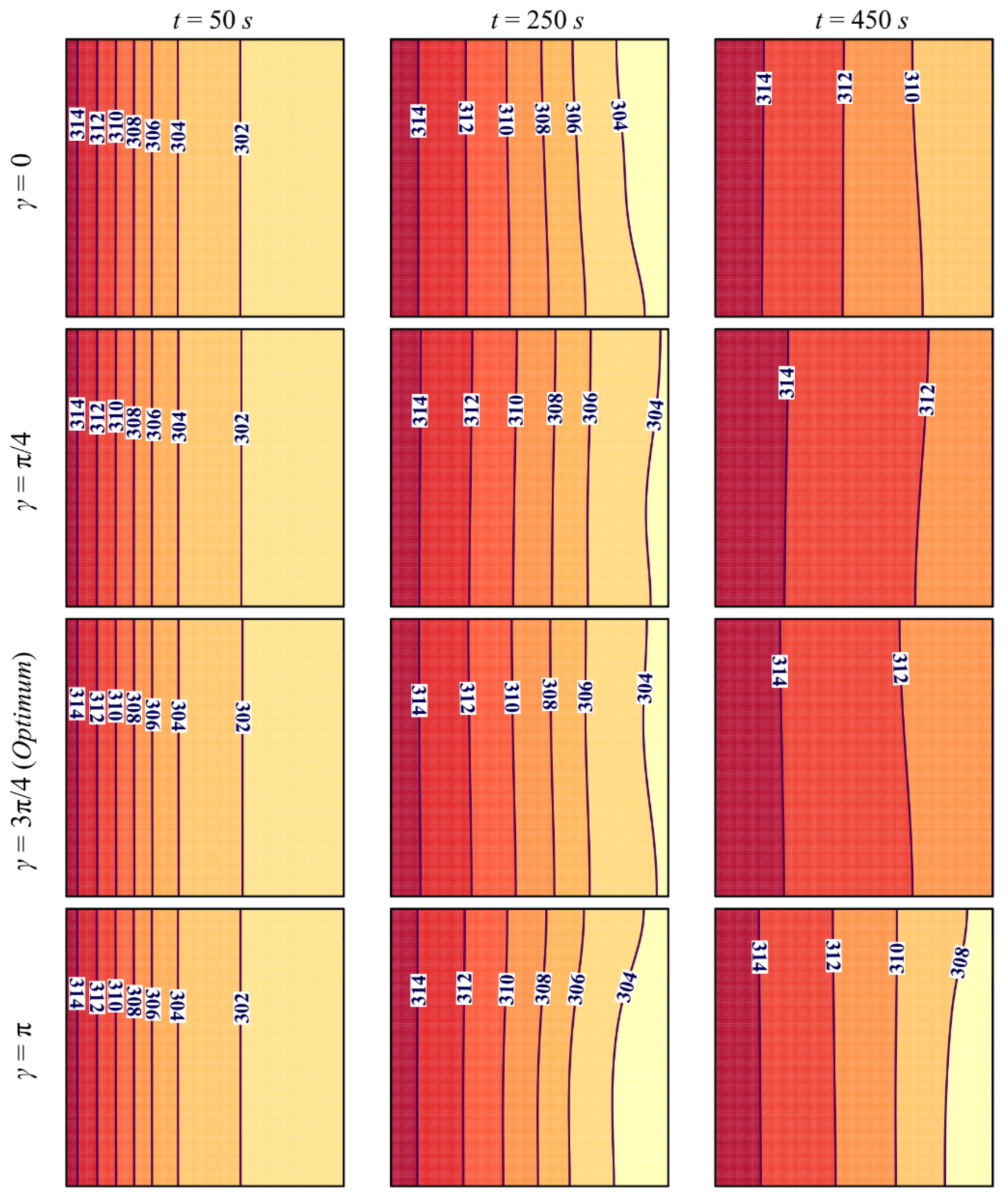
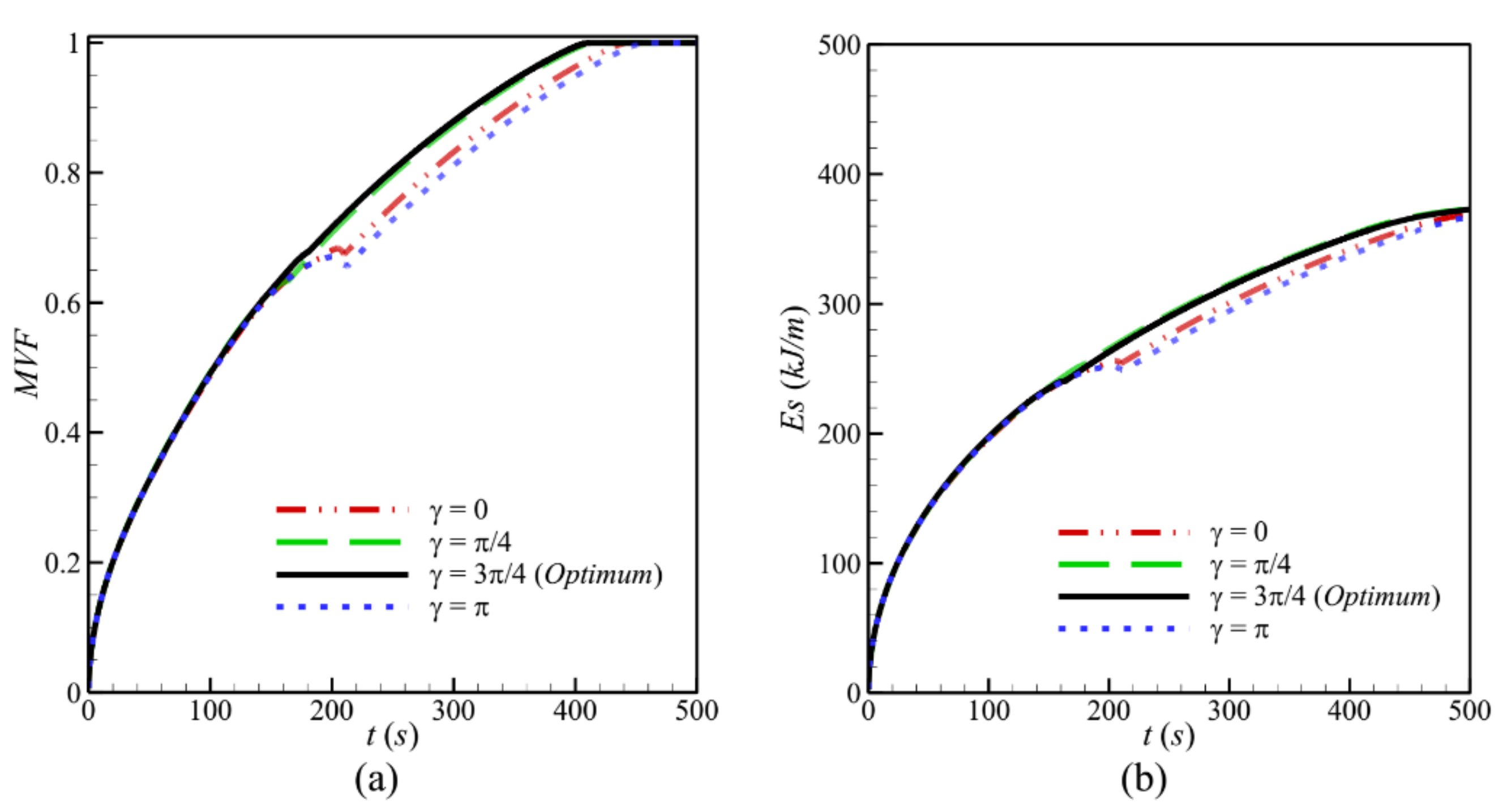
- Tilting the cavity has a limited effect on the flow and thermal behavior of NePCM, mainly in the initial stages. This effect becomes more apparent when the convective heat transfer starts taking place, and the charging power can be improved when the inclination angle is γ = π/4 or γ = 3π/4 compared with the cases of γ = 0 and γ = π.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Nomenclature
| Latin Symbols | |
| a | slope of porosity |
| Amush | mushy constant (kg m−3 s−1) |
| b | constant parameter |
| cp | heat capacity (J kg−1 K−1) |
| Dl | fiber diameter (m) |
| Dp | pore diameter (m) |
| F | mushy source term (kg m−3 s−1) |
| gravity acceleration vector (m s−2) | |
| hf | latent heat (kJ kg−1) |
| I | identity matrix |
| L | length of the domian (m) |
| MVF | normalized liquid fraction |
| n | surface normal |
| p | pressure (Pa) |
| PPI | pore density (pore per inch) |
| t | time (s) |
| TU | temperature uniformity index (K) |
| velocity vector (m s−1) | |
| VFna | volume fraction of nanoadditives |
| W | width of the domain (m) |
| x | x-axis (m) |
| y | y-axis (m) |
| Greek Symbols | |
| β | thermal expansion coefficient of liquid PCM (K−1) |
| γ | inclination angle (rad) |
| liquid fraction | |
| Γ | a small value |
| Δθmel | melting temperature range of PCM (K) |
| ε | porosity |
| θ | temperature (K) |
| ι | dummy variable for Equation (8) |
| κ | permeability (m2) |
| λ | thermal conductivity (W m−1 K−1) |
| μ | dynamic viscosity (Pa s) |
| ρ | density (kg m−3) |
| Subscripts | |
| ave | average |
| eff | effective properties of the PCM and metal foam |
| initial | initial condition |
| l | PCM in liquid state |
| mel | melting |
| mf | metal foam |
| na | nanoadditives |
| npcm | nano-enhanced phase change material |
| pcm | phase change material |
| s | PCM in solid state |
| Superscript | |
| T | Transpose of matrix |
References
- Sharma, A.; Tyagi, V.V.; Chen, C.; Buddhi, D. Review on thermal energy storage with phase change materials and applications. Renew. Sustain. Energy Rev. 2009, 13, 318–345. [Google Scholar] [CrossRef]
- Fan, L.; Khodadadi, J.M. Thermal conductivity enhancement of phase change materials for thermal energy storage: A review. Renew. Sustain. Energy Rev. 2011, 15, 24–46. [Google Scholar] [CrossRef]
- Agyenim, F.; Hewitt, N.; Eames, P.; Smyth, M. A review of materials, heat transfer and phase change problem formulation for latent heat thermal energy storage systems (LHTESS). Renew. Sustain. Energy Rev. 2010, 14, 615–628. [Google Scholar] [CrossRef]
- Sharifi, N.; Bergman, T.L.; Faghri, A. Enhancement of PCM melting in enclosures with horizontally-finned internal surfaces. Int. J. Heat Mass Transf. 2011, 54, 4182–4192. [Google Scholar] [CrossRef]
- Sciacovelli, A.; Gagliardi, F.; Verda, V. Maximization of performance of a PCM latent heat storage system with innovative fins. Appl. Energy 2015, 137, 707–715. [Google Scholar] [CrossRef]
- Kurnia, J.C.; Sasmito, A.P.; Jangam, S.V.; Mujumdar, A.S. Improved design for heat transfer performance of a novel phase change material (PCM) thermal energy storage (TES). Appl. Therm. Eng. 2013, 50, 896–907. [Google Scholar] [CrossRef]
- Raul, A.; Jain, M.; Gaikwad, S.; Saha, S.K. Modelling and experimental study of latent heat thermal energy storage with encapsulated PCMs for solar thermal applications. Appl. Therm. Eng. 2018, 143, 415–428. [Google Scholar] [CrossRef]
- Raj, A.; Srinivas, M.; Jayaraj, S. CFD modeling of macro-encapsulated latent heat storage system used for solar heating applications. Int. J. Therm. Sci. 2019, 139, 88–104. [Google Scholar] [CrossRef]
- Mettawee, E.-B.S.; Assassa, G.M. Thermal conductivity enhancement in a latent heat storage system. Sol. Energy 2007, 81, 839–845. [Google Scholar] [CrossRef]
- Sanusi, O.; Warzoha, R.; Fleischer, A.S. Energy storage and solidification of paraffin phase change material embedded with graphite nanofibers. Int. J. Heat Mass Transf. 2011, 54, 4429–4436. [Google Scholar] [CrossRef]
- Rostami, S.; Afrand, M.; Shahsavar, A.; Sheikholeslami, M.; Kalbasi, R.; Aghakhani, S.; Shadloo, M.S.; Oztop, H.F. A review of melting and freezing processes of PCM/nano-PCM and their application in energy storage. Energy 2020, 211, 118698. [Google Scholar] [CrossRef]
- Frusteri, F.; Leonardi, V.; Vasta, S.; Restuccia, G. Thermal conductivity measurement of a PCM based storage system containing carbon fibers. Appl. Therm. Eng. 2005, 25, 1623–1633. [Google Scholar] [CrossRef]
- Mesalhy, O.; Lafdi, K.; Elgafy, A.; Bowman, K. Numerical study for enhancing the thermal conductivity of phase change material (PCM) storage using high thermal conductivity porous matrix. Energy Convers. Manag. 2005, 46, 847–867. [Google Scholar] [CrossRef]
- Ebadi, S.; Tasnim, S.H.; Aliabadi, A.A.; Mahmud, S. An experimental investigation of the charging process of thermal energy storage system filled with PCM and metal wire mesh. Appl. Therm. Eng. 2020, 115266. [Google Scholar] [CrossRef]
- Gopalan, K.S.; Eswaran, V. Numerical investigation of thermal performance of PCM based heat sink using structured porous media as thermal conductivity enhancers. Int. J. Therm. Sci. 2016, 104, 266–280. [Google Scholar] [CrossRef]
- Liu, Z.; Yao, Y.; Wu, H. Numerical modeling for solid–liquid phase change phenomena in porous media: Shell-and-tube type latent heat thermal energy storage. Appl. Energy 2013, 112, 1222–1232. [Google Scholar] [CrossRef]
- Deng, Z.; Liu, X.; Zhang, C.; Huang, Y.; Chen, Y. Melting behaviors of PCM in porous metal foam characterized by fractal geometry. Int. J. Heat Mass Transf. 2017, 113, 1031–1042. [Google Scholar] [CrossRef]
- El Idi, M.M.; Karkri, M. Heating and cooling conditions effects on the kinetic of phase change of PCM embedded in metal foam. Case Stud. Therm. Eng. 2020, 21, 100716. [Google Scholar] [CrossRef]
- Huang, X.; Lin, Y.; Alva, G.; Fang, G. Thermal properties and thermal conductivity enhancement of composite phase change materials using myristyl alcohol/metal foam for solar thermal storage. Sol. Energy Mater. Sol. Cells 2017, 170, 68–76. [Google Scholar] [CrossRef]
- Martinelli, M.; Bentivoglio, F.; Caron-Soupart, A.; Couturier, R.; Fourmigue, J.-F.; Marty, P. Experimental study of a phase change thermal energy storage with copper foam. Appl. Therm. Eng. 2016, 101, 247–261. [Google Scholar] [CrossRef]
- Xiao, X.; Zhang, P.; Li, M. Effective thermal conductivity of open-cell metal foams impregnated with pure paraffin for latent heat storage. Int. J. Therm. Sci. 2014, 81, 94–105. [Google Scholar] [CrossRef]
- Sheikholeslami, M. Numerical modeling of nano enhanced PCM solidification in an enclosure with metallic fin. J. Mol. Liq. 2018, 259, 424–438. [Google Scholar] [CrossRef]
- Kok, B. Examining effects of special heat transfer fins designed for the melting process of PCM and Nano-PCM. Appl. Therm. Eng. 2020, 170, 114989. [Google Scholar] [CrossRef]
- Huu-Quan, D.; Sheremet, M.; Kamel, M.S.; Izadi, M. Investigation of thermal-hydro dynamical behavior on nano-encapsulated PCM suspension: Effect of fin position, fractioning and aspect ratio. Chem. Eng. Process. Process Intensif. 2020, 157, 108122. [Google Scholar] [CrossRef]
- Mahdi, J.M.; Mohammed, H.I.; Hashim, E.T.; Talebizadehsardari, P.; Nsofor, E.C. Solidification enhancement with multiple PCMs, cascaded metal foam and nanoparticles in the shell-and-tube energy storage system. Appl. Energy 2020, 257, 113993. [Google Scholar] [CrossRef]
- Al-Jethelah, M.; Ebadi, S.; Venkateshwar, K.; Tasnim, S.; Mahmud, S.; Dutta, A. Charging nanoparticle enhanced bio-based PCM in open cell metallic foams: An experimental investigation. Appl. Therm. Eng. 2019, 148, 1029–1042. [Google Scholar] [CrossRef]
- Li, Z.; Shahsavar, A.; Al-Rashed, A.A.; Talebizadehsardari, P. Effect of porous medium and nanoparticles presences in a counter-current triple-tube composite porous/nano-PCM system. Appl. Therm. Eng. 2020, 167, 114777. [Google Scholar] [CrossRef]
- Yang, J.; Yang, L.; Xu, C.; Du, X. Numerical analysis on thermal behavior of solid–liquid phase change within copper foam with varying porosity. Int. J. Heat Mass Transf. 2015, 84, 1008–1018. [Google Scholar] [CrossRef]
- Mahdi, J.M.; Nsofor, E.C. Multiple-segment metal foam application in the shell-and-tube PCM thermal energy storage system. J. Energy Storage 2018, 20, 529–541. [Google Scholar] [CrossRef]
- Marri, G.K.; Balaji, C. Experimental and numerical investigations on the effect of porosity and PPI gradients of metal foams on the thermal performance of a composite phase change material heat sink. Int. J. Heat Mass Transf. 2021, 164, 120454. [Google Scholar] [CrossRef]
- Choi, S.-K.; Kim, S.-O.; Lee, T.-H.; Dohee-Hahn. Computation of the natural convection of nanofluid in a square cavity with homogeneous and nonhomogeneous models. Numer. Heat Transf. Part A Appl. 2014, 65, 287–301. [Google Scholar] [CrossRef]
- Nield, D.A.; Bejan, A. Convection in Porous Media; Springer: Berlin/Heidelberg, Germany, 2017. [Google Scholar]
- Ranut, P. On the effective thermal conductivity of aluminum metal foams: Review and improvement of the available empirical and analytical models. Appl. Therm. Eng. 2016, 101, 496–524. [Google Scholar] [CrossRef]
- Zheng, H.; Wang, C.; Liu, Q.; Tian, Z.; Fan, X. Thermal performance of copper foam/paraffin composite phase change material. Energy Convers. Manag. 2018, 157, 372–381. [Google Scholar] [CrossRef]
- Gupta, M.; Singh, V.; Kumar, R.; Said, Z. A review on thermophysical properties of nanofluids and heat transfer applications. Renew. Sustain. Energy Rev. 2017, 74, 638–670. [Google Scholar] [CrossRef]
- Bertrand, O.; Binet, B.; Combeau, H.; Couturier, S.; Delannoy, Y.; Gobin, D.; Lacroix, M.; Le Quéré, P.; Médale, M.; Mencinger, J. Melting driven by natural convection A comparison exercise: First results. Int. J. Therm. Sci. 1999, 38, 5–26. [Google Scholar] [CrossRef]








| Properties | Coconut Oil (Measured) | Metal Foam | CuO Nano Additives | |
|---|---|---|---|---|
| Liquid (32 C) | Solid (15 C) | |||
| Cp (JkgK−1) | 2010 | 3750 | 386 | 540 |
| (kgm−1) | 914 | 920 | 8900 | 6500 |
| k (Wm−1K−1) | 0.166 | 0.228 | 380 | 18 |
| (Nsm−2) | 0.0326 | - | - | - |
| hf (kJkg−1) | 103 | - | - | - |
| Tme (ΔTme) | - | 24 C | - | - |
| Pr | 394.73 | - | - | - |
| Factors | Control Parameters | Level 1 | Level 2 | Level 3 | Level 4 | Level 5 |
|---|---|---|---|---|---|---|
| A | VFna | 0.00 | 0.01 | 0.02 | 0.03 | 0.04 |
| B | εavg | 0.800 | 0.825 | 0.850 | 0.875 | 0.9 |
| C | a | −4 | −2 | 0 | 2 | 4 |
| D | γ | 0 | π/4 | π/2 | 3π/4 | π |
| E | PPI | 10 | 15 | 20 | 25 | 30 |
| Experiment Number | Control Parameters | Time (s) When MVF = 0.9 | ES (kJ/m) | P (kW/m) | ||||
|---|---|---|---|---|---|---|---|---|
| VFna | εavg | a | γ | PPI | ||||
| 1 | 0.00 | 0.800 | −4 | 0 | 10 | 480 | 320.30 | 0.667 |
| 2 | 0.00 | 0.825 | −2 | π/4 | 15 | 488 | 328.86 | 0.674 |
| 3 | 0.00 | 0.850 | 0 | 2π/4 | 20 | 521 | 337.71 | 0.648 |
| 4 | 0.00 | 0.875 | 2 | 3π/4 | 25 | 627 | 347.45 | 0.554 |
| 5 | 0.00 | 0.900 | 4 | π | 30 | 773 | 359.82 | 0.466 |
| 6 | 0.01 | 0.800 | −2 | 2π/4 | 25 | 397 | 320.90 | 0.808 |
| 7 | 0.01 | 0.825 | 0 | 3π/4 | 30 | 404 | 329.27 | 0.815 |
| 8 | 0.01 | 0.850 | 2 | π | 10 | 470 | 338.52 | 0.720 |
| 9 | 0.01 | 0.875 | 4 | 0 | 15 | 579 | 349.09 | 0.603 |
| 10 | 0.01 | 0.900 | −4 | π/4 | 20 | 4460 | 335.91 | 0.075 |
| 11 | 0.02 | 0.800 | 0 | π | 15 | 351 | 320.95 | 0.914 |
| 12 | 0.02 | 0.825 | 2 | 0 | 20 | 428 | 329.95 | 0.772 |
| 13 | 0.02 | 0.850 | 4 | π/4 | 25 | 437 | 339.40 | 0.776 |
| 14 | 0.02 | 0.875 | −4 | 2π/4 | 30 | 1288 | 332.20 | 0.258 |
| 15 | 0.02 | 0.900 | −2 | 3π/4 | 10 | 1174 | 342.28 | 0.292 |
| 16 | 0.03 | 0.800 | 2 | π/4 | 30 | 324 | 321.24 | 0.991 |
| 17 | 0.03 | 0.825 | 4 | 2π/4 | 10 | 358 | 330.39 | 0.922 |
| 18 | 0.03 | 0.850 | −4 | 3π/4 | 15 | 774 | 325.11 | 0.420 |
| 19 | 0.03 | 0.875 | −2 | π | 20 | 795 | 334.15 | 0.420 |
| 20 | 0.03 | 0.900 | 0 | 0 | 25 | 810 | 343.61 | 0.424 |
| 21 * | 0.04 | 0.800 | 4 | 3π/4 | 20 | 318 | 321.79 | 1.012 |
| 22 | 0.04 | 0.825 | −4 | π | 25 | 615 | 317.63 | 0.517 |
| 23 | 0.04 | 0.850 | −2 | 0 | 30 | 606 | 326.23 | 0.538 |
| 24 | 0.04 | 0.875 | 0 | π/4 | 10 | 830 | 335.39 | 0.404 |
| 25 | 0.04 | 0.900 | 2 | 2π/4 | 15 | 712 | 345.21 | 0.485 |
| Experiment Number | Control Parameters | Time When MVF = 0.9 | ES (kJ/m) | P (kW/m) | |||||
|---|---|---|---|---|---|---|---|---|---|
| Parameter Study | VFna | εavg | a | γ | PPI | ||||
| 1 | VFna | 0.00 | 0.800 | 4 | 3π/4 | 20 | 351.511 | 329.927 | 0.9386 |
| 2 | 0.01 | 0.800 | 4 | 3π/4 | 20 | 334.002 | 327.870 | 0.9816 | |
| 3 | 0.02 | 0.800 | 4 | 3π/4 | 20 | 369.538 | 325.911 | 0.8819 | |
| 4 | 0.03 | 0.800 | 4 | 3π/4 | 20 | 365.244 | 323.935 | 0.8869 | |
| 5 | εavg | 0.04 | 0.825 | 4 | 3π/4 | 20 | 392.582 | 328.438 | 0.8366 |
| 6 | 0.04 | 0.850 | 4 | 3π/4 | 20 | 467.525 | 335.255 | 0.7171 | |
| 7 | 0.04 | 0.875 | 4 | 3π/4 | 20 | 528.626 | 342.399 | 0.6477 | |
| 8 | 0.04 | 0.900 | 4 | 3π/4 | 20 | 688.149 | 350.656 | 0.5096 | |
| 9 | a | 0.04 | 0.800 | −4 | 3π/4 | 20 | 469.522 | 312.043 | 0.6646 |
| 10 | 0.04 | 0.800 | −2 | 3π/4 | 20 | 407.366 | 314.557 | 0.7722 | |
| 11 | 0.04 | 0.800 | 0 | 3π/4 | 20 | 348.865 | 316.916 | 0.9084 | |
| 12 | 0.04 | 0.800 | 2 | 3π/4 | 20 | 338.125 | 319.286 | 0.9443 | |
| 13 | γ | 0.04 | 0.800 | 4 | 0 | 20 | 347.665 | 321.838 | 0.9257 |
| 14 | 0.04 | 0.800 | 4 | π/4 | 20 | 315.240 | 321.787 | 1.0208 | |
| 15 | 0.04 | 0.800 | 4 | 2π/4 | 20 | 353.908 | 334.902 | 0.9463 | |
| 16 | 0.04 | 0.800 | 4 | π | 20 | 360.902 | 321.827 | 0.8917 | |
| 17 | PPI | 0.04 | 0.800 | 4 | 3π/4 | 10 | 312.557 | 321.807 | 1.0296 |
| 18 | 0.04 | 0.800 | 4 | 3π/4 | 15 | 391.438 | 321.881 | 0.8223 | |
| 19 | 0.04 | 0.800 | 4 | 3π/4 | 25 | 346.688 | 321.853 | 0.9284 | |
| 20 | 0.04 | 0.800 | 4 | 3π/4 | 30 | 307.910 | 321.748 | 1.0449 | |
| 21 | Optimum case | 0.04 | 0.800 | 4 | 3π/4 | 20 | 319.425 | 321.766 | 1.0073 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ghalambaz, M.; Mehryan, S.A.M.; Hajjar, A.; Fteiti, M.A.; Younis, O.; Sardari, P.T.; Yaïci, W. Latent Heat Thermal Storage in Non-Uniform Metal Foam Filled with Nano-Enhanced Phase Change Material. Sustainability 2021, 13, 2401. https://doi.org/10.3390/su13042401
Ghalambaz M, Mehryan SAM, Hajjar A, Fteiti MA, Younis O, Sardari PT, Yaïci W. Latent Heat Thermal Storage in Non-Uniform Metal Foam Filled with Nano-Enhanced Phase Change Material. Sustainability. 2021; 13(4):2401. https://doi.org/10.3390/su13042401
Chicago/Turabian StyleGhalambaz, Mohammad, S. A. M. Mehryan, Ahmad Hajjar, Mehdi A. Fteiti, Obai Younis, Pouyan Talebizadeh Sardari, and Wahiba Yaïci. 2021. "Latent Heat Thermal Storage in Non-Uniform Metal Foam Filled with Nano-Enhanced Phase Change Material" Sustainability 13, no. 4: 2401. https://doi.org/10.3390/su13042401
APA StyleGhalambaz, M., Mehryan, S. A. M., Hajjar, A., Fteiti, M. A., Younis, O., Sardari, P. T., & Yaïci, W. (2021). Latent Heat Thermal Storage in Non-Uniform Metal Foam Filled with Nano-Enhanced Phase Change Material. Sustainability, 13(4), 2401. https://doi.org/10.3390/su13042401







