An Efficient and Robust Current Control for Polymer Electrolyte Membrane Fuel Cell Power System
Abstract
1. Introduction
2. Materials and Methods
2.1. Polymer Electrolyte Membrane Fuel Cell
2.2. DC-DC Boost Converter
2.3. Control Design
2.3.1. PI Control
2.3.2. Integral Fast Terminal Sliding Mode Control (IFTSMC)
2.3.3. IFTSMC Stability Proof
2.4. Digital Filter Design
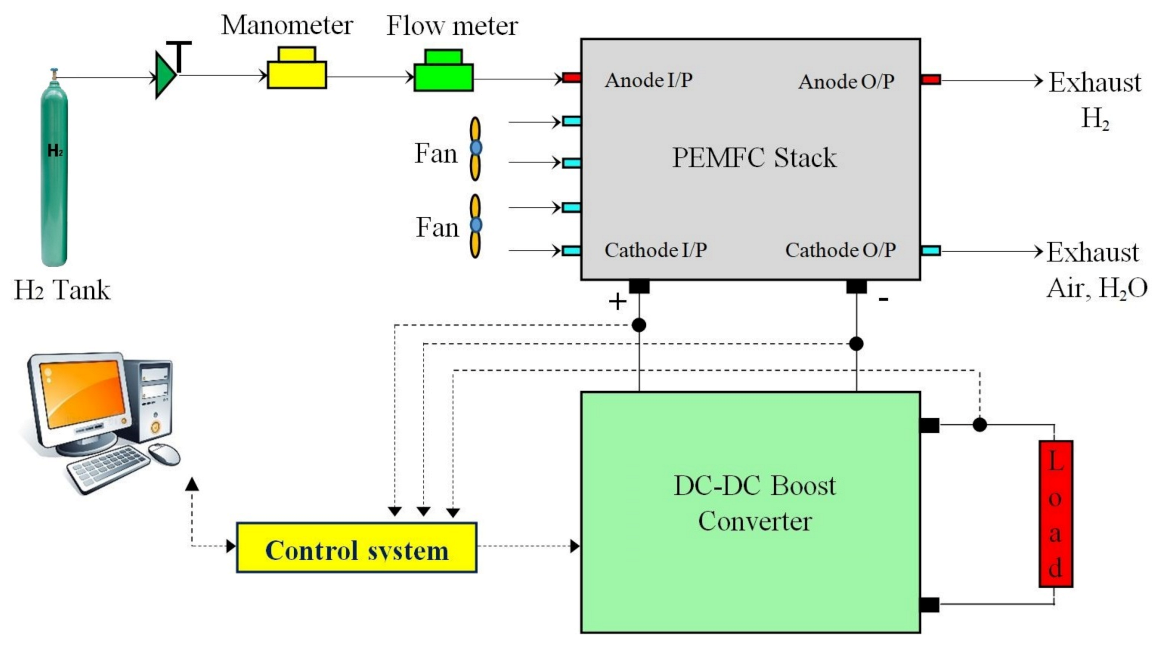
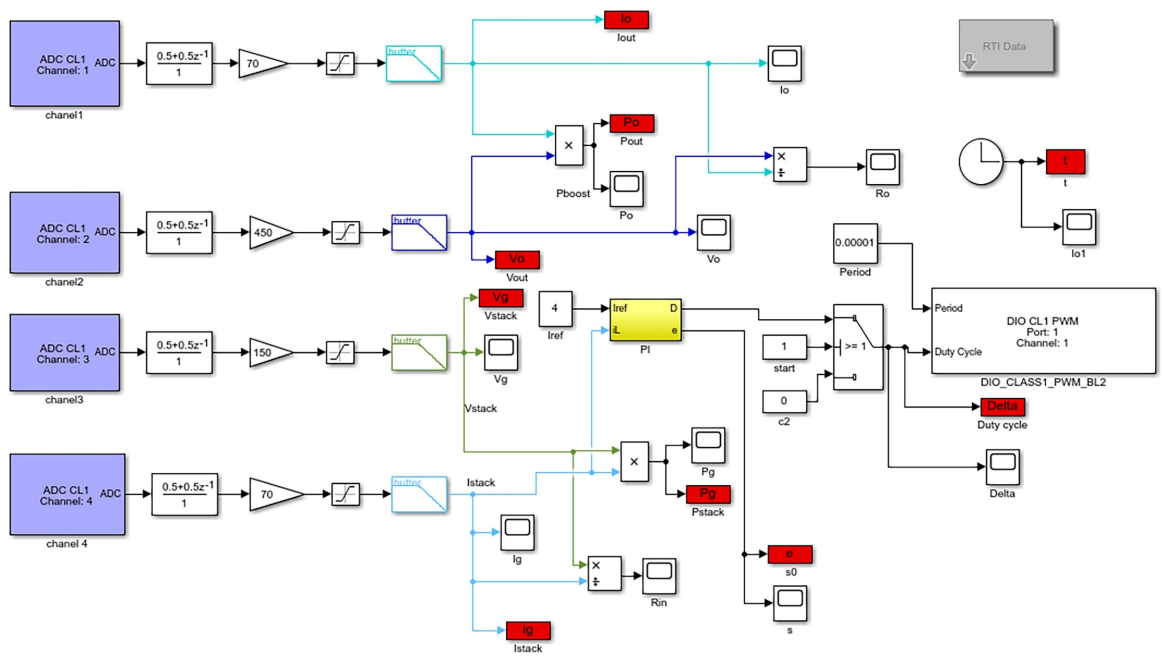
2.5. Description of the Test Bench
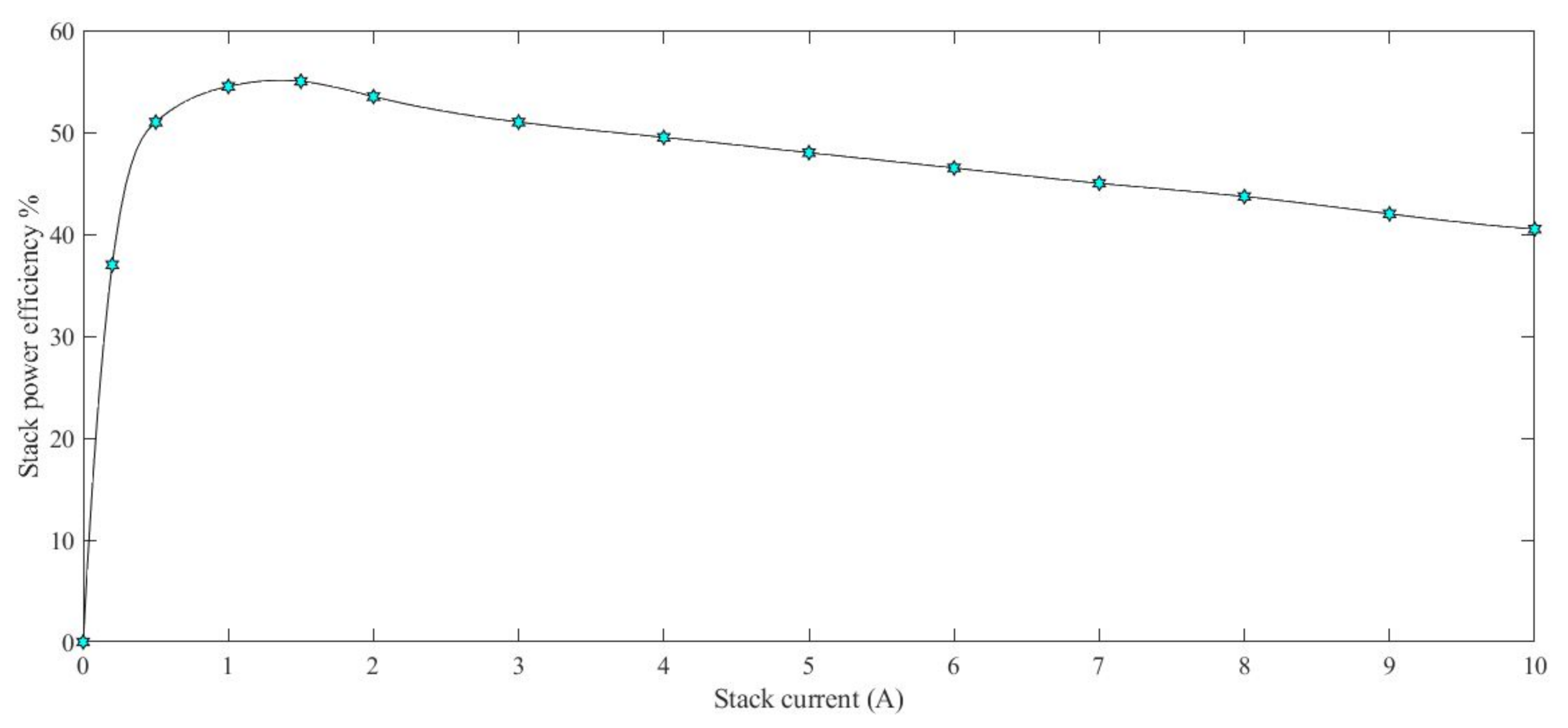
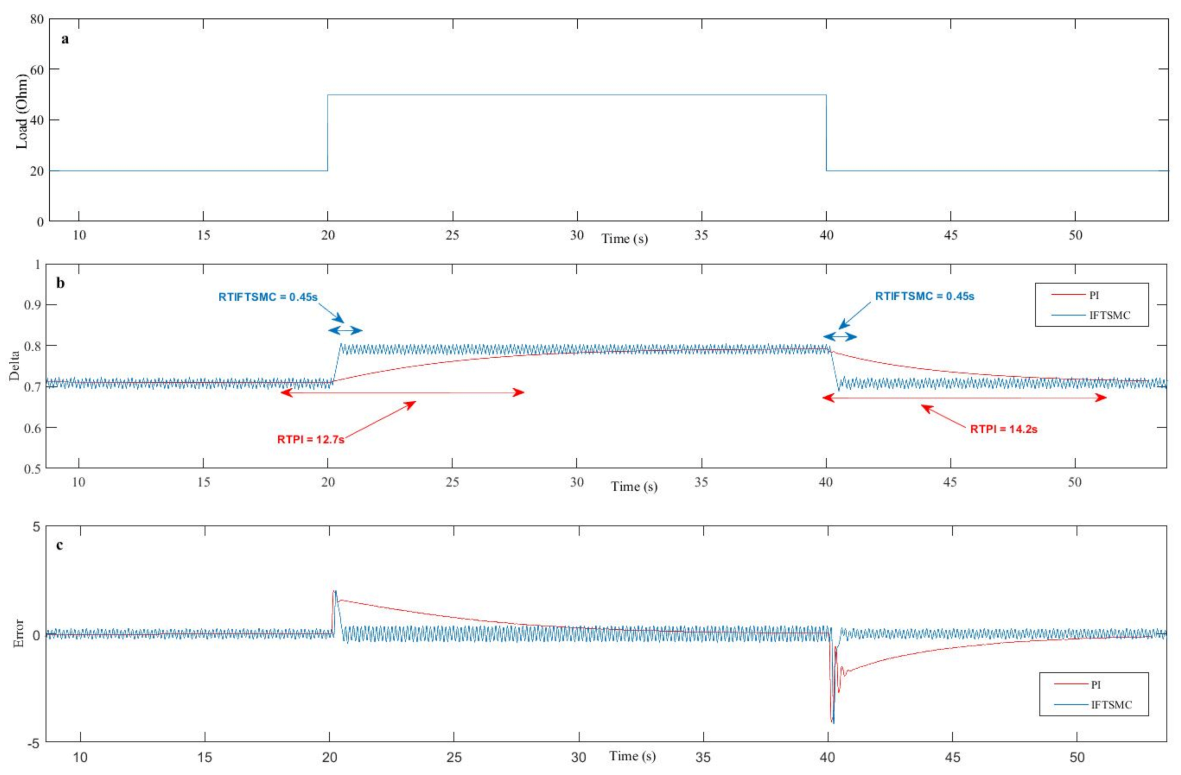
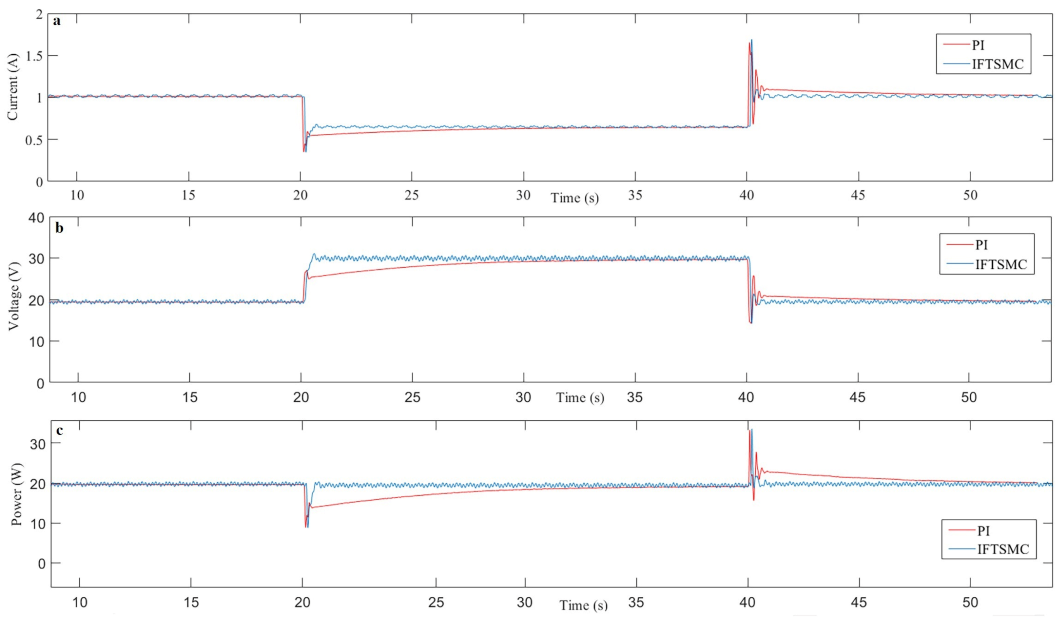
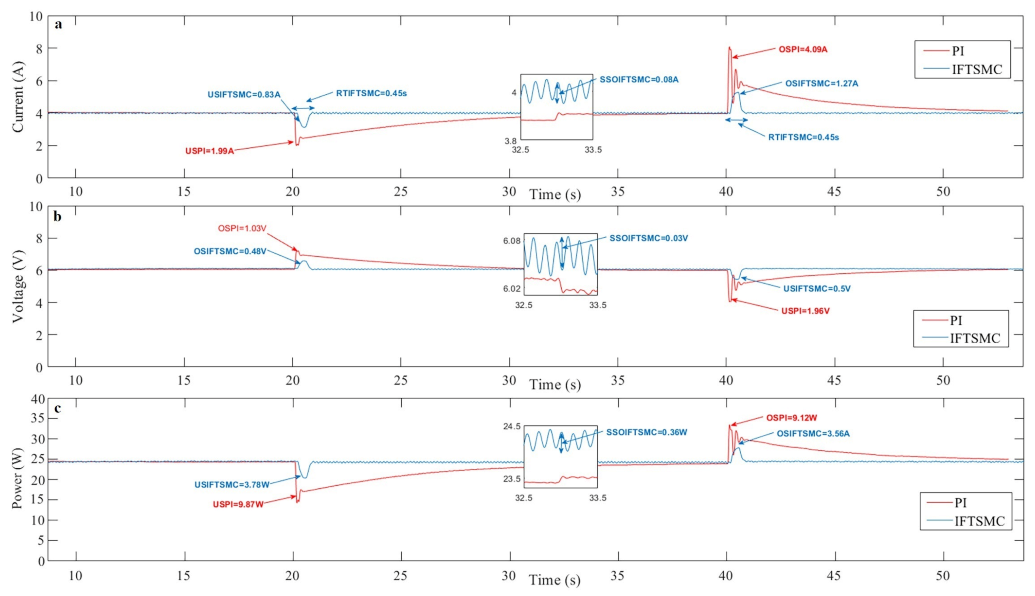
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| PEMFC | polymer electrolyte membrane fuel cell |
| PI | proportional-integral |
| IFTSMC | integral fast terminal sliding mode control |
| PEMFCs | proton exchange membrane fuel cells |
| PWM | pulse width modulation |
| PID | proportional-integral derivative |
| FOPID | fractional-order proportional-integral-derivative |
| TZTP | two-zero/three-pole |
| PID-SSA | PID using slap swarm algorithm |
| IRA | incremental resistance algorithm |
| GAO | grey antlion optimizer |
| GWM | grey wolf optimizer |
| MBA | mine-blast algorithm |
| FLC | fuzzy logic control |
| P&O | perturb and observe |
| FLC-PSO | fuzzy logic control based on particle swarm optimization |
| ANFIS | adaptive neuro-fuzzy inference system |
| SMC | sliding mode control |
| HOSM-QC | high order sliding mode based on quasi-continuous algorithm |
| HOSM-TA | high order sliding mode based on twisting algorithm |
| HOSM-STA | high order sliding mode based on super-twisting algorithm |
| TSMCs | terminal sliding mode controls |
| DTSMC | distributed terminal sliding mode controller |
| PFTC | proportional finite-time control |
| PACC | proportional asymptotic convergent contro |
| PIFTC | proportional-integral finite-time contro |
| FTSMC | fast terminal sliding mode control |
| ITSMC | integral terminal sliding mode control |
| CLF | control Lyapunov function |
| TDE | time delay estimation |
| LHV | hydrogen lower heating value |
| MOSFET | metal oxide semiconductor field effect transistor |
| CCM | continuous-conduction-mode |
| DCM | discontinuous-conduction-mode |
| TSMC | terminal sliding mode |
| DAC | digital to analog converter |
| ADC | analog to digital converter |
References
- Anderson, T.R.; Hawkins, E.; Jones, P.D. CO2, the greenhouse effect and global warming: From the pioneering work of Arrhenius and Callendar to today’s Earth System Models. Endeavour 2016, 40, 178–187. [Google Scholar] [CrossRef]
- Kaberger, T. Progress of renewable electricity replacing fossil fuels. Glob. Energy Interconnect. 2018, 1, 48–52. [Google Scholar]
- Reddy, B.M.; Samuel, P. Modeling and Simulation of Proton Exchange Membrane Fuel Cell Hybrid Electric Vehicle; Springer: Berlin/Heidelberg, Germany, 2020; pp. 281–291. [Google Scholar]
- Delgado, S.; Lagarteira, T.; Mendes, A. Air Bleeding Strategies to Increase the Efficiency of Proton Exchange Membrane Fuel Cell Stationary Applications Fuelled with CO ppm-levels. Int. J. Electrochem. Sci. 2020, 15, 613–627. [Google Scholar] [CrossRef]
- Mardle, P.; Ji, X.; Wu, J.; Guan, S.; Dong, H.; Du, S. Thin film electrodes from Pt nanorods supported on aligned N-CNTs for proton exchange membrane fuel cells. Appl. Catal. B Environ. 2020, 260, 118031. [Google Scholar] [CrossRef]
- García-Olivares, A.; Solé, J.; Samsó, R.; Ballabrera-Poy, J. Sustainable European transport system in a 100% renewable economy. Sustainability 2020, 12, 5091. [Google Scholar] [CrossRef]
- Lee, D.; Lin, K.C. How to Transform Sustainable Energy Technology into a Unicorn Start-Up: Technology Review and Case Study. Sustainability 2020, 12, 3018. [Google Scholar] [CrossRef]
- Rastayesh, S.; Bahrebar, S.; Blaabjerg, F.; Zhou, D.; Wang, H.; Dalsgaard Sørensen, J. A System Engineering Approach Using FMEA and Bayesian Network for Risk Analysis—A Case Study. Sustainability 2020, 12, 77. [Google Scholar] [CrossRef]
- Friedrich, K.A.; Kallo, J.; Schirmer, J.; Schmitthals, G. Fuel cell systems for aircraft application. ECS Trans. 2009, 25, 193. [Google Scholar] [CrossRef]
- Akinyele, D.; Olabode, E.; Amole, A. Review of Fuel Cell Technologies and Applications for Sustainable Microgrid Systems. Inventions 2020, 5, 42. [Google Scholar] [CrossRef]
- Kester, W.; Erisman, B.; Thandi, G. Section 4 Switched Capacitor Voltage Converters. Switched Capacitor Voltage Converters. Available online: https://www.analog.com/media/en/training-seminars/design-handbooks/Practical-Design-Techniques-Power-Thermal/Section4.pdf (accessed on 14 November 2020).
- Belhaj, F.Z.; El Fadil, H.; Idrissi, Z.E.; Koundi, M.; Gaouzi, K. Modeling, Analysis and Experimental Validation of the Fuel Cell Association with DC-DC Power Converters with Robust and Anti-Windup PID Controller Design. Electronics 2020, 9, 1889. [Google Scholar] [CrossRef]
- Derbeli, M.; Sbita, L.; Farhat, M.; Barambones, O. Proton exchange membrane fuel cell—A smart drive algorithm. In Proceedings of the 2017 International Conference on Green Energy Conversion Systems (GECS), Hammamet, Tunisia, 23–25 March 2017; pp. 1–5. [Google Scholar]
- Derbeli, M.; Barambones, O.; Sbita, L. A Robust Maximum Power Point Tracking Control Method for a PEM Fuel Cell Power System. Appl. Sci. 2018, 8, 2449. [Google Scholar] [CrossRef]
- Derbeli, M.; Barambones, O.; Farhat, M.; Sbita, L. Efficiency Boosting for Proton Exchange Membrane Fuel Cell Power System Using New MPPT Method. In Proceedings of the 10th International Renewable Energy Congress (IREC), Sousse, Tunisia, 26–28 March 2019; pp. 1–4. [Google Scholar]
- Derbeli, M.; Farhat, M.; Barambones, O.; Sbita, L. Control of PEM fuel cell power system using sliding mode and super-twisting algorithms. Int. J. Hydrog. Energy 2017, 12, 8833–8844. [Google Scholar] [CrossRef]
- Silaa, M.Y.; Derbeli, M.; Barambones, O.; Cheknane, A. Design and Implementation of High Order Sliding Mode Control for PEMFC Power System. Energies 2020, 13, 4317. [Google Scholar] [CrossRef]
- Derbeli, M.; Barambones, O.; Farhat, M.; Ramos-Hernanz, J.A.; Sbita, L. Robust high order sliding mode control for performance improvement of PEM fuel cell power systems. Int. J. Hydrog. Energy 2020, 45, 29222–29234. [Google Scholar] [CrossRef]
- Derbeli, M.; Barambones, O.; Ramos-Hernanz, J.A.; Sbita, L. Real-time implementation of a super twisting algorithm for PEM fuel cell power system. Energies 2019, 12, 1594. [Google Scholar] [CrossRef]
- Shotorbani, A.M.; Ghassem-Zadeh, S.; Mohammadi-Ivatloo, B.; Hosseini, S.H. A distributed secondary scheme with terminal sliding mode controller for energy storages in an islanded microgrid. Int. J. Electr. Power Energy Syst. 2017, 93, 352–364. [Google Scholar] [CrossRef]
- Gudey, S.K.; Gupta, R. Recursive fast terminal sliding mode control in voltage source inverter for a low-voltage microgrid system. IET Gener. Transm. Distrib. 2016, 10, 1536–1543. [Google Scholar] [CrossRef]
- Armghan, H.; Yang, M.; Armghan, A.; Ali, N.; Wang, M.Q.; Ahmad, I. Design of integral terminal sliding mode controller for the hybrid AC/DC microgrids involving renewables and energy storage systems. Int. J. Electr. Power Energy Syst. 2020, 119, 105857. [Google Scholar] [CrossRef]
- Derbeli, M.; Farhat, M.; Barambones, O.; Sbita, L. Control of proton exchange membrane fuel cell (pemfc) power system using pi controller. In Proceedings of the International Conference on Green Energy Conversion Systems (GECS), Hammamet, Tunisia, 23–25 March 2017; pp. 1–5. [Google Scholar]
- Cruz Rojas, A.; Lopez Lopez, G.; Gomez-Aguilar, J.F.; Alvarado, V.M.; Sandoval Torres, C.L. Control of the air supply subsystem in a PEMFC with balance of plant simulation. Sustainability 2017, 9, 73. [Google Scholar] [CrossRef]
- Rezk, H.; Fathy, A. Performance improvement of PEM fuel cell using variable step-size incremental resistance MPPT technique. Sustainability 2020, 12, 5601. [Google Scholar] [CrossRef]
- Wan, Z.; Chang, H.; Shu, S.; Wang, Y.; Tang, H. A review on cold start of proton exchange membrane fuel cells. Energies 2014, 7, 3179–3203. [Google Scholar] [CrossRef]
- Louzazni, M.; Al-Dahidi, S.; Mussetta, M. Fuel Cell Characteristic Curve Approximation Using the Bézier Curve Technique. Sustainability 2020, 12, 8127. [Google Scholar] [CrossRef]
- Seyed Mahmoudi, S.M.; Sarabchi, N.; Yari, M.; Rosen, M.A. Exergy and exergoeconomic analyses of a combined power producing system including a proton exchange membrane fuel cell and an organic rankine cycle. Sustainability 2019, 11, 3264. [Google Scholar] [CrossRef]
- Wilberforce, T.; Olabi, A.G. Design of Experiment (DOE) Analysis of 5-Cell Stack Fuel Cell Using Three Bipolar Plate Geometry Designs. Sustainability 2020, 12, 4488. [Google Scholar] [CrossRef]
- Khatib, T.; Elmenreich, W.; Mohamed, A. Simplified iv characteristic tester for photovoltaic modules using a dc-dc boost converter. Sustainability 2017, 9, 657. [Google Scholar] [CrossRef]
- Derbeli, M.; Barambones, O.; Silaa, M.Y.; Napole, C. Real-Time Implementation of a New MPPT Control Method for a DC-DC Boost Converter Used in a PEM Fuel Cell Power System. Actuators 2020, 9, 105. [Google Scholar] [CrossRef]
- Erickson, R.W.; Maksimovic, D. Fundamentals of Power Electronics; Springer Science: Berlin/Heidelberg, Germany, 2007. [Google Scholar]
- Sarikhani, A.; Allahverdinejad, B.; Hamzeh, M.; Afjei, E. A continuous input and output current quadratic buck-boost converter with positive output voltage for photovoltaic applications. Sol. Energy 2019, 188, 19–27. [Google Scholar] [CrossRef]
- Derbeli, M.; Mrad, I.; Sbita, L.; Barambones, O. PEM fuel cell efficiency boosting—Robust MPP tracking. In Proceedings of the 9th International Renewable Energy Congress (IREC), Hammamet, Tunisia, 20–22 March 2018; pp. 1–5. [Google Scholar]
- Derbeli, M.; Charaabi, A.; Barambones, O.; Sbita, L. Optimal Energy Control of a PEM Fuel Cell/Battery Storage System. In Proceedings of the 10th International Renewable Energy Congress (IREC), Sousse, Tunisia, 26–28 March 2019; pp. 1–5. [Google Scholar]
- Chavero-Navarrete, E.; Trejo-Perea, M.; Jáuregui-Correa, J.C.; Carrillo-Serrano, R.V.; Rios-Moreno, J.G. Pitch Angle Optimization by Intelligent Adjusting the Gains of a PI Controller for Small Wind Turbines in Areas with Drastic Wind Speed Changes. Sustainability 2019, 11, 6670. [Google Scholar] [CrossRef]
- Aguilar-Mejía, O.; Minor-Popocatl, H.; Tapia-Olvera, R. Comparison and Ranking of Metaheuristic Techniques for Optimization of PI Controllers in a Machine Drive System. Appl. Sci. 2020, 10, 6592. [Google Scholar] [CrossRef]
- Arfaoui, J.; Rezk, H.; Al-Dhaifallah, M.; Ibrahim, M.N.; Abdelkader, M. Simulation-Based Coyote Optimization Algorithm to Determine Gains of PI Controller for Enhancing the Performance of Solar PV Water-Pumping System. Energies 2020, 13, 4473. [Google Scholar] [CrossRef]
- Venkataraman, S.T.; Gulati, S. Control of nonlinear systems using terminal sliding modes. Appl. Sci. 1993, 115, 554–560. [Google Scholar] [CrossRef]
- Slotine, J.J.E.; Li, W. Applied Nonlinear ControlPrentice Hall: Englewood Cliffs, NJ, USA; 1991Volume 199, p. 106354.
- Utkin, V.; Jürgen, G.; Ma, S. Sliding Mode Control in Electro-Mechanical Systems; CRC Press: Boca Raton, FL, USA, 1999; Volume 34. [Google Scholar]
- Rizi, M.T.; Eliasi, H. Nonsingular terminal sliding mode controller for voltage and current control of an islanded microgrid. Electr. Power Syst. Res. 2020, 185, 106354. [Google Scholar] [CrossRef]
- Feng, Y.; Yu, X.; Man, Z. Non-singular terminal sliding mode control of rigid manipulators. Automatica 2002, 38, 2159–2167. [Google Scholar] [CrossRef]
- Yu, X.; Man, Z. Fast terminal sliding-mode control design for nonlinear dynamical systems. IEEE Trans. Circuits Syst. I Fundam. Theory Appl. 2002, 49, 261–264. [Google Scholar]
- Zhao, H.; Zhang, L.; Liu, J.; Zhang, C.; Cai, J.; Shen, L. Design of a Low-Order FIR Filter for a High-Frequency Square-Wave Voltage Injection Method of the PMLSM Used in Maglev Train. Electronics 2020, 9, 729. [Google Scholar] [CrossRef]





| Reference | Year | Controller | Converter | Features | Drawbacks |
|---|---|---|---|---|---|
| Ref. [12] | 2020 | PID | DC/DC buck and boost converters | - Easy to implement. - Low computational requirements. - The most common used in the industry. | - Sensitive when facing large load variation. - Inappropriate gains leads to the instability of the system. - Tuning the controller parameters is difficult. |
| Ref. [13] | 2017 | FLC | DC/DC boost converter | - Easy to understand. - It simplifies implementation. - Similar to human reasoning. - Simple to extend by adding new rules. | - Human expertise is required to achieve a suitable accuracy - The system states have to be known. - It is not always accurate since the results are perceived as a guess. - Stability is not guaranteed. |
| Ref. [14] | 2018 | BSTP | DC/DC boost converter | - Popular technique for high order systems. - Guaranteed stability design through Lyapunov function. - Uncertainties could be handled to a certain level. | - Complex Lyapunov function. - High design complexity - The exact mathematical model of the system is required - Sensitive to parameter variation. - Necessity of measuring all the state variables. |
| Ref. [15] | 2019 | SMC | DC/DC boost converter | - Simple structure. - Easy parameter tuning. - Applicable for a wide range of nonlinear systems. - Robust to uncertainties and disturbances. - Stability is guaranteed. | - Excessive chattering effect. - Unguaranteed finite time convergence. - The trajectories are not robust against perturbations during the reaching phase. |
| Ref. [17] Ref. [18] Ref. [19] | 2020 2020 2019 | QC TA STA | DC/DC boost converter | - Chattering reduction in comparison with SMC. - Finite time convergence. - Robust to parameter uncertainties and disturbances. | - Complex design. - Unable to use for first-order systems. - Precise and accurate response is not guaranteed. - Complex stability demonstration. |
| Ref. [20] | 2017 | DTSMC | Voltage source converter | - Finite time convergence. - Capable of reducing the chattering. - Robust to parameter uncertainties and disturbances. | - Slow convergence speed. - Requires the knowledge of the system boundary uncertainties. - Convergence problem may occur in case if the system states move away from the equilibrium. - Problem of intrinsic singularity. |
| Ref. [21] | 2016 | FTSMC | DC/AC inverter | - Finite time convergence. - Fast convergence rate. - Capable of reducing the chattering. - Robust to uncertainties and disturbances. | - Problem of intrinsic singularity. - Can not be applied to higher order systems. - The boundary information of system uncertainties is usually required to be known in advance. - Problem of intrinsic singularity. |
| Ref. [22] | 2020 | ITSMC | AC/DC inverter | - Finite time convergence. - High tracking accuracy. - Robust to parameter uncertainties and disturbances. - Applicable to high order systems. | - Slow convergence rate. - Requires the knowledge of the system boundary uncertainties. - Problem of intrinsic singularity. |
| FC50 Characteristics | Electrical Characteristics | ||
|---|---|---|---|
| Type of cell | Proton exchange membrane | Operating voltage | 2.5–9 V |
| Cooling system | Ventilators | Operating current | 0–10 A |
| Fuel type | Pure hydrogen | Rated. Output power | 40 Watt |
| Dimensions W × H × D | 120 mm × 103 mm × 135 mm | Max. Output power | 50 Watt |
| Weight | 1150 g | Open-circuit voltage | 9.0 V |
| Flow meter | Kit of 15 bar | ||
| Precision | 0.8% of the quantified value | Inlet pressure | 1–15 bar |
| Range of measuring | 10–1000 sml/min | Outlet pressure | 0.4–0.8 bar |
| Thermal | Kit of 200 bar | ||
| Operating temperature | +15– 50 | Inlet pressure | 200 bar |
| Max. Start temperature | + 45 | Outlet pressure | 1–15 bar |
| Fuel detector | Detector | ||
| Recommended purity | 5 with | Type of sensors | 4% |
| input pressure | 0.4–8 bar (5.8–11.6 psig) | Measuring principle | 3 electrode sensor |
| consumption | Max. 700 sml/min (at , 1013 bar) | Operating range | 0–4% |
| Parameter | Value |
|---|---|
| Inductance | 6 μH |
| Input capacitor | 1500 μF |
| Output capacitor | 3000 μF |
| Max. Switching frequency | 25,000 HZ |
| Max. Input voltage | = 60 V |
| Max. Iput current | = 30 A |
| Max. Output voltage | = 250 V |
| Max. Output current | = 30 A |
| IFTSMC | PI |
|---|---|
| − |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Silaa, M.Y.; Derbeli, M.; Barambones, O.; Napole, C.; Cheknane, A.; Gonzalez De Durana, J.M. An Efficient and Robust Current Control for Polymer Electrolyte Membrane Fuel Cell Power System. Sustainability 2021, 13, 2360. https://doi.org/10.3390/su13042360
Silaa MY, Derbeli M, Barambones O, Napole C, Cheknane A, Gonzalez De Durana JM. An Efficient and Robust Current Control for Polymer Electrolyte Membrane Fuel Cell Power System. Sustainability. 2021; 13(4):2360. https://doi.org/10.3390/su13042360
Chicago/Turabian StyleSilaa, Mohammed Yousri, Mohamed Derbeli, Oscar Barambones, Cristian Napole, Ali Cheknane, and José María Gonzalez De Durana. 2021. "An Efficient and Robust Current Control for Polymer Electrolyte Membrane Fuel Cell Power System" Sustainability 13, no. 4: 2360. https://doi.org/10.3390/su13042360
APA StyleSilaa, M. Y., Derbeli, M., Barambones, O., Napole, C., Cheknane, A., & Gonzalez De Durana, J. M. (2021). An Efficient and Robust Current Control for Polymer Electrolyte Membrane Fuel Cell Power System. Sustainability, 13(4), 2360. https://doi.org/10.3390/su13042360







