Abstract
This work demonstrates a techno-economical assessment of wind energy potential for four passes of Tamil Nadu (Aralvaimozhi, Shencottah, Palghat, and Cumbum) with uncertainty factors. First, a potential assessment was carried out with time-series data, and the Weibull parameters, such as c (scale) and k (shape), were determined using the modern-era retrospective analysis for research and applications (MEERA) data set. Using these parameters, the mean speed, most probable speed, power density, maximum energy-carrying speed of wind power were determined. From the analysis, it was observed that all four passes had better wind parameters; notably, the Aralvaimozhi pass attained a better range of about 6.563 m/s (mean wind speed), 226 W/m2 (wind power density), 6.403 m/s (most probable wind speed), and 8.699 m/s (max wind speed). Further, uncertainty factors, such as the probability of exceedance (PoE), wind shear co-efficient (WSC), surface roughness, and wake loss effect (WLE), were evaluated. The value of PoE was found to be within the bound for all the locations, i.e., below 15%. In addition, the ranged of WSC showed a good trend between 0.05 and 0.5. Moreover, the surface length of the passes was evaluated and recorded to be 0.0024 m with a 73% energy index. Further, output power, annual energy production (AEP), capacity factor (CF), and cost of wind energy of all four passes were computed using different wind turbine ratings in two cases, i.e., with and without WLE. It was observed that there was a huge profit in loss from all the four locations due to WLE that was estimated to be Rupees (Rs.) 10.07 crores without considering interest components and Rs. 13.66 crores with interest component at a 10% annual rate of interest.
1. Introduction
Due to the continuous growth of populations and technological developments, the consumption rate of electricity increases rapidly every year that affects the ecological factors based on the power generation scheme. Specifically, fossil fuel-based power generation increases greenhouse gas emissions that affect climatic conditions due to pollution particles [1,2]. Among the emissions, carbon dioxide (CO2) is a significant pollutant that causes severe changes in the earth’s atmosphere behavior [3,4,5]. Recently, global economies and industries have proclaimed that they target to condense their emissions down to net-zero by 2050 or soon after. To drive this target further, the International Energy Agency (IEA) is planning to announce the first wide-ranging road map for the global energy sector to grasp net-zero by 2050 [6]. In addition, the International Renewable Energy Agency (IRENA) launched a road map to 2050 for global energy transformation in 2019. It is targeted for immediate deployable, cost-effective alternatives for nations to fulfill climate commitments and reduce the growth of global temperatures. The predicted energy revolution can also reduce net costs and fetch substantial socioeconomic benefits, likely augmented economic growth, job creation, and overall welfare gains [7].
For a few decades, the evolution of renewable energy resource (RER) additions on the global energy mix has shown a significant rise, notably from the year 2001. Among the available installed capacity of RER, solar photovoltaic (SPV) and wind energy show greater dominance in their global renewable energy mix markedly from the year 2010, as demonstrated in Figure 1. At present, the potential for renewable energy production from WES is estimated between 630,720 and 1,489,200 TWh/year globally [8]. Due to the abundant availability of wind energy resources, some of the countries, namely China, Brazil, the United States of America, and India, attained a higher magnitude of installed capacity, as illustrated in Figure 2.
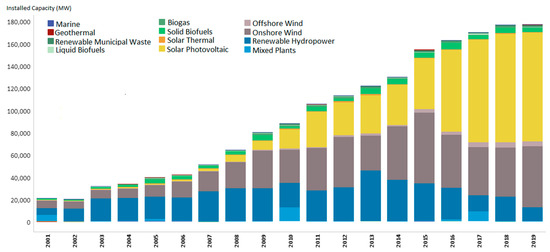
Figure 1.
Evolution of global renewable energy.
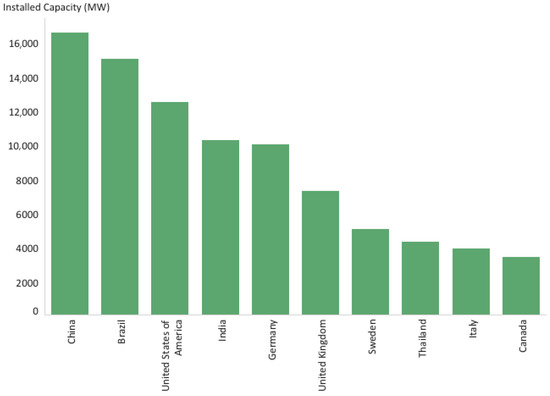
Figure 2.
Top ten countries with higher wind energy installed capacity.
India is one of the leading countries in the world to stack a higher ratio of RER in its energy mix and records greater growth of WES since 2001 (Figure 3) [9]. The Indian Energy Agency (public organization) has aimed to achieve 60 GW of power generation through WES by 2022 from their total RER capacity of 175 GW [10]. At present, onshore wind energy capacity contributes about 37.69 GW as of March 2020 [11]. Though the onshore WES accelerates commendably, India struggles to raise the wind energy capacity both offshore and nearshore. However, some of the Indian states hold higher potential and the MNRE announced a clear roadmap to attain an offshore wind energy capacity of 5 GW targeting the year 2032 [12].
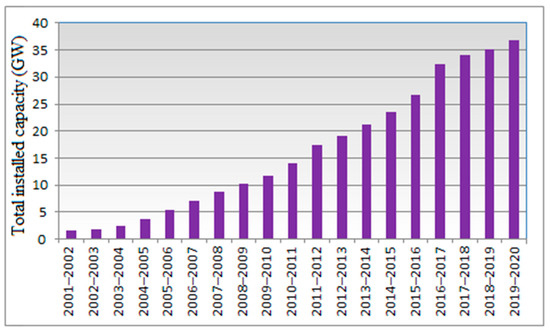
Figure 3.
Evolution of installed capacity of wind energy growth in India (GW).
As stated earlier, India has a great potential for wind resources that are distributed diversely; there are some notable states in India, which play a vital role in wind power production, specifically Tamil Nadu. The total renewable installed capacity of the state is estimated to be 15.79 GW as of January 2020 [13]. The mix of the RER shows a greater stack by wind power, about 8.5 GW from the total RER installed capacity, as shown in Figure 4. Moreover, the potential estimation of the state is found to be great about 33.79 GW at 100 m hub height, i.e., 11.25 GW from the wasteland, 22.15 GW from cultivable land, and 0.39 GW from forest areas [14].
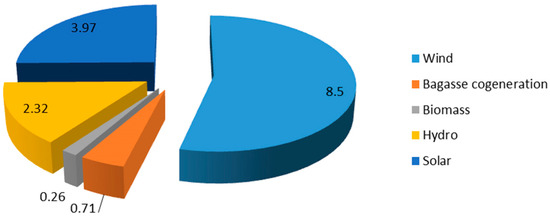
Figure 4.
Energy mix of Tamilnadu from renewable sources in GW.
Additionally, repowering of WES in Tamilnadu sites can enhance the potential further by optimum utilization of wind energy resources using the appropriate framework. Recently, Tamilnadu Generation Corporation (TANDEDCO) announced the guidelines for repowering by replacing old turbines (200 kW to 600 kW) with new ones, which are higher rated between 750 kW to 2100 kW [15]. In addition, the conventional spacing for micro sittings is revised in their policy from 5D/7D to possibly 3D/5D (D-Diameter of the rotor turbine). Due to this emerging policy, the cost of energy may decline to some extent. However, it is imperative to evaluate the technical parameters of wind behavior and turbine performances. Considering these concerns, this work aims to investigate the wind and turbine characteristics of selected sites in Tamilnadu state with the following objectives:
- To investigate the wind characteristics of the selected sites using the Weibull distribution function for the years 2000 to 2019;
- To analyze the probability of exceedance (PoE);
- To investigate the surface roughness of the selected sites;
- To estimate the wind shear coefficient;
- To find the percentage of WLE;
- To evaluate the output power, AEP, and capacity factor of the selected turbines from all locations;
- To compute the total loss in profit due to WLE
Based on the stated objectives, this paper is organized as follows: Section 2 describes the literature report of the work, and Section 3 illustrates the data collection, site descriptions of the selected locations, and wind turbine selection. Further, Section 4 demonstrates the detailed method of wind characteristics analysis and the estimation method of technical and economical parameters. Subsequently, results and discussions are made using different factors in Section 5. Lastly, conclusions are made using the attained outcome in Section 6.
2. Literature Review
There are various works published relating to the potential assessment and power extraction on specified locations. Some of the recent and notable works of literature are discussed below (Table 1):

Table 1.
Existing literature reports.
Considering all the inferences and limitations of the existing literature reports, computation of energy output, cost of generation, capacity factor, and loss in profit were not demonstrated with uncertainty factors by the researchers. In addition, the uncertainty factors, namely, the probability of exceedance (PoE), surface roughness, and wake loss effect of the selected locations, were not exposed extensively. Further, micro sitting in wind farms resulting in a greater wake loss effect (WLE) that can reduce the net annual energy production (AEP) and increase the total energy cost. A recent survey report described that the European offshore wind projects offer a higher rate of WLE between 25% and 60% [29]. Typically, about 20% to 30% WLE were estimated in onshore projects of North America [30]. Consolidating these inferences, this work targets to evaluate the uncertainty factors and loss in profit due to WLE extensively for the selected locations of Tamilnadu. Further, wind resource assessment is carried out using probability density functions (PDF) to detect the supreme fitting measurement. Largely, Weibull and Rayleigh distributions methods are adapted in recent studies. Particularly, the Weibull method takes the upper hand because it can be incorporated easily with commercial wind investigation software [1].
3. Case Study
3.1. Data Collection and Site Descriptions
The development of a wind farm for any site needs some key requirements, notably wind data investigation and precise wind energy potential assessment. For effective application of wind turbines, a characteristic of the local wind flow analysis is essential. The annual energy generation of the turbine hinges on various factors, such as wind velocity, hub height above the ground level, winds gusting effect, and micro siting of wind energy generations.
Globally, India ranks fourth in wind energy production due to its abundant wind potential throughout the years. The most important zones are the Western Ghats and Himalaya mountains, but the features and importance of Western Ghats represent the geomorphic and biophysical ecological system, which is much older than the great Himalaya Mountains. Moreover, these Western were recognized as world heritage sites by UNESCO [31] and declared as one among “hotspots” of diversity within the species in the world. These Western Ghat’s locations of equatorial tropical evergreen forests act as a wall, intercepting the monsoon winds from the South-west during late summer. The western coast covers approximately 30–50 km inland, and the Western Ghats traverse through the Indian states of Tamilnadu, Kerala, Goa, Karnataka, Gujarat, and Maharashtra. The total surface of 140,000 km2 and 1600 km long stretch is covered by these mountains [32]. The chain of mountains, also called wind passes, comprises a gap that produces more wind speed due to compressed air formation on the side of the mountains. These gaps increase the wind speed considerably, and this effect is termed the “tunnel effect”. Among other states of Western Ghats, Tamilnadu plays a major role in wind energy production [13], which stands top in the country due to its abundant wind energy availability and multiple potential sites by nature. Consolidating all these inferences, this work targets the potential assessment of four key wind passes of Tamilnadu, namely the Palghat gap (S1), Cumbum (S2), Shencottah (S3), and Aralvaimozhi (S4), as described in Figure 5 [33]. The wind speeds of all passes are commendable, as illustrated in the figure with a maximum rate of 9.75 m/s. In addition, the state is situated at the Southeastern Indian peninsula, which has high humidity and temperature around the year, with an annual rainfall of 911.6 mm of southwest monsoon from June to September and northeast monsoon from October to December. The field temperatures of the sites are between 20 °C to 38 °C [34]. Further, the geographical description of the selected wind passes is displayed in Table 2.
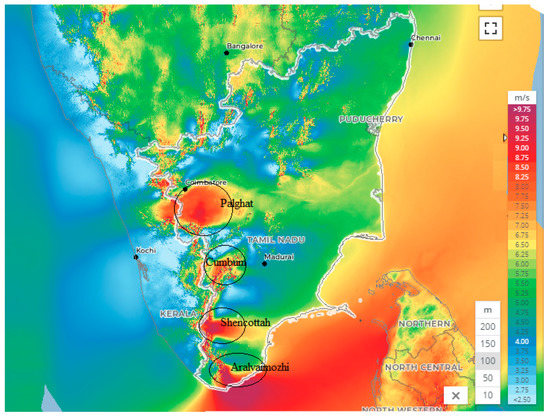
Figure 5.
Potential locations of wind passes in Tamilnadu (Global Wind Atlas—January 2021).

Table 2.
Site selection and its description.
The historical time-series datasets were investigated from the Weibull distribution function using wind navigator in the Windographer software. The potential wind sites were identified through the Global Wind Atlas map as described above. Using Windographer [35], the MEERA data were taken for all the four locations, i.e., Aralvaimozhi, Shencottah, Palghat, and Cumbum. From the analysis, the frequency and hours per year of the wind speed, yearly speed variation, the variation of scale and shape factor, dominant wind direction as per the wind rose diagram were calculated. Further, the annual mean wind speeds of the four passes observed at various heights, such as 100 m, 70 m, and 50 m, are illustrated in Figure 6. It was observed that the mean wind speed of Aralvaimozhi, Shencottah, and Palghat exceeded 8 m/s except for the Cumbum Pass that attained a maximum wind of 7 m/s; notably, the Aralvaimozhi Pass had a good rate of wind speed throughout the year, particularly from January to March and April to September. Although the wind speed variations were observed between different heights of the hub, but not greater range. Considering these inferences, all four passes have a greater potential for wind energy conversion.
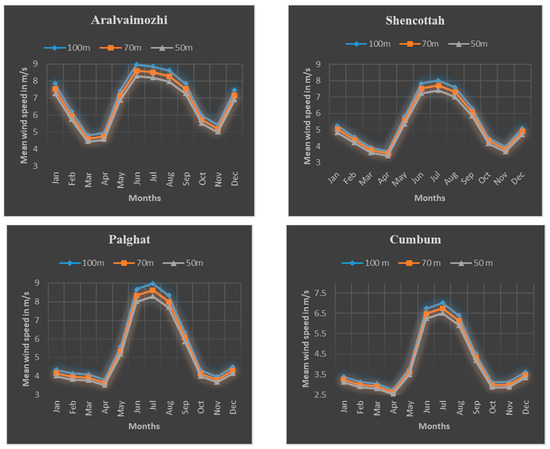
Figure 6.
Seasonal wind speeds of all four passes at 100 m, 70 m, and 50 m.
3.2. Wind Turbine Selection
A total of 30 wind turbines were considered for this study based on the available data from all four passes ranging between 600 kW to 2.3 MW. The comprehensive descriptions of different wind turbines adopted in four passes are tabulated in Table 3. It was observed that the wind turbines were placed at different hub heights between 48.1 m to 85 m. Moreover, the rotor diameter, cut-in-speed, cut-out-speed, and rated speed of the individual turbine are illustrated in Table 3. The key objective of this work was to demonstrate a potential assessment of the four wind passes by adapting different turbine specifications from wind farms to estimate the least-cost generating machine and location, considering the uncertainty factors.

Table 3.
Characteristics of selected wind turbines.
4. Methodology
4.1. Wind Characteristics—Weibull Parameter Analyses
For effective fitting of actual wind data, the distribution method has been adopted for a few decades. The characteristics of wind in any site can be analyzed using the probability distribution function (PDF). The behavior of speed data sets are corresponding to a random variable, intermittent, and continuous variation in time. Weibull function parameters are determined using different PDF viz. gamma, maximum-likelihood, log-normal, method of moment, Rayleigh, and three-parameter beta. Among these, the Weibull distribution function is utilized widely and accepted for an extensive range of wind speed data [36]. The most pivotal parameters of Weibull functions are k (shape parameter-dimensionless) and c (scale parameter in m/s), and these need to be evaluated [37,38]. The Weibull PDF can be evaluated using the following equation:
where v is the wind speed in m/s.
The Weibull distribution’s cumulative function is presented below [39]:
The approximation methods were adopted to measure the Weibull parameters after determining the variance and mean speed of the wind data as represented in Equations (3) and (4). The “k” and “c” parameters were assessed from these equations [40]. Weibull shape parameter (k) is the width of the distribution, and the scale parameter (c) determines the nature of the windy location. The shape factor can be computed using Equation (3):
where is the average wind speed in m/s, and the scale parameter is determined using the relation below [40]:
The average speed () and standard deviation (σ) of the wind is computed from Weibull parameters of the probability distribution function using Equation (5) and Equation (6), respectively [40]:
where Γ denotes a gamma function that can be computed using the below equation [41]:
The power density of wind plays a vital role in influencing the available wind potential at any site that can be evaluated as follows [42]:
where the term N denotes the number of wind data sets.
To assess the wind energy resource available at a particular location, it was necessary to assess the power density. It gives the available energy of the location that meets the wind energy conversion to electricity. With the help of the Weibull distribution function, the measurement of wind speed and the power density (W/m2) is determined using the following equation [41,42]:
where the term A denotes the rotor area in m2 and ρ terms a standard air density of the site.
The peak value of the probability density function is denoted by the most probable wind speed (Vmp) and is calculated using Equation (10) [43]:
The maximum energy (Vmax) carrying wind speed is used to choose the proper rating/design of the turbine. It can be derived as follows [43]:
4.2. Estimation of Technical and Economic Parameters
The power extraction from the wind energy system is evaluated using Equation (12) according to wind speed and rated power of the individual turbine.
where PR is the rated power of the turbine in Watts, Vi denotes the cut-in-speed of the wind in m/s, Vo represents the cut-out-speed of the wind in m/s, and the term VR denotes the average wind speed in m/s. The cost analysis is carried out using the cost of energy (COE) per kWh, and it can be determined by the following expression:
where PVC states the Present value cost that can be derived as follows:
where I represents the investment cost, r denotes a discount rate, Comr is the cost of operation and maintenance, the term i states the inflation rate, S defines the salvage values, and n defines the lifetime of the turbine. The cost breaks up of the per kW turbine is illustrated in Table 4.

Table 4.
Cost breakdown of turbine (per kW).
Annual energy production (AEP) cost is an important term to investigate the annual performance of the wind turbine. It can be computed as follows:
Then the capacity factor (CF) is defined as the ratio between the average output powers to the rated power of the wind turbine. It is dimensionless and can be expressed as follows:
5. Results and Discussions
This section describes the wind characteristics of the selected locations using Weibull “k” and “c” parameters. Subsequently, uncertainty factors of all four sites are described in detail to verify the feasibility of the effective energy conversion. In addition, the wake loss effect is demonstrated that helps to find the net AEP reduction for the entire lifetime of the project.
5.1. Wind Characteristics of Selected Passes
The historical time-series datasets are investigated from the Weibull distribution function using wind navigator using the Windographer software. From the analysis, the frequency and hours per year of the wind speed, yearly speed variation, the variation of scale and shape factor, dominant wind direction as per wind rose diagram, and the category of wind power class are analyzed.
5.1.1. Frequency Distribution
The frequency distribution of the wind speed gives the time interval, which was used to examine the energy potential in the wind at a particular location. The frequency distribution parameters were random, intermittent and the wind speeds varied by season, hours of a day, and weather events. This variation shows the time–wind speed correlation. Further, the wind speed frequency distribution can be analyzed statistically by concerning the speed of measured wind and time interval.
After estimating the distribution pattern of the wind speed, it was easy to investigate the potential along with the economic feasibility of a specified site. The output power of the wind turbine is a function of variable wind speed and is calculated based on the average wind speed or by analyzing the measurement of real-time data of frequency distribution of wind speed. The Weibull frequency distribution process is a widely used PDF to examine the characteristics of wind speed and to estimate the power density. The shape factor (k) was used for measuring the shape of the frequency distribution. The wind speed was concentrated and narrowly distributed for higher k values and widely distributed for the low value of k. The shape parameter (k) was large for sites with a constant or low variation of speed. The quality of wind was determined by the scale factor c, and its value was directly proportional to wind speed, i.e., high windy sites had high scale factors, while low wind sites had low scale factors. The PDF was deployed to project the total annual average output power by consolidating the power produced on an hourly basis at any wind speed [44]. Based on these inferences, the wind speed frequency distribution of all four wind passes, i.e., Aralvaimozhi, Shencottah, Palghat, and Cumbum, were analyzed at a hub height of 50 m and illustrated in Figure 7 using the Weibull distribution process.
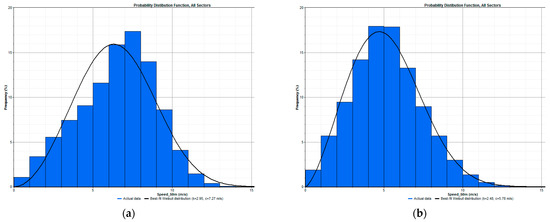
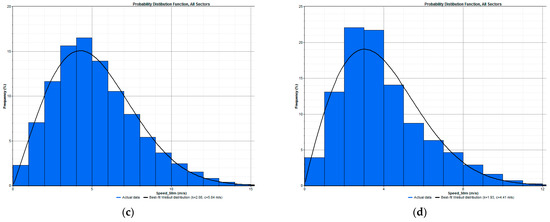
Figure 7.
Probability distribution functions (PDF) for (a) Aralvaimozhi (b) Shencottah (c) Palghat and (d) Cumbum.
From the PDF, the Weibull parameters, such as mean speeds and Weibull “k” and “c” parameters with an annual variation for four different wind passes, are depicted in Table 5. It was observed that the yearly highest value of the average wind speed at Aralvaimozhi wind pass showed a great value of about 7.034 m/s in the year 2004, and the lowest wind speed (mean) was recorded at the Cumbum location, i.e., 3.669 m/s in the year 2008.

Table 5.
“k” and “c” parameters of all four sites.
From Figure 8 and Figure 9, it is investigated that the Weibull “k” and “c” factor varied from 2.59 to 3.458 with a mean of 2.995 and 6.70 to 7.809 with a mean of 7.334 for Aralvaimozhi wind pass 2.089 to 2.738 with a mean of 2.478 and 5.348 to 6.172 with a mean of 5.813 for Shencottah pass,1.77 to 2.505 with a mean of 2.085 and 5.453 to 6.225 with a mean of 5.813 for Palghat pass and Cumbum pass 1.671 to 2.424 with a mean of 1.949 and 4.146 to 4.754 with a mean of 4.422, respectively analyzed for 20 years from the period 2000 to 2019. After finding the Weibull parameters “k” and “c”, it was possible to estimate the wind power density that was one of the vital indicators to describe the consistency of wind nature throughout the period (i.e., month, season, or year), which helps in the classification of wind power class in the four passes as depicted in Table 6.
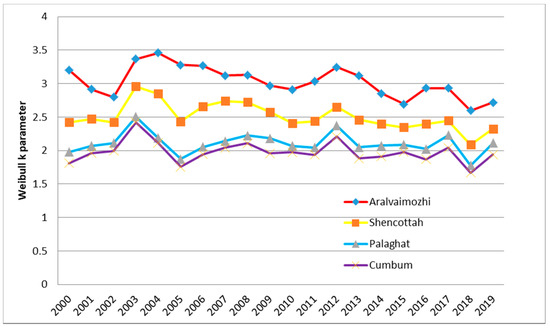
Figure 8.
Weibull shape parameter—k (annual variation).
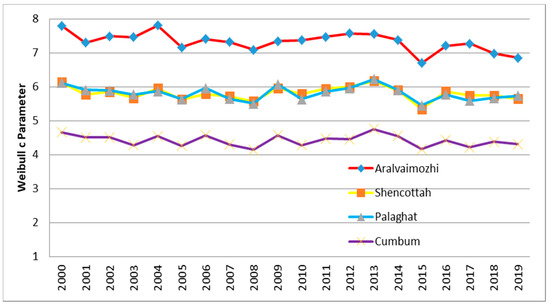
Figure 9.
Weibull scale parameter—c (annual variation).

Table 6.
Wind speed characteristics of wind passes in Tamil Nadu, India at 50 meters’ hub height.
5.1.2. Wind Rose Analysis
Wind or energy rose analysis provides the optimum placement of a wind turbine to maximize the energy and thereby decrease the wake losses. Before installing the wind turbines, past information of the prevailing wind direction (energy rose) is required that can maximize the energy production annually. Hence, wind direction investigation plays a vital role in the assessment of potential in the wind energy system. The status of the wind direction is if the wind is blowing from the same direction frequently, the rotation of the nacelle to face the wind through the yaw control mechanism is reduced, in turn ultimately reduces the wear and tear of the turbine components. The frequency distribution wind direction is usually represented in a polar form known as a wind rose. The wind rose plots divide each segment of the polar plot in the percentage of the frequency the wind is blowing in the speed range. These plots can be plotted by dividing the wind sample data into a suitable number of sectors (here in this investigation, the number of the sector is taken as 16) and computing the statistical share of each sector. From this analysis, the dominant direction of the wind from which the maximum energy can be explored will be known [45]. The wind rose is a graph depicting the time distribution of the direction and the azimuthal distribution of the wind speed in a specific location. A wind rose displays the anemometer data for sitting analysis, such as direction and wind speed. The distribution of wind speed and the wind direction at a particular location for time obtain graphically from the wind rose diagram. From the analysis, the dominant wind direction at 50 m hub height in the four wind passes is presented in Figure 10a–d. The wind rose diagrams also show the frequency of wind energy harvested from each direction is indicated by the concentric circles to the percentage.
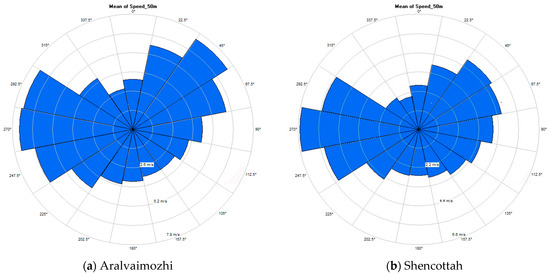
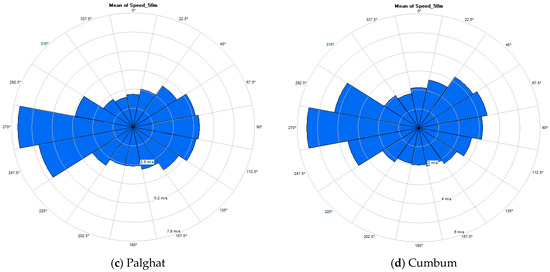
Figure 10.
Wind rose diagram.
From Figure 10a,b, it was concluded that the dominant wind direction indicated in this diagram were 270° and 45° in Aralvaimozhi and Shencottah wind pass locations. In Figure 10c,d, 270° and 67.5° are the dominant wind directions in Palghat and Cumbum wind passes. The wind rose analysis showed that the frequency of wind in calm conditions was depicted in the center and proved that the northwest direction contribution was more in all the four wind pass locations. It was summarized that most of the wind directions where the wind was the strongest were northwest.
Table 7 depicts the wind rose analysis, and it is clear that the maximum average speeds in all the four wind passes are dominant in the sector 270° with an average frequency of more than 25 percent.

Table 7.
The wind rose analysis of wind pass location in Tamil Nadu.
5.2. Uncertainty Factors of Selected Wind Pass
The energy conversion in a wind farm is stochastic and requires statistical analysis to estimate the technical and economic feasibilities. An assessment of uncertainties in wind energy conversion helps to identify the accurate value of the system and acts as a crucial factor to figure the profitability for the investors. Considering these facts, this subsection describes the various uncertainty factors that can affect the annual energy production and cost of generation of all selected locations.
The general definition of uncertainty is a measure of the random fluctuations of repeated measurement or the variability of the difference between predictions and observations of a process around the mean of those measurements or predictions. The calculation of the estimative energy production from a wind farm terrain is subject to uncertainties that must be accounted for to assess the risk of investments based on the accuracy of the estimated energy production. The main objective of considering these factors is to present the sources of uncertainty in the production of the energy estimate process for wind farms to identify the expected improvement in energy reliability and reduce the financial risks of the projects. The estimation of the annual energy production (AEP) and capacity factor is an important task to determine the assessment of uncertainties in the windy site. The techno-economic analyses of the wind-energy system involved in the study sites employ computation of the present value cost (PVC) relating to the AEP.
5.2.1. Probability of Exceedance (PoE)
There are several steps adopted to evaluate the total energy yield from WES, but every step of the applied approach is subject to uncertainties. Moreover, it is crucial to compute the accurate exceedance probabilities for the identification and quantification of uncertainties.
The resulting central or “P50” approximation of wind speed at any location has two major potential errors, such as resource measurement and/or modeling and interannual inconsistency of the renewable resource. The second category, i.e., the annual inconsistency of resources, refers to the variability of the wind resource over time, particularly up to a lifetime of the project that has significant variations from one year to another. It is a known fact that there is no accurate model to forecast those changes. In this context, uncertainty is calculated to account for interannual variation over the wind farm lifetime. The longer the lifespan of the project is, the more likely it is to reach the P50 in cumulated production.
The AEP predicted by wind data analysis has a 50% PoE, which is expressed as P50. This represents an energy value with a 50% probability of being exceeded. It is important to notice that the total uncertainty is related to the energy value in P50. The net AEP in P90 translates to a 90% probability of being attained or exceeded. It is recommended that the total uncertainty of the project should be around 15%. The higher the value of total uncertainty, the higher the difference between P50 and the other levels of probability of exceedance. In the case of P75, the AEP has a 25% probability of not reaching the AEP.
For any probability of exceedance level Pα, the equation is as follows:
where
P50 = P50 energy production estimate;
Zα,∞ = Standard normal distribution value for (1 − α) confidence level with infinite degrees of freedom;
σT = total uncertainty surrounding the central estimate of wind or solar generation (from Equation (17)).
Considering these facts, the probability of exceedance (POE) of all selected locations/passes are analyzed by placing ABL at 50 m and illustrated in Figure 11.
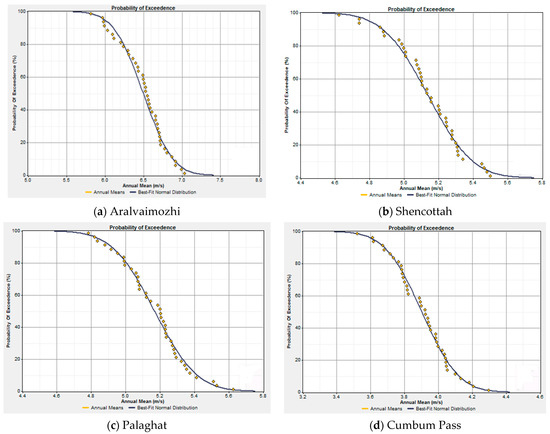
Figure 11.
Probability of exceedance (PoE) of all passes.
From the observed PoE of all passes, the percentage of uncertainty due to annual wind variations was estimated and is shown in Figure 12. As stated earlier, the uncertainty factor of any site should not exceed 15%. Attesting this statement, the uncertainty factors of Aralvaimozhi, Shencottah, Palghat, and Cumbum show good trends because they attained about 10.9%, 9.2%, 8.7%, and 10.3%, respectively. Among the four passes, the Palghat pass showed the least percentage of uncertainty. Overall, all four sites are suitable for wind energy resource assessment that offers low-risk to the investors and stakeholders.
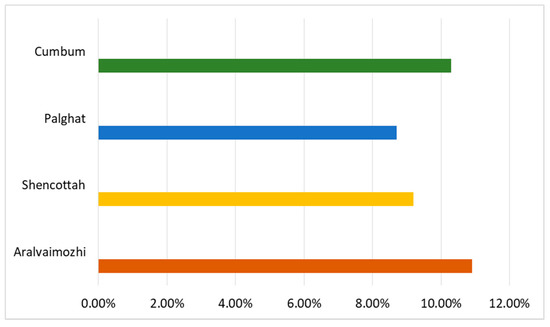
Figure 12.
Percentage of uncertainties of all passes.
5.2.2. Surface Roughness
The roughness of the terrain is influenced by obstacles like trees, buildings, and the effect of terrain contours like water surfaces, grass, shrubs, bushes, etc., affects the wind speed. Moreover, the orography of the passes determines the wind potential of the individual sites. In addition, the wind speed characteristics are widely affected by the ridges, cliffs, hills, etc., and the orography plays a vital role in setting the wind turbines in the specific site.
The roughness of a terrain surface can be parameterized by a single length scale and the roughness length (Z0), and the influence of, which on the wind speed profile is given by the logarithmic wind profile. It can be determined by the length and the terrain surface characteristics, including vegetation, built-up areas, and soil and water surfaces. Moreover, the roughness length is not constant but changes with foliation, growth of vegetation, snow cover, and sea state, etc. This should be taken into account in any climatological analysis.
The length of the roughness is defined by the height above the ground in meters at, which the wind speed is theoretically equal to zero. The roughness class is expressed in terms of roughness length in meters (Z0) and is given as follows:
The roughness class of any site can be derived from the roughness length and its terrain surface characteristics, as illustrated in Table 8.

Table 8.
Analysis of roughness class.
Considering all these inferences, the roughness class of the four wind pass locations, such as Aralvaimozhi, Shencottah, Palghat, and Cumbum passes, are studied. These locations are greatly influenced by the gaps and gorges and traverse through the Western Ghats with continuous mountain ranges and interrupted by the gaps, as shown in Figure 13.
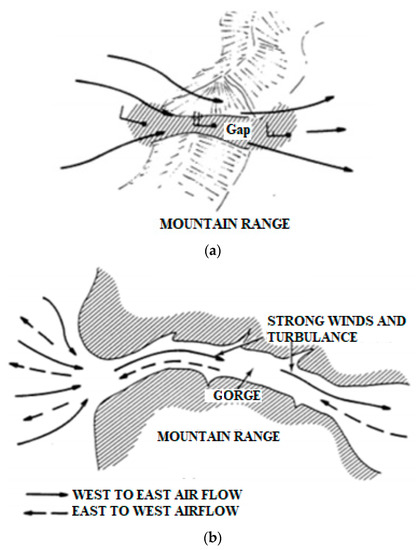
Figure 13.
(a) Gap and (b) gorge of the selected pass.
Due to these impacts, more wind speed is influenced by the “tunneling effect”. The ground class comes under the open terrain with smooth surface characteristics, such as concrete runways in airports, mowed grass, and some parts of grounds are with slight complex terrain in the four wind pass locations. In addition, these sites are majorly influenced by the Gaps and Gorges. With these references, the roughness lengths of all the four passes are found to be 0.0024 m, and it falls under the class of 0.5 that have the potential of 73% energy index.
5.2.3. Wind Shear Coefficient (WSC)
The variation in wind speed and direction is known as wind shear. Wind shear coefficients are derived by taking wind speeds at two different heights. Wind shear values are never constant; this is similar to the case of a wind profile, but it varies with the mean wind speed, the direction of the wind flow, atmospheric condition, the time of the day, the nature of the terrain, humidity, pressure, temperature and also the wind direction. The most general method to represent the variation of wind speed with the hub height can be represented by a power law:
where V1 and V2 are the mean wind speeds at heights of h1 and h2, respectively. The value depends on surface roughness and atmospheric stability. It should be within the range of 0.05 to 0.5. In addition, it depends upon the diurnal cycle of air above the ground. Due to the Diurnal hot and cooling cycle, it is clear that WSC is higher during the night and lower during the daytime. Over the 24 h of the day, the heating and cooling cycle of the air adjacent to the earth influences the wind shear coefficient. Figure 14 shows the wind shear coefficient annual variation in the four wind pass locations. It is inferred that in all the four wind pass locations, the wind shear is in the range of 0.1, and it is within the range.
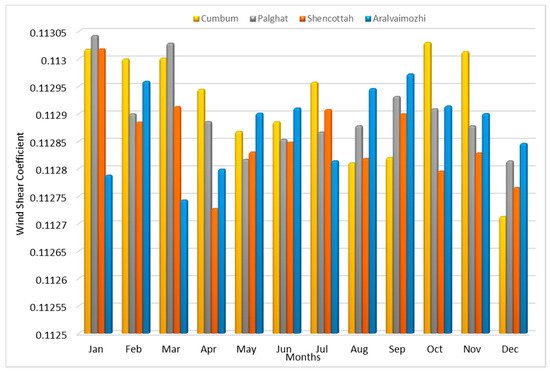
Figure 14.
Variation of wind shear coefficients with respect to the months in the four wind pass locations.
5.2.4. Wake Loss Effect (WLE)
The flow of wind in the wind farm is not uniform due to different types of terrain. Moreover, the placement of wind turbines in an array not facing the uniform wind resources and offers a wake effect. Specifically, downstream turbines receive a condensed wind resource when compared with upstream wind turbines that affect the overall efficiency of the conversion system. Theoretically, WLE is defined as the ratio between total generation with no wakes and actual generation with wake effect.
To increase the energy production, the wind farms layout (micro sittings) can be optimized, which in turn reduce the wake effects, both internal and external to the project. Figure 15 shows the wind farm array layout in the terrain that demonstrates the micro sitting with an inter-turbine spacing of a 7D*5D array configuration. Here, D denotes the rotor diameter of the turbine. Micro sitting is an important consideration while designing the wind farm, which in turn improves the wind park efficiency. The efficiency of the wind park is defined as the ratio between the actual energy extracted from the wind farm to the total energy yield. The proper sitting of several wind turbines in a certain orientation in an array improves the parking efficiency with reduced WLE because the main influencing factors of the wake loss are downwind spacing and crosswind spacing that are related to the turbine rotor diameter (D) configuration and its sittings.
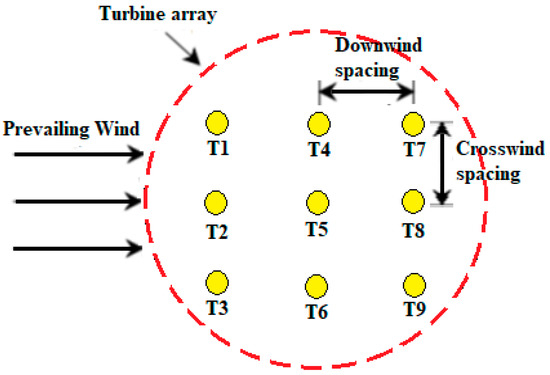
Figure 15.
Turbine array configuration.
There are various models to estimate the wake loss effect from wind farms with different accuracy levels. The notable models are as follows: Katic–Jensen model [46], Eddy viscosity model [47], Frandsen model [48], deep-array wake model [49], and Larsen model [50]. These models use simplified computation steps to estimate the wake effect accurately. Based on the real-time data retrieved from the wind farm investors from all four passes, the wake loss effects of Individual turbines from Aralvaimozhi, Shencottah, Palghat, and Cumbum passes are displayed in Figure 16.
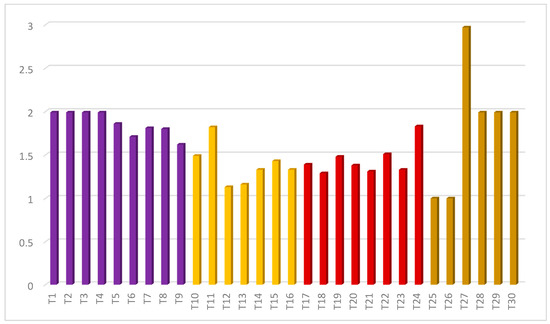
Figure 16.
Wake loss effect on turbines (%).
From the image, it is observed that the wake loss percentage on turbines shows greater variations. Particularly, Shencottah and Palghat pass concede the least percentage of wake loss when compared with Aralvaimozhi and Cumbum passes. Based on the observed percentages, the technical and economic characteristics of all turbines are evaluated in the following sections.
5.3. Technical Assessment
The technical characteristics of the selected wind turbine for all four passes are analyzed under two categories, namely with and without wake loss effect (WLE). The electrical parameters, such as output power, annual energy production (AEP), and capacity factor (CF) of individual turbines, are evaluated in detail. The output power of the wind turbines from all locations is estimated for both cases and represented in Figure 17. Among thirty turbines, T9 generates more power, about 440 kW, due to the better wind characteristic of Aralvaimozhi pass throughout the year. All four passes show a greater reduction in their output based on the characteristics of the WLE on each turbine. Further, AEP shows similar trends in their net rate variations between both cases based on the turbine output characteristics, as represented in Figure 18.
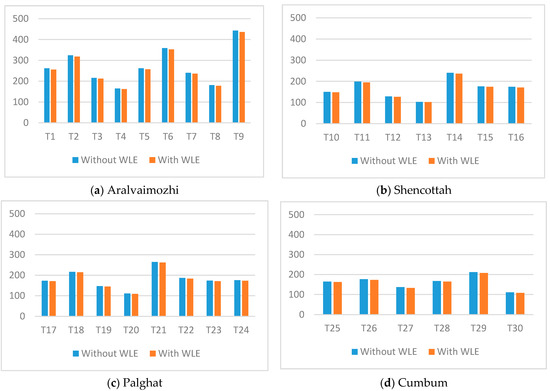
Figure 17.
Output power of the wind turbines (kW).
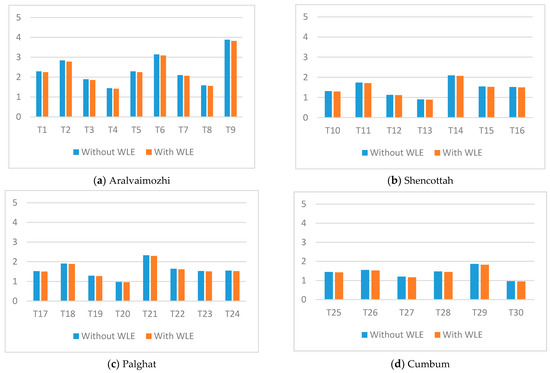
Figure 18.
Annual energy production (AEP) in kWh.
Further, the capacity factors of all wind turbines are examined for both cases using the relationship between average output generation to the rated values of the machine. The CF of the Aralvaimozhi shows improved characteristics for all turbines (T1 to T9) due to their superior value of rated wind speed, as illustrated in Figure 19.
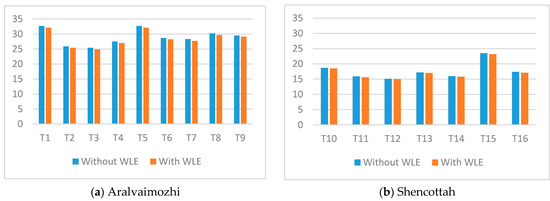
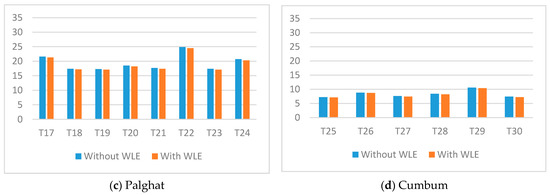
Figure 19.
Capacity factor.
Furthermore, the percentage variations of turbine output, AEP, and CF between both cases (with and without WLE) are shown in Figure 20 to demonstrate the effect of WLE. From the image, it is perceived that the Cumbum pass has a severe influence on WLE because the power output of the wind turbines is reduced up to 2.06%. Similarly, AEP and CF are reduced up to 1.96% and 2.0%, respectively. On other hand, Shencottah and Palghat display less percentage variation due to their reduced WLE.
Figure 20.
Percentage variation due to wake loss effect (WLE).
5.4. Economic Assessment (EA)
As stated in the above section, the EA of WECS depends on various factors due to the geographical parameters of the sites. Although the WECS requires free fuel, it involves a high magnitude investment cost. In addition, the selected sites should be suitable for a different range of turbines, notably from small standalone to large wind power plants. Before investment, the investors wanting a meticulous investigation of a wind farm to estimate their profit at the end of the lifetime of the project. Considering these implications, economic investigations of the wind turbines at different locations are studied for two cases, such as with and without the WLE effect. This analysis aims to estimate the total loss in profit for the investors due to the WLE, specifically where poor micro sittings were executed. Though optimized micro sittings are used in a wind farm, the investor can identify the actual AEP and CoE of the selected locations and selected wind turbines. Therefore, economic characteristics, such as CoE, AEP, and loss in profit of all the selected wind turbines from all four passes are scrutinized and illustrated in Table 9.

Table 9.
Economical characteristics of selected wind turbines.
It was observed that the CoE of the turbine T1 and T5 showed the least level among other turbines in the Aralvaimozhi pass for both with and without WLE. Further, among the turbines in Shencottah pass, turbine T15 conceded the least cost of CoE, about Rs. 1.970, and this was increased to Rs. 1.999 due to WLE. The wind turbines T22 and T28 offered a reduced cost of energy, about Rs. 1.863 and Rs. 0.966 for Palghat and Cumbum passes, respectively and showed the same trend with WLE. Among the turbines from all passes, turbine T28 at Cumbum passed, performing well with the least CoE because it comprised a better cut-in-speed and rated speed of 4.5 m/s and 16 m/s, respectively, when compared with other wind turbines.
Further, the WLE reduces the total AEP of the individual turbine, and it is found to be more for T9, T11, T21, and T29 for Aralvaimozhi (−62,967 kWh), Shencottah (−31,680 kWh), Palghat (−30,498 kWh), and Cumbum (−37,038 kWh) passes, respectively and this is due to the increased WLE of the specified turbines. The total loss of AEP from all four passes is found to be high, i.e., −8, 87, 836 kWh. Due to the increase of CoE and reduction of AEP, there is a great loss in profit for the wind farm investors at the end of the project lifetime. The total losses in profit from Aralvaimozhi, Shencottah, Palghat, and Cumbum passes are estimated to be Rs. 3.20 crores, Rs. 1.94 cores, Rs. 2.20 crores, and Rs. 2.71 crores, respectively. Consolidating the total losses from all passes, it is found to be Rs. 10.07 crores, which is a great loss in profit for the wind farm investors.
The above estimation of profit loss is furnished without considering the interest components. By considering 10% annual interest for the loss incurred due to WLE, a total loss is increasing rapidly for every year and estimated to be Rs.13.66 crores at the end of the 25th year, i.e., end of the project lifetime, as illustrated in Figure 21.
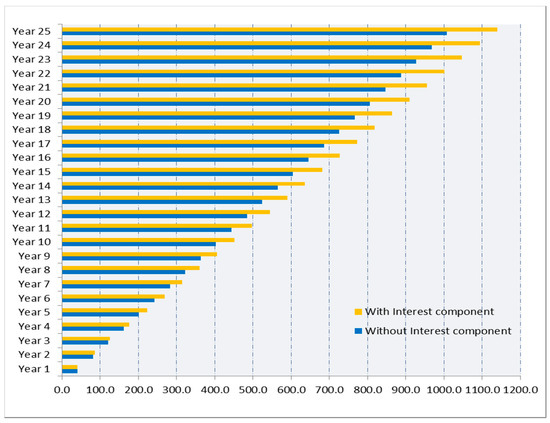
Figure 21.
Loss in profit with a 10% annual interest rate.
Consolidating all the inferences from the results and discussions, a small reduction of WLE offers great profit for the wind farm investors due to the increasing AEP and decreasing CoE. In addition, the proposed objectives were achieved as described below:
- The wind energy potential of the selected location of Tamilnadu, such as Aralvaimozhi, Palghat, Shencottah, and Cumbum, was studied and found to be great in all locations;
- The uncertainty factors, such as PoE, WSC, and surface roughness of all the four passes were in the acceptable band;
- The percentage of WLE was computed for all four passes;
- Considering the computed WLE, output power, AEP, CF, and loss in profit were evaluated.
Based on the attained results, it is recommended that the wind farm investors should investigate and reduces the wake loss using innovative optimization techniques. There are some possible measures to overcome these challenges, notably by adapting optimizing wind Farm control strategies because optimization methods can discover the global maximum or minimum of a function effectively. There are many heuristic and stochastic methods are adopted for optimal micro sitting, notably improved Park wake model optimization, dynastic optimization algorithm (DOA), non-dominated Sorting genetic algorithm-III (NSGA-III), binary particle swarm optimization (BPSO), two-echelon model [30,51,52], etc. However, the hybrid optimization techniques are not demonstrated greatly, and therefore the future work can be extended to adapt hybrid optimization technique for a micro sitting of wind turbines with WLE as the main factor.
Moreover, some notable limitations need to be considered before demonstrating the outcome of this work, such as the underdeveloped grid and its boundary. These may lead to a suboptimal evacuation of power that may incur heavy financial risk to the investors and government agencies. To overcome these challenges, existing infrastructure needs to be upgraded, i.e., prioritize anticipatory investment in grid expansion (Green energy corridors) to evacuate the generated power optimally.
6. Conclusions
In this paper, historical time-series, wind direction and speed data (2000–2019) for 20 years were considered for investigating the four wind passes in Tamil Nadu. Based on these Weibull parameters, the mean speed, power density, most probable wind speed, maximum energy-carrying speed, annual wind variation, and dominant wind direction in the wind passes are determined. The results are summarized as the following:
- The wind power density of Aralvaimozhi, Shencottah, Palghat, and Cumbum were recorded as 226 W/m2, 122 W/m2, 142 W/m2, and 66 W/m2, respectively;
- Mean wind speeds were recorded at the height of 50 (Aralvaimozhi location (6.653 m/s), Shencottah (5.164 m/s), Palghat (5.146 m/s) and Cumbum location (3.912 m/s));
- Among the four passes, the highest annual mean wind speed was registered at the Aralvaimozhi pass (7.304 m/s), and the lowest level was recorded at the Cumbum pass (3.669 m/s);
- The dominant wind speed was very strong in the northwest (270°) in all four wind passes.
- The uncertainty factors of all the four passes show the least percentage, i.e., less than 15%;
- The roughness lengths of all four passes were estimated to be 0.0024 m, which falls under the class of 0.5 with the potential of 73% energy index;
- In all four passes, WSCs were within the range, i.e., less than 0.1;
- The WLE reduces the total output power, AEP, and CF the most in Aralvaimozhi and Cumbum, and the least in Shencottah and Palghat;
- The total loss in profit was estimated to be Rs. 10.07 crores and Rs. 13.66 crores for with and without interest components, respectively, due to the WLE of all four passes.
From these summarized results, the Aralvaimozhi wind pass location has a huge potential with higher advantages for setting up the wind plant for exploring more power. In addition, the preliminary investigation should carry out in all four passes for the application of repowering using emerging optimization techniques that may reduce the WLE extensively.
Author Contributions
Conceptualization: V.S.S.B.; methodology: V.S.S.B.; software: V.S.S.B.; validation: N.J.S.; formal analysis: N.J.S.; data curation: K.R.; writing—original draft preparation: K.R.; writing—review and editing: M.H.A.; supervision: M.H.A. and M.-K.K.; funding acquisition: M.-K.K. All authors have read and agreed to the published version of the manuscript.
Funding
This research was supported by Basic Science Research Program through the National Research Foundation of Korea (NRF), funded by the Ministry of Education (2020R1A2C1004743). This research was also supported by the Korea Electric Power Corporation (Grant number: R19XO01-37).
Institutional Review Board Statement
Not aaplicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Acknowledgments
The authors would like to thank V. Sridhar, Project Assistant, National Institute of Wind Energy (NIWE), India for providing relevant information for this research. The authors would also like to express their gratitude to the editor-in-chief, editors, and reviewers for their comments and suggestions that helped to improve the quality of a manuscript.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Raju, K.; Elavarasan, R.M.; Mihet-Popa, L. An Assessment of Onshore and Offshore Wind Energy Potential in India Using Moth Flame Optimization. Energies 2020, 13, 3063. [Google Scholar] [CrossRef]
- Subramanian, S.; Sankaralingam, C.; Elavarasan, R.M.; Vijayaraghavan, R.R.; Raju, K.; Mihet-Popa, L. An Evaluation on Wind Energy Potential Using Multi-Objective Optimization-Based Non-Dominated Sorting Genetic Algorithm III. Sustainability 2021, 13, 410. [Google Scholar] [CrossRef]
- Gul, M.; Tai, N.; Huang, W.; Nadeem, M.H.; Yu, M. Assessment of Wind Power Potential and Economic Analysis at Hyderabad in Pakistan: Powering to Local Communities Using Wind Power. Sustainability 2019, 11, 1391. [Google Scholar] [CrossRef]
- Anthony, M.; Prasad, V.; Raju, K.; Alsharif, M.H.; Geem, Z.W.; Hong, J. Design of Rotor Blades for Vertical Axis Wind Turbine with Wind Flow Modifier for Low Wind Profile Areas. Sustainability 2020, 12, 8050. [Google Scholar] [CrossRef]
- Elavarasan, R.M.; Selvamanohar, L.; Raju, K.; Vijayaraghavan, R.R.; Subburaj, R.; Nurunnabi, M.; Khan, I.A.; Afridhis, S.; Hariharan, A.; Pugazhendhi, R.; et al. A Holistic Review of the Present and Future Drivers of the Renewable Energy Mix in Maharashtra, State of India. Sustainability 2020, 12, 6596. [Google Scholar] [CrossRef]
- Net Zero by 2050 Plan for Energy Sector is Coming. Available online: https://www.iea.org/commentaries/net-zero-by-2050-plan-for-energy-sector-is-coming (accessed on 10 February 2021).
- Global Energy Transformation: A Roadmap to 2050 (2019 Edition). Available online: https://www.irena.org/publications/2019/Apr/Global-energy-transformation-A-roadmap-to-2050-2019Edition (accessed on 10 February 2021).
- Bataineh, K.M.; Dalalah, D. Assessment of wind energy potential for selected areas in Jordan. Renew. Energy 2013, 59, 75–81. [Google Scholar] [CrossRef]
- NIWE. Available online: https://niwe.res.in/assets/Docu/India’s_Wind_Potential_Atlas_at_120m_agl.pdf (accessed on 29 January 2021).
- Ministry of New and Renewable Energy (MNRE). India-Paris Agreement Commitments, the Government of India. MNRE Annual Report 2018–19; MNRE: New Dehli, India, 2019.
- Ministry of New and Renewable Energy (MNRE). Programme Scheme Wise Physical Progress in 2019–20 and Cu-mulative up to March 2020; MNRE: New Dehli, India, 2020.
- From Zero To Five Gw—Offshore Wind Outlook For Gujarat And Tamil Nadu 2018–2032. Available online: https://gwec.net/wp-content/uploads/2021/01/GWEC_From-Zero-to-Five-GW-offshore-wind-outlook-for-Gujarat-and-Tamil-Nadu_2017.pdf (accessed on 30 January 2021).
- Tamilnadu Energy Development Agency. 2020. Available online: www.teda.in (accessed on 4 January 2021).
- National Institute of Wind Energy. 2020. Available online: https://niwe.res.in/department_wra_100magl.php (accessed on 4 January 2021).
- TANGEDCO. Available online: https://www.tangedco.gov.in/linkpdf/mpno3of2019.pdf (accessed on 13 January 2021).
- Yu, J.; Fu, Y.; Yu, Y.; Wu, S.; Wu, Y.; You, M.; Guo, S.; Li, M. Assessment of Offshore Wind Characteristics and Wind Energy Potential in Bohai Bay, China. Energies 2019, 12, 2879. [Google Scholar] [CrossRef]
- Kumar, M.B.H.; Balasubramaniyan, S.; Padmanaban, S.; Holm-Nielsen, J.B. Wind Energy Potential Assessment by Weibull Parameter Estimation Using Multiverse Optimization Method: A Case Study of Tirumala Region in India. Energies 2019, 12, 2158. [Google Scholar] [CrossRef]
- De Andrade, C.F.; Dos Santos, L.F.; Macedo, M.V.S.; Rocha, P.A.C.; Gomes, F.F. Four heuristic optimization algorithms applied to wind energy: Determination of Weibull curve parameters for three Brazilian sites. Int. J. Energy Environ. Eng. 2018, 10, 1–12. [Google Scholar] [CrossRef]
- Mohammadi, K.; Alavi, O.; McGowan, J.G. Use of Birnbaum-Saunders distribution for estimating wind speed and wind power probability distributions: A review. Energy Convers. Manag. 2017, 143, 109–122. [Google Scholar] [CrossRef]
- Abas, H.; Vahid, R.; Simin, R. Wind energy potential assessment in order to produce electrical energy for case study in Divandareh, Iran. In Proceedings of the International Conference on Renewable Energy Research and Applications, Milwakuee, WI, USA, 19–22 October 2014. [Google Scholar]
- Okeniyi, J.O.; Ohunakin, O.S.; Okeniyi, E.T. Assessments of Wind-Energy Potential in Selected Sites from Three Geopolitical Zones in Nigeria: Implications for Renewable/Sustainable Rural Electrification. Sci. World J. 2015, 2015, 581679. [Google Scholar] [CrossRef]
- Rezaeiha, A.; Montazeri, H.; Blocken, B. A framework for preliminary large-scale urban wind energy potential assessment: Roof-mounted wind turbines. Energy Convers. Manag. 2020, 214, 112770. [Google Scholar] [CrossRef]
- Hulio, Z.H.; Jiang, W. Wind energy potential assessment for KPT with a comparison of different methods of determining Weibull parameters. Int. J. Energy Sect. Manag. 2020, 14, 59–84. [Google Scholar] [CrossRef]
- Chen, X.; Foley, A.; Zhang, Z.; Wang, K.; O’Driscoll, K. An assessment of wind energy potential in the Beibu Gulf considering the energy demands of the Beibu Gulf Economic Rim. Renew. Sustain. Energy Rev. 2020, 119, 109605. [Google Scholar] [CrossRef]
- Teimourian, A.; Bahrami, A.; Teimourian, H.; Vala, M.; Huseyniklioglu, A.O. Assessment of wind energy potential in the southeastern province of Iran. Energy Sourcespart A Recover. Util. Environ. Eff. 2019, 42, 329–343. [Google Scholar] [CrossRef]
- Idriss, A.I.; Ahmed, R.A.; Omar, A.I.; Said, R.K.; Akinci, T.C. Wind energy potential and micro-turbine performance analysis in Djibouti-city, Djibouti. Eng. Sci. Technol. Int. J. 2020, 23, 65–70. [Google Scholar] [CrossRef]
- Saeed, M.A.; Ahmed, Z.; Zhang, W. Wind energy potential and economic analysis with a comparison of different methods for determining the optimal distribution parameters. Renew. Energy 2020, 161, 1092–1109. [Google Scholar] [CrossRef]
- Deep, S.; Sarkar, A.; Ghawat, M.; Rajak, M.K. Estimation of the wind energy potential for coastal locations in India using the Weibull model. Renew. Energy 2020, 161, 319–339. [Google Scholar] [CrossRef]
- Mark, S. A Multi-Project Validation Study of Vaisala’s Wake Loss Estimation Method; Vaisala: Vantaa, Finland, 2019. [Google Scholar]
- Nygaard, N.G. Systematic Quantification of Wake Model Uncertainty. In Proceedings of the EWEA Offshore, Bella Center Copenhagen, Copenhagen, Denmark, 10–12 March 2015. [Google Scholar]
- UNESCO. World Heritage List, “Western Ghats”. Available online: https://whc.unesco.org/en/list/1342/ (accessed on 29 January 2020).
- Ramachandra, T.V.; Ganesh, H. Sustainable Decentralised Green Energy Options for Western Ghats. Sahy-Adri E-New 2017, 43, 1–26. [Google Scholar]
- Global Wind Atlas. Available online: https://globalwindatlas.info/area/India/Tamil%20Nadu (accessed on 29 January 2021).
- Palaneeswari, T. Wind Power Development in Tamil Nadu. Int. J. Res. Soc. Sc. 2008, 8, 661–673. [Google Scholar]
- Windographer. Available online: https://www.ul.com/resources/apps/windographer (accessed on 29 January 2021).
- Bagiorgas, H.S.; Giouli, M.; Rehman, S.; Al-Hadhrami, L.M. Weibull parameters estimation using four different meth-ods and most energy-carrying wind speed analysis. Int. J. Green Energy 2011, 8, 529–554. [Google Scholar] [CrossRef]
- Mahmood, F.H.; Resen, A.K.; Khamees, A.B. Wind characteristic analysis based on Weibull distribution of Al-Salman site, Iraq. Energy Rep. 2020, 6, 79–87. [Google Scholar] [CrossRef]
- Gul, M.; Tai, N.; Huang, W.; Nadeem, M.H.; Yu, M. Evaluation of Wind Energy Potential Using an Optimum Approach based on Maximum Distance Metric. Sustainability 2020, 12, 1999. [Google Scholar] [CrossRef]
- Soulouknga, M.; Doka, S.; Revanna, N.; Djongyang, N.; Kofane, T.C. Analysis of wind speed data and wind energy potential in Faya-Largeau, Chad, using Weibull distribution. Renew. Energy 2018, 121, 1–8. [Google Scholar] [CrossRef]
- Islam, M.; Saidur, R.; Rahim, N. Assessment of wind energy potentiality at Kudat and Labuan, Malaysia using Weibull distribution function. Energy 2011, 36, 985–992. [Google Scholar] [CrossRef]
- Alcala, G.; Perea-Moreno, A.J.; Hernandez-Escobedo, Q. Wind resource assessment using Weibull function for different periods of the day in the Yucatan Peninsula. Chem. Eng. Trans. 2019, 76, 1003–1008. [Google Scholar]
- Akdağ, S.A.; Güler, Ö. Calculation of Wind Energy Potential and Economic Analysis by Using Weibull Distribution—A Case Study from Turkey. Part 1: Determination of Weibull Parameters Energy Sources, Part B: Economics, Planning, and Policy. Energy Sources 2009, 4, 1–8. [Google Scholar] [CrossRef]
- Ozay, C.; Celiktas, M.S. Statistical analysis of wind speed using two-parameter Weibull distribution in Alacati region. Energy Convers. Manag. 2016, 121, 49–54. [Google Scholar] [CrossRef]
- Al Ameri, A.; Ounissa, A.; Nichita, C.; Djamal, A. Power Loss Analysis for Wind Power Grid Integration Based on Weibull Distribution. Energies 2017, 10, 463. [Google Scholar] [CrossRef]
- Kutty, S.S.; Khan, M.G.M.; Ahmed, M.R. Estimation of different wind characteristics parameters and accurate wind resource assessment for Kadavu, Fiji. Aims Energy 2019, 7, 760–791. [Google Scholar] [CrossRef]
- Jensen, N. A Note on Wind Generator Interaction Tech; RisΦ National Laboratory: Roskilde, Denmark, 1983; pp. 1–16. [Google Scholar]
- Ainslie, F.F. Calculating the flow field in the wake of wind turbines. J. Wind Eng. Ind. Aerodyn. 1988, 27, 213–224. [Google Scholar] [CrossRef]
- Frandsen, S.; Barthelmie, R.; Pryor, S.; Rathmann, O.; Larsen, S.; Højstrup, J.; Thøgersen, M. Analytical modelling of wind speed deficit in large offshore windfarms. Wind Energy 2006, 9, 39–53. [Google Scholar] [CrossRef]
- Brower, M.C.; Robinson, N.M. The Open Wind Deep-Array Wake Model-Development and Validation; AWS Truepower: Albany, NY, USA, 2012; pp. 1–16. [Google Scholar]
- LGC. A Simple Stationary Semi-Analytical Wakemodel; Risø National Laboratory for Sustainable Energy, Technical University of Denmark: Roskilde, Denmark, 2009. [Google Scholar]
- Zhang, Y.; Hu, Y.; Wang, F.; Liu, Y. Research and Application of Micro-sitting optimization Model in Low Wind Speed Regions. In Proceedings of the 2020 12th IEEE PES Asia-Pacific Power and Energy Engineering Conference (APPEEC), Nanging, China, 20–23 September 2020; pp. 1–6. [Google Scholar]
- Massan, S.-U.-R.; Wagan, A.I.; Shaikh, M.M. A new metaheuristic optimization algorithm inspired by human dynasties with an application to the wind turbine micrositing problem. Appl. Soft Comput. 2020, 90, 106176. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).