A Hesitant Fuzzy Combined Compromise Solution Framework-Based on Discrimination Measure for Ranking Sustainable Third-Party Reverse Logistic Providers

Abstract

Customers’ pressure, social responsibility, and government regulations have motivated the enterprises to consider the reverse logistics (RL) in their operations. Recently, companies frequently outsource their RL practices to third-party reverse logistics providers (3PRLPs) to concentrate on their primary concern and diminish costs. However, to select the suitable 3PRLP candidate requires a multi-criteria decision making (MCDM) process involving uncertainty owing to the presence of many associated aspects. In order to choose the most appropriate sustainable 3PRLP (S3PRLP), we introduce a hybrid approach based on the classical Combined Compromise Solution (CoCoSo) method and propose a discrimination measure within the context of hesitant fuzzy sets (HFSs). This approach offers a new process based on the discrimination measure for evaluating the criteria weights. The efficiency and practicability of the present approach are numerically demonstrated by solving an illustrative case study of S3PRLPs selection under a hesitant fuzzy environment. Moreover, sensitivity and comparative studies are presented to highlight the robustness and strength of the introduced methodology. The result of this work concludes that the introduced methodology can recommend a more feasible performance when facing with determinate and inconsistent knowledge and qualitative data.

1. Introduction

Over the last two decades, supply chain management (SCM) has been popularized as a significant part of every company, no matter whether the size of the company is large or small. SCM encompasses the planning and management of all supply chain activities engaged in sourcing and procurement, conversion, and all logistics management activities with the objective of maximizing customer value, creating net value, and achieving a sustainable competitive advantage [1]. Logistics, one of the core components of effective SCM, is not only delivering the merchandise but also proffering the opportunity for stock to be returned to the suppliers through a feedback loop. Along with the requirement or prospective for the recycling of redundant stock, emergent global environmental concerns and increasing revenues from effective product returns strategies have encouraged some industrialists and researchers to originate a novel concept termed as “reverse logistics (RL)”. It stands for all the processes or activities associated with the reuse of products and materials. RL is the process of scheduling, implementing, and controlling the well-organized, cost-effective flow of raw materials, in-process inventory, finished merchandise, and related information for returned products in reverse flow of the classical supply chain in order to recover value and get the competitive advantage [2]. Effective RL is believed to result in direct benefits, consisting of enhanced customer satisfaction, decreased resource investment levels, increased protection level of the environment with recycling and proper disposal, and reductions in storage and distribution costs [3,4].

The pressure of increasing costs of enterprises, commercial competition, globalization of business activities, legislative pressure, and customers are compelling the companies to pay increasing attention to their RL activities. The companies have three different modes to handle their RL operations, which are (i) handle them in-house; (ii) manage them through a reliable logistics subsidiary or group company, either by setting up or buying an associated logistics firm [1], and (iii) outsource this function to an exterior provider [5]. Nonetheless, several enterprises struggle for implementing RL in house because they do not have adequate capacity to manage this function. Moreover, there are massive risks involved in setting up or buying a logistics firm, and doing so may have a negative consequence on the company’s core business, particularly its economic and operational features. Indeed, outsourcing the company’s RL operations may be important to facilitate a company for pursuing financial efficiency, operational investments, and sustainable long-term development. One of the essential decisions that must be made with RL activities is the selection of appropriate third party reverse logistics provider (3PRLP). The suitable 3PRLP candidate offers benefits in terms of operational and resource efficiency, cost reduction, improvement in performance, organizational competitiveness, and long-term development of the company [2,4]. Thus, the 3PRLP selection decision can be a strategic issue faced by supply chain executives in retaining organizational strategic competitive advantage. The process of choosing a proper sustainable 3PRLP (S3PRLP) can be treated as a multi-criteria decision making (MCDM) due to the presence of multiple qualitative and quantitative criteria.

Uncertainty common occurs in the S3PRLP selection process. The fuzzy set theory [6] has been successfully implemented to solve the uncertain 3PRLP selection problem. Sometimes, the decision-making experts (DMEs) might assess the Belongingness Degree (BD) of an object to a set of various distinct degrees in numerous real-life circumstances because of their individual attention, time restrictions, and deficiency of information. For example, if a group of DMEs is required to offer the BD of a particular opinion to an adult age cluster, the first DME wishes 0.65, another 0.70, and the last one does not recommend the BD due to the time restrictions and deficiency of knowledge/information/data [7]. To handle this issue, the doctrine of HFSs was given by Torra and Narukawa [8], which offers the BD to comprise various distinct assessment degrees. As the extension of FSs, HFSs have gained much interest from the researchers in dealing with the ambiguity that occurred in daily life problems. It is represented by a BD and signified by a set of possible degrees. Recently, it is revealing that the HFSs have powerfully associated to the existing concepts, namely, Intuitionistic Fuzzy Sets (IFSs) [9], Type-2 Fuzzy Sets (T2FSs) [10], and Fuzzy Multi Sets (FMSs) [11]. As stated by Torra [7], the prime concern to invent HFSs is that when describing the BD of an object, the complexity of generating the BD is not a margin of error (previously seen in IFSs) or specific possibility distribution (previously seen in T2FSs) on the possibility degrees, but a possible degrees’ set. Owing to the association with mentioned extended FSs, HFSs are distinguished as IFSs when it is a non-void closed interval; in specific concerns, HFSs can describe FMSs, even if the laws for FMSs do not implement properly to HFSs. Since its appearance, a great number of studies have been conducted within the HFSs context. However, there is no study regarding the proposed hesitant fuzzy-based decision-making methodology for selecting a desirable S3PRLP alternative over a set of multiple conflicting criteria.

In the process of selecting an ideal S3PRLP alternative, it is expected to deal with the compromise of performance values of partner candidates over incompatible or diverse influencing factors. In several situations, a comprehensive study on the fundamental properties of compromise solutions can assist the MCDM procedure. Presently, lots of MCDM techniques have been introduced to investigate the compromise solutions, such as the VlseKriterijumska Optimizacija I Kompromisno Resenje (VIKOR), Technique for Order of Preference by Similarity to Ideal Solution (TOPSIS), COmbinative Distance-based Assessment (CODAS), EDAS (Evaluation Based on Distance from Average Solution), and Complex Proportional Assessment (COPRAS). Nonetheless, the preference ordering of the candidates attained by these techniques may fluctuate extensively owing to the variation of weight distribution of the criteria. In other words, the consistency and stability of the outcomes obtained by these approaches are restricted [12,13]. To conquer this issue, Yazdani et al. [14] introduced the idea of Combined Compromise Solution (CoCoSo) approach, which mingles the combined compromise decision-making algorithm with some aggregation strategies to get a versatile compromise solution. The compromise solution acquired by the CoCoSo approach is consistent with that attained by other MCDM approaches, but it is not simply influenced by the amendment of weight distribution of criteria. This means that the CoCoSo approach has high reliability and stability regarding the ranking of alternatives.

In a real-life S3PRLP selection process, there are various cases wherein people feel doubtful or hesitant for one or another reason, which makes it complex for them to reach agreement on a final judgment. In other words, it is often hard for a panel of experts that comprises numerous DMEs to acquire suitable and realistic outcomes against a set of provider candidates over multiple qualitative and quantitative criteria. Moreover, in reality, it is difficult to evaluate the 3PRLP candidates and choose a desirable one(s) because of the existence of multiple conflicting factors, lack of information, and time limitation. Consequently, there is a need to establish an appropriate framework for handling the 3PRLP selection problem with uncertainty from sustainable viewpoints. In order to overcome the above-discussed shortcomings, this study focuses under a hesitant fuzzy sets (HFSs) context, as the HFS theory is one of the remarkable tools for handling the hesitant information that arises in practical applications. For ranking of the alternatives, the classical CoCoSo method has high stability and reliability regarding the preference ordering of the alternatives. Thus, in this work, we develop an integrated hesitant fuzzy-based CoCoSo methodology that can efficiently tackle the intrinsic uncertainty and the hesitancy in DME’s opinions and provide a compromise solution for the S3PRLP selection problem. Since the weight determination of criteria has a momentous impact on the decision outcomes, thus, this paper proposes a new hesitant fuzzy discrimination measure-based formula to calculate the criteria weights. The proposed method in this study offers an easy calculation process with accurate and consistent results for assessing S3PRLPs. In this perspective, the major contributions are listed as follows:

• A novel integrated HF-CoCoSo methodology is introduced for solving MCDM problems with HFSs.
• An HF-discrimination measure based framework is employed for evaluating the criteria weights.
• The proposed method is implemented to choose an optimal S3PRLP for an automobile manufacturing company within the HFS context.
• At last, comparison with extant approaches and sensitivity assessment are studied to confirm the reliability and practicability of the outcomes.

The present manuscript is systematized as follows: Section 2 confers the comprehensive reviews associated to the present study. Section 3 discusses the fundamentals of the HFSs. Section 4 pioneers an innovative HF-CoCoSo technique for solving MCDM problems under an HFSs environment. Section 5 discusses a decision-making example related to the S3PRLPs selection problem with uncertainty. In addition, comparative and sensitivity analyses are conferred at the end of this section. Lastly, Section 6 suggests the conclusions and scope for future research.

2. Preliminaries

The current section presents comprehensive literatures related to this study.

2.1. Hesitant Fuzzy Set (HFS)

As the extension of FSs, HFSs [7,8] have gained much interest from the researchers in dealing with the ambiguity occurred in daily life problems. It is represented by a BD and signified by a set of possible degrees. Next, a great number of studies have been considered and applied under the HFSs context. For instance, Xia and Xu [15] and Xia et al. [16] presented a set of Aggregation Operators (AOs) on HFSs. Xu and Xia [17,18] pioneered the distance measure on HFSs and discussed the relationship between different information measures. He et al. [19] and Sun [20] presented the HF-power geometric and normalized geometric Bonferroni mean operators and used them to handle MCDM problems under HFS settings. Liao et al. [21] introduced the measures of correlation on HFSs. Li et al. [22] and Hu et al. [23] discussed several hesitant fuzzy information measures. Cuiping et al. [24] constructed several novel prioritized AOs. Yu [25] firstly offered the notion of HF-Heronian mean operators. Lv et al. [26] firstly suggested the conception of a feature vector and then studied the hesitant fuzzy information measures. Wang [27] used the combination of similarity measures and applied the synthetical procedure for HFSs. In addition, they used their formula for clustering analysis within the HFSs context.

Currently, HFS has extensively been employed in decision-making applications owing to its usefulness in articulating the ambiguous information. Afterward, numerous techniques have been presented to elucidate the MCDM problems under the HFSs environment. Lan et al. [28] suggested an innovative MCDM model with a new priority degree formula under HFSs environment. Mousavi et al. [29] introduced the HF-Elimination and Choice Expressing the REality (HF-ELECTRE) technique to assess the renewable energy source assessment problem. Wu et al. [30] employed a modified HF-VIKOR-based model for prioritizing engineering characteristics of an electric vehicle. It is worthwhile to say that various theoretical and practical reasoning can be simplified with the help of a uniformly typical HFS, which was articulated by Alcantud and Torra [31]. Cheng [32] recommended a novel autocratic approach using group recommendations for HFSs to deal with the green hotel assessment problems. Liu et al. [33] initiated the hesitant fuzzy cognitive maps and showed how to use it to explore the risk factors that arise in an electric power system. With the implementation of the HF-Complex Proportional Assessment (HF-COPRAS) method, Mishra et al. [34] assessed and presented the ranking order of the service quality alternatives for vehicle insurance companies. In a further study, Mishra et al. [35] designed an innovative framework within the HFSs environment to evaluate and prioritize green supplier alternatives. Farhadinia and Herrera-Viedma [36] re-defined the existing definition of extended HFS by employing the Cartesian product of HFS. Wang et al. [37] extended the group emergency decision-making (GEDM) method using hesitant fuzzy numbers. Mokhtia et al. [38] adapted the Ridge, least absolute shrinkage and selection operator (LASSO), and Elastic Net regression techniques for the task of choosing a feature. Çolak and Kaya [39] proposed a hybrid technique to solve the energy storage technology selection problem within the HFS setting. Mardani et al. [40] proposed a combined structure based on different approaches with HFS to assess the digital health intervention during the COVID-19 pandemic. Wu et al. [41] designed a trust-based social network group decision-making methodology with HF preference relations to the Water–Energy–Food nexus estimation. Narayanamoorthy et al. [42] gave a latest ranking scheme, named as HF-Multi-Objective Optimization on the basis of Simple Ratio Analysis (HF-MOOSRA), for evaluating and choosing an ideal bio-medical waste disposal treatment method. Rani et al. [43] assessed and prioritized the sustainable suppliers by employing the HF-Step-wise Weight Assessment Ratio Analysis-COPRAS methodology. Demirel et al. [44] proposed an innovative Choquet integral-based hesitant fuzzy decision-making method to prevent soil erosion. To deal with the hydrogen underground storage site selection decision-making problem under an interval type-2 HFS domain, Deveci [45] introduced a multi-criteria decision support system based on interval type-2 HFS. In the literature, several other models have been discussed within the HFSs setting [46,47].

2.2. Combined Compromise Solution (CoCoSo) Method

Existing studies offer various MCDM approaches for dealing with the practical MCDM issues. However, the preference results obtained by the extant decision-making approaches [48,49] have low reliability and stability due to change of weight distributions of criteria, which may be irrational for DEs to opt an ideal option. To surmount this limitation, Yazdani et al. [14] initiated a novel CoCoSo method that offers effective and simple calculation steps to deal with the uncertain information in a logical way. It integrates the two most prominent MCDM models, which are simple additive weighting (SAW) and exponentially weighted product (EWP). In recent times, copious scholarly articles have focused their interest on the development and application of the CoCoSo method. For instance, Yazdani et al. [50] introduced the decision making trial and evaluation laboratory (DEMATEL) and best worst method (BWM)-based gray extension of the CoCoSo approach to select the ideal supplier in construction management. In a further study, Wen et al. [13] originated a collective methodology by combining the CoCoSo model and hesitant linguistic fuzzy set and then applied it to a decision-making problem. Peng and Smarandache [51] developed a novel neutrosophic soft CoCoSo method for China’s rare earth industry security assessment. Liao et al. [52] introduced an innovative Pythagorean fuzzy CoCoSo method for the selection of cold chain logistics delivery center. Alrasheedi et al. [53] suggested a novel IVIF-CoCoSo technique for assessing the green growth indicators to accomplish sustainable development in the manufacturing region. Rani and Mishra [54] gave a single-valued neutrosophic CoCoSo method for evaluating sustainable waste electrical and electronics equipment recycling partners. In a recent study, Liu et al. [55] evaluated and selected an appropriate medical waste treat technology by using a Pythagorean fuzzy CoCoSo approach.

From the aforementioned discussion, we can see that an integrated method based on the CoCoSo approach with HFSs can additionally improve the practicality of the CoCoSo approach with uncertain decision-making settings.

2.3. Sustainable Third-Party Reverse Logistics Provider (S3PRLP) Assessment

The S3PRLP assessment problem is a complex MCDM problem due to the participation of numerous decisive factors. To choose the optimal S3PRLP option and enhance the precision and consistency of the outcomes, lots of new MCDM procedures have been considered and utilized to several fields [56,57,58]. FSs and their generalizations have expansively been employed to manage the uncertain and vague information that occurs in realistic MCDM processes. Efendigil et al. [59] designed a two-way method by integrating artificial neural networks and fuzzy logic for the evaluation of an ideal 3PRLP alternative. Govindan [60] designed a fuzzy-based procedure for assessing the 3PRLP selection problem. Govindan and Murugesan [61] used the fuzzy extent assessment approach for choosing the desirable 3PRLP for a battery manufacturing industry. Corresponding to AHP and TOPSIS approaches, Senthil et al. [62] suggested a combined model for evaluating an ideal reverse logistics contractor. Uygun et al. [63] planned and selected an outsourcing provider for a telecommunications business by employing DEMATEL and ANP methods for FSs. Mavi et al. [64] presented the SWARA method for weighting the assessment criteria of 3PRLP in the plastics industry and further ranked the S3PRLP alternatives through the MOORA model within FSs. Tavana et al. [65] suggested a combined method with the integration of ANP and gray superiority and inferiority methods on IFSs for the assessment of the 3PRLPs selection process. Li et al. [66] used a combined cumulative prospect doctrine with hybrid information MCDM methodology for the evaluation of 3PRLPs from sustainability perspectives. Zarbakhshnia et al. [67] weighted the assessment criteria through the fuzzy-SWARA method and ranked the S3PRLPs by employing the COPRAS method under a fuzzy environment. Zhang and Su [68] introduced a dominance degree-based heterogeneous linguistic model to assess the best S3PRLP for a car manufacture industry. On the basis of fuzzy AHP and gray MOORA, Zarbakhshnia et al. [69] originated a collective MCDM method for assessing the S3PRLP alternatives. Chen et al. [1] suggested a new multi-perspective multi-attribute decision-making support system for the evaluation and prioritization of 3PRLPs under an HF linguistic term set environment. Mishra et al. [70] gave a combined framework with CRITIC and EDAS methods for Fermatean fuzzy sets (FFSs) to deal the S3PRLP selection problem in which the attributes and DEs’ weights are completely unknown.

3. Preliminaries

The present section is dedicated to describing the fundamental definitions and operations of HFSs. The concept of HFSs was pioneered by Torra [7] and Torra and Narukawa [8], to handle the problems where the BD of an element to a given set includes some diverse values.

Definition 1

[7].An HFS on the fixed universal set $\Omega$ is often expressed by the following mathematical form:

$$S=\left\{\langle v,h_S\left(v\right)\rangle :v\in \Omega \right\},$$

(1)

where $h_S\left(v\right)$, called as a hesitant fuzzy element (HFE), is a set of some values in $[0,1]$, denoting the possible BD of an element $v\in \Omega$ to the set S. Based on the set of all HFEs of S, the HFS S can be defined as $S=\left\{\langle v,\underset{k\in h_S\left(v\right)}{\cup }\left\{k\right\}\rangle :v\in \Omega \right\}$.

Example 1.

If $\Omega =\{v_1,v_2,v_3\}$ is the fixed universal set, $h(v_1)=\{0.2,0.4,0.5\}$, $h(v_2)=\{0.3,0.4\}$ and $h(v_3)=\{0.3,0.2,0.5,0.6\}$ are the HFEs of $v_i(i=1,2,3,4)$ to a set S, respectively. Then, the set S can be considered as an HFS and mathematically represented as $S=\left\{\langle v_1,\{0.2,0.4,0.5\}\rangle ,\langle v_2,\{0.3,0.4\}\rangle ,\langle v_3,\{0.3,0.2,0.5,0.6\}\rangle \right\}$.

Definition 2

[7,15].Let $h,h_1,h_2\in HFEs\left(Y\right)$. Then, the operations on HFEs are discussed as follows:

(a)	$h^c={\displaystyle \underset{\kappa \in h}{{\displaystyle \cup }}\left\{1-\kappa \right\}};$
(b)	$h_1\cup h_2={\displaystyle \underset{{\kappa }_1\in h_1,{\kappa }_2\in h_2}{{\displaystyle \cup }}\max \left\{{\kappa }_1,{\kappa }_2\right\}};$
(c)	$h_1\cap h_2={\displaystyle \underset{{\kappa }_1\in h_1,{\kappa }_2\in h_2}{{\displaystyle \cup }}\min \left\{{\kappa }_1,{\kappa }_2\right\}};$
(d)	$\lambda h={\displaystyle \underset{\kappa \in h}{{\displaystyle \cup }}\left\{1-{\left(1-\kappa \right)}^{\lambda }\right\}},\lambda >0;$
(e)	$h^{\lambda }={\displaystyle \underset{\kappa \in h}{{\displaystyle \cup }}\left\{{\kappa }^{\lambda }\right\}},\lambda >0;$
(f)	$h_1\oplus h_2={\displaystyle \underset{{\kappa }_1\in h_1,{\kappa }_2\in h_2}{{\displaystyle \cup }}\left\{{\kappa }_1+{\kappa }_2-{\kappa }_1{\kappa }_2\right\}};$
(g)	$h_1\otimes h_2={\displaystyle \underset{{\kappa }_1\in h_1,{\kappa }_2\in h_2}{{\displaystyle \cup }}\left\{{\kappa }_1{\kappa }_2\right\}}.$

Definition 3

[21].For a given HFE $h(v)$, the score and variance functions are given by the following expressions (2) and (3):

$$\wp \left(h(v)\right)=\frac{1}{l\left(h(v)\right)}{\displaystyle {\sum }_{\kappa \in h(v)}\kappa },$$

(2)

$$\Im \left(h(v)\right)=\frac{1}{l\left(h(v)\right)}\sqrt{{\displaystyle {\sum }_{{\kappa }_i,{\kappa }_j\in h}{\left({\kappa }_i-{\kappa }_j\right)}^2}},$$

(3)

where $l\left(h(v)\right)$ is the number of elements in $h(v)$.

Inspired by the idea of score and variance functions, a comparative procedure is obtained as follows:

(i)

If $\wp \left(h_1\right)>\wp \left(h_2\right)$, then $h_1>h_2$,

(ii)

If $\wp \left(h_1\right)=\wp \left(h_2\right)$, then

a)

If $\Im \left(h_1\right)>\Im \left(h_2\right)$, then $h_1<h_2$,

b)

If $\Im \left(h_1\right)=\Im \left(h_2\right)$, then $h_1=h_2$.

Definition 4

[15,21].Consider a set of HFEs $E=\left\{h_1,h_2,\dots ,h_n\right\}$, then, the HF weighted average (HFWA) and HF weighted geometric (HFWG) operators are as follows:

$$HFWA\left(h_1,h_2,\dots ,h_n\right)=\underset{j=1}{\overset{n}{\oplus }}{\varphi }_j{h}_j={\displaystyle \underset{{\kappa }_1\in h_1,{\kappa }_2\in h_2,\dots ,{\kappa }_n\in h_n}{{\displaystyle \cup }}\left\{1-{\displaystyle \prod _{j=1}^n{\left(1-{\kappa }_j\right)}^{{\varphi }_j}}\right\}},$$

(4)

$$HFWG\left(h_1,h_2,\dots ,h_n\right)=\underset{j=1}{\overset{n}{\otimes }}{\left(h_j\right)}^{{\varphi }_j}={\displaystyle \underset{{\kappa }_1\in h_1,{\kappa }_2\in h_2,\dots ,{\kappa }_n\in h_n}{{\displaystyle \cup }}\left\{{\displaystyle \prod _{j=1}^n{\left({\kappa }_j\right)}^{{\varphi }_j}}\right\}}.$$

(5)

The measure of the discrimination of two HFSs is defined axiomatically with the following axioms similar to the case of FSs and IFSs [71,72,73].

-

It is a nonnegative and symmetric mapping of the two compared sets.

-

It becomes zero when the two sets coincide.

-

It decreases when the two subsets become “more similar” in some sense.

Definition 5

[74].For all $R,S,T\in HFSs(\Omega )$, a function $D:HFS(\Omega )\times HFS(\Omega )\to \mathbb{R}$ is said to be an HF—Discrimination measure if it satisfies

(J1).	$D\left(R,S\right)=D\left(S,R\right);$
(J2).	$D\left(R,R\right)=0;$
(J3).	$\max \left\{D\left(R\cup T,S\cup T\right),D\left(R\cup T,S\cap T\right)\right\}\le D\left(R,S\right).$

Definition 6.

Consider $R,S\in HFSs(\Omega )$. In the following, Xu and Xia [17] presented a HF-distance measure:

$$d\left(R,S\right)=\frac{1}{n}{\displaystyle \sum _{i=1}^n\left[\frac{1}{l\left(h(v_i)\right)}{\displaystyle \sum _{j=1}^{l_y}\left|{\hslash }_R^{\sigma (j)}\left(v_i\right)-{\hslash }_S^{\sigma (j)}\left(v_i\right)\right|}\right]}.$$

(6)

4. New Discrimination Measure for HFSs

The divergence measure is one of the important research contents in FS theory and has a broad application background. For HFSs, Xu and Xia [18] firstly pioneered the concept of divergence measure. Mishra et al. [34,35] proposed some entropy and divergence measures for HFSs and applied them to a service quality assessment and green supplier selection problem, respectively. Kobza et al. [70] studied a new axiomatic definition of HF divergence measure and proposed some divergence measures under an HFS context. Recently, Mishra et al. [75] studied an HF divergence measure-based Additive Ratio Assessment approach for a COVID-19 medication problem. To overcome the drawbacks of existing measures, this section introduces a new discrimination measure for HFSs.

In the following, a parametric symmetric discrimination measure between HFSs R and S with $\gamma >0 \left(\gamma \ne 2\right)$ is proposed:

$$\begin{array}{l}D\left(R,S\right)=\\ \frac{1}{n}{\displaystyle \sum _{i=1}^n\left(\frac{1}{l\left(h(v_i)\right)\left(2^{\left(1-\gamma /2\right)}-1\right)}{\displaystyle \sum _{j=1}^{l\left(h(v_i)\right)}\left[\begin{array}{l}{\left(\frac{{\left(h_R^{\sigma \left(j\right)}\left(v_i\right)\right)}^2+{\left(h_S^{\sigma \left(j\right)}\left(v_i\right)\right)}^2}{2}\right)}^{\gamma /2}-\frac{{\left(h_R^{\sigma \left(j\right)}\left(v_i\right)\right)}^{\gamma }+{\left(h_S^{\sigma \left(j\right)}\left(v_i\right)\right)}^{\gamma }}{2}\\ \end{array}\right]}\right)}.\end{array}$$

(7)

Theorem 1.

Let $R,S\in HFSs(\Omega )$, then measure $D\left(R,S\right);\gamma >0\left(\gamma \ne 2\right)$, as presented by (7), which is a discrimination measure for HFSs.

Proof. 

To prove this theorem, the function $D\left(R,S\right);\gamma >0\left(\gamma \ne 2\right)$ has to satisfy all the postulates of Definition 5. □

(D₁). For any two real numbers $\alpha ,\beta \in \mathbb{R}$, the following inequalities assure:

$${\left(\frac{{\alpha }^2+{\beta }^2}{2}\right)}^{\gamma /2}\ge \frac{{\alpha }^{\gamma }+{\beta }^{\gamma }}{2},\mathrm{for}\gamma <2\mathrm{and}{\left(\frac{{\alpha }^2+{\beta }^2}{2}\right)}^{\gamma /2}\le \frac{{\alpha }^{\gamma }+{\beta }^{\gamma }}{2},\mathrm{for}\gamma >2.$$

(8)

In addition, we have

$$\frac{1}{n\left(2^{\left(1-\gamma /2\right)}-1\right)}>0,\mathrm{for}\gamma <2\mathrm{and}\frac{1}{n\left(2^{\left(1-\gamma /2\right)}-1\right)}<0,\mathrm{for}\gamma >2.$$

(9)

Let $R,S\in HFSs(\Omega )$, we know that $h_R^{\sigma \left(j\right)},h_S^{\sigma \left(j\right)}:\Omega \to \left[0,1\right]$, which implies that

$${\left(\frac{{\left(h_R^{\sigma \left(j\right)}\left(v_i\right)\right)}^2+{\left(h_S^{\sigma \left(j\right)}\left(v_i\right)\right)}^2}{2}\right)}^{\gamma /2}\ge \frac{{\left(h_R^{\sigma \left(j\right)}\left(v_i\right)\right)}^{\gamma }+{\left(h_S^{\sigma \left(j\right)}\left(v_i\right)\right)}^{\gamma }}{2},\mathrm{for}\gamma <2$$

(10)

and

$${\left(\frac{{\left(h_R^{\sigma \left(j\right)}\left(v_i\right)\right)}^2+{\left(h_S^{\sigma \left(j\right)}\left(v_i\right)\right)}^2}{2}\right)}^{\gamma /2}\ge \frac{{\left(h_R^{\sigma \left(j\right)}\left(v_i\right)\right)}^{\gamma }+{\left(h_S^{\sigma \left(j\right)}\left(v_i\right)\right)}^{\gamma }}{2},\mathrm{for}\gamma >2.$$

(11)

Therefore, for each $v_i\in \Omega$, we combine Equations (9)–(11), and therefore, we have

$$\frac{1}{n}{\displaystyle \sum _{i=1}^n\left(\frac{1}{l\left(h(v_i)\right)\left(2^{\left(1-\gamma /2\right)}-1\right)}{\displaystyle \sum _{j=1}^{l\left(h(v_i)\right)}\left[\begin{array}{l}{\left(\frac{{\left(h_R^{\sigma \left(j\right)}\left(v_i\right)\right)}^2+{\left(h_S^{\sigma \left(j\right)}\left(v_i\right)\right)}^2}{2}\right)}^{\gamma /2}-\frac{{\left(h_R^{\sigma \left(j\right)}\left(v_i\right)\right)}^{\gamma }+{\left(h_S^{\sigma \left(j\right)}\left(v_i\right)\right)}^{\gamma }}{2}\\ \end{array}\right]}\right)}\ge 0.$$

(12)

From Equation (7), we obtain $D\left(R,S\right)\ge 0$.

(D₂). It is obvious from Definition 5.

(D₃). Suppose that $R=S$, therefore, $h_R^{\sigma \left(j\right)}\left(v_i\right)=h_S^{\sigma \left(j\right)}\left(v_i\right)$, for each $i=1,2,\dots ,n,j=1,2,\dots ,l\left(h(v_i)\right)$. Then, Equation (7) becomes

$$D\left(R,S\right)=\frac{1}{n}{\displaystyle \sum _{i=1}^n\left(\frac{1}{l\left(h(v_i)\right)\left(2^{\left(1-\gamma /2\right)}-1\right)}{\displaystyle \sum _{j=1}^{l\left(h(v_i)\right)}\left[\begin{array}{l}{\left(\frac{{\left(h_R^{\sigma \left(j\right)}\left(v_i\right)\right)}^2+{\left(h_S^{\sigma \left(j\right)}\left(v_i\right)\right)}^2}{2}\right)}^{\gamma /2}-\frac{{\left(h_R^{\sigma \left(j\right)}\left(v_i\right)\right)}^{\gamma }+{\left(h_S^{\sigma \left(j\right)}\left(v_i\right)\right)}^{\gamma }}{2}\\ \end{array}\right]}\right)}=0.$$

Conversely, assume $D\left(R,S\right)=0$,

$$\iff \frac{1}{n}{\displaystyle \sum _{i=1}^n\left(\frac{1}{l\left(h(v_i)\right)\left(2^{\left(1-\gamma /2\right)}-1\right)}{\displaystyle \sum _{j=1}^{l\left(h(v_i)\right)}\left[{\left(\frac{{\left(h_R^{\sigma \left(j\right)}\left(v_i\right)\right)}^2+{\left(h_S^{\sigma \left(j\right)}\left(v_i\right)\right)}^2}{2}\right)}^{\gamma /2}-\frac{{\left(h_R^{\sigma \left(j\right)}\left(v_i\right)\right)}^{\gamma }+{\left(h_S^{\sigma \left(j\right)}\left(v_i\right)\right)}^{\gamma }}{2}\right]}\right)}=0,$$

$$\iff {\left(\frac{{\left(h_R^{\sigma \left(j\right)}\left(v_i\right)\right)}^2+{\left(h_S^{\sigma \left(j\right)}\left(v_i\right)\right)}^2}{2}\right)}^{\gamma /2}-\frac{{\left(h_R^{\sigma \left(j\right)}\left(v_i\right)\right)}^{\gamma }+{\left(h_S^{\sigma \left(j\right)}\left(v_i\right)\right)}^{\gamma }}{2}=0.$$

This is possible if and only if $h_R^{\sigma \left(j\right)}\left(v_i\right)=h_S^{\sigma \left(j\right)}\left(v_i\right)$, $i=1,2,\dots ,n,j=1,2,\dots ,l\left(h(v_i)\right)$. This proves that $R=S$.

Theorem 2.

Let $R,S,T\in HFSs(\Omega )$. Then, the discrimination measure $D\left(R,S\right);\gamma >0\left(\gamma \ne 2\right)$, given by (6), holds the following postulates:

(P1).$D\left(R,S\right)\le D\left(R,T\right)$ and $D\left(S,T\right)\le D\left(R,T\right)$, for $R\subseteq S\subseteq T$;

Proof. 

Since $R\subseteq S\subseteq T$, therefore, $h_R^{\sigma \left(j\right)}\left(v_i\right)\le h_S^{\sigma \left(j\right)}\left(v_i\right)\le h_T^{\sigma \left(j\right)}\left(v_i\right)$, and thus, from Equation (7), we obtain. □

$$D\left(R,S\right)=\frac{1}{n}{\displaystyle \sum _{i=1}^n\left(\frac{1}{l\left(h(v_i)\right)\left(2^{\left(1-\gamma /2\right)}-1\right)}{\displaystyle \sum _{j=1}^{l\left(h(v_i)\right)}\left[{\left(\frac{{\left(h_R^{\sigma \left(j\right)}\left(v_i\right)\right)}^2+{\left(h_S^{\sigma \left(j\right)}\left(v_i\right)\right)}^2}{2}\right)}^{\gamma /2}-\frac{{\left(h_R^{\sigma \left(j\right)}\left(v_i\right)\right)}^{\gamma }+{\left(h_S^{\sigma \left(j\right)}\left(v_i\right)\right)}^{\gamma }}{2}\right]}\right)}$$

$$\le \frac{1}{n}{\displaystyle \sum _{i=1}^n\left(\frac{1}{l\left(h(v_i)\right)\left(2^{\left(1-\gamma /2\right)}-1\right)}{\displaystyle \sum _{j=1}^{l\left(h(v_i)\right)}\left[{\left(\frac{{\left(h_R^{\sigma \left(j\right)}\left(v_i\right)\right)}^2+{\left(h_T^{\sigma \left(j\right)}\left(v_i\right)\right)}^2}{2}\right)}^{\gamma /2}-\frac{{\left(h_R^{\sigma \left(j\right)}\left(v_i\right)\right)}^{\gamma }+{\left(h_T^{\sigma \left(j\right)}\left(v_i\right)\right)}^{\gamma }}{2}\right]}\right)}=D\left(R,T\right).$$

Thus, $D\left(R,S\right)\le D\left(R,T\right),\forall T\in HFS(\Omega )$. In the same way, we can prove $D\left(S,T\right)\le D\left(R,T\right),\forall T\in HFS(\Omega )$.

(P2).$D\left(R\cup S,R\cap S\right)=D\left(R,S\right)$;

(P3).$D\left(R\cup S,T\right)\le D\left(R,T\right)+D\left(S,T\right),\forall T\in HFS(\Omega )$;

(P4).$D\left(R\cap S,T\right)\le D\left(R,T\right)+D\left(S,T\right),\forall T\in HFS(\Omega )$;

Proof. 

To verify (P2)–(P4), we partition the universe of discourse $\Omega$ into two disjoint sets ${\Omega }_1$ and ${\Omega }_2$, where ${\Omega }_1=\left\{v_i|v_i\in \Omega ,R\left(v_i\right)\subseteq S\left(v_i\right)\right\}$ and ${\Omega }_2=\left\{v_i|v_i\in \Omega ,S\left(v_i\right)\subseteq R\left(v_i\right)\right\}$. □

$$D\left(R\cup S,R\cap S\right)$$

$$=\frac{1}{n}{\displaystyle \sum _{i=1}^n\left(\frac{1}{l\left(h(v_i)\right)\left(2^{\left(1-\gamma /2\right)}-1\right)}{\displaystyle \sum _{j=1}^{l\left(h(v_i)\right)}\left[{\left(\frac{{\left(h_{R\cup S}^{\sigma \left(j\right)}\left(v_i\right)\right)}^2+{\left(h_{R\cap S}^{\sigma \left(j\right)}\left(v_i\right)\right)}^2}{2}\right)}^{\gamma /2}-\frac{{\left(h_{R\cup S}^{\sigma \left(j\right)}\left(v_i\right)\right)}^{\gamma }+{\left(h_{R\cap S}^{\sigma \left(j\right)}\left(v_i\right)\right)}^{\gamma }}{2}\right]}\right)}$$

$$=\frac{1}{n}{\displaystyle \sum _{v_i\in {\Omega }_1}\left(\frac{1}{l\left(h(v_i)\right)\left(2^{\left(1-\gamma /2\right)}-1\right)}{\displaystyle \sum _{j=1}^{l\left(h(v_i)\right)}\left[{\left(\frac{{\left(h_S^{\sigma \left(j\right)}\left(v_i\right)\right)}^2+{\left(h_R^{\sigma \left(j\right)}\left(v_i\right)\right)}^2}{2}\right)}^{\gamma /2}-\frac{{\left(h_S^{\sigma \left(j\right)}\left(v_i\right)\right)}^{\gamma }+{\left(h_R^{\sigma \left(j\right)}\left(v_i\right)\right)}^{\gamma }}{2}\right]}\right)}$$

$$+\frac{1}{n}{\displaystyle \sum _{v_i\in {\Omega }_2}\left(\frac{1}{l\left(h(v_i)\right)\left(2^{\left(1-\gamma /2\right)}-1\right)}{\displaystyle \sum _{j=1}^{l\left(h(v_i)\right)}\left[{\left(\frac{{\left(h_R^{\sigma \left(j\right)}\left(v_i\right)\right)}^2+{\left(h_S^{\sigma \left(j\right)}\left(v_i\right)\right)}^2}{2}\right)}^{\gamma /2}-\frac{{\left(h_R^{\sigma \left(j\right)}\left(v_i\right)\right)}^{\gamma }+{\left(h_S^{\sigma \left(j\right)}\left(v_i\right)\right)}^{\gamma }}{2}\right]}\right)}.$$

This implies that $D\left(R\cup S,R\cap S\right)=D\left(R,S\right)$. Hence, (P2) is proved.

Again, from Equation (7), for each $T\in HFS(\Omega )$, we get

$$D\left(R\cup S,T\right)$$

$$=\frac{1}{n}{\displaystyle \sum _{i=1}^n\left(\frac{1}{l\left(h(v_i)\right)\left(2^{\left(1-\gamma /2\right)}-1\right)}{\displaystyle \sum _{j=1}^{l\left(h(v_i)\right)}\left[{\left(\frac{{\left(h_{R\cup S}^{\sigma \left(j\right)}\left(v_i\right)\right)}^2+{\left(h_T^{\sigma \left(j\right)}\left(v_i\right)\right)}^2}{2}\right)}^{\gamma /2}-\frac{{\left(h_{R\cup S}^{\sigma \left(j\right)}\left(v_i\right)\right)}^{\gamma }+{\left(h_T^{\sigma \left(j\right)}\left(v_i\right)\right)}^{\gamma }}{2}\right]}\right)}$$

$$=\frac{1}{n}{\displaystyle \sum _{v_i\in {\Omega }_1}\left(\frac{1}{l\left(h(v_i)\right)\left(2^{\left(1-\gamma /2\right)}-1\right)}{\displaystyle \sum _{j=1}^{l\left(h(v_i)\right)}\left[{\left(\frac{{\left(h_S^{\sigma \left(j\right)}\left(v_i\right)\right)}^2+{\left(h_T^{\sigma \left(j\right)}\left(v_i\right)\right)}^2}{2}\right)}^{\gamma /2}-\frac{{\left(h_S^{\sigma \left(j\right)}\left(v_i\right)\right)}^{\gamma }+{\left(h_T^{\sigma \left(j\right)}\left(v_i\right)\right)}^{\gamma }}{2}\right]}\right)}$$

$$+\frac{1}{n}{\displaystyle \sum _{y_i\in Y_2}\left(\frac{1}{l\left(h(v_i)\right)\left(2^{\left(1-\gamma /2\right)}-1\right)}{\displaystyle \sum _{j=1}^{l\left(h(v_i)\right)}\left[{\left(\frac{{\left(h_R^{\sigma \left(j\right)}\left(v_i\right)\right)}^2+{\left(h_T^{\sigma \left(j\right)}\left(v_i\right)\right)}^2}{2}\right)}^{\gamma /2}-\frac{{\left(h_R^{\sigma \left(j\right)}\left(v_i\right)\right)}^{\gamma }+{\left(h_T^{\sigma \left(j\right)}\left(v_i\right)\right)}^{\gamma }}{2}\right]}\right)}.$$

It implies that $D\left(R\cup S,T\right)\le D\left(R,T\right)+D\left(S,T\right),\forall T\in HFS(\Omega )$. Hence, the property (P3) is proved.

Similarly, we can prove the property (P4).

(P5).$D\left(R\cap T,S\cap T\right)\le D\left(R,S\right),\forall T\in HFS(\Omega )$;

(P6).$D\left(R\cup T,S\cup T\right)\le D\left(R,S\right),\forall T\in HFS(\Omega )$.

Proof. 

To prove (P5) and (P6), the universal set $\Omega$ is partitioned into the following eight subsets:

$$\Omega =\left\{v_i\in \Omega |R\left(v_i\right)\le S\left(v_i\right)=T\left(v_i\right)\right\}\cup \left\{v_i\in \Omega |R\left(v_i\right)=T\left(v_i\right)\le S\left(v_i\right)\right\}$$

$$\cup \left\{v_i\in \Omega |R\left(v_i\right)\le S\left(v_i\right)<T\left(v_i\right)\right\}\cup \left\{v_i\in \Omega |R\left(v_i\right)\le T\left(v_i\right)<S\left(v_i\right)\right\}$$

$$\cup \left\{v_i\in \Omega |S\left(v_i\right)<R\left(v_i\right)\le T\left(v_i\right)\right\}\cup \left\{v_i\in \Omega |S\left(v_i\right)\le T\left(v_i\right)<R\left(v_i\right)\right\}$$

$$\cup \left\{v_i\in \Omega |T\left(v_i\right)<R\left(v_i\right)\le S\left(v_i\right)\right\}\cup \left\{v_i\in \Omega |T\left(v_i\right)<S\left(v_i\right)<R\left(v_i\right)\right\},$$

which are denoted by ${\Delta }_1,{\Delta }_2,\dots ,{\Delta }_8$. According to Mishra et al. [34,35], for every ${\Delta }_j;j=1\left(1\right)8$,

$${\left(\frac{{\left(h_R^{\sigma \left(j\right)}\left(v_i\right)\right)}^2+{\left(h_S^{\sigma \left(j\right)}\left(v_i\right)\right)}^2}{2}\right)}^{\gamma /2}\ge \frac{{\left(h_R^{\sigma \left(j\right)}\left(v_i\right)\right)}^{\gamma }+{\left(h_S^{\sigma \left(j\right)}\left(v_i\right)\right)}^{\gamma }}{2},\mathrm{for}\gamma <2$$

(13)

$${\left(\frac{{\left(h_R^{\sigma \left(j\right)}\left(v_i\right)\right)}^2+{\left(h_S^{\sigma \left(j\right)}\left(v_i\right)\right)}^2}{2}\right)}^{\gamma /2}\ge \frac{{\left(h_R^{\sigma \left(j\right)}\left(v_i\right)\right)}^{\gamma }+{\left(h_S^{\sigma \left(j\right)}\left(v_i\right)\right)}^{\gamma }}{2},\mathrm{for}\gamma >2.$$

(14)

□

Therefore, from (P1), we obtain

$D\left(R\cap T,S\cap T\right)\le D\left(R,S\right)$ and $D\left(R\cup T,S\cup T\right)\le D\left(R,S\right),\forall T\in HFS(\Omega )$.

Since measure $D\left(R,S\right)$ holds all the essential postulates of Definition 5, hence, $D\left(R,S\right)$ is a valid discrimination measure for HFSs.

5. Hesitant Fuzzy Combined Compromise Solution (HF-CoCoSo) Approach

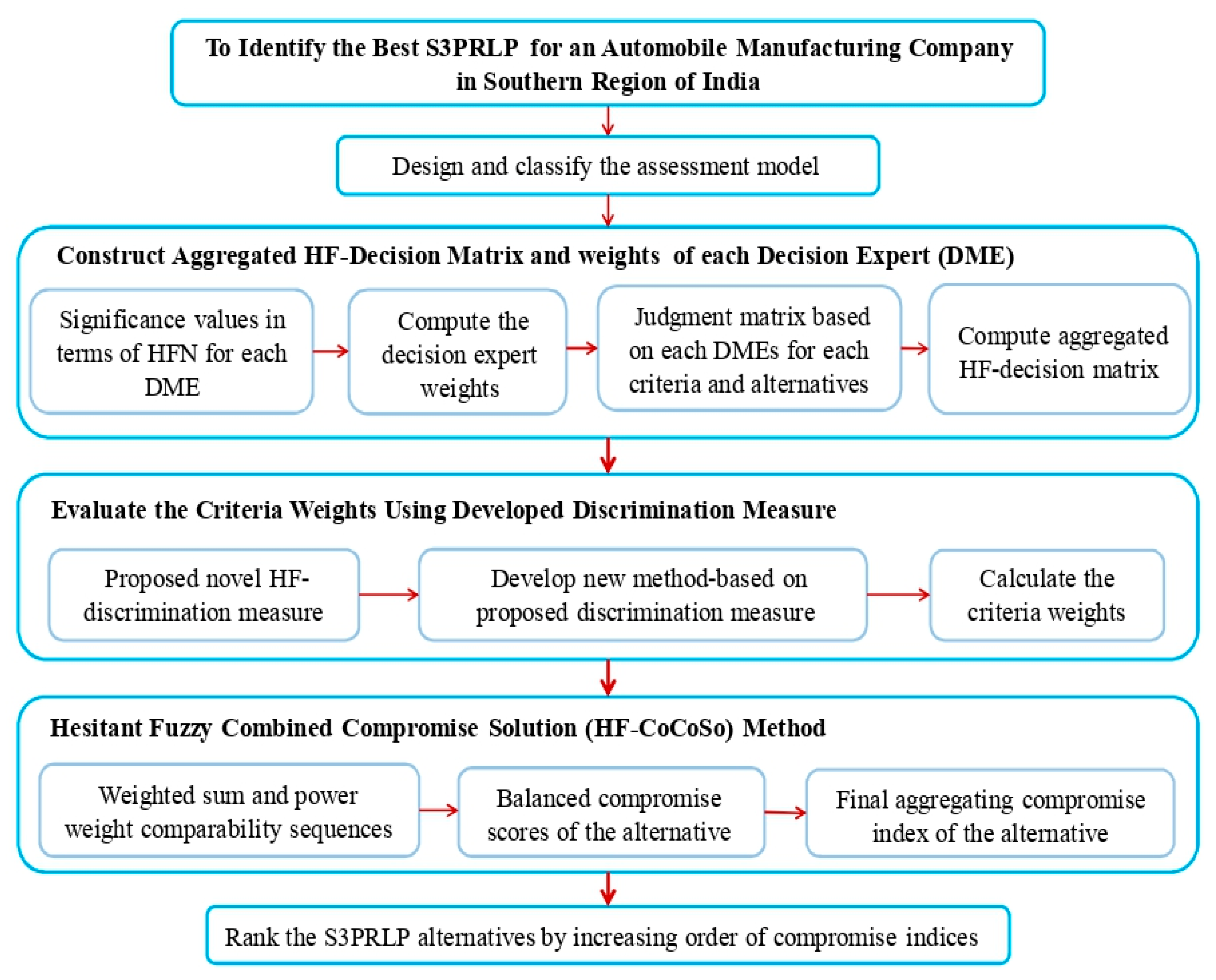
In the current section, we offer an extended decision-making model, named as the hesitant fuzzy CoCoSo (HF-CoCoSo) approach, for dealing with the MCDM problems under an HF environment. For this purpose, we combine the CoCoSo approach [76,77,78] with the notions and operations of the HFNs, score function, and proposed discrimination measure within an HFS setting. The calculation procedure of the developed approach is presented as follows (see Figure 1):

Step 1: Problem description.

Consider a team of $\ell$ DMEs $\left\{P_1,P_2,\dots ,P_{\ell }\right\}$ to determine the best choice among a set of ‘m’ alternatives $\left\{M_1,M_2,\dots ,M_m\right\}$ over a criteria set $\left\{H_1,H_2,\dots ,H_n\right\}$. Create a decision matrix $Z=\left(z_{ij}\right)$ based on linguistic terms for assessing the alternatives over the criteria, where $i=1,2,\dots ,m,j=1,2,\dots ,n$. Convert the linguistic matrix into an HF-decision matrix (HF-DM) $\Pi =\left(x_{ij}\right),i=1,2,\dots ,m,j=1,2,\dots ,n$.

Step 2: Determine crisp DMEs’ weights.

For the evaluation of kth DME, let $h_k\left(v\right)=\left\{\kappa :\kappa \in h_k\left(v\right)\right\}$ be the hesitant fuzzy number (HFN). Then, the weight of the kth DME is obtained by using the expression

$${\lambda }_k=\frac{{\displaystyle {\sum }_{{\kappa }_a\in h}{\kappa }_a}}{{\displaystyle \sum _{k=1}^{\ell }\left({\displaystyle {\sum }_{{\kappa }_a\in h}{\kappa }_a}\right)}},k=1,2,\dots ,\ell ,a=1,2,\dots ,l\left(h(v)\right).$$

(15)

Clearly, ${\lambda }_k\ge 0$ and ${\displaystyle \sum _{k=1}^{\ell }{\lambda }_k=1}$.

Step 3: Create the aggregated HF-DM.

Here, we combine all the individuals’ matrices ${\Pi }_k=\left(x_{ij}^k\right);k=1,2,\dots ,l\left(h(v)\right)$ and create the aggregated HF-DM $M=\left(y_{ij}\right)$, $i=1,2,\dots ,m$, $j=1,2,\dots ,n$, where $M=\underset{k=1}{\overset{\ell }{\oplus }}{\lambda }_k{M}_k$, and

$$y_{ij}={\displaystyle \underset{{\kappa }_1\in y_{ij}^k,{\kappa }_2\in h_{ij}^k,\dots ,{\kappa }_a\in h_{ij}^k}{\cup }\left\{1-{\displaystyle \prod _{k=1}^{\ell }{\left(1-y_{ij}^k\right)}^{{\lambda }_k}}\right\}}.$$

(16)

Step 4: Determine the criteria weights.

In the following, we present a combined criteria weight-determining method based on objective and subjective weighting methods.

Step 4.1: To estimate the objective criteria weights, we execute the following process by employing the proposed HF-discrimination measure (7):

$${\varpi }_j=\frac{{\displaystyle \sum _{i=1}^m\left(\frac{1}{m-1}{\displaystyle \sum _{k=1}^{m}D\left(y_{ij},y_{kj}\right)}\right)}}{{\displaystyle \sum _{j=1}^n{\displaystyle \sum _{i=1}^m\left(\frac{1}{m-1}{\displaystyle \sum _{k=1}^{m}D\left(y_{ij},y_{kj}\right)}\right)}}},j=1,2,\dots ,n.$$

(17)

Step 4.2: Calculate the subjective criteria weights.

To compute the subjective criteria weight, first, we compute the importance degree $\left({\kappa }_j\right)$ of each criterion H_j. For this, create the individual importance degree matrix $\left({\eta }_j^k\right)$ for kth expert by using the process

$${\eta }_j^k={\left[\begin{array}{c}{\eta }_1^k\\ {\eta }_2^k\\ ⋮\\ {\eta }_n^k\end{array}\right]}_{1\times n},$$

(18)

where ${\eta }_j^k$ is the importance degree of criterion H_j given by kth expert, $j=1,2,\dots ,n$, $k=1,2,\dots ,\ell$. To estimate the subjective weight, we get

$${\vartheta }_j=HFW{A}_{\lambda }\left({\eta }_j^1,{\eta }_j^2,\dots ,{\eta }_j^{\ell }\right).$$

(19)

Let ${\eta }_j^k=\left(h_{ij}^k\right)$ be the decision importance, where $h_{ij}^k=\left\{{\kappa }_k:{\kappa }_k\in h_{ij}^k\right\},k=1,2,\dots ,\ell$ is an HFN. Then, we find the overall importance degree as follows:

$${\vartheta }_j={\left(h_{ij}\right)}^{*}={\displaystyle \underset{{\kappa }_1\in h_{i1}^k,{\kappa }_2\in h_{i2}^k,\dots ,{\kappa }_n\in h_{in}^k}{\cup }\left\{1-{\displaystyle \prod _{k=1}^{\ell }{\left(1-{\kappa }_k\right)}^{{\lambda }_k}}\right\}}.$$

(20)

Here, ${\kappa }_j={\left(h_{ij}\right)}^{*}$ is an HFN.

Step 4.3: Evaluate the overall importance degree $\left({\eta }_j\right)$ of criteria H_j.

Next, we calculate the score value $s\left({\vartheta }_j\right)$ by employing Equation (2). Thus, we calculate the importance degree as follows:

$${\eta }_j=\frac{s\left({\vartheta }_j\right)}{{\displaystyle {\sum }_{j=1}^{n}s\left({\vartheta }_j\right)}};j=1,2,\dots ,n.$$

(21)

Step 4.4: Determine the final weight of criteria.

With the use of using Equations (16)–(20), the formula for the computation of combined weight is

$$w_j=\tau {\varpi }_j+\left(1-\tau \right){\eta }_j,$$

(22)

where ${\varpi }_j$ represents the objective weight obtained by the proposed discrimination measure of evaluation of the jth criterion, ${\eta }_j$ represents the subjective weight of the jth criterion expressed by DEs, $\tau \left(0\le \tau \le 1\right)$ represents the adjustment coefficient, and its value can be chosen along with the actual situation of the group decision and $0\le w_j\le 1$.

Step 5: Construct the normalized aggregated HF-DM.

To create the normalized aggregated HF-DM $\mathbb{R}={\left({\varsigma }_{ij}\right)}_{m\times n}$, we have utilized the following expression:

$${\varsigma }_{ij}=\{\begin{array}{l}{y}_{ij}, \mathrm{for} \mathrm{benefit} \mathrm{criterion}\\ {\left(y_{ij}\right)}^c=1-y_{ij}, \mathrm{for} \mathrm{cost} \mathrm{criterion}.\end{array}$$

(23)

Step 6: Determine the weighted sum and power weight comparability sequences.

In the following, we present the weighted sum measure (WSM) (or sum of the weighted comparability sequence) ${\mathsf{\Lambda }}_i^{(1)}$ for each candidate:

$${\mathsf{\Lambda }}_i^{(1)}=\underset{j=1}{\overset{n}{\oplus }}{w}_j{\varsigma }_{ij}.$$

(24)

Next, we present the weighted product measure (WPM) (or amount of the power weight of comparability sequence) ${\mathsf{\Lambda }}_i^{(2)}$ for each candidate, which is given as

$${\mathsf{\Lambda }}_i^{(2)}=\underset{j=1}{\overset{n}{\otimes }}{w}_j{\varsigma }_{ij}.$$

(25)

Step 7: Computation of relative weights or balanced compromise scores.

Next, three appraisal score strategies are presented to formulate the relative weights of the alternative, which are derived as follows:

$$C_i^{\left(1\right)}=\frac{s\left({\mathsf{\Lambda }}_i^{(1)}\right)+s\left({\mathsf{\Lambda }}_i^{(2)}\right)}{{\displaystyle \sum _{i=1}^m\left(s\left({\mathsf{\Lambda }}_i^{(1)}\right)+s\left({\mathsf{\Lambda }}_i^{(2)}\right)\right)}},$$

(26)

$$C_i^{\left(2\right)}=\frac{s\left({\mathsf{\Lambda }}_i^{(1)}\right)}{\underset{i}{\min }s\left({\mathsf{\Lambda }}_i^{(1)}\right)}+\frac{s\left({\mathsf{\Lambda }}_i^{(2)}\right)}{\underset{i}{\min }s\left({\mathsf{\Lambda }}_i^{(2)}\right)},$$

(27)

$$C_i^{\left(3\right)}=\frac{\gamma s\left({\mathsf{\Lambda }}_i^{(1)}\right)+\left(1-\gamma \right)s\left({\mathsf{\Lambda }}_i^{(2)}\right)}{\underset{i}{\gamma \max }s\left({\mathsf{\Lambda }}_i^{(1)}\right)+\left(1-\gamma \right)\underset{i}{\max }s\left({\mathsf{\Lambda }}_i^{(2)}\right)},$$

(28)

where $\gamma \in [0,1]$ is compromise decision mechanism coefficient. Generally, we take $\gamma =0.5$. Here, Equation (26) articulates the arithmetic mean of sums of WSM and WPM scores, whilst Equation (27) articulates a sum of relative scores of WSM and WPM compared to the best. Equation (28) expresses the balanced compromise of WSM and WPM models scores.

Step 8: Estimate the final aggregating compromise index.

The final aggregating compromise index $C_i$ is computed as

$$C_i={\left(C_i^{\left(1\right)}{C}_i^{\left(2\right)}{C}_i^{\left(3\right)}\right)}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$3$}\right.}+\frac{1}{3}\left(C_i^{\left(1\right)}+C_i^{\left(2\right)}+C_i^{\left(3\right)}\right).$$

(29)

Lastly, prioritize the candidates according as the increasing values of aggregating compromise index $C_i$.

Step 9: End.

6. Case Study of S3PRLP Selection

To show the application of the introduced MCDM framework, an empirical case study of 3PRLP selection is carried out for an automobile manufacturing company (XYZ). This company is located in the southern region of India that endorses economic and social development. Its manufacturing chain is long and has a great level of relevance to other businesses. This automobile company is effectual for promoting employment and motivating consumption, and it acts as a momentous part in the social and economic growth of the country. Simultaneously, it entails large-scale production escorted by a huge flow of raw materials, parts, finished products, and scrap materials. Reverse logistics is vastly associated to scrap waste and flawed products related to the manufacturing process. As a result of the speedy growth of the automotive businesses, the general public has paid great interest to the automobile reverse logistics. The management of recollected defective and scrapped cars is strongly associated with the individual security and ecological protection, and consequently, study on the development of automobile reverse logistics is a significant process to fulfill the customers’ demands, enhance the corporate competitiveness, conserve the natural resources, and protect the atmosphere.

The company XYZ currently has a well-built marketing system and a trustworthy reverse logistics network. The company lacks material resources, manpower, experience, and capital in logistics practices, particularly reverse logistics practices, and this has motivated the company to outsource its reverse logistics business to a proficient 3PRLP for reducing costs and enhancing its core competitiveness. The company executives are facing some difficulties in choosing the 3PRLP and in managing successful reverse logistics practices in a green and sustainable supply chain during the network. The improper reverse logistics practices may result in environmental pollution, global warming, etc. In order to choose a suitable 3PRLP option, the company XYZ posted a tender notice to invite 3PRLPs to participate in the reverse logistics services. Accordingly, lots of potential alternatives are contributed in the tender. To assess the candidate 3PRLPs appropriately, the company formed a team of three professionals (P₁, P₂, P₃). After establishing the expert team, six candidate providers (M₁, M₂, M₃, M₄, M₅, M₆) are identified for a further evaluation process. These alternatives are evaluated based on the following 13 criteria: Green warehousing (H₁), Pollution control cost (H₂), Green product and eco-design cost (H₃), RL cost (H₄), Green R&D and innovation (H₅), Air emissions (H₆), Environmental management system (H₇), Flexibility (H₈), Quality (H₉), Financial risk (H₁₀), Health and safety practices (H₁₁), Social responsibility (H₁₂), and Employment Practices (H₁₃). In this example, the criteria S₂, S₃, S₄, S₆, and S₁₀ are of cost type, and the rest all are of the benefit type. Next, the implementation procedures of the proposed HF-CoCoSo model for assessing the S3PRLPs are expressed as follows.

Table 1. Linguistic ratings for the importance of criteria and experts.

LVs	HFEs	DMEs Risk Preferences
		Pessimist	Moderate	Optimist
Very high (VH)	[0.85, 1.00]	0.85	0.925	1.00
High (H)	[0.70, 0.85]	0.70	0.775	0.85
Medium (M)	[0.55, 0.70]	0.55	0.625	0.70
Low (L)	[0.40, 0.55]	0.40	0.475	0.55
Very low (VL)	[0.25, 0.40]	0.25	0.325	0.40

and

Table 2. Linguistic variables for the importance of criteria and alternatives.

LVs	HFEs	DMEs Risk Preferences
		Pessimist	Moderate	Optimist
Extremely preferable (EP)	[0.90, 1.00]	0.90	0.95	1.00
Strong preferable (SP)	[0.75, 0.90]	0.75	0.825	0.90
Preferable (P)	[0.60, 0.75]	0.60	0.675	0.75
Moderately preferable (MP)	[0.50, 0.60]	0.50	0.55	0.60
Moderate (M)	[0.40, 0.50]	0.40	0.45	0.50
Moderately undesirable (MU)	[0.30, 0.40]	0.30	0.35	0.40
Undesirable (U)	[0.20, 0.30]	0.20	0.25	0.30
Strong undesirable (SU)	[0.10, 0.20]	0.10	0.15	0.20
Extremely undesirable (EU)	[0.00, 0.10]	0.00	0.05	0.10

present the linguistic terms (LTs) and their consequent HFEs for the rating of relative significance of criteria and 3PRLP candidate assessment to the given decision-making problem, respectively. As a result of the qualitative [34] and quantitative [79] nature of evaluation factors, imprecise information, and lack of time, it is easy for the DMEs to articulate their opinions based on linguistic values (LVs) [33].

Suppose the DMEs’ weights are given by LVs, which as {H, VH, M}. Consequently, with the use of Table 2, Equations (6) and (15), the crisp weights of the DMEs are obtained as {λ₁ = 0.3333, λ₂ = 0.2689, λ₃ = 0.3978}. The linguistic decision matrix is presented in

Table 3. Linguistic decision matrix given by different experts for sustainable third-party reverse logistics provider (S3PRLP) evaluation.

Criteria	DMEs	M1	M2	M3	M4	M5	M6
H1	P1	MP	M	MU	MP	M	MP
	P2	M	MU	P	MU	P	SU
	P3	P	MP	M	P	MU	MU
H2	P1	MP	MU	MP	MP	P	U
	P2	SP	MP	P	M	MU	MP
	P3	P	U	MU	P	P	U
H3	P1	U	M	M	P	P	M
	P2	MP	SP	MU	M	MU	P
	P3	M	P	M	P	M	MU
H4	P1	M	MU	U	M	P	M
	P2	M	U	P	MU	U	P
	P3	MP	MU	U	U	MP	M
H5	P1	M	M	M	MP	MP	M
	P2	SP	M	MU	M	P	MP
	P3	M	SU	M	SU	MU	M
H6	P1	MP	P	M	MP	SP	SP
	P2	M	MP	MU	U	MU	U
	P3	P	M	SP	P	U	MP
H7	P1	MU	P	MP	M	SU	P
	P2	MP	M	SP	SU	MP	M
	P3	P	SP	P	M	M	SU
H8	P1	SP	EP	MP	P	M	M
	P2	M	P	P	MP	P	P
	P3	P	MP	P	M	SP	P
H9	P1	MP	EP	SP	M	MP	SP
	P2	SP	MP	MP	MU	M	M
	P3	P	MU	U	M	M	M
H10	P1	MU	MP	P	MU	P	SP
	P2	MP	M	M	MP	U	M
	P3	M	P	MU	P	MU	MU
H11	P1	MP	P	M	SP	MU	P
	P2	P	MP	MP	MP	P	MP
	P3	SP	P	MU	M	MU	SP
H12	P1	U	P	M	P	P	M
	P2	SP	SP	SP	M	MP	U
	P3	M	MU	P	MP	M	MP
H13	P1	MU	SP	MU	P	MP	MP
	P2	SP	MP	P	MU	P	MU
	P3	P	M	SP	SU	M	M

.

With the use of Equation (16), we combine the individuals’ opinions given in Table 3 and then create an aggregated HF-DM in

Table 4. Aggregated HF-decision matrix (HF-DM) for 3PRLP candidates over criteria.

	M1	M2	M3	M4	M5	M6
H1	0.584	0.461	0.497	0.499	0.476	0.401
H2	0.680	0.424	0.543	0.564	0.557	0.396
H3	0.472	0.641	0.461	0.581	0.484	0.476
H4	0.527	0.372	0.470	0.384	0.524	0.524
H5	0.581	0.368	0.455	0.425	0.539	0.523
H6	0.548	0.571	0.579	0.527	0.526	0.575
H7	0.527	0.652	0.665	0.423	0.439	0.472
H8	0.660	0.740	0.663	0.555	0.652	0.581
H9	0.665	0.699	0.581	0.424	0.505	0.579
H10	0.444	0.603	0.507	0.539	0.449	0.552
H11	0.686	0.621	0.488	0.619	0.466	0.675
H12	0.559	0.609	0.653	0.561	0.539	0.470
H13	0.651	0.606	0.632	0.416	0.555	0.477

.

In order to determine the significance degrees of considered criteria, firstly, we have calculated the objective weights, which are given as ${\varpi }_j$ = (0.0479, 0.1329, 0.0630, 0.0808, 0.0918, 0.0082, 0.1315, 0.0370, 0.1137, 0.0493, 0.0973, 0.0438, and 0.1027).

Based on the above-discussed objective weights (${\varpi }_j$) and the subjective weights given by

Table 5. Linguistic values (LVs) for criteria performance.

Criteria	LVs Given by DMEs			HFNs Given by DMEs			$\mathit{s}\left({\mathit{\kappa }}_{\mathit{j}}\right)$	${\mathit{\eta }}_{\mathit{j}}$
	P1	P2	P3	P1	P2	P3
H1	MU	MP	P	0.35	0.55	0.675	0.575	0.0769
H2	MP	M	P	0.50	0.45	0.75	0.625	0.0835
H3	U	MP	M	0.25	0.55	0.50	0.472	0.0631
H4	MP	M	P	0.50	0.45	0.675	0.584	0.0781
H5	M	MP	M	0.40	0.60	0.50	0.528	0.0706
H6	MU	P	P	0.35	0.60	0.675	0.592	0.0791
H7	U	P	SP	0.30	0.60	0.75	0.623	0.0833
H8	SP	M	SP	0.75	0.40	0.825	0.734	0.0981
H9	P	MP	P	0.60	0.55	0.675	0.639	0.0854
H10	U	P	MP	0.30	0.60	0.55	0.524	0.0700
H11	MP	M	SP	0.50	0.45	0.75	0.625	0.0835
H12	MU	MP	M	0.40	0.55	0.50	0.509	0.0680
H13	MP	M	MU	0.50	0.45	0.35	0.452	0.0604

, the combined weights of the criteria are estimated as below:

w_j = (0.0624, 0.1082, 0.0630, 0.0794, 0.0812, 0.0437, 0.1074, 0.0675, 0.0996, 0.0597, 0.0904, 0.0559, 0.0815).

As the criteria H₂, H₃, H₄, H₆, and H₁₀ are of non-benefit, and the rest all are of the benefit-type criteria; therefore, by using Table 4 and Equation (23), the normalized aggregated HF-DM is depicted in

Table 6. Normalized aggregated HF-DM for S3PRLP selection.

	M1	M2	M3	M4	M5	M6
H1	0.584	0.461	0.497	0.499	0.476	0.401
H2	0.320	0.576	0.457	0.436	0.443	0.604
H3	0.528	0.359	0.539	0.419	0.516	0.524
H4	0.473	0.628	0.530	0.616	0.476	0.476
H5	0.581	0.368	0.455	0.425	0.539	0.523
H6	0.452	0.429	0.421	0.473	0.474	0.425
H7	0.527	0.652	0.665	0.423	0.439	0.472
H8	0.660	0.740	0.663	0.555	0.652	0.581
H9	0.665	0.699	0.581	0.424	0.505	0.579
H10	0.556	0.397	0.493	0.461	0.551	0.448
H11	0.686	0.621	0.488	0.619	0.466	0.675
H12	0.559	0.609	0.653	0.561	0.539	0.470
H13	0.651	0.606	0.632	0.416	0.555	0.477

.

On the basis of Equations (24)–(29), the overall computational steps of the HF-CoCoSo approach has been determined and presented in

Table 7. Overall aggregation and combined compromise ranking results.

Option	${\mathbf{\Lambda }}_{\mathit{i}}^{(1)}$	${\mathbf{\Lambda }}_{\mathit{i}}^{(2)}$	${\mathit{C}}_{\mathit{i}}^{\left(1\right)}$	${\mathit{C}}_{\mathit{i}}^{\left(2\right)}$	${\mathit{C}}_{\mathit{i}}^{\left(3\right)}$	${\mathit{C}}_{\mathit{i}}$	Ranking
M1	0.5676	0.5437	0.1747	2.3004	0.9818	1.8857	2
M2	0.5811	0.5508	0.1779	2.3428	1.0000	1.9206	1
M3	0.5551	0.5414	0.1724	2.2701	0.9688	1.8608	3
M4	0.4888	0.4773	0.1519	2.0000	0.8535	1.6394	6
M5	0.5079	0.5015	0.1587	2.0899	0.8918	1.7130	5
M6	0.5292	0.5172	0.1645	2.1663	0.9245	1.7758	4

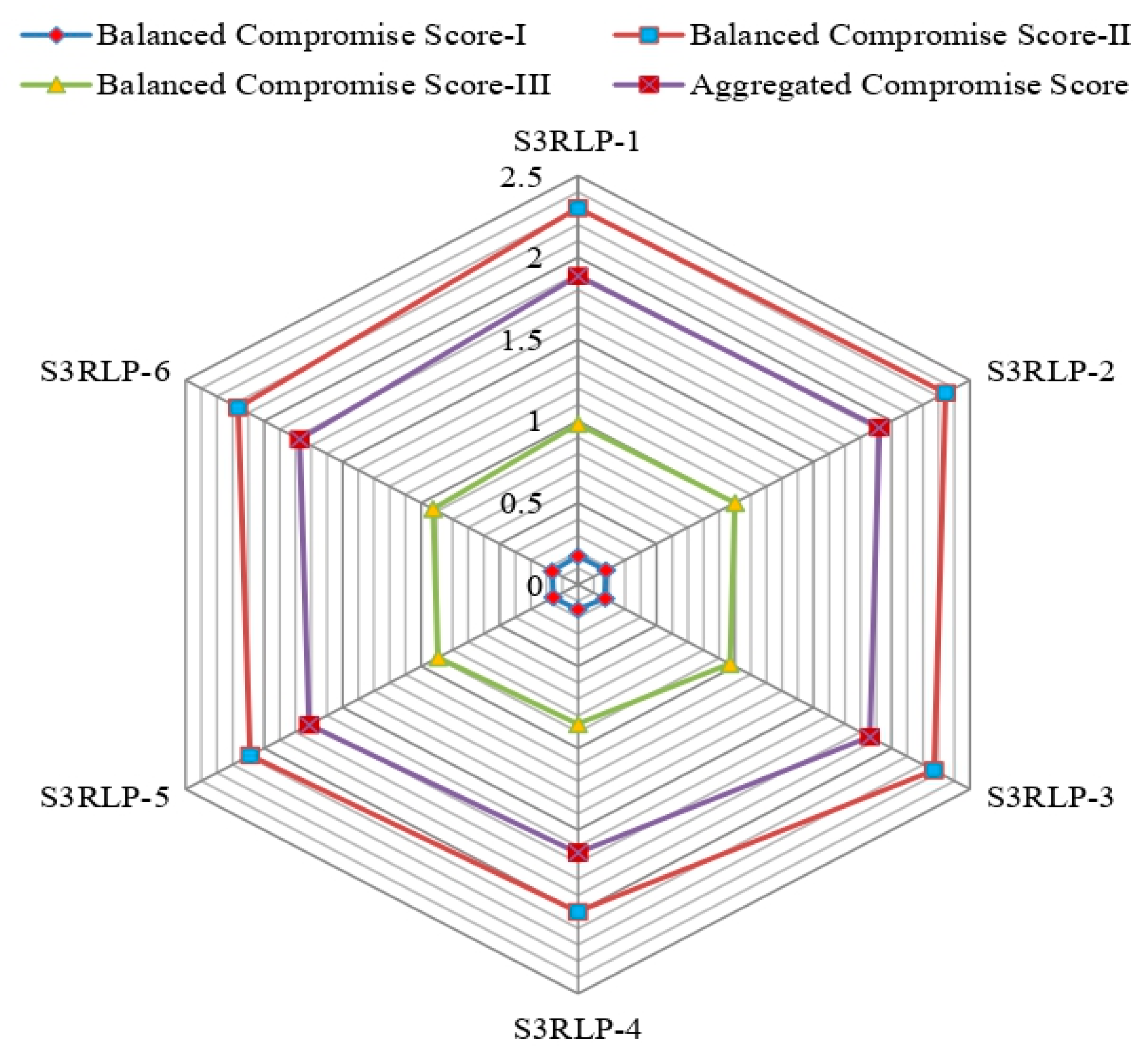
. Along with the values of increasing values of aggregating compromise index $C_i$, the prioritization order of the S3PRLP candidates is $M_2\succ M_1\succ M_3\succ M_6\succ M_5\succ M_4$ and thus, the option $M_2$ is the suitable, sustainable 3PRLP option. Here, Figure 2 shows the variation of compromise degrees with different measures of the proposed HF-CoCoSo method.

6.1. Comparative Study

In the current section, we compare the introduced HF-CoCoSo method with some of the existing methods, namely HF-TOPSIS developed by Xu and Zhang [80] and HF-COPRAS presented by Mishra et al. [34].

6.1.1. HF-TOPSIS Method

The structure of the HF-TOPSIS method is as follows:

Step 1–4: Same as HF-CoCoSo methodology.

Step 5: Determine the HF-positive ideal solution (HF-PIS) and HF-negative ideal solution (HF-NIS).

The HF-PIS and HF-NIS are computed by the following expressions (30) and (31):

$${\xi }^{+}=\{\begin{array}{l}\underset{i=1,2,\dots ,m}{\max }{y}_{ij} \mathrm{for} \mathrm{benefit} \mathrm{criterion} H_b\\ \underset{i=1,2,\dots ,m}{\min }{y}_{ij} \mathrm{for} \mathrm{cost} \mathrm{criterion} H_n\end{array}$$

(30)

$${\xi }^{-}=\{\begin{array}{l}\underset{i=1,2,\dots ,m}{\min }{y}_{ij} \mathrm{for} \mathrm{benefit} \mathrm{criterion} H_b\\ \underset{i=1,2,\dots ,m}{\max }{y}_{ij} \mathrm{for} \mathrm{cost} \mathrm{criterion} H_n,\end{array}$$

(31)

Step 6: Calculation of discrimination measures from HF-PIS and HF-NIS

By means of Equation (7), calculate the weighted discrimination measure $D\left(y_{ij},{\xi }^{+}\right)$ among the options $M_i\left(i=1,2,\dots ,m\right)$ and the HF-PIS ${\xi }^{+}$ and the Discrimination measure $D\left(y_{ij},{\xi }^{-}\right)$ among the options $M_i\left(i=1,2,\dots ,m\right)$ and the HF-AIS ${\xi }^{-}$.

Step 7: Estimation off relative closeness coefficient (CF).

With the use of Equation (30), the relative CC of each candidate is calculated, which is given as:

$$CF\left(M_i\right)=\frac{D\left(y_{ij},{\xi }^{-}\right)}{D\left(y_{ij},{\xi }^{-}\right)+D\left(y_{ij},{\xi }^{-}\right)},i=1,2,\dots ,m.$$

(32)

Step 8: Selection of optimal alternative

Opt the maximum value, symbolized by $CF\left(M_k\right)$, among the values $CF\left(M_i\right),i=1,2,\dots ,m$. Thus, $M_k$ is the optimal choice.

Step 9: End.

From Table 4 and Equations (30) and (31), HF-PIS and HF-NIS are appraised. Next, the entire procedural steps of HF-TOPSIS [80] framework are described in

Table 8. Overall outcomes of HF-Technique for Order of Preference by Similarity to Ideal Solution (HF-TOPSIS) framework.

Option	$\mathit{D}\left({\mathit{y}}_{\mathit{i}\mathit{j}},{\mathit{\xi }}^{+}\right)$	$\mathit{D}\left({\mathit{y}}_{\mathit{i}\mathit{j}},{\mathit{\xi }}^{-}\right)$	$\mathit{C}\mathit{F}\left({\mathit{M}}_{\mathit{i}}\right)$	Ranking
M1	0.132	0.133	0.502	3
M2	0.093	0.145	0.610	1
M3	0.119	0.104	0.465	4
M4	0.153	0.083	0.352	6
M5	0.142	0.090	0.387	5
M6	0.101	0.137	0.577	2

.

Thus, the final ordering of the S3PRLP candidates is $M_2\succ M_6\succ M_1\succ M_3\succ M_5\succ M_4$. Therefore, the most suitable alternative is M₂.

6.1.2. HF-COPRAS Method

The structure of the HF-COPRAS method is as follows:

Step 1–4: Same as HF-CoCoSo framework.

Step 5: Sum the values of criteria for benefit and cost.

Let $\Delta =\left\{1,2,\dots ,k\right\}$ be a collection of criteria, the greater values of which are finer. Then, determine the following index for each candidate:

$${\delta }_i^{\left(1\right)}=\underset{j=1}{\overset{k}{\oplus }}{w}_j{y}_{ij},i=1,2,\dots m.$$

(33)

Let $\nabla =\left\{k+1,k+2,\dots ,n\right\}$ be a set of criteria, the lesser values of which are finer. Then, estimate the following index for each candidate:

$${\delta }_i^{\left(2\right)}=\underset{j=k+1}{\overset{n}{\oplus }}{w}_j{y}_{ij},i=1,2,\dots ,m.$$

(34)

Here, k, n, and $w_j$ denote the number of benefit criteria, total number of criteria, and weight of the jth criterion.

Step 6: Determine the relative weight.

The relative weight of ith candidate is computed by

$${\mathsf{ƛ}}_i=s\left({\delta }_i^{\left(1\right)}\right)+\frac{\underset{i}{\min }s\left({\delta }_i^{\left(2\right)}\right){\displaystyle \sum _{i=1}^{m}s\left({\delta }_i^{\left(2\right)}\right)}}{s\left({\delta }_i^{\left(2\right)}\right){\displaystyle \sum _{i=1}^m\frac{\underset{i}{\min }s\left({\delta }_i^{\left(2\right)}\right)}{s\left({\delta }_i^{\left(2\right)}\right)}}},i=1,2,\dots ,m.$$

(35)

where $s\left({\delta }_i^{\left(1\right)}\right)$ and $s\left({\delta }_i^{\left(2\right)}\right)$ are the score values of ${\delta }_i^{\left(1\right)}$ and ${\delta }_i^{\left(2\right)},$ respectively.

Step 7: Compute the priority order.

The greater relative weight ${\mathsf{ƛ}}_i$ of the alternative, the higher the priority of the alternative. In the case of ${\mathsf{ƛ}}_{\max }$, the satisfaction degree is maximum.

Step 8: Evaluate the utility degree.

The utility degree of each alternative is

$${\eta }_i=\frac{{\mathsf{ƛ}}_i}{{\mathsf{ƛ}}_{\max }}\times 100\%,i=1,2,\dots ,m.$$

(36)

Step 9: End.

With the use of Equations (33)–(36), the overall procedures of the HF-COPRAS approach are calculated and presented in

Table 9. The overall computational results of the HF-Complex Proportional Assessment (HF-COPRAS) method.

Option	${\mathit{\delta }}_{\mathit{i}}^{\left(1\right)}$	${\mathit{\delta }}_{\mathit{i}}^{\left(2\right)}$	${\mathbf{ƛ}}_{\mathit{i}}$	${\mathit{\eta }}_{\mathit{i}}$	Ranking
M1	0.464	0.254	0.670	96.63	2
M2	0.460	0.224	0.693	100.00	1
M3	0.435	0.224	0.667	96.30	3
M4	0.352	0.230	0.578	83.45	6
M5	0.377	0.227	0.607	87.59	5
M6	0.391	0.213	0.635	91.70	4

.

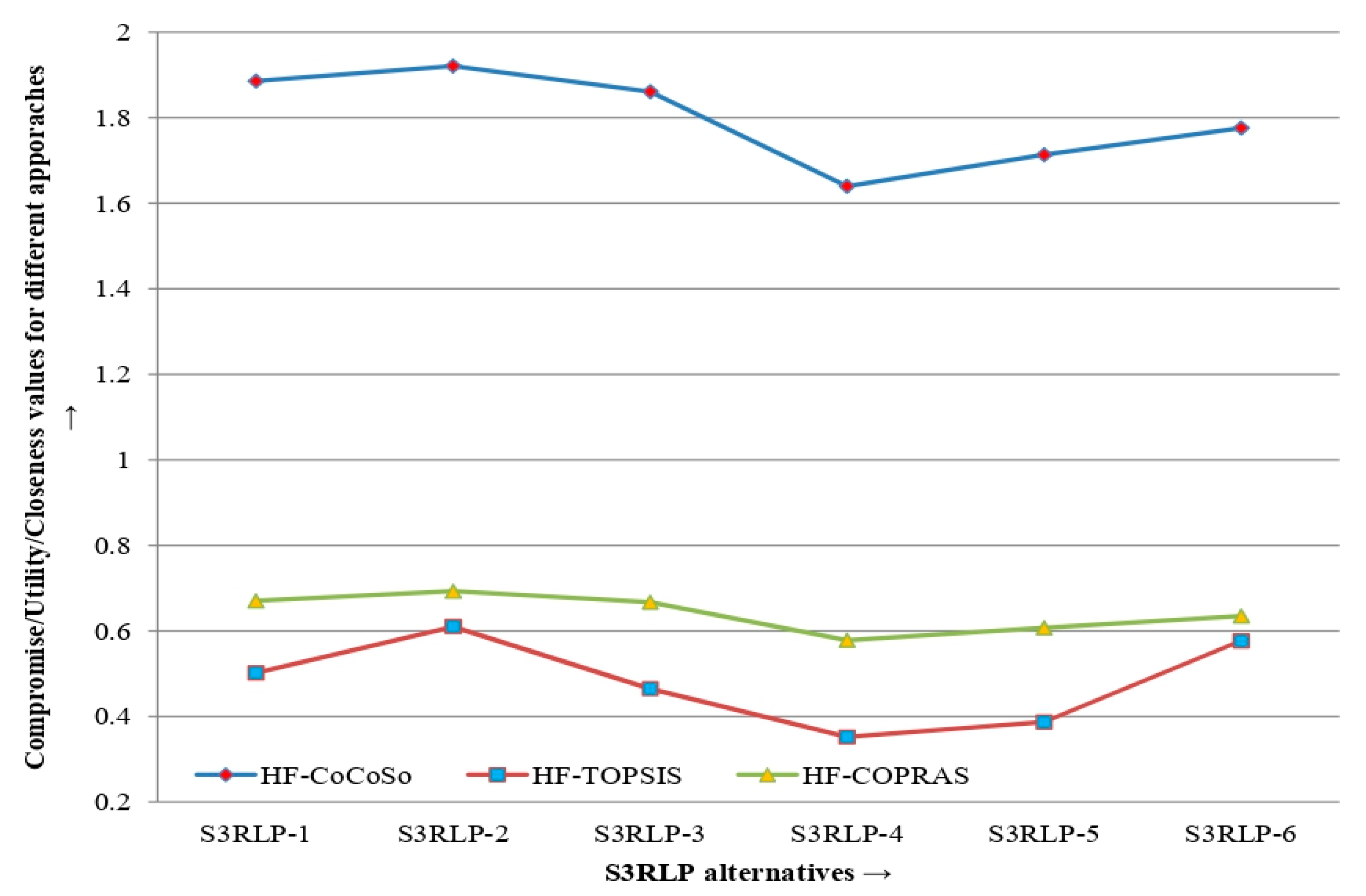
Thus, the ranking of the S3PRLP candidates is $M_2\succ M_1\succ M_3\succ M_6\succ M_5\succ M_4$. The ranking reflects that the alternative M₂ is the best alternative. Figure 3 presents the comparison of score values of S3PRLP alternatives with various methods.

The outcomes of the developed method are given as follows:

⮚

The proposed approach utilizes a comparability sequence, and then, the weights are aggregated through two manners. One of them follows the usual multiplication rule, and the second one narrates the weighted power of the distance from the comparability sequence. To validate the preference order, we have defined three different measures (aggregation strategy) for a given alternative. At the ultimate, a cumulative equation reports a ranking. There is not any algorithm among MCDM tools supporting this kind of aggregation. Each strategy would offer a ranking score, which would be further improved by a complete ranking index. This procedure is based on a combination of compromise attitudes.

⮚

The CoCoSo methodology has the potential to entail the DMEs’ estimations into decision-making processes, whilst the COPRAS technique is incapable of doing so.

⮚

The hesitancy degree is considered independently significant in the complete implementation process, and preference ordering of the candidates is obtained using the transaction degrees of all three parameters.

⮚

Assessment of criteria weights is one of the main challenges in the MCDM process. In the developed method, the objective weights, which are determined by new discrimination measure-based formula and the subjective weights, which are expressed by DMEs, are combined, and the aggregated weights are employed in the extended CoCoSo framework.

7. Conclusions

Increasing environmental awareness and the rapidly growing utilization of natural resources have motivated businesses to focus on sustainable SCM. As a result of the restraints related to their technology, own capital, or knowledge, some businesses outsource their RL activities. However, the selection of the correct S3PRLP alternative among a set of alternatives over multiple qualitative and quantitative criteria is an important and uncertain MCDM problem. The objective of the study is to recommend an MCDM methodology for evaluating the S3PRLP assessment problem with HFNs information. To do this, firstly, an innovative HF-CoCoSo approach is introduced by combining the traditional CoCoSo method, HFSs’ operators, and discrimination measure under HFSs settings. The weights of the criteria have been assessed by combining a proposed discrimination measure-based objective weighting method and a subjective method given by experts. Then, an illustrative case study of S3PRLP evaluation and selection problem has been discussed within HFS settings, which expresses the applicability and viability of the current method. The effectiveness of the introduced approach has been justified by comparison with extant methods. Finally, sensitivity assessment has also been discussed to show the stability of the proposed approach.

The shortcomings of this study are (i) the number of DMEs engaged in the present case study was small; (ii) the interrelationships between the criteria were not taken into deliberation, and (iii) the BDs of a certain element are not necessarily real numbers; this may bound the application range of the developed technique to some extent. Thus, further study will need to be carried out to enhance the precision of the decision-making selection problem by considering these factors. We can extend our study by incorporating objective and subjective criteria weights under different fuzzy environment. In addition, we will suggest some methods such as GLDS, DNMA, or MULTIMOORA to assess the S3PRLP selection problem. In addition, we will apply the developed methodology to other applications, such as sustainable biomass crop selection, renewable energy technology selection, and others.