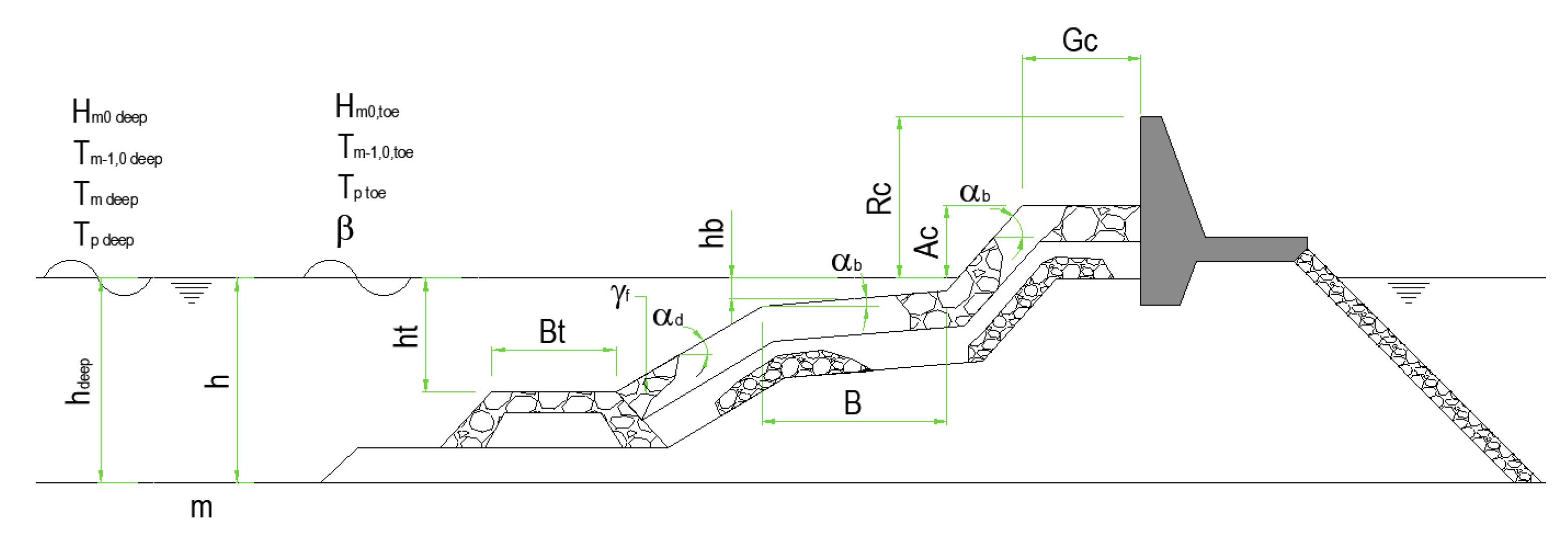
3.1. Obtaining the Reduced Dimension of the Input Vector
A first step will be to carry out a correlational analysis, by obtaining the correlation matrix. The information it provides is sufficient to make decisions about discarding some variables, but not enough to others, so it is necessary to resort to more sophisticated techniques such as those that will be used later. The existing correlations of the different explanatory variables with the variable to be predicted are very low (maximum
r value of 0.322), which shows the high non-linearity of the process to be analyzed (
Table 3).
In general, the correlation coefficients between the different variables that make up the set of input variables are low, or very low, reaching only significant correlation values in the following pairs of values:
B and Bh: referred to the dimensions of the berm (0.999)
h and ht: referred to depth at the toe of the structure or the submergence of the toe (0.91)
Tm t and Tm1 t: period values at the toe of the structure (0.63)
D and γf: variables related to the size and roughness factors (0.777)
Rc and Ac: variables relative to freeboard (0.860)
Cotαincl, cotαexcl, cotαd: variables related to the slope geometry (0.828 to 0.921)
Regarding PCA analysis,
Table 4 represents the contribution of each variable to the first eight principal components, together with their correspondent eigenvalues and the cumulative variance explained by them. The total variance cumulated by them is higher than 75%, that is one of the criteria accepted in practice for stablishing the contributing limit to an effective model. Another adopted criterion will be that the variance explained by them be major than the mean, so major than one, rule also proportionated by the first eight components.
The first component (F1) explains 15.09% of the variance and is dominated by variables related with the period, slope of the structure and by the wave steepness. The second component (F2) with a similar percentage of the variance explained (13.55%) is dominated by variables related with the submergence and cotαexcl. And the third component (F3) explains 12.64% of the total variance and is dominated by the variables cotαincl and Ac.
The analysis of the correlation circle, that corresponds to a projection of the initial variables of the first two factors of the PCA onto a two-dimensional plane, provides relevant information that allows observing correlations between the variables and interpreting the axes, or main factors, and thus being able to eliminate correlations that could be redundant and therefore detrimental to the predictability of the model. For the present case, it is shown, in the correlation circle (in the projection of both F1 and F2 axes) (See
Figure 3a), that the percentage of variability represented by the first two factors is not particularly high (28.64%). Therefore, to avoid a misinterpretation of the graphics, it also requires a visualization in axes 1 and 3, and interpretation of the influence of presence or absence of certain parameters (See
Figure 3b).
Both plots confirm the results shown in
Table 4, without a significant relevance of the variables, accompanied by a lack of clear interpretation of the axes, but on the other hand, with the evidence of certain interesting relationships between the variables.
It can be seen that there is a strong grouping between the variables related to the period (Tm1.0t; Tp t; Tm t), with a high positive correlation between them, a trivial matter already detected in the correlation matrix, which at least allows reducing their number, in any case keeping only one of them. Another group with a strong positive correlation is composed of those variables related to the geometric characterization of the slope (cotαincl; cotαexcl; cotαd) on which it will act in a similar way. The same procedure can be carried out with the variables relative to the width of the berm and its horizontal projection (B; Bh), and from which it is inferred that only variable B will be preserved. The grouping of variables in the correlation circle, in the projection of both axes F1 and F2, seems to determine the lack of correlation between the variables that make up the most obvious groupings, with similar direct cosines, such as those determined by cotαincl, cotαexcl, cotαd, and those like: cotαu, tanαB, Hm0 t. The foregoing leads to considering that both groupings of variables must be present in the input space, although with the particular restrictions indicated previously for some of them. The spectral wave steepness variable (Hm0 t/Lm1 t), negatively correlated with the freeboard variables (Rc, Ac), should be kept as above. Finally, the strong link between the width of the crest and the characteristic size of the protection elements in the breakwater is clearly reflected along with its strong link with the F2 axis.
The projection on the F1 and F3 axes explain a total variability of 27.7%, which is a percentage very similar to that explained by the previous projection (F1 and F2). Additionally, in this projection the correlations established for the first circle of projections are maintained, even the observed groupings are very similar. This robustness in the projection reaffirms the initial idea of finally discarding several of these correlated variables.
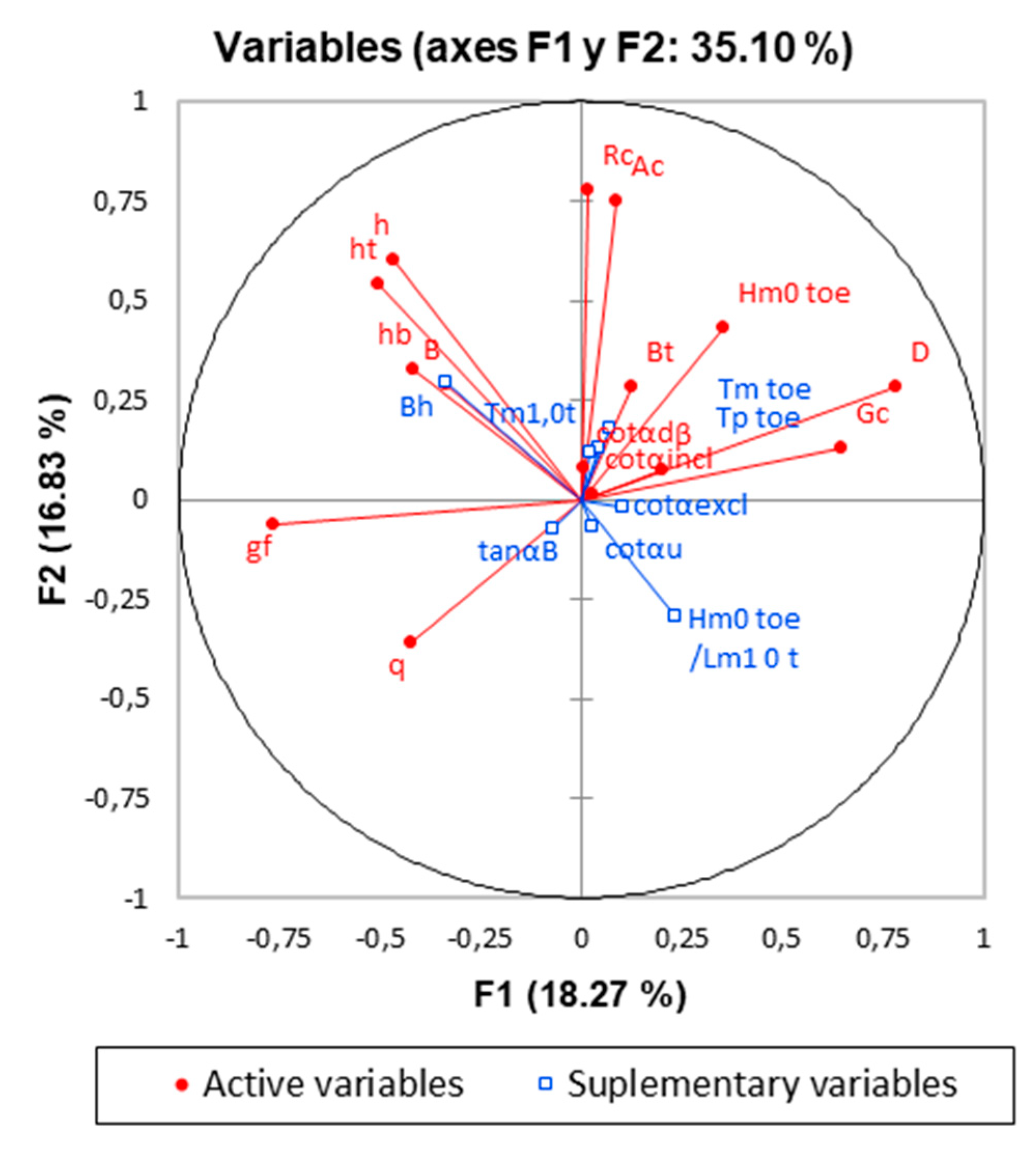
A technique that is usually used when the information provided by the PCA analysis carried out on the total of the variables is not very informative, is to consider the contribution of some variables whose contribution is doubted, such as that of supplementary variables studying the effect of their elimination on the projection space. In this case, the input space is censored by considering as supplementary variables all those that have shown an evident correlation in the previous projections.
Figure 4 shows the new correlation circle with this elimination step applied.
Figure 4 demonstrates that the variability explained by the first two factors increases slightly with a total of the variance explained equal to 35.10%. Additionally, that there is strong linking between variables relates with freeboard parameters and F1 axis, which could explain the major variance in the sample. The above, and its comparison with the initial projections, indicates that a reduction in dimensionality may be beneficial for the explanation of the problem without a significant loss of information [
53], and therefore this reasoning can be valid for the composition of a model with a smaller input dimension.
Alternatively, the application of a Kohonen network model on the same input pattern space, with a dimension of 23 factors (all of which come from the previous pre-processing processes), will indirectly allow the interpretation of the relationships existing at the level of self-similarity between input patterns, in a two-dimensional projection, where every pixel in that 2-dimensional map is characterized by a multidimensional vector. Information that will ultimately allow the reduction of the dimensionality of the entrance space, either by interpretation of these detected relationships, or by confirmation of those already detected using the PCA technique.
For the specific purposes of the present study, the constructed model, built with a Gaussian neighborhood function in every node, has been carried out using the following training scheme, characterized by two different phases [
66], where each set is shown 500 times to the SOM. During the training phase, the complete preprocessed data set is shown 500 times to the SOM, built with a Gaussian neighborhood function in every node. The first of these, or rough adjustment phase, is performed with a learning rate with values in the range between 0.9 to 0.1, and with a neighborhood ratio that varies from 2 to 1, and with an extension of training up to 100 times. The second or fine-tuning phase is completed with a unique learning rate of
η = 0.01, with a neighborhood ratio of 0, and with training extension up to 100 epochs. With this, the total length of the training will be: 100 + 100 = 200 times. The dimension of the input tile for this model will be 25 × 25 units (625 total units).
The following figure (
Figure 5) shows the different component planes obtained after network training, with a total of 23 units (one for each component variable of the input and output space).
From the analysis of these component planes the existence of several evident relationships between the variables is deduced. The first of these concerns the parameters related to the definition of the slopes of the dykes and which comparatively shows the existence of a direct and significant correlation across the entire range of the data between the variables (cotαexcl, cotαincl, cotαd). A reason why the information contributed by them can be redundant, and informs which two of them should be discarded. However, it is noteworthy that another of the variables related to that group of parameters, which refers to the cotangent of the slope of the structure in the part of the slope above the berm (cotαu), presents a projection pattern that is notoriously different from the previous ones, but without a distinctive response in the component plane, so it should not be taken into account.
Another very significant relationship detected by the SOM is the one that shows the component planes of the roughness factor variables (
γf) and the mean diameter (
D). The comparison of both planes shows the existence of a negative correlation between them, and thus the greater sizes, the lower the roughness factor. This relationship is evidence in the existing empirical knowledge and taken into account [
32,
41], but it is comforting to confirm that the ANN is capable of detecting it as well. Both parameters should be preserved a priori.
The next detected relationship is the one between the width of the berm (B) and its projected width (Bh), and that is also preserved across the data range. Therefore, only one of them should be selected, discarding the other.
It could be thought that, based on design criteria, there was a direct relationship between the width of the berm and the width of the toe (
Bt), or with the width of the crest, however, this has not been detected at the data base analyzed for the crest width of the structure, so this supposed relationship will be discarded. While the existence of a partial correlation, at least in a region of the projection plane, between the variables of the berm width and the width of the bench (see
Figure 5) is detected, which indicates that some of the breakwaters that have been tested have been designed with a theoretical pattern that relates both variables. The foregoing forces not discarding these variables, but to keep them in the input space, since this relationship is partial in the sample space it is necessary to preserve that differentiation.
A last relationship highlighted (
Figure 5), and also expected by the existing empirical knowledge, is the one presented by the depth variables at the toe of the structure (
h), and the one that define the submergence of it (
ht). In this case, as expected, its correlation is direct or positive. However, the lack of correlation between both variables and the berm (
hb) is also striking, therefore, following the above reasoning, at least two of them should be maintained, discarding the third of them.
In view of the results obtained and interpreted after applying both the PCA technique and the SOM maps, a reduction in the size of the input patterns can be achieved. It results in a final dimension of the input vector of 15 parameters (see
Table 5).
3.2. Model Selection
The results obtained after the training process of the different architectures tested for each model, show better performance of the aggregate model (Model I) over the disaggregated model (Model II), both in terms of error and correlation, as shown in
Table 6,
Table 7 and
Table 8, and
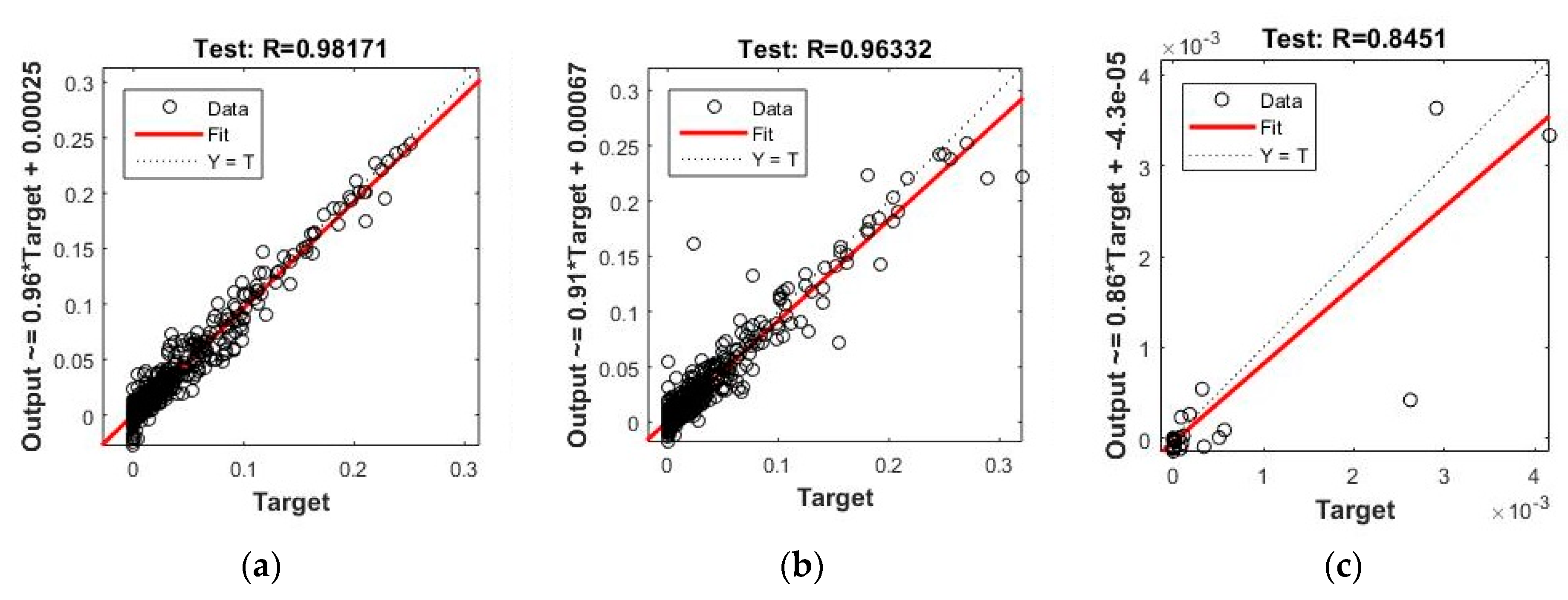
Figure 6, in which is possible to distinguish the results for each of the subsets used in the cross-verification process: Training (TR), Verification (V), Test (T) of the better Model I.
The finally selected architecture for Model I, based on the results obtained, is an MLP network with 15 input variables, 25 neurons in the hidden layer, and a single neuron in the output layer (see
Table 6,
Table 7 and
Table 8, with the trial results to determine the best architecture in the results of the different models proposed).
The results are shown in the form of correlation plots for test subset in
Figure 6. Noting that for the test subset the correlation values are greater than 0.98. Although they are similar to those obtained for sub model II.1 (0.96), they are much higher than those obtained with sub model II.2 (0.84). The results in terms of error (MSE) are similar for both model I (3.85 × 10
−5) and model II (3.82 × 10
−5), with the known exception that the MSE is not an absolute statistic, but a relative one [
64].
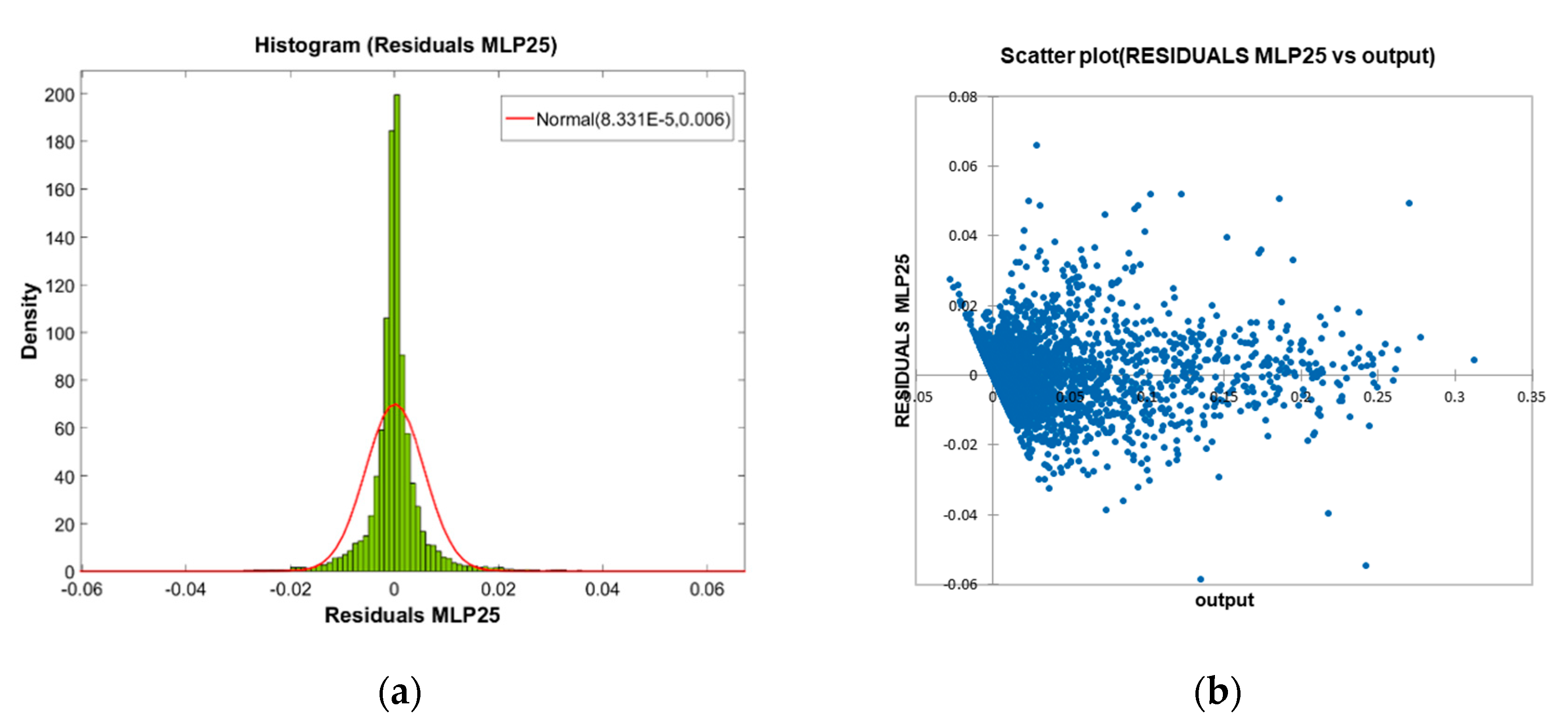
The analysis of the residuals establishes, as a desirable objective for an ideal model, that its distribution be carried out according to a pattern as close as possible to a normal distribution as a clear indicator of the absence of any hidden trend or bias in the modelling performed. In the present case, a careful analysis of this distribution shows that although it is close to normal, it does not fit significantly to it. This is demonstrated by the chi-square and Kolmogorov-Smirnov fit tests carried out, and that they are presented below (see
Table 9), together with their correspondent graphical adjustment (
Figure 7a).
The graphical analysis of the scatter plot of the residuals (
Figure 7b) shows adequate behavior across the entire response range, except in the range of low values of overtopping rate, for which it does show a certain tendency towards non-compliance with the hypothesis of constant variance of the residuals. This heteroscedasticity may be linked to scale problems in the tests or introduced by iso-energetic sequences of waves [
60,
61], since the behavior of the prediction for very low overtopping rates has been associated with high levels of uncertainty [
69], or may be due to the need to perform further specific transformations on the input variables beyond those already applied in the present study [
25].
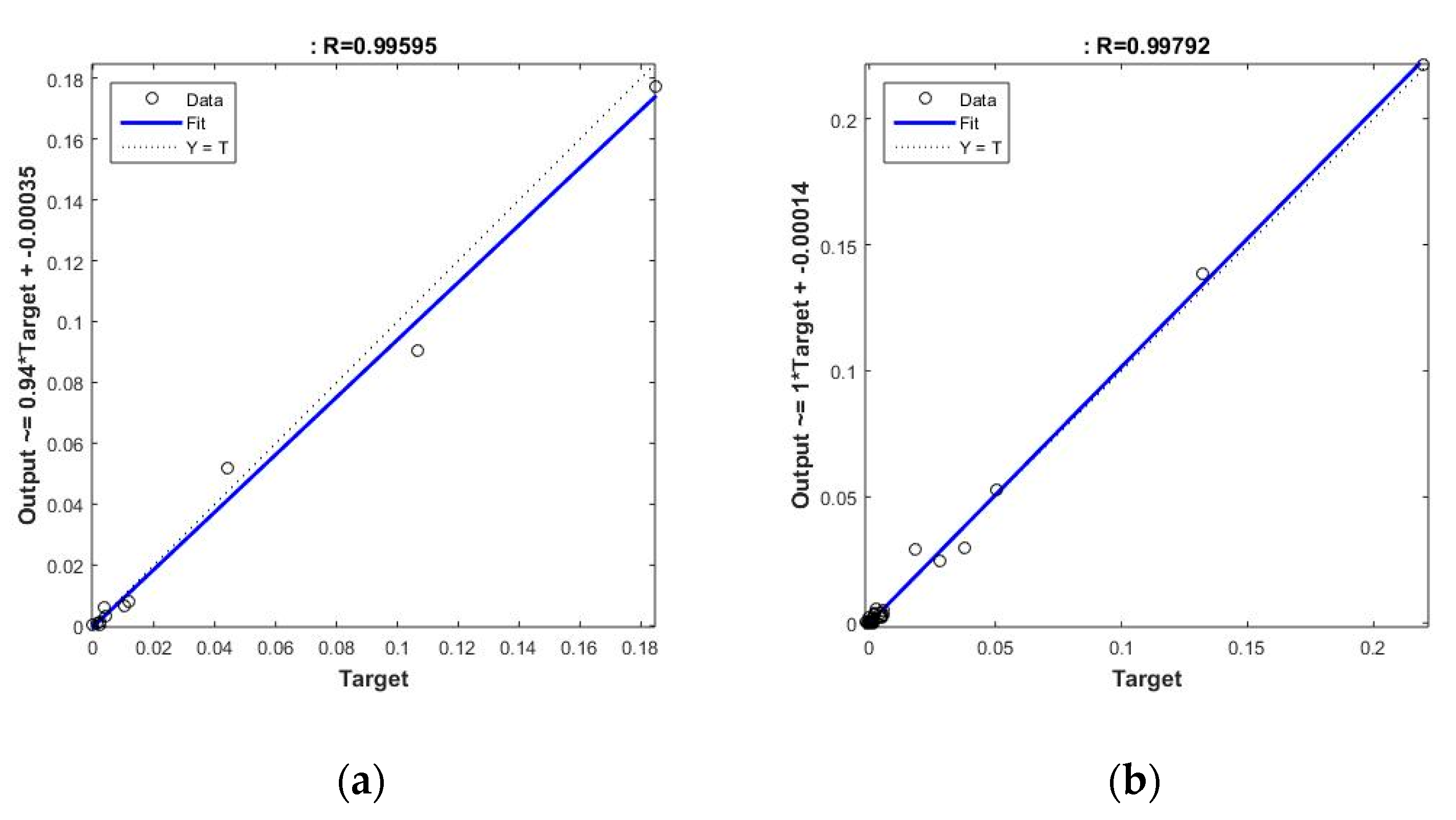
An extra validation test performed on an additional sample of 100 patterns, and with the selected ANN, provides good performance, with correlations of 0.98, which could validate its generalizability. However, what is more interesting, after classifying the component patterns into two different classes, the first one corresponding to tests on seawalls, and the second corresponding to sloped breakwaters, they show a similar aspect and is very suitable for the prediction of the overtopping rate on both (see
Figure 8). Thus, the results for the typology of seawalls provides a correlation coefficient of 0.996, while for slope breakwaters it provides a similar result of 0.998.
3.3. Sensitivity Analysis
Finally, a sensitivity analysis is carried out on the selected ANN, specifically on the component parameters of the input vector. This analysis is performed using a pruning technique, and the ratio that was proposed for this purpose:
where
is the sensibility ratio, and
the error function value for the trained network. In this case, the MSE is chosen as the error criterion to define the sensitivity ratio.
This procedure is especially useful when the input variables are essentially independent of each other [
64], and conversely, the more interdependencies there are between the variables, the less reliable they will be. Hence, among other reasons, the importance of the previously performed dimensionality reduction procedure, which now supports the application of that sensitivity analysis.
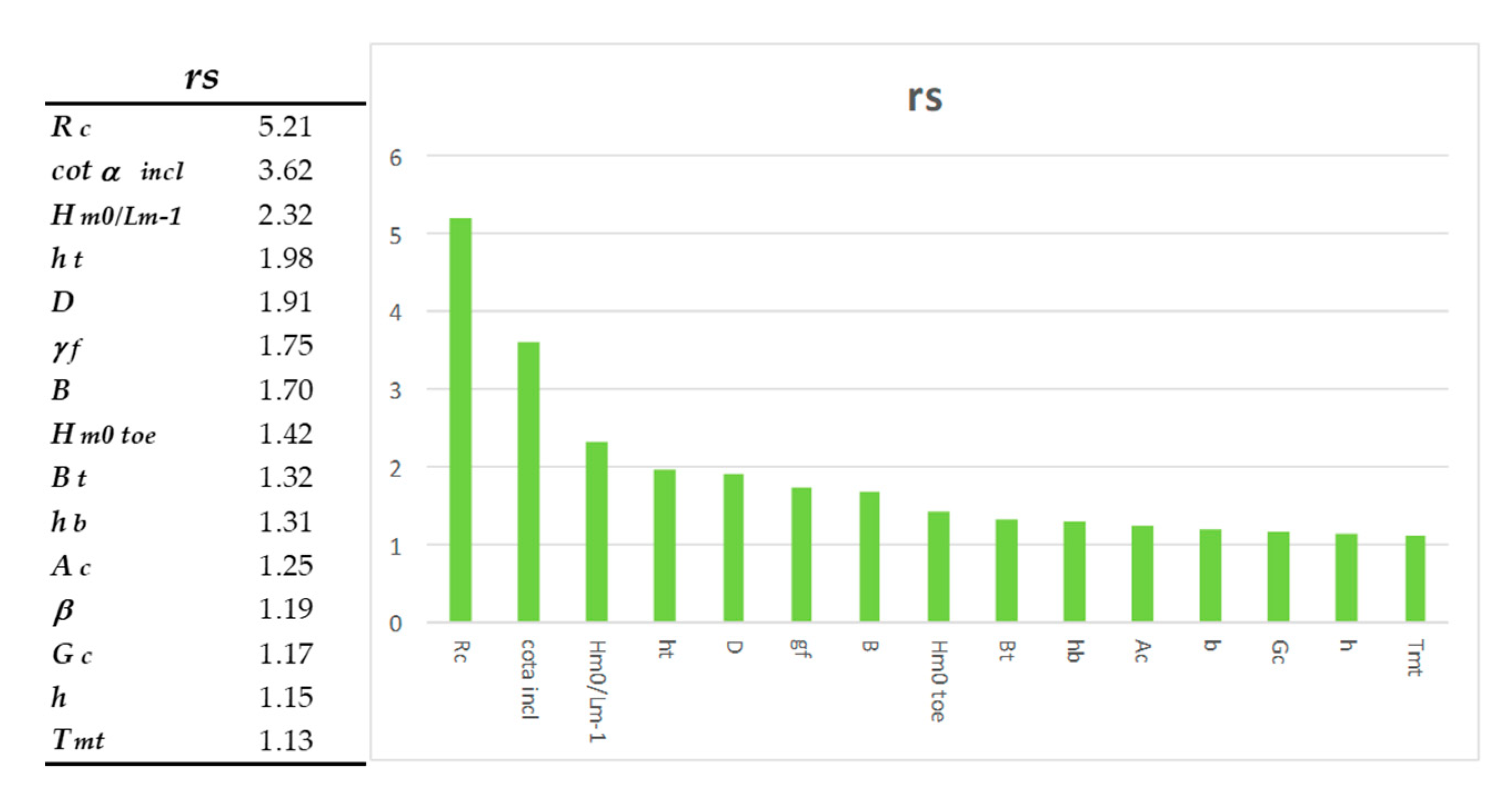
It is observed in the
Figure 9 that all the variables have a significance ratio greater than 1.05, which according to that criterion implies that all the variables are significant a priori, and that therefore it would be desirable to maintain them for adequate network performance. The above has a clear derivative, which is to suppose that the process of dimensionality reduction has been successful, since any of the existing variables will provide enough relevant information and their elimination may imply worse predictive capacity of the network.
Beyond the previous observations, it is noted that the most influential variable is the freeboard of the wall with respect to swl (
Rc), an issue that is confirmed by PCA analysis. It is noteworthy that a variable closely related to it, the other freeboard parameter, the crest height with respect to swl (
Ac), is quite far, in terms of significance, from the parameter
Rc. This fact is relevant since in some works [
59] it has been determined that the scale effect seems to depend a lot on the superior geometry of the breakwater. This results in many more significant associated effects on small overtopping rates, which are incidentally, also the most numerous in the database. Given this, and to try to mitigate these effects as much as possible, some authors propose the dimensionless of these variables [
25,
30,
59].
Another significantly interesting variable is the average cotangent where the contribution of the berm (
cotαincl) is considered [
42,
59]. Similarly of interest, the wave steepness (
Hm0/Lm−1) is highlighted. In addition to these, are both parameters related to roughness (and in essence, to the porosity of the mantle) where their close relationship with overtopping is already known empirically [
32], and which in turn have a substantial dependence on the dimensionless freeboard (
Rc/Hm0).
Overall, the results are consistent in terms of the significance of these parameters with similar studies carried out with different preprocessing techniques [
30]. And it should be mentioned that some parameters in this study are may be penalized, due to the fact that they have been poorly represented in the database. For example, this happens with the wave incidence angle parameter (
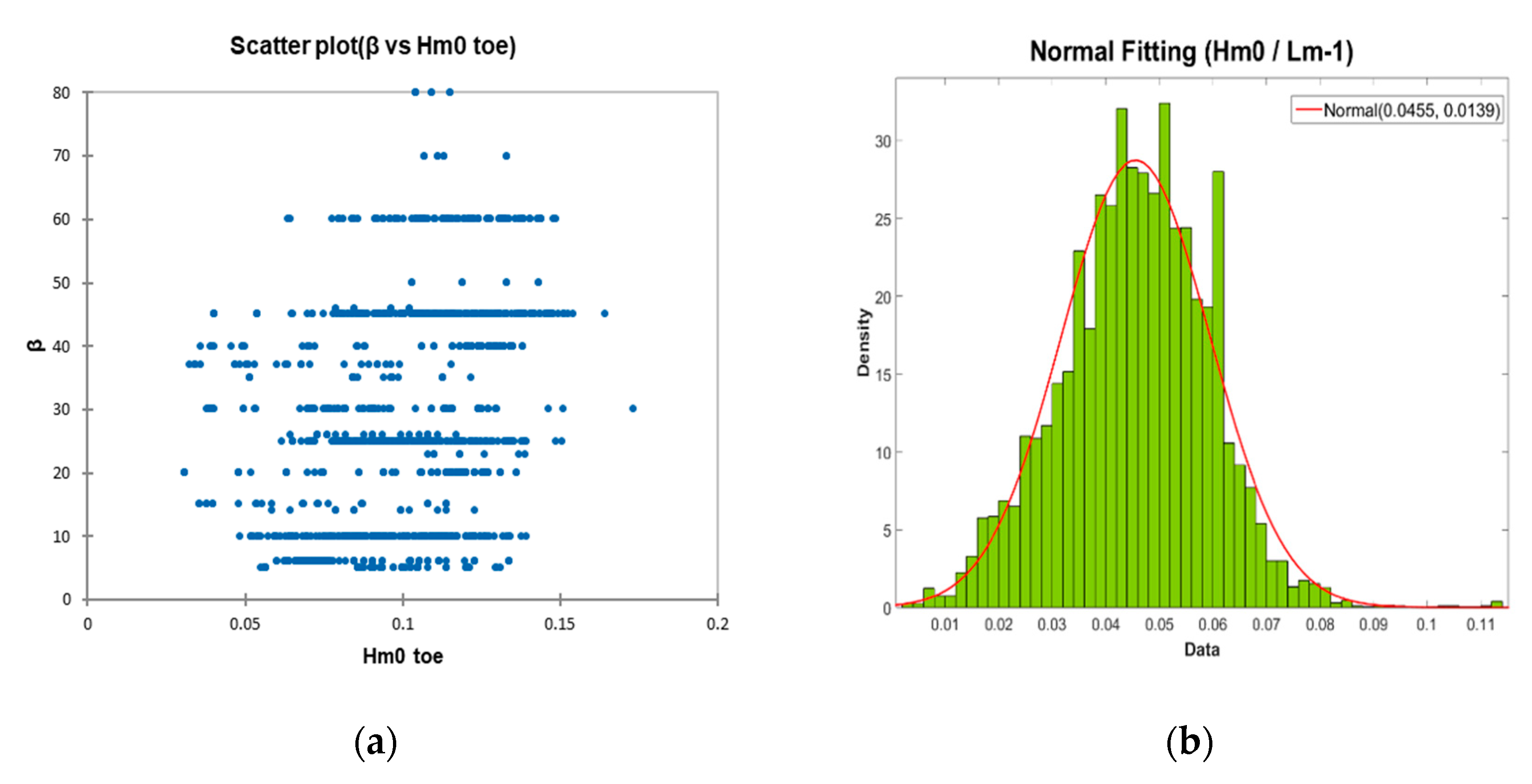
β) that shows a significant lack of data in some ranges of that continuous variable. In the following figure (see
Figure 10a) the distribution of the aforementioned parameter with respect to the significant wave height at the toe structure (
Hmo t) is presented since, as Van der Meer cites [
48], this relationship is strongly related to the overtopping phenomenon, and shows the existence of poor representability in the ranges greater than 50°.
The importance given to the dimensionless parameter of the wave steepness, particularly for wave overtopping energy conversion [
70], which has good representation in the database, both in its distribution and in the quality of that distribution (normalized distribution), should also be highlighted (see
Figure 10b). Faced with possible uncertainties associated with scale phenomena [
59], although the parameter’s existence in the field of validity is remarkable with values over 0.07 that are physically not possible as the wave breaks on steepness [
56], the use of wave steepness as a variable is recommended. This also represents the effects induced by local breakage and waves [
25], and is therefore strongly related with the overtopping.
Due to the fact that for wave overtopping conversion the maximum overtopping rates correlated with the lower
Rc/Hs relationships [
71] are highly desirable. These will generally be associated with low crested structures, specifically with
Rc/Hs lower than 1. It would be desirable that the training sample be well represented in this range, as does happen, and is shown in the following figure (
Figure 11a). Checking the model for those exceedance rates corresponding to the range in the previously mentioned sample of 100 extra cases (corresponding to a total of 57 cases), the result is encouraging, with values of the correlation coefficient greater than 0.98, as shown in the
Figure 11b.
Thus, and in accordance with the above mentioned, any future improvement in the model should necessarily focus on that data range. This desired approach is in practice the opposite of what is usually done for defense structures.
Another crucial issue related to the generation of the data is the need to make the range of data tested wide enough to include extraordinary events, given that ANNs are usually unable to extrapolate beyond the range of the data used for training [
65,
72]. This ensures that they always work in the expected range, avoiding poor predictions when the validation data contain values outside of the range of those used for training. In this sense, there is a preponderance of low flow rates that reinforces the idea of a disaggregated approach in future models.