Accuracy and Predictive Power of Sell-Side Target Prices for Global Clean Energy Companies

Abstract

Target prices are often provided as a support for stock recommendations by sell-side analysts which represent an explicit estimate of the expected future value of a company’s stock. This research focuses on mean target prices for stocks contained in the Standard and Poor’s Global Clean Energy Index during the time period from 2009 to 2020. The accuracy of mean target prices for these global clean energy stocks at any point during a 12-month period (Year-Highest) is 68.1% and only 46.6% after exactly 12 months (Year-End). A random forest and an SVM classification model were trained for both a Year-End and a Year-Highest target and compared to a random model. The random forest demonstrates the best results with an average accuracy of 73.24% for the Year-End target and 81.15% for the Year-Highest target. The analysis of the variables shows that for all models the mean target price is the most relevant variable, whereas the number of target prices appears to be highly relevant as well. Moreover, the results indicate that following the rare positive predictions of the random forest for the highest target return groups (“30% to 70%” and “Above 70%”) may potentially represent attractive investment opportunities.

1. Introduction

Investors aiming to invest in the stock market to buy a company’s stock face the challenge to select companies that will be successful in the future and whose stock will appreciate over time. Brokerage firms spend a considerable amount of resources, including money, on stock analysis, recommendations, and target prices, which suggests that these institutions and their clients see value in such research [1,2]. For that reason, investors and academics alike have been interested in the value of sell-side analysts’ reports [3]. In this context, sell-side analyst refers to analysts employed by financial institutions such as banks, brokers, and asset management firms, which also sell securities such as stocks to their clients. These analysts provide research reports on stocks to the clients of their institution [4], which contain information about the future of these companies [5]. Their reports frequently include three elements: (1) an earnings forecast, (2) a stock recommendation, and (3) a target price for the stock [5,6,7], which are the result of their own evaluation of a company [6]. Stock recommendations usually come in five distinct levels (“Strong Buy”, “Buy”, “Hold”, “Sell”, “Strong Sell”) [1,4,5,8], whereas the target price is provided as a support for the stock recommendation and is explicitly mentioning the expected stock value [3,6,9], usually, for the next 12 months [2,7]. Target prices often accompany stock recommendations, but previous research suggests that not all analyst reports contain target prices [5]. In particular, their inclusion in reports is more likely in case of positive recommendations (e.g., 70% for upgrades vs. 35% for downgrades [3] or 84% for “Strong Buy”/79% “Buy” vs. 27% for “Hold” [6]). However, when target prices are included in a report, it is intuitive that higher target prices for stocks are generally associated with more favorable stock recommendations [6].

Previous research has covered different aspects of stock recommendations and target prices. This includes investigating the individual analyst’s ability to make recommendations and set target prices [7,10,11] as well as the performance of recommendations of different institutions [8], and the value or abnormal returns associated with stock recommendations [1,12] even when analysts face conflicts of interest [13].

It was shown that, even though analysts appear to be reluctant to make “Sell” (and “Strong Sell”) and “Hold” recommendations and tend to focus on “Buy” recommendations (and “Strong Buy”) [3,5,14] (e.g., “Buy” and “Strong Buy” account for 70.8% [5] or 68% [3] of all recommendations), their recommendations appear to have value. In particular, there are stock price reactions to recommendations (and recommendation revisions) [14] and investors can benefit from such recommendations [1,4] e.g., by buying highly rated stocks and by selling lowly rated ones [1].

In terms of target prices, the link between target prices and stock recommendations [6], factors affecting the accuracy of target prices [2], the impact of price targets and recommendation revisions [3,4,5], the impact of different valuation models on the target price [9], and the dispersion of target prices as a risk measure [15] are examples of research works found in the literature. Moreover, research has indicated that target prices and target price revisions contain new and valuable information [3,5]. However, the fact that target prices may contain relevant information for the stock market and investors does not necessarily mean that target prices are accurate [11]. Moreover, as pointed out by Bonini et al. [2], the ability to forecast future stock prices using analyst target prices is a neglected topic in the literature. The accuracy of target prices, meaning whether stock price meet target prices after or during the forecast period (e.g., a 12-month period), as well as their (absolute) forecast error, meaning how far the stock prices are away from the predicted target prices, depends on different factors. First, in terms of the institutions issuing target prices, highly reputable institutions tend to issue more accurate target prices (those target prices with positive implied return only) [11]. The evidence towards individual analysts’ ability to suggest accurate target prices is limited. Bradshaw, Brown, and Huang [7] find some statistical evidence supporting a persistent differential ability of analysts in terms of accurate target price predictions, but these were shown to be trivial economically. Besides, as may be expected, analyst-specific optimism has a negative impact on the accuracy of target prices [11]. This may be linked to the fact that analysts’ target prices may be used strategically [11] e.g., to create a “hype” around a stock [5] and may not always reflect the actual belief of analysts (e.g., similar for recommendations where a “Buy” recommendation is issued instead of a more suitable “Hold”/”Sell” one [13]). In terms of analyst research, the level of detail of research reports is positively affecting the target price accuracy [11] and the number of analysts providing research appears to improve the information quality [16], which may potentially also affect the target price accuracy positively. In terms of the company covered, recommendations for stocks associated with a larger price-to-book value (P/B), which can be called “glamour” stocks (e.g., technology companies) show lower forecast accuracy [11], which may be problematic given that research suggests that sell-side analysts tend to recommend such stocks more often [12]. Apart from that, setting accurate target prices appears to be especially challenging for companies that are loss-making (not earning profits) [2]. Volatility appears to impact target price accuracy as well, with lower volatility of the stock price leading to a higher accuracy [7,11]. The positive development of the stock market as a whole also affects the accuracy of target prices positively [7], which is in line with the finding that the forecast error of analysts increases during negative market environments [17]. Lastly, in terms of the target price, the accuracy and magnitude of the forecast error seem to be higher the larger the difference between the target price and current stock price (implied growth in stock price) [2,5,11].

This research work focuses on the accuracy and predictive power of target prices, specifically consensus information, meaning mean target prices. As mentioned previously, research on target price accuracy is very limited. Apart from that, the vast majority of previous research on target price accuracy has centered on individual analysts and/or individual target prices. There is some research on using consensus recommendations (e.g., the mean of recommendations) [1,12] but no research appears to have been done on using the consensus of target prices and determining the accuracy of such an aggregate estimate for the future stock price. In recent years private investors have also had easy and free access to many financial websites (e.g., Yahoo Finance, finanzen.net) that provide such mean target prices and related information [6] and make such an investigation also relevant for private investors, as well as academics and practitioners. Apart from that, no work appears to have been done using classification algorithms with target prices, which are very intuitive from an investors’ perspective since they can be used for the binary decision (yes/no) whether to invest in a stock or to refrain from doing so. This study aims to address this research gap by using mean target prices and measuring the accuracy of these consensus estimates as well as using classification methods (with embedded feature selection) to build a model to predict when mean target prices will be met and when they might be missed. Moreover, the variables that are relevant for the prediction will be determined to gain further insights into potential factors that may affect the probability that a mean target price is met.

The emphasis of this work is on clean energy stocks which have attracted increased attention due to the Paris Agreement [18] and the rise of clean energy technologies as a response to the threat imposed by climate change. The road to the Paris Agreement extended multiple years, starting from around 2009 with the Copenhagen Accord [19]. The agreement was adopted by 196 Parties (almost every nation) in December 2015 to address climate change and its harmful impacts, and about 190 of those countries formally approved it [20]. The agreement sets up an ambitious target to limit the increase in mean global temperature to well below 2 °C above pre-industrial levels by reducing global greenhouse gas emissions. Among other measures, this includes ramping up efforts to accelerate the implementation of clean and sustainable energy technologies.

2. S&P Global Clean Energy Index

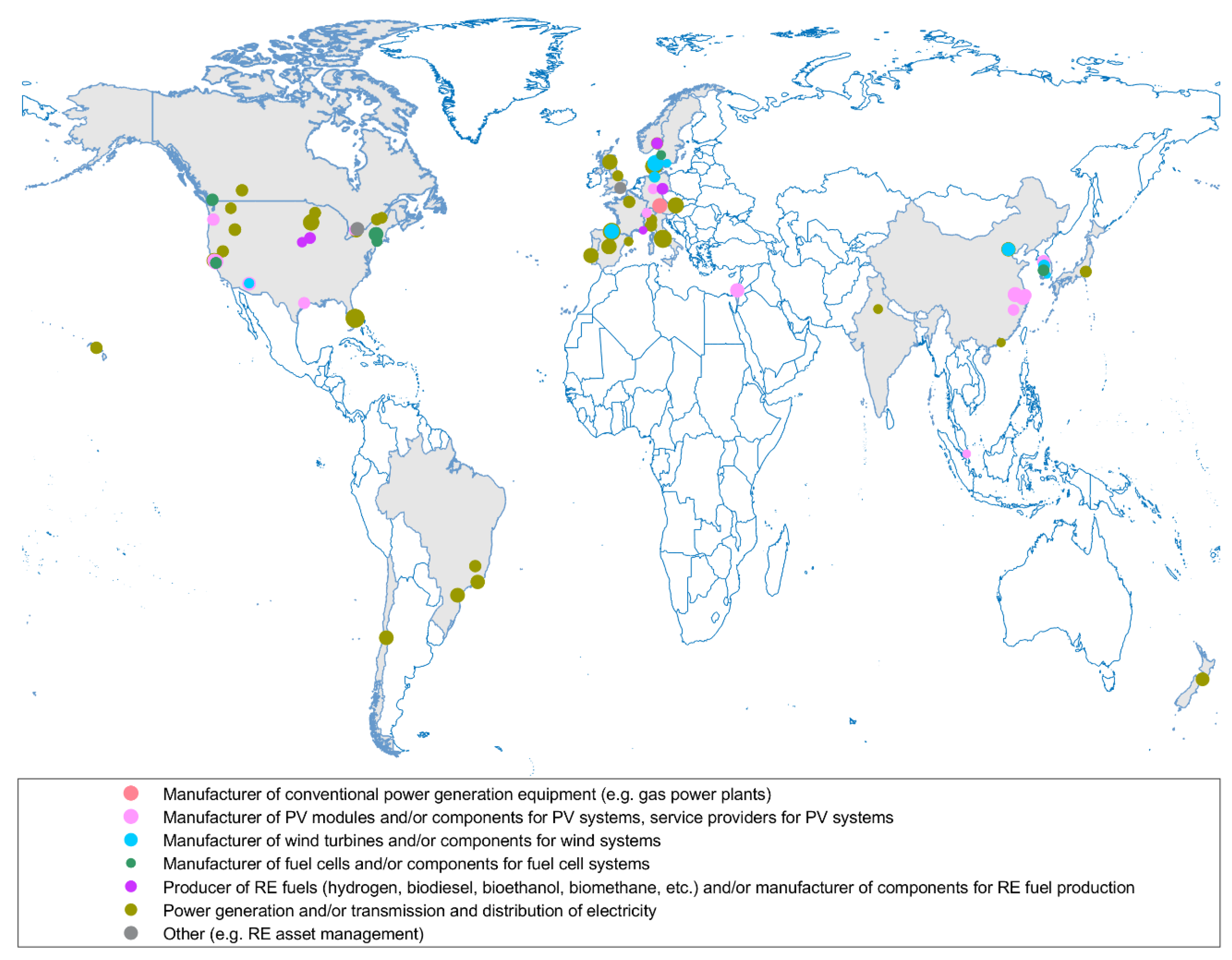
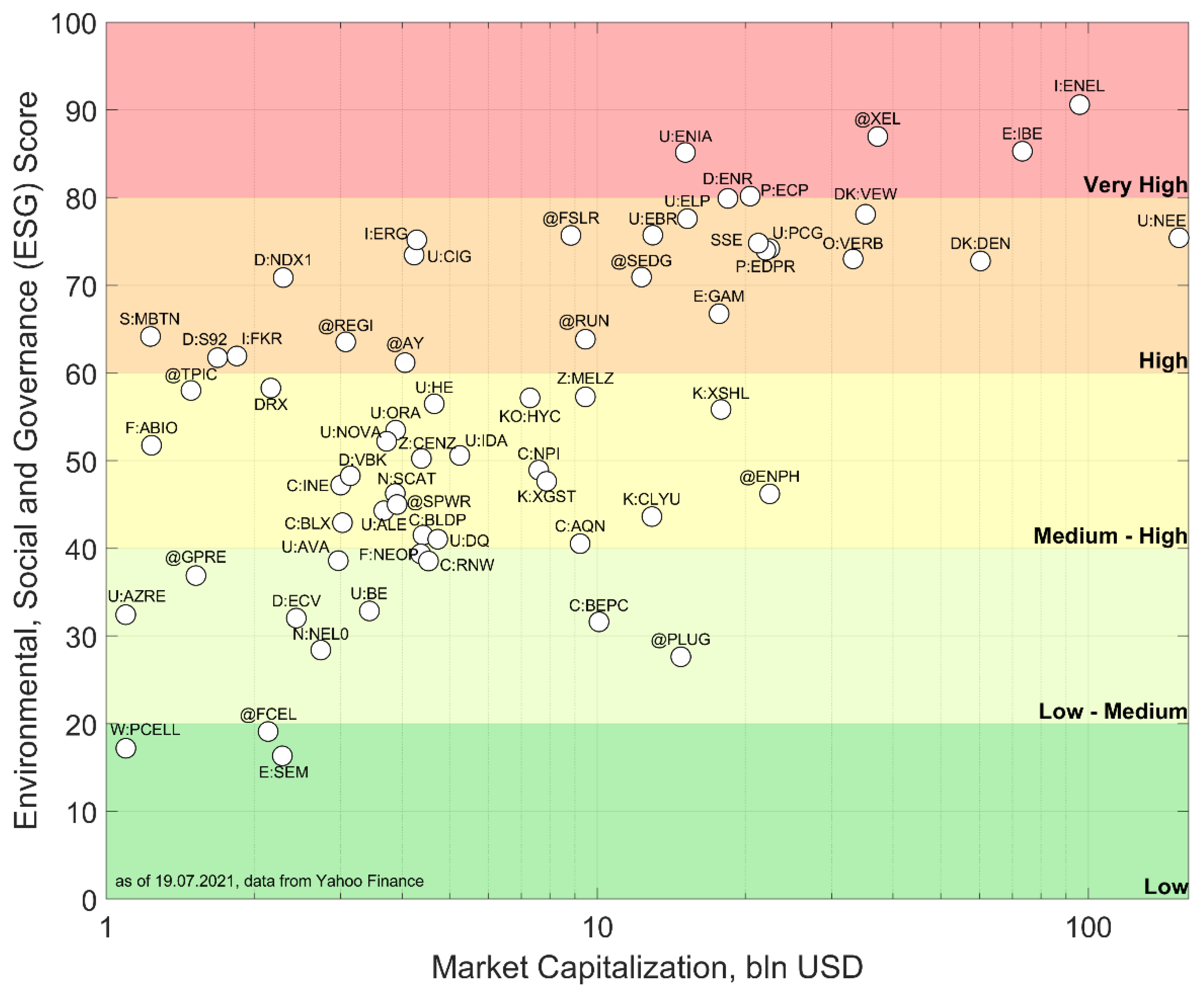
The Standard and Poor’s Global Clean Energy Index (USD) is an equity index launched in 2007 that aims to measure the performance of companies in developed and emerging markets that have businesses linked to global clean energy [21,22]. In particular, companies contained in the index are “involved in the production of clean energy or provision of clean energy technology and equipment” [22]. Figure 1 displays the geographical location of the headquarters of the companies (as of July 2021) contained in the S&P Global Clean Energy Index. Gray color highlights the countries with headquarters in them and the marker size reflects the relative size of the company in terms of the market capitalization, as obtained from Yahoo Finance [23].

Out of the 81 companies included in this study, the headquarters of 28 companies are located in Europe (in Austria, Denmark, France, Germany, Italy, Norway, Portugal, Spain, Sweden, Switzerland, and United Kingdom). The headquarters of another 28 companies can be found in North America (in Canada and the United States). Finally, there are 15 headquarters in Northeast Asia (in China, South Korea, and Japan), 4 in South America (in Brazil and Chile), 3 in Southeast Asia (in New Zealand and Singapore), 3 in MENA (in Israel), and 1 in SAARC (in India). The largest number of companies (20) are headquartered in the United States (24.7%). In contrast to that, none of the 81 companies in the index is headquartered in Africa or the Eurasian regions. However, the authors of this study acknowledge that these companies may operate/have subsidiaries in African or Eurasian countries.

In terms of the business activity, about 52% of the companies are involved (directly or through their subsidiaries) in the power generation process, which includes the development, construction, and operation of power plants as well as the subsequent transmission and distribution of electrical energy. The second-largest group of companies (about 21% of the companies) are linked to the manufacturing of solar PV systems and their components (for instance, production of monocrystalline and polycrystalline silicon for solar PV cells, solar PV modules, inverters, storage systems, software, etc.). Apart from that, the third-largest group (10% of the companies) are developers of wind power generation systems. This group consists of companies, which, for example, design and manufacture blades and wind towers, construct wind turbines and wind farms, as well as provide various services to wind power generation companies.

Figure 2 displays the market capitalization of the companies and their corresponding Environmental, Social, and Governance (ESG) scores obtained from Thompson Reuters Datastream (see Appendix A 

Table A1. Selected variables from Thompson Reuters Datastream.

Name	Variables	Type	Description
IBES Number of Price Targets	PTNE	Target Price	Indicates IBES Number of Price Targets.
IBES Price Target High Value	PTHI	Target Price	Indicates IBES Price Target high value.
IBES Price Target Low Value	PTLO	Target Price	Indicates IBES Price Target low value.
IBES Price Target Mean	PTMN	Target Price	Indicates IBES Price Target mean value.
IBES Price Target Standard Deviation	PTSED	Target Price	Indicates IBES Price Target Standard deviation.
Price Target Up since last monthly values	PTUP1M	Target Price	-
Price Target down since last monthly values	PTDN1M	Target Price	-
Price/Earnings Ratio (Adjusted)	PE	Other Financial	This is the price divided by the earnings rate per share at the required date.
MSCI World Price Index	MSWRLD$, PI	Other Financial	Price Index of the MSCI world stock market index.
ESG Score	TRESGS	ESG	Refinitiv’s ESG Score is an overall company score based on the self-reported information in the environmental, social, and corporate governance pillars.

).

The ESG score takes values from 0 to 100 and is based on self-reported (but verifiable) information of companies on their performance in terms of environmental, social, and governance indicators. In particular, the environmental score contains components such as “resource use” and “emissions”, the social score elements such as “workforce” and “human rights”, and the governance component for instance the “corporate social responsibility (CSR) strategy” [24]. The point labels are the Datastream symbols for the companies (shorter than the complete company names) and the levels of ESG scores (from “Low” to “Very high”) were artificially created for this study for better representation of the ESG scores. The y-axis is on a logarithmic scale. In general, companies with larger market capitalization tend to be associated with higher Environmental, Social, and Governance (ESG) scores. One possible explanation for this could be that the operations of larger companies might be more in the public’s attention and more exposed, which may create pressure from stakeholders such as society, civil organizations, as well as from (potential) investors. Additionally, larger companies might be able to allocate larger financial resources to reporting tools for ESG rating agencies (for instance, to provide higher quality and more comprehensive data to better fit the ESG measurement systems). Apart from that, it could be that the management enumeration of larger companies may be more tied to the accomplishment of ESG-based objectives, thus incentivizing a stronger focus on ESG-conform activities and behavior.

3. Data

The data for this study are from the 81 constituents of the S&P Global Clean Energy Index from 1 January 2009 until 30 June 2021. The start of the time period was selected as the year 2009 since this year marks the beginning of the steps leading up to the Paris Agreement [19]. The time-series data were obtained from the Thompson Reuters “Datastream” service with daily frequency. The variables downloaded for the companies consist of target price information (from the “Institutional Brokers Estimate System” (IBES)), company-related information such as the stock price, and the price-earnings (PE) ratio, as well as the MSCI world index, which is a broad global equity index. A complete list of the “raw” variables (incl. symbols) downloaded from Datastream can be found in Appendix A Table A1.

Target prices are most commonly set for the estimated stock price in 12 months [2,7]. Thus, taking an investor’s perspective, only the information related to target prices from 1 January 2009 until 30 June 2020 were considered (a year shorter than the entire period) and compared with the actual stock prices after one year (1 January 2010 to 30 June 2021). This way, up to 2999 observations were available per company (less for those that did not have any target price information at certain points in time).

The focus of this work is on mean target prices (consensus price target) since they represent analysts’ average estimated price of a stock in the future. In order to avoid including the same target prices for a company on consecutive days, the number of observations was reduced to the initial observation of a company and each observation for which the mean target price had changed compared to the previous observation—so at least a single revision/adjustment of a stock price has taken place. This decreased the number of observations to 0 to 139 per company with 5 out of 81 companies having 0 observations due to a lack of any target prices before the end of June 2020. For the (1:1) American depository receipt (ADR) of “Companhia Paranaense Denga” (Brazil), usually only a single target price was available, which was for unknown reasons consistently below the actual price (on average 80%) and, thus, was not further considered. (This issue could not be resolved by adjusting the target prices using the USD—BRL exchange rate.) For the remaining 75 companies the mean number of observations is about 77 and, overall, the data set contained 5810 observations. All target price variables (target mean price, target low price, target high price) were converted to target returns by calculating the “implied return” each of them represents compared to the corresponding current stock price. This was done in line with previous research (e.g., [7]), so that the targets of companies with target prices of different magnitude can be compared more easily. It was ensured that both the stock prices and target prices were in the same currency (usually the domestic currency) before the target returns were calculated. The list of all variables used for modeling, the corresponding pre-processing, and values are presented in

Table 1. Variables and pre-processing.

No	Variable Name	Pre-Processing	Values
1	No Targets	None	Integer, [1, 39]
2	Mean Target Return	Converted from Target Price to Target Return	Continuous, [−92.3%, 1384%]
3	Low Target Return	Converted from Target Price to Target Return	Continuous, [−99.4%, 363.6%]
4	High Target Return	Converted from Target Price to Target Return	Continuous, [−90.5%, 2403%]
5	Std Target Ratio	Converted to Ratio by dividing by Mean Target Price	Continuous, [0, 1.07]
6	Target Up 1 Month	None	Integer, [0, 22]
7	Target Down 1 Month	None	Integer, [0, 29]
8	Low Target Above Price	Converted to binary (if Low > Current Price, then 1, else 0)	Binary, “0” (70.6%), “1” (29.4%)
9	High Target Below Price	Converted to binary (if High < Current Price, then 1, else 0)	Binary, “0” (92.4%), “1” (7.6%)
10	PE Ratio	None (Nearest known imputation)	Continuous, [0.3, 1766]
11	MSCI World Return	Converted from Index price to Index Return (previous 12 months)	Continuous, [−45.6%, 53.7%]
12	Class (Year-End)	If Price (year-end) >= Target Price, then 1, else 0	Binary, “0” (51.3%), “1” (48.7%)
13	Class (Year-Highest)	If Price (during year) >= Target Price, then 1, else 0	Binary, “0” (30.8%), “1” (69.2%)

.

Two additional variables were created: “Low Target Above Price” and “High Target Below Price”. The first reflects that even the lowest target price of analysts exceeds the current stock price, highlighting a consensus that the stock may be undervalued and suggesting a possibly positive outlook for a company. The second reflects that even the highest target price provided by analysts is below the current stock price, indicating a potentially overvalued stock.

There are two separate targets for the classification that are based on the mean target price. The first target (“Year-End”) is binary and reflects whether a stock’s price after 12 months is as high or higher than the (initial) mean target price suggested (“1”) or whether it did not reach the target price (“0”). The second target (“Year-Highest”) is also binary, but represents whether the highest stock price accomplished during the entire 12-month interval is as high or higher than the initial mean target price (“1”) or whether it was at no point during that year as high as the mean target price (“0”). In other words, the first target focuses exclusively on the year-end stock price whereas the second target emphasizes the largest stock price during the entire 12-month period. Using these two perspectives for the accuracy of target price was also taken in [2,7], whereas a focus on any point during the year—which is termed in this study “Year-Highest”—was pursued in [5,11].

4. Target Price Analysis

4.1. Analysis of Target Returns and Coverage

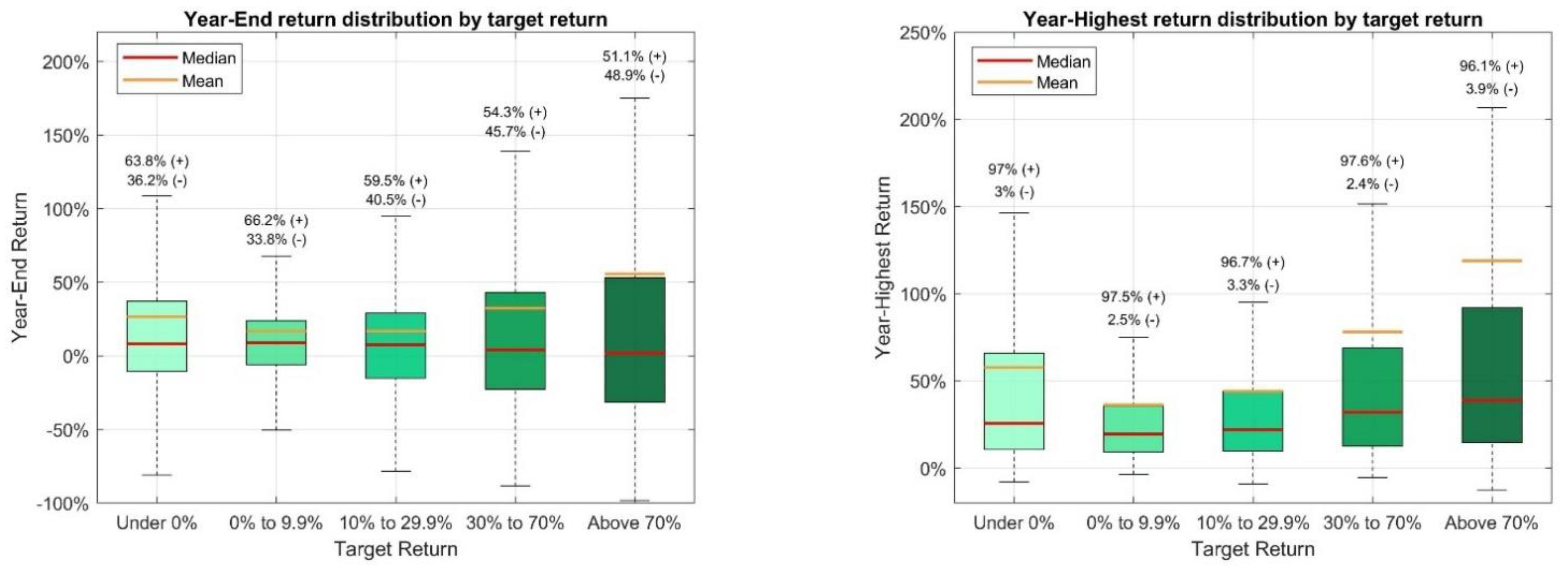
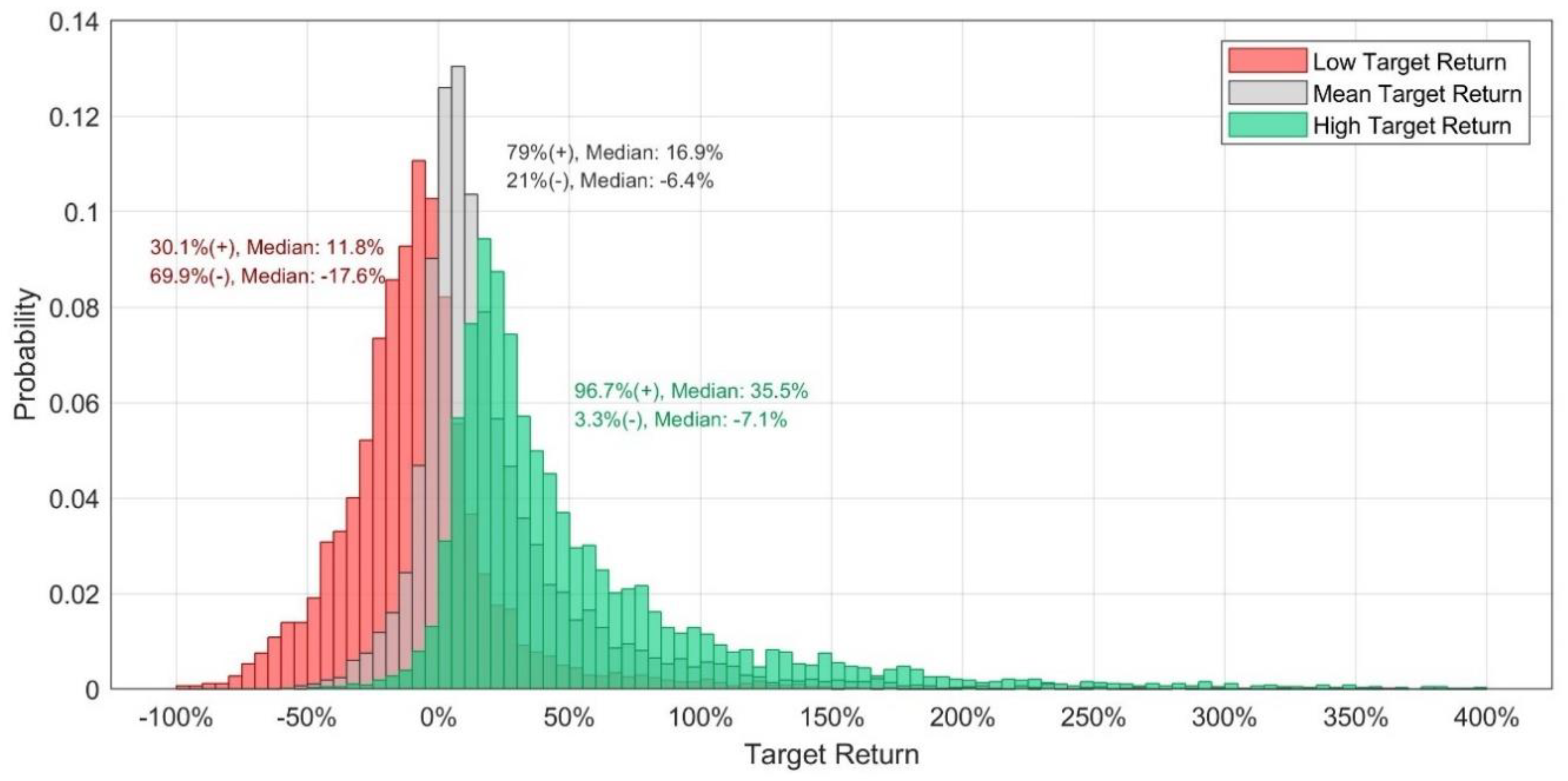
The average mean target return for the clean energy companies is 22.23% compared to the stock price at that time. It is unsurprising that the average low return is −8.12%, considerably lower, and the average high return is 58.20%, considerably higher than that. However, as Figure 3 illustrates, the magnitude of low, mean, and high target returns can differ considerably.

It is apparent that the low target return distribution has the lowest mean and earliest peak of all distributions, followed by the mean target return and, lastly, the high target return. The first interesting observation is that low, mean, and high target returns can all be below and above the current stock price (=0% target return). For the low target prices, about 70% are below zero—implying an expected decline of the stock price over the next year. However, roughly 30% of the low target returns show the expectation of a positive return over the next year. Since the low target price reflects the lowest expectation of all analysts covering the stock, the low target price exceeding the current stock price may reflect the consensus belief of all analysts that the stock is undervalued. (It may be noted that at any point some target prices may have been provided days or weeks before the date of the observation and, thus, can potentially reflect outdated beliefs of the analysts that may be corrected in the future. Additionally, mean target prices, especially when based on numerous separate analyst target prices, may react slowly to changing market conditions or stock information since this may require many analysts to revise their target prices in a timely manner in order to affect the mean target price considerably and rapidly.) For the mean and high target prices, most implied returns are positive. About 79% of the mean target returns exceed zero and for the high price, this percentage even amounts to 96.7%. It is interesting to note that high prices tend to be highly positive but there appears to be also a small tail for target returns below zero. A high target return below zero, which is only the case for roughly 3.3% of the observations, reflects that all current analyst targets indicate that the stock is likely overvalued and will decline within the next year. It is noteworthy that all, the largest high target return (2403.5%), the largest mean target return (1835.0%), and the largest low target (363.6%) are linked to the stock of “Fuelcell Energy”. In this extreme example, the target prices were lagging behind the stock price, which had declined considerably to new lows in mid-June of 2019. In general, for those 3.3% observations with a high price below the current price, the stock prices had increased or recovered from a decline and the target prices were lagging behind this surge. Similarly, the reason for some low target prices (about 4%) being 50% or higher over the current stock price was a decline in the stock price and the mean target prices’ delayed correction for this decline. Moreover, both these cases—stock prices exceeding the high price considerably and low prices exceeding the stock price considerably tend both to be associated with a low number of analysts covering them (usually 1–2 analysts).

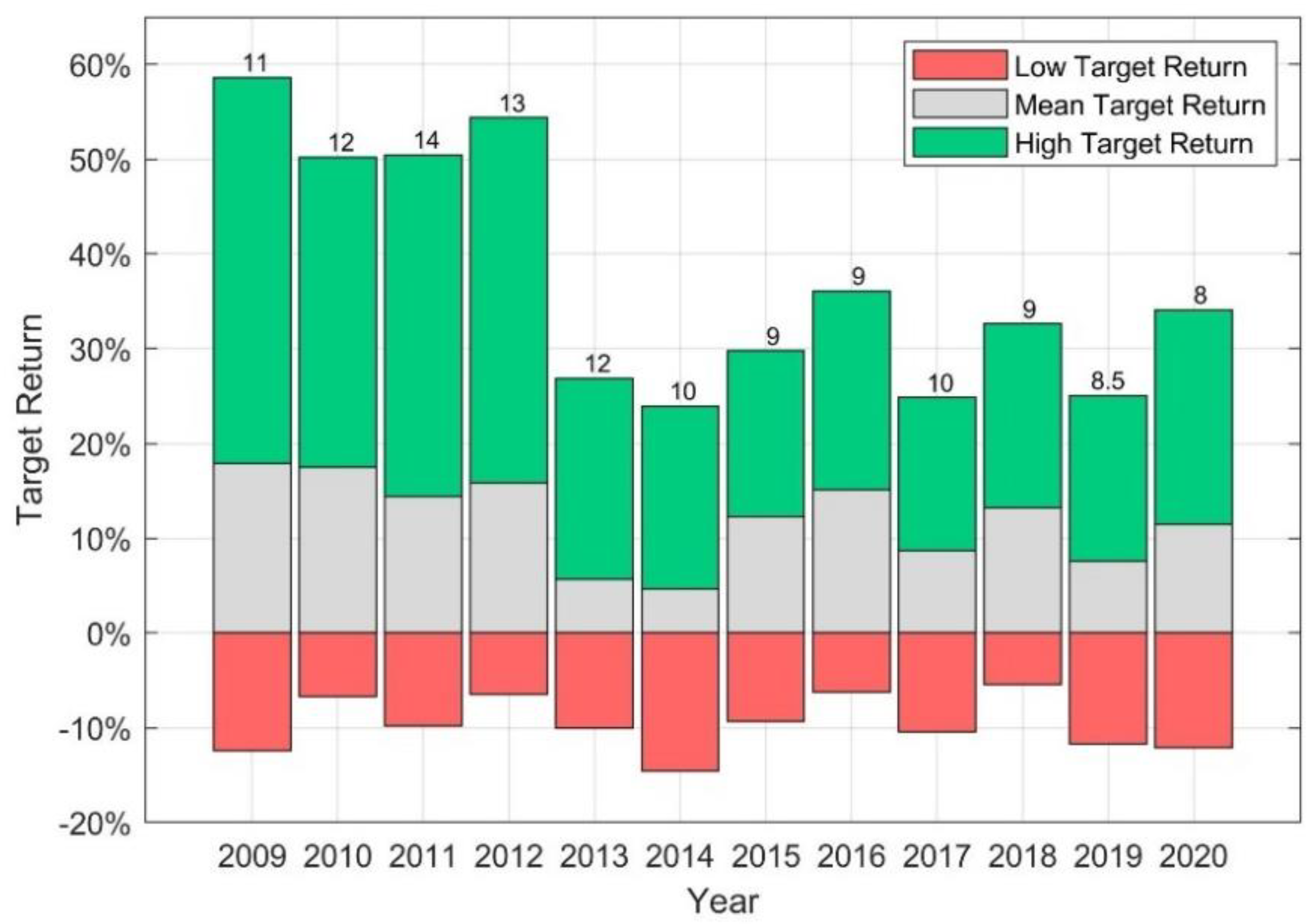
Figure 4 shows the median low, mean, and high target return as well as the median number of analysts covering a stock for each year.

It is apparent that the target returns vary between years, with the high returns appearing most optimistic between 2009 and 2012 with medians around 50%. The low target return is with median values between −5.4% and −14.6%, consistently negative, whereas the median values for the mean and high target returns are consistently positive. The median for the mean target return ranges from 4.6% to 17.9% and for the high target return even from 24.0% to 58.7%. The median number of analysts covering a stock is between (about) 9 to 14. Overall, the median number of analyst target prices at any time is 10, the minimum 1 and the maximum number of analyst targets is 39.

4.2. Analysis of Target Price Accuracy

This research will consider two forms of accuracy (or hit rate), meaning whether the target price was met (=hit) or not (=miss)—which is a binary class label with only two outcomes. The first version, referred to as “Year-End”, focuses on whether the stock price has reached the target price 12 months after a change in the mean target price (Yes/No). The second version, referred to as “Year-Highest”, determines whether the stock price met the target price (Yes/No) at any point during the 12 months after a change in the mean target price. In the previous literature, the measure for achieving the target price at year-end was termed “TPMetEnd” and for accomplishing it at any point during the year “TPMetAny” [7].

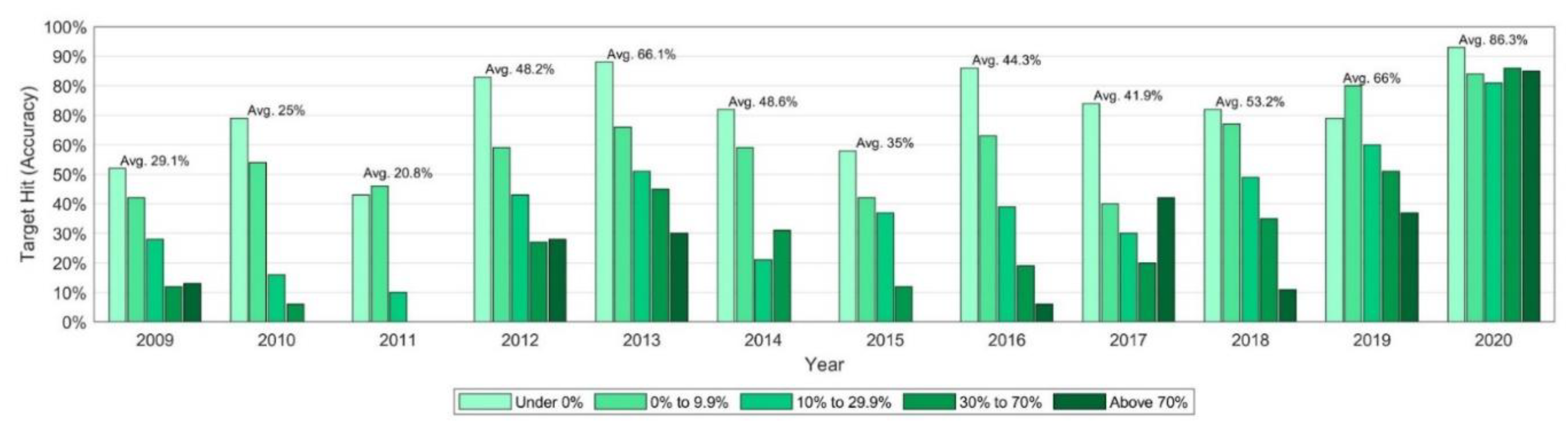
For the given 75 clean energy companies and target prices over the time period from 2009 to 2020, the mean accuracy for the Year-End target is 46.6% whereas the mean accuracy for the Year-Highest setup is 68.1%. It is unsurprising that the accuracy for the Year-Highest target is higher than that of the Year-End given that it measures whether the target price is met at any time during the 12-month window (including at year-end) whereas the Year-End target only measures the accuracy at a single point in time, at the end of the 12-month period. A comparison of the implied return of target prices and the accuracies found in previous studies is displayed in

Table 2. Target price and accuracy comparison.

Authors	Companies	Target	TPMetEnd	TPMetAny	Period
Bradshaw [6]	US	36.0%	-	-	1996 to 1999
Asquith, Mikhail, and Au [5]	Global	32.9%	-	54.3%	1997 to 1999
Brav & Lehavy [3]	US	32.9% (28.0% 1)	-	-	1997 to 1999
Gleason, Johnson, and Li [9]	US	32.0%	-	-	1997 to 2003
Bonini, Bianchini, and Salvi [2]	Italy	14.9%	20.0%	33.1%	2000 to 2006
Bradshaw, Brown, and Huang [7]	US	24.0%	38.0%	64.0%	2000 to 2009
Kerl [11]	Germany	18.1%	-	56.5%	2002 to 2004
This Study	Global (Clean Energy)	22.2%	46.6% (41.5% 2)	68.1% (62.5% 3)	2009 to 2020

¹ Brav and Lehavy [3] report a one-year-ahead target price that is 28% larger than the current stock price and 32.9% higher than the preannouncement stock price (2-days prior recommendation/target price announcement). ² Excluding the year 2020, which is exceptional due to the COVID-19 pandemic. ³ Excluding the year 2020, which is exceptional due to the COVID-19 pandemic.

(ordered by the period). The previous studies covered different time periods and it is apparent that the average implied return is considerably higher in time periods extending from 1997 compared to all that exclude years before 2000. Only a few studies reported the accuracy of target prices and the results for the clean energy stocks covered in this study seem to be in line with these results, especially the most recent ones from Bradshaw, Brown, and Huang [7] and Kerl [11]. Since 2020 appears to have been an extraordinary year with also a very high accuracy (see Figure 5) the accuracy values excluding this year are also presented, which are even closer to the results found in the literature.

It is noteworthy that Bradshaw, Brown, and Huang [7] also provide the additional inside that TPMetEnd and TPMetAny differ considerably in down and up markets with up markets resulting in accuracies of 50% and 71% whereas down markets lead to accuracies of only 17% and 49%.

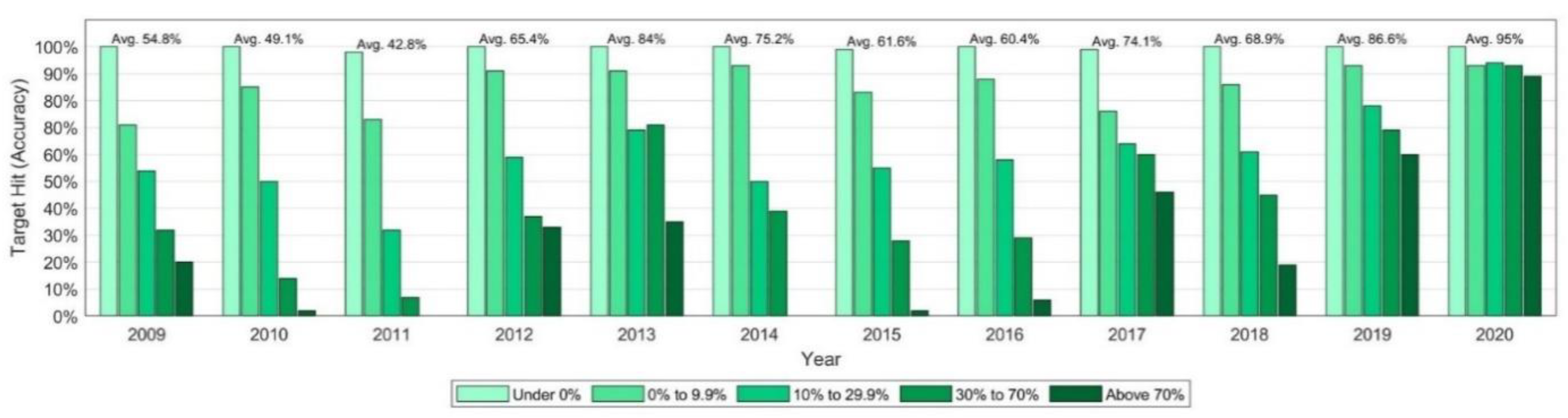
In the following, the accuracy of the target prices (and, thus, of the target returns) is analyzed overall and by the magnitude of the mean target return, to determine if the predicted return appears to be linked to the accuracy of the prediction. The groups for the mean target return are (1) “Under 0%”, reflecting an average estimate of no stock price increase, (2) from “0% up to 9.9%”—with the upper limit being the rounded median of the target return (11.5%), (3) from “10% to 29.9%”—representing approximately the range from the median to the third quartile (29.8%), (4) “30% to 70%”—with the upper limit being roughly the third quartile +1.5 times the interquartile range (72.2%), which is a common limit for outliers, and (5) target returns “Above 70%”, which could statistically be considered outliers.

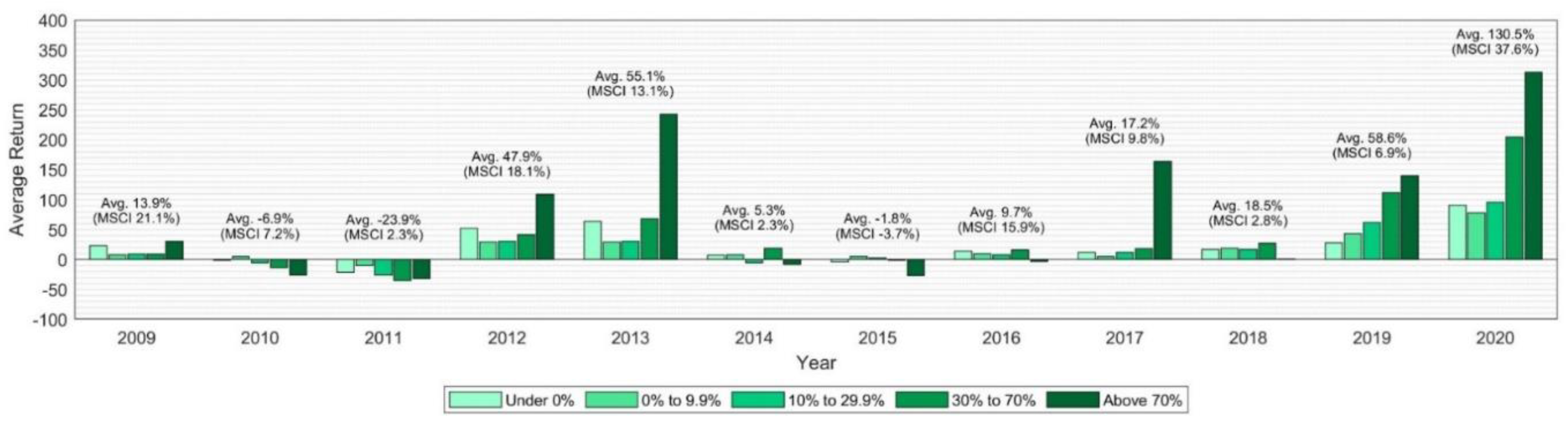
Figure 5 displays, for the Year-End target, the accuracy for each of the target return groups and for each year, and Figure 6 illustrates the average (actual) return achieved by the stocks in these target return groups. The first figure illustrates that the average accuracy of target prices can differ considerably between years (from 20.8% in 2011 to 86.3% in 2020) and generally differs considerably among target return groups. For most years, the accuracy for the “Under 0%” target return group has the highest accuracy, followed by the “0% to 9.9%” target return, which roughly represents all positive returns up to the median target return. In contrast to that, the two highest return groups, “30% to 70%” and the “Above 70%”, usually are characterized by the lowest accuracy and often show 2–3 times lower accuracies than the two highest target return groups. Combining this information with the average Year-End returns for stocks in Figure 6 shows that the return group “Above 70%” has the most extreme average returns (independent of the target being hit or missed), showing in six years the highest average return and in three the lowest average return.

It is noteworthy that average Year-End returns are moderately positively correlated (0.77, 0.44 excl. 2020) with the average MSCI world performance during the same time period. (The MSCI world performance is not the MSCI world return during that calendar year but the average of the 1-year return of the MSCI for the 12-month time period starting at the time of each of the target prices. Thus, the performance is the average return of the MSCI world from different starting points in that year up to 12 months in the future. For instance, if the mean target price changes in March, the MSCI world return from that point in time until March of the subsequent year is recorded. This is done so that the actual return of stocks in a given timeframe can be compared with the MSCI world return in exactly the same timeframe.) In particular, in nine out of eleven years with a positive average MSCI world performance, the average return for clean energy stocks is positive as well, whereas for the one year with a negative average MSCI world performance the clean energy stocks’ performance is also negative. However, as Figure 6 shows, the magnitude of positive and negative returns for clean energy stocks appears to be larger than that of the MSCI world index. The average accuracy and return for the Year-End target by target return group is displayed in

Table 3. Average accuracy and return by target return group (Year-End class).

Target Return Group	Under 0%	0% to 9.9%	10% to 29.9%	30% to 70%	Above 70%
Average Accuracy	73.1%	57.8%	37.9%	25.9%	17.1%
Average Return	26.6%	16.9%	16.8%	32.5%	55.7%
Average Hit Return	47.9%	40.2%	67.0%	156.9%	353.0%
Average Miss Return	−31.3%	−15.1%	−13.8%	−11.0%	−5.4%

.

The decrease in the average accuracy for stocks belonging to higher target return groups is in line with previous findings indicating that demonstrated that the predicted growth in the stock price is negatively impacting the forecast accuracy [2,5,11]. It is interesting to see that the average accuracy for the target prices gradually decreases with the magnitude of the implied target returns, but the same does not hold true for the average returns. The reason for that is two-fold: first, the average hit return, meaning the average return when the target price is met (=hit), tends to increase with the target return group and (2) the average miss return, meaning the average return achieved when the target price is not met, increases considerably with the target return group and, thus, is less negative. Both of these developments appear plausible. For the average hit return, the result appears plausible given that meeting higher return targets by definition means that returns below the target return group are excluded from the hit average. For instance, the average return of stocks that met their target price “Above 70%” by definition need to have achieved at least a return of 70%. In contrast, it is plausible that the average miss returns are on average negative and it appears intuitive that they increase with the target return group given that with higher return groups they may include higher returns that were still not meeting the target return. For instance, by definition, not accomplishing a return in the target return group “30% to 70%” means that returns of up to 29.9% can be contained in the miss returns. Moreover, it appears plausible that stocks with very high mean target prices tend to have higher average returns if they miss their high targets than stocks that miss considerably lower targets.

Overall, it is interesting to see that the higher average hit and average miss returns tend to outweigh the decrease in the average accuracies so that even when target prices are rarely met (e.g., in the “30% to 70%” and “Above 70%” target return group), the average hit return is so high, and the average miss return is still not so low as to lead to a lower average return overall. In other words, clean energy stocks in the groups with higher mean target returns, which represent a more favorable analyst expectation than groups with lower mean target returns, also tend to be associated with higher average returns until the end of the corresponding 12-month period. This trend still holds true if target prices from the exceptional year 2020 are excluded. However, this information only provides an incomplete picture of the returns in the target return groups. It is noteworthy that while the average return tends to be higher for higher target return groups, the distribution tends to be wider, with the median showing a decreasing trend and the share of Year-End returns below zero is increasing for higher target return groups (see Figure A1 in Appendix A). The fact that the mean tends to be further from the median for higher target return groups in the most extreme case for the “Above 70%” target return the mean even exceeds the third quartile shows that there is a long tail at the higher end of the returns. Thus, higher average returns are based on a comparably small number of very high Year-End returns. This illustrates that the risk associated with stocks in higher target return groups increases but so does the potential reward, as highlighted by the average returns.

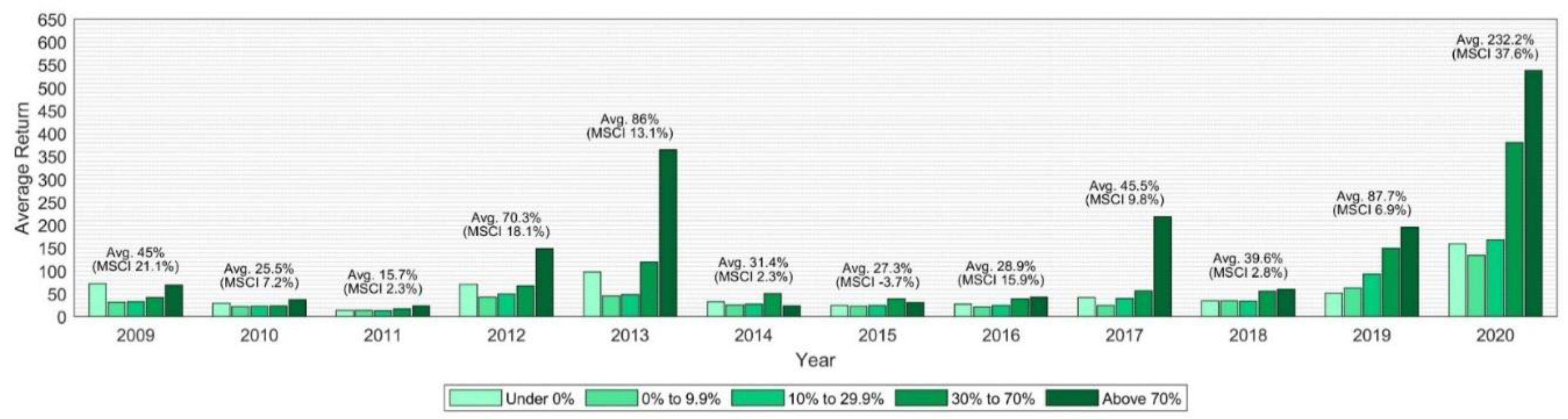
The next step is the analysis of the Year-Highest class that represents whether the target price is met at any time during the 12-month period after the mean target price changes. Figure 7 displays for the Year-Highest target the accuracy for each of the target return groups and for each year, and Figure 8 illustrates the average of the highest achievable (actual) return by the stocks in these target return groups during the 12-month period.

The average accuracies (target hit rates) are considerably less variable for the Year-Highest class than for the Year-End class and are also consistently higher in each year (see also Figure 5). The average accuracy ranges from 42.8% (2011) to 95% (in 2020) with an overall average return of 68.1%. The average accuracy for the “Under 0%” target return group is essentially 100% every year given that the stock price is already exceeding the target price at the start. The only exceptions are three observations for which the target return is only 0.2% to 5.1% below the stock price, which drops below it during the first day and never recovers from it. The tendency that lower target return groups are more likely to be met is even stronger for the Year-Highest target. It is noteworthy that the average accuracy for the “Above 70%” target return group is still often 2–3 times smaller than for the “Under 0%” and “0% to 9.9%” target return group. The average (highest) returns achievable displayed in Figure 8 follow a similar pattern to those for the average returns by Year-End in terms of the higher magnitude of average returns for the “Above 70%” target return group. The average returns for each target return group and year are positive, highlighting that, on average, stocks during the 12-month period at some point increased over their initial stock price. The correlation between the average Year-Highest returns with the MSCI world performance is still strongly to moderately positive (0.80, 0.41 excl. 2020).

The average accuracy and return for the Year-Highest target by target return group is displayed in

Table 4. Average accuracy and return by target return group (Year-Highest class).

Target Return Group	Under 0%	0% to 9.9%	10% to 29.9%	30% to 70%	Above 70%
Average Accuracy	99.8%	85.1%	59.6%	39.9%	21.8%
Average Return	57.8%	36.4%	44.1%	78.1%	118.9%
Average Hit Return	57.9%	42.3%	68.4%	168.6%	420.3%
Average Miss Return	−4.1%	2.6%	8.4%	18.0%	35.1%

. Similar to the Year-End average accuracies, the Year-Highest average accuracies also decline for higher target return groups. Moreover, the trend of higher average returns for higher target return groups can also be observed. Similar to the Year-End average accuracies, the Year-Highest average accuracies also decline for higher target return groups. Moreover, the trend of higher average returns for higher target return groups can also be observed.

Similar to the Year-End average accuracies, the Year-Highest average accuracies also decline for higher target return groups. Moreover, the trend of higher average returns for higher target return groups can also be observed. The average returns for the Year-Highest class are for each target return group higher than those of the Year-End class (see Table 4), which is intuitive given that these correspond to the highest stock price during an entire year and not just those at the end of the year. The same holds true for the average hit returns and the average miss returns, which are all positive (with the single exception of the average miss return for the “Under 0%” target return group which, by definition, cannot be positive). As for the Year-End target, for the Year-Highest target the average hit and miss rates increase as the target return group increases. This highlights that clean energy stocks in the groups with higher mean target returns, which represent a more favorable analyst expectation than groups with lower mean target returns, also tend to achieve higher stock price increases over their 12-month periods. It is noteworthy that both the average as well as the median return increases with higher target return groups, highlighting that the distribution has a longer tail for the high positive returns (see Figure A1 in Appendix A). However, in contrast to the Year-End returns, the share of negative returns remains at a low, close to constant level for all target return groups.

From an investor’s perspective, it is interesting to note that the Year-End returns represent the returns achieved by investing in a stock at the time where the mean target price is updated and simply holding it for the 12-month period (passive management). In contrast, the Year-Highest returns embody the highest return accomplishable during the 12-month period starting from the change of the mean target price and, thus, may require extensive monitoring and optimal market timing to be accomplished (active management). This was also pointed out by Bonini et al. [2], who stated that it is effectively not possible for investors to determine when the maximum price (or minimum price) of a stock is accomplished.

5. Feature Selection

Feature selection refers to the process of selecting features (=variables) that are relevant for a task and, thus, discarding irrelevant or redundant features from a data set [25,26,27,28,29]. This differentiates feature selection from another dimensionality reduction approach termed feature extraction. Feature extraction transforms the existing features into “new” ones and, subsequently, keeps only some of these new features, whereas feature selection chooses a subset of the original features to retain [30,31,32]. Using feature selection is generally associated with several advantages and motivations such as (1) improving (or at least not considerably decreasing) the error of the final model [33,34,35,36,37], (2) increasing the speed of model training, and obtaining more simple models from the data [33,34,35,36], (3) reducing computational cost and data storage requirements [33,34,35], and (4) obtaining more easily visualizable and interpretable data [33,34,35,38,39].

When feature selection is applied in the context of supervised learning, such as classification or regression, it is referred to as supervised feature selection [30,39]. Supervised feature selection can be divided into three types: filter, wrapper, and embedded methods [31,39,40,41]. Filter methods are part of the pre-processing of the data and only use the characteristics of features to determine their relevance, thus, they do nit involve any learning algorithm (e.g., classifier) [31,39,41,42]. Wrapper methods deploy the learning algorithm as a “blackbox” to evaluate different feature subsets (e.g., using classification accuracy) and to select the best performing one [39,43,44,45,46]. Embedded methods are as wrapper methods classifier-dependent, but unlike wrapper methods, they are part of the model training of the learning algorithm itself [25,33,47,48]. Thus, the feature subset generated by embedded methods can be seen as a byproduct of model training [47].

This research will use commonly known embedded feature selection methods, in particular random forests and support vector machines with recursive feature elimination (RFE), to train the classification models for this study. The software used for coding is Matlab version 2020a.

6. Classification Models

6.1. Random Forest

Random forests were suggested by Breiman [49] and are an ensemble of so-called decision trees [50]. A common algorithm to create decision trees is CART [51], but others exist as well [52,53]. A decision tree is a machine learning method that starts at the so-called “root” node and uses at each step the best binary split of a variable to create two child nodes [50]. This split can be considered a rule that aims to make resulting partitions of the data more “pure” in terms of the distribution of classes in each of them. This procedure is repeated until a stopping criterion is met [50], for instance, that each partition is “pure”, meaning that only a single class is present. Following the resulting path of rules that are applied to each new observation leads them to a so-called “leaf” or “terminal node” which is associated with one class (either pure or majority in that partition) [52,54,55]. Thus, following the path branched out from the root node determines the class membership of an observation. This procedure of iteratively using binary splits to create “purer” partitions of the data is called “recursive partitioning” meaning that it creates regions of the instance space that belong to each of the classes in a classification problem [50,52,55].

A decision tree has multiple advantages, such as its easy interpretability due to the rules it provides for its class assignments [52,54], its ability to handle numerical and discrete variables, and that it does not require assumptions about the underlying distributions [52]. However, decision trees are sensitive to small perturbations of the data (high variance) [56] and, thus, tend to overfit.

The aim of a random forest is to overcome this weakness of decision trees by combining multiple decision trees and aggregating their class predictions [50,56]. The idea of random forests is an extension of bagging [50]. Bagging stands for “bootstrap aggregation”, where “bootstrap” refers to randomly sampling observations with replacement from the training data to obtain multiple data sets of the same size as the original training data, whereas “aggregation” highlights that the results from training models on these bootstraps are averaged (=aggregated) [56]. The difference in random forests to classical bagging is that not only observations are randomly drawn from the original data but also the variables are randomly sampled (except for the target variable) [50,56]. This procedure aims to reduce the correlation between trees to obtain de-correlated trees [56]. The algorithm for a random forest [50,56] (in the context of classification) is illustrated in Algorithm 1. The algorithm illustrates that a set of decision trees are used that each cast their vote and the most common class vote is used as the class prediction for the random forest (majority voting) [56].

Algorithm 1 Random forest for classification
1. For t = 1 to T (number of decision trees in the random forest)
	1.1. Take a bootstrap sample of the training data
	1.2. Use the bootstrap sample to fit a decision tree by repeating the following steps (recursive partitioning) until a stopping criterion for the tree is met
		1.2.1. Select a subset of the variables (denoted m) of all variables (denoted p) in the bootstrap sample
		1.2.2. Determine the best binary split for any of the m variables (best splitting criterion value e.g., purity)
		1.2.3. Split the node into two child nodes using the variable and variable value for the best binary split
	End
2. Assign observations to classes by taking each tree’s class prediction and using a majority vote (most common class prediction) over all decision trees (=votes) to determine the class label

For this study, the number of decision trees in the random forest is set to 50. The minimum number of observations at each leaf node (minimum leaf size) is an optimized hyperparameter over the values $\left\{1, 10, 20, 50, 250, 1000, 2905\right\}$, where 2905 is the number of samples divided by two (rounded down). The Gini diversity index (GDI) is selected as the splitting criterion, the technique for variable selection (step 1.2.1. in Algorithm 1) is the interaction test [57], and the number of variables selected randomly (m) from the bootstrap sample is $\sqrt{p}$ where p is the number of all variables in the data set [50,56].

6.2. Support Vector Machine—Recursive Feature Elimination

The support vector machine (SVM) originated in the work of Boser, Guyon, and Vapnik [58] and Cortes and Vapnik [59]. The general idea of an SVM is to create a decision boundary (hyperplane) that maximizes the margin between itself and the closest observations (=data points) of each of the classes [54]. The points that are closest to the boundary and, thus, are on the margin are called “support vectors” [60]. It is noteworthy that the input variables, denoted x, are often mapped into a higher-dimensional feature space using a (nonlinear) mapping that can be denoted as $\varphi ()$. Following the notation in [59,61], the decision function f for a data set x can be defined as

$$f\left(x\right)=w\varphi \left(x\right)+b$$

(1)

where w are the weights for the optimal hyperplane (decision surface) that separates the classes with the largest margin, $\varphi ()$ is a function that transforms the input, and b is the bias value. The bias is the average over the marginal support vectors and can be calculated using the weights $w$ [60]. The weights $w$ for the optimal hyperplane are calculated as

$$w={\displaystyle \sum }_i{y}_i{\alpha }_i\varphi \left(x_i\right)$$

(2)

where $x_i$ is a support vector, ${\alpha }_i$ is the weight for the support vector $x_i$, and $y_i$ is the class label $ϵ\left\{-1,1\right\}$ corresponding to the support vector [59,60]. The weights of the support vectors $\alpha$ are the parameters of an SVM, which are optimized using convex optimization [60]. For details on the optimization problem behind an SVM, please see [56,61].

The weight vector w for the hyperplane will be used in recursive feature elimination to determine the ranking of features. Recursive feature elimination using a support vector machine (SVM-RFE) was introduced by Guyon et al. [60]. It deploys a greedy backward elimination procedure where in each step an SVM is trained and the variable with the lowest squared weight $w^2$ is removed from the set of the remaining variables [48,60,62,63]. Thus, $w^2$ can be regarded as a ranking criterion for the variables [60]. It is noteworthy that in each step one or more variables can be removed [48,60]. Thus, SVM-RFE is inherently different from random forests: the former starts with a complete variable set and iteratively removes one (or multiple) variable(s) whereas the latter functions by iteratively selecting variables. The algorithm for SVM-RFE is depicted in Algorithm 2 (similar to [48,60]).

Algorithm 2 Support vector machine—recursive feature elimination (SVM-RFE)
For m = 1 to M (number of features to remove)
	1. Train an SVM on the training data with the remaining features (s) (initially all features p)
	2. Determine the ranking criterion $w^2$ from the trained SVM
		2.1. Obtain the weights $\alpha$ of the support vectors from the trained SVM
		2.2. Calculate the weight vector $w$ of the optimal hyperplane $\left(w={\displaystyle \sum }_i{\alpha }_i{y}_i\varphi \left(x_i\right)\right)$
	3. Remove the variable associated with the smallest $w^2$ from the set of the remaining features s
End

The logic behind this procedure is that $w^2$ estimates the effect of each variable on the objective function (sensitivity) with larger values indicating more important variables so that the resulting variable subset leads to the best class separation with the SVM classifier [48,60]. The number of variables to retain can either be user-specified (and the number of variables to remove would, thus, be all variables minus the number of variables to retain) [62,63] or the algorithm can be run until a single variable is left and the optimal subset can be selected using cross-validation as the subset leading to the highest validation accuracy. For this study, the variables are standardized using the weighted mean and weighted standard deviation, and the optimal variable subset is determined using cross-validation.

7. Experimental Results and Analysis

7.1. Model Performance and Feature Importance

The performance of the random forest (RF) and SVM are compared to a simple random approach using the two-class probabilities. In particular, for each observation, a random uniform number is generated and if its value is below or equal to the first class’s probability, it is assigned to that class, and otherwise, it is assigned to the second class. This approach is taken to compare the random forest and SVM with a random approach but still account for the class sizes (especially for the Year-Highest class, which has a higher share of observations with the positive target class). The average classification accuracy, precision, and recall for the three models are displayed for each of the two targets (“Year-End” and “Year-Highest”) in

Table 5. Model results for the Year-End and the Year-Highest targets.

Model	Target	Accuracy ± Std 1	Avg Precision	Avg Recall
RF	Year-End	73.24 ± 1.63 ***	72.19	69.3
SVM	Year-End	65.90 ± 1.75 ***	62.21	68.45
Random	Year-End	50.02 ± 2.09	46.34	50.02
RF	Year-Highest	81.15 ± 1.57 ***	84.51	88.55
SVM	Year-Highest	75.77 ± 1.28 ***	76.15	93.8
Random	Year-Highest	56.49 ± 1.93	68.02	56.49

¹ The notation ‘***’ refer to 0.1% significance level corresponding to a one-sided Welch’s test of the accuracy of RF and SVM versus the accuracy of the Random model for a specific target, respectively.

. The results are based on 20 runs of a nested cross-validation (10-fold cross-validation split for the external and also the nested cross-validation).

The results for the Year-End target show that the random forest is, with an average accuracy of 73.24%, the most accurate model. The linear SVM model performs noticeably worse than the random forest. However, using the one-sided Welch’s test, it can be demonstrated that both the random forest and the SVM are highly significantly (***) more accurate than the random model (p-value < 0.999). The average precision and recall are also the highest for the random forest model with both values being around 70%. This indicates that the model correctly predicts around 70% of the actual target price hits (recall) and that also about 70% of the positive predictions are actual hits (precision). For the Year-Highest target, the ranking of the methods is the same, with the random forest performing the best in terms of accuracy and, both the random forest and SVM show average accuracies that are highly significantly more accurate than that of the random model (p-value < 0.999). It is noteworthy that all metrics—average accuracy, average precision, and average recall are higher for all methods for the Year-Highest target than for the Year-End target. This is likely based on the fact that it is an easier classification task to determine if a certain target price is exceeded at some point during a time period than for only one point in time (year-end).

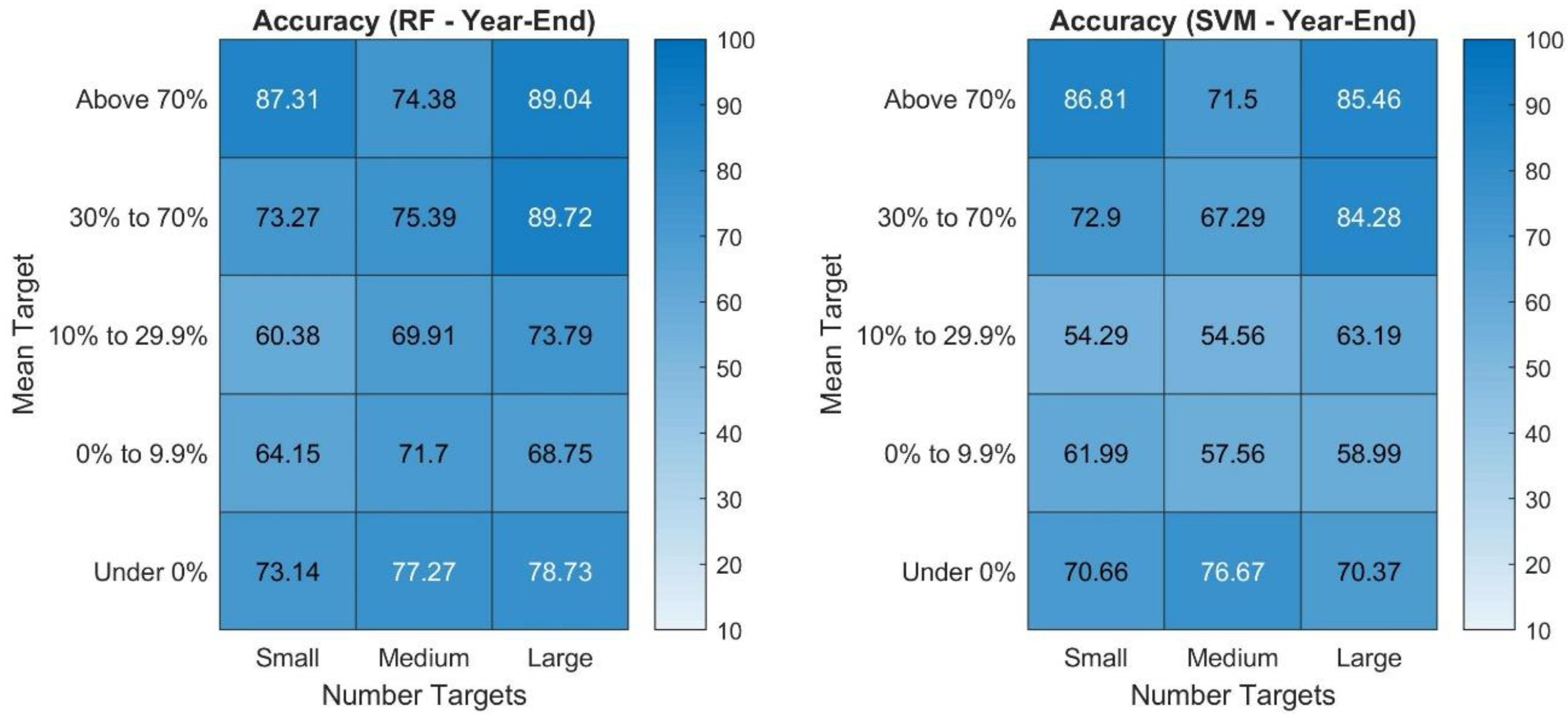
The next question investigated is that of the feature importance, meaning, which variables are relevant and used by each of the two machine learning algorithms for their models. The relevance of features (=variables) for these two models for both targets is displayed in Figure 9.

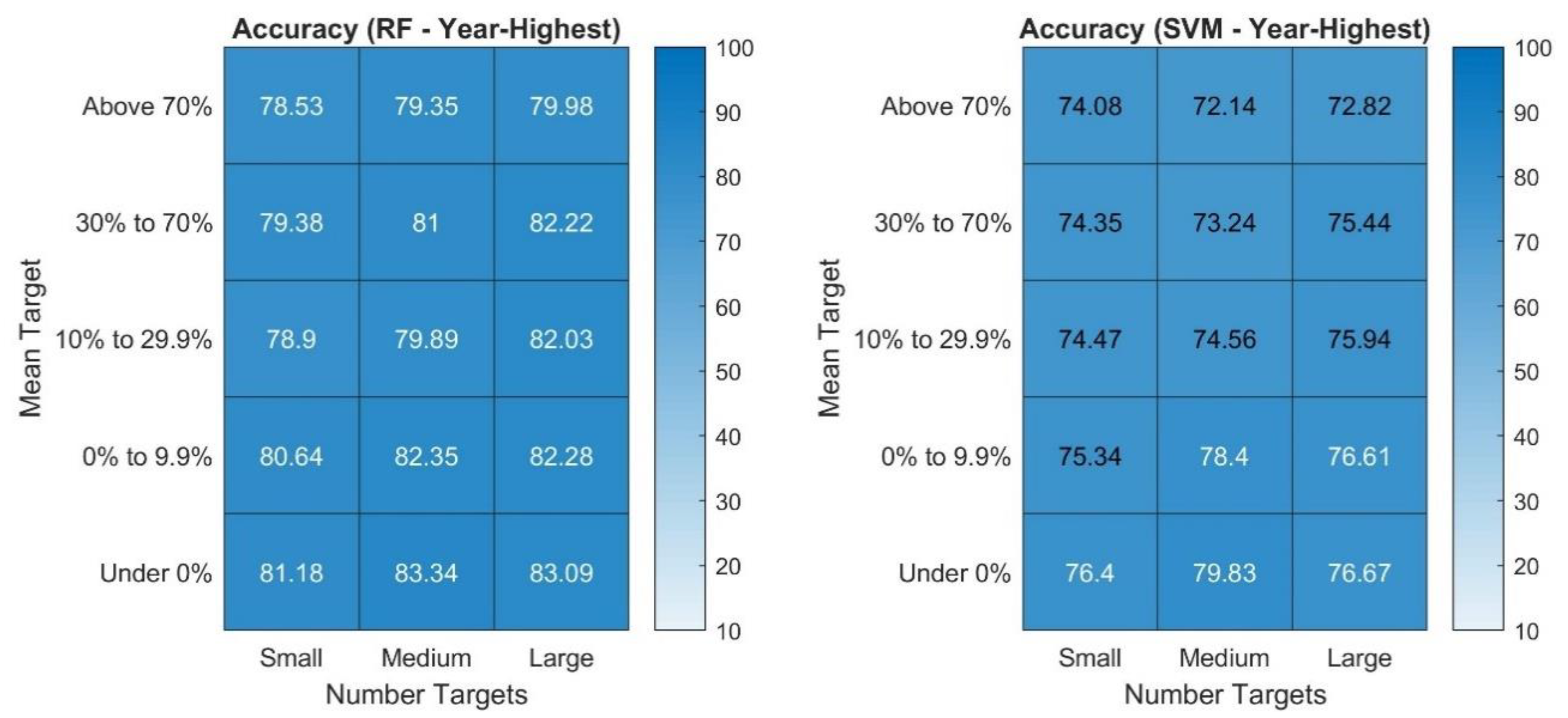
The feature importance scores illustrate that for both the Year-End and the Year-Highest random forest and SVM models the most relevant variable is the mean target price of the stock. This may not be surprising given that (1) the mean target was the target price used to set up both of the targets and (2) it represents a consensus of analysts about the expected (average) stock price in the future. For the random forest model, the number of target prices was the second most relevant variable whereas for the SVM models it was only the third most relevant one. In order to analyze the obtained model performances in more detail and understand for which type of observations the model works particularly well, the overall accuracy accomplished is broken down by the mean target price and the number of target prices. This breakdown for the random forest and SVM model with the Year-End target is presented in Figure 10. The categories for the number of targets were created with the help of the 33rd and 67th percentile of the number of analysts covering a stock as cut-off points. Thus, the number of targets is considered “Small” when an observation is covered by 1–6 analysts, “Medium” for 7–14 analysts, and “Large” when 15 or more analysts’ target prices are available.

The results show that for both the random forest and SVM model, the average accuracies tend to be the highest for the very high mean target prices (“Above 70%” and “30% to 70%), followed by the lowest mean target prices (“Under 0%), which imply a decrease from the current stock price. Both models rarely predict the positive class (target price met) for observations with very high and high mean target prices (“Above 70%”, “30% to 70%)—but the SVM is in that case more extreme by almost never predicting a “hit” for these return groups (see in Figure A3 in Appendix A). Moreover, the precision of the random forest for these return groups tends to be rather high, indicating that when it predicts a hit (which it does not do often), then it is often correct with that prediction (see in Figure A2 in Appendix A). This holds true especially for stocks with high target returns (“30% to 70%”, “Above 70%”) and that are highly covered meaning that there are 15 or more (recent) analyst prices at that time available for it. These two subgroups show a precision of 84.95% and 93.06%, indicating that positive predictions are in the vast majority of cases correct. It should be pointed out that the random forest model can also be considered prudent since the recall is not high for instance 37.53% and 25.97% for these subgroups highlighting that often observations for stocks that hit their target prices are not predicted as positive. These results are very different for the SVM model for the Year-End target, which almost never predicts a positive outcome for the high return groups and even when it does, the precision is generally low. Thus, the high accuracies achieved with the SVM for the high return groups are almost exclusively based on predicting a negative outcome (which is the majority class label for these return groups). This likely makes this model less attractive for potential investors since correctly predicting hits of a target price provides usually more information than the miss. In particular, a hit states a minimum return achieved (the target return) to be an actual hit, whereas a miss does not provide other information than that the return is lower than the target return, which can still be positive or be negative (exception (“Under 0%”)).

The two models are also very accurate on observations with a mean target that is below the current stock price (“Under 0%”). For these observations the model tends to predict the positive class (target price met) in 90% to 100% of the cases and, thus, unsurprisingly correctly predicts most observations that are actually positive. The observations “Under 0%” have a high share of stocks that after one year are at or above the target price, which may indicate that the mean target price is accurate or even too pessimistic. However, investors should keep in mind that the target price is below the current price, so this does not necessarily reflect an investment opportunity. However, the average actual return associated with these observations is over 26% (within 12 months) with 63.9% of observations in that group showing a positive return instead of a decline over the 12-month period.

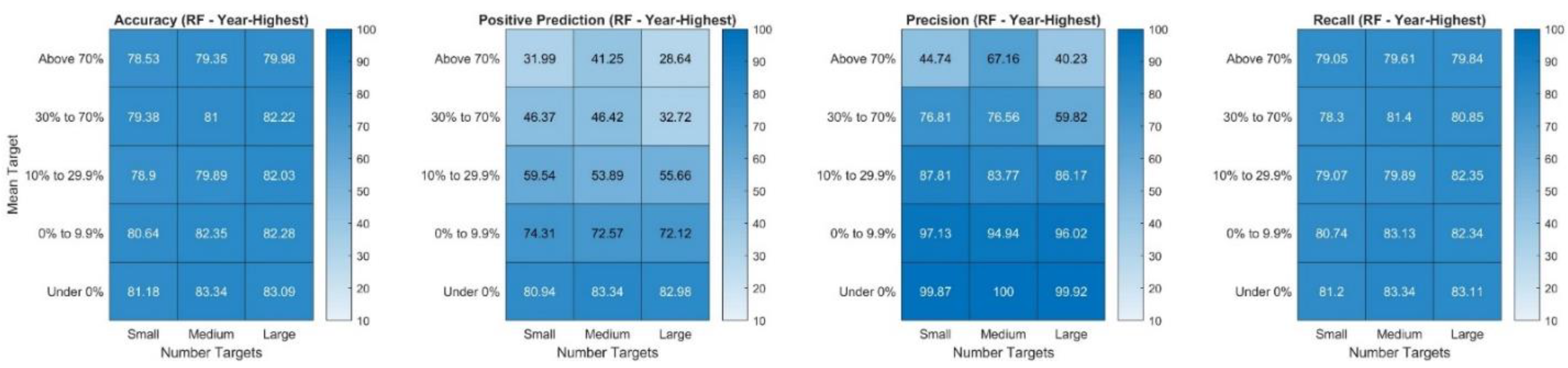
This breakdown for the random forest and SVM model with the Year-Highest target is presented in Figure 11.

The average accuracy of both models is not just higher for the Year-Highest target than for the Year-End target (see Table 5) but there also seems to be clearly less variation among the average accuracy values for different subgroups. It is interesting to note what for both models there are more positive predictions for the high return groups, but the recall for them tends to be lower (see Figure A4 and Figure A5 in Appendix A). However, the opposite is true for the moderate return groups such as “10% to 29.9%” or “0% to 9.9%” which tend to have the same or a larger share of positive predictions for the Year-Highest than for the Year-End target but have a higher recall. This means that for these moderate return groups the share of positive predictions that turn out to the correct is higher. The simple reason for the higher accuracy and precision on these moderate return groups is likely the fact that the magnitude of the estimated increase is not that high, and the stock price has an entire year to reach it at least at a single point in time. Since stock prices tend to fluctuate over a year, it appears plausible that especially low to moderate increases can happen at least temporarily during that entire time period. This also highlights the main problem of models using the Year-Highest target: investors do not know at which time and for how long targets may be met, thus requiring strict and continuous monitoring of the stock prices and optimal market timing to accomplish the results suggested by the Year-Highest model. However, if this is possible for an investor, then the predictions especially for the moderate target groups may be of interest due to the high precision.

7.2. Performance Comparison

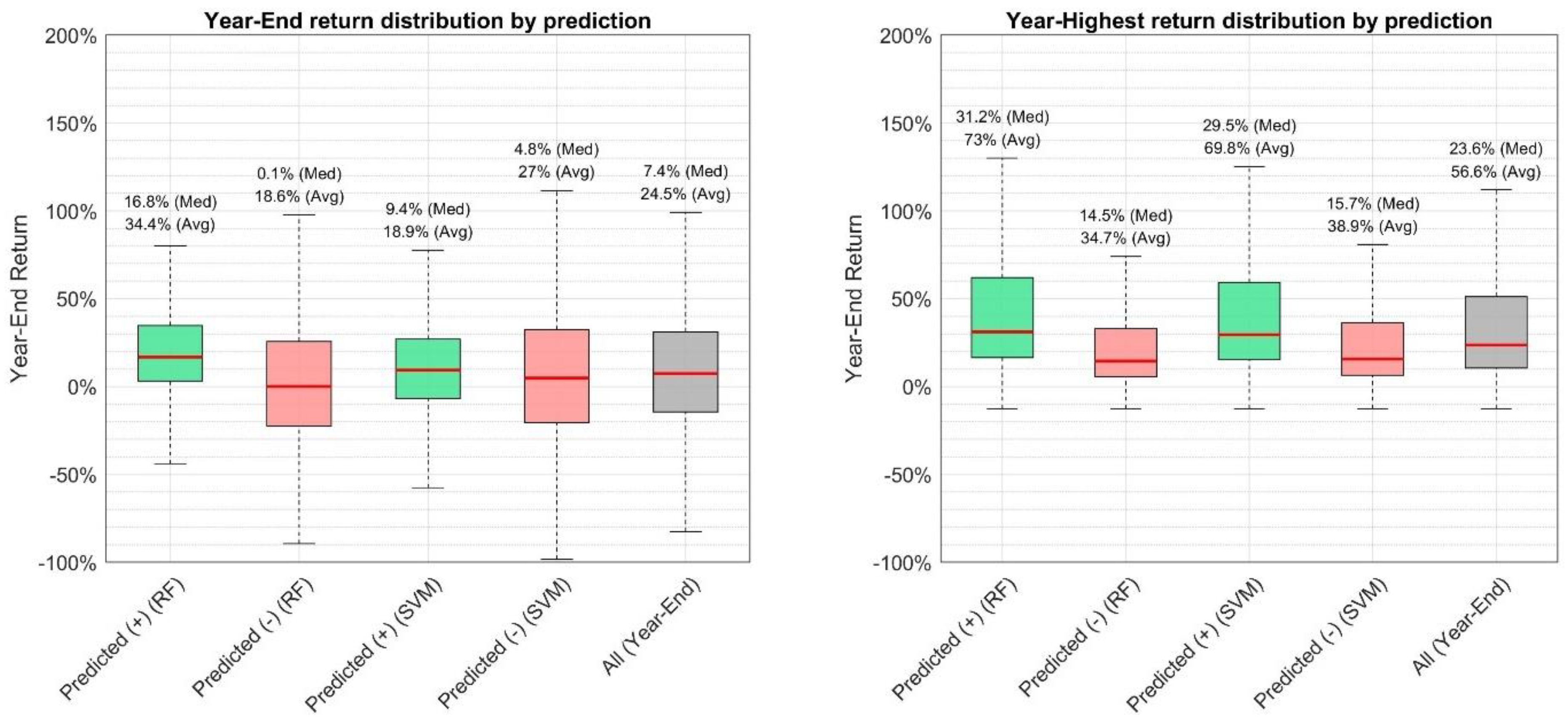
From an investor’s perspective, the accuracy of a classifier is only of secondary importance compared to its usefulness as a support tool for investment decisions. Figure 12 shows the Year-End and Year-Highest return distributions for positive and negative predictions conducted by the random forest and SVM model. Since the target return group “Under 0%” is assumed not to be of interest for investors since correctly predicting that a stock may reach its target price, which is lower than the current price, is likely of limited investment value, these observations are not included in the return distributions presented in Figure 12.

For the Year-End, especially the random forest, which was the most accurate model for this target, showed the most interesting distributions. In particular, positive predictions of the random forest did not just have a clearly higher median and mean than all returns (in grey), the first quartile also exceeds zero (3.2%). This means that less than 25% of the stocks for which the model predicted that the target price would be reached, experienced a negative return over the subsequent year. In contrast, the negative predictions lead to a median year-end return close to zero. Thus, close to 50% of the observations were characterized with a negative return whereas overall this is only the case for about 39.4% of observations. For the SVM the average year-end return is lower than that of all observations and the third quartile for negative predictions is larger than for positive ones, indicating that the top 25% of returns for negative predictions are actually higher than for positive predictions. It is noteworthy that for both the random forest and the SVM the distribution of negative predictions is wider, reflecting that for negative predictions there is a wide variety of returns that can be obtained.

For the Year-Highest returns, the distributions look clearly different than for the Year-End returns. Both the random forest and the SVM show higher median and average returns than overall. Moreover, the positive predictions are characterized by a larger variation of the returns. Again, the random forest shows better performance in terms of the actual returns. However, it should be kept in mind that these are the Year-Highest returns, which means that the corresponding high stock prices are accomplished at some point during the year, likely not at year-end and not necessarily for a prolonged period of time. Thus, achieving such returns might be extremely challenging. In this regard, the Year-End returns might be of larger interest for investors since they only require the implementation of a buy-and-hold strategy and do not necessarily require additional monitoring.

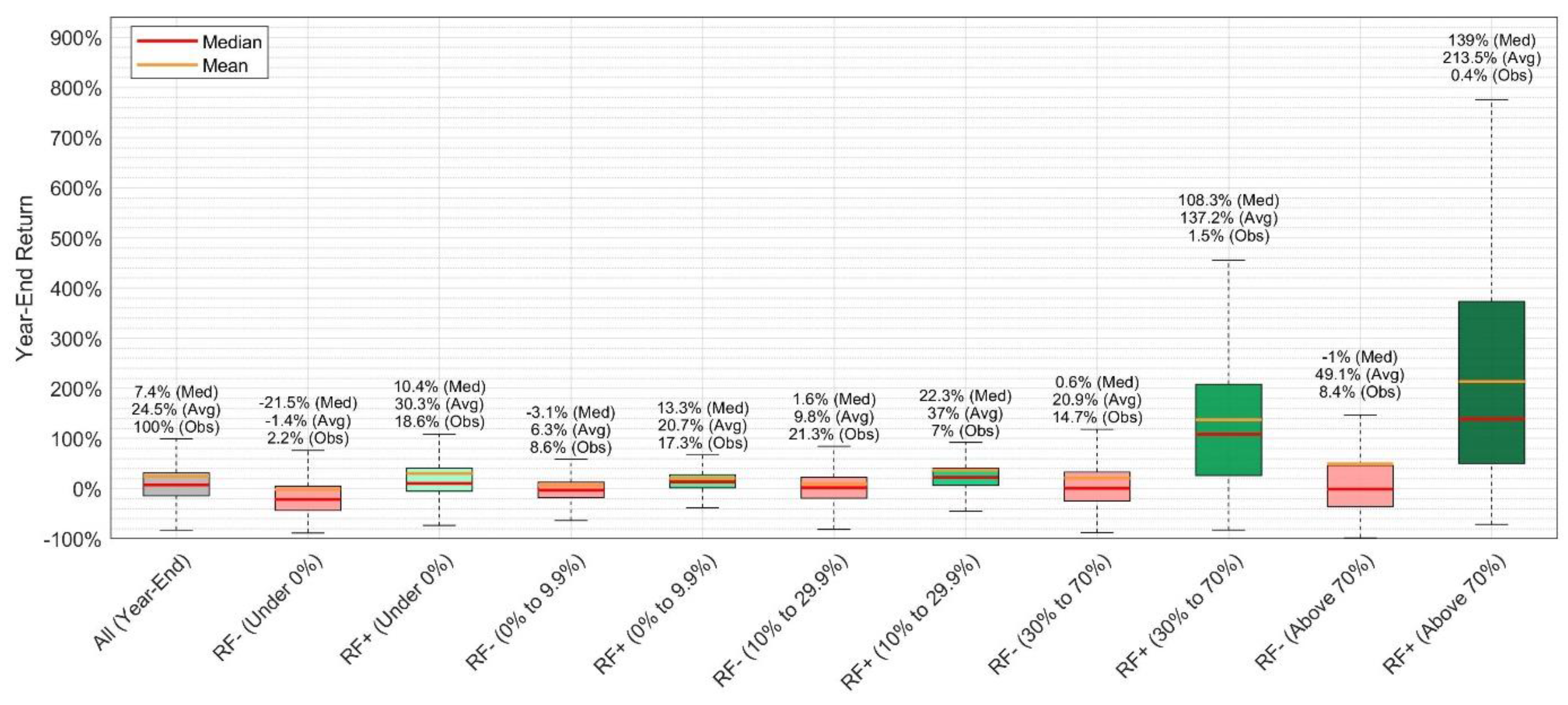
The subsequent analysis will, thus, focus on the Year-End returns achieved using the most accurate model, the random forest. Figure 13 depicts the Year-End return by target return group accomplished with negative and positive predictions of the random forest.

It is apparent that the median and average return by year-end is considerably higher for positive predictions of the random forest for stocks with target prices between “30% to 70%” and those “Above 70%”. The shares of these predictions compared to all predictions made are overall very low, 1.5% and 0.4%, respectively. However, they appear of interest as it suggests a potentially higher return for stocks with high target prices for which the random forest predicts that they will meet the target price. Positive predictions are with a share of only 4.1% even within the “Above 70%” target return low (0.4% overall). Thus, positive predictions for “Above 70%” target returns are very rare but appear to be associated with very high average and median returns.

This finding was manually verified for companies in this group (positive prediction and “Above 70%” target return), which were characterized by the highest returns (200% or higher). Of the 12 companies that were contained in this subset, these extremely high positive returns were observed during recoveries of the stock prices which were prior over 90% below their all-time highs (e.g., Vestas Wind Systems A/S in 2012, SunPower Corp. in 2012 and 2019, Enphase Energy in 2017, First Solar in 2012). Apart from that, some companies simply experienced a stock price surge to new all-time highs after 2020, which has been an exceptional year due to the COVID-19 pandemic (e.g., Enphase Energy, Sunrun Inc, Bloom Energy Corp., Sunnova Energy International). Thus, the results appear plausible, but this does not necessarily mean that they are repeatable.

Figure 14 allows a more detailed look at the positive return predictions of the random forest in terms of hits and misses.

It is unsurprising that when the model correctly predicts a target price being met (i.e., a hit), the returns achieved are higher than when a misclassification occurs (i.e., a miss). Moreover, it is intuitive that correctly predicting higher return groups leads on average to higher returns. Having said that, it is noteworthy that the magnitude of the actual returns in the “30% to 70% and the “Above 70%” target return group are very high—on average 195.2% and 296.5% respectively. However, the magnitude of the returns associated with misses appears even more interesting. The average returns are in general negative, but their magnitude decreases for higher target return groups. In other words, the higher the target return group, the smaller the consequences of misclassifications. This appears plausible given that higher average target returns reflect a higher confidence of analysts in a company’s stock. Moreover, a higher target return also means that the range of positive returns a stock can accomplish while not meeting the target price is larger. The extreme case is the “Above 70%” target return group for which the average return of misclassifications is still positive with an average return of 18.6% and a median return of even 28%. The low or even positive average returns for misclassifications is one of the contributing factors for the overall high average returns of positive predictions for high return groups. Lastly, it is noteworthy that the share of hits for the positive predictions (=precision) is often around 70% and appears rather consistent throughout the return groups. This indicates that independently of the magnitude of the return group the positive predictions of the random forest model are largely correct.

From an investors’ point of view, it should be kept in mind that clean energy stocks represent a relatively new asset class that tends to be very volatile [64]. Moreover, the performance of clean energy companies is linked to the (crude) oil price where the oil price has a unidirectional short-term causality on the price of alternative energy companies [65] and the volatility of the oil price affects the profitability of these stocks [66]. Apart from that, previous research found that the volatility of the oil market (e.g., measured by OVX) impacts the volatility of clean energy companies [67] and vice versa [68] and that this spillover effect of volatility is stronger than the spillover effect of returns [69]. Moreover, during the COVID-19 pandemic, the volatility spillovers appear to have intensified [66]. Apart from the (crude) oil market, technology stocks, and investor sentiment towards renewable energy have been shown to affect the stocks of cleantech companies as well [69,70]. Finally, it is noteworthy that hedging against adverse movements of clean energy stocks can be possible using the volatility index VIX or crude oil [64] and that clean energy companies can be part of profitable hedging strategies themselves [68] as well as contributing to portfolio diversification, e.g., in times of extreme market events (e.g., a pandemic) [66].

8. Conclusions

In this paper, the accuracy and predictive power of mean target prices for the stocks of companies contained in the Standard and Poor’s Global Clean Energy (USD) index were investigated. This study shows that the mean target prices for these stocks during the timeframe from 2009 to 2020 are on average 22.2% above the current stock price. This is in line with recent research works that cover time periods after 2000, whereas studies covering partially or entirely the 1990s show higher implied returns for target prices. The Year-End accuracy of 46.6% (41.5% excl. 2020) shows that only less than half of the mean target prices were met by year-end, whereas the Year-Highest accuracy of 68.1% (62.5% excl. 2020) highlights that close to two thirds of mean target prices are met at some point during the 12 months. These results are similar to those found in recent research, illustrating that the accuracy for global clean energy stocks is not considerably different than those of different cross-sections of stocks in different stock markets. In line with previous research, the average accuracy of target prices decreases as the implied target return increases, meaning that relatively higher target prices are less likely to be met.

Subsequently, a random forest and an SVM classification model were trained using both the Year-End and the Year-Highest target for the mean target prices and were compared to a random model. The random forest leads in both cases to the highest classification accuracy but both the SVM and random forest are highly significantly more accurate than the random model. Unsurprisingly, the best average accuracy of 73.24% for the Year-End target is lower than the best average accuracy of 81.15% for the Year-Highest target. This appears to reflect that meeting a target price at any point during the 12-month period is easier to predict than meeting the target price only at a single point, at the end of the 12-month period. The analysis of the variables shows that for all models the mean target price is the most relevant variable, whereas the number of target prices appears to be relevant as well. This is in line with previous research that suggested that the implied return of target prices and the number of analysts covering a stock are linked to the accuracy of target prices. A detailed analysis of the results in terms of these two variables for the Year-End target indicates for the random forest that this model is particularly accurate for the high target returns (“30% to 70%” and “Above 70%”), especially when the number of target prices is high (coverage of at least 15 analysts). For these subsets, only a few positive predictions are made but those are in the vast majority of cases correct. Thus, it is unsurprising that the actual mean and median returns for high target return groups are considerably higher than for all observations. These high actual returns are based on extremely high mean and median returns for actual hits and close to positive or even positive returns when positive predictions for high target returns are incorrect. Consequently, following the rare positive predictions of the random forest for the highest target return groups (“30% to 70%” and “Above 70%”) may represent potentially attractive investment opportunities.

Some limitations apply to the results of this study. First, the results are obtained for a selection of clean energy stocks, which may not be generalizable for stocks in other sectors or even all clean energy stocks. Moreover, the results are in line with recent research but show clear differences to older research, highlighting that the implied returns and accuracies may differ in various time periods and may also be different in the future. For future research, a set of global stocks from a wider range of sectors can be investigated to confirm the findings. Moreover, additional variables linked to the company and the past stock performance can be included for the classification model, and investment strategies following the corresponding model predictions can be presented.