Impact of an Innovative Solution for the Interruption of 3-D Point Thermal Bridges in Buildings on Sustainability
Abstract
:1. Introduction
2. Thermal Bridges
Point Thermal Bridges
- q Heat flow in W/m2;
- heat transfer coefficient in W/ (m2. K).
- q Heat flow in W/m2;
- the inside or outside temperature in K;
- the temperature of the interior or exterior surface in K;
- the interior or exterior heat transfer resistance in m2. K/W.
- L3D is the linear thermal transmittance determined from the 3-D calculation of a 3-D building structure separating the two environments in W/K;
- Ui is the heat transfer coefficient of a 1D building structure separating two environments in W/ (m2. K);
- Ai area over which the value applies Ui in m2;
- Ψj linear loss coefficient W/(m. K);
- lj the length of the geometric model over which the value applies Ψj in m;
- Nj number of 2D building structures;
- Ni number of 1D building structures.
3. Calculation Method for the Analysis of Point Thermal Bridges
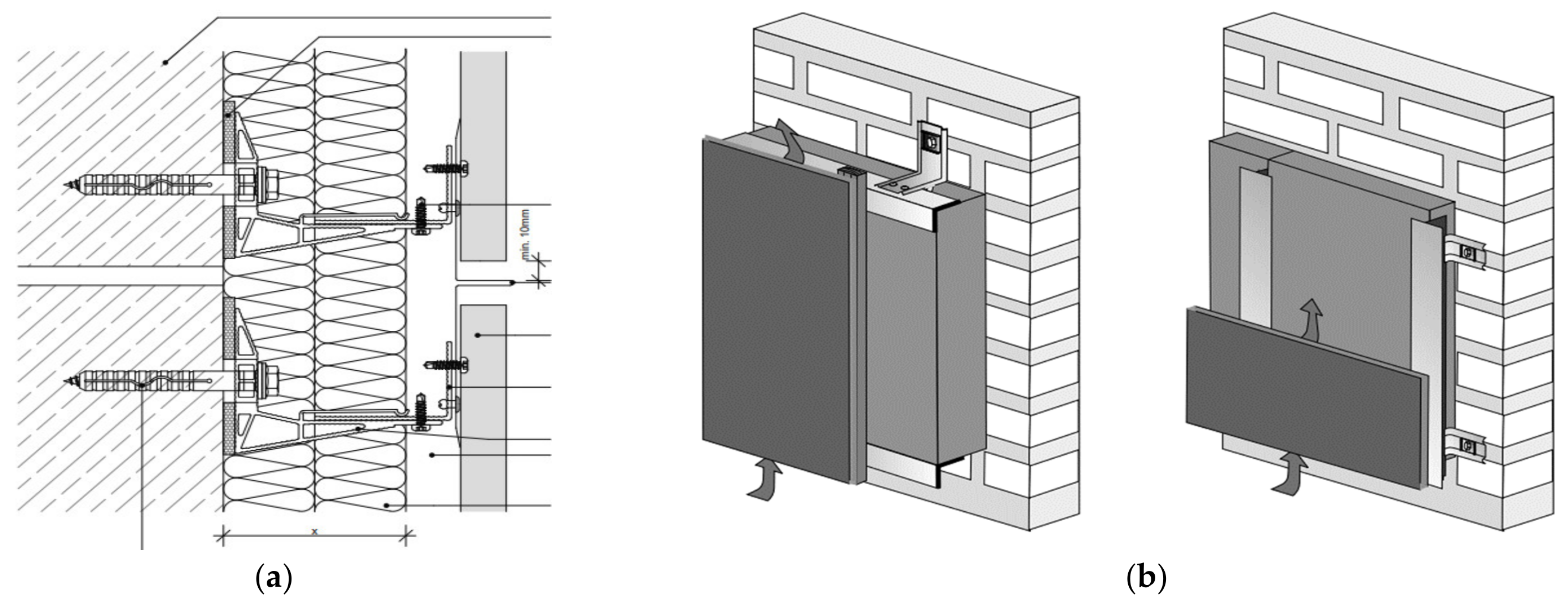
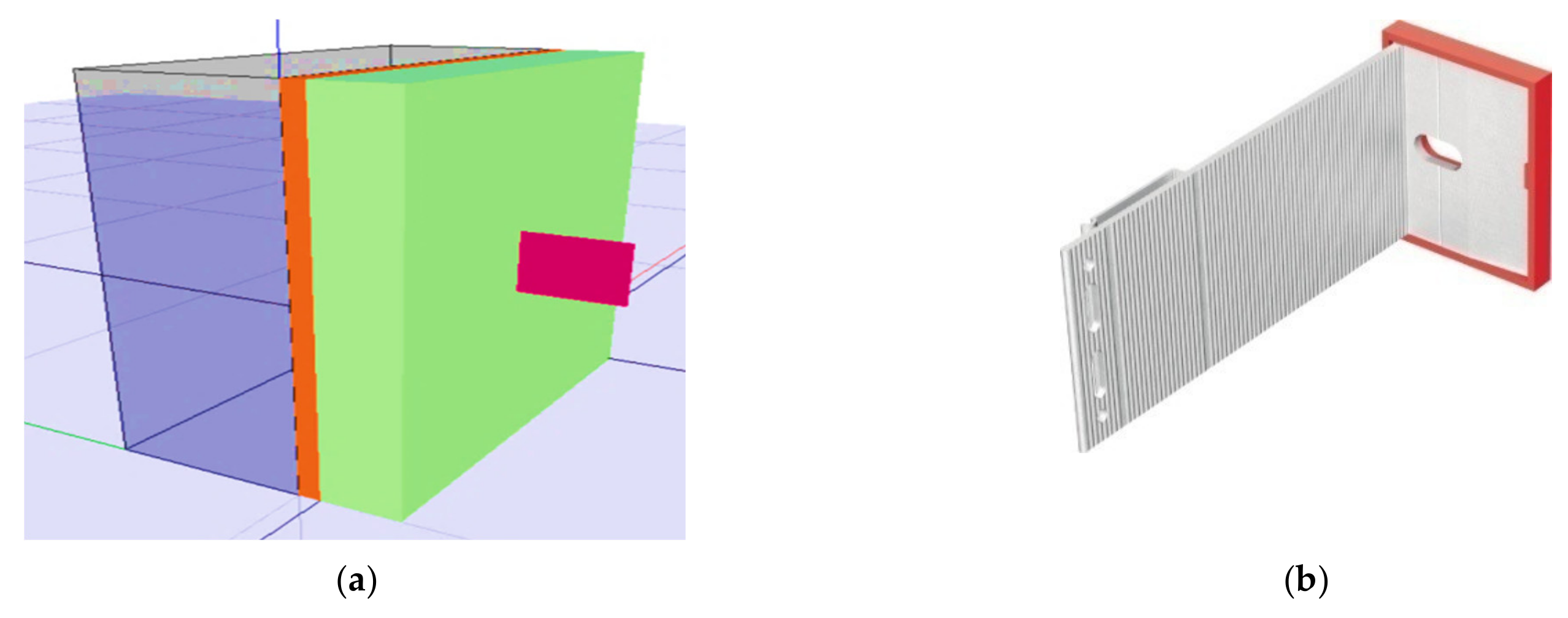
3.1. Description of Samples Used in the Calculation Method of Point Thermal Bridges
3.2. Calculation Analysis of Individual Variants
3.2.1. Hilti Anchor Analysis without Interrupting Point Thermal bridges
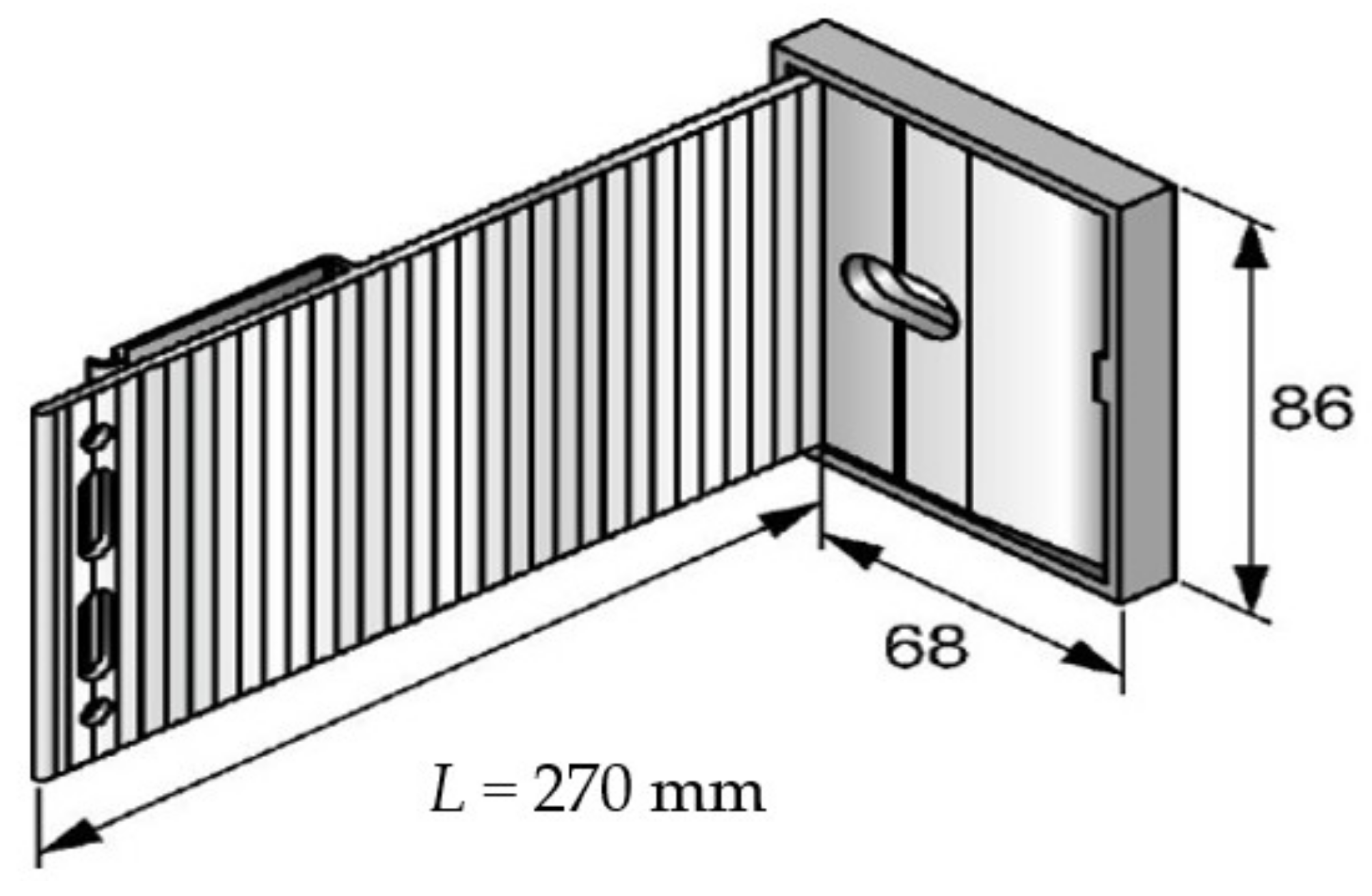
3.2.2. Analysis of an Anchor from Hilti with the Break of Point Thermal Bridges—A Technical Solution from Hilti
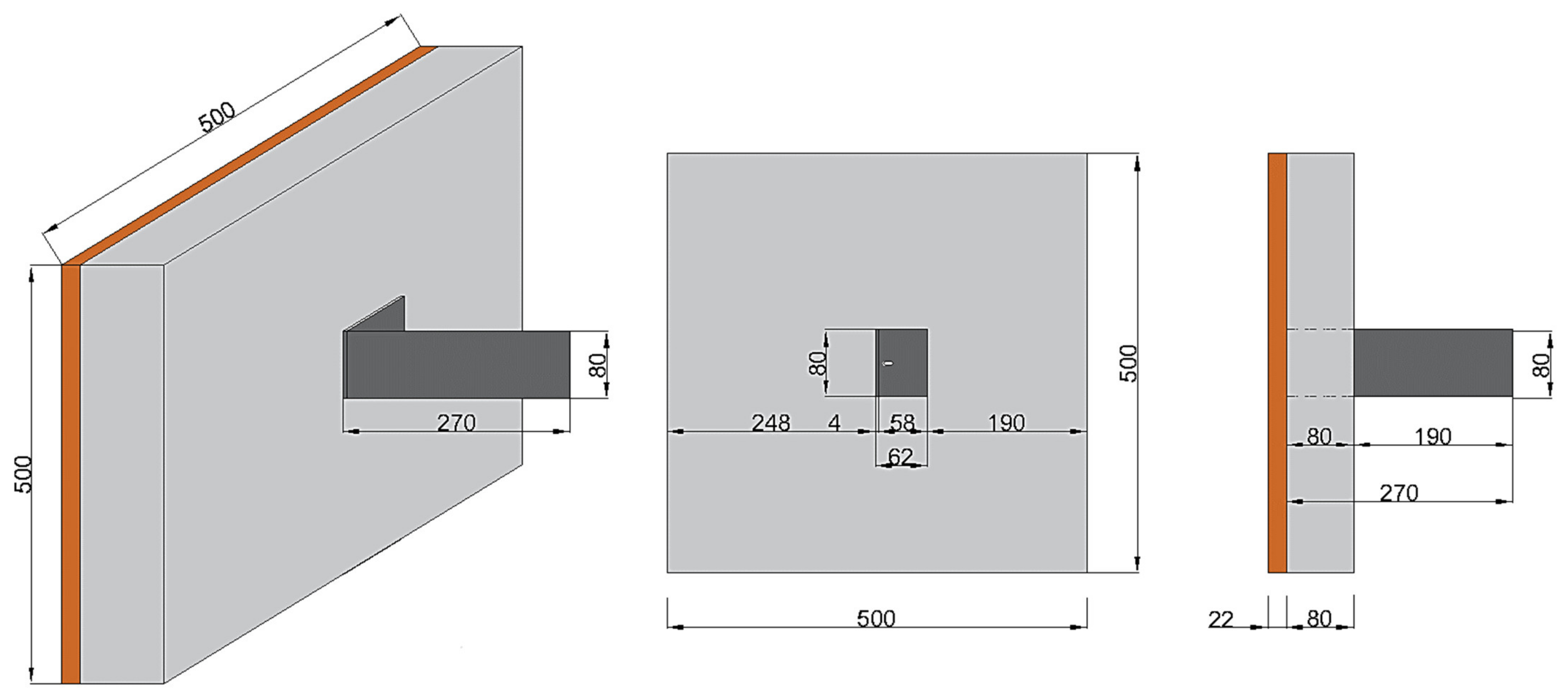
3.2.3. Analysis of an Anchor from the Hilti Company with Break of Point Thermal Bridges—Technical Solution of the Author of the Article (Patent)
3.2.4. Comparison of Results for Individual Variants
3.3. Influence of Point 3-D Thermal Bridges on Heat Losses through Heat Transfer for Different Variants of Ventilated Façade by Rockwool
4. Experimental Method for the Analysis of Point Thermal Bridges
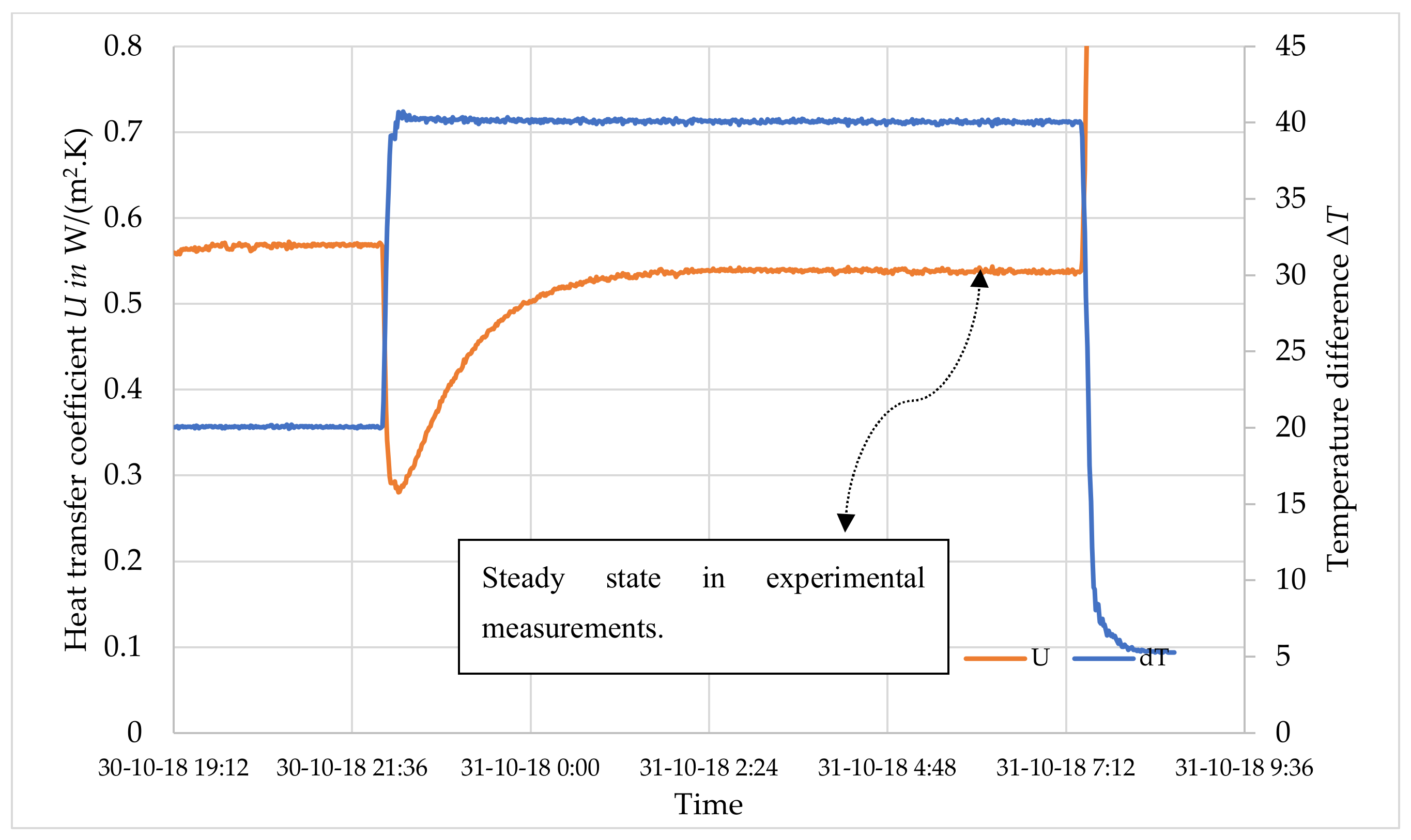
Experimental Measurements
5. Discussion
6. Conclusions
7. Patents
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- European Union. Energy Efficiency: Energy Performance of Buildings. Directive 2002/91/EC; European Union: Brussels, Belgium, 2002. [Google Scholar]
- European Union. Energy End-Use Efficiency and Energy Services and Repealing Council Directive 93/76/EEC. Directive 2006/32/EC; European Union: Brussels, Belgium, 2006. [Google Scholar]
- European Union. Energy Performance of Buildings. Directive 2010/31/EC; European Union: Brussels, Belgium, 2010. [Google Scholar]
- Tadeu, A.; Simões, I.; Simões, N.; Prata, J. Simulation of dynamic linear thermal bridges using a boundary element method model in the frequency domain. Energy Build. 2011, 43, 3685–3695. [Google Scholar] [CrossRef]
- Theodosiou, T.G.; Tsikaloudaki, A.G.; Kontoleon, K.J.; Bikas, D.K. Thermal bridging analysis on cladding systems for building facades. Energy Build. 2015, 109, 377–384. [Google Scholar] [CrossRef]
- Theodosiou, T.G.; Papadopoulos, A.M. The impact of thermal bridges on the energy demand of buildings with double brick wall constructions. Energy Build. 2008, 40, 2083–2089. [Google Scholar] [CrossRef]
- ISO. Thermal Bridges in Building Construction—Linear Thermal Transmittance—Simplified Methods and Default Values. UNI EN ISO 14683:2018; ISO Copyright Office: Geneva, Switzerland, 2018. [Google Scholar]
- ISO. Thermal Bridges in Buildings e Thermal Flows and Superficial Temperatures e Detailed Calculations, EN ISO 10211; ISO Copyright Office: Geneva, Switzerland, 2018. [Google Scholar]
- Magrini, A.; Magnani, L.; Pernetti, R. The effort to bring existing buildings towards the A class: A discussion on the application of calculation methodologies. Appl. Energy 2012, 97, 438–450. [Google Scholar] [CrossRef]
- ISO. Thermal Performance of the Building Components e Thermal Dynamic Characteristics e Methods of Calculation, EN ISO 13786; ISO Copyright Office: Geneva, Switzerland, 2008. [Google Scholar]
- Rockwool. 2021. Available online: https://cdn01.rockwool.sk/siteassets/rw-sk/dokumenty/cad-detaily/rw-detaily-prevetravane-fasady_sk.pdf?f=20181206102116 (accessed on 19 September 2021).
- Martin, K.; Erkoreka, A.; Flores, I.; Odriozola, M.; Sala, J.M. Problems in the calculation of thermal bridges in dynamic conditions. Energy Build. 2011, 43, 529–535. [Google Scholar] [CrossRef]
- Hassid, S. Thermal bridges in homogeneous walls: A simplified approach. Build. Environ. 1989, 24, 259–264. [Google Scholar] [CrossRef]
- Hassid, S. Thermal bridges across multilayer walls: An integral approach. Build. Environ. 1990, 25, 143–150. [Google Scholar] [CrossRef]
- Sempey, H.V.A.; Pauly, M.; Mora, L. Comparison of different methods for calculating thermal bridges: Application to wood-frame buildings. Build. Environ. 2015, 93, 339–348. [Google Scholar] [CrossRef]
- Kosny, J. Advances in residential wall technologies—Simple ways of decreasing the whole building energy consumption. ASHRAE Trans. 2001, 107, 421–432. [Google Scholar]
- Mao, G. Thermal Bridges. Efficient Models for Energy Analysis in Buildings; Department of Building Sciences, Kunglika Tekniska Högskolan: Stockholm, Sweden, 1997. [Google Scholar]
- Ben Larbi, A. Statistical modelling of heat transfer for thermal bridges of buildings. Energy Build. 2005, 37, 945–951. [Google Scholar] [CrossRef]
- Kosny, J.; Kossecka, E. Multi-dimensional heat transfer through complex building envelope assemblies in hourly energy simulation programs. Build. Environ. 2002, 34, 445–454. [Google Scholar] [CrossRef]
- Carpenter, S.C.; Schumacher, C. Characterization of Framing Factors for Wood-Framed Low-Rise Residential Buildings. ASHRAE Trans. 2003, 109, 101. [Google Scholar]
- Kosny, J. A New Whole Wall R-value Calculator, An Integral Part of the Interactive Internet-Based Building Envelope, Materials Database for Whole-Building Energy Simulation Programs. 2004. Available online: http://citeseerx.ist.psu.edu/viewdoc/download?doi=10.1.1.135.8046&rep=rep1&type=pdf (accessed on 19 September 2021).
- Buday, P.; Ingeli, R.; Čekon, M. Influence of Thermal Break Element Applied in Balcony Slab on Internal Surface Temperature. Adv. Mater. Res. 2014, 1057, 79–86. [Google Scholar] [CrossRef]
- Buday, P.; Ingeli, R. Balcony systems (isokorb) impact on energy need for heating and economic valuation. Appl. Mech. Mater. 2016, 820, 146–151. [Google Scholar] [CrossRef]
- Ingeli, R.; Vavrovič, B.; Čekon, M.; Paulovičová, L. Thermal Bridges Minimizing through Window Jamb in Low Energy Buildings. Appl. Mech. Mater. 2014, 899, 66–69. [Google Scholar] [CrossRef]
- Juráš, P. Lightweight timber-framed wall and impact of ventilated cladding on the possibility of reducing summer overheating in Central Europe. E3S Web Conf. 2020, 172, 03-D09. [Google Scholar] [CrossRef]
- Čurpek, J.; Čekon, M.; Hraška, J. PCM Integrated in BiPV Ventilated Facąde Concepts: Experimental Test Cell Platform and Initial Full-Scale Measurements. IOP Conf. Ser. Earth Environ. Sci. 2019, 290, 012072. [Google Scholar] [CrossRef]
- Sanjuan, C.; Suárez, M.J.; González, M.; Pistono, J.; Blanco, E. Energy performance of an open-joint ventilated façade compared with a conventional sealed cavity façade. Sol. Energy 2011, 85, 1851–1863. [Google Scholar] [CrossRef]
- Ascione, F.; Bianco, N.; de Masi, R.F.; Rossi, F.d.; Vanoli, G.P. Simplified state space representation for evaluating thermal bridges in building: Modelling, application, and validation of a methodology. Appl. Therm. Eng. 2013, 61, 344–354. [Google Scholar] [CrossRef]
- Ben-Nakhi, A.E. Minimizing thermal bridging through window systems in buildings of hot regions. Appl. Therm. Eng. 2002, 22, 989–998. [Google Scholar] [CrossRef]
- Hilti-20.11.2020. Available online: https://www.hilti.cz/c/CLS_FACADE_MOUNTING_SYSTEMS/CLS_BRACKETS/r5325 (accessed on 19 September 2021).
- ÚNMS, SR. Thermal Protection of Buildings. Thermal Performance of Buildings and Components. Part 2: Functional Requirements; Office for Standardization, Metrology and Testing of the Slovak Republic: Bratislava, Slovakia, 2019. [Google Scholar]
- Mumaw, J.R. Calibrated hot box: An effective means for measuring thermal conductance in large wall sections. In American Society for Testing and Materials, ASTM STP 544, Heat Transmission Measurements in Thermal Insulations; ASTM: West Conshohocken, PA, USA, 1974; pp. 193–211. [Google Scholar]
- Klems, J.H. A calibrated hot box for testing window systems—Construction calibration and measurements on prototype high-performance windows. In Proceedings of the ASHRAE/DOE-ORNL Conference on Thermal Performance of the Exterior Envelopes of Buildings, Kissimmee, FL, USA, 3–5 December 1979; pp. 338–346. [Google Scholar]
- Fang, X.D. A study of the U-factor of the window with a high-reflectivity venetian blind. Sol. Energy 2000, 68, 207–214. [Google Scholar] [CrossRef]
- Psi-Therm 2D Enterprise 2017, PLUS Psi-Therm 3D 2017. Available online: https://www.psitherm.uk/psi-features/psi-therm-3D-features (accessed on 19 September 2021).
- Zarr, R.R.; Burch, D.M.; Faison, T.K.; Arnold, C.E.; O’Connell, M.E. Calibration of the NBS calibrated hot box. J. Test. Eval. 1997, 15, 167–177. [Google Scholar]
- Aviram, D.P.; Fried, A.N.; Roberts, J.J. Thermal properties of a variable cavity wall. Build. Environ. 2001, 36, 1057–1072. [Google Scholar] [CrossRef]











| Material Number | Material Description | Thermal Conductivity λ in W/ (m. K) | Comment |
|---|---|---|---|
| 1. | OSB board hr. 22 mm | 0.20 | Data were used from the material manufacturer. |
| 2. | Anchor—from HILTI | 160 | Data were used from the material manufacturer. |
| 3. | Pad thermal barrier—Hilti. | 0.117 | Data were used from the material manufacturer. |
| 4. | Polystyrene foam EPS F | 0.039 | Data were used from the material manufacturer. |
| 5. | Plastic coated anchor | 49 1 | Patented application of the author of this work. |
| Variant | Description | Variant Image | Comment |
|---|---|---|---|
| 1. | Variant without the use of an anchoring element | No anchor was used in the given variant. | |
| 2. | Anchor without modifications to eliminate the thermal point 3-D bridge. |  | The anchor material is made of aluminum with high thermal conductivity. |
| 3. | Anchor with modification to eliminate thermal point 3-D bridge. |  | The anchor material is made of aluminum with high thermal conductivity and with the interruption of the thermal bridge by means of a pad. |
| 4. | Anchor with modification to eliminate thermal point 3-D bridge. |  | The anchor material is made of aluminum with high thermal conductivity and with interruption of the thermal bridge by means of plastic coating of the anchor. This proposal is the property of the author of the work. |
| Variant | Heat Transfer Coefficient U in W/ (m2. K). | The Difference between the Simulated Values Relative to the Variant no. 1 in % | Comment |
|---|---|---|---|
| 1. | 0.429 | 0 | - |
| 2. | 0.585 | 36.36% | This is a calculation of the increase from the value of the first variant (0.429–100% and 0.585–136.36%). Increase the heat transfer coefficient is 36.36% |
| 3. | 0.543 | 26.57% | This is a calculation of the increase from the value of the first variant (0.429–100% and 0.543–126.57%). Increase the heat transfer coefficient is 26.57% |
| 4. | 0.550 | 29.37% | This is a calculation of the increase from the value of the first variant (0.429–100% and 0.550–129.37%). Increase the heat transfer coefficient is 29.37% |
| Variant | Description of the Supporting Structure | Thermal Insulation | Thermal Insulation Thickness in mm | Number of Anchors |
|---|---|---|---|---|
| 1. | Reinforced concrete structure (λ = 1.58 W/ (m. K)) 200 mm | Thermal insulation (λD = 0.033 W/ (m. K)) | 140, 200 | 0, 1, 2, 3 |
| 2. | Reinforced concrete structure (λ = 1.58 W/ (m. K)) 200 mm | Thermal insulation (λD = 0.035 W/ (m. K)) | 140, 200 | 0, 1, 2, 3 |
| Geometry of the Building | Values |
|---|---|
| Total floor area A in m2 | 335.8 |
| Total built-up volume V in m3 | 1074.56 |
| Construction height h in m | 3.2 |
| Total heat exchange envelope in m2 | 693 |
| Shape factor | 0.64 |
| Area of wall in m2 | 314.6 |
| Number of Anchors | Heat Loss in W/K | Percentage Increase to 0 Number of Anchors in% |
|---|---|---|
| 0 | 54.74 | - |
| 1 | 70.16 | 28.16 |
| 2 | 87.46 | 59.77 |
| 3 | 100.67 | 83.90 |
| Number of Anchors | Energy Need for Heating in kWh/ (m2. a) | Percentage Increase to 0 Number of Anchors in% |
|---|---|---|
| 0 | 34.81 | - |
| 1 | 39.48 | 13.41 |
| 2 | 43.53 | 25.05 |
| 3 | 46.64 | 33.98 |
| Variant | Description of the Variants | Heat Flow q in W/m2 | Temperature Difference ΔT | Heat Transfer Coefficient U in W/ (m2. K) |
|---|---|---|---|---|
| 2. | Anchor without modification to eliminate thermal point 3-D bridge. | 2.32 | 38.616 | 0.578 |
| 3. | Anchor with modification to eliminate thermal point 3-D bridge. | 20.703 | 38.553 | 0.537 |
| 4. | Anchor with modification to eliminate thermal point 3-D bridge. | 21.052 | 38.744 | 0.543 |
| Variant | Heat Transfer Coefficient U in W/ (m2. K). | The Difference between the Calculated Values Relative to the Variant n. 3 in% |
|---|---|---|
| 2. | 0.578 | - |
| 3. | 0.537 | - |
| 4. | 0.543 | 1.117 * |
| Variant | Heat Transfer Coefficient U in W/ (m2. K) from Experimental Measurement | Heat Transfer Coefficient U in W/ (m2. K) from 3-D Simulation | Increase the Heat Transfer Coefficient in% |
|---|---|---|---|
| 3. | 0.537 | 0.543 | 1.117 * |
| 4. | 0.543 | 0.550 | 1.289 * |
| Variant | Heat Transfer Coefficient U in W/ (m2. K). | The Difference between the Calculated Values Relative to the Variant n. 1 in% | The Difference between the Calculated Values Relative to the Variant n. 2 in% |
|---|---|---|---|
| 1. | 0.429 | 0 | - |
| 2. | 0.585 | 36.36 * | - |
| 3. | 0.543 | 26.57 * | 7.73 * |
| 4. | 0.550 | 29.37 * | 6.36 * |
| Variant | Heat Transfer Coefficient U in W/ (m2. K). | The Difference between the Calculated Values Relative to the Variant n. 1 in% | The Difference between the Calculated Values Relative to the Variant n. 3 in% |
|---|---|---|---|
| 1. | 0.429 | 0 | - |
| 2. | 0.585 | 36.36 * | - |
| 3. | 0.543 | 26.57 * | - |
| 4. | 0.550 | 29.37 * | 1.29 * |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ingeli, R.; Gašparík, J.; Paulovičová, L. Impact of an Innovative Solution for the Interruption of 3-D Point Thermal Bridges in Buildings on Sustainability. Sustainability 2021, 13, 11561. https://doi.org/10.3390/su132111561
Ingeli R, Gašparík J, Paulovičová L. Impact of an Innovative Solution for the Interruption of 3-D Point Thermal Bridges in Buildings on Sustainability. Sustainability. 2021; 13(21):11561. https://doi.org/10.3390/su132111561
Chicago/Turabian StyleIngeli, Rastislav, Jozef Gašparík, and Lucia Paulovičová. 2021. "Impact of an Innovative Solution for the Interruption of 3-D Point Thermal Bridges in Buildings on Sustainability" Sustainability 13, no. 21: 11561. https://doi.org/10.3390/su132111561
APA StyleIngeli, R., Gašparík, J., & Paulovičová, L. (2021). Impact of an Innovative Solution for the Interruption of 3-D Point Thermal Bridges in Buildings on Sustainability. Sustainability, 13(21), 11561. https://doi.org/10.3390/su132111561








