Learning Analytics for Diagnosing Cognitive Load in E-Learning Using Bayesian Network Analysis
Abstract
:1. Introduction
1.1. Cognitive Load Theory
1.2. Learning Analysis for Diagnostic Information Using Bayesian Network Analysis
1.3. Research Objectives
- (1)
- Does BN estimate a learner’s levels of extraneous, intrinsic, and germane cognitive load?
- (2)
- Does BN predict a learner’s academic achievement based on the patterns of three cognitive load components?
2. Methods
2.1. Participants
2.2. Data Analysis
2.3. Measures
3. Results
3.1. Descriptive Statistics
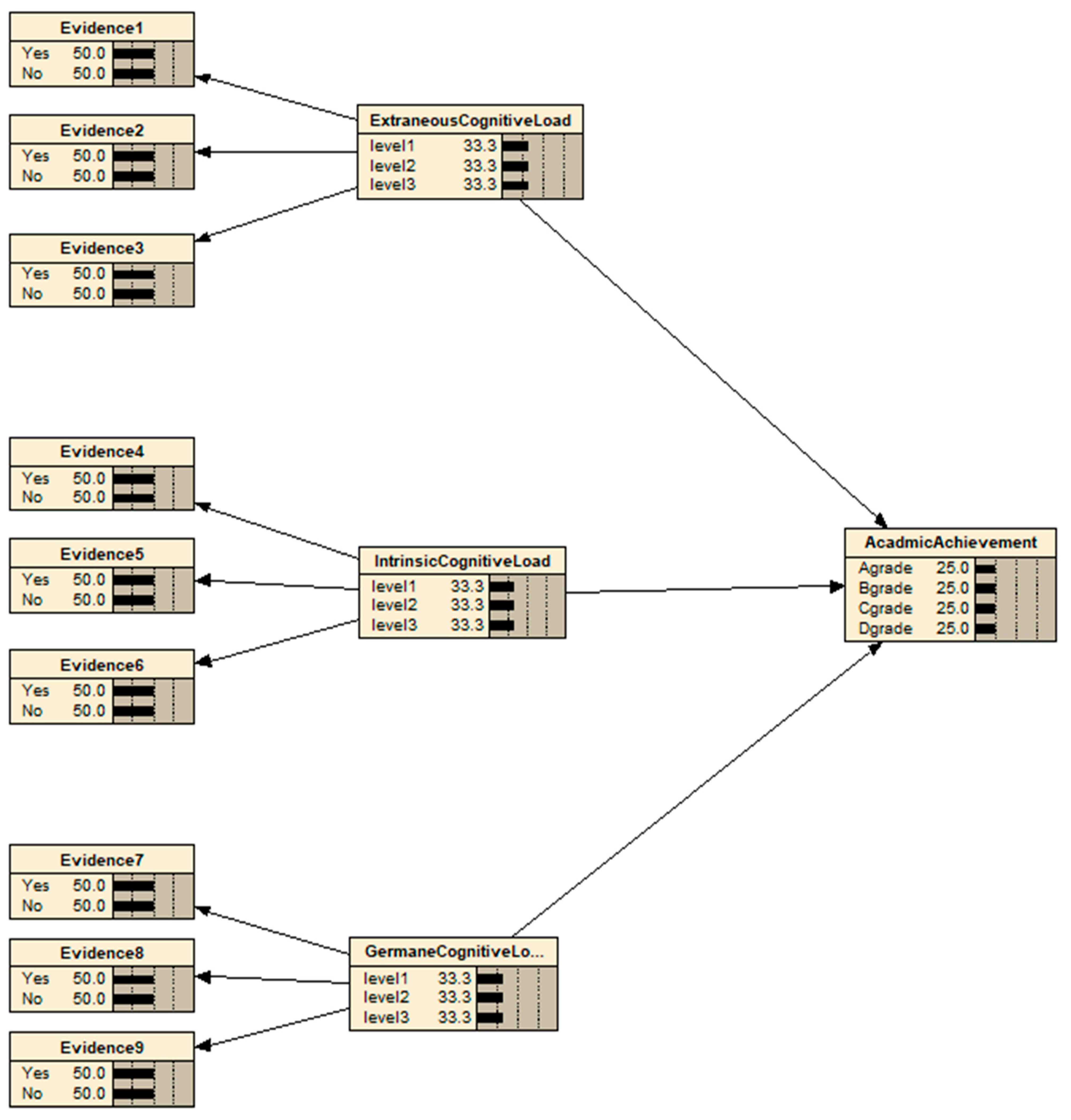
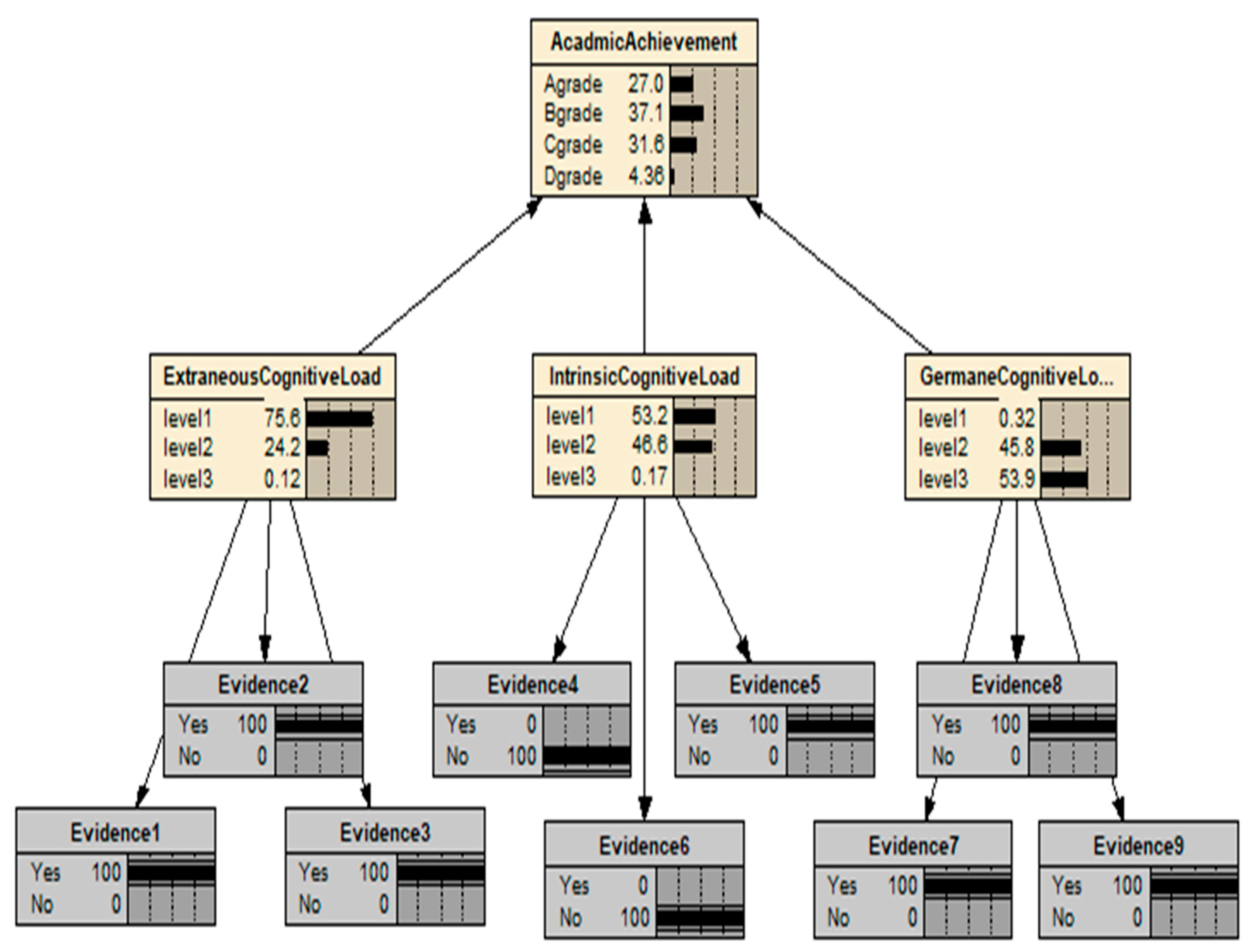
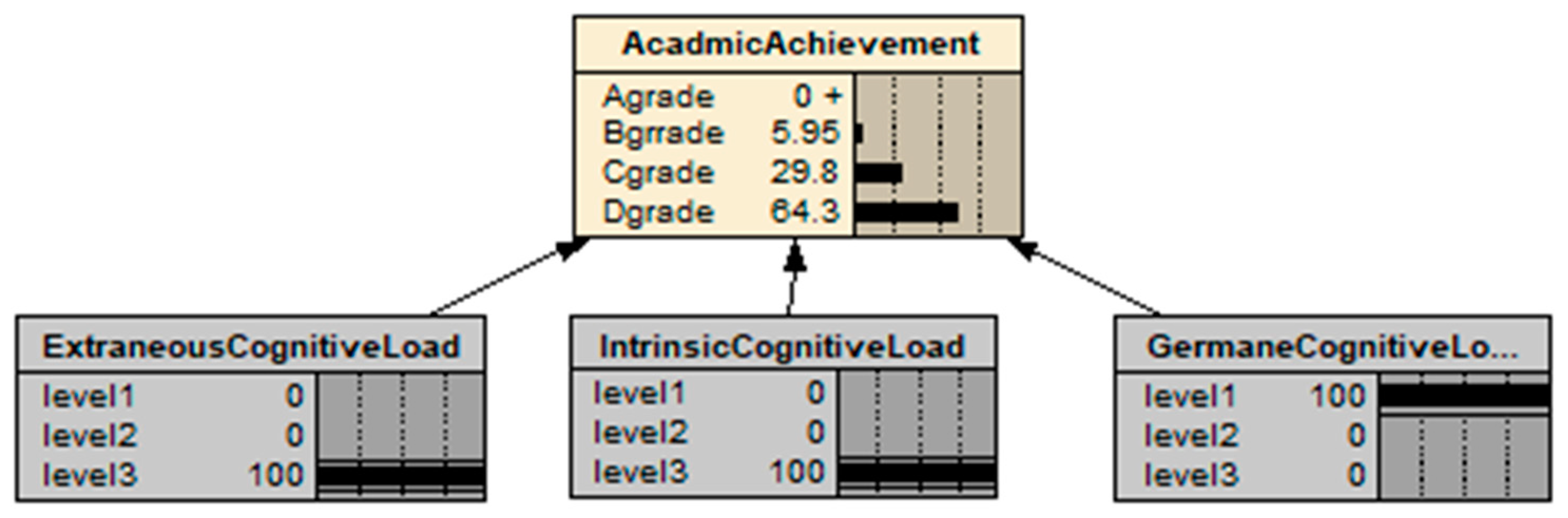
3.2. Bayesian Network Analysis for Diagnostic Information about the Cognitive Load
4. Discussion
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Gherheș, V.; Stoian, C.E.; Fărcașiu, M.A.; Stanici, M. E-learning vs. face-to-face learning: Analyzing students’ preferences and behaviors. Sustainability 2021, 13, 4381. [Google Scholar] [CrossRef]
- Ali, W. Online and remote learning in higher education institutes: A necessity in light of COVID-19 pandemic. High. Educ. 2020, 10, 16–25. [Google Scholar] [CrossRef]
- Portuguez Castro, M.; Gómez Zermeño, M.G. Challenge based learning: Innovative pedagogy for sustainability through e-learning in higher education. Sustainability 2020, 12, 4063. [Google Scholar] [CrossRef]
- Jacques, S.; Ouahabi, A.; Lequeu, T. Remote Knowledge Acquisition and Assessment during the COVID-19 Pandemic. Int. J. Eng. Pedagog. 2020, 10, 120–138. [Google Scholar] [CrossRef]
- Lee, J.; Song, H.-D.; Hong, A.J. Exploring factors, and indicators for measuring students’ sustainable engagement in e-learning. Sustainability 2019, 11, 985. [Google Scholar] [CrossRef] [Green Version]
- Ananga, P. Pedagogical Considerations of E-Learning in Education for Development in the Face of COVID-19. Int. J. Technol. Educ. Sci. 2020, 4, 310–321. [Google Scholar] [CrossRef]
- Bartolomé, A.; Castañeda, L.; Adell, J. Personalization in educational technology: The absence of underlying pedagogies. Int. J. Educ. Technol. High. Educ. 2018, 15, 1–17. [Google Scholar] [CrossRef]
- Kalyuga, S. Cognitive load theory: How many types of load does it really need? Educ. Psychol. Rev. 2011, 23, 1–19. [Google Scholar] [CrossRef]
- Paas, F.; Renkl, A.; Sweller, J. Cognitive load theory and instructional design: Recent developments. Educ. Psychol. 2003, 38, 1–4. [Google Scholar] [CrossRef]
- Kalyuga, S.; Chandler, P.; Sweller, J. When redundant on-screen text in multimedia technical instruction can interfere with learning. Hum. Factors 2004, 46, 567–581. [Google Scholar] [CrossRef]
- Moreno, R.; Park, B. Cognitive load theory: Historical development and relation to other theories. In Cognitive Load Theory; Plass, J., Moreno, R., Brünken, R., Eds.; Cambridge University Press: Cambridge, UK, 2010; pp. 9–28. [Google Scholar]
- Brünken, R.; Plass, J.L.; Moreno, R. Current issues and open questions in cognitive load research. In Cognitive Load Theory; Plass, J., Moreno, R., Brünken, R., Eds.; Cambridge University Press: Cambridge, UK, 2010; pp. 253–272. [Google Scholar]
- Leppink, J.; Paas, F.; van der Vleuten, C.P.; van Gog, T.; van Merriënboer, J.J. Development of an instrument for measuring different types of cognitive load. Behav. Res. Methods 2013, 45, 1058–1072. [Google Scholar] [CrossRef]
- Kalyuga, S.; Chandler, P.; Sweller, J. Managing split-attention and redundancy in multimedia instruction. Appl. Cognit. Psychol. 1999, 13, 351–371. [Google Scholar] [CrossRef] [Green Version]
- Sweller, J. Cognitive load theory, learning difficulty, and instructional design. Learn. Instr. 1994, 4, 295–312. [Google Scholar] [CrossRef]
- Sweller, J.; Chandler, P.; Tierney, P.; Cooper, M. Cognitive load as a factor in the structuring of technical material. J. Exp. Psychol. 1990, 119, 176–192. [Google Scholar] [CrossRef]
- Almond, R.G.; Mislevy, R.J.; Steinberg, L.S.; Williamson, D.M.; Yan, D. Bayesian Networks in Educational Assessment; Springer: New York, NY, USA, 2015. [Google Scholar]
- Reichenberg, R. Dynamic Bayesian networks in educational measurement: Reviewing and advancing the state of the field. Appl. Meas. Educ. 2018, 31, 335–350. [Google Scholar] [CrossRef]
- Brünken, R.; Plass, J.L.; Leutner, D. Direct measurement of cognitive load in multimedia learning. Educ. Psychol. 2003, 38, 53–61. [Google Scholar] [CrossRef]
- De Jong, T. Cognitive load theory, educational research, and instructional design: Some food for thought. Instr. Sci. 2010, 38, 105–134. [Google Scholar] [CrossRef] [Green Version]
- Moreno, R. Cognitive load theory: More food for thought. Instr. Sci. 2010, 38, 135–141. [Google Scholar] [CrossRef]
- Mayer, R.E. Multimedia Learning; Cambridge University Press: Cambridge, UK, 2009. [Google Scholar]
- Sweller, J. Cognitive load during problem solving: Effects on learning. Cogn. Sci. 1988, 12, 257–285. [Google Scholar] [CrossRef]
- Cierniak, G.; Scheiter, K.; Gerjets, P. Explaining the split-attention effect: Is the reduction of extraneous cognitive load accompanied by an increase in germane cognitive load? Comput. Hum. Behav. 2009, 25, 315–324. [Google Scholar] [CrossRef]
- Sweller, J. Element interactivity and intrinsic, extraneous, and germane cognitive load. Educ. Psychol. Rev. 2010, 22, 123–138. [Google Scholar] [CrossRef]
- Sweller, J.; van Merriënboer, J.J.; Paas, F. Cognitive architecture and instructional design. Educ. Psychol. Rev. 1998, 10, 251–296. [Google Scholar] [CrossRef]
- Sweller, J.; van Merriënboer, J.J.; Paas, F. Cognitive architecture and instructional design: 20 years later. Educ. Psychol. Rev. 2019, 31, 261–292. [Google Scholar] [CrossRef] [Green Version]
- Sweller, J.; Ayres, P.; Kalyuga, S. Measuring cognitive load. In Cognitive Load Theory; Sweller, J., Ayres, P., Kalyuga, S., Eds.; Springer: New York, NY, USA, 2011; pp. 71–85. [Google Scholar]
- Berthold, K.; Renkl, A. Instructional aids to support a conceptual understanding of multiple representations. J. Educ. Psychol. 2009, 101, 70–87. [Google Scholar] [CrossRef] [Green Version]
- Paas, F.; van Gog, T.; Sweller, J. Cognitive load theory: New conceptualizations, specifications, and integrated research perspectives. Educ. Psychol. Rev. 2010, 22, 115–121. [Google Scholar] [CrossRef] [Green Version]
- Atkinson, R.K.; Renkl, A.; Merrill, M.M. Transitioning from studying examples to solving problems: Effects of self-explanation prompts and fading worked-out steps. J. Educ. Psychol. 2003, 95, 774–783. [Google Scholar] [CrossRef] [Green Version]
- Van Merriënboer, J.J.; Kester, L.; Faas, F. Teaching complex rather than simple tasks: Balancing intrinsic and germane load to enhance transfer of learning. Appl. Cogn. Psychol. 2006, 20, 343–352. [Google Scholar] [CrossRef]
- Paas, F.; Tuovinen, J.E.; Tabbers, H.; Van Gerven, P.W. Cognitive load measurement as a means to advance cognitive load theory. Educ. Psychol. 2003, 38, 63–71. [Google Scholar] [CrossRef]
- Paas, F.; van Merriënboer, J.J.; Adam, J.J. Measurement of cognitive load in instructional research. Percept. Mot. Skills 1994, 79, 419–430. [Google Scholar] [CrossRef]
- Paas, F.; van Merriënboer, J.J. The efficiency of instructional conditions: An approach to combine mental effort and performance measures. Hum. Factors 1993, 35, 737–743. [Google Scholar] [CrossRef]
- Paas, F.; van Merriënboer, J.J. Variability of worked examples and transfer of geometrical problem-solving skills: A cognitive-load approach. J. Educ. Psychol. 1994, 86, 122–133. [Google Scholar] [CrossRef]
- Kjaerulff, U.B.; Madsen, A.L. Probabilistic Networks for Practitioners: A Guide to Construction and Analysis of Bayesian Networks and Influence Diagrams; Springer: New York, NY, USA, 2007. [Google Scholar]
- Murphy, K.P. Dynamic Bayesian Networks: Representation, Inference and Learning; University of California: Berkeley, CA, USA, 2002. [Google Scholar]
- Norsys Software Corp. Netica V. 4.16. Available online: http://www.norsys.com (accessed on 15 July 2021).
- Dempster, A.P.; Laird, N.M.; Rubin, D.B. Maximum likelihood from incomplete data via the EM algorithm. J. R. Stat. Soc. Ser. B Stat. Methodol. 1997, 39, 1–38. [Google Scholar]
- Mislevy, R.J.; Almond, R.G.; Lukas, J. A brief introduction to evidence-centered design. ETS Res. Rep. Ser. 2003, 1, i-29. [Google Scholar] [CrossRef]
- Mislevy, R.J.; Haertel, G.D.; Riconscente, M.M.; Rutstein, D.W.; Ziker, C. Assessing Model-Based Reasoning Using Evidence-Centered Design; Springer Nature: London, UK, 2017. [Google Scholar]
- Choi, Y.; Cho, Y.I. Learning Analytics Using Social Network Analysis and Bayesian Network Analysis in Sustainable Computer-Based Formative Assessment System. Sustainability 2020, 12, 7950. [Google Scholar] [CrossRef]
- Van Merriënboer, J.J.; Sweller, J. Cognitive load theory and complex learning: Recent developments and future directions. Educ. Psychol. Rev. 2005, 17, 2. [Google Scholar] [CrossRef]

| Percent | Count | ||
|---|---|---|---|
| Educational Level | 1 Year | 45.0% | 315 |
| 2 Year | 22.3% | 156 | |
| 3 Year | 16.1% | 113 | |
| 4 Year | 16.6% | 116 | |
| Age | 20 s | 37.7% | 264 |
| 30 s | 31.0% | 217 | |
| 40 s | 16.7% | 117 | |
| 50 s | 14.6% | 102 | |
| Gender | Male | 65.1% | 456 |
| Female | 35.0% | 245 | |
| Job Status | Full Time | 49.3% | 345 |
| Part Time | 30.9% | 216 | |
| No | 19.9% | 139 |
| Mean (SD) | Skewness | Kurtosis | |
|---|---|---|---|
| Intrinsic Cognitive Load | 1.46 (0.90) | 0.073 | −0.75 |
| Extraneous Cognitive Load | 1.65 (1.01) | −0.186 | −1.04 |
| Germane Cognitive Load | 1.79 (0.92) | −0.25 | −0.83 |
| Academic Achievement | 2.59 (0.93) | −0.04 | −0.87 |
| Sub-Factor | Intrinsic Cognitive Load | Extraneous Cognitive Load | Germane Cognitive Load | Academic Achievement |
|---|---|---|---|---|
| Intrinsic Cognitive Load | 1 | 0.006 | −0.061 | −0.135 ** |
| Extraneous Cognitive Load | 1 | −0.005 | −0.156 ** | |
| Germane Cognitive Load | 1 | 0.069 | ||
| Academic Achievement | 1 |
| Status | Academic Achievement |
|---|---|
| A grade | 18.5 |
| B grade | 34.7 |
| C grade | 33.5 |
| D grade | 13.3 |
| Intrinsic Cognitive Load | Extraneous Cognitive Load | Germane Cognitive Load | |
|---|---|---|---|
| Level 1 | 39.7 | 30.9 | 10.2 |
| Level 2 | 59.7 | 53.8 | 67.5 |
| Level 3 | 0.60 | 15.3 | 22.3 |
| Item 1 | Item 2 | Item 3 | Item 4 | Item 5 | Item 6 | Item 7 | Item 8 | Item 9 | |
|---|---|---|---|---|---|---|---|---|---|
| Yes | 60.3 | 53.7 | 50.7 | 55.3 | 57.1 | 33.5 | 58.0 | 63.4 | 51.5 |
| No | 39.7 | 46.3 | 49.3 | 44.7 | 42.9 | 66.5 | 42.0 | 36.6 | 48.5 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Choi, Y.; Kim, J. Learning Analytics for Diagnosing Cognitive Load in E-Learning Using Bayesian Network Analysis. Sustainability 2021, 13, 10149. https://doi.org/10.3390/su131810149
Choi Y, Kim J. Learning Analytics for Diagnosing Cognitive Load in E-Learning Using Bayesian Network Analysis. Sustainability. 2021; 13(18):10149. https://doi.org/10.3390/su131810149
Chicago/Turabian StyleChoi, Younyoung, and Jigeun Kim. 2021. "Learning Analytics for Diagnosing Cognitive Load in E-Learning Using Bayesian Network Analysis" Sustainability 13, no. 18: 10149. https://doi.org/10.3390/su131810149
APA StyleChoi, Y., & Kim, J. (2021). Learning Analytics for Diagnosing Cognitive Load in E-Learning Using Bayesian Network Analysis. Sustainability, 13(18), 10149. https://doi.org/10.3390/su131810149






